Mapping Long-Term Dynamics of Population and Dwellings Based on a Multi-Temporal Analysis of Urban Morphologies
Abstract
1. Introduction
2. Methodological Framework
2.1. Data Sources
- Topographic raster maps (historical data): The maps should be at a scale of 1: 25,000 or larger and should contain the building footprints cartographically represented as solid, hatched or coloured areal symbols.
- Land use data (current data): A polygon data set for the seamless description of land use at the urban block level. This data set can usually be derived from digital landscape models from NMCAs at a scale of 1:10,000 to 1:25,000.
- Building model (current data): 2D building footprints or 3D building model in Level of Detail 1 (LoD1).
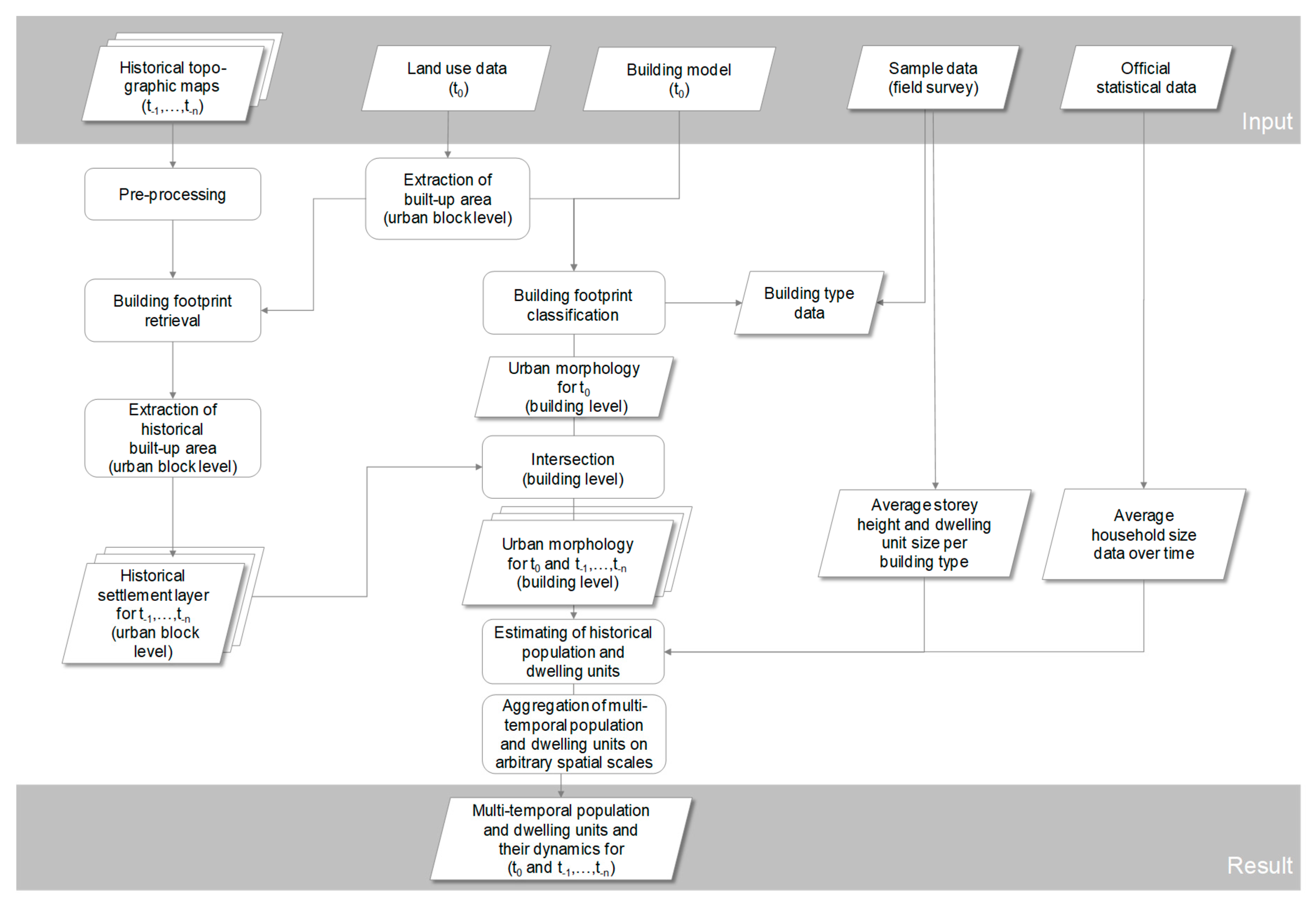
2.2. General Workflow
2.3. Pre-Processing of the Topographic Maps
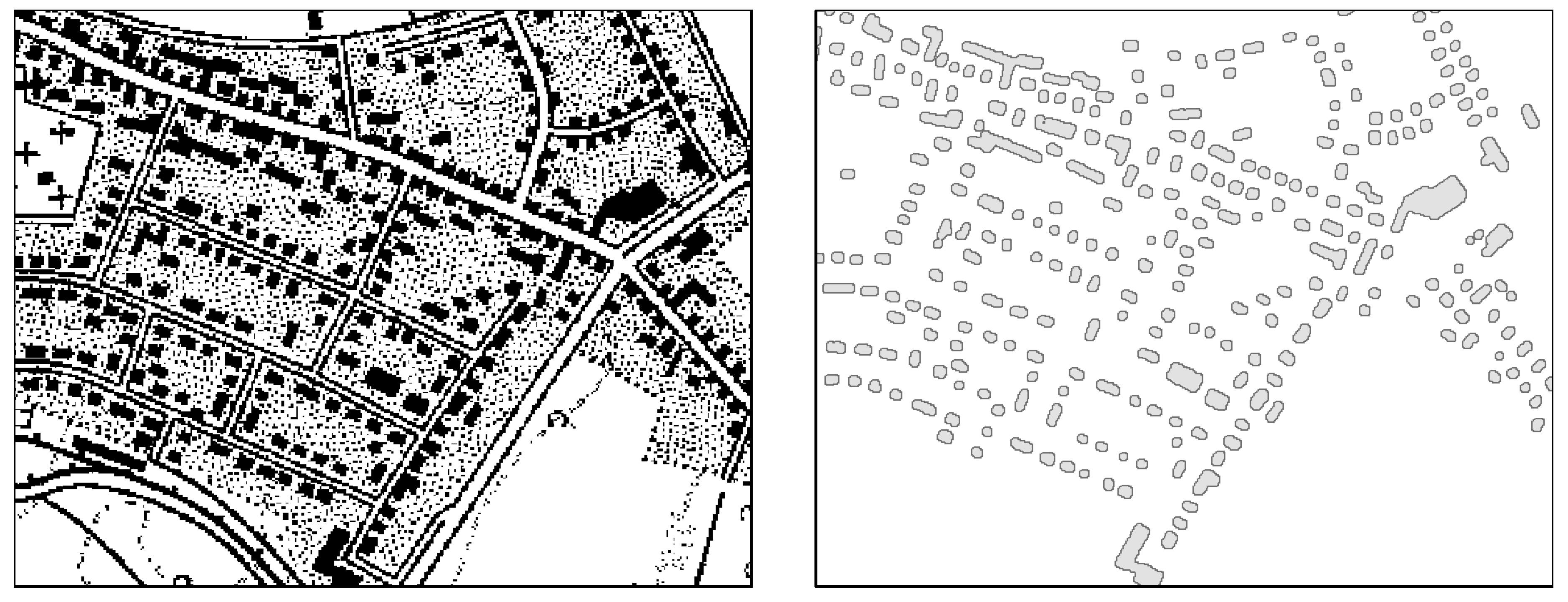
2.4. Building Footprint Retrieval
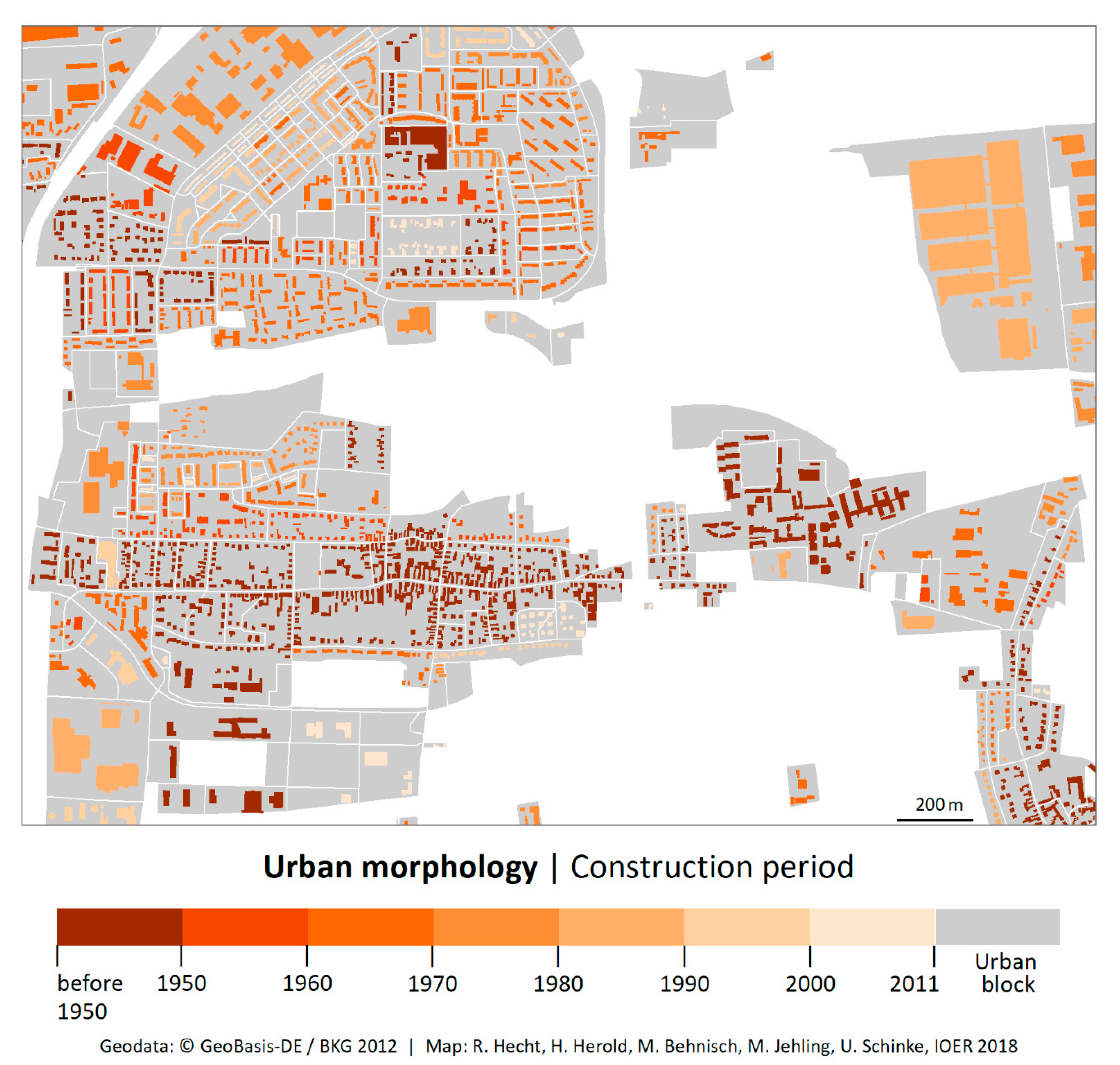
2.5. Derivation of Building Age
- Calculating the built-up coverage: For each urban block and time slice, the built-up coverage (proportion of building area in the block area) is calculated based on a spatial intersection of the extracted building footprints from the topographic maps and the urban block geometry taken from the ATKIS® Basic DLM. The calculated built-up coverages over time form the basis for determining the time of first construction of an urban block. The block-based calculation avoids building-by-building comparisons over time, which may be impossible due to the varying map quality, layout and positional inaccuracies across the time series.
- Determination of a threshold value: For distinguishing between built-up and not built-up at a specific time, a threshold value needs to be applied. The optimal threshold value was determined by performing a Receiver Operating Characteristic (ROC) analysis on given reference data. The reference data include a map of built-up areas for the year 1970. Together with the calculated built-up coverages, they were input data for the ROC analysis. Thus, an optimum threshold value of 0.025 was determined, that is, only from a built-up coverage of 2.5% is an area regarded as built-up (with a sensitivity of 0.948 and a specificity of 0.785).
- Historical settlement layer: In this step, the urban blocks of all time slices are classified according to built-up and not built-up by applying the threshold value to the built-up coverage values. Subsequently, the time of first construction is determined on the basis of the development pattern. The result is the historical settlement layer.
- Historical urban morphology at the building level: In a final step, the buildings are intersected with the historical settlement layer at the urban block level and the age data are attached to the building layer (see Figure 3).
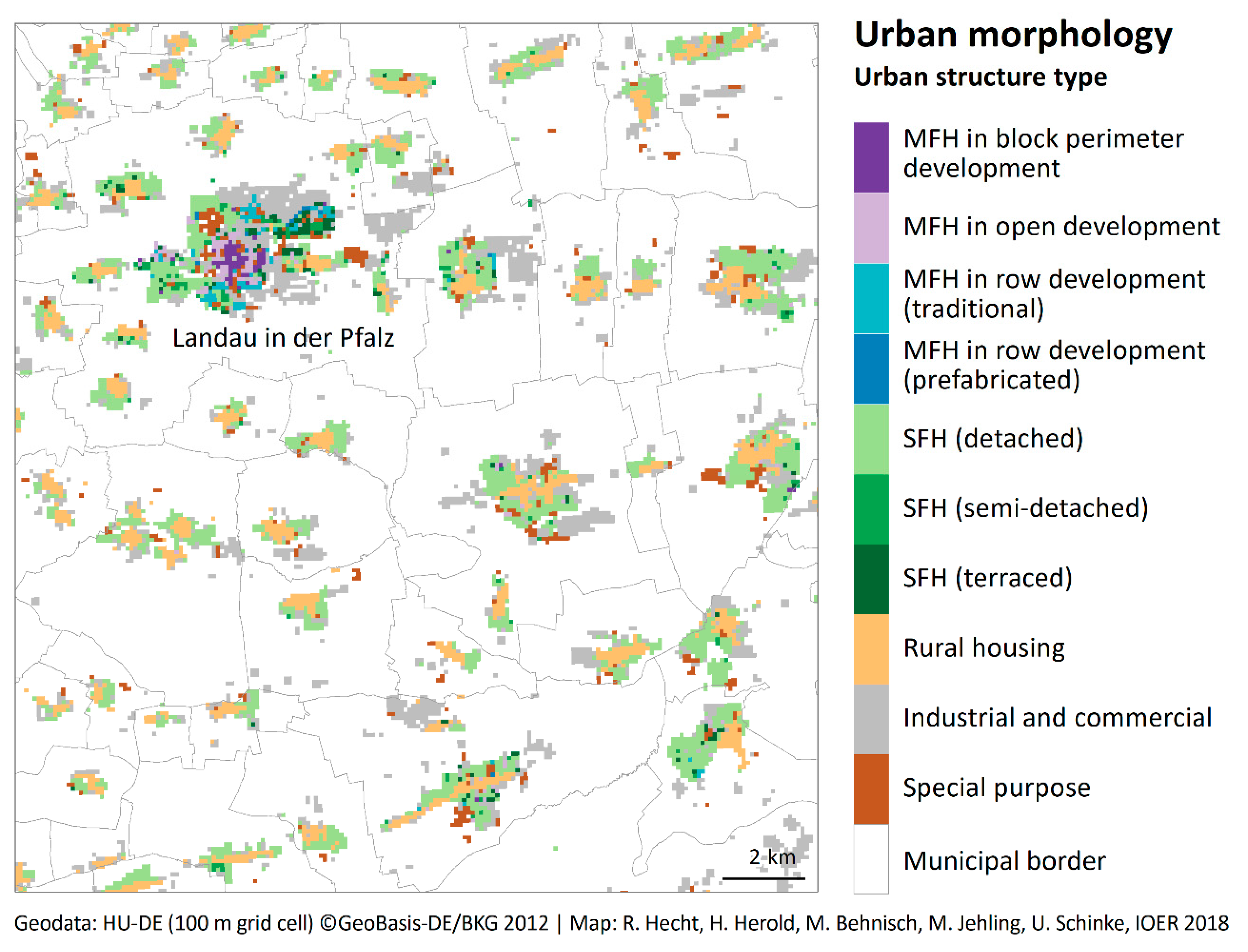
2.6. Classification of Building Footprints
2.7. Calculation of the Number of Dwellings and Inhabitants
- Mean story height (sh)
- Conversion factor (cf)
- Dwelling unit size (dz)
- Household size (hh)
2.8. Aggregation
3. Study Area and Data Sets
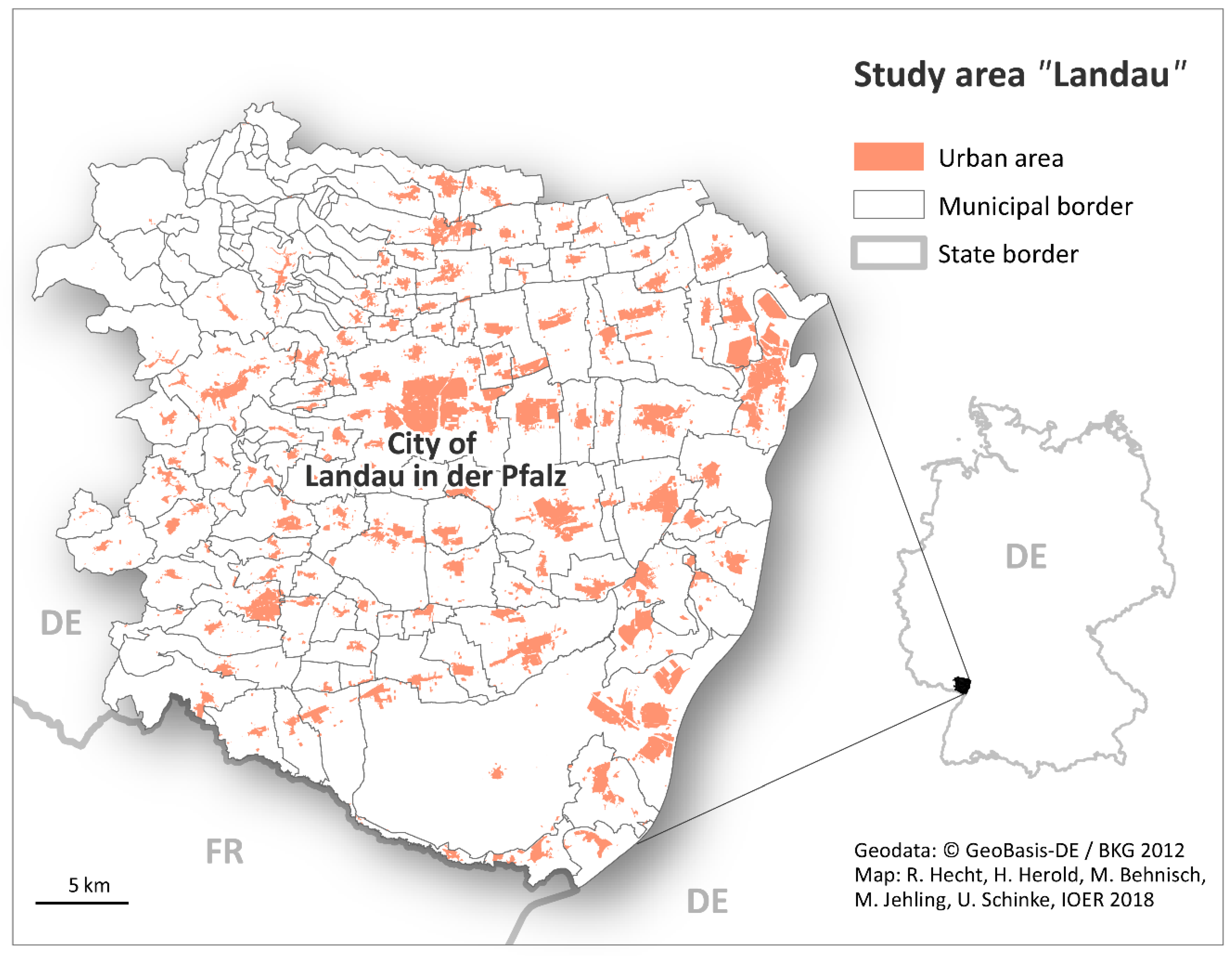
3.1. Study Area
3.2. Data Sets
- Building data: 3D building model in LoD1 from the year 2012
- Land use data: Digital Landscape Model of the German Authoritative Topographic-Cartographic Information System (ATKIS base DLM) from the year 2012
- Topographic raster maps: German topographic maps (TK 25) at a scale of 1:25,000 from the years 1950, 1960, 1970, 1980, 1990 and 2000.
- Field survey data: Data set of 603 buildings with information on the average story height and average size of dwelling units per building type. This data was used to parameterize the model.
- Grid cell based statistical census data: Population and number of dwelling units at the level of 100 m grid cells based on the INSPIRE Geographical Grid System. The data are taken from Zensus2011.de, which is provided by the Federal Statistical Office (Destatis). These data are used for the validation of the estimates of the historical population and dwelling units.
- Official statistics at the municipal level: Current and historical statistical data on population and household size obtained from the Federal Statistical Office of Rhineland-Palatinate. These data are used for the validation of the historical estimates.
4. Results
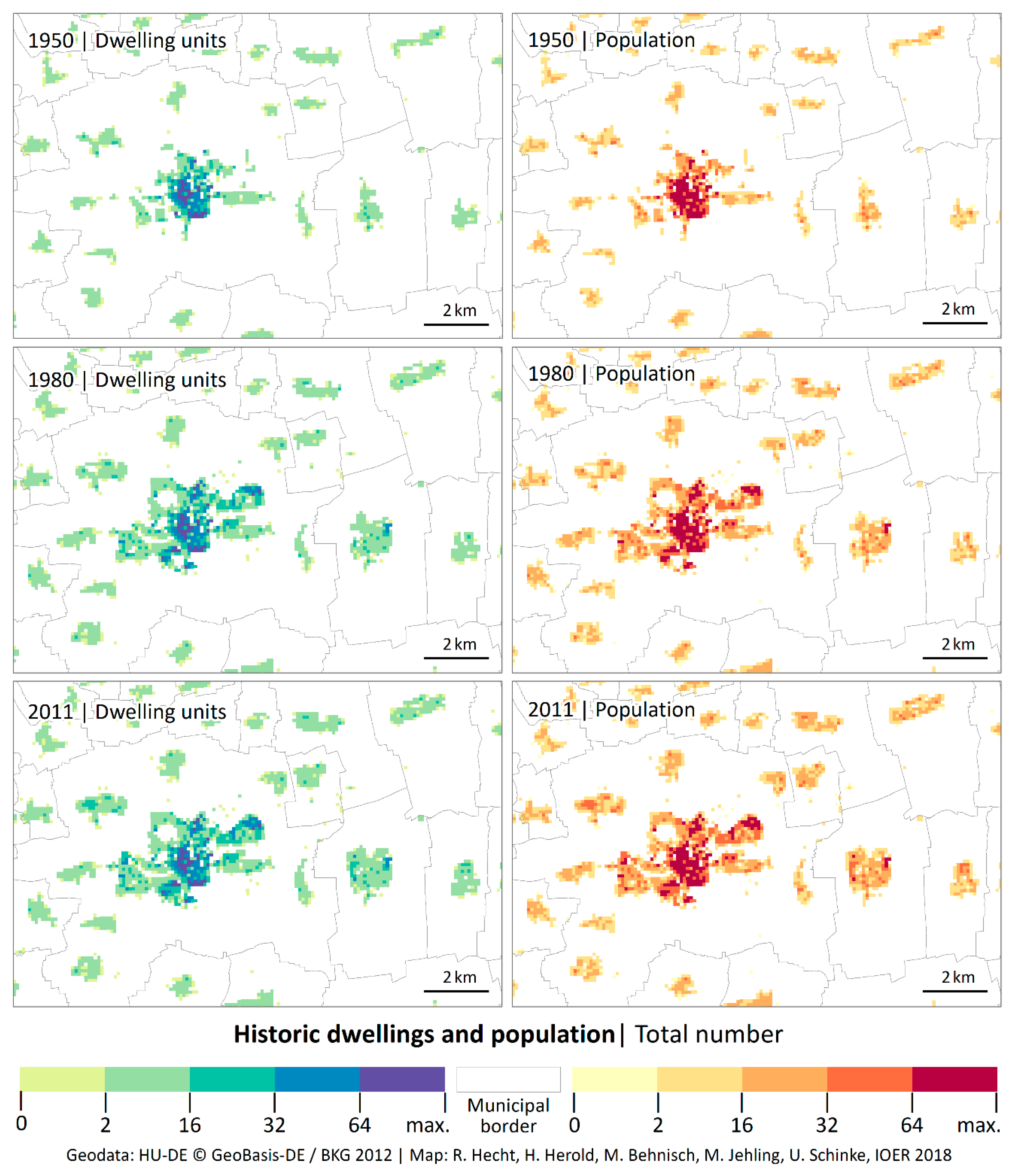
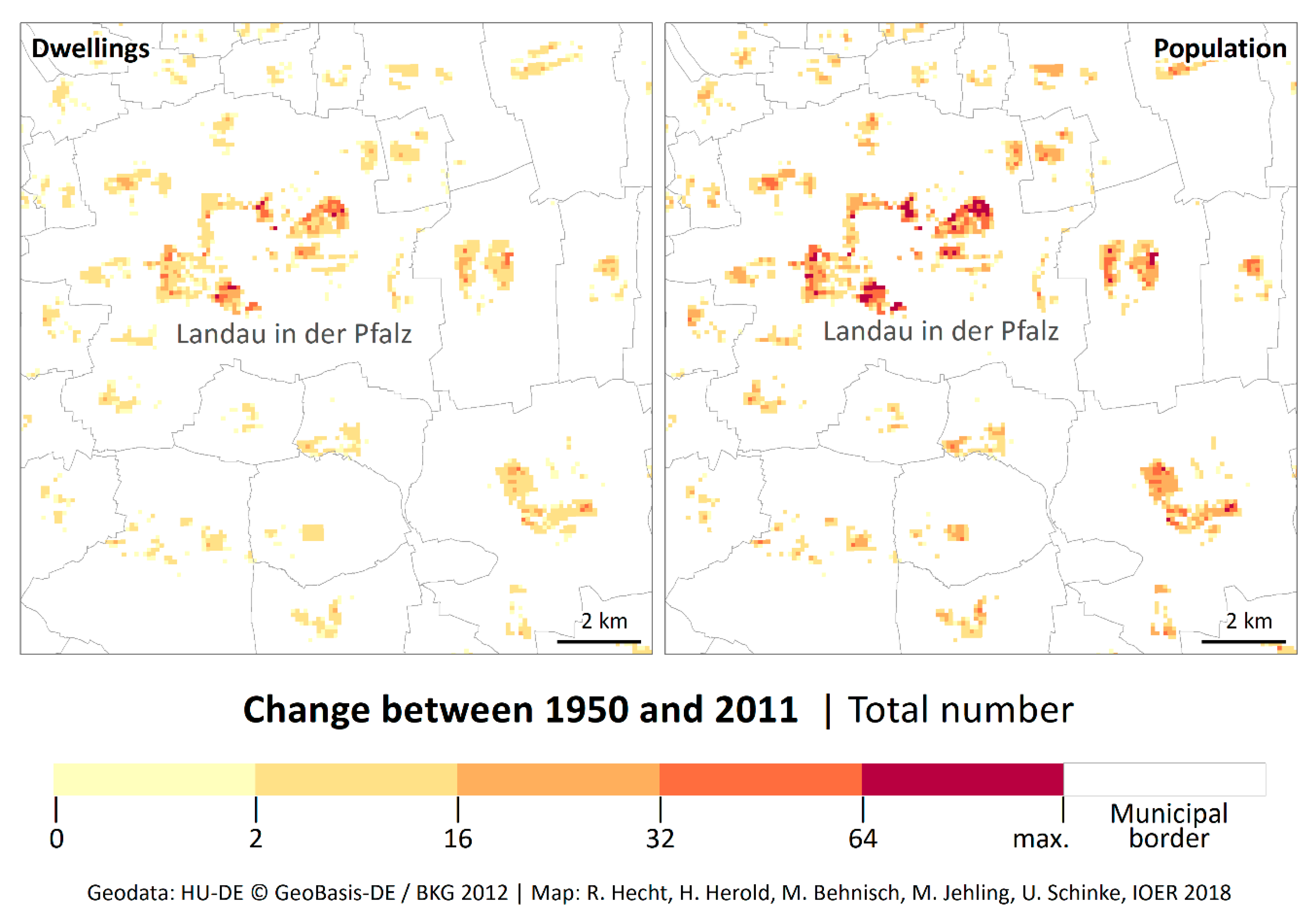
4.1. Historical Population and Dwellings and Dynamics
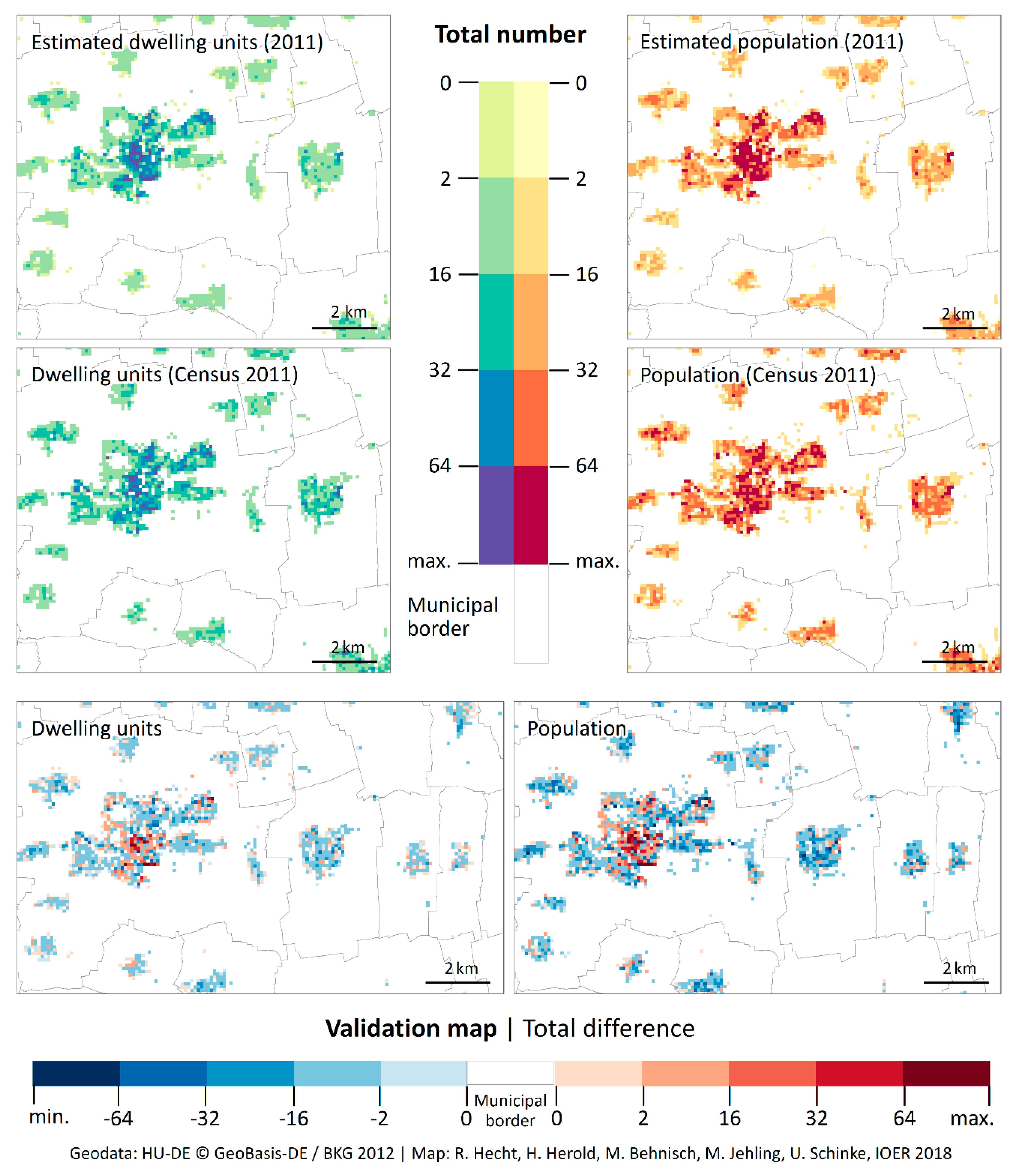
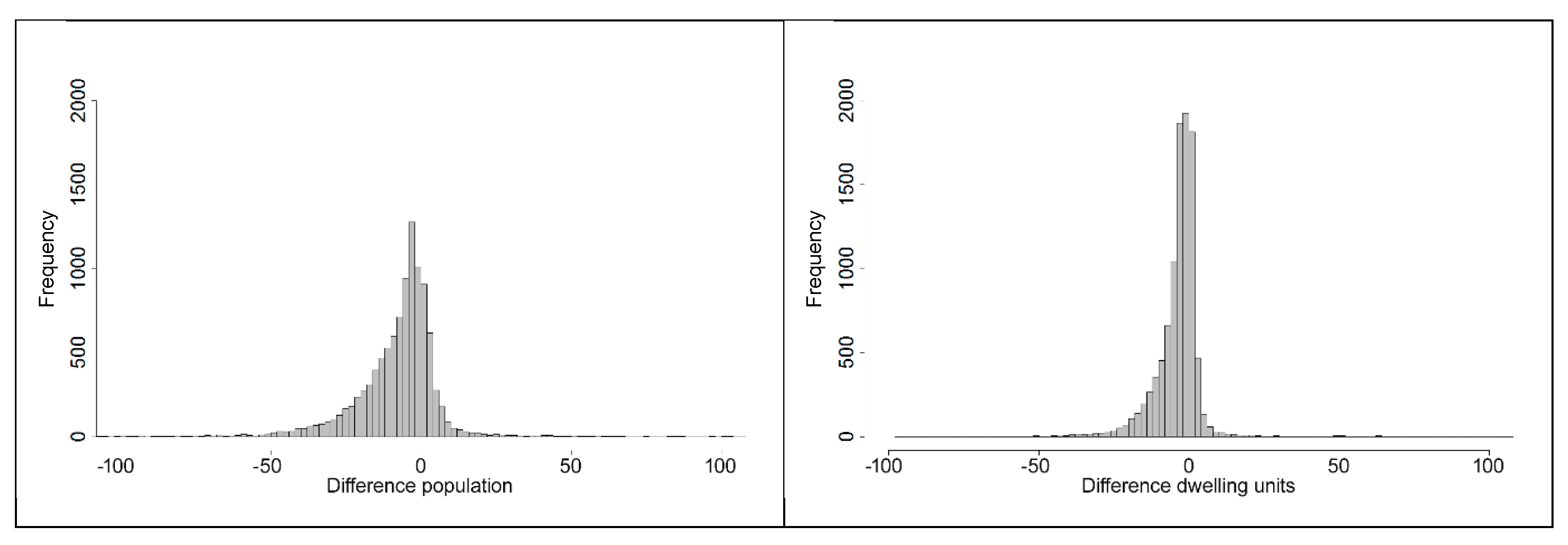
4.2. Cell-Based Validation of the Current State Using Census Data 2011
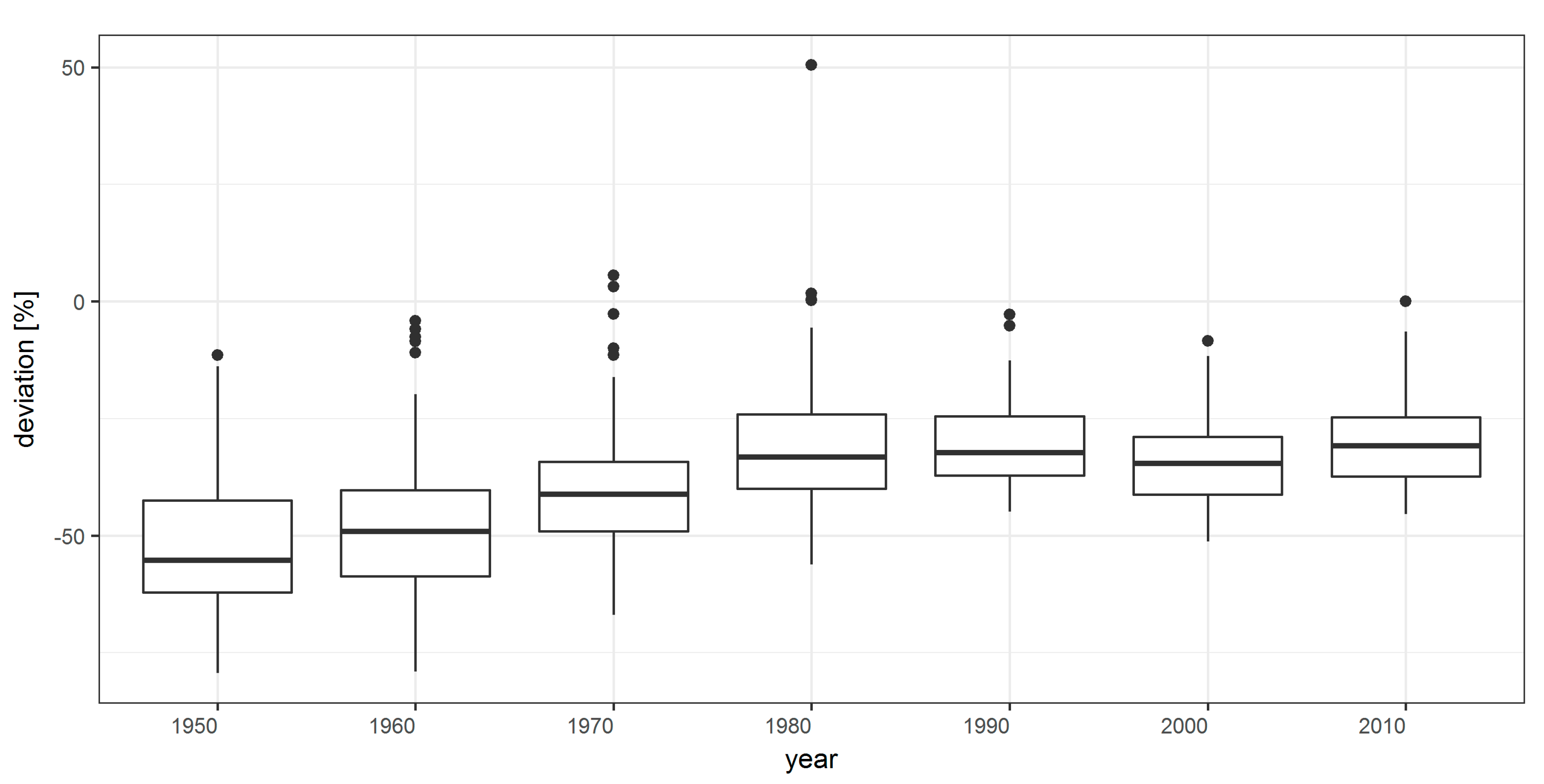
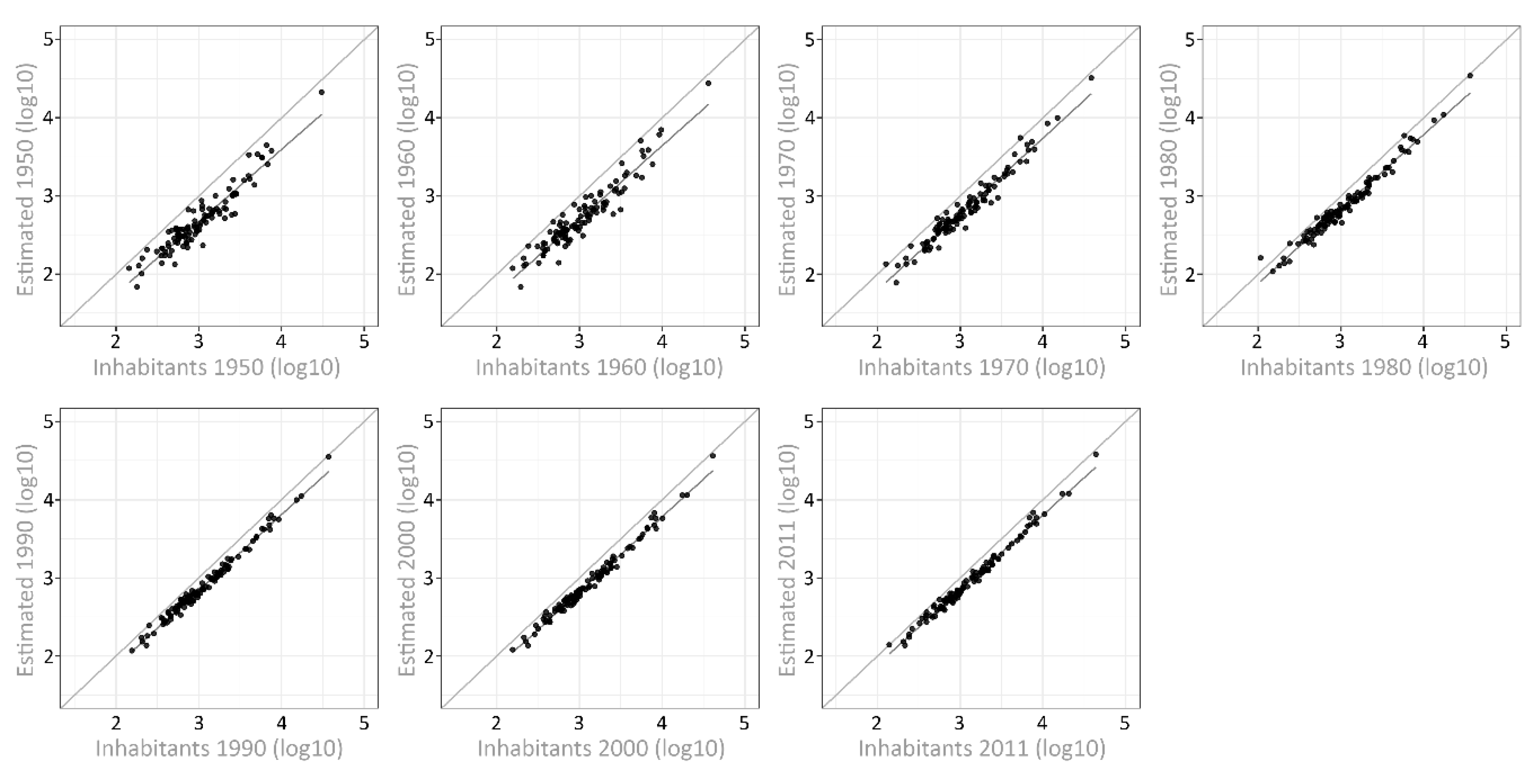
4.3. Validation of the Population Dynamics
5. Discussion
5.1. Limitations
5.2. Transferability
5.3. Field of Applications
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ahola, T.; Virrantaus, K.; Krisp, J.M.; Hunter, G.J. A spatio-temporal population model to support risk assessment and damage analysis for decision-making. Int. J. Geogr. Inf. Sci. 2007, 21, 935–953. [Google Scholar] [CrossRef]
- Cockx, K.; Canters, F. Incorporating spatial non-stationarity to improve dasymetric mapping of population. Appl. Geogr. 2015, 63, 220–230. [Google Scholar] [CrossRef]
- Crols, T.; Vanderhaegen, S.; Canters, F.; Engelen, G.; Poelmans, L.; Uljee, I.; White, R. Downdating high-resolution population density maps using sealed surface cover time series. Landsc. Urban Plan. 2017, 160, 96–106. [Google Scholar] [CrossRef]
- Renner, K.; Schneiderbauer, S.; Pruß, F.; Kofler, C.; Martin, D.; Cockings, S. Spatio-temporal population modelling as improved exposure information for risk assessments tested in the Autonomous Province of Bolzano. Int. J. Disaster Risk Reduct. 2018, 27, 470–479. [Google Scholar] [CrossRef]
- Evans, S.; Liddiard, R.; Steadman, P. 3DStock: A new kind of three-dimensional model of the building stock of England and Wales, for use in energy analysis. Environ. Plan. B 2017, 44, 227–255. [Google Scholar] [CrossRef]
- Beck, A.; Long, G.; Boyd, D.S.; Rosser, J.F.; Morley, J.; Duffield, R.; Sanderson, M.; Robinson, D. Automated classification metrics for energy modelling of residential buildings in the UK with open algorithms. Environ. Plan. B 2018. [Google Scholar] [CrossRef]
- Ekamper, P. Using cadastral maps in historical demographic research: Some examples from the Netherlands. Hist. Fam. 2010, 15, 1–12. [Google Scholar] [CrossRef]
- Jehling, M.; Hecht, R.; Herold, H. Assessing urban containment policies within a suburban context—An approach to enable a regional perspective. Land Use Policy 2018, 77, 846–858. [Google Scholar] [CrossRef]
- Pan, H.; Deal, B.; Chen, Y.; Hewings, G. A Reassessment of urban structure and land-use patterns: Distance to CBD or network-based?—Evidence from Chicago. Reg. Sci. Urban Econ. 2018, 70, 215–228. [Google Scholar] [CrossRef]
- Alahmadi, M.; Atkinson, P.; Martin, D. Estimating the spatial distribution of the population of Riyadh, Saudi Arabia using remotely sensed built land cover and height data. Comput. Environ. Urban Syst. 2013, 41, 167–176. [Google Scholar] [CrossRef]
- Wu, S.; Qiu, X.; Wang, L. Population Estimation Methods in GIS and Remote Sensing: A Review. GISci. Remote Sens. 2005, 42, 80–96. [Google Scholar] [CrossRef]
- Eicher, C.L.; Brewer, C.A. Dasymetric Mapping and Areal Interpolation: Implementation and Evaluation. Cartogr. Geogr. Inf. Sci. 2001, 28, 125–138. [Google Scholar] [CrossRef]
- Maantay, J.A.; Maroko, A.R.; Herrmann, C. Mapping Population Distribution in the Urban Environment: The Cadastral-based Expert Dasymetric System (CEDS). Cartogr. Geogr. Inf. Sci. 2007, 34, 77–102. [Google Scholar] [CrossRef]
- Langford, M.; Unwin, D.J. Generating and mapping population density surfaces within a geographical information system. Cartogr. J. 1994, 31, 21–26. [Google Scholar] [CrossRef]
- Fisher, P.F.; Langford, M. Modelling the Errors in Areal Interpolation between Zonal Systems by Monte Carlo Simulation. Environ. Plan. A 1995, 27, 211–224. [Google Scholar] [CrossRef]
- Holt, J.B.; Lo, C.P.; Hodler, T.W. Dasymetric Estimation of Population Density and Areal Interpolation of Census Data. Cartogr. Geogr. Inf. Sci. 2004, 31, 103–121. [Google Scholar] [CrossRef]
- Mennis, J. Generating Surface Models of Population Using Dasymetric Mapping. Prof. Geogr. 2003, 55, 31–42. [Google Scholar]
- Tatem, A.J.; Noor, A.M.; von Hagen, C.; Di Gregorio, A.; Hay, S.I. High Resolution Population Maps for Low Income Nations: Combining Land Cover and Census in East Africa. PLoS ONE 2007, 2, e1298. [Google Scholar] [CrossRef] [PubMed]
- Gallego, F.J. A population density grid of the European Union. Popul. Environ. 2010, 31, 460–473. [Google Scholar] [CrossRef]
- Langford, M.; Higgs, G.; Radcliffe, J.; White, S. Urban population distribution models and service accessibility estimation. Comput. Environ. Urban Syst. 2008, 32, 66–80. [Google Scholar] [CrossRef]
- Meinel, G.; Hecht, R.; Herold, H. Analyzing building stock using topographic maps and GIS. Build. Res. Inf. 2009, 37, 468–482. [Google Scholar] [CrossRef]
- Zoraghein, H.; Leyk, S. Data-enriched interpolation for temporally consistent population compositions. GISci. Remote Sens. 2018, 32. [Google Scholar] [CrossRef]
- Lwin, K.; Murayama, Y. A GIS Approach to Estimation of Building Population for Micro-spatial Analysis. Trans. GIS 2009, 13, 401–414. [Google Scholar] [CrossRef]
- Ural, S.; Hussain, E.; Shan, J. Building population mapping with aerial imagery and GIS data. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 841–852. [Google Scholar] [CrossRef]
- Kunze, C.; Hecht, R. Semantic enrichment of building data with volunteered geographic information to improve mappings of dwelling units and population. Comput. Environ. Urban Syst. 2015, 53, 4–18. [Google Scholar] [CrossRef]
- Biljecki, F.; Arroyo Ohori, K.; Ledoux, H.; Peters, R.; Stoter, J. Population Estimation Using a 3D City Model: A Multi-Scale Country-Wide Study in the Netherlands. PLoS ONE 2016, 11, e0156808. [Google Scholar] [CrossRef] [PubMed]
- Bhaduri, B.; Bright, E.; Coleman, P.; Urban, M.L. LandScan USA: A high-resolution geospatial and temporal modeling approach for population distribution and dynamics. GeoJournal 2007, 69, 103–117. [Google Scholar] [CrossRef]
- Greger, K. Spatio-Temporal Building Population Estimation for Highly Urbanized Areas Using GIS: Spatio-Temporal Building Population Estimation. Trans. GIS 2015, 19, 129–150. [Google Scholar] [CrossRef]
- Batista e Silva, F.; Marín Herrera, M.A.; Rosina, K.; Ribeiro Barranco, R.; Freire, S.; Schiavina, M. Analysing spatiotemporal patterns of tourism in Europe at high-resolution with conventional and big data sources. Tour. Manag. 2018, 68, 101–115. [Google Scholar] [CrossRef]
- Morton, T.A.; Yuan, F. Analysis of population dynamics using satellite remote sensing and US census data. Geocarto Int. 2009, 24, 143–163. [Google Scholar] [CrossRef]
- Leyk, S.; Uhl, J.H. HISDAC-US, historical settlement data compilation for the conterminous United States over 200 years. Sci. Data 2018, 5, 180175. [Google Scholar] [CrossRef] [PubMed]
- Herold, H. Geoinformation from the Past; Springer: Wiesbaden, Germany, 2018; ISBN 978-3-65-820569-0. [Google Scholar]
- Hecht, R.; Kunze, C.; Hahmann, S. Measuring Completeness of Building Footprints in OpenStreetMap over Space and Time. ISPRS Int. J. Geo-Inf. 2013, 2, 1066–1091. [Google Scholar] [CrossRef]
- Deseilligny, M.P.; Mariani, R.; Labiche, J.; Mullot, R. Topographic maps automatic interpretation: Some proposed strategies. In Graphics Recognition Algorithms and Systems; Lecture Notes in Computer Science; Tombre, K., Chhabra, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1389, pp. 175–193. ISBN 978-3-54-064381-4. [Google Scholar]
- Illert, A. Automatic Digitization of Large Scale Maps. In Proceedings of the Auto-Carto 10, London, UK, 25–28 March 1991; pp. 113–122. [Google Scholar]
- Herold, H.; Roehm, P.; Hecht, R. Georeferenced Maps as a Source for High Resolution Urban Growth Analyses. In Proceedings of the 25th ICA International Cartographic Conference, Paris, France, 3–8 July 2011; pp. 1–5. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2008; ISBN 978-0-13-168728-8. [Google Scholar]
- Hecht, R.; Meinel, G.; Buchroithner, M. Automatic identification of building types based on topographic databases—A comparison of different data sources. Int. J. Cartogr. 2015, 1, 18–31. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hecht, R. Automatische Klassifizierung von Gebäudegrundrissen: Ein Beitrag zur Kleinräumigen Beschreibung der Siedlungsstruktur; Rhombos-Verl.: Berlin, Germany, 2014; Volume 63, ISBN 978-3-94-410163-7. [Google Scholar]
- Korda, M. (Ed.) Städtebau; Vieweg+Teubner Verlag: Wiesbaden, Germany, 1999; ISBN 978-3-32-296807-4. [Google Scholar]
- GeoBasis-DE. Digital Base Landscape Model; Documentation from 20.09.2011; Federal Agency for Cartography and Geodesy: Frankfurt, Germany, 2011; Available online: http://www.geodatenzentrum.de/docpdf/basis-dlm_eng.pdf (accessed on 12 December 2018).
- Zhang, X.; Ai, T.; Stoter, J.; Zhao, X. Data matching of building polygons at multiple map scales improved by contextual information and relaxation. ISPRS J. Photogramm. Remote Sens. 2014, 92, 147–163. [Google Scholar] [CrossRef]
- Schinke, U.; Herold, H.; Meinel, G.; Prechtel, N. Analysis of European Topographic Maps for Automatic Acquisition of Urban Land Use Information. In Proceedings of the 26th ICA International Cartographic Conference, Dresden, Germany, 25–30 August 2013. [Google Scholar]
- Whitworth, A.; Carter, E.; Ballas, D.; Moon, G. Estimating uncertainty in spatial microsimulation approaches to small area estimation: A new approach to solving an old problem. Comput. Environ. Urban Syst. 2017, 63, 50–57. [Google Scholar] [CrossRef]
- Hassler, U.; Kohler, N. The ideal of resilient systems and questions of continuity. Build. Res. Inf. 2014, 42, 158–167. [Google Scholar] [CrossRef]
- Hudson, P. Urban Characterisation; Expanding Applications for, and New Approaches to Building Attribute Data Capture. Hist. Environ. Policy Pract. 2018, 9, 306–327. [Google Scholar] [CrossRef]
- Aksözen, M.; Hassler, U.; Kohler, N. Reconstitution of the dynamics of an urban building stock. Build. Res. Inf. 2017, 45, 239–258. [Google Scholar] [CrossRef]
- Roumpani, F.; Hudson, P.; Hudson-Smith, A. The Use of Historical Data in Rule-Based Modelling for Scenarios to Improve Resilience within the Building Stock. Hist. Environ. Policy Pract. 2018, 9, 328–345. [Google Scholar] [CrossRef]
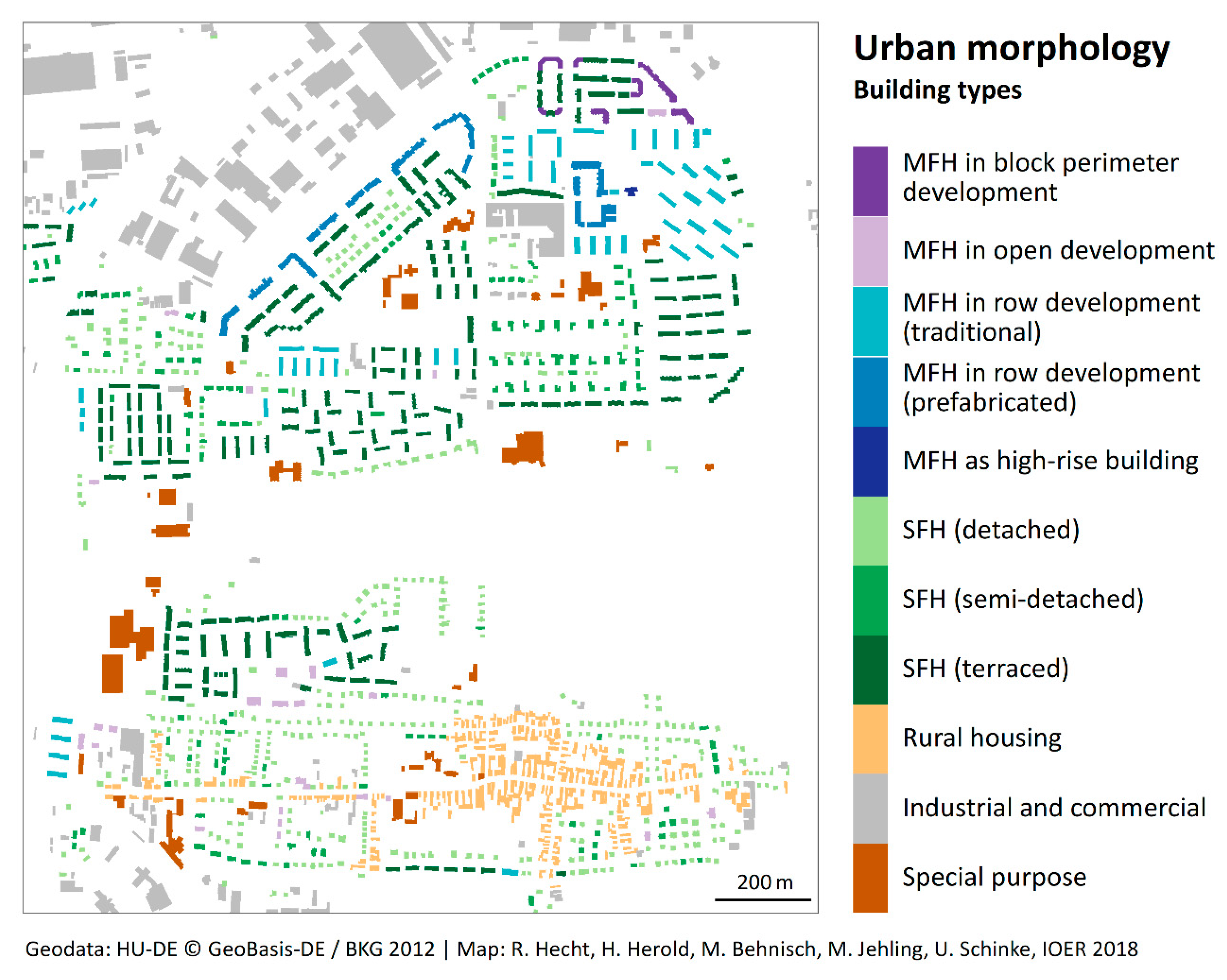
| Building Type | Story Height (sh) in m | Conversion Factor (cf) | Dwelling Unit Size (dz) in m2 | Household Size 1 (hh) |
|---|---|---|---|---|
| MFH in block perimeter dev. | 4.40 | 0.80 | 100.76 | 2.03 |
| MFH in open dev. | 4.59 | 0.80 | 109.70 | 2.03 |
| MFH in row dev. (traditional) | 4.00 | 0.80 | 62.20 | 2.03 |
| MFH in row dev. (prefabricated) | 4.00 | 0.80 | 104.72 | 2.03 |
| SFH (detached) | 5.55 | 0.80 | 112.21 | 2.03 |
| SFH (semi-detached) | 5.18 | 0.80 | 88.73 | 2.03 |
| SFH (terraced) | 4.95 | 0.80 | 88.21 | 2.03 |
| Rural housing | 5.78 | 0.34 | 150.00 | 2.03 |
| Estimation Error | Min | 1% | 5% | 10% | 25% | 50% | Mean | Std. Dev. | 75% | 90% | 95% | 99% | Max |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Population | −346 | −60 | −33 | −24 | −13 | −5 | −7.82 | 17.43 | 0 | 4 | 7 | 26 | 244 |
| Dwelling units | −98 | −31 | −16 | −12 | −5.5 | −2.0 | −3.27 | 8.32 | 1 | 2 | 4 | 14 | 118 |
| Urban Structure Type | No. of Pixels | Mean No. of Inhabitants (est.) | Mean No. of Inhabitants (ref.) | Rel. diff. Inhabitants (est.-ref.) | Mean No. of Dwellings (est.) | Mean No. of Dwellings (ref.) | Rel. Diff. Dwellings (est.-ref.) |
|---|---|---|---|---|---|---|---|
| Single-family housing (1) | 5594 | 18.53 | 24.54 | −24.5% | 9.13 | 11.17 | −18.3% |
| Multi-family housing in block perimeter development (2) | 108 | 97.41 | 87.09 | 11.8% | 48.08 | 38.98 | 23.3% |
| Multi-family-housing in open structure (3) | 196 | 48.17 | 58.42 | −17.5% | 23.73 | 29.84 | −20.5% |
| Multi-family-housing in row development (4) | 162 | 82.21 | 84.85 | −3.1% | 40.51 | 39.69 | 2.1% |
| Rural housing (5) | 2601 | 16.60 | 29.24 | −43.2% | 8.17 | 14.25 | −42.6% |
| Non-residential (6) | 6067 | 2.41 | 4.55 | −47.0% | 1.18 | 2.04 | −42.0% |
| No buildings | 102,596 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Year | Median | Mean | Std. Deviation | IQR |
|---|---|---|---|---|
| 1950 | −55.22 | −51.22 | 14.83 | 19.57 |
| 1961 | −49.00 | −47.59 | 15.91 | 18.43 |
| 1970 | −41.11 | −40.24 | 13.47 | 14.90 |
| 1979 | −33.14 | −31.00 | 13.92 | 15.94 |
| 1989 | −32.26 | −30.67 | 9.04 | 12.60 |
| 2000 | −34.51 | −33.99 | 8.75 | 12.26 |
| 2010 | −30.83 | −29.73 | 9.23 | 12.63 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hecht, R.; Herold, H.; Behnisch, M.; Jehling, M. Mapping Long-Term Dynamics of Population and Dwellings Based on a Multi-Temporal Analysis of Urban Morphologies. ISPRS Int. J. Geo-Inf. 2019, 8, 2. https://doi.org/10.3390/ijgi8010002
Hecht R, Herold H, Behnisch M, Jehling M. Mapping Long-Term Dynamics of Population and Dwellings Based on a Multi-Temporal Analysis of Urban Morphologies. ISPRS International Journal of Geo-Information. 2019; 8(1):2. https://doi.org/10.3390/ijgi8010002
Chicago/Turabian StyleHecht, Robert, Hendrik Herold, Martin Behnisch, and Mathias Jehling. 2019. "Mapping Long-Term Dynamics of Population and Dwellings Based on a Multi-Temporal Analysis of Urban Morphologies" ISPRS International Journal of Geo-Information 8, no. 1: 2. https://doi.org/10.3390/ijgi8010002
APA StyleHecht, R., Herold, H., Behnisch, M., & Jehling, M. (2019). Mapping Long-Term Dynamics of Population and Dwellings Based on a Multi-Temporal Analysis of Urban Morphologies. ISPRS International Journal of Geo-Information, 8(1), 2. https://doi.org/10.3390/ijgi8010002





