An INS/Floor-Plan Indoor Localization System Using the Firefly Particle Filter
Abstract
1. Introduction
2. Related Work
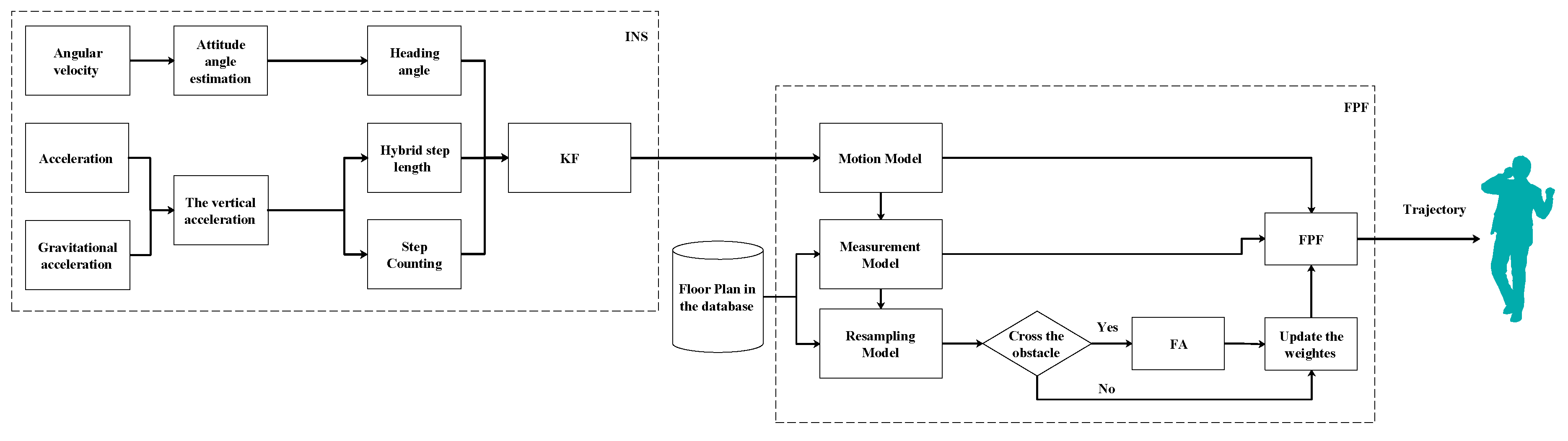
3. System Model
3.1. INS for an Indoor Positioning System
3.1.1. Attitude Angle Estimation
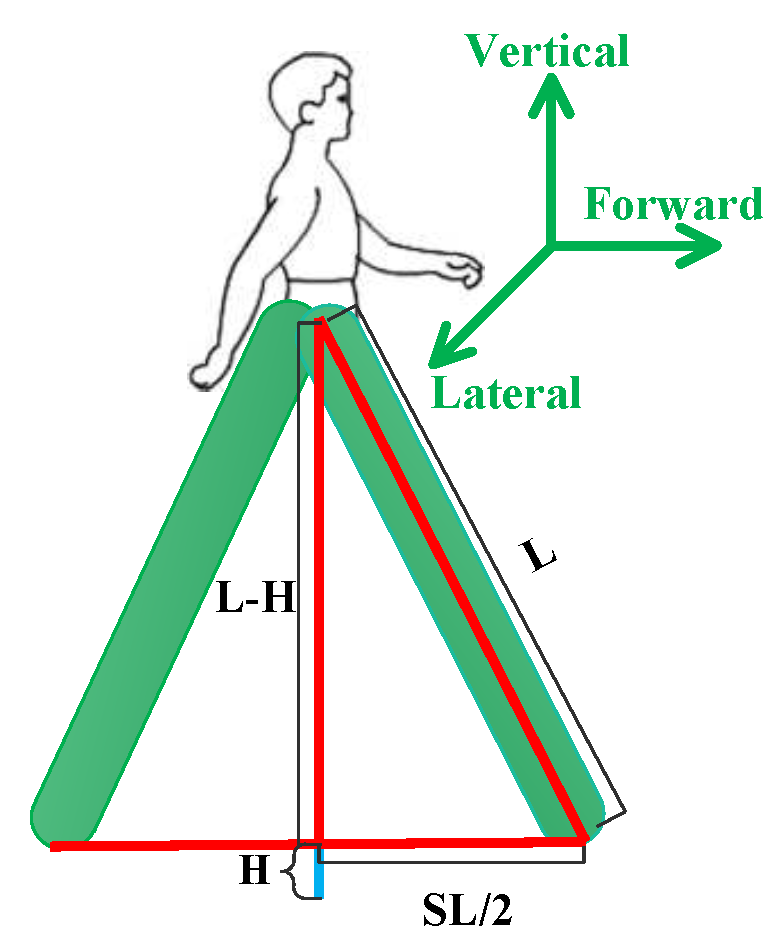
3.1.2. Hybrid Step Length Module
3.1.3. Step Counting Module
3.2. KF for Indoor Positioning Systems
3.3. FPF for Indoor Positioning Systems
| Algorithm 1 KF. |
| Input: Acceleration and angular velocity from the inertial sensor 1. Extract the vertical acceleration. 2. Detect zero vertical velocity point. 3. Loop KF 4. Use estimated sensor error to compensate measurements. 5. Update the quaternion based on the angular velocity. 6. Use the update quaternion to calculate the attitude of the navigation system. 7. Update the state transition matrix. 8. Calculate KF gain when zero vertical velocity is detected. 9. Update the filter state covariance matrix. 10. End KF 11. Calculate the step length. 12. Calculate a user’s position using dead-reckoning. |
3.3.1. The Basic Principle of PF
3.3.2. Motion Model
3.3.3. Measurement Model
3.3.4. Resampling Model
| Algorithm 2 FPF. |
| 1. Collect acceleration and angular velocity. 2. Load a floor plan information in the database. 3. FPF initialization. 4. Particle state transition. 5. According to the position relationship between the particles and a floor plan, the particles are divided into crossing-obstacle particles and non-crossing-obstacle particles. 6. Use FA to modify the crossing-obstacle particles. 7. Update the particle weights. 8. Resampling. 9. Estimate the location of a user. 10. If the condition is not finished, go to Step 4; otherwise, end FPF. |
4. Experiments and Discussion
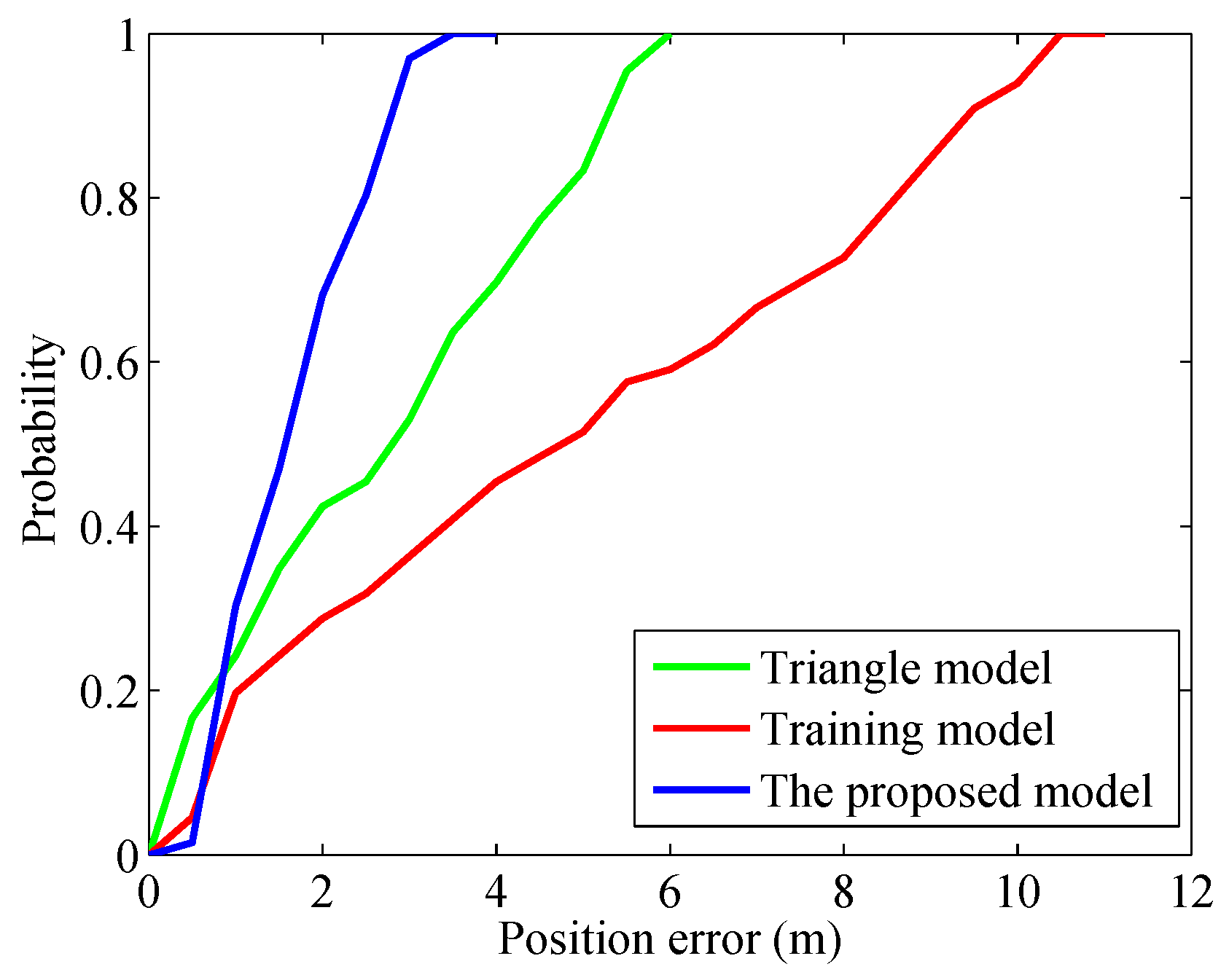
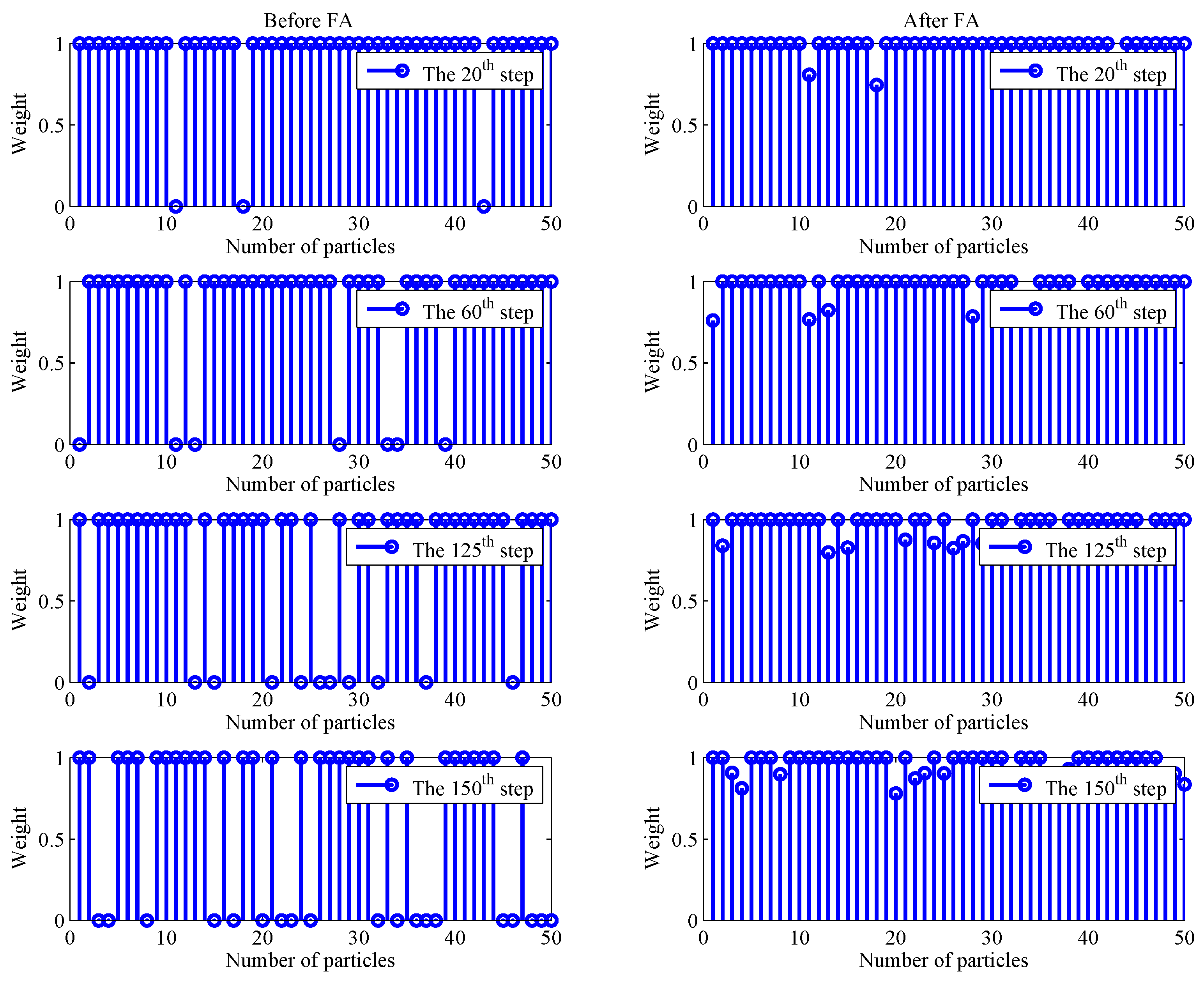
4.1. Weights Experiment
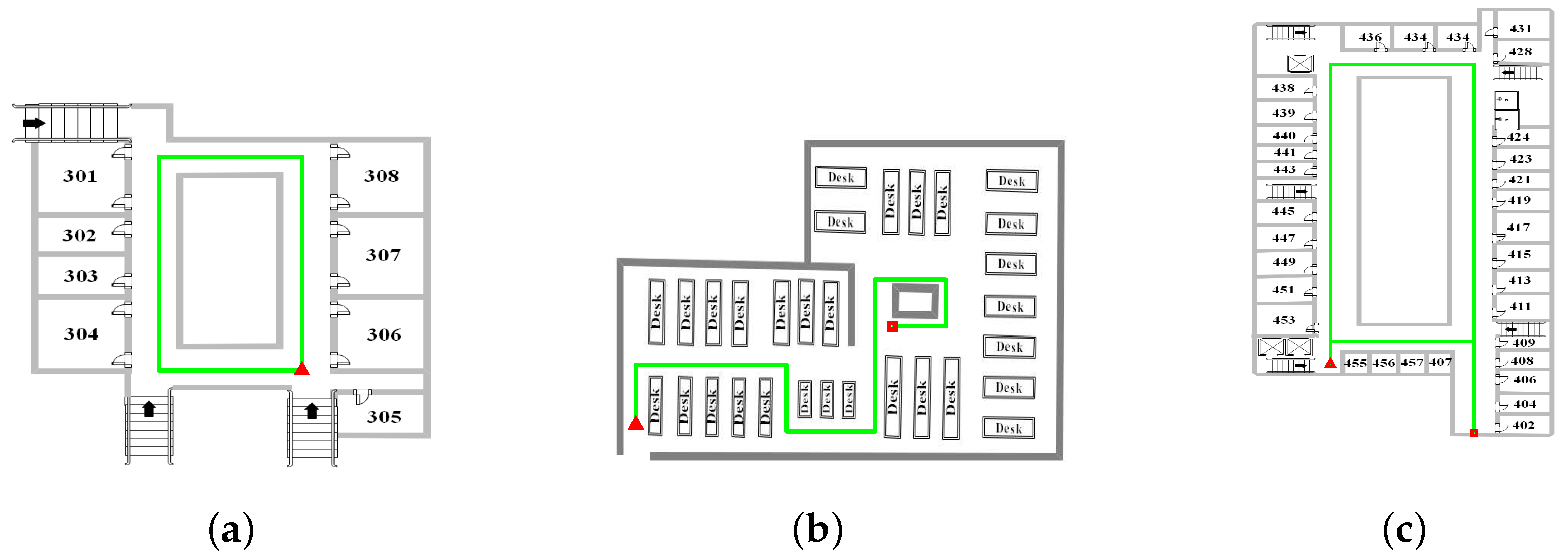
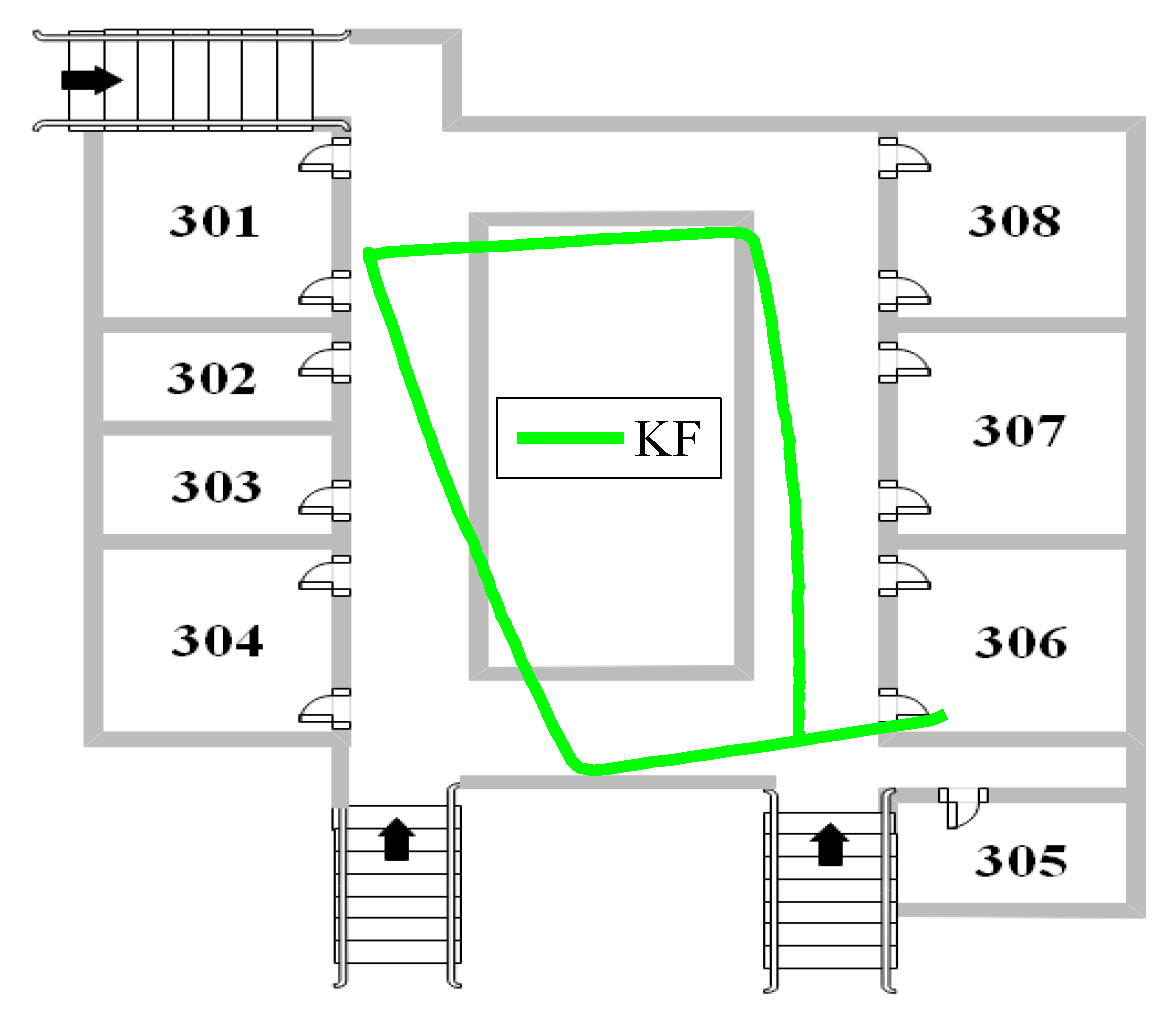
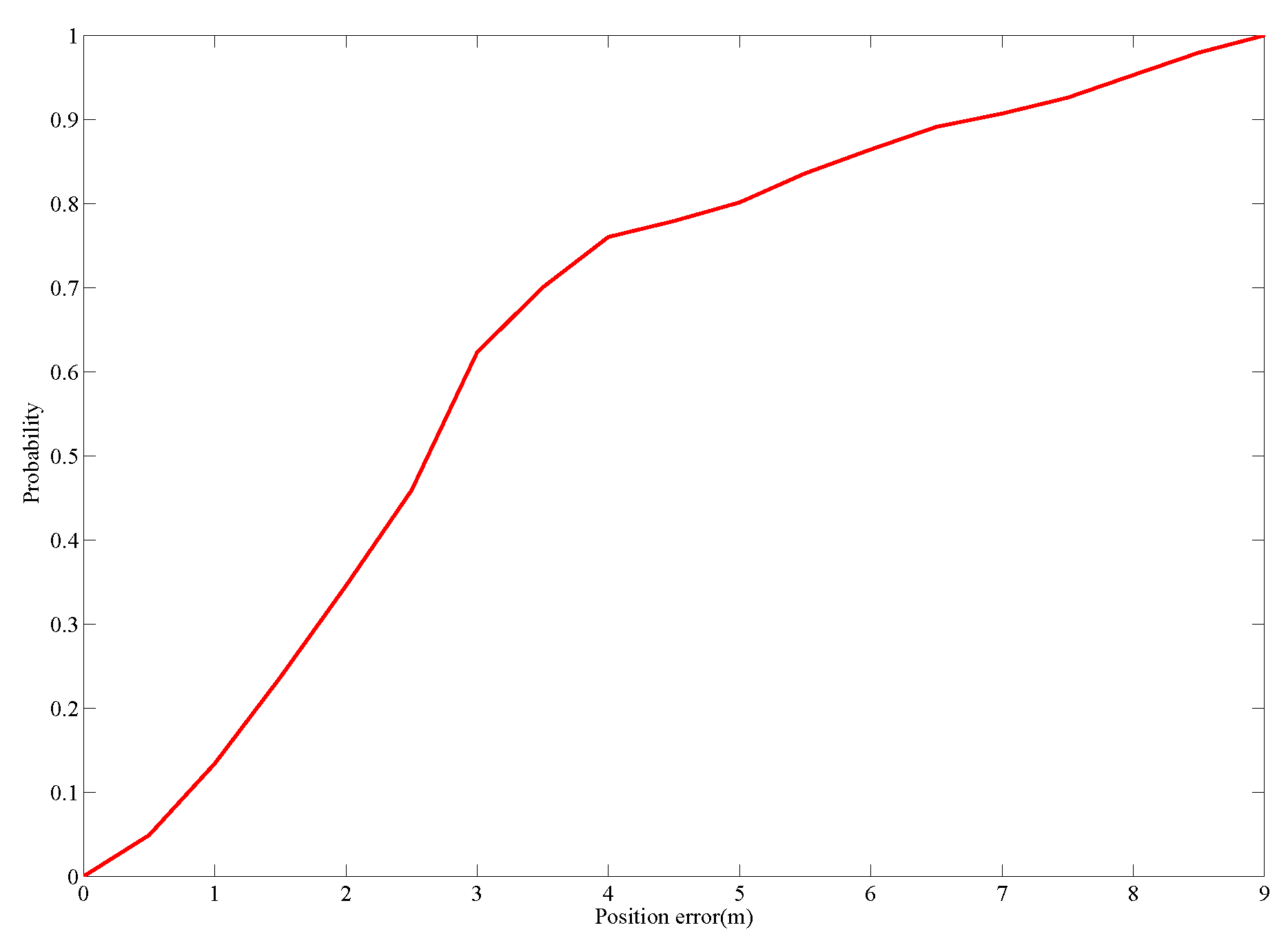
4.2. Walking Experiment at the Teaching Building
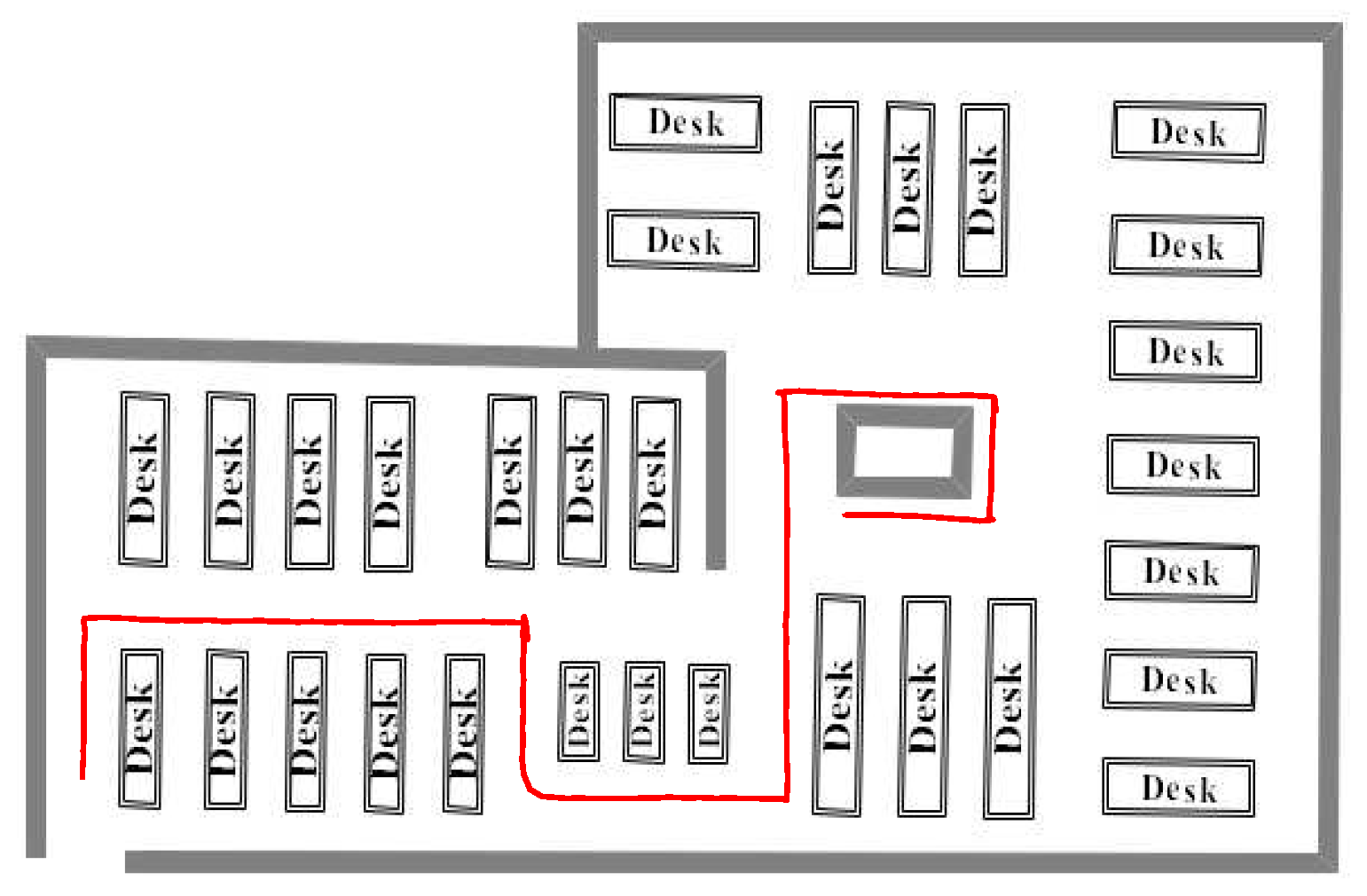
4.3. Walking Experiment at the Study Room
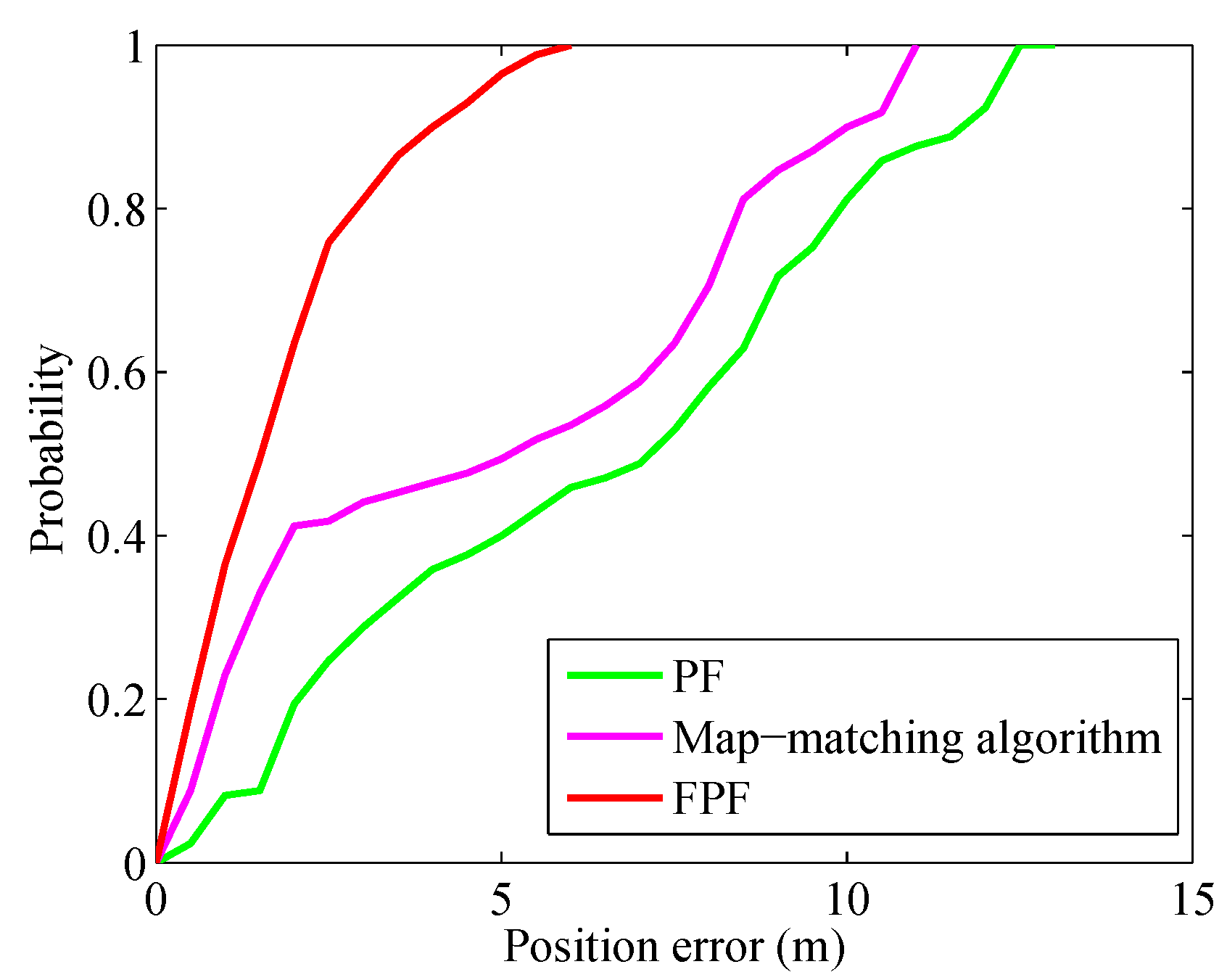
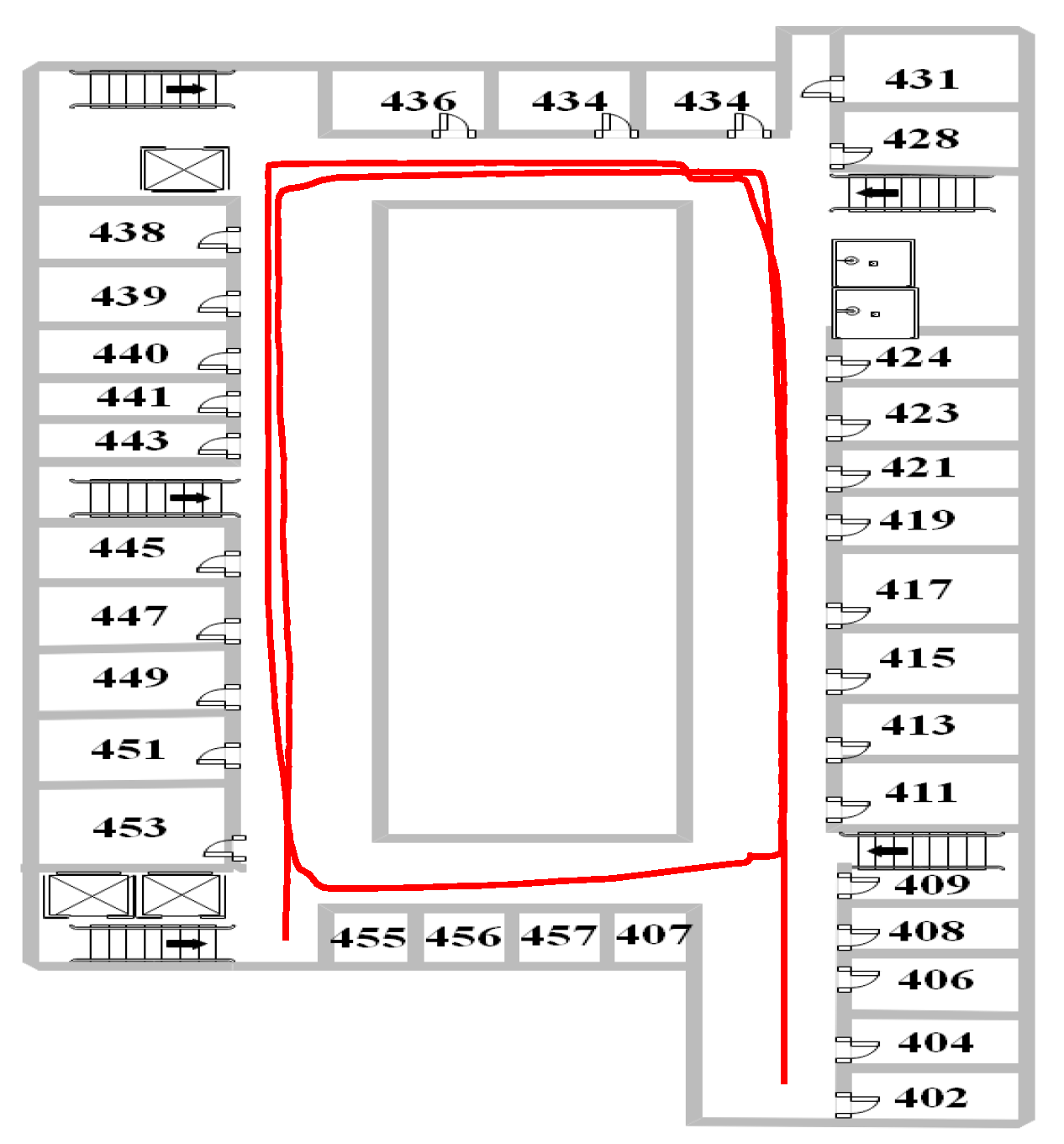
4.4. Walking Experiment at the Office Building
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| INS | Inertial Navigation System |
| KF | Kalman Filter |
| FPF | Firefly Particle Filter |
| MaLoc | Magnetic fingerprint-based indoor Localization |
| WLS | Weighted Least Squares |
| PF | Particle Filter |
| FA | Firefly Algorithm |
| CDF | Cumulative Distribution Function |
| RMSE | Root Mean Square Error |
| CEP | Circular Error Probability |
References
- Chiang, K.W.; Liao, J.K.; Huang, S.H.; Chang, H.W.; Chu, C.H. The Performance Analysis of Space Resection-Aided Pedestrian Dead Reckoning for Smartphone Navigation in a Mapped Indoor Environment. ISPRS Int. J. Geo-Inf. 2017, 6, 43. [Google Scholar] [CrossRef]
- Li, Z.; Liu, C.; Gao, J.; Li, X. An Improved WiFi/PDR Integrated System Using an Adaptive and Robust Filter for Indoor Localization. ISPRS Int. J. Geo-Inf. 2016, 5, 224. [Google Scholar] [CrossRef]
- Xie, H.; Gu, T.; Tao, X.; Ye, H.; Lu, J. A reliability-augmented particle filter for magnetic fingerprinting based indoor localization on smartphone. IEEE T. Mobile. Comput. 2016, 15, 1877–1892. [Google Scholar] [CrossRef]
- Sheinker, A.; Ginzburg, B.; Salomonski, N.; Frumkis, L.; Kaplan, B.Z.; Moldwin, M.B. A method for indoor navigation based on magnetic beacons using smartphones and tablets. Measurement 2016, 81, 197–209. [Google Scholar] [CrossRef]
- Gozick, B.; Subbu, K.P.; Dantu, R.; Maeshiro, T. Magnetic maps for indoor navigation. IEEE T. Instrum. Meas. 2011, 60, 3883–3891. [Google Scholar] [CrossRef]
- Subbu, K.P.; Gozick, B.; Dantu, R. LocateMe: Magnetic-fields-based indoor localization using smartphones. ACM Trans. Intell. Syst. Technol. 2013, 4, 73:1–73:27. [Google Scholar] [CrossRef]
- Fang, S.H.; Lin, T.N. A dynamic system approach for radio location fingerprinting in wireless local area networks. IEEE Trans. Commun. 2010, 58, 1020–1025. [Google Scholar] [CrossRef]
- Khalajmehrabadi, A.; Gatsis, N.; Akopian, D. Modern WLAN fingerprinting indoor positioning methods and deployment challenges. IEEE Commun. Surv. Tutor. 2017, 19, 1974–2002. [Google Scholar] [CrossRef]
- Li, H.; Chen, X.; Jing, G.; Wang, Y.; Cao, Y.; Li, F.; Zhang, X.; Xiao, H. An indoor continuous positioning algorithm on the move by fusing sensors and Wi-Fi on smartphones. Sensors 2015, 15, 31244–31267. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Ou, G.; Peng, A.; Zheng, L.; Shi, J. An INS/WiFi Indoor Localization System Based on the Weighted Least Squares. Sensors 2018, 18, 1458. [Google Scholar] [CrossRef] [PubMed]
- Bahl, P.; Padmanabhan, V.N. RADAR: An in-building RF-based user location and tracking system. In Proceedings of the Nineteenth Annual Joint Conference of the IEEE Computer and Communications Societies, Tel Aviv, Israel, 26–30 March 2000; pp. 775–784. [Google Scholar]
- Zheng, L.X.; Wu, Z.H.; Zhou, W.C.; Weng, S.L.; Zheng, H.R. A Smartphone Based Hand-Held Indoor Positioning System. In Frontier Computing; Springer: Singapore, 2016; pp. 639–650. [Google Scholar]
- Zheng, L.X.; Zhou, W.C.; Tang, W.W.; Zheng, X.C.; Peng, A.; Zheng, H.R. A 3D indoor positioning system based on low-cost MEMS sensors. Simul. Model Pract. Th. 2016, 65, 45–56. [Google Scholar] [CrossRef]
- Yu, C.; Lan, H.; Liu, Z.; El-Sheimy, N.; Yu, F. Indoor map aiding/map matching smartphone navigation using auxiliary particle filter. In Proceedings of the China Satellite Navigation Conference (CSNC) 2016 Proceedings, Changsha, China, 18–20 May 2016; Sun, J., Liu, J., Fan, S., Wang, F., Eds.; Springer: Singapore, 2016; Volume 1. [Google Scholar]
- Ali, N.; Othman, M.A.; Husain, M.N.; Misran, M.H. A review of firefly algorithm. ARPN J. Eng. Appl. Sci. 2014, 9, 1732–1736. [Google Scholar]
- Kang, X.; Huang, B.; Qi, G. A Novel Walking Detection and Step Counting Algorithm Using Unconstrained Smartphones. Sensors 2018, 18, 297. [Google Scholar] [CrossRef] [PubMed]
- Song, J.W.; Park, C.G. Enhanced pedestrian navigation based on course angle error estimation using cascaded Kalman filters. Sensors 2018, 18, 1281. [Google Scholar] [CrossRef] [PubMed]
- Foxlin, E. Pedestrian tracking with shoe-mounted inertial sensors. IEEE Comput. Graph. 2005, 25, 33–46. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, W.; Shen, Q.; Li, T.; Chang, H. A handheld inertial pedestrian navigation system with accurate step modes and device poses recognition. IEEE Sens. J. 2015, 15, 1421–1429. [Google Scholar] [CrossRef]
- Borenstein, J.; Ojeda, L. Heuristic drift elimination for personnel tracking systems. J. Navig. 2010, 63, 591–606. [Google Scholar] [CrossRef]
- Jiménez, A.R.; Seco, F.; Zampella, F.; Prieto, J.C.; Guevara, J. Improved heuristic drift elimination with magnetically-aided dominant directions (MiHDE) for pedestrian navigation in complex buildings. J. Locat. Based Serv. 2012, 6, 186–210. [Google Scholar] [CrossRef]
- Li, Y.; Zhuang, Y.; Lan, H.; Niu, X.; El-Sheimy, N. A profile-matching method for wireless positioning. IEEE Commun. Lett. 2016, 20, 2514–2517. [Google Scholar] [CrossRef]
- Li, Y.; Zhuang, Y.; Lan, H.; Zhang, P.; Niu, X.; El-Sheimy, N. Self-Contained Indoor Pedestrian Navigation Using Smartphone Sensors and Magnetic Features. IEEE Sens. J. 2016, 16, 7173–7182. [Google Scholar] [CrossRef]
- Xie, H.; Gu, T.; Tao, X.; Ye, H.; Lv, J. MaLoc: A practical magnetic fingerprinting approach to indoor localization using smartphones. In Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing, New York, NY, USA, 13–17 September 2014; pp. 243–253. [Google Scholar]
- Chen, G.; Meng, X.; Wang, Y.; Zhang, Y.; Tian, P.; Yang, H. Integrated Wifi/PDR/Smartphone Using an Unscented Kalman Filter Algorithm for 3d Indoor Localization. Sensors 2015, 15, 24595–24614. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.S.; Ju, H.; Park, C.G. Map assisted PDR/Wi-Fi fusion for indoor positioning using smartphone. Int. J. Control. Autom. 2017, 15, 627–639. [Google Scholar] [CrossRef]
- Tian, Q.; Salcic, Z.; Wang, K.I.K.; Pan, Y. A hybrid indoor localization and navigation system with map matching for pedestrians using smartphones. Sensors 2015, 15, 30759–30783. [Google Scholar] [CrossRef] [PubMed]
- Bao, H.; Wong, W.C. A novel map-based dead-reckoning algorithm for indoor localization. J. Sens. Actuator Netw. 2014, 3, 44–63. [Google Scholar] [CrossRef]
- Yu, C.; El-Sheimy, N.; Lan, H.; Liu, Z. Map-Based Indoor Pedestrian Navigation Using an Auxiliary Particle Filter. Micromachines 2017, 8, 225. [Google Scholar] [CrossRef]
- Pinchin, J.; Hide, C.; Moore, T. A particle filter approach to indoor navigation using a foot mounted inertial navigation system and heuristic heading information. In Proceedings of the 2012 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sydney, Australia, 13–15 November 2012; pp. 1–10. [Google Scholar]
- Li, F.; Zhao, C.; Ding, G.; Gong, J.; Liu, C.; Zhao, F. A Reliable and Accurate Indoor Localization Method Using Phone Inertial Sensors. In Proceedings of the 2012 ACM Conference on Ubiquitous Computing, Pittsburgh, PA, USA, 5–8 September 2012; pp. 421–430. [Google Scholar]
- Yang, X.S. Firefly algorithms for multimodal optimization. In Stochastic Algorithms: Foundations and Applications, Proceedings of the 5th International Symposium on Stochastic Algorithms (SAGA 2009), Sapporo, Japan, 26–28 October 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Gao, M.L.; He, X.H.; Luo, D.S.; Jiang, J.; Teng, Q.Z. Object tracking using firefly algorithm. IET Comput. Vis. 2015, 7, 227–237. [Google Scholar] [CrossRef]
- Gao, M.L.; Li, L.L.; Sun, X.M.; Yin, L.J.; Li, H.T.; Luo, D.S. Firefly algorithm (FA) based particle filter method for visual tracking. Optik 2015, 126, 1705–1711. [Google Scholar] [CrossRef]
- Shin, E. Estimation Techniques for Low-Cost Inertial Navigation. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2005. [Google Scholar]
- Chung, H.Y.; Hou, C.C.; Chen, Y.S. Indoor intelligent mobile robot localization using fuzzy compensation and Kalman filter to fuse the data of gyroscope and magnetometer. IEEE Trans. Ind. Electron. 2015, 62, 6436–6447. [Google Scholar] [CrossRef]
- Jiménez, A.R.; Seco, F.; Prieto, J.C.; Guevara, J. Indoor pedestrian navigation using an INS/EKF framework for yaw drift reduction and a foot-mounted IMU. In Proceedings of the 2010 7th Workshop on Positioning Navigation and Communication (WPNC), Dresden, Germany, 11–12 March 2010; pp. 135–143. [Google Scholar]
- Zhou, T.; Peng, D.; Xu, C.; Zhang, W.; Shen, J. Adaptive particle filter based on Kullback–Leibler distance for underwater terrain aided navigation with multi-beam sonar. IET Radar. Sonar. Nav. 2018, 4, 433–441. [Google Scholar] [CrossRef]
- Jo, H.; Cho, H.M.; Jo, S.; Kim, E. Efficient Grid-Based Rao–Blackwellized Particle Filter SLAM With Interparticle Map Sharing. IEEE-ASME Trans. Mechatron. 2018, 23, 714–724. [Google Scholar] [CrossRef]
- Yin, S.; Zhu, X. Intelligent particle filter and its application to fault detection of nonlinear system. IEEE Trans. Ind. Electron. 2015, 62, 3852–3861. [Google Scholar] [CrossRef]
- Park, S.; Hwang, J.P.; Kim, E.; Kang, H.J. A new evolutionary particle filter for the prevention of sample impoverishment. IEEE Trans. Evol. Comput. 2009, 13, 801–809. [Google Scholar] [CrossRef]
- ISO/IEC 18305:2016. Information Technology—Real Time Locating Systems—Test and Evaluation of Localization and Tracking Systems. Available online: https://www.iso.org/standard/62090.html (accessed on 10 May 2018).
- Zheng, L.; Zhou, W.; Tang, W.; Zheng, X.; Yang, H.; Pu, S.; Li, C.; Tang, B.; Chen, Y. A foot-mounted sensor based 3D indoor positioning approach. In Proceedings of the 2015 IEEE Twelfth International Symposium on Autonomous Decentralized Systems (ISADS), Taichung, Taiwan, 25–27 March 2015; pp. 145–150. [Google Scholar]
- Davidson, P.; Collin, J.; Takala, J. Application of particle filters for indoor positioning using floor plans. In Proceedings of the 2010 Ubiquitous Positioning Indoor Navigation and Location Based Service (UPINLBS), Kirkkonummi, Finland, 14–15 October 2010; pp. 1–4. [Google Scholar]


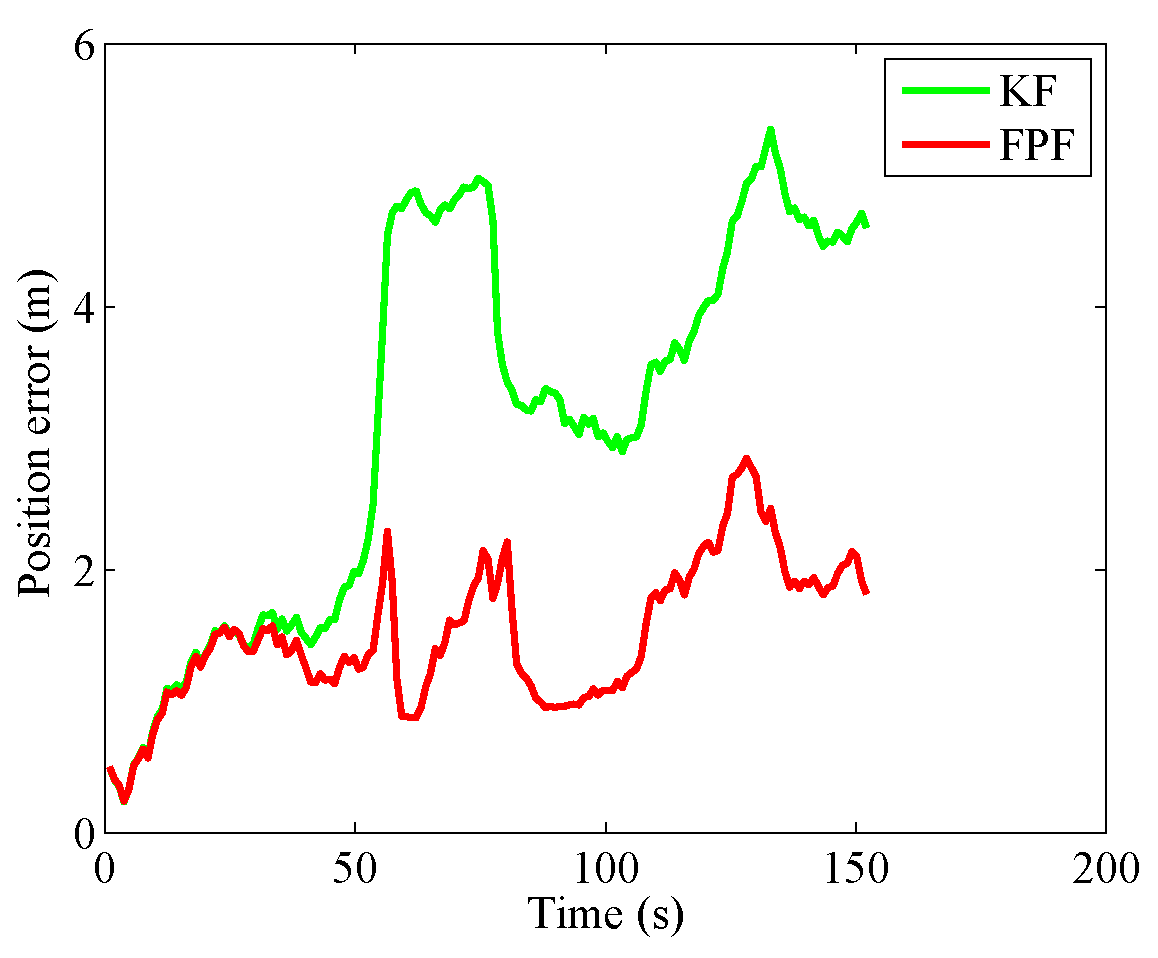
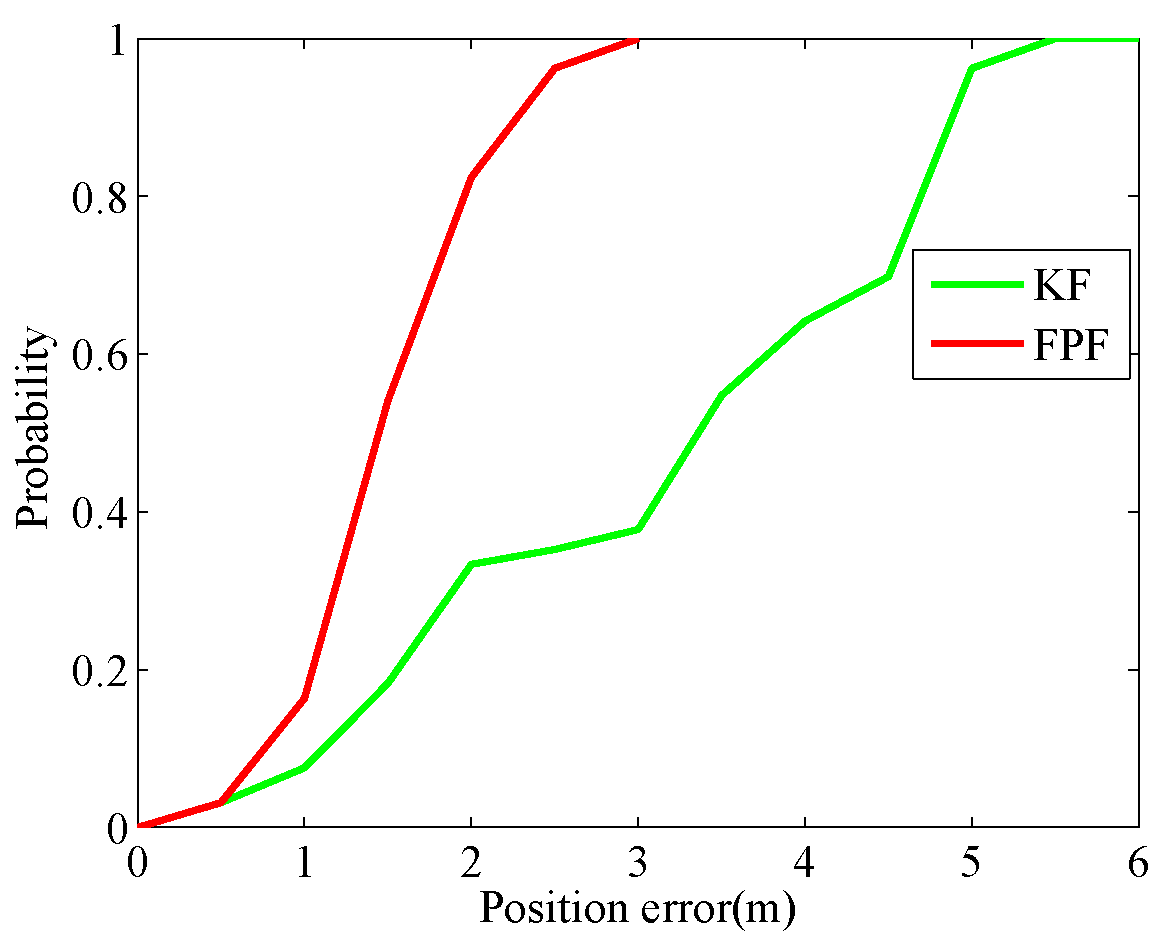
| Error | The Average Error | RMSE | Maximum Error | CEP (95%) |
|---|---|---|---|---|
| KF | 3.13 | 3.46 | 5.35 | 4.97 |
| FPF | 1.5 | 1.6 | 2.85 | 2.44 |
| Error | The Average Error | RMSE | Maximum Error | CEP (95%) |
|---|---|---|---|---|
| PF | 6.35 | 7.37 | 12.37 | 12.14 |
| Map-matching algorithm | 4.89 | 6.14 | 10.74 | 10.62 |
| FPF | 1.8 | 2.27 | 5.59 | 4.75 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Ou, G.; Peng, A.; Zheng, L.; Shi, J. An INS/Floor-Plan Indoor Localization System Using the Firefly Particle Filter. ISPRS Int. J. Geo-Inf. 2018, 7, 324. https://doi.org/10.3390/ijgi7080324
Chen J, Ou G, Peng A, Zheng L, Shi J. An INS/Floor-Plan Indoor Localization System Using the Firefly Particle Filter. ISPRS International Journal of Geo-Information. 2018; 7(8):324. https://doi.org/10.3390/ijgi7080324
Chicago/Turabian StyleChen, Jian, Gang Ou, Ao Peng, Lingxiang Zheng, and Jianghong Shi. 2018. "An INS/Floor-Plan Indoor Localization System Using the Firefly Particle Filter" ISPRS International Journal of Geo-Information 7, no. 8: 324. https://doi.org/10.3390/ijgi7080324
APA StyleChen, J., Ou, G., Peng, A., Zheng, L., & Shi, J. (2018). An INS/Floor-Plan Indoor Localization System Using the Firefly Particle Filter. ISPRS International Journal of Geo-Information, 7(8), 324. https://doi.org/10.3390/ijgi7080324





