Task-Oriented Visualization Approaches for Landscape and Urban Change Analysis
Abstract
1. Introduction
- A classification of low-level tasks is developed that frequently occur in the course of landscape and urban change analysis. This not only takes into account remotely sensed and other categorical data (such as land use classes), but also quantitative data such as (geo-) statistical numbers.
- An assignment of suitable visualization methods or map types to the given change analysis tasks is developed. These comprehensive and generalizable recommendations follow the idea of using maps effectively and efficiently, thus improving the overall visual/manual processing part of the analysis. This aspect, together with the aforementioned task classification, follows the frequently expressed demand for “identifying a ‘right’ visualization type for the data/purpose/audience” [4] (p. 126), [3] (p. 130).
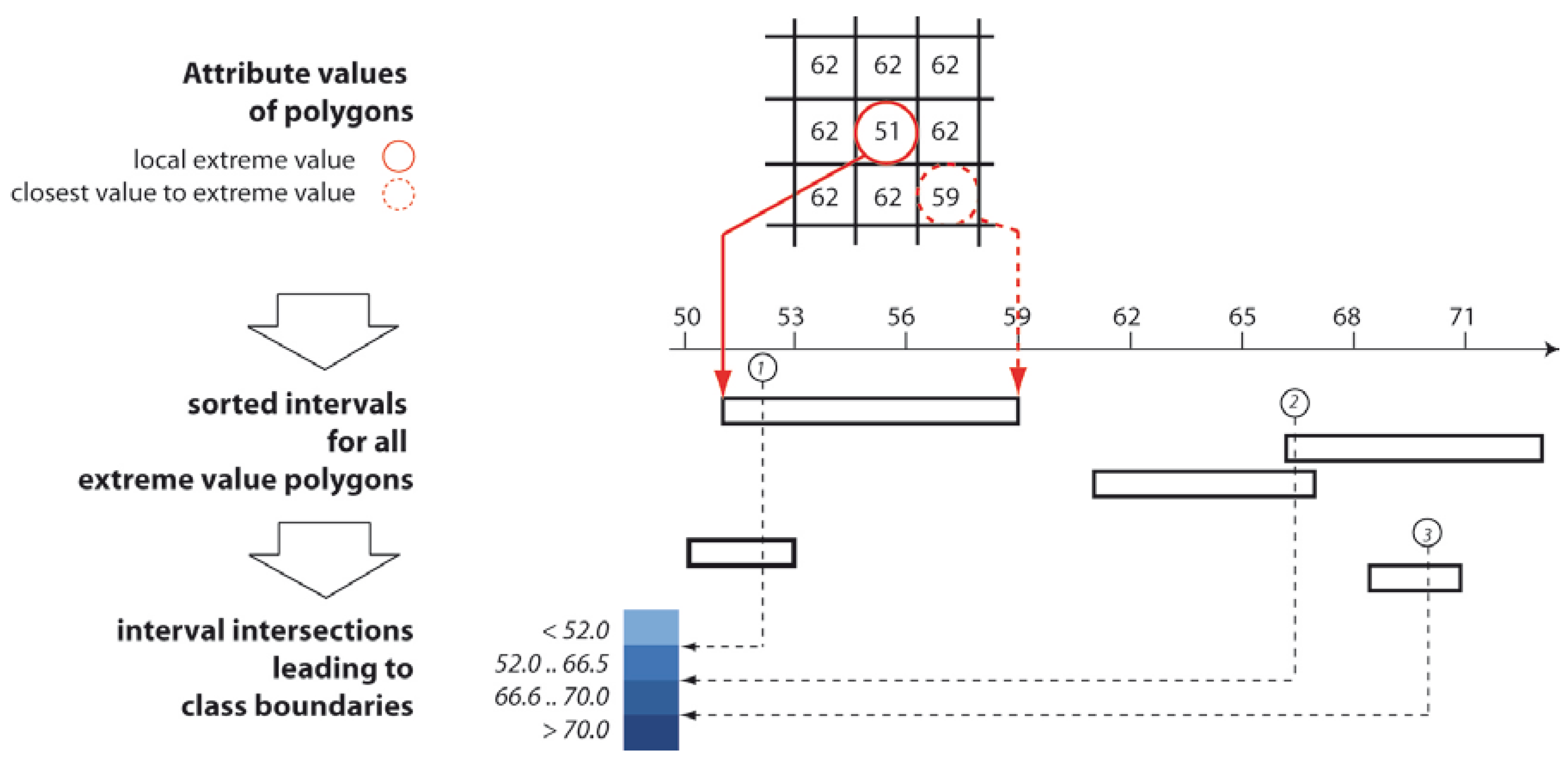
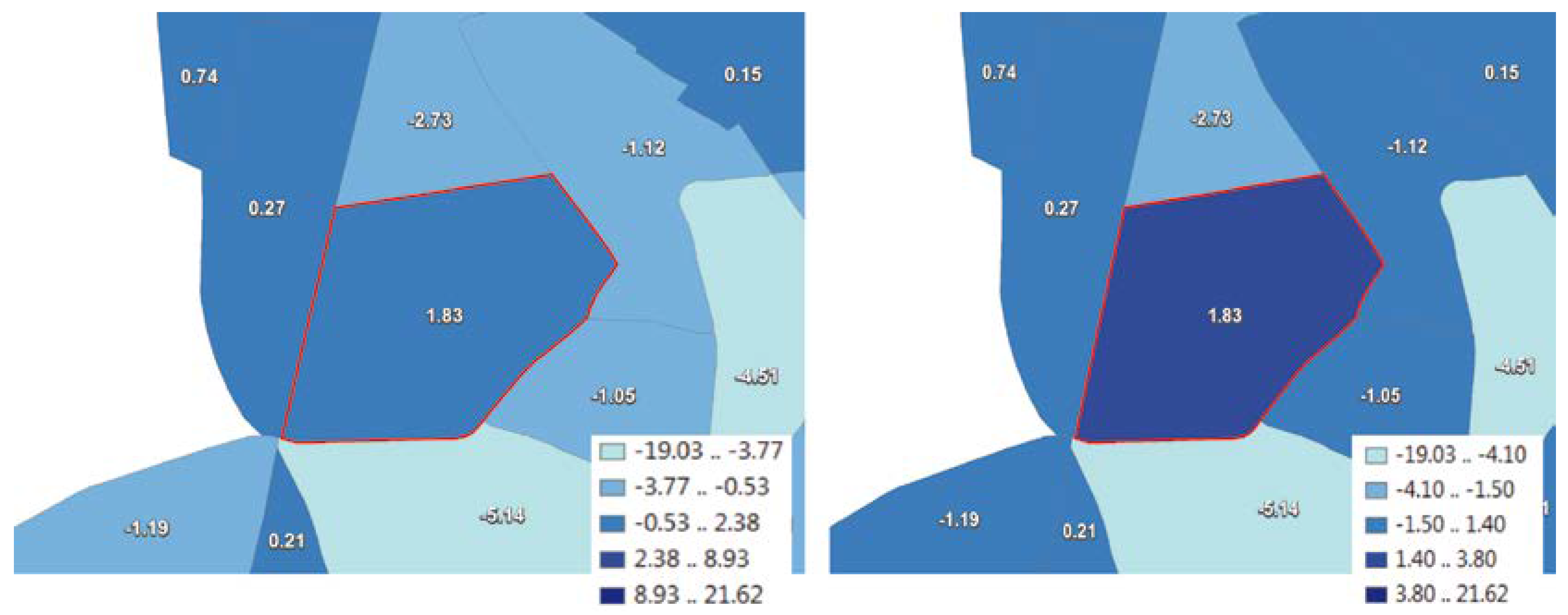
- It is stressed that not only the pure graphical representation, but also the corresponding pre-processing of the data is of great importance. This aspect is demonstrated by the step of data classification prior visualization by emphasizing the need for and development of an algorithmic solution to the problem of preserving spatial properties such as local extreme values or hot spots, which could be lost in maps with conventional data classification methods.
2. Previous Work
3. Classification of Change Analysis Tasks
- Existential change: “What kind of existential change of hot spots can be observed in Canadian provinces between 1950 and 2000?”
- Unspecified class changes: “What changes in hot spot classes (such as very significant, significant, etc.) can be observed in Canadian provinces between 1950 and 2000?
- Specified class change: “In Canadian provinces between 1950 and 2000, is there any change between very significant hot spots (Getis Ord Index z-score above 2.0) and very significant cold spots (Getis Ord Index z-score below −2.0)?”
- Change in relative value: “What is the change in Getis Ord Index z-core for describing hot spots in Canadian provinces between 1950 and 2000?”
- Existential change: “What kind of existential changes in lakes can be observed in Canada in 1950, 1960, 1970 and 1980?”
- Change in absolute values: What is the average population change in Canadian provinces between 1950 and 2000 in 10-year-increments?
4. Visualizing Outputs of Change Analysis
4.1. Guiding Principles
- A rather fundamental aspect relates to the question of whether spatial context (e.g., spatial distribution of changes in the scene) is relevant for the specific application. This leads either to the need for cartographic visualization (either as a single map or as linked views), or to the explicit abandonment of a map-like representation.
- The visualization should be tailored to the tasks or questions that relate to the specific application. This requires a predetermined classification of tasks that often occur in the context of change analysis. This task-oriented approach is becoming increasingly apparent as the complexity of applications increases and workflows should be still effective and efficient.
- In terms of efficiency, explicit visualization of changes should be made where possible. For example, instead of displaying two maps of different points in time side-by-side and asking the users to detect changes themselves, changes should be explicitly displayed in a difference map in order to free human resources for interpretation tasks.
- More technically, the visualization should minimize eye-movements. During these movements (called saccades), cognitive reception of information is not possible and, even worse, a typical loss of exact locations can occur as one moves from one map to another.
- One should also consider an appropriate degree of interaction functionalities—again, to allow efficient use.
- In this context, the tools should also enable users to save and annotate on findings for further interpretation and comparison [19] (p. 38).
4.2. Recommendations for Representing Bi-Temporal Changes
4.3. Recommendations for Representing Multi-Temporal Changes
5. Data Processing Prior Visualization
5.1. Problem Statement
- a proper choice of time intervals (e.g., to avoid smoothing effects due to long time lags or a large redundancy due to short time lags),
- a meaningful aggregation of spatial units,
- the definition of thresholds (e.g., to separate an actual change from random behavior), or simply,
- an appropriate cartographical generalization.
5.2. Task-Oriented Data Classification Methods
6. Conclusions
6.1. Summary
6.2. Future Directions
- Big data is characterized by a complex and less structured appearance. As an example, earlier in this paper, the benefits of difference maps also in the case of multi-temporal scenes that lead to (n − 1)! maps were pointed out. This increases the need for a compact and generalized presentation. In this context, the role of maps and Cartography needs to be emphasized again as maps are well-accepted means of reducing and generalizing data to a usable minimum. On the other hand, methods for visualization, for interacting with them as well as for pre-processing (e.g., data classification or generalization) are not sufficiently integrated in big data platforms yet. This is also due to the fact that many GIS methods are not able to deal with extremely large amounts of data [3,19].
- The core goal of inductive big data analytics is to detect and interpret patterns, correlations and other information. For this purpose, an extended task-oriented approach is certainly helpful, especially at early stages in dealing with big data for getting an overview. However, again, existing methods for overview purposes are not suited for big data cases yet [19].
- With the increasing volume and variety of data, the consideration of inherent uncertainties (i.e., veracity) becomes more and more important [40]. This is particularly important in change analysis where a distinction must always be made between actual changes and differences due to uncertain input information and modeling operations. In earlier studies, we have already made attempts in this direction by reviewing the various methods for uncertainty visualization [41]; however, more application scenarios are needed along with usability testing.
Funding
Conflicts of Interest
References
- Andrienko, G.; Andrienko, N.; Keim, D.; MacEachren, A.M.; Wrobel, S. Challenging Problems of Geospatial Visual Analytics. J. Vis. Lang. Comput. 2011, 22, 251–256. [Google Scholar] [CrossRef]
- Zhang, L.; Stoffel, A.; Behrisch, M.; Mittelstadt, S.; Schreck, T.; Pompl, R. Visual analytics for the big data era—A comparative review of state-of-the-art commercial systems. In Proceedings of the 2012 IEEE Conference on Visual Analytics Science and Technology (VAST), Seattle, WA, USA, 14–19 October 2012; pp. 173–182. [Google Scholar]
- Li, S.; Dragicevic, S.; Castro, F.A.; Sester, M.; Winter, S.; Coltekin, A.; Cheng, T. Geospatial big data handling theory and methods: A review and research challenges. ISPRS J. Photogramm. Remote Sens. 2016, 115, 119–133. [Google Scholar] [CrossRef]
- Çöltekin, A.; Bleisch, S.; Andrienko, G.; Dykes, J. Persistent challenges in geovisualization—A community perspective. Int. J. Cartogr. 2017, 3, 115–139. [Google Scholar] [CrossRef]
- Keim, D.; Kohlhammer, J.; Ellis, G.; Mansmann, F. Mastering the Information Age—Solving Problems with Visual Analytics; Eurographics Association: Goslar, Germany, 2011; ISBN 978-3-905673-77-7. [Google Scholar]
- Schiewe, J. Geovisualization and geovisual analytics: The interdisciplinary perspective on cartography. Kartogr. Nachr. 2013, 122–126. [Google Scholar]
- Tiede, D. A new geospatial overlay method for the analysis and visualization of spatial change patterns using object-oriented data modeling concepts. Cartogr. Geogr. Inf. Sci. 2014, 41, 227–234. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Fu, T.; Blaschke, T.; Li, M.; Tiede, D.; Zhou, Z.; Ma, X.; Chen, D. Evaluation of feature selection methods for object-based land cover mapping of unmanned aerial vehicle imagery using random forest and support vector machine classifiers. ISPRS Int. J. Geo Inf. 2017, 6, 51. [Google Scholar] [CrossRef]
- Krüger, T.; Meinel, G.; Schumacher, U. Land-use monitoring by topographic data analysis. Cartogr. Geogr. Inf. Sci. 2013, 40, 220–228. [Google Scholar] [CrossRef]
- MacEachren, A.M.; Kraak, M.-J. Research challenges in geovisualization. Cartogr. Geogr. Inf. Sci. 2001, 28, 3–12. [Google Scholar] [CrossRef]
- Peuquet, D.J. It’s about time: A conceptual framework for the representation of temporal dynamics in geographic information systems. Ann. Assoc. Am. Geogr. 1994, 84, 441–461. [Google Scholar] [CrossRef]
- Andrienko, N.; Andrienko, G. Exploratory Analysis of Spatial and Temporal Data: A Systematic Approach; Springer: Heidelberg, Germany, 2006; ISBN 978-3-540-31190-4. [Google Scholar]
- Andrienko, N.; Andrienko, G.; Gatalsky, P. Impact of data and task characteristics on design of spatio-temporal data visualization tools. In Exploring Geovisualization; Dykes, J., MacEachren, A.M., Kraak, M.-J., Eds.; Elsevier: New York, NY, USA, 2005; pp. 201–222. ISBN 9780080445311. [Google Scholar]
- Von Landesberger, T.; Bremm, S.; Andrienko, N.; Andrienko, G.; Tekusova, M. Visual analytics methods for categoric spatio-temporal data. In Proceedings of the IEEE Conference on Visual Analytics Science and Technology (VAST), Seattle, WA, USA, 14–19 October 2012; pp. 183–192. [Google Scholar]
- Zurita-Milla, R.; Blok, C.; Retsios, V. Geovisual analytics of satellite image time series. In Proceedings of the 2012 International Congress on Environmental Modelling and Software, Leipzig, Germany, 1–5 July 2011; pp. 1431–1438. [Google Scholar]
- Green, K. Change matters. Photogramm. Eng. Remote Sens. 2011, 77, 305–309. [Google Scholar]
- Bogucka, E.P.; Jahnke, M. Feasibility of the space-time cube in temporal cultural landscape visualization. ISPRS Int. J. Geo Inf. 2017, 7, 209. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). 1995. Available online: http://www.cipr.rpi.edu/research/publications/Woods/MPEGcontrib/S15.doc (accessed on 12 May 2018).
- Robinson, A.C.; Demsar, U.; Moore, A.B.; Buckley, A.; Jiang, B.; Field, K.; Kraak, M.-J.; Camboin, S.P.; Sluter, C.R. Geospatial big data and cartography: Research challenges and opportunities for making maps that matter. Int. J. Cartogr. 2017, 3, 32–60. [Google Scholar] [CrossRef]
- Slocum, T.A.; McMaster, R.B.; Kessler, F.C.; Howard, H.H. Thematic Cartography and Geovisualization; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Slocum, T.A.; Blok, C.; Jiang, B.; Koussoulakou, A.; Montello, D.; Fuhrmann, S.; Hedley, N. Cognitive and usability issues in geovisualization. Cartogr. Geogr. Inf. Sci. 2001, 28, 61–75. [Google Scholar] [CrossRef]
- MacEachren, A.M.; Boscoe, F.P.; Haug, D.; Pickle, L.W. Geographic visualization: Designing manipulable maps for exploring temporally varying georeferenced statistics. In Proceedings of the IEEE Symposium on Information Visualization, Research Triangle, CA, USA, 19–20 October 1998; pp. 87–94. [Google Scholar]
- Jenny, B.; Stephen, D.M.; Muehlenhaus, I.; Marston, B.E.; Sharma, R.; Zhang, E.; Jenny, H. Design principles for origin-destination flow maps. Cartogr. Geogr. Inf. Sci. 2016, 62–75. [Google Scholar] [CrossRef]
- Opach, T. Semantic and pragmatic aspects of transmitting information by animated maps. In Proceedings of the ICA International Cartographic Conference, A Coruna, Spain, 9–16 July 2005. [Google Scholar]
- Harrower, M. Cognitive limits of animated maps. Cartographica 2007, 42, 349–357. [Google Scholar] [CrossRef]
- Goldsberry, K.; Battersby, S. Issues of change detection in animated choropleth maps. Cartographica 2009, 44, 201–215. [Google Scholar] [CrossRef]
- Fish, C.; Goldsberry, K.P.; Battersby, S. Change blindness in animated choropleth maps: An empirical study. Cartogr. Geogr. Inf. Sci. 2011, 38, 350–362. [Google Scholar] [CrossRef]
- Armstrong, M.P.; Xiao, N.; Bennett, D.A. Using genetic algorithms to create multicriteria class intervals for choropleth maps. Ann. Assoc. Am. Geogr. 2003, 91, 595–623. [Google Scholar] [CrossRef]
- Smith, R.M. Comparing traditional methods for selecting class intervals on choropleth maps. Prof. Geogr. 1986, 38, 62–67. [Google Scholar] [CrossRef]
- Monmonier, M. Contiguity-biased class-interval selection and location allocation models. Geogr. Rev. 1972, 62, 203–228. [Google Scholar] [CrossRef]
- Jenks, G.; Caspall, F. Error on choroplethic maps: Definition, measurement, reduction. Ann. Assoc. Am. Geogr. 1971, 61, 217–244. [Google Scholar] [CrossRef]
- Andrienko, G.; Andrienko, N.; Savinov, A. Choropleth maps: Classification revisited. In Proceedings of the ICA International Cartographic Conference, Rome, Italy, 2–7 September 2001. [Google Scholar]
- Cromley, R.G. A comparison of optimal classification strategies for choroplethic displays of spatially aggregated data. Int. J. Geogr. Inf. Syst. 1996, 10, 405–424. [Google Scholar] [CrossRef]
- MacEachren, A.M. Some Truth with Maps: A Primer on Symbolization and Design. Available online: http://www.cartographicperspectives.org/index.php/journal/article/view/cp20-patton/936 (accessed on 12 May 2018).
- Schiewe, J. Data classification for highlighting polygons with local extreme values in choropleth maps. In Advances in Cartography and GIScience; Peterson, M.P., Ed.; Lecture Notes in Geoinformation and Cartography; Springer: Heidelberg, Germany, 2017; pp. 449–459. [Google Scholar]
- Schiewe, J. Preserving attribute value differences of neighboring regions in classified choropleth maps. Int. J. Cartogr. 2016, 2, 6–19. [Google Scholar] [CrossRef]
- Beucher, S.; Meyer, F. The morphological approach to segmentation: The watershed transformation. In Mathematical Morphology in Image Processing; Dougherty, E., Ed.; Marcel Dekker Inc.: New York, NY, USA, 1993; pp. 433–481. ISBN 08247-87242. [Google Scholar]
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Kinkeldey, C.; Schiewe, J.; Gerstmann, H.; Götze, C.; Kit, O.; Lüdecke, M.; Taubenböck, H.; Wurm, M. Evaluating the use of uncertainty visualization for exploratory analysis of land cover change: A qualitative expert user study. Comput. Geosci. 2015, 84, 46–53. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, A.; Zhou, X.; Zhang, M. Challenges and prospects of uncertainties in spatial big data analytics. Ann. Am. Assoc. Geogr. 2018. [Google Scholar] [CrossRef]
- Kinkeldey, C.; MacEachren, A.M.; Schiewe, J. How to assess visual communication of uncertainty? A systematic review of geospatial uncertainty visualisation user studies. Cartogr. J. 2015, 51, 372–386. [Google Scholar] [CrossRef]
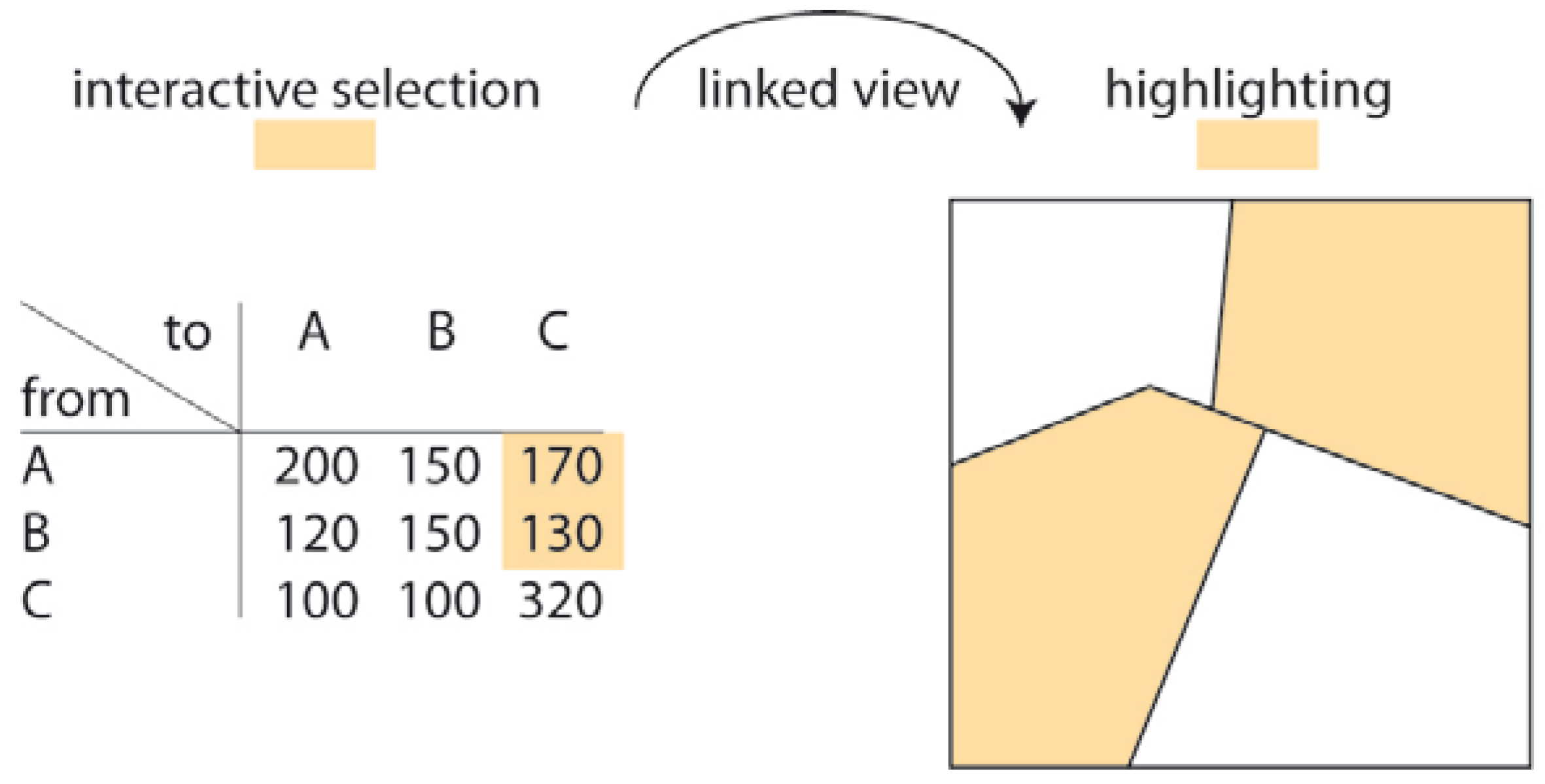
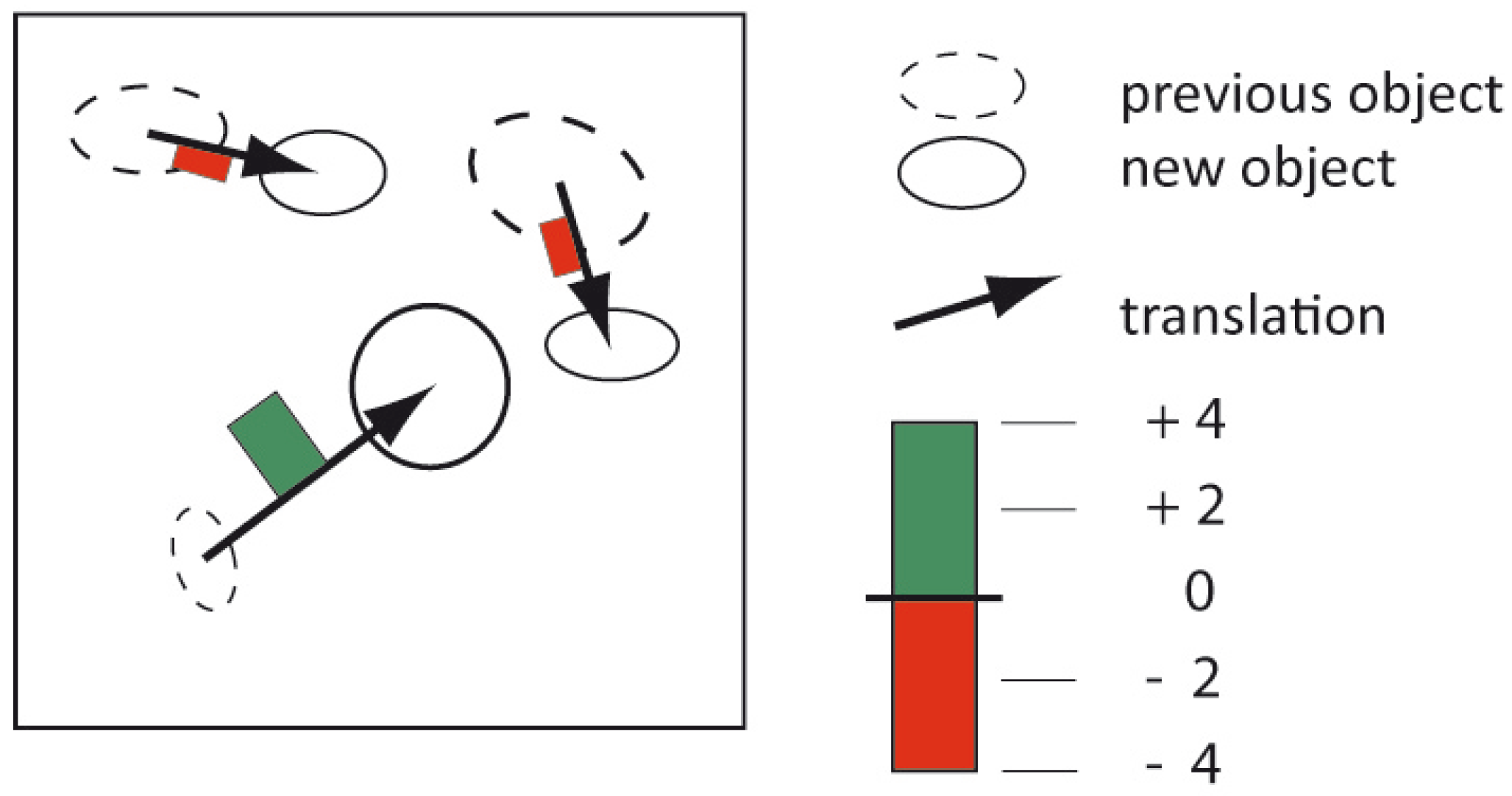
| Change Feature | Feature Value | Example Change Questions: When ⊕ Where ➲ What |
|---|---|---|
| 1a Existential change | gain/loss/none | What kind of existential change of forest areas can be observed in Canadian provinces between 1950 and 2000? |
| 1b Unspecified class change | <from/to class name (s)> | What class changes can be observed in Canadian provinces between 1950 and 2000? |
| 1c Specified class change (from/to) | yes/no | Is there any class change between forest and urban in Canadian provinces between 1950 and 2000? |
| 1d Change of absolute value | <difference> OR: increase/decrease/constant OR: <max/min difference> | What is the population change in Canadian provinces between 1950 and 2000? What kind of population change can be observed in Canadian provinces between 1950 and 2000? What maximum population change in Canadian provinces can be observed between 1950 and 2000? |
| 1e Change of relative value | <difference > OR: increase/decrease/constant OR: <max/min difference> | What is the change of population density in Canadian provinces between 1950 and 2000? What kind of change of population density can be observed in Canadian provinces between 1950 and 2000? What maximum change of population density can be observed in Canadian provinces between 1950 and 2000? |
| Change Feature | Feature Value | Example Change Questions: When ⊕ What ➲ Where |
|---|---|---|
| 2a Region | <region name> OR <co-ordinate list, bounding box> | In which Canadian provinces did the population change between 1950 and 2000? |
| 2b Location | <location name> OR <co-ordinate> | In which Canadian cities did the population change between 1950 and 2000? |
| 2c Translation | <distance and direction of translation> | Which movements of grassland can be observed between 1950 and 2000 in Canadian provinces? |
| Change Feature | Feature Value | Example Change Questions: Where ⊕ What ➲ When |
|---|---|---|
| 3a Date | <date> | In which year between 1940 and 2000 was the maximum population number reached in Canadian provinces? |
| 3b Duration | <duration> | How long did it take to double the population in Canadian provinces since 1900? |
| 3c Time-interval (bi-temporal) | <time interval> | In which decade between 1900 and 2000 was the maximum increase in population in Canadian provinces? |
| 3d Time series (multi-temporal) | <time series> | In which successive years can we observe an increase and then a decrease in population numbers in Canadian provinces within the entire time span between 1900 and 2000? |
| 3e Change in duration | <duration 1, duration 2> | What is the time period difference to increase the population about 10% in the neighboring countries compared to France? |
| Change Feature | Example Change Question | Visualization | |
|---|---|---|---|
| Map Type | Example | ||
| 4a Existential change | What kind of existential change of forest areas can be observed in Canadian provinces between 1950 and 2000? | Mosaic map |  |
| 4b Unspecified class change | What class changes can be observed in Canadian provinces between 1950 and 2000? | Symbol map/micro diagrams | 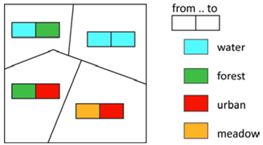 |
| 4c Specified class change (from/to) | Is there any class change between forest and urban in Canadian provinces between 1950 and 2000? | (Binary) mosaic map (possibly linked with change matrix) | 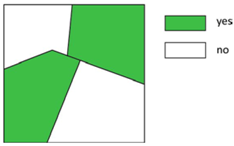 |
| 4d Change of absolute value | (1) What is the population change in Canadian provinces between 1950 and 2000? | (Bi-polar) Proportional Symbol map |  |
| (2) What kind of population change can be observed in Canadian provinces between 1950 and 2000? | Mosaic map | rf. to 4a | |
| 4e Change of relative value | (1) What is the change of population density in Canadian provinces between 1950 and 2000? | (Bi-polar) Choropleth map |  |
| (2) What kind of change of population density can be observed in Canadian provinces between 1950 and 2000? | Mosaic map | rf. to 4a | |
| Change Feature | Example Change Question | Visualization | |
|---|---|---|---|
| Map Type | Example | ||
| 5a Region | In which Canadian provinces did the population change between 1950 and 2000? | (Binary) mosaic map | 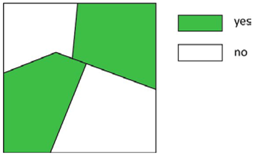 |
| 5b Location | In which Canadian cities did the population change between 1950 and 2000? | (Binary) Point map |  |
| 5c Trans-lation | Which relocations of grassland can be observed between 1950 and 2000 in Canadian provinces? | Origin-desti-nation flow maps | 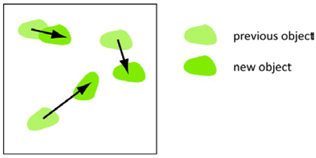 |
| Change Feature | Example Change Question | Visualization | |
|---|---|---|---|
| Map Type | Example | ||
| 6a Date | In which year between 1940 and 2000 was the maximum population number reached in Canadian provinces? | Choropleth map |  |
| 6b Duration | How long did it take to double the population in Canadian provinces since 1900? | Proportional Symbol map |  |
| 6c Time-interval (bi-temporal) | In which decade between 1900 and 2000 was the maximum increase in population in Canadian provinces? | Symbol map (micro diagrams) | 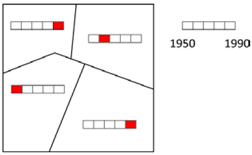 |
| 6d Time series (multi-temporal) | In which successive years can we observe an increase and then a decrease in population numbers in Canadian provinces in the entire time span between 1900 and 2000? | Symbol map (micro diagrams) | 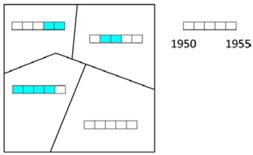 |
| 6e Change in duration | What is the time period difference to increase the population about 10% in the neighboring countries compared to France? | (Bipolar) Choropleth map | 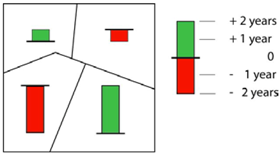 |
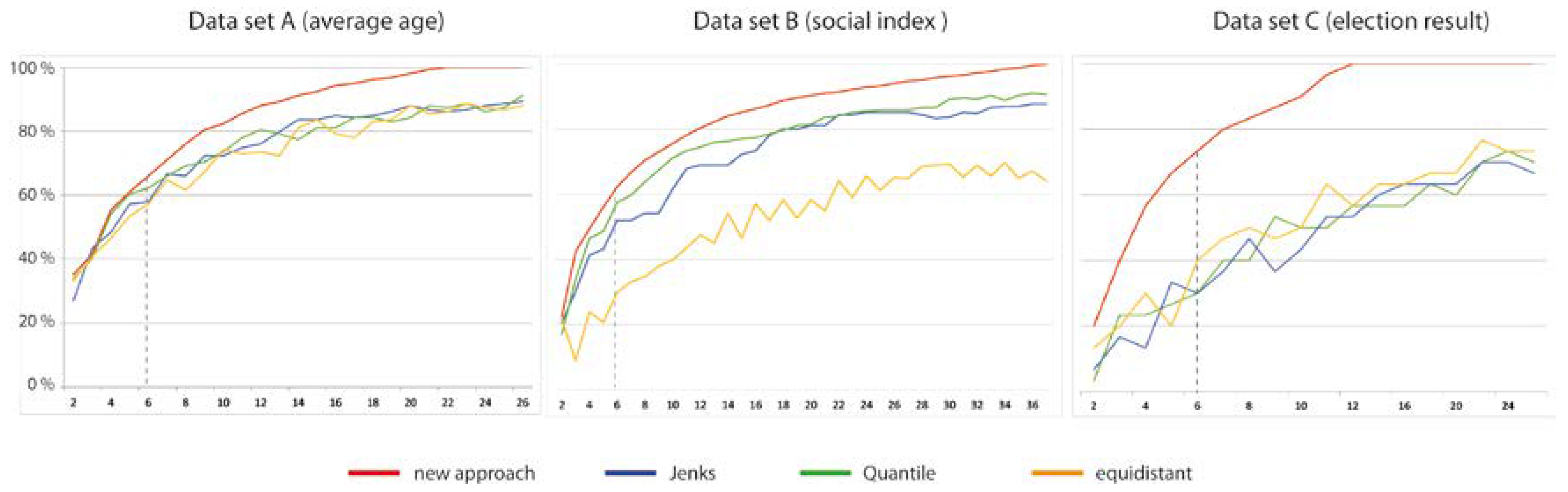
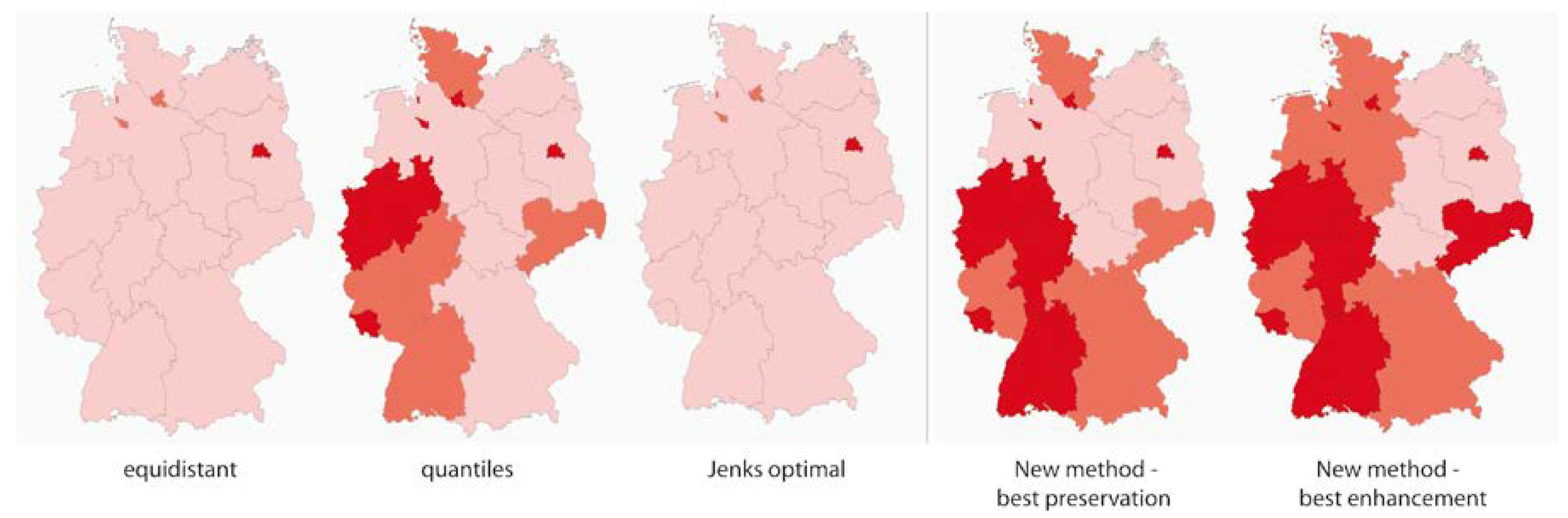
| Data Set | Input Data Set | Proposed Method: No. of Classes to Preserve All Extreme Values | |
|---|---|---|---|
| No. of Polygons | No. of Local Extreme Values | ||
| A: Average age | 439 | 159 (36%) | 22 |
| B: Social index | 847 | 271 (32%) | 37 |
| C: Election result | 103 | 30 (29%) | 12 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schiewe, J. Task-Oriented Visualization Approaches for Landscape and Urban Change Analysis. ISPRS Int. J. Geo-Inf. 2018, 7, 288. https://doi.org/10.3390/ijgi7080288
Schiewe J. Task-Oriented Visualization Approaches for Landscape and Urban Change Analysis. ISPRS International Journal of Geo-Information. 2018; 7(8):288. https://doi.org/10.3390/ijgi7080288
Chicago/Turabian StyleSchiewe, Jochen. 2018. "Task-Oriented Visualization Approaches for Landscape and Urban Change Analysis" ISPRS International Journal of Geo-Information 7, no. 8: 288. https://doi.org/10.3390/ijgi7080288
APA StyleSchiewe, J. (2018). Task-Oriented Visualization Approaches for Landscape and Urban Change Analysis. ISPRS International Journal of Geo-Information, 7(8), 288. https://doi.org/10.3390/ijgi7080288





