Temporal Variations and Associated Remotely Sensed Environmental Variables of Dengue Fever in Chitwan District, Nepal
Abstract
:1. Introduction
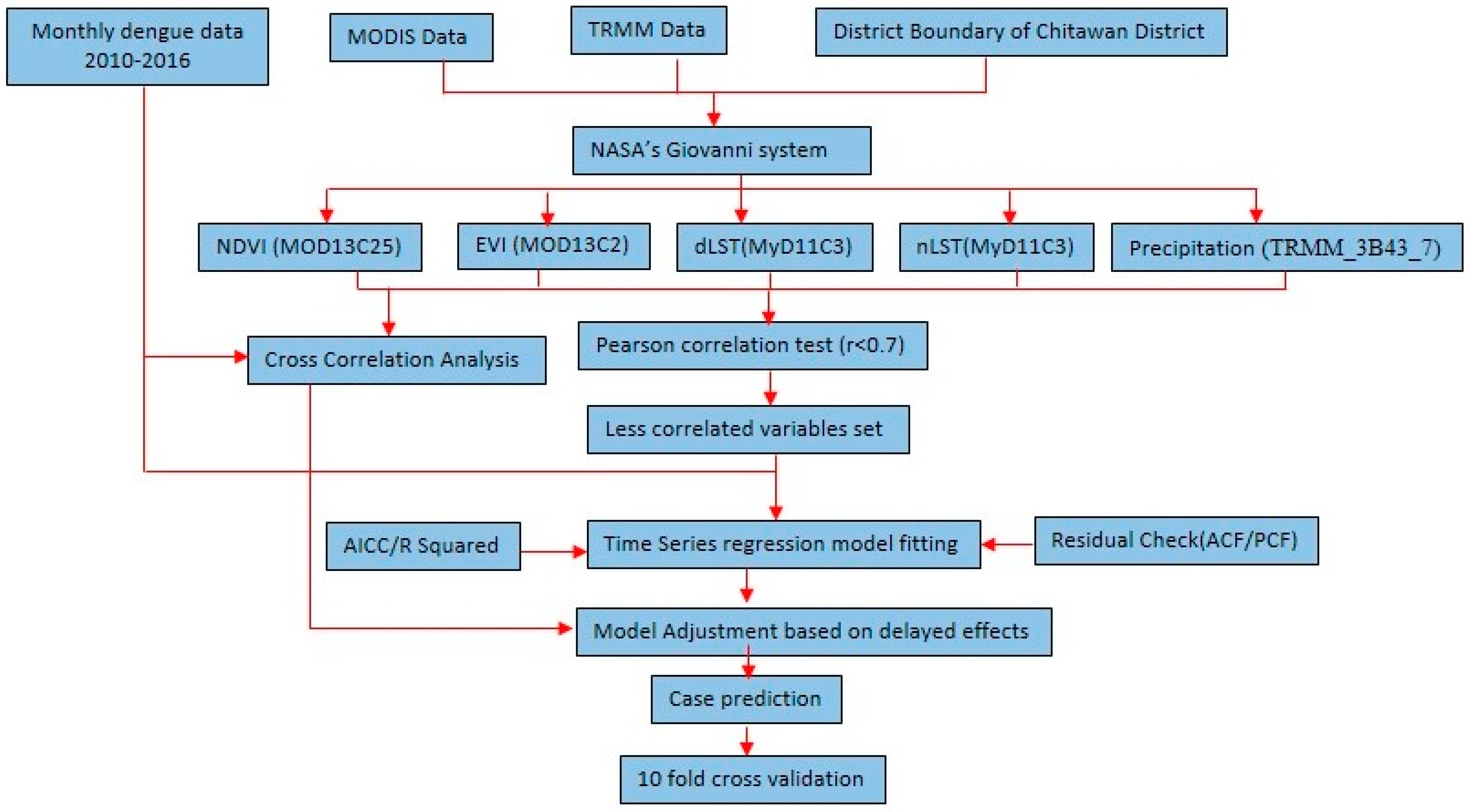
2. Materials and Methods
2.1. Study Area
2.2. Dengue Data
2.3. Remote Sensing Data
2.4. Statistical Analysis
3. Results
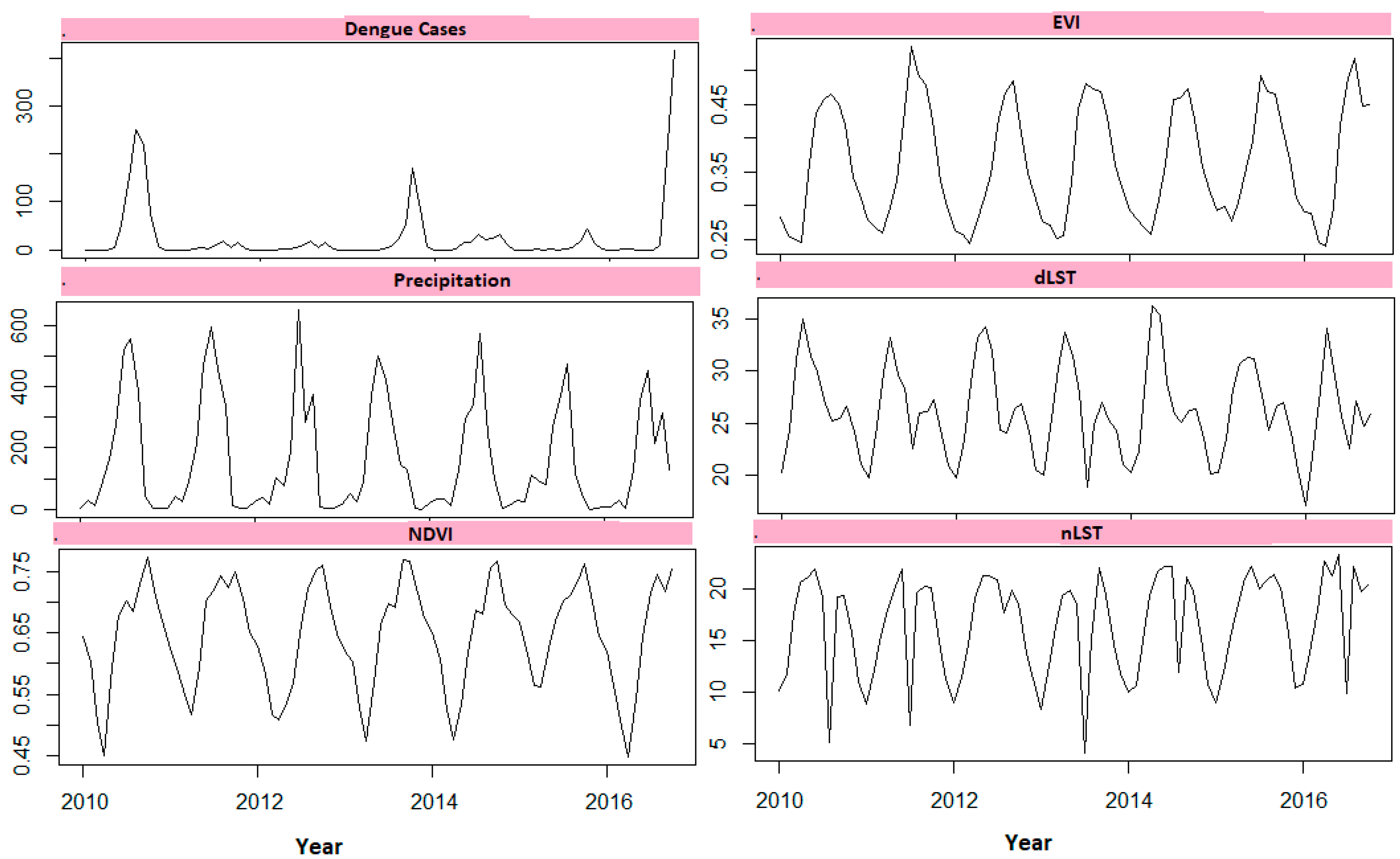
3.1. Descriptive Statistics
3.2. Cross Correlation Analysis and Lagged Association
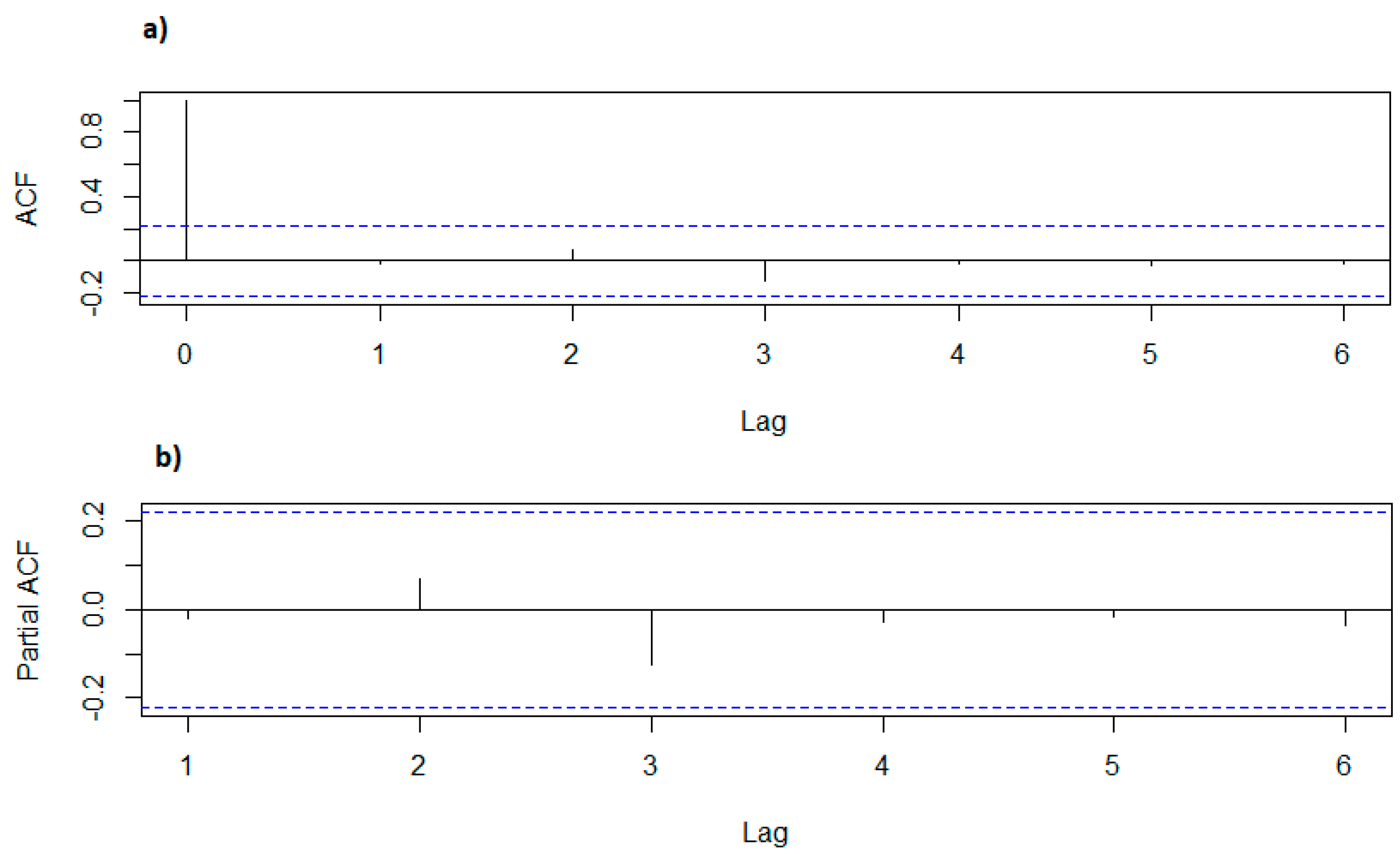
3.3. Model Fitting, Model Selection and Residual Diagnosis
3.4. Prediction
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wilder-Smith, A.; Murray, N.A.E.; Quam, M.B. Epidemiology of dengue: Past, present and future prospects. Clin. Epidemiol. 2013, 5, 299–309. [Google Scholar] [CrossRef] [PubMed]
- Bhatt, S.; Gething, P.W.; Brady, O.J.; Messina, J.P.; Farlow, A.W.; Moyes, C.L.; Drake, J.M.; Brownstein, J.S.; Hoen, A.G.; Sankoh, O.; et al. The global distribution and burden of dengue. Nature 2013, 496, 504–507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Messina, J.P.; Brady, O.J.; Pigott, D.M.; Golding, N.; Kraemer, M.U.G.; Scott, T.W.; Wint, G.R.W.; Smith, D.L.; Hay, S.I. The many projected futures of dengue. Nat. Rev. Microbiol. 2015, 13, 230–239. [Google Scholar] [CrossRef] [PubMed]
- Naish, S.; Dale, P.; Mackenzie, J.S.; McBride, J.; Mengersen, K.; Tong, S. Climate change and dengue: A critical and systematic review of quantitative modelling approaches. BMC Infect. Dis. 2014, 14, 167. [Google Scholar] [CrossRef] [PubMed]
- Regis, L.N.; Acioli, R.V.; Silveira, J.C.; de Melo-Santos, M.A.V.; da Cunha, M.C.S.; Souza, F.; Batista, C.A.V.; Barbosa, R.M.R.; de Oliveira, C.M.F.; Ayres, C.F.J.; et al. Characterization of the spatial and temporal dynamics of the dengue vector population established in urban areas of Fernando de Noronha, a Brazilian oceanic island. Acta Trop. 2014, 137, 80–87. [Google Scholar] [CrossRef] [PubMed]
- Morin, C.W.; Comrie, A.C.; Ernst, K. Climate and Dengue Transmission: Evidence and Implications. Environ. Health Perspect. 2013, 121, 1264–1272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Méndez-Lázaro, P.; Muller-Karger, F.; Otis, D.; McCarthy, M.; Peña-Orellana, M. Assessing Climate Variability Effects on Dengue Incidence in San Juan, Puerto Rico. Int. J. Environ. Res. Public. Health 2014, 11, 9409–9428. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gubler, D.J. Epidemic dengue/dengue hemorrhagic fever as a public health, social and economic problem in the 21st century. Trends Microbiol. 2002, 10, 100–103. [Google Scholar] [CrossRef]
- Eastin, M.D.; Delmelle, E.; Casas, I.; Wexler, J.; Self, C. Intra- and Interseasonal Autoregressive Prediction of Dengue Outbreaks Using Local Weather and Regional Climate for a Tropical Environment in Colombia. Am. J. Trop. Med. Hyg. 2014, 91, 598–610. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gharbi, M.; Quenel, P.; Gustave, J.; Cassadou, S.; Ruche, G.L.; Girdary, L.; Marrama, L. Time series analysis of dengue incidence in Guadeloupe, French West Indies: Forecasting models using climate variables as predictors. BMC Infect. Dis. 2011, 11, 166. [Google Scholar] [CrossRef] [PubMed]
- Banu, S.; Guo, Y.; Hu, W.; Dale, P.; Mackenzie, J.S.; Mengersen, K.; Tong, S. Impacts of El Niño Southern Oscillation and Indian Ocean Dipole on dengue incidence in Bangladesh. Sci. Rep. 2015, 5, 16105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chuang, T.-W.; Chaves, L.F.; Chen, P.-J. Effects of local and regional climatic fluctuations on dengue outbreaks in southern Taiwan. PLoS ONE 2017, 12, e0178698. [Google Scholar] [CrossRef] [PubMed]
- Midekisa, A.; Senay, G.; Henebry, G.M.; Semuniguse, P.; Wimberly, M.C. Remote sensing-based time series models for malaria early warning in the highlands of Ethiopia. Malar. J. 2012, 11, 165. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Linthicum, K.J.; Anyamba, A.; Tucker, C.J.; Kelley, P.W.; Myers, M.F.; Peters, C.J. Climate and satellite indicators to forecast Rift Valley fever epidemics in Kenya. Science 1999, 285, 397–400. [Google Scholar] [CrossRef] [PubMed]
- Cheong, Y.; Burkart, K.; Leitão, P.; Lakes, T. Assessing Weather Effects on Dengue Disease in Malaysia. Int. J. Environ. Res. Public. Health 2013, 10, 6319–6334. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chien, L.-C.; Yu, H.-L. Impact of meteorological factors on the spatiotemporal patterns of dengue fever incidence. Environ. Int. 2014, 73, 46–56. [Google Scholar] [CrossRef] [PubMed]
- Fuller, D.O.; Troyo, A.; Beier, J.C. El Niño Southern Oscillation and vegetation dynamics as predictors of dengue fever cases in Costa Rica. Environ. Res. Lett. 2009, 4, 014011. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beck, L. Remote Sensing and Human Health: New Sensors and New Opportunities. Emerg. Infect. Dis. 2000, 6, 217–227. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Estallo, E.L.; Ludueña-Almeida, F.F.; Visintin, A.M.; Scavuzzo, C.M.; Lamfri, M.A.; Introini, M.V.; Zaidenberg, M.; Almirón, W.R. Effectiveness of normalized difference water index in modelling Aedes aegypti house index. Int. J. Remote Sens. 2012, 33, 4254–4265. [Google Scholar] [CrossRef]
- Sewe, M.O.; Ahlm, C.; Rocklöv, J. Remotely Sensed Environmental Conditions and Malaria Mortality in Three Malaria Endemic Regions in Western Kenya. PLoS ONE 2016, 11, e0154204. [Google Scholar] [CrossRef] [PubMed]
- Nygren, D.; Stoyanov, C.; Lewold, C.; Månsson, F.; Miller, J.; Kamanga, A.; Shiff, C.J. Remotely-sensed, nocturnal, dew point correlates with malaria transmission in Southern Province, Zambia: A time-series study. Malar. J. 2014, 13, 231. [Google Scholar] [CrossRef] [PubMed]
- Acharya, B.; Cao, C.; Xu, M.; Khanal, L.; Naeem, S.; Pandit, S. Present and Future of Dengue Fever in Nepal: Mapping Climatic Suitability by Ecological Niche Model. Int. J. Environ. Res. Public. Health 2018, 15, 187. [Google Scholar] [CrossRef] [PubMed]
- Department of Health Services. Government of Nepal Annual Health Report (2015/2016); Department of Health Services: Kathmandu, Nepal, 2017.
- Central Bureau of Statistics (CBS). National Population Census 2011 Household National Report; Central Bureau of Statistics (CBS): Kathmandu, Nepal, 2011.
- Pandey, B.D.; Rai, S.K.; Morita, K.; Kurane, I. First case of Dengue virus infection in Nepal. Nepal Med. Coll. J. NMCJ 2004, 6, 157–159. [Google Scholar] [PubMed]
- Midekisa, A.; Beyene, B.; Mihretie, A.; Bayabil, E.; Wimberly, M.C. Seasonal associations of climatic drivers and malaria in the highlands of Ethiopia. Parasit. Vectors 2015, 8, 339. [Google Scholar] [CrossRef] [PubMed]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The Tropical Rainfall Measuring Mission (TRMM) Sensor Package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar] [CrossRef]
- Acker, J.; Soebiyanto, R.; Kiang, R.; Kempler, S. Use of the NASA Giovanni Data System for Geospatial Public Health Research: Example of Weather-Influenza Connection. ISPRS Int. J. Geo-Inf. 2014, 3, 1372–1386. [Google Scholar] [CrossRef] [Green Version]
- Banu, S.; Hu, W.; Guo, Y.; Hurst, C.; Tong, S. Projecting the impact of climate change on dengue transmission in Dhaka, Bangladesh. Environ. Int. 2014, 63, 137–142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, C.; Yang, L.; Ou, C.-Q.; Li, L.; Zhuang, Y.; Yang, J.; Zhou, Y.-X.; Qian, J.; Chen, P.-Y.; Liu, Q.-Y. Malaria incidence from 2005–2013 and its associations with meteorological factors in Guangdong, China. Malar. J. 2015, 14, 116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Talagala, T. Distributed Lag Nonlinear Modelling Approach to Identify Relationship between Climatic Factors and Dengue Incidence in Colombo District, Sri Lanka. Epidemiol. Biostat. Public Health 2015, 12. [Google Scholar] [CrossRef]
- Burnham, K.P. Multimodel Inference: Understanding AIC and BIC in Model Selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013. [Google Scholar]
- Pandey, B.D.; Nabeshima, T.; Pandey, K.; Rajendra, S.P.; Shah, Y.; Adhikari, B.R.; Gupta, G.; Gautam, I.; Tun, M.M.N.; Uchida, R.; et al. First Isolation of Dengue Virus from the 2010 Epidemic in Nepal. Trop. Med. Health 2013, 41, 103–111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buczak, A.L.; Koshute, P.T.; Babin, S.M.; Feighner, B.H.; Lewis, S.H. A data-driven epidemiological prediction method for dengue outbreaks using local and remote sensing data. BMC Med. Inform. Decis. Mak. 2012, 12, 124. [Google Scholar] [CrossRef] [PubMed]
- Silva, F.D.; dos Santos, A.M.; da Graça Carvalhal Frazão Corrêa, C.; de Jesus Mendes Caldas, A. Temporal relationship between rainfall, temperature and occurrence of dengue cases in São Luís, Maranhão, Brazil. Ciênc. Saúde Coletiva 2016, 21, 641–646. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laureano-Rosario, A.E.; Garcia-Rejon, J.E.; Gomez-Carro, S.; Farfan-Ale, J.A.; Muller-Karger, F.E. Modelling dengue fever risk in the State of Yucatan, Mexico using regional-scale satellite-derived sea surface temperature. Acta Trop. 2017, 172, 50–57. [Google Scholar] [CrossRef] [PubMed]
- Qi, X.; Wang, Y.; Li, Y.; Meng, Y.; Chen, Q.; Ma, J.; Gao, G.F. The Effects of Socioeconomic and Environmental Factors on the Incidence of Dengue Fever in the Pearl River Delta, China, 2013. PLoS Negl. Trop. Dis. 2015, 9, e0004159. [Google Scholar] [CrossRef] [PubMed]
- Schuster, G.; Ebert, E.E.; Stevenson, M.A.; Corner, R.J.; Johansen, C.A. Application of satellite precipitation data to analyse and model arbovirus activity in the tropics. Int. J. Health Geogr. 2011, 10, 8. [Google Scholar] [CrossRef] [PubMed]
- Troyo, A.; Fuller, D.O.; Calderón-Arguedas, O.; Solano, M.E.; Beier, J.C. Urban structure and dengue incidence in Puntarenas, Costa Rica. Singap. J. Trop. Geogr. 2009, 30, 265–282. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roslan, N.S.; Latif, Z.A.; Dom, N.C. Dengue Cases Distribution Based on Land Surface Temperature and Elevation. In Proceedings of the 2016 7th IEEE Control and System Graduate Research Colloquium (ICSGRC), Shah Alam, Malaysia, 8 August 2016; pp. 87–91. [Google Scholar]
- Herbreteau, V.; Salem, G.; Souris, M.; Hugot, J.-P.; Gonzalez, J.-P. Thirty years of use and improvement of remote sensing, applied to epidemiology: From early promises to lasting frustration. Health Place 2007, 13, 400–403. [Google Scholar] [CrossRef] [PubMed]
- Rotela, C.; Fouque, F.; Lamfri, M.; Sabatier, P.; Introini, V.; Zaidenberg, M.; Scavuzzo, C. Space–time analysis of the dengue spreading dynamics in the 2004 Tartagal outbreak, Northern Argentina. Acta Trop. 2007, 103, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Arboleda, S.; Nicolas, J.-O.; Peterson, A.T. Mapping Environmental Dimensions of Dengue Fever Transmission Risk in the Aburrá Valley, Colombia. Int. J. Environ. Res. Public. Health 2009, 6, 3040–3055. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bøgh, C.; Lindsay, S.W.; Clarke, S.E.; Dean, A.; Jawara, M.; Pinder, M.; Thomas, C.J. High spatial resolution mapping of malaria transmission risk in the Gambia, west Africa, using LANDSAT TM satellite imagery. Am. J. Trop. Med. Hyg. 2007, 76, 875–881. [Google Scholar] [PubMed]
- Nakhapakorn, K.; Tripathi, N.K. An information value based analysis of physical and climatic factors affecting dengue fever and dengue haemorrhagic fever incidence. Int. J. Health Geogr. 2005, 4, 13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Estallo, E.L.; Benitez, E.M.; Lanfri, M.A.; Scavuzzo, C.M.; Almiron, W.R. MODIS Environmental Data to Assess Chikungunya, Dengue, and Zika Diseases Through Aedes (Stegomia) aegypti Oviposition Activity Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5461–5466. [Google Scholar] [CrossRef]
- Sharma, S.P. Dengue outbreak affects more than 7000 people in Nepal. BMJ 2010, 341, c5496. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.Z.; Roytman, L.; Kadik, A.; Rosy, D.A. Environmental data analysis and remote sensing for early detection of dengue and malaria. In Sensing Technologies for Global Health, Military Medicine, and Environmental Monitoring IV, Proceedings of the SPIE Sensing Technology and Applications, Baltimore, ML, USA, 5–9 MAY 2014; Southern, Š.O., Mentzer, M.A., Rodriguez-Chavez, I., Wotring, V.E., Eds.; SPIE: Baltimore, ML, USA, 2014; p. 91121C. [Google Scholar]
- Shi, Y.; Liu, X.; Kok, S.-Y.; Rajarethinam, J.; Liang, S.; Yap, G.; Chong, C.-S.; Lee, K.-S.; Tan, S.S.Y.; Chin, C.K.Y.; et al. Three-Month Real-Time Dengue Forecast Models: An Early Warning System for Outbreak Alerts and Policy Decision Support in Singapore. Environ. Health Perspect. 2015, 124, 1369. [Google Scholar] [CrossRef] [PubMed]
- Lowe, R.; Barcellos, C.; Coelho, C.A.S.; Bailey, T.C.; Coelho, G.E.; Graham, R.; Jupp, T.; Ramalho, W.M.; Carvalho, M.S.; Stephenson, D.B.; et al. Dengue outlook for the World Cup in Brazil: An early warning model framework driven by real-time seasonal climate forecasts. Lancet Infect. Dis. 2014, 14, 619–626. [Google Scholar] [CrossRef]
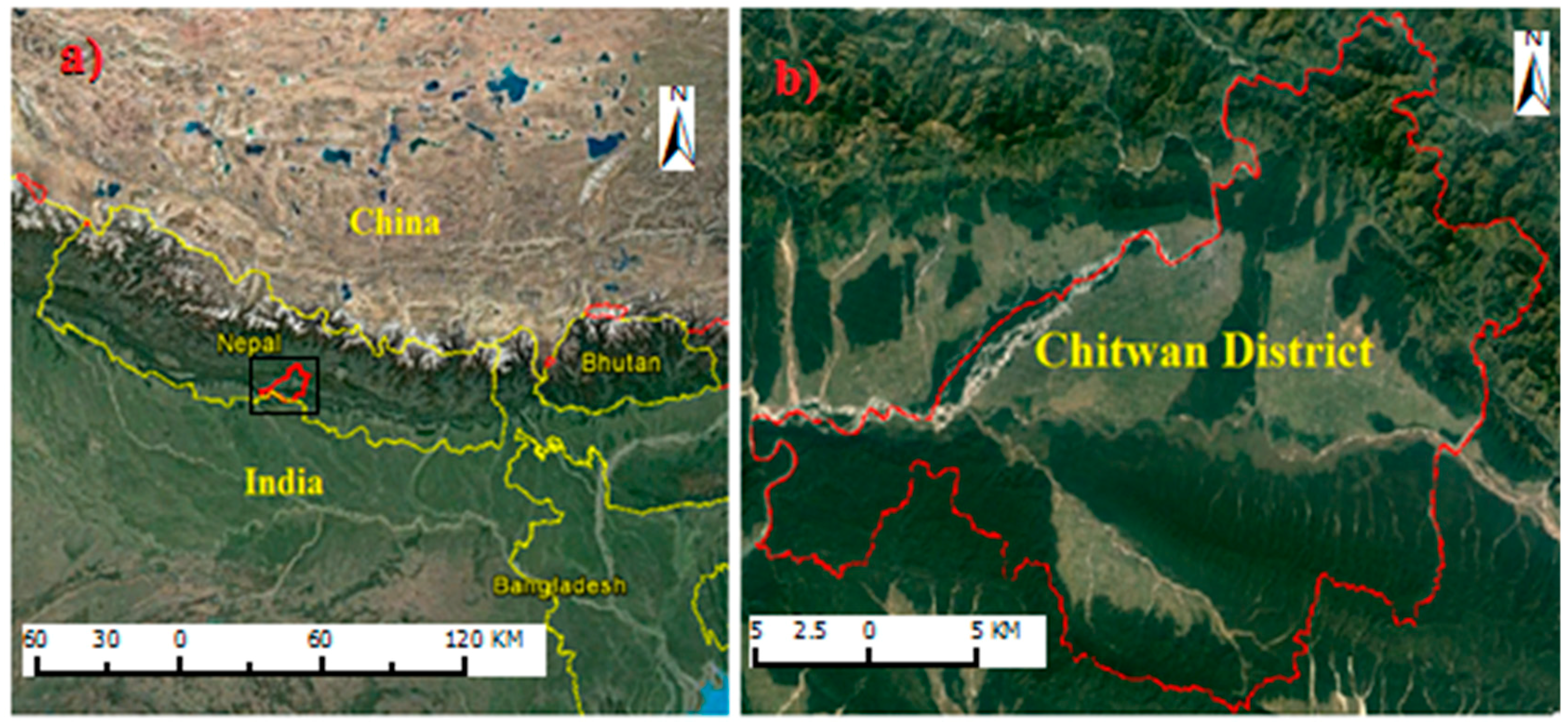

| Satellite | Sensor | Product | Indicator | Temporal Period | Total Month |
|---|---|---|---|---|---|
| Terra | MODIS | MOD13C25 | NDVI | January2010 to December 2016 | 82 |
| Terra | MODIS | MOD13C25 | EVI | January 2010 to December 2016 | 82 |
| Acqua | MODIS | MYD11C3 | nLST | January 2010 to December 2016 | 82 |
| Acqua | MODIS | MYD11C3 | dLST | January 2010 to December 2016 | 82 |
| TRMM | TRMM | TRMM_3B43_7 | Precipitation | January 2010 to December 2016 | 82 |
| Percentiles | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Variables | Min. | Mean | Max. | 5% | 25% | 50% | 75% | 95% | 99% |
| Dengue | 0.00 | 25.59 | 415.00 | 0.00 | 0.00 | 1.50 | 14.75 | 169.00 | 401.63 |
| Precipitation | 0.00 | 160.70 | 651.80 | 1.16 | 12.48 | 85.64 | 285.66 | 522.14 | 647.28 |
| EVI | 0.24 | 0.36 | 0.53 | 0.25 | 0.28 | 0.34 | 0.45 | 0.49 | 0.53 |
| NDVI | 0.45 | 0.64 | 0.77 | 0.50 | 0.58 | 0.66 | 0.71 | 0.76 | 0.77 |
| nLST | 4.19 | 16.44 | 23.22 | 8.91 | 11.92 | 17.99 | 20.28 | 22.10 | 23.17 |
| dLST | 17.10 | 26.26 | 36.20 | 20.06 | 23.66 | 25.90 | 29.29 | 34.07 | 36.13 |
| Variables | Precipitation | NDVI | EVI | nLST | dLST |
|---|---|---|---|---|---|
| Precipitation | 1.000 | ||||
| NDVI | 0.303 | 1.000 | |||
| EVI | 0.731 | 0.789 | 1.000 | ||
| nLST | 0.213 | 0.030 | 0.295 | 1.000 | |
| dLST | 0.067 | −0.530 | −0.122 | 0.723 | 1.000 |
| Lag Months | Lag 0 | Lag 1 | Lag 2 | Lag 3 | Lag 4 | Lag 5 | Lag 6 |
|---|---|---|---|---|---|---|---|
| NDVI | 0.368 * | 0.296 * | 0.2 | 0.001 | −0.246 | −0.454 | −0.491 |
| EVI | 0.365 * | 0.421 * | 0.41 * | 0.245 * | −0.031 | −0.302 | −0.407 |
| dLST | −0.041 | 0.016 | 0.08 | 0.081 | 0.258 * | 0.358 * | 0.268 * |
| nLST | −0.041 | 0.016 | 0.08 | 0.081 | 0.258 | 0.358 * | 0.268 |
| Precipitation | 0.23 * | 0.351 * | 0.33 * | 0.318 * | 0.137 | −0.087 | −0.222 |
| Model | Variables in the Model | AIC | Adjusted R-Squared | Deviance Explained (%) |
|---|---|---|---|---|
| Model1 | Precipitationt0 | 1604.89 | 0.67 | 79.50 |
| Model2 | NDVIt0 | 1750.27 | 0.58 | 77.30 |
| Model3 | EVIt0 | 1749.79 | 0.57 | 77.30 |
| Model4 | dLSTt0 | 1735.57 | 0.61 | 77.50 |
| Model5 | nLSTt0 | 1717.53 | 0.55 | 77.80 |
| Model6 | NDVIt0 + nLSTt0 | 1736.55 | 0.60 | 77.50 |
| Model7 | NDVIt0 + dLSTt0 | 1693.00 | 0.54 | 78.20 |
| Model8 | NDVIt0 + Precipitationt0 | 1540.612 | 0.713 | 80.5 |
| Model9 | nLSTt0 + Precipitationt0 | 1601.104 | 0.656 | 79.6 |
| Model10 | dLSTt0 + Precipitationt0 | 1263.099 | 0.845 | 84.7 |
| Model11 | nLSTt0 + EVIt0 | 1737.437 | 0.64 | 77.5 |
| Model12 | dLSTt0 + EVIt0 | 1699.155 | 0.53 | 78.1 |
| Model13 | Precipitationt0 + nLSTt0 + NDVIt0 | 1542.57 | 0.71 | 80.5 |
| Model14 * | Precipitationt0 + dLSTt0 + NDVIt0 | 1256.66 | 0.848 | 84.8 |
| Model15 ** | Precipitationt1 + dLSTt5 + NDVIt0 | 682.160 | 0.87 | 89.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acharya, B.K.; Cao, C.; Xu, M.; Khanal, L.; Naeem, S.; Pandit, S. Temporal Variations and Associated Remotely Sensed Environmental Variables of Dengue Fever in Chitwan District, Nepal. ISPRS Int. J. Geo-Inf. 2018, 7, 275. https://doi.org/10.3390/ijgi7070275
Acharya BK, Cao C, Xu M, Khanal L, Naeem S, Pandit S. Temporal Variations and Associated Remotely Sensed Environmental Variables of Dengue Fever in Chitwan District, Nepal. ISPRS International Journal of Geo-Information. 2018; 7(7):275. https://doi.org/10.3390/ijgi7070275
Chicago/Turabian StyleAcharya, Bipin Kumar, Chunxiang Cao, Min Xu, Laxman Khanal, Shahid Naeem, and Shreejana Pandit. 2018. "Temporal Variations and Associated Remotely Sensed Environmental Variables of Dengue Fever in Chitwan District, Nepal" ISPRS International Journal of Geo-Information 7, no. 7: 275. https://doi.org/10.3390/ijgi7070275







