1. Introduction
The severe landslides affecting the Mila Basin (located in the North-East region of Algeria) have created serious threats not only to the environment and human settlements but also inflicted economic burdens to local authorities by the non-ending reconditioning and restoration projects. In addition, these landslides affect the current landscape evolution of the basin; therefore, predicting and delineating landslides are crucial tasks to reduce their associated damages. However, landslide prediction and delineation remain challenging tasks in the basin due to the complex nature of landslides.
Fortunately, the advancements achieved in machine learning and Geographic Information Systems (GIS) in the last decade have provided a plethora of quantitative methods and techniques for landslide modeling. Consequently, various models have been proposed and implemented successfully for modeling landslides that help in understanding landslide patterns and their triggering mechanism [
1]. The literature reviews showed that physical-based models are capable of delivering the highest prediction accuracy [
2]. Nonetheless, for large-scale analysis (similar to this case study), physical-based models require a fair amount of detailed data information to provide reliable results, which is unbelievably expensive [
3]. As a result, statistical and machine learning models can be considered a viable option to use. Basically, machine learning methods for landslide are based on the assumption that “
previous, current and future landslide failures do not happen randomly or by chance, but instead, failures follow patterns and share common geotechnical behaviors under similar conditions of the past and the present” [
4]. This requires collecting and preparing an accurate and large database (i.e., a geospatial database of landslide inventory and conditioning factors) with maximum details available. Then, models based on these methods are trained and validated using that database and the resulting models are used to generate landslide occurrence probability grids [
2].
Machine learning (ML) is one of the most effective methods for solving non-linear geo-spatial problems like landslides susceptibility, using either regression or classification. In fact, ML has proven to be ideal for addressing large-scale analysis problems where theoretical knowledge about the problem is still incomplete [
5]. After all, ML methods do require a significant number of conditioning factors to obtain reliable results. In the literature, several studies have been able to implement and compare machine learning models in landslide susceptibility modeling such as Artificial Neural Networks (NNET) [
1,
6,
7]; Support Vector Machines (SVM) [
1,
6,
8,
9,
10]; Decision Trees (DT) [
3,
11]; Logistic Regression (LR) [
1,
8,
11]; and ensemble methods such as Boosted Trees (BT) [
11,
12], and Random Forest (RF) [
3,
8,
11]. Despite the availability of some research concerning machine learning techniques and methods, no solid agreement about which method or technique is the most suitable for a landslide-prone area prediction has been identified [
13]. Nevertheless, there’s “
No free lunch” (NFL) (according to Wolpert [
14], NFL can be explained as: “
any two algorithms are equivalent when their performance is averaged across all possible problems”) when it comes to machine learning in general and the spatial prediction of landslides in particular due to the high level of uncertainty behind the process. In fact, no single or particular model can be depicted as the most suitable for all case scenarios. Selecting the most suitable method for landslide spatial prediction depends essentially on the underlined scientific goal for the case study [
15]. Additionally, the prediction accuracy of landslide modeling is influenced not only by the quality of the landslide inventories and the influencing factors, but also the fundamental quality of the machine learning algorithm used [
2]. Therefore, exploring and experimenting with new methods and techniques for spatially predicting this hazard is highly necessary.
The main goal of this study is to investigate and compare five machine learning algorithms, Random Forest (RF), Gradient Boosting Machine (GBM), Logistic Regression (LR), Artificial Neural Network (NNET), and Support Vector Machine (SVM) for landslide susceptibility mapping at the Mila Basin (Algeria). Additionally, this study aims to implement a meta-modeling approach using Sequential Model-Based Optimization (SMBO) for models that configure hyperparameters. Unlike similar studies [
1,
3,
5,
6,
7,
8,
9,
10,
11,
12,
16], this approach supports automated expensive hyperparameter optimization in order to provide a useful framework with a reproducible and unbiased optimization process. Moreover, it is important to note that the Mila Basin has suffered (and still) from various landslide disaster problems during the last five years; however, no significant attempt has been conducted to understand the phenomenon.
6. Discussions
The most effective way to reduce casualties and economic losses resulting from landslides are landslide risk planning and management; therefore, high-quality landslide susceptibility maps are an important tool [
57]. However, it is still a challenge to produce high accuracy landslide susceptibility maps at a regional scale due to the complex nature of landslides and it is widely recognized that the prediction quality of landslides is dependent on the algorithm used. Thus, although various methodologies for producing landslide susceptibility maps have been developed, the prediction accuracy of these methods is still debated [
49]. Therefore, in the present study, five classifications algorithms (GBM, LR, NNET, RF, and SVM) were investigated and compared for landslide susceptibility mapping at Mila Basin.
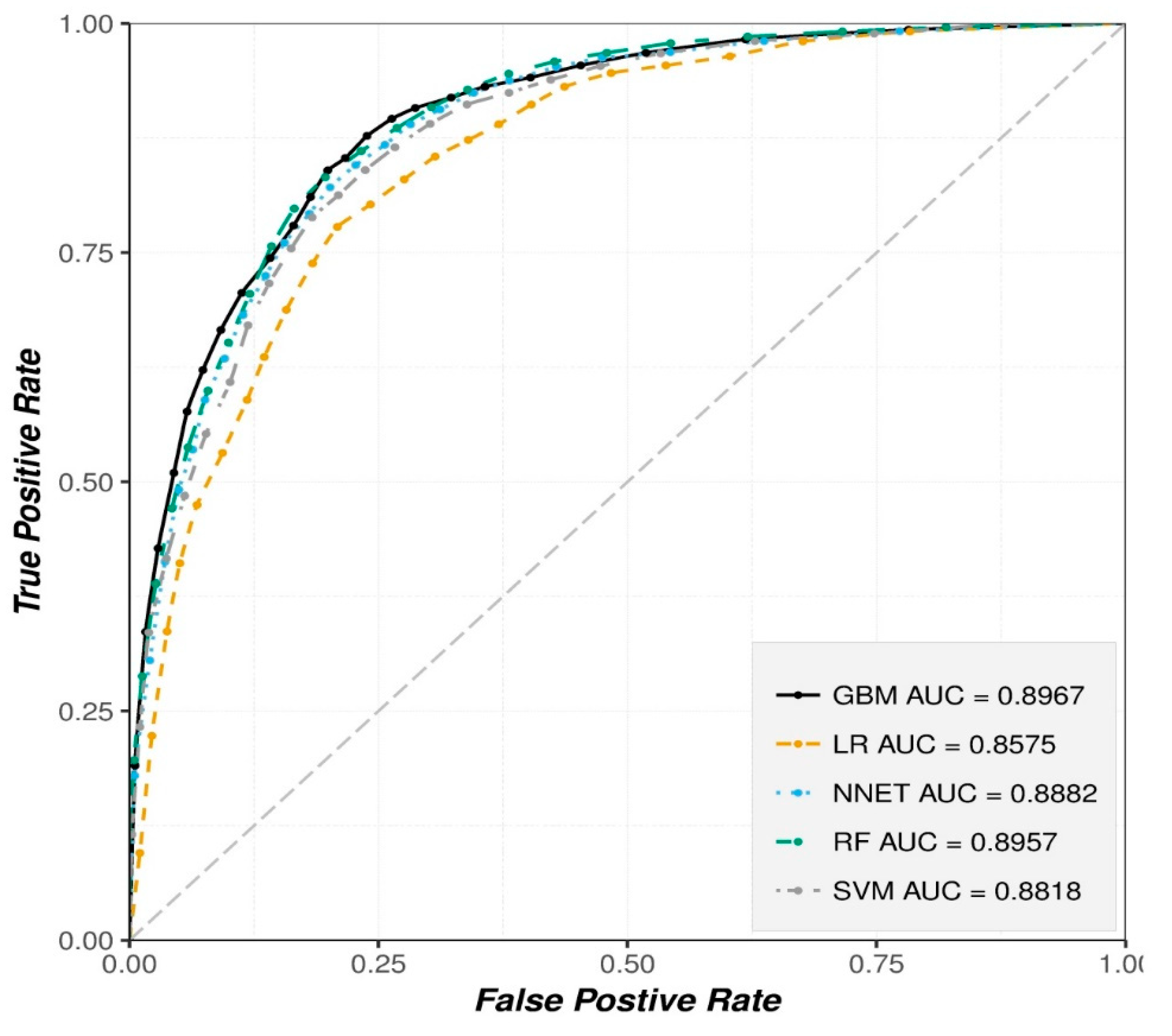
The results obtained in this study (see
Table 8 and
Figure 9) show that all the implemented models achieved high performance (AUC > 0.88, Acc > 80% and kappa > 0.60). However, two ensemble trees models (GBM and RF) yielded the highest prediction results compared to the others. This better performance is confirmed to be statistically significant with the used Wilcoxon signed-rank test. This finding is in agreement with the results from recent studies i.e., in ([
58,
59,
60,
61]) that reported that the ensemble models outperform single machine learning models. In contrast to GBM and RF, LR consistently yields the lowest results compared to the other implemented models. This finding is in line with the literature where LR achieves the worst, if not the poorest, performance of all models [
6,
9,
11,
16,
62].
The better-fit and higher performance of GBM and RF compared to LR, NNET, and SVM in this research is due to the divide-and-conquer approach that the assembling technique implements in both models (i.e., benefiting from aggregating weak learners to solve the issue). In fact, the main causes of error in the landslide modeling at the basin scale in this study is due to noise and the uncertainty that existed in the landslide conditioning factor maps (which were collected from various sources and scales). It is still difficult to eliminate the noise and uncertainty, though several fuzzy modeling approaches have been proposed. However, ensemble learning, RF, and GBM, which use the random sampling with replacement strategy, could minimize these due to their diversity and stability [
63], which are two key issues of ensemble learning. Thus, both RF and GBM are capable models that work well over noise and uncertainty environments [
64] such as landslide modeling; therefore, they are robust and better than the other models in this study.
Generally, GBM models offer similar or even better performance results than RF, but the large number of sensitive parameters and the tendency to easily over-fit makes it difficult to implement it right out the box compared to RF, which is easier to implement and less prone to both over-fitting and outliers. Additionally, some studies [
65] have found that GBM performs exceptionally well when the dimensionality is low (≈4000 predictors). Above that, RF has the best overall performance. Notably, the results obtained by SVM for typical binary landslide susceptibility problems are very satisfying. Even if it is lower than GBM, RF, and NNET, it is still relevant compared to the results produced by similar studies [
1,
6,
8,
9,
10]. NNET, on the other hand, unsurprisingly outperforms SVM and LR, but fails to capture the underlying model of the input data like RF and GBM, simply because neural networks need a large number of observations. However, in the case of landslides, the observation events are scarce and very hard to obtain. On top of samples being scarce, the most recent landslide susceptibility studies [
7,
9,
16] do not benefit from the full potential of NNET by implementing NNET models with vanilla “
Backpropagation” or one of its variances for the weight adjustments. In fact, Back-propagation based NNET are extremely slow to converge, which leads to a long execution time and a heavy computational load, not to mention both a large number of parameters to tune in and the special input data preparation required. Unlike Back-propagation NNETs, the implemented feed forward BFGS NNET are faster to converge with fewer hyperparameters to tune in and provided arguably better results than similar studies that implemented NNET [
7,
9,
16].
In the end, it is widely accepted that no single or particular model can be depicted as the most suitable for all case scenarios. For example, the LR model is simple, fast, easy to implement, and is only able to capture the linear relationship between the conditioning factors and the landslide susceptibility. The merit of LR is that it does not compulsorily require a normal distribution data. Additionally, both continuous and discrete data types can be used as an input for the LR model. However, landslides are complex phenomena with non-linear mechanisms. SVMs are useful non-linear classifiers whose goal is not only to correctly classify landslide instances, but also to keep the distance between instances and keep the separation of the hyperplane at a maximum. This makes SVM models appealing for susceptibility evaluation considering the number of hyperparameters to tune in. However, if those hyperparameters are inappropriately set, SVM will often lead to unsatisfactory results. NNET models are very effective for simulating non-linear complex phenomena with multiple conditioning factors (preferably continuous input dataset). However, being a black box model and the large number of samples required to obtain a reliable model are the only downsides to this kind of model. Ensemble tree models (GBM and RF) offer excellent performance with decent interpretability and a moderate number of hyperparameters to tune in but require a considerable time budget (they require a lot of time to converge, especially if used on large-scale analyses). Though some studies (such as in [
66]) highly recommend RF and GBM due to the outstanding performance, they suggest that a rather fast and simple model, such as LR would be much better than advanced machine learning models.
7. Conclusions
This research paper provided a framework for comparing and assessing five machine-learning methods (GBM, LR, NNET, RF, and SVM) for the landslide susceptibility assessment in the Mila Basin. The achieved results demonstrate that there is a significant difference between the implemented models. Even if the obtained results are underlined with a clear objective of comparing and assessing those models, finding the most suitable model for the case study was very challenging as it does not depend solely on the performance results, but also on the high level of uncertainty behind landslide modeling and the limitation and caveats that come with each model.
The two ensemble tree models (RF and GBM) were proven the most suitable models for this case study when comparing them to the remaining models (NNET, SVM, and LR), as they significantly outperformed the rest of the models based on the excellent performance results achieved. Despite that, the remaining three models are considered viable options, as they are adequately capable of satisfactory performance compared to similar studies. Summing up, the obtained landslide susceptibility maps by the implemented models can be used as a preliminary planning framework for planners in the study area or as a technical framework for countermeasures and regulatory policies by decision makers to minimize the damages introduced by either existing or future landslides by the Mila and Constantine municipalities.
Overall, the results of this study have demonstrated the effectiveness of all Five ML technique classifiers, especially ensemble tree models such as the GBM and RF algorithms for the assessment of landslide susceptibility. In terms of future work, we will consider the following issues: (1) exploring other machine learning algorithms; (2) including more landslide observation cases if possible; (3) introduce more richness to the input data pool, such as deformation formations based on InSAR space born imagery.