2DPR-Tree: Two-Dimensional Priority R-Tree Algorithm for Spatial Partitioning in SpatialHadoop
Abstract
:1. Introduction
2. Related Work
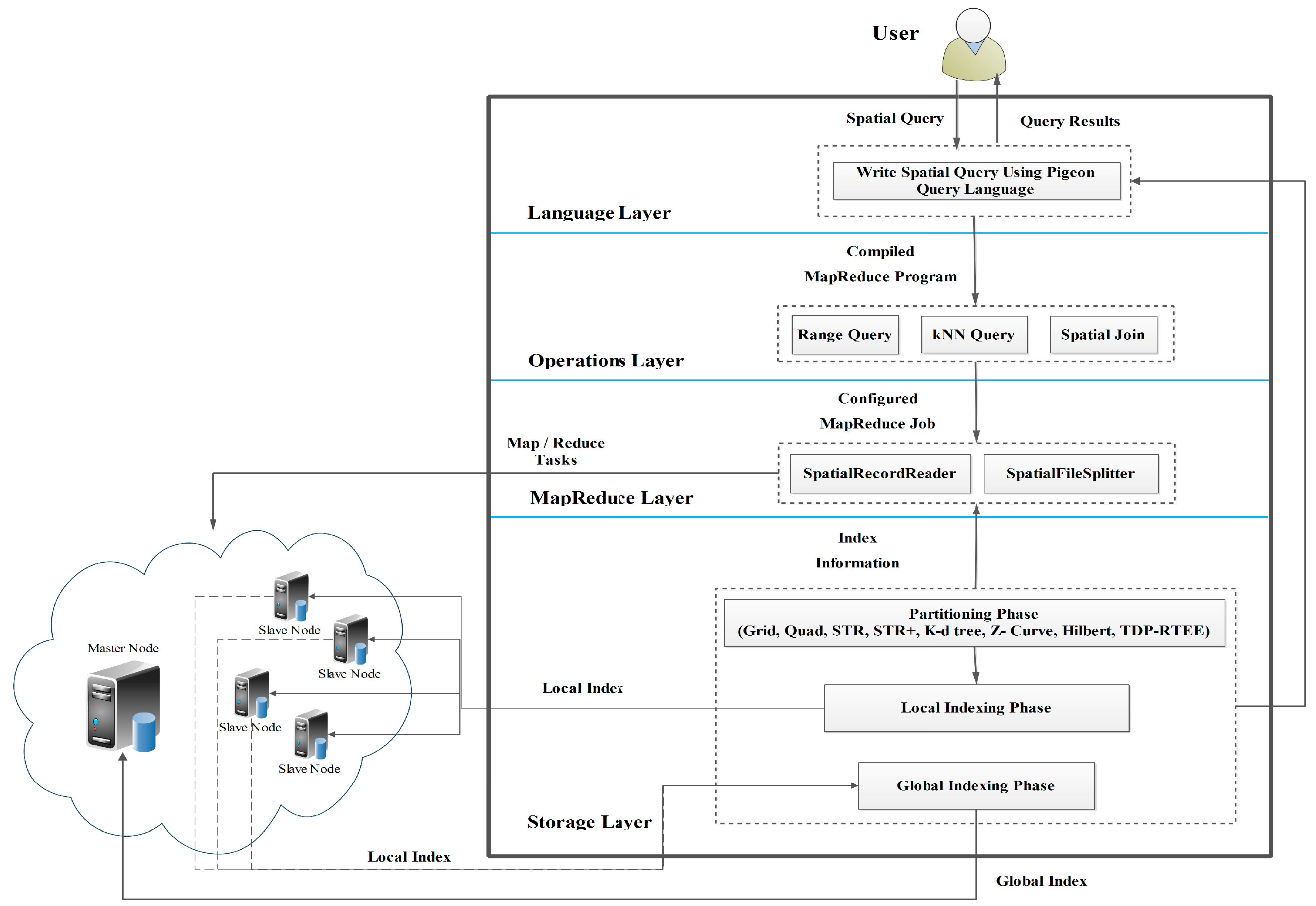
3. The Overall Architecture of SpatialHadoop
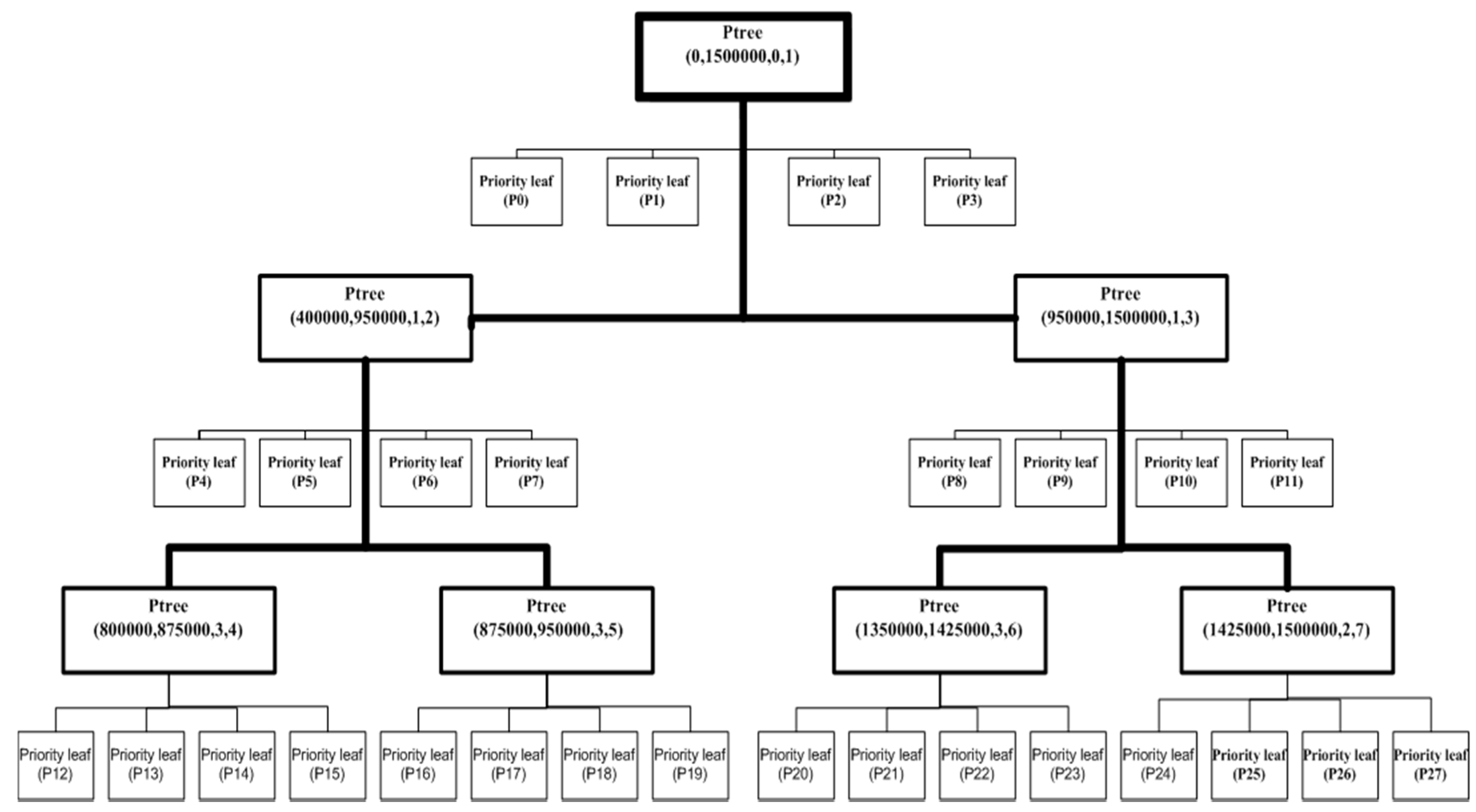
4. The Priority R-Tree
- Extract the B four-dimensional points in S* with minimal xmin-coordinates and store them in the first priority leaf .
- Extract the B four-dimensional points among the rest of the points with minimal ymin-coordinates and store them in the second priority leaf .
- Extract the B four-dimensional points among the rest of the points with maximal xmax-coordinates and store them in the third priority leaf .
- Finally, extract the B four-dimensional points among the rest of the points with maximal ymax-coordinates and store them in the fourth priority leaf .
| Algorithm 1 PR-tree index creation working steps. | |
| 1 | Function PRTreeIndex(S, PN) |
| 2 | Input: S = {R1, ...., RN}, PN |
| 3 | Output: A priority search tree (Stack of nodes) |
| 4 | Method: |
| 5 | B← np / PN |
| 6 | Foreach rectangle R 𝛜 S do // prepare S* |
| 7 | R* ← (RXmin, Rymin, Rxmax, Rymax) |
| 8 | S*← R* // store R* in S* |
| 9 | End For |
| 10 | RN ← Initial node with start_index = 0,end_index = S*.length and depth = 0 |
| 11 | STACK.push(RN) |
| 12 | While (STACK is not empty) |
| 13 | Nd← pop(STACK) |
| 14 | If (Nd.size ≤ B) // where Nd.size = Nd.end_index - Nd.start_index |
| 15 | leaf ←create a single leaf // TS consists of a single leaf; |
| 16 | Else If (Nd.size ≤ 4B) |
| 17 | b←⌈(Nd.size)/4⌉ |
| 18 | Recursively sort and extract the B points in S* in a leaf node according to xmin, ymin, xmax and ymax |
| 19 | Else |
| 20 | Recursively sort and extract the B points in S* in a leaf node according to xmin, ymin, xmax, and ymax |
| 21 | µ← (Nd.size - 4B)/2 |
| 22 | TS< (Nd.start_index + (4*B), Nd.start_index + (4*B) + µ,Nd.depth+1) |
| 23 | TS> (Nd.start_index + (4*B) + µ, Nd.end_index,Nd.depth+1) |
| 24 | STACK.push (TS< and TS>) |
| 25 | End if |
| 26 | End while |
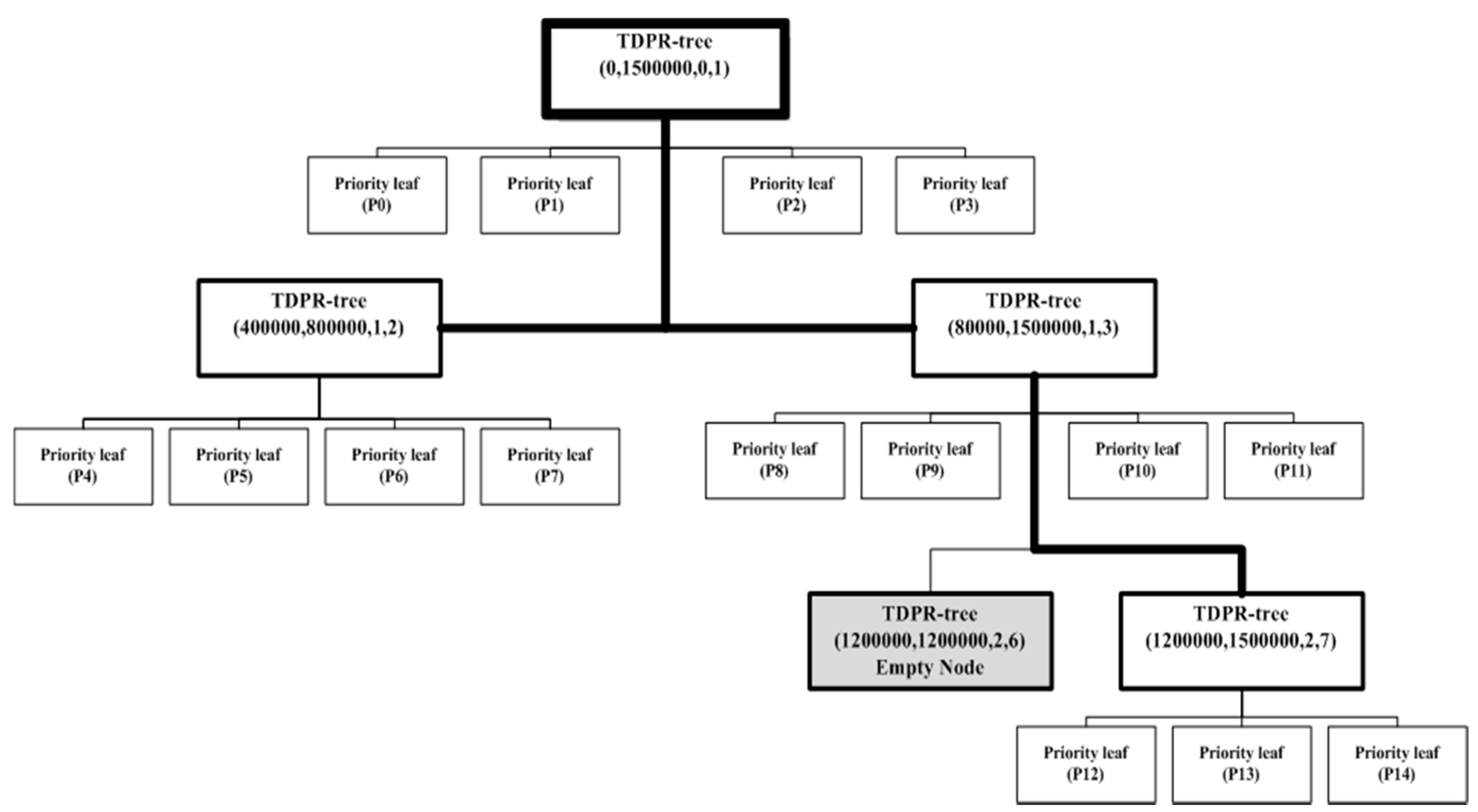
5. The 2DPR-Tree Technique in SpatialHadoop
- The first priority leaf stores the left-extreme B shapes with minimal x-coordinates.
- The second priority leaf stores the bottom-extreme B shapes with minimal y-coordinates.
- The third priority leaf stores the right-extreme B shapes with maximal x-coordinates.
- The fourth priority leaf stores the top-extreme B shapes with maximal y-coordinates.
- In separating the rest of the n-4B shapes into two parts in light of our present tree depth, the first part contains the number of shapes equal to µ calculated as in line 32, and the second part contains the rest of the n-4B shapes. The same plan is utilized in finding the KD-Tree:
- (a)
- If ((depth % 4) == 0) split based on the ascending order of the x-coordinate (left extraordinary).
- (b)
- If ((depth % 4) == 1) split based on the ascending order of the y-coordinate (bottom extraordinary).
- (c)
- If ((depth % 4) == 2) split based on the descending order of the x-coordinate (right extraordinary).
- (d)
- If ((depth % 4) == 3) split based on the descending order of the y-coordinate (top extraordinary).
| Algorithm 2 2DPR-Tree index creation working steps. | |
| 1 | Function 2DPRTreeIndex (S, PN) |
| 2 | Input:S = {R1, ...., RN}, PN |
| 3 | Output: A 2DPR-tree(Stack of nodes) |
| 4 | Method: |
| 5 | B ← np / PN |
| 6 | Foreachrectangle R𝛜S do // prepare S* |
| 7 | R* ← R.getCenterPoint(); // converting each rectangle to a 2D point |
| 8 | ← R* // store R* in S* |
| 9 | End For |
| 10 | RN← Initial node with start_index = 0 and end_index = S*. length and depth = 0 |
| 11 | STACK.push (RN) |
| 12 | While (STACK is not empty) |
| 13 | Nd ← pop (stack) |
| 14 | If(Nd.size ≤ B) //where Nd.size = Nd.end_index - Nd.start_index |
| 15 | leaf ← create a single leaf //TS comprises a single leaf; |
| 16 | Else If (Nd.size ≤ 4B) |
| 17 | Sort (the S* points, X, ASC) |
| 18 | Extract (the B points in S* with the minimal X coordinate, leaf ) |
| 19 | If ((Nd.size – B) ≤ B) |
| 20 | Sort (the rest S* points, Y, ASC) |
| 21 | leaf ← create a leaf with the rest S* points |
| 22 | Else |
| 23 | Sort (the rest S* points, Y, ASC) |
| 24 | Extract (the B points in S* with the minimal Y coordinate, leaf |
| 25 | If ((Nd.size – 2B) ≤ B) |
| 26 | Sort (the rest S* points, X, DESC) |
| 27 | leaf ← create a leaf with the rest S* points |
| 28 | Else |
| 29 | Sort (the rest S* points, X, DESC) |
| 30 | Extract (the B points in S* with the maximal X coordinate, leaf ) |
| 31 | Sort (the rest S* points, Y, DESC) |
| 32 | leaf ← create a leaf with the rest S* points |
| 33 | End if |
| 34 | End if |
| 35 | Else |
| 36 | µ← |
| 37 | If ((Nd.depth % 4) == 0) |
| 38 | split by the x coordinate (left extraordinary) |
| 39 | Else If ((Nd.depth % 4) == 1) |
| 40 | split by the y coordinate (bottom extraordinary) |
| 41 | Else If ((Nd.depth % 4) == 2) |
| 42 | split by the x coordinate backward (right extraordinary) |
| 43 | Else |
| 44 | split by the y coordinate backward (top extraordinary) |
| 45 | End If |
| 46 | TS< (Nd.start_index + (4*B), Nd.start_index + (4*B) + µ, Nd.depth+1) |
| 47 | TS>(Nd.start_index + (4*B) + µ, Nd.end_index, Nd.depth+1) |
| 48 | STACK.push (TS< and TS>) |
| 49 | End if |
| 50 | End while |
6. Experimentation
6.1. Experimental Setup
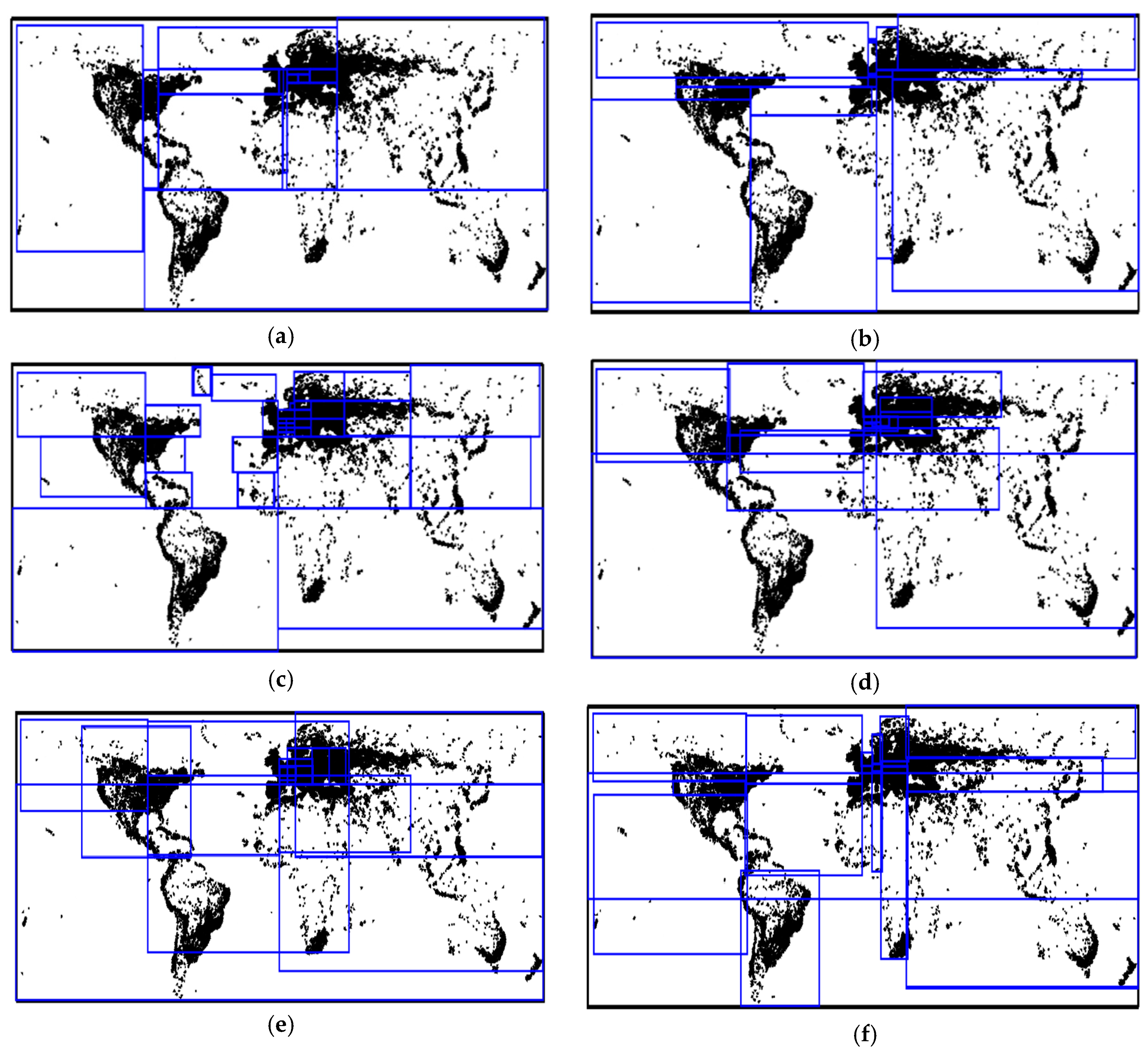
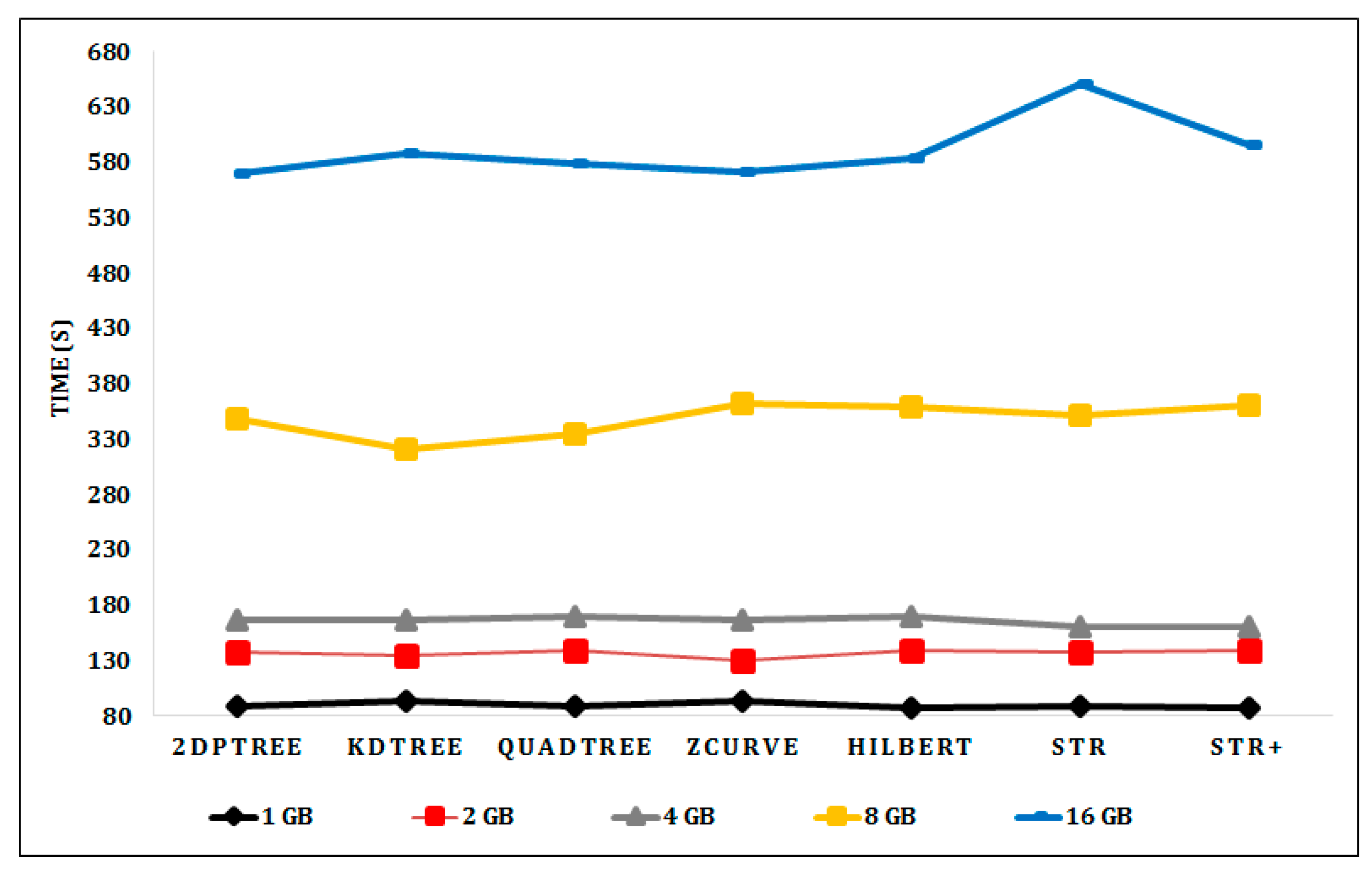
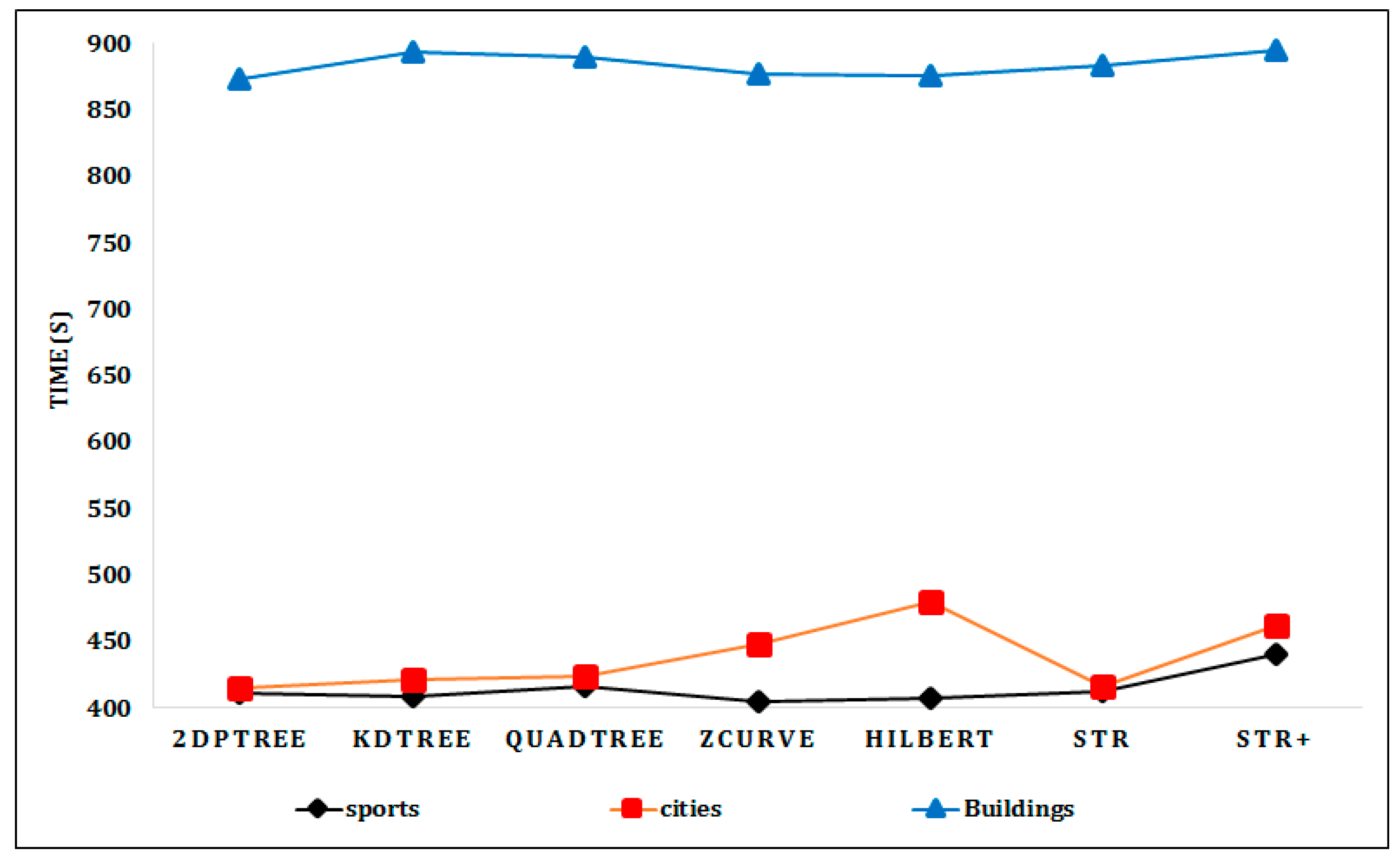
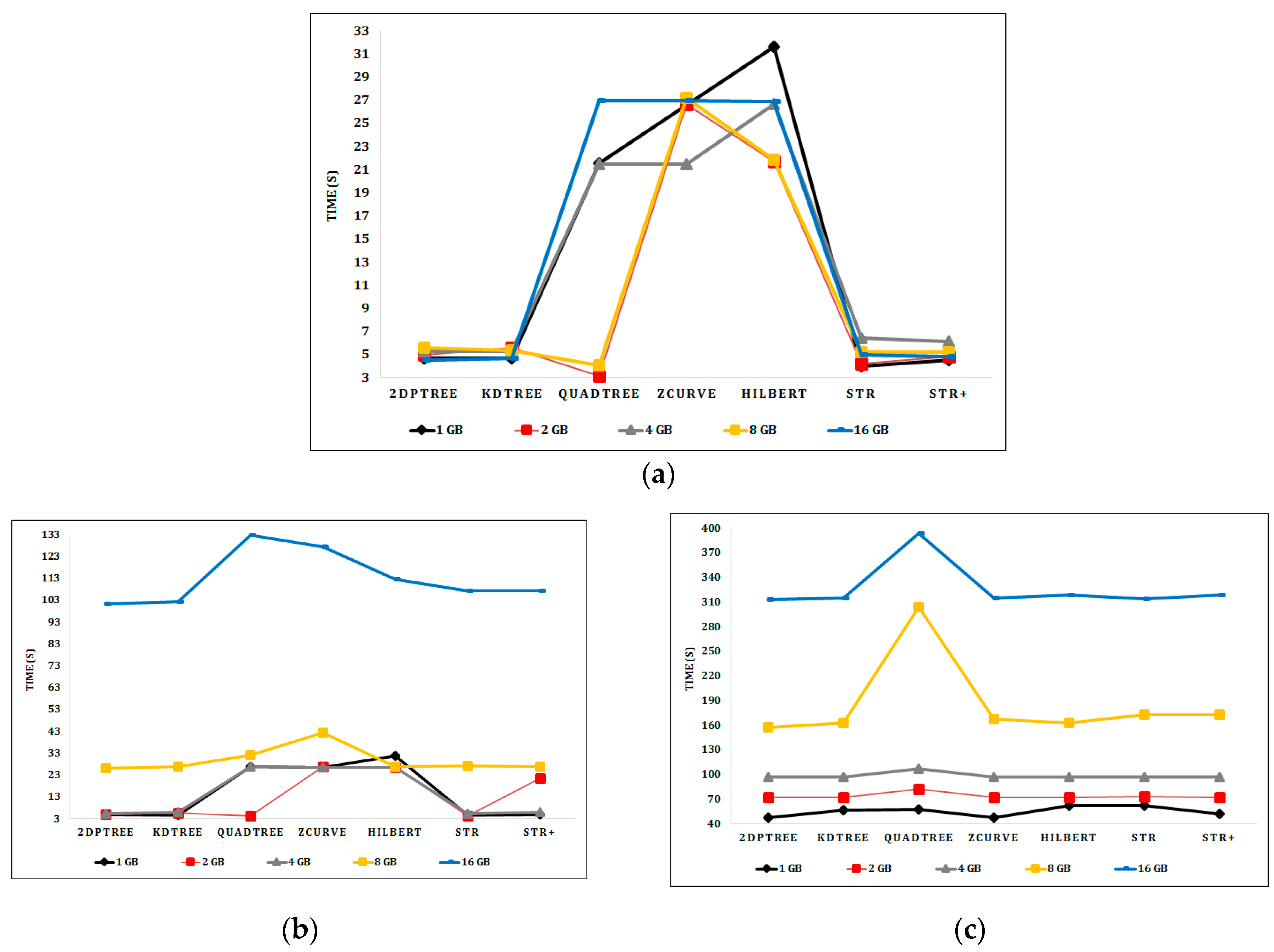
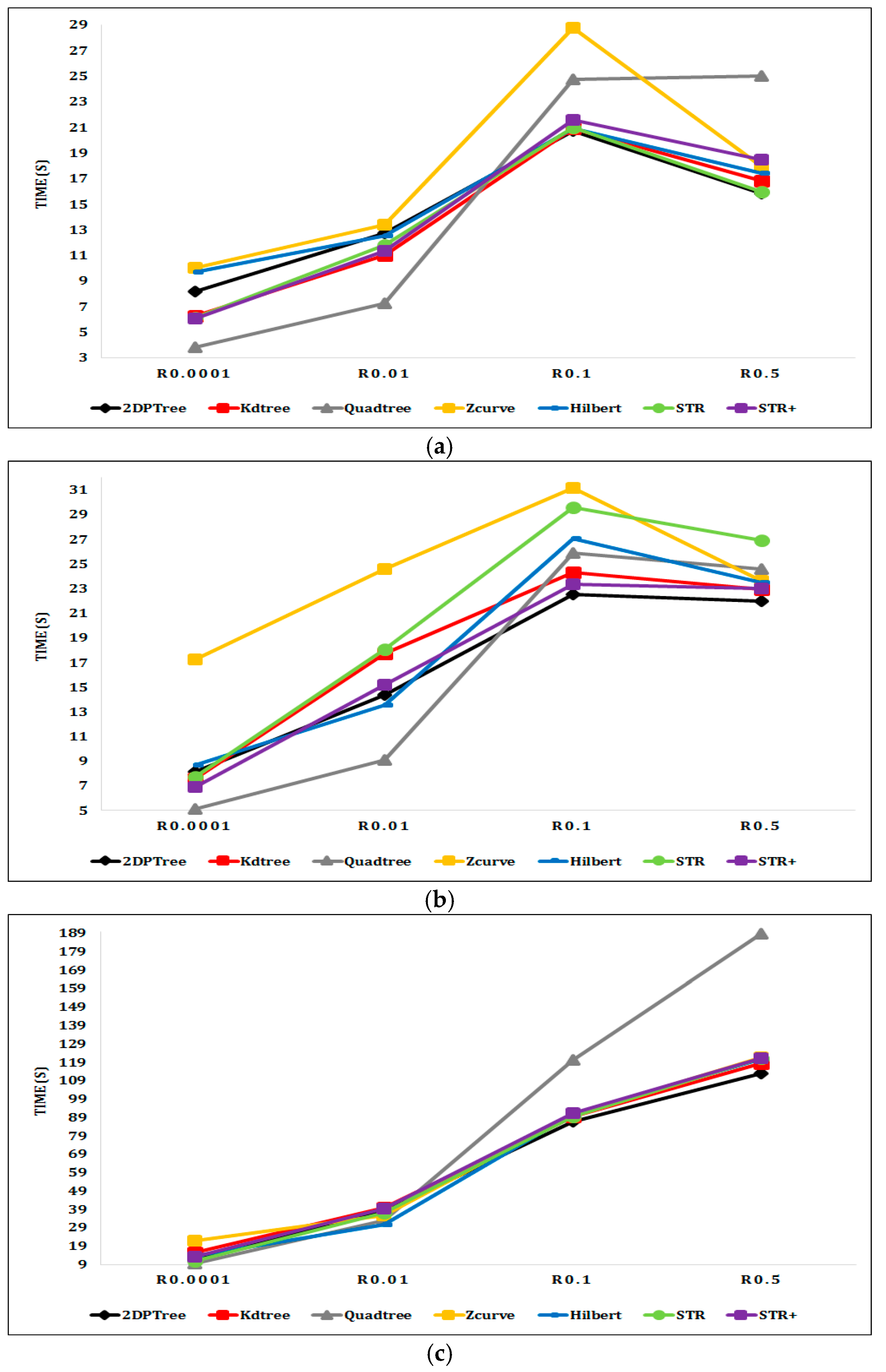
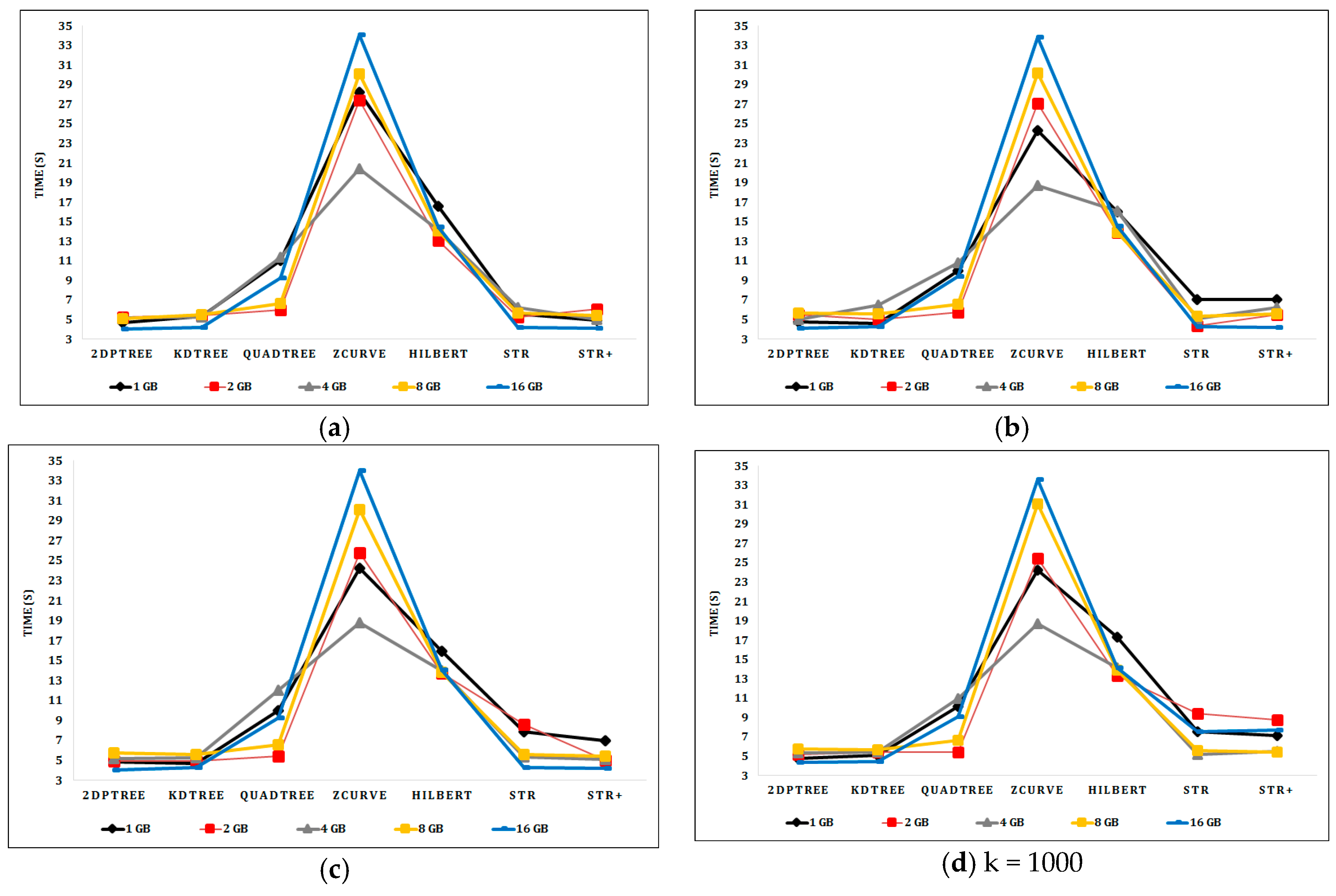
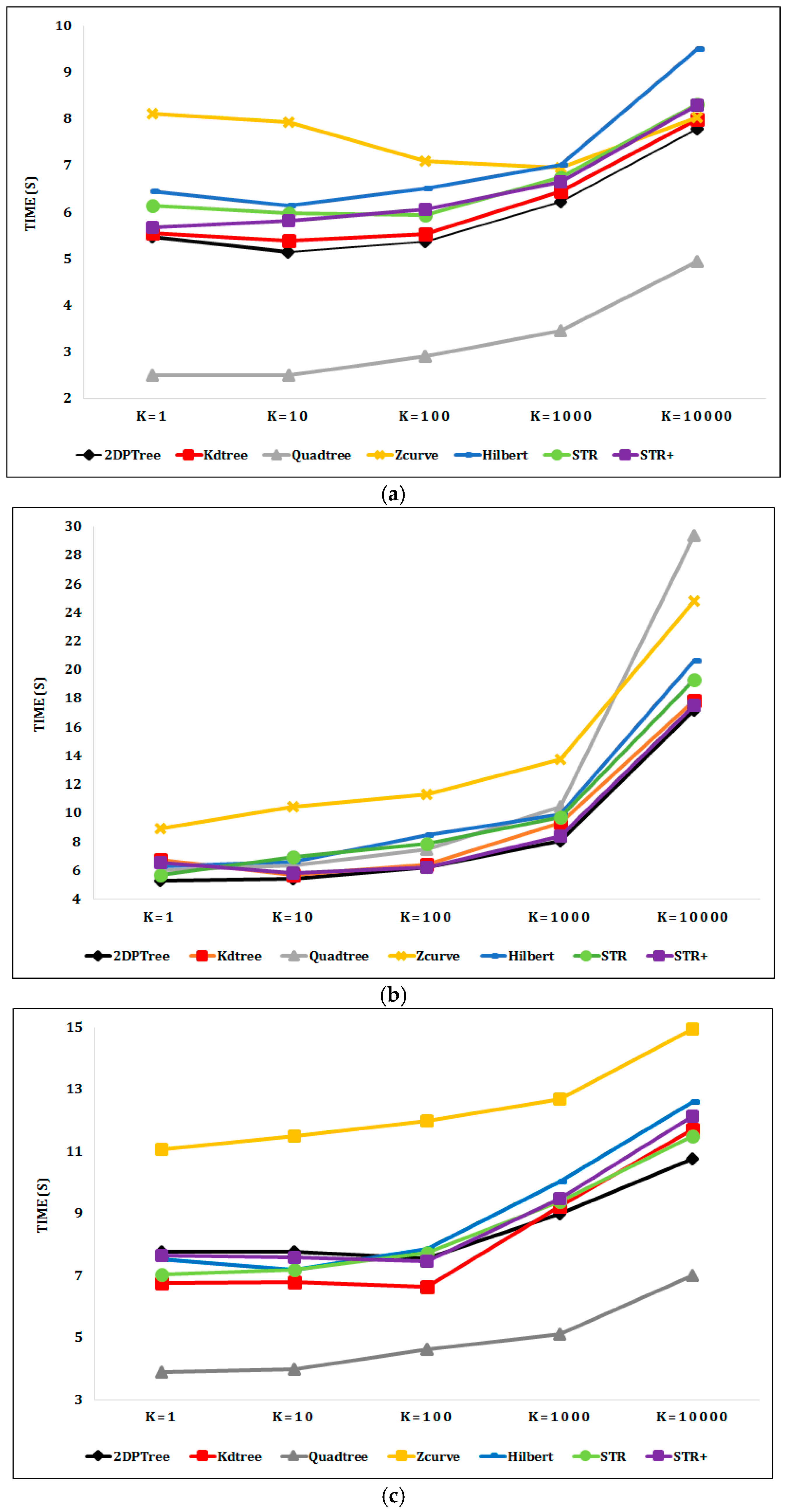
6.2. Experimental Results
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Cary, A.; Yesha, Y.; Adjouadi, M.; Rishe, N. Leveraging cloud computing in geodatabase management. In Proceedings of the IEEE International Conference on Granular Computing, San Jose, CA, USA, 14–16 August 2010. [Google Scholar]
- Li, Z.; Hu, F.; Schnase, J.L.; Duffy, D.Q.; Lee, T.; Bowen, M.K.; Yang, C. A spatiotemporal indexing approach for efficient processing of big array-based climate data with mapreduce. Int. J. Geogr. Inf. Sci. 2017, 31, 17–35. [Google Scholar] [CrossRef]
- Haynes, D.; Ray, S.; Manson, S. Terra populus: Challenges and opportunities with heterogeneous big spatial data. In Advances in Geocomputation: Geocomputation 2015–the 13th International Conference; Griffith, D.A., Chun, Y., Dean, D.J., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 115–121. [Google Scholar]
- Katzis, K.; Efstathiades, C. Resource management supporting big data for real-time applications in the 5g era. In Advances in Mobile Cloud Computing and Big Data in the 5g Era; Mavromoustakis, C.X., Mastorakis, G., Dobre, C., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 289–307. [Google Scholar]
- White, T. Hadoop: The Definitive Guide; O’Reilly Media: Scbastopol, CA, USA, 2015. [Google Scholar]
- Thusoo, A.; Sarma, J.S.; Jain, N.; Shao, Z.; Chakka, P.; Anthony, S.; Liu, H.; Wyckoff, P.; Murthy, R. Hive: A warehousing solution over a map-reduce framework. Proc. VLDB Endow. 2009, 2, 1626–1629. [Google Scholar] [CrossRef]
- Li, F.; Ooi, B.C.; Ozsu, M.T.; Wu, S. Distributed data management using mapreduce. ACM Comput. 2014, 46, 31–42. [Google Scholar] [CrossRef]
- Doulkeridis, C.; Nrvag, K. A survey of large-scale analytical query processing in mapreduce. VLDB J. 2014, 23, 355–380. [Google Scholar] [CrossRef]
- Eldawy, A.; Li, Y.; Mokbel, M.F.; Janardan, R. Cg_hadoop: Computational geometry in mapreduce. In Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Orlando, FL, USA, 5–8 November 2013; pp. 294–303. [Google Scholar]
- Dean, J.; Ghemawat, S. Mapreduce: Simplified data processing on large clusters. Commun. ACM 2008, 51, 107–113. [Google Scholar] [CrossRef]
- Wang, K. Accelerating spatial data processing with mapreduce. In Proceedings of the 2010 IEEE 16th International Conference on ICPADS, Shanghai, China, 8–10 December 2010. [Google Scholar]
- Eldawy, A.; Mokbel, M.F. Spatialhadoop: A mapreduce framework for spatial data. In Proceedings of the ICDE Conference, Seoul, Korea, 13–17 April 2015; pp. 1352–1363. [Google Scholar]
- Maleki, E.F.; Azadani, M.N.; Ghadiri, N. Performance evaluation of spatialhadoop for big web mapping data. In Proceedings of the 2016 Second International Conference on Web Research (ICWR), Tehran, Iran, 27–28 April 2016; pp. 60–65. [Google Scholar]
- Aly, A.M.; Elmeleegy, H.; Qi, Y.; Aref, W. Kangaroo: Workload-aware processing of range data and range queries in hadoop. In Proceedings of the Ninth ACM International Conference on Web Search and Data Mining, San Francisco, CA, USA, 22–25 February 2016; pp. 397–406. [Google Scholar]
- Zhang, S.; Han, J.; Liu, Z.; Wang, K.; Feng, S. Spatial queries evaluation with mapreduce. In Proceedings of the 2009 Eighth International Conference on Grid and Cooperative Computing, Lanzhou, China, 27–29 August 2009; pp. 287–292. [Google Scholar]
- Ma, Q.; Yang, B.; Qian, W.; Zhou, A. Query processing of massive trajectory data based on mapreduce. In Proceedings of the First International Workshop on Cloud Data Management, Hong Kong, China, 2 November 2009; pp. 9–16. [Google Scholar]
- Akdogan, A.; Demiryurek, U.; Banaei-Kashani, F.; Shahabi, C. Voronoi-based geospatial query processing with mapreduce. In Proceedings of the 2010 IEEE Second International Conference on Cloud Computing Technology and Science, Indianapolis, IN, USA, 30 November–3 December 2010; pp. 9–16. [Google Scholar]
- Nodarakis, N.; Rapti, A.; Sioutas, S.; Tsakalidis, A.K.; Tsolis, D.; Tzimas, G.; Panagis, Y. (a)knn query processing on the cloud: A survey. In Algorithmic Aspects of Cloud Computing: Second International Workshop, Algocloud 2016, Aarhus, Denmark, August 22, 2016, Revised Selected Papers; Sellis, T., Oikonomou, K., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 26–40. [Google Scholar]
- Ray, S.; Simion, B.; Brown, A.D.; Johnson, R. A parallel spatial data analysis infrastructure for the cloud. In Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Orlando, FL, USA, 5–8 November 2013; pp. 284–293. [Google Scholar]
- Ray, S.; Simion, B.; Brown, A.D.; Johnson, R. Skew-resistant parallel in-memory spatial join. In Proceedings of the 26th International Conference on Scientific and Statistical Database Management, Aalborg, Denmark, 30 June–2 July 2014; pp. 1–12. [Google Scholar]
- Vo, H.; Aji, A.; Wang, F. Sato: A spatial data partitioning framework for scalable query processing. In Proceedings of the 22nd ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Dallas, TX, USA, 4–7 November 2014; pp. 545–548. [Google Scholar]
- Pertesis, D.; Doulkeridis, C. Efficient skyline query processing in spatialhadoop. Inf. Syst. 2015, 54, 325–335. [Google Scholar] [CrossRef]
- Eldawy, A.; Alarabi, L.; Mokbel, M.F. Spatial partitioning techniques in spatialhadoop. In Proceedings of the International Conference on Very Large Databases, Kohala Coast, HI, USA, 31 August–4 September 2015. [Google Scholar]
- Eldawy, A.; Mokbel, M.F. The ecosystem of spatialhadoop. SIGSPATIAL Spec. 2015, 6, 3–10. [Google Scholar] [CrossRef]
- Randolph, W.; Chandrasekhar Narayanaswaml, F.; Kankanhalll, M.; Sun, D.; Zhou, M.-C.; Yf Wu, P. Uniform Grids: A Technique for Intersection Detection on Serial and Parallel Machines. In In Proceedings of the Auto Carto 9, Baltimore, Maryland, 2–7 April 1989; pp. 100–109. [Google Scholar]
- Singh, H.; Bawa, S. A survey of traditional and mapreduce based spatial query processing approaches. SIGMOD Rec. 2017, 46, 18–29. [Google Scholar] [CrossRef]
- Tan, K.-L.; Ooi, B.C.; Abel, D.J. Exploiting spatial indexes for semijoin-based join processing in distributed spatial databases. IEEE Trans. Knowl. Data Eng. 2000, 12, 920–937. [Google Scholar]
- Zhang, R.; Zhang, C.-T. A brief review: The z-curve theory and its application in genome analysis. Curr. Genom. 2014, 15, 78–94. [Google Scholar] [CrossRef] [PubMed]
- Meng, L.; Huang, C.; Zhao, C.; Lin, Z. An improved hilbert curve for parallel spatial data partitioning. Geo-Spat. Inf. Sci. 2007, 10, 282–286. [Google Scholar] [CrossRef]
- Liao, H.; Han, J.; Fang, J. Multi-dimensional index on hadoop distributed file system. In Proceedings of the 2010 IEEE Fifth International Conference on Networking, Architecture, and Storage, Macau, China, 15–17 July 2010; pp. 240–249. [Google Scholar]
- Guttman, A. R-trees: A dynamic index structure for spatial searching. SIGMOD Rec. 1984, 14, 47–57. [Google Scholar] [CrossRef]
- Beckmann, N.; Kriegel, H.-P.; Schneider, R.; Seeger, B. The r*-tree: An efficient and robust access method for points and rectangles. SIGMOD Rec. 1990, 19, 322–331. [Google Scholar] [CrossRef]
- Leutenegger, S.T.; Lopez, M.A.; Edgington, J. Str: A simple and efficient algorithm for r-tree packing. In Proceedings of the 13th International Conference on Data Engineering, Birmingham, UK, 7–11 April 1997; pp. 497–506. [Google Scholar]
- Giao, B.C.; Anh, D.T. Improving sort-tile-recursive algorithm for r-tree packing in indexing time series. In Proceedings of the the 2015 IEEE RIVF International Conference on Computing & Communication Technologies–Research, Innovation, and Vision for Future (RIVF), Can Tho, Vietnam, 25–28 January 2015; pp. 117–122. [Google Scholar]
- Sellis, T. The r+-tree: A dynamic index for multidimensional objects. In Proceedings of the 13th International Conference on Very Large Data Bases, Brighton, UK, 1–4 September 1987; pp. 507–518. [Google Scholar]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar] [CrossRef]
- Olston, C.; Reed, B.; Srivastava, U.; Kumar, R.; Tomkins, A. Pig latin: A not-so-foreign language for data processing. In Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada, 9–12 June 2008; pp. 1099–1110. [Google Scholar]
- Arge, L.; Berg, M.D.; Haverkort, H.J.; Yi, K. The priority r-tree: A practically efficient and worst-case optimal r-tree. ACM Trans. Algorithms 2008, 4, 9. [Google Scholar] [CrossRef]
- Agarwal, P.K.; Berg, M.D.; Gudmundsson, J.; Hammar, M.; Haverkort, H.J. Box-trees and r-trees with near-optimal query time. Discre. Comput. Geom. 2002, 28, 291–312. [Google Scholar] [CrossRef]
- Davies, J. Implementing the Pseudo Priority r-Tree (pr-tree), a Toy Implementation for Calculating Nearest Neighbour on Points in the x-y Plane. Available online: http://juliusdavies.ca/uvic/report.html (accessed on 18 August 2017).
- Amazon. Amazon ec2. Available online: http://aws.amazon.com/ec2/ (accessed on 10 January 2018).
| Dimension | Category | Grid | Quad Tree | Z Curve | Hilbert Curve | STR | STR+ | KD-Tree | 2DPR-Tree |
|---|---|---|---|---|---|---|---|---|---|
| Partition Boundary | overlapping | √ | √ | √ | √ | ||||
| non-overlapping | √ | √ | √ | √ | |||||
| Search Strategy | top-down | N/A | N/A | √ | √ | ||||
| bottom-up | N/A | N/A | √ | √ | √ | √ | |||
| Split Criterion | space-oriented | √ | √ | ||||||
| space-filling curve (SFC)-oriented | √ | √ | |||||||
| data-oriented | √ | √ | √ | √ |
| Symbol | Description |
|---|---|
| S | Set of rectangles in the working file |
| N | Rectangles number in S. |
| np | The number of shapes/points to be indexed |
| PN | Partition number calculated by dividing the size of working file by the file block size as each partition should fit into only one file block |
| B | Number of shapes/points assigned for each partition or file block calculated as np/PN |
| Set of 4D points (a point for each rectangle in S) | |
| Set of 2D points (a 2D point for each rectangle in S) | |
| RN | Initial node (root) with start index = 0 and end index = S*. length and depth = 0 |
| µ | Median (the divider that splits the rest of the points into two almost equal sized subsets) |
| Name | Data Size | Records No. | Average Record Size | Description |
|---|---|---|---|---|
| Buildings | 28.2 GB | 115 M | 263 bytes | Boundaries of all buildings |
| Cities | 1.4 GB | 171 K | 8.585 KB | Boundaries of postal code areas (mostly cities) |
| Sports | 590 MB | 1.8 M | 343 bytes | Boundaries of sporting areas |
| File Size (GB) | Partitions NO | ||||
|---|---|---|---|---|---|
| 1 GB | 2 GB | 4 GB | 8 GB | 16 GB | |
| 2DPR-Tree | 10 | 20 | 39 | 77 | 154 |
| KD-Tree | 10 | 20 | 39 | 77 | 154 |
| Quadtree | 16 | 64 | 64 | 256 | 256 |
| Z-curve | 10 | 20 | 39 | 77 | 154 |
| Hilbert | 10 | 20 | 39 | 77 | 154 |
| STR & STR+ | 12 | 20 | 42 | 81 | 156 |
| Real Dataset | Partitions NO | ||
|---|---|---|---|
| Sports | Cities | Buildings | |
| 2DPR-Tree | 6 | 14 | 252 |
| KD-Tree | 6 | 14 | 252 |
| Quadtree | 25 | 34 | 705 |
| Z-curve | 6 | 14 | 252 |
| Hilbert | 6 | 14 | 252 |
| STR & STR+ | 6 | 18 | 252 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elashry, A.; Shehab, A.; Riad, A.M.; Aboul-Fotouh, A. 2DPR-Tree: Two-Dimensional Priority R-Tree Algorithm for Spatial Partitioning in SpatialHadoop. ISPRS Int. J. Geo-Inf. 2018, 7, 179. https://doi.org/10.3390/ijgi7050179
Elashry A, Shehab A, Riad AM, Aboul-Fotouh A. 2DPR-Tree: Two-Dimensional Priority R-Tree Algorithm for Spatial Partitioning in SpatialHadoop. ISPRS International Journal of Geo-Information. 2018; 7(5):179. https://doi.org/10.3390/ijgi7050179
Chicago/Turabian StyleElashry, Ahmed, Abdulaziz Shehab, Alaa M. Riad, and Ahmed Aboul-Fotouh. 2018. "2DPR-Tree: Two-Dimensional Priority R-Tree Algorithm for Spatial Partitioning in SpatialHadoop" ISPRS International Journal of Geo-Information 7, no. 5: 179. https://doi.org/10.3390/ijgi7050179
APA StyleElashry, A., Shehab, A., Riad, A. M., & Aboul-Fotouh, A. (2018). 2DPR-Tree: Two-Dimensional Priority R-Tree Algorithm for Spatial Partitioning in SpatialHadoop. ISPRS International Journal of Geo-Information, 7(5), 179. https://doi.org/10.3390/ijgi7050179





