Estimating the Performance of Random Forest versus Multiple Regression for Predicting Prices of the Apartments
Abstract
:1. Introduction
2. Case Study and Data Description
Explanatory Variables
3. Methods
3.1. Hedonic Price Model
3.2. Principal Component Analysis
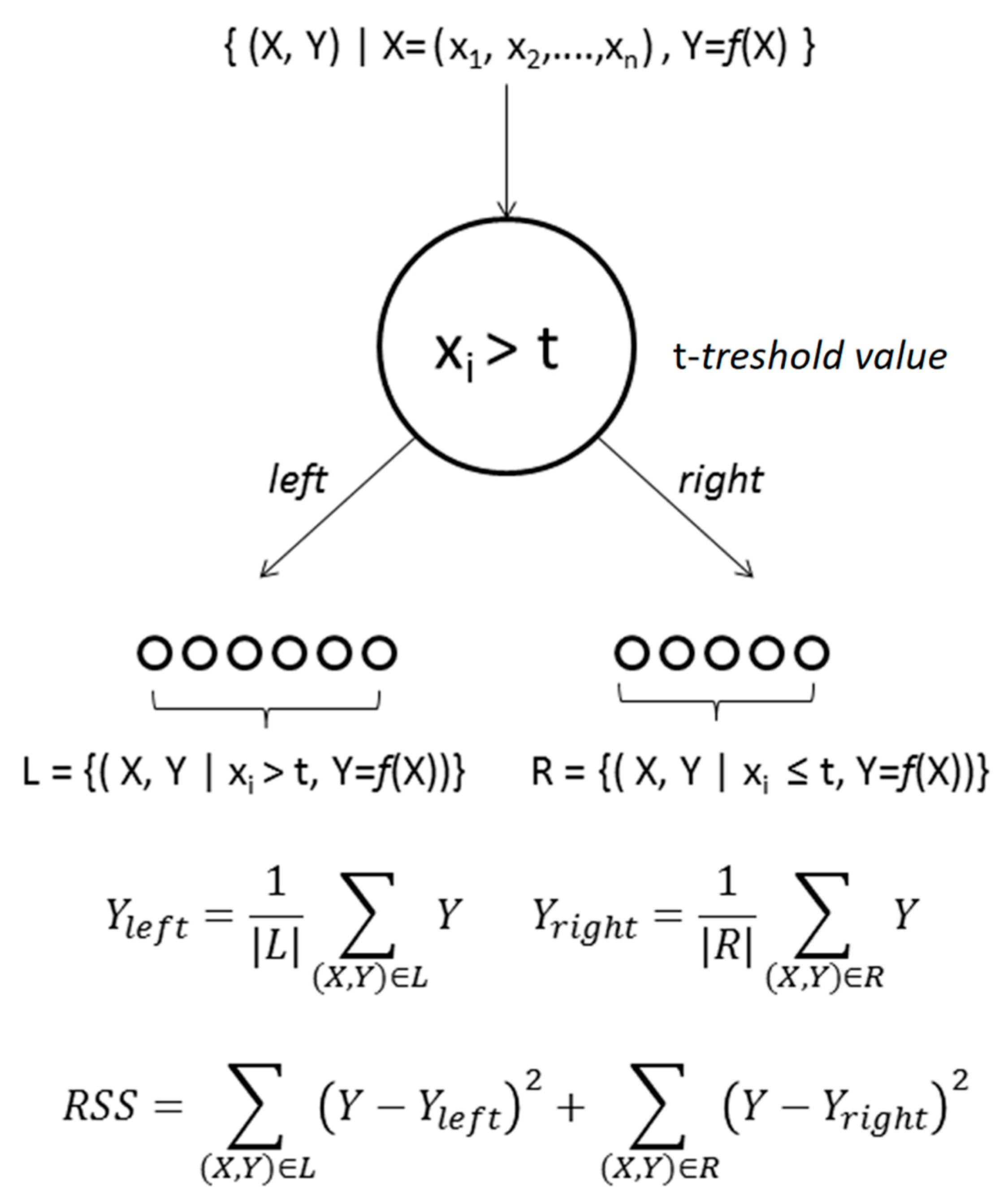
3.3. Random Forest
3.4. Model Performance Measures
3.5. R Language Environment
4. Results and Discussion
4.1. OLS Model Interpretation
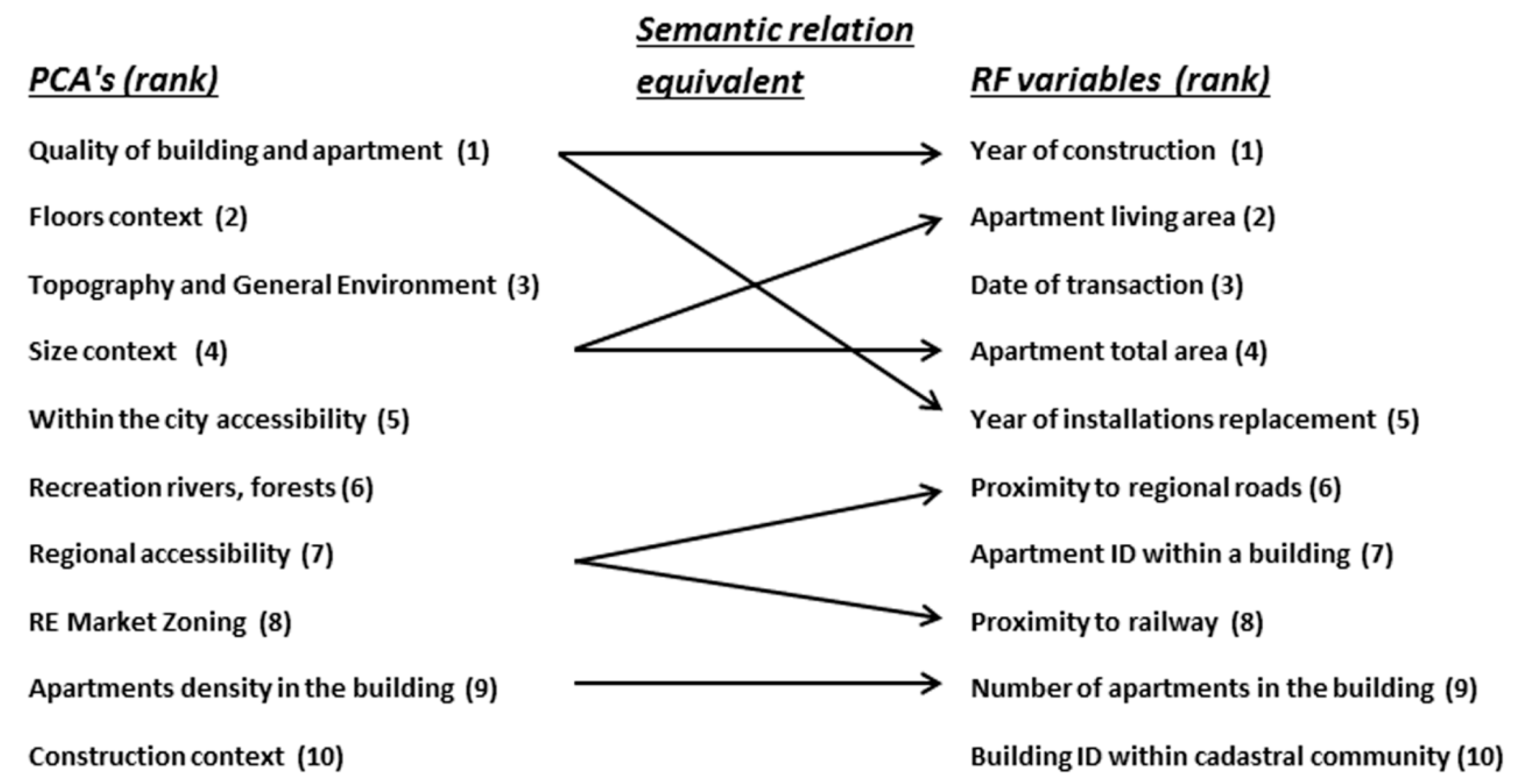
4.2. Random Forest Model Interpretation
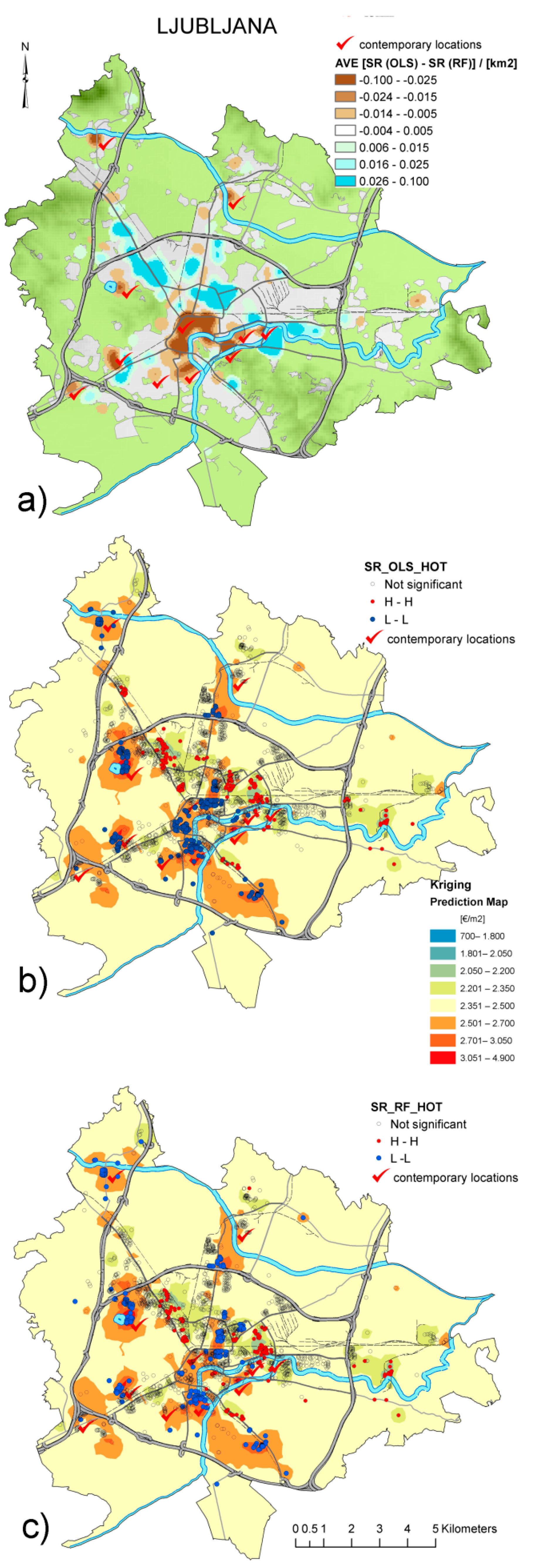
4.3. The Comparison of OLS and RF Performance
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lake, I.R.; Lovett, A.A.; Bateman, I.J.; Day, B. Using GIS and large-scale digital data to implement hedonic pricing studies. Int. J. Geogr. Inf. Sci. 2000, 14, 521–541. [Google Scholar] [CrossRef]
- Din, A.; Hoesli, M.; Bender, A. Environmental variables and real estate prices. Urban. Stud. 2001, 38, 1989–2000. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, R. Impacts of Street-Visible Greenery on Housing Prices: Evidence from a Hedonic Price Model and a Massive Street View Image Dataset in Beijing. ISPRS Int. J. Geo-Inf. 2018, 7, 104. [Google Scholar] [CrossRef]
- Schernthanner, H.; Asche, H.; Gonschorek, J.; Scheele, L. Spatial modeling and geovisualization of rental prices for real estate portals. In Computational Science and Its Applications—ICCSA 2016; Gervasi, O., Ed.; Springer: Cham, Switzerland, 2016; Volume 9788. [Google Scholar] [CrossRef]
- Bajat, B.; Kilibarda, M.; Pejović, M.; Samardžić Petrović, M. Spatial Hedonic Modeling of Housing Prices Using Auxiliary Maps. In Spatial Analysis and Location Modeling in Urban and Regional Systems; Thill, J.C., Ed.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 97–122. [Google Scholar]
- Meen, G. Spatial housing economics: A survey. Urban. Stud. 2016, 53, 1987–2003. [Google Scholar] [CrossRef]
- Tay, D.P.; Ho, D.K. Artificial intelligence and the mass appraisal of residential apartments. J. Prop. Valuat. Invest. 1992, 10, 525–540. [Google Scholar] [CrossRef]
- Do, A.Q.; Grudnitski, G. A neural network approach to residential property appraisal. Real Estate Appraiser 1992, 58, 38–45. [Google Scholar]
- Borst, R.A. Artificial neural networks in mass appraisal. J. Prop. Tax Assess. Adm. 1995, 1, 5–15. [Google Scholar]
- Chiarazzo, V.; Caggiani, L.; Marinelli, M.; Ottomanelli, M. A Neural Network based model for real estate price estimation considering environmental quality of property location. Transp. Res. Proc. 2014, 3, 810–817. [Google Scholar] [CrossRef]
- Yalpir, S.; Durduran, S.S.; Unel, F.B.; Yolcu, M. Creating a Valuation Map in GIS Through Artificial Neural Network Methodology: A Case Study. Acta Montan. Slovaca 2014, 19, 89–99. [Google Scholar]
- Fan, G.Z.; Ong, S.E.; Koh, H.C. Determinants of house price: A decision tree approach. Urban. Stud. 2006, 43, 2301–2315. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; p. 768. [Google Scholar]
- Kontrimas, V.; Verikas, A. The mass appraisal of the real estate by computational intelligence. Appl. Soft Comput. 2011, 11, 443–448. [Google Scholar] [CrossRef]
- Yu, D.; Wu, C. Incorporating Remote Sensing Information in Modeling House Values. Photogramm. Eng. Remote Sens. 2006, 72, 129–138. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Antipov, E.A.; Pokryshevskaya, E.B. Mass appraisal of residential apartments: An application of Random forest for valuation and a CART-based approach for model diagnostics. Expert Syst. Appl. 2012, 39, 1772–1778. [Google Scholar] [CrossRef]
- Yoo, S.; Im, J.; Wagner, J.E. Variable selection for hedonic model using machine learning approaches: A case study in Onondaga County, NY. Landsc. Urban Plan. 2012, 107, 293–306. [Google Scholar] [CrossRef]
- Lake, I.R.; Lovett, A.A.; Bateman, I.J.; Langford, I.H. Modelling environmental influences on property prices in an urban environment. Comput. Environ. Urban. Syst. 1998, 22, 121–136. [Google Scholar] [CrossRef]
- Lancaster, K.J. A new approach to consumer theory. J. Polit. Econ. 1966, 74, 132–157. [Google Scholar] [CrossRef]
- Rosen, S. Hedonic Prices and Implicit Markets: Product Differentiation in Pure Competition. J. Polit. Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Se Can, A.; Megbolugbe, I. Spatial dependence and house price index construction. J. Real Estate Financ. Econ. 1997, 14, 203–222. [Google Scholar] [CrossRef]
- Zuur, A.F.; Ieno, E.N.; Elphick, C.S. A protocol for data exploration to avoid common statistical problems. Methods Ecol. Evol. 2010, 1, 3–14. [Google Scholar] [CrossRef]
- Kaiser, H.F. The application of electronic computers to factor analysis. Educ. Psychol. Meas. 1960, 20, 141–151. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by random Forest. R News 2002, 2, 18–22. [Google Scholar]
- Moore, J.W. Performance comparison of automated valuation models. J. Prop. Tax Assess. Adm. 2006, 3, 43–59. [Google Scholar]
- International Association of Assessing Officers. Guidance on International Mass Appraisal and Related Tax Policy. 2014. Available online: http://www.iaao.org/media/Standards/International_Guidance.pdf (accessed on 3 March 2018).
- Kuhn, M. Caret package. J. Stat. Softw. 2008, 28, 1–16. [Google Scholar]
- Orton, T.; Pringle, M.; Bishop, T. A one-step approach for modelling and mapping soil properties based on profile data sampled over varying depth intervals. Geoderma 2016, 262, 174–186. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman and Hall: New York, NY, USA, 1986; p. 175. [Google Scholar]
- Getis, A.; Ord, J.K. The Analysis of Spatial Association by Use of Distance Statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]

| Variables | Description | Type | VIF |
|---|---|---|---|
| ID_cadas_com | Unique cadastral community ID | neighborhood | 2.0803 |
| ID_building | Building ID within cadas. community | neighborhood | 1.6505 |
| ID_appartment | Apartment ID within a building | structural | 1.3362 |
| floors_total | Total number of floors in the building | structural | 4.2064 |
| year built | Year of construction | time/structural | 1.1748 |
| year_ren_roof | Year of roof replacement | time/structural | 3.1731 |
| year_ren_face | Year of facade insulation | time/structural | 1.4340 |
| constr_type | Construction type (brick, concrete, wood) | structural | 2.0259 |
| Elevator | Elevator | structural | 1.0439 |
| house_type | Housing type (single, double, raw) | structural | 2.8378 |
| no_appart | Number of apartments in building | structural | 1.0815 |
| Northing | N coordinate (mathematical) | neighborhood | 2.4851 |
| Easting | E coordinate (mathematical) | neighborhood | 667.249 * |
| trans_date | Date of transaction (contract) | time | 46.5974 * |
| market zone | Real estate market zone | neighborhood | 1.0117 |
| floor_appartment | Apartment floor number | structural | 1.8006 |
| position_type | Position in building (basement, ground, middle, penthouse) | structural | 7.4933 * |
| Duplex | Apartment in 2 floors | structural | 1.4334 |
| Rooms | Number of rooms in apartment | structural | 1.0680 |
| living_area | Apartment living area | structural | 2.5412 |
| total area | Apartment total area | structural | 11.3511 * |
| year_ren_wind | Year of windows replacement | time/structural | 9.6525 * |
| year_ren_inst | Year of installation replacement | time/structural | 2.0041 |
| floor_above_ground | Apartment above ground floor | structural | 2.4321 |
| dist_Airport | Prox. (Euclidian distance) to airport | accessability | 5.2100 * |
| dist_Public transport | Prox. to city bus station | accessability | 726.2465 * |
| Elevation | Elevation above sea level | environmental | 2.1488 |
| dist_Schools | Prox. to university facilities | accessability | 6.8582 * |
| dist_Highway entr. | Prox. to highway entrance | accessability | 1.2613 |
| dist_Highway | Prox. to highway lane | environmental | 68.622 * |
| dist_Railway | Prox. to railway | environmental | 67.061 * |
| dist_Recreation | Prox. to green areas, forest | accessability | 2.0475 |
| dist_Main roads | Prox. to main city roads | accessability | 3.5815 |
| dist_Regional road | Prox. to regional roads | accessability | 5.5086 * |
| dist_River | Prox. to river banks | environmental | 3.3402 |
| Variables | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | PC9 | PC10 | h2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ID_cadas_com | −0.04 | 0.01 | −0.05 | 0 | 0.09 | 0.84 | 0.09 | −0.03 | 0 | 0.02 | 0.72 |
| ID_builing | 0.27 | 0.1 | −0.25 | 0.05 | 0.1 | 0.16 | −0.12 | 0.31 | −0.6 | −0.02 | 0.65 |
| ID_appartment | 0.07 | 0.23 | −0.07 | 0 | −0.06 | 0.02 | −0.05 | 0.22 | 0.52 | 0.01 | 0.39 |
| floors_total | 0.05 | 0.83 | 0.05 | −0.09 | −0.14 | 0.1 | 0.03 | −0.02 | 0.22 | −0.08 | 0.78 |
| floor_entrance | 0 | 0.27 | 0.25 | 0 | −0.22 | 0.05 | 0.17 | −0.1 | −0.05 | 0.22 | 0.28 |
| year built | 0.85 | 0.11 | 0 | −0.03 | 0.13 | 0.04 | −0.12 | 0 | 0.04 | −0.01 | 0.76 |
| year_ren_roof | 0.62 | −0.04 | 0.02 | 0.05 | 0.04 | −0.09 | −0.05 | 0.02 | −0.08 | −0.04 | 0.41 |
| year_ren_face | 0.75 | 0.1 | 0.06 | −0.01 | 0.09 | −0.12 | −0.08 | 0.07 | −0.02 | −0.05 | 0.62 |
| constr_type | −0.05 | 0.03 | −0.06 | −0.05 | −0.02 | 0 | 0.04 | −0.07 | −0.1 | 0.64 | 0.44 |
| elevator | 0.28 | 0.7 | 0.07 | 0.01 | −0.03 | 0.06 | 0.15 | 0.02 | 0.05 | −0.09 | 0.61 |
| house_type | −0.03 | −0.07 | 0.12 | 0.04 | −0.08 | −0.04 | 0.09 | −0.03 | −0.08 | 0.51 | 0.31 |
| no_appart | 0.13 | 0.55 | −0.11 | −0.15 | −0.07 | 0.01 | −0.11 | 0.19 | 0.53 | −0.14 | 0.71 |
| northing | 0.08 | 0.07 | 0.84 | −0.03 | 0.3 | 0.09 | −0.1 | −0.16 | 0.14 | −0.03 | 0.88 |
| easting | −0.04 | 0.09 | −0.49 | −0.06 | 0.19 | 0.19 | 0.25 | −0.41 | 0.42 | 0.05 | 0.73 |
| trans_date | −0.03 | 0.02 | 0.07 | −0.03 | −0.03 | −0.05 | 0.09 | −0.04 | −0.16 | −0.46 | 0.26 |
| market zone | −0.02 | 0.05 | −0.07 | −0.12 | −0.09 | 0.16 | −0.19 | 0.71 | 0.01 | −0.09 | 0.6 |
| floor_appartment | −0.03 | 0.91 | 0.02 | −0.02 | −0.05 | 0.02 | −0.01 | −0.02 | 0.02 | −0.01 | 0.83 |
| postion_type | −0.04 | 0.4 | −0.02 | 0.05 | −0.02 | −0.06 | −0.02 | 0 | −0.29 | 0.15 | 0.28 |
| duplex | 0.02 | −0.02 | 0 | 0.32 | 0.03 | 0 | −0.02 | −0.01 | −0.1 | 0.05 | 0.12 |
| rooms | 0.02 | −0.03 | −0.01 | 0.85 | 0.02 | −0.01 | 0 | −0.02 | 0.06 | −0.02 | 0.73 |
| living_area | −0.02 | −0.01 | 0 | 0.95 | −0.02 | −0.02 | 0.08 | −0.02 | 0.02 | −0.02 | 0.92 |
| total area | 0.02 | −0.02 | 0 | 0.94 | −0.01 | −0.02 | 0.09 | 0 | 0.02 | −0.02 | 0.89 |
| year_ren_wind | 0.83 | 0.01 | 0.01 | 0 | 0.02 | 0.06 | −0.02 | −0.05 | 0.04 | 0.05 | 0.7 |
| year_ren_inst | 0.86 | 0 | 0.01 | 0.02 | 0.06 | 0.03 | −0.02 | −0.02 | 0.05 | 0.06 | 0.75 |
| floor_above_ground | −0.05 | 0.81 | 0 | −0.03 | −0.01 | −0.03 | −0.07 | −0.01 | 0.04 | −0.04 | 0.67 |
| dist_Airport | −0.07 | −0.06 | −0.92 | 0.01 | −0.17 | −0.06 | 0.13 | 0.06 | −0.04 | 0.04 | 0.91 |
| dist_Public transport | 0.1 | −0.04 | 0.06 | 0.01 | 0.72 | −0.02 | 0.11 | −0.12 | −0.12 | −0.07 | 0.59 |
| Elevation | −0.02 | −0.01 | 0.82 | 0.04 | −0.09 | 0.05 | −0.22 | 0.29 | −0.16 | 0.02 | 0.84 |
| dist_Schools | 0.15 | −0.09 | −0.07 | 0.05 | 0.34 | −0.08 | −0.05 | 0.26 | −0.02 | 0.34 | 0.35 |
| dist_Highway entr. | −0.13 | −0.01 | −0.24 | 0.08 | 0.05 | −0.01 | 0.92 | −0.13 | −0.01 | 0.02 | 0.94 |
| dist_Highway | −0.14 | 0.02 | −0.24 | 0.06 | −0.02 | 0.01 | 0.91 | −0.12 | 0.01 | 0.02 | 0.93 |
| dist_Railway | 0.04 | −0.09 | 0.26 | 0.06 | 0.21 | −0.29 | −0.02 | 0.54 | 0.2 | 0.08 | 0.54 |
| dist_Recreation | 0.08 | −0.04 | 0.07 | −0.01 | 0.75 | 0.33 | −0.2 | −0.05 | 0.01 | −0.06 | 0.73 |
| dist_Main roads | 0.12 | −0.17 | 0.2 | 0.05 | 0.82 | −0.22 | 0.09 | 0.12 | 0.04 | 0.04 | 0.84 |
| dist_Regional road | −0.23 | 0.07 | 0.09 | 0 | −0.49 | −0.07 | 0.5 | 0.5 | 0.04 | 0 | 0.81 |
| dist_River | −0.07 | 0.08 | 0.42 | −0.06 | −0.13 | 0.74 | −0.17 | 0.08 | 0 | 0 | 0.79 |
| SS loadings | 3.44 | 3.38 | 3.07 | 2.71 | 2.49 | 2.34 | 1.67 | 1.66 | 1.4 | 1.15 | |
| Proportion Var | 0.1 | 0.09 | 0.09 | 0.08 | 0.07 | 0.07 | 0.05 | 0.05 | 0.04 | 0.03 |
| OLS | RF | |||
|---|---|---|---|---|
| Train | Test | Train | Test | |
| SR | 1.0447 | 1.0465 | 1.0191 | 1.0197 |
| MAPE [%] | 16.85 | 17.48 | 7.04 | 7.27 |
| COD [%] | 16.52 | 17.12 | 7.05 | 7.28 |
| R2 | 0.23 | 0.57 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Čeh, M.; Kilibarda, M.; Lisec, A.; Bajat, B. Estimating the Performance of Random Forest versus Multiple Regression for Predicting Prices of the Apartments. ISPRS Int. J. Geo-Inf. 2018, 7, 168. https://doi.org/10.3390/ijgi7050168
Čeh M, Kilibarda M, Lisec A, Bajat B. Estimating the Performance of Random Forest versus Multiple Regression for Predicting Prices of the Apartments. ISPRS International Journal of Geo-Information. 2018; 7(5):168. https://doi.org/10.3390/ijgi7050168
Chicago/Turabian StyleČeh, Marjan, Milan Kilibarda, Anka Lisec, and Branislav Bajat. 2018. "Estimating the Performance of Random Forest versus Multiple Regression for Predicting Prices of the Apartments" ISPRS International Journal of Geo-Information 7, no. 5: 168. https://doi.org/10.3390/ijgi7050168
APA StyleČeh, M., Kilibarda, M., Lisec, A., & Bajat, B. (2018). Estimating the Performance of Random Forest versus Multiple Regression for Predicting Prices of the Apartments. ISPRS International Journal of Geo-Information, 7(5), 168. https://doi.org/10.3390/ijgi7050168





