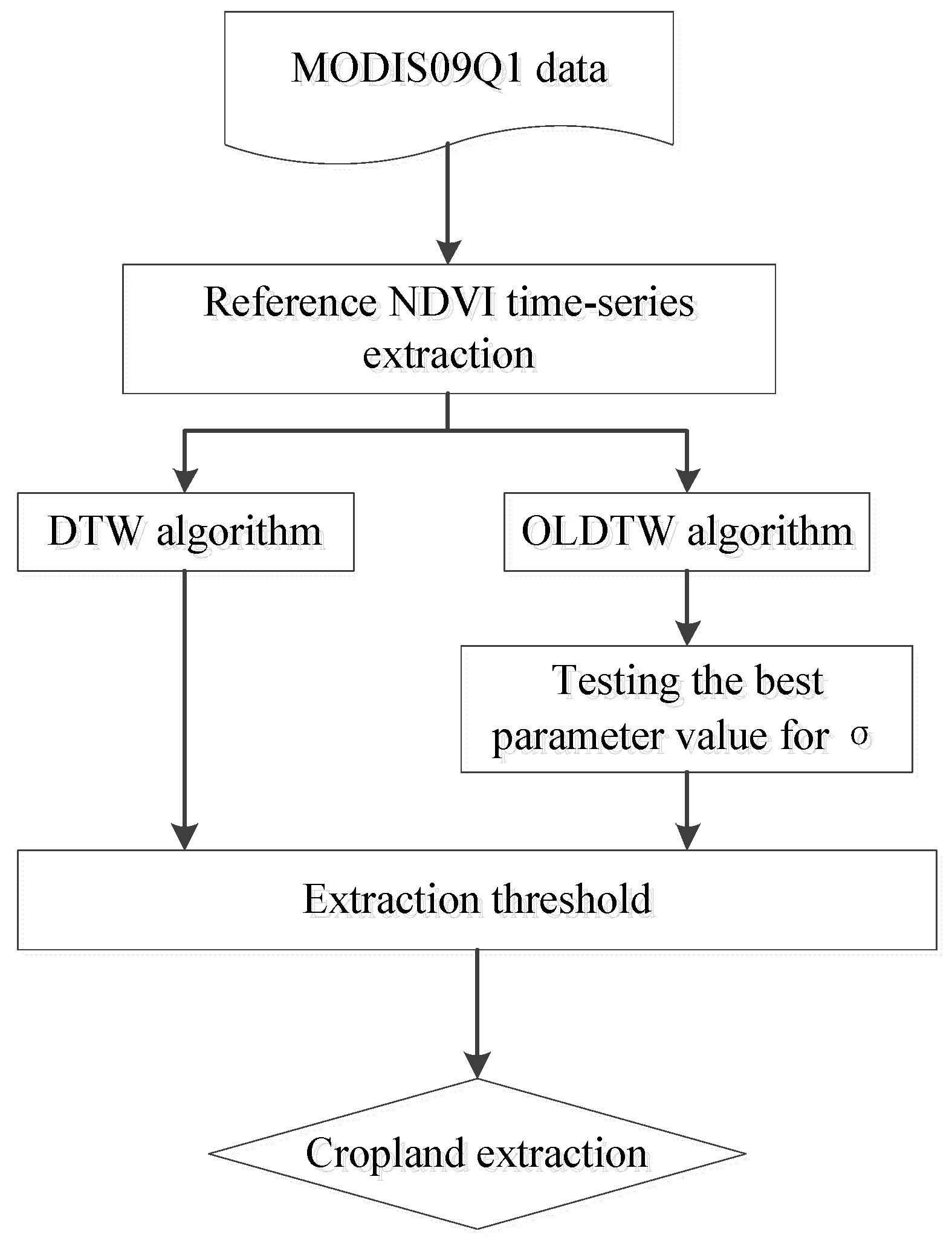
2.3.2. Review of Original Dynamic Time Warping
DTW uses a dynamic programming technique to find the minimal distance between two time series, where sequences are warped by stretching or shrinking the time dimension [
37]. The DTW algorithm is described below.
Suppose that we have two time series, i.e., C = {c1, c2, …, cm} and Q = {q1, q2, …, qn}, with respective lengths of m and n. We construct an m × n matrix Am×n and define the distance between each element as aij = d(Ci, Qj) = . In the matrix Am×n, a warping path is set by a group of adjacent matrix elements, and notes for ω = {ω1, ω2, ..., ωk} and the kth element in ω are defined as ωk = (aij)k; this path must satisfy the following conditions:
Monotonicity constraint: ωk = aij, ωk+1 = ai’j’, then i’ ≥ i and j’ ≥ j
Endpoint constraint: ω1 = a11, ωK = amn
Continuity constraint: ωk = aij, ωk+1 = ai’j’; then i’ ≤ i + 1 and j’ ≤ j + 1.
Thus, DTW(C, Q) = min
. The DTW algorithm can be summarized by applying ideal dynamic programming to find the best (i.e., least bending) cost path, as shown in Equation (2):
where i = 2, 3, …, m and represents the row index of the matrix and j = 2, 3, …, n and represents the column index of the matrix. D(i, j) is the minimum cumulative value of the warping paths.
The greater the distance between two time series, the more dissimilar the two time series are. The lower the distance between the two time series, the more similar the two time series are.
2.3.3. Local Weighting Added to the Seasonal Cycle Section
● General frame of the OLWDTW method
In the original version of DTW distance, the warping path is not limited by windows [
31]. We call the original DTW (ODTW) algorithm the open-boundary DTW method. Although many applications use the window-restricted DTW for the best warping path search, we used the open-boundary DTW in this study and did not restrict the warping path.
Sunlight, heat, and moisture conditions in Southeast Asia can affect when crops are planted. Identification of crops in remote sensing images of Southeast Asia should focus on the shape of the seasonal cycle rather than focusing on the beginning or the ending time of the seasonal cycle. For example, rice plantation could last from the 30th to 150th day of the year. It also could last from the 150th to 270th day. In either case, the seasonal growth cycle shape is similar. Enhancing the effect of the seasonal growth cycle when comparing the NDVI time series, while keeping the open-boundary characteristic of the original DTW algorithm, should help better recognize croplands. To enhance the effect of the seasonal cycle when comparing the NDVI cycle’s similarities, this locally weighted open-boundary DTW adds a coefficient σ to the section of the reference NDVI time series of crop types.
In
Section 2.3.2, suppose time series C is the reference crop growth NDVI time series. C = {c
1, c
2, …, c
m} and the growing season is from time
to time
, thus
. Add the coefficient σ to the section of the reference NDVI time series of crop types and Equation (3) becomes:
After running many tests using different values of σ, we found that for different crop types’ NDVI time series, the value of σ was different. The effectiveness of the OLWDTW method is illustrated by picking an NDVI time series from the satellite data and manually making a curve. As shown in
Figure 3, the reference curve is the rice paddy cultivation field picked from the satellite data. The rice paddy curve is a man-made curve where the seasonal growth section on the curve from day 161 to day 345 is the same as the reference rice paddy curve picked from the satellite data. Using the original DTW algorithm comparing the distance between the reference rice paddy field curve with the manually made rice paddy curve and the dryland curve, the distance values are 0.5008 and 1.4333.
According to the reference rice paddy cultivation field, the growing season of a rice paddy field is from day 161 to day 345, so
and
in Equation (3) are 20 and 43. Using the OLWDTW method to enhance the seasonal section on the curve according to Equation (3), we tested using different values of
and the result is shown in
Table 1. As the parameter
grows, the value of OLWDTW distance are invariant between the reference curve with the rice paddy curve where the seasonal growth curve is the same as the reference curve. Not unexpectedly, the distance increases between the reference curve of the rice paddy field and the dryland crop field curve.
From the test above we can conclude that the open-boundary DTW is beneficial to cropland identification in flexible cropping conditions. The OLWDTW better distinguishes different crops. It seems to be that, as the value of increases, the rice paddy is increasingly better distinguished from dryland crops. However, in the real world, the seasonal growth cycles are not identical to the reference time series’ seasonal growth section cycle. In real-world testing we find that to make the best intra-class and inter-class distinction between crops and other land cover types, there exists an optimal value to distinguish cropland types.
● Parameter value selection for OLWDTW method
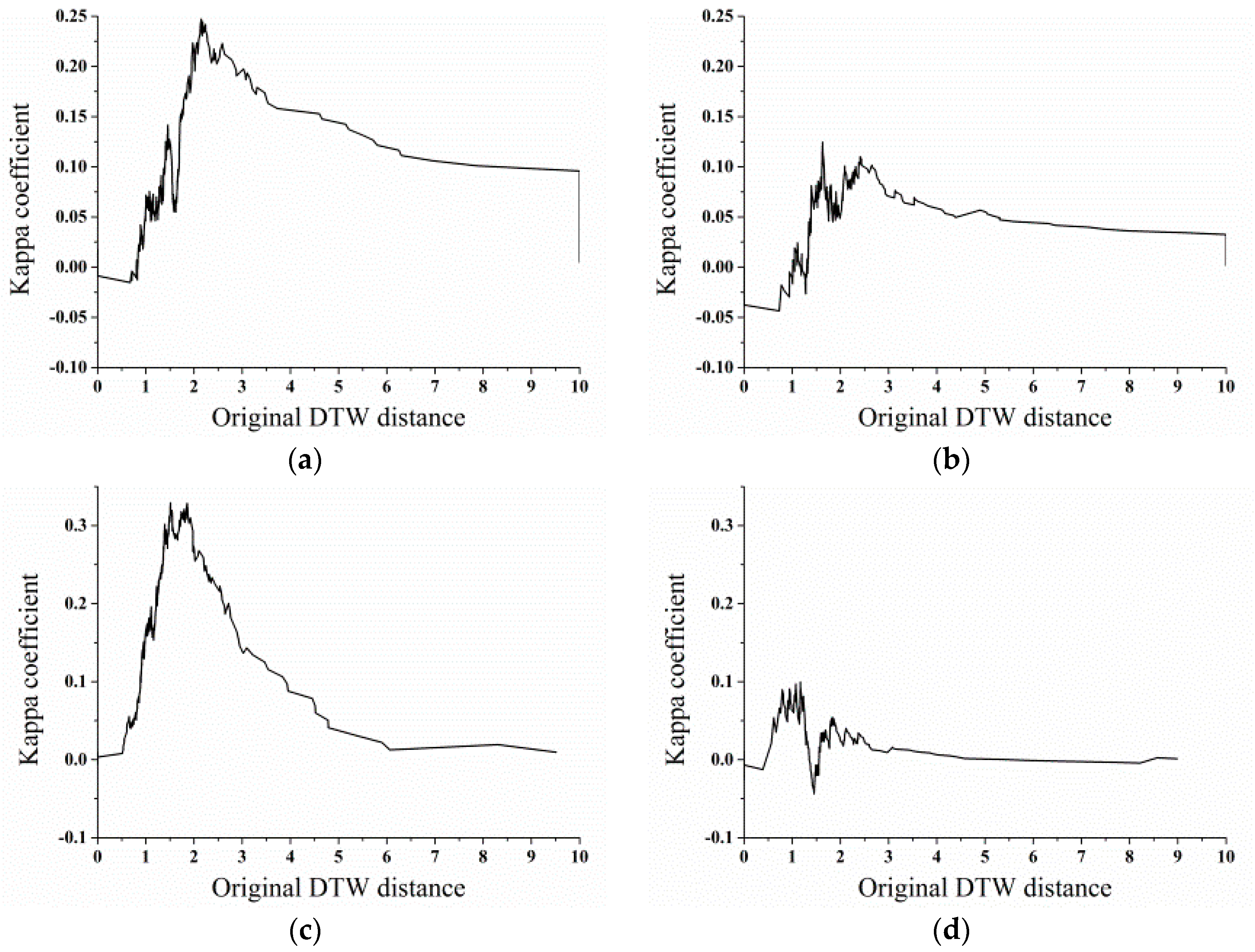
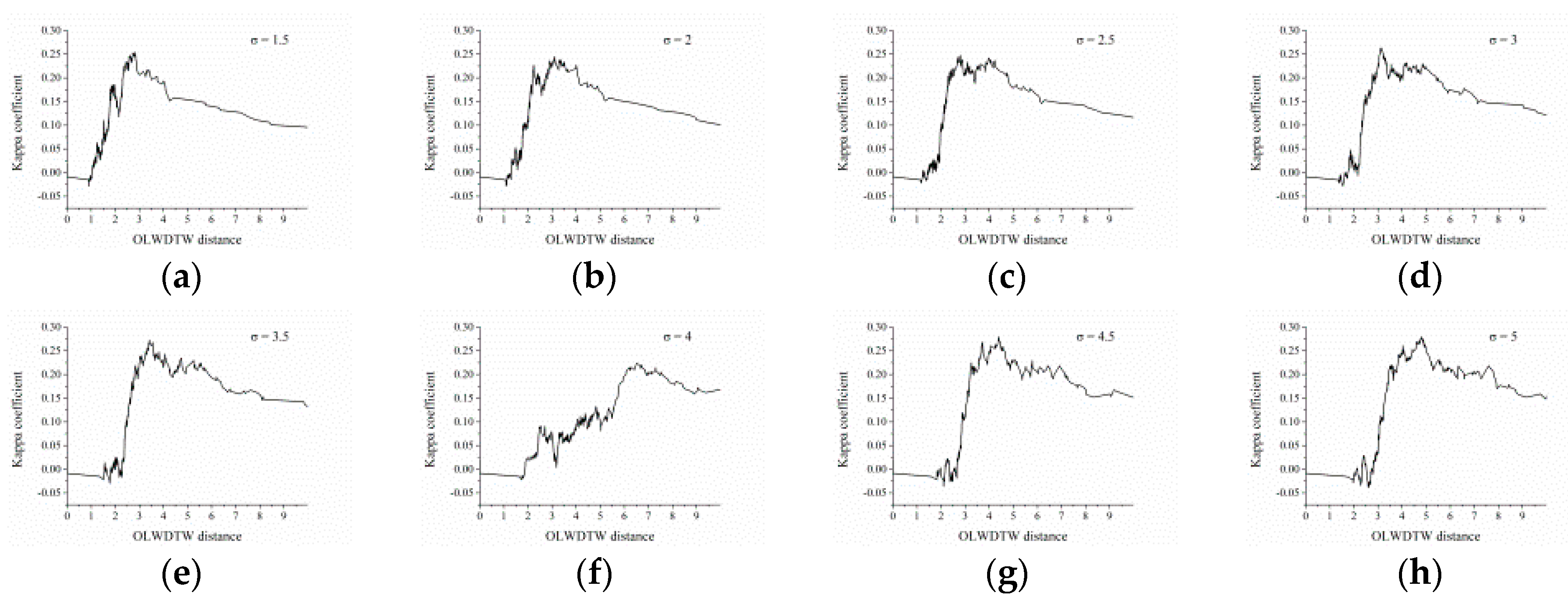
For the OLWDTW method, the major problem is selecting the
value to achieve the highest classification accuracy. In this paper, we repeatedly tested the performance of OLWDTW under different
values for 300 sample points in test site 1 and 300 sample points in test site 2, using the sample points to obtain the distance of the pixel’s NDVI time series with the reference NDVI time series. The performance is evaluated by the kappa coefficient. This step is to obtain the value of
and use this parameter to achieve the highest classification accuracy of cropland by the OLWDTW method. The kappa coefficient was defined as the proportion of agreements between paired observations, corrected for chance agreement as estimated from the marginal frequencies over the K response categories [
38,
39]. The equation to calculate the kappa coefficient is shown in Equation (4):
where
is the observed agreement and
is the chance agreement.
Calculation of the observed agreement
is shown in Equation (5). Calculation of the chance agreement
is shown in Equation (6):
where n is the total number of observations, a is the number of agreements of observation 1 and observation 2 on a positive category, b is the number of agreements of observation 1 and observation 2 on a negative category, c is the number of negative category of observation 1 but positive category on observation 2, d is the number of positive category of observation 1 but negative category on observation 2 and as shown in
Table 2.
Before explaining how to select the parameter , we should first explain how to select the threshold on the similarity measure map to obtain the highest classification accuracy. The method is simple. It first compares the similarity between each pixel’s NDVI time series with the reference NDVI time series using the ODTW/OLWDTW distance method. The lower the value of the distance between a pixel’s NDVI time series with the reference NDVI time series, the more likely the pixel is to belong to the land cover type of the reference NDVI time series. The second step of our method is to select a threshold value. Those pixels with distance values higher than the threshold are considered to not belong to the cropland type of the reference NDVI time series. Those pixels with distance values lower than the threshold are considered to belong to the cropland type of the reference NDVI time series so that when we select the threshold value, it guarantees the highest kappa coefficient value. The threshold is obtained in three steps:
Arrange the randomly selected sample points by distance to the reference NDVI time series.
Calculate the kappa coefficient by hypothesizing the threshold from the first value arranged in the distance list to the last value of the distance.
Ensure the threshold value brings the highest kappa coefficient.
As shown in
Table 3, assume that 10 sample points are randomly selected. They have two attributes. The first is the true classification of whether the pixel belongs to the crop type of the reference NDVI time series (“True classification” in the first column in
Table 3). The second attribute is the distance between the pixels’ NDVI time series and the reference NDVI time series (“Distance value” in the second column in
Table 3). Threshold is the distance value to be used. For example, if the threshold value is 0.99, then the threshold classification result value at 0.99 is 0 (“Threshold classification result” in the third column in
Table 3) and the rest of the distance value is 1. Then the first row is correctly classified (the true classification result is 0 and the classification result with a threshold distance of 0.99 is 0), while the second row is misclassified because the true classification result is 0 and the classification result with distance value 0.99 is 1. Thus, the third row, sixth row, seventh row, ninth row and tenth row are correctly classified. The second row, fourth row, fifth row and eighth row are misclassified. Then according to Equation (4), the kappa coefficient value is 0. If the threshold value is 1.17, then the threshold classification result value of 0.99 and in 1.17 is 0 and the remaining distance value is 1. The kappa coefficient is 0.2 and so on. In
Table 3, when the threshold distance value is 1.52, the kappa coefficient reached its highest value of 0.6 so the threshold we use is 1.52.
Obtaining the value of achieves the highest cropland classification accuracy using the OLWDTW method. We tested values from 1.5 to 5 and increased by 0.5. Selecting the highest kappa coefficient then selecting the value of resulted in the highest kappa coefficient.