Studying the Association between Green Space Characteristics and Land Surface Temperature for Sustainable Urban Environments: An Analysis of Beijing and Islamabad
Abstract
:1. Introduction
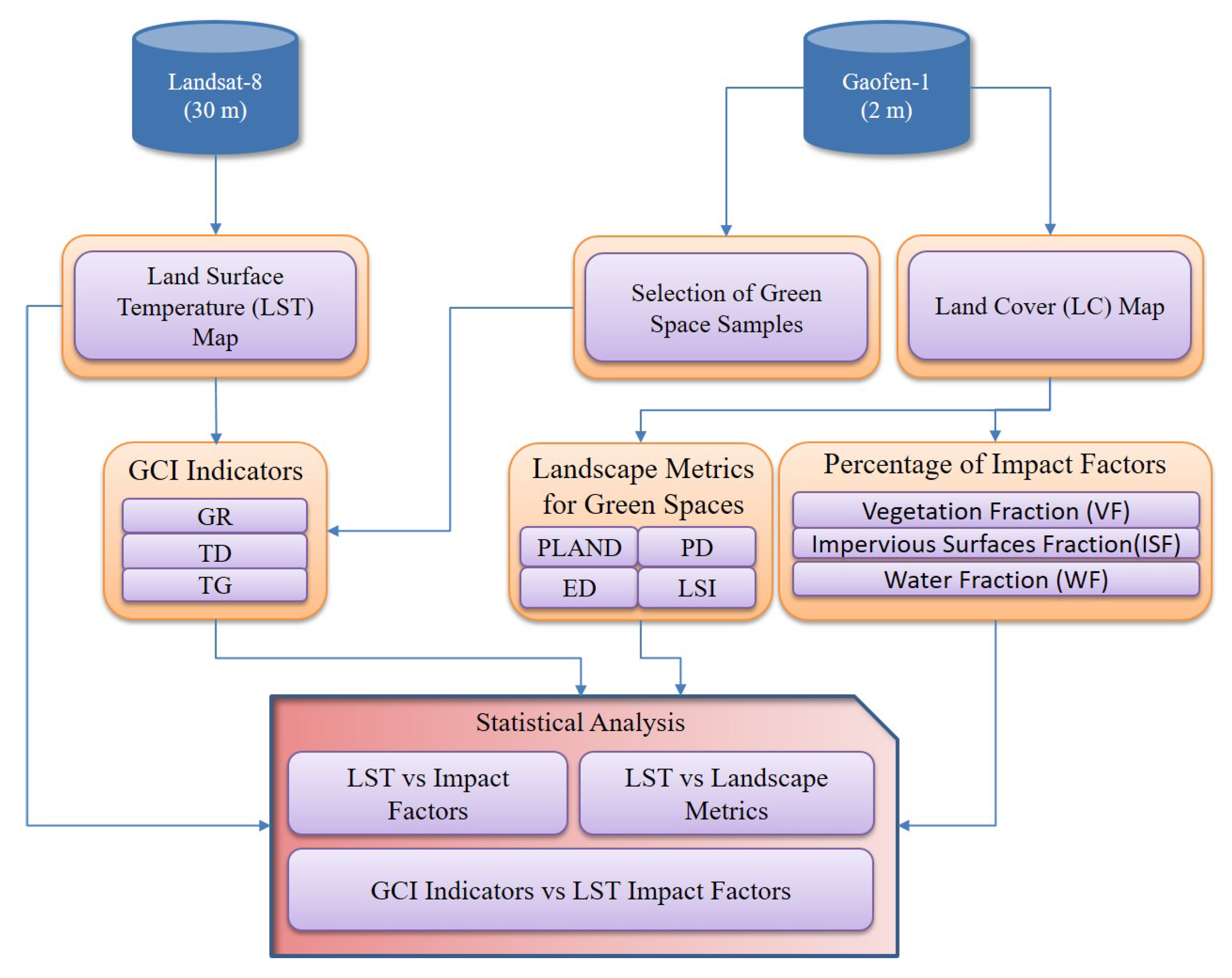
2. Materials and Methods
2.1. Study Area
2.2. Satellite Data Sources
2.3. Methodological Approach
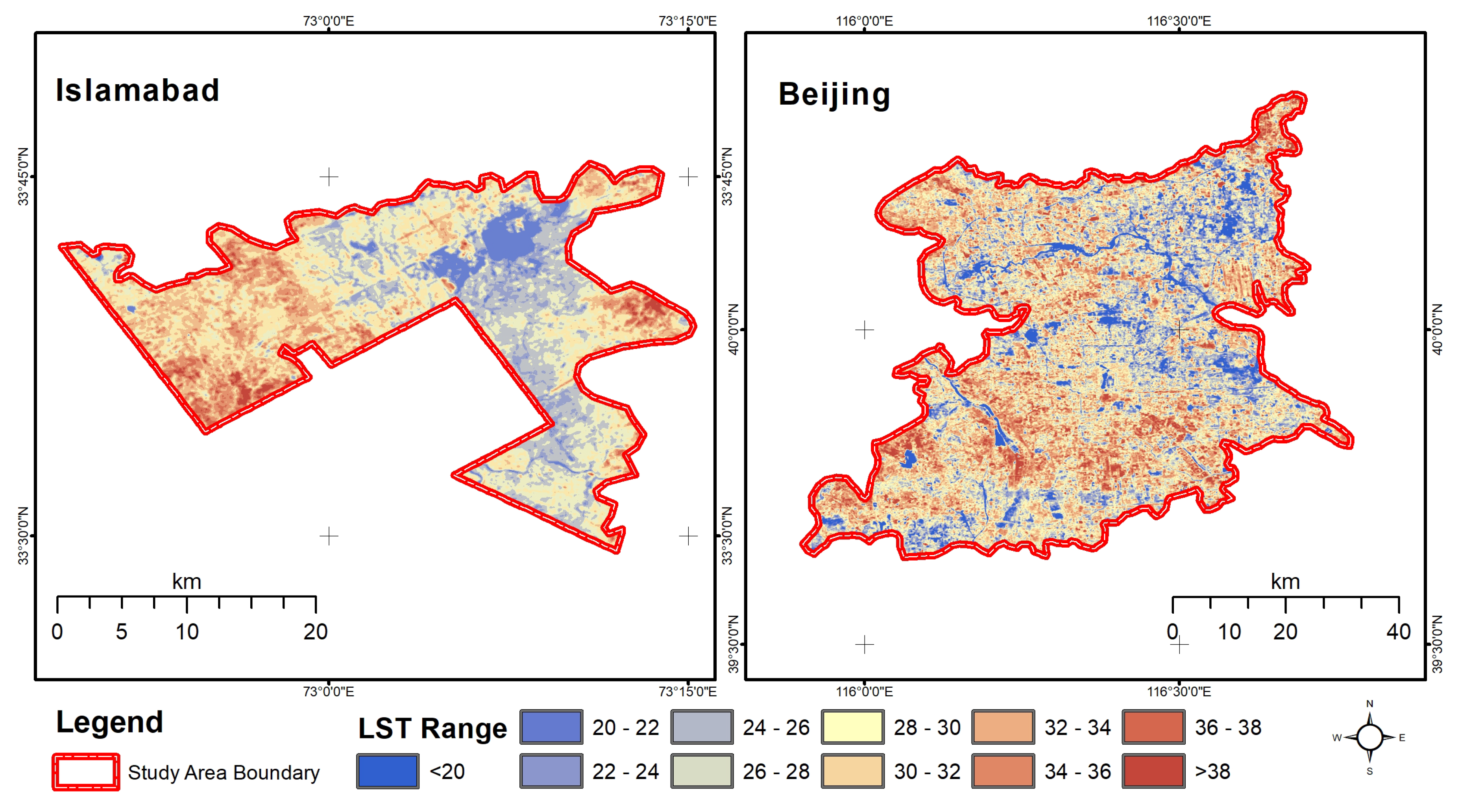
2.4. Land Surface Temperature (LST) Retrieval
- , , , , , and = the split-window coefficients;
- = brightness temperature of band 10 (Kelvin K);
- = brightness temperature of band 11 (Kelvin K);
- = mean value of Land Surface Emissivity (LSE) of TIR bands;
- W = content of water vapors in the atmosphere;
- = difference between LSE of bands 10 and 11.
2.4.1. Brightness Temperature ()
- = reflectance of band 10 or 11;
- = band-specific multiplicative rescaling factor;
- = the additive rescaling factor.
- , = thermal conversion constants. These are different for both TIR bands and are given in the metadata files;
- = radiance of Top of the Atmosphere (ToA).
2.4.2. Land Surface Emissivity (LSE)
- = Normalized Difference Vegetation Index;
- = reclassified NDVI value for soil;
- = reclassified NDVI value for vegetation.
2.4.3. NDVI Threshold
- = mean LSE;
- = difference in LSE.
2.5. Statistical Approach
- and = probability distribution for whole function;
- s = support of variable.
- and = marginal probability density functions;
- = joint probability density function of x and y.
- = probability of an event for of possible values from a definite set .
- and = marginal probability density functions;
- = joint probability density function of x and y.
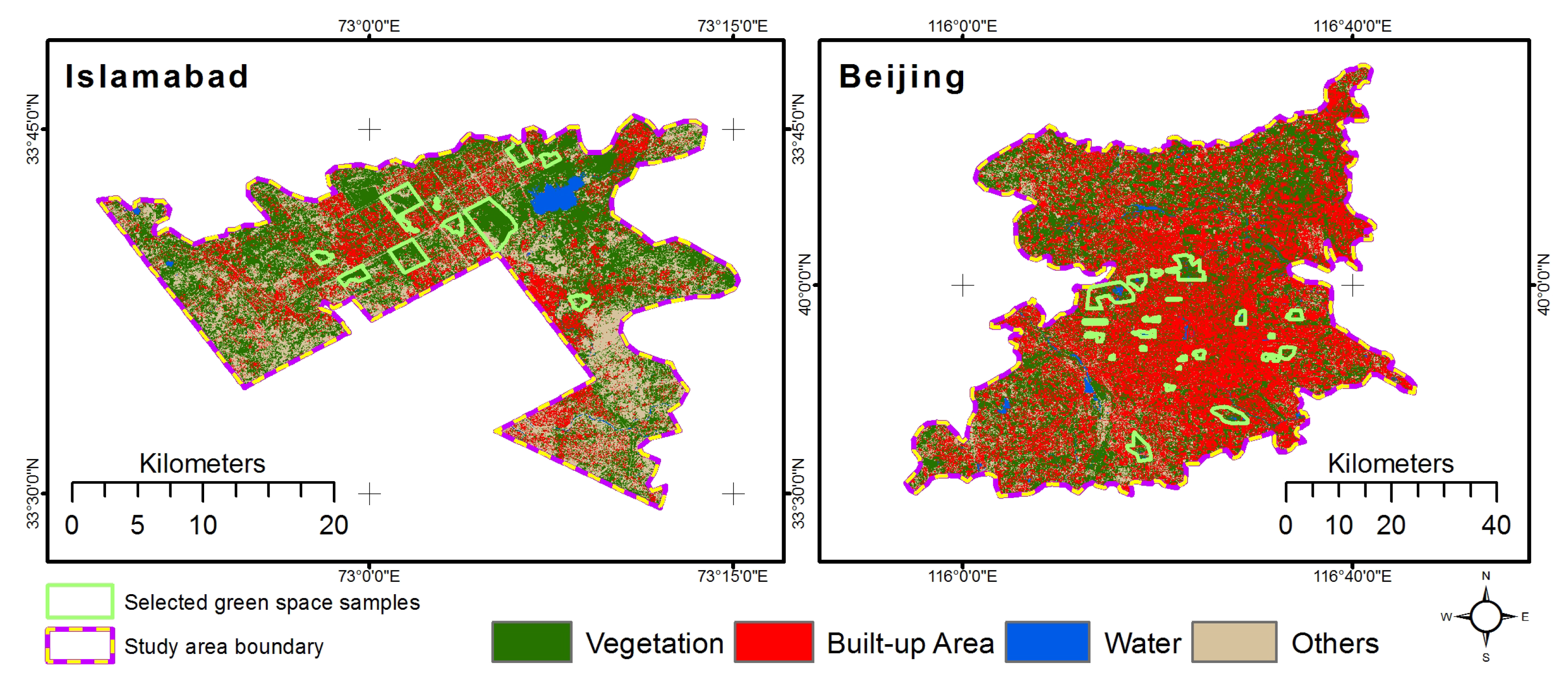
2.6. Land Cover Classification
2.7. Green Space Characteristics, Indicators, and Impact Factors
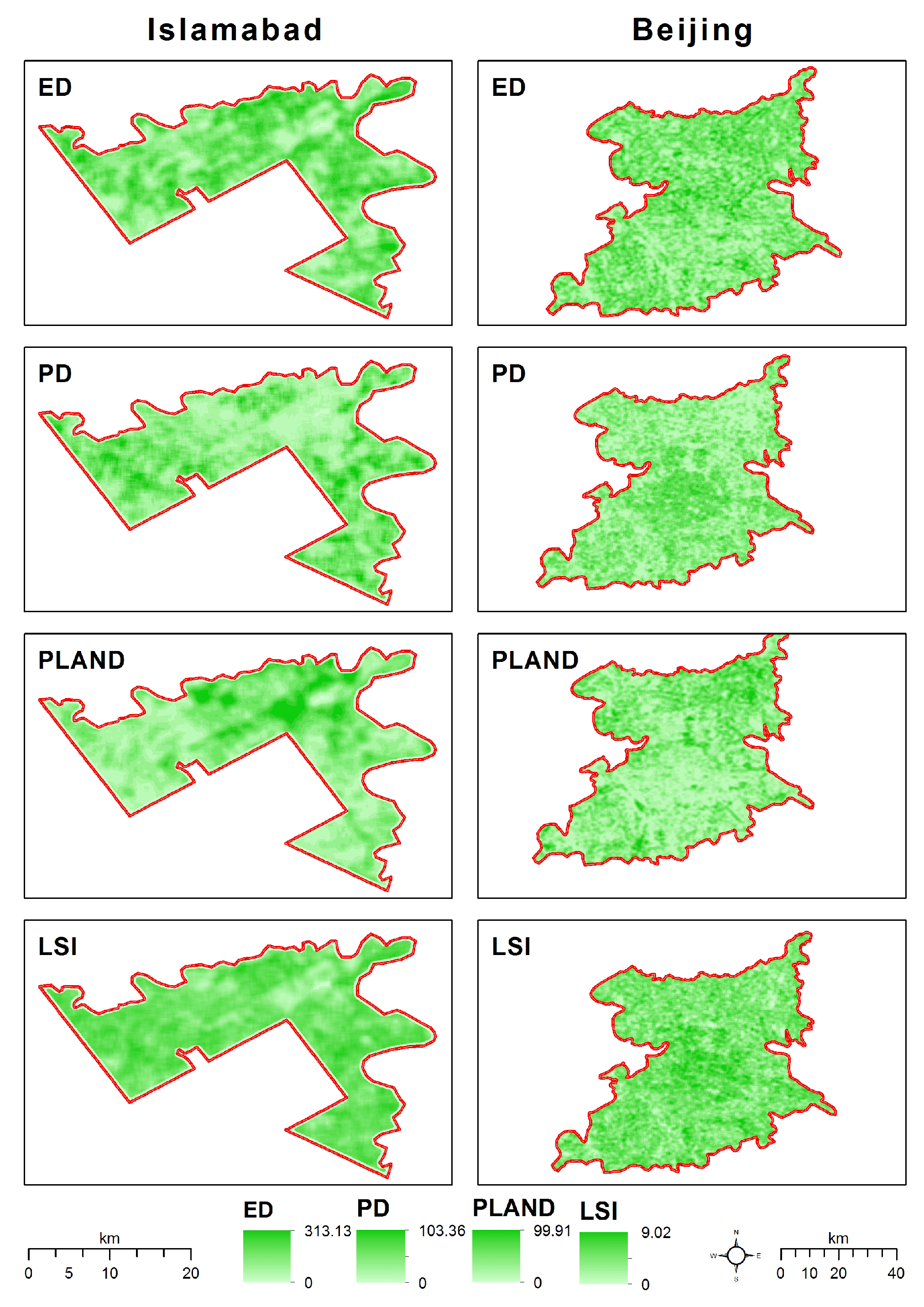
2.7.1. Green Space Spatial Patterns
2.7.2. GCI Indicators and LST Impact Factors
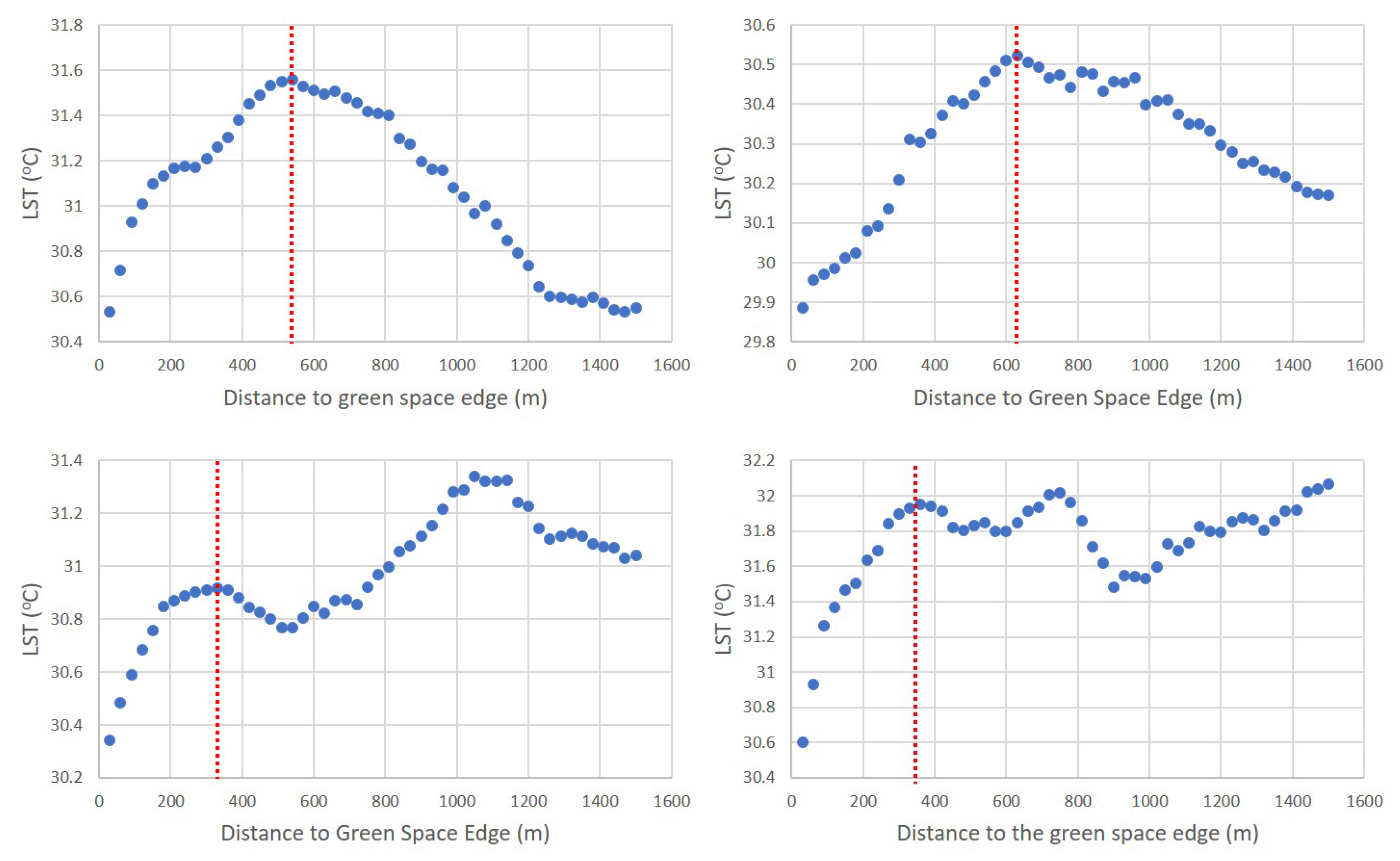
- Green Space Range (GR): The distance between green space edge and the first drop in temperature outside the green space. It is measured in km.
- Temperature Difference (TD): The LST difference between the first drop in temperature and the average temperature of the green space interior. It is measured in C.
- Temperature Gradient (TG): The temperature drop per unit distance in the surrounding areas. It is measured in C/km.
- Green Space Area (GSA)
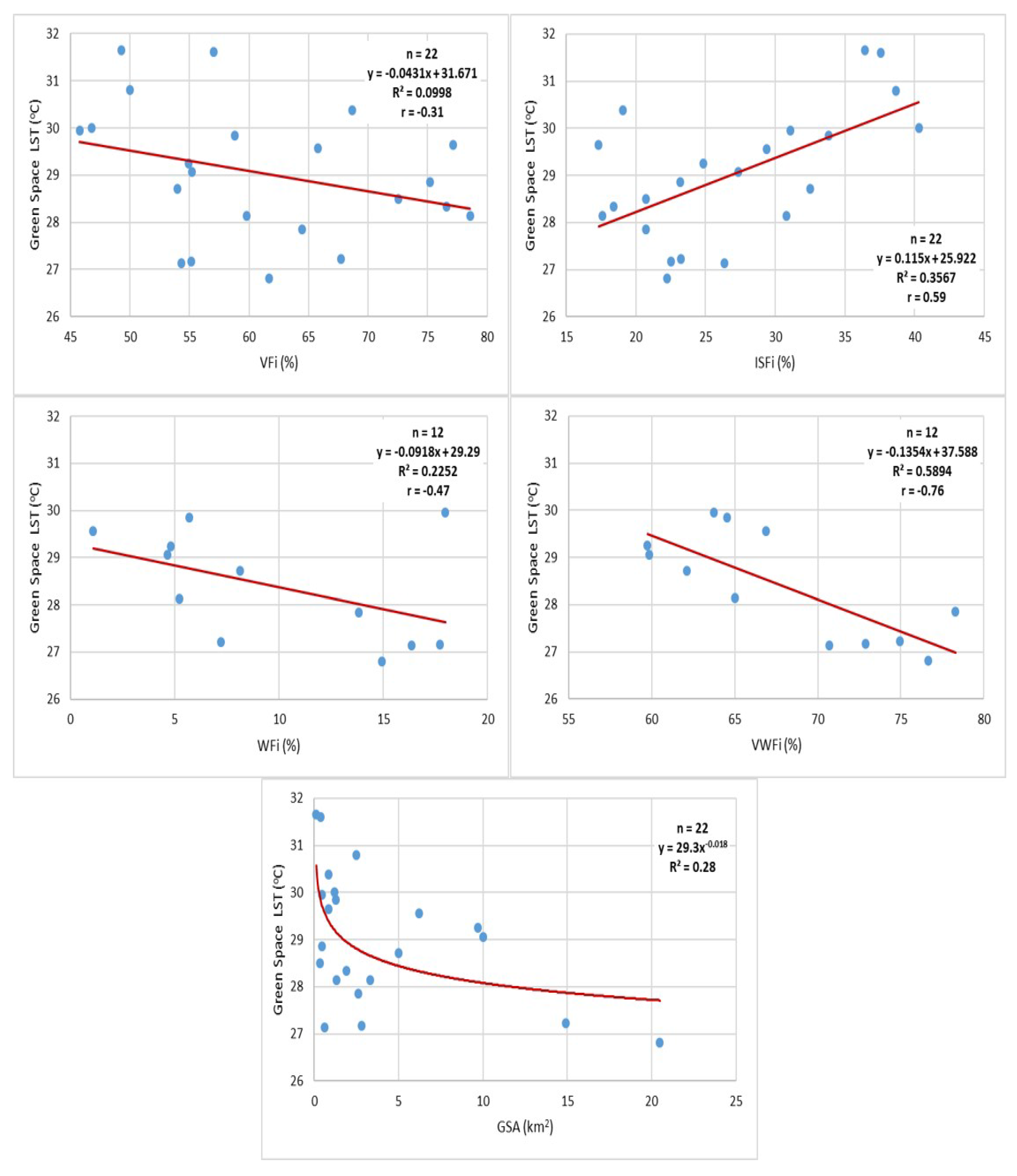
- Vegetation fraction within the green space boundary (VFi)
- Water body fraction within the green space boundary (WFi)
- Impervious surface fraction within the green space boundary (ISFi)
- The combined effect of vegetation and water fractions within the green space boundary (VWFi)
- Vegetation fraction outside the green space boundary (VFo)
- Water body fraction outside the green space boundary (WFo)
- Impervious surface fraction outside the green space boundary (ISFo)
- The combined effect of vegetation and water fractions outside the green space boundary (VWFo)
3. Results
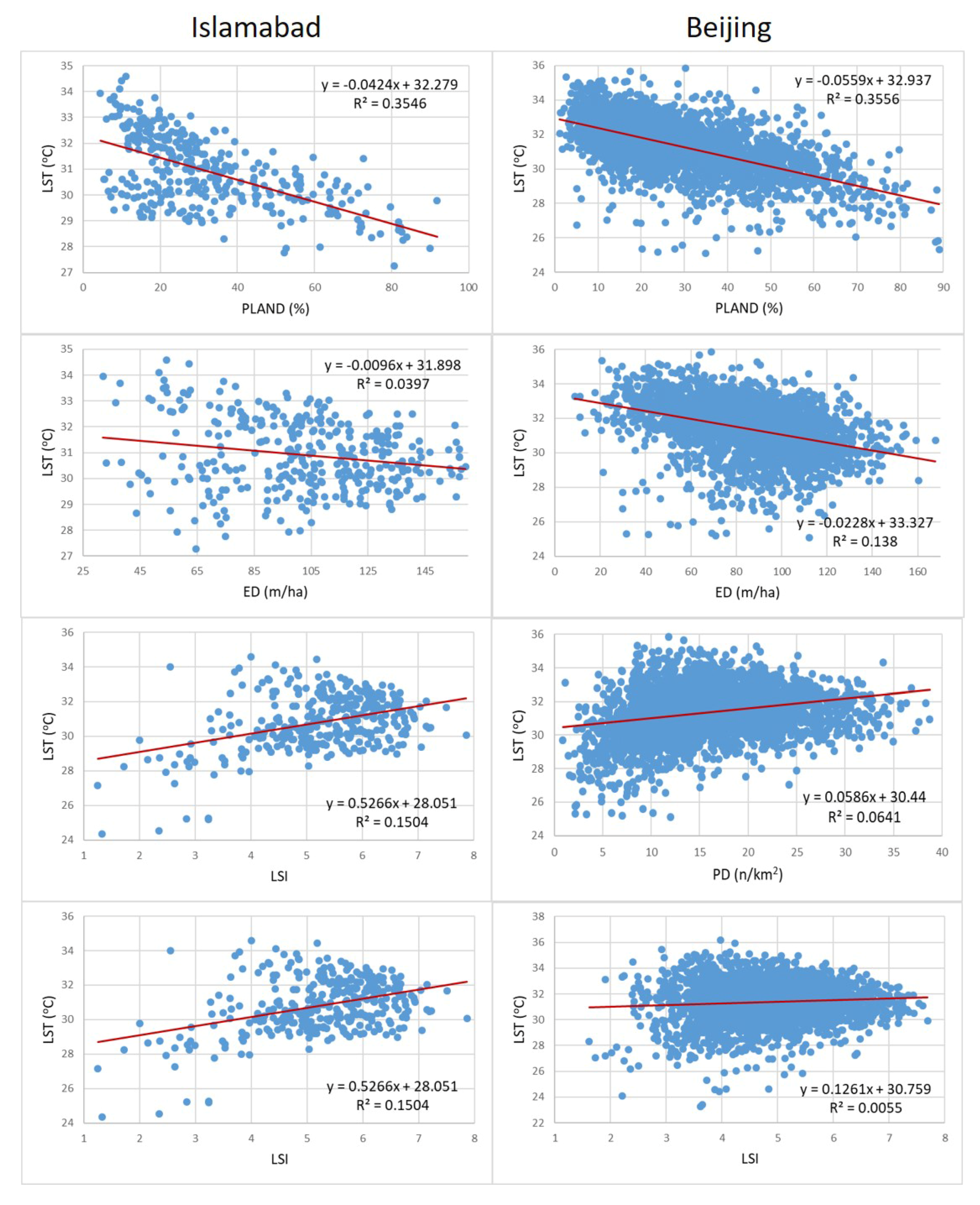
3.1. Correlation between Green Space Spatial Patterns and LST
3.2. Characteristics of Green Spaces and GCI Effect
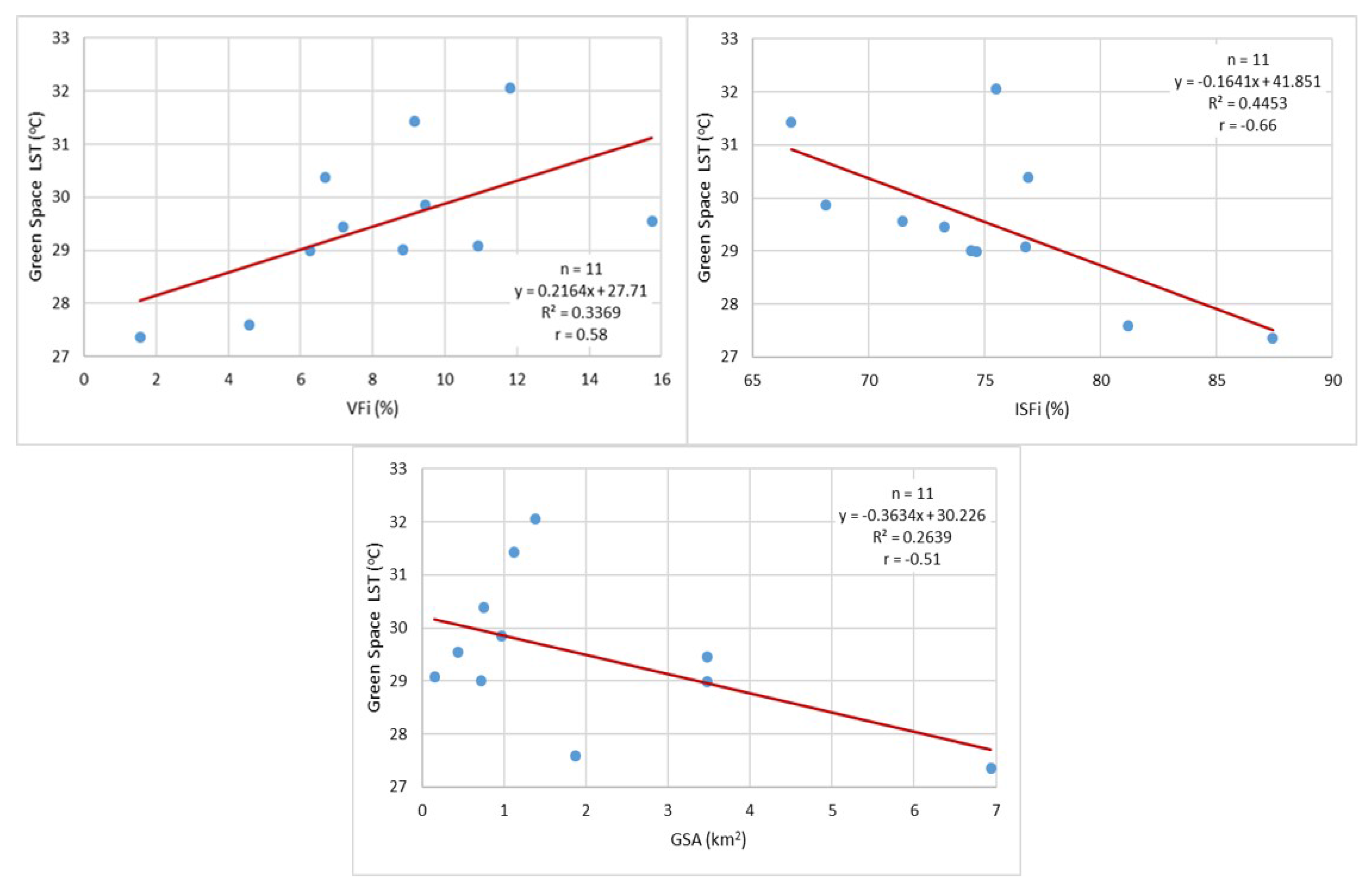
3.2.1. Relation between Surface Temperature of Green Space and Impact Factors
3.2.2. Relation between LST Impact Factors and GCI Indicators
4. Discussion
4.1. Green Space Spatial Patterns and LST
4.2. GCI Indicators and LST Impact Factors
4.3. Urban Planning Implications
5. Conclusions
- (1)
- Complex shapes of green space and more fragmentation supports the SUHI phenomena because green spaces with square shape, less fragmentation, and a greater percentage of vegetation contribute to reducing the surface thermal impacts.
- (2)
- Increase in the GSA by considering the threshold (2-km for Islamabad and 5-km for Beijing) increases the green space efficiency because, when GSA crosses a certain threshold, the SUHI mitigation efficiency starts increasing.
- (3)
- The green space efficiency depends on interior characteristics as well as those of the surrounding environment. To strengthen the cooling effect and efficiency with the help of GCI, urban designers should consider the increase in vegetation fraction, decrease in impervious surfaces fraction, and increase the water bodies fraction inside and around green spaces.
- (4)
- When designing the future urban layout of Islamabad, the construction of artificial lakes within urban green spaces would be beneficial, as is the case with Beijing.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Frank, A. Tracing socioeconomic pattern of urban development: issues, problems and methods of spatio-temporal urban analysis. In Proceedings of the Geoinformatics Conference, Ann Arbor, MI, USA, 10–12 March 1999; pp. 1–12. [Google Scholar]
- Orville, R.E.; Huffines, G.; Nielsen-Gammon, J.; Zhang, R.; Ely, B.; Steiger, S.; Read, W. Enhancement of cloud-to-ground lightning over Houston, Texas. Geophys. Res. Lett. 2001, 28, 2597–2600. [Google Scholar] [CrossRef]
- Meyer, W.B.; Turner, B.L. Changes in Land Use and Land Cover: A Global Perspective; Cambridge University Press: Cambridge, UK, 1994; Volume 4. [Google Scholar]
- Grove, J.M.; Burch, W.R. A social ecology approach and applications of urban ecosystem and landscape analyses: A case study of Baltimore, Maryland. Urban Ecosystems 1997, 1, 259–275. [Google Scholar] [CrossRef]
- Breuste, J.; Feldmann, H.; Uhlmann, Q. Urban Ecology; Springer: Berlin, Germany, 1998. [Google Scholar]
- Bhatta, B. Analysis of Urban Growth and Sprawl from Remote Sensing Data; Advances in Geographic Information Science; Springer-Verlag: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Moriyama, M.; Tanaka, T.; Iwasaki, M. The mitigation of UHI intensity by the improvement of land use plan in the urban central area: Application to Osaka City, Japan. In Proceedings of the Second International Conference on Countermeasures to Urban Heat Islands (SICCUHI), Berkeley, CA, USA, 21–23 September 2009. [Google Scholar]
- Freire, M. Urban planning: Challenges in developing countries. In Proceedings of the International Congress on Human Development, Madrid, Spain, 3–5 August 2006. [Google Scholar]
- Stewart, I.D. A systematic review and scientific critique of methodology in modern urban heat island literature. Int. J. Climatol. 2011, 31, 200–217. [Google Scholar] [CrossRef]
- Tran, H.; Uchihama, D.; Ochi, S.; Yasuoka, Y. Assessment with satellite data of the urban heat island effects in Asian mega cities. Int. J. Appl. Earth Obs. Geoinform. 2006, 8, 34–48. [Google Scholar] [CrossRef]
- Cui, Y.Y.; de Foy, B. Seasonal variations of the urban heat island at the surface and the near-surface and reductions due to urban vegetation in Mexico City. J. Appl. Meteorol. Climatol. 2012, 51, 855–868. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Ouyang, Z.; Xu, W.; Zheng, H. Spatial pattern of greenspace affects land surface temperature: evidence from the heavily urbanized Beijing metropolitan area, China. Landsc. Ecol. 2012, 27, 887–898. [Google Scholar] [CrossRef]
- Elsayed, I.S.M. Effects of population density and land management on the intensity of urban heat islands: A case study on the city of Kuala Lumpur, Malaysia. In Application of Geographic Information Systems; InTech: London, UK, 2012. [Google Scholar]
- Zhou, B.; Diego, R.; Jürgen, P.K. The role of city size and urban form in the surface urban heat island. Sci. Rep. 2017, 7, 4791. [Google Scholar] [CrossRef] [PubMed]
- Solecki, W.D.; Rosenzweig, C.; Parshall, L.; Pope, G.; Clark, M.; Cox, J.; Wiencke, M. Mitigation of the heat island effect in urban New Jersey. Global Environ. Chang. part B Environ. Hazards 2005, 6, 39–49. [Google Scholar] [CrossRef]
- Oke, T.R. City size and the urban heat island. Atmos. Environ. 1973, 7, 769–779. [Google Scholar] [CrossRef]
- Howard, L. The Climate of London, Deduced from Meteorological Observations, Made at Different Places in the Neighbourhood of the Metropolis; W. Phillips: London, UK, 1818; Volume 2, pp. 1818–1820. [Google Scholar]
- Oke, T.R. The Heat Island of the Urban Boundary Layer: Characteristics, Causes and Effects. In Wind climate in cities; Cermak, J.E., Davenport, A.G., Plate, E.J., Viegas, D.X., Eds.; Springer: Dordrecht, The Netherlands, 1995; pp. 81–107. [Google Scholar]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Akbari, H.; Pomerantz, M.; Taha, H. Cool surfaces and shade trees to reduce energy use and improve air quality in urban areas. Sol. Energy 2001, 70, 295–310. [Google Scholar] [CrossRef]
- Wong, N.H.; Yu, C. Study of green areas and urban heat island in a tropical city. Habitat Int. 2005, 29, 547–558. [Google Scholar] [CrossRef]
- Bowler, D.E.; Buyung-Ali, L.; Knight, T.M.; Pullin, A.S. Urban greening to cool towns and cities: A systematic review of the empirical evidence. Landsc. Urban Plan. 2010, 97, 147–155. [Google Scholar] [CrossRef]
- Bonan, G.B. Effects of land use on the climate of the United States. Clim. Chang. 1997, 37, 449–486. [Google Scholar] [CrossRef]
- Hamada, S.; Ohta, T. Seasonal variations in the cooling effect of urban green areas on surrounding urban areas. Urban For. Urban Green. 2010, 9, 15–24. [Google Scholar] [CrossRef]
- Chen, A.; Yao, X.A.; Sun, R.; Chen, L. Effect of urban green patterns on surface urban cool islands and its seasonal variations. Urban For. Urban Green. 2014, 13, 646–654. [Google Scholar] [CrossRef]
- Zhang, X.; Zhong, T.; Feng, X.; Wang, K. Estimation of the relationship between vegetation patches and urban land surface temperature with remote sensing. Int. J. Remote Sens. 2009, 30, 2105–2118. [Google Scholar] [CrossRef]
- Yu, C.; Hien, W.N. Thermal benefits of city parks. Energy Build. 2006, 38, 105–120. [Google Scholar] [CrossRef]
- Oliveira, S.; Andrade, H.; Vaz, T. The cooling effect of green spaces as a contribution to the mitigation of urban heat: A case study in Lisbon. Build. Environ. 2011, 46, 2186–2194. [Google Scholar] [CrossRef]
- Kantzioura, A.; Kosmopoulos, P.; Zoras, S. Urban surface temperature and microclimate measurements in Thessaloniki. Energy Build. 2012, 44, 63–72. [Google Scholar] [CrossRef]
- Li, J.; Song, C.; Cao, L. Impacts of landscape structure on surface urban heat islands: A case study of Shanghai, China. Remote Sens. Environ. 2011, 115, 3249–3263. [Google Scholar] [CrossRef]
- Cao, X.; Onishi, A.; Chen, J.; Imura, H. Quantifying the cool island intensity of urban parks using ASTER and IKONOS data. Landsc. Urban Plan. 2010, 96, 224–231. [Google Scholar] [CrossRef]
- Lu, J.; Li, C.; Yang, Y.; Zhang, X.; Jin, M. Quantitative evaluation of urban park cool island factors in mountain city. J. Cent. South Univ. 2012, 19, 1657–1662. [Google Scholar] [CrossRef]
- Connors, J.P.; Galletti, C.S.; Chow, W.T.L. Landscape configuration and urban heat island effects: assessing the relationship between landscape characteristics and land surface temperature in Phoenix, Arizona. Landsc. Ecol. 2013, 28, 271–283. [Google Scholar] [CrossRef]
- Wong, N.H.; Jusuf, S.K.; Win, A.A.L.; Thu, H.K.; Negara, T.S. Environmental study of the impact of greenery in an institutional campus in the tropics. Build. Environ. 2007, 42, 2949–2970. [Google Scholar] [CrossRef]
- Jonsson, P. Vegetation as an urban climate control in the subtropical city of Gaborone. Int. J. Climatol. 2004, 24, 1307–1322. [Google Scholar] [CrossRef]
- Turner, M.G. Landscape ecology: What is the state of the science? Ann. Rev. Ecol. Evol. Sens. 2005, 36, 319–344. [Google Scholar] [CrossRef]
- Gustafson, E.J. Quantifying landscape spatial pattern: What is the state of the art? Ecosystems 1998, 1, 143–156. [Google Scholar] [CrossRef]
- Zhibin, R.; Haifeng, Z.; Xingyuan, H.; Dan, Z.; Xingyang, Y. Estimation of the Relationship Between Urban Vegetation Configuration and Land Surface Temperature with Remote Sensing. J. Indian Soc. Remote Sens. 2015, 43, 89–100. [Google Scholar] [CrossRef]
- Maimaitiyiming, M.; Ghulam, A.; Tiyip, T.; Pla, F.; Latorre-Carmona, P.; Halik, Ü.; Caetano, M. Effects of green space spatial pattern on land surface temperature: Implications for sustainable urban planning and climate change adaptation. ISPRS J. Photogramm. Remote Sens. 2014, 89, 59–66. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, G.; Cadenasso, M.L. Does spatial configuration matter? Understanding the effects of land cover pattern on land surface temperature in urban landscapes. Landsc. Urban Plan. 2011, 102, 54–63. [Google Scholar] [CrossRef]
- Zhao, C.; Fu, G.; Liu, X.; Fu, F. Urban planning indicators, morphology and climate indicators: A case study for a north-south transect of Beijing, China. Build. Environ. 2011, 46, 1174–1183. [Google Scholar] [CrossRef]
- Chang, C.R.; Li, M.H.; Chang, S.D. A preliminary study on the local cool island intensity of Taipei city parks. La ndsc. Urban Plan. 2007, 80, 386–395. [Google Scholar] [CrossRef]
- Beijing Statistics Bureau. Beijing Statistical Yearbook 2015; China Statistics Press: Beijing, China, 2015.
- Xia, X.A.; Chen, H.B.; Wang, P.C.; Zhang, W.X.; Goloub, P.; Chatenet, B.; Eck, T.F.; Holben, B.N. Variation of column-integrated aerosol properties in a Chinese urban region. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Memon, G.R. Education in Pakistan: The key issues, problems and the new challenges. J. Manag. Soc. Sci. 2007, 3, 47–55. [Google Scholar]
- Shah, M.H.; Nazia, S. Seasonal behaviours in elemental composition of atmospheric aerosols collected in Islamabad, Pakistan. Atmos. Res. 2010, 95, 210–223. [Google Scholar] [CrossRef]
- Jin, M.; Li, J.; Wang, J.; Shang, R. A practical split-windowalgorithmfor retrieving land surface temperature from Landsat-8 data and a case study of an urban area in China. Remote Sens. 2015, 7, 4371–4390. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Rozenstein, O.; Qin, Z.; Derimian, Y.; Karnieli, A. Derivation of land surface temperature for Landsat-8 TIRS using a split window algorithm. Sensors 2014, 14, 5768–5780. [Google Scholar] [CrossRef] [PubMed]
- Du, C.; Ren, H.Z.; Qin, Q.M.; Meng, J.J.; Li, J. Split-window algorithm For estimating land surface temperature from Landsat 8 TIRs data. In Proceedings of the 2014 IEEE International Geosciences and Remote Sensing Symposium, Quebec, QC, Canada, 13–18 July 2014. [Google Scholar]
- Jimenez-Munoz, J.C.; Sobrino, J.A.; Skokovic, D.; Matter, C.; Cristobal, J. Land surface temperature retrieval methods fromLandsat-8 Thermal Infrared Sensor data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1840–1843. [Google Scholar] [CrossRef]
- Wang, F.; Qin, Z.; Song, C.; Tu, L.; Karnieli, A.; Zhao, S. An improved mono-window algorithm for land surface temperature retrieval from Landsat 8 thermal infrared sensor data. Remote Sens. 2015, 7, 4268–4289. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. Int. J. Remote Sens. 2001, 22, 3719–3746. [Google Scholar] [CrossRef]
- Skokovic, D.; Sobrino, J.A.; Jimenez-Munoz, J.C.; Soria, G.; Julien, Y.; Mattar, C.; Cristobal, J. Calibration and Validation of Land Surface Temperature for Landsat 8—TIRS Sensor. In Proceedings of the Land product Validation and Evolution, Frascati, Italy, 28–30 January 2014. [Google Scholar]
- Strehl, A.; Ghosh, J. Cluster ensembles—A knowledge reuse framework for combining partitionings. J. Mach. Learn. Res. 2002, 3, 93–99. [Google Scholar]
- Pluim, J.P.W.; Maintz, J.B.A.; Viergever, M.A. Mutual-Information-Based Registration of Medical Images: A Survey. IEEE Trans. Med. Imag. 2003, 22, 986–1004. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.; Thomas, J. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 1991. [Google Scholar]
- Allaby, M. A Dictionary of Earth Sciences, 3rd ed.; Oxford University Press Inc.: New York, NY, USA, 2008; p. 460. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Section 14.7.3. Conditional Entropy and Mutual Information. In Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007; ISBN 978-0-521-88068-8. [Google Scholar]
- White, J.V.; Steingold, S.; Fournelle, C.G. Performance metrics for group-detection algorithms. In Proceedings of the 36th Symposium on the Interface, Baltimore, MD, USA, 26–29 May 2004. [Google Scholar]
- Sridhar, D.V.; Bartlett, E.B.; Seagrave, R.C. Information theoretic subset selection for neural network models. Comput. Chem. Eng. 1998, 22, 613–626. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Strehl, A.; Ghosh, J. Cluster ensembles—a knowledge reuse framework for combining multiple partitions. J. Mach. Learn. Res. 2003, 3, 583–617. [Google Scholar]
- Yang, Z.; Dong, J.; Liu, J.; Zhai, J.; Kuang, W.; Zhao, G.; Qin, Y. Accuracy Assessment and Inter-Comparison of Eight Medium Resolution Forest Products on the Loess Plateau, China. ISPRS Int. J. Geo Inf. 2017, 6, 152. [Google Scholar] [CrossRef]
- Tilahun, A.; Teferie, B. Accuracy assessment of land use land cover classification using google earth. Am. J. Environ. Prot. 2015, 4, 193–198. [Google Scholar] [CrossRef]
- McGarigal, K.; Cushman, S.A.; Neel, M.C.; Ene, E. FRAGSTATS: Spatial Pattern Analysis Program for Categorical Maps, Computer Software Program Produced by the Authors at the University of Massachusetts. 2002. Available online: http://www.umass.edu/landeco/research/fragstats/fragstats.html (accessed on 6 August 2016).
- Riva-Murray, K.; Riemann, R.; Murdoch, P.; Fischer, J.M.; Brightbill, R. Landscape characteristics affecting streams in urbanizing regions of the Delaware River Basin (New Jersey, New York, and Pennsylvania, US). Landsc. Ecol. 2010, 25, 1489–1503. [Google Scholar] [CrossRef]
- Du, H.; Cai, W.; Xu, Y.; Wang, Z.; Wang, Y.; Cai, Y. Quantifying the Cool Island Effects of Urban Green Spaces Using Remote Sensing Data. Urban For. Urban Green. 2017, 27, 24–31. [Google Scholar]
- Yang, C.; He, X.; Wang, R.; Yan, F.; Yu, L.; Bu, K.; Zhang, S. The Effect of Urban Green Spaces on the Urban Thermal Environment and Its Seasonal Variations. Forests 2017, 8, 153. [Google Scholar] [CrossRef]
- Chen, X.L.; Zhao, H.M.; Li, P.X.; Yin, Z.Y. Remote sensing image-based analysis of the relationship between urban heat island and land use/cover changes. Remote Sens. Environ. 2006, 104, 133–146. [Google Scholar]
- Huang, G.; Zhou, W.; Cadenasso, M.L. Is everyone hot in the city? Spatial pattern of land surface temperatures, land cover and neighborhood socioeconomic characteristics in Baltimore, MD. J. Environ. Manage. 2011, 92, 1753–1759. [Google Scholar] [CrossRef] [PubMed]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature–vegetation abundance relationship for urban heat island studies. Remote Sens. Environ. 2004, 89, 467–483. [Google Scholar] [CrossRef]
- Kim, J.H.; Gu, D.; Sohn, W.; Kil, S.H.; Kim, H.; Lee, D.K. Neighborhood landscape spatial patterns and land surface temperature: An empirical study on single-family residential areas in Austin, Texas. Int. J. Environ. Res. Pub. Health 2016, 13, 880. [Google Scholar] [CrossRef] [PubMed]
- Kong, F.; Yin, H.; James, P.; Hutyra, L.R.; He, H.S. Effects of spatial pattern of greenspace on urban cooling in a large metropolitan area of eastern China. Landsc. Urban Plan. 2014, 128, 35–47. [Google Scholar] [CrossRef]
- Jin, M.S.; Kessomkiat, W.; Pereira, G. Satellite-Observed urbanization characters in Shanghai, China: Aerosols, urban heat island effect, and land-Atmosphere interactions. Remote Sens. 2011, 3, 83–99. [Google Scholar] [CrossRef]
- Jayalakshmy, M.S.; Philip, J. Thermophysical properties of plant leaves and their influence on the environment temperature. Int. J. Thermophys. 2010, 31, 2295–2304. [Google Scholar] [CrossRef]
- Notice of Beijing Municipal Bureau of Landscape and Forestry on Printing and Distributing the Work Plan of Urban Greening in 2016. Available online: http://www.bjyl.gov.cn/zwgk/fgwj/qtwj/201602/t20160202_176411.shtml (accessed on 14 September 2017).
- 13th Five-Year, Landscape and Greening Plan of Beijing. Available online: http://news.xinhuanet.com/local/2016-01/06/c_128600299.htm (accessed on 14 September 2017).
- Tong, H.; Liu, H.; Li, Y.; Sang, J.; Hu, F. Acyuality of summer urban heat island and the impact of urban planning wedge-shaped greenland to reducing the intensity of urban heat island in Beijing. J. Appl. Meteorol. Sci. 2005, 16, 257–266. (In Chinese) [Google Scholar]
| Satellite Name | Spectral Mode | Spatial Resolution (m) |
|---|---|---|
| Multispectral | 30 × 30 | |
| Landsat-8 (OLI) | Panchromatic | 15 × 15 |
| Thermal Infrared | 100 × 100 | |
| Multispectral | 8 × 8 | |
| Gaofen-1 (GF-1) | Panchromatic | 2 × 2 |
| Constant | Value |
|---|---|
| −0.268 | |
| 1.3780 | |
| 0.1830 | |
| 54.300 | |
| −2.238 | |
| −129.2 | |
| 16.400 |
| Emissivity | Band 10 | Band 11 |
|---|---|---|
| 0.971 | 0.977 | |
| 0.987 | 0.989 |
| Class Name | Islamabad (%) | Beijing (%) |
|---|---|---|
| Vegetation | 48.59 | 21.83 |
| Built-up area | 19.58 | 64.26 |
| Water | 1.58 | 1.12 |
| Others | 30.25 | 12.79 |
| Class Name | No. of Samples | Total Sample Area (Ha) | User’s Accuracy (%) | Producer’s Accuracy (%) |
|---|---|---|---|---|
| Green space | 85 | 78.2 | 89.43 | 88.24 |
| Built-up area | 42 | 31.5 | 85.81 | 82.65 |
| Water | 12 | 9.1 | 80.34 | 85.41 |
| Others | 28 | 20.9 | 79.01 | 77.34 |
| Total | 167 | 139.7 | ||
| Overall accuracy | 83.6 |
| Class Name | No. of Samples | Total Sample Area (Ha) | User’s Accuracy (%) | Producer’s Accuracy (%) |
|---|---|---|---|---|
| Green space | 147 | 139.6 | 90.13 | 91.39 |
| Built-up area | 110.1 | 31.5 | 84.81 | 85.51 |
| Water | 10 | 7.3 | 85.37 | 79.34 |
| Others | 61 | 44.7 | 75.72 | 81.46 |
| Total | 341 | 301.7 | ||
| Overall accuracy | 84.01 |
| Landscape Metric | Calculation | Description |
|---|---|---|
| Percentage of Landscape (Compositional) | PLAND = 100/A × a | Percentage of landscape quantifies the proportional abundance of green spaces in the landscape (%) |
| Edge Density (Configurational) | ED = () e | Total length (border not included) of all edge segments of green space per hectare (m/ha) |
| Patch Density (Configurational) | PD = n/A x 10 | Number of green space patches divided by total landscape area (n/km ) |
| Landscape Shape Index (Configurational) | LSI = 0.25 () | It gives a standardized measure of edge density or total edge, which adjusts the size of a landscape |
| Landscape Metrics | Islamabad | Beijing |
|---|---|---|
| PLAND | −0.59 | −0.60 |
| ED | −0.20 | −0.37 |
| PD | 0.43 | 0.26 |
| LSI | 0.39 | 0.08 |
| Landscape Metrics | Land Surface Temperature (LST) | NMI of Islamabad | NMI of Beijing |
|---|---|---|---|
| PLAND | 0.77 | 0.76 | |
| ED | LST | 0.75 | 0.71 |
| PD | 0.57 | 0.38 | |
| LSI | 0.66 | 0.51 |
| GCI | GSA | VFi | ISFi | WFi | VWFi | VFo | ISFo | WFo | VWFo |
|---|---|---|---|---|---|---|---|---|---|
| GR | 0.72 | 0.042 | −0.32 | 0.37 | 0.66 | 0.57 | −0.32 | 0.73 | 0.77 |
| TD | 0.18 | 0.14 | −0.36 | 0.65 | 0.64 | 0.1 | 0.18 | 0.62 | 0.6 |
| TG | −0.43 | −0.21 | 0.22 | 0.57 | −0.06 | −0.51 | 0.34 | 0.23 | −0.3 |
| GCI | GSA | VFi | ISFi | VFo | ISFo |
|---|---|---|---|---|---|
| GR | 0.87 | 0.67 | −0.68 | 0.28 | −0.3 |
| TD | 0.48 | 0.81 | −0.69 | 0.09 | 0.06 |
| TG | −0.45 | 0.16 | 0.28 | −0.06 | 0.25 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naeem, S.; Cao, C.; Qazi, W.A.; Zamani, M.; Wei, C.; Acharya, B.K.; Rehman, A.U. Studying the Association between Green Space Characteristics and Land Surface Temperature for Sustainable Urban Environments: An Analysis of Beijing and Islamabad. ISPRS Int. J. Geo-Inf. 2018, 7, 38. https://doi.org/10.3390/ijgi7020038
Naeem S, Cao C, Qazi WA, Zamani M, Wei C, Acharya BK, Rehman AU. Studying the Association between Green Space Characteristics and Land Surface Temperature for Sustainable Urban Environments: An Analysis of Beijing and Islamabad. ISPRS International Journal of Geo-Information. 2018; 7(2):38. https://doi.org/10.3390/ijgi7020038
Chicago/Turabian StyleNaeem, Shahid, Chunxiang Cao, Waqas Ahmed Qazi, Mehdi Zamani, Chen Wei, Bipin Kumar Acharya, and Asid Ur Rehman. 2018. "Studying the Association between Green Space Characteristics and Land Surface Temperature for Sustainable Urban Environments: An Analysis of Beijing and Islamabad" ISPRS International Journal of Geo-Information 7, no. 2: 38. https://doi.org/10.3390/ijgi7020038
APA StyleNaeem, S., Cao, C., Qazi, W. A., Zamani, M., Wei, C., Acharya, B. K., & Rehman, A. U. (2018). Studying the Association between Green Space Characteristics and Land Surface Temperature for Sustainable Urban Environments: An Analysis of Beijing and Islamabad. ISPRS International Journal of Geo-Information, 7(2), 38. https://doi.org/10.3390/ijgi7020038







