Optimising Citizen-Driven Air Quality Monitoring Networks for Cities
Abstract
1. Introduction
- We extended the optimisation method proposed by Gupta et al. [27] by incorporating wide-spread distribution aspects (in addition to LUR’s predictor error aspects) into the placement of low-cost citizen sensors for air quality monitoring.
- We demonstrated the applicability of the proposed optimisation method in two practical scenarios: starting a new volunteered geographic information (VGI)-based air quality monitoring campaign; and finding out where to place new sensors to extend the existing VGI-based air quality monitoring network from the city of Stuttgart, Germany.
2. Related Work
2.1. Citizen Participation/VGI
2.2. Air Quality Monitoring Methods
3. Material
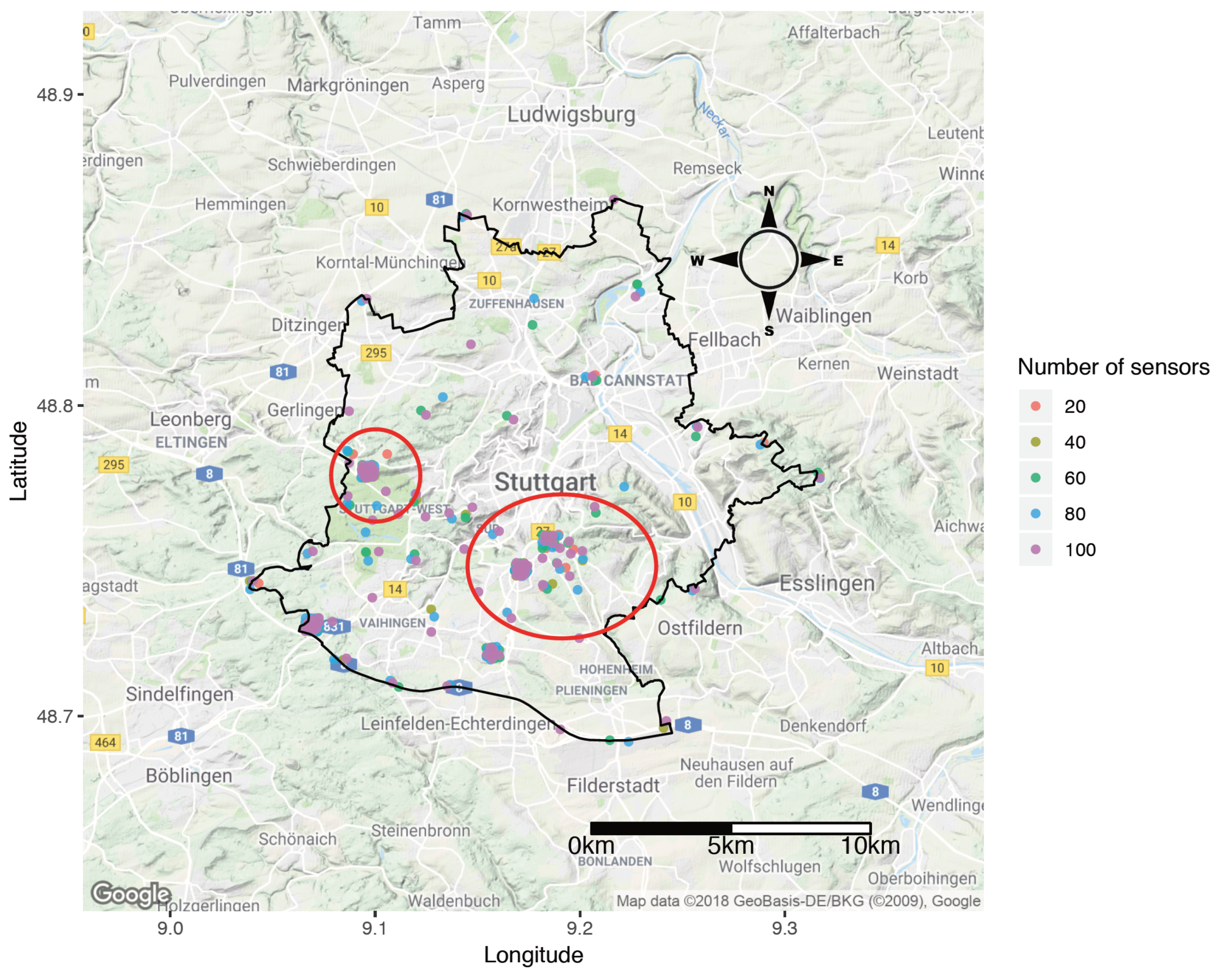
3.1. Study Area
3.2. Data
3.2.1. Citizen-Generated Air Pollution Data
3.2.2. Land Use Regression (LUR) Variables Open Data
- y is an n × 1 vector with air pollution observations at low-cost sensor locations for any particular instance (where, in our case, weekly mean concentration was used);
- X is an n × k matrix with observations of k independent variables for the n sensor locations;
- is a k × 1 vector with unknown parameters; and
- is an n × 1 vector of residuals, assumed to be distributed independently and identically.
4. Method
4.1. Optimisation Objective Function
- prediction error; and
- widespread distribution aspect.
4.1.1. Prediction Error Aspect
4.1.2. Widespread Distribution Aspect
- Input of a number of points (N) with a different spatial configuration as selected in each iteration of SSA.
- Compute the distance matrix for all points.
- Identify the second minimum value in each row of the matrix, as the distance matrix will contain the first minimum value as 0.
- Compute the mean of the minimum values from each row and column of the distance matrix.
- Compute the inverse of the mean value.
- A LUR model is selected/developed (using the air pollution ground data from low-cost sensors and predictor variables). If ground data are not available for LUR creation, already existing LUR models can be selected (arbitrarily or by considering models containing specific predictor variables which are significant for the study area).
- Initial monitoring station locations are defined as the input, consisting of N observations, which can also be feed in as a whole number.
- The study area A is discretised and the candidate locations are defined based on the resolution expected for the study area.
- Random point selection in each iteration starts and calculates the objective function values using SSA.
- The design of each previously selected configuration during the optimisation is modified until the network design is accepted based on the objective function value.
- A design will be accepted if it reduces the prediction error as well as distribute the sensor in a wide-spread fashion, depending on the weight assigned to each objective as per Equation (5).
- The optimisation continues to iterate and find the set of optimal locations until the new energy value reaches the minimum and is not changing in further iterations based on the energy transition and other annealing parameters.
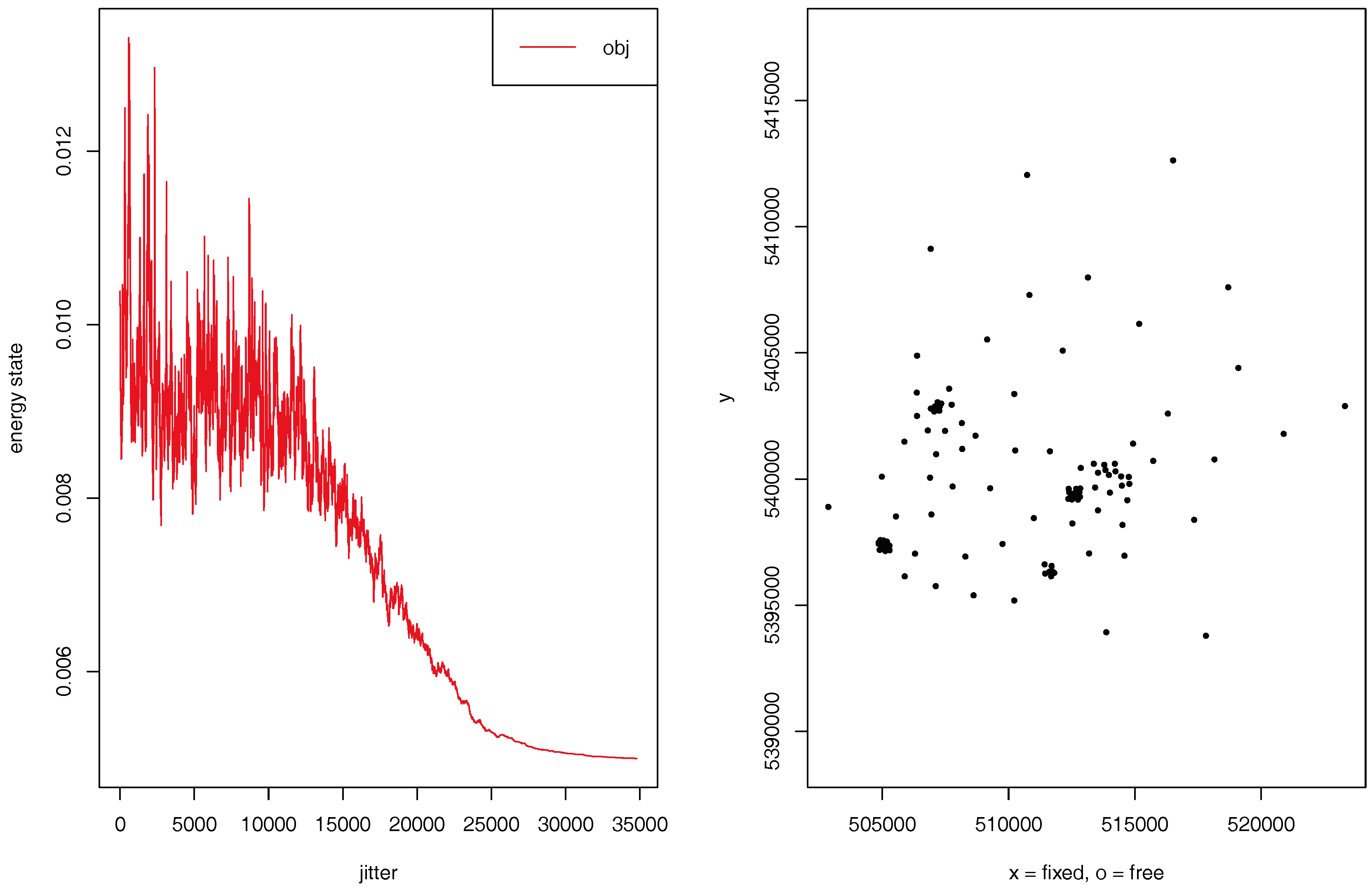
4.2. Optimisation Process
- Starting a new VGI campaign
- How many sensors should be deployed?
- Which locations are significant for deployment?
- Finding out where to place new VGI sensors to extend the existing network
4.2.1. Optimisation for Starting a New VGI Campaign
How Many Sensors Should Be Deployed?
Which Locations Are Significant?
4.2.2. Optimisation While Placing New VGI Sensors to Extend an Existing Network?
5. Results
5.1. Starting a New VGI Campaign
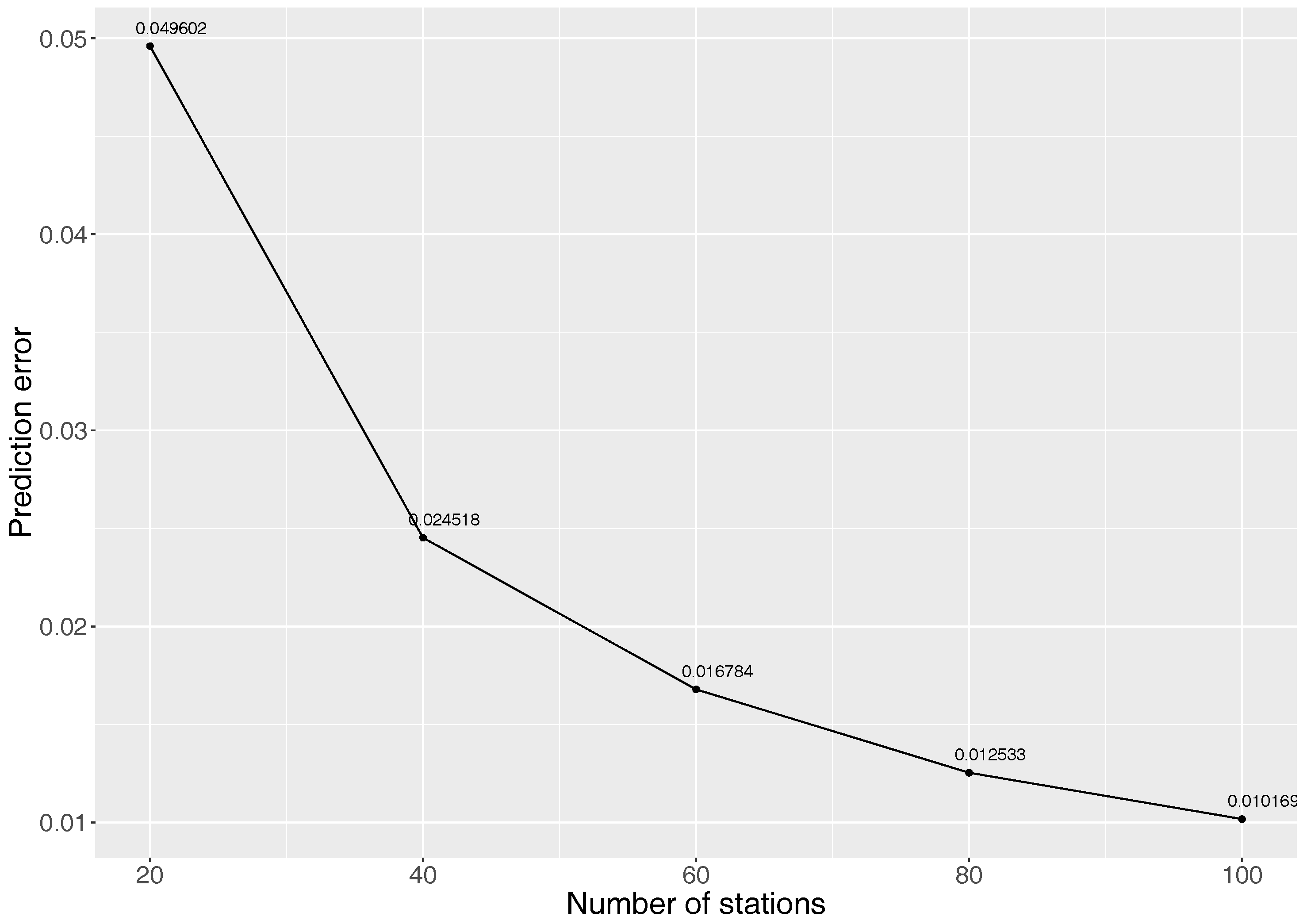
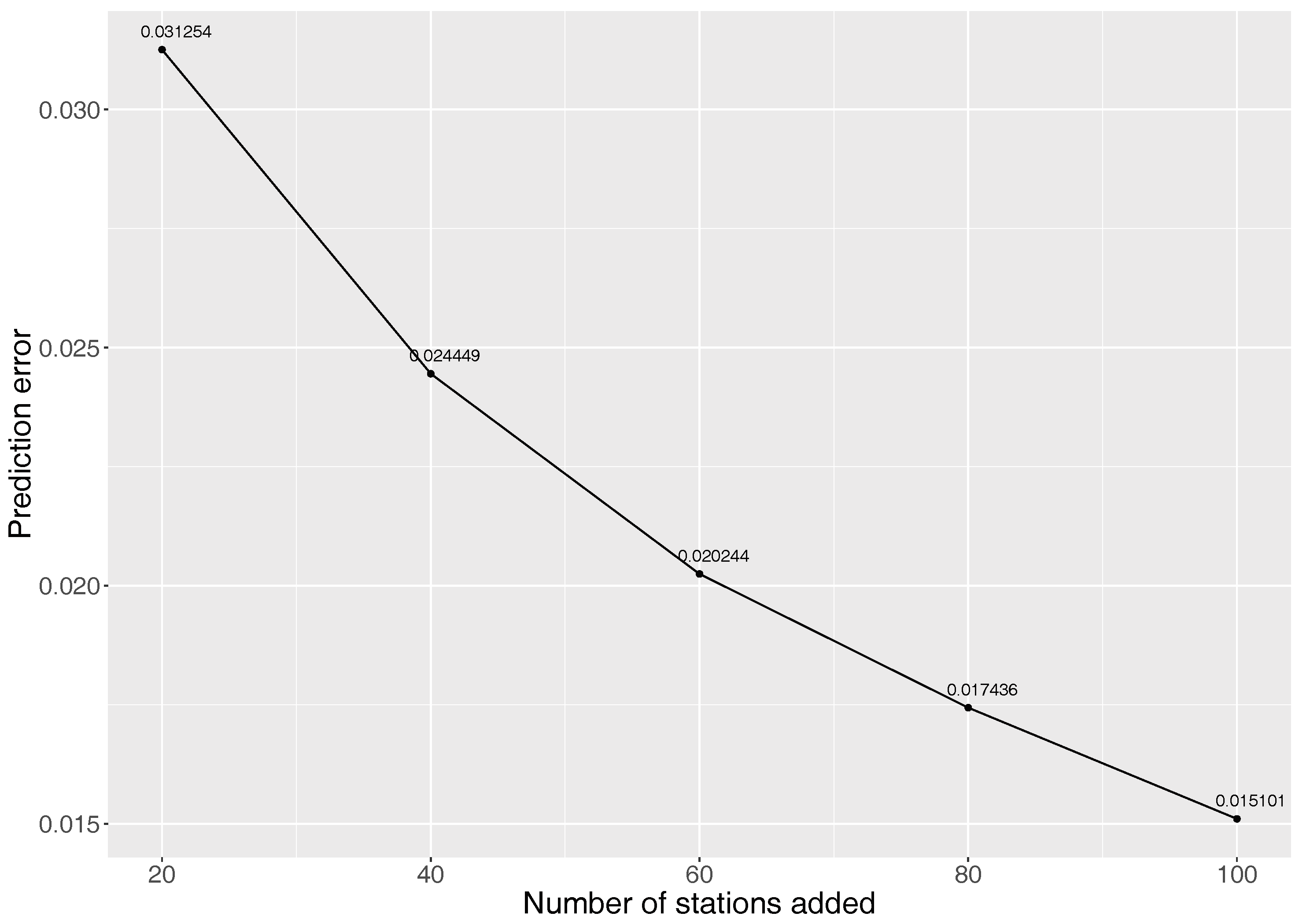
5.1.1. How Many Sensors Should Be Deployed?
5.1.2. Location Significance
5.2. Finding Out Where to Place New VGI Sensors
6. Discussion
6.1. Significance
6.2. Limitation and Outlook
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ESCAPE | European study of cohorts for air pollution effects |
| IMSD | Inverse mean shortest distance |
| LUR | Land Use Regression |
| OLS | Ordinary Least Squares |
| Particulate matter (PM) that have a diameter of less than 2.5 micrometers | |
| QoL | Quality of Life |
| SQRALT | Square root of altitude |
| SSA | Spatial Simulated Annealing |
| USEPA | United States Environmental Protection Agency |
| VGI | Volunteered Geographic Information |
| WHO | World Health Organisation |
| WLS | Weighted Least square |
Appendix A
Appendix B
References
- Molina, L.T.; Molina, M.J.; Slott, R.S.; Kolb, C.E.; Gbor, P.K.; Meng, F.; Singh, R.B.; Galvez, O.; Sloan, J.J.; Anderson, W.P.; et al. Air quality in selected megacities. J. Air Waste Manag. Assoc. 2004, 54, 1–73. [Google Scholar] [CrossRef]
- Barer, M. Why Are Some People Healthy and Others Not? Routledge: Abingdon, UK, 2017. [Google Scholar]
- Brown, J.; Bowman, C. Integrated Science Assessment for Ozone and Related Photochemical Oxidants; US Environmental Protection Agency: Washington, DC, USA, 2013.
- Bauernschuster, S.; Hener, T.; Rainer, H. When labor disputes bring cities to a standstill: The impact of public transit strikes on traffic, accidents, air pollution, and health. Am. Econ. J. Econ. Policy 2017, 9, 1–37. [Google Scholar] [CrossRef]
- WHO. WHO Releases Country Estimates on Air Pollution Exposure and Health Impact; WHO: Geneva, Switzerland, 2016. [Google Scholar]
- Jerrett, M.; Arain, M.A.; Kanaroglou, P.; Beckerman, B.; Crouse, D.; Gilbert, N.L.; Brook, J.R.; Finkelstein, N.; Finkelstein, M.M. Modeling the intraurban variability of ambient traffic pollution in Toronto, Canada. J. Toxicol. Environ. Health Part A 2007, 70, 200–212. [Google Scholar] [CrossRef] [PubMed]
- Hamra, G.B.; Laden, F.; Cohen, A.J.; Raaschou-Nielsen, O.; Brauer, M.; Loomis, D. Lung cancer and exposure to nitrogen dioxide and traffic: A systematic review and meta-analysis. Environ. Health Perspect. 2015, 123, 1107. [Google Scholar] [CrossRef] [PubMed]
- Khreis, H.; Kelly, C.; Tate, J.; Parslow, R.; Lucas, K.; Nieuwenhuijsen, M. Exposure to traffic-related air pollution and risk of development of childhood asthma: A systematic review and meta-analysis. Environ. Int. 2017, 100, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Bauer, K.; Bosker, T.; Dirks, K.N.; Behrens, P. The impact of seating location on black carbon exposure in public transit buses: Implications for vulnerable groups. Transp. Rese. Part D Transp. Environ. 2018, 62, 577–583. [Google Scholar] [CrossRef]
- Conti, G.O.; Heibati, B.; Kloog, I.; Fiore, M.; Ferrante, M. A review of AirQ Models and their applications for forecasting the air pollution health outcomes. Environ. Sci. Pollut. Res. 2017, 24, 6426–6445. [Google Scholar] [CrossRef] [PubMed]
- Mayer, H. Air pollution in cities. Atmos. Environ. 1999, 33, 4029–4037. [Google Scholar] [CrossRef]
- Van Nunen, E.; Vermeulen, R.; Tsai, M.Y.; Probst-Hensch, N.; Ineichen, A.; Davey, M.; Imboden, M.; Ducret-Stich, R.; Naccarati, A.; Raffaele, D.; et al. Land use regression models for ultrafine particles in six European areas. Environ. Sci. Technol. 2017, 51, 3336–3345. [Google Scholar] [CrossRef] [PubMed]
- Wolf, K.; Cyrys, J.; Harciníková, T.; Gu, J.; Kusch, T.; Hampel, R.; Schneider, A.; Peters, A. Land use regression modeling of ultrafine particles, ozone, nitrogen oxides and markers of particulate matter pollution in Augsburg, Germany. Sci. Total Environ. 2017, 579, 1531–1540. [Google Scholar] [CrossRef] [PubMed]
- Weichenthal, S.; Van Ryswyk, K.; Goldstein, A.; Bagg, S.; Shekkarizfard, M.; Hatzopoulou, M. A land use regression model for ambient ultrafine particles in Montreal, Canada: A comparison of linear regression and a machine learning approach. Environ. Res. 2016, 146, 65–72. [Google Scholar] [CrossRef] [PubMed]
- Jiao, W.; Hagler, G.; Williams, R.; Sharpe, R.; Brown, R.; Garver, D.; Judge, R.; Caudill, M.; Rickard, J.; Davis, M.; et al. Community Air Sensor Network (CAIRSENSE) project: Evaluation of low-cost sensor performance in a suburban environment in the southeastern United States. Atmos. Meas. Tech. 2016, 9, 5281–5292. [Google Scholar] [CrossRef]
- Snyder, E.G.; Watkins, T.H.; Solomon, P.A.; Thoma, E.D.; Williams, R.W.; Hagler, G.S.; Shelow, D.; Hindin, D.A.; Kilaru, V.J.; Preuss, P.W. The Changing Paradigm of Air Pollution Monitoring; ACS Publications: Washington, DC, USA, 2013. [Google Scholar]
- Yi, W.Y.; Lo, K.M.; Mak, T.; Leung, K.S.; Leung, Y.; Meng, M.L. A survey of wireless sensor network based air pollution monitoring systems. Sensors 2015, 15, 31392–31427. [Google Scholar] [CrossRef] [PubMed]
- Shusterman, A.A.; Teige, V.E.; Turner, A.J.; Newman, C.; Kim, J.; Cohen, R.C. The BErkeley Atmospheric CO2 Observation Network: Initial evaluation. Atmos. Chem. Phys. 2016, 16, 13449–13463. [Google Scholar] [CrossRef]
- Fang, X.; Bate, I. Issues of using wireless sensor network to monitor urban air quality. In Proceedings of the First ACM International Workshop on the Engineering of Reliable, Robust, and Secure Embedded Wireless Sensing Systems, Delft, The Netherlands, 6–8 November 2017; pp. 32–39. [Google Scholar]
- Castell, N.; Dauge, F.R.; Schneider, P.; Vogt, M.; Lerner, U.; Fishbain, B.; Broday, D.; Bartonova, A. Can commercial low-cost sensor platforms contribute to air quality monitoring and exposure estimates? Environ. Int. 2017, 99, 293–302. [Google Scholar] [CrossRef] [PubMed]
- Schneider, P.; Castell, N.; Vogt, M.; Dauge, F.R.; Lahoz, W.A.; Bartonova, A. Mapping urban air quality in near real-time using observations from low-cost sensors and model information. Environ. Int. 2017, 106, 234–247. [Google Scholar] [CrossRef] [PubMed]
- Clements, A.L.; Griswold, W.G.; Rs, A.; Johnston, J.E.; Herting, M.M.; Thorson, J.; Collier-Oxandale, A.; Hannigan, M. Low-cost air quality monitoring tools: from research to practice (a workshop summary). Sensors 2017, 17, 2478. [Google Scholar] [CrossRef] [PubMed]
- Watkins, T. DRAFT Roadmap for Next Generation Air Monitoring; Environmental Protection Agency: Washington, DC, USA, 2013.
- Kanaroglou, P.S.; Jerrett, M.; Morrison, J.; Beckerman, B.; Arain, M.A.; Gilbert, N.L.; Brook, J.R. Establishing an air pollution monitoring network for intra-urban population exposure assessment: A location-allocation approach. Atmos. Environ. 2005, 39, 2399–2409. [Google Scholar] [CrossRef]
- Bonney, R.; Shirk, J.L.; Phillips, T.B.; Wiggins, A.; Ballard, H.L.; Miller-Rushing, A.J.; Parrish, J.K. Next steps for citizen science. Science 2014, 343, 1436–1437. [Google Scholar] [CrossRef] [PubMed]
- Elwood, S.; Goodchild, M.F.; Sui, D.Z. Researching volunteered geographic information: Spatial data, geographic research, and new social practice. Ann. Assoc. Am. Geogr. 2012, 102, 571–590. [Google Scholar] [CrossRef]
- Gupta, S.; Pebesma, E.; Mateu, J.; Degbelo, A. Air Quality Monitoring Network Design Optimisation for Robust Land Use Regression Models. Sustainability 2018, 10, 1442. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Li, L. Assuring the quality of volunteered geographic information. Spat. Stat. 2012, 1, 110–120. [Google Scholar] [CrossRef]
- Sieber, R.E.; Haklay, M. The epistemology(s) of volunteered geographic information: A critique. Geo Geogr. Environ. 2015, 2, 122–136. [Google Scholar] [CrossRef]
- Senaratne, H.; Mobasheri, A.; Ali, A.L.; Capineri, C.; Haklay, M.M. A review of volunteered geographic information quality assessment methods. Int. J. Geogr. Inf. Sci. 2017, 31, 139–167. [Google Scholar] [CrossRef]
- Haklay, M. How good is volunteered geographical information? A comparative study of OpenStreetMap and Ordnance Survey datasets. Environ. Plan. B Plan. Des. 2010, 37, 682–703. [Google Scholar] [CrossRef]
- Jackson, S.; Mullen, W.; Agouris, P.; Crooks, A.; Croitoru, A.; Stefanidis, A. Assessing completeness and spatial error of features in volunteered geographic information. ISPRS Int. J. Geo-Inf. 2013, 2, 507–530. [Google Scholar] [CrossRef]
- Gupta, S.; Pebesma, E.; Mateu, J.; Degbelo, A. Connecting Citizens and Housing Companies for Fine-grained Air Quality Sensing. GI_Forum J. Geogr. Inf. Sci. 2018, in press. [Google Scholar]
- Gabrys, J.; Pritchard, H. Just Good Enough Data and Environmental Sensing: Moving Beyond Regulatory Benchmarks toward Citizen Action. Int. J. Spat. Data Infrastruct. Res. 2018, 13, 4–14. [Google Scholar]
- Jovašević-Stojanović, M.; Bartonova, A.; Topalović, D.; Lazović, I.; Pokrić, B.; Ristovski, Z. On the use of small and cheaper sensors and devices for indicative citizen-based monitoring of respirable particulate matter. Environ. Pollut. 2015, 206, 696–704. [Google Scholar] [CrossRef] [PubMed]
- Lisjak, J.; Schade, S.; Kotsev, A. Closing data gaps with citizen science? Findings from the Danube region. ISPRS Int. J. Geo-Inf. 2017, 6, 277. [Google Scholar] [CrossRef]
- Budde, M.; Schankin, A.; Hoffmann, J.; Danz, M.; Riedel, T.; Beigl, M. Participatory Sensing or Participatory Nonsense?: Mitigating the Effect of Human Error on Data Quality in Citizen Science. IMWUT 2017, 1, 39. [Google Scholar] [CrossRef]
- Hoek, G.; Beelen, R.; De Hoogh, K.; Vienneau, D.; Gulliver, J.; Fischer, P.; Briggs, D. A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmos. Environ. 2008, 42, 7561–7578. [Google Scholar] [CrossRef]
- Wang, M.; Beelen, R.; Eeftens, M.; Meliefste, K.; Hoek, G.; Brunekreef, B. Systematic evaluation of land use regression models for NO2. Environ. Sci. Technol. 2012, 46, 4481–4489. [Google Scholar] [CrossRef] [PubMed]
- Basagaña, X.; Rivera, M.; Aguilera, I.; Agis, D.; Bouso, L.; Elosua, R.; Foraster, M.; de Nazelle, A.; Nieuwenhuijsen, M.; Vila, J.; et al. Effect of the number of measurement sites on land use regression models in estimating local air pollution. Atmos. Environ. 2012, 54, 634–642. [Google Scholar] [CrossRef]
- Hystad, P.; Setton, E.; Cervantes, A.; Poplawski, K.; Deschenes, S.; Brauer, M.; van Donkelaar, A.; Lamsal, L.; Martin, R.; Jerrett, M.; et al. Creating national air pollution models for population exposure assessment in Canada. Environ. Health Perspect. 2011, 119, 1123. [Google Scholar] [CrossRef] [PubMed]
- Jerrett, M.; Arain, A.; Kanaroglou, P.; Beckerman, B.; Potoglou, D.; Sahsuvaroglu, T.; Morrison, J.; Giovis, C. A review and evaluation of intraurban air pollution exposure models. J. Expo. Sci. Environ. Epidemiol. 2005, 15, 185. [Google Scholar] [CrossRef] [PubMed]
- Peng, J.; Hu, M.; Wang, Z.; Huang, X.; Kumar, P.; Wu, Z.; Guo, S.; Yue, D.; Shang, D.; Zheng, Z.; et al. Submicron aerosols at thirteen diversified sites in China: size distribution, new particle formation and corresponding contribution to cloud condensation nuclei production. Atmos. Chem. Phys. 2014, 14, 10249–10265. [Google Scholar] [CrossRef]
- Official Journal of the European Union. Directive 2008/50/EC of the European Parliament and of the Council of 21 May 2008 on Ambient Air Quality and Cleaner Air for Europe; Official Journal of the European Union: Brussels, Belgium, 2008. [Google Scholar]
- Goldstein, I.F.; Landovitz, L. Analysis of air pollution patterns in New York City—I. Can one station represent the large metropolitan area? Atmos. Environ. 1977, 11, 47–52. [Google Scholar] [CrossRef]
- Ott, D.K.; Kumar, N.; Peters, T.M. Passive sampling to capture spatial variability in PM10–2.5. Atmos. Environ. 2008, 42, 746–756. [Google Scholar] [CrossRef]
- Chong, C.Y.; Kumar, S.P. Sensor networks: Evolution, opportunities, and challenges. Proc. IEEE 2003, 91, 1247–1256. [Google Scholar] [CrossRef]
- Borrego, C.; Costa, A.; Ginja, J.; Amorim, M.; Coutinho, M.; Karatzas, K.; Sioumis, T.; Katsifarakis, N.; Konstantinidis, K.; De Vito, S.; et al. Assessment of air quality microsensors versus reference methods: The EuNetAir joint exercise. Atmos. Environ. 2016, 147, 246–263. [Google Scholar] [CrossRef]
- Spinelle, L.; Gerboles, M.; Villani, M.G.; Aleixandre, M.; Bonavitacola, F. Field calibration of a cluster of low-cost commercially available sensors for air quality monitoring. Part B: NO, CO and CO2. Sens. Actuators B Chem. 2017, 238, 706–715. [Google Scholar] [CrossRef]
- Borrego, C.; Coutinho, M.; Costa, A.M.; Ginja, J.; Ribeiro, C.; Monteiro, A.; Ribeiro, I.; Valente, J.; Amorim, J.; Martins, H.; et al. Challenges for a new air quality directive: The role of monitoring and modelling techniques. Urban Clim. 2015, 14, 328–341. [Google Scholar] [CrossRef]
- Benis, K.Z.; Fatehifar, E.; Shafiei, S.; Nahr, F.K.; Purfarhadi, Y. Design of a sensitive air quality monitoring network using an integrated optimization approach. Stoch. Environ. Res. Risk Assess. 2016, 30, 779–793. [Google Scholar] [CrossRef]
- Weissert, L.; Salmond, J.; Miskell, G.; Alavi-Shoshtari, M.; Grange, S.; Henshaw, G.; Williams, D. Use of a dense monitoring network of low-cost instruments to observe local changes in the diurnal ozone cycles as marine air passes over a geographically isolated urban centre. Sci. Total Environ. 2017, 575, 67–78. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Shusterman, A.A.; Lieschke, K.J.; Newman, C.; Cohen, R.C. The berkeley atmospheric CO2 observation network: Field calibration and evaluation of low-cost air quality sensors. Atmos. Meas. Tech. Discuss. 2017. [Google Scholar] [CrossRef]
- Baden-Württemberg, S.L. Bevölkerung und Erwerbstätigkeit. Available online: https://www.statistik-bw.de/Service/Veroeff/Statistische_Berichte/312616001.pdf (accessed on 15 August 2018).
- Deutsche Welle. Stuttgart: Germany’s ‘Beijing’ for Air Pollution? Available online: https://www.dw.com/en/stuttgart-germanys-beijing-for-air-pollution/a-18991064 (accessed on 19 August 2018).
- Deutsche Welle. Germany’s Stuttgart Asks Residents to Leave Car at Home Amid High Air Pollution. Available online: https://www.dw.com/en/germanys-stuttgart-asks-residents-to-leave-car-at-home-amid-high-air-pollution/a-18986437 (accessed on 19 August 2018).
- City of Stuttgart. Measuring Points. Available online: https://www.stadtklima-stuttgart.de/index.php?air_clean_air_plan_measuring_points (accessed on 17 August 2018).
- Umbelt Bundesamt. Current Concentrations of Air Pollutants in Germany. Available online: https://www.umweltbundesamt.de/en/data/current-concentrations-of-air-pollutants-in-germany#/ (accessed on 5 August 2018).
- OK Labs. Measure Air Quality Yourself Nearly Finished With Your Help. Available online: https://luftdaten.info/en/home-en/ (accessed on 12 August 2018).
- OK Labs. Data Archive. Available online: https://archive.luftdaten.info (accessed on 10 August 2018).
- OK Labs. Measurement Accuracy. Available online: https://luftdaten.info/messgenauigkeit/ (accessed on 11 August 2018).
- Geofabrik GmbH Karlsruhe. Downloads. Available online: https://www.geofabrik.de/data/download.html (accessed on 19 August 2018).
- OpenStreetMap Contributors. Planet Dump Retrieved from https://planet.osm.org. Available online: https://www.openstreetmap.org (accessed on 19 August 2018).
- Open.NRW. NRW: Zensusatlas 2011—Bundesweite. Available online: https://www.europeandataportal.eu/data/en/dataset/https-ckan-govdata-de-dataset-fe865d7e-90ff-508b-92b5-92819a8f6d2b (accessed on 19 August 2018).
- Bundesamt für Kartographie und Geodäsie. Open Data—Freie Daten und Dienste des BKG. Available online: http://www.geodatenzentrum.de/geodaten/gdz_rahmen.gdz_div?gdz_spr=deu&gdz_akt_zeile=5&gdz_anz_zeile=1&gdz_unt_zeile=0&gdz_user_id=0 (accessed on 9 August 2018).
- Copernicus. CORINE Land Cover. Available online: https://land.copernicus.eu/pan-european/corine-land-cover (accessed on 17 August 2018).
- Van Groenigen, J.W. Constrained Optimisation of Spatial Sampling: A Geostatistical Approach; ITC Publication: Enschede, The Netherlands, 1999. [Google Scholar]
- Heuvelink, G.B.M.; Jiang, Z.; De Bruin, S.; Twenhöfel, C.J.W. Optimization of mobile radioactivity monitoring networks. Int. J. Geogr. Inf. Sci. 2010, 24, 365–382. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2014; Volume 326. [Google Scholar]
- Mitchell, G.; Dorling, D. An environmental justice analysis of British air quality. Environ. Plan. A 2003, 35, 909–929. [Google Scholar] [CrossRef]
- Kumar, P.; Morawska, L.; Martani, C.; Biskos, G.; Neophytou, M.; Di Sabatino, S.; Bell, M.; Norford, L.; Britter, R. The rise of low-cost sensing for managing air pollution in cities. Environ. Int. 2015, 75, 199–205. [Google Scholar] [CrossRef] [PubMed]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Pebesma, E.; Bivand, R.S. Classes and Methods for Spatial Data in R: The sp Package. R News 2005, 5, 9–13. [Google Scholar]
- Pebesma, E. sf: Simple Features for R. R Package Version 0.5-5. 2018. Available online: https://CRAN.R-project.org/package=sf (accessed on 10 June 2018).
- French, J. SpatialTools: Tools for Spatial Data Analysis, R Package Version 1.0.2; 2015. Available online: https://CRAN.R-project.org/package=SpatialTools (accessed on 10 June 2018).
- Samuel-Rosa, A.; dos Anjos, L.H.C.; de Mattos Vasques, G.; Heuvelink, G.B.M.; Pebesma, E.; Skoien, J.; French, J.; Roudier, P.; Brus, D.; Lark, M. Package ‘Spsann’. 2017. Available online: https://cran.r-project.org/web/packages/spsann/spsann.pdf (accessed on 12 June 2018).
- Gupta, S. VGI-AQM-Optimisation. Available online: https://github.com/geohealthshivam/VGI-AQM-Optimisation (accessed on 30 August 2018).
- Eeftens, M.; Tsai, M.Y.; Ampe, C.; Anwander, B.; Beelen, R.; Bellander, T.; Cesaroni, G.; Cirach, M.; Cyrys, J.; de Hoogh, K.; et al. Spatial variation of PM2. 5, PM10, PM2. 5 absorbance and PMcoarse concentrations between and within 20 European study areas and the relationship with NO2–Results of the ESCAPE project. Atmos. Environ. 2012, 62, 303–317. [Google Scholar] [CrossRef]
- Wu, H.; Reis, S.; Lin, C.; Heal, M.R. Effect of monitoring network design on land use regression models for estimating residential NO2 concentration. Atmos. Environ. 2017, 149, 24–33. [Google Scholar] [CrossRef]
- Beelen, R.; Hoek, G.; Pebesma, E.; Vienneau, D.; de Hoogh, K.; Briggs, D.J. Mapping of background air pollution at a fine spatial scale across the European Union. Sci. Total Environ. 2009, 407, 1852–1867. [Google Scholar] [CrossRef] [PubMed]
- Tuia, D.; Pozdnoukhov, A.; Foresti, L.; Kanevski, M. Active learning for monitoring network optimization. In Spatio-Temporal Design: Advances in Efficient Data Acquisition; Wiley Online Library: Hoboken, NJ, USA, 2012; pp. 285–318. [Google Scholar]
- FLAMENCO Project. Citizen Observatory—Home of the Flamenco Project. Available online: http://citizen-observatory.be (accessed on 25 August 2018).



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, S.; Pebesma, E.; Degbelo, A.; Costa, A.C. Optimising Citizen-Driven Air Quality Monitoring Networks for Cities. ISPRS Int. J. Geo-Inf. 2018, 7, 468. https://doi.org/10.3390/ijgi7120468
Gupta S, Pebesma E, Degbelo A, Costa AC. Optimising Citizen-Driven Air Quality Monitoring Networks for Cities. ISPRS International Journal of Geo-Information. 2018; 7(12):468. https://doi.org/10.3390/ijgi7120468
Chicago/Turabian StyleGupta, Shivam, Edzer Pebesma, Auriol Degbelo, and Ana Cristina Costa. 2018. "Optimising Citizen-Driven Air Quality Monitoring Networks for Cities" ISPRS International Journal of Geo-Information 7, no. 12: 468. https://doi.org/10.3390/ijgi7120468
APA StyleGupta, S., Pebesma, E., Degbelo, A., & Costa, A. C. (2018). Optimising Citizen-Driven Air Quality Monitoring Networks for Cities. ISPRS International Journal of Geo-Information, 7(12), 468. https://doi.org/10.3390/ijgi7120468




