1. Introduction
Urban planners are making efforts to make cities livable for residents; They are also making efforts to predict future population change. Therefore, it is important to detect the shrinkage or growth of a population and to estimate the effects of urban development on future populations. However, it is difficult to follow urban development quickly to estimate the effects of urban development on future residential mobility.
Previous studies have shown that the urban form influences both non-work travel behavior [
1,
2,
3,
4] and residential mobility [
5,
6]. The amenities of residential neighborhoods reduce the need for non-work travel to distant places and increase the number of in-migrants. For example, if shopping centers and parks are located in a neighborhood, residents do not have to go to shopping centers and parks located far away. Such convenience also contributes to an increase in residential movements to such a location.
We consider that the analysis of non-work travel contributes to the prediction of future residential mobility.
Figure 1 shows our hypothesis on the causal relationship between urban form, non-work human mobility and residential mobility. Changes in urban form (e.g., the amenities of a neighborhood) could be a cause of changes in non-work human mobility (e.g., average travel time and diversity of destinations). Changes in non-work human mobility could be a cause of changes in residential mobility (e.g., the number of people who relocate to each place). Therefore, we consider it possible to create an index based on mobility data to estimate the influence of urban development on residential mobility. Since human mobility changes quickly according to urban changes, such as the opening of shopping centers, we consider that mobility data enable us to quickly predict the outcome of urban development. Therefore, the causal influence of changes in urban form on future residential movements can be quickly predicted, if it is possible to create such an index based on mobility data collected within a short period. Opportunities for analyzing massive real-time mobility data are increasing due to the automatic collection of mobility data such as smart card data of public transportation. Therefore, we consider that massive collected mobility data can contribute to the prediction of future residential mobility.
This study attempts to investigate a method for creating an index that not only correlates with future residential movements, but also has causal influence on future residential movements. Creating an index based on human mobility data will make it possible to predict the influence of urban development on future residential movements.
We propose a method called travel cost method for multiple places (TCM4MP) by extending the conventional travel cost method (TCM). In previous studies, TCM was used for inferring the benefit of a recreational site [
7,
8] and the opportunity cost of travel time [
9,
10]. We consider that the opportunity cost of travel time on non-working days reflects the convenience and amenities of a neighborhood.
Opportunity cost is the loss of potential gain from other alternatives when one alternative is chosen. In this paper, we focus on the opportunity cost of travel time on non-working days. When people choose to travel to a distant place from the location of their residences, they lose potential gain that could be obtained by engaging in activities in the residential neighborhood. Therefore, the opportunity cost of travel time is high if various types of amenities are accessible in the residential neighborhood. For example, the opening of a shopping center increases the opportunity cost of travel time, because people can spend enjoyable time at the shopping center. People prefer to spend time in the residential neighborhood rather than to travel to distant places, if they can engage in enjoyable activities in the residential neighborhood.
TCM4MP is proposed to estimate the opportunity cost of travel time that varies according to the departure place. Conventional TCM does not assume that the opportunity cost of travel time varies according to the departure place. We consider such estimation as possible due to the use of massive mobility data. We assume that the opportunity cost of travel time on non-working days reflects the convenience and amenities of a neighborhood. Therefore, we consider that the opportunity cost of travel time has a causal influence on future residential movements.
The contributions of this paper are summarized as follows:
We propose a method to infer the opportunity cost of travel time on non-working days that varies according to the departure place by extending the conventional travel cost method.
We examine the extent to which the opportunity cost of travel time contributes to the prediction of future residential movements.
We compare the contribution of opportunity cost to the prediction of the number of people who relocate to each place with other types of indices derived from smart card data of public transportation. It is insufficient to examine the contribution of the opportunity cost of travel time to the prediction of future residential movements only through the correlation to the number of people who relocate to each place. We infer a causal relation between the number of residential moves, the opportunity cost of travel time and other indices that highly correlate with the number of residential moves. Thus, the research questions that we address in this paper are as follows:
RQ1: Does the opportunity cost of travel time calculated by an extended travel cost method contribute to the prediction of the number of people who relocate to each place compared to the current population and other indices?
RQ2: Does the opportunity cost of travel time have a causal influence on the number of people who relocate to each place compared to the current population and other indices?
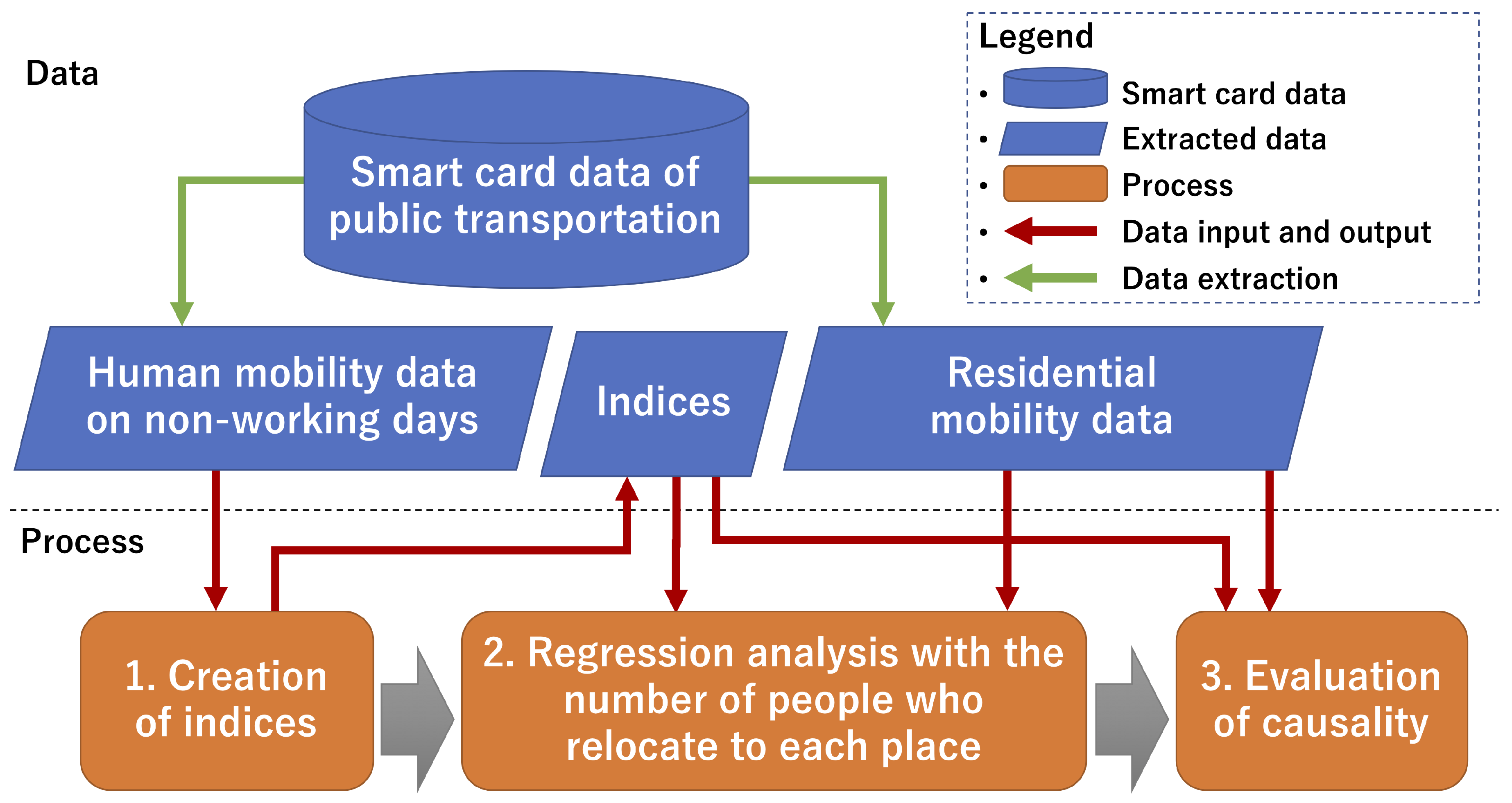
Figure 2 is a flowchart of this study. We extract human mobility data on non-working days and residential mobility data from smart card data of public transportation. Indices for the prediction of residential movements are created. We create a regression model for each index using human mobility data on non-working days. Then, we perform the evaluation of causality between the number of people who relocate to each place and the created indices.
The remainder of this paper is organized as follows:
Section 2 reviews previous studies.
Section 3 describes the proposed method.
Section 4 explains the baselines and evaluation method.
Section 5 explains the data that we use.
Section 6 describes the data preprocessing method.
Section 7 reports on the results.
Section 8 discusses the implications and limitations of our study.
Section 9 draws our conclusions.
2. Related Works
2.1. Travel Cost Method and Opportunity Cost of Travel Time
Travel is considered as a demand derived from the desire to engage in activities at destinations [
11]. According to Becker’s theory of the allocation of time [
12], people allocate their limited time to activities to maximize utility. Since travel time is considered wasteful or unproductive [
10], it is interpreted as a necessary evil to obtain benefits from activities at destinations. The travel cost method (TCM) is widely used for measuring the benefit of recreational sites [
7,
8] and for measuring the opportunity cost of travel time [
9,
10]. The method assumes that the ratio or the number of visits to a site and the cost of travel, including time and money, presents a demand curve. Regression analysis is performed for measuring the benefits of destinations and the opportunity cost of travel time. On the other hand, some studies [
13,
14,
15] note that people spend time on productive or enjoyable activities while traveling using rapidly growing information and communication technologies (ICTs) such as smart phones, laptop computers, portable music players and gaming devices. Therefore, the opportunity cost of travel time may differ based on such activities during traveling. In regard to methodologies developed in the behavioral sciences, discrete choice models are used to analyze individuals’ destination choices of non-working trips, incorporating the opportunity cost of travel time into the utility models [
16]. The methodologies are also useful for the analysis of the choices of residential locations.
In our research, we measure the opportunity cost of travel time for multiple departure places using the smart card data of public transportation. Such measurement has never been performed in previous studies, and it requires an extension of the conventional TCM. In addition, we measure the opportunity cost of travel time for different demographic groups using gender and age data. The influence of the development of ICTs could be reflected in the difference in the opportunity cost of travel time among different demographic groups.
2.2. Interaction between Urban Form and Travel Behavior
In regard to the interaction between urban form and travel behavior, previous studies argue that urban form affects non-work travel behavior [
1,
2,
3,
4]. According to these studies, the ratio of people who walk on non-working days is strongly related to land use diversity, intersection density and the number of destinations within walking distance. On the other hand, while other studies [
17,
18,
19,
20,
21] also acknowledge that urban form influences non-work travel behavior, they argue that attitudes toward travel behavior and preferences in residential location are more strongly associated with travel than are land use characteristics. These studies suggest that such preferences could affect residential choice. For example, people who prefer to drive may choose to live in suburban areas and travel by car, and people who prefer to walk may choose to live in areas with mixed land use and higher neighborhood accessibility. Mokhtarian and Cao [
22] note the difficulty in finding causality between attitudinal factors, residential locations and non-work travel behavior. They recommend the usage of longitudinal structural equation modeling for causal analysis. Krizek [
23] performed a longitudinal analysis of the travel behavior of the same households to find causal relations between urban form and travel behavior. The findings of the study suggested that households changed travel behavior when exposed to differing urban forms. In particular, locating to areas with higher neighborhood accessibility decreases vehicle miles traveled (VMT) and person miles traveled (PMT). In addition, Handy et al. [
24] acknowledged that residential self-selection plays an important role in influencing individuals’ travel decisions, but they also suggested that mixed land uses tend to discourage auto travel.
Regarding our research, public transportation is the dominant measure for moving in the area where data that we use are collected. We assume that the opportunity cost of travel time increases when amenities and convenience in the neighborhood are high. In addition, we assume that convenience and amenities in the neighborhood contribute to an increase in the number of people who relocate to the place. Our study does not assume that preferences for residential locations and travel behavior differ among people. Our study does not incorporate automobile travel, nor does it incorporate the difference in preferences for travel behavior and residential location. Therefore, it is necessary to further develop our method if applied to areas where people have varying preferences for travel behavior.
2.3. Influential Factors on Residential Mobility
Influential factors on residential mobility and residential demand have long been studied [
5,
6]. By applying hedonic modeling, the influence of crime [
25], consumption amenities [
26,
27,
28], neighborhood parks [
29], social capital [
30], walkability [
31] and air quality [
32] have been discussed. The relations between lifestyles, neighborhood characteristics and the choice of residential location have been studied by modeling individual or household choices regarding residential location [
33,
34,
35].
Jacobs [
36] qualitatively argued that the ideal neighborhood is one that is walkable with many mixed uses and a diverse community. Walk Score [
37], a publicly available website, has been introduced to quantitatively assess neighborhood walkability. Walk Score assigns neighborhood walkability scores based on distance to amenities and pedestrian friendliness (e.g., population density, road metrics) using data from Google, Education.com, Open Street Map, the U.S. Census and Localeze. According to Gilderbloom et al. [
31], Walk Score has positive impacts on housing values, crime rates, livability and economic resilience, so it is an efficient tool to plan new urban forms to make a city livable and active.
We consider that the opportunity cost of travel time reflects consumption amenities, neighborhood parks and walkability. However, crime rate and air quality are not reflected in mobility data. We consider that the benefit of our method is that it only requires mobility data for predicting residential mobility and that it does not require additional secondary data such as information about neighborhood amenities and road metrics.
2.4. Gap in the Literature
In previous studies, data were collected through survey. It is costly and time consuming to collect survey data. The availability of a large amount of mobility data collected from mobile phones and smart cards of public transportation has been rapidly increasing.
Recent studies created indices for estimating urban characteristics using automatically collected mobility data. For example, Smith et al. [
38] created an index for estimating community well-being by calculating the diversity of destinations people visit based on the smart card data of public transportation. Zhong et al. [
39] created indices of the centrality of mobility for each station using a network science approach from the smart card data of public transportation. Yabe et al. [
40] measured the fragility of people flows to plan future investments in infrastructure appropriately based on locational data collected from mobile phones. The benefit of such indices is as follows: First, we can detect urban changes without surveys, which cost time and money. Second, we can evaluate the result of investments in urban development and predict future outcomes. Third, we can obtain knowledge about the nature of urban systems using those indices.
To the best of our knowledge, no method has been proposed to create an index based on mobility data to predict future residential movements. We propose a method called TCM4MP (travel cost method for multiple places) to infer the opportunity cost of travel time that varies according to the given place as an index for predicting the number of people who relocate to each place.
Our study assumes that the opportunity cost of travel time on non-working days reflects the convenience and amenities of the neighborhood. The opportunity cost of travel time is the potential loss of benefit by traveling to distant places. Therefore, the opportunity cost of travel time is affected by the convenience and amenities of the neighborhood. On the other hand, we note that this assumption has a limitation. According to Walsh et al. [
9], the opportunity cost of travel time on non-working days is also affected by other factors. For example, individuals with flexible work hours appear to have a lower opportunity cost of travel time than those whose work hours are fixed. Similarly, persons who are in school, retired or unemployed have a lower opportunity cost of travel time. In addition, the opportunity cost of travel time is proportional to wage rate. If such factors differ widely according to places, the opportunity cost of travel time is affected by those factors. It is necessary to evaluate the relation between the opportunity cost of travel time and neighborhood amenities. We consider that such a comparison is possible using Walk Score.
Our study is motivated by previous studies in the domain of transportation engineering and urban economics; however, the aim of our study is practical use. The final objective of our study is to contribute to the detection and prediction of changes in the trends of residential mobility. We consider that the current population of each place also correlates with the number of people who relocate to each place. However, this changes slowly compared to changes in travel behavior; therefore, it does not contribute to the early detection and prediction of changes in the trends of residential mobility. We compare our proposed method with other indices derived from smart card data in terms of correlation and causality to the number of people who relocate to each place.
3. Method
3.1. Measurement of Opportunity Cost of Travel Time
Conventional studies using TCM do not assume that the opportunity cost of travel time varies according to the departure place. In addition, these studies usually calculate the benefit of one recreational site. Equation (
1) is the equation of a demand curve defined in a conventional travel cost method.
In this equation, denotes the visitation rate to a recreational site per person who lives in place i, C denotes the benefit one can obtain by visiting the recreational site and denotes the time it takes to travel from place i to the recreational site. B denotes the opportunity cost of travel time per unit time, and D denotes the set of departure places.
We propose a method called TCM4MP by extending Equation (
1) to measure the values of the opportunity cost that differ according to the departure place. Equation (
2) is derived by assuming that the opportunity cost of travel time differs according to the departure place and by incorporating the values of the benefits of multiple arrival places.
In this equation, is a parameter that represents the opportunity cost of people who live in departure place i. is a parameter that represents the benefit that one can obtain by visiting arrival place j. denotes the logarithm of the average number of movements from departure place i to arrival place j per person, and A denotes the set of arrival places.
It is impossible to determine the values of
by simply applying linear regression analysis. We assume that the parameters
and
follow normal distributions as in Equations (
3) and (
4).
In these equations,
,
,
and
are hyperparameters. All the parameters and hyperparameters are inferred by applying the hierarchical Bayesian inference method to Equations (
2)–(
4) using mobility data on non-working days. In this study, we use statistical software, Stan [
41], for Bayesian inference, which is based on No-U-Turn sampler (NUTS) [
42], an extension of Hamiltonian Monte Carlo (HMC) [
43]. Thus, the values of the opportunity cost of travel time
are obtained.
The opportunity cost can be obtained separately according to people’s demographic information. Our method divides mobility data according to demographic information about their gender and age, and we calculate for each demographic group. We let k denote a demographic group, and denotes the opportunity cost of people living in place i in demographic group k.
3.2. Decision of the Prediction Model
We assume that the opportunity cost of travel time reflects the convenience of the place. We also consider that the number of people who relocate to a place correlates with the convenience of the place. In addition, we consider that the convenience of a place varies depending on gender and age. Therefore, we use the opportunity cost of the travel time to a place for the prediction of the number of people who relocate to that place.
We create a power regression model
for opportunity cost (O) to predict the amount of future residential mobility by Equation (
5).
Note that
denotes the number of people in demographic group
k who relocate to place
i. The parameters
and
are unconditioned to place
i. We consider that power regression is suitable because of the assumption that the number of residential movements is proportional to the product of the population of two areas (a gravity model [
44]) and the assumption that the distribution of a population follows the power law (Zipf’s law [
45]). The parameters are calculated using the Levenberg–Marquardt algorithm [
46].
4. Baselines and Evaluation Methods
4.1. Baselines
We evaluate how much the predictor using the opportunity cost () contributes to the prediction of residential mobility by comparing it with other indices. We compare it with predictors using the following three indices:
Population (P): This index is simply the number of current residents in place i. We let denote the number of residents of demographic group k living in place i.
Average travel time (A): This index is a simplification of the opportunity cost of travel time. We let denote the multiplicative inverse of travel time per person.
Entropy (E): According to Smith et al. [
38], the diversity of places people visit reflects the well-being of the community. The index is as follows:
In Equation (
6),
is the set of places user
u visited, and
is the proportion of all
u’s visits to place
j. The numerator in this equation is the Shannon entropy. In Equation (
7),
is the set of users who live in place
i. We let
denote the entropy of places users in demographic group
k living in place
i visit.
As with Equation (
5), prediction models
,
and
are determined by power regression.
4.2. Evaluation of the Correlation and Causal Relation between the Number of Relocations and the Predictors
First, we evaluate the correlation between a predictor and the number of people who relocate to each place. If we found predictors that highly correlate with the number of people who relocate to each place, we perform causal inference between the predictors and the number of residential moves.
We apply the linear non-Gaussian acyclic model (LiNGAM) [
47] for the causal inference. By applying LiNGAM, causal relations between variables are obtained as described in Equation (
8).
In this equation, is an observed variable. The variable is an exogenous variable (random variable) having a non-Gaussian distribution, and is the strength of the causal connection from to . The objective of causal inference is to determine .
The key difference between LiNGAM and earlier works on causal inference is that LiNGAM assumes that exogenous variables are non-Gaussian. Under this assumption, it is possible to estimate a causal ordering of variables using passive observational data alone without any prior information on a causal ordering of the variables.
In our study, denotes either the number of residential moves or the value of a predictor for predicting the number of residential moves. By applying LiNGAM, we obtain the causal networks between the number of residential moves and predictors that highly correlate with the number of residential moves. We use causal networks obtained using LiNGAM for the evaluation of the causal influence of each predictor on the number of residential moves.
5. Data
We use the smart card data of public transportation in the Kansai Area of Japan. The data are from March–April 2016 and from March–April 2017. There are two types of smart cards in this area. One type of smart card requires applicants to submit their personal information when applying to obtain the card. We use data collected from that type of smart card. The data include information about the user’s ID, user’s age, user’s gender, the postal code of the location of the user’s residence, boarding station, boarding time, alighting station and alighting time. The data were completely anonymized before being provided to us by the railway companies.
The data include 1024 stations held by 14 railway companies and 3 agencies of city governments. The locations of the stations are shown in
Figure 3.
The demographic composition of the card holders is given in
Table 1. The number of male card holders and that of female card holders exceed one million in both 2016 and 2017.
We compare the demographic composition of the smart card data and that of the data published by the government of Osaka City. We categorize the smart card data by gender and ages in groups of 10 years. Osaka City has 24 wards. We therefore further divide the smart card data according to the ward in which each card holder’s residence is located. We compare the number of residents by ward for each demographic group.
Table 2 shows the correlation coefficients between the number of each demographic group of the smart card data and that of the governmental data. We assume that smart card data reflect real demographic compositions.
In this paper, we use smart card data collected from March–May 2016 for obtaining predictors for the amount of future residential mobility. We recognize residential moves between 2016 and 2017 by the changes in stations at which card holders most frequently board for the first time on a day.
We do not use data on individuals younger than 20 or older than 79 because we assume that most of these people do not relocate to other areas by their own will. In the following, we divide card holders into demographic groups by gender and in age groups of 10 years.
6. Data Pre-Processing
This section explains the data pre-processing procedure for the smart card data that we used. Some thresholds used in this section are arbitrarily set, and we do not investigate a method to find such suitable thresholds automatically in this paper. Further research is needed to investigate a method to find suitable thresholds automatically.
6.1. Decision of Travel Time between Two Stations
We determine the time it takes to travel from departure station
to arrival station
by
defined in Equation (
9).
In this equation, denotes a set of all the values of durations for traveling from departure station to arrival station . denotes the median of .
6.2. Grouping Departure Stations, Arrival Stations and Smart Card Holders
We group departure stations by the physical proximity between stations and similarity of boardings by smart card holders. Departure station
and departure station
are grouped together when Equation (
10) or (
11) is satisfied.
In Equation (
10),
denotes the distance between departure station
and departure station
in meters. In Equation (
11),
denotes a set of smart card holders who had boarded at departure station
for the first time on a day during the period from March–May 2016 (we assume that a station that a user boards at for the first time on a day is located near the user’s residential location). Equation (
10) means that the distance between departure station
and departure station
is less than 300 m. Equation (
11) means that the number of smart card users who have boarded at both departure station
and departure station
is greater than 10% of the number of smart card holders who had boarded at departure station
and that of smart card users who had boarded at departure station
.
We group arrival stations by the physical proximity and walkability between stations. Arrival station
and arrival station
are grouped together when Equation (
12) or (
13) is satisfied.
In Equation (
13),
denotes the set of all the values of the duration between a user alighting at station
and the time the user subsequently board at station
. Equation (
13) means that the minimum period between when users alight at station
and when the users subsequently board at station
is less than 30 min. We assume that this means that people can walk from station
to station
within 30 min. This is based on a fare system employed by many Japanese railway companies that additional fare is not required for a transit within 30 min.
Finally, 599 groups of departure stations and 541 groups of arrival stations are obtained. In the following, the group of departure stations is simply referred to as the departure place, and the group of arrival stations is simply referred to as the arrival place.
We determine the time it takes to travel from departure place
i to arrival place place
j by Equation (
14).
In this equation, denotes the set of all stations in departure place i, and denotes the set of all stations in arrival place j.
We also group smart card holders. Smart card holders are grouped by the stations at which they most frequently board for the first time on a day.
In this equation, denotes the number of days user u boards at place k. This equation means that user u is grouped into set when the number of days user u boards at departure place i is the highest among all the departure places.
In addition, we exclude the data of user if place i is far from the location of his/her residence estimated by his/her postal code. In this study, we set the threshold to 5000 m.
6.3. Removing Records of Arrival Stations that Each User Frequently Visits
We apply the travel cost method to the data of non-work travel. Therefore, we apply the method to data collected on holidays and weekends. However, some people commute to work on holidays or weekends. To remove such records, we count the number of days each user has alighted at each station. We ignore the records of the stations at which a user frequently alighted. The records of arrival place
j of user
u that satisfy Equation (
16) are ignored.
In this equation, denotes the number of days (including weekdays) user u has alighted at arrival station j. s denotes the number of all the days in the period of the data.
Table 3 shows the number of valid users obtained after data preprocessing.
7. Results
7.1. Results of the Regression of the Predictors to the Number of Residential Moves
Table 4 shows the results of the regression analyses between the number of residential movements
and predictors
,
,
and
. The predictor using opportunity cost (O) was superior to other baselines for the data of male individuals of all ages and female individuals less than 60 years old. On the other hand, the predictor using population (P) scored the highest for the data of female individuals who are 60 or older.
The coefficients of determination of the predictors using opportunity cost (O) and population (P) were higher than 0.6, but the other predictors were lower than 0.6.
7.2. Causal Influences on the Number of Residential Moves
We measured causal influences from the two predictors using opportunity cost (O) and population (P) on the number of residential moves using linear non-Gaussian acyclic model (LiNGAM) [
47]. LiNGAM assumes that exogenous variables are non-Gaussian. We tested whether the predictors and the number of residential moves satisfied this assumption. It is impossible to test the distributions of exogenous variables. Therefore, we tested the distributions of observed variables instead.
The Shapiro–Wilk test [
48] was used to test normality. The Shapiro–Wilk test tests the null hypothesis that a sample came from a normal distribution. The null hypothesis of this test was that the population of the data was normally distributed. If the
p-value was less than the chosen alpha level, then the null hypothesis was rejected, and there was evidence that the data tested were not from a normally distributed population.
Table 5 shows the results of the Shapiro–Wilk test. Every
p-value listed in
Table 5 is small enough to conclude that the predictors O and P and the number of residential moves to each place (M) did not follow a normal distribution.
In addition to non-Gaussianity, LiNGAM assumes that relations between variables are linear. The linearity between the number of residential moves (
) and the predictor O (
) and the linearity between the number of residential moves (
) and the predictor P (
) have already been confirmed, as shown in
Table 4. In regards to the relation between the two predictors (
and
), the correlation coefficient is shown in
Table 6. It was high enough to assume that the relation between the two predictors was linear. Therefore, we considered that the values satisfied the assumption of LiNGAM.
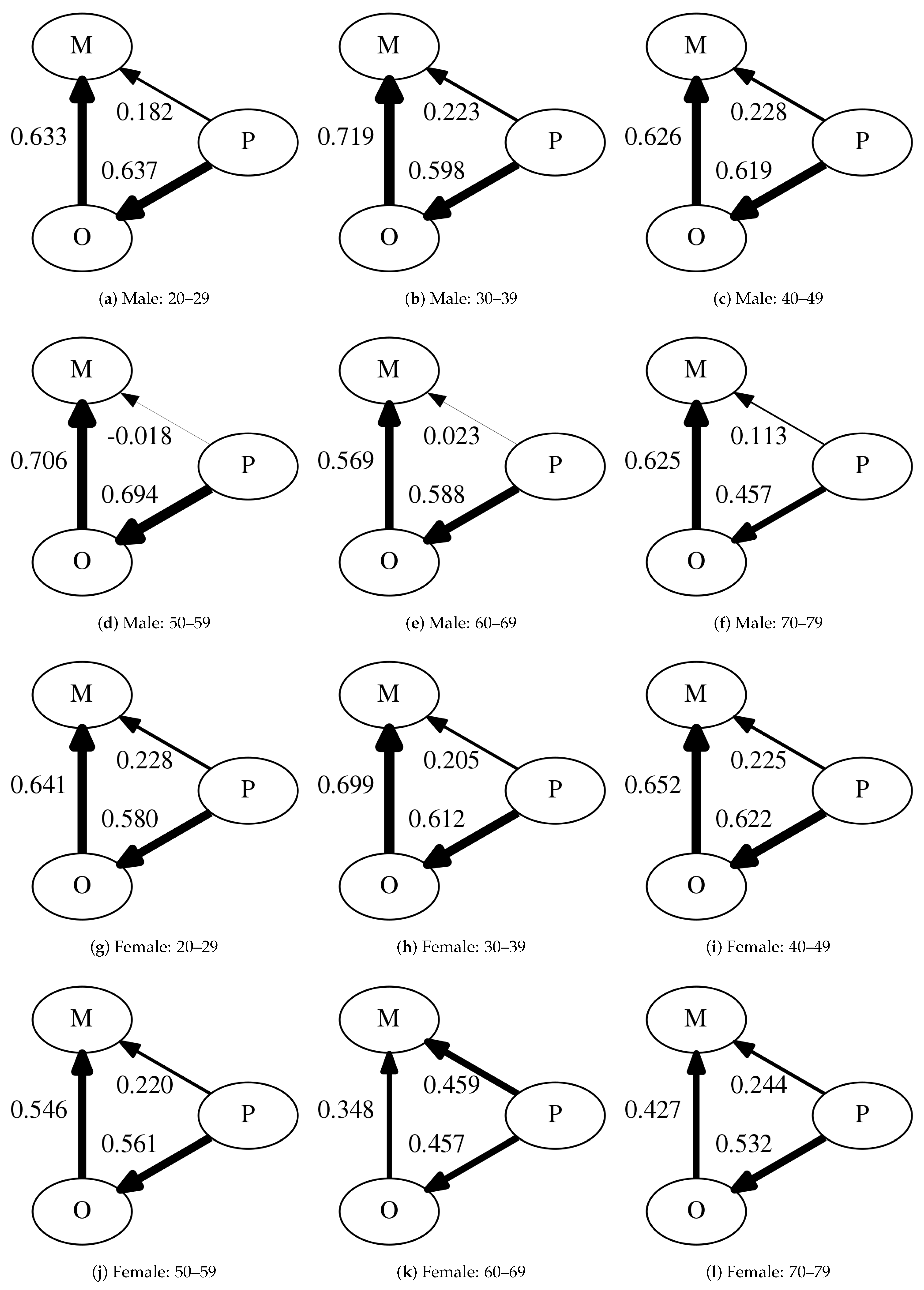
Figure 4 shows the results of the application of LiNGAM. The directions of the obtained causal networks were the same for every demographic group. The number of people who relocated to each place (M) was affected by both the predictor using the opportunity cost of travel time (O) and the predictor using the current population (P). The strength of causality from O to M was greater from P to M except for the demographic group of female individuals between 60 and 69 years of age. In addition, the strength of causality from P to O was greater from P to M except for the demographic group of female individuals between 60 and 69 years of age.
We measured the reproducibility of the results. First, we examined the reproducibility of the directions of causal networks. We repeated the experiment by making 1000 causal networks for each demographic group by randomly taking 400 departure places out of 599 departure places and making causal networks using the data of 400 selected departure places. The results are shown in
Table 7. The first type of network has the same causal directions as the network that we obtained using all the departure places. The number of individuals in the first type in the network was 1000 for the demographic groups of male individuals less than 70 years of age and female individuals less than 60 years of age. On the other hand, the number of individuals in the first type of network for the groups of male individuals in their 70s was 772. Therefore, there might be missing causal factors for the demographic group; thus, it is necessary to seek other causal factors to incorporate.
Next, we examined the reproducibility of the order of the strength between the causalities to the number of residential moves from the opportunity cost of travel time and current population. We conducted the same random sampling until we obtained 1000 networks whose directions of causality were the same as the network that we obtained using all the departure places.
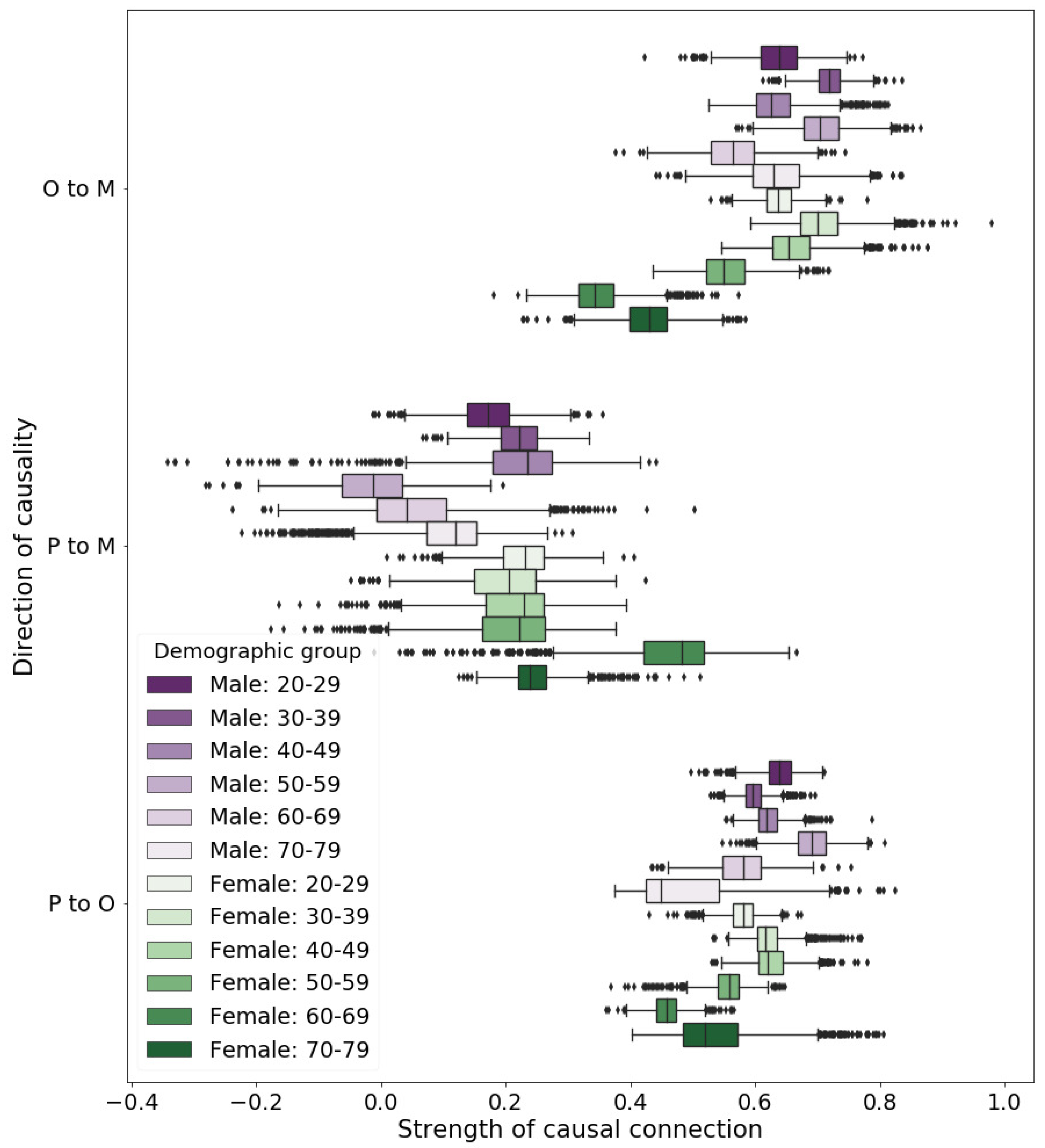
Figure 5 shows the ranges of the strengths of causality. Comparing the medians of the strengths of causality to the number of residential moves, the orders were consistent with the results obtained using all the departure places, as shown in
Figure 4. The ranges of the causalities (O→M and P→M) overlapped only in regards to the demographic group of female individuals 60 years or older. Therefore, we concluded it was certain that the causal strength of O→M was greater than P→M, and the causal strength of P→O was greater than that of P→M, except for the demographic group of female individuals 60 years or older. We cannot draw the conclusion for the demographic group of female individuals 60 years or older.
8. Discussion
We have observed that the opportunity cost of travel time has strong causality to the number of people who relocate to each place. In addition, the index is influenced by the current population in each place. We assume that this is because a more heavily populated area will be more convenient because commercial developers and residential developers focus on such areas. This leads to the conclusion that most of the influence from the current population on residential mobility is mediated indirectly through the opportunity cost of travel time. The opportunity cost of travel time is calculated from non-work travel behavior in a short period of time (three months), and it directly reflects the effects of urban development such as the construction of parks and the development of commercial facilities. Therefore, the opportunity cost of travel time is an efficient and effective index for predicting future residential mobility.
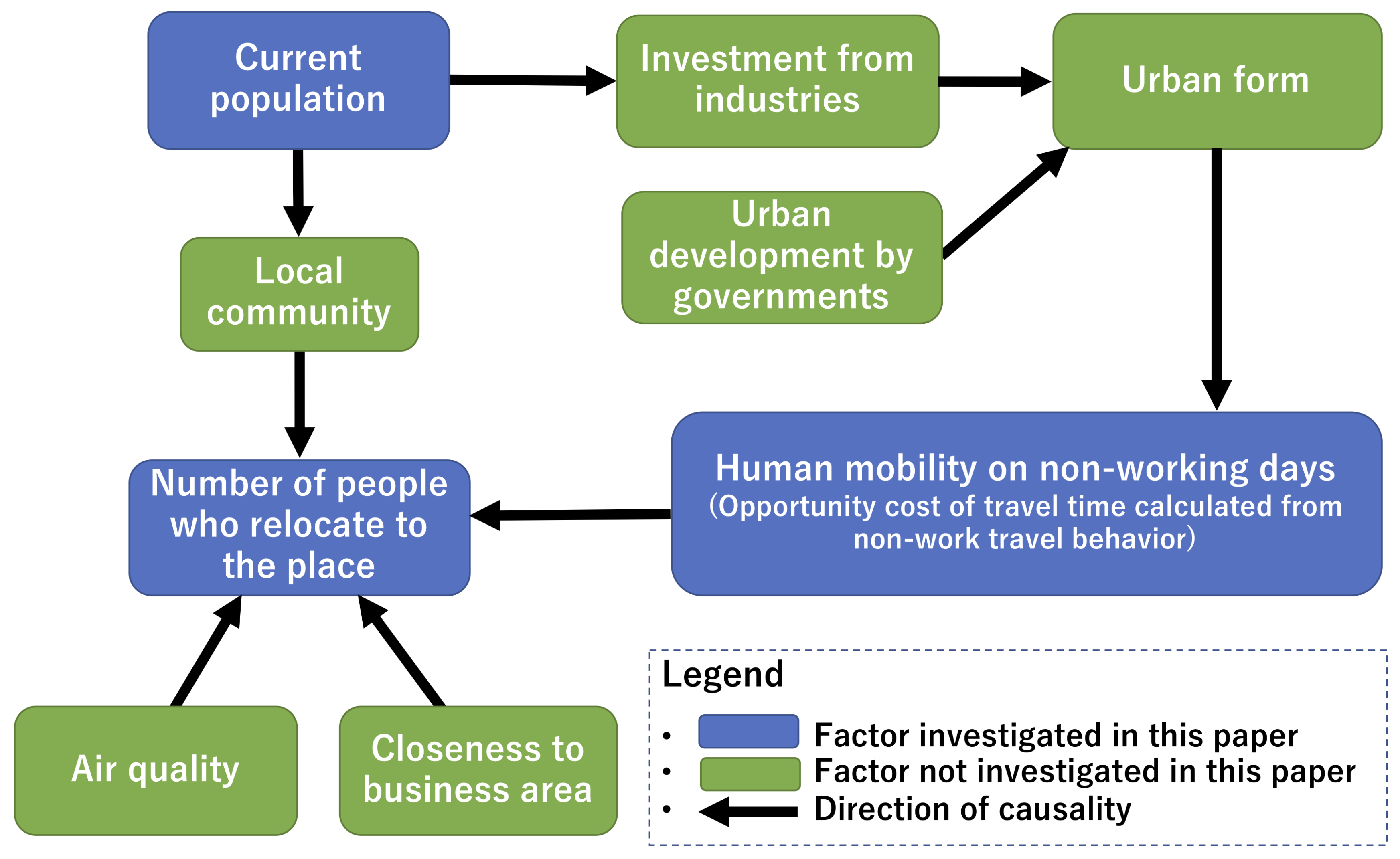
We can list many other factors that are not investigated in our paper.
Figure 6 includes some factors related to residential mobility that were not investigated in this paper. The factors in green are not investigated in our paper.
Human mobility on non-working days is influenced by urban form such as amenities of the neighborhood and land use diversity. Urban form is influenced by investment from both industries and governments. Industries tend to invest in areas with high population densities. Therefore, investment from industries is influenced by the current population. Governments can change the trend of residential movements by investing in urban development.
There is also causality from the current population to the number of people who relocate to each place that is not mediated through non-work human mobility. Residential movement is influenced by land prices and the social capital of the local community. These factors are influenced by the current population. We assume that these causalities could be why the causality from O to M is not always greater than that from P to M in regard to the demographic group of female individuals 60 years or older.
There are also factors influencing residential mobility not being mediated by human mobility on non-working days and the current population. For example, closeness to business areas and air quality could have strong causality to residential mobility.
We note that further investigation needs to test the settings of thresholds and their influence on the results. In this paper, we arbitrarily set thresholds for: (1) grouping stations and smart card holders; (2) extracting non-working trips; and (3) selecting predictors for a causal analysis. In regard to grouping stations and card holders, the results may change according to the thresholds. In regard to extracting non-working trips, many business areas also have many commercial facilities in the neighborhood. Therefore, it is difficult to distinguish non-working trips using smart card data of public transportation. The results of our study may be biased by such factors. In regard to selecting predictors for a causal analysis, we select predictors whose correlation coefficients with the number of people who relocate to each place is high. It is difficult to determine whether the relation between two variables is linear. In our analysis, the correlation coefficient between every combination of the three variables (P, O, and M) is very high, but it is manually determined. When our method is applied to other data, the selection of variables for causal analysis must be carefully done.
9. Conclusions
In this work, we have investigated a method for creating an index based on mobility data to estimate the effects of urban development on residential movements. The contributions of this work are summarized as follows:
We have extended the conventional travel cost method to estimate the opportunity cost of travel time as a function of the departure place.
We have confirmed that both the current population and the opportunity cost of travel time contribute to the prediction of the number of relocations.
We have confirmed that most of the causal influence from the current population to residential mobility is mediated indirectly through the opportunity cost of travel time. Therefore, the opportunity cost of travel time is more effective at estimating changes in residential mobility caused by urban development.
Our method is aimed at predicting future residential mobility and detecting future changes in residential mobility. The method can also be used to evaluate urban development. In planning of a new urban form, discrete choice models for destination choices [
16] and housing choices [
49] are suitable means. In addition, Walk Score [
37] can also contribute to planning a new urban form.
We note some limitations of our work. First, the opportunity cost of travel time is influenced by not only urban form, but also other factors such as people’s disposable time and activities using ICTs while traveling (e.g., mobile phones and potable gaming devices). Second, residential mobility is determined by other factors such as closeness to business areas and air quality. Third, the causal networks are not theoretically derived; therefore, it is necessary to analyze the causalities from a theoretical perspective.
Our future work will investigate which factors of urban form influence the opportunity cost of travel time. In addition, further research is needed to extend the method to include other types of transportation such as automobiles.
Recent smart city initiatives are aimed at using a mixture of various types of data to solve a mixture of various urban problems, such as transportation, energy use and the economy [
50]. Especially, the European Commission proposes an integrated approach to connect policies and resources at EU, national, regional and local levels to promote smart city solutions [
51]. Analyzing the relationships between human mobility and residential mobility marks an important step towards understanding urban dynamics and, thereby, helps planning and managing of public transport and economic development. Despite the above limitations, our proposed method is beneficial to urban planners for estimating the effects of urban development and detecting the shrinkage and growth of populations.