Analyzing OpenStreetMap Road Data and Characterizing the Behavior of Contributors in Ankara, Turkey
Abstract
:1. Introduction
2. Study Description
2.1. The Study Area and OSM Road Data Structure
2.2. Evaluation Methods
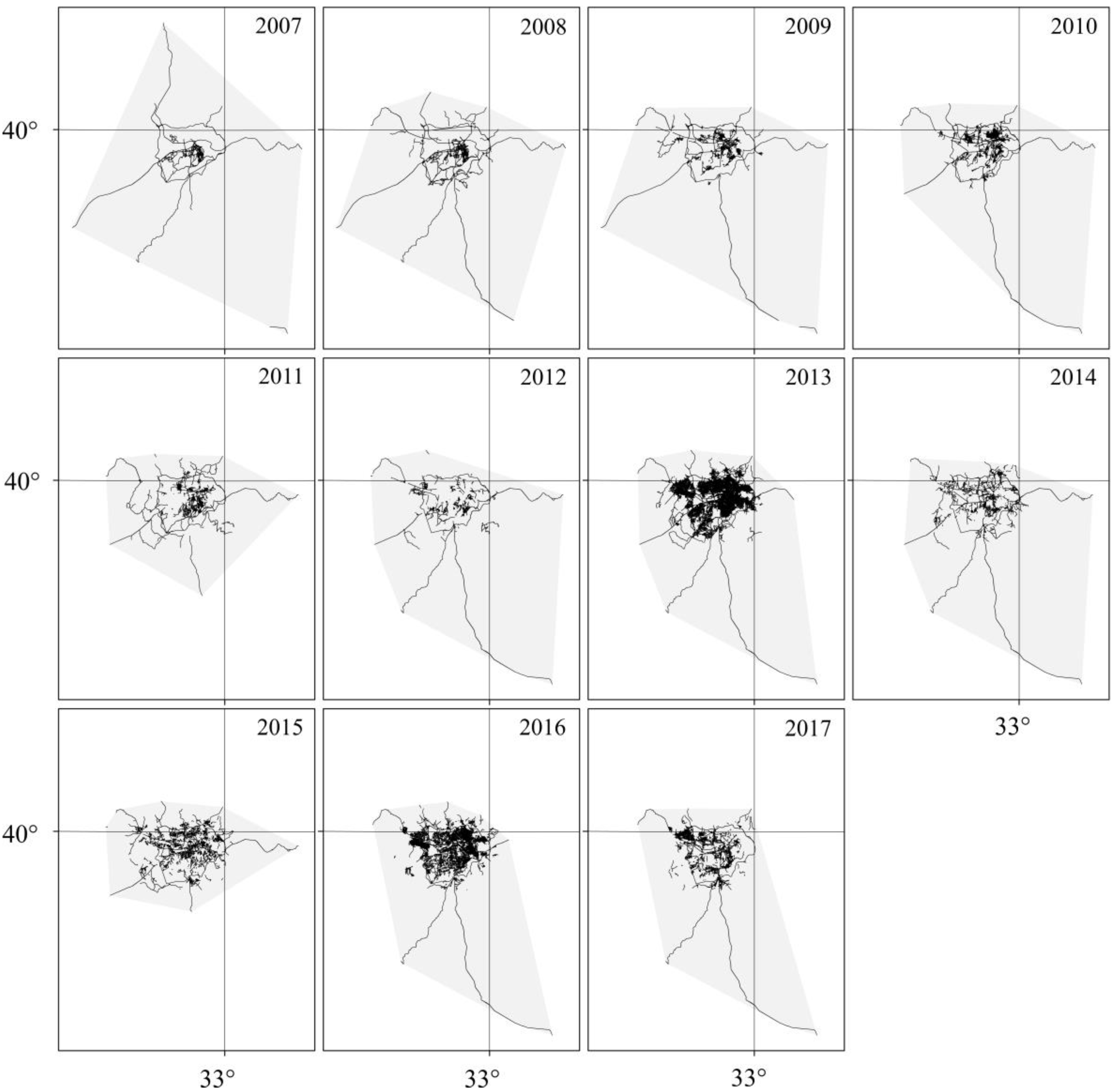
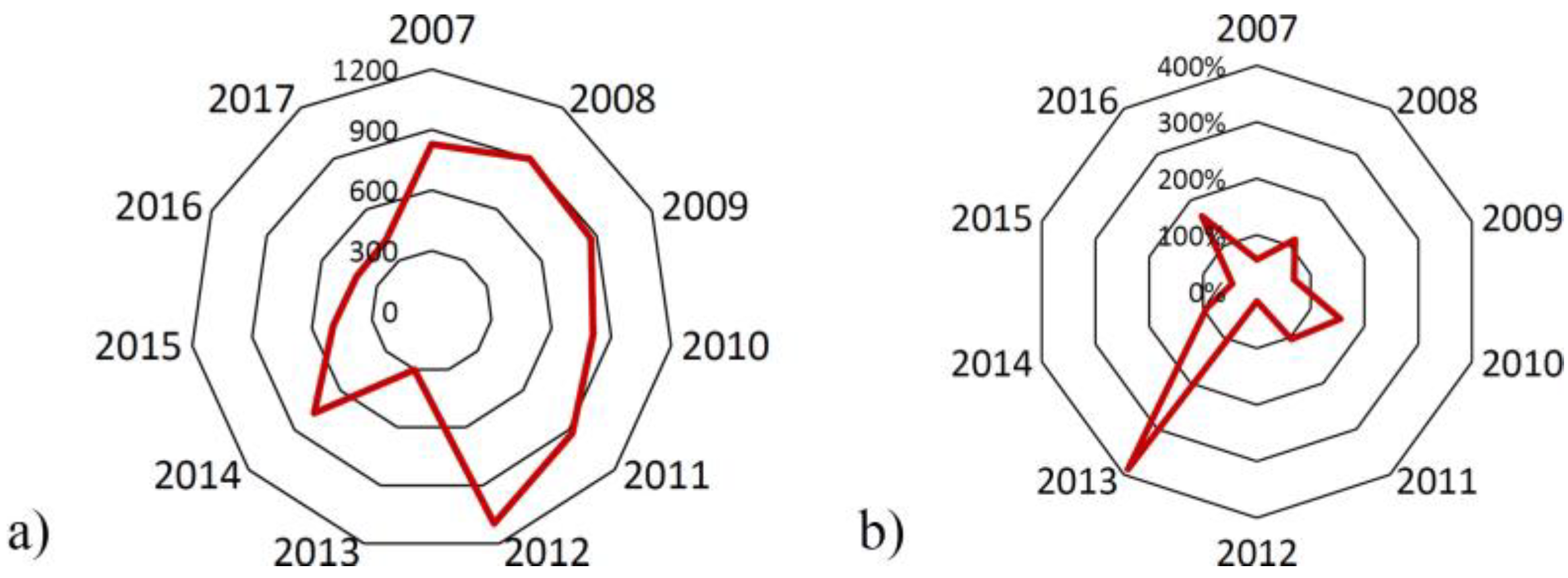
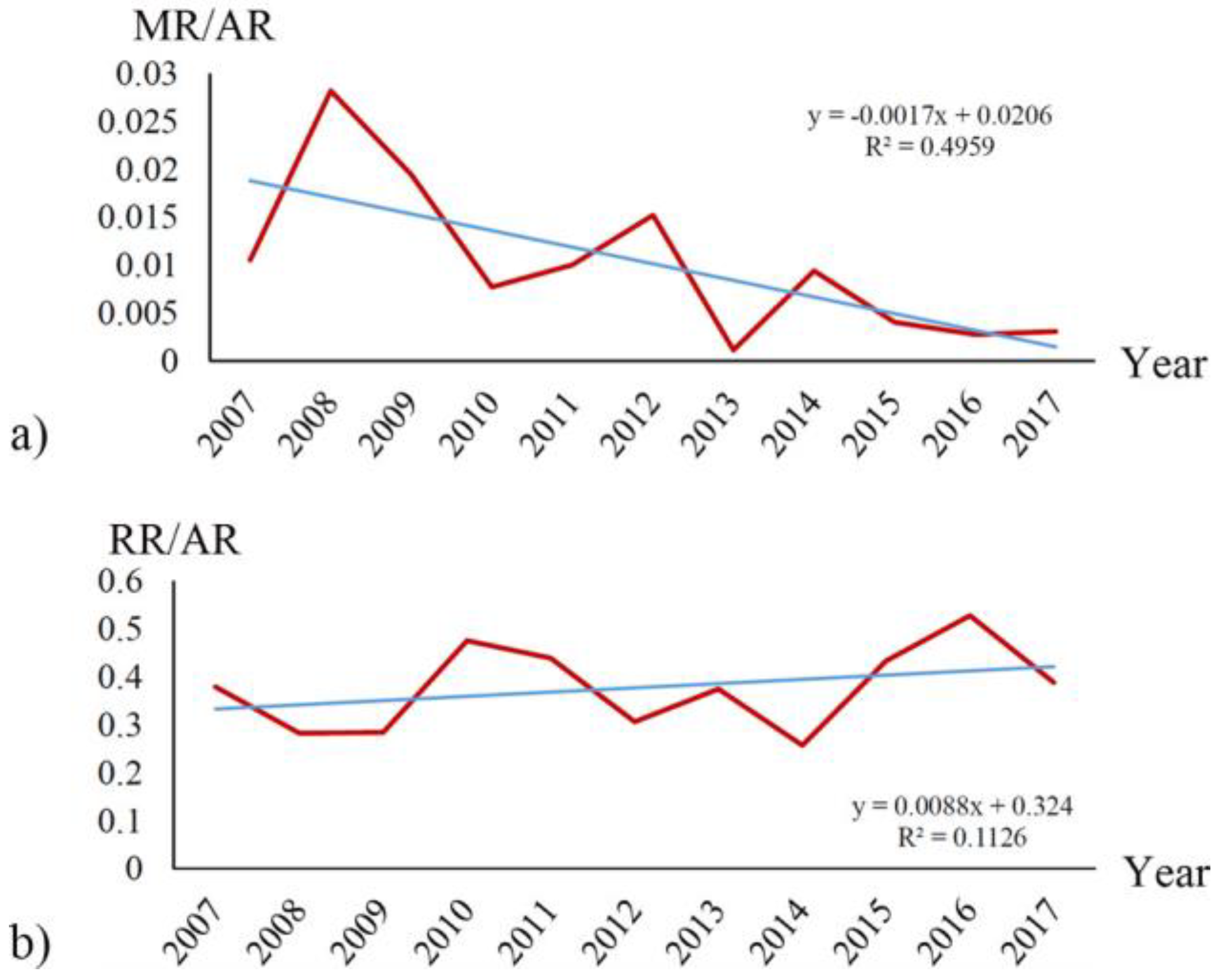
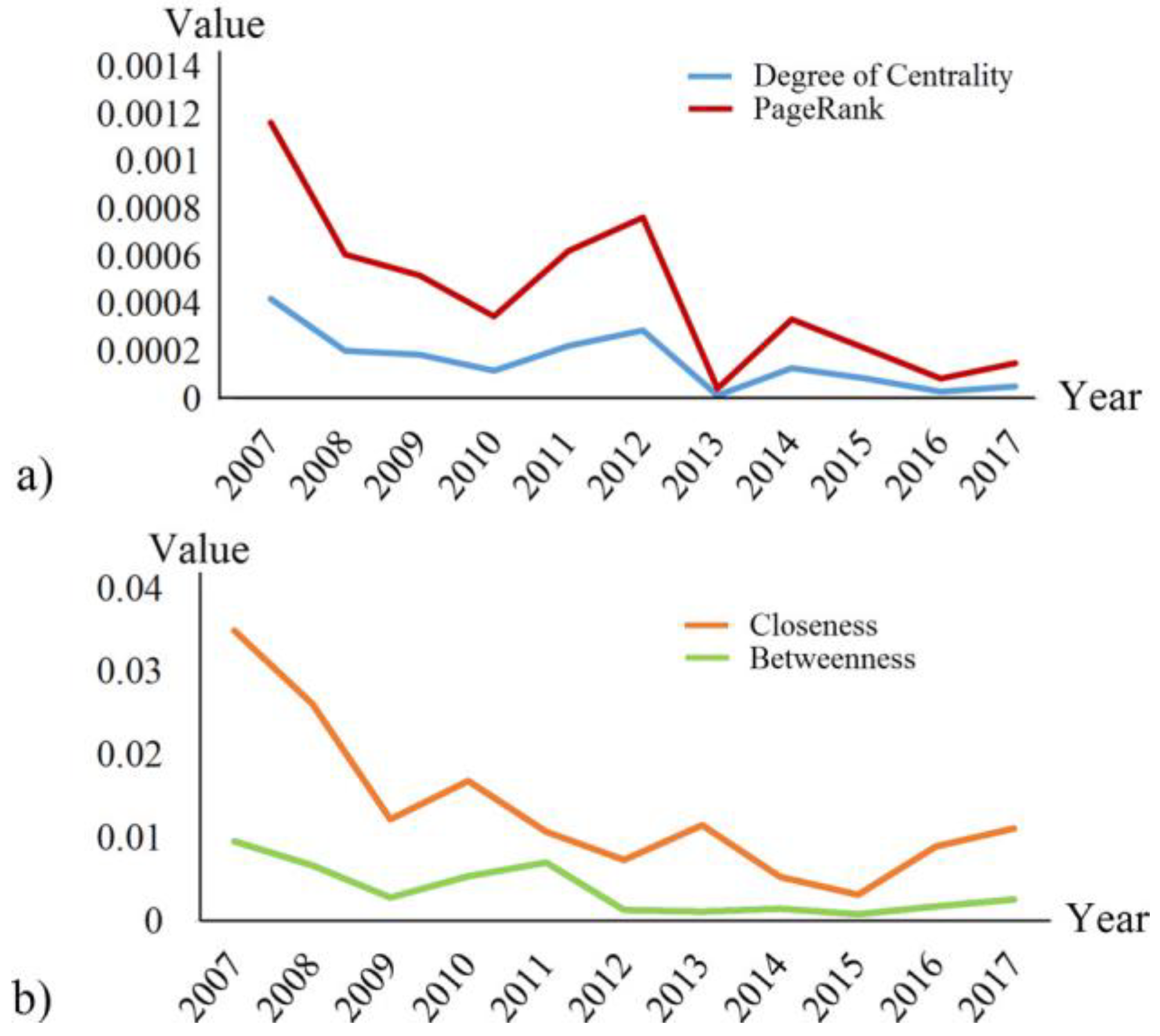
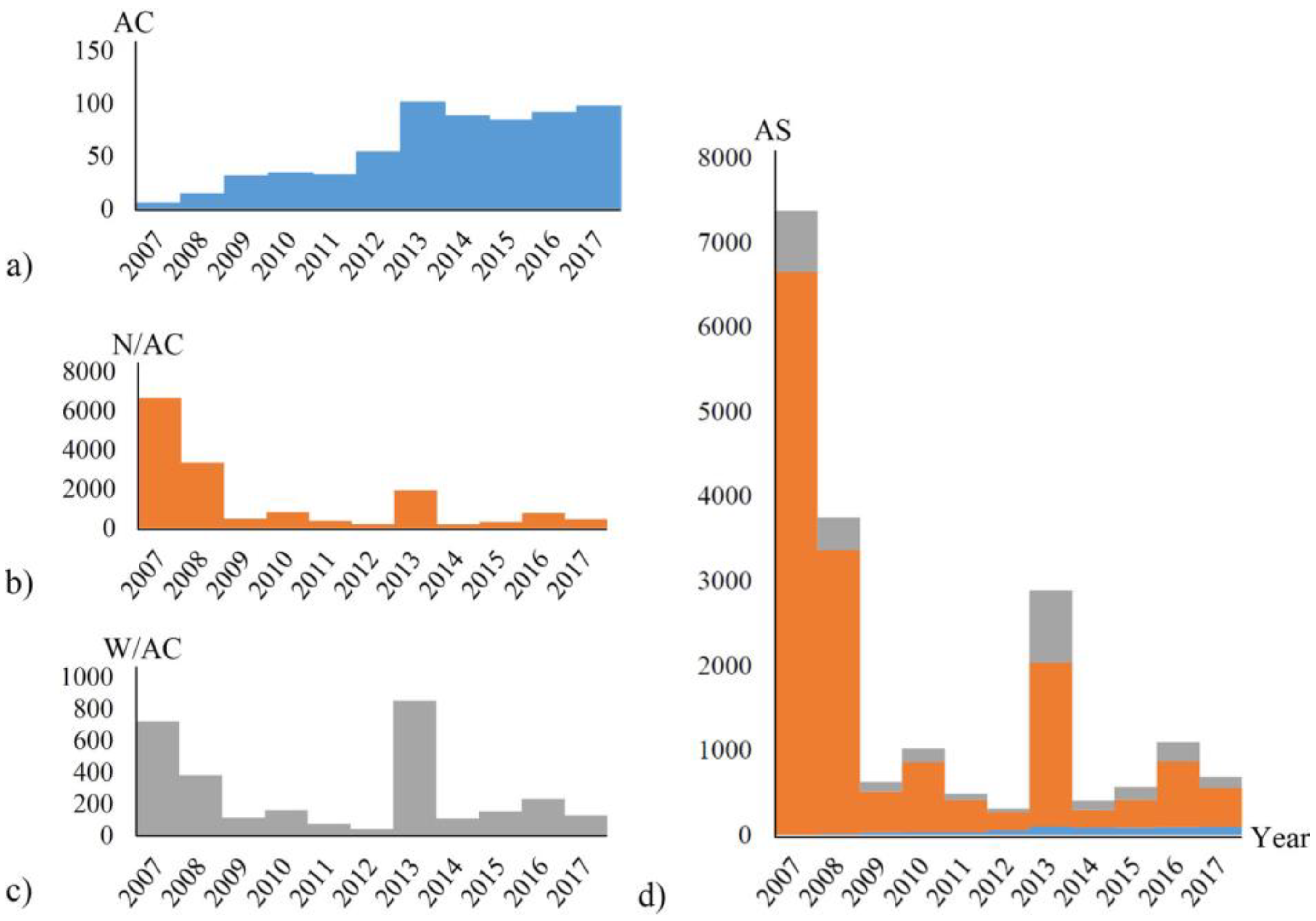
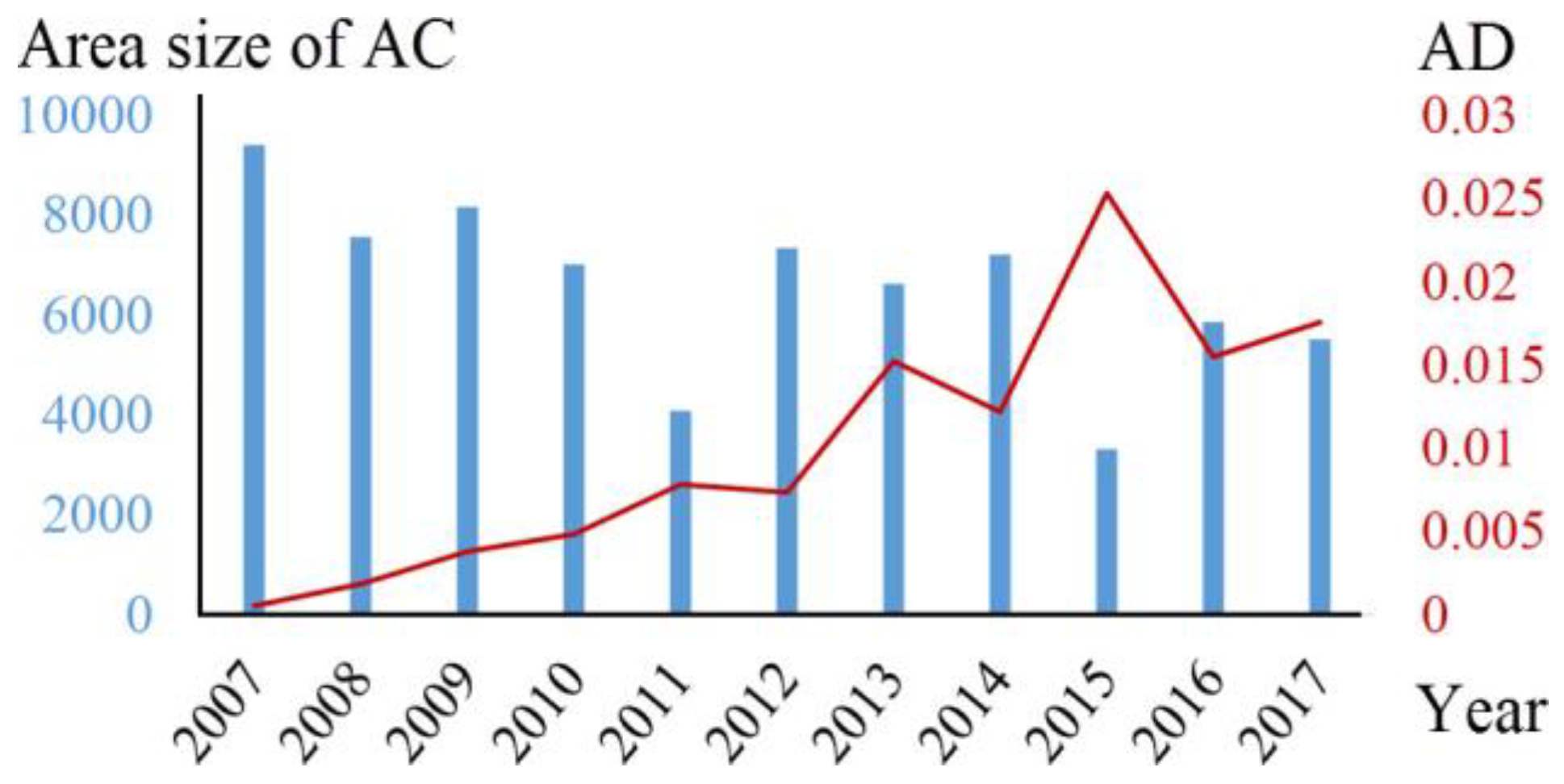
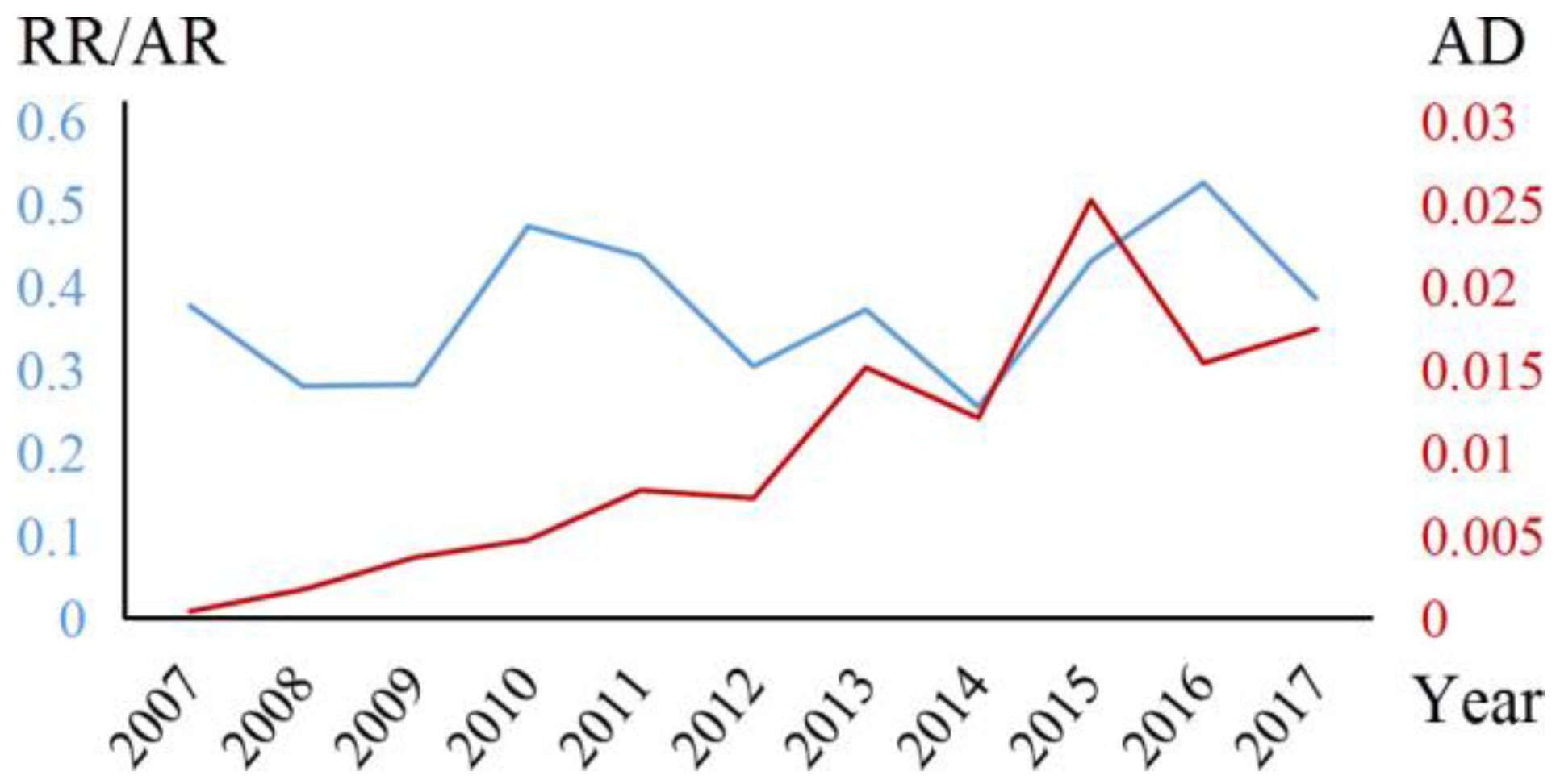
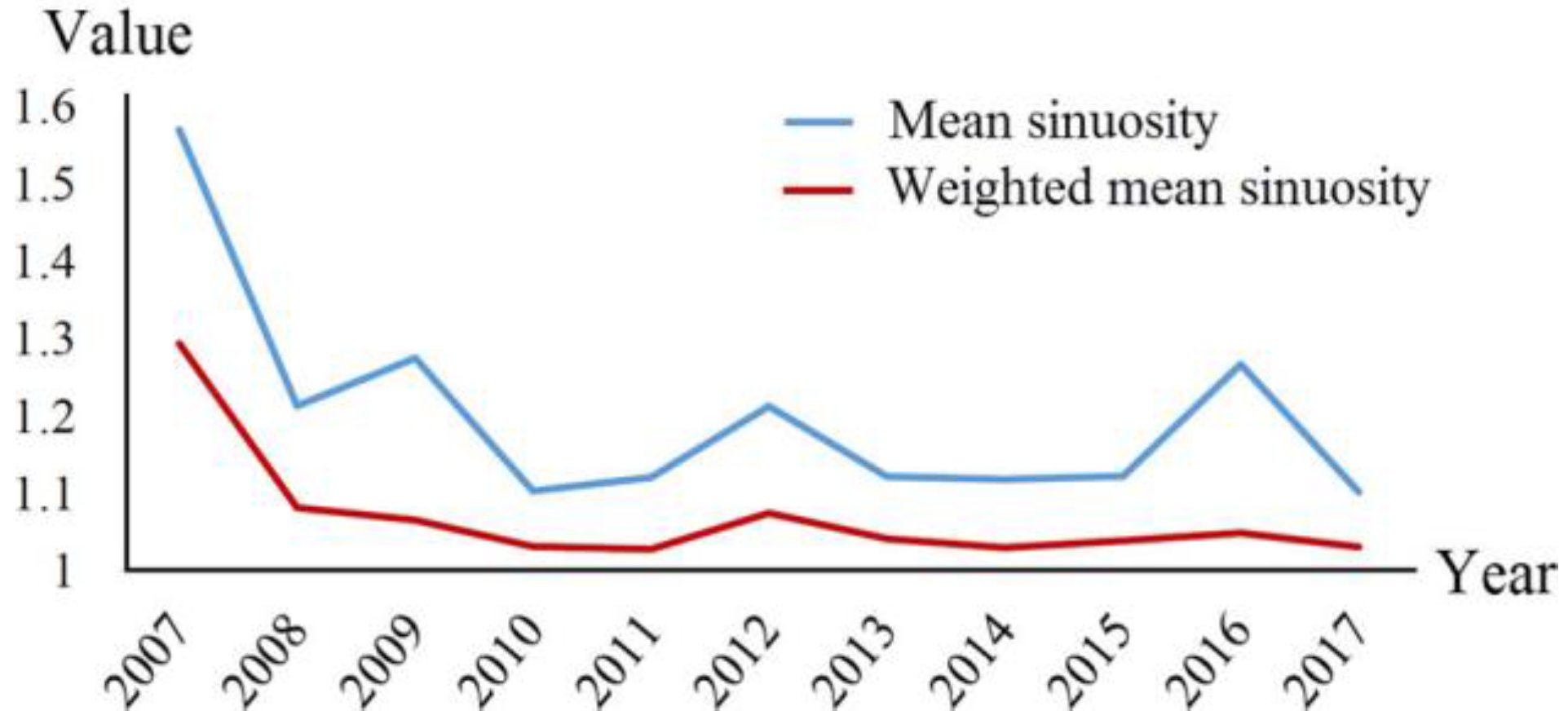
3. Evaluation of OSM Road Data and Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, P.; Jia, T.; Qin, K.; Shan, J.; Jiao, C. Statistical analysis on the evolution of OpenStreetMap road networks in Beijing. Phys. A 2015, 420, 59–72. [Google Scholar] [CrossRef]
- Goodchild, M.F. Citizens as sensors: The world of volunteered geography. GeoJournal 2007, 69, 211–221. [Google Scholar] [CrossRef]
- Heipke, C. Crowdsourcing geospatial data. ISPRS J. Photogramm. Remote Sens. 2010, 65, 550–557. [Google Scholar] [CrossRef]
- Neis, P.; Zielstra, D. Recent developments and future trends in volunteered geographic information research: The case of OpenStreetMap. Future Internet 2014, 6, 76–106. [Google Scholar] [CrossRef] [Green Version]
- Budhathoki, N. Participants’ Motivations to Contribute Geographic Information in an Online Community. Ph.D. Thesis, University of Illinois, Urbana-Champaign, Urbana, IL, USA, 2010. [Google Scholar]
- Degrossi, L.C.; Albuquerque, J.P.; Rocha, R.S.; Zipf, A. A taxonomy of quality assessment methods for volunteered and crowdsourced geographic information. Trans. GIS 2018, 22, 542–560. [Google Scholar] [CrossRef] [PubMed]
- Buhl, J.; Gautrais, J.; Reeves, N.; Solé, R.V.; Valverde, S.; Kuntz, P.; Theraulaz, G. Topological patterns in street networks of self-organized urban settlements. Eur. Phys. J. B 2006, 49, 513–522. [Google Scholar] [CrossRef]
- Crucitti, P.; Latora, V.; Porta, S. Centrality in networks of urban streets. Chaos 2006, 16, 015113. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B. A topological pattern of urban street networks: Universality and peculiarity. Phys. A 2007, 384, 647–655. [Google Scholar] [CrossRef] [Green Version]
- Barthélemy, M.; Flammini, A. Modeling urban street patterns. Phys. Rev. Lett. 2008, 100, 138702. [Google Scholar] [CrossRef]
- Masucci, A.P.; Smith, D.; Crooks, A.; Batty, M. Random planar graphs and the London street network. Eur. Phys. J. B 2009, 71, 259–271. [Google Scholar] [CrossRef] [Green Version]
- Erath, A.; Löchl, M.; Axhausen, K.W. Graph-theoretical analysis of the Swiss road and railway networks over time. NETS 2009, 9, 379–400. [Google Scholar] [CrossRef]
- von Ferber, C.; Holovatch, T.; Holovatch, Y.; Palchykov, V. Modeling metropolis public transport. In Traffic and Granular Flow’07; Appert-Rolland, C., Chevoir, F., Gondret, P., Lassarre, S., Lebacque, J.P., Schreckenberg, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 709–719. ISBN 978-3-540-77073-2. [Google Scholar]
- Soh, H.; Lim, S.; Zhang, T.; Fu, X.; Lee, G.K.K.; Hung, T.G.G.; Di, P.; Prakasam, S.; Wong, L. Weighted complex network analysis of travel routes on the Singapore public transportation system. Phys. A 2010, 389, 5852–5863. [Google Scholar] [CrossRef]
- Masucci, A.P.; Stanilov, K.; Batty, M. Limited urban growth: London’s street network dynamics since the 18th century. PLoS ONE 2010, 8, e69469. [Google Scholar] [CrossRef] [PubMed]
- Strano, E.; Nicosia, V.; Latora, V.; Porta, S.; Barthélemy, M. Elementary processes governing the evolution of road networks. Sci. Rep. 2012, 2, 296. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Senaratne, H.; Mobasheri, A.; Ali, A.L.; Capineri, C.; Haklay, M. A review of volunteered geographic information quality assessment methods. Int. J. Geogr. Inf. Sci. 2017, 31, 139–167. [Google Scholar] [CrossRef]
- Haklay, M. How good is volunteered geographical information? A comparative study of OpenStreetMap and Ordnance Survey datasets. Environ. Plan. B 2010, 37, 682–703. [Google Scholar] [CrossRef]
- Girres, J.F.; Touya, G. Quality assessment of the French OpenStreetMap dataset. Trans. GIS 2010, 14, 435–459. [Google Scholar] [CrossRef]
- Neis, P.; Zielstra, D.; Zipf, A. The street network evolution of crowdsourced maps: OpenStreetMap in Germany 2007–2011. Future Internet 2012, 4, 1–21. [Google Scholar] [CrossRef]
- Corcoran, P.; Mooney, P.; Bertolotto, M. Analysing the growth of OpenStreetMap networks. Spa. Stat. 2013, 3, 21–32. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Malczewski, J. Accuracy evaluation of the Canadian OpenStreetMap road networks. Int. J. Geospat. Environ. Res. 2018, 5. [Google Scholar] [CrossRef]
- Neis, P.; Zipf, A. Analyzing the contributor activity of a volunteered geographic information project — The case of OpenStreetMap. ISPRS Int. J. Geo-Inf 2012, 1, 146–165. [Google Scholar] [CrossRef]
- Rehrl, K.; Gröechenig, S.; Hochmair, H.; Leitinger, S.; Steinmann, R.; Wagner, A. A conceptual model for analyzing contribution patterns in the context of VGI. In Progress in location-based services; Krisp, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 373–388. ISBN 978-3-642-34203-5. [Google Scholar]
- Steinmann, R.; Gröchenig, S.; Rehrl, K.; Brunauer, R. Contribution profiles of voluntary mappers in OpenStreetMap. In Proceedings of the Action and Interaction in Volunteered Geographic Information (ACTIVITY) Workshop, Leuven, Belgium, 14–17 May 2013; pp. 1–6. [Google Scholar]
- Arsanjani, J.J.; Mooney, P.; Helbich, M.; Zipf, A. An exploration of future patterns of the contributions to OpenStreetMap and development of a contribution index. Trans. GIS 2015, 19, 896–914. [Google Scholar] [CrossRef]
- Bégin, D.; Devillers, R.; Roche, S. Contributors’ enrollment in collaborative online communities: The case of OpenStreetMap. Geo-Spat. Inf. Sci. 2017, 20, 282–295. [Google Scholar] [CrossRef]
- Turkish Statistical Institute. Available online: http://www.tuik.gov.tr/UstMenu.do?metod=temelist (accessed on 20 July 2018).
- Porta, S.; Crucitti, P.; Latora, V. The network analysis of urban streets: A primal approach. Environ. Plann. B Plann. Des. 2006, 33, 705–725. [Google Scholar] [CrossRef]
- Porta, S.; Crucitti, P.; Latora, V. The network analysis of urban streets: A dual approach. Phys. A 2006, 369, 853–866. [Google Scholar] [CrossRef] [Green Version]
- Bavelas, A. A mathematical model for group structures. Appl. Anthropol. 1948, 7, 16–30. [Google Scholar] [CrossRef]
- Porta, S.; Crucitti, P.; Latora, V. Multiple centrality assessment in Parma: A network analysis of paths and open spaces. Urban Des. Int. 2008, 13, 41–50. [Google Scholar] [CrossRef] [Green Version]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Networks 1979, 1, 215–239. [Google Scholar] [CrossRef]
- Al, U.; Sezen, U.; Soydal, I. The evaluation of scientific publications of Turkey using social network analysis method. [Originally in Turkish: Türkiye’nin bilimsel yayınlarının sosyal ağ analizi yöntemiyle değerlendirilmesi]. Hacet. Uni. Edeb. Fak. Derg. 2012, 29, 53–71. [Google Scholar]
- Brandes, U. On variants of shortest-path betweenness centrality and their generic computation. Soc. Networks 2008, 30, 136–145. [Google Scholar] [CrossRef] [Green Version]
- Okamoto, K.; Chen, W.; Li, X.Y. Ranking of closeness centrality for large-scale social networks. In International Workshop on Frontiers in Algorithmics; Preparata, F.P., Wu, X., Yin, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 186–195. ISBN 978-3-540-69310-9. [Google Scholar]
- De Sousa, S.; Kropatsch, W.G. Graph-based point drift: Graph centrality on the registration of point-sets. Pattern Recognit. 2015, 48, 368–379. [Google Scholar] [CrossRef]
- Mueller, J.E. An introduction to the hydraulic and topographic sinuosity indexes. Ann. Assoc. Am. Geogr. 1968, 58, 371–385. [Google Scholar] [CrossRef]
- Osmium Tool-osmcode. Available online: https://osmcode.org/osmium-tool/ (accessed on 11 September 2018).
- NetworkX python package. Available online: https://networkx.github.io/ (accessed on 11 September 2018).
| 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of roads | 1706 | 2766 | 2519 | 3890 | 2195 | 1776 | 37910 | 3834 | 6416 | 16990 | 10070 |
| Length of new roads (km) | 1413.7 | 2486.6 | 2185.5 | 3146.8 | 2026.2 | 1947.9 | 11472 | 2955.6 | 3164.4 | 6979.3 | 4223.6 |
| Mean length (m) | 828.7 | 899.0 | 867.6 | 808.9 | 923.1 | 1096.8 | 302.6 | 770.9 | 493.2 | 410.8 | 419.4 |
| 1.010 | 1.776 | 1.561 | 2.248 | 1.447 | 1.391 | 8.194 | 2.111 | 2.260 | 4.985 | 3.017 | |
| Temporal completeness (%) | 57 | 114 | 69 | 155 | 104 | 17 | 388 | 93 | 45 | 165 | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hacar, M.; Kılıç, B.; Şahbaz, K. Analyzing OpenStreetMap Road Data and Characterizing the Behavior of Contributors in Ankara, Turkey. ISPRS Int. J. Geo-Inf. 2018, 7, 400. https://doi.org/10.3390/ijgi7100400
Hacar M, Kılıç B, Şahbaz K. Analyzing OpenStreetMap Road Data and Characterizing the Behavior of Contributors in Ankara, Turkey. ISPRS International Journal of Geo-Information. 2018; 7(10):400. https://doi.org/10.3390/ijgi7100400
Chicago/Turabian StyleHacar, Müslüm, Batuhan Kılıç, and Kadir Şahbaz. 2018. "Analyzing OpenStreetMap Road Data and Characterizing the Behavior of Contributors in Ankara, Turkey" ISPRS International Journal of Geo-Information 7, no. 10: 400. https://doi.org/10.3390/ijgi7100400
APA StyleHacar, M., Kılıç, B., & Şahbaz, K. (2018). Analyzing OpenStreetMap Road Data and Characterizing the Behavior of Contributors in Ankara, Turkey. ISPRS International Journal of Geo-Information, 7(10), 400. https://doi.org/10.3390/ijgi7100400







