Towards an Affordance-Based Ad-Hoc Suitability Network for Indoor Manufacturing Transportation Processes
Abstract
:1. Introduction and Motivation
2. Relevant Work and Research Approach
2.1. Relevant Work
2.2. Research Approach
3. Indoor Manufacturing Space and Manufacturing Processes
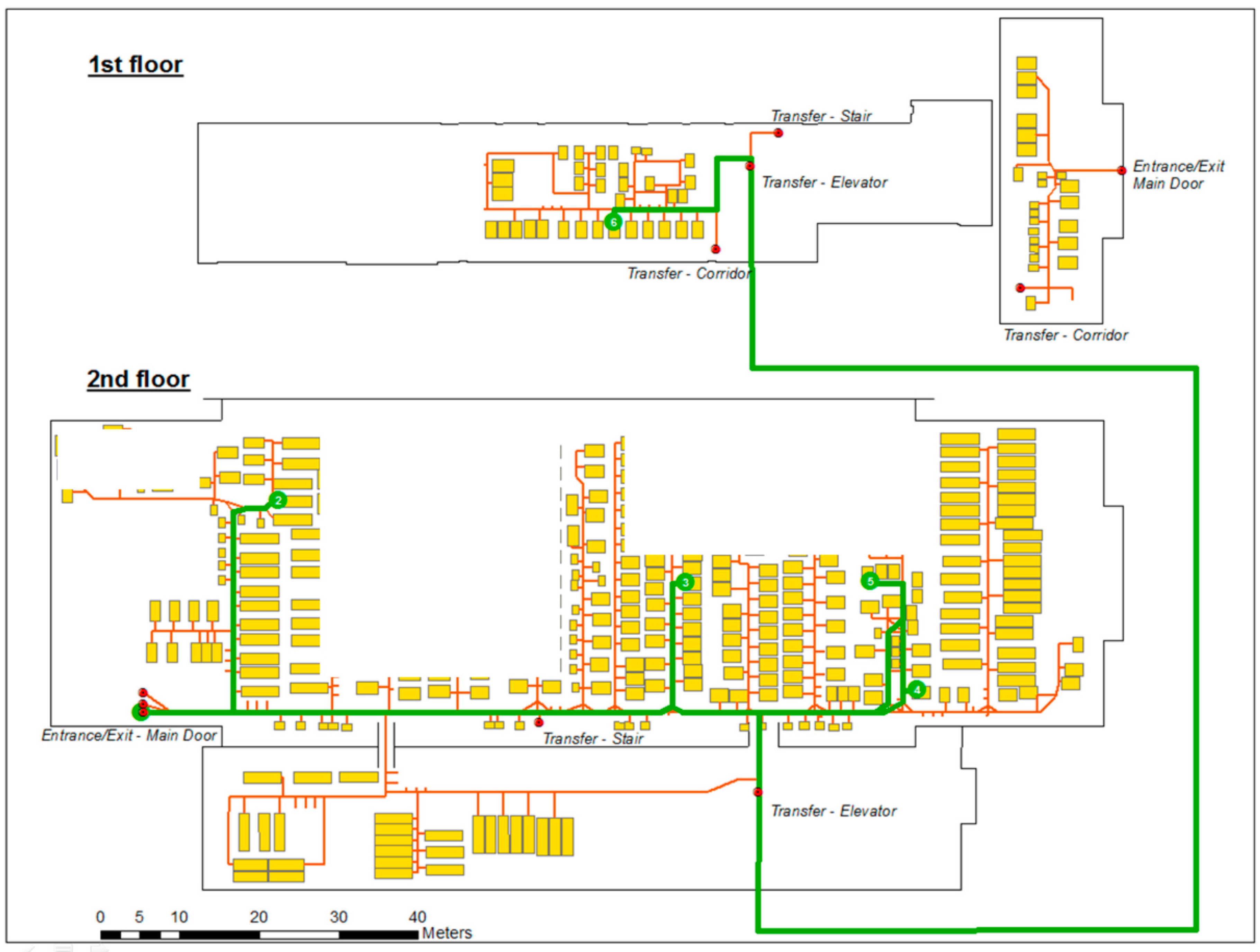
3.1. Indoor Space of the Manufacturing Environment Under Rreview
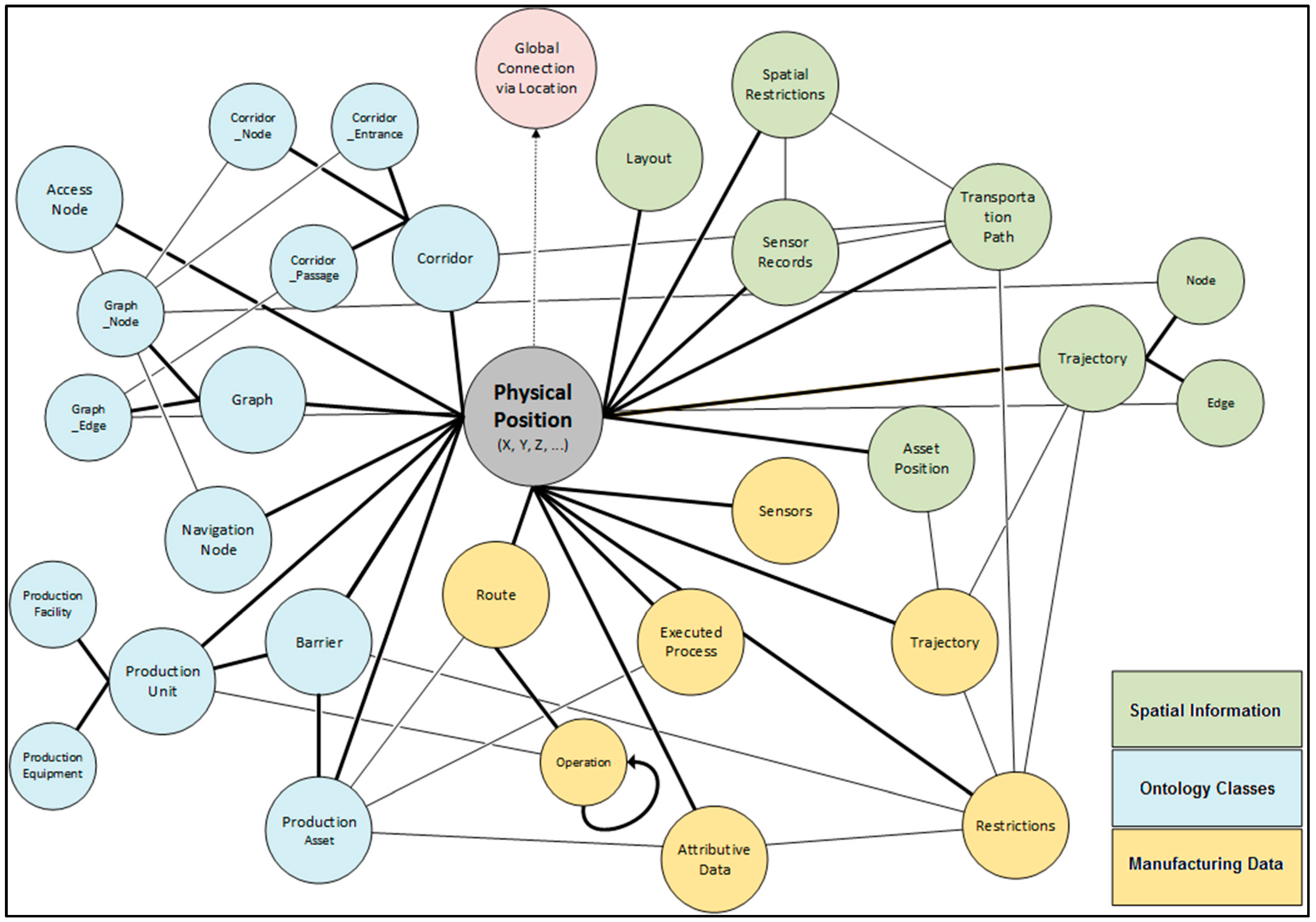
3.2. Spatial Cyberinfrastructure for Manufacturing Data
4. Methodology for Affordance-Based Spatial Suitability Calculation
4.1. Ontologies and Affordances
“The affordances of the environment are what it offers the animal, what it provides or furnishes, whether for good or ill”.([11], p. 127)
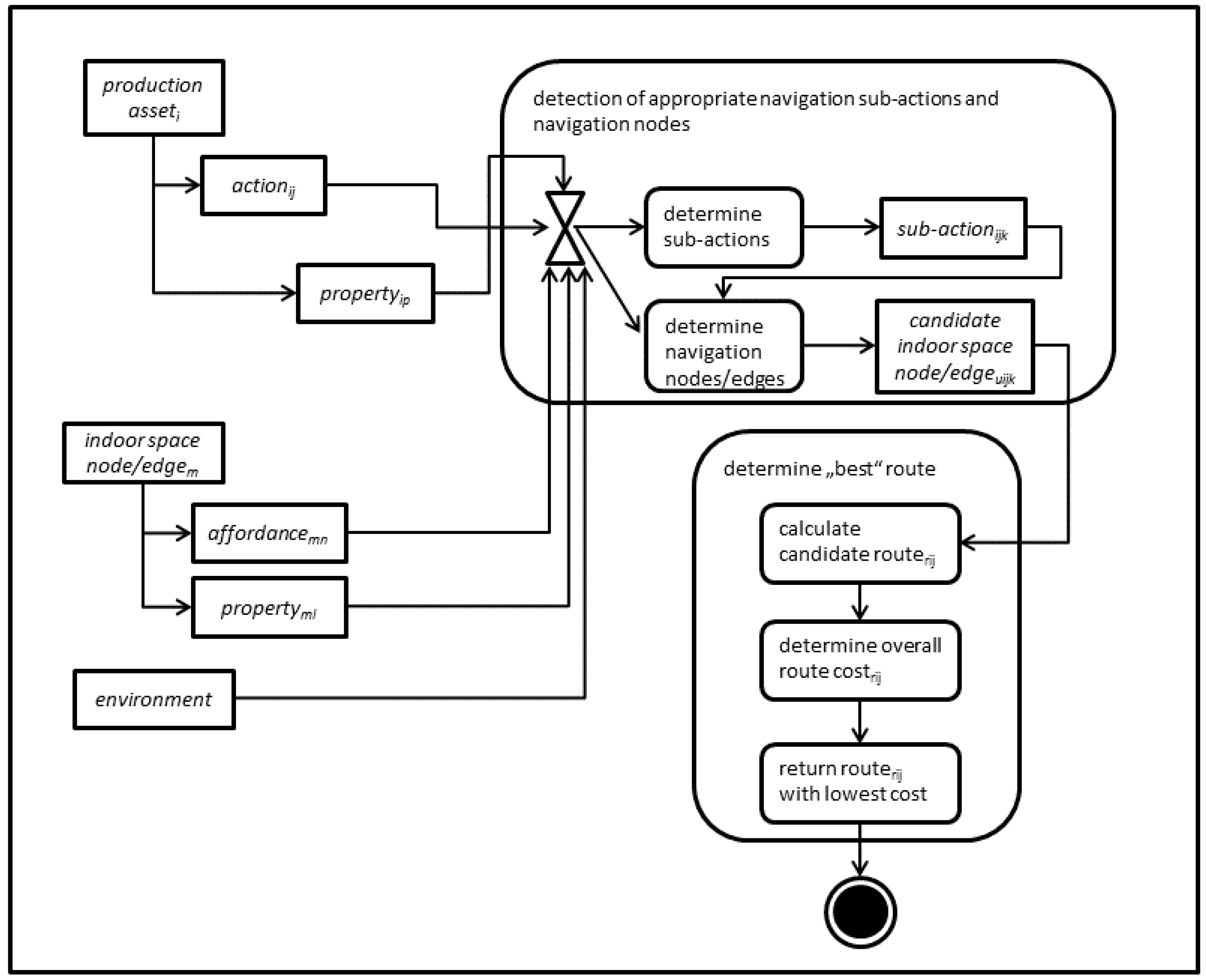
4.2. Determination of Spatial Suitability
- Product type: The product type provides implicit information on the manipulation of the production assets. Specific types need to be handled with care, as they might break easily. Thus, transportation over stairs or “bumpy” cleanroom sections are restricted. Other types are able to move through contaminated or low quality cleanroom areas due to a specific enclosure. The mentioned enclosure has to be carried with both hands, which means that the operator is not able to open doors. In addition, the product type defines other impediments to transport, such as air quality or contamination risks.
- List of manufacturing operations: This information stores the sequence of manufacturing processes that have to be carried out. As several processes can be performed on several pieces of equipment, the resulting quality of the manufacturing processes may differ. Hence, each production asset should choose a production equipment that fits ’best’ in terms of manufacturing quality.
4.3.The Ad-Hoc Aspect
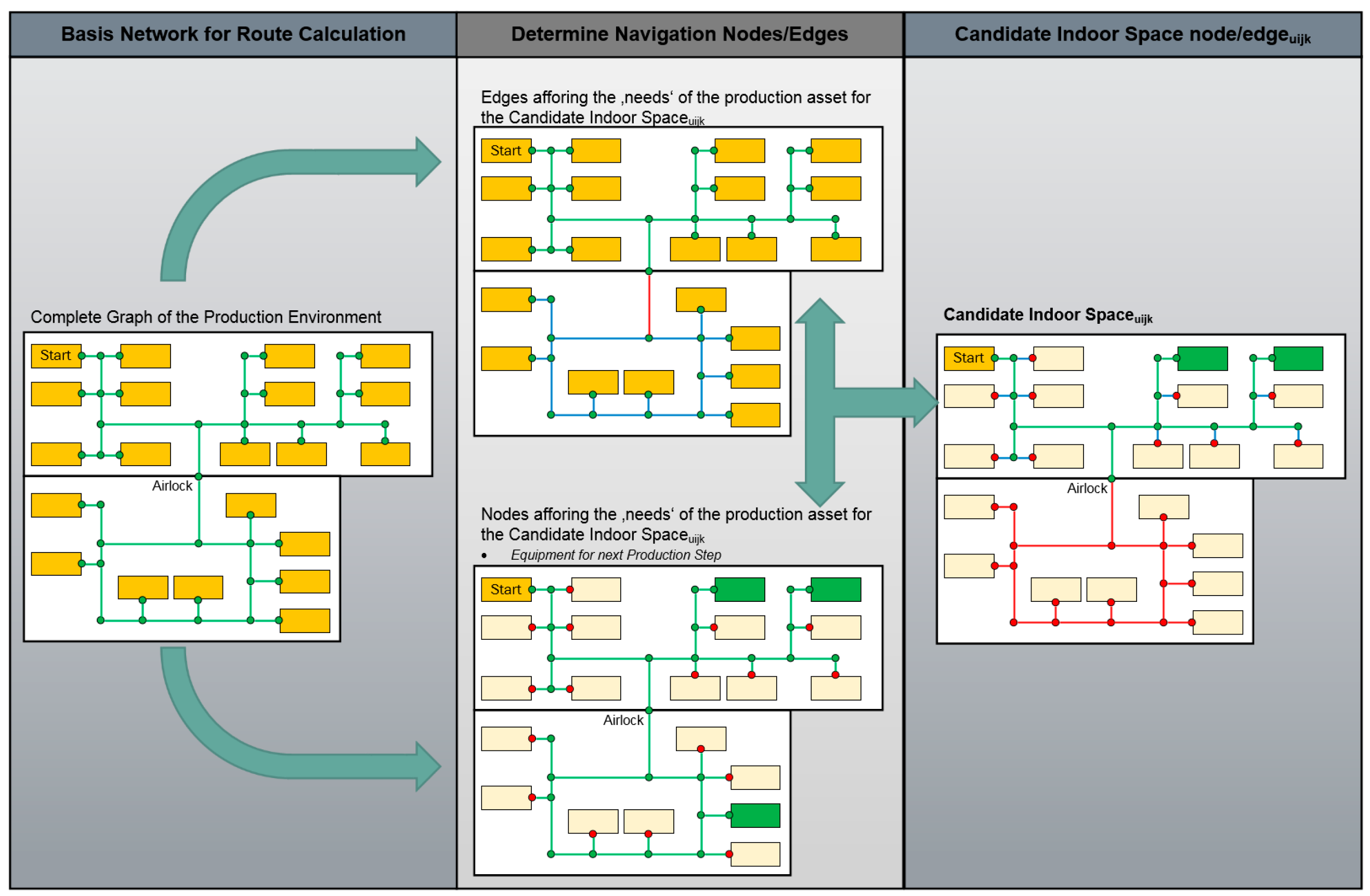
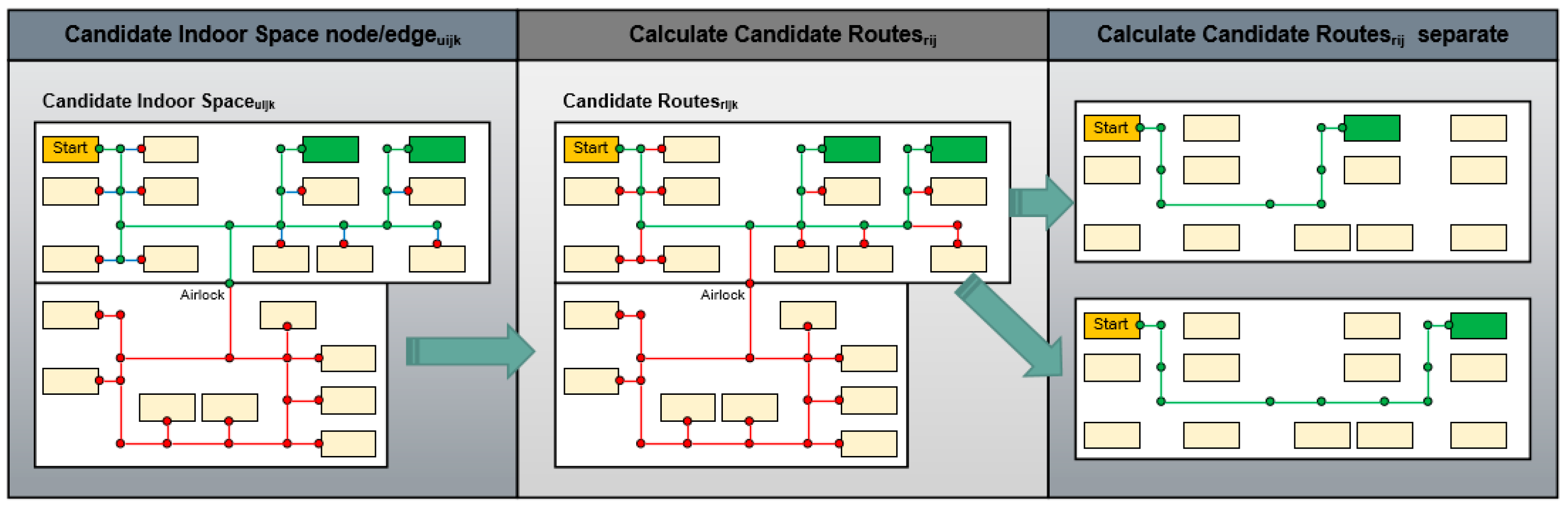
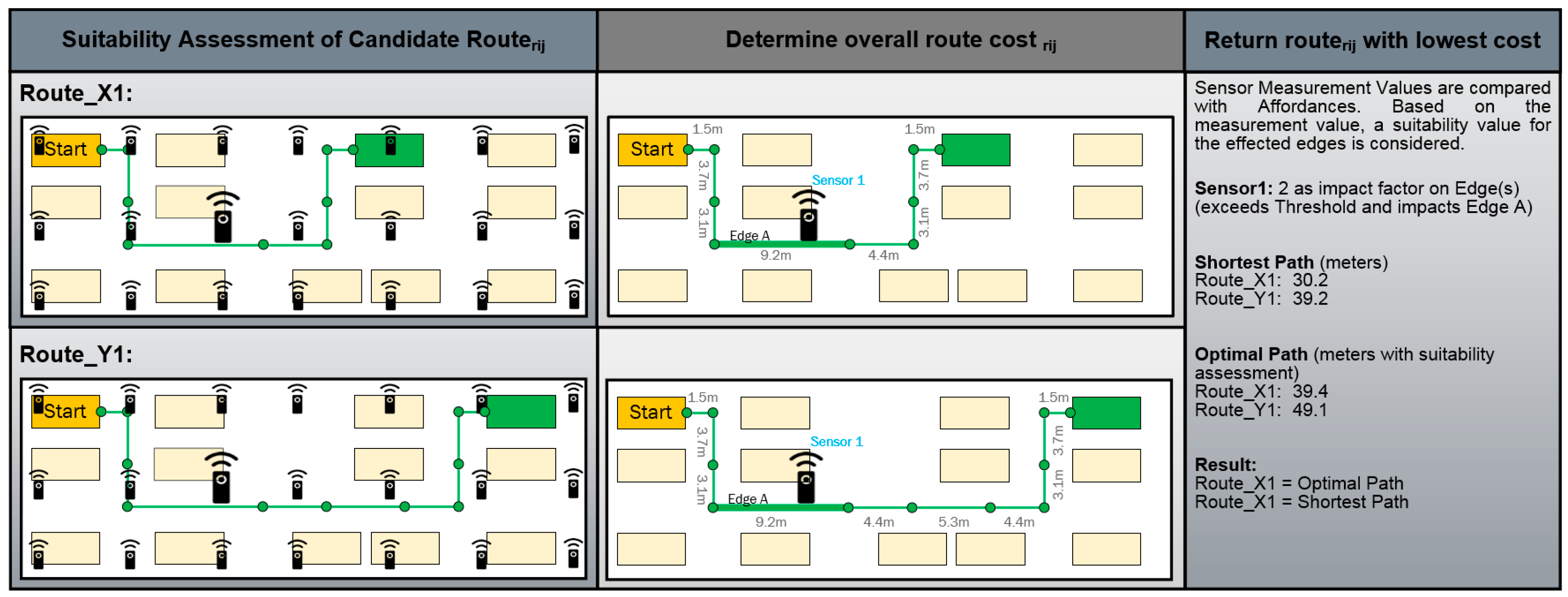
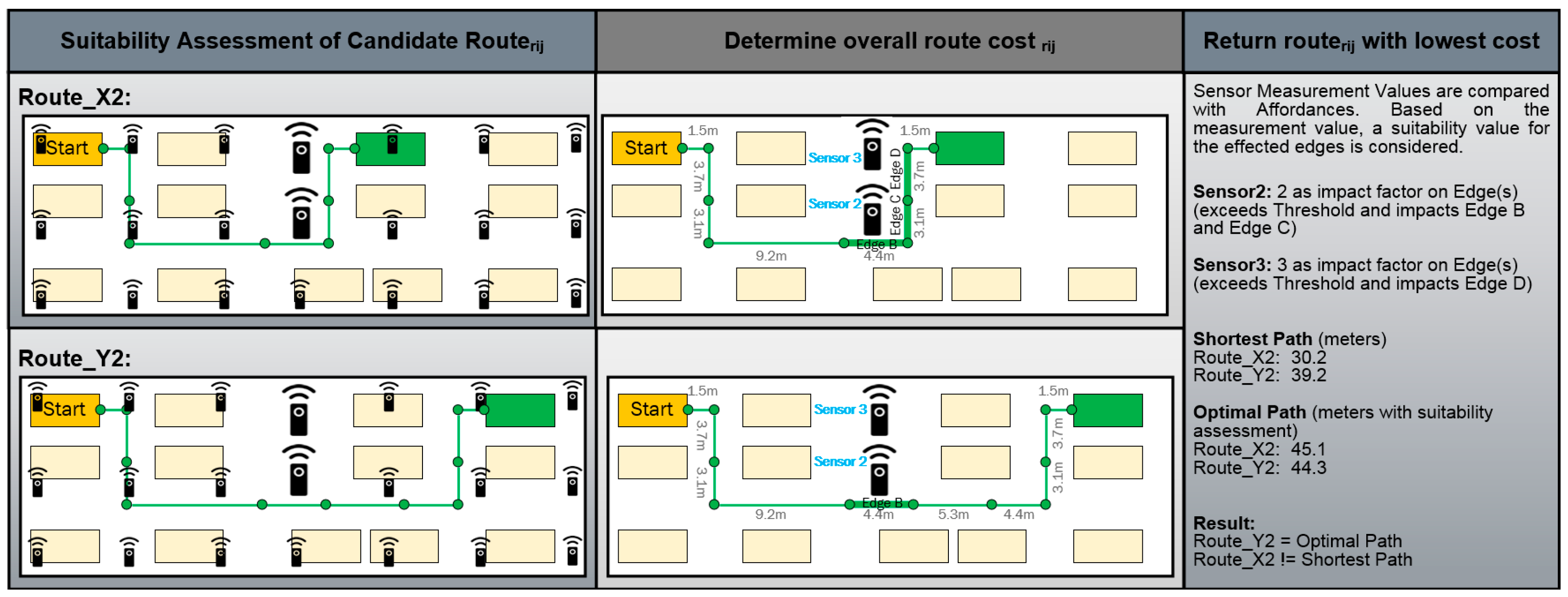
5. Analysis of the Affordance-Based Spatial Suitability Network for Shortest Path Calculation
6. Case Study: Optimal Path Calculation in a Manufacturing Environment
6.1. Implementation of the Ad-Hoc Suitability Network for a Smart Transportation Process in a Flexible Manufacturing Environment
6.2. Use-Case: Optimal Route Decision Based on Affordances and the Ad-Hoc Suitability Network
7. Conclusions and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jenkins, P.L.; Phillips, T.J.; Mulberg, E.J.; Hui, S.P. Activity patterns of Californians: Use of and proximity to indoor pollutant sources. Atmos. Environ. Part A Gen. Top. 1992, 26, 2141–2148. [Google Scholar] [CrossRef]
- Klepeis, N.E.; Nelson, W.C.; Ott, W.R.; Robinson, J.P.; Tsang, A.M.; Switzer, P.; Behar, J.V.; Hern, S.C.; Engelmann, W.H. The National Human Activity Pattern Survey (NHAPS): A resource for assessing exposure to environmental pollutants. J. Expo. Anal. Environ. Epidemiol. 2001, 11, 231–252. [Google Scholar] [CrossRef] [PubMed]
- Scholz, J.; Schabus, S. An indoor navigation ontology for production assets in a production environment. In Proceedings of the 8th International Conference on Geographic Information Science, GIScience 2014, Vienna, Austria, 24–26 September 2014; Duckham, M., Pebesma, E., Stewart, K., Frank, A.U., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 204–220. [Google Scholar]
- Schabus, S.; Scholz, J. Geographic Information Science and technology as key approach to unveil the potential of Industry 4.0: How location and time can support smart manufacturing. In Proceedings of the 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO), Colmar, France, 21–23 July 2015; Volume 2, pp. 463–470. [Google Scholar]
- Schabus, S.; Scholz, J.; Skupin, A. Spatial-temporal Patterns of Production Assets in an Indoor Production Environment. In Proceedings of the Workshop “Analysis of Movement Data’14” Workshop at GIScience, Vienna, Austria, 14 February 2014. [Google Scholar]
- Nyström, R.H.; Harjunkoski, I.; Kroll, A. Production optimization for continuously operated processes with optimal operation and scheduling of multiple units. Comput. Chem. Eng. 2006, 30, 392–406. [Google Scholar] [CrossRef]
- Li, W.; Goodchild, M.F.; Raskin, R. Towards geospatial semantic search: Exploiting latent semantic relations in geospatial data. Int. J. Digit. Earth 2014, 7, 17–37. [Google Scholar] [CrossRef]
- May, G.S.; Spanos, C.J. Fundamentals of Semiconductor Manufacturing and Process Control; John Wiliey & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Geng, H. Semiconductor Manufacturing Handbook; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Gibson, J.J. The Theory of Affordances. In Perceiving, Acting, and Knowing; Shaw, R., Bransford, J., Eds.; Lawrence Erlbaum Associates Inc.: Mahwah, NJ, USA, 1977; pp. 67–82. [Google Scholar]
- Gibson, J.J. The Ecological Approach to Visual Perception: Classic Edition; Psychology Press: New York, NY, USA, 2014. [Google Scholar]
- Jonietz, D.; Timpf, S. An affordance-based simulation framework for assessing spatial suitability. In Proceedings of the International Conference on Spatial Information Theory, Scarborough, UK, 2–6 September 2013; Springer: Berlin, Germany, 2013; pp. 169–184. [Google Scholar]
- Jonietz, D.; Timpf, S. On the relevance of Gibson’s affordance concept for geographical information science (GISc). Cognit. Process. 2015, 16, 265–269. [Google Scholar] [CrossRef] [PubMed]
- Jonietz, D.; Schuster, W.; Timpf, S. Modelling the suitability of urban networks for pedestrians: An affordance-based framework. In Geographic Information Science at the Heart of Europe; Vandenbroucke, D., Bucher, B., Crompvoets, J., Eds.; Springer: Berlin, Germany, 2013. [Google Scholar]
- Davis, J.; Edgar, T.; Porter, J.; Bernaden, J.; Sarli, M. Smart manufacturing, manufacturing intelligence and demand-dynamic performance. Comput. Chem. Eng. 2012, 47, 145–156. [Google Scholar] [CrossRef]
- Scholl, A.; Becker, C. State-of-the-art exact and heuristic solution procedures for simple assembly line balancing. Eur. J. Oper. Res. 2006, 168, 666–693. [Google Scholar] [CrossRef]
- Osswald, S.; Weiss, A.; Tscheligi, M. Designing wearable devices for the factory: Rapid contextual experience prototyping. In Proceedings of the International Conference on Collaboration Technologies and Systems (CTS), San Diego, CA, USA, 20–24 May 2013; pp. 517–521. [Google Scholar]
- Raubal, M. Ontology and epistemology for agent-based wayfinding simulation. Int. J. Geogr. Inf. Sci. 2001, 15, 653–665. [Google Scholar] [CrossRef]
- Raubal, M.; Worboys, M. A formal model of the process of wayfinding in built environments. In Spatial Information Theory. Cognitive and Computational Foundations of Geographic Information Science; Springer: Berlin, Germany, 1999; pp. 381–399. [Google Scholar]
- Worboys, M. Modeling indoor space. In Proceedings of the 3rd ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness, New York, NY, USA, 1 Novomber 2011. [Google Scholar]
- Yang, L.; Worboys, M. Generation of navigation graphs for indoor space. Int. J. Geogr. Inf. Sci. 2015, 29, 1737–1756. [Google Scholar] [CrossRef]
- Stoffel, E.P.; Schoder, K.; Ohlbach, H.J. Applying hierarchical graphs to pedestrian in-door navigation. In Proceedings of the 16th ACM SIG Spatial International Conference on Advances in Geographic Information Systems, Irvine, CA, USA, 5–7 Novomber 2008; p. 54. [Google Scholar]
- Lorenz, B.; Ohlbach, H.J. A hybrid spatial model for representing indoor environments. In Proceedings of the International Symposium on Web and Wireless Geographical Information Systems, Hong Kong, China, 4–5 December 2006; Springer: Berlin, Germany, 2006; pp. 102–112. [Google Scholar]
- Becker, T.; Nagel, C.; Kolbe, T.H. A multilayered space-event model for navigation in indoor spaces. In 3D Geo-Information Sciences; Springer: Berlin, Germany, 2009; pp. 61–77. [Google Scholar]
- Stoffel, E.P.; Lorenz, B.; Ohlbach, H.J. Towards a semantic spatial model for pedestrian indoor navigation. In Proceedings of the International Conference on Conceptual Modeling, Auckland, New Zealand, 5–9 November 2007; Springer: Berlin, Germany, 2007; pp. 328–337. [Google Scholar]
- Yang, L.; Worboys, M. A navigation ontology for outdoor-indoor space:(work-in-progress). In Proceedings of the 3rd ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness, New York, NY, USA, 1 November 2011; pp. 31–34. [Google Scholar]
- Howell, I.; Batcheler, B. Building Information Modeling Two Years Later-Huge Potential, Some Success and Several Limitations. Available online: http://www.laiserin.com/features/bim/newforma_bim.pdf (accessed on 15 June 2017).
- Uschold, M.; Gruninger, M. Ontologies: Principles, methods and applications. Knowl. Eng. Rev. 1996, 11, 93–136. [Google Scholar] [CrossRef]
- Smith, B. Objects and their environments: From Aristotle to ecological ontology. In Life Motion Socio-Economic Units: Gisdata; Frank, A.U., Ed.; Taylor & Francis: Abingdon, UK, 2011; Volume 8. [Google Scholar]
- Gruber, T.R. A translation approach to portable ontology specification. Knowl. Acquis. 1993, 5, 199–220. [Google Scholar] [CrossRef]
- Davis, E. Representations of Commonsense Knowledge; Morgan Kaufmann: Burlington, MA, USA, 1990. [Google Scholar]
- Bishr, Y.; Kuhn, W. Ontology-based modelling of geospatial information. In Proceedings of the 3rd AGILE Conference on Geographic Information Science, Helsinki, Finland, 26–28 May 2000. [Google Scholar]
- Grenon, P.; Smith, B. SNAP and SPAN: Towards dynamic spatial ontology. Spat. Cognit. Comput. 2004, 4, 69–104. [Google Scholar] [CrossRef]
- Liu, L.; Zlatanova, S. An Approach for Indoor Path Computation among Obstacles that Considers User Dimension. ISPRS Int. J. Geo-Inf. 2015, 4, 2821–2841. [Google Scholar] [CrossRef]
- Kostic, N.; Scheider, S. Automated generation of indoor accessibility information for mobility-impaired individuals. In AGILE 2015; Bacao, F., Santos, Y.M., Painho, M., Eds.; Springer: Berlin, Germany, 2015; pp. 235–252. [Google Scholar]
- Turner, A.; Penn, A. Encoding natural movement as an agent-based system: An investigation into human pedestrian behaviour in the built environment. Environ. Plan. B Plan. Des. 2002, 29, 473–490. [Google Scholar] [CrossRef]
- Kapadia, M.; Singh, S.; Hewlett, W.; Faloutsos, P. Egocentric affordance fields in pedestrian steering. In Proceedings of the 2009 Symposium on Interactive 3D Graphics and Games, Boston, MA, USA, 27 February–1 March 2009. [Google Scholar]
- Kim, N.; Joo, J.; Rothrock, L.; Wysk, R.; Son, Y.-J. Human behavioral simulation using affordance-based agent model. In Proceedings of the International Conference on Human-Computer Interaction, Vancouver, BC, Canada, 9–14 July 2011. [Google Scholar]
- Richter, K.-F.; Winter, S.; Santosa, S. Hierarchical representations of indoor space. Environ. Plan. B Plan. Des. 2011, 38, 1052–1070. [Google Scholar] [CrossRef]
- Hu, Y.; Janowicz, K.; Carral, D.; Scheider, S.; Kuhn, W.; Berg-Cross, G.; Hitzler, P.; Dean, M.; Kolas, D. A geo-ontology design pattern for semantic trajectories. In Proceedings of the International Conference on Spatial Information Theory, Scarborough, UK, 2–6 September 2013; pp. 438–456. [Google Scholar]
- Cyganiak, R.; Jentzsch, A. Linking Open Data Cloud Diagram. LOD Community. 2011, Volume 12. Available online: http://lod-cloud (accessed on 15 June 2017).
- Schabus, S.; Scholz, J. Spatially-Linked Manufacturing Data to support Data Analysis. GI_Forum 2017, 2017, 126–140. [Google Scholar] [CrossRef]
- Koffka, K. Principles of Gestalt Psychology; Harcourt Brace: New York, NY, USA, 1935. [Google Scholar]
- Jordan, T.; Raubal, M.; Gartrell, B.; Egenhofer, M. An affordance-based model of place in GIS. In Proceedings of the Eight International Symposium on Spatial Data Handling, Vancouver, BC, Canada, 12–15 July 1998; Volume 38, pp. 98–109. [Google Scholar]
- Kemke, C. About the Ontology of Actions; Technical Report MCCS-01-328; Computing Research Laboratory, New Mexico State University: Las Cruces, NM, USA, 2001. [Google Scholar]
- Leontiev, N. Activity, Consciousness, and Personality; Prentice-Hall: Upper Saddle River, NJ, USA, 1978. [Google Scholar]
- Nishi, Y.; Doering, R. Handbook of Semiconductor Manufacturing Technology, 2nd ed.; CRC Press: New York, NY, USA; Basel, Switzerland, 2000. [Google Scholar]
- Tsetsos, V.; Anagnostopoulos, C.; Kikiras, P.; Hasiotis, P.; Hadjiefthymiades, S. A human-centered semantic navigation system for indoor environments. In Proceedings of the IEEE International Conference on Pervasive Services (ICPS), Santorini, Greece, 11–14 July 2005. [Google Scholar]
- Vanclooster, A.; Ooms, K.; Viaene, P.; Fack, V.; van de Weghe, N.; de Maeyer, P. Evaluating Suitability of the least risk path algorithm to support cognitive wayfinding in indoor space: An empirical study. Appl. Geogr. 2014, 53, 128–140. [Google Scholar]
| Classical Dijkstra | Ad-Hoc Network Using Dijkstra | Comparison | |
|---|---|---|---|
| Basis: G—Graph V—Vertices E—Edges | G (V, E) | GAH (VAH, EAH) | GAH < G |
| Complexity: (optimal) | O = (|V| × log(|V|) + |E|) | OAH = (|VAH| × log(|VAH|) + |EAH|) | OAH < O |
| Abstract Example: | 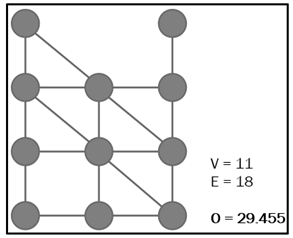 | 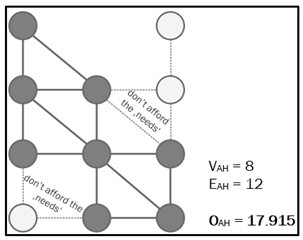 | OAH < O 17.915 < 29.455 |
| Single Transportation Process in ~1/4 of one production hall: (Affordances of Vertices and Nodes considered for the “candidate indoor space nodes/edgesuijk”) | For each transportation process of a production asset, the complete graph-based network is considered for the shortest path calculation. Spatial Suitability is calculated for the complete graph.  V = 123 E = 123 O = 380.058 | At the beginning, the candidate indoor space nodes/edgesuijk is calculated based on the ‘personalized’ ad-hoc network. Therefore, first the edges have to afford the ‘needs’. Second, for each calculation equipments have to affor the ‘needs’ for the operation. Spatial suitability is calculated for the candidate indoor space nodes/edgesuijk.  VAH = 68 EAH = 68 OAH = 137.832 | “One transportation path calculation, each asset has a few hundred of them.” OAH < O 137.832 < 380.058 |
| Calculation considering one production hall: (Assumption based on the previous example) | V = (123 × 4) = 492 E = (123 × 4) = 492 O = 1816.446 | VAH = (68 × 4) = 272 EAH = (68 × 4) = 272 OAH = 934.202 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scholz, J.; Schabus, S. Towards an Affordance-Based Ad-Hoc Suitability Network for Indoor Manufacturing Transportation Processes. ISPRS Int. J. Geo-Inf. 2017, 6, 280. https://doi.org/10.3390/ijgi6090280
Scholz J, Schabus S. Towards an Affordance-Based Ad-Hoc Suitability Network for Indoor Manufacturing Transportation Processes. ISPRS International Journal of Geo-Information. 2017; 6(9):280. https://doi.org/10.3390/ijgi6090280
Chicago/Turabian StyleScholz, Johannes, and Stefan Schabus. 2017. "Towards an Affordance-Based Ad-Hoc Suitability Network for Indoor Manufacturing Transportation Processes" ISPRS International Journal of Geo-Information 6, no. 9: 280. https://doi.org/10.3390/ijgi6090280
APA StyleScholz, J., & Schabus, S. (2017). Towards an Affordance-Based Ad-Hoc Suitability Network for Indoor Manufacturing Transportation Processes. ISPRS International Journal of Geo-Information, 6(9), 280. https://doi.org/10.3390/ijgi6090280





