An Adaptive Sweep-Circle Spatial Clustering Algorithm Based on Gestalt
Abstract
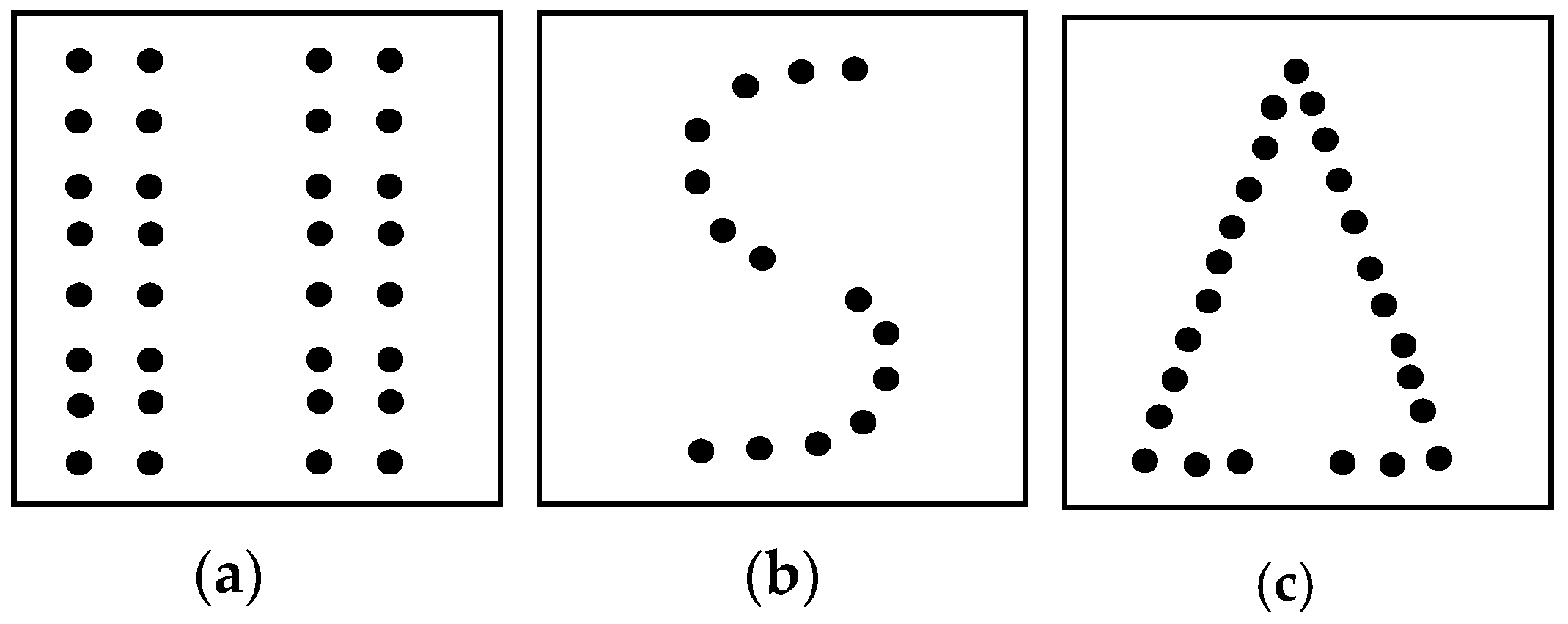
:1. Introduction
2. Related work
2.1. Plane-Sweep Techniques
2.2. Sweep-Circle Algorithm
2.3. Data Stream Technique
2.4. Sweep-Line Clustering Algorithm
3. ASC Algorithm
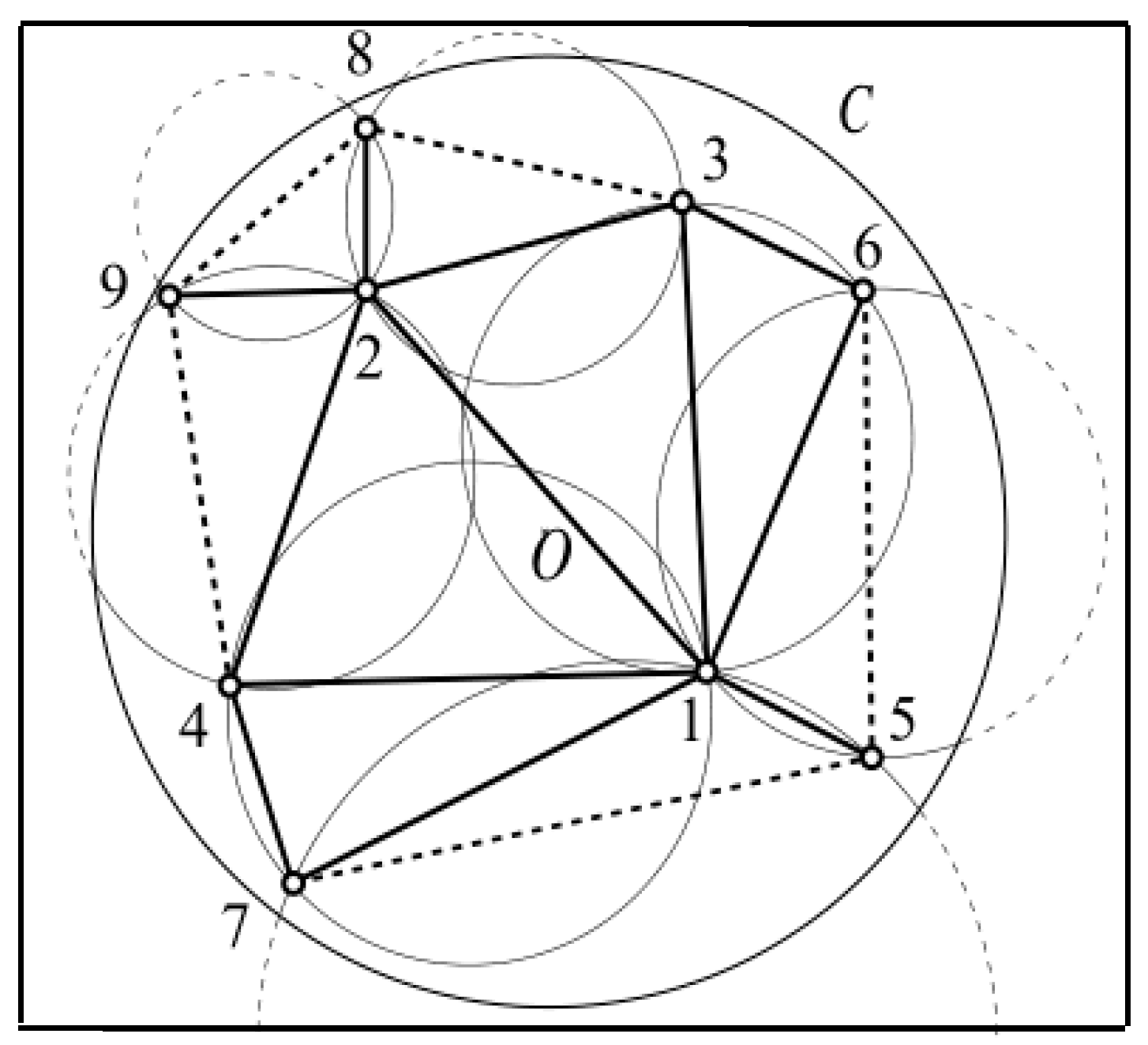
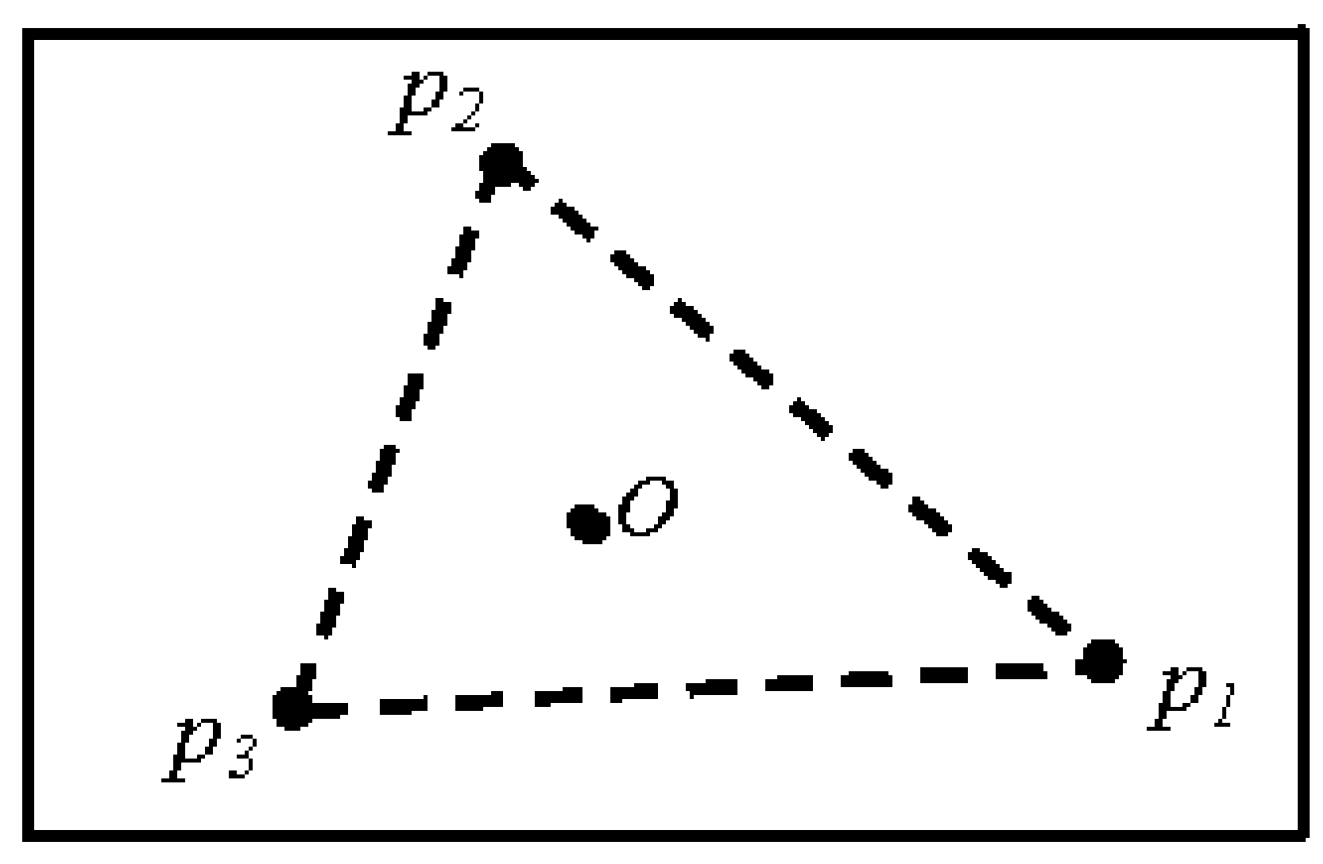
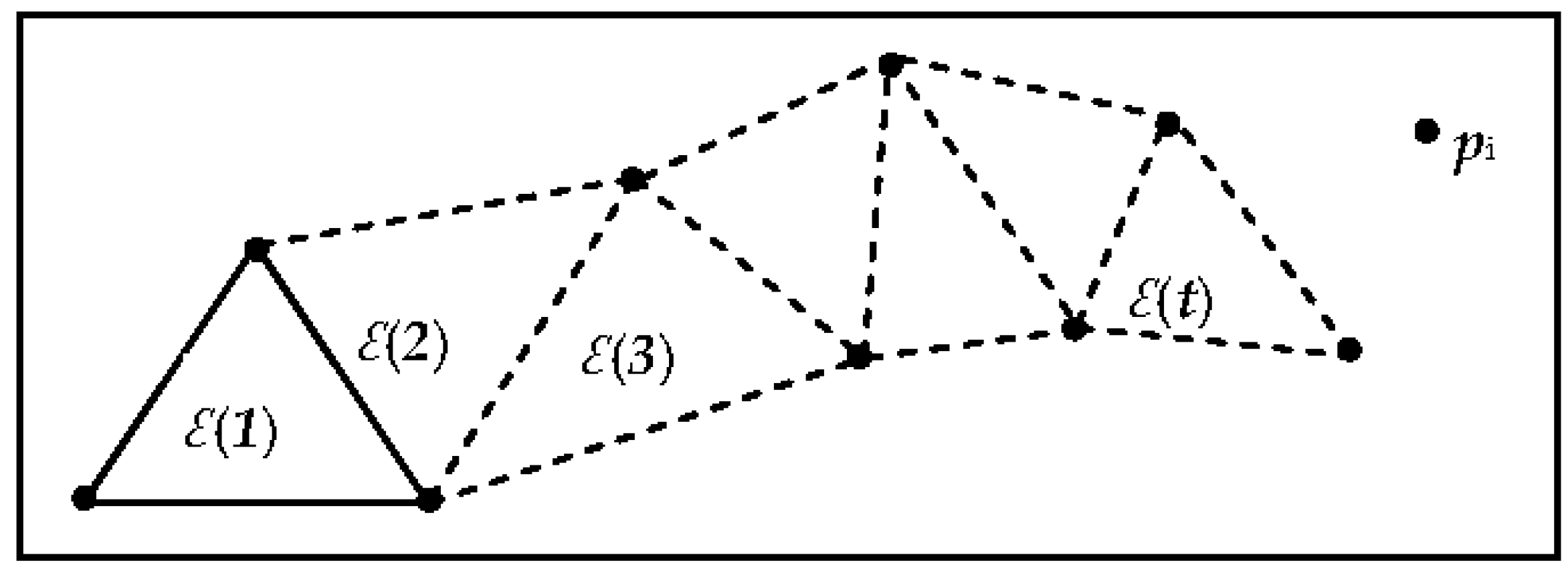
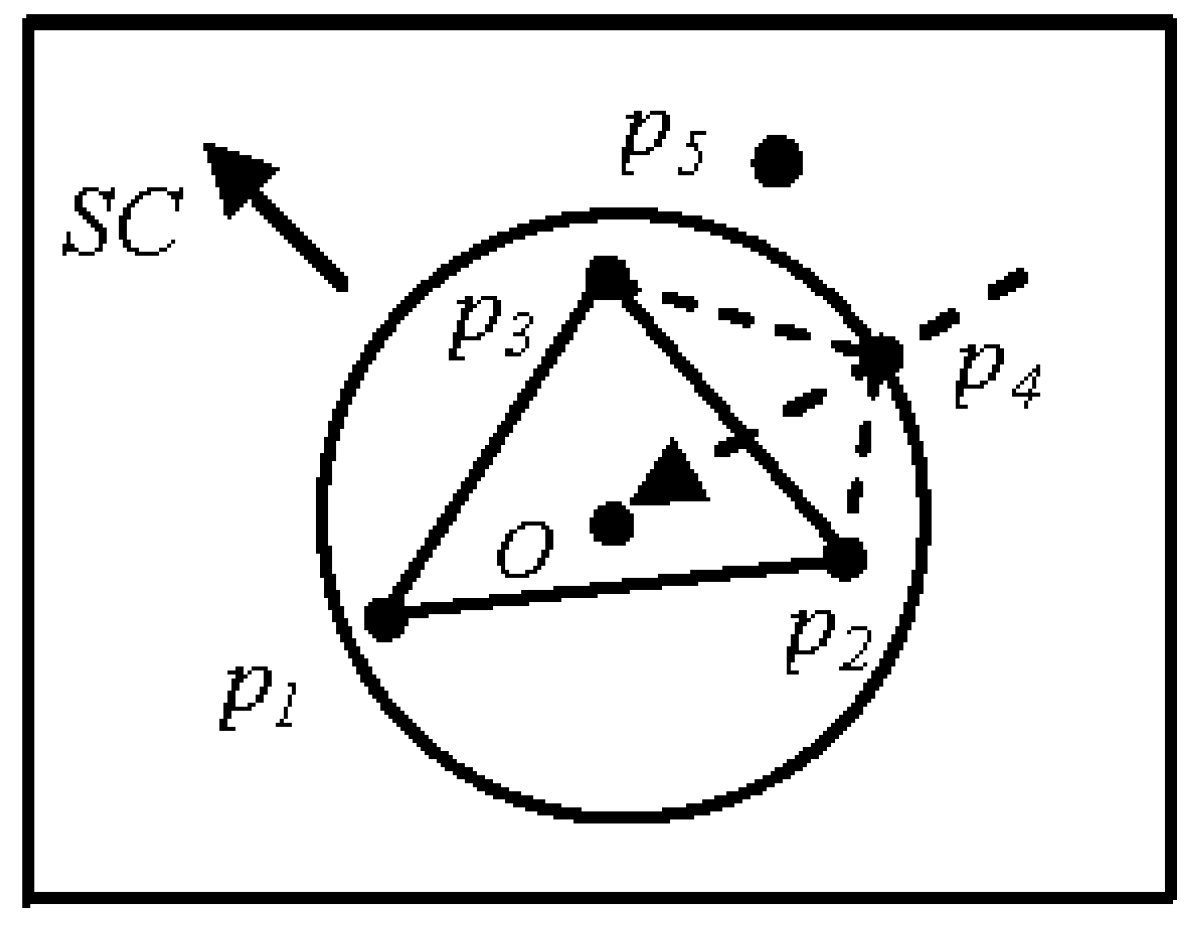
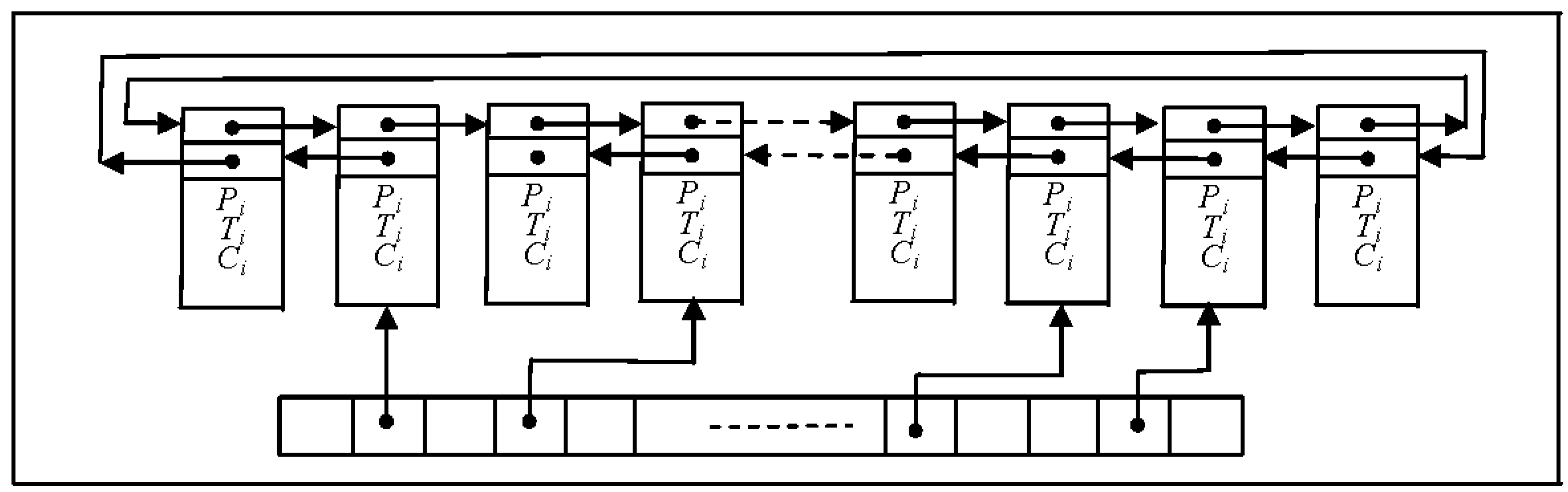
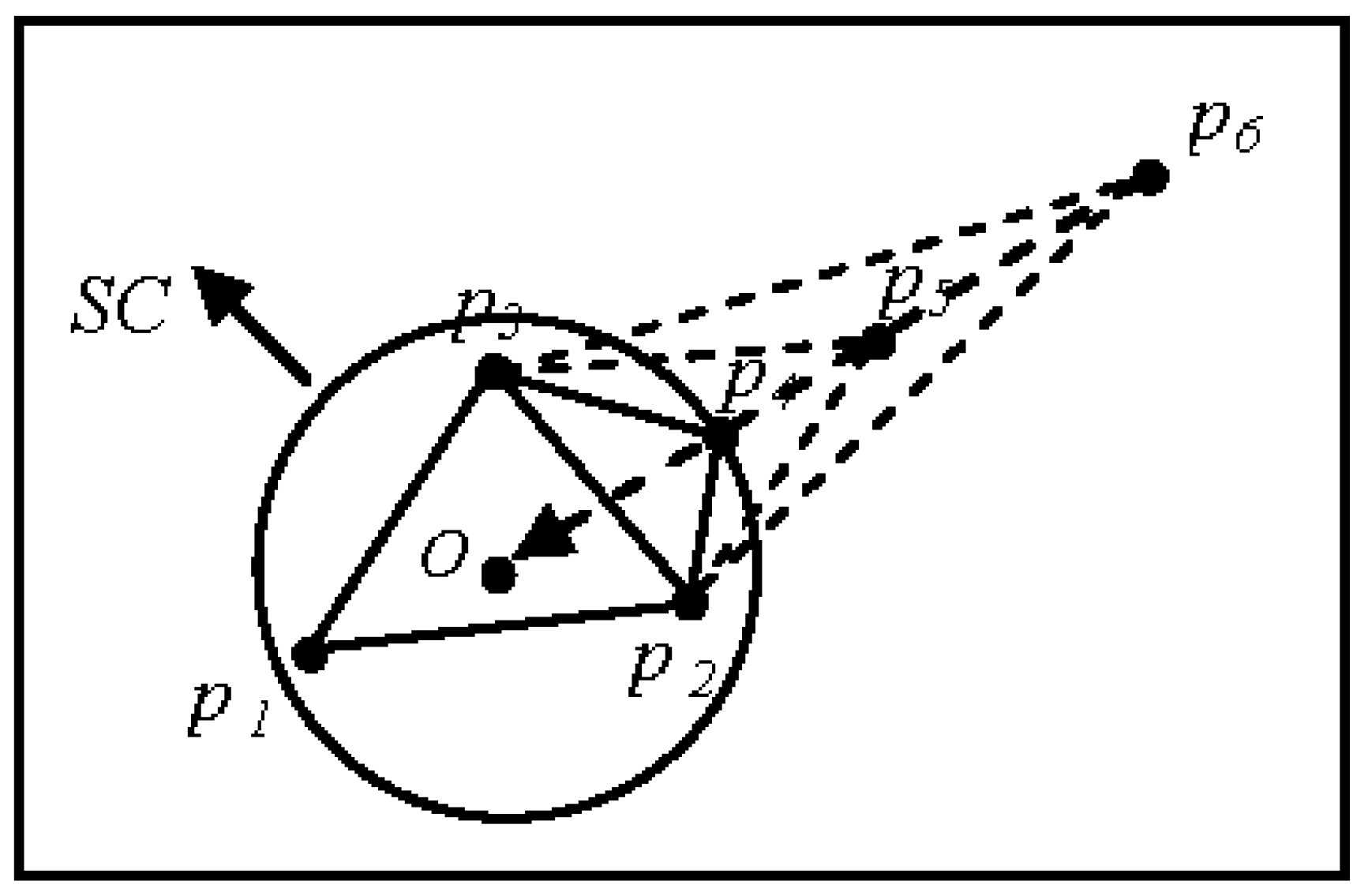
3.1. Basic Concepts and Initialization
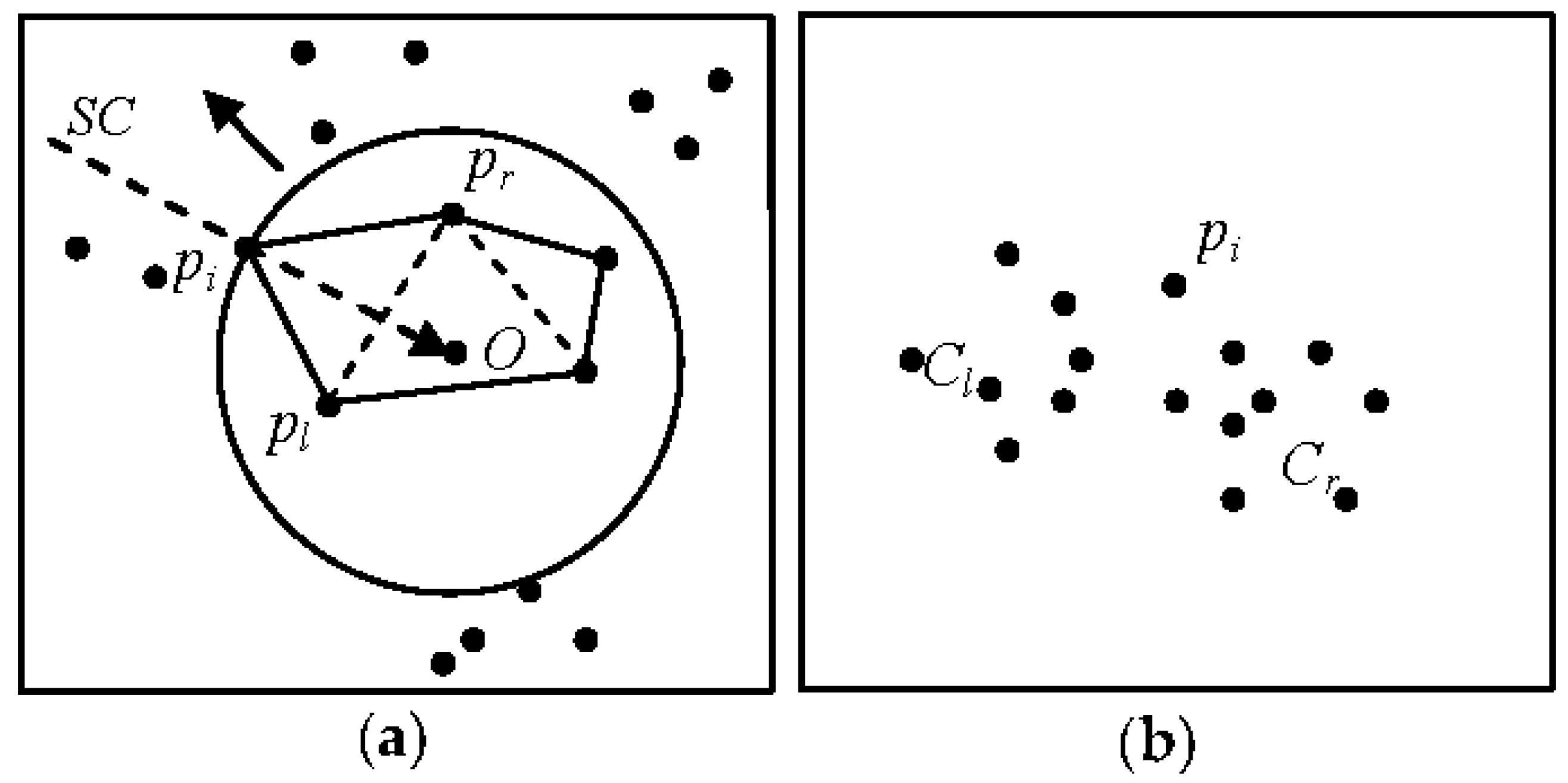
3.2. Clustering
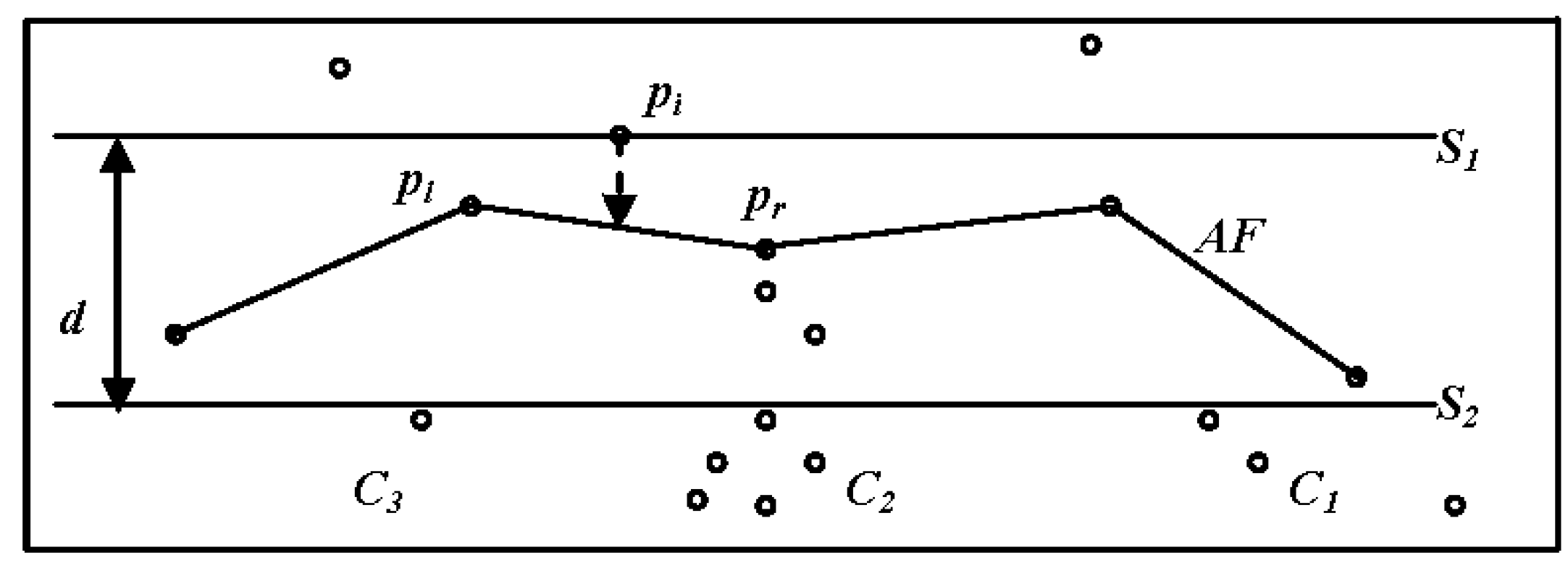
- dist (pi,pl) > (t) and dist (pi,pr) > (t), where pi is the first element of a new cluster.
- dist (pi,pl) > (t) and dist (pi,pr) ≤ (t), where the right side of pi is assigned to a cluster (Cr) (Figure 8b).
- dist (pi,pl) ≤ (t) and dist (pi,pr) > (t), where the left side of pi is assigned to a cluster (C1) (Figure 8b).
- dist (pi,pl) ≤ (t) and dist (pi,pr) ≤ (t), where if pl and pr are members of the same cluster, before pi is placed into the same cluster. Otherwise, pi is a merging point between left and right clusters [41].
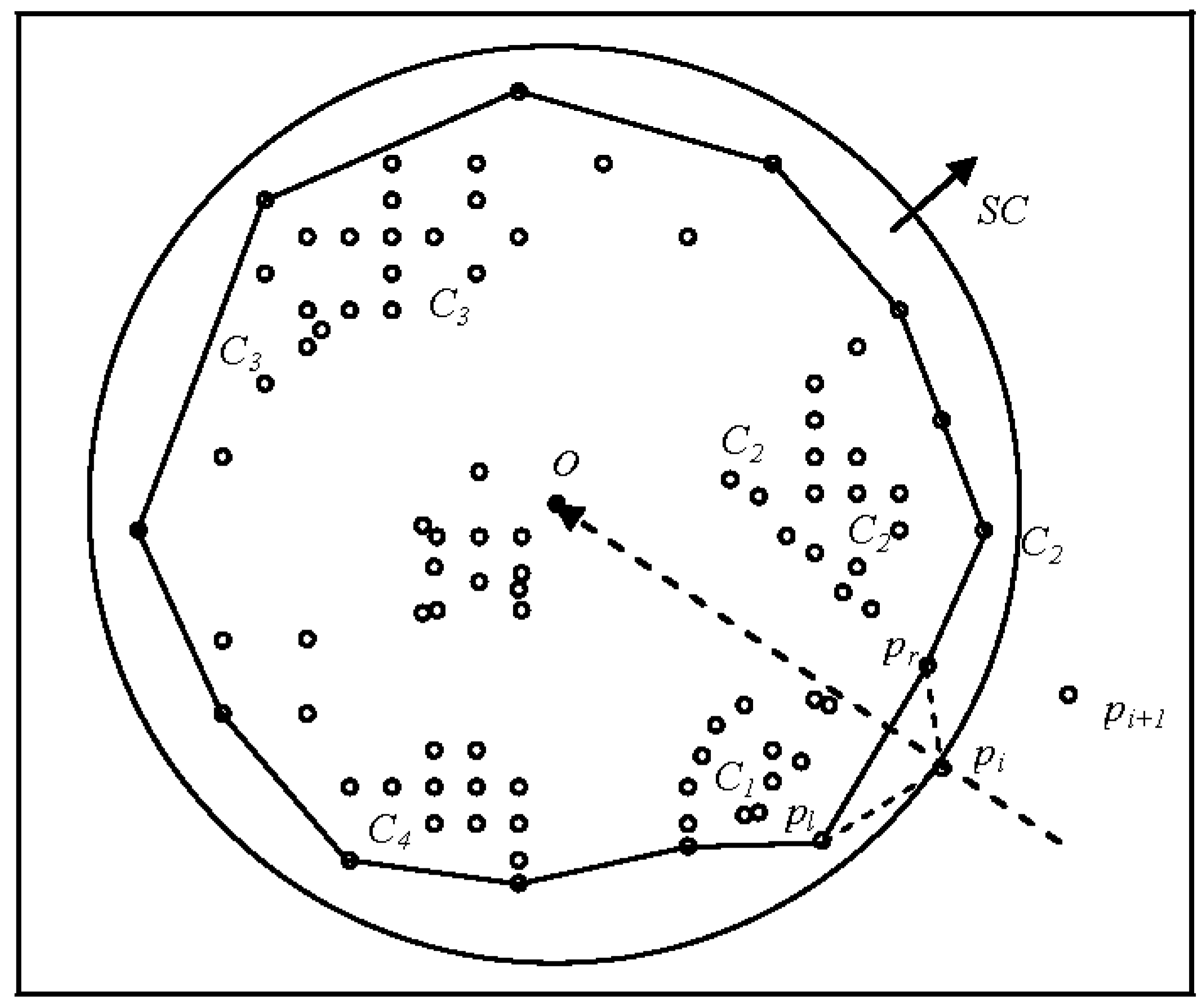
3.3. Merging Clusters
3.4. Point Collinearity
| Algorithm 1. ASC clustering algorithm. |
| Input: The 2D set S = {p1,p2,p3,···,pn} of n points |
| Output: C |
| Initialization: |
| 1: select the pole O |
| 2: calculate pi (ri,θi) for points in S |
| 3: sort the S according to r |
| 4: create the first triangle |
| 5: compute (t) ,t←1,t < (n − 3) |
| 6:CL←Ø, CR←Ø,CN←Ø, CS←Ø |
| Clustering: |
| 7: for i ←4 to n do |
| 8: (t) = 1/3 Lt |
| 9: project pi on the frontier; hits the edge (pl, pr) |
| 10: if d (pi,pl) > (t) and d (pi,pr) > (t) then |
| 11: CN←CN∪pi |
| 12: end if |
| 13: if d (pi,pl) > (t) and d (pi,pr) ≤ (t) then |
| 14: CR←CR∪pi |
| 15: end if |
| 16: if d (pi,pl) ≤ (t) and d (pi,pr) > (t) then |
| 17: CL←CL∪pi |
| 18: end if |
| 19: if d (pi,pl) ≤ (t) and d (pi,pr) ≤ (t) then |
| 20: CS←CS∪pi |
| 21: end if |
| 22: create triangle ∆i,l,r |
| 23: t←t + 1 |
| 24: end for |
| Merging: |
| 25: C←CL∪CR∪CN∪CS |
4. ASC-Based Stream Clustering
- The large data set S is divided into a sequence of data blocks S = {X1,X2,…,Xi} according to the memory size. A load monitor [53] ensures that the loading of spatial data fits the main memory.
- ASC is applied to each data block Xi to form atom clusters Ci = {C1,C2,…,Cl}.
- It is assumed that the user provides a suitable threshold value and the clustering number K is set in advance for the obtained atom clusters. ASC is repeatedly implemented until forming a final (macro) space cluster by processing retrieval queries from the cluster indexes into the adjacent data blocks.
5. Results and Discussion
5.1. Time Complexity Analysis
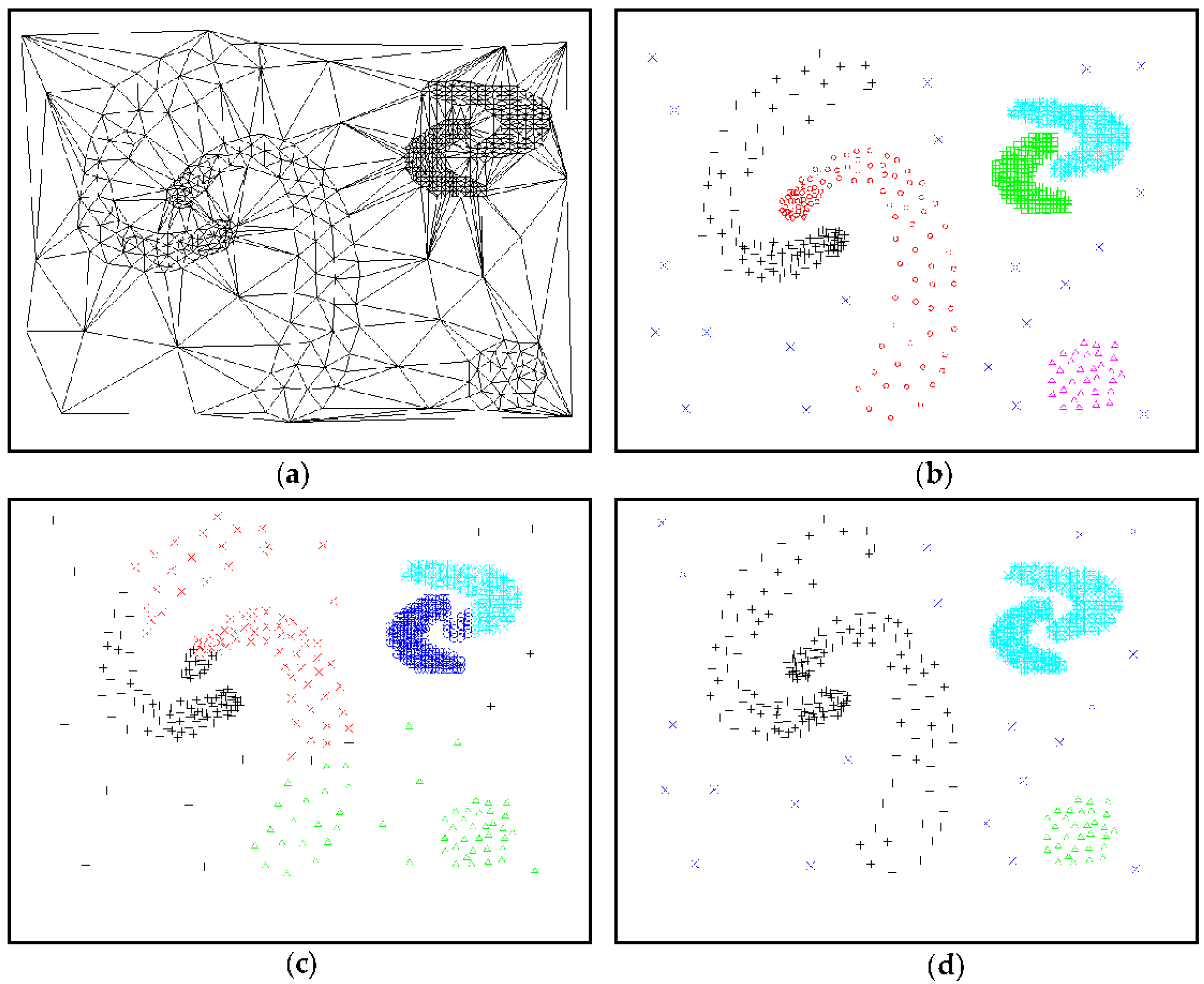
5.2. Comparison and Analysis of Experimental Results
5.3. CPU Time
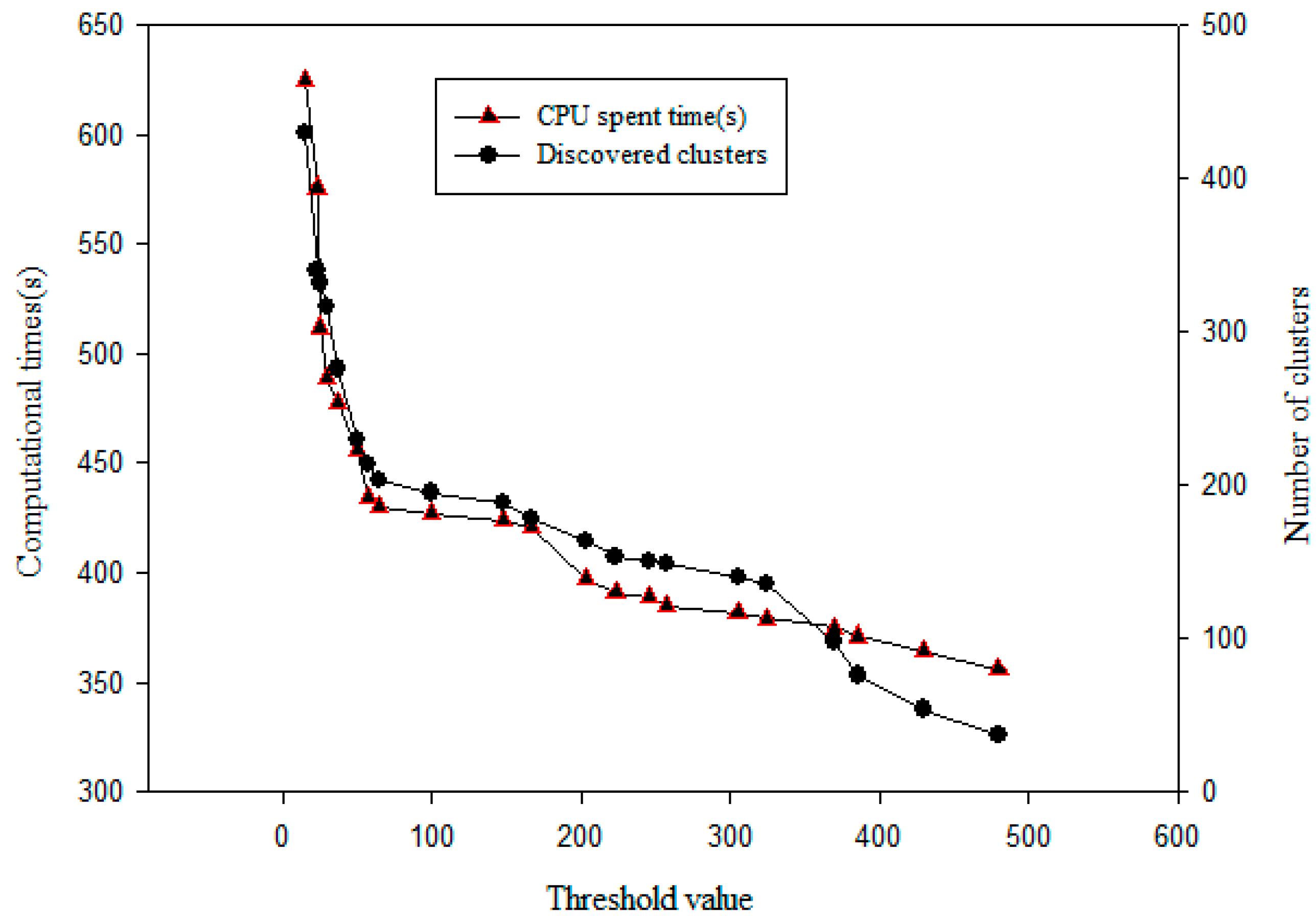
5.3.1. CPU Time Spent for Clustering
5.3.2. CPU Time Spent for ASC-Based Stream Clustering
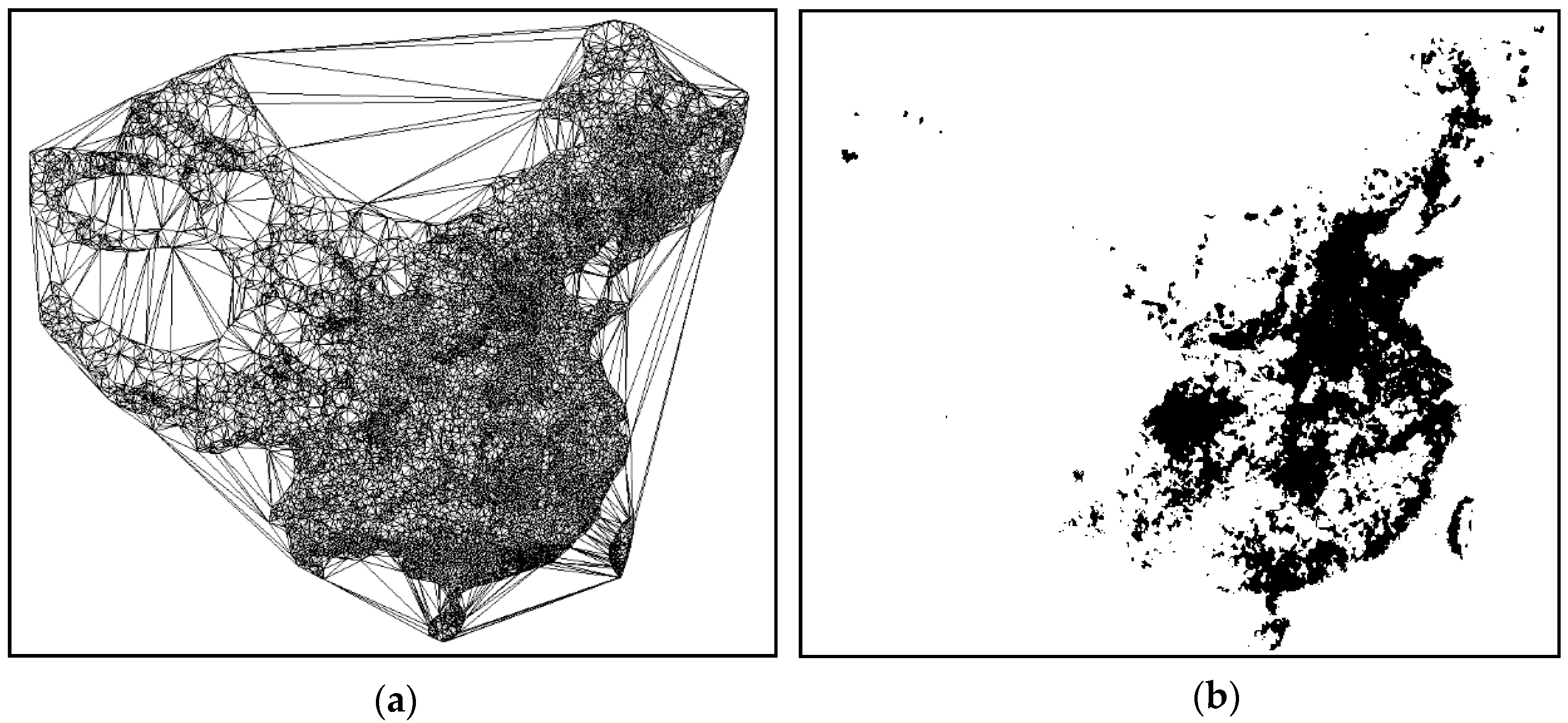
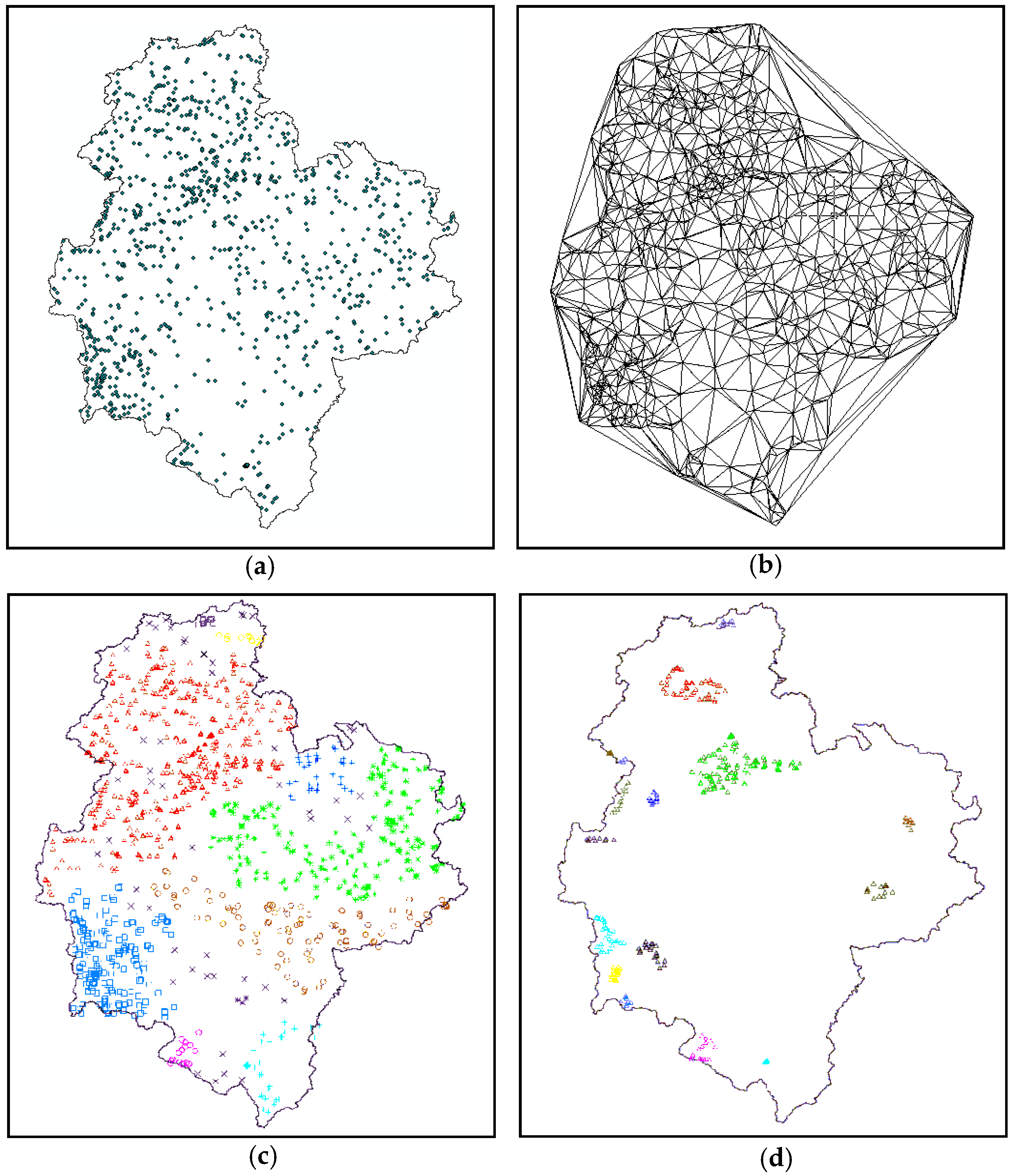
6. Practical Applications of ASC
7. Conclusions
- The Gestalt theory was successfully applied to enhance the adaptability of the spatial clustering algorithm. Both the sweep-circle technique and the dynamic threshold setting was employed to detect spatial clusters.
- The ASC algorithm can automatically locate clusters in a single pass, rather than through modifying the initial model (i.e., via minimal spanning tree, Delaunay triangulation or Voronoi diagram). The algorithm could quickly adapt to identify arbitrarily-shaped clusters and could locate the non-homogeneous density characteristics of spatial data without necessitating a priori knowledge or parameters. The time complexity of the ASC algorithm was approximately O (nlogn), where n is the size of the spatial database.
- Scalability in ASC was not limited to the size of the data set, which demonstrated that the algorithm is suitable for data streaming technology to cluster large, dynamic spatial data sets.
- The proposed algorithm was efficient, feasible, easily understood and easily implemented.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Han, J.; Kamber, M.; Pei, J. Data Mining, 3rd ed.; Morgan Kaufmann: Boston, MA, USA, 2012. [Google Scholar]
- Chen, J.; Lin, X.; Zheng, H.; Bao, X. A novel cluster center fast determination clustering algorithm. Appl. Soft Comput. 2017, 57, 539–555. [Google Scholar]
- Deng, M.; Liu, Q.; Cheng, T.; Shi, Y. An adaptive spatial clustering algorithm based on Delaunay triangulation. Comput. Environ. Urban Syst. 2011, 35, 320–332. [Google Scholar] [CrossRef]
- Liu, Q.; Deng, M.; Shi, Y. Adaptive spatial clustering in the presence of obstacles and facilitators. Comput. Geosci. 2013, 56, 104–118. [Google Scholar] [CrossRef]
- Bouguettaya, A.; Yu, Q.; Liu, X.; Zhou, X.; Song, A. Efficient agglomerative hierarchical clustering. Expert Syst. Appl. 2015, 42, 2785–2797. [Google Scholar] [CrossRef]
- MacQueen, J. Some Methods for Classification and Analysis of Multivariate Observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1965 and 27 December 1965–7 January 1966; pp. 281–297. [Google Scholar]
- Ng, R.T.; Han, J. Efficient and effective clustering methods for spatial data mining. In Proceedings of the 20th International Conference on Very Large Data Bases, Santiago de Chile, Chile, 12–15 September 1994; pp. 144–155. [Google Scholar]
- Guha, S.; Rastogi, R.; Shim, K. Cure: An efficient clustering algorithm for large databases. Inf. Syst. 1998, 26, 35–58. [Google Scholar] [CrossRef]
- Zhang, T. Birch: An efficient data clustering method for very large databases. In Proceedings of the 1996 ACM SIGMOD international conference on Management of data, Montreal, QC, Canada, 4–6 June 1999; pp. 103–114. [Google Scholar]
- Karypis, G.; Han, E.-H.; Kumar, V. Chameleon: Hierarchical clustering using dynamic modeling. Computer 1999, 32, 68–75. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Date Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.-P.; Sander, J. Optics: Ordering points to identify the clustering structure. In Proceedings of the 1999 ACM SIGMOD International Conference on Management of Data, Philadelphia, PA, USA, 31 May–3 June 1999; pp. 49–60. [Google Scholar]
- Hinneburg, A.; Keim, D.A. An Efficient Approach to Clustering in Large Multimedia Databases with Noise. In Proceedings of the 4th International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 27–31 August 1998; pp. 58–65. [Google Scholar]
- Zahn, C.T. Graph-theoretical methods for detecting and describing gestalt clusters. IEEE Trans. Comput. 1971, C-20, 68–86. [Google Scholar] [CrossRef]
- Estivill-Castro, V.; Lee, I. Autoclust: Automatic clustering via boundary extraction for mining massive point-data sets. In Proceedings of the 5th International Conference on Geocomputation, London, UK, 23–25 August 2000. [Google Scholar]
- Kang, I.-S.; Kim, T.-W.; Li, K.-J. A spatial data mining method by delaunay triangulation. In Proceedings of the 5th ACM International Workshop on Advances in Geographic Information Systems, Las Vegas, NV, USA, 10–14 November 1997; pp. 35–39. [Google Scholar]
- Wang, W.; Yang, J.; Muntz, R.R. Sting: A statistical information grid approach to spatial data mining. In Proceedings of the 23rd International Conference on Very Large Data Bases, Athens, Greece, 25–29 August 1997; pp. 186–195. [Google Scholar]
- Sheikholeslami, G.; Chatterjee, S.; Zhang, A. Wavecluster: A multi-resolution clustering approach for very large spatial databases. In Proceedings of the 24rd International Conference on Very Large Data Bases, New York, NY, USA, 24–27 August 1998; pp. 428–439. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the em algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–38. [Google Scholar]
- Gennari, J.H.; Langley, P.; Fisher, D. Models of incremental concept formation. Artif. Intell. 1989, 40, 11–61. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Schikuta, E. Grid-clustering: An efficient hierarchical clustering method for very large data sets. In Proceedings of the 13th International Conference on Pattern Recognition, Vienna, Austria, 25–29 August 1996; pp. 101–105. [Google Scholar]
- Pei, T.; Zhu, A.X.; Zhou, C.; Li, B.; Qin, C. A new approach to the nearest-neighbour method to discover cluster features in overlaid spatial point processes. Int. J. Geogr. Inf. Sci. 2006, 20, 153–168. [Google Scholar] [CrossRef]
- Tsai, C.-F.; Tsai, C.-W.; Wu, H.-C.; Yang, T. Acodf: A novel data clustering approach for data mining in large databases. J. Syst. Softw. 2004, 73, 133–145. [Google Scholar] [CrossRef]
- Estivill-Castro, V.; Lee, I. Amoeba: Hierarchical clustering based on spatial proximity using delaunaty diagram. In Proceedings of the 9th International Symposium on Spatial Data Handling, Beijing, China, 10–12 August 2000. [Google Scholar]
- Estivill-Castro, V.; Lee, I. Argument free clustering for large spatial point-data sets via boundary extraction from delaunay diagram. Comput. Environ. Urban Syst. 2002, 26, 315–334. [Google Scholar] [CrossRef]
- Wei, C.P.; Lee, Y.H.; Hsu, C.M. Empirical comparison of fast partitioning-based clustering algorithms for large data sets. Expert Syst. Appl. 2003, 24, 351–363. [Google Scholar] [CrossRef]
- Li, D.; Yang, X.; Cui, W.; Gong, J.; Wu, H. A novel spatial clustering algorithm based on Delaunay triangulation. In Proceedings of the International Conference on Earth Observation Data Processing and Analysis (ICEODPA), Wuhan, China, 28–30 December 2008; Volume 7285, pp. 728530–728539. [Google Scholar]
- Liu, D.; Nosovskiy, G.V.; Sourina, O. Effective clustering and boundary detection algorithm based on delaunay triangulation. Pattern Recognit. Lett. 2008, 29, 1261–1273. [Google Scholar] [CrossRef]
- Nosovskiy, G.V.; Liu, D.; Sourina, O. Automatic clustering and boundary detection algorithm based on adaptive influence function. Pattern Recognit. 2008, 41, 2757–2776. [Google Scholar] [CrossRef]
- Xu, D.; Tian, Y. A comprehensive survey of clustering algorithms. Ann. Data Sci. 2015, 2, 165–193. [Google Scholar] [CrossRef]
- Zhao, Q.; Shi, Y.; Liu, Q.; Fränti, P. A grid-growing clustering algorithm for geo-spatial data. Pattern Recognit. Lett. 2015, 53, 77–84. [Google Scholar] [CrossRef]
- Bolaños, M.; Forrest, J.; Hahsler, M. Clustering large datasets using data stream clustering techniques. In Data Analysis, Machine Learning and Knowledge Discovery; Spiliopoulou, M., Schmidt-Thieme, L., Janning, R., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 135–143. [Google Scholar]
- Preparata, F.P.; Ian, S.M. Computational geometry: An Introduction; Springer-Verlag New York: New York, NY, USA, 1985. [Google Scholar]
- Žalik, B. An efficient sweep-line delaunay triangulation algorithm. Comput.-Aided Des. 2005, 37, 1027–1038. [Google Scholar] [CrossRef]
- Alfred, U. A mathematician’s progress. Math. Teach. 1966, 59, 722–727. [Google Scholar]
- Shamos, M.I.; Hoey, D. Geometric intersection problems. In Proceedings of the 17th Annual Symposium on Foundations of Computer Science, Houston, TX, USA, 25–27 October 1976; pp. 208–215. [Google Scholar]
- Bentley, J.L.; Ottmann, T.A. Algorithms for reporting and counting geometric intersections. IEEE Trans. Comput. 1979, C-28, 643–647. [Google Scholar] [CrossRef]
- Fortune, S. A sweepline algorithm for voronoi diagrams. Algorithmica 1987, 2, 153–174. [Google Scholar] [CrossRef]
- Zhou, P. Computational geometry algorithm design and analysis. In Computational Geometry Algorithm Design and Analysis, 4th ed.; Tsinghua University Press: Beijing, China, 2011. [Google Scholar]
- Žalik, K.R.; Žalik, B. A sweep-line algorithm for spatial clustering. Adv. Eng. Softw. 2009, 40, 445–451. [Google Scholar] [CrossRef]
- Biniaz, A.; Dastghaibyfard, G. A faster circle-sweep delaunay triangulation algorithm. Adv. Eng. Softw. 2012, 43, 1–13. [Google Scholar] [CrossRef]
- Adam, B.; Kauffmann, P.; Schmitt, D.; Spehner, J.-C. An increasing-circle sweep-algorithm to construct the Delaunay diagram in the plane. In Proceedings of the 9th Canadian Conference on Computational Geometry (CCCG), Kingston, ON, Canada, 11–14 August 1997. [Google Scholar]
- Guha, S.; Mishra, N.; Motwani, R.; O’Callaghan, L. Clustering data streams. In Proceedings of the 41st Annual Symposium on Foundations of Computer Science, Redondo Beach, CA, USA, 12–14 November 2000; pp. 359–366. [Google Scholar]
- O’Callaghan, L.; Mishra, N.; Meyerson, A.; Guha, S.; Motwani, R. Streaming-data algorithms for high-quality clustering. In Proceedings of the 18th International Conference on Data Engineering, San Jose, CA, USA, 26 February–1 March 2002; pp. 685–694. [Google Scholar]
- Zengyou, H.E.; Xiaofei, X.U.; Deng, S. Squeezer: An efficient algorithm for clustering categorical data. J. Comput. Sci. Technol. 2002, 17, 611–624. [Google Scholar]
- Guha, S.; Meyerson, A.; Mishra, N.; Motwani, R.; O’Callaghan, L. Clustering data streams: Theory and practice. IEEE Trans. Knowl. Data Eng. 2003, 15, 515–528. [Google Scholar] [CrossRef]
- Ding, S.; Zhang, J.; Jia, H.; Qian, J. An adaptive density data stream clustering algorithm. Cogn. Comput. 2016, 8, 30–38. [Google Scholar] [CrossRef]
- Zheng, L.; Huo, H.; Guo, Y.; Fang, T. Supervised adaptive incremental clustering for data stream of chunks. Neurocomputing 2016, 219, 502–517. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Ellis, W.D. A Source Book of Gestalt Psychology; Kegan Paul, Trench, Trubner & Company: London, UK, 1938; p. 403. [Google Scholar]
- Hathaway, R.J.; Bezdek, J.C. Extending fuzzy and probabilistic clustering to very large data sets. Comput. Stat. Data Anal. 2006, 51, 215–234. [Google Scholar] [CrossRef]
- Cho, K.; Jo, S.; Jang, H.; Kim, S.M.; Song, J. Dcf: An efficient data stream clustering framework for streaming applications. In Proceedings of the 17th International Conference on Database and Expert Systems Applications, Kraków, Poland, 4–8 September 2006; pp. 114–122. [Google Scholar]



| Category | Typical Algorithm | Shape of Suitable Data Set | Discovery of Clusters with Even Density | Scalability | Requirement of Prior Knowledge | Sensitive to Noise/Outlier | for Large-Scale Data | Complexity (Times) |
|---|---|---|---|---|---|---|---|---|
| Partition | K-means | Convex | No | Middle | Yes | Highly | Yes | Low |
| CLARANS | Convex | No | Middle | Yes | Little | Yes | High | |
| Hierarchy | BIRCH | Convex | No | High | Yes | Little | Yes | Low |
| CURE | Arbitrary | No | High | Yes | Little | Yes | Low | |
| CHAMELEON | Arbitrary | Yes | High | Yes | Little | No | High | |
| Density | DBSCAN | Arbitrary | No | Middle | Yes | Little | Yes | Middle |
| OPTICS | Arbitrary | Yes | Middle | Yes | Little | Yes | Middle | |
| DENCLUE | Arbitrary | No | Middle | Yes | Little | Yes | Middle | |
| Graph theory | MST | Arbitrary | Yes | High | Yes | Highly | Yes | Middle |
| AMEOBA | Arbitrary | Yes | High | No | Little | No | Middle | |
| AUTOCLUST | Arbitrary | Yes | High | No | Little | No | Middle | |
| Grid | STING | Arbitrary | No | High | Yes | Little | Yes | Low |
| CLIQUE | Arbitrary | No | High | Yes | Moderately | No | Low | |
| WaveCluster | Arbitrary | No | High | Yes | Little | Yes | Low | |
| Model | EM | Convex | No | Middle | Yes | Highly | No | Low |
| Data Set | Points | CPU Time (s) |
|---|---|---|
| Figure 13 | 264 | 0.014 |
| Figure 11 | 8000 | 0.074 |
| Figure 12b | 10,000 | 0.116 |
| Figure 12c | 10,000 | 0.124 |
| Figure 12d | 10,000 | 0.243 |
| Figure 14 | 15,067 | 0.457 |
| Dataset | ASC | AUTOCLUST | ||
|---|---|---|---|---|
| Clustering Time | DT Time | Clustering Time | Total (s) | |
| 10,000 | 0.249 | 0.026 | 0.314 | 0.340 |
| 20,000 | 0.422 | 0.082 | 2.450 | 2.532 |
| 50,000 | 0.941 | 0.287 | 5.125 | 5.412 |
| 100,000 | 2.653 | 0.607 | 14.234 | 14.841 |
| 200,000 | 5.324 | 2.290 | 61.124 | 63.414 |
| Data Set Algorithm | 100,000 | 200,000 | ||
|---|---|---|---|---|
| ASC | Žalik | ASC | Žalik | |
| Initialization | 0.646 | 0.717 | 1.597 | 2.700 |
| Clustering | 1.026 | 1.944 | 2.715 | 7.242 |
| Merging | 0.481 | 0.624 | 1.012 | 2.332 |
| Total | 2.153 | 3.285 | 5.324 | 12.274 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, Q.; Deng, S.; Zheng, Z. An Adaptive Sweep-Circle Spatial Clustering Algorithm Based on Gestalt. ISPRS Int. J. Geo-Inf. 2017, 6, 272. https://doi.org/10.3390/ijgi6090272
Zhan Q, Deng S, Zheng Z. An Adaptive Sweep-Circle Spatial Clustering Algorithm Based on Gestalt. ISPRS International Journal of Geo-Information. 2017; 6(9):272. https://doi.org/10.3390/ijgi6090272
Chicago/Turabian StyleZhan, Qingming, Shuguang Deng, and Zhihua Zheng. 2017. "An Adaptive Sweep-Circle Spatial Clustering Algorithm Based on Gestalt" ISPRS International Journal of Geo-Information 6, no. 9: 272. https://doi.org/10.3390/ijgi6090272
APA StyleZhan, Q., Deng, S., & Zheng, Z. (2017). An Adaptive Sweep-Circle Spatial Clustering Algorithm Based on Gestalt. ISPRS International Journal of Geo-Information, 6(9), 272. https://doi.org/10.3390/ijgi6090272







