The IMU/UWB Fusion Positioning Algorithm Based on a Particle Filter
Abstract
:1. Introduction
2. UWB and IMU Fusion Algorithm
2.1. Problem Description
- As indicated by Sample in the corresponding flowchart, perform the sampling according to the distribution state transition equation.
- As indicated by Evaluate in the corresponding flowchart, update the weight of every particle according to the observation model and the observation values.
- As indicated by Resample in the corresponding flowchart, use the resampling method to restrain the particle attenuation.
2.2. The Velocity and Direction of the Virtual Odometer Method
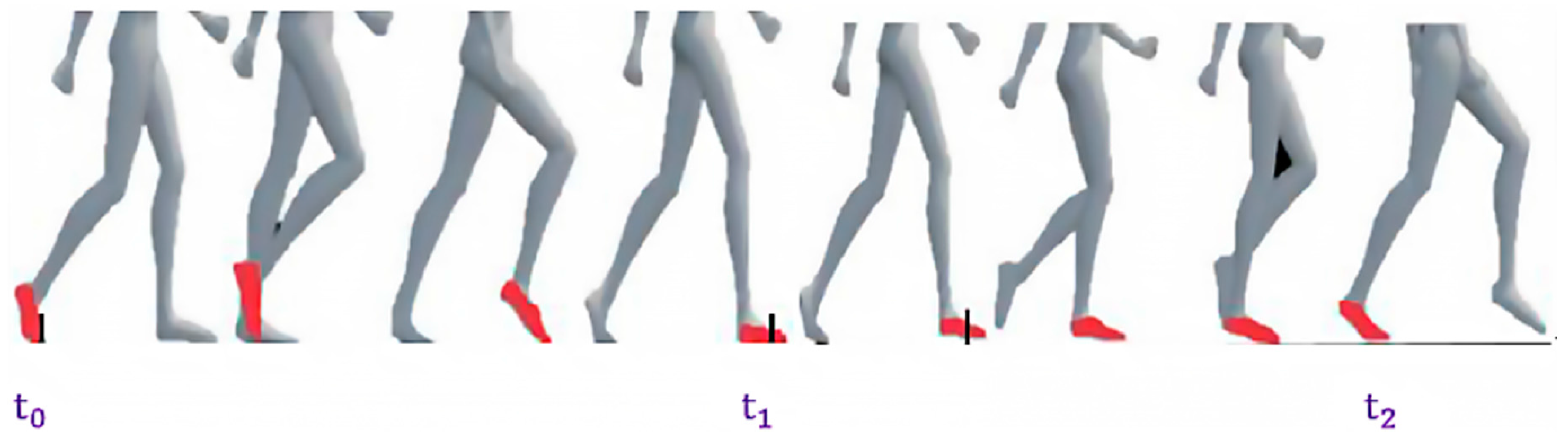
2.3. The ZUPT-Based Algorithm in the IMU
- 1:
- k ≔ 0
- 2:
- Initial;
- 3:
- While
- 4:
- k ≔ k + 1
- 5:
- 6:
- ≔
- 7:
- if(ZeroVelocity() = True)
- 8:
- 9:
- 10:
- 11:
- VirtualOdometer() // The virtual odometer method provided in Section 2.2
- 12:
- 13:
- end if
- 14:
- end while
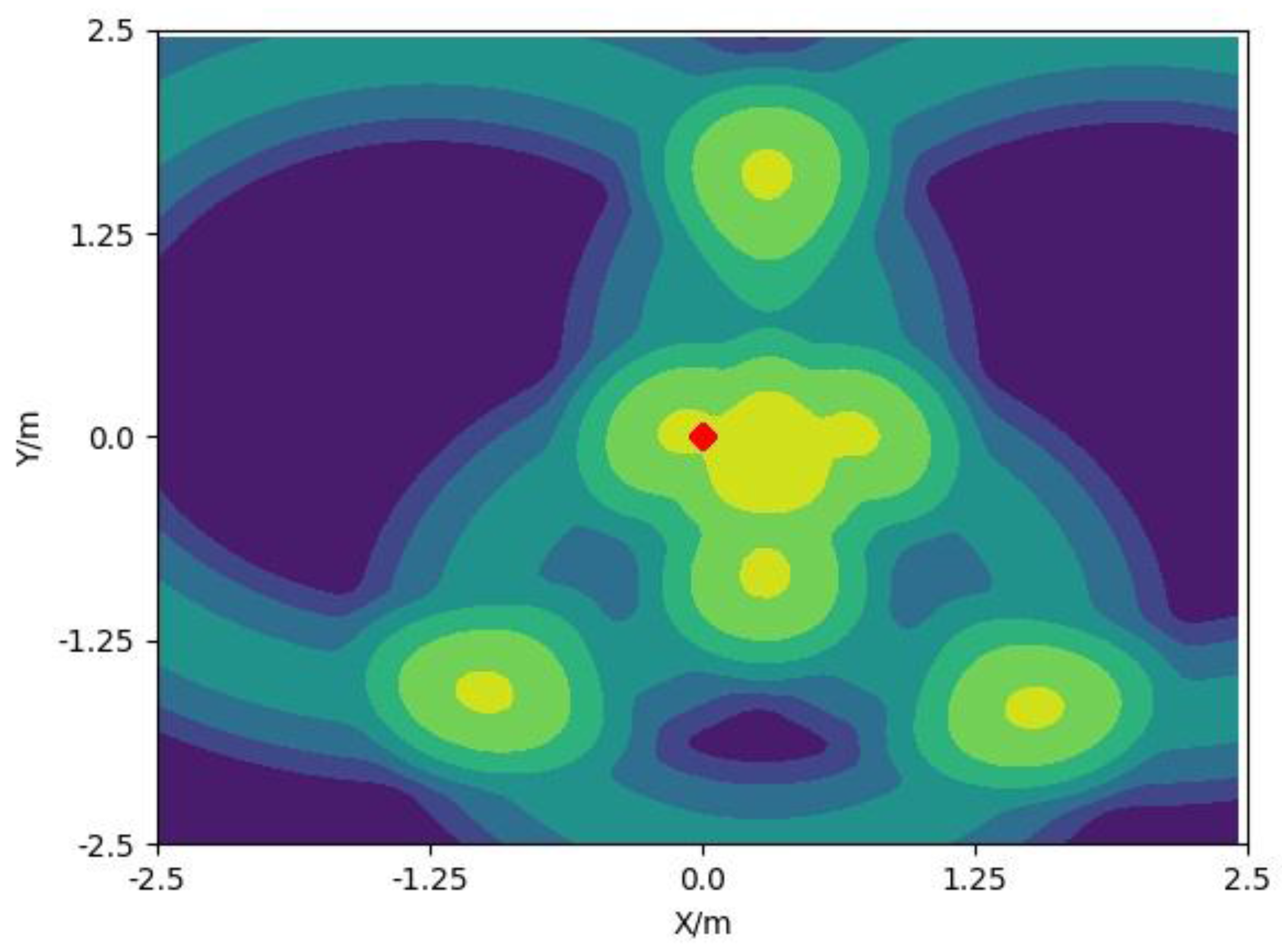
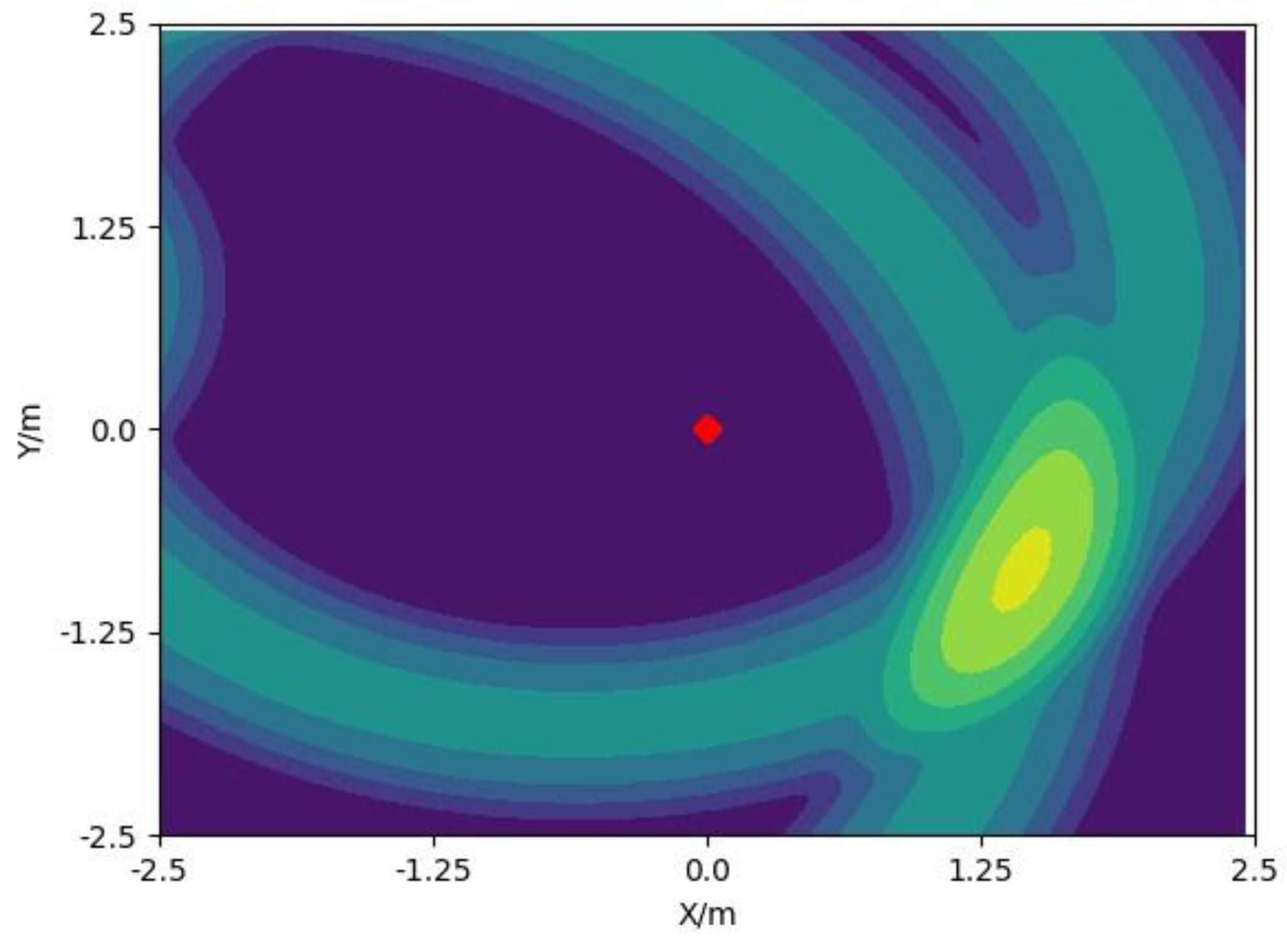
2.4. The Fusion of UWB and IMU Based on Particle Filter
3. Experiments and Results
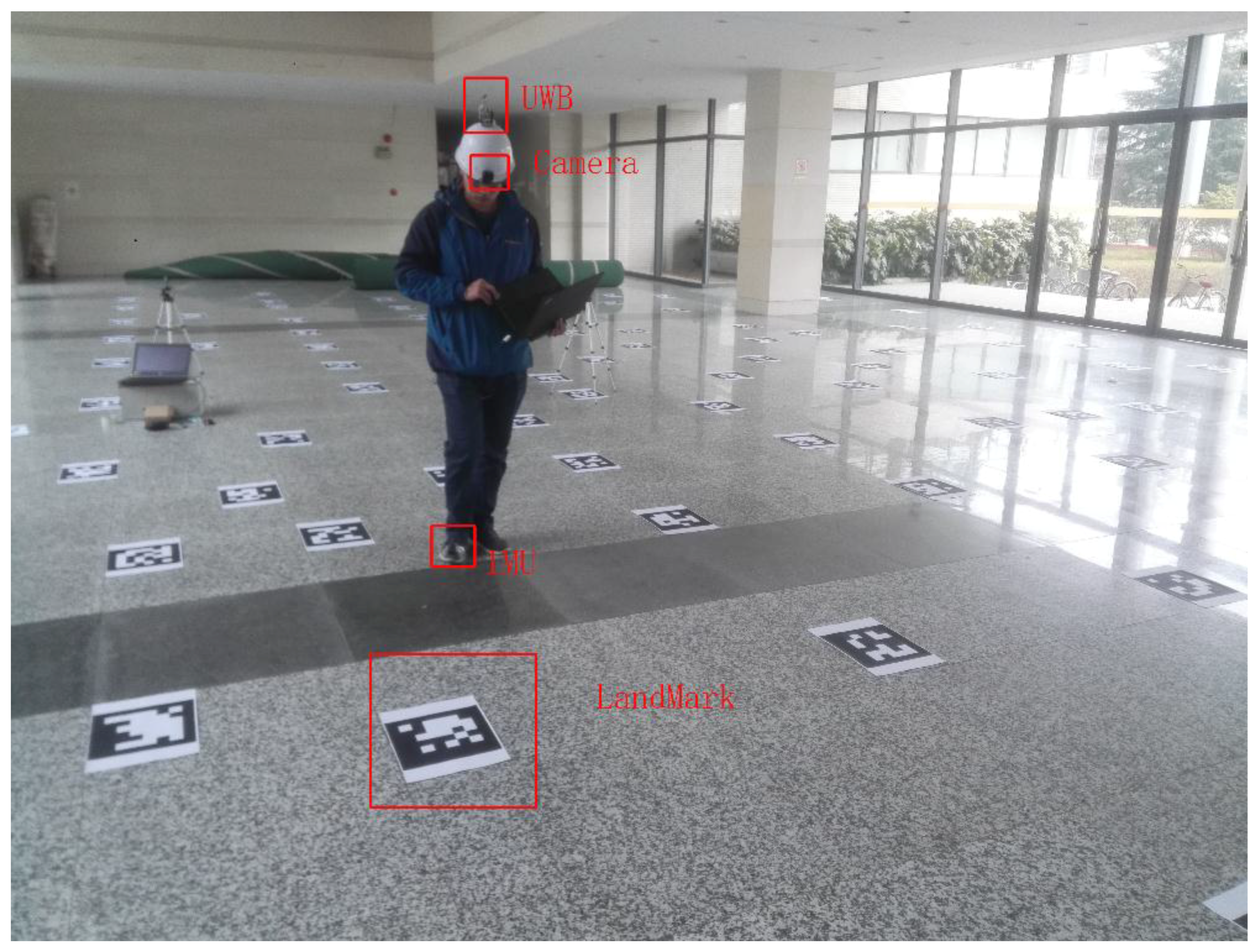
3.1. Experimental Scene and Method
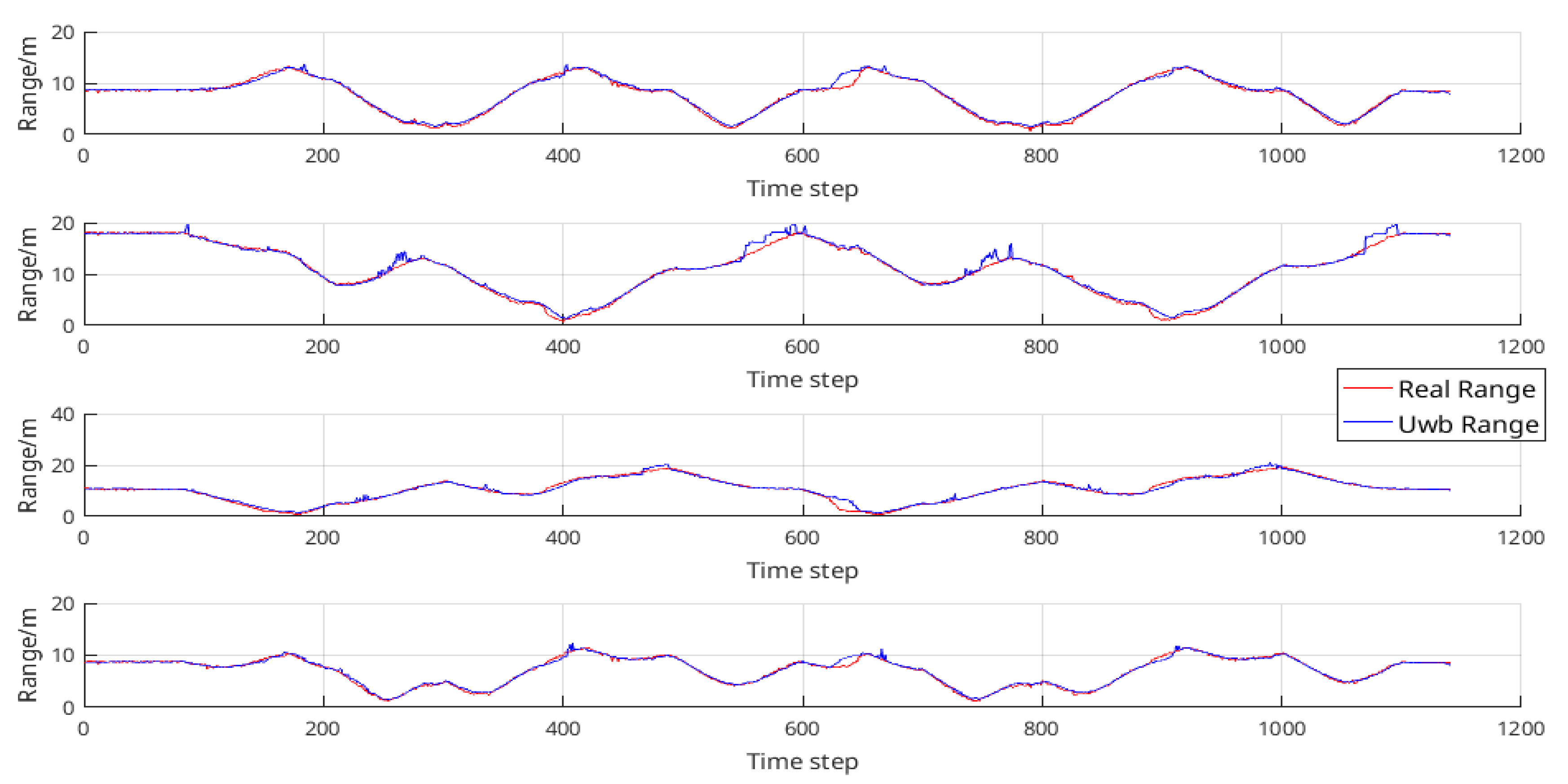
3.2. The Acquisition of the Real Trajectory
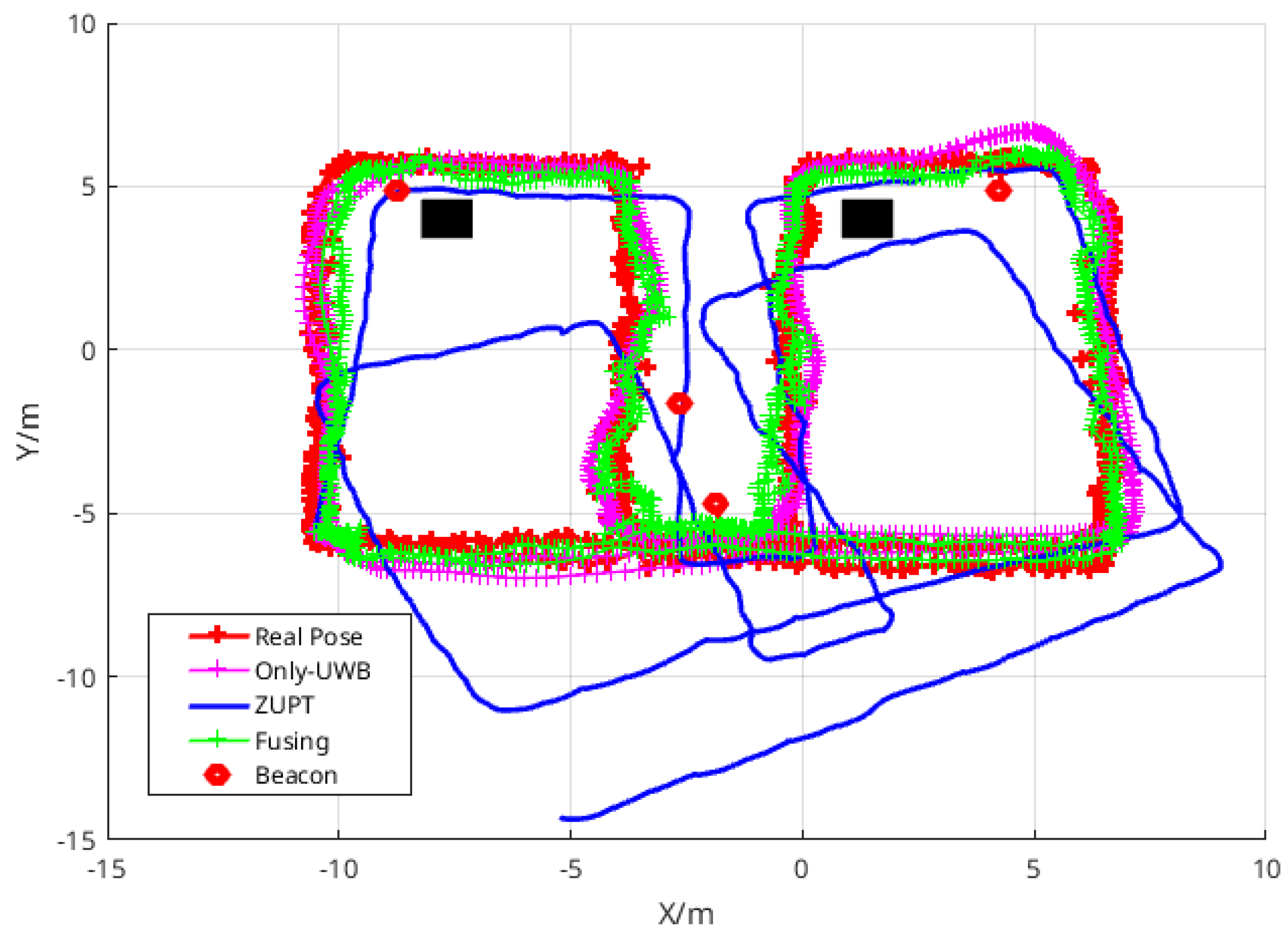
3.3. Experimental Results and Comparison
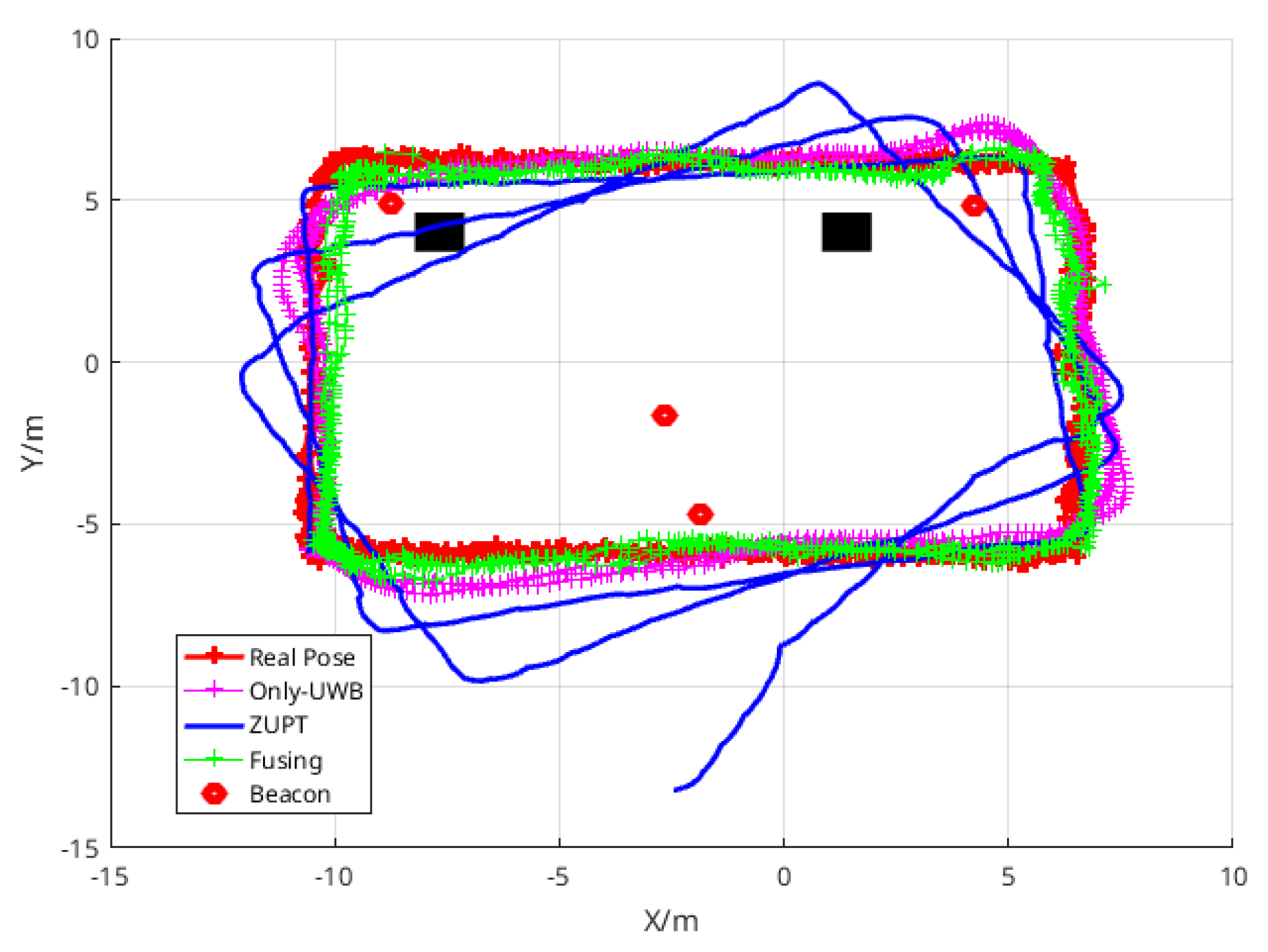
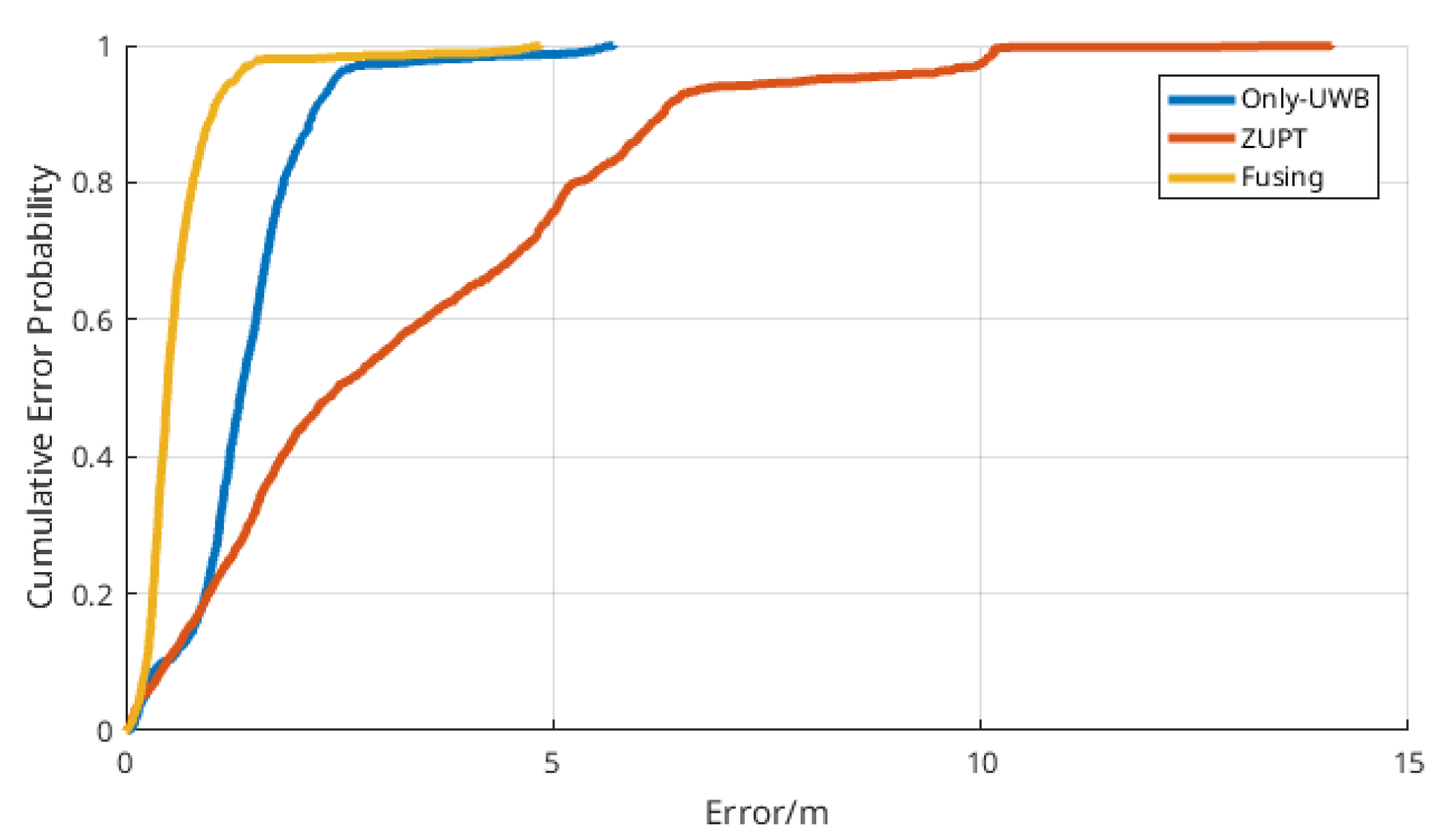
3.3.1. Comparison of the Various Algorithms in Path I
3.3.2. Comparison of the Various Algorithms in Path II
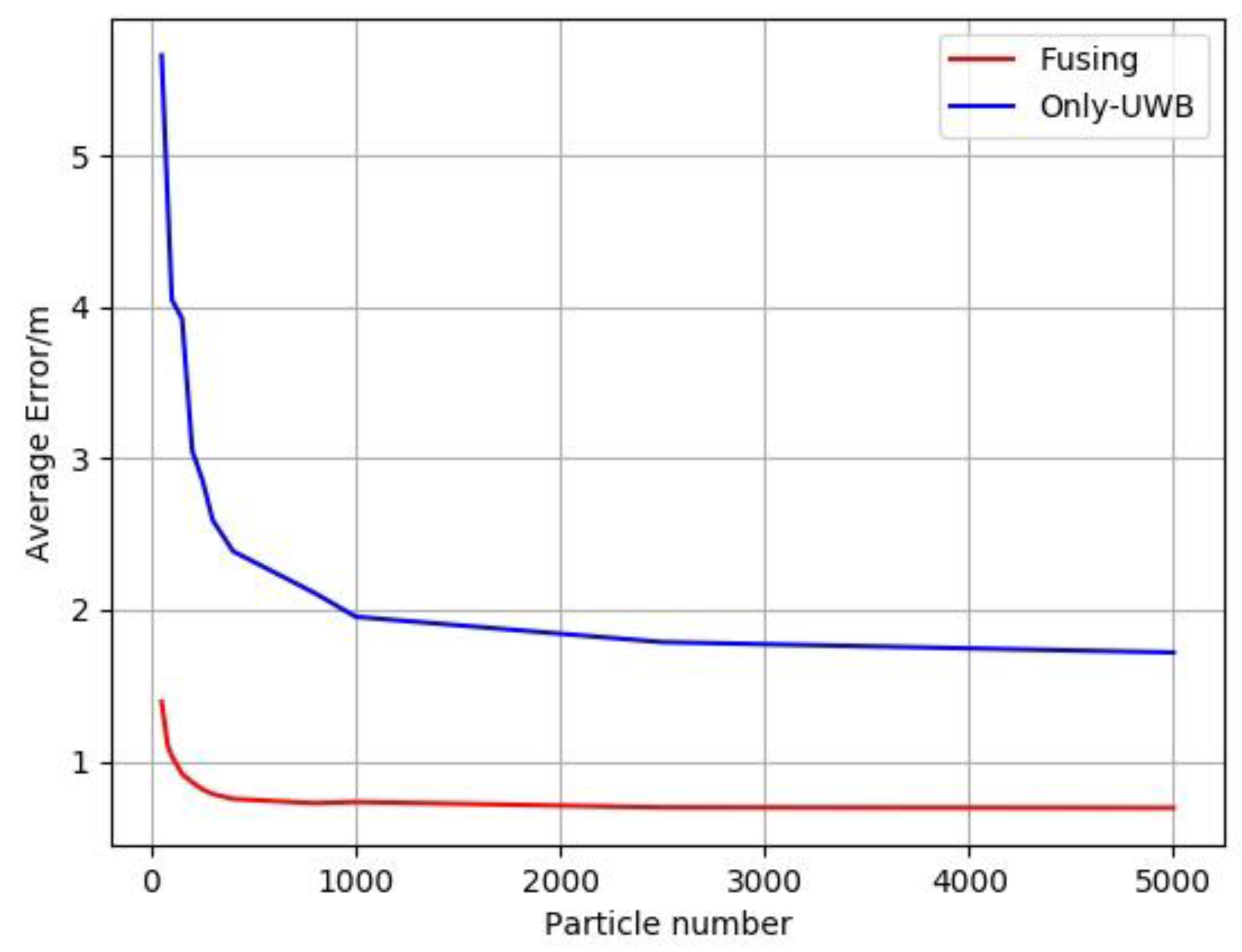
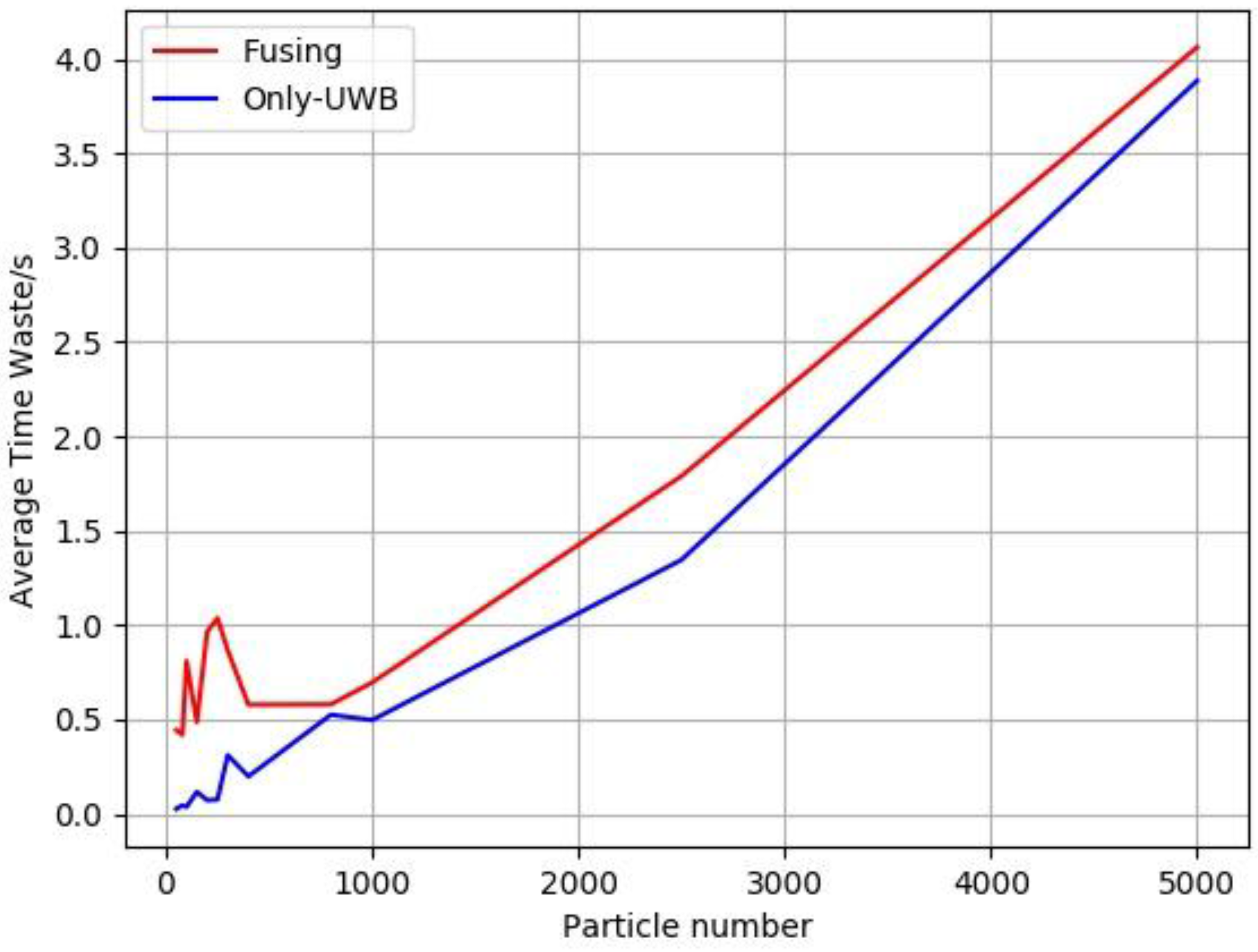
3.3.3. The influence of the Number of Particles on the Positioning Result
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nilsson, J.O.; Skog, I.; Händel, P.; Hari, K.V.S. Foot-mounted INS for everybody—An open-source embedded implementation. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Myrtle Beach, SC, USA, 23–26 April 2012; pp. 140–145. [Google Scholar]
- Skog, I.; Nilsson, J.O.; Händel, P. Pedestrian tracking using an IMU array. In Proceedings of the 2014 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 6–7 January 2014. [Google Scholar]
- Huang, C.; Liao, Z.; Zhao, L. Synergism of INS and PDR in self-contained pedestrian tracking with a miniature sensor module. IEEE Sens. J. 2010, 10, 1349–1359. [Google Scholar] [CrossRef]
- Mezentsev, O.; Lachapelle, G.; Collin, J. Pedestrian dead reckoning—A solution to navigation in GPS signal degraded areas? Geomatica 2005, 59, 175–182. [Google Scholar]
- Zampella, F.; De Angelis, A.; Skog, I.; Zachariah, D.; Jimenez, A. A constraint approach for UWB and PDR fusion. In Proceedings of the 2012 International Conference on Indoor Positioning and Indoor Navigation, IPIN 2012—Conference Proceedings, Sydney, Australia, 13–15 November 2012. [Google Scholar]
- Li, X.; Xie, L.; Chen, J.; Han, Y.; Song, C. A ZUPT Method Based on SVM Regression Curve Fitting for SINS; IEEE: Piscataway, NJ, USA, 2014; pp. 754–757. [Google Scholar]
- Hellmers, H.; Eichhorn, A. IMU/Magnetometer Based 3D Indoor Positioning for Wheeled Platforms in NLoS Scenarios; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Kang, W.; Nam, S.; Han, Y.; Lee, S. Improved heading estimation for smartphone-based indoor positioning systems. In Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications PIMRC, Sydney, Australia, 9–12 September 2012; pp. 2449–2453. [Google Scholar]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. Visual-lidar Odometry and Mapping: Low-drift, Robust, and Fast. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2174–2181. [Google Scholar]
- Mur-Artal, R.; Tardos, J.D. Probabilistic Semi-Dense Mapping from Highly Accurate Feature-Based Monocular SLAM. In Proceedings of the Robotics Science and Systems (RSS), Rome, Italy, 13–17 July 2015. [Google Scholar]
- Wagle, N.; Frew, E.W. A Particle Filter Approach to WiFi Target Localization. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Toronto, ON, Canada, 2–5 August 2010; pp. 1–12. [Google Scholar]
- Bekkelien, A. Bluetooth Indoor Positioning. Master’s Thesis, University of Geneva, Geneva, Switzerland, 2012. [Google Scholar]
- Yu, K.; Montillet, J.; Rabbachin, A.; Cheong, P.; Oppermann, I. UWB location and tracking for wireless embedded networks. Signal Process. 2006, 86, 2153–2171. [Google Scholar] [CrossRef]
- Zhou, Y.; Law, C.L.; Guan, Y.L.; Chin, F. Indoor elliptical localization based on asynchronous UWB range measurement. IEEE Trans. Instrum. Meas. 2011, 60, 248–257. [Google Scholar] [CrossRef]
- Blanco, J.L.; Galindo, C.; Fern, J.A.; Moreno, F.A.; Mart, J.L. Mobile Robot Localization based on Ultra-Wide-Band Ranging : A Particle Filter Approach. Robot. Auton. Syst. 2009, 57, 496–507. [Google Scholar]
- Zwirello, L.; Ascher, C.; Trommer, G.F.; Zwick, T. Study on UWB/INS integration techniques. In Proceedings of the 8th Workshop on Positioning Navigation and Communication 2011, WPNC, Dresden, Germany, 7–8 April 2011; pp. 13–17. [Google Scholar]
- Skog, I.; Händel, P.; Nilsson, J.-O.; Rantakokko, J. Zero-velocity detection—An algorithm evaluation. IEEE Trans. Biomed. Eng. 2010, 57, 2657–2666. [Google Scholar] [CrossRef] [PubMed]
- Garrido-Jurado, S.; Muñoz-Salinas, R.; Madrid-Cuevas, F.J.; Marín-Jiménez, M.J. Automatic generation and detection of highly reliable fiducial markers under occlusion. Pattern Recognit. 2014, 47, 2280–2292. [Google Scholar] [CrossRef]
- Kümmerle, R.; Rainer, K.; Grisetti, G.; Konolige, K. G2o:A general framework for graph optimization. In Proceedings of the IEEE International Conference on Robotics and Automation Shanghai International Conference Center, Shanghai, China, 9–13 May 2011; pp. 1–19. [Google Scholar]
- Bacik, J.; Durovsky, F.; Fedor, P.; Perdukova, D. Autonomous flying with quadrocopter using fuzzy control and ArUco markers. Intell. Serv. Robot. 2017, 10, 185–194. [Google Scholar] [CrossRef]

| Algorithm | Mean Error (m) | Standard Deviation of Errors (m) | Time of Offline Calculation (s) |
|---|---|---|---|
| ZUPT | 3.09 | 2.69 | 0.192 |
| Only-UWB | 1.63 | 0.936 | 3.05 |
| Fusing | 0.708 | 0.660 | 3.22 |
| Algorithm | Mean Error (m) | Standard Deviation of Errors (m) | Time of Offline Calculation (s) |
|---|---|---|---|
| ZUPT | 3.20 | 2.50 | 0.212 |
| Only-UWB | 1.76 | 0.970 | 3.80 |
| Fusing | 0.726 | 0.661 | 4.12 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, X. The IMU/UWB Fusion Positioning Algorithm Based on a Particle Filter. ISPRS Int. J. Geo-Inf. 2017, 6, 235. https://doi.org/10.3390/ijgi6080235
Wang Y, Li X. The IMU/UWB Fusion Positioning Algorithm Based on a Particle Filter. ISPRS International Journal of Geo-Information. 2017; 6(8):235. https://doi.org/10.3390/ijgi6080235
Chicago/Turabian StyleWang, Yan, and Xin Li. 2017. "The IMU/UWB Fusion Positioning Algorithm Based on a Particle Filter" ISPRS International Journal of Geo-Information 6, no. 8: 235. https://doi.org/10.3390/ijgi6080235
APA StyleWang, Y., & Li, X. (2017). The IMU/UWB Fusion Positioning Algorithm Based on a Particle Filter. ISPRS International Journal of Geo-Information, 6(8), 235. https://doi.org/10.3390/ijgi6080235





