Implementation of Algorithm for Satellite-Derived Bathymetry using Open Source GIS and Evaluation for Tsunami Simulation
Abstract
:1. Introduction
2. System Environment
2.1. GRASS Python Scripting Library
2.2. R Packages
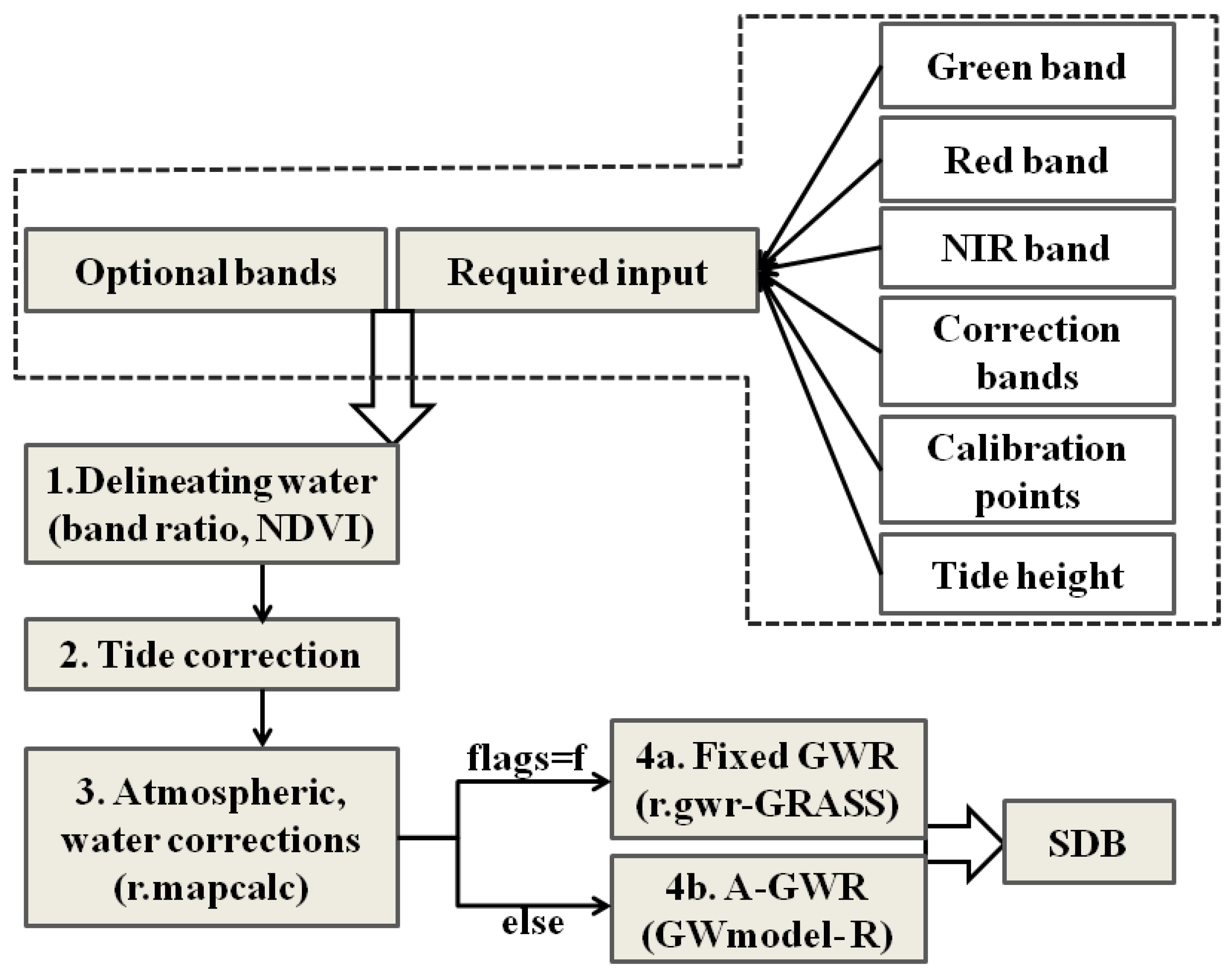
3. Implementation of SDB Model as GRASS GIS Module
3.1. Delineation of Water Region
3.2. Tide Correction
3.3. Atmospheric and Water Corrections
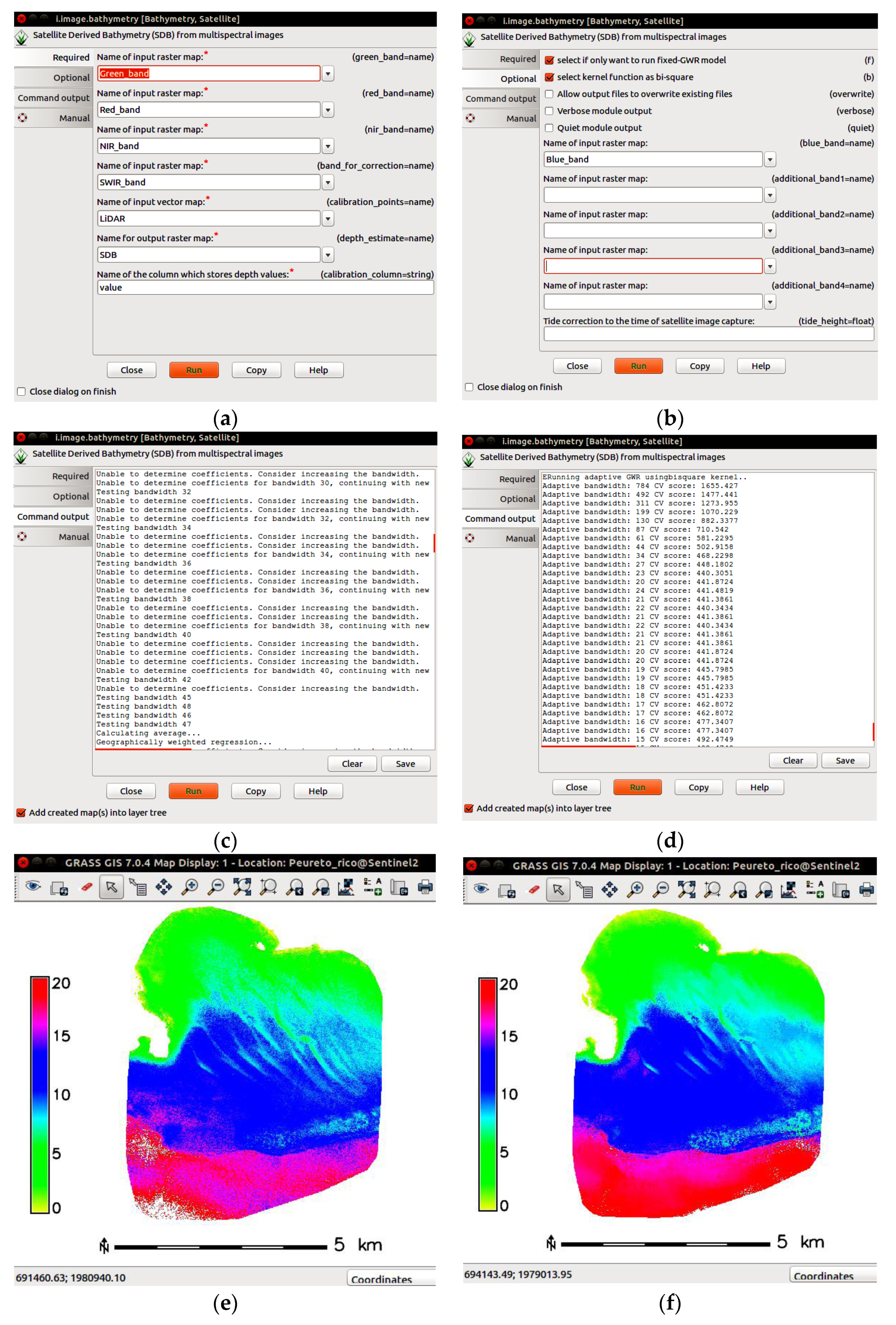
3.4. Geographical Weighted Regression
3.4.1. Fixed-GWR
3.4.2. Adaptive-GWR
4. Validation of Implemented SDB Algorithm
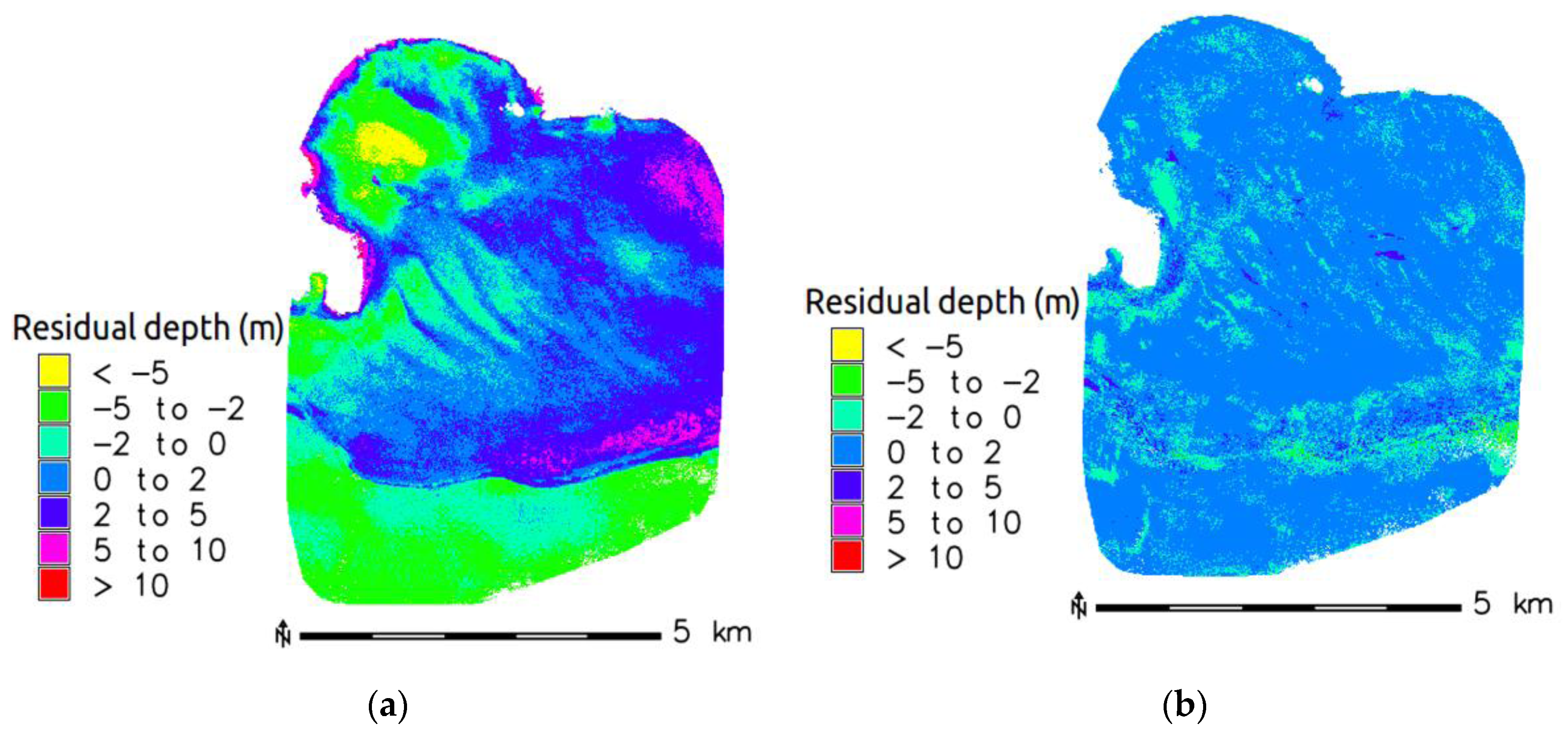
4.1. Puerto Rico, Northeastern Caribbean Sea
4.2. Iwate Prefecture, Japan
5. Application for Integrated Coastal Relief Model and Tsunami Simulation
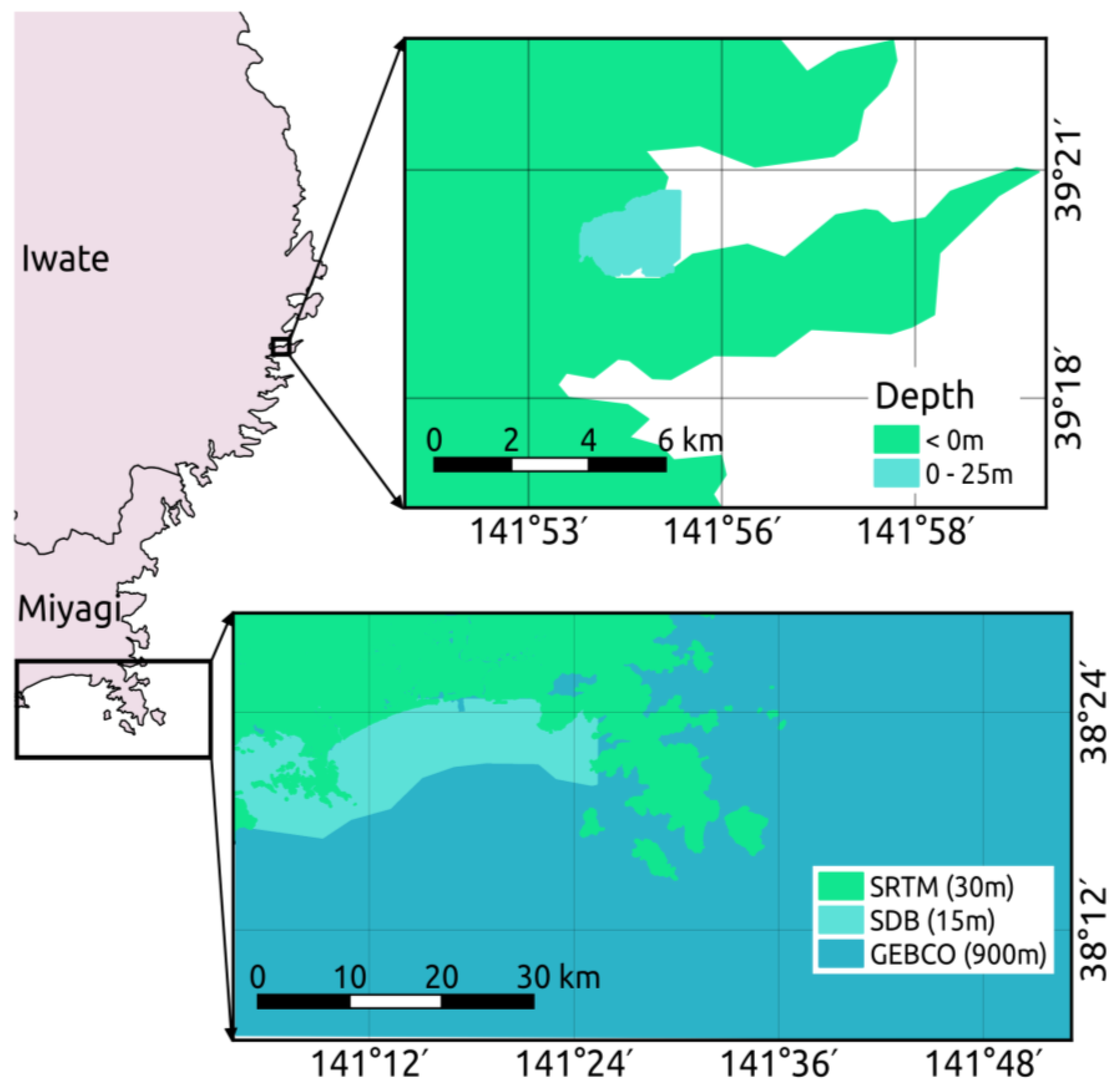
5.1. Study Area and Data Usage
5.2. Integrated Coastal Relief Model
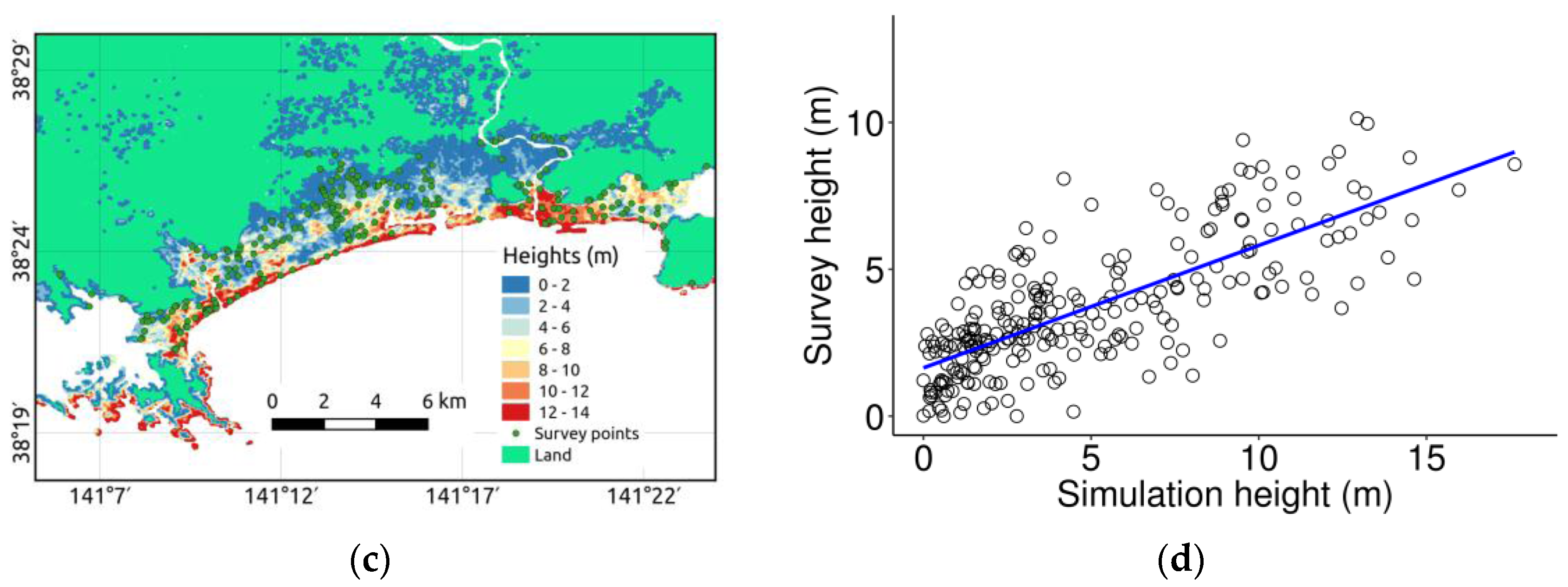
5.3. Tsunami Simulation
6. Result and Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lyzenga, D.R. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and Landsat data. Int. J. Remote Sens. 1981, 2, 72–82. [Google Scholar] [CrossRef]
- Baban, S.M.J. The evaluation of different algorithms for bathymetric charting of lakes using Landsat imagery. Int. J. Remote Sens. 1993, 14, 2263–2273. [Google Scholar] [CrossRef]
- Benny, A.H.; Dawson, G.J. Satellite imagery as an aid to bathymetric charting in the Red Sea. Cartogr. J. 1983, 20, 5–16. [Google Scholar] [CrossRef]
- Muslim, A.M.; Foody, G.M. DEM and bathymetry estimation for mapping a tide-coordinated shoreline from fine spatial resolution satellite sensor imagery. Int. J. Remote Sens. 2008, 29, 4515–4536. [Google Scholar] [CrossRef]
- Philpot, W.D. Bathymetric mapping with passive multispectral imagery. Appl. Opt. 1989, 28, 1569–1579. [Google Scholar] [CrossRef] [PubMed]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Clark, R.K.; Faye, T.H.; Walker, C.L. Bathymetry using thematic mapper imagery. Ocean Opt. IX 1988, 925, 229–231. [Google Scholar]
- Stoffle, R.W.; Halmo, D.B. Satellite Monitoring of Coastal Marine Ecosystems: A Case from the Dominican Republic; Consortium for Integrated Earth Science Information Network (CIESIN): Saginaw, Michigan, 1991. [Google Scholar]
- Lyzenga, D.R.; Malinas, N.R.; Tanis, F.J. Multispectral bathymetry using a simple physically based algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Gholamalifard, M.; Esmaili Sari, A.; Abkar, A.; Naimi, B. Bathymetric modeling from satellite imagery via single band algorithm (SBA) and principal components analysis (PCA) in southern Caspian Sea. Int. J. Environ. Res. 2013, 7, 877–886. [Google Scholar]
- Vinayaraj, P.; Raghavan, V.; Masumoto, S.; Glejin, J. Comparative evaluation and refinement of algorithm for water depth estimation using medium resolution remote sensing data. Int. J. Geoinform. 2015, 11, 17–29. [Google Scholar]
- Kanno, A.; Tanaka, Y. Modified lyzenga’s method for estimating generalized coefficients of satellite-based predictor of shallow water depth. IEEE Geosci. Remote Sens. Lett. 2012, 9, 715–719. [Google Scholar] [CrossRef]
- Monteys, X.; Harris, P.; Caloca, S.; Cahalane, C. Spatial prediction of coastal bathymetry based on multispectral satellite imagery and multibeam data. Remote Sens. 2015, 7, 13782–13806. [Google Scholar] [CrossRef]
- Brunsdon, A.C.; Fotheringham, S.; Charlton, E.M. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 283–297. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Charlton, M.E.; Brunsdon, C. Geographically weighted regression: A natural evolution of the expansion method for spatial data analysis. Environ. Plann. 1998, 30, 1905–1927. [Google Scholar] [CrossRef]
- Lu, B.; Harris, P.; Charlton, M.; Brunsdon, C. The GWmodel R package: Further topics for exploring spatial heterogeneity using geographically weighted models. Geo-Spat. Inf. Sci. 2014, 17, 85–101. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, K.; Mcdermid, G.J.; Hay, G.J. The influence of sampling density on geographically weighted regression: A case study using forest canopy height and optical data. Int. J. Remote Sens. 2012, 33, 2909–2924. [Google Scholar] [CrossRef]
- Yrigoyen, C.C.; Rodrigouz, I.G.; Otera, J.V. Modeling spatial variations in household disposable income with geographically weighted regression. Estad. Esp. 2008, 50, 321–360. [Google Scholar]
- Su, H.; Liu, H.; Lei, W.; Philipi, M.; Heyman, W.; Beck, A. Geographically adaptive inversion model for improving bathymetric retrieval from multispectral satellite imagery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 465–476. [Google Scholar] [CrossRef]
- Vinayaraj, P.; Raghavan, V.; Masumoto, S. Satellite derived bathymetry using adaptive-geographically weighted regression model. Mar. Geod. 2016, 39, 458–478. [Google Scholar] [CrossRef]
- Neteler, M.; Bowman, H.; Landa, M.; Metz, M. GRASS GIS: A multi-purpose open source GIS. Environ. Model. Softw. 2012, 31, 124–130. [Google Scholar] [CrossRef]
- Python Software Foundation. 2016. Available online: https://www.python.org/ (accessed on 07 January 2017).
- Zambelli, P.; Gebbert, S.; Ciolli, M. Pygrass: An object oriented Python Application Programming Interface (API) for Geographic Resources Analysis Support System (GRASS) Geographic Information System (GIS). ISPRS Int. J. Geo-Inf. 2013, 2, 201–219. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Bivand, R. Interface between GRASS 7 Geographical Information System and R 2015. Available online: https://cran.r-project.org/web/packages/rgrass7/ (accessed on 07 January 2017).
- Gollini, I.; Lu, B.; Charlton, M.; Brunsdon, C.; Harris, P. GWmodel: An R Package for exploring spatial heterogeneity using geographically weighted models. J. Stat. Softw. 2015, 63, 1548–7660. [Google Scholar] [CrossRef]
- Harris, P.; Fotheringham, A.S.; Crespo, R.; Charlton, M. The use of geographically weighted regression for spatial prediction: an evaluation of models using simulated data Sets. Math. Geosci. 2010, 42, 657–680. [Google Scholar] [CrossRef]
- Harris, P.; Brunsdon, C.; Fotheringham, A.S. Links, comparisons and extensions of the geographically weighted regression model when used as a spatial predictor. Stoch. Environ. Res. Risk Assess. 2011, 25, 123–138. [Google Scholar] [CrossRef]
- Costa, B.M.; Battista, T.A.; Pittman, S.J. Comparative evaluation of airborne lidar and ship-based multibeam sonar bathymetry and intensity for mapping coral reef ecosystems. Remote Sens. Environ. 2009, 113, 1082–1100. [Google Scholar] [CrossRef]
- Griffin, J.D.; Latief, H.; Kongko, W.; Harig, S.; Horspool, N.; Hanung, R.; Rojali, A. An evaluation of onshore digital elevation models for modeling tsunami inundation zones. Front. Earth Sci. 2015, 3, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Akio, O.; Takenori, S.; Hidekatsu, Y.; Takeyoshi, N.; Shinji, S. Severe erosion of sandbar at Unosumai River mouth, Iwate, due to 2011 Tohoku tsunami. In Proceedings of the 7th International Conference on Coastal Dynamics, Arcachon, France, 24–28 June 2013.
- Mori, N.; Takahashi, T. Nationwide post event survey and analysis of the 2011 Tohoku earthquake tsunami. Coast. Eng. J. 2012, 54, 1250001. [Google Scholar] [CrossRef]
- Shuttle Radar Topography Mission1 Arc-Second Global. 2015. Available online: https://lta.cr.usgs.gov/SRTM1Arc (accessed on 07 January 2017).
- Nielsen, O.; Roberts, S.; Gray, D.; McPherson, A.; Hitchman, A. Hydrodynamic modeling of coastal inundation. In MSSANZ International Congress on Modelling and Simulation; Modelling and Simulation Society of Australia and New Zealand: Melbourne, VIC, Australia, 2005; pp. 518–523. [Google Scholar]
- Goto, C.; Ogawa, Y.; Shuto, N.; Imamura, F. IUGG/IOC Time Project: Numerical Method of Tsunami Simulation with the Leap-Frog Scheme; IOC Manuals and Guides No. 35; IOC of UNESCO Publish: Paris, France, 1997. [Google Scholar]
- Rakowsky, N.; Androsov, A.; Fuchs, A.; Harig, S.; Immerz, A.; Danilov, S. Operational tsunami modelling with TsunAWI—recent developments and applications. Nat. Hazards Earth Syst. Sci. 2013, 13, 1629–1642. [Google Scholar] [CrossRef] [Green Version]
- Grilli, S.T.; Harris, J.C.; Tajalli Bakhsh, T.S.; Masterlark, T.L. Numerical simulation of the 2011 Tohoku tsunami based on a new transient FEM co-seismic source: Comparison to far and near-field observations. Appl. Geophys. 2013, 170, 1333–1359. [Google Scholar] [CrossRef]


| Data | Date | Res.(m) | Estimation Bands | Correction Band |
|---|---|---|---|---|
| Landsat-8 | 31 October 2014 | 30 | 0.43–0.45 μm (coastal) | 1.57–1.65 μm (SWIR) |
| 30 | 0.45–0.51 μm (blue) | |||
| 30 | 0.53–0.59 μm (green) | |||
| 30 | 0.64–0.67 μm (red) | |||
| 30 | 0.85–0.88 μm (NIR) | |||
| Sentinel-2 | 25 December 2015 | 10 | 0.44–0.53 μm (blue) | 1.53–1.68 μm (SWIR) |
| 10 | 0.53–0.58 μm (green) | |||
| 10 | 0.64–0.68 μm (red) | |||
| 20 | 0.69–0.71 μm (Red-edge) | |||
| 20 | 0.73–0.74 μm (Red-edge) | |||
| 10 | 0.76–0.90 μm (NIR) | |||
| ASTER | 10 September 2010 | 15 | 0.52–0.60 μm (green) | 0.76–0.86 μm (NIR) |
| 15 | 0.63–0.69 μm (red) |
| Case Studies | Global Model | GWR Model | ||||
|---|---|---|---|---|---|---|
| R | R2 | RMSE (m) | R | R2 | RMSE (m) | |
| Puerto Rico | 0.86 | 0.74 | 2.53 | 0.99 | 0.98 | 0.61 |
| Iwate | 0.80 | 0.65 | 3.59 | 0.97 | 0.94 | 1.50 |
| Miyagi | 0.78 | 0.61 | 3.18 | 0.93 | 0.87 | 1.65 |
| Area | Data | Kernel | GWR Model | Time (m) | SDB Results | ||
|---|---|---|---|---|---|---|---|
| R | R2 | RMSE (m) | |||||
| Puerto Rico | Sentinel-2 | Gaussian | Fixed-GWR | 2.22 | 0.99 | 0.98 | 0.67 |
| A-GWR | 180.00 | 0.99 | 0.98 | 0.62 | |||
| Bi-square | Fixed-GWR | 2.24 | 0.99 | 0.98 | 0.64 | ||
| A-GWR | 184.00 | 0.99 | 0.98 | 0.61 | |||
| Iwate | Landsat-8 | Gaussian | Fixed-GWR | 2.50 | 0.86 | 0.74 | 2.91 |
| A-GWR | 6.00 | 0.96 | 0.93 | 1.54 | |||
| Bi-square | Fixed-GWR | 2.50 | 0.88 | 0.77 | 2.77 | ||
| A-GWR | 5.55 | 0.97 | 0.94 | 1.50 | |||
| Miyagi | ASTER | Gaussian | Fixed-GWR | 3.02 | 0.91 | 0.83 | 1.93 |
| A-GWR | 265.00 | 0.89 | 0.80 | 2.20 | |||
| Bi-square | Fixed-GWR | 3.08 | 0.93 | 0.87 | 1.65 | ||
| A-GWR | 255.00 | 0.91 | 0.84 | 1.95 | |||
| Case Studies | Reference Depth | GWR Model | ||||||
|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | STD | Min | Max | Mean | STD | |
| Puerto Rico | 0.80 | 20.20 | 10.89 | 4.89 | 0.82 | 20.10 | 10.83 | 4.94 |
| Iwate | 0.48 | 26.51 | 11.95 | 5.89 | 0.53 | 26.29 | 11.99 | 6.00 |
| Miyagi | 2.00 | 19.00 | 11.95 | 4.90 | 1.51 | 17.41 | 12.10 | 3.45 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poliyapram, V.; Raghavan, V.; Metz, M.; Delucchi, L.; Masumoto, S. Implementation of Algorithm for Satellite-Derived Bathymetry using Open Source GIS and Evaluation for Tsunami Simulation. ISPRS Int. J. Geo-Inf. 2017, 6, 89. https://doi.org/10.3390/ijgi6030089
Poliyapram V, Raghavan V, Metz M, Delucchi L, Masumoto S. Implementation of Algorithm for Satellite-Derived Bathymetry using Open Source GIS and Evaluation for Tsunami Simulation. ISPRS International Journal of Geo-Information. 2017; 6(3):89. https://doi.org/10.3390/ijgi6030089
Chicago/Turabian StylePoliyapram, Vinayaraj, Venkatesh Raghavan, Markus Metz, Luca Delucchi, and Shinji Masumoto. 2017. "Implementation of Algorithm for Satellite-Derived Bathymetry using Open Source GIS and Evaluation for Tsunami Simulation" ISPRS International Journal of Geo-Information 6, no. 3: 89. https://doi.org/10.3390/ijgi6030089
APA StylePoliyapram, V., Raghavan, V., Metz, M., Delucchi, L., & Masumoto, S. (2017). Implementation of Algorithm for Satellite-Derived Bathymetry using Open Source GIS and Evaluation for Tsunami Simulation. ISPRS International Journal of Geo-Information, 6(3), 89. https://doi.org/10.3390/ijgi6030089





