Extraction of Road Intersections from GPS Traces Based on the Dominant Orientations of Roads
Abstract
1. Introduction
2. Related Work
3. Proposed Method
3.1. Road Skeleton Extraction
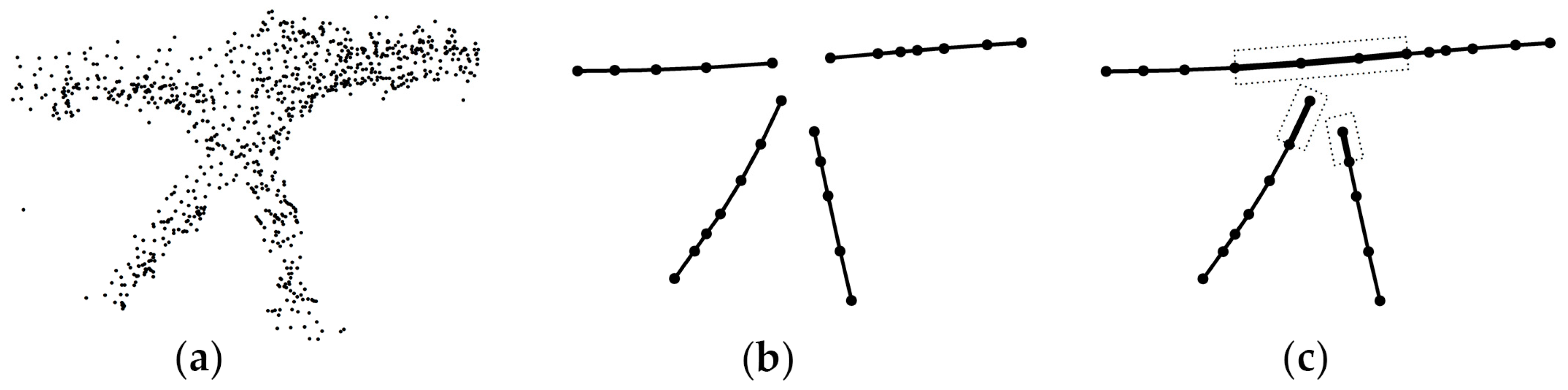
3.1.1. Simplification of Scattered Points
3.1.2. Road Skeleton Segmentation
3.2. Orientation-Based Extraction of Intersections
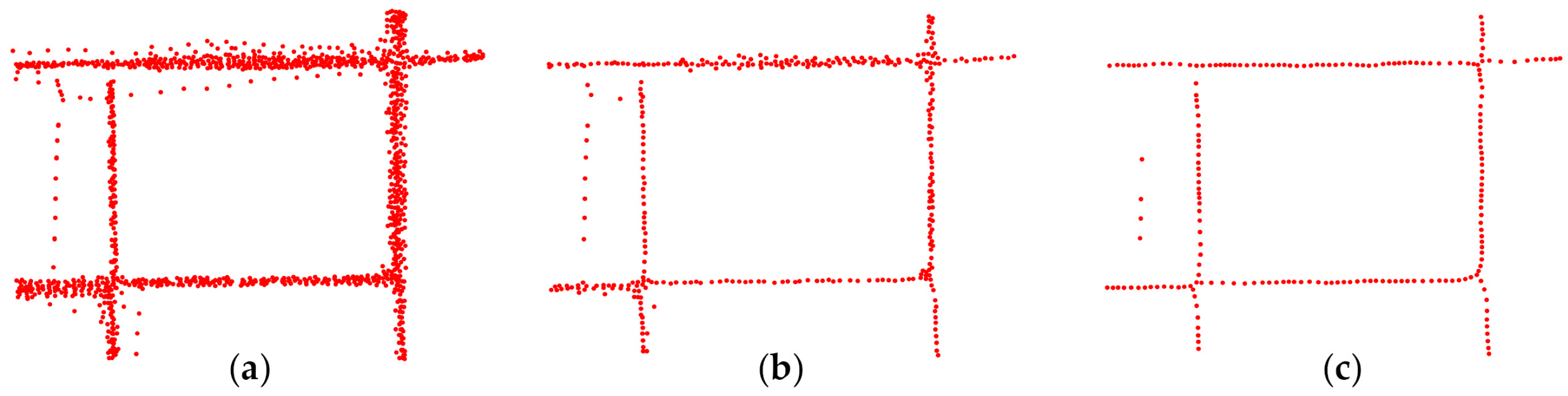
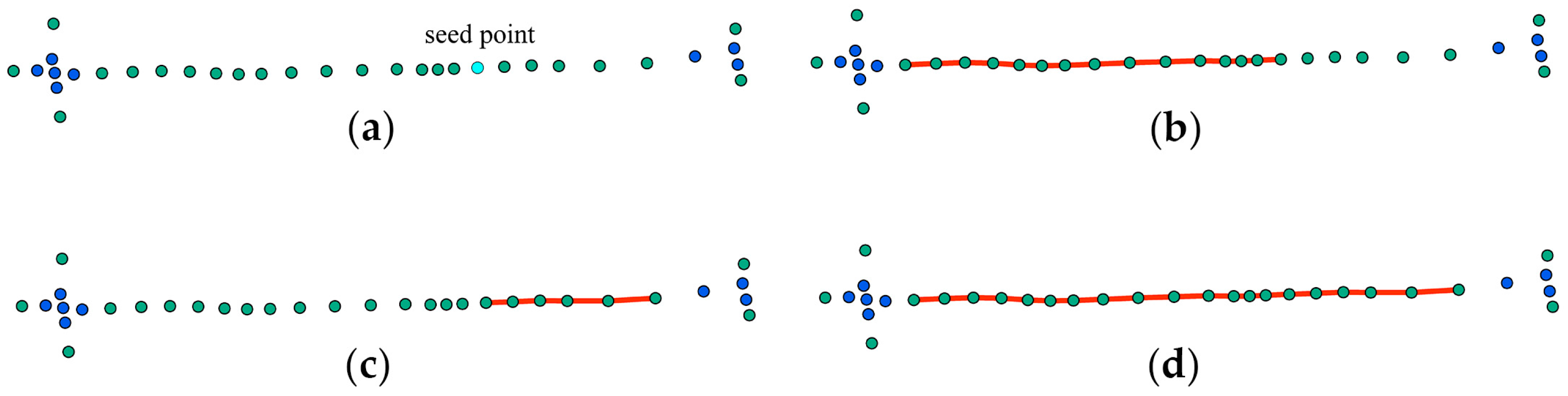
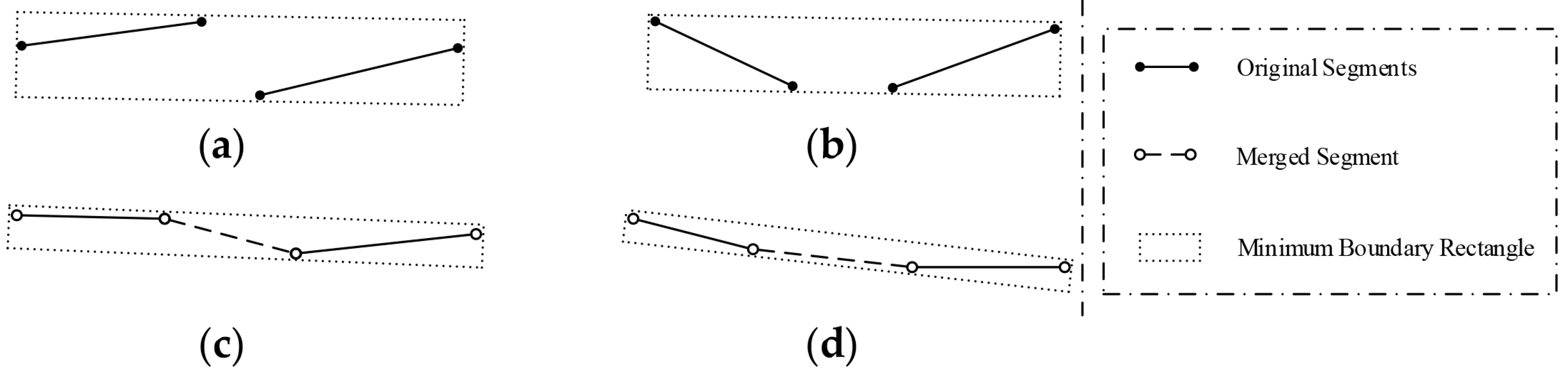
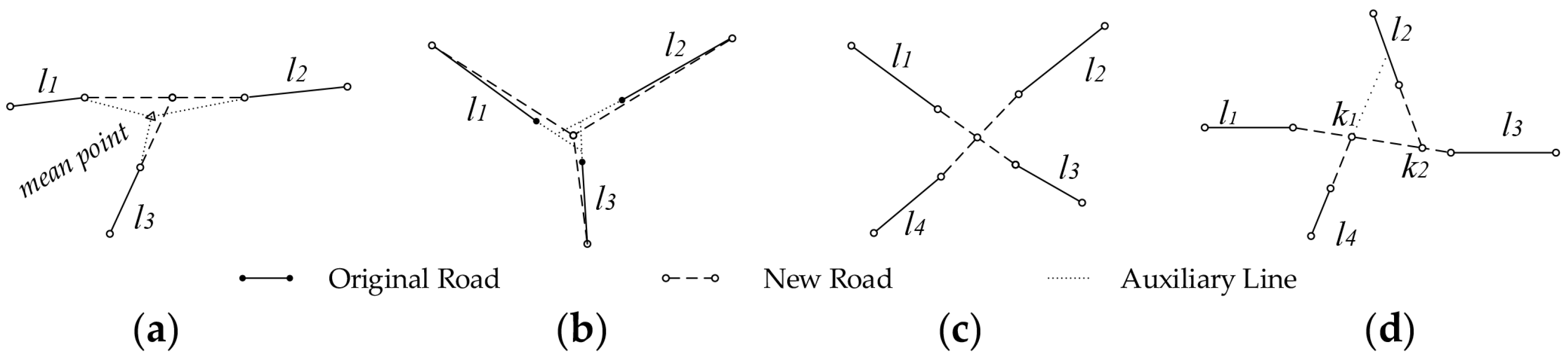
3.2.1. Identification of Collinear Segments
3.2.2. Detecting the Locations of Intersections
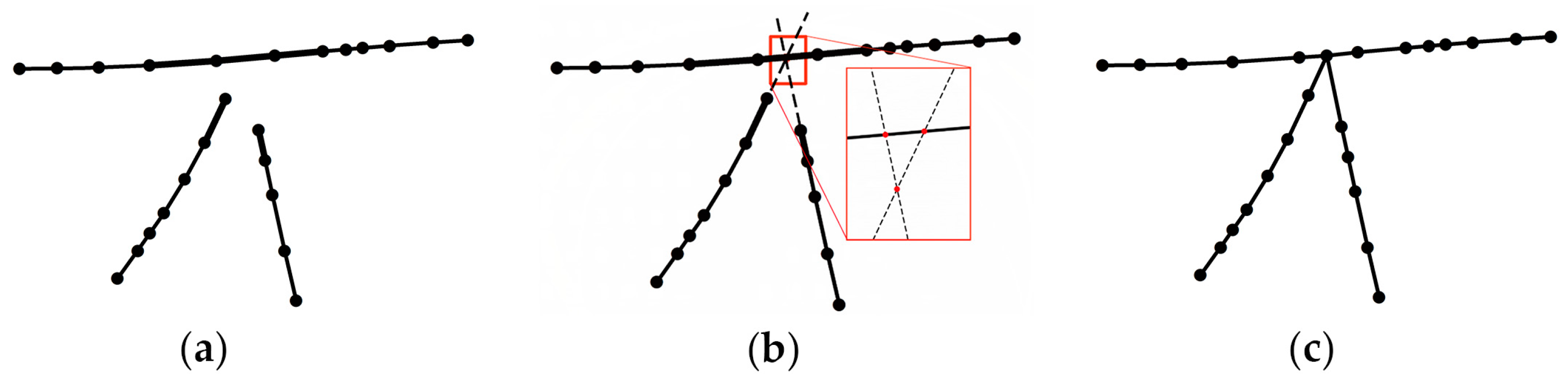
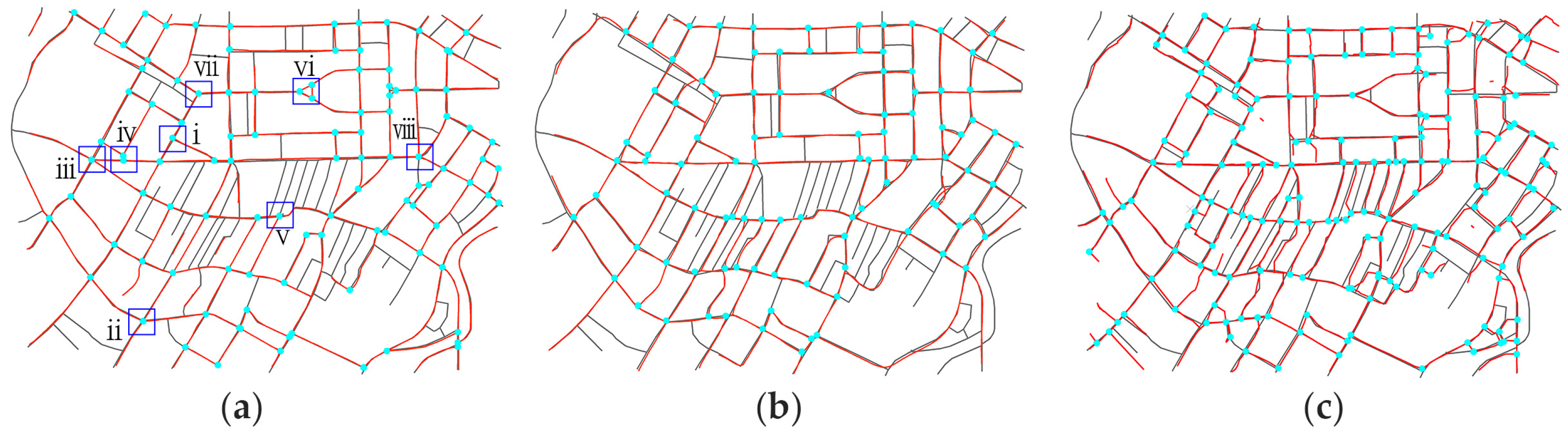
- In the first case, all the segments intersect at one point exactly, as illustrated in Figure 7a,c.
- In the second case, the segments intersect at multiple sub-intersections and the sub-intersections are all near the road intersection position, as illustrated in Figure 7b.
- In the third case, the segments intersect at multiple sub-intersections but some of the sub-intersections are not near the road intersection (i.e., outliers and noise), as illustrated in Figure 7d.
- For the first situation, which is illustrated in Figure 7a,c, the location of the road intersection is the intersection point of the road segments (i.e., the crossroad, T-intersection and turn).
- For the second situation, which is illustrated in Figure 7b, the location of the road intersection is the centroid of the multiple sub-intersections of all road segments.
- For the third situation, which is illustrated in Figure 7d, before merging the sub-intersections, outliers and noise must be removed (Section 3.1.2 states that a road segment cannot cross through the intersection area where feature points have a smaller linearity value; thus, the sub-intersection defined by the intersection of road segment and the dashed line in Figure 6d is discarded). Hierarchical clustering [39] is then performed to calculate the remaining intersections (sets of data are grouped by maximizing the similarity among similar clusters and minimizing the similarity between different clusters), and the centroids of the clusters are then used as the intersections. As illustrated in Figure 7d, the remaining two sub-intersections, and , are autonomous fragmented parts that preserve an irregular intersection because they are divided into two clusters.
4. Experiments and Discussion
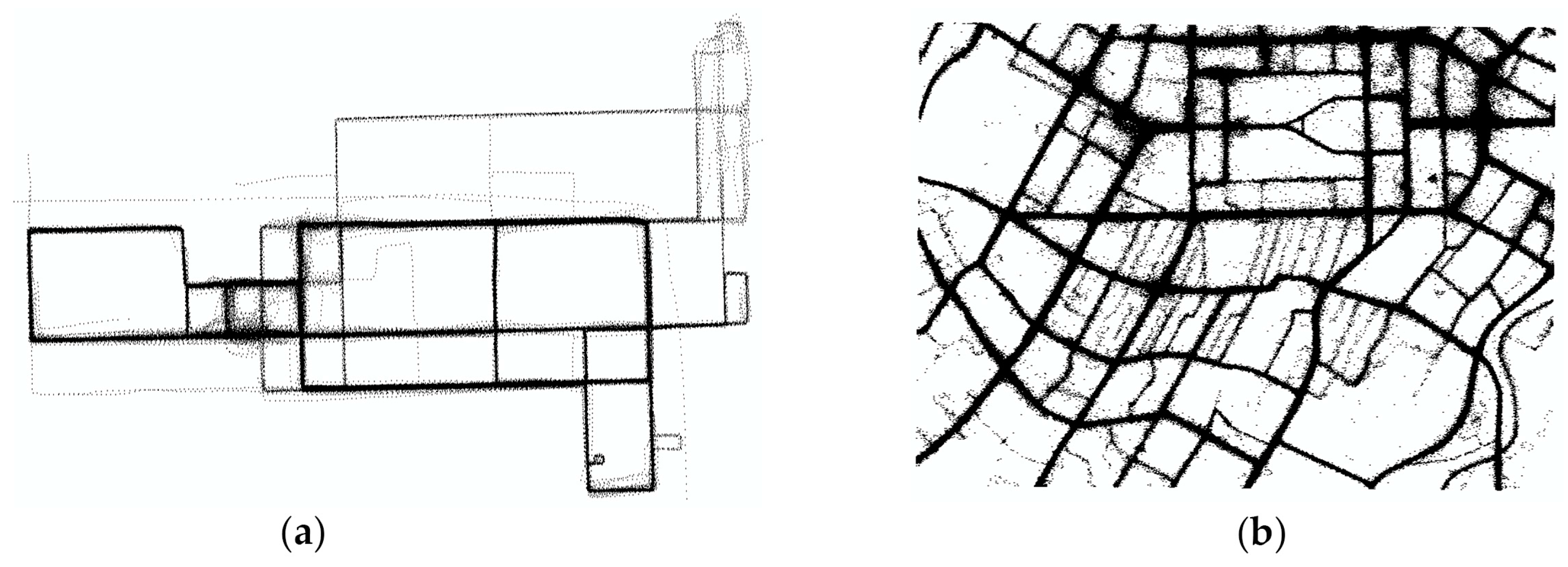
4.1. Datasets
4.2. Evaluation Method
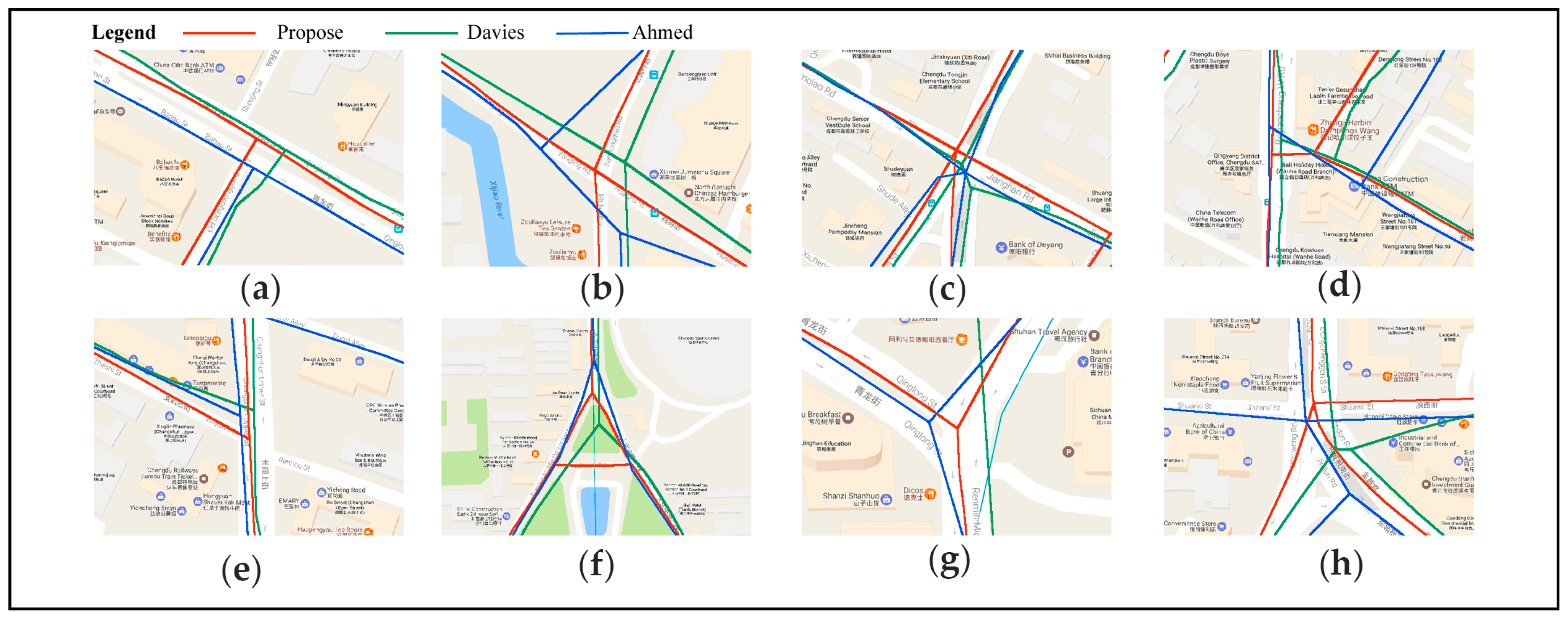
4.3. Comparison and Discussion
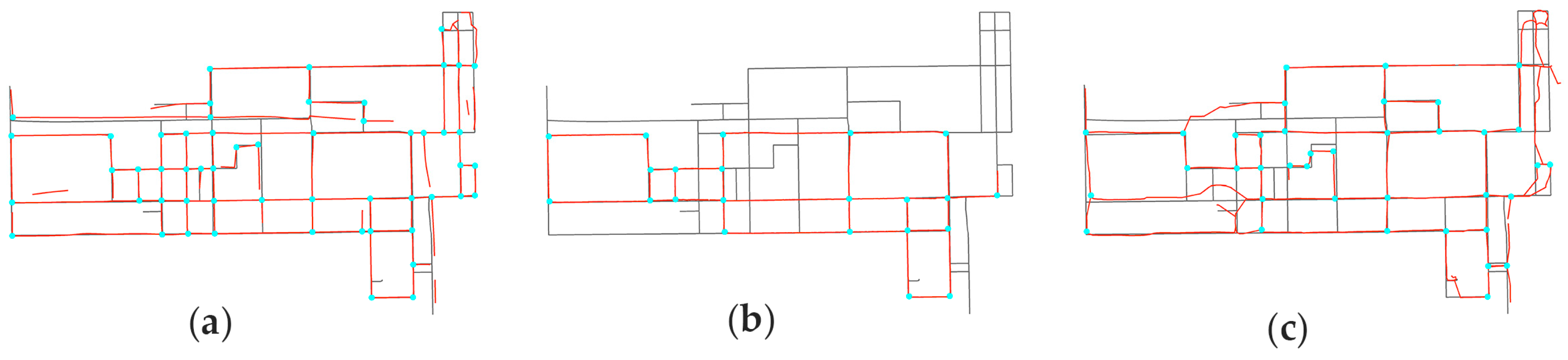
4.3.1. Visual Inspection
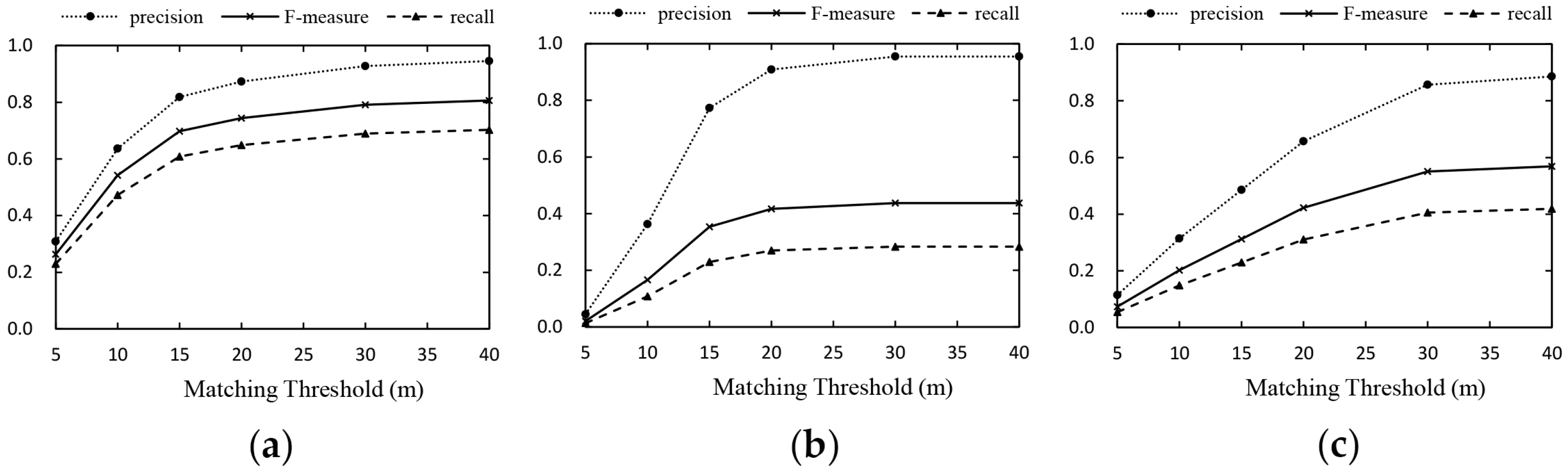
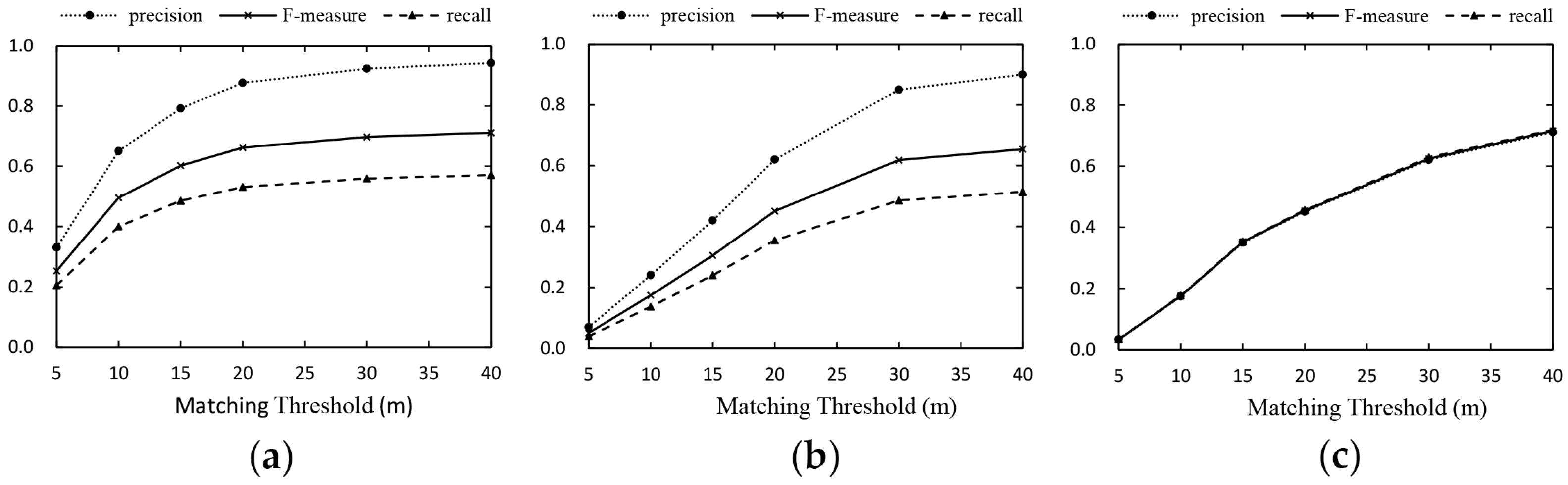
4.3.2. Accuracy Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Guo, T.; Iwamura, K.; Koga, M. Towards high accuracy road maps generation from massive GPS traces data. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 667–670. [Google Scholar]
- Wang, Y.; Liu, X.; Wei, H.; Forman, G.; Chen, C.; Zhu, Y. Crowdatlas: Self-updating maps for cloud and personal use. In Proceedings of the International Conference on Mobile Systems, Applications, and Services, Taipei, Taiwan, 25–28 June 2013; pp. 27–40. [Google Scholar]
- Matisziw, T.; Demir, E. Inferring network paths from point observations. Int. J. Geogr. Inf. Sci. 2012, 26, 1–18. [Google Scholar] [CrossRef]
- Li, L.; Xing, X.; Xia, H.; Huang, X. Entropy-weighted instance matching between different sourcing points of interest. Entropy 2016, 18, 45. [Google Scholar] [CrossRef]
- Tong, X.; Liang, D.; Xu, G.; Zhang, S. Positional accuracy improvement: A comparative study in shanghai, china. Int. J. Geogr. Inf. Sci. 2011, 25, 1147–1171. [Google Scholar] [CrossRef]
- Nagai, Y.; Itoh, M.; Inagaki, T. Adaptive driving support via monitoring of driver behavior and traffic conditions. Trans. Soc. Automot. Eng. Jpn. 2008, 39, 393–398. [Google Scholar]
- Ahmed, M.; Karagiorgou, S.; Pfoser, D.; Wenk, C. A comparison and evaluation of map construction algorithms using vehicle tracking data. Geoinformatica 2014, 19, 601–632. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, Y.; Lu, F. Geometric-based approach for integrating VGI POIs and road networks. Int. J. Geogr. Inf. Sci. 2014, 28, 126–147. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, L.; Xie, X.; Ma, W.Y. Mining interesting locations and travel sequences from GPS trajectories. In Proceedings of the International Conference on World Wide Web, Madrid, Spain, 20–24 April 2009; pp. 791–800. [Google Scholar]
- You, Q.; Krumm, J. Transit Tomography Using Probabilistic Time Geography: Planning Routes without a Road Map. J. Locat. Based Serv. 2014, 12, 211–228. [Google Scholar] [CrossRef]
- Herrera, J.C.; Work, D.B.; Herring, R.; Ban, X.; Jacobson, Q.; Bayen, A.M. Evaluation of traffic data obtained via GPS-enabled mobile phones: The mobile century field experiment. Transp. Res. Part C Emerg. Technol. 2010, 18, 568–583. [Google Scholar] [CrossRef]
- Das, S.; Mirnalinee, T.T.; Varghese, K. Use of salient features for the design of a multistage framework to extract roads from high-resolution multispectral satellite images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3906–3931. [Google Scholar] [CrossRef]
- Unsalan, C.; Sirmacek, B. Road network detection using probabilistic and graph theoretical methods. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4441–4453. [Google Scholar] [CrossRef]
- Boichis, N.; Viglino, J.M.; Cocquerez, J.P. Knowledge based system for the automatic extraction of road intersections from aerial images. Int. Arch. Photogramm. Remote Sens. 2000, XXXIII, 27–34. [Google Scholar]
- Hu, J.; Razdan, A.; Femiani, J.C.; Cui, M.; Wonka, P. Road network extraction and intersection detection from aerial images by tracking road footprints. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4144–4157. [Google Scholar] [CrossRef]
- Efentakis, A.; Brakatsoulas, S.; Grivas, N.; Lamprianidis, G.; Patroumpas, K.; Pfoser, D. Towards a flexible and scalable fleet management service. In Proceedings of the Sixth ACM SIGSPATIAL International Workshop on Computational Transportation Science, Orlando, FL, USA, 5–8 November 2013; pp. 79–84. [Google Scholar]
- Fathi, A.; Krumm, J. Detecting road intersections from GPS traces. In Geographic Information Science: 6th International Conference, Giscience 2010, Zurich, Switzerland, September 14–17, 2010, Proceedings; Fabrikant, S.I., Reichenbacher, T., van Kreveld, M., Schlieder, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 56–69. [Google Scholar]
- Ahmed, M.; Wenk, C. Constructing street networks from GPS trajectories. In Proceedings of the European Conference on Algorithms, Ljubljana, Slovenia, 10–12 September 2012; pp. 60–71. [Google Scholar]
- Wu, J.; Zhu, Y.; Tao, K.; Wang, L. Detecting road intersections from coarse-gained GPS traces based on clustering. J. Comput. 2013, 8, 2959–2965. [Google Scholar] [CrossRef]
- Xie, X.; Bingyungwong, K.; Aghajan, H.; Veelaert, P.; Philips, W. Inferring directed road networks from GPS traces by track alignment. ISPRS Int. J. Geo-Inf. 2015, 4, 2446–2471. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.; Song, X.; Raghavan, V. Automatic intersection and traffic rule detection by mining motor-vehicle GPS trajectories. Comput. Environ. Urban Syst. 2017, 64, 19–29. [Google Scholar] [CrossRef]
- Davies, J.J.; Beresford, A.R.; Hopper, A. Scalable, distributed, real-time map generation. Pervasive Comput. IEEE 2006, 5, 47–54. [Google Scholar] [CrossRef]
- Xie, X.; Liao, W.; Aghajan, H.; Veelaert, P.; Philips, W. Detecting road intersections from GPS traces using longest common subsequence algorithm. ISPRS Int. J. Geo-Inf. 2017, 6, 1. [Google Scholar] [CrossRef]
- Tang, L.; Ren, C.; Liu, Z.; Li, Q. A road map refinement method using delaunay triangulation for big trace data. ISPRS Int. J. Geo-Inf. 2017, 6, 45. [Google Scholar] [CrossRef]
- Chiang, Y.Y.; Knoblock, C.A. Automatic extraction of road intersection position, connectivity, and orientations from raster maps. In Proceedings of the ACM Sigspatial International Symposium on Advances in Geographic Information Systems, ACM-GIS 2008, Irvine, CA, USA, 5–7 November 2008; p. 22. [Google Scholar]
- Shi, J.; Malik, J. Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 22, 888–905. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Xu, X. A density-based algorithm for discovering clusters a density-based algorithm for discovering clusters in large spatial databases with nois. In Proceedings of the International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Cheng, Y. Mean shift, mode seeking, and clustering. IEEE Trans. Pattern Anal. Mach. Intell. 1995, 17, 790–799. [Google Scholar] [CrossRef]
- Qiu, J.; Wang, R. Automatic extraction of road networks from GPS traces. Photogramm. Eng. Remote Sens. 2016, 82, 593–604. [Google Scholar] [CrossRef]
- Wang, J.; Yu, Z.; Zhang, W.; Wei, M.; Tan, C.; Dai, N.; Zhang, X. Robust reconstruction of 2d curves from scattered noisy point data. Comput.-Aided Des. 2014, 50, 27–40. [Google Scholar] [CrossRef]
- Funke, S.; Ramos, E.A. Reconstructing a collection of curves with corners and endpoints. In Proceedings of the Twelfth Acm-Siam Symposium on Discrete Algorithms, Washington, DC, USA, 7–9 January 2001; pp. 344–353. [Google Scholar]
- Koutaki, G.; Uchimura, K.; Hu, Z. Road Updating from High Resolution Aerial Imagery Using Road Intersection Model. Available online: http://www.isprs.org/proceedings/xxxvi/5-w1/papers/25.pdf (accessed on 9 December 2017).
- Zourlidou, S.; Sester, M. Intersection detection based on qualitative spatial reasoning on stopping point clusters. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B2, 269–276. [Google Scholar]
- Luan, X.; Fan, H.; Yang, B.; Li, Q. Arterial roads extraction in urban road networksbased on shape analysis. Geomat. Inf. Sci. Wuhan Univ. 2014, 39, 327–331. [Google Scholar]
- Regnauld, N. Généralisation du Bâti: Structure Spatiale de Type Graphe et Représentation Cartographique. Ph.D. Thesis, Provence University, Marseille, France, 1998. [Google Scholar]
- Campbell, J. Map Use and Analysis, 4th ed.; McGraw Hill: Boston, MA, USA, 2001; ISBN 0-073-03748-6. [Google Scholar]
- Touya, G. A road network selection process based on data enrichment and structure detection. Trans. GIS 2010, 14, 595–614. [Google Scholar] [CrossRef]
- Karypis, G.; Han, E.H.; Kumar, V. Chameleon: Hierarchical clustering using dynamic modeling. Computer 2002, 32, 68–75. [Google Scholar] [CrossRef]
- Biagioni, J.; Eriksson, J. Map inference in the face of noise and disparity. In Proceedings of the 20th International Conference on Advances in Geographic Information Systems, Redondo Beach, CA, USA, 6–9 November 2012; pp. 79–88. [Google Scholar]
- Biagioni, J.; Eriksson, J. Inferring road maps from global positioning system traces. Transp. Res. Rec. J. Transp. Res. Board 2012, 2291, 61–71. [Google Scholar] [CrossRef]
- OpenStreetMap. Available online: Http://www.openstreetmap.org/ (accessed on 11 May 2017).


| Area | Method | Extracted/Truth 1 | Number of Matched Intersections with the Threshold Distance (m) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 30 | 40 | 50 | |||
| Chicago | Proposed | 55/74 | 17 | 35 | 45 | 48 | 51 | 52 | 52 |
| Davies | 28/74 | 1 | 8 | 17 | 20 | 21 | 21 | 21 | |
| Ahmed | 38/74 | 4 | 11 | 17 | 23 | 30 | 31 | 31 | |
| Chengdu | Proposed | 106/175 | 35 | 69 | 84 | 93 | 98 | 100 | 102 |
| Davies | 100/175 | 7 | 24 | 42 | 62 | 85 | 90 | 92 | |
| Ahmed | 177/175 | 6 | 31 | 62 | 80 | 110 | 126 | 138 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Li, D.; Xing, X.; Yang, F.; Rong, W.; Zhu, H. Extraction of Road Intersections from GPS Traces Based on the Dominant Orientations of Roads. ISPRS Int. J. Geo-Inf. 2017, 6, 403. https://doi.org/10.3390/ijgi6120403
Li L, Li D, Xing X, Yang F, Rong W, Zhu H. Extraction of Road Intersections from GPS Traces Based on the Dominant Orientations of Roads. ISPRS International Journal of Geo-Information. 2017; 6(12):403. https://doi.org/10.3390/ijgi6120403
Chicago/Turabian StyleLi, Lin, Daigang Li, Xiaoyu Xing, Fan Yang, Wei Rong, and Haihong Zhu. 2017. "Extraction of Road Intersections from GPS Traces Based on the Dominant Orientations of Roads" ISPRS International Journal of Geo-Information 6, no. 12: 403. https://doi.org/10.3390/ijgi6120403
APA StyleLi, L., Li, D., Xing, X., Yang, F., Rong, W., & Zhu, H. (2017). Extraction of Road Intersections from GPS Traces Based on the Dominant Orientations of Roads. ISPRS International Journal of Geo-Information, 6(12), 403. https://doi.org/10.3390/ijgi6120403






