Belgium through the Lens of Rail Travel Requests: Does Geography Still Matter?
Abstract
:1. Introduction
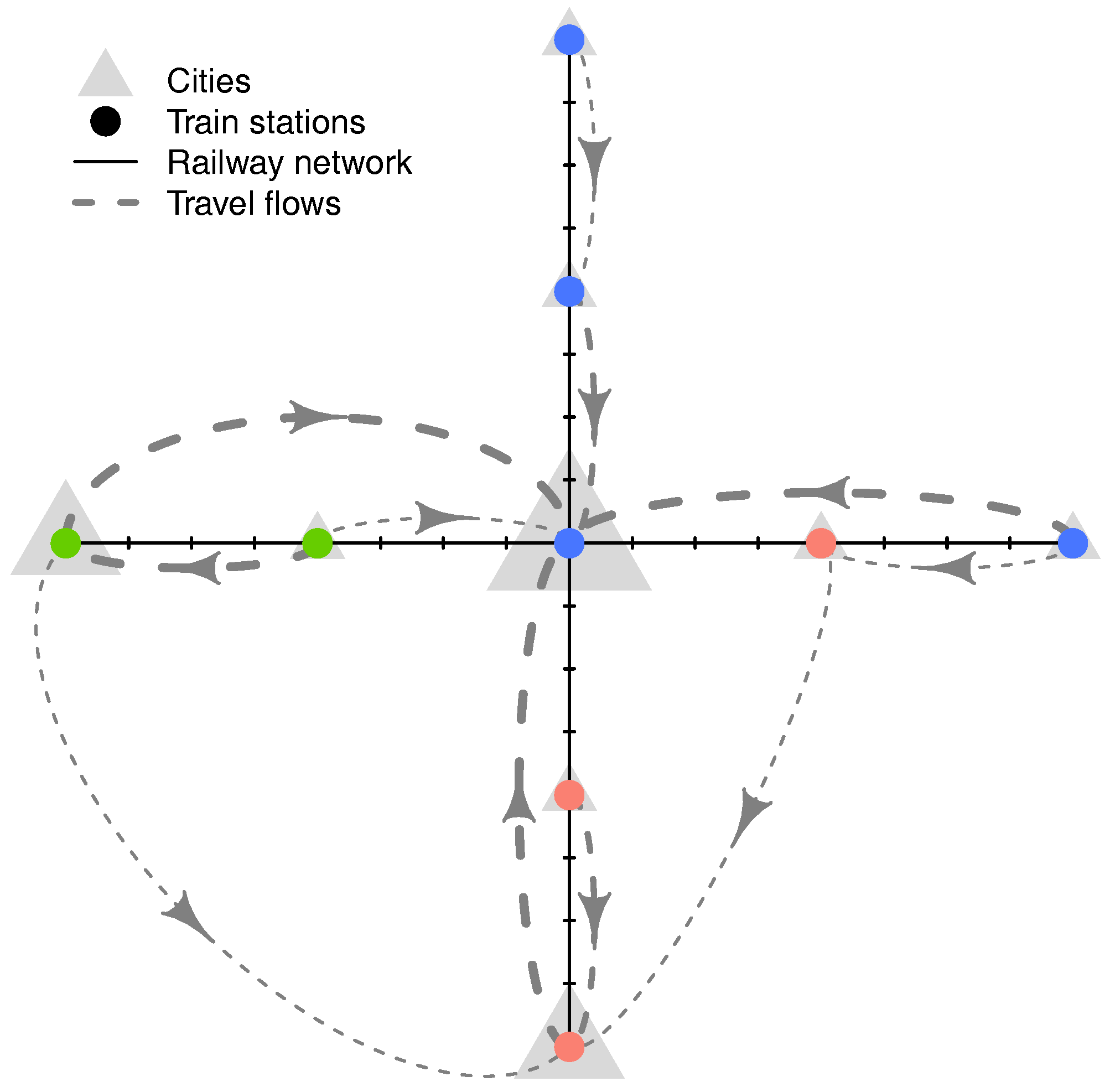
2. Travel Requests versus Travel Flows
3. Data and Methodology
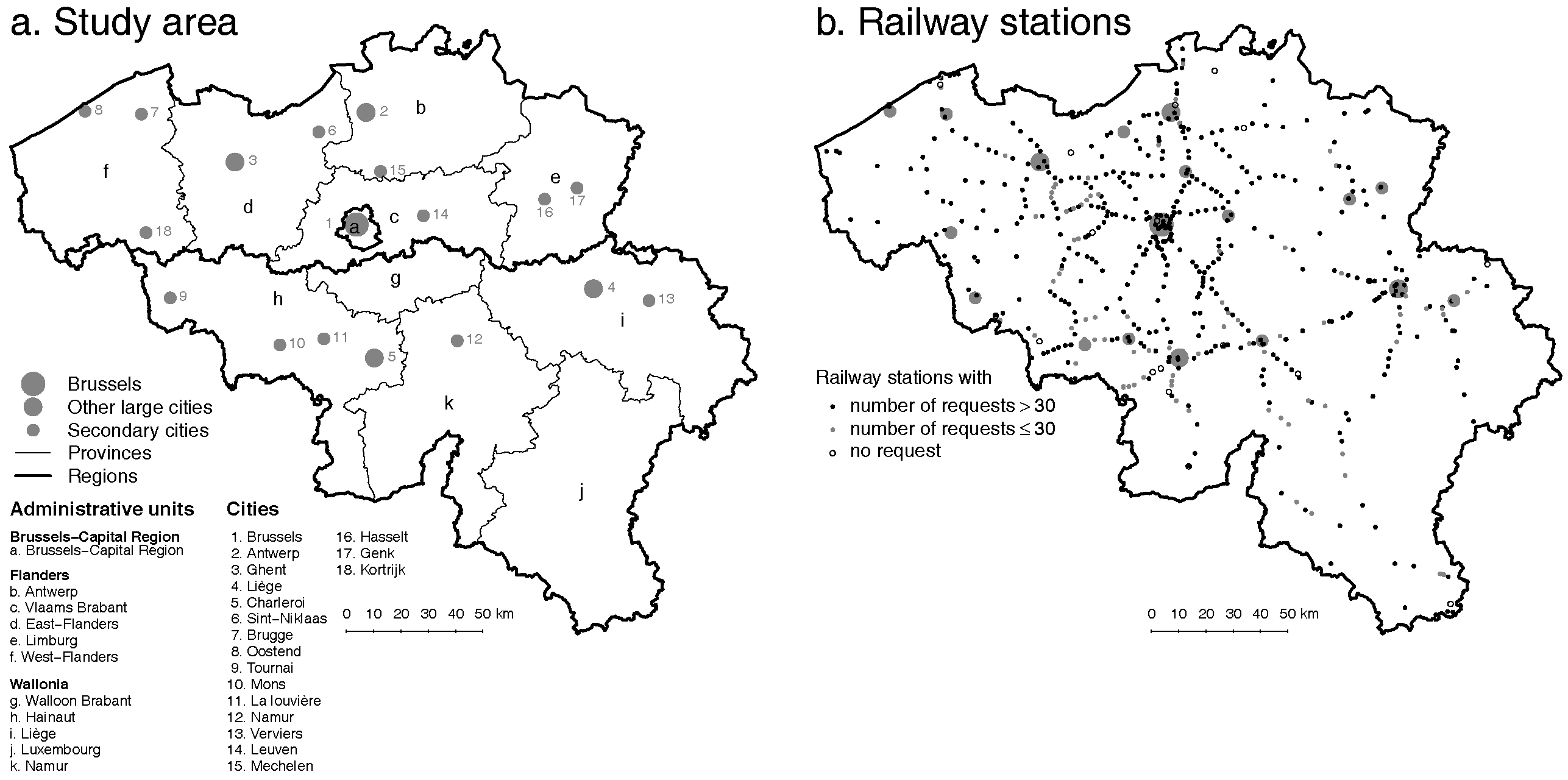
3.1. Urban and Railway Structures of Belgium
3.2. The iRail Dataset
3.2.1. Data Collection
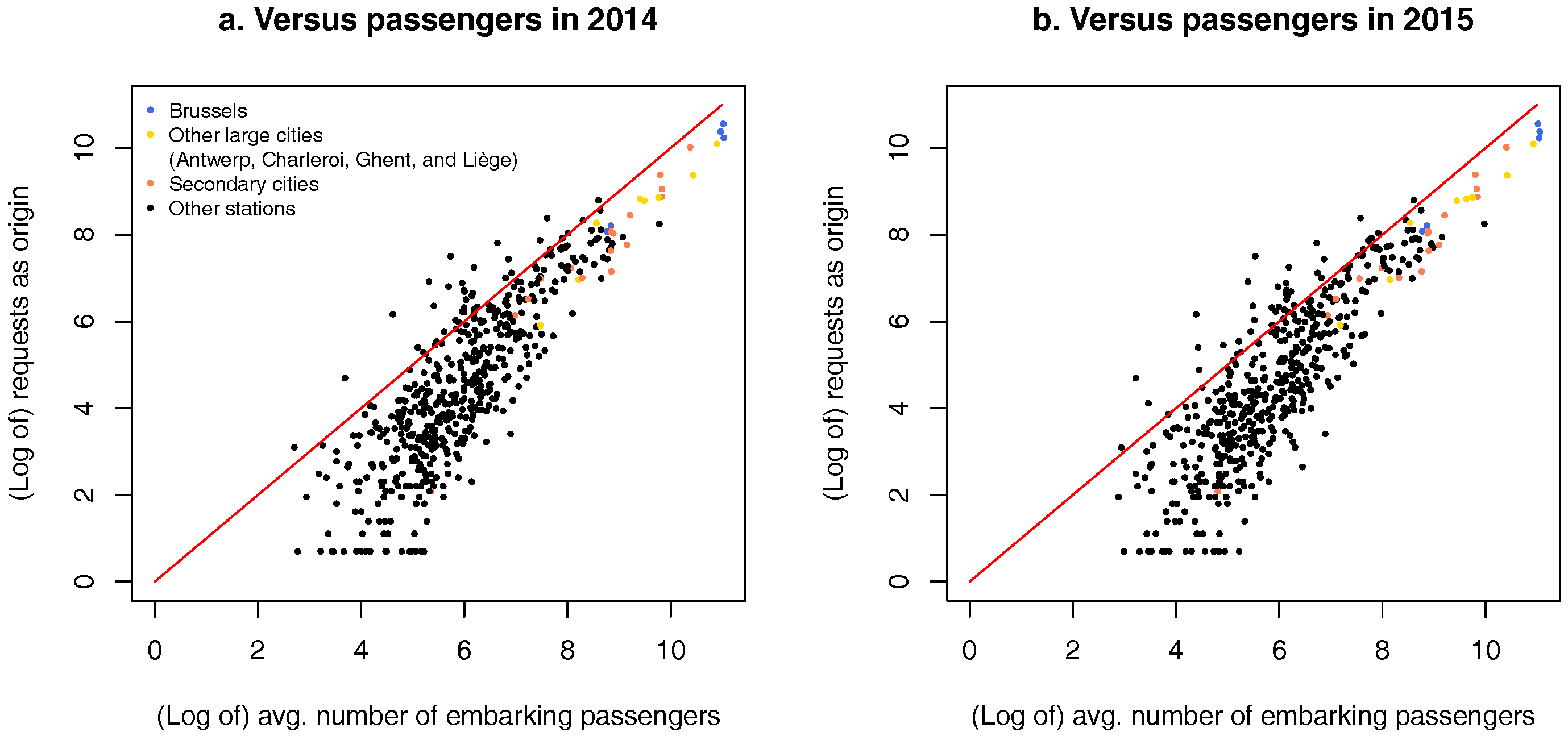
3.2.2. Calibration
3.3. Methodology
3.3.1. Subsets of the Case Study
3.3.2. Community Detection
3.3.3. Attributes of the Communities
4. Results
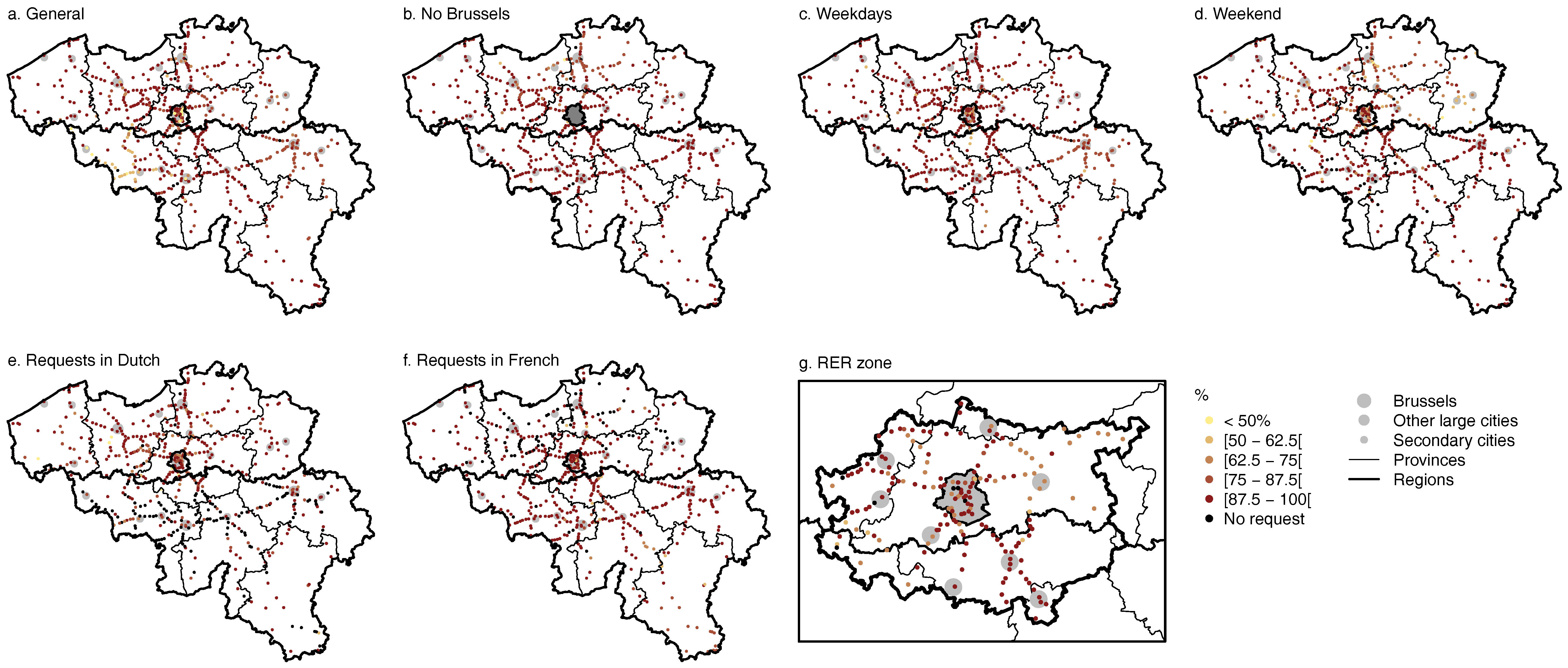
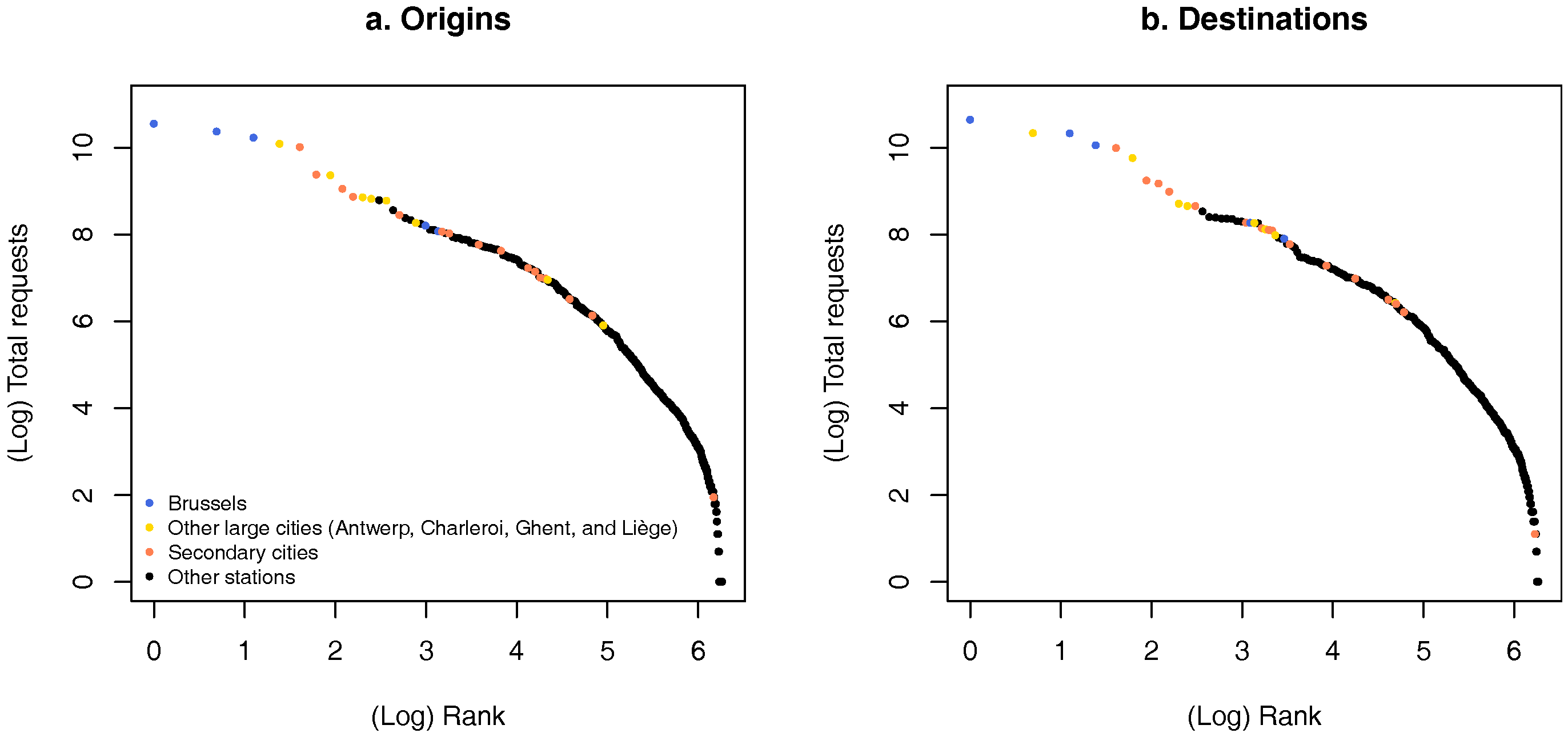
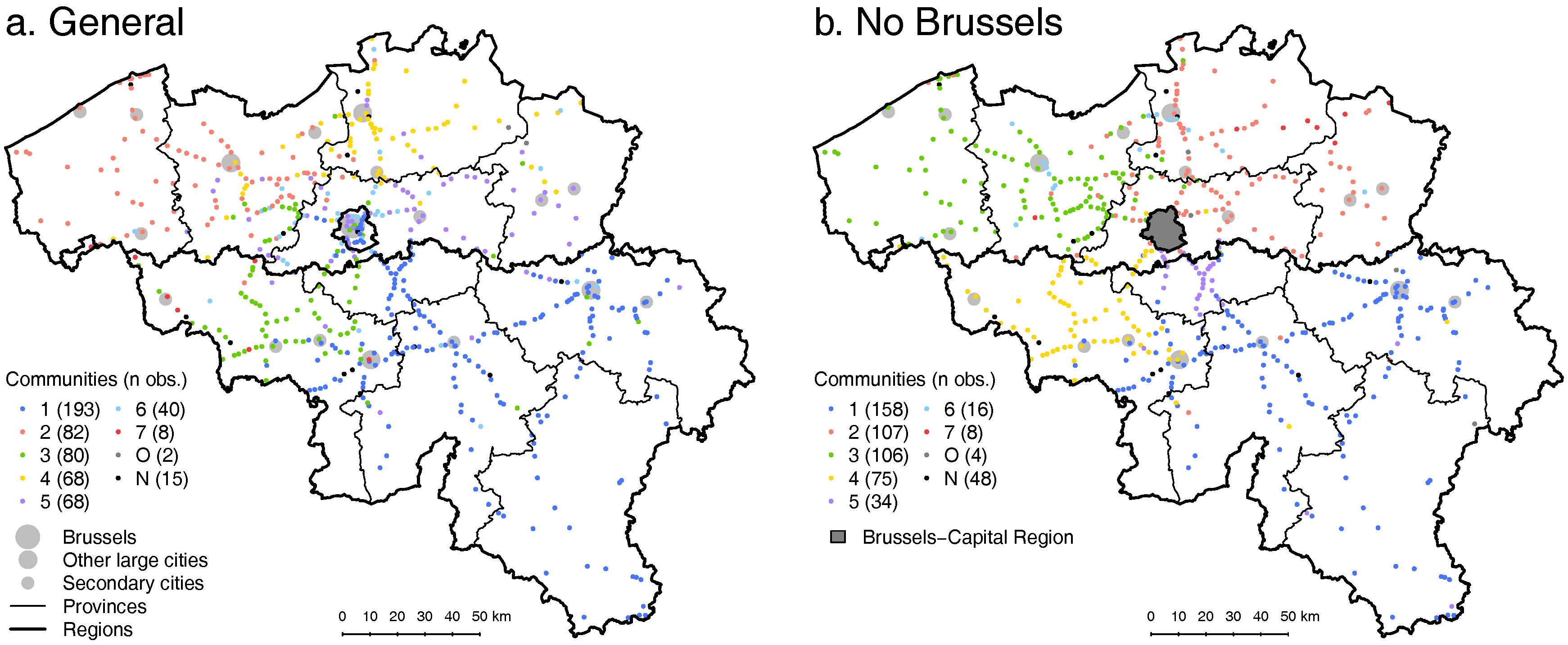
4.1. All Requests
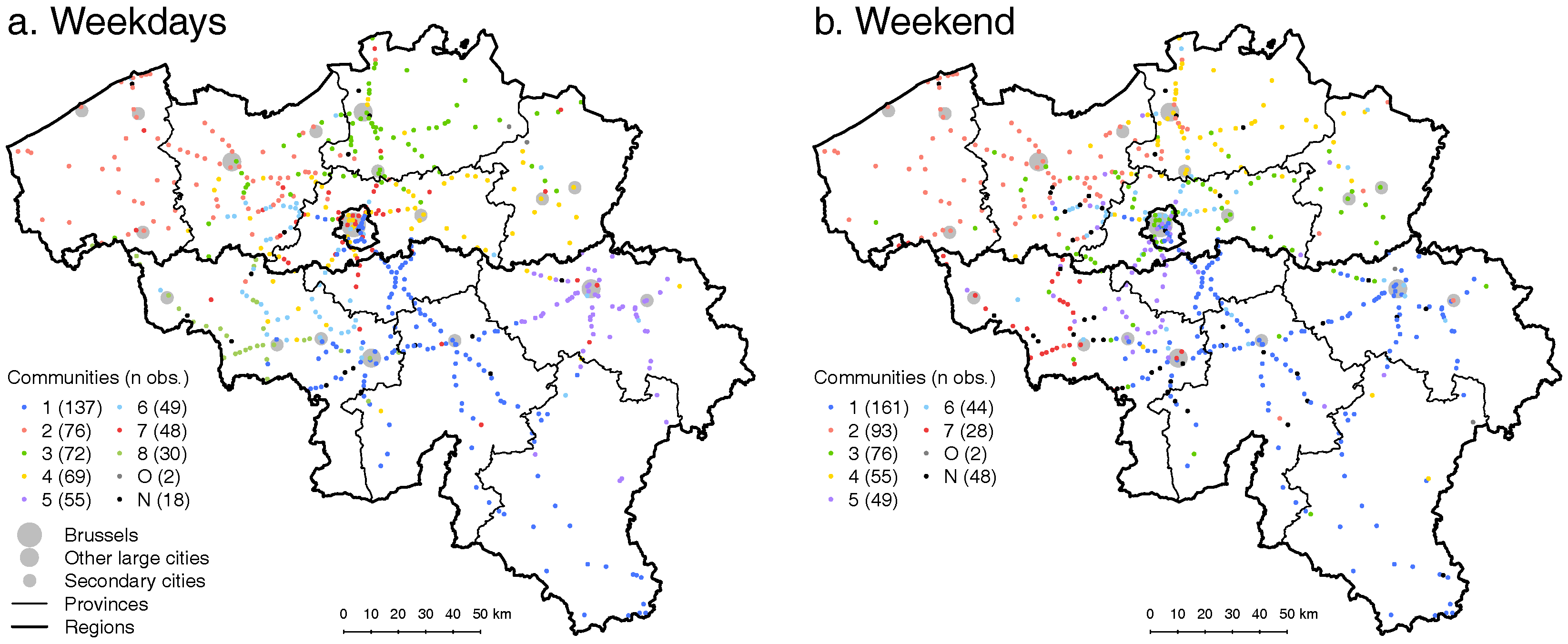
4.2. Temporal Variations
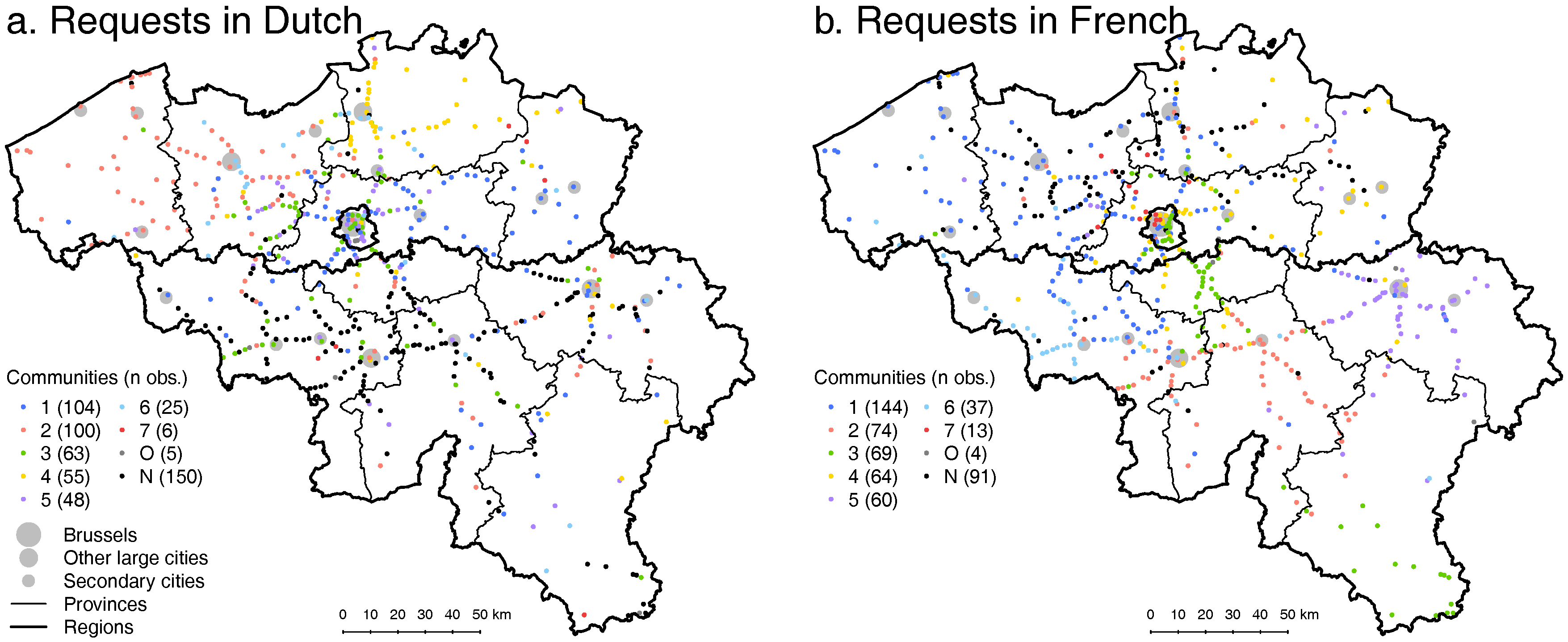
4.3. Linguistic Variations
4.4. Regional Variations: The RER Zone
5. Discussion
5.1. Urban- or Network-Oriented Communities?
5.2. Implications for Policy Decisions
5.3. Challenges and Paths for Future Research
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BCR | Brussels-Capital Region |
| ICT | Information and communication technologies |
| RER | Réseau Express Régional |
| SNCB | Belgian National Railway Company |
Appendix A
| Subsets | By Communities | Global Network | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| General | Namur | Ghent | Brussels | Antwerp | Brussels | Brussels | Tournai | Brussels | |
| (Namur) | (Gent-Sint-Pieters) | (Bruxelles-Midi) | (Antwerpen-Centraal) | (Bruxelles-Central) | (Bruxelles-Nord) | (Tournai) | (Bruxelles-Central) | ||
| No Brussels | Namur | Ghent | Antwerp | Mons | Ottignies | Antwerp | Mol | Antwerp | |
| (Namur) | (Gent-St-Pieters) | (Antwerpen-Centraal) | (Mons) | (Ottignies) | (Antwerpen-Berchem) | (Mol) | (Antwerpen-Centraal) | ||
| Weekdays | Namur | Ghent | Antwerp | Brussels | Liège | Brussels | Brussels | Mons | Brussels |
| (Namur) | (Gent-St-Pieters) | (Antwerpen-Centraal) | (Bruxelles-Central) | (Liège-Guillemins) | (Bruxelles-Midi) | (Bruxelles-Nord) | (Mons) | (Bruxelles-Central) | |
| Weekend | Namur | Ghent | Brussels | Antwerp | Brussels | Brussels | Mons | Brussels | |
| (Namur) | (Gent-St-Pieters) | (Bruxelles-Central) | (Antwerpen-Centraal) | (Bruxelles-Midi) | (Bruxelles-Nord) | (Mons) | (Bruxelles-Central) | ||
| Dutch | Leuven | Ghent | Brussels | Antwerp | Brussels | Antwerp | Zonhoven | Ghent | |
| (Leuven) | (Gent-St-Pieters) | (Bruxelles-Midi) | (Antwerpen-Centraal) | (Bruxelles-Nord) | (Antwerpen-Berchem) | (Zonhoven) | (Gent-StPieters) | ||
| French | Brussels | Namur | Ottignies | Brussels | Liège | Mons | Brussels | Brussels | |
| (Bruxelles-Midi) | (Namur) | (Ottignies) | (Bruxelles-Nord) | (Liège-Guillemins) | (Mons) | (Simonis) | (Bruxelles-Midi) | ||
| RER | Ottignies | Brussels | Brussels | Brussels | Brussels | Brussels | |||
| (Ottignies) | (Bruxelles-Nord) | (Bruxelles-Midi) | (Bruxelles-Central) | (Jette) | (Bruxelles-Central) | ||||
References
- Klapka, P.; Halás, M.; Erlebach, M.; Tonev, P.; Bednar, M. A multistage agglomerative approach for defining functional region of the Czech republic: The use of 2001 commuting data. Morav. Geogr. Rep. 2014, 22, 2–13. [Google Scholar]
- Farmer, C.; Fotheringham, A.S. Network-based functional regions. Environ. Plan. A 2011, 43, 2723–2741. [Google Scholar] [CrossRef]
- Konjar, M.; Lisec, A.; Drobne, S. Methods for delineation of functional regions using data on commuters. In Proceedings of the 13th AGILE International conference on Geographic Information Science, Guimaraes, Portugal, 11–14 May 2010.
- Coombes, M. From City-region concept to boundaries for governance: The English case. Urban Stud. 2013, 52, 1113–1133. [Google Scholar] [CrossRef]
- Thomas, I.; Cotteels, C.; Jones, J.; Peeters, D. Revisiting the Extension of the Brussels urban agglomeration: New methods, new data... new results? e-Belgeo 2013, 1–2, 1–11. [Google Scholar] [CrossRef]
- Thomopoulos, N.; Givoni, M.; Rietveld, P. ICT for Transport: Opportunities and Threats; Edward Elgar Publishing: Cheltenham, UK, 2015. [Google Scholar]
- Kitchin, R. The Data Revolution: Big Data, Open Ddata, Data Infrastructures and Their Consequences; Sage: Thousand Oaks, CA, USA, 2014. [Google Scholar]
- Vanoutrive, T.; Malderen, L.V.; Jourquin, B.; Thomas, I.; Verhetsel, A.; Witlox, F. Rail commuting to workplaces in Belgium: A multilevel approach. Int. J. Sustain. Transp. 2012, 6, 67–87. [Google Scholar] [CrossRef]
- Bergstrand, J.H. The gravity equation in international trade: Some microeconomic foundations and empirical evidence. Rev. Econ. Stat. 1985, 67, 474–481. [Google Scholar] [CrossRef]
- Grasland, C.; Beauguitte, L. Modelling attractiveness of global places: A worldwide survey on 9000 undergraduate students. In Proceedings of the 50th European Congress of the Regional Science Association International on: Sustainable Regional Growth and Development in the Creative Knowledge Economy, Jönköping, Sweden, 19–23 August 2010.
- Giraud, T.; Commenges, H. SpatialPosition: Spatial Position Models. R Package Version 1.0. 2015. Available online: http://CRAN.R-project.org/package=SpatialPosition (accessed on 9 September 2016).
- Cervero, R.; Wu, K.L. Polycentrism, commuting, and residential location in the San Francisco Bay area. Environ. Plan. A 1997, 29, 865–886. [Google Scholar] [CrossRef] [PubMed]
- Wang, F. Modeling commuting patterns in Chicago in a GIS environment: A job accessibility perspective. Prof. Geogr. 2000, 52, 120–133. [Google Scholar] [CrossRef]
- Wang, F. Explaining intraurban variations of commuting by job proximity and workers’ characteristics. Environ. Plan. B Plan. Des. 2001, 28, 169–182. [Google Scholar] [CrossRef]
- Sohn, J. Are commuting patterns a good indicator of urban spatial structure? J. Transp. Geogr. 2005, 13, 306–317. [Google Scholar] [CrossRef]
- Mathä, T.; Wintr, L. Commuting flows across bordering regions: A note. Appl. Econ. Lett. 2009, 16, 735–738. [Google Scholar] [CrossRef]
- Dujardin, C. Effet de frontière et intégration spatiale: Les migrations alternantes et la frontière linguistique en Belgique. L’espace Géogr. 2001, 2001, 307–320. [Google Scholar]
- Rodrigue, J.P.; Comtois, C.; Slack, B. The Geography of Transport Systems; Routledge: London, UK, 2013. [Google Scholar]
- Spiekermann, K.; Wegener, M. The shrinking continent: New time—space maps of europe. Environ. Plan. B Plan. Des. 1994, 21, 653–673. [Google Scholar] [CrossRef]
- Spiekermann, K.; Wegener, M. Trans-European networks and unequal accessibility in Europe. Eur. J. Reg. Dev. 1996, 4, 35–42. [Google Scholar]
- Vickerman, R. High-speed rail in Europe: Experience and issues for future development. Ann. Reg. Sci. 1997, 31, 21–38. [Google Scholar] [CrossRef]
- Givoni, M. Development and impact of the modern High-speed train: A review. Transp. Rev. 2006, 26, 593–611. [Google Scholar] [CrossRef]
- Levinson, D.M. Accessibility impacts of high-speed rail. J. Transp. Geogr. 2012, 22, 288–291. [Google Scholar] [CrossRef]
- Blondel, V.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large network. J. Stat. Mech. Theory. Exp. 2008, 2008, 10008. [Google Scholar] [CrossRef]
- Guimera, R.; Mossa, S.; Turtschi, A.; Amaral, L.N. The worldwide air transportation network: Anomalous centrality, community structure, and cities’ global roles. Proc. Natl. Acad. Sci. USA 2005, 102, 7794–7799. [Google Scholar] [CrossRef] [PubMed]
- Verhetsel, A.; Van Hecke, E.; Halleux, J.M.; Decroly, J.M.; Merenne-Schoumaker, B. Noyaux D’habitats et région Urbaines Dans Une Belgique Urbanisée; Technical Report, Monographie de L’enquète Socio-Économique 2001; SPF Economie: Brussels, Belgium, 2009.
- Van Hecke, E.; Thomas, I.; Beelen, M.; Halleux, J.M.; Lambotte, J.M.; Rixhon, G.; Verhetsel, A. Le Mouvement Pendulaire en Belgique; Technical Report, Monographie de L’enquète Socio-Économique 2001; SPF Economie: Brussels, Belgium, 2009.
- Verhetsel, A.; Thomas, I.; Beelen, M. Commuting in Belgian metropolitan areas. J. Transp. Land Use 2010, 2, 109–131. [Google Scholar] [CrossRef]
- Federal Highway Administration. National Household Travel Survey 2016. Available online: https://www.nationalhouseholdtravelsurvey.com/l (accessed on 9 September 2016).
- Cornelis, M. Belgian Daily Mobility-BELDAM. 2012. Available online: http://www.belspo.be/belspo/organization/Publ/pub_ostc/agora/ragjj150_fr.pdf (accessed on 9 September 2016).
- Ahem, A.; Weyman, G.; Redelbach, M.; Schulz, A.; Akkermans, L.; Vannacci, L.; Anoyrkati, E.; van Grinsven, A. Analysis of National Travel Statistics in Europe. 2013. Available online: http://publications.jrc.ec.europa.eu/repository/bitstream/JRC83304/tch-d2.1_final.pdf (accessed on 9 September 2016).
- Hubert, J.P.; Armoogum, J.; Axhausen, K.W.; Madre, J.L. Immobility and mobility seen through trip-based versus time-use surveys. Transp. Rev. 2008, 28, 641–658. [Google Scholar] [CrossRef]
- Gerike, R.; Gehlert, T.; Leisch, F. Time use in travel surveys and time use surveys—Two sides of the same coin? Transp. Res. Part A Policy Prac. 2015, 76, 4–24. [Google Scholar] [CrossRef]
- Roth, C.; Kang, S.M.; Batty, M.; Barthelemy, M. Structure of urban movements: Polycentric activity and entangled hierarchical flows. PLoS ONE 2011, 6, e15923. [Google Scholar] [CrossRef] [PubMed]
- Long, Y.; Thill, J. Combining smart card data and household travel survey to analyze jobs-housing relationships in Beijing. Comput. Environ. Urban Syst. 2015, 53, 19–35. [Google Scholar] [CrossRef]
- Sun, S.; Duan, Z.; Yang, D.; Li, W. Polycentricity of the urban structure: Spatial movements analysis in Shanghai with smart card data. In Proceedings of the 21st World Congress on Intelligent Transport Systems, ITSWC 2014: Reinventing Transportation in Our Connected World, Detroit, MI, USA, 7–11 September 2014.
- SNCB. Available online: http://www.belgianrail.be/en (accessed on 9 November 2016).
- DGSIE. Population—Chiffres Population 2010–2016. Available online: http://statbel.fgov.be/fr/modules/publications/statistiques/population/population_-_chiffres_population_2010_-_2012.jsp (accessed on 9 September 2016).
- Thisse, J.F.; Thomas, I. Bruxelles au sein de l’économie belge: Un bilan. Reflets Perspect. Econ. 2010, 80, 1–18. [Google Scholar]
- Van der Herten, B. Le Temps du Train, 175 ans de Chemins de fer en Belgique, 75e Anniversaire de la SNCB; Presses Universitaires de Louvain: Louvain la Neuve, Belgium, 2001. [Google Scholar]
- Denis, J. (Ed.) Geographie de la Belgique; Bulletin du Credit Communal: Brussels, Belgium, 1992; p. 616.
- National Geography Committee. A Concise Geography of Belgium; Academia Press: Ghent, Belgium, 2012; p. 46. [Google Scholar]
- Infrabel. Railway Lines. Available online: http://www.infrabel.be/en/about/our-rail-network/railway-lines (accessed on 9 September 2016).
- SNCB. SNCB 2015 Activities Report. 2015. Available online: http://www.belgianrail.be/en/corporate/~/media/1212C2ABEFCA4BC0A236781FECE168E5.ashx (accessed on 9 September 2016).
- iRail. Available online: https://irail.be/ (accessed on 9 November 2016).
- iRail API. Available online: https://hello.irail.be/api/1-0/ (accessed on 9 November 2016).
- Colpaert, P.; Chua, A.; Verborgh, R.; Mannens, E.; Van de Walle, R.; Vande Moere, A. What public transit API logs tell us about travel flows. In Proceedings of the 25th International Conference Companion on World Wide Web. International World Wide Web Conferences Steering Committee, Montreal, QC, Canada, 11–15 April 2016; pp. 873–878.
- SNCB. Nombre de Voyageurs Montes Par Gare en 2014. Available online: https://www.belgianrail.be/fr/~/media/73AECBB3473141C1AA565C122AB6259C.ashx (accessed on 9 September 2016).
- SNCB. Nombre de Voyageurs Montes Par Gare en 2015. Available online: http://www.belgianrail.be/fr/~/media/8F764D77F60F48B188A8742652C6E48F.ashx (accessed on 9 September 2016).
- Delvenne, J.C.; Schaub, M.T.; Yaliraki, S.N.; Barahona, M. The stability of a graph partition: A dynamics-based framework for community detection. In Dynamics On and Of Complex Networks; Springer: Berlin, Germany, 2013; Volume 2, pp. 221–242. [Google Scholar]
- Lancichinetti, A.; Radicchi, F.; Ramasco, J.J.; Fortunato, S. Finding statistically significant communities in networks. PLoS ONE 2011, 6, e18961. [Google Scholar] [CrossRef] [PubMed]
- Traag, V.; Van Dooren, P.; Nesterov, Y. Narrow scope for resolution-limit-free community detection. Phys. Rev. E 2011, 84, 016114. [Google Scholar] [CrossRef] [PubMed]
- Traag, V.A.; Krings, G.; Van Dooren, P. Significant scales in community structure. Sci. Rep. 2013, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Cunningham, P. Community detection: Effective evaluation on large social networks. J. Complex Netw. 2014, 2, 19–37. [Google Scholar] [CrossRef]
- Good, B.H.; de Montjoye, Y.A.; Clauset, A. Performance of modularity maximization in practical contexts. Phys. Rev. E 2010, 81, 046106. [Google Scholar] [CrossRef] [PubMed]
- Ana, L.; Jain, A.K. Robust data clustering. In Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Madison, WI, USA, 18–20 June 2003; Volume 2.
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Blondel, V.; Krings, G.; Thomas, I. Regions and borders of mobile telephony in Belgium and in the Brussels metropolitan zone. Brussels Stud. 2010, 42, 1–12. [Google Scholar]
- De Witte, A.; Macharis, C.; Mairesse, O. How persuasive is free public transport?: A survey among commuters in the Brussels Capital Region. Transp. Policy 2008, 15, 216–224. [Google Scholar] [CrossRef]
- Vandenbulcke, G.; Dujardin, C.; Thomas, I.; de Geus, B.; Degraeuwe, B.; Meeusen, R.; Panis, L.I. Cycle commuting in Belgium: Spatial determinants and share-cycling strategies. Transp. Res. Part A Policy Pract. 2011, 45, 118–137. [Google Scholar] [CrossRef]
- SNCB. S-Train. Available online: http://www.belgianrail.be/en/ /media/91715610D054471E8B2D70D3CD3B6562.pdf (accessed on 9 September 2016).
- J.C. RER a Bruxelles: Quel etait le projet? Qu’en est-il maintenant? Available online: https://www.rtbf.be/info/regions/bruxelles/detail_rer-a-bruxelles-quel-etait-le-projet-qu-en-est-il-maintenant?id=9202743 (accessed on 9 September 2016).
- Ordonnance Portant Assentiment à la Convention du 4 Avril 2003 Entre l’Etat fédéral, la Région Flamande, la Région Wallone et la Région de Bruxelles-Capitale, Visant à mettre en Oeuvre le Programme du Réseau Express R’egional de, Vers, Dans et Autour de Bruxelles; Moniteur Belge: Brussels, Belgium, 2004.
- Huff, D.L. A probabilistic analysis of shopping center trade areas. Land Econ. 1963, 39, 81–90. [Google Scholar] [CrossRef]
- Attout, X. RER: Scenario catastrophe en vue? Le Soir 2016. Available online: http://www.lesoir.be/1264492/article/actualite/regions/brabant-wallon/2016-07-12/rer-scenario-catastrophe-en-vue (accessed on 9 September 2016).
- Jan Peumans (N-VA): Il serait bon de regionaliser la SNCB. Le Soir 2015. Available online: http://www.lesoir.be/933608/article/actualite/belgique/politique/2015-07-11/jan-peumans-n-vail-serait-bon-regionaliser-sncb (accessed on 9 September 2016).
- RTBF. Une Regionalisation de la SNCB Est-Elle Possible? Available online: https://www.rtbf.be/info/belgique/detail_une-regionalisation-de-la-sncb-est-elle-realisable?id=9178419 (accessed on 9 September 2016).
- Kitchin, R. The real-time city? Big data and smart urbanism. GeoJournal 2014, 79, 1–14. [Google Scholar] [CrossRef]
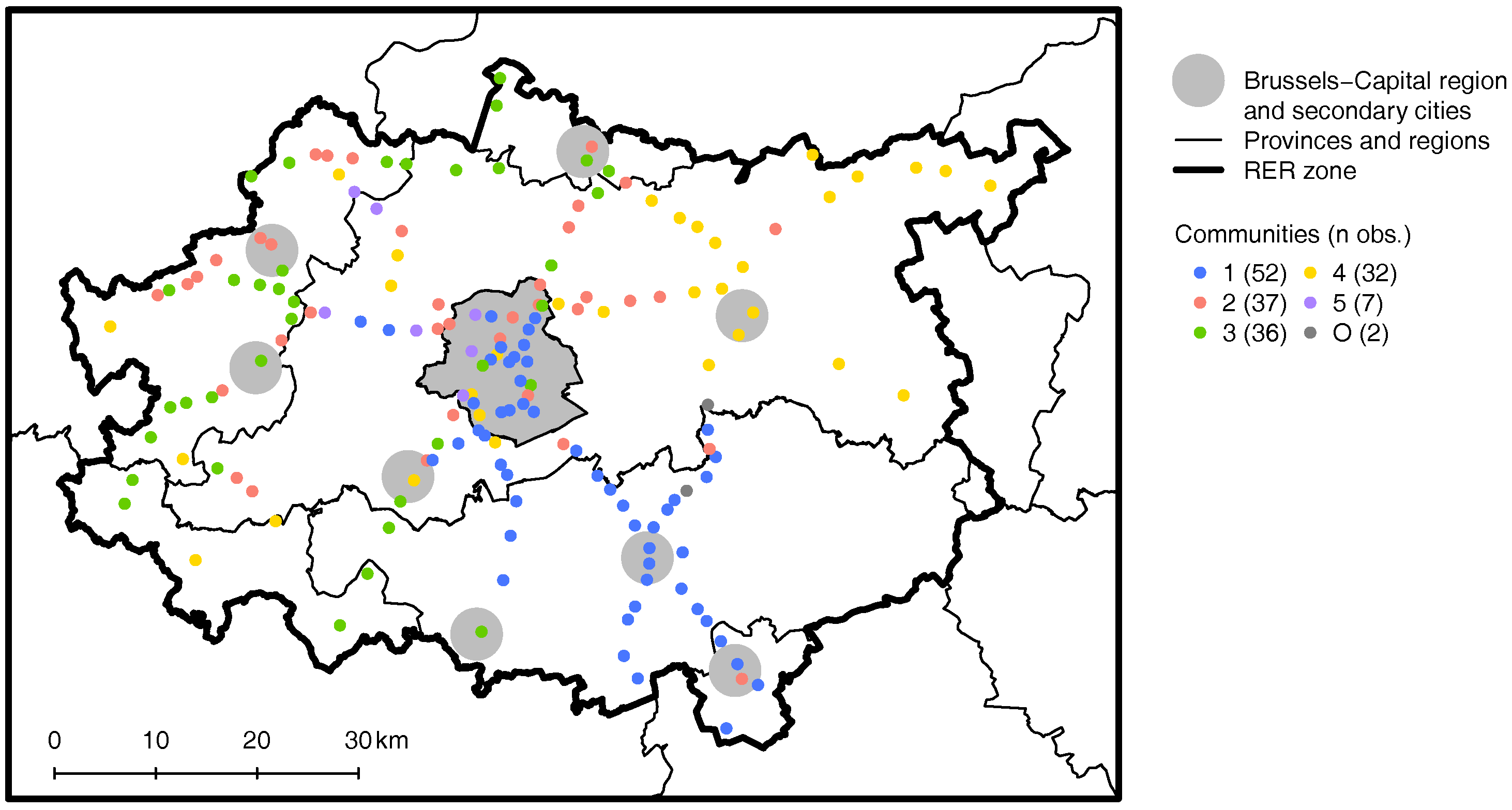
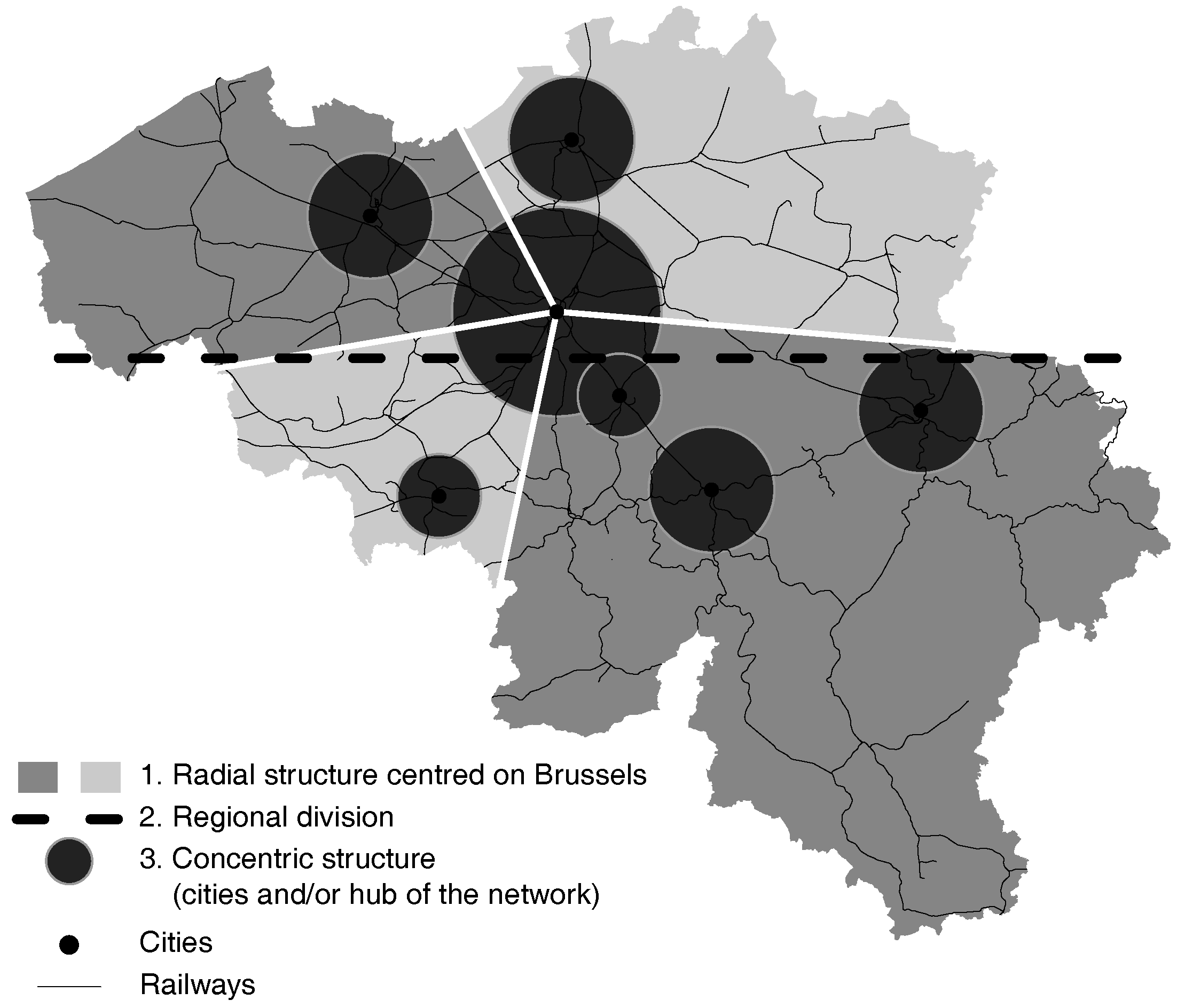
| Subsets | Number of | Modularity | NMI | |||
|---|---|---|---|---|---|---|
| Requests | Stations | O/D Pairs | Communities | (0 to 1) | (with General Subset) | |
| General | 551,301 | 541 | 13,770 | 7 | 0.30 | / |
| No Brussels | 265,013 | 508 | 9600 | 7 | 0.51 | 0.53 |
| Weekdays | 419,184 | 538 | 12,262 | 8 | 0.34 | 0.79 |
| Weekend | 132,117 | 508 | 7374 | 7 | 0.35 | 0.58 |
| Dutch | 297,710 | 406 | 7473 | 7 | 0.29 | 0.38 |
| French | 196,185 | 465 | 6927 | 7 | 0.41 | 0.32 |
| RER | 204,731 | 166 | 3614 | 5 | 0.25 | 0.58 |
| Subsets | By Communities | Global Mean | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| General | 89.6 | 98.8 | 83.3 | 91.9 | 87.4 | 99.5 | 44.7 | 90.2 | |
| (14.1) | (3.78) | (19.5) | (14.0) | (9.58) | (2.19) | (0.00) | (14.9) | ||
| No Brussels | 99.4 | 88.8 | 97.8 | 99.5 | 96.7 | 73.6 | 100 | 95.9 | |
| (4.11) | (12.1) | (8.10) | (2.25) | (1.58) | (7.13) | (0.00) | (9.22) | ||
| Weekdays | 96.8 | 98.9 | 93.2 | 96.2 | 81.1 | 96.8 | 91.1 | 90.5 | 94.3 |
| (8.44) | (4.43) | (10.4) | (8.92) | (0.00) | (7.78) | (16.8) | (6.11) | (9.90) | |
| Weekend | 97.1 | 91.9 | 81.3 | 79.3 | 97.4 | 90.9 | 88.4 | 90.8 | |
| (9.49) | (16.9) | (17.7) | (8.21) | (7.94) | (16.0) | (11.5) | (14.6) | ||
| Dutch | 92.3 | 94.7 | 73.5 | 96.2 | 97.7 | 100 | 98.48 | 91.8 | |
| (13.5) | (8.06) | (5.06) | (9.10) | (5.93) | (0.00) | (0.00) | (12.2) | ||
| French | 99.6 | 95.8 | 89.1 | 95.7 | 100 | 91.2 | 94.1 | 96.0 | |
| (2.90) | (11.1) | (13.9) | (8.87) | (0.00) | (5.39) | (14.3) | (9.28) | ||
| RER | 97.5 | 95.3 | 92.7 | 74.1 | 64.5 | 90.1 | |||
| (9.03) | (9.12) | (14.1) | (0.00) | (0.00) | (13.7) | ||||
| Subsets | By Communities | Global Mean | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| General | 32.9 | 42.2 | 29.3 | 32.8 | 32.7 | 30.1 | 46.1 | 42.8 | |
| (30.8) | (27.4) | (19.1) | (27.0) | (20.0) | (26.0) | (11.3) | (32.6) | ||
| No Brussels | 30.8 | 41.6 | 31.1 | 31.8 | 9.9 | 56.9 | 33.6 | 44.4 | |
| (23.1) | (27.9) | (21.9) | (18.5) | (11.2) | (38.3) | (34.7) | (36.5) | ||
| Weekdays | 30.5 | 42.4 | 33.1 | 32.6 | 25.5 | 30.7 | 27.6 | 38.0 | 42.0 |
| (31.0) | (27.6) | (27.0) | (19.8) | (16.3) | (19.7) | (24.2) | (17.8) | (31.9) | |
| Weekend | 33.7 | 46.7 | 35.5 | 26.3 | 28.1 | 31.3 | 41.1 | 45.3 | |
| (32.9) | (31.4) | (22.0) | (20.2) | (19.0) | (26.2) | (16.4) | (34.3) | ||
| Dutch | 34.4 | 42.9 | 20.1 | 24 | 26.0 | 54.6 | 104.8 | 43. 8 | |
| (21.0) | (28.7) | (15.5) | (17.3) | (16.3) | (36.0) | (8.4) | (31.4) | ||
| French | 35.9 | 29.5 | 31.3 | 35.3 | 23.2 | 39.1 | 12.4 | 39.9 | |
| (25.7) | (23.9) | (41.3) | (27.8) | (13.1) | (17.5) | (7.8) | (33.3) | ||
| RER | 14.4 | 16.6 | 20.3 | 28.3 | 15.1 | 22.7 | |||
| (10.7) | (11.5) | (8.3) | (14.1) | (5.9) | (13.0) | ||||
| Subsets | By Communities | Global Mean | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| General | 0.68 | 0.61 | 0.56 | 0.61 | 0.56 | 0.48 | 0.45 | 0.61 | |
| (0.16) | (0.18) | (0.18) | (0.17) | (0.18) | (0.13) | (0.21) | (0.18) | ||
| No Brussels | 0.72 | 0.68 | 0.66 | 0.70 | 0.67 | 0.51 | 0.57 | 0.68 | |
| (0.12) | (0.14) | (0.13) | (0.13) | (0.15) | (0.10) | (0.07) | (0.14) | ||
| Weekdays | 0.67 | 0.57 | 0.61 | 0.52 | 0.67 | 0.46 | 0.47 | 0.58 | 0.59 |
| (0.17) | (0.18) | (0.18) | (0.20) | (0.16) | (0.17) | (0.13) | (0.21) | (0.19) | |
| Weekend | 0.67 | 0.65 | 0.52 | 0.57 | 0.53 | 0.49 | 0.56 | 0.60 | |
| (0.16) | (0.16) | (0.17) | (0.17) | (0.18) | (0.14) | (0.15) | (0.18) | ||
| Dutch | 0.54 | 0.57 | 0.48 | 0.55 | 0.49 | 0.48 | 0.50 | 0.53 | |
| (0.17) | (0.18) | (0.19) | (0.23) | (0.16) | (0.12) | (0.11) | (0.18) | ||
| French | 0.60 | 0.58 | 0.63 | 0.52 | 0.64 | 0.62 | 0.60 | 0.59 | |
| (0.16) | (0.20) | (0.19) | (0.13) | (0.16) | (0.21) | (0.23) | (0.18) | ||
| RER | 0.60 | 0.48 | 0.57 | 0.55 | 0.29 | 0.54 | |||
| (0.19) | (0.18) | (0.19) | (0.23) | (0.11) | (0.21) | ||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jones, J.; Cloquet, C.; Adam, A.; Decuyper, A.; Thomas, I. Belgium through the Lens of Rail Travel Requests: Does Geography Still Matter? ISPRS Int. J. Geo-Inf. 2016, 5, 216. https://doi.org/10.3390/ijgi5110216
Jones J, Cloquet C, Adam A, Decuyper A, Thomas I. Belgium through the Lens of Rail Travel Requests: Does Geography Still Matter? ISPRS International Journal of Geo-Information. 2016; 5(11):216. https://doi.org/10.3390/ijgi5110216
Chicago/Turabian StyleJones, Jonathan, Christophe Cloquet, Arnaud Adam, Adeline Decuyper, and Isabelle Thomas. 2016. "Belgium through the Lens of Rail Travel Requests: Does Geography Still Matter?" ISPRS International Journal of Geo-Information 5, no. 11: 216. https://doi.org/10.3390/ijgi5110216
APA StyleJones, J., Cloquet, C., Adam, A., Decuyper, A., & Thomas, I. (2016). Belgium through the Lens of Rail Travel Requests: Does Geography Still Matter? ISPRS International Journal of Geo-Information, 5(11), 216. https://doi.org/10.3390/ijgi5110216





