1. Introduction
Spatial patterns of species presence have been a central theme for long time in a variety of disciplines, such as ecology, biogeography, evolution, and management. Therefore, there is much interest in predicting the distribution of species, for which methods have been developed, including several modeling approaches widely known as species distribution models (SDMs) [
1,
2]. Typically, SDMs relate spatially-limited records of the presence or abundance of a species to environmental variables (e.g., temperature) that control its distribution. The relationships established may then be used to predict the presence of the species across unsurveyed areas [
3].
Error and uncertainty abound in SDM-based analysis. Barry and Elith [
4] classify the sources of error and uncertainty embedded in SDMs into two main categories: deficiencies in the data and deficiencies introduced by the specification of the model. In the first category, common problems include missing variables [
4], small sample size [
5,
6], biased samples [
7], incorrectly located species records [
6], lack of absence records [
8], and disagreement between the scale (grain/extent) of the species data and the modeling setup [
1,
6,
9]. The second category includes possible discrepancies between the model used and the “true” model (e.g., if the model used is linear and the true relationship between species presence and variables is quadratic) and the modeling approach (e.g., envelope, distance-based, and regression) [
4].
In this paper, attention is focused on the deficiencies in data, namely the species data. The quality of species data is often compromised for a variety of reasons. For example, commonly used datasets, such as those obtained from museums, herbariums, and atlases, often include only presence records (
i.e., spatial reference where the species was detected), frequently resulting from
ad hoc compilations of records collected occasionally without information on the species’ absence and survey effort; the latter is relevant since easily-accessible areas (e.g., near roads) are often more surveyed than remote areas, which leads to spatially-biased samples [
8,
10].
A variety of impacts of species data deficiencies on SDMs have been studied and a range of mitigation solutions have been proposed. For example, modeling methods have been developed that use presence-only data [
11]; the impact of limited sample size in modeling have been studied [
5,
12]; and solutions have been proposed for the problem of incorrectly located species records [
13], uneven sampling effort [
14,
15,
16], spatial autocorrelation [
17,
18,
19,
20], and scales [
21,
22]. However, not all deficiencies in species data sets have been fully studied. One key problem that has attracted little attention yet may be common is that of species misidentification. Species misidentification is a particular type of false positive error, which occurs when a species is recorded as being present at a location where it is in fact absent. An example of a false positive error other than species misidentification is double-counting of individuals (e.g., when aural point counts are used to detect birds [
23]). Here, the concern is when a species is simply misidentified.
False positive errors have, in general, been largely neglected [
24]. One of the reasons why false positive errors are commonly neglected is that there is a tendency to believe that they are small and, thus, viewed as having negligible impact. However, that is not always true. With regard to species misidentification, substantial error rates have been reported in the literature. For example, ∼7% for plants [
25], ∼20% for sharks [
26], 23% for hawks [
27], ∼27% for freshwater mussels [
28], and ∼70% for robber flies [
29]. The magnitude of the problem of species misidentification varies as a function of several factors, namely the surveyor’s level of expertise and the species involved. For example, in a study addressing the causes of species misidentification in vegetation monitoring, Scott and Hallam [
30] found an average misidentification rate of 2.7%–25.6% depending on surveyors’ expertise. Furthermore, Scott and Hallam [
30] found high misidentification rates (e.g., >14%) for specific categories of plants, such as lower plants and particular trees.
A rare example of a study that addressed the impacts of species misidentification on research using SDMs is that of Ensing,
et al. [
31] in a study that predicted the potential distribution of an invasive species in North America. Ensing,
et al. [
31] found that the species distribution modeled using all of the presence records available (possibly including misidentifications) was substantially larger than that based only on records regarded as taxonomically “reliable”. A similar conclusion is drawn by Molinari-Jobin,
et al. [
32] using reliable and non-reliable data to predict the distribution of the Eurasian lynx in the Alps with site-occupancy modeling.
The effects of species misidentification on studies using SDMs are, however, still to be fully understood. A key issue is whether the misidentification committed is arbitrary or systematic. Arbitrary misidentification refers here to errors that lack a clear pattern, specifically, when the source of error vary. For example, the presumed presence of a species may involve confusion with several species, recorded by different surveyors with different expertise, and following inconsistent methodologies [
31,
32]. Systematic misidentification refers to the systematically confusion of one species with another. Systematic species misidentification can happen especially when two species are both morphologically similar and sympatric. For example, misidentifications of white marlin (
Tetrapturus albidus) have occurred for a long time with the morphologically similar and sympatric roundscale spearfish (
T. georgii); as a result, the two species were unknowingly assessed and managed as a species group [
33].
When systematic species misidentification occurs, the spatial data of the misidentified species systematically “contaminates” the spatial data of the species of interest. It is expected that the effects of contaminated data on modeling are related to the distribution of the species confused. For example, if the contaminating species has a broader distribution than the species of interest, its erroneous inclusion in the data set will expand the predicted distribution of the species of interest, as Ensing,
et al. [
31] and Molinari-Jobin,
et al. [
32] concluded. However, if the contaminating species has a narrower distribution than the species of interest, it will possibly have the opposite effect. Ultimately, the SDM predictions would be expected to be shifted towards the distribution of the contaminating species. Furthermore, the magnitude of the effects will also be expected to vary as a function of the rate of species misidentification from potentially negligible impact if misidentification is rare to large if misidentification is common. The latter issue has not been studied in detail. For example, the results of Ensing,
et al. [
31] and Molinari-Jobin,
et al. [
32] were based on data with unknown rates of species misidentification. This paper focuses on the impacts of systematic species misidentification of variable rate on SDM predictions of species presence using presence-only data.
2. Material and Methods
To explore the effects of species misidentification error on species distribution modeling, a series of analyses were undertaken. The analyses focused on the effects of misidentification error on the predicted distribution of a species of interest and its potential impact on practical applications that use SDMs to select regions for various purposes such as management of endangered species. Specifically, four analyses were performed in which the modeling results obtained with data regarded as a gold standard (
i.e., error-free) were compared to the results obtained with data contaminated with misidentification error. To ensure that the misidentification error could be known and characterized accurately to enable a rigorous assessment of the impacts of species misidentification on modeling a set of simulated datasets were used, but a real dataset is also used to provide an illustrative case study of the importance of the topic. Six rates,
r, of species misidentification (contamination) were used: 1, 2, 4, 8, 16, and 32%; all inside the range of values reported in the literature highlighted above. All analyses were undertaken using a widely used species distribution model: maximum entropy (MaxEnt) [
11].
Figure 1.
Study area and species data used: (a) island of São Miguel in the Azores, Portugal; and (b) location of the Cyathea cooperi (orange squares) and C. medullaris (blue dots) presence recorded in São Miguel between September 2011 and May 2012. Note: grey background represents the island relief as bright tones for high altitude and insolation and dark tones for opposite conditions.
Figure 1.
Study area and species data used: (a) island of São Miguel in the Azores, Portugal; and (b) location of the Cyathea cooperi (orange squares) and C. medullaris (blue dots) presence recorded in São Miguel between September 2011 and May 2012. Note: grey background represents the island relief as bright tones for high altitude and insolation and dark tones for opposite conditions.
2.1. Real Data
The real data used in this study relate to the island of São Miguel in the Azores (Portugal). The Azores is an archipelago of volcanic origin located in the North Atlantic Ocean, about 1500 km west from mainland Portugal (
Figure 1a). The Azorean climate is temperate oceanic with a mean annual temperature of 17 °C at sea level, decreasing with altitude. Relative humidity is high and rainfall ranges from 1000 to well above 3000 mm yr
−1, increasing with altitude and from east to west [
34,
35]. São Miguel is the largest island (745 km
2), and its highest peak stands 1103 m high in the East (
Figure 1b).
The real species data used were collected in a field survey conducted between September 2011 and May 2012 across São Miguel in order to increase the knowledge about the presence of tree ferns, which are alien to the Azores. The presence of tree ferns was detected during field surveys undertaken by car and on foot. Thus, the species datasets resulted from ad hoc compilations of records collected occasionally without information on the species’ absence and survey effort.
The species of interest (hereafter referred to as target species) is
Cyathea cooperi (351 individuals recorded).
C. cooperi is a tree fern considered as problematic because of its invasiveness [
36] and is one of the top 100 invasive alien species with management priority in European Macaronesia [
34].
C. cooperi can be confused with
C. medullaris, which was identified for the first time in the Azores in the 2011/2012 survey (32 records). These two species are morphologically similar, with a further 141 records labeled only as
Cyathea sp. as their exact species was not clear. Finally, samples of another tree fern species,
Dicksonia antartica, were obtained (59 individuals recorded) which could be useful in modeling.
The presence of
C. medullaris casts doubts upon past studies on the presence of
C. cooperi in São Miguel because misidentifications may have happened historically. The situation is particularly possible because of the high number of specimens identified as
C. medullaris in an apparently self-supporting population, which makes it unlikely that it was introduced recently. The presence of
C. cooperi was recorded in a range of environments while
C. medullaris was less dispersed geographically. In particular,
C. medullaris was mainly observed at high altitude while
C. cooperi was observed at all altitudes (
Figure 1b). Note there are no guaranties the datasets of
C. cooperi and
C. medullaris are free of misidentification error. All specimens difficult to identify were labeled as
Cyathea sp. but errors may have been made. For practical reasons, in this paper these data sets were used as if there were no error.
Environmental variables were selected for modeling the distribution of tree ferns. Climatic data were obtained from the model “Clima Insular à Escala Local” (CIELO) [
37]. CIELO models local scale climate variables using data from synoptic coastal meteorological stations, and is available in raster format with 100 m spatial resolution (details are found at [
38]). Specifically, the following six climatic variables were used: precipitation (mm) and mean maximum temperature (°C) of the warmest quarter, precipitation (mm) and mean minimum temperature (°C) of the coldest quarter, and the annual mean of the minimum and maximum relative humidity (%). These data were used as they are basic climate variables of the type known to affect plant species distribution. In addition, a set of topographic variables was derived within a geographical information system (ESRI ArcGIS 9.3) based on a digital elevation model available in the CIELO database: slope (%), winter hillshade, summer hillshade, and curvature. Hillshade is a simulation of the lighting conditions on the surface dictated by the topography and the position of the Sun (the winter and summer solstices were considered). Curvature is the second derivative of the surface, thus highlighting flat, convex, and concave areas. These variables were used as indicators of local environmental conditions known to affect plant species distribution that were not available for this study, such as available soil water and insolation.
2.2. Simulated Data
Real species datasets are typically flawed in some fashion, specifically in relation to issues, such as data quality and sampling bias. Hence, to further illustrate the importance of species misidentification on SDMs predictions, simulated species data were generated with well-defined characteristics. A target species and a contaminating species were simulated as being at equilibrium with the environment, that is, the species were defined as present at all locations ecologically suitable, thus satisfying the equilibrium assumption of most SDMs [
1,
3].
The environmental suitability for the presence of both the simulated target and contaminating species was calculated for each location of the island. A location is defined here as a raster cell
i of the environmental data used. Environmental suitability was defined similarly as in Varela,
et al. [
16], that is, as a function of the species response to the multiplicative interaction of two environmental variables: precipitation (P) and temperature (T). Specifically, the species’ response to each variable was defined using normal curves (of mean μ and standard deviation σ), and the environmental suitability at location
i (S
i) was defined as the product of those two responses, which may be expressed as S
i = P
iT
i.
For the simulated target species, μ and σ of P (μP, σP) and T (μT, σT) were defined, respectively, equal to the mean and standard deviation of the precipitation and mean maximum temperature of the warmest quarter (introduced above) of the whole archipelago of the Azores. Thus, μP = 314.77, σP = 162.90, μT = 21.83, and σT = 1.79.
For the simulated contaminating species, the mean and standard deviation of P and T varied in standard deviation units in relation to the simulated target species defined above. Specifically, a specific contaminating species was simulated within five scenarios (scenarios I–V) as the impact of species misidentification would be expected to depend on the ecological difference between the species niches confused.
Figure 2 shows the mean and standard deviation of P and T, and the resulting niche for the simulated target and contaminating species in all the scenarios. Specifically, the niche of the simulated contaminating species was defined relative to the simulated target species as being wider (scenarios I and III) and narrower (scenarios II and V). Both species have the same niche breadth in scenario IV. In addition, scenarios III, IV, and V define the simulated contaminating species with a shift in niche optimum, preferring cooler and wetter environmental conditions than the simulated target species. As a result of the scenarios defined, the niche of the simulated target and contaminating species were expected to diverge. The Bhattacharyya distance [
39] was used to measure the divergence between the niches, which increased across the scenarios—the Bhattacharyya distance between the niche of the simulated target and contaminating species of scenarios I–V was 3.5 × 10
−3, 9.4 × 10
−3, 34.6 × 10
−3, 95.7 × 10
−3, and 138.8 × 10
−3 respectively.
Figure 2.
The ecological niche of the simulated target and contaminating species in five scenarios (ellipses show the 95% probability regions). The niche of the target species was defined as the multiplicative interaction of precipitation (P) and temperature (T). The response of the target species to P and T was defined using normal curves where the mean μ and standard deviation σ of P (μP, σP) and T (μT, σT) are 314.77 and 162.90, and 21.83 and 1.79, respectively. For the simulated contaminating species, μ and σ of P and T varied in standard deviation units in relation to the simulated target species as shown in each scenario (for example, the normal curve of P in scenario III used a mean value of μP + σP and a standard deviation of 2σP).
Figure 2.
The ecological niche of the simulated target and contaminating species in five scenarios (ellipses show the 95% probability regions). The niche of the target species was defined as the multiplicative interaction of precipitation (P) and temperature (T). The response of the target species to P and T was defined using normal curves where the mean μ and standard deviation σ of P (μP, σP) and T (μT, σT) are 314.77 and 162.90, and 21.83 and 1.79, respectively. For the simulated contaminating species, μ and σ of P and T varied in standard deviation units in relation to the simulated target species as shown in each scenario (for example, the normal curve of P in scenario III used a mean value of μP + σP and a standard deviation of 2σP).
The environmental suitability of the simulated species defined above was used to create a presence-only sample for each species, needed for modeling with MaxEnt. A total of 1000 records (locations) were sampled for each species. The locations were selected through a weighted random sampling, using the environmental suitability of the locations (S
i) as weights. Thus, locations with high suitability for the species had a higher chance of being selected and, hence, the samples indicated ecological preferences of the species. In addition, the same strategy was used to create a testing sample for the purpose of estimating the prediction accuracy of the MaxEnt results while using simulated data. However, here there was the opportunity of generating data for absences as well as presences, allowing the calculation of standard accuracy measures such as the area under the receiver operating characteristic curve (AUC) [
40]. A total of 1000 presences and 1000 absences were generated in the same manner outlined above, but using the inverse of environmental suitability (1 − S
i) as weights for generating the absences (
i.e., locations with low environmental suitability for the species had a higher chance of being selected).
2.3. Modeling Procedures
MaxEnt (version 3.3.3k; [
41]) was used in this study as it is one of the most popular methods to model species distributions. MaxEnt finds the species spatial distribution of maximum entropy (
i.e., closest to uniform), subject to a set of constraints determined by the species data in use [
11], which is equivalent to minimizing, in the environmental space, the relative entropy between the probability density estimated from the presence data and that one estimated from the landscape, or from a sample thereof, called background [
42].
The default values of the MaxEnt’s parameters were used, except the feature types and output format. The term “feature” refers to an expanded set of transformations of the original environmental variables used, such as the product of all possible pair-wise combinations of variables [
42]. Only the “hinge” feature type was used as it, alone, produces results similar to all the other feature types available in the software [
43]. The ‘raw’ output format was used and interpreted as relative probability or a suitability index at a location for the presence of a species [
44,
45,
46]. In addition, a “target-group” background was defined in the case of the real data to address sample bias. The target-group considered were the tree ferns detected in the island, including
C. cooperi,
C. medullaris,
Cyathea sp., and
D. antartica. The aim of a “target-group” background is to include spatial bias in the background as embedded in the presence-only data so that both become spatially biased in a similar manner. This procedure reduces the potential for the MaxEnt predictions to resemble the spatial bias included in the species data [
43,
47]. A total of 10,000 records (locations) were selected across the island through a weighted random sampling using as probability weights the inverse distance from the location to the closest tree fern presence identified in the field survey. In this way, locations closer to sampled locations were more likely to be selected and hence more represented in the background.
MaxEnt was used within bootstrapping procedures. Bootstrapping allows calculating measures of variance such as confidence intervals useful to reflect the expected uncertainty of estimates produced based on field samples. The number of bootstrap replicates used with the real and simulated species was 250 and 500, respectively. Each of the bootstrap replicates randomly selected 200 records from the species samples to create a bootstrap sample with a specific species misidentification rate, r. First, the bootstrap sample did not included error (r = 0%), that is the bootstrap samples randomly selected 200 records from either the C. cooperi data set or the sample defined for the simulated target species. Then, the bootstrapping samples included increasing rates of error, from 1% to 32%. For example, each bootstrap sample with 1% of error contained 198 random records of the target species and two random records of the contaminating species. Thus, in the case of real data, the random records selected from the C. cooperi dataset were contaminated with records randomly selected from the C. medullaris dataset. However, here, the rate of 32% was not possible to investigate because each species record could be selected only one time per iteration to avoid duplicates, and at least 64 records of C. medullaris were needed while it has only 32 records. In the case of the simulated data, bootstrapping was applied in each scenario, meaning that the random records selected from the sample defined for the simulated target species were contaminated with records randomly selected from the sample of the simulated contaminating species defined in the relevant scenario.
Finally, predictions were produced for the contaminating species, which is equivalent to an error rate of 100%. In the case of the real data, a bootstrapping procedure was not applied here as the dataset of C. medullaris has only 32 records, which were used simultaneously to produce a model predicting the presence of C. medullaris across the island. In the case of the simulated data, predictions for the contaminating species defined in each scenario were calculated within a bootstrapping procedure similar to that described above, with bootstrap samples of size 200 randomly selected only from the sample of the contaminating species defined in the relevant scenario.
Each bootstrapping procedure created 250 or 500 MaxEnt outputs, which needed to be summarized. Each location
i in the island was assigned the mean value of the predictions calculated in the bootstrapping procedures for the real and simulated species. The mean of the predictions were kept for further analysis and are, hereafter, simply referred to as “predictions”. The 95% confidence intervals around the predictions were also calculated for each location. Additionally, the predictions were ranked in order of magnitude. Thus, the modeling results could be used in two different ways, based on either the value of the predictions or their relative rank order. These two distinct ways of representing SDM outputs are commonly considered in real-world applications [
48,
49].
Table 1 summarizes the modeling definitions applied.
Table 1.
Summary of the modeling setup performed with MaxEnt.
Table 1.
Summary of the modeling setup performed with MaxEnt.
| Modeling setup | Real data | Simulated data |
|---|
| Target species | Cyathea cooperi
(351 records) | Target species
(1000 records) |
| Contaminating scenarios | 1 | 5 (I, II, III, IV and V) |
| Contaminating species | Cyathea medullaris
(32 records) | Contaminating species of scenarios I–V
(1000 records each) |
| Mis-identification rates r | 7 (0, 1, 2, 4, 8, 16 and 100%) | 8 (0, 1, 2, 4, 8, 16, 32 and 100%) |
| Bootstrapping replicates | 250 * | 500 |
| Bootstrap sample size | 200 * | 200 |
| SDMs outputs produced | 7 | 36 (7 settings of r (i.e., r > 0) times 5 scenarios plus one model without contamination (i.e., r = 0)) |
Lastly, the accuracy of the predictions produced using the simulated data were measured through the calculation of the AUC as it is widely used. Specifically, for each scenario and error rate 50 presences and 50 absences were randomly sampled 100 times from the testing sample to calculate 100 AUC values by means of the R package PresenceAbsence [
50]. The mean of the 100 AUC values was calculated for each scenario and error rate and are hereafter referred to as “AUC values”.
2.4. Analyses
Two analyses (A and B) were performed to understand the nature of the effects of species misidentification on MaxEnt predictions. Another two analyses (C and D) were performed to assess the magnitude of the effects and their potential impacts of practical applications. The four analyses (
Table 2) were performed for the results obtained with the real and simulated data.
Table 2.
Summary of the analyses performed to examine the impacts of misidentification on the MaxEnt predictions.
Table 2.
Summary of the analyses performed to examine the impacts of misidentification on the MaxEnt predictions.
| Analysis | Purpose | Methods |
|---|
| A | Understanding whether species misidentification caused a contraction or expansion of the predicted distribution of the target species. | Comparison of the estimate of the probability density function of the predictions produced with and without contaminated data. Estimates were obtained with the kernel method, namely the Gaussian smoothing kernel [51]. |
| B | Identifying the direction of the contraction or expansion effects identified in Analysis A, namely whether the contaminating data shifted the MaxEnt predictions of the species presence towards the distribution of the contaminating species. | Calculation of Schoener’s D comparing the MaxEnt predictions produced using contaminated data (1%≤ r ≤32%) to both the predictions produced using the gold standard data set (r = 0%) and the contaminating species (r = 100%). |
| C | Assessing the magnitude of the effects identified in the previous two analyses. | Number of pixels for which the MaxEnt predictions produced using contaminated data and the gold standard data set differed significantly (i.e., the 95% confidence interval of the SDM predictions did not overlapped). |
| D | Assessing the potential impacts of species misidentification on practical applications that use SDM based analysis to identify priority areas such as in management. | Identification of the omission and commission errors committed using contaminated data while defining priority areas (i.e., the MaxEnt predictions that ranked in the top decile). |
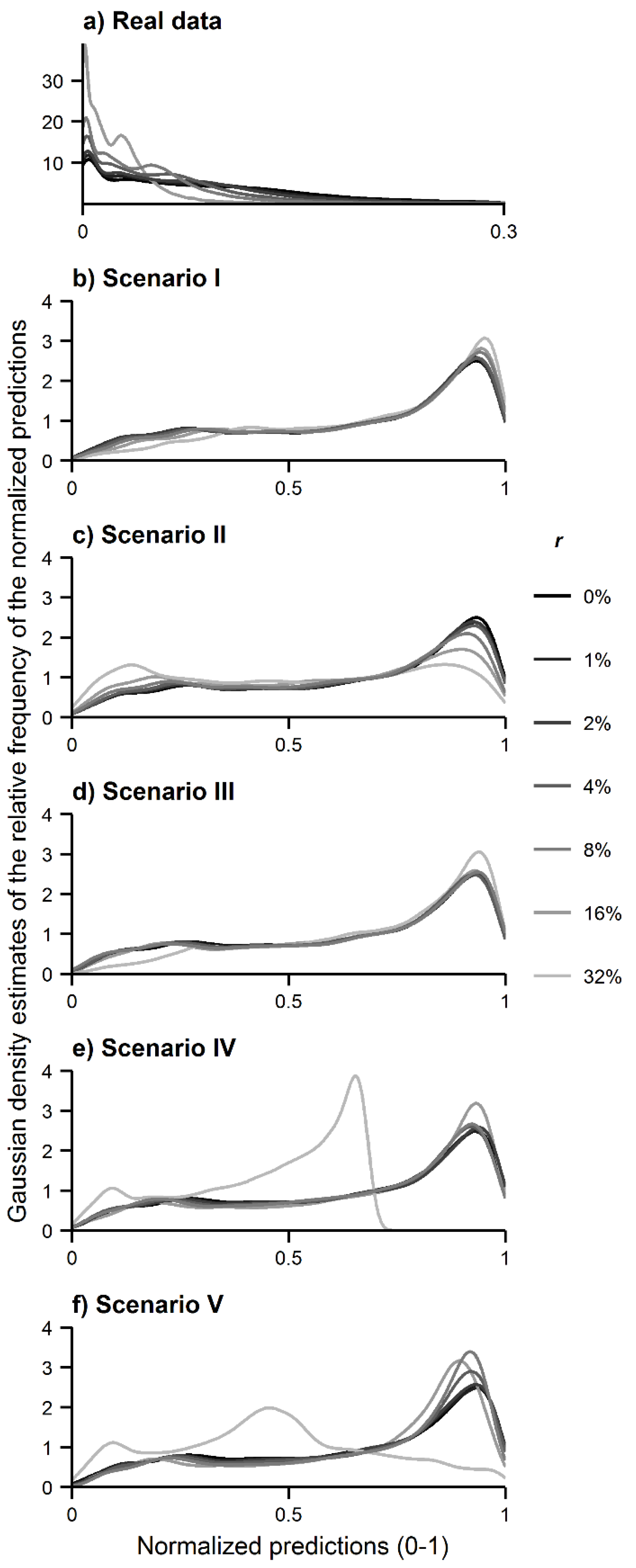
The relative frequency of the predicted values produced by MaxEnt across the island was examined in Analysis A. The comparison between the relative frequency of the predicted values produced with and without contaminated data allows for understanding of whether species misidentification caused a contraction or expansion of the predicted distribution of the target species. Specifically, when contraction occurs, the relative frequency of low prediction values is expected to increase at the expense of a decrease of the frequency of high prediction values; with expansion the opposite occurs. The Gaussian kernel density estimates of the prediction values were, thus, calculated by means of the R package ggplot2 [
52]; kernel density estimates are close to histograms but facilitate legibility and interpretation.
The direction of the contraction or expansion effects were analyzed in Analysis B, namely whether species misidentification shifted the MaxEnt predictions of the species presence towards the distribution of the contaminating species. Schoener’s
D [
53,
54] was used to compare the predictions produced using contaminated data (1%≤
r ≤32%) to both the predictions produced using the gold standard data set (
r = 0%) and the contaminating species (
r = 100%). The calculation of Schoener’s
D is based on normalized prediction values (all predictions should sum to 1) and may be expressed as
D = 1 − 1/2∑|p
Xi − p
Yi|, where p
Xi and p
Yi are the normalized prediction values on location
i of the SDM outputs being compared. Thus, Schoener’s
D ranges between 0 and 1 and provides a measure of the similarity of two modeling outputs in the geographic space.
The MaxEnt outputs produced using contaminated data (1% ≤ r ≤ 32%) were, in Analysis C, compared again in the geographic space to the MaxEnt outputs produced using the gold standard data set (r = 0%). However, analysis C provides a measure of the magnitude of the effects identified in the previous analyses. The difference between the predictions obtained with and without contaminated data for a given location i was considered insignificant if the 95% confidence intervals of the predictions overlapped. The proportion of the locations of São Miguel whose predictions differed significantly was calculated.
Finally, the potential impacts of species misidentification on practical applications such as management were considered in Analysis D. Specifically, this analysis focused on only the locations that ranked in top decile (i.e., 10%), as an example, as sites with relatively higher prediction values are commonly targeted, such as for surveillance of early invasions of alien species. Such locations are hereafter referred to as priority areas. The omission and commission errors committed by MaxEnt in the definition of priority areas were calculated through the comparison of the location of the priority areas defined with and without contaminated data. Omission error is the proportion of the locations defined as priority areas using the gold standard data set but not when using contaminated data. Commission error is the proportion of the locations defined as priority areas using contaminated data but not when using the gold standard dataset.
3. Results
The results of the analyses performed show that the use of spatial data of a species contaminated with records of another species changed the predicted distribution of interest. Analysis A shows that the predicted distribution of the target species either contracted or expanded as the density estimates calculated were shifted towards lower or higher prediction values (
Figure 3). The size of the effects observed was, as expected, positively related to the size of the misidentification rate, whereas the type of effect observed—contraction or expansion—was dependent on the distribution of the contaminating species. Contraction tended to occur only when the contaminating species was less dispersed than the target species while, conversely, expansion tended to occur when the contaminating species was more dispersed than the target species. Some examples are evident from the results. With regard to the real data, the predicted distribution of the target species
C. cooperi contracted when modeled with contaminating records of
C. medullaris (
Figure 3a), which has a limited distribution in São Miguel.
Figure 3a shows that the relative frequency of high prediction values decreased whereas the relative frequency of low values increased as a function of the error rate. With regard to the simulated data, similar results were observed, for example, in scenario II (
Figure 3c), in which the niche of the contaminating species was defined as narrow relative to that of the target species. On the contrary, in scenarios I and III, in which the contaminating species had a wider niche than the target species, the predicted distribution of the target species expanded.
Figure 3b,d shows that the relative frequency of high prediction values increased in scenario I and III as a function of the misidentification rate.
Figure 3.
Gaussian kernel density estimates of the MaxEnt predictions: (a) real data; (b) simulated data in scenario I; (c) simulated data in scenario II; (d) simulated data in scenario III; (e) simulated data in scenario IV; and (f) simulated data in scenario V.
Figure 3.
Gaussian kernel density estimates of the MaxEnt predictions: (a) real data; (b) simulated data in scenario I; (c) simulated data in scenario II; (d) simulated data in scenario III; (e) simulated data in scenario IV; and (f) simulated data in scenario V.
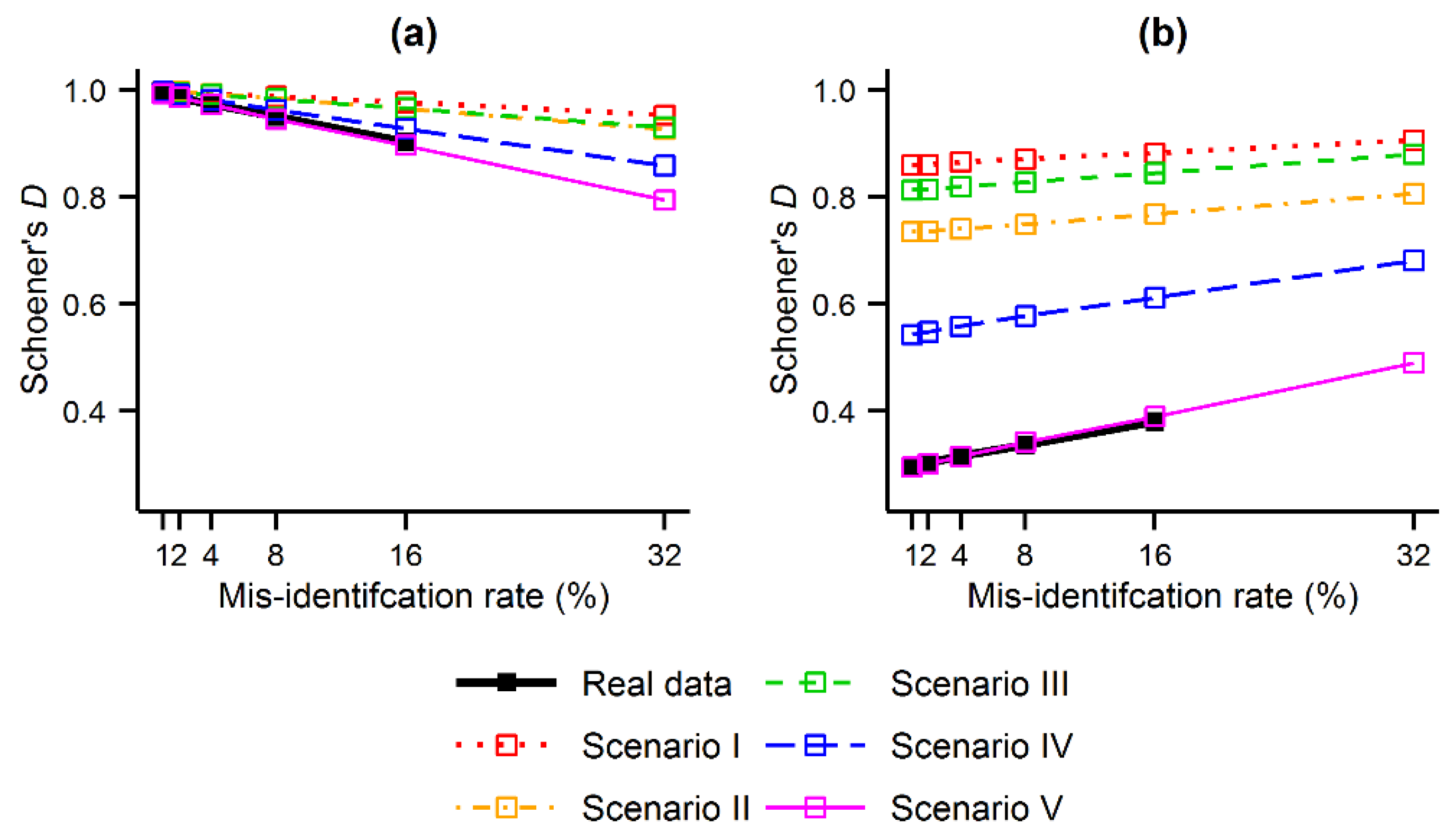
The second analysis performed, Analysis B, focused on the direction of the contraction and expansion effects identified, and shows that the predicted distribution of the target species contracted or expanded towards the distribution of the contaminating species.
Figure 4 shows that the predicted distribution of the target species was progressively shifted towards the distribution of the contaminating species as the misidentification rate increased. Specifically, Schoener’s
D showed that the MaxEnt outputs became less similar to those produced using the gold standard data set, as expected, and became more similar to the outputs produced for the contaminating species. For example, as regards the tree ferns,
Figure 4a shows that the similarity between the MaxEnt output obtained with
r = 1% and that obtained with the gold standard data set (
r = 0% ) is very high (Schoener’s
D ∼1). As the value of
r increased, the value of Schoener’s
D decreased. That is, the distribution of
C. cooperi predicted with increasing rates of error diverged progressively from the actual distribution of the species. On the contrary, in
Figure 4b, the similarity between the MaxEnt output obtained using
r = 1% and that obtained for the contaminating species (
r = 100%) was very low (Schoener’s
D ∼0.3), but increased with increasing values of
r. This means that the use of misidentified records caused the predicted distribution of
C. cooperi to become more similar to the distribution of the contaminating species
C. medullaris. These trends observed in
Figure 4 were in general consistent across the real data and the scenarios of the simulated data. The influence of the niche of the species was, in the context of Analysis B, irrelevant as the ecological distance between the niches of the target and contaminating species was expected to change merely the magnitude of the Schoener’s
D values; in all cases Schoener’s
D showed that the predicted distribution was shifted towards the distribution of the contaminating species, which meets the purpose of the analysis.
Figure 4.
Similarity (Schoener’s D) between the MaxEnt outputs produced with and without contaminated data: (a) comparison between the contaminated outputs (1% ≤ r ≤ 32%) and those produced using the gold standard data set (r = 0%); and (b) comparison between the contaminated outputs (1% ≤ r ≤ 32%) and those produced using the contaminating species (r = 100%).
Figure 4.
Similarity (Schoener’s D) between the MaxEnt outputs produced with and without contaminated data: (a) comparison between the contaminated outputs (1% ≤ r ≤ 32%) and those produced using the gold standard data set (r = 0%); and (b) comparison between the contaminated outputs (1% ≤ r ≤ 32%) and those produced using the contaminating species (r = 100%).
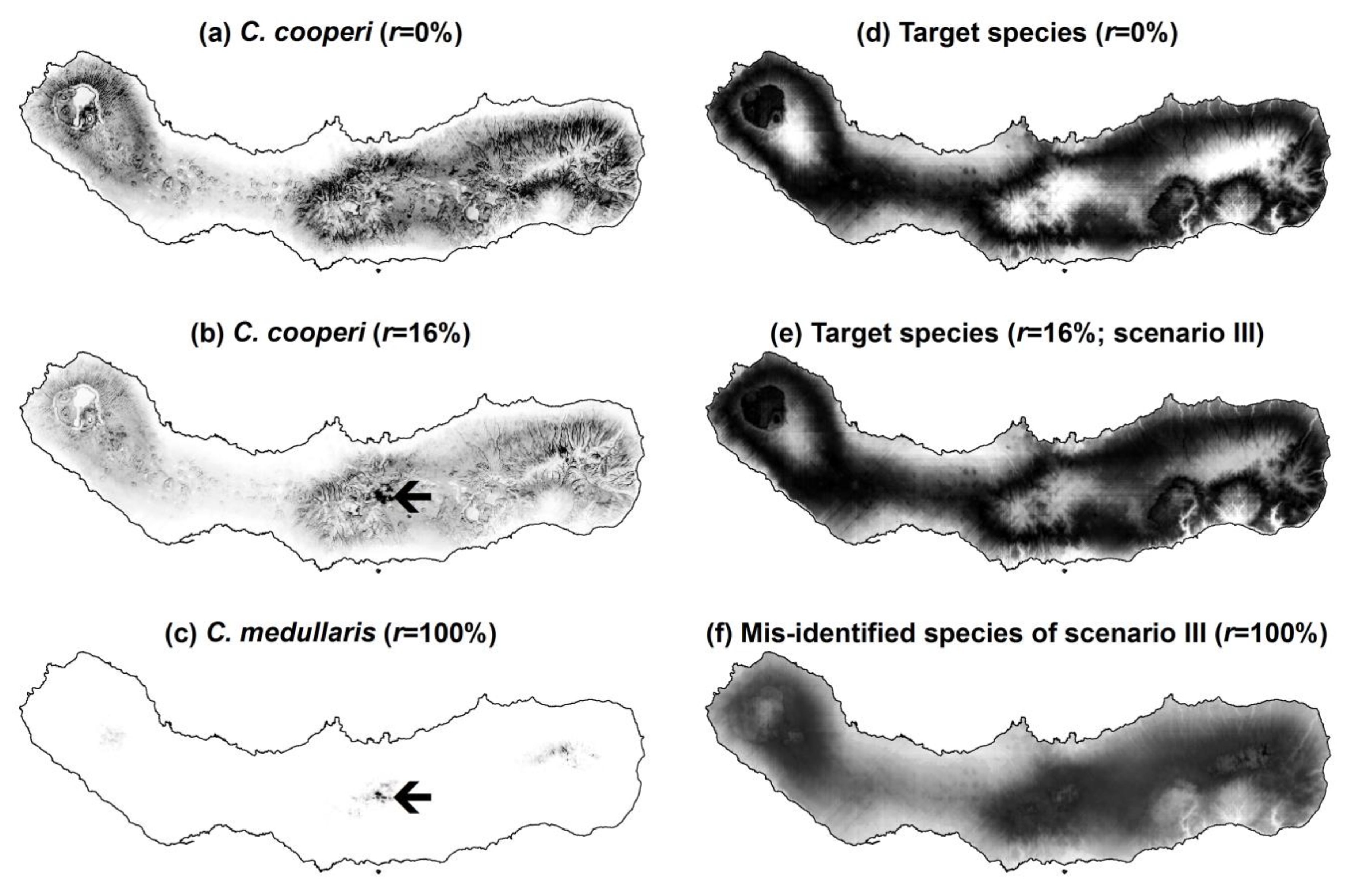
The effects identified in Analysis A and B are visually evident in the maps produced by MaxEnt, and some examples are shown in
Figure 5. With regard to the real data, in which the contaminating species was less widely distributed than the target species, the use of contaminated data led MaxEnt to produce lower prediction values of the target species presence across the island. That is, the predicted distribution of
C. cooperi contracted (
Figure 5a,b). Moreover, the locations of São Miguel that present relatively higher prediction values in
Figure 5b (
r = 16%), highlighted by an arrow, correspond to the locations of higher prediction values for the contaminating species
C. medullaris (
Figure 5c). This means that the misidentified records shifted the predictions of presence of
C. cooperi towards those of
C. medullaris. Similar effects were visible in the results obtained with the simulated data. However, the simulated data also allowed assessment of scenarios in which the niche of the contaminating species was broader than that of the target species. In this situation the predicted distribution of the target species expanded (
Figure 5d,e), particularly to zones at altitude in scenarios III–V because the distribution of the contaminating species was simulated to include such environments (
Figure 2 and
Figure 5f).
Figure 5.
Some examples of predictions of presence of the real and simulated species produced by MaxEnt: (a) predictions of presence of C. cooperi produced using the gold standard data set (r = 0%); (b) predictions of presence of C. cooperi produced using contaminated data (r = 16%); (c) predictions of presence of the contaminating species C. medullaris (r = 100%); (d) predictions of presence of the simulated target species using the gold standard data set (r = 0%); (e) predictions of presence of the simulated target species using contaminated data in scenario III (r = 16%); and (f) predictions of presence of the simulated contaminating species in scenario III (r = 100%); Notes: greyscale from black (high prediction values) to white (low prediction values). Black arrows in parts (b) and (c) highlight an area where the influence of the distribution of the contaminating species over that of the target species is particularly noted when using contaminated data.
Figure 5.
Some examples of predictions of presence of the real and simulated species produced by MaxEnt: (a) predictions of presence of C. cooperi produced using the gold standard data set (r = 0%); (b) predictions of presence of C. cooperi produced using contaminated data (r = 16%); (c) predictions of presence of the contaminating species C. medullaris (r = 100%); (d) predictions of presence of the simulated target species using the gold standard data set (r = 0%); (e) predictions of presence of the simulated target species using contaminated data in scenario III (r = 16%); and (f) predictions of presence of the simulated contaminating species in scenario III (r = 100%); Notes: greyscale from black (high prediction values) to white (low prediction values). Black arrows in parts (b) and (c) highlight an area where the influence of the distribution of the contaminating species over that of the target species is particularly noted when using contaminated data.
The magnitude of the contraction and expansion effects shown above was assessed in Analysis C. The proportion of predictions (
i.e., locations) that differed significantly when using the gold standard data set and contaminated data was, as expected, positively related to the size of the misidentification rate (
Figure 6). However, the effects were very pronounced as a small increase of the misidentification rate caused a large proportion of predictions to differ significantly across São Miguel. For example, 1% of misidentified records used to model the distribution of
C. cooperi changed significantly the MaxEnt predictions in only 1% of the locations of the island (
Figure 6b); increasing
r to 4 and 16% the proportion of significant differences increased to 24 and 77% of the locations respectively (
Figure 6c,d). The results obtained with the simulated species were similar, and also allowed assessment of the influence of the niche of the contaminating species. The proportion of significant differences observed in the MaxEnt predictions increased from scenarios I–V (
Figure 6a). That is, the proportion of predictions that differed significantly when using contaminated data increased, following the increasing ecological distance observed between the niches of the simulated target and contaminating species across scenarios I–V.
Figure 6.
Magnitude of the effects caused by species mis-identification on the MaxEnt predictions: (a) proportion of the predictions that differed significantly at the various misidentification rates for the real and simulated species; (b) location of the predictions that changed significantly (in black) for C. cooperi using the misidentification rate of 1%; (c) Location of the predictions that changed significantly (in black) for C. cooperi using the misidentification rate of 4%; and (d) location of the predictions that changed significantly (in black) for C. cooperi using the misidentification rate 16%.
Figure 6.
Magnitude of the effects caused by species mis-identification on the MaxEnt predictions: (a) proportion of the predictions that differed significantly at the various misidentification rates for the real and simulated species; (b) location of the predictions that changed significantly (in black) for C. cooperi using the misidentification rate of 1%; (c) Location of the predictions that changed significantly (in black) for C. cooperi using the misidentification rate of 4%; and (d) location of the predictions that changed significantly (in black) for C. cooperi using the misidentification rate 16%.
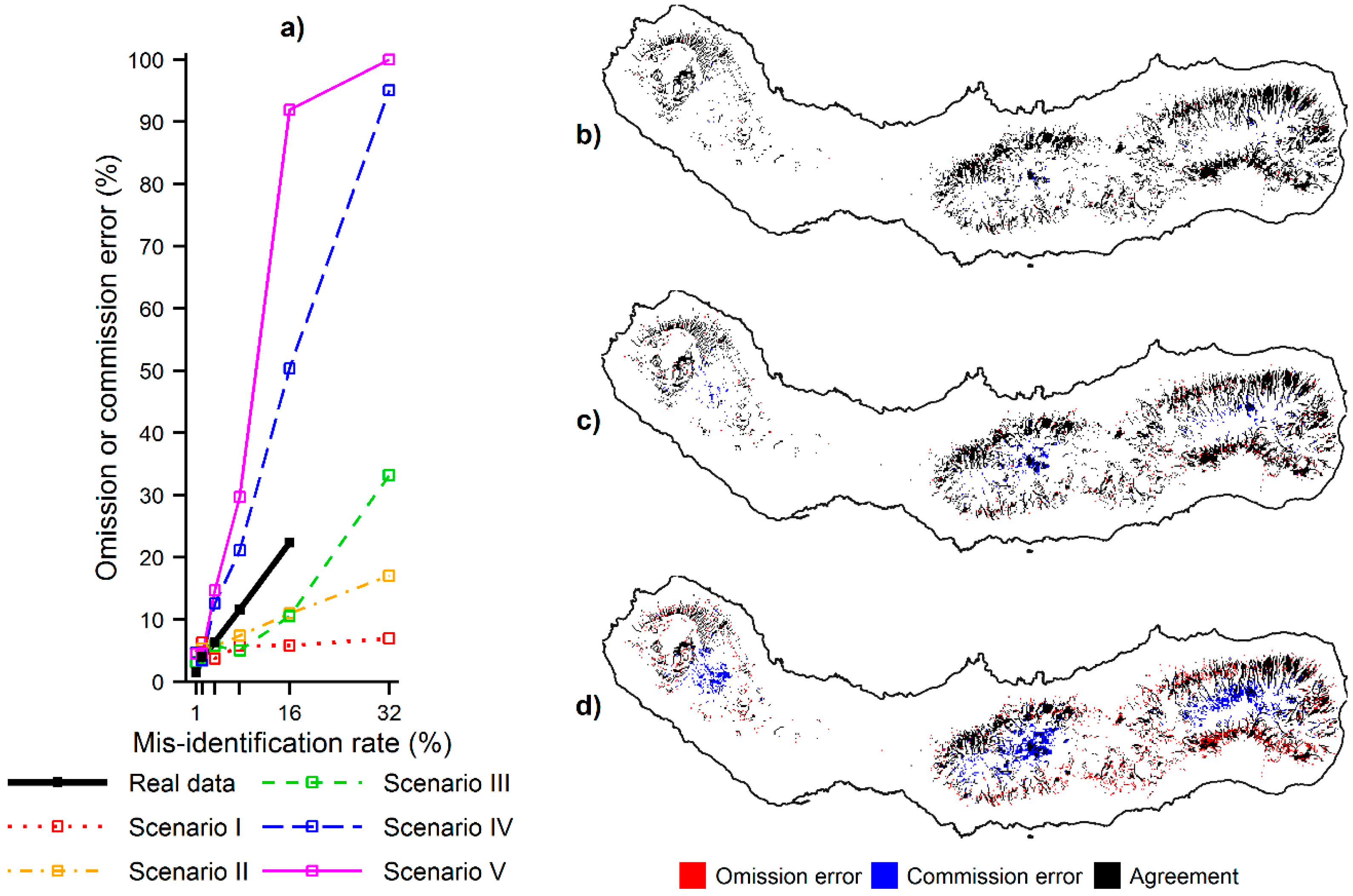
The last analysis performed, Analysis D, focused on the potential impact that the effects identified above may have on practical applications.
Figure 7 shows that the omission and commission errors made while defining priority areas, for example useful for environmental management, increased progressively as the misidentification rate increased. Locations of high relative probability of the species presence were erroneously left out of the set of priority areas when contaminated data was used (omission errors), while locations of low relative probability of the species presence were erroneously included in the set of priority areas when contaminated data was used (commission errors). Furthermore, the results also showed that the size and location of the omission and commission errors depended on the distribution of the species confused. With regard to the simulated data, the size of the errors was positively related to the ecological distance between the niches of the target and contaminating species. Specifically, the errors increased from scenarios I–V (
Figure 7a), which corresponds to an increasing ecological distance between the niches. The location of the errors was associated with the ecological preferences of the species. Omission errors tended to appear at locations preferred by the target species but not the contaminating species and commission errors tended to appear in opposite conditions. For example,
Figure 7b–d show the location of the omission and commission errors committed while defining priority areas for
C. cooperi with imperfect data. As the misidentification rate increased, the higher ranked predictions appeared progressively in the interior part of São Miguel, where
C. medullaris occurs. These commission errors occurred at the expense of omission errors located elsewhere. Note that the real data used is a case in which the niche of the contaminating species is less widely distributed relative to that of the target species and, thus, the predicted distribution of
C. cooperi contracted (
Figure 3a). As a result, the location of the omission and commission errors reflects the contraction of a broader species distribution towards the narrow environments associated to the records of the contaminating species.
Figure 7.
Omission and commission errors committed by MaxEnt while defining priority areas using contaminated data: (a) omission or commission error committed at the various misidentification rates for the real and simulated species; (b) location of the omission and commission errors committed for C. cooperi using the misidentification rate of 1%; (c) location of the omission and commission errors committed for C. cooperi using the mis-identification rate of 4%; and (d) location of the omission and commission errors committed for C. cooperi using the misidentification rate of 16%. Note: The priority areas that were correctly defined using contaminated data are shown in black in parts (b), (c) and (d).
Figure 7.
Omission and commission errors committed by MaxEnt while defining priority areas using contaminated data: (a) omission or commission error committed at the various misidentification rates for the real and simulated species; (b) location of the omission and commission errors committed for C. cooperi using the misidentification rate of 1%; (c) location of the omission and commission errors committed for C. cooperi using the mis-identification rate of 4%; and (d) location of the omission and commission errors committed for C. cooperi using the misidentification rate of 16%. Note: The priority areas that were correctly defined using contaminated data are shown in black in parts (b), (c) and (d).
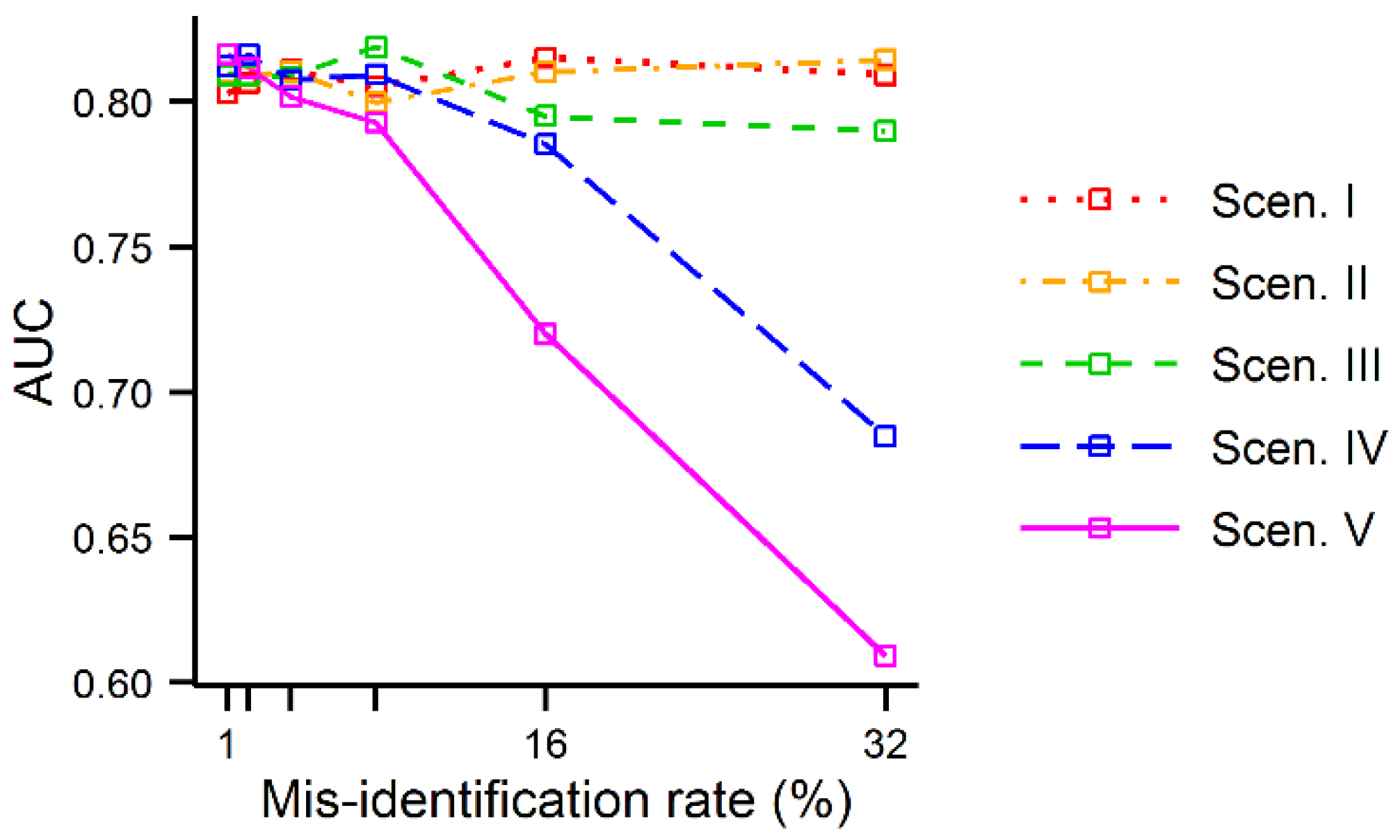
Finally, the impacts of misidentification error identified and measured in analyses A-D were less apparent in the AUC values calculated using the simulated data. Although the AUC values tended to decrease as the error rate,
r, increased, as expected, the AUC values were constant until
r was large. Only when the error rate was 16% in scenarios IV and V the AUC values clearly started to decrease (
Figure 8).
Figure 8.
AUC values of the MaxEnt outputs produced using the simulated data as a function of the misidentification error rate.
Figure 8.
AUC values of the MaxEnt outputs produced using the simulated data as a function of the misidentification error rate.
4. Discussion
Systematic misidentification of species and consequent production of contaminated spatial datasets impacts negatively on species distribution modeling. Species misidentification errors may act to change the predicted distribution of the target species while shifting the predicted distribution towards that of the contaminating species. The magnitude and direction of the changes is positively related to both the misidentification rate and the ecological difference between the distributions of the species confused.
Expansion of the predicted distribution of a species caused by misidentification errors have already been reported in the literature [
31,
32]. Here, however, it is evident that contraction can occur if the contaminating species is less widely dispersed than the target species. For example, Analysis A showed contraction effects in the MaxEnt results produced with real data (
Figure 3a), in which the contaminating species was less widely distributed than the target species (
Figure 1b). It is thus expected that systematic species misidentification error can often act to contract the predicted distribution of a target species since less-dispersed contaminating species may be rare and unfamiliar species and, hence, may be more prone to misidentification, more than well-known species.
Although the effects of species misidentification outlined above may be not surprising, their magnitude may be larger than anticipated. Even low misidentification rates, smaller than the average rates reported in the literature (e.g., 6.8% for plants in Archaux,
et al. [
25]), may correspond to marked changes on the outputs of SDMs (
Figure 6). Worryingly, the rates of species misidentification embedded in species data sets may not be small. For example, a species misidentification rate of ∼70% is reported in Meier and Dikow [
29] for robber flies. The results presented in this paper show that misidentification rates of such size may be expected to have a very large impact on the SDMs’ predictions. Furthermore, the impacts of misidentification error on SDMs’ predictions may go largely unnoticed while assessing their accuracy. The results obtained with the simulated data show that a measure such as the AUC may not indicate any problem with the predictions even if the testing dataset used is free of error as in this study. Therefore, systematic species misidentification addressed in this paper could be a dangerous source of error in species distribution modeling as there may be no means available for its detection once a species dataset is used as if free of error.
Perhaps the main finding of this study is that the occurrence of misidentification errors in species data may compromise the goal behind the application of SDMs. For example, if the SDMs’ predictions are regarded as an estimate of probability [
45], small rates of misidentification error may significantly change the prediction values produced, resulting in erroneous estimates of the probability of the species presence in much of the area in study. This was evident in the results for Analysis C above (
Figure 6). Alternatively, the SDMs’ predictions may be regarded as ordinal, which is enough to identify areas with relatively higher probability of a species presence. In this case, SDMs are required to solve a simpler problem, which is to rank locations by order of probability of a species. The latter was the focus of Analysis D, which showed that systematic misidentification may also influence negatively the rank of the predictions and hence the identification of priority areas (
Figure 7). Critically, misidentification errors may cause priority areas to include locations where the species is unlikely to actually occur, thus wasting efforts and resources, and overlooking locations where the species is likely to occur, thus possibly compromising the effectiveness of management actions.
The location of omission and commission errors committed while defining priority areas relate to the direction of the contraction or expansion effects outlined above. The latter was the focus of Analysis B, which showed that the predicted distribution of the target species was shifted towards the distribution of the contaminating species (
Figure 4). As a result, areas incorrectly identified as priority areas (commission error) will tend to appear in locations close to environments ideal for the contaminating species. Locations that are worth of attention will tend, on the other hand, to be overlooked (omission error) across regions associated with environments preferred by the target species. This is evident, for example, in
Figure 7d, which shows that the commission errors of the priority areas defined for
C. cooperi appeared at altitude, in the interior of the island, where the contaminating species
C. medullaris was detected (
Figure 1b).
The four analyses performed with both real and simulated data show that the occurrence of systematic misidentification errors in species data is expected to degrade SDMs predictions in a wide variety of circumstances; the real dataset represented a common situation in which the species were not at equilibrium and the sample was spatially biased, while the simulated dataset represented a situation in which the species were at equilibrium and the sample unbiased.
Some solutions for the problem of misidentification error may be used yet with strong drawbacks. For example, if information on the reliability of the source of the data or the confidence of the labeling is available, only high confidence cases may be considered like in Ensing,
et al. [
31] and Molinari-Jobin,
et al. [
32]. However, high confidence cases may include misidentification error as well, or exclude cases difficult to identify but correctly identified. This is especially true when species are identified by people only (
i.e., without any help such as genetic analysis), which makes species identification vulnerable to human error. For example, a surveyor may unwittingly misidentify a case with great confidence and
vice versa. Actually, the expertise of botanists involved in species identification has been referred to as a relevant cause of species misidentifications [
25,
28,
30]. Data acquired in circumstances such as the emerging framework of citizen science [
55] need, therefore, careful consideration as surveyors with highly variable skill levels are often involved [
56]. Alternatively, outlier analysis may be used as a means for the detection and removal of suspicious records [
57]. Outliers may, however, correspond to records of the species of interest. For example, outliers may correspond to individuals at the forefront of an invasion and thus provide important information that should be taken into account [
58]. Note that records seen as outliers among records collected across regions of interest (e.g., an island) may be, after all, highly similar to records of the species collected across a larger region. Thus, it is important to take into considerations the entire range of environmental conditions known to be used by the species [
59]. This is not sufficient, however, if a species is introduced into new regions where it meets no constraints [
60], such as predation and competition, and thus has the opportunity of using new environments. Changing the modeling approach is also a possibility and thus occupancy models may be considered. This type of model allows for misidentification errors [
24], but are demanding in data, such as several surveys over time, which may not be logistically possible or not applicable if biodiversity databases are used [
8,
10]. The present study, therefore, highlights that investment on quality should be a continuous concern with regard to data collection.