1. Introduction
Uncertainty is resulted from not knowing the exact degree of the discrepancy between geographic data and the geographic reality which these data are intended to represent. The quality of geographic data is affected by positional, attribute, or temporal accuracy, consistency, completeness, or lineage [
1,
2]. Limitation in human knowledge and capacities, instruments, analysis techniques, and the financial budget can all introduce uncertainty into geographic data. Uncertainty can be propagated or amplified during the process of data management, analysis, and visualization. Despite the fact that uncertainty exists widely in geographic data, it is often disregarded during analysis and decision making [
3]. Without proper consideration of uncertainty in geographic data, a policy decision may be inappropriate and may affect people’s lives dramatically.
In the past thirty years, researchers in Geographic Information Sciences and Systems (GIS) and the related fields have made great progress in defining, measuring, modeling and visualizing uncertainty in geographic data. Uncertainty was identified as one of the long-term research priorities by the University Consortium of Geographic Information Science (UCGIS) in 1996 [
4]. Researchers concluded that appropriate visualization of uncertainty can help map users understand uncertainty and make more informed decisions [
5,
6]. Various methods for uncertainty visualization have been developed and their effectiveness has been tested [
5,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16]. However, there are some gaps in literature regarding how map users may prefer the different visualization techniques and the potential impact of map users’ background on their decision making using uncertainty maps. Particularly, the existing studies failed to address two important questions: (1) which uncertainty visualization method(s) is preferred by map users, and (2) does GIS knowledge and training affect map users’ decision making using uncertainty maps.
The study reported in this paper was conducted to examine the preference for the different visualization methods for representing uncertainty in geographic data and to examine if GIS knowledge and training affects map users’ ability to incorporate uncertainty for better decision making. A survey of 72 undergraduate students was conducted in April 2012 at Texas State University. The findings can provide guidelines for visualizing uncertainty on bivariate maps to encourage informed decision making.
2. Literature Review
Evans [
5] stated that it was map designers’ responsibility to provide uncertainty information to map users so that decisions could be made with the awareness of the data limitation. In the past thirty years, many empirical researches focused on developing effective methods to visualize uncertainty on a map [
5,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16]. Among these studies, MacEachren suggested three types of uncertainty visualization methods: map pairs, bivariate maps and dynamic representations [
17]. Map pairs use one map to represent data and the other map to represent the associated uncertainty [
9,
11,
13]. Bivariate maps report data and uncertainty with one map by using two different visual variables to represent data and uncertainty [
5,
7,
9,
11]. Dynamic representation shows a sequence of possible realizations continuously on a computer screen [
5,
9,
10,
12,
13,
18]. Among these three types of methods, dynamic representation is mostly limited to digital environment. Bivariate maps were found by multiple studies, e.g., [
16,
19] to be easier and more accurate in presenting data and uncertainty than map pairs.
Different visual variables can be used for representing uncertainty on bivariate maps. Bertin suggested location, size, value, texture, color, orientation, and shape [
20]. MacEachren suggested edge crispness (fuzziness), fill clarity, fog, and resolution [
17]. Gershon suggested boundary (thickness, texture, and color), transparency, animation, and extra dimensionality [
21]. Among the above visual variables, size and color value may be more appropriate for depicting uncertainty in numerical data [
17]. Texture was found to be effective on binary maps to represent the existence of uncertainty [
11]. The study by Schweizer and Goodchild [
7] and that by MacEachren
et al. [
11] found that an integral representation using one color attribute to represent data and another to represent uncertainty was ineffective and difficult for map users to identify data and uncertainty. Leitner and Buttenfield [
6] supported using lighter color to display high level of certainty. However, in Kubicek and Sasinka’s study [
16], the majority of the participants preferred lighter color for more uncertain information. MacEachren and others [
22] suggested that opaque objects are better to represent certainty and transparent objects are better for uncertainty. Overall, there is a lack of consensus in literature regarding which visual variable is best at depicting uncertainty and how uncertainty should be visualized on bivariate maps.
A few studies have examined how decision making could be affected by the visualization of uncertainty. Evans [
5] conducted a survey asking the participants to select a site with plenty of hardwood trees. Working with maps of land use classification and their reliability information, most of the participants made correct decisions, and they acknowledged the helpfulness of uncertainty information for their decision making. Leitner and Buttenfield [
6] tested how time, correctness, and confidence in decision making were affected by uncertainty visualization. Their study showed that the number of the survey participants who made correct decisions increased significantly when uncertainty was reported on the map; this was achieved without increasing decision-making time. They concluded that uncertainty visualization added clarity rather than complexity to a map. However, in a study by Viard
et al. [
19], the participants did not make better decisions when uncertainty information was applied. The authors concluded that, to add value for decision making, visualization of uncertainty should be carefully designed and with minimal burden on map users.
The existing literature seems suggesting that visualization of uncertainty can improve decision making when the uncertainty information is properly presented [
5,
6,
19]. However, map users’ ability to understand the uncertainty information that is depicted on maps may impact the quality of decision making. This aspect has been neglected by previous studies and the factors that contribute to map users’ ability to understand and use uncertainty have been under-investigated. Blenkinsop
et al. [
18] and Kubicek and Sasinka [
16] found that experienced GIS users performed better in identifying uncertainty information on maps. The GIS novices in the study by Blenkinsop
et al. [
18] reported that they could not understand the map due to their unfamiliarity with the concept of uncertainty. Contradictory to these two studies, Evans [
5] found no significant difference between GIS novices and experienced GIS users in decision making with uncertainty maps.
3. Method
Through a survey, this study examined the preference of map users for different visual variables for reporting uncertainty on bivariate maps. Moreover, this study investigated if and how map users’ GIS background may impact their capability in using uncertainty for decision making. This section of the paper explains the development of the uncertainty maps that were used in the survey, the design and implementation of the survey, and the techniques that were employed to analyze the survey data.
3.2. Survey Design and Participants
There are two tasks in the survey: a visualization task (Survey Part 1) and a decision-making task (Survey Part 2). The two tasks were fulfilled through two phases in sequence. The visualization task was achieved in phase one in order to investigate how the different uncertainty visualization methods for bivariate maps are preferred by map users. The decision-making task was for phase two and examines map users’ performance on incorporating uncertainty into decision making. The survey participants were asked to complete the visualization task first so that the application of a visual variable in a map in Part 2 would not impact their choice for uncertainty visualization in Part 1.
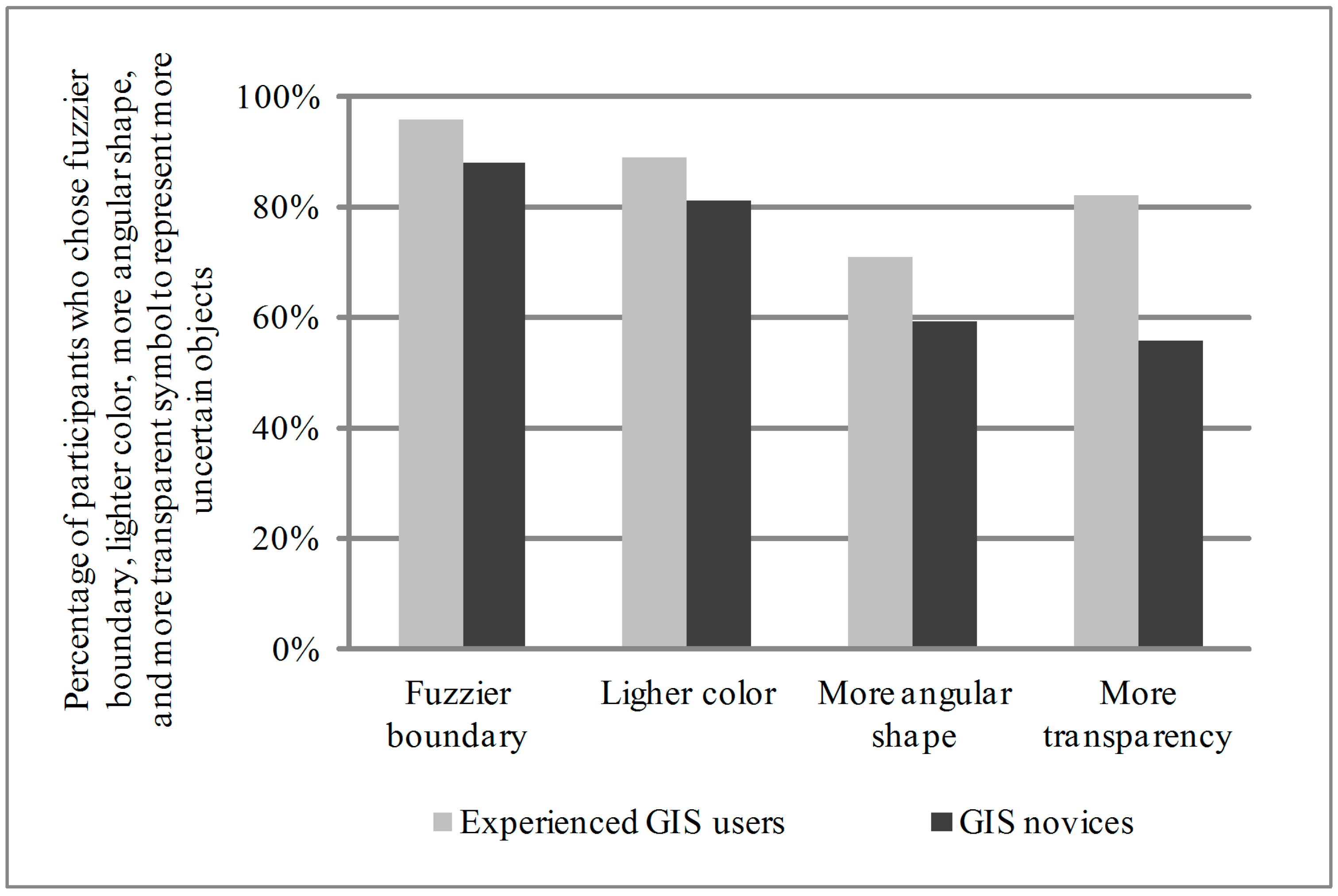
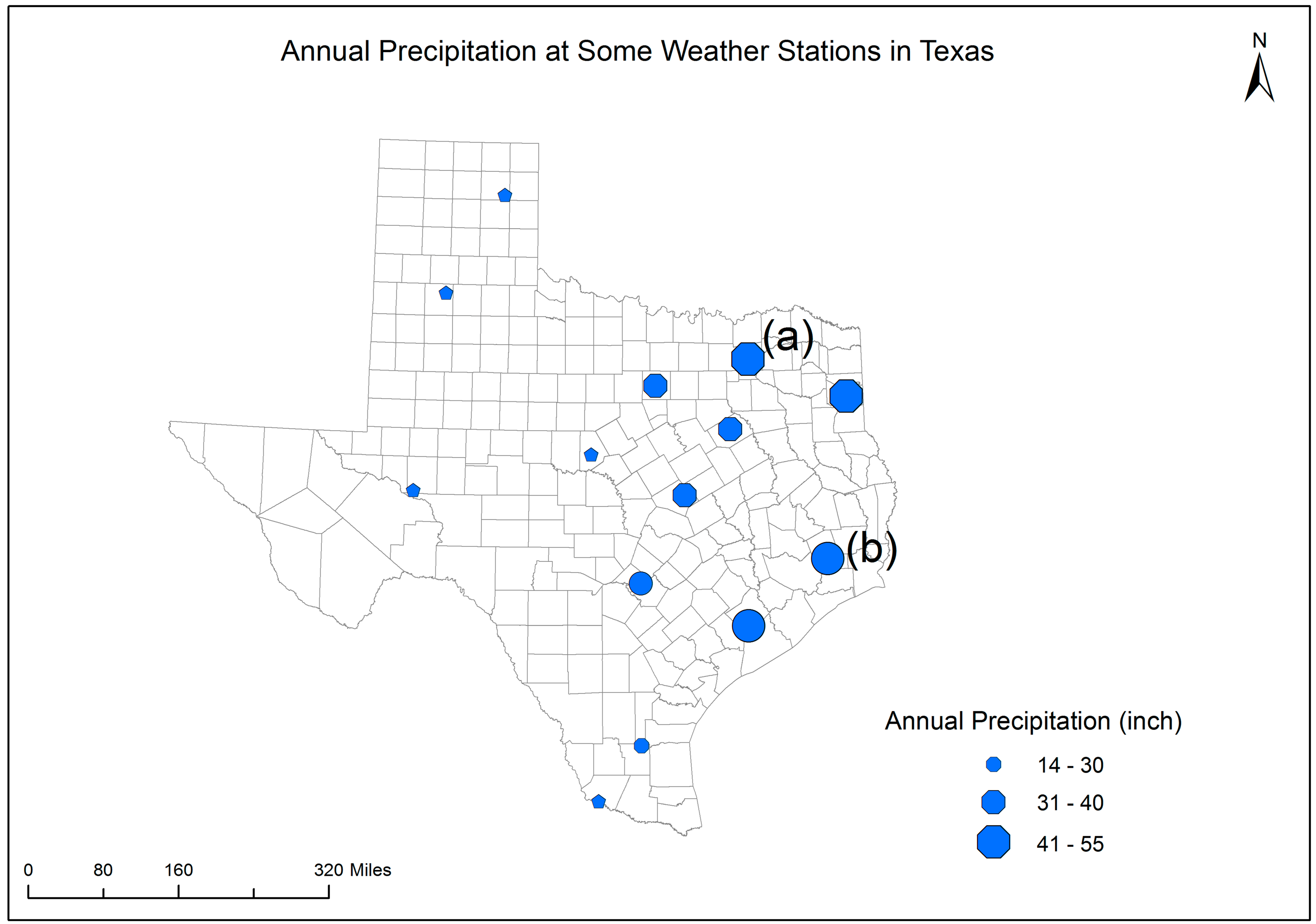
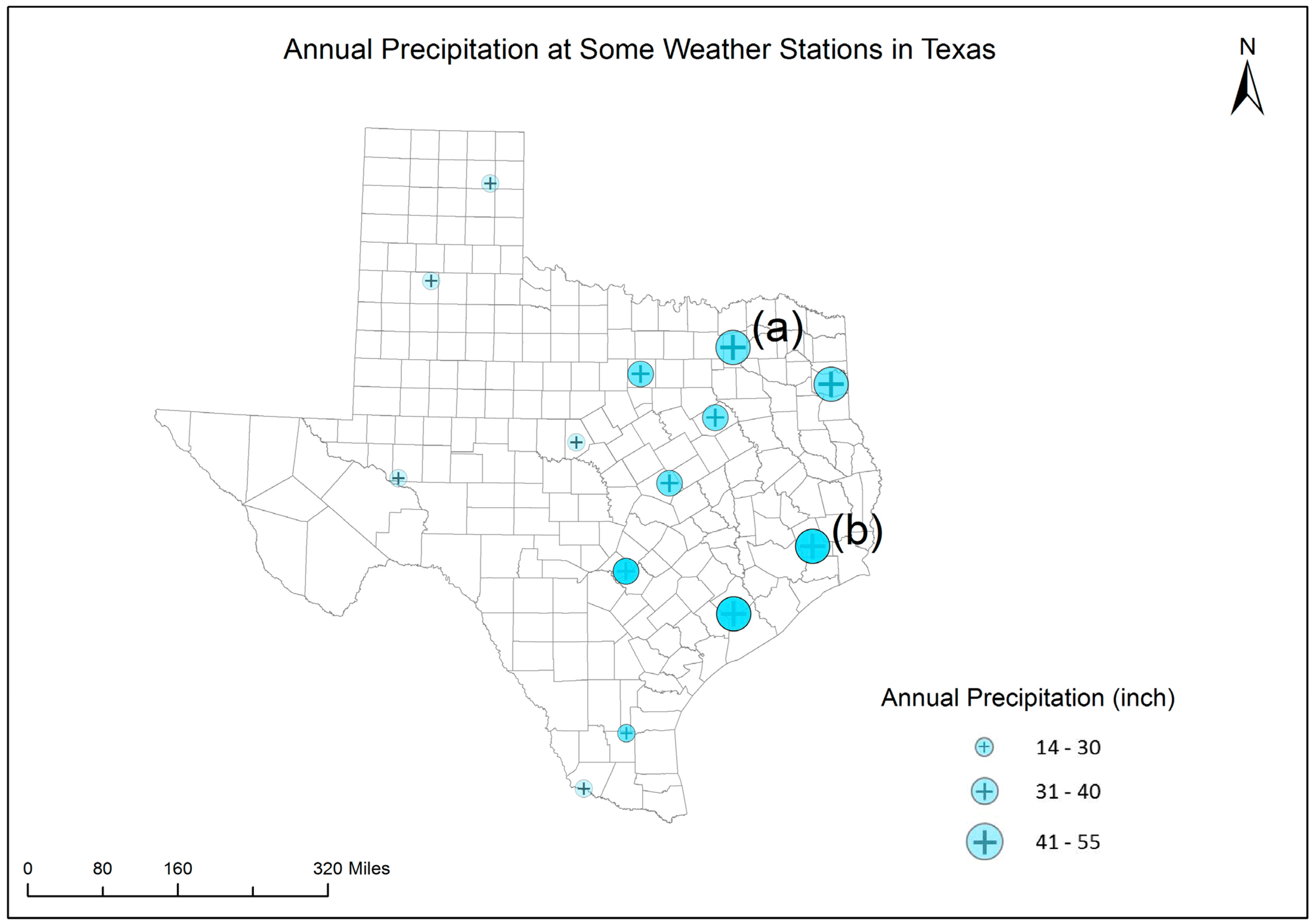
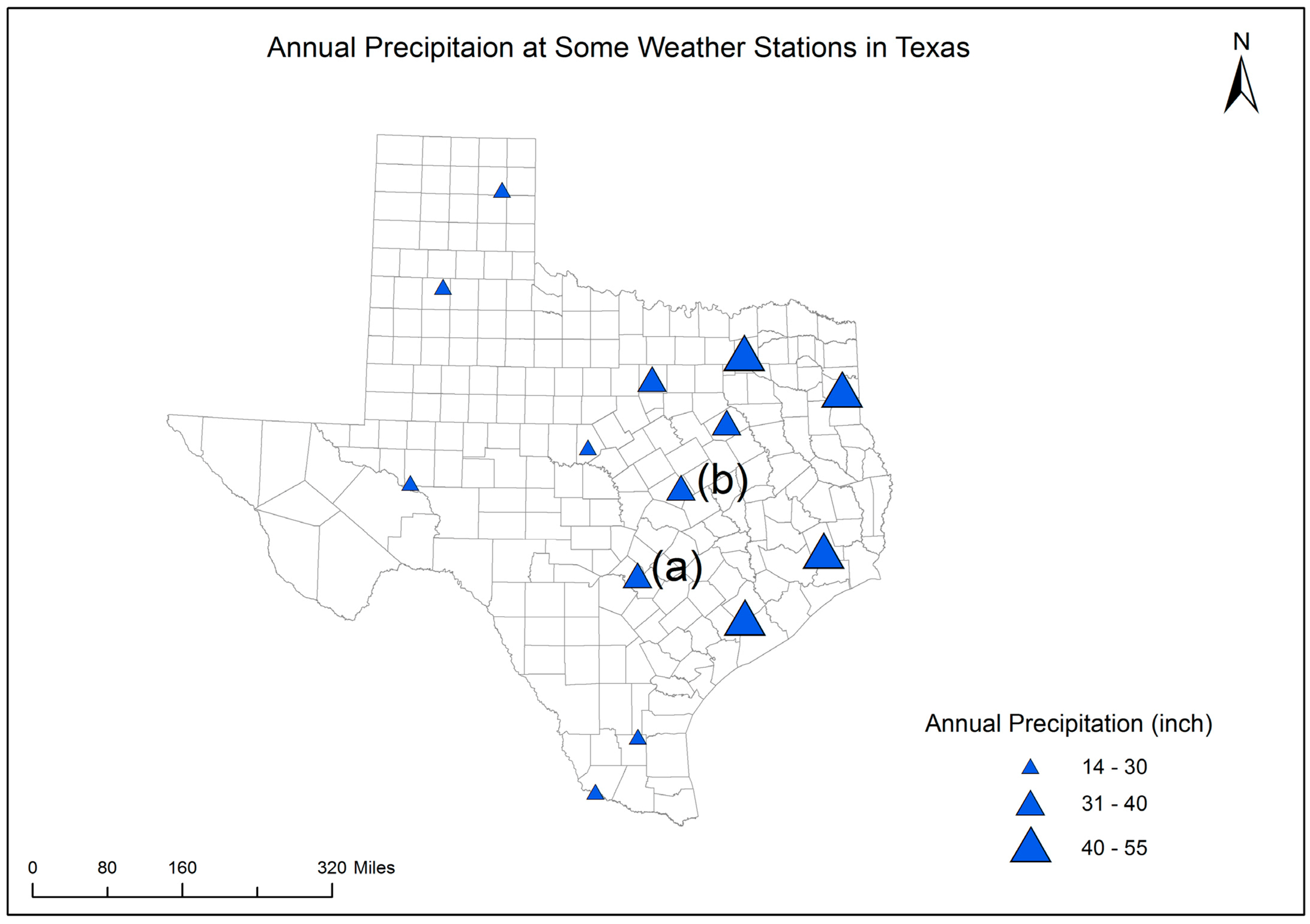
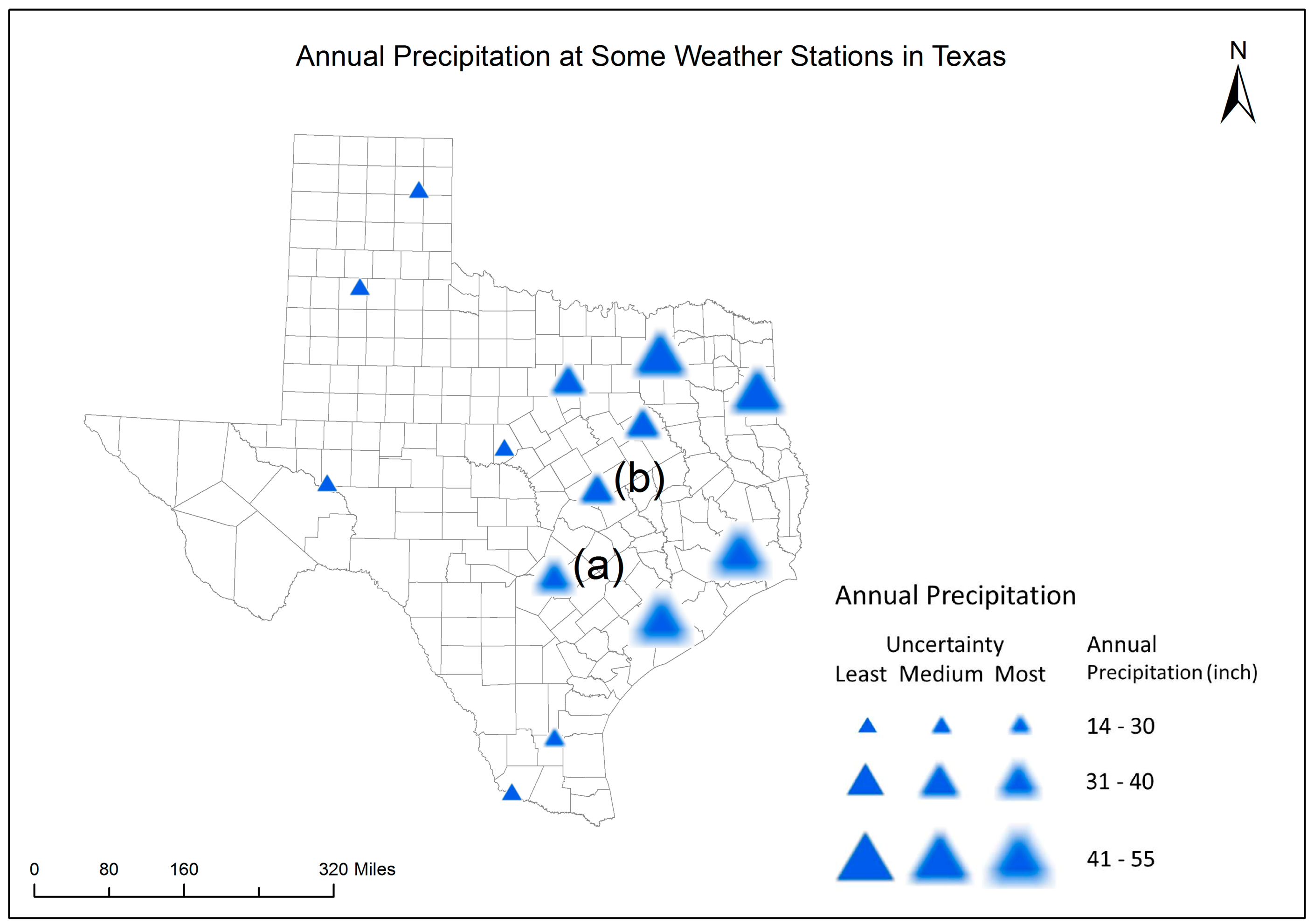
In the visualization task (Part 1), maps 1–4 were provided to the participants. No contextual information about areal precipitation or the associated uncertainty of the precipitation data were shown on the maps. Each map was followed by one question asking which directional change of a visual variable is perceived to be associated with a high level of uncertainty. The four questions were: “Do fuzzier boundary or less fuzzy boundary symbols indicate a high level of uncertainty?”, “Do darker colored or lighter colored symbols indicate a high level of uncertainty?”, “Do more angular or less angular (i.e., more circular) shape symbols represent a high level of uncertainty?”, and “Do more transparent or less transparent symbols represent a high level of uncertainty?”. Finally, after viewing all four maps, the participants were asked to rank the four maps from the most preferred uncertainty visualization to the least preferred.
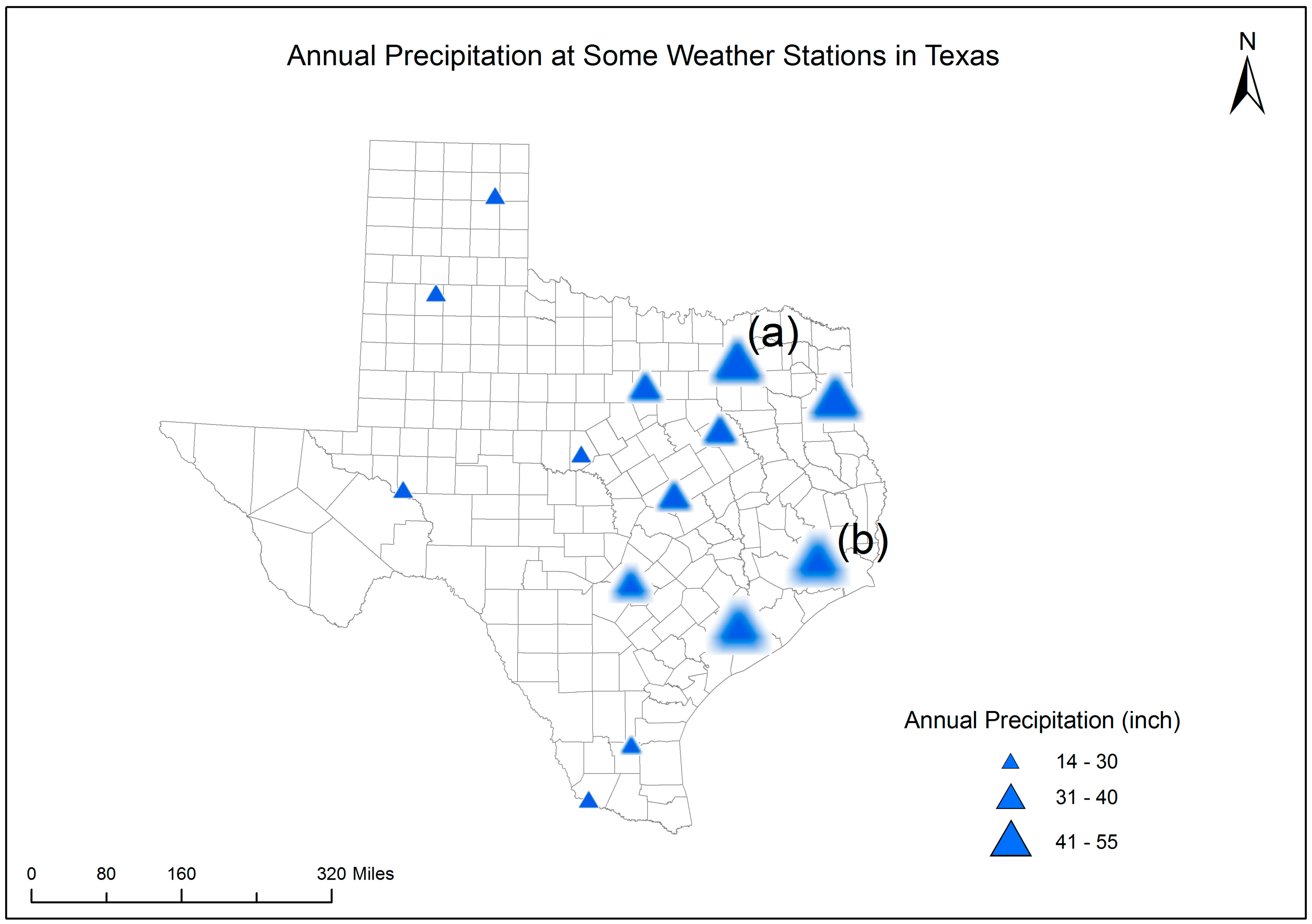
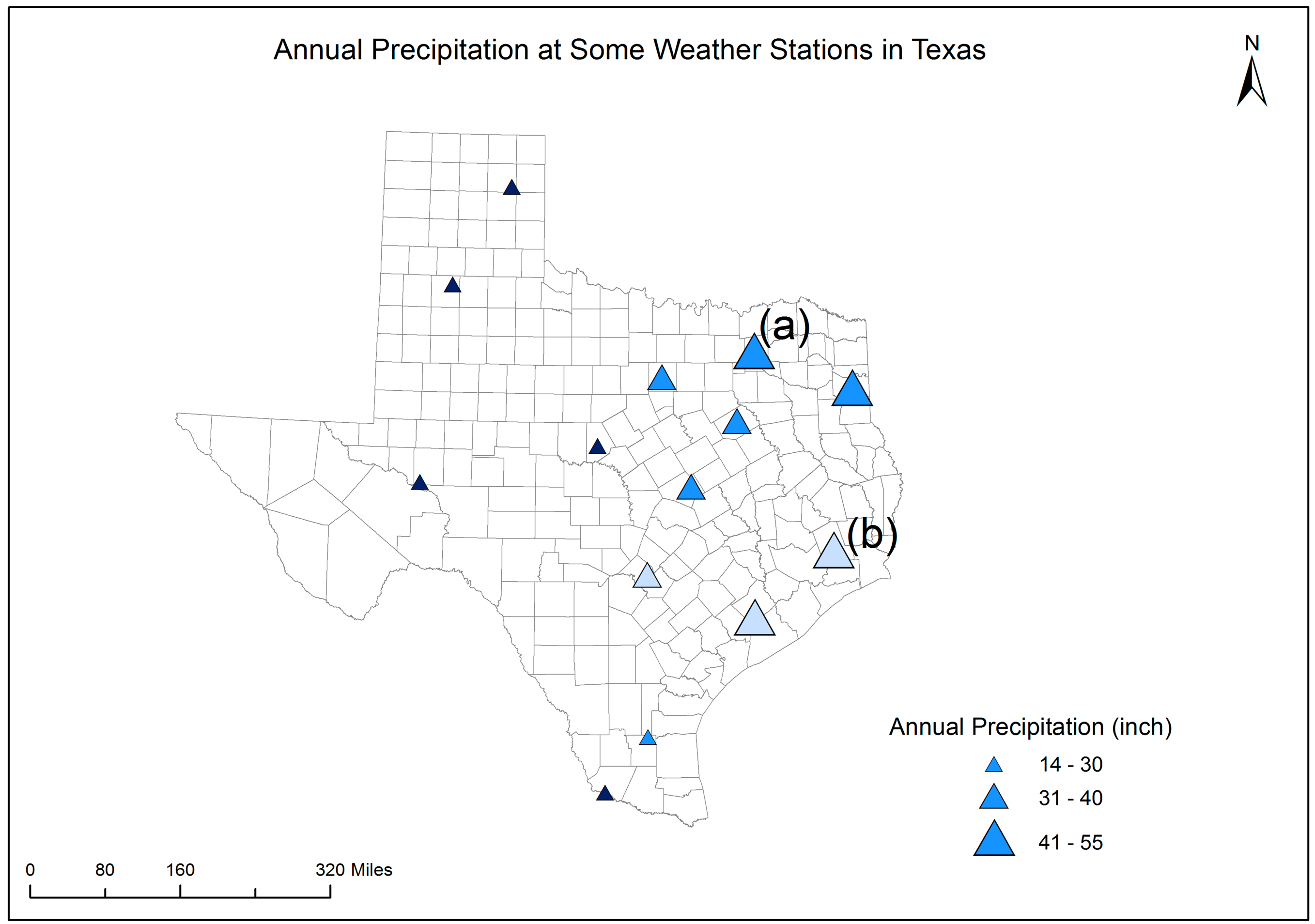
In the decision-making task (Part 2), the participants were asked to choose a better place between the two candidate places to grow a pseudo type of crop. This type of crop was assumed to require an annual precipitation of between 31 and 40 inches. Both candidate places were predicted to have the same perfect level of precipitation for the crop, but with different prediction uncertainty. Map 1 shows the predicted annual precipitation only. Without showing the prediction uncertainty, place (a) and place (b) were expected to be equally good for growing the crop. Map 2 shows both prediction and uncertainty information and was presented to the participants after they finished working with Map 1. On Map 2, the fuzzier boundary symbol at place (a) indicates that the prediction has a higher level of uncertainty than the prediction at place (b). Therefore, place (b) was supposed to be better than place (a) for growing the crop. The last three questions in Part 2 of the survey were used to examine the participants’ perception towards and capabilities in using uncertainty information in decision making.
With the approval from the Institutional Review Board (IRB) of the authors’ university, the survey was conducted on campus in late April of 2012. The participants included 72 undergraduate students from two World Geography classes, one Remote Sensing class, and two Advanced GIS classes. These classes were chosen to balance the participants’ GIS background needed for this study. According to the GIS course sequence design and requirements at the authors’ university, a student would have taken one or more GIS courses before being able to enroll in the Remote Sensing or the Advanced GIS courses. The World Geography course falls outside of the GIS-related course sequence and does not have such pre-requisite. Of the 72 students who finished the survey, 28 students would have taken three or more GIS/Cartography/Remote Sensing classes by the end of the spring 2012 semester. They were grouped as Experienced GIS Users. A total of 32 students never had any GIS related classes. They were grouped as GIS Novices. The remaining 12 students would have taken one or two GIS related classes by the end of the spring 2012 semester. Aiming at examining the potential impact of GIS knowledge and training on map users’ preference for visualization of uncertainty information and the impact on their decision making with uncertainty information, these 12 students were excluded from further analyses. For informational purposes, the data from their surveys are reported in
Appendix II.
3.3. Analysis Methods
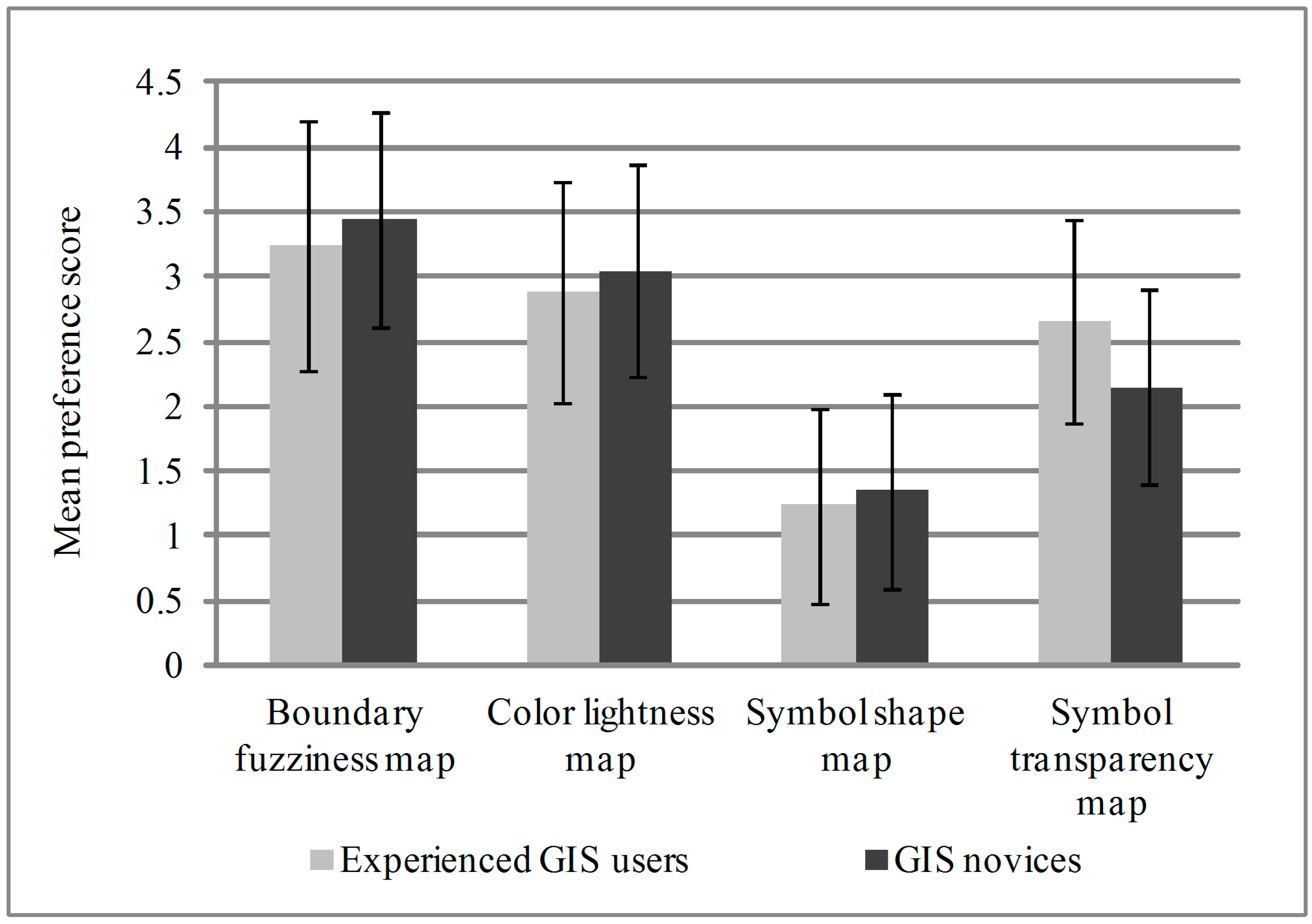
The ranks of the four maps in the responses to Question 5 in Survey Part 1 were coded into preference scores. Among the 60 surveys included in the analyses, 37 participants provided valid rankings. For each valid response, a map ranked first is the most preferred map for reporting uncertainty and receives a preference score of 4; a map ranked the fourth is the least preferred and receives a preference score of 1. Kendall’s coefficient of concordance [
24,
25,
26] was applied to these 37 sets of preference scores to examine the strength of the agreement among the participants regarding preferences for the four bivariate map visualization methods for uncertainty.
For each of the uncertainty maps in Part 1 of the survey, analyses were conducted to investigate the preference difference between the Experienced GIS Users group and the GIS Novices group. The participants’ ranking of preference for the four uncertainty visualization methods were summarized for both groups and are reported in
Table 1. Chi-square Test of Homogeneity [
26] was used to compare the preferences of the Experienced GIS Users and the GIS Novices. However, the problem of small expected frequency exists for all four maps. This problem was corrected by combining adjacent columns in the contingency table to achieve a greater expected cell frequency [
26].
Table 1.
Number of preference ranking for the four maps.
Table 1.
Number of preference ranking for the four maps.
| Visual Variable | Participant Group | Least Preferred | 2nd-Least Preferred | 2nd-Most Preferred | Most Preferred |
|---|
| Boundary fuzziness map | Experienced GIS Users | 1 | 3 | 4 | 9 |
| GIS Novices | 1 | 1 | 6 | 12 |
| Color lightness map | Experienced GIS Users | 0 | 7 | 5 | 5 |
| GIS Novices | 0 | 6 | 7 | 7 |
| Symbol shape map | Experienced GIS Users | 15 | 1 | 0 | 1 |
| GIS Novices | 16 | 1 | 3 | 0 |
| Symbol transparency map | Experienced GIS Users | 1 | 6 | 8 | 2 |
| GIS Novices | 3 | 12 | 4 | 1 |
5. Conclusions
This paper investigated map users’ perception and preference for different visual variables on bivariate uncertainty maps, and further examined if GIS knowledge and training had an impact on map users’ ability to understand uncertainty and use uncertainty maps for decision making. Precipitation data from Texas was collected and used to make several precipitation prediction maps with various uncertainty levels. A survey was conducted among the college students at the authors’ university. Data was collected on map users’ preferences for visual variables for reporting uncertainty on bivariate maps and on how well uncertainty information can be used by the participants for decision making. Kendall’s coefficient of concordance and Chi-square test of homogeneity were applied to the survey data. The results showed that boundary fuzziness was the most preferred visual variable for uncertainty representation on bivariate maps followed by color lightness. It was highly agreeable to the participants that fuzzier boundaries and lighter colors were associated with a high level of uncertainty. The Experienced GIS Users had a higher success rate than the GIS Novices in decision making, with or without uncertainty information. It is believed that GIS knowledge and training enhanced the Experienced GIS Users’ capability in decision making using maps. Most participants reported a positive attitude towards using uncertainty information for decision making.
The result of this case study is very positive. Uncertainty information was highly appreciated by most participants, even though it is a complex concept and often hard for some people to use for decision making. It is believed that with a carefully designed training session on geographic data quality and a proper explanation on the map background and its uncertainty aspect, the general public may be able to understand an uncertainty map better and further incorporate the uncertainty information into their decision making.
It should be noted that the conclusions of this study were drawn from a survey using one particular dataset. Although this is a commonly adopted practice in literature, e.g., [
5,
6,
7,
14], the properties of any dataset may affect the survey results and thus the findings from a study. Therefore, cautions must be applied when extending the findings from this study to uncertainty visualization and decision making using other datasets. Future studies are needed to investigate how dataset properties may impact users’ preference for uncertainty visualization and their decision making with uncertainty information. Finally, the authors recognize that the choices listed as possible reasons for not willing to use uncertainty information for decision making (last question for Part 2 of the survey) are limited and may appear to be guiding. Note that these choices were included to reflect the findings from existing literature. Being the last question on the entire survey, the possible impact on the survey participants’ responses should be limited.