Impacts of Scale on Geographic Analysis of Health Data: An Example of Obesity Prevalence
Abstract
:1. Introduction and Problem Statements
2. Data
- Derived BMI data—data from a five-year cycle of all holders of driver’s licenses in Summit County, Ohio was obtained from Ohio Bureau of Motor Vehicles (OBMV) for 2008–2012 for public health purposes. Drivers in Ohio need to renew their licenses once every five years. By including data (age, height, weight, and home address) of all adults (16 years and older) in a five-year cycle, we basically captured everyone who had a driver’s license in the county during the study period. It should be noted that this data set does not include derived BMI for population age 15 and below or those who do not hold driver’s licenses. Over 480,000 addresses and associated data were geocoded to latitude/longitude coordinates. BMI was calculated for each record. Those records with BMI equal to and over 30 are selected and included in the dataset of obese population as this study focuses only on the distribution of obese population. Since self-reported heights are typically biased upward (≈1 inch) while self-reported weights are biased downward (≈10 lbs) in large surveys such as those reported by Ossiander et al. [23], the BMI’s from the OBMV data may underestimate the true prevalence of obesity in Summit County. However, we have no reason to expect that the bias is large or strongly associated with socio-economic status (SES). For this reason, we included in this study only records of license holders who were between 16 and 21 of age at the time when their licenses were first issued. This, of course, still assumes that the self-reported weights and heights are still subject to the same potential bias as stated earlier.
- Socio-economic Data—we extracted the five-year data (2007–2011) from the American Community Survey to form a data set that contains both census tract and census block group data, including population counts, population counts with college or higher education attainment, median family income, unemployment, and percentages of white population.
- Census tract and census block group boundary files from the 2010 TIGER/Line files by the US Census Bureau.
3. Analysis and Results
3.1. Spatial Distribution of Obese Population and Geographic Scales
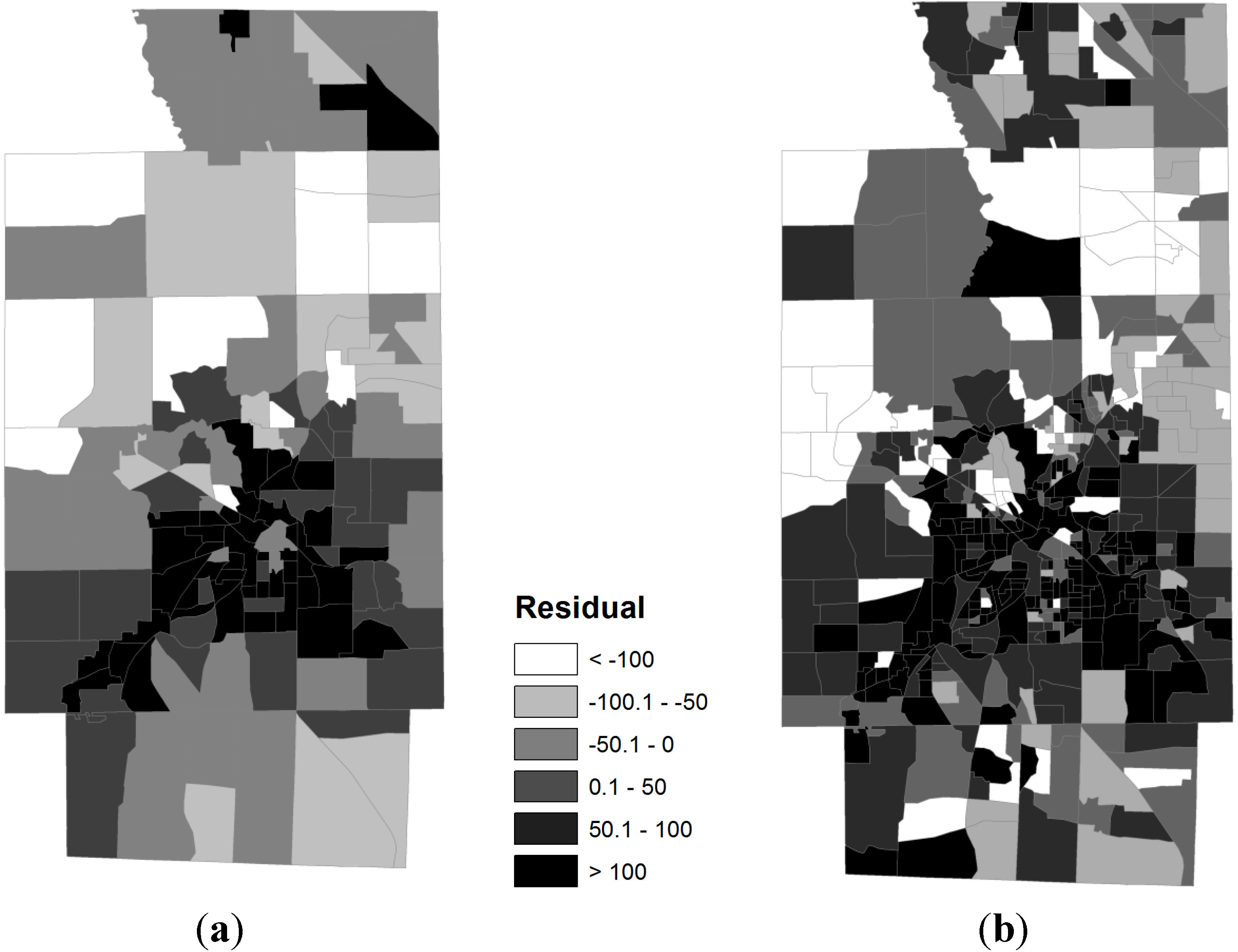
3.2. Spatial Relationships between Obese Population and SES Attributes
- Population density (POPDEN)
- Percent white population (RWHITE)
- Median family income (MEDINC)
- Percent with bachelor degree or higher (RGEBA)
- Percent unemployed (RUNEMP)
| Adj-R2 | Regression Model | |
|---|---|---|
| Bgroups | 0.40 | −RGEBA |
| 0.41 | −MEDINC | |
| 0.36 | +RUNEMP | |
| Tracts | 0.66 | −RGEBA |
| 0.65 | −MEDINC | |
| 0.62 | +RUNEMP |
| Obesity_Ratio = Function ( RGEBA, MEDINC, RUNEMP) | |||
|---|---|---|---|
| GWR | R2 | Adjusted-R2 | AICc |
| Block Groups | 0.4937 | 0.4650 | 5101.32 |
| Tracts | 0.7301 | 0.7070 | 1395.61 |
| OLS | R2 | Adjusted-R2 | AICc |
| Block Groups | 0.4415 | 0.4378 | 5114.80 |
| Tracts | 0.6968 | 0.6899 | 1400.02 |
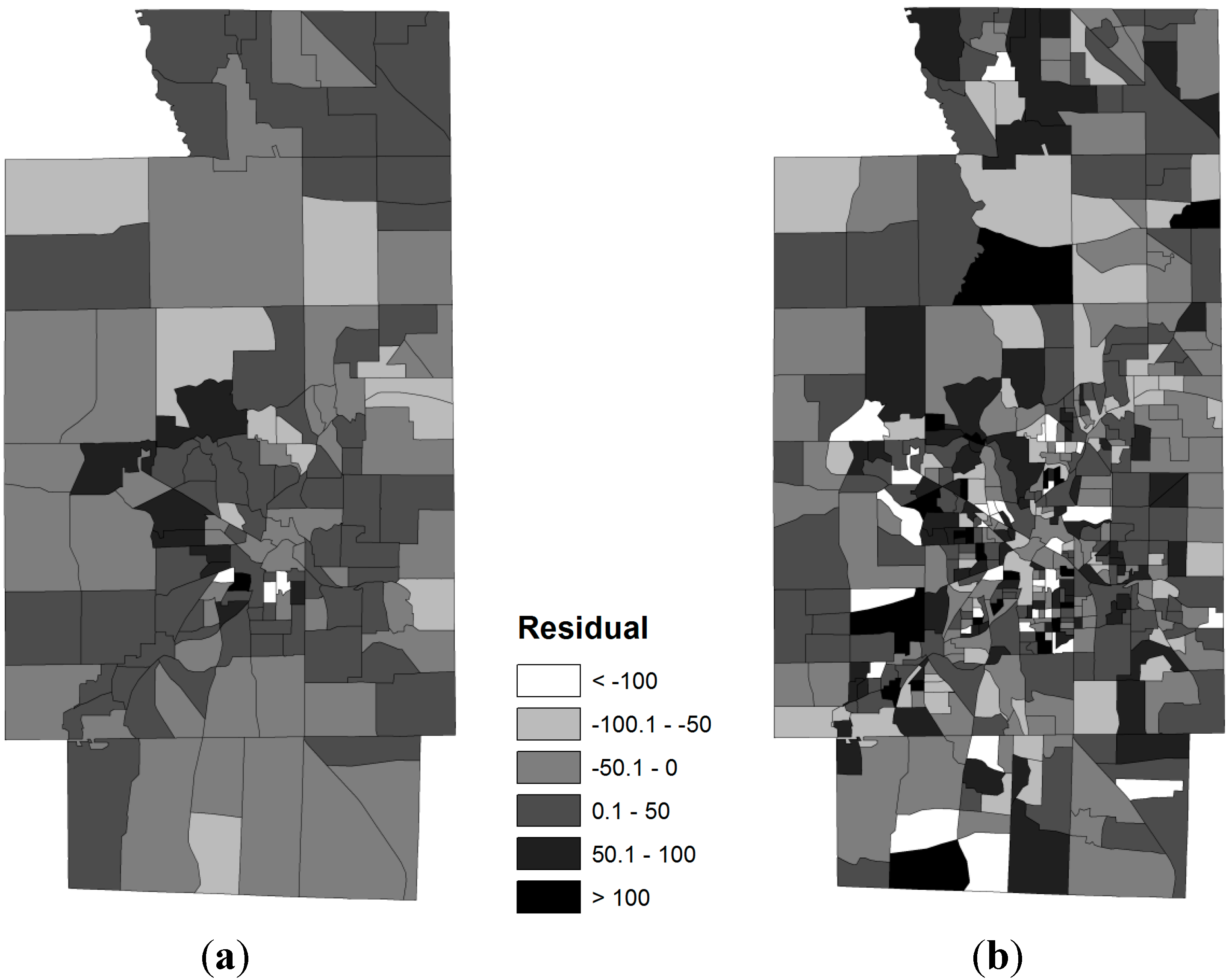
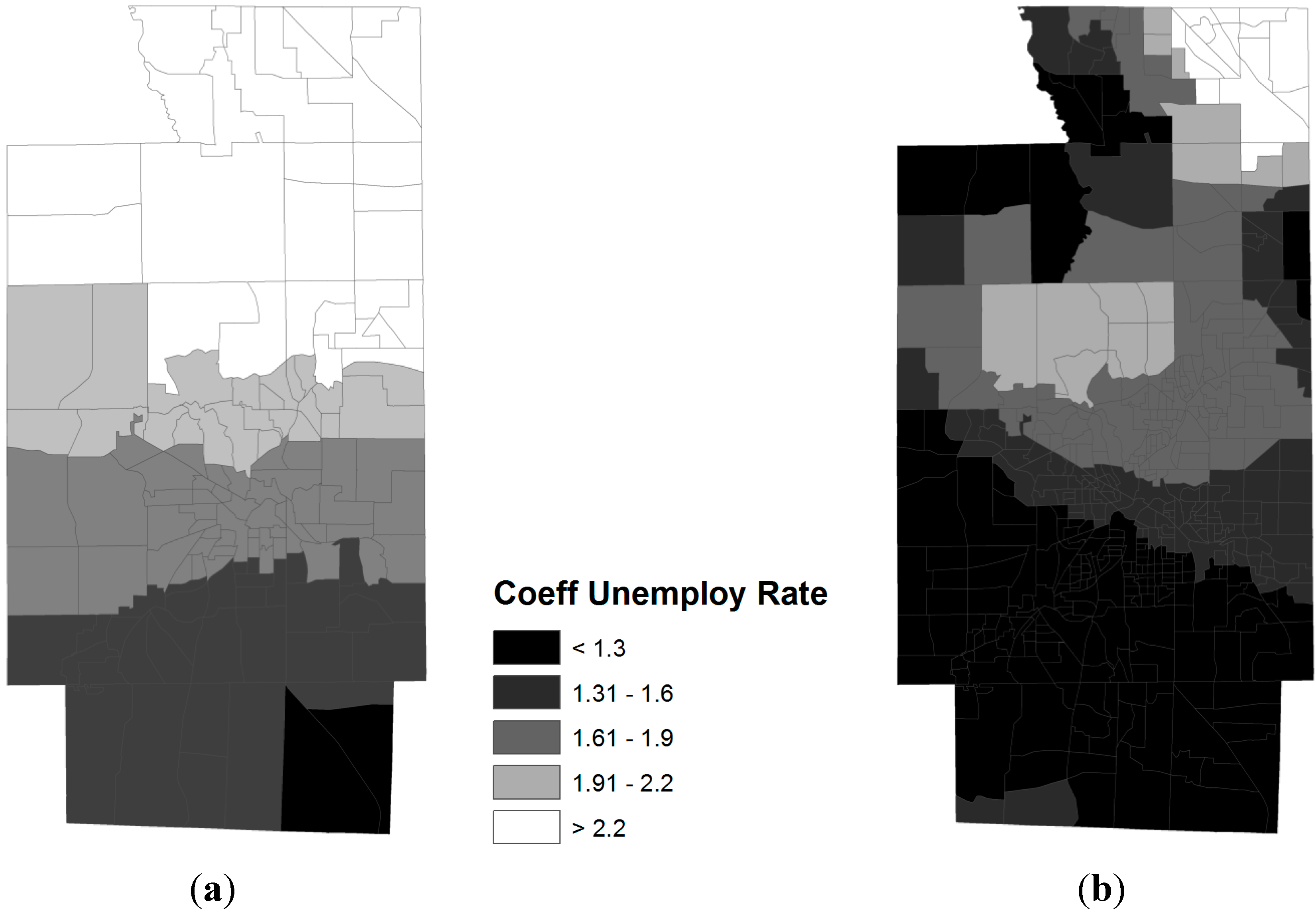
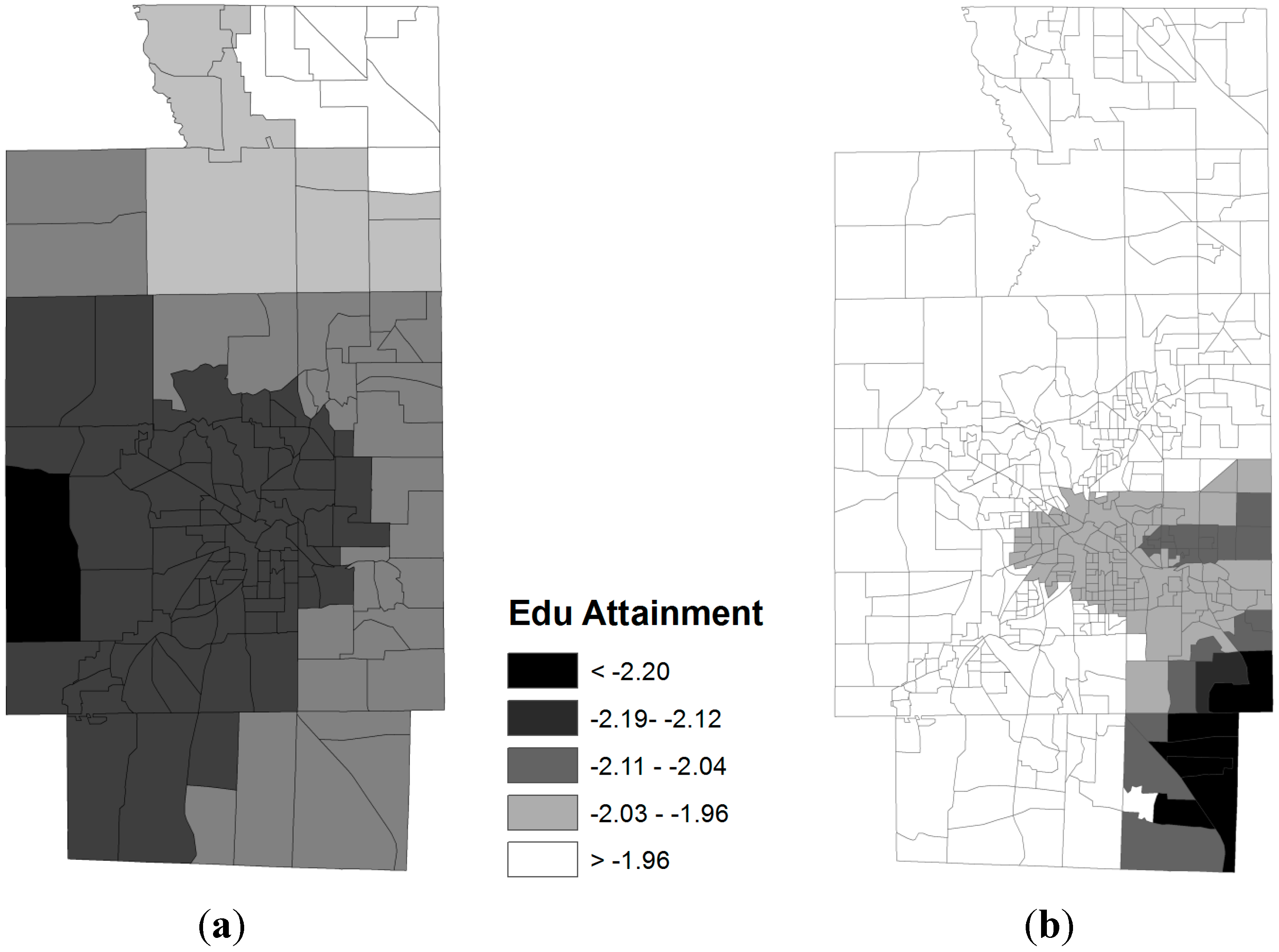
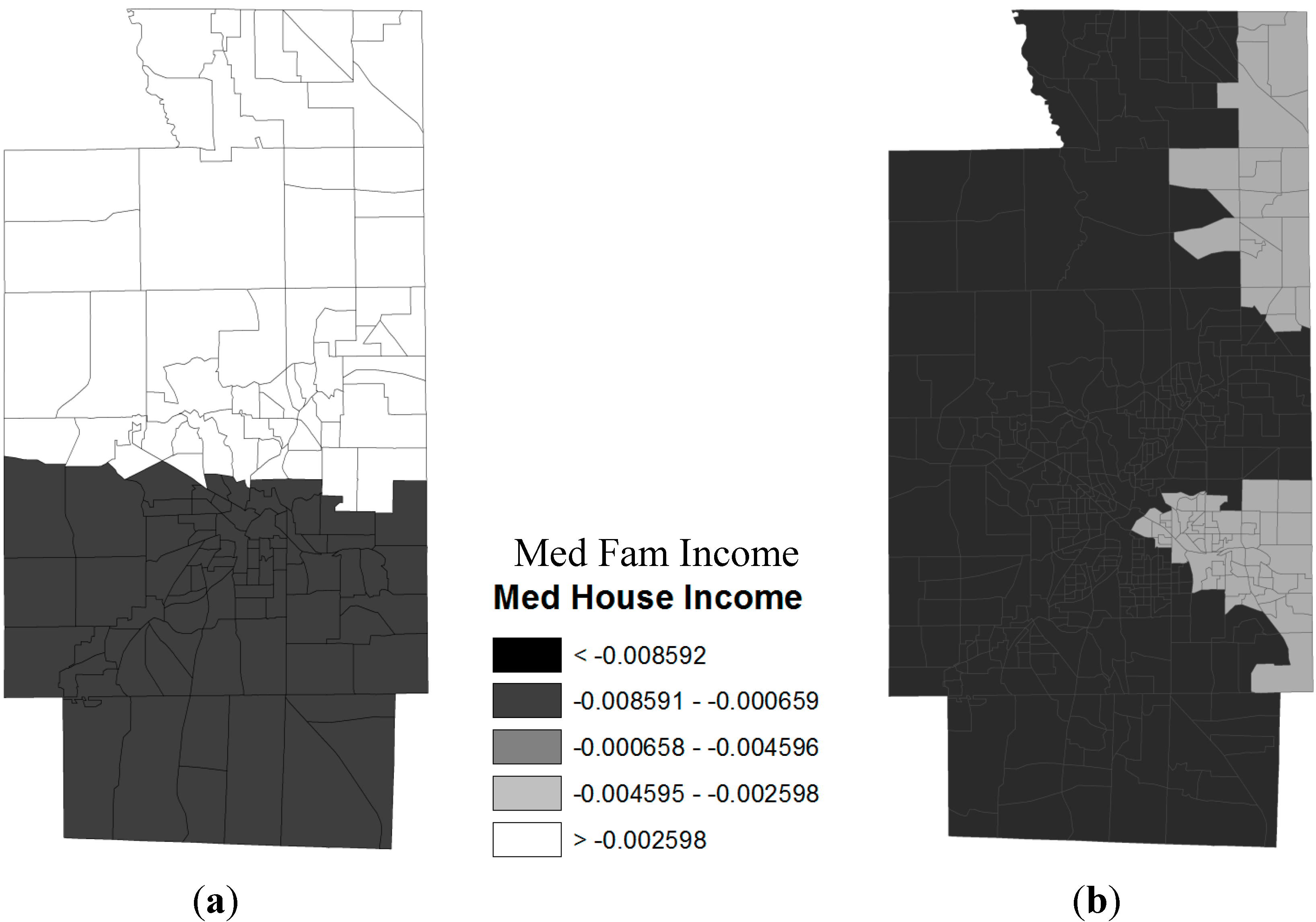
4. Discussion and Concluding Remarks
| Statistics for CV | Block Group Level | Tract Level |
|---|---|---|
| Minimum | 0.0137 | 0.0250 |
| Maximum | 2.2572 | 0.8192 |
| Average | 0.2703 | 0.1305 |
Author Contributions
Conflicts of Interest
References
- Wong, D. The modifiable areal unit problem (MAUP). In The SAGE Handbook of Spatial Analysis; Fotheringham, A.S., Rogerson, P.A., Eds.; Sage: London, UK, 2009; pp. 105–123. [Google Scholar]
- Cockings, S.; Martin, D. Zone design for environment and health studies using pre-aggregated data. Soc. Sci. Med. 2005, 60, 2729–2742. [Google Scholar] [PubMed]
- Anderson, B.; Rafferty, A.P.; Lyon-Callo, S.; Fussman, C.; Imes, G. Fast-food consumption and obesity among Michigan adults. Prev. Chronic Dis. 2011, 8, A71. [Google Scholar] [PubMed]
- Fine, L.J.; Philogene, G.S.; Gramling, R.; Coups, E.J.; Sinha, S. Prevalence of multiple chronic disease risk factors: 2001 National Health Interview Survey. Am. J. Prev. Med. 2004, 27, 18–24. [Google Scholar] [PubMed]
- Flegal, K.M.; Carroll, M.D.; Ogden, C.; Johnson, C.L. Prevalence and tends in obesity among US adults, 1999–2000. J. Am. Med. Assoc. 2002, 288, 1723–1727. [Google Scholar]
- Hedley, A.A.; Ogden, C.L.; Johnson, C.L.; Carroll, M.D.; Curtin, L.R.; Flegal, K.M. Prevalence of overweight and obesity among US children, adolescents, and adults, 1999–2002. J. Am. Med. Assoc. 2004, 291, 2847–2850. [Google Scholar]
- Ogden, C.L.; Flegal, K.M.; Carroll, M.D.; Johnson, C.L. Prevalence and trends in overweight among US children and adolescents, 1999–2000. J. Am. Med. Assoc. 2002, 288, 1728–1732. [Google Scholar]
- Ogden, C.L.; Carroll, M.D.; Kit, B.K.; Flegal, K.M. Prevalence of obesity and trends in body mass index among US children and adolescents, 1999–2010. J. Am. Med. Assoc. 2012, 307, 483–490. [Google Scholar] [CrossRef]
- Flynn, M.A.T.; McNeil, D.A.; Maloff, B.; Mutasingwa, D.; Wu, M.; Ford, C.; Tough, S.C. Reducing obesity and related chronic disease risk in children and youth: A synthesis of evidence with “best practice” recommendations. Obes. Rev. 2006, 7, 7–66. [Google Scholar] [CrossRef] [PubMed]
- Must, A.; Spadano, J.; Coakley, E.H.; Field, A.E.; Colditz, G.; Dietz, W.H. The disease burden associated with overweight and obesity. J. Am. Med. Assoc. 1999, 282, 1523–1529. [Google Scholar]
- Rippe, J.M.; Crossley, S.; Ringer, R. Obesity as a chronic disease: Modern medical and lifestyle management. J. Am. Diet. Assoc. 1998, 98, S9–S15. [Google Scholar] [PubMed]
- Wang, Y.; Mi, J.; Shan, X.-Y.; Wang, Q.J.; Ge, K.-Y. Is China facing an obesity epidemic and the consequences? The trends in obesity and chronic disease in China. Int. J. Obes. 2007, 31, 177–188. [Google Scholar]
- World Health Organization. Obesity: Preventing and Managing the Global Epidemic. Available online: http://libdoc.who.int/trs/WHO_TRS_984.pdf (accessed on 24 November 2013).
- Eckel, R.H.; Krauss, R.M. American Heart Association call to action: Obesity as a major risk factor for coronary heart disease. Circulation 1998, 98, 2099–2100. [Google Scholar] [PubMed]
- Martinez, J.A. Body-weight regulation: Causes of obesity. Proc. Nutr. Soc. 2000, 59, 337–345. [Google Scholar] [CrossRef] [PubMed]
- Obe, C.W. Causes of obesity. In Obesity and Weight Management in Primary Care; Waine, C., Ed.; Blackwell Science: Oxford, UK, 2008; p. 118. [Google Scholar]
- Sonya, A.G.; Mensinger, G.; Huang, S.H.; Kumanyika, S.K.; Stettler, N. Fast-food marketing and children’s fast-food consumption: Exploring parents’ influences in an ethnically diverse sample. J. Public Policy Mark. 2007, 26, 221–235. [Google Scholar]
- Wilding, J. Causes of obesity. Pract. Diabetes Int. 2001, 18. [Google Scholar] [CrossRef]
- Wright, S.M.; Aronne, L.J. Causes of obesity. Abdom. Imaging 2012, 37, 730–732. [Google Scholar] [CrossRef] [PubMed]
- Sobal, J.; Stunkard, A.J. Socioeconomic status and obesity: A review of literature. Psychol. Bull. 1989, 105, 260–275. [Google Scholar] [PubMed]
- Zhang, Q.; Wang, Y. Trends in the association between obesity and socioeconomic status in US adults: 1971–2000. Obes. Res. 2004, 12, 1622–1632. [Google Scholar] [PubMed]
- McLaren, L. Socioeconomic status and obesity. Epidemiol. Rev. 2007, 29, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Ossiander, E.M.; Emanuel, I.; O’Brian, W.; Malone, K. Driver’s license as a source of data on height and weight. Econ. Hum. Biol. 2004, 2, 219–227. [Google Scholar] [CrossRef] [PubMed]
- Pearce, J.; Witten, K. Geographies of Obesity: Environmental Understandings of the Obesity Epidemic; Ashgate Publishing Ltd.: Burlinton, VT, USA, 2010; p. 331. [Google Scholar]
- Fotheringham, A.S.; Wong, D.W.S. The modifiable areal unit problem in multivariate statistical analysis. Environ. Plan. A 1991, 23, 1025–1044. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M. Geographically weighted regression. J. R. Stat. Soc. Ser. D 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
- ESRI. Available online: http://www.esri.com (accessed on 10 October 2014).
- Lam, N.S.-N. Fractals and scale in environmental assessment and monitoring. In Scale and Geographic Inquiry: Nature, Society and Method; Sheppard, E., McMaster, R.B., Eds.; John Wiley and Sons: New York, NY, USA, 2008; pp. 23–40. [Google Scholar]
- Sun, M.; Wong, D.W.S. Incorporating data quality information in mapping the American Community Survey data. Cartogr. Geogr. Inf. Sci. 2010, 37, 285–300. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Alnasrallah, M.; Wong, D.; Beaird, H.; Logue, E. Impacts of Scale on Geographic Analysis of Health Data: An Example of Obesity Prevalence. ISPRS Int. J. Geo-Inf. 2014, 3, 1198-1210. https://doi.org/10.3390/ijgi3041198
Lee J, Alnasrallah M, Wong D, Beaird H, Logue E. Impacts of Scale on Geographic Analysis of Health Data: An Example of Obesity Prevalence. ISPRS International Journal of Geo-Information. 2014; 3(4):1198-1210. https://doi.org/10.3390/ijgi3041198
Chicago/Turabian StyleLee, Jay, Mohammad Alnasrallah, David Wong, Heather Beaird, and Everett Logue. 2014. "Impacts of Scale on Geographic Analysis of Health Data: An Example of Obesity Prevalence" ISPRS International Journal of Geo-Information 3, no. 4: 1198-1210. https://doi.org/10.3390/ijgi3041198
APA StyleLee, J., Alnasrallah, M., Wong, D., Beaird, H., & Logue, E. (2014). Impacts of Scale on Geographic Analysis of Health Data: An Example of Obesity Prevalence. ISPRS International Journal of Geo-Information, 3(4), 1198-1210. https://doi.org/10.3390/ijgi3041198





