Forecast-Driven Enhancement of Received Signal Strength (RSS)-Based Localization Systems
Abstract
: Real-time user localization in indoor environments is an important issue in ambient assisted living (AAL). In this context, localization based on received signal strength (RSS) has received considerable interest in the recent literature, due to its low cost and energy consumption and to its availability on all wireless communication hardware. On the other hand, the RSS-based localization is characterized by a greater error with respect to other technologies. Restricting the problem to localization of AAL users in indoor environments, we demonstrate that forecasting with a little user movement advance (for example, when the user is about to leave a room) provides significant benefits to the accuracy of RSS-based localization systems. Specifically, we exploit echo state networks (ESNs) fed with RSS measurements and trained to recognize patterns of user’s movements to feed back to the RSS-based localization system.1. Introduction
Wireless sensor networks (WSNs) are an important source of context information, which find important applications in smart environments and ambient assisted living (AAL) [1]. In these applications, WSNs can monitor various parameters of the user and his/her home, including physiological parameters, movements and activities [2]. Among all parameters of interest for AAL, user localization and tracking are some of the most important (it is essential to supply the AAL services in the appropriate location). Unfortunately, this cannot be achieved by the widely used, satellite-based global positioning systems, since they do not achieve the required accuracy in indoor environments, where AAL applications typically operate. For this reason, most localization systems for AAL rely on WSN [3].
WSN-based solutions are constructed by deploying a set of fixed sensors (called anchors) in the user environment and a sensor on the user itself (called the mobile), and they estimate the (unknown) location of the mobile with respect to the anchors, whose position is known. This estimation exploits measurements of physical quantities related to beacon packets exchanged between the mobile and the anchors. Radio signal measurements are typically the received signal strength (RSS), the angle of arrival (AOA), the time of arrival (TOA) and the time difference of arrival (TDOA). Although AOA or TDOA can guarantee high localization precision, they require specific and complex hardware. This is a major drawback in particular in AAL applications, which are deeply involved with user monitoring and, thus, may suffer from complex and too invasive hardware. In this work, we consider localization-based on RSS, since it does not require any special hardware and is available in most standard wireless devices. Furthermore, the measurement of RSS has almost a null impact on power consumption, sensor size and cost, and for these reasons, it has received considerable interest in the recent literature [4].
Although simple, the RSS-based indoor localization algorithms are not sufficient by themselves, since RSS measurements are affected by noise, which makes localization information imprecise. This problem is due both to the multipath effects of indoor environments and to the fact that the body of the user affects the radio signal propagation with irregular patterns, depending on the orientation of the user, the orientation of the antenna, etc.
An approach to improve the accuracy of RSS-based localization consists of exploiting context information that might be produced by other sensors of AAL applications. For example, if the user turns on the light, the AAL system identifies the user position very precisely (although for a short time), and this information can be used to feed back to the localization system in order to adjust its parameters and improve further measurements [4]. However, this improvement is only opportunistic, as the information used to feed back to the localization system is available only sporadically and in the presence of appropriate sensors in the applications (e.g., on the doors, light switches, etc.).
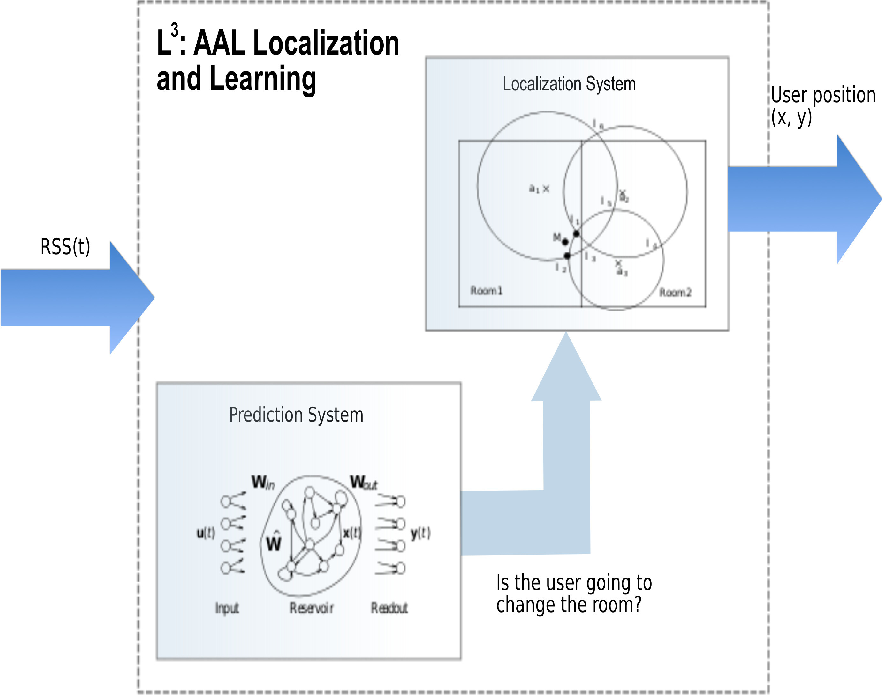
In this work we take into consideration machine learning models to predict some activities of the user that imply a specific position of the user in the environment, and we use this information to feed back to the localization system. Specifically, we exploit recurrent neural networks (RNNs) [5] to process RSS information in order to predict whether the user is going to leave the current room, assuming that such a decision depends on the user movement pattern. This information is then given to the localization algorithm, which, leveraging on it, improves the localization accuracy (Figure 1).
We present the results of a set of experiments in a real indoor environment aimed at producing a sufficiently large dataset to be used for the training of an RNN, and we assess its accuracy in a predictive classification of user movement patterns and cost. In particular, we evaluate the cost in terms of the number of anchors that are necessary to achieve the desired accuracy in the prediction and in terms of the degree of independence of these predictions from errors in the actual deployment of the anchors, which has a direct impact on deployment costs. In our experiments, we show that our approach provides optimal accuracy with four anchors, but it can already provide good accuracy, even with a single anchor.
Later, we present the results of experiments that leverage the proposed prediction system together with an RSS localization algorithm, showing how the combination of these two elements increases the overall accuracy of the RSS-based localization.
2. Related Works
In order to increase their accuracy, current RSS-based localization techniques exploit information coming from the surrounding environment. In [6], the authors describe an opportunistic RSS-based localization method. The basic idea consists of allowing mobile users to opportunistically exchange location information when they happen to be in the radio range and to exploit this information in order to improve their self-localization accuracy. The authors show that opportunistic localization paradigm is effective in enhancing the node’s localization accuracy in indoor environments, even though the performance increment is strongly dependent on the node’s mobility patterns, the heterogeneity of the opportunistic nodes and the accuracy of the ranging.
Another approach, called COAL (Context Aware Localization) [7], exploits a different kind of context information. In particular, COAL leverages the user programs (such as an ongoing event, seminar schedule or personal agenda) to facilitate the user localization. By employing this context information, the authors significantly reduce the localization frequency, thus reducing energy consumption, while maintaining a high degree of accuracy.
Other approaches employ additional sensory data, such as sound and light, to identify a location [8]. Learning techniques are often used to train the system and increase accuracy. Examples include EEMSS [9] and CenceMe [10]. CenceMe combines the inference of the presence of mobiles using sensor-enabled mobile phones with the information shared through social networking applications, such as Facebook and MySpace.
In [4], the authors exploit context information produced by devices that monitor the user activities as part of AAL applications. Such devices provide information about opening/closing of refrigerators, doors or light switches.
Differently from the above works, in our approach, we do not use additional sources of information, but we simply rely on the same RSS information that is used for localization to infer by an RNN additional information that is localization-related and use this information to feed back to the localization system.
3. L3—AAL Localization and Learning
The proposed L3 system is composed of two subsystems, namely, the Prediction subsystem and the Localization subsystem. The Prediction subsystem (described in Section 3.1) is based on the Reservoir Computing paradigm, while the Localization subsystem (described in Section 3.2) exploits a well-known trilateration algorithm. In practice, the key idea is to predict the user movements in order to provide to the localization algorithm the knowledge about the room in which the user is entering. This knowledge is leveraged by the localization system as an additional input.
3.1. The Prediction Subsystem
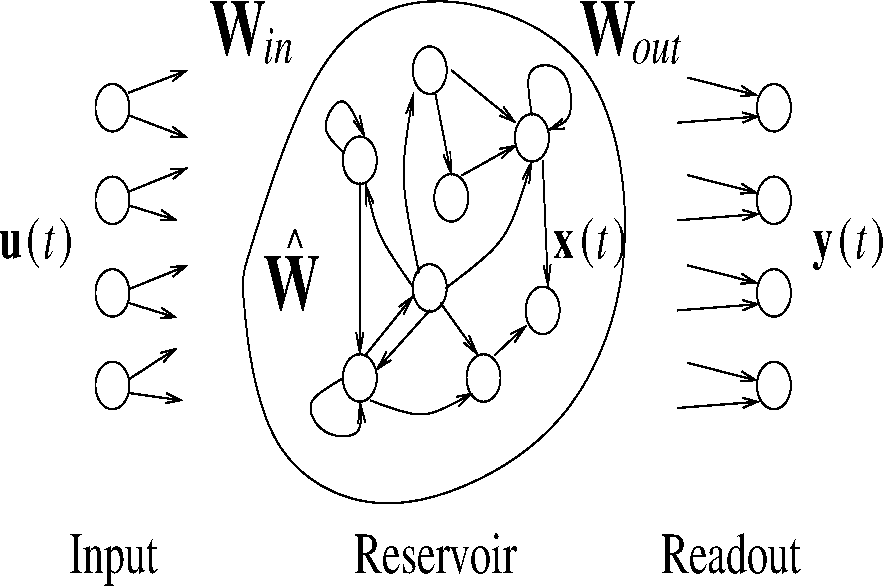
Reservoir Computing (RC) is a computational paradigm covering several models in the recurrent neural network (RNN) family, which are characterized by the presence of a large and sparsely connected hidden reservoir layer of recurrent non-linear units, which are read by means of some read-out mechanism, i.e., typically a linear combination of the reservoir outputs. With respect to traditional RNN training, where all weights are adapted, RC performs learning mainly on the output weights, leaving those in the reservoir untrained. As other RNNs, RC models are well suited for modeling of dynamical systems and, in particular, for temporal data processing. As the movement prediction problem discussed in this paper is, from a machine learning perspective, a time-series prediction task, we are naturally interested in analyzing and discussing the effectiveness of the RC paradigm on such a scenario. In particular, we focus on the computationally-efficient echo state networks (ESNs) [11–13], which are one of the best-known RC models, which are characterized by an input layer of NU units, a hidden reservoir layer of NR untrained recurrent non-linear units and a readout layer of NY feed-forward linear units (see Figure 2). Within a time-series prediction task, the untrained reservoir acts as a fixed non-linear temporal expansion function, implementing an encoding process of the input sequence into a state space where the trained linear readout is applied. Standard ESN reservoirs are built from simple additive units with a sigmoid activation function that, however, has been shown to weakly model the temporal evolution of slow dynamical systems [14]. In particular, [5] have shown that indoor user movements can be best modeled by a leaky integrator type of RC network (LI-ESNs) [14]. Given an input sequence s = [u(1), …, u(n)] over the input space, , at each time step t = 1, …, n, the LI-ESN reservoir computes the following state transition:
For a binary classification task over sequential data, the linear readout is applied only after the encoding process computed by the reservoir is terminated, by using:
The reservoir is initialized to satisfy the so-called Echo State Property (ESP) [11]. The ESP asserts that the reservoir state of an ESN driven by a long input sequence only depends on the input sequence itself. Dependencies on the initial states are progressively forgotten after an initial transient (the reservoir provides an echo of the input signal). A sufficient and a necessary condition for the reservoir initialization is given in [11]. Usually, only the necessary condition is used for reservoir initialization, whereas the sufficient condition is often too restrictive [11]. The necessary condition for the ESP is that the system governing the reservoir dynamics of Equation (1) is locally asymptotically stable around the zero state, 0 ∈ . By setting = (1−a)I + a , where a is the leaking rate parameter, the necessary condition is satisfied whenever the following constraint holds:
In sequence classification tasks, each training sequence is presented to the reservoir for a number of Ntransient consecutive times, to account for the initial transient. The final reservoir states corresponding to the training sequences are collected in the columns of matrix X, while the vector, ytarget, contains the corresponding target classifications (at the end of each sequence). The linear readout is therefore trained to solve the least squares linear regression problem:
Usually, Moore-Penrose pseudo-inversion of matrix X or ridge regression are used to train the readout [13].
3.2. The Localization Subsystem
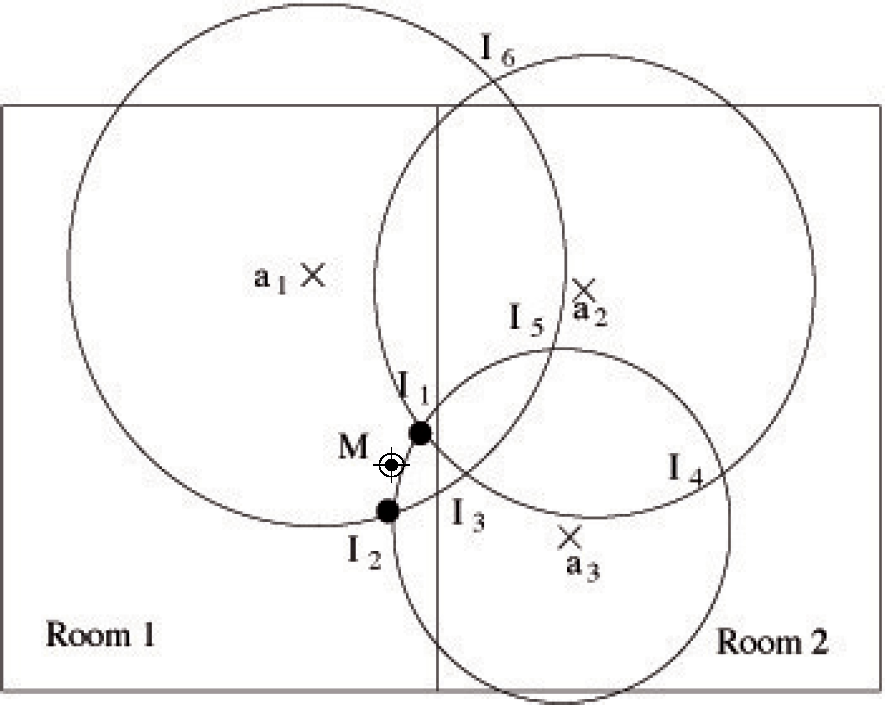
In order to take into account the knowledge coming from the Prediction subsystem about the room in which the user is or he/she is entering, we consider two localization algorithms, one based on multilateration and the other one based on fingerprinting, which uses least mean squares (LMS in the following). Each of these algorithms may be augmented with context information. The modified algorithms use the output of the Prediction subsystem in order to establish the room where the user currently is in at any moment. An example of how the multilateration algorithm works is shown in Figure 3 (for the sake of simplicity, this figure is depicted disregarding the effect of the wall attenuation). The three anchors, a1, a2 and a3, with a greater RSS are selected, and only two out of the six intersection points (I1 and I2) are considered, since they are in the room indicated by the Prediction subsystem. The intersection points are treated as point masses, and the mobile position M is then estimated, evaluating the centroid of all masses. Of course there exists a chance that all the intersection points are outside the room (however, this never happened in all our experiments). In this case, the input data are not consistent and, depending on the requirements of the localization system, there are different possible alternatives; for example, the system may return an inconsistency or it may return the last known position, etc.
The LMS algorithm, on the other hand, exploits an RSS map of the environment that is computed during the deployment of the localization system. This map is a list of pairs <coordinate, RSS tuple> that, for a given point of coordinates (x, y) in the environment, expresses an N-tuple of RSS measurements among each of the N anchors, ai, and the mobile at that point. Typically, this list is computed at the nodes of a regular grid in the environment, and its granularity depends on the precision required by the localization. At runtime, the LMS algorithm takes the N-tuple of measured RSS < r1, r2, …, rN >, and it finds in the list the RSS tuple that minimizes the mean square error between the two tuples. Then, it outputs the corresponding coordinate pair (x, y). In the LMS algorithm, only the pairs <coordinate, RSS tuple> computed in the room indicated by the Prediction subsystem are used.
4. Scenario
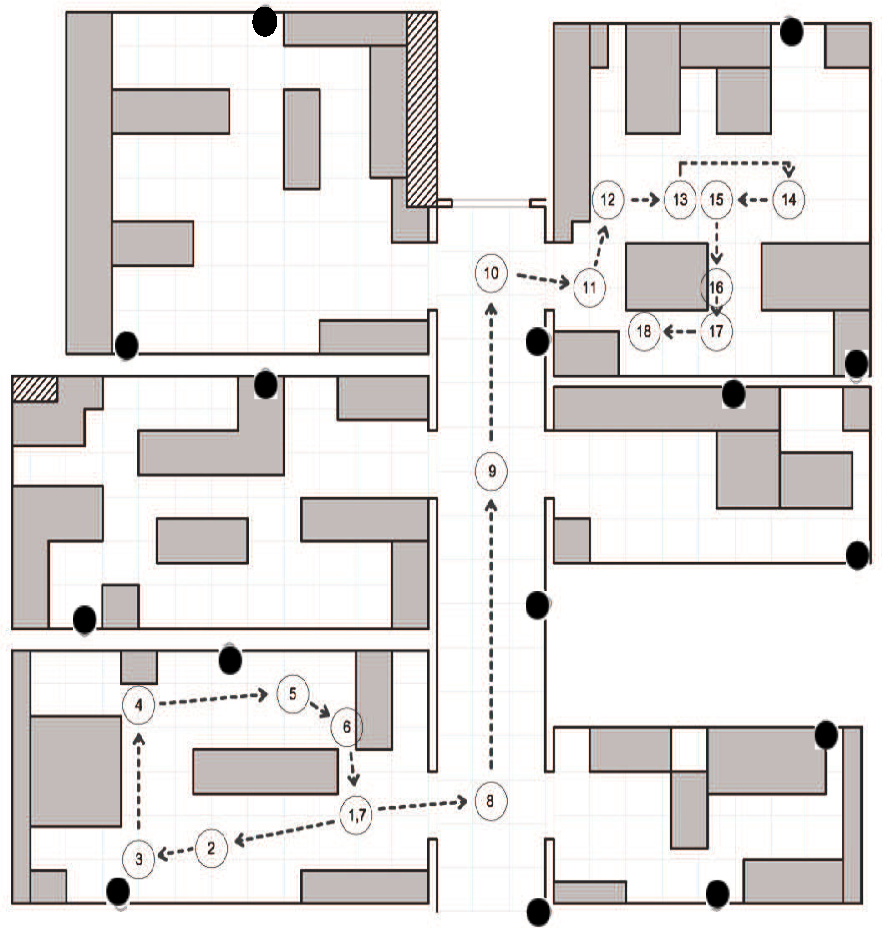
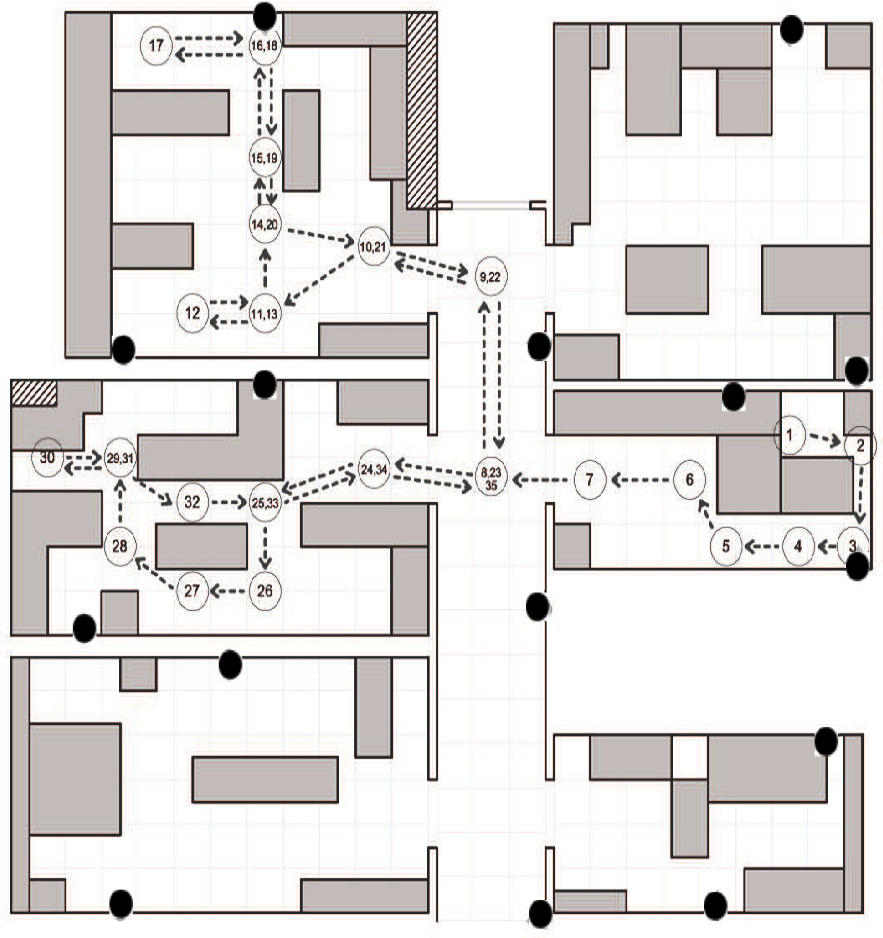
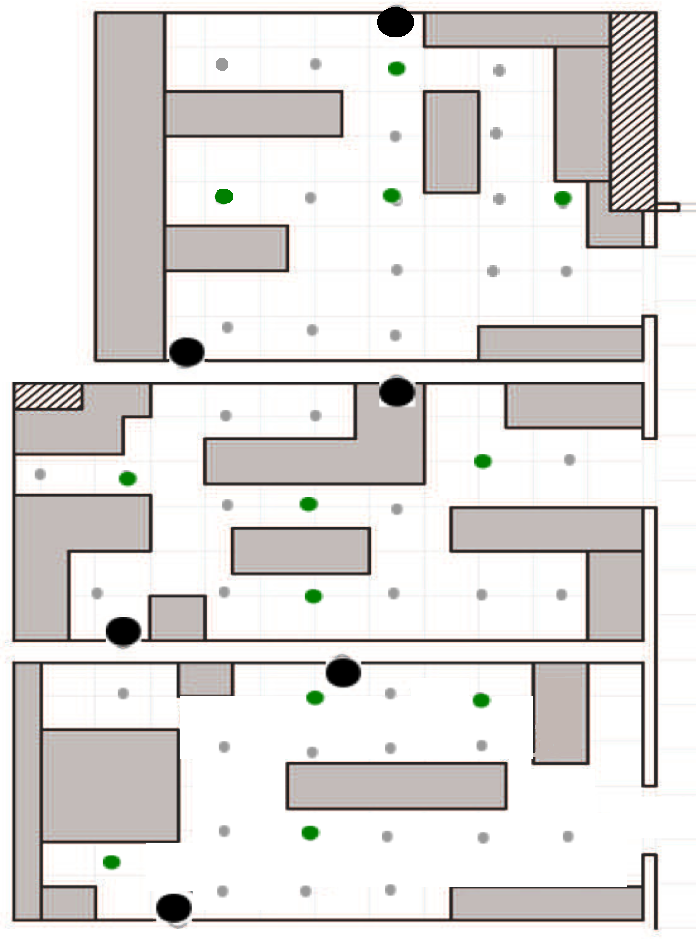
A measurement campaign has been performed on the first floor of the the ISTIinstitute of CNRin the Pisa Research Area, in Italy. The scenario is a typical office environment comprising six rooms with different geometries, as depicted in Figure 4. Rooms contain typical office furniture: desks, chairs, cabinets and monitors. From the point of view of wireless communications, this is a harsh environment, due to the multi-path reflections caused by walls and the interference produced by electronic devices. Experimental measurements have been performed by a sensor network of 15 IRISnodes embedding a Chipcon AT86RF230 radio subsystem that implements the IEEE 802.15.4 standard [15]. Fifteen sensors, in the following anchors, are located in fixed positions in the environment (as depicted in Figure 4), and one sensor is placed on the user, hereafter called the mobile. The height of the anchors has been set to 1.5 m from the ground, and the mobile was worn on the chest of the user. The user moves along free paths to facilitate with a constant speed of about 1 m/s. The measurement campaign comprises experiments on six different rooms with a total surface of about 100 m2. Experiments consist in measuring the RSS between anchors and the mobile for the two selected paths, hereby referred to as the first and second path. Figures 4 and 5 show the position and the orientation of the anchors deployed in the environment, as well as the performing path for the fist and second path, respectively. We collected RSS samples by sending a beacon packet from the anchors to the mobile at regular intervals, eight times per second, using the full transmission power of the IRIS nodes.
5. Experimental Results
This section describes the results of the experiments conducted in the scenarios drawn in the previous section.
During the experiments, we performed specific measurements for the evaluation of the performance of the Prediction subsystem, both in terms of predictive classification accuracy and cost. In a second set of experiments, we evaluated the performance in terms of the localization accuracy of the L3 localization system, for the two selected paths of the scenarios. Moreover, we quantified how the prediction system increases the overall accuracy with respect to both trilateration and fingerprinting methods.
5.1. Location Forecasting Accuracy
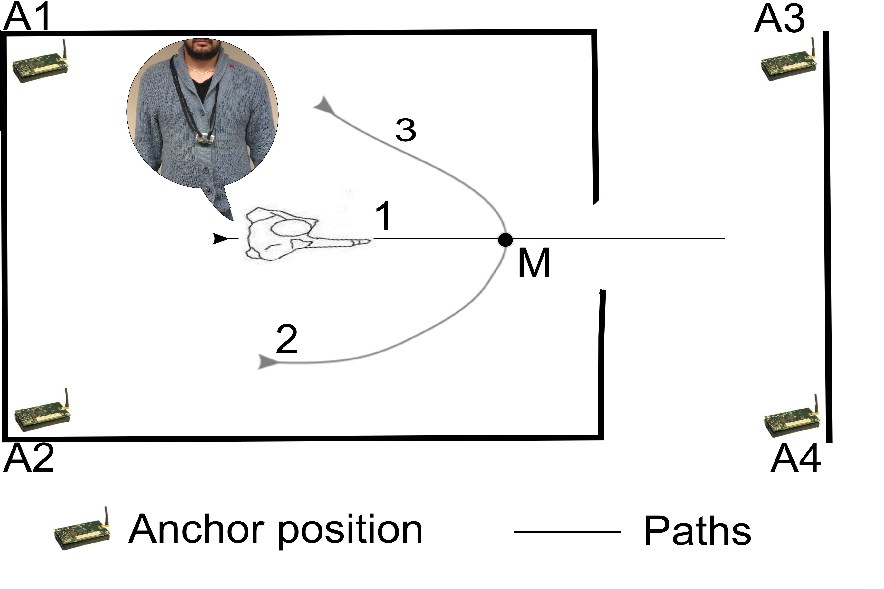
In order to evaluate the performance in terms of prediction accuracy, we performed experiments consisting of the measurement of the RSS between a set of four anchors and the mobile for a set of repeated user movements. The measurement campaign comprises experiments on six different rooms, hereby referred as dataset 1, 2, 3, 4, 5 and 6. Figure 6 shows the anchors deployed in a room and the set of three prototypal trajectories of the user (numbered from 1 to 3). The straight path (labeled 1) ran from inside the room to outside and yielded to a change in the spatial context of the user (i.e., to a room exit). The curved paths (labeled as 2 and 3, in the figure) preserved the spatial context (i.e., are within the same room). Table 1 summarizes the number of experiments for the six different rooms (corresponding to datasets 1–6) and for each path. Note that, due to physical constraints, dataset 1 does not have the curved path in the room denoted as path 3. The number of paths leading to a room exit, with respect to those that preserve the spatial context, is given in Table 1 and labeled as Tot. Exit and Tot. Unchanged, respectively. Each path produces a trace of RSS measurements that is marked when the user reaches a point (denoted with M in Figure 6) located at 0.6 m from the door. Overall, the experiment produced about 5,000 RSS samples from each of the four anchors and for each dataset. The marker, M, is the same for all the movements; therefore, different paths cannot be distinguished based only on the RSS values collected at M.
The experimental scenario and the gathered RSS measures are used to feed a binary classification task on time series for movement forecasting. The RSS values from the four anchors are organized into sequences of varying length (see Table 1) corresponding to trajectory measurements from the starting point until marker M. A target classification label is associated with each input sequence to indicate whether the user is about to exit the room or not. In particular, target class +1 is associated with location changing movements (i.e., path 1 in Figure 6), while label −1 is used to denote location preserving paths (i.e., paths 2 and 3 in Figure 6).
In [5], the baseline performance of different ESN models on user movement prediction with a small two-room dataset has been analyzed. Such an analysis suggests that the LI-ESN model, described in Section 3.1, is best suited to deal with slowly changing RSS time series. Therefore, in the remainder of the section, we limit our analysis to the assessment of a leaky-integrated model, with meta-parameters chosen as in [5]. In particular, we consider LI-ESNs comprising reservoirs of NR = 500 units and a 10% of randomly generated connectivity, spectral radius ρ = 0.99, input weights in [−1, 1] and leaking rate a = 0.1. Results refer to the average of 10 independent and randomly guessed reservoirs. The readout (NY = 1) is trained using pseudo-inversion and ridge regression with regularization parameter λ ∈ {10−i|i = 1, 3, 5, 7}.
Input data comprise time series of four dimensional RSS measurements (NU = 4) corresponding to the four anchors in Figure 6, normalized in the range [−1, 1] independently for each dataset. Normalized RSS sequences are fed to the LI-ESN network only until the marker signal, M.
We used the data collected in the experiment to train an RC to forecast whether the user will exit the room or not when he reaches point M. In particular, to test the ability of RC to generalize its prediction to unseen indoor environments, we define an experimental evaluation setup, where RC training is performed on RSS measurements corresponding to only two rooms of the scenarios, while the experiments in the remaining rooms are used to test the generalization capability of the RC model. Specifically, we have defined two experimental settings (ESs) that are intended to assess the predictive performance of the LI-ESNs when training/test data comes from both uniform (ES1) and previously unseen ambient configurations (ES2), i.e., providing an external test set. Setting ES1 comprises datasets 1, 2, 3 and 4 to form a single dataset of 210 sequences. This leads to a training set of a size of 168 and a test set of a size of 42, with stratification on the path types. The readout regularization parameter of ES1 is set to λ = 10−1, on a (33%) validation set extracted from the training samples. In setting ES2, we use the LI-ESN with the readout regularization selected in the ES1. We train it on the union of datasets 1, 2, 3 and 4 (i.e., four rooms), and we use dataset 5 and 6 as an external test set (with measurements from two unknown environments). Table 2 reports the mean test accuracy for both the ESs. An excellent predictive performance is achieved for ES1, which is coherent with the results reported in [5]. This seems to indicate that the LI-ESN approach, on the one hand, scales well as the number of training environments increases, while, on the other hand, it is robust to changes to the training room configurations. Note that RSS trajectories for different rooms are, typically, consistently different, and, as such, the addition of novel rooms strongly exercises the short-term memory of the reservoirs and their ability to encode complex dynamical signals.
The result on the ES2 setting is more meaningful, as it shows that the performance of the LI-ESN model can be generalized to unknown environments. Specifically, the model reaches a predictive accuracy of about 90% on the external test comprising unseen ambient configurations. Table 3 describes the confusion matrix of the external test-set in ES2, averaged over the reservoir guesses and expressed as percentages over the number of test samples. This allows appreciating the equilibrium of the predictive performance, which has comparable values for both classes. Note that total accuracy is obtained as the sum over the diagonal, while error is computed from the sum of the off-diagonal elements.
5.2. Localization Results
Leveraging the prediction system trained with the previous ad hoc measurement campaign (ES2), we evaluate the accuracy of the proposed L3 localization system by using both the trilateration and the LMS algorithms. The localization performance is evaluated in terms of the localization error ϵ, which is the distance between the point where the mobile actually is and the point identified by the localization algorithm. This is the metric that is most commonly used in the literature: while not necessarily the most significant for practical applications, it allows an easy comparison between different methods in different environments. Let the Cumulative Distribution Function (CDF) of ϵ be the probability that the localization error takes on a value less than or equal to x meters. Figures 7 and 8 show the CDF of the localization error ϵ by using both the L3 and the trilateration or the LMS algorithms, with or without the prediction system, respectively.
5.2.1. Trilateration Results
One of the factors influencing the RSS values is the distance between the anchor (emitter) and the mobile (receiver), as this distance causes an attenuation in RSS values. Therefore, it is mandatory to determine the dependence among those RSS values and the distance between the emitter and the receiver. This attenuation, caused by the distance between the emitter and the receiver, is known as path loss, and it is generally modeled to be inversely proportional to the distance between the emitter and the receiver raised to a certain exponent, known as the path loss exponent [16] or path loss gradient [17]. Other factors that affect RSS values are the wall attenuation factor and the attenuation at a reference distance. The path loss in decibels between a given anchor and a given mobile can be expressed as:
The objective of calibration is to adapt the theoretical propagation model (Equation (6)) to the environment where it is actually used. The parameters of the propagation model (Equation (6)) are: r0 (RSS measured at 1 m), α (the path loss exponent) and lw (the attenuation factor for the wall, w). r0 should be estimated in a generic environment similar to the one in which we are going to carry out the location, since it only depends on the physical properties of the devices’ hardware. The other parameters have been estimated by using the automatic virtual calibration procedure described in [4] that does not require human intervention. This methods leverages the communications among the anchors (whose position is a priori known) to evaluate the parameters of the Equation (6).
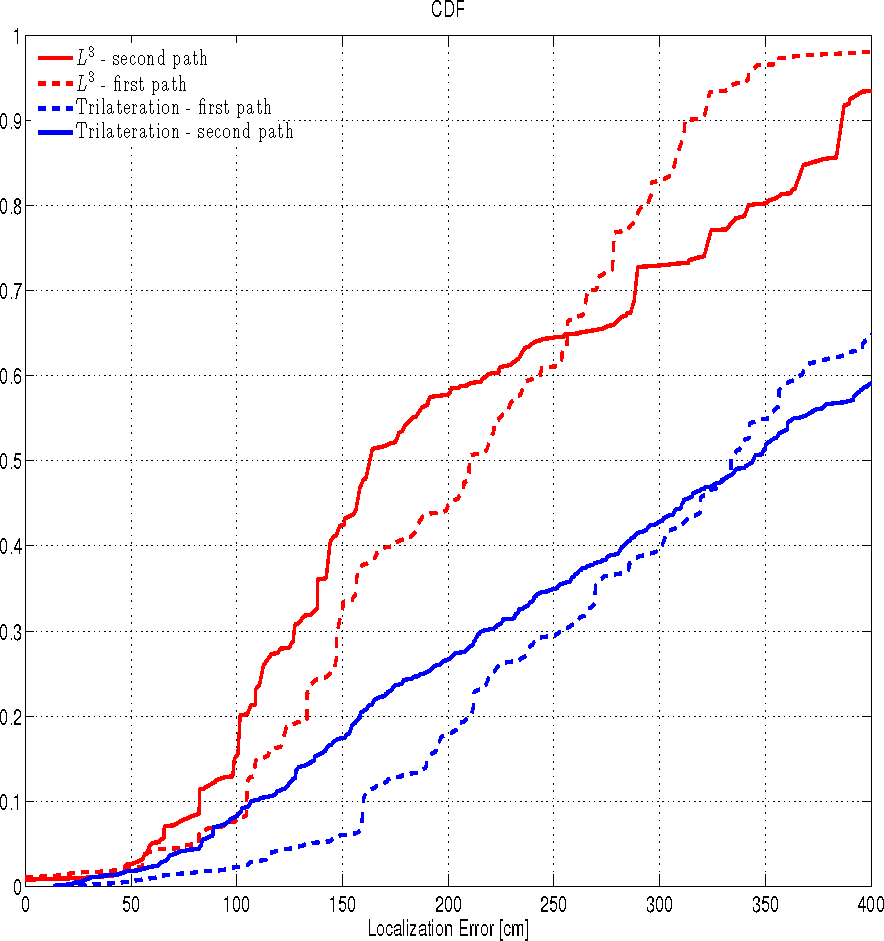
After calibration, the performance of both the L3 and the trilateration algorithm, with or without the prediction system on two paths (Figures 4 and 5) have been evaluated. As highlighted in Figure 7, we can see that in 50% of the cases, the localization error ϵ of L3 in the two paths is below 2.2 m and 1.6 m, while without exploiting the prediction system, ϵ is below 3.4 and 3.5 in 50% of the cases. Therefore, the use of the prediction system improves the localization accuracy by about 47%. The localization accuracy is increased in both paths, in particular, the median localization error of path 1 is decreased by 1.9 m, while the ϵ of path 2 is decreased by 1.2 m. If we look at Figure 7 from the point of view of usability, in this setting and with a target localization error of 2 m, the common trilateration technique without the prediction system is practically unusable, as it gives correct results in less than 25% of the cases. On the other hand, with the same target error, L3 achieves the goal barely more than half of the times. For more restricted accuracy requirements, for example, ϵ < 1.5 m, we can see that the use of the prediction system significantly improves the overall localization accuracy (on the order of 75%), but it is not sufficient to make the localization system usable, as the error is always greater than 1.5 m in more than 50% of the cases.
5.2.2. LMS Results
The calibration of the LMS algorithm consisted in a set of measures between an anchor and a point of a grid with side of about 1 m (Figure 9). These measures have been memorized to create the RSS map <coordinate, RSS tuple> of the environment that, for a given point of a coordinate (x,y) in the environment, expresses an N-tuple of RSS measurements among each anchor and the mobile at that point. Each measure collected about 1,000 RSS measurements, where every RSS measurement was the average of 32 consecutively received samples. Samples were obtained by sending a beacon packet from the anchor to the mobile at regular intervals, 32 times per second.
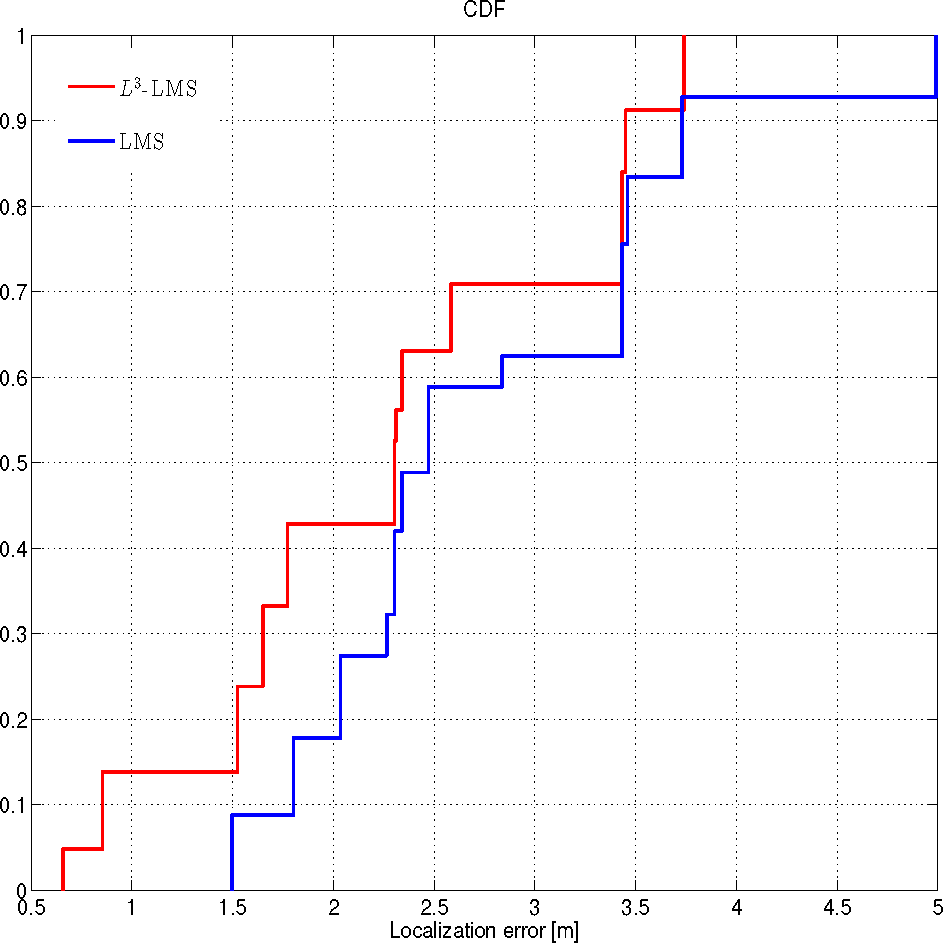
In order to evaluate how the prediction system improves the localization accuracy of an RSS-based localization systems, the performance of the LMS algorithm has been evaluated for a static target, i.e., the users stay in the same position for at least 30 s. As highlighted in Figure 8, we can see that in 50% of the cases, the localization error ϵ of L3 is below 2.2 m, while without exploiting the prediction system, ϵ is below 2.3 in 50% of the cases. Therefore, the use of the prediction system improves the localization accuracy by about 10%.
If we look at Figure 8 from the point of view of usability, in this setting and with a target localization error of 2 m, the LMS technique without the prediction system is practically unusable, as it gives correct results in less than 20% of the cases. On the other hand, with the same target error, L3 achieves the goal barely more than half the times (i.e., 43% of the cases). In this case the prediction system improves the localization accuracy by about 20%. Moreover, the maximum error we achieved was about 3.7 m when the L3 was used against 5 m without the prediction system.
5.3. Calibration Overhead
Tuning our system for a specific environment requires two main activities: the calibration of the localization subsystem and the calibration of the prediction subsystem.
In our experiments, the calibration of the localization subsystem required the collection of RSS samples in a grid of points placed 1 m from each other, to cover a total space of about 50 m2. Thus, the total number of points in the grid was about 50. For each point, we took RSS measurements by exchanging data between the anchors and the mobile for 3 min. Just for the measurements, the calibration time was 2.5 h. This, however, does not include the time required to replace the mobile device at each point, to restart the measurements and to execute the calibration.
The calibration of the prediction subsystem instead took around 6 h of work, mainly spent simulating the movements of a user along the different paths. This latter time of calibration is particularly important, because this is the additional overhead required to improve the localization accuracy of the fingerprinting method. Furthermore, the same amount of time could be spent to improve the localization subsystem with more conventional methods, by augmenting the resolution of the grid of points (i.e., using more reference points for fingerprinting).
We observe, however, that the calibration of the fingerprinting needs to be executed during the deployment phase, before the user can actually use the system, while the calibration of the prediction subsystem does not have this requirement, as it can be overlapped with a period of actual use of the system by the user (during this period, the localization system based on fingerprinting works alone, with reduced performances).
Specifically, the calibration of the prediction subsystem requires traces of RSS measurements that precede the event in which the user exits from a room/environment. The precise detection of the occurrence of such an event can be achieved in different ways; for example, it can be used in any near-field communication mechanism (RFID-based or others), with the reader placed near the doors and the tagon the user. Whenever the reader detects the tag, this is taken as an indication of an “exit” event. Consequently, the previous few seconds of RSS measurements (in our experiments, 6 s) are taken as a sample of an “exit” event. Any other sequence of RSS measurements can be taken as a negative “exit” event. Such an automatic method of data collection had the drawback that it requires an additional subsystem, which, however, is only temporarily deployed to acquire the necessary data in the first days of use and can be removed once the predictive subsystem is fully calibrated.
Hence, in this configuration, the time required to appropriately calibrate the prediction subsystem is almost transparent to the user (he/she only need to wear an RFID tag or a similar device for a limited period of time). On the other hand, the time required to perform a deeper fingerprinting of the environment has a stronger impact on the user, as it is the time of the inactivity of the system and requires an invasive intervention in the user environment, due to human operators performing the fingerprinting.
6. Conclusions and Discussions
We have presented an RC approach to user movement prediction in indoor environments, based on RSS traces collected by low-cost WSN devices. We exploit the ability of LI-ESNs in capturing the temporal dynamics of slowly changing noisy RSS measurements to yield to very accurate predictions of the user spatial context. The performance of the proposed model has been tested on challenging real-world data comprising RSS information collected in real environments.
We have shown that the LI-ESN approach is capable of generalizing its predictive performance to training information related to multiple setups. More importantly, it can effectively generalize movement forecasting to previously unseen environments, as shown by the external test-set assessment. Such flexibility is of paramount importance for the development of practical smart-home solutions, as it allows one to consistently reduce the installation and setup costs. For instance, we envisage a scenario in which an ESN-based localization system is trained off-line (e.g., in the laboratory/factory) on RSS measurements captured on a (small) set of sample rooms. Then, the system is deployed and put into operation into its target environment, reducing the need of an expensive fine tuning phase.
In order to evaluate how the prediction system increases the performance of an RSS-based localization system, we have made measurements in a typical office environment consisting of six adjacent rooms with furniture.
We considered a common trilateration and a fingerprinting localization algorithm, and we evaluated them, both with and without the previous trained prediction system. The information used by the localization system consists in knowing whether the user is exiting from the current room. Measurements show that the trilateration algorithm, coupled with this information, provides more usable performance, in that it gives the correct result about 80% of the time for a target localization error of 3 m. Moreover, the proposed L3 localization system leveraging the prediction movements improves the accuracy by about 47% with respect to an RSS-based trilateration localization system that does not exploit it. We then evaluated the performance of a fingerprinting localization algorithm with and without the prediction system. In order to really show how the prediction system improves the localization accuracy of an RSS-based localization system, the performance has been evaluated for a static target, i.e., the users stays in the same position for at least 30 s. Even if this is a more suitable case for the RSS-based localization algorithms, the accuracy increases by about 10%.
While, the computational cost is a minor detail, since we envision a dedicated server, which elaborates all this information and these algorithms, an analysis of the calibration cost is required. Usually, the RSS-based localization algorithms need to be calibrated. In this paper, we exploited the automatic virtual calibration for the trilateration localization system (therefore, without calibration cost) [4], and we calibrated the fingerprinting localization system by creating an RSS map of about 50 entries. Despite the calibration of the RSS-based localization systems that depend on the techniques used, the proposed L3 system needs to be further calibrated. Indeed, the prediction system has been trained with about 100 straight paths and 100 curved paths. Even if the calibration phase is time expensive, it makes the RSS-base localization systems (both trilateration and fingerprinting techniques) usable.
Conflict of Interest
The authors declare no conflict of interest.
References
- Van Den Broek, G.; Cavallo, F.; Wehrmann, C. AALIANCE Ambient Assisted Living Roadmap; IOS Press: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Barsocchi, P. Position recognition to support bedsores prevention. IEEE J. Biomed. Health Informa. 2013, 17, 53–59. [Google Scholar]
- Alvarez-Garcia, J.A.; Barsocchi, P.; Chessa, S.; Salvi, D. Evaluation of localization and activity recognition systems for ambient assisted living: The experience of the 2012 EvAAL competition. JAISE 2013, 5, 119–132. [Google Scholar]
- Barsocchi, P.; Lenzi, S.; Chessa, S.; Furfari, F. Automatic virtual calibration of range-based indoor localization systems. Wirel. Commun. Mob. Comput. 2012, 12, 1546–1557. [Google Scholar]
- Gallicchio, C.; Micheli, A.; Barsocchi, P.; Chessa, S. User Movements Forecasting by Reservoir Computing Using Signal Streams Produced by Mote-Class Sensors. In MOBILIGHT; Ser, J.D., Jorswieck, E.A., Miguez, J., Matinmikko, M., Palomar, D.P., Salcedo-Sanz, S., Gil-Lopez, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 81, pp. 151–168. [Google Scholar]
- Zorzi, F.; Zanella, A. Opportunistic Localization: Modeling and Analysis, Proceedings of the IEEE 69th Vehicular Technology Conference, Barcelona, Spanish, 26–29 April 2009.
- Liu, Y.; Lu, S.; Liu, Y. COAL: Context Aware Localization for High Energy Efficiency in Wireless Networks, Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Cancun, Quintana Roo, Mexico, 28–31 March 2011; pp. 2030–2035.
- Azizyan, M.; Constandache, I.; Roy Choudhury, R. SurroundSense: Mobile Phone Localization via Ambience Fingerprinting, Proceedings of the 15th Annual International Conference on Mobile Computing and Networking (MobiCom ’09), Beijing, China, 20–25 September 2009; ACM: New York, NY, USA; pp. 261–272.
- Wang, Y.; Jacobson, Q.A.; Lin, J.; Hong, J.; Annavaram, M.; Krishnamachari, B.; Sadeh, N. A Framework of Energy Efficient Mobile Sensing for Automatic User State Recognition, Proceedings of the International Conference on Mobile Systems, Applications and Services (MobiSys), Krakov, Poland, 22–25 June 2009.
- Miluzzo, E.; Lane, N.D.; Fodor, K.; Peterson, R.; Lu, H.; Musolesi, M.; Eisenman, S.B.; Zheng, X.; Campbell, A.T. Sensing Meets Mobile Social Networks: The Design, Implementation and Evaluation of the CenceMe Application, Proceedings of the 6th ACM Conference on Embedded network Sensor Systems (SenSys ’08), Raleigh, North Carolina, USA, 5–7 November 2008; ACM: New York, NY, USA; pp. 337–350.
- Jaeger, H. The “Echo State” Approach to Analysing and Training Recurrent Neural Networks; Technical Report; GMD—German National Research Institute for Computer Science: Darmstadt, Germany, 2001. [Google Scholar]
- Jaeger, H.; Haas, H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science 2004, 304, 78–80. [Google Scholar]
- Lukosevicius, M.; Jaeger, H. Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 2009, 3, 127–149. [Google Scholar]
- Jaeger, H.; Lukosevicius, M.; Popovici, D.; Siewert, U. Optimization and applications of echo state networks with leaky-integrator neurons. Neural Netw. 2007, 20, 335–352. [Google Scholar]
- Crossbow Technology Inc, Available at: http://www.xbow.com accessed on 10 October 2013.
- Pahlavan, K.; Levesque, A.H. Wireless Information Networks; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Li, X. RSS-based location estimation with unknown pathloss model. IEEE Trans. Wirel. Commun 2006, 5, 3626–3633. [Google Scholar]
| Path Type | Dataset 1 | Dataset 2 | Dataset 3 | Dataset 4 | Dataset 5 | Dataset 6 |
|---|---|---|---|---|---|---|
| 1 | 26 | 26 | 26 | 26 | 27 | 27 |
| 2 | 26 | 13 | 13 | 14 | 12 | 13 |
| 3 | – | 13 | 13 | 14 | 12 | 13 |
| Tot. Exit | 26 | 26 | 26 | 26 | 27 | 27 |
| Tot. Unchanged | 26 | 26 | 26 | 28 | 24 | 26 |
| ES1 | ES2 |
|---|---|
| 95.95%(±3.54) | 89.52%(±4.48) |
| LI-ESN Prediction | |||
|---|---|---|---|
| +1 | −1 | ||
| Actual | +1 | 44.04%(±5.17) | 7.88%(±5.17) |
| −1 | 2.60%(±2.06) | 45.48%(±2.06) | |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Barsocchi, P.; Chessa, S.; Micheli, A.; Gallicchio, C. Forecast-Driven Enhancement of Received Signal Strength (RSS)-Based Localization Systems. ISPRS Int. J. Geo-Inf. 2013, 2, 978-995. https://doi.org/10.3390/ijgi2040978
Barsocchi P, Chessa S, Micheli A, Gallicchio C. Forecast-Driven Enhancement of Received Signal Strength (RSS)-Based Localization Systems. ISPRS International Journal of Geo-Information. 2013; 2(4):978-995. https://doi.org/10.3390/ijgi2040978
Chicago/Turabian StyleBarsocchi, Paolo, Stefano Chessa, Alessio Micheli, and Claudio Gallicchio. 2013. "Forecast-Driven Enhancement of Received Signal Strength (RSS)-Based Localization Systems" ISPRS International Journal of Geo-Information 2, no. 4: 978-995. https://doi.org/10.3390/ijgi2040978
APA StyleBarsocchi, P., Chessa, S., Micheli, A., & Gallicchio, C. (2013). Forecast-Driven Enhancement of Received Signal Strength (RSS)-Based Localization Systems. ISPRS International Journal of Geo-Information, 2(4), 978-995. https://doi.org/10.3390/ijgi2040978






