Asymmetric Fingerprint Scheme for Vector Geographic Data Based on Smart Contracts

Abstract

Existing vector geographic data transaction schemes are typically merchant-controlled, hindering fair ownership tracing and impartial arbitration. To address this, we propose an asymmetric digital fingerprinting scheme based on smart contracts. In our approach, the user encrypts a proof fingerprint with a public key and sends it to the merchant; the merchant leverages the additive homomorphic property of the Paillier cryptosystem to embed the encrypted user fingerprint into an encrypted portion of the vector data while embedding a tracking fingerprint into the plaintext portion. The combined data is delivered to the user, who uses their private key to decrypt the encrypted part and obtain the plaintext data containing both fingerprints. This design enables tracing of unauthorized distribution without exposing the user’s fingerprint in plaintext, preventing malicious accusations. By leveraging blockchain immutability and smart contract automation, the scheme supports secure, transparent transactions and decentralized arbitration without third-party involvement, thereby reducing collusion risk and protecting both parties’ rights.

1. Introduction

Vector geographic data, as a fundamental component of national infrastructure and a key strategic resource, plays a vital role in land planning, urban governance, disaster early warning, and resource management [1,2,3]. However, the rapid proliferation in both the scale and complexity of such data has introduced significant challenges in ownership, secure circulation, and transaction regulation. Unauthorized acquisition and redistribution have become increasingly prevalent, while real-time monitoring and enforcement in digital environments remain difficult, substantially weakening the rights holders’ ability to assert control [4,5,6]. Recent official case analyses and regulatory inspections have revealed that the leakage and uncontrolled circulation of sensitive surveying and mapping data occur repeatedly in practice, involving multiple institutions and application scenarios. Typical incidents include staff copying classified terrain datasets onto internet-connected computers, scanning confidential maps into ordinary office systems, or uploading large numbers of classified geological maps to commercial websites. In several publicly reported cases, dozens of sensitive datasets were found to have been disseminated beyond authorized environments. In addition, national security warnings have indicated that certain foreign geographic information software deployed in key sectors continuously collects and transmits sensitive Chinese geographic data to external servers without authorization. These cases, spanning data production, storage, and dissemination stages, demonstrate that once geographic data become digitized, traditional administrative or contractual controls are often insufficient to observe data flows or prevent unauthorized redistribution in real time. These further underscore the necessity of technical mechanisms that can bind usage accountability directly to the data itself.

To address these challenges, merchants commonly embed digital watermarks into geographic data to verify ownership and enable post-infringement tracing [7]. Representative approaches include the normalization-based method proposed by Yan et al., which enhances robustness against geometric transformations while preserving spatial accuracy [8], and the multiple watermarking scheme developed by Wang et al., which embeds watermark information through coordinate mapping and domain subdivision to support hierarchical protection [9]. Despite their effectiveness in ownership verification, such watermarking methods primarily focus on post-infringement identification and exhibit limited resistance to collusion attacks. When multiple authorized users collude to redistribute data, embedded watermarks may be intentionally weakened or removed, rendering these schemes ineffective for reliably identifying illegal copiers.

To solve this problem, digital fingerprint technology has emerged, which has gained the ability to resist collusion attacks through a special encoding mechanism [10]. Most existing schemes are symmetric, with the merchant generating and embedding fingerprints. For example, Chen et al. proposed GD-PBIBD encoding, which can resist single-user attacks and nonlinear attacks while effectively identifying all colluders [11]. Similarly, Zhang et al. proposed a multi-level fingerprint algorithm that maps the high bits of normalized coordinates to the distribution level to cope with multi-level distribution [12]. However, this type of method has obvious security risks: the merchant has the user’s fingerprint and may maliciously embed the fingerprint into any data to frame the user. To alleviate this problem, an asymmetric fingerprint scheme has been proposed, in which the merchant and the user jointly generate and embed the fingerprint so that the merchant cannot fully grasp the user’s fingerprint [13]. When a dispute occurs, most existing solutions require arbitration to be carried out by a third-party agency, but there is a possibility that the third-party agency may collude with one party and interfere with the arbitration results.

Blockchain technology is decentralized, tamper-proof, and transparent. With the emergence of smart contract platforms such as Ethereum, its role has expanded from simple data recording to decentralized copyright registration, trusted transactions, and automatic verification. Therefore, it can effectively replace the position of third-party institutions in the dispute resolution process [14,15]. In recent years, a large number of studies have explored the application of blockchain in the field of trusted data transactions. Jiang et al. designed a high-performance copyright system based on a consortium chain, integrating smart contracts to achieve automatic transactions and revenue distribution [16]. Wu et al. proposed a privacy-preserving blockchain framework using zero-knowledge proofs and encryption to ensure data confidentiality alongside transactional transparency [17]. Ouyang developed a dual-chain system to support cross-chain copyright registration and verification, addressing the interoperability challenges in heterogeneous blockchain environments [18]. Xiang et al. proposed a flexible copyright trading protocol on Ethereum, incorporating encrypted data, deposit payments, and automated arbitration to protect both transaction integrity and user rights [19].

At present, there are a lot of studies on copyright protection schemes based on blockchain in the multimedia field [20,21,22,23]. However, the underlying design assumptions of these approaches are generally incompatible with the characteristics of vector geographic data. Multimedia files are typically treated as indivisible bitstreams, enabling hash-based binding or watermark embedding without compromising semantic integrity. In contrast, vector geographic data are composed of precise coordinate sequences, topological relationships, and semantic attributes, all of which must remain numerically consistent to preserve spatial accuracy. Even minor perturbations introduced by conventional watermarking or fingerprinting techniques may distort geometric structures or violate topological consistency constraints. Moreover, file-level blockchain binding strategies are ill-suited to the complex processing workflows commonly applied to geographic data, including reprojection, tiling, simplification, and incremental updates. These structural and operational disparities render existing multimedia-oriented blockchain schemes ineffective for vector geographic datasets. Consequently, there is a clear need to develop an asymmetric fingerprinting mechanism specifically tailored to the intrinsic properties of vector geographic data in order to enable secure, reliable, and trustworthy data transactions.

The main contributions of this paper are summarized as follows:

• An asymmetric fingerprinting scheme is proposed in which the merchant and the user jointly participate in fingerprint generation and embedding. This design prevents the merchant from obtaining the complete user fingerprint, thereby eliminating the inherent risk of fingerprint forgery and framing that exists in conventional symmetric fingerprinting schemes.
• A blockchain-enabled smart contract framework is developed to integrate fingerprint binding, data delivery, and automated dispute arbitration into a unified execution process. By embedding responsibility attribution logic directly into smart contracts, the proposed framework provides tamper-resistant, transparent, and third-party-free copyright protection for vector geographic data transactions.
• A collaborative technical framework is constructed by integrating GD-PBIBD-based fingerprint encoding, Paillier homomorphic encryption, and blockchain technology. Within this framework, GD-PBIBD encoding enhances resistance to collusion attacks, homomorphic encryption enables privacy-preserving fingerprint generation and tracing, and blockchain technology ensures verifiable execution and auditability. Collectively, these components enable accountable and trustworthy data transactions while preserving the geometric accuracy of vector geographic data.

The remainder of this paper is organized as follows. Section 2 introduces the Paillier cryptosystem and collusion-resistant fingerprint coding techniques. Section 3 presents the overall system model and the blockchain-based smart contract framework. Section 4 describes the proposed asymmetric fingerprint embedding and extraction algorithms for vector geographic data in detail. Section 5 reports the experimental setup and performance evaluation results. Finally, Section 6 concludes the paper.

2. Related Work

2.1. Paillier Encryption

Homomorphic encryption algorithms can embed encrypted fingerprints into encrypted digital products without exposing unencrypted fingerprints in the process. Therefore, they are widely used in the construction of asymmetric fingerprint schemes [24]. The current homomorphic encryption algorithms are divided into three types: additive homomorphism, multiplicative homomorphism, and full homomorphism. Among them, although the full homomorphic algorithm has the characteristics of both additive homomorphism and multiplicative homomorphism, it is not efficient and is not suitable for vector map data containing a large number of data points [25]. The multiplicative homomorphic encryption algorithm represented by RSA multiplies the encrypted vector map and the encrypted fingerprint to achieve the embedding effect, which has a great impact on the accuracy. At the same time, the principle of RSA determines that it cannot directly encrypt 0 and 1, and the fingerprint sequence needs to be preprocessed, which is a cumbersome process. Considering all factors, the additive homomorphic encryption algorithm is the best solution. Therefore, this article selects the most widely used and efficient Paillier encryption algorithm. The specific encryption and decryption process is as follows:

Step 1: Randomly select two unequal large prime numbers p and q. The selection of p and q needs to satisfy the condition (1), where gcd() is the greatest common divisor of the two numbers. The coordinate value data of vector data is usually large, so the generated large prime number also needs to be large enough; otherwise, the encrypted result will not be decrypted. The time required for encryption and decryption will also increase with the increase in large prime numbers, so it is necessary to generate a suitable large prime number according to the actual needs of the data.

$$\gcd \left(pq,\left(p-1\right)\left(q-1\right)\right)=1$$

(1)

where p and q are two unequal large prime numbers generated randomly.

Step 2: Calculate the product n of $p$ and $q$ and the least common multiple $\lambda$ of $(p-1)$ and $(q-1)$.

Step 3: Randomly select an integer $g\in Z_{n^2}^{*}$, where $Z_{n^2}^{*}$ represents the set of all integers less than $n^2$ that are coprime to $n^2$.

Step 4: Calculate $\mu$ according to Formula (2), where $L\left(x\right)=(x-1)/n$. Obtain the public key $(n, g)$ and private key $(\lambda , \mu )$. The private key is kept secret by the user, while the public key can be published publicly. Therefore, the public key is usually used to encrypt data, and the private key is used to decrypt it to ensure the security of the data.

$$\mu ={\left(L\right(g^{\lambda } mod n^2\left)\right)}^{-1} mod n$$

(2)

where $g$ is a randomly selected integer in the set $Z_{n^2}^{*}$, $\lambda$ is the least common multiple of $\left(p-1\right)$ and $\left(q-1\right)$, and $n$ is the product of $p$ and $q$.

Step 5: When encrypting plaintext $m$, a number $r$ that satisfies $\gcd \left(r,n\right)=1$ is randomly selected, and the ciphertext $c$ is calculated according to Formula (3). It can be seen from the formula that a random number $r$ is generated each time encryption is performed, so the ciphertext $c$ after each encryption of the same plaintext $m$ is different, ensuring data security.

$$c=g^m·r^n mod n^2$$

(3)

Step 6: When the ciphertext $c$ needs to be decrypted, the plaintext $m$ is calculated according to Formula (4):

$$m=L\left(c^{\lambda } mod n^2\right)·\mu mod n$$

(4)

Because $r$ is randomly generated each time encryption is performed, different ciphertexts will be generated after encrypting the same plaintext, which ensures the security of the ciphertext. The additive homomorphism of Paillier encryption is shown in Formula (5):

$$D\left(E\left(m_1,r_1\right)·E\left(m_2,r_2\right)\right)=m_1+m_2$$

(5)

where $D\left(x\right)$ means decrypting $x$, and $E\left(x\right)$ means encrypting $x$. Therefore, multiplying the ciphertext of $m_1$ and $m_2$ can obtain the ciphertext value of the plaintext addition of $m_1$ and $m_2$. This paper will use this feature of Paillier encryption to embed the watermark in the encrypted domain.

2.2. Fingerprint Encoded

To resist collusion attacks among buyers, merchants typically encode buyer-related information using collusion-resistant codes [26]. In this paper, two types of fingerprints are embedded into vector maps: a tracking fingerprint generated by the merchant and an accusation fingerprint generated by the buyer. The tracking fingerprint must support efficient traitor tracing and strong collusion resistance, while the accusation fingerprint serves as legal evidence in copyright disputes and imposes no strict encoding requirements. For simplicity, both fingerprints adopt the same encoding scheme in experiments.

The paper employs collusion-resistant fingerprint coding using I code and PD-PBIBD code chunking [27]. The buyer codes are generated using the GD-PBIBD code, which is a code set that arranges $v$ elements into $b$ subsets, each of size $k$, and repeats each element $r$ times, so that each pair of elements within a group occurs ${\lambda }_1$ times and between groups ${\lambda }_2$ times [28]. Where $v$ represents the code length, $b$ represents the number of buyers, and $(k-1)$ represents the number of colluders that can resist. It is common practice to set ${\lambda }_1=0$ and ${\lambda }_2=1$. $\left(s^p,s^{2p-2},s^{p-1},s,0,1\right)$ GD-PBIBD is the set of fingerprint encodings consisting of $s^{2p-2}$ buyers, capable of resisting $s-1$ colluders, and with a code length of $s^p$. Where $s$ is a prime number and $p$ is a positive integer greater than 2. Buyer codes of appropriate lengths at all levels are constructed by varying the parameters $s$,$p$. The total number of rows of the code word matrix indicates the number of buyers that can be accommodated, and each row is a unique fingerprint sequence of a buyer. Each row represents a unique fingerprint sequence of a buyer, where the buyer is identified by the different position of “0”.

The I code matrix is obtained by complementing the orthogonal matrix of the corresponding criteria to form the grouping code, based on the number of buyers to be accommodated. The grouping code should be constructed in such a way that each fingerprint has a group to which it belongs and belongs to only one group. To construct the I code of $s^p\times s^{p-1}$ accommodating $s^{2p-2}$ buyers, take $s^{p-1}$ as a zone group in turn, resulting in $s^{p-1}$ zone groups. To improve fingerprint retrieval efficiency, it is necessary to first confirm that the fingerprint belongs to the corresponding zone group and then traverse that group.

The buyer code is spliced with the group code to create a fingerprint code with a length of ${(s^p+s}^{p-1})$ and a buyer capacity of $s^{2p-2}$. This coding method can resist collusion attacks. At the same time, it can quickly locate the zone group through the I code and then use the GD-PBIBD code to accurately find the colluders, improving the efficiency of detecting the colluders.

Upon receiving a purchase request, the merchant selects a fingerprint from its database, embeds it into the data, and records the transaction. If an illegal copy is found, the embedded fingerprint is extracted and compared against the merchant’s records to trace the transaction. However, since the tracking fingerprint is generated unilaterally by the merchant, it supports tracing but lacks evidentiary validity for formal accusations.

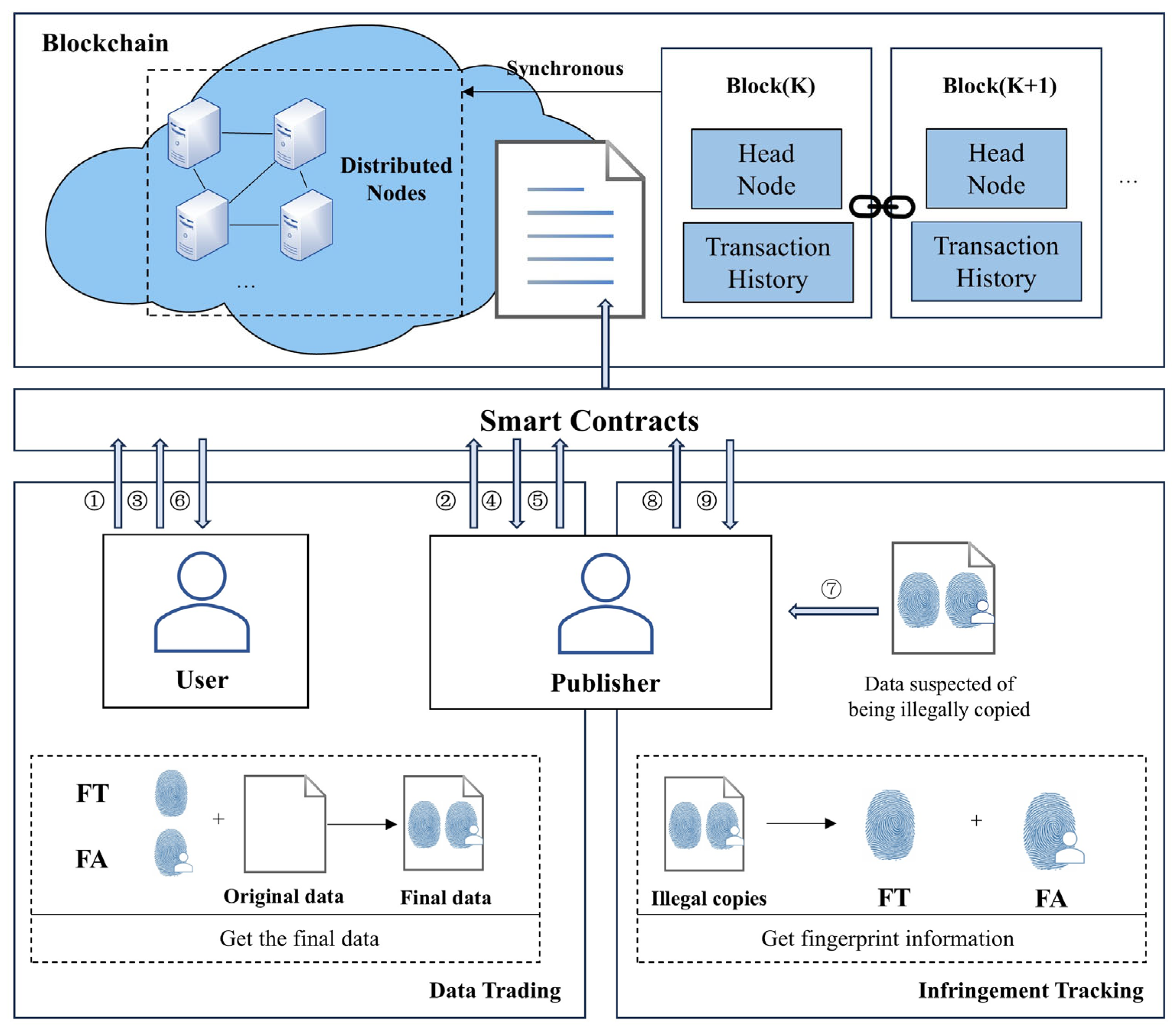
3. Overall Scheme Design and Smart Contract Framework

This section presents the overall scheme design of the proposed asymmetric fingerprinting framework for vector geographic data, with a focus on its implementation through smart contracts. Before introducing the detailed contract mechanisms, we first clarify the adversary model and the security objectives that the proposed scheme aims to achieve. Based on these assumptions and goals, the subsequent subsections describe how the proposed scheme coordinates fingerprint generation, encrypted data delivery, transaction execution, and dispute arbitration within a blockchain-based framework.

3.1. Adversary Model and Security Objectives

In the considered transaction scenario of vector geographic data, two types of participants are regarded as potentially dishonest: the data merchant and the data users. After legally obtaining vector data, a data user may maliciously redistribute the licensed data to unauthorized parties or collude with other users to attenuate, manipulate, or remove the embedded fingerprints in order to evade source tracing. Meanwhile, the data merchant is not assumed to be fully trustworthy and may attempt to deliberately embed forged fingerprints into distributed data so as to falsely accuse an honest user, which constitutes a typical framing attack. In contrast, the blockchain infrastructure and the deployed smart contracts are assumed to execute correctly according to their predefined logic, providing immutable and publicly verifiable transaction records.

Based on the above adversary model, the proposed scheme is designed to simultaneously achieve several essential security objectives. First, when unauthorized redistribution of vector geographic data occurs, the embedded fingerprint should be reliably extracted to uniquely identify the source of data leakage, thereby ensuring effective traceability. Second, the scheme must prevent any party, including the data merchant, from forging valid fingerprints to falsely accuse honest users so as to guarantee resistance against framing attacks. Third, even in the presence of collusion among multiple malicious users, the embedded fingerprint should remain robust against collective removal or manipulation, ensuring collusion resistance. At the same time, the privacy of user fingerprints must be preserved such that no single party can independently obtain the complete fingerprint information. In addition, the transaction process should guarantee fairness and non-repudiation, ensuring that neither party can deny its participation or tamper with the transaction outcome after execution. Finally, the binding relationships among the vector data, fingerprint information, and transaction records must be tamper-resistant and auditable so that the entire transaction and tracing process can be transparently verified through the blockchain.

3.2. Smart Contract Overview

Smart contracts are self-executing protocols based on blockchain technology that encode contract terms into program logic and automatically execute when predefined conditions are met [29]. Contract codes and rules are publicly stored on the chain and verified by all nodes through a consensus mechanism to ensure that they are tamper-proof and transparent [30,31,32]. Incorporating smart contracts into the asymmetric digital fingerprint framework of vector geographic data can significantly improve the automation, traceability and credibility of data transactions. Once the data is embedded with an asymmetric fingerprint and encrypted, its related copyright metadata can be registered on the chain, and the transaction process is managed by smart contracts. Legal access or dissemination of data can trigger automatic verification of fingerprint ownership, generate an on-chain timestamp and record transaction activities. In the event of a copyright dispute, the system can perform detection and arbitration procedures according to predefined rules, thereby improving execution efficiency. This integration not only simplifies the transaction process and enhances transparency but also supports reliable copyright protection without relying on centralized intermediaries.

3.3. Smart Contract Process

The proposed smart contract consists of two components: the transaction contract and the infringement tracking and arbitration contract. As illustrated in Figure 1, steps ①–⑥ correspond to the transaction contract, during which both parties exchange information and complete the data delivery via the smart contract. Steps ⑦–⑨ pertain to the infringement tracking and arbitration contract, where the merchant extracts evidence and submits it to the contract to complete the arbitration process.

Initially, the user sends a purchase request to the smart contract, which is received by the merchant. Subsequently, the user encrypts their fingerprint information using their public key and transmits both the encrypted fingerprint and the public key to the contract. The merchant retrieves this information from the contract and embeds both the encrypted user fingerprint and their own fingerprint into the vector map. The resulting map is uploaded to the InterPlanetary File System (IPFS), and the returned IPFS address is sent back to the smart contract. The user then obtains the address from the contract, downloads the required data, and confirms the completion of the transaction upon successful verification.

If the merchant identifies a potentially unauthorized copy, they employ fingerprint extraction algorithms to retrieve their own fingerprint from the suspect data. Based on the fingerprint records stored in the database, the merchant can identify the possible source of the unauthorized distribution. If the suspected user denies involvement, the merchant submits the extracted user fingerprint to the smart contract, which then executes the arbitration process to reach a final decision. Figure 1 shows the overall framework of the scheme. Algorithm 1 presents the detailed execution procedure of the proposed trade contract, including party initialization, confirmation, and message exchange.

The transaction contract is primarily responsible for establishing the transactional relationship between the merchant and the user, as well as facilitating the transfer of vector geospatial data. This component corresponds to Steps ①–⑥ in the workflow, and the detailed process is as follows:

Step 1: Upon identifying a vector map that meets their requirements, the user initiates a purchase request to the merchant via the smart contract.

Step 2: The merchant, upon receiving the request, either confirms the transaction—thus proceeding to the next step—or rejects the transaction, in which case the contract is terminated.

Step 3: The user encrypts their unique fingerprint using their own public key and uploads both the encrypted fingerprint and the corresponding public key to the smart contract.

Step 4: The merchant retrieves the user’s public key and encrypted fingerprint from the contract. Then, a fingerprint is selected from the merchant’s own fingerprint database and embedded into the vector map together with the user’s encrypted fingerprint.

Step 5: The merchant uploads the fingerprint-embedded vector map to the InterPlanetary File System (IPFS), obtains the corresponding IPFS address, and submits it to the smart contract.

Step 6: The user receives the IPFS address from the smart contract, downloads the data from IPFS, decrypts the content using their private key, and confirms the completion of the transaction.

The infringement tracking and arbitration contract is responsible for identifying the source of unauthorized copies and, in cases where the suspected infringer denies involvement, conducting arbitration based on submitted evidence via the smart contract.

Step 7: When the merchant identifies a suspected unauthorized copy, they extract the embedded merchant fingerprint using a fingerprint extraction algorithm. The extracted fingerprint is then matched against the merchant’s transaction database to determine the identity of the suspected infringer.

Step 8: If the suspected user denies the infringement, the merchant encrypts the extracted user fingerprint and submits it to the smart contract. The contract then compares it against the original fingerprint submitted by the user during the transaction.

Step 9: The merchant receives the verdict from the smart contract and completes the arbitration process

Algorithm 1. Trade Contract Execution Process

Input: B, S, message Output: status, events 1:  if (buyer == 0 × 0 and seller == 0 × 0) then 2:      if (B == 0 × 0 or S == 0 × 0 or B == S) then reject “Invalid parties” end if 3:      if (caller != B and caller != S) then reject “Only buyer or seller can initialize” end if 4:      buyer ← B 5:      seller ← S 6:      status ← Confirming 7:  else 8:      if (B != buyer or S != seller) then reject “Parties already set” end if 9:  end if 10: if (caller == buyer) then 11:      buyerConfirmed ← true 12:      emit BuyerConfirmed(buyer) 13: else if (caller == seller) then 14:      sellerConfirmed ← true 15:      emit SellerConfirmed(seller) 16: else 17:      reject “Only buyer or seller can confirm” 18: end if 19: if (buyerConfirmed and sellerConfirmed) then 20:      status ← Confirmed 21:      if (message != “”) then 22:          if (caller == buyer) then emit MessageSent(buyer, seller, message) 23:          else emit MessageSent(seller, buyer, message) 24:          end if 25:      end if 26: end if

4. Asymmetric Fingerprint Algorithm Design

In this work, two distinct types of fingerprint information are embedded simultaneously into a single vector map: the merchant’s fingerprint for ownership identification and the buyer’s fingerprint for post-distribution arbitration. To prevent the buyer’s arbitration-oriented fingerprint from being disclosed to the merchant, the buyer first generates a Paillier public–private key pair and provides only the public key to the merchant. The buyer’s fingerprint is then encrypted under the Paillier public key prior to embedding. After encryption, the fingerprint sequence is transformed into a non-patterned real-valued series, rendering conventional watermark embedding rules inapplicable. Consequently, the encrypted buyer fingerprint is embedded through homomorphic operations performed by the merchant without access to the plaintext fingerprint, thereby ensuring the non-framing property of the proposed scheme.

Directly encrypting the entire vector map would, however, prevent the embedding of the merchant’s plaintext fingerprint into the ciphertext data. To enable the simultaneous embedding of both fingerprint types without mutual interference and to ensure reliable extraction, the proposed scheme applies a polar coordinate transformation to the vector map and partitions the transformed data into two segments. These segments are used to separately embed the encrypted buyer fingerprint and the plaintext merchant fingerprint, respectively. Given that asymmetric encryption typically incurs substantially higher computational overhead than symmetric encryption, encrypting only a portion of the transformed data effectively reduces overall computational cost while preserving the security requirements of the arbitration-oriented fingerprint. The complete algorithmic workflow of the proposed scheme is illustrated in Figure 2.

In summary, the buyer generates and retains the Paillier public–private key pair and is responsible for fingerprint generation and decryption during the arbitration process, while only the public key is disclosed to the merchant. The merchant performs homomorphic embedding operations using the buyer’s public key without access to the plaintext buyer fingerprint or the private key. The merchant independently embeds its own plaintext fingerprint, and neither party can obtain the complete fingerprint information of the other, thereby ensuring both cryptographic security and functional separation.

4.1. Fingerprint Embedding

To ensure that both fingerprint sequences can be embedded into the vector map without interfering with each other and to guarantee the correct extraction of fingerprint information, this paper divides the vector data into two parts and embeds each fingerprint into a separate portion. Furthermore, given that asymmetric encryption typically incurs higher computational costs than symmetric encryption, encrypting only a subset of the data can significantly reduce the overall encryption time without compromising security.

The specific fingerprint embedding procedure is as follows:

Step 1: Read the vector geospatial dataset M and extract the coordinate point sets X and Y.

Step 2: Select two stable points P₁ and P₂, and compute their midpoint to serve as the origin P of the polar coordinate system.

Step 3: As shown in Figure 3, P is used as the origin to convert all coordinate points (x, y) into the polar coordinate system (r, θ) according to Equations (6) and (7).

$$r=\sqrt{x^2+y^2}$$

(6)

$$\theta =\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}(y/x)$$

(7)

where x and y represent the Cartesian coordinates of the point, r denotes the radial distance in the polar coordinate system, and θ is the polar angle.

Step 4: Classify the coordinate points based on the parity of the first n digits of their radial distances. The vector map is thereby divided into two subsets: M₁, comprising points whose first n digits of the radial distance are odd, and M₂, containing the remaining points.

Step 5: For all coordinates $(r_{m1},{\theta }_{m1})$ in M₁, embed the tracking fingerprint FT according to the indexing strategy defined in Equation (8). The fingerprint embedding operation is then performed using Equation (9):

$${index}_{r_{m1}}=int\left(r_{m1}/100\right)\%len\left(FT\right)$$

(8)

$${r_{m1}}^{\prime }=\{\begin{array}{c}{r}_{m1}\left(i\right)-\mathrm{R}/2,FT\left({index}_{r_{m1}}\right)=0 and mod\left(r_{m1}\left(i\right),\mathrm{R}\right)>R/2 \\ r_{m1}\left(i\right),FT\left({index}_{r_{m1}}\right)=0 and mod\left(r_{m1}\left(i\right),R\right)\le R/2\\ r_{m1}\left(i\right)+R/2,FT\left({index}_{r_{m1}}\right)=1 and mod\left(r_{m1}\left(i\right),R\right)\le R/2\\ r_{m1}\left(i\right),FT\left({index}_{r_{m1}}\right)=1 and mod\left(r_{m1}\left(i\right),R\right)>R/2\end{array}$$

(9)

where $FT$ is the binary tracking fingerprint sequence and $len\left(FT\right)$ is its length. $FT\left({index}_{r_{m1}}\right)$ denotes the fingerprint bit assigned to the $i$-th coordinate by Equation (8). $R$ is the quantization constant.

Step 6: Scale all coordinates in M₂, denoted as $(r_{m2},{\theta }_{m2})$, by a factor of ${10}^k$, where k is a precision-control parameter selected according to the required coordinate accuracy of the vector data. Then, use Equation (10) to encrypt both the arbitration fingerprint FA and the radial distance $r_{m2}$:

$$E\left(FA\right)=g^{DF}·r^n mod n^2$$

(10)

$$E\left(r_{m2}\right)=g^{r_{m2}}·r^n mod n^2$$

(11)

where FA and $r_{m2}$ are the inputs to be encrypted, and g, r, and n are parameters chosen according to the specifications detailed in Section 2.1.

Step 7: Utilize the additive homomorphic property of Paillier encryption to embed the arbitration fingerprint FA into the encrypted data using Equation (12):

$${r_{m2}}^{\prime }=E\left(r_{m2},r_1\right)·E\left(FA,r_2\right)=E(r_{m2}+FA)$$

(12)

Step 8: Combine the modified encrypted coordinates ${r_{m1}}^{\prime }$ and ${r_{m2}}^{\prime }$ to form the final vector map $M\mathrm{’}$, which is then delivered to the user.

4.2. Fingerprint Extraction

Upon receiving the delivered vector map, the user first decrypts the encrypted portion ${r_{m2}}^{\prime }$ using Equation (13). Subsequently, all coordinates are transformed back to the Cartesian coordinate system using Equations (14) and (15), thereby reconstructing a usable vector map.

$$D\left(E\right(r_{m2}+FA\left)\right)=L\left({E(r_{m2}+FA)}^{\lambda } mod n^2\right)·\mu mod n$$

(13)

$$x=rcos\theta$$

(14)

$$y=rsin\theta$$

(15)

When the merchant detects an illegal copy, fingerprint extraction can be performed to determine ownership and identify the infringing party. The merchant extracts the tracking fingerprint $FT$ to identify the responsible user. If the user denies involvement, the arbitration fingerprint $FA$ is further extracted for evidence in the arbitration process. The detailed procedure is as follows:

Step 1: As in the embedding process, convert the vector coordinates into the polar coordinate system. The dataset is then partitioned into subsets M₁, and M₂ using the same classification rules.

Step 2: The tracking fingerprint FT is extracted from ${r_{m1}}^{\prime }$ using the indexing strategy in Equation (8) and the extraction rule defined in Equation (16):

$$W\left(i\right)=\{\begin{array}{c}W\left(i\right)+1,mod\left({r_{m1}}^{\prime },R\right)>R/2\\ W\left(i\right)-1,mod\left({r_{m1}}^{\prime },R\right)\le R/2\end{array}$$

(16)

where W denotes the extracted fingerprint sequence, i is the index determined by the mapping function, and R is the quantization factor consistent with the embedding phase.

Step 3: The final fingerprint sequence is determined via a majority voting mechanism. This fingerprint can then be used to identify the illegal merchant.

To identify the infringing party, the regional code embedded in the fingerprint is first used to narrow down the search to a specific area. The extracted fingerprint is then compared with those stored in the regional fingerprint database. The party whose fingerprint has the smallest Hamming distance from the extracted one is identified as the colluder.

If the suspected user denies involvement, arbitration fingerprint verification is triggered. Note that arbitration fingerprint extraction requires access to the plaintext vector data, which can only be obtained after the user decrypts the map using Equation (13). The extraction process is as follows:

Step 1: The arbitration fingerprint is extracted based on the parity of the decrypted radial distance values ${x^{\prime }}_{fa}$, as expressed in Equation (17). Since values were quantized to even numbers during embedding, a value of 1 would convert an even integer into an odd one [33]. Thus, fingerprint bits can be determined by examining whether the integer component is odd or even:

$$FA\left(index\right)=\{\begin{array}{c}FA\left(index\right)+1,D\left({r_{m2}}^{\prime }\right)\%2=1\\ FA\left(index\right)-1,D\left({r_{m2}}^{\prime }\right)\%2=0\end{array}$$

(17)

where FA is the extracted fingerprint sequence, $index$ is the fingerprint position calculated according to the index relationship, and $D\left({r_{m2}}^{\prime }\right)$ is the decrypted polar diameter containing the fingerprint.

Step 2: The final arbitration fingerprint is again determined by majority voting.

Throughout the protocol, the arbitration fingerprint is known only to the user and is transmitted solely in its encrypted form using the user’s public key. As a result, if the merchant successfully extracts the user’s fingerprint from an illegal copy, it serves as irrefutable evidence of infringement, rendering any denial by the user invalid.

5. Experiments and Analysis

To evaluate the soundness of the proposed fingerprinting protocol, two dimensions of assessment are considered: the evaluation of the asymmetric fingerprint scheme and the evaluation of algorithmic performance. The former focuses on analyzing the protocol’s procedural integrity—examining whether any vulnerabilities may disrupt the workflow or lead to the leakage of private information between transacting parties. The latter involves a series of experiments designed to assess the security and robustness of the algorithm. Specifically, it includes evaluating the variation in coordinate points of the vector map before and after fingerprint embedding, as well as determining whether the embedded fingerprints can be accurately extracted following various types of attacks. These evaluations collectively highlight the strengths and limitations of the proposed method.

5.1. Analysis of Asymmetric Fingerprint Schemes

The proposed asymmetric fingerprinting scheme embeds fingerprint information after encrypting the data, a design approach that shares conceptual similarities with the commutative cipher watermarking technique, as both involve the encryption of data and the embedding of copyright-related information [34]. However, most existing commutative cipher watermarking approaches rely on symmetric encryption, in which the same key is used for both encryption and decryption. Under such schemes, the merchant must transmit both the encrypted data and the decryption key to the user, making the key transmission a critical point of vulnerability. If the symmetric key is intercepted during transmission, the confidentiality of the encrypted data is entirely compromised.

In contrast, the scheme presented in this work adopts the Paillier cryptosystem, which is an asymmetric encryption method. The fundamental distinction lies in the use of separate keys: a public key for encryption and a private key for decryption. In the proposed data transmission protocol, only the encrypted data and the public key are transmitted; the private key is securely retained by the user. As a result, even if the communication channel is compromised, the encrypted data cannot be decrypted without access to the user’s private key, thereby preserving the confidentiality of the data. Moreover, even if a malicious merchant embeds a user’s encrypted fingerprint into other data, the resulting ciphertext remains unusable without the corresponding private key. Consequently, the merchant cannot extract or utilize the embedded fingerprint for framing legitimate users. This design significantly enhances security compared to symmetric watermarking schemes based on commutative ciphers.

In asymmetric encryption, the private key serves as the core component of cryptographic security. If compromised, the merchant could potentially misuse the private key to falsely implicate legitimate users. Therefore, safeguarding the user’s private key is of paramount importance. The private key should be stored in a highly secure environment, such as a hardware security module (HSM), which transfers sensitive key management and cryptographic operations from software to physical devices, offering robust protection through physical and logical security mechanisms. Alternatively, access control mechanisms may be employed to restrict unauthorized access to sensitive components. As long as the correspondence between the public and private keys is maintained, storing them separately can also be a viable and secure approach.

5.2. Prototype System Implementation

Based on the framework proposed in Section 3, a prototype trusted transaction system for vector geographic data was implemented to demonstrate the overall system operation process. The system adopts an Ethereum-compatible blockchain as the underlying execution platform and integrates smart contracts with a front-end demonstration interface. The implementation encompasses both smart contract development and deployment, as well as the construction of a user-facing interface that supports transaction execution and post-delivery arbitration. The smart contracts are implemented in Solidity and deployed within the blockchain environment, where they are responsible for transaction execution, on-chain evidence recording, and dispute handling. The front-end prototype system provides two primary functional modules: a trading module and an arbitration module, which together illustrate the operational workflow of the proposed scheme.

As shown in Figure 4, the trading module demonstrates the complete transaction workflow. During the transaction phase, the buyer inputs identity-related information and cryptographic parameters, while the merchant supplies the corresponding data identifier and vector data file. The system then generates and encrypts a user-specific fingerprint, binds it to the transaction process, and invokes the smart contract to execute the data trading operation. Upon successful execution, transaction identifiers, data hashes, and related state information are immutably recorded on-chain, thereby forming verifiable delivery evidence to support subsequent traceability.

Following data delivery, potential infringement disputes can be processed through the arbitration module, as illustrated in Figure 5. At this stage, the merchant initiates an arbitration request by submitting the relevant transaction identifier, the suspected user address, and the associated evidence data. The smart contract subsequently performs verification based on on-chain transaction records and fingerprint-related information. The arbitration outcome, including responsibility attribution and the corresponding verdict, is generated and recorded on-chain, providing technically verifiable evidence to support regulatory supervision or legal proceedings.

By integrating transaction execution, on-chain evidence preservation, and dispute arbitration, the prototype system offers a clear and practical demonstration of how the proposed asymmetric fingerprint scheme operates within a blockchain-enabled environment. This system-level implementation complements the algorithmic validation and performance evaluation results, providing an intuitive and comprehensive illustration of the overall system operation process.

5.3. Smart Contract Performance Evaluation

To evaluate the feasibility and cost characteristics of the proposed scheme in a blockchain environment, this study conducts a comparative analysis against an existing blockchain-based spatial data trading framework in which smart contracts constitute the core mechanism for transaction execution and settlement (Liu et al., 2022) [35]. Both schemes are implemented and tested under identical experimental settings to ensure a fair and reproducible comparison. Encrypted vector geographic data embedded with transaction-party fingerprints are stored off-chain using the InterPlanetary File System (IPFS), while only essential identifiers and transaction records are maintained on-chain. All smart contracts are developed in Solidity and deployed on a local Ethereum test network instantiated via Ganache, which provides predefined accounts for contract deployment and transaction execution. The comparison focuses on two primary performance indicators: contract deployment cost and overall runtime cost. Functional differences between the schemes are considered jointly to examine the relationship between on-chain cost and system capability. The corresponding results are summarized in

Table 1. Comparison of Blockchain Performance and Functionality.

Comparison Category	Evaluation Indicator	Proposed Scheme	Liu et al., [35]
Performance	Deployment cost	2,762,930 Gas	2,666,636 Gas
	Runtime cost	552,030 Gas	349,542 Gas
Functionality	Post-delivery responsibility traceability	Leaked data can be traced back to specific transaction participants	Data redistribution cannot be traced after transaction completion
	On-chain recording of data delivery evidence	Delivery identifiers are recorded on-chain together with transaction states	Delivery actions and outcomes are not recorded
	Technical non-repudiation capability	User fingerprints are cryptographically bound to transaction processes	Only asset registration and transaction records are maintained
	Infringement dispute handling mechanism	Technical judgments are produced via on-chain fingerprint comparison	Disputes rely on off-chain manual or legal procedures

.

With respect to deployment cost, the proposed scheme requires 2,762,930 gas, compared with 2,666,636 gas for the reference scheme. Both values remain within the same order of magnitude, indicating that the introduction of fingerprint management and infringement arbitration logic does not impose a substantial additional burden during system initialization. Given that contract deployment is a one-time expense, this marginal difference is unlikely to affect long-term system operation or scalability.

In terms of overall runtime cost, the proposed scheme incurs a total on-chain cost of 552,030 gas to complete a full business process, including transaction execution and infringement arbitration when triggered. By contrast, the reference scheme requires 349,542 gas within its supported functional scope. The higher runtime cost of the proposed scheme primarily arises from the inclusion of post-delivery accountability and dispute handling mechanisms, rather than from inefficiencies in transaction execution. The reference scheme focuses on completing the transaction process through smart contracts and does not record delivery evidence or support infringement tracing, resulting in lower on-chain costs but more limited functionality.

From a functional perspective, the proposed scheme strengthens post-transaction control by cryptographically binding user fingerprints to transaction records and recording delivery identifiers on-chain. This design enables technical responsibility determination in cases of data leakage or unauthorized redistribution. Infringement disputes can further be processed through smart contracts, with arbitration outcomes immutably recorded on-chain as verifiable technical evidence. In contrast, the reference scheme primarily relies on off-chain procedures to address post-transaction disputes and lacks built-in technical mechanisms to constrain or verify data redistribution behavior.

Overall, the proposed scheme demonstrates that the integration of post-delivery accountability mechanisms into blockchain-based spatial data trading can be achieved with a manageable increase in on-chain cost. The observed rise in runtime gas consumption is directly attributable to the incorporation of additional functionalities, namely fingerprint binding, delivery evidence recording, and arbitration result preservation, rather than to inefficiencies in transaction execution. This design effectively extends the role of smart contracts beyond transaction settlement toward lifecycle-level responsibility management, a capability that is particularly important for trusted circulation scenarios involving high-value geographic information data.

5.4. Algorithm Performance Analysis

To verify the generality and effectiveness of the proposed algorithm, experiments were conducted on three vector maps of different types. The basic characteristics of these maps are summarized in

Table 2. Experimental data information table.

Data	Type	Size/KB	The Number of Vertices	The Number of Features
A	Point	377	13,769	13,769
B	Polyline	6917	338,986	29,625
C	Polygon	1140	70,084	581

. The Paillier cryptosystem was adopted as the homomorphic encryption method. The encryption results are illustrated in Figure 6, where Figure 6a–c represent the original (unencrypted) data, and Figure 6d–f show the corresponding data after encryption.

The experiment analyzed the performance of the proposed algorithm from three perspectives: data accuracy analysis, encryption and decryption efficiency analysis, and robustness analysis. Hamming distance is employed as the evaluation metric to determine whether the fingerprint information is correctly extracted. As a fundamental concept in information theory, the Hamming distance measures the number of differing bits between two fingerprint sequences at corresponding positions. It provides a quantitative measure of the similarity between sequences and objectively evaluates the accuracy of fingerprint extraction [36].

Accordingly, during performance evaluation, the robustness of the algorithm is assessed by computing the Hamming distances between the extracted fingerprint sequences $f_{A1}, {f_{B1}, f}_{A2}, f_{B2}, f_{A3}, f_{B3}$ and the original fingerprints $FT$ and $FA$. The computation of the Hamming distance is defined in Equation (18):

$$D\left(x,y\right)={\sum }_{k-1}^n{x}_k\oplus y_k$$

(18)

where $x_k$ and $y_k$ respectively represent a certain bit of the two fingerprint sequences, and $\oplus$ represents the bitwise XOR operation. $D\left(x,y\right)$ represents the Hamming distance of the two fingerprints, and a Hamming distance of 0 proves that the fingerprint information was extracted correctly.

• Data precision and parameter sensitivity analysis

To evaluate the impact of fingerprint embedding on the precision and usability of vector geospatial data, a multi-dimensional error analysis is conducted, and the results are summarized in Table 2. Since the proposed scheme embeds fingerprint information directly into coordinate values after polar coordinate transformation, slight numerical perturbations are inevitable.

As shown in

Table 3. Results of data precision and parameter sensitivity analysis.

Data	n	Max Deviation	RMSE	Points with Deviation < 0.0001 m (%)	Total Number of Data Points
A	2	5.449575 × 10−5	1.884387 × 10−5	100%	13,769
	3	5.285191 × 10−5	1.879556 × 10−5	100%
	4	5.449575 × 10−5	1.886346 × 10−5	100%
B	2	7.428597 × 10−6	1.390115 × 10−6	100%	338,986
	3	7.428597 × 10−6	1.394993 × 10−6	100%
	4	7.221957 × 10−6	1.397788 × 10−6	100%
C	2	5.072406 × 10−5	2.253388 × 10−5	100%	70,084
	3	5.125154 × 10−5	2.274152 × 10−5	100%
	4	5.072406 × 10−5	2.263077 × 10−5	100%

, for all tested datasets, including point, line, and polygon data, and for all parameter settings (n = 2, 3, and 4), the maximum coordinate deviation is consistently smaller than 0.0001 m, and the root mean square error (RMSE) remains on the order of 10⁻⁵–10⁻⁶ m. Notably, 100% of the data points exhibit coordinate deviations smaller than 0.0001 m in all experiments, indicating that the proposed scheme preserves geometric accuracy without introducing outliers or abnormal distortions.

In addition, Table 3 provides experimental evidence for the selection of the embedding parameter n. The parameter n controls the parity-based partitioning of radial distances in the polar coordinate domain, thereby influencing the distribution of embedding positions. The experimental results demonstrate that, within the tested range (n = 2–4), variations in n do not lead to significant differences in maximum deviation or RMSE, and data precision remains stable across different parameter choices. This indicates that n can be flexibly selected to balance embedding robustness and computational efficiency without compromising data accuracy.

Overall, by jointly considering maximum deviation, RMSE, deviation distribution, and total data scale, the proposed scheme exhibits negligible impact on the precision and usability of vector geospatial data.

2.

Encryption and decryption efficiency analysis

This study employs the Paillier cryptosystem to encrypt both vector map data and fingerprint information. The security of this algorithm is based on the computational hardness of large integer factorization. Consequently, using larger prime numbers to generate the public and private keys enhances security but also increases the computational cost of encryption and decryption. To evaluate the efficiency of the algorithm, five polyline datasets with varying numbers of vertices were used. As shown in

Table 4. Analysis results of encryption and decryption efficiency.

Data	Number of Coordinates to Be Encrypted	Number of Elements to be Encrypted	Encryption Time (s)	Decryption Time (s)
1	12,685	3734	0.59	0.44
2	24,898	6724	1.15	0.88
3	50,704	10,654	2.45	1.95
4	105,422	17,911	4.86	3.48
5	249,595	31,512	11.80	9.74
6	425,900	44,734	20.42	16.91
7	841,486	76,985	42.61	33.31

, the proposed method performs efficiently on small datasets, but the processing time increases as the data volume grows. The average encryption speed across the experimental datasets was 0.598 MB/s, while the average decryption speed was 0.715 MB/s. Although the performance is lower than that of common symmetric encryption schemes, it remains within an acceptable range for practical use.

3.

Algorithm robustness experiment

To comprehensively assess the robustness of the proposed algorithm against common geometric transformations, a series of experiments involving translation, scaling, cropping, point insertion/deletion, and rotation were conducted. As summarized in

Table 5. Attack experimental results.

Degree of Attack	Fingerprint Type	Point	Polyline	Polygon
500 m along the X-axis	Tracking fingerprints	${D(FT,f}_{A1})=0$	${D(FT,f}_{A2})=0$	${D(FT,f}_{A3})=0$
	Accuse fingerprints	${D(FA,f}_{B1})=0$	${D(FA,f}_{B2})=0$	${D(FA,f}_{B3})=0$
500 m along the Y-axis	Tracking fingerprints	${D(FT,f}_{A1})=0$	${D(FT,f}_{A2})=0$	${D(FT,f}_{A3})=0$
	Accuse fingerprints	${D(FA,f}_{B1})=0$	${D(FA,f}_{B2})=0$	${D(FA,f}_{B3})=0$
Scaling 0.5	Tracking fingerprints	${D(FT,f}_{A1})=0$	${D(FT,f}_{A2})=0$	${D(FT,f}_{A3})=0$
	Accuse fingerprints	${D(FA,f}_{B1})=0$	${D(FA,f}_{B2})=0$	${D(FA,f}_{B3})=0$
Scaling 2.0	Tracking fingerprints	${D(FT,f}_{A1})=0$	${D(FT,f}_{A2})=0$	${D(FT,f}_{A3})=0$
	Accuse fingerprints	${D(FA,f}_{B1})=0$	${D(FA,f}_{B2})=0$	${D(FA,f}_{B3})=0$
Clipping 10%	Tracking fingerprints	${D(FT,f}_{A1})=0$	${D(FT,f}_{A2})=0$	${D(FT,f}_{A3})=0$
	Accuse fingerprints	${D(FA,f}_{B1})=0$	${D(FA,f}_{B2})=0$	${D(FA,f}_{B3})=0$
Clipping 30%	Tracking fingerprints	${D(FT,f}_{A1})=0$	${D(FT,f}_{A2})=0$	${D(FT,f}_{A3})=0$
	Accuse fingerprints	${D(FA,f}_{B1})=0$	${D(FA,f}_{B2})=0$	${D(FA,f}_{B3})=0$
Add 20%	Tracking fingerprints	${D(FT,f}_{A1})=0$	${D(FT,f}_{A2})=0$	${D(FT,f}_{A3})=0$
	Accuse fingerprints	${D(FA,f}_{B1})=0$	${D(FA,f}_{B2})=0$	${D(FA,f}_{B3})=0$
Add 40%	Tracking fingerprints	${D(FT,f}_{A1})=0$	${D(FT,f}_{A2})=0$	${D(FT,f}_{A3})=0$
	Accuse fingerprints	${D(FA,f}_{B1})=0$	${D(FA,f}_{B2})=0$	${D(FA,f}_{B3})=0$
Delete20%	Tracking fingerprints	${D(FT,f}_{A1})=0$	${D(FT,f}_{A2})=0$	${D(FT,f}_{A3})=0$
	Accuse fingerprints	${D(FA,f}_{B1})=0$	${D(FA,f}_{B2})=0$	${D(FA,f}_{B3})=0$
Delete 40%	Tracking fingerprints	${D(FT,f}_{A1})=0$	${D(FT,f}_{A2})=0$	${D(FT,f}_{A3})=0$
	Accuse fingerprints	${D(FA,f}_{B1})=0$	${D(FA,f}_{B2})=0$	${D(FA,f}_{B3})=0$
Rotate 60°	Tracking fingerprints	${D(FT,f}_{A1})=0$	${D(FT,f}_{A2})=0$	${D(FT,f}_{A3})=0$
	Accuse fingerprints	${D(FA,f}_{B1})=0$	${D(FA,f}_{B2})=0$	${D(FA,f}_{B3})=0$
Rotate 120°	Tracking fingerprints	${D(FT,f}_{A1})=0$	${D(FT,f}_{A2})=0$	${D(FT,f}_{A3})=0$
	Accuse fingerprints	${D(FA,f}_{B1})=0$	${D(FA,f}_{B2})=0$	${D(FA,f}_{B3})=0$

, the fingerprint information remained consistently extractable under all tested conditions, demonstrating strong resilience.

For translation attacks, vector data were shifted by 500 m along the X and Y axes, respectively. In scaling experiments, the data were resized to 0.5× and 2× their original dimensions. In both cases, the embedded fingerprints were accurately recovered, which can be attributed to the inherent translation and scaling invariance properties of the polar coordinate representation employed in the algorithm. Furthermore, robustness against data loss was verified through cropping operations, where up to 30% of the data was randomly removed. The extracted fingerprint sequences still exhibited a Hamming distance of zero from the original, confirming that the redundant embedding strategy and compact code length effectively mitigate the impact of partial data loss. Similarly, the algorithm demonstrated strong resistance to point insertion and deletion, which are common in vector data simplification or densification processes. Even with 40% of the coordinate points altered, fingerprint extraction remained error-free. Finally, the algorithm’s resilience to rotation was validated across multiple angles. Thanks to the preprocessing step involving polar coordinate transformation, the fingerprint maintained full rotational invariance, with the extracted sequences perfectly matching the originals.

4.

Comparative experiment

Table 6. Robustness capability comparison under typical attacks.

Attack Type	Proposed Scheme	Reference [15]	Reference [31]
Translation	√	√	√
Scaling	√	√	√
Clipping	√	√	√
Add Point	√	√	√
Delet Point	√	√	√
Rotate	√	×	×
Collusion attacks	√	×	√
Impact on data precision	Low	Low	Medium
traceability	High	Medium	Medium
Efficiency	Low	High	High

presents a capability-oriented comparison between the proposed scheme and two representative fingerprinting methods. Unlike purely numerical robustness evaluations, this comparison focuses on whether a scheme can fundamentally support specific attack scenarios and functional requirements.

As shown in Table 6, Reference [15] demonstrates basic robustness against common geometric modifications but fails to resist rotation and collusion attacks, due to its reliance on symmetric fingerprint generation and the absence of invariant coordinate representations. Reference [31] improves resistance to collusion attacks by adopting asymmetric fingerprinting; however, its fingerprint embedding strategy introduces relatively larger coordinate perturbations, resulting in the highest impact on data precision among the three schemes. They both rely on a trusted third party to perform dispute arbitration and infringement determination.

By contrast, the proposed scheme simultaneously supports rotation invariance and collusion resistance, while maintaining a low impact on data precision. More importantly, it uniquely integrates buyer and seller dispute arbitration and traceability mechanisms, enabling reliable post-distribution accountability in data trading scenarios. It should be noted that the proposed scheme incurs higher computational overhead than the reference methods, mainly due to the use of homomorphic encryption.

6. Conclusions

This paper presents an asymmetric fingerprinting scheme for vector geospatial data that integrates blockchain technology and smart contracts to achieve secure, transparent, and traceable transactions. The proposed scheme embeds two types of fingerprints: a tracking fingerprint generated by the merchant for identifying unauthorized users, and a proof fingerprint generated and encrypted by the user through the additive homomorphic property of the Paillier cryptosystem. This structure prevents the merchant from accessing the user’s fingerprint in plaintext, thereby avoiding false accusations and improving the credibility of copyright protection. In cases of copyright disputes, the embedded information can be extracted and verified through smart contract–based automated arbitration, eliminating the need for third-party intervention. Experimental results demonstrate that the dual-fingerprint mechanism preserves the geometric accuracy of vector data and exhibits robustness against common attacks, offering a practical and effective approach to geospatial data copyright protection. Future work will focus on optimizing the computational efficiency of the encryption and embedding processes and extending the proposed scheme to broader geospatial data types and distributed application scenarios.