Context-Aware Knowledge Graph Learning for Point-of-Interest Recommendation

Abstract

Existing point-of-interest (POI) recommendation methods often fail to capture complex contextual dependencies and suffer from severe data sparsity in location-based social networks (LBSNs). To address these limitations, this study proposes a Context-Aware Knowledge Graph Learning (CKGL) method that integrates multi-dimensional semantic information, spatio-temporal dependencies, and social relationships into a unified knowledge graph framework. First, the Context-Aware Knowledge Graph Construction (CKGC) module builds a unified POI knowledge graph that captures heterogeneous relationships among users, POIs, regions of interest (ROIs), and social links. Then, the Context-Aware Knowledge Graph Embedding (CKGE) module, based on the Translational Distance Model with Relation-Specific Spaces (TransR), learns relation-specific embeddings of entities to preserve heterogeneous semantics. Next, a Spatio-Temporal Gated Graph Neural Network (STG-GNN) captures temporal dynamics and spatial dependencies in user check-in behaviors, while the Relation-Aware Graph Attention Network (RA-GAT) enhances multi-relational reasoning and information aggregation across heterogeneous relations. Extensive experiments on two real-world LBSN datasets, Gowalla and Brightkite, demonstrate that CKGL significantly outperforms several baseline models on Recall and Normalized Discounted Cumulative Gain (NDCG), validating its effectiveness in capturing contextual semantics and improving recommendation accuracy under sparse and complex scenarios.

1. Introduction

With the rapid advancement of mobile technologies and social media platforms, location-based social networks (LBSNs) have become an integral part of daily life. Within LBSNs, users share real-time activity information across multiple modalities, including geographic locations, text, images, and videos. These interactions generate large-scale datasets containing check-in times, venues, and place categories, enriching check-in data with semantic information. Points of Interest (POIs), which are the core elements of LBSNs, typically refer to specific geographic entities such as restaurants, hotels, and parks. Accurately predicting users’ potential POIs based on check-in data has become a key research focus in the field of recommender systems.

Unlike traditional recommendation tasks, user behavior in LBSNs exhibits distinct spatio-temporal dynamics and social correlations. On the one hand, check-in behavior is influenced by temporal and spatial factors, displaying periodicity and geographic clustering. On the other hand, social relationships among users significantly impact POI selection, as the check-in activities of friends can implicitly influence individual decision-making. Therefore, integrating contextual information—such as temporal, spatial, and social factors—is crucial for improving POI recommendation accuracy. However, existing approaches still face several challenges:

(1)

Data sparsity: Check-in data is inherently sparse, making it difficult to model user interests effectively using only check-in records.

(2)

Underutilization of contextual information: Many existing methods focus on static user–POI relationships without adequately capturing the dynamic spatio-temporal context embedded in check-ins.

(3)

Limited integration of social influence: Social correlations among users are often oversimplified, resulting in an inadequate capture of preference propagation among friends.

In recent years, knowledge graphs (KGs) have emerged as a powerful tool for representing users, POIs, and their interrelations in a structured manner [1]. KGs enhance the representation of complex relationships and enable the propagation of user preferences through graph structures, helping to alleviate the challenges of data sparsity and limited contextual modeling [2].

To address these challenges, we propose a Context-Aware Knowledge Graph Learning-Based POI Recommendation (CKGL) method. This approach fully leverages multi-dimensional contextual information to improve the accuracy of POI recommendations. The key contributions of this work are as follows:

(1)

Multi-dimensional context integration: We construct a knowledge graph that incorporates user social networks, temporal sequences, and geographical information, enhancing the semantic representation capability of the data.

(2)

Spatio-temporal feature modeling: We introduce a Spatio-Temporal Gated Graph Neural Network (STG-GNN) to model user check-in sequences, capturing both temporal dependencies and spatial influences on user behavior.

(3)

Social influence propagation: We apply a Graph Attention Network (GAT) to optimize the propagation of preferences between user groups and POI regions, thus enhancing the personalization of recommendations.

Extensive experiments on the Gowalla and Brightkite datasets demonstrate that the proposed CKGL method significantly outperforms state-of-the-art baselines in terms of precision and recall, validating its effectiveness in handling sparse data and complex contextual information.

The remainder of this paper is organized as follows. Section 2 reviews related work on POI recommendation. Section 3 introduces the overall framework of the proposed CKGL method. Section 4 elaborates on the technical details of the model, including knowledge graph construction, embedding learning, and graph neural network design. Section 5 presents the experimental setup, evaluation metrics, and results analysis. Section 6 concludes the paper and discusses potential directions for future research.

2. Related Work

In the context of LBSNs, the task of POI recommendation presents multiple challenges arising from diverse user preferences, dynamic spatio-temporal characteristics, and data sparsity. These challenges demand higher adaptability and robustness from recommender systems. The development of POI recommendation has evolved from traditional collaborative filtering (CF) to deep learning and graph-based models, with each stage improving the ability to model complex contextual relationships.

Early research primarily relied on collaborative filtering techniques. The classic CF algorithm proposed by Amazon [3] had a profound impact on the evolution of recommender systems. To enhance performance, subsequent studies integrated additional contextual factors into CF. For example, Ye et al. [4] incorporated users’ social relationships and the spatial clustering of POIs into a Naïve Bayes-based CF model, while Gao et al. [5] introduced temporal effects by considering the correlations between check-in times and locations. However, due to the high sparsity of LBSN data, traditional CF methods struggle to achieve accurate and personalized recommendations.

To mitigate data sparsity, matrix factorization (MF) models were introduced into POI recommendation. Guo et al. [6] incorporated social relationships into singular value decomposition (SVD), while Cheng et al. [7] fused geographical factors with MF to improve recommendation accuracy. As user behavioral data became increasingly complex, traditional two-dimensional MF models exhibited limited expressive power. To address this issue, Luan et al. [8] introduced high-order tensor factorization to incorporate contextual information, and Li et al. [9] proposed a fourth-order tensor factorization ranking method to jointly model user–POI interactions and temporal dependencies, effectively capturing both long-term and short-term user preferences. Nevertheless, high-order tensor computations often entail heavy parameter tuning and high computational costs, reducing model efficiency.

With the rapid progress of deep learning, a variety of neural architectures have been adopted for POI recommendation, such as Recurrent Neural Networks (RNNs) [10], Long Short-Term Memory Networks (LSTMs) [11], Graph Convolutional Networks (GCNs) [12], and Graph Attention Networks (GATs) [13]. Sequential models such as RNNs have shown remarkable ability in capturing the spatio-temporal dependencies of user check-in data. For instance, Lu et al. [14] used RNNs to model the sequential patterns of user visits, integrating POI order information with user preferences. Cui et al. [15] also employed RNNs to learn behavioral patterns from temporal sequences, improving recommendation accuracy. More recently, multi-dimensional POI recommendation approaches have emerged, integrating social network information into the model l_j ∈ L k sign. Liu et al. [16] leveraged pre-training and random-walk-based embeddings to incorporate social relationships, thereby enhancing recommendation precision. In addition to sequential neural models, some studies have explored POI recommendation by jointly considering sequential and geographical influences. For example, Qin et al. [17] proposed DisenPOI, which models user mobility by disentangling the sequential and geographical factors. Ju et al. [18] introduced a kernel-based substructure exploration approach to investigate higher-order spatial relationships among POIs using kernel methods.

In parallel, graph-based approaches [19,20,21] have demonstrated strong capability in modeling complex relational structures within LBSNs. Representative techniques such as DeepWalk [22], Node2Vec [23], and LINE [24] learn node embeddings through random walks or structure-preserving objectives, capturing both local and global graph structures. To better integrate multi-source heterogeneous information, researchers have further explored hybrid graph-based frameworks. For instance, Yang et al. [25] enhanced Graph Neural Networks (GNNs) to model social information propagation on user interaction graphs, thereby capturing both the direct and indirect influence among users. Wu et al. [26] proposed a GCN-based recommendation model that jointly extracts structural, geographic, and demographic features; and Wang et al. [27] developed the Knowledge Graph Attention Network (KGAT), which connects users and POI through knowledge graph structures. Building on this, Chen et al. [28] constructed a Spatial–Temporal Knowledge Graph (STKG) to model both long-term and short-term user preferences, while Liu et al. [29] designed KDRank, a knowledge-driven user-aware POI recommendation model that effectively captures latent user preferences in complex social networks.

In summary, although existing studies have achieved substantial progress—particularly in modeling social relationships, temporal sequences, and spatial dependencies—three key limitations remain:

(1)

Contextual information is often insufficiently integrated, leading to a lack of fine-grained understanding of user behaviors.

(2)

Relation modeling in sparse data environments tends to be coarse-grained, reducing recommendation robustness.

(3)

The ability to fuse multi-source heterogeneous data remains limited.

These limitations hinder the comprehensive representation of complex associations between users and POIs. To overcome these challenges, this paper proposes the CKGL method, which achieves a deeper integration of multi-dimensional contextual information, enhanced spatio-temporal behavior modeling, and improved relation representation learning.

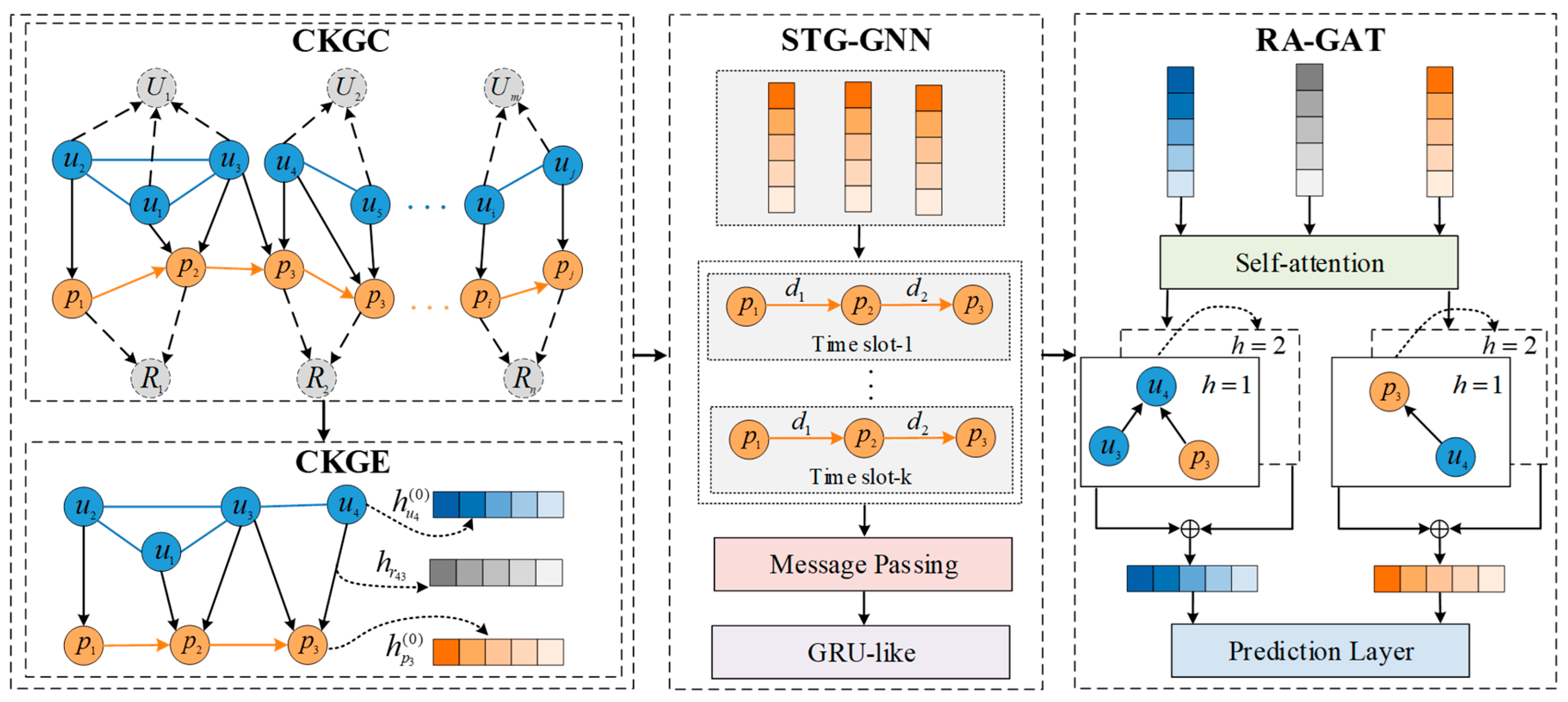
3. Overview

This section provides an overview of the CKGL method for POI recommendation. As illustrated in Figure 1, the overall framework consists of four main components: (1) Context-Aware Knowledge Graph Construction (CKGC), (2) Context-Aware Knowledge Graph Embedding (CKGE), (3) STG-GNN, and (4) the Relation-Aware Graph Attention Network (RA-GAT). These components are designed to work collaboratively to capture multi-dimensional contextual information and accurately infer users’ latent preferences for POIs.

(1)

The first component, CKGC, constructs a context-aware knowledge graph (KG) that integrates multiple types of entities and relations, including users, POIs, check-in behaviors, POI categories, and temporal contexts. To enhance the expressiveness of the graph, additional edges are added to represent spatial and temporal dependencies, as well as social relationships among users. This comprehensive graph structure provides a unified representation of heterogeneous contextual information and serves as the foundation for subsequent embedding learning.

(2)

Based on the constructed KG, the second component focuses on embedding learning. To capture the semantics of different relations among entities, CKGL employs the Translational Distance Model with Relation-Specific Spaces (TransR) embedding model [30] to project entities and relations into a continuous low-dimensional space while preserving relation-specific semantics. This embedding process captures latent dependencies among users and POIs and enables the model to represent multi-relational information in a unified space. The learned embeddings serve as the initial input for subsequent graph neural network modeling, allowing high-level features to be propagated and aggregated effectively.

(3)

The third component, STG-GNN, is designed to capture higher-order spatio-temporal dependencies within the knowledge graph. It introduces a gated mechanism to control the flow of spatial and temporal information during message propagation, ensuring that both short-term and long-term dependencies are adaptively modeled. By aggregating neighborhood information through the gating mechanism, the model learns context-aware representations that reflect users’ evolving user interests and temporal preferences. STG-GNN effectively enhances the spatial–temporal reasoning ability of CKGL, providing richer behavioral representations for recommendation.

(4)

The final component, RA-GAT, further refines the learned embeddings by introducing relation-specific attention weights. Unlike conventional GATs that treat all neighboring nodes equally, RA-GAT distinguishes different relation types and assigns adaptive weights according to their semantic importance. Through this relation-aware attention mechanism, the model selectively amplifies informative connections while suppressing less relevant ones, thereby improving the interpretability and accuracy of recommendations. Ultimately, CKGL fuses multi-source contextual information—spatial, temporal, and social—within RA-GAT to generate a personalized ranking of candidate POIs for each user.

4. The Proposed POI Recommendation Method

This section elaborates on the proposed CKGL method for POI recommendation. Based on the overall framework introduced in Section 3, the technical details of each component are presented in detail. We first describe the CKGC, which serves as the structural foundation of CKGL.

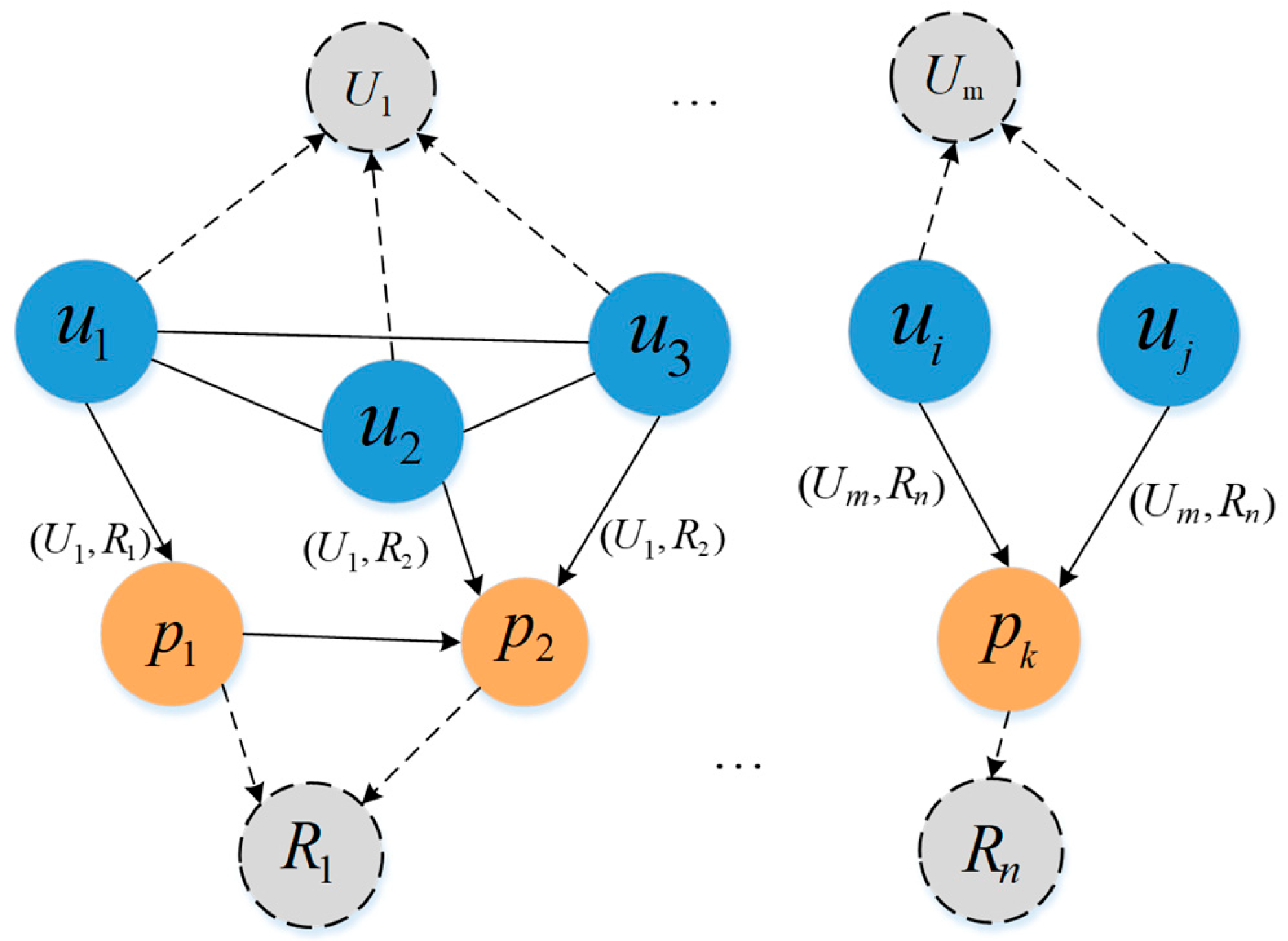
4.1. Context-Aware Knowledge Graph Construction

To effectively capture the complex associations between users and POIs across spatial, temporal, and social dimensions, a context-aware POI knowledge graph is constructed, as illustrated in Figure 2. The graph consists of four types of nodes: user-group nodes, user nodes, POI nodes, and region-of-interest (ROI) nodes. Here, a user group represents a cluster of users exhibiting similar behaviors across social, temporal, and spatial dimensions, while an ROI denotes a spatial region formed by aggregating geographically adjacent POIs.

The graph defines the following four types of relations:

(1)

User–User Group (membership relation): User groups are generated by clustering users according to behavioral similarity, and each user is connected to the corresponding group. User groups represent collective preference patterns at the group level, which helps alleviate data sparsity and enhances the generalization capability of the recommendation model. Details of user-group construction are presented in Section 4.1.1.

(2)

User–User (social relation): This relation is constructed based on friendships in social networks, representing the propagation and mutual influence of preferences among users.

(3)

POI–ROI (belonging relation): POIs are clustered into ROIs using spatial clustering, and each POI is linked to its corresponding ROI. ROIs capture the spatial organization of POIs, reflecting how individual POIs are spatially grouped into higher-level regional structures. ROIs enrich the representation of geographical contextual semantics within the knowledge graph. The details of ROI construction are described in Section 4.1.2.

(4)

POI–POI (temporal sequence relation): User check-in times are discretized into multiple time slots, and directed edges are established between consecutive POIs according to the visit order within each slot. This relation characterizes the temporal evolution of user mobility patterns and models’ sequential dependencies between POIs. The time-slot division follows the discretization method proposed in our previous work [31], where one day is divided into 96 time slots.

The constructed knowledge graph integrates user check-in sequences, the geographical distribution of POIs, and the social network structure among users. By capturing multi-source heterogeneous information, it provides rich contextual semantic support for subsequent embedding learning and graph-based recommendation.

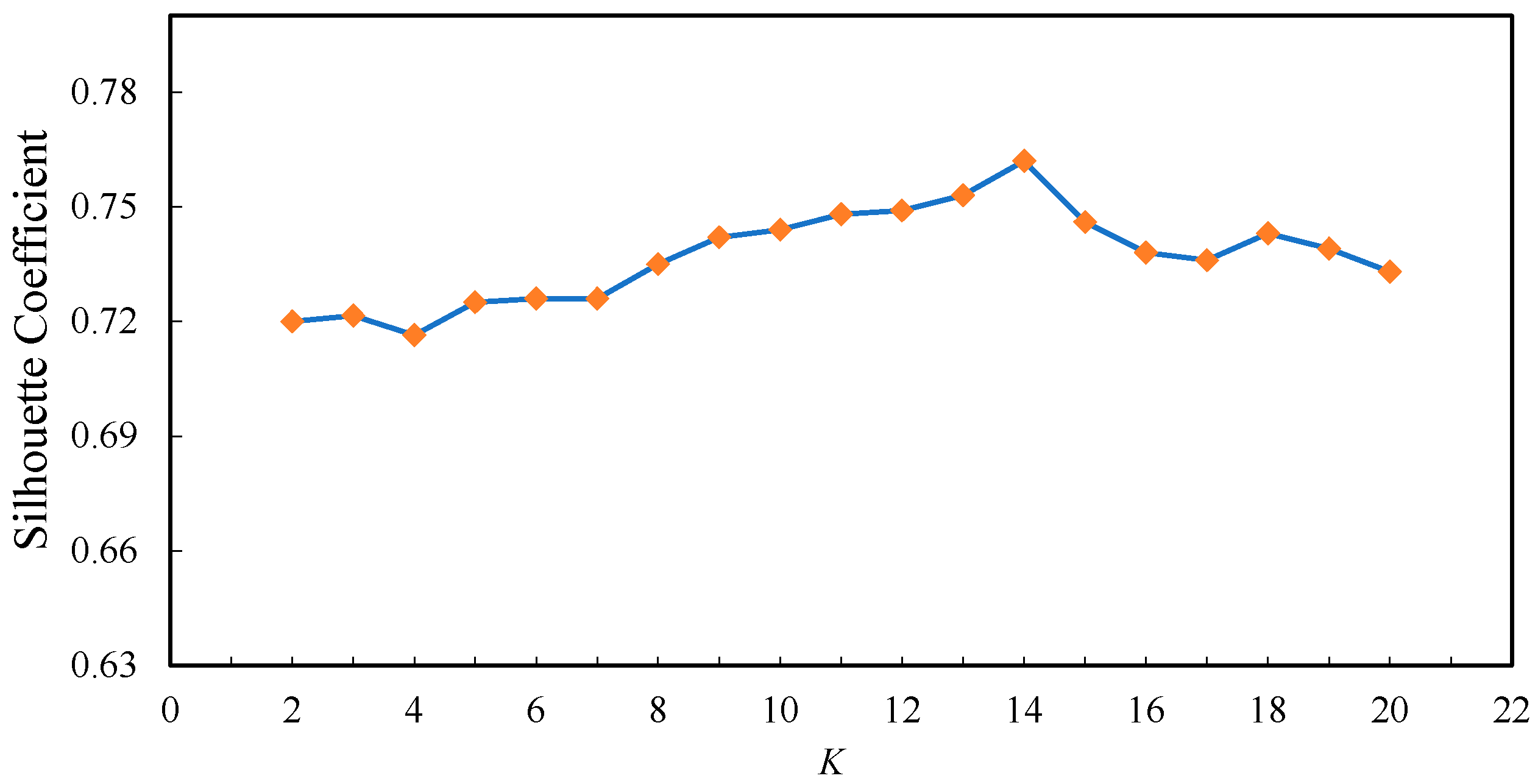
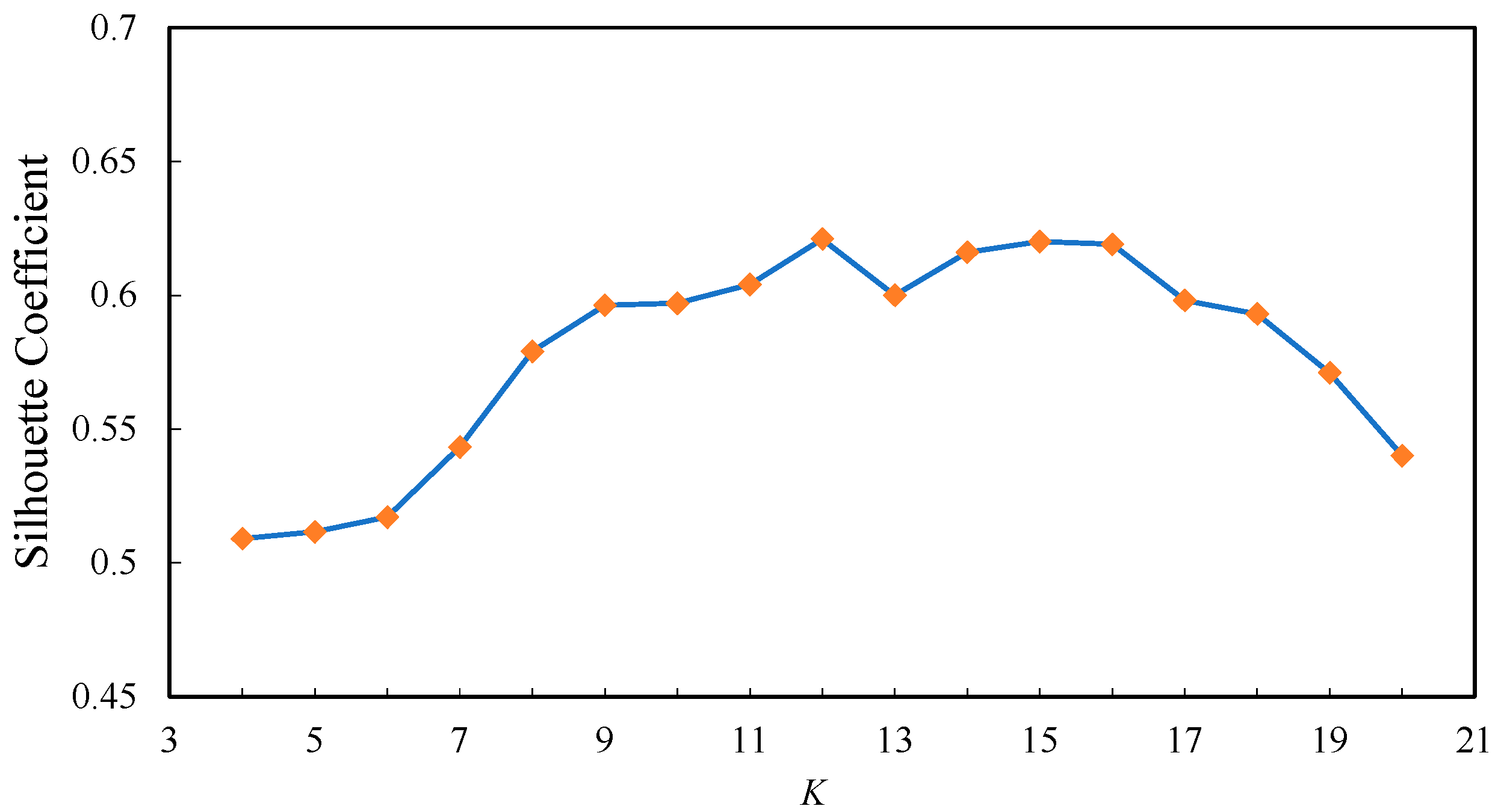
4.1.1. User Group Clustering Based on Similarity Measures

To effectively capture user behavioral similarities across social, temporal, and spatial dimensions, this study applies a spectral clustering algorithm to group users. The clustering results are represented as “user-group” nodes in the knowledge graph. This process enables the discovery of latent group-level preference structures, thereby alleviating the problem of data sparsity.

To quantify the similarity between users, this study adopts the user similarity computation model proposed in our previous work [31]. This model integrates three dimensions of similarity—social, spatial, and temporal—to jointly represent user correlations. The overall similarity between user $u_i$ and user $u_j$ is defined in Equation (1):

$$si{m}_{u_i-u_j}=sim{u}_{u_i-u_j}+sim{l}_{u_i-u_j}+sim{t}_{u_i-u_j}$$

(1)

where $sim{u}_{u_i-u_j}$, $sim{l}_{u_i-u_j}$, and $sim{t}_{u_i-u_j}$ represent the social, spatial, and temporal similarities between users $u_i$ and $u_j$, respectively. The detailed formulations of these similarity measures can be found in [31]. Since all similarity components are normalized to the same numerical scale, their magnitudes are directly comparable; therefore, a simple summation is adopted to maintain stability while avoiding the introduction of additional weighting hyperparameters that could increase model complexity and tuning sensitivity.

Based on the computed similarities, we apply a standard spectral clustering algorithm to group users. Specifically, a similarity graph is constructed, and the eigengap heuristic [32] is employed to determine the optimal number of clusters. The resulting user clusters are represented as “user-group” nodes in the knowledge graph, which helps alleviate data sparsity by capturing higher-level shared preference structures.

4.1.2. ROI Clustering Based on Spatial Proximity

In practical scenarios, users tend to visit POIs that are geographically close to each other. Following this behavioral pattern, this study applies the K-means [33] clustering algorithm to group POIs in LBSNs according to spatial proximity, thereby forming ROIs. To quantify spatial similarity between POIs, the Euclidean distance based on geographic coordinates is employed. The distance between any two POIs is as defined in Equation (2):

$$k(i,j)={‖p_i-p_j‖}^2=\sqrt{{(x_i-x_j)}^2+{(y_i-y_{\mathrm{j}})}^2}$$

(2)

where $(x_i,y_i)$ and $(x_j,y_j)$ denote the geographic coordinates of POIs $p_i$ and $p_j$, respectively. POIs that are closer in space generally exhibit higher spatial similarity and are thus more likely to be grouped into the same ROI.

To enhance clustering performance, the silhouette coefficient is adopted to determine the optimal number of clusters $K$, thereby partitioning the POI set $P$ into $K$ ROIs, as expressed in Equation (3):

$$P=\left\{R_1,R_2,R_3,\dots ,R_K\right\}$$

(3)

Through this process, spatially adjacent POIs are aggregated into ROIs, which serve as supplementary semantic entities in the construction of the knowledge graph. These ROIs reflect the geographical aggregation structure of POIs and enhance the representational capacity of the knowledge graph in modeling spatial contextual semantics.

4.2. Context-Aware Knowledge Graph Embedding

To enhance the structural expressiveness of the knowledge graph and alleviate the sparsity of check-in data, this study proposes a context-aware graph embedding approach based on entity clustering.

Specifically, two semantic entities, the “user group” and “ROI”, are introduced to semantically enrich the original triplet structure (user, check-in relation, POI). The triplet is reformulated as (user, check-in relation of the user group in an ROI, POI), which captures the check-in behavior of a user’s affiliated group within a specific region of interest. This reformulated structure extends individual check-in activities to user-group-level preference modeling.

The clustering-based enhancement strategy not only mitigates the problem of data sparsity but also enriches the interaction semantics between users and POIs, thereby improving the context awareness and representational capacity of the knowledge graph.

During the embedding construction stage, this study adopts the TransR model to perform vectorized representation learning of entities and relations within the knowledge graph. To achieve context-aware representation, three categories of semantic triplets are constructed and jointly trained within a unified embedding framework, enabling the model to capture multi-dimensional interaction patterns between users and POIs across social, spatial, and temporal dimensions:

(1)

Social relationships between users: (user, friendship relation, user);

(2)

Check-in relationships based on spatially clustered user groups: (user, user-group–ROI check-in relation, POI);

(3)

POI sequential visit relationships: (POI, sequential check-in relation, POI).

Each triplet can be represented as $(h,r,t)$, where $h$ and $t$ denote the head and tail entities, respectively, and $r$ represents the semantic relation connecting them.

The core idea of TransR is to introduce an independent projection matrix $M_r\in R^{k\times d}$ for each relation $r$, which maps the head and tail entities from the entity space into the corresponding relation space while preserving their translational properties, as defined in Equation (4):

$$h_r=M_{r}h,t_r=M_{r}t$$

(4)

where $h_r$ and $t_r$ denote the projection vectors of entities $h$ and $t$ in the relation-specific space, and $M_r$ is the projection matrix associated with relation $r$.

During the embedding training process, a margin-based ranking loss is employed to enhance the model’s ability to discriminate between positive and negative triplets. The scoring functions for positive and negative samples are as defined in Equations (5) and (6):

$$f_r(h,t)={‖h_r+r_{s-t}-t_r‖}_2^2$$

(5)

$$f_{r^{\prime }}(h^{\prime },t^{\prime })={‖{h_r}^{\prime }+{r_{s-t}}^{\prime }-{t_r}^{\prime }‖}_2^2$$

(6)

Here, $f_r(h,t)$ denotes the score function of a positive triplet, where $h_r$, $t_r$, and $r_{s-t}$ are the embedding vectors of the head entity (user), tail entity (POI), and their semantic relation, respectively. Similarly, $f_{r^{\prime }}(h^{\prime },t^{\prime })$ represents the score function of a negative triplet, where ${h_r}^{\prime }$, ${t_r}^{\prime }$, and ${r_{s-t}}^{\prime }$ denote the embeddings of the corrupted entity and relation.

The final optimization objective is expressed as Equation (7):

$$L_{KG}={\displaystyle \sum _{\left(h,r,t\right)\in S}{\displaystyle \sum _{\left(h^{\prime },r^{\prime },t^{\prime }\right)\in S^{\prime }}\max }}\left(0,f_r(h,t)+\gamma -f_{r^{\prime }}\left(h^{\prime },t^{\prime }\right)\right)$$

(7)

where $L_{KG}$ denotes the margin-based loss function, $S$ and $S^{\prime }$ represent the sets of positive and negative samples, respectively, and $\gamma$ is the margin hyperparameter. Through this embedding construction process, CKGL effectively captures the semantic heterogeneity of multiple relations in the knowledge graph, as well as the dynamic evolution of user interests. These learned embedding provide high-quality initialization for the subsequent attention aggregation module used in downstream recommendation tasks.

4.3. Spatio-Temporal Gated Graph Neural Network

Considering the significant influence of temporal and spatial factors on check-in behaviors, this study improves upon the original Gated Graph Neural Network (G-GNN) model [34] by developing an STG-GNN. The proposed model jointly incorporates temporal and spatial contextual information to update node representations within the check-in graph.

In the temporal dimension, the check-in sequences of each user within different time slots are modeled separately. Each user’s check-ins within a given time slot are treated as an independent check-in subgraph, representing the local temporal sequence of visits. Since check-in behaviors within the same time slot typically exhibit temporal similarity, this design ensures that the constructed subgraphs maintain temporal consistency and contextual relevance.

In the spatial dimension, users tend to check in at geographically proximate POIs. Therefore, a distance-based edge weighting mechanism is incorporated into the message-passing layer of G-GNN. Specifically, in each user’s check-in subgraph, the weights of the input and output edges associated with POI nodes are adjusted according to geographic distance, thereby generating a spatially enriched check-in subgraph.

Based on the check-in data of user $u_i$, the check-in sequence $S_u$ is obtained, as defined in Equation (8):

$$S_{u_i}=\{p_{t_T^1}^{u_i},p_{t_T^2}^{u_i},\mathrm{\dots },p_{t_T^{\left|S\right|}}^{u_i}\}$$

(8)

where $p_{t_T^{\left|S\right|}}^{u_i}$ denotes the POI visited by user $u_i$ at time point $t_T^{\left|S\right|}$, and $\left|S\right|$ represents the total number of POIs visited within time slot $T$.

To incorporate spatial information, this study redesigns the computation of adjacency weights within the check-in subgraph. For a location node $v_i$, the normalized weight of an incoming edge from node $v_j$ to $v_i$ is denoted as $e_{ij}^{in}$, as defined in Equation (9), where $N_{in}(i)$ represents the set of predecessor nodes of $v_i$. Similarly, the normalized weight of an outgoing edge from node $v_i$ to $v_j$ is denoted as $e_{ij}^{out}$, as defined in Equation (10), where $N_{out}(i)$ represents the set of successor nodes of $v_i$.

$$e_{ij}^{in}={\displaystyle \frac{W(v_j,v_i)}{{\displaystyle \sum _{k\in N_{in}(i)}W(v_k,v_i)}}}$$

(9)

$$e_{ij}^{out}={\displaystyle \frac{W(v_i,v_j)}{{\displaystyle \sum _{k\in N_{out}(i)}W(v_i,v_k)}}}$$

(10)

Here, $W(v_i,v_j)$ denotes the distance-based edge weight between POI node $v_i$ and $v_j$, which reflects their geographic distance. The weight is calculated as in Equation (11):

$$W(v_i,v_j)=\left\{\begin{array}{c}\exp (-{\displaystyle \frac{{‖p_{v_i}-p_{v_j}‖}^2-△l}{△l}})\\ 1\end{array}\right.\begin{array}{c},{‖p_{v_i}-p_{v_j}‖}^2>△l\\ ,{‖p_{v_i}-p_{v_j}‖}^2\le △l\end{array}$$

(11)

where $p_{v_i}$ and $p_{v_j}$ represent the geographic coordinates of nodes $v_i$ and $v_j$, respectively, and $△l$ is a distance threshold factor. The value of $W(v_i,v_j)$ ranges within (0,1]. In practice, the distance threshold $△l$ is empirically determined in a dataset-specific manner according to the spatial distribution characteristics of POIs in each dataset. The setting is adopted to capture local spatial influence while preventing the constructed check-in subgraph from becoming excessively spares or overly dense, and it does not introduce additional trainable parameters.

Using the above formulation, the adjacency matrices of each check-in subgraph, denoted as $W_{S_{-}}A$, is constructed. As shown in Equation (12), $W_{S_{-}}{A}^{in}$ represents the in-degree adjacency matrix, where each element corresponds to $e_{ji}^{in}$ calculated by Equation (9). Similarly, $W_{S_{-}}{A}^{out}$ represents the out-degree adjacency matrix, where each element corresponds to $e_{ij}^{out}$ calculated by Equation (10).

$$W_{S_{-}}A=\left[W_{S_{-}}{A}^{in},W_{S_{-}}{A}^{out}\right]$$

(12)

Based on the adjacency matrix $W_{S_{-}}A$ incorporating geographic distance, the input embedding vector corresponding to the i-th check-in location of user $u_i$ in sequence $S$ is computed as in Equation (13):

$$a_{S_i}^u=concat(W_{S_{-}}{A}_i^{in}[p_{t_T^1}^{u_i},p_{t_T^2}^{u_i},\mathrm{\dots },p_{t_T^{\left|S\right|}}^{u_i}]W_S^{in},W_{S_{-}}{A}_i^{out}[p_{t_T^1}^{u_i},p_{t_T^2}^{u_i},\mathrm{\dots },p_{t_T^{\left|S\right|}}^{u_i}]W_S^{out})$$

(13)

where $W_{S_{-}}{A}_i^{in}$ and $W_{S_{-}}{A}_i^{out}$ denote the i-th row of the in-degree and out-degree adjacency matrices, respectively. $[p_{t_T^1}^{u_i},p_{t_T^2}^{u_i},\mathrm{\dots },p_{t_T^{\left|S\right|}}^{u_i}]$ represents the check-in sequence of user $u_i$ within time slot $T$, and $\left|S\right|$ denotes the length of the sequence. $W_S^{in}$ and $W_S^{out}$ are learned parameter matrices.

STG-GNN extends the G-GNN framework to capture temporal dependencies in user check-in behaviors. At each time step, a gated unit updates the node representation by integrating the current check-in embedding, the previous hidden state within the same time slot, and aggregated messages from spatially neighboring POIs. This gating mechanism adaptively balances new observations and historical patterns, enabling the model to preserve long-term behavioral contexts while reflecting recent movement dynamics. All parameters are trained in an end-to-end manner.

Furthermore, the TransR model introduced in Section 4.2 is utilized to initialize entity embeddings, which are subsequently fed into the gated neural network. Through this mechanism, multiple check-in subgraphs are constructed and processed, yielding the embedding matrix $V_p=\{x_{p_1},x_{p_2},x_{p_3},\mathrm{\dots }{x}_{p_N}\}$, where $x_{p_i}$ denotes the final embedding of the i-th POI node.

4.4. Relation-Aware Graph Attention Network

Building on the spatio-temporal embeddings obtained from the STG-GNN, this section introduces an RA-GAT to further enhance multi-relational reasoning within the context-aware knowledge graph. The RA-GAT focuses on differentiating heterogeneous relations among entities and integrating edge-level semantic features into the attention mechanism, thereby improving both the interpretability and accuracy of POI recommendation.

In conventional GAT model, the attention coefficient between two nodes is computed solely based on their node features, while edge features are ignored. However, in the context-aware knowledge graph, edges encode rich semantics, including friendship links, check-in relations, and sequential visit relations, which reflect users’ dynamic preference. To fully exploit this relational information, RA-GAT introduces an edge-enhanced, relation-aware attention mechanism in which both node and edge features jointly contribute to the computation of attention weights. The fused vector $x_{ij}$ is constructed as shown in Equation (14):

$$x_{ij}=W_n{h}_i‖W_n{h}_j‖W_r{r}_{ij}$$

(14)

where $W_n$ and $W_r$ are trainable weight matrices, $h_i$ and $h_j$ denote the node feature vectors of node $i$ and node $j$, respectively. $r_{ij}$ represents the edge feature between the nodes, and the symbol ‖ indicates vector concatenation. The fused vector $x_{ij}$ is obtained by concatenating the linearly transformed features of nodes $i$ and $j$, along with their corresponding edge feature, explicitly capturing both node semantics and relational information for subsequent attention computation.

The attention coefficient $a_{ij}$ is then obtained by Equation (15):

$$a_{ij}={\displaystyle \frac{\exp (\mathrm{LeakyReLU}(c^T{x}_{ij}))}{{\displaystyle {\sum }_{k\in N(i)}\exp (\mathrm{LeakyReLU}(c^T{x}_{ik}))}}}$$

(15)

where $c^T$ is a learnable weight vector, and LeakyReLU denotes a nonlinear activation function. The softmax normalization ensures that the attention coefficients over all neighboring of nodes $i$ sum to 1.

The edge-aware aggregation function is expressed in Equation (16):

$$h_{N_i}=\sigma ({\displaystyle \sum _{j\in N(i)}{a}_{ij}(W_h{h}_j+W_r{r}_{ij})})$$

(16)

where $W_h$ and $W_r$ are trainable matrices for node and edge features, respectively, and $\sigma (·)$ is a nonlinear activation function.

Through this mechanism, RA-GAT dynamically adjusts the influence of each neighbor according to both its node representation and relation-specific edge semantics. To simulate preference propagation in social networks, a message propagation and aggregation process is performed.

For a central node $i$, messages from its first-order neighbors are aggregated as in Equation (17):

$$f_{Bi-Interaction}=\mathrm{LeakyReLU}(W_1(h_i+h_{N_i}))+\mathrm{LeakyReLU}(W_2(h_i\odot h_{N_i}))$$

(17)

where $W_1$ and $W_2$ are trainable parameter matrices, and $\odot$ denotes element-wise multiplication.

To capture higher-order dependencies, multi-layer propagation is applied. The representation of node $i$ at layer $l$ is updated from layer $(l-1)$ using Equations (18) and (19):

$$h_i^{(l)}=f(h_i^{(l-1)},h_{N_i}^{(l-1)})$$

(18)

$$h_{N_i}^{(l-1)}={\displaystyle \sum _{j\in N(i)}{a}_{ij}(W_h{h}_j^{(l-1)}+W_r{r}_{ij})}$$

(19)

where $h_j^{(l-1)}$ is the feature vector of the neighbor node $j$ at the (l-1)-th layer, and $h_{N_i}^{(l-1)}$ denotes the attention-weighted aggregated embedding of neighbors. This iterative propagation enables RA-GAT to model multi-hop relational influences across the knowledge graph.

After $L$ layers of message propagation and aggregation, each user node $u_i$ and POI node $p$ obtain multi-level representations, as shown in Equations (20) and (21):

$$h_{u_i}^{\ast }=h_{u_i}^{(0)}‖h_{u_i}^{(1)}‖\mathrm{\dots }‖h_{u_i}^{(L)}$$

(20)

$$h_p^{\ast }=h_p^{(0)}‖h_p^{(1)}‖\mathrm{\dots }‖h_p^{(L)}$$

(21)

where ‖ denotes concatenation, and $L$ specifies the number of aggregation layers controlling the propagation depth.

The matching score between user $u_i$ and POI $p$ is computed through their embedding inner product as in Equation (22):

$${\widehat{y}}_{(u_i,p)}=h_{u_i}^{{\ast }^{\top }}{h}_p^{\ast }$$

(22)

To train the recommendation component based on users’ implicit feedback, a binary cross-entropy loss is employed as in Equation (23):

$$L_{BCE}=-{\displaystyle \sum _{(u_i,p)}{y}_{(u_i,p)}\log ({\widehat{y}}_{(u_i,p)})+(1-y_{(u_i,p)})\log (1-{\widehat{y}}_{(u_i,p)})}$$

(23)

where $y_{(u_i,p)}$ denotes the ground-truth interaction (1 if the user has visited the POI, 0 otherwise), and ${\widehat{y}}_{(u_i,p)}$ represents the predicted probability that user $u_i$ visits POI $p$.

Finally, the joint optimization objective integrates the margin-based ranking loss from the knowledge graph embedding stage with the above recommendation loss, as in Equation (24):

$$L_{CKGL}=L_{KG}+L_{BCE}+\lambda \parallel \Theta {\parallel }_2^2$$

(24)

where $\Theta$ is the set of trainable parameters, and $\lambda$ is a regularization coefficient controlling the L2 norm penalty. The regularization coefficient $\lambda$ is tuned within a predefined range on the validation set, and the value that yields the best validation performance is selected for all experiments.

Through this relation-aware, edge-enhanced attention mechanism, RA-GAT effectively fuses spatial, temporal, and social contexts learned from previous modules. It captures fine-grained semantic relations and high-order structural dependencies within the knowledge graph, thereby providing a unified and interpretable representation foundation for personalized POI recommendation in CKGL.

5. Experiments and Analysis

To evaluate the performance and effectiveness of the proposed CKGL method, a series of comparative experiments were conducted on real-world LBSN datasets.

5.1. Datasets

Two publicly available LBSN datasets, Gowalla and Brightkite, were used for evaluation. The Gowalla dataset contains user check-in records from February 2009 to October 2010, while the Brightkite dataset spans from 1 October 2009 to 30 September 2010. Both datasets include user–POI interactions, POI coordinates, and social relationships.

To ensure data quality and reduce sparsity, users and POIs with few interactions were filtered out. In Gowalla, users with fewer than 15 check-ins and POIs with fewer than 10 check-ins were removed. In Brightkite, users and POIs with fewer than 10 check-ins were excluded.

The statistical information of the preprocessed datasets is summarized in

Table 1. Statistical information of the datasets.

Dataset	Gowalla	Brightkite
Number of users	5628	4844
Number of POIs	31,803	7675
Number of friendship relations	46,001	93,036
Number of check-ins	620,683	388,148

.

5.2. Computing Environment

All experiments were conducted on a Linux-based system with two NVIDIA RTX 4090 GPUs, each featuring 24 GB of memory. The models were implemented using PyTorch (version 2.1.2) with CUDA support, with the CUDA driver version 12.6 and PyTorch installed with CUDA 12.1 and cuDNN 8.9.2. For each dataset, the training process typically converged in approximately 6 h.

5.3. Evaluation Metrics

The performance of CKGL and baseline methods was evaluated using two widely adopted $\mathrm{top}-k$ metrics: $\mathrm{Recall}@k$ and Normalized Discounted Cumulative Gain ($\mathrm{NDCG}@k$).

$\mathrm{Recall}@k$ measures the proportion of visited POIs appearing in the $\mathrm{top}-k$ recommendation list, as defined in Equation (25):

$$\mathrm{Recall}@k={\displaystyle \frac{1}{\left|U\right|}}{\displaystyle \sum _{u_i\in U}\frac{|R(u_i)\cap T(u_i)|}{|T(u_i)|}}$$

(25)

where $U$ denotes the user set, $R(u_i)$ is the $\mathrm{top}-k$ recommended POIs for user $u_i$, and $T(u_i)$ is the POIs actually visited by user $u_i$.

$\mathrm{NDCG}@k$ evaluates ranking quality by considering both relevance and position of recommended items, as defined in Equation (26):

$$\mathrm{NDCG}@k={\displaystyle \frac{1}{\left|U\right|}}{\displaystyle \frac{\mathrm{DCG}@k}{\mathrm{IDCG}@k}}$$

(26)

where $\mathrm{DCG}@k$ and $\mathrm{IDCG}@k$ denote the Discounted Cumulative Gain (DCG) and the Ideal DCG, respectively, given by Equations (27) and (28):

$$\mathrm{DCG}@k={\displaystyle \sum _{i=1}^k\frac{rel(i)}{{\log }_2(i+1)}}$$

(27)

$$\mathrm{IDCG}@k={\displaystyle \sum _{i=1}^k\frac{re{l}^{ideal}(i)}{{\log }_2(i+1)}}$$

(28)

where $rel(i)$ denotes the relevance of the i-th recommended POI for user $u_i$, and $re{l}^{ideal}(i)$ is its ideal relevance.

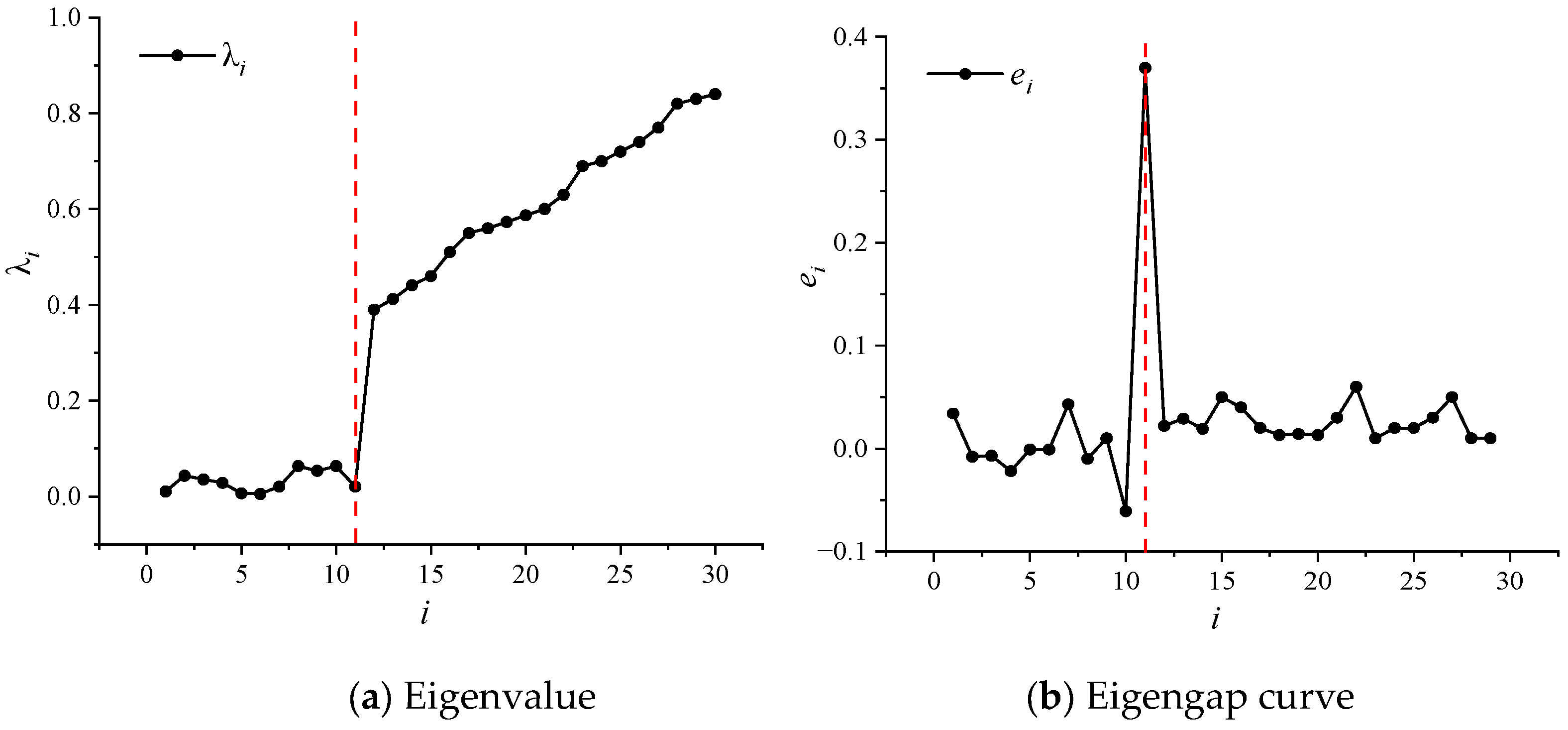
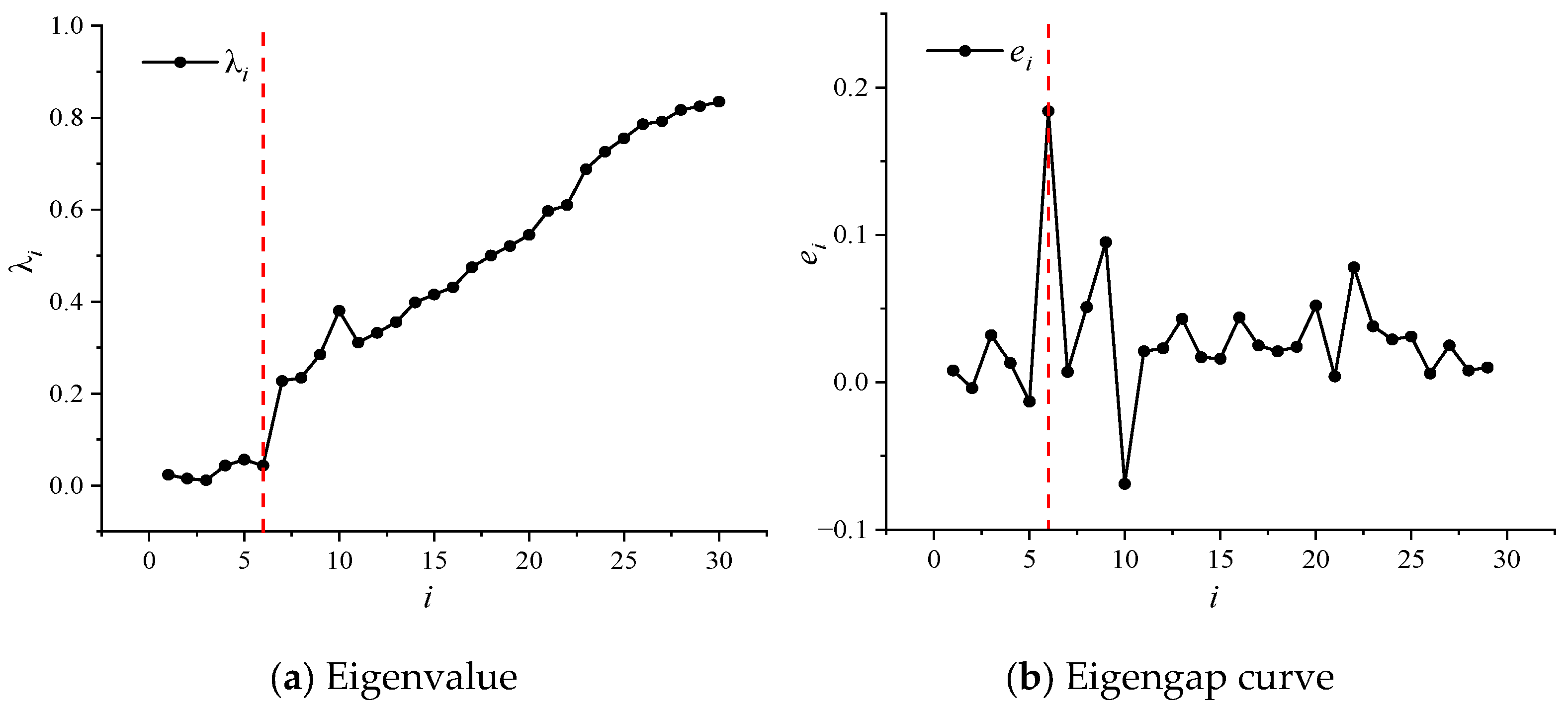
5.4. Knowledge Graph Parameters

Before embedding entities and relations into the knowledge graph, two key parameters need to be determined: the number of user clusters and the ROI clustering parameter. These parameters directly affect the structural granularity and semantic richness of the constructed knowledge graph.

To determine the optimal ROI clustering parameter, this study evaluates the clustering performance on the Gowalla and Brightkite datasets using the silhouette coefficient, which jointly measures intra-cluster compactness and inter-cluster separation. The coefficient value ranges from −1 to 1, where a value close to 1 indicates that samples within a cluster are compact and well separated from other clusters, reflecting a high clustering quality. For a given sample $i$, the silhouette coefficient is defined in Equation (29):

$$S(i)={\displaystyle \frac{b(i)-a(i)}{\max \{a(i),b(i)\}}}$$

(29)

where $a(i)$ denotes the average distance between $i$ and other samples within the same cluster, and $b(i)$ represents the minimum average dissimilarity distance between $i$ and all other clusters. The overall silhouette coefficient is obtained by averaging the coefficients of all samples.

By testing different values of the clustering parameter $K$, and using the Euclidean distance as the distance metric, the K-means results on the Gowalla dataset (Figure 3) show that the silhouette coefficient stabilizes when $K=14$. Therefore, the ROI clustering parameter $K$ for Gowalla is set to 14, grouping POIs into 14 ROI clusters. Similarly, for the Brightkite dataset (Figure 4), stability is achieved when $K=12$, and clustering parameter is set accordingly.

To further determine the number of user clusters, eigenvalue decomposition was performed on the normalized Laplacian of the user similarity matrix. The first 30 eigenvalues and their corresponding eigengaps were plotted, as shown in Figure 5 and Figure 6 below. The eigenvalues increase smoothly for smaller index values; however, a distinct jump emerges at the point where the adjacent eigengap reaches its maximum. According to the eigengap heuristic, when the largest gap occurs between the i-th and (i + 1)-th eigenvalues, the optimal number of user clusters can be determined as C = i.

Specifically, for the Gowalla dataset, the largest eigengap appears at the 11th eigenvalue, and the number of user clusters is therefore set to $C=11$. Similarly, for the Brightkite dataset, the largest eigengap occurs at the 6th eigenvalue, resulting in $C=6$. These findings indicate that the eigengap heuristic provides an effective and stable approach for determining the optimal number of user clusters, ensuring the rationality of the clustering process and providing a reliable foundation for subsequent ROI partitioning and knowledge graph construction.

5.5. Experimental Results and Analysis

To evaluate the effectiveness of the proposed CKGL method for POI recommendation, seven representative baseline models are selected for comparison:

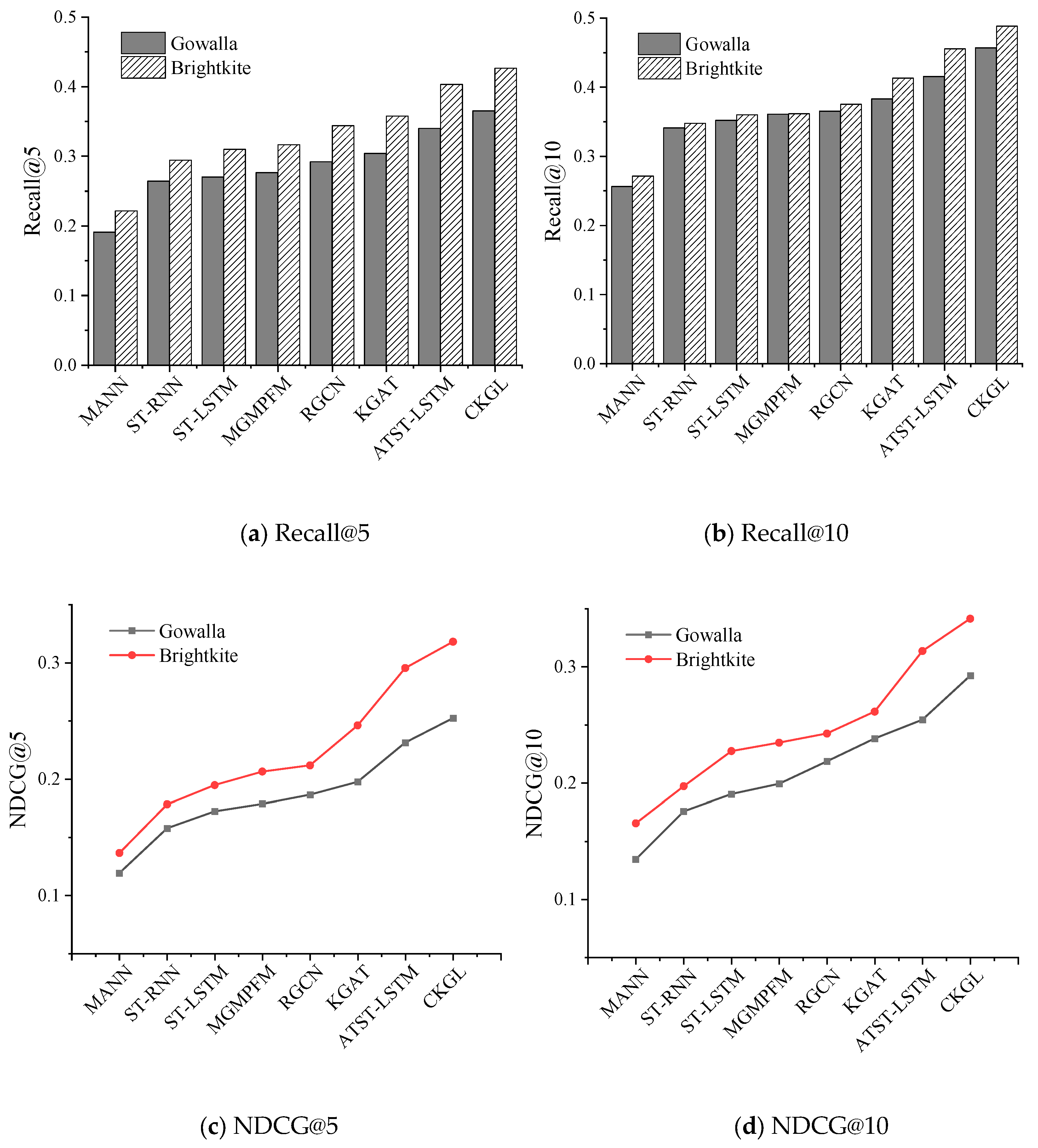
• MANN [35]: Introduces a memory mechanism into the recommendation system and integrates it with collaborative filtering.
• ST-RNN [36]: Models local spatio-temporal contexts using time-dependent transition matrices for different temporal intervals and distance-dependent matrices for geographical distances.
• ST-LSTM [37]: Proposes a spatio-temporal gated network (STGN) that models personalized sequential patterns based on users’ long-term and short-term preferences.
• MGMPFM [7]: A matrix factorization-based POI recommendation method that employs a multi-center Gaussian model to capture the geographical influence of users’ check-in behaviors.
• RGCN [38]: Extends the GCN to handle heterogeneous relationships within graphs.
• KGAT [27]: Incorporates attention mechanisms and knowledge graph information to enhance user–POI interaction modeling.
• ATST-LSTM [39]: Based on an LSTM network, integrates spatio-temporal information and attention mechanisms to capture sequential patterns in users’ check-in behaviors.

5.5.1. Performance Comparison

The experimental results on the Gowalla and Brightkite datasets are summarized in

Table 2. Comparative results on the Gowalla dataset.

Model	Gowalla
	Recall@5	Recall@10	NDCG@5	NDCG @10
MANN	0.1907	0.2562	0.1193	0.1345
ST-RNN	0.2643	0.3413	0.1577	0.1756
ST-LSTM	0.2702	0.3523	0.1723	0.1905
MGMPFM	0.2765	0.3612	0.1787	0.1993
RGCN	0.2922	0.3655	0.1865	0.2185
KGAT	0.3042	0.3833	0.1975	0.2382
ATST-LSTM	0.3402	0.4156	0.2312	0.2543
CKGL	0.3652	0.4572	0.2523	0.2924

and

Table 3. Comparative results on the Brightkite dataset.

Model	Brightkite
	Recall@5	Recall@10	NDCG@5	NDCG @10
MANN	0.2217	0.2715	0.1365	0.1654
ST-RNN	0.2945	0.3479	0.1783	0.1971
ST-LSTM	0.3101	0.3602	0.1947	0.2274
MGMPFM	0.3166	0.3618	0.2064	0.2346
RGCN	0.3441	0.3755	0.2117	0.2425
KGAT	0.3577	0.4133	0.2461	0.2614
ATST-LSTM	0.4033	0.4557	0.2955	0.3136
CKGL	0.4266	0.4885	0.3182	0.3414

. CKGL consistently outperforms the baseline models in terms of $\mathrm{Recall}@k$ and $\mathrm{NDCG}@k$. For instance, on the Gowalla dataset, CKGL achieves improvements over the best-performing baseline model ATST-LSTM by 7.35%, 10.01%, 9.13%, and 14.99% on $\mathrm{Recall}@5$, $\mathrm{Recall}@10$, $\mathrm{NDCG}@5$, and $\mathrm{NDCG}@10$, respectively. On the Brightkite dataset, the corresponding improvements are 5.78%, 7.17%, 7.68%, and 8.86%. These results demonstrate the robustness and generalization capability of CKGL across different datasets.

As shown in Figure 7, the overall performance ranking is CKGL > ATST-LSTM > KGAT > RGCN > MGMPFM > ST-LSTM > ST-RNN > MANN. MANN, which only combines a memory mechanism with collaborative filtering, fails to capture complex contextual dependencies and thus exhibits the weakest performance. ST-RNN incorporates temporal and spatial transition modeling but struggles to represent long-term user behavior sequences effectively. ST-LSTM introduces a spatio-temporal gating mechanism that distinguishes long- and short-term user preferences, leading to moderate improvement.

MGMPFM strengthens spatial modeling through a Gaussian-based geographic influence function but overlooks semantic and social contextual factors. RGCN extends GCN to heterogeneous relational scenarios, allowing for multi-type relation modeling, yet underemphasizes the relative importance of different relational features. KGAT leverages attention mechanisms and knowledge graphs to capture richer user–POI interactions, effectively alleviating data sparsity and outperforming traditional GCN-based models. ATST-LSTM integrates attention-enhanced spatio-temporal learning to model users’ sequential behaviors more precisely.

Compared with these methods, CKGL achieves significant improvements in POI recommendation accuracy and interpretability through the following three aspects:

(1)

Multi-source contextual fusion: CKGL integrates user behavior, geographical location, and social network data within a unified knowledge graph, enabling the model to capture richer contextual semantics and structured representations between users and POIs.

(2)

Spatio-temporal graph modeling: By incorporating the STG-GNN network, CKGL effectively models the complex temporal evolution and spatial dependencies of user check-in behaviors, providing a finer representation of user behavioral dynamics.

(3)

Relation-aware graph attention mechanism: CKGL adopts a relation-aware graph attention mechanism to refine the aggregation of heterogeneous relational information, thereby enhancing both the accuracy and interpretability of user preference propagation across the knowledge graph.

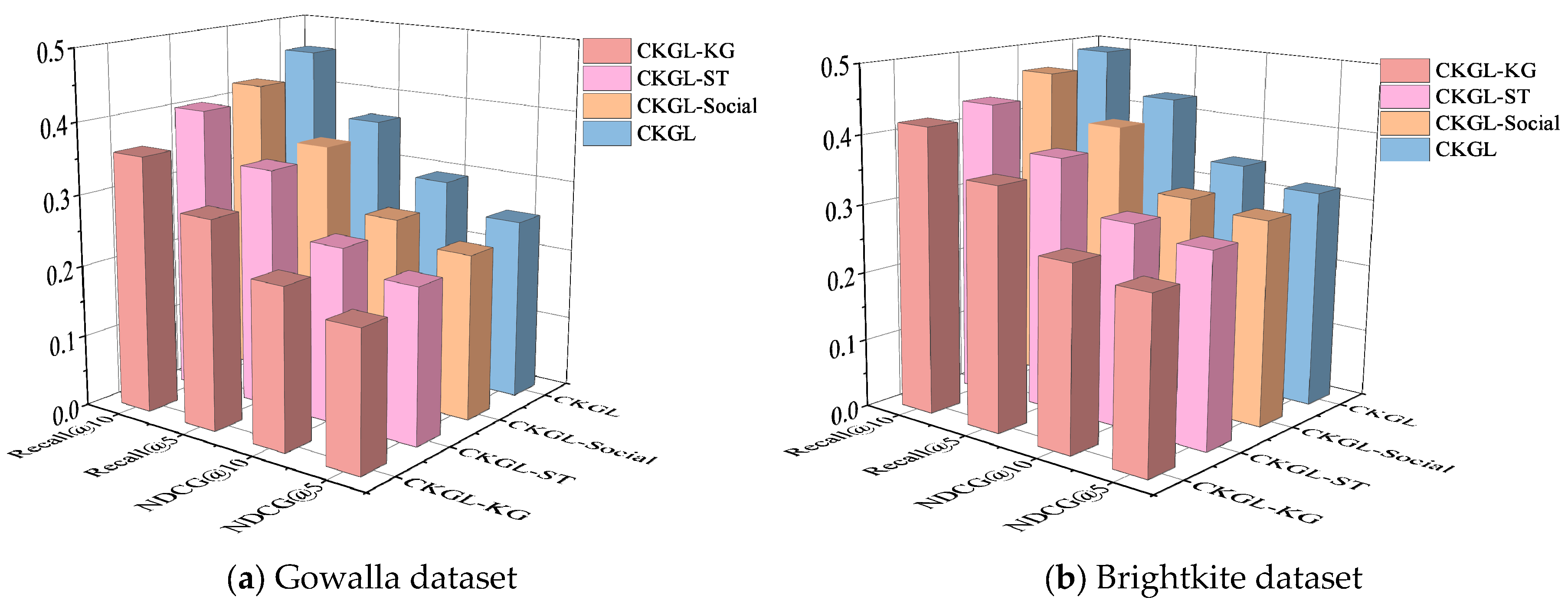
5.5.2. Ablation Study

To further verify the effectiveness of each module in the proposed CKGL framework, three ablation variants were designed:

• CKGL-KG: This variant retains only the basic structural relations in the knowledge graph, including user check-ins and geographical associations between POIs, while excluding the semantic enrichment introduced by entity clustering and multi-relational embedding.
• CKGL-ST: This variant models sequential user–POI relationships but omits the STG-GNN module for spatio-temporal feature extraction, without integrating temporal dynamics and spatial dependencies.
• CKGL-Social: This variant focuses solely on social relationships within the knowledge graph, without incorporating POI-related or spatio-temporal relational information.

The experimental results on the Gowalla and Brightkite datasets are presented in

Table 4. Ablation results on the Gowalla dataset.

Model	Gowalla
	Recall@5	Recall@10	NDCG@5	NDCG @10
CKGL-KG	0.2912	0.3579	0.1934	0.2236
CKGL-ST	0.3347	0.4023	0.2167	0.2471
CKGL-Social	0.3475	0.4216	0.2313	0.2611
CKGL	0.3652	0.4572	0.2523	0.2924

and

Table 5. Ablation results on the Brightkite dataset.

Model	Brightkite
	Recall@5	Recall@10	NDCG@5	NDCG @10
CKGL-KG	0.3523	0.4172	0.2514	0.2677
CKGL-ST	0.3721	0.4332	0.2825	0.2981
CKGL-Social	0.4001	0.4663	0.3005	0.3122
CKGL	0.4266	0.4885	0.3182	0.3414

. Across all evaluation metrics, CKGL consistently achieves the highest performance, demonstrating the effectiveness of its integrated framework.

As shown in Figure 8, CKGL significantly outperforms the three baseline variants on both datasets. The overall performance ranking is CKGL > CKGL-Social > CKGL-ST > CKGL-KG. This result indicates that the joint modeling of semantic relations, spatio-temporal dependencies, and social interactions contributes substantially to the improvement of recommendation accuracy.

Among the three modules, the largest performance gap is observed between CKGL and CKGL-KG, emphasizing the essential role of knowledge graph embedding in capturing semantic associations between users and POIs. By refining relational structures and introducing semantic entities such as user-group and ROI nodes, CKGL provides richer user–POI representations for downstream prediction.

Although CKGL-KG performs slightly worse than CKGL-ST, their performance difference remains relatively small, suggesting that the spatio-temporal patterns of user check-ins exert a significant influence on recommendation outcomes. Effectively modeling periodic temporal regularities and geographically constrained check-in behaviors can further enhance predictive accuracy.

Compared with the other variants, CKGL-Social exhibits a moderate performance decline, indicating that the model relies less on explicit social relationships. This can be attributed to two factors: first, user similarity derived from social interactions is already embedded in the knowledge-graph structure; and second, spatio-temporal dependencies captured by STG-GNN strengthen user behavioral representations, thereby diminishing the marginal effect of social information in the final recommendation process.

From a cross-dataset perspective, the performance differences are more pronounced on the Gowalla dataset than on Brightkite, showing that CKGL demonstrates stronger adaptability and robustness when dealing with sparser check-in data.

6. Conclusions

This study proposed the CKGL method to address the challenges of contextual semantic modeling and data sparsity in POI recommendation. By integrating multi-dimensional semantics, spatio-temporal dependencies, and social relationships within a unified knowledge graph, CKGL enabled a more comprehensive representation of user preferences and POI interactions. The method combined context-aware graph construction and embedding with spatio-temporal gated propagation and relation-aware attention mechanisms, effectively capturing heterogeneous relations, and improving both recommendation accuracy and interpretability. Extensive experiments conducted on two real-world LBSN datasets, Gowalla and Brightkite, demonstrated that CKGL consistently outperformed several representative baseline models in terms of recall and NDCG, confirming its robustness and generalization capability in sparse and dynamic environments. Overall, CKGL provides a flexible and extensible framework for modeling complex user–POI interactions in LBSNs.

Future research will explore incorporating additional contextual dimensions, such as user emotions, textual reviews, and cross-domain behavioral cues, to enrich semantic representation and further improve the recommendation quality. Additionally, incorporating dynamic data streams, such as real-time user behavior or temporal changes in POIs, could enhance the model’s adaptability and performance over time. Furthermore, extending CKGL with contrastive and transferable graph representation learning represents a promising direction to enhance its scalability and applicability in large-scale recommendation scenarios. Finally, investigating the scalability of CKGL to larger, more diverse datasets will be crucial to assessing its practical application in real-world setting.