The Integrated Choice and Latent Variable Model for Exploring the Mechanisms of Pedestrian Route Choice

Abstract

The Integrated Choice and Latent Variable (ICLV) model has been widely applied in travel behavior studies, yet its use in understanding pedestrian route choice remains very limited. This paper seeks to address this gap by analyzing data from a series of controlled pedestrian route choice experiments. Four groups of experimental runs were designed, each involving two route options. The first three groups introduced specific controls: bottlenecks, distance constraints, and extra rewards, while the fourth group, without any imposed control, focused on the influence of route geometry (lengths and widths). For each group, we developed measurement and structural models, followed by three comparative models: a binary logit model using only measured variables (MV model), a model using only latent variables (LV model), and the ICLV model that integrates both. Across all the four scenarios, the adjusted R² values have been improved from 0.286/0.135/0.108/0.035 (MV model) to 0.329/0.161/0.111/0.056 (ICLV model), and the ICLV model can provide interpretable results. These findings highlight the value of incorporating latent constructs based on Structural Equation Modelling (SEM), which enhances the explanatory power of pedestrian route choice models. Moreover, the differences in significant latent variables across various experimental settings offers further insights into the distinct mechanisms underlying pedestrian decision-making under varying conditions.

1. Introduction

In urban transportation systems, pedestrian route choice behavior not only affects walking efficiency but also relates to road safety, spatial utilization, and the quality of pedestrian environments. A deeper understanding of how pedestrians choose their routes can help reveal the human-centered logic behind travel behavior, and offer practical insights for improving walkability and shaping more responsive urban planning strategies.

The existing studies on pedestrian route choice have primarily relied on Discrete Choice Models (DCM), which emphasize factors such as distance, safety, built environment attributes, and crowd dynamics, as highlighted in some systematic review [1]. Additionally, theoretical frameworks have been proposed to outline the principles governing pedestrian decisions, including information perception, integration, and response mechanisms [2]. However, these traditional approaches often overlook unobservable latent constructs and lack an in-depth analysis of the mechanism of variables. This limitation underscores the need for more advanced modeling frameworks that integrate both observable and latent variables to better capture the complexities of pedestrian behavior.

To address this gap, this study explores the use of ICLV models with data collected from a series of controlled pedestrian route choice experiments. These experiments were conducted in 2020 and 2021, resulting in a dataset suitable for both DCM and SEM. In our previous work [3], we examined the performance of various logit models using this dataset. Building on that, this paper further considers the use of SEM to capture latent constructs influencing decision-making. Unlike DCMs, which often assume utility maximization, the ICLV framework incorporates unobservable factors, providing a more comprehensive understanding of pedestrian behavior.

Therefore, the main research objectives of this paper are:

(1)

Build a meaningful and systematic structure for understanding pedestrian route choice behavior in the controlled experiments by SEM and ICLV models.

(2)

Propose a new ICLV model which could be better than previous model without SEM structure.

The rest of this paper is organized as follows. The literature review about the studies of pedestrian route choice behavior and related challenges is given in Section 2. Section 3 describes the methodology, including the conceptual framework, study design, and detailed methodology about the results of case study. A more in-depth discussion will be presented in Section 4. The conclusion and future work are given in Section 5.

2. Literature Review

2.1. DCMs in Pedestrian Route Choice

Traditionally, DCMs have been utilized to analyze pedestrian route choice behavior, commonly assuming that users act as utility maximizers [4]. For example, King and Bode [5] revealed that pedestrians tend to avoid busier and more distant locations, and Haghani and Sarvi [6] examined the multinomial logit (MNL) model’s structure and determined that the impact of decision rule specification was less crucial than hypothetical bias. Some researchers have also resorted to principles like random regret minimization [7]. Since MNL model is based on the Independence of Irrelevant Alternatives (IIA) assumption [8], which may not hold in pedestrian decision-making, more flexible models have been widely adopted to better account for behavioral heterogeneity, such as mixed logit [9] and latent class models [10]. For instance, Haghani and Sarvi [11] examined pedestrian egress behavior in crowded environments and found that while route choice in non-emergency situations was primarily influenced by proximity to the destination, crowd avoidance became a dominant factor during emergencies.

2.2. ICLV Models in Transportation Studies

In recent years, the ICLV model has gained increasing attention in transportation research as an extension of traditional DCMs. By incorporating latent factors such as attitudes, norms, and emotions—which are difficult to observe directly but significantly influence decision-making [12,13]—the ICLV framework enhances behavioral realism. SEM is used to estimate the measurement and structural components of these latent constructs, which are then integrated into utility functions to improve model explanatory power. This approach has been applied in various contexts, ranging from mode choice behaviors to vehicle adoption and policy evaluations.

One prominent area of application is understanding mode choice and travel behaviors, where ICLV models help capture the interplay between environmental factors, perceptions, and decision-making. For instance, Malik et al. [14] used ICLV models to assess how residential environment and vehicle ownership preferences affect ride-hailing use for non-work trips. Similarly, Liu et al. [15] demonstrated that ICLV models outperform traditional multinomial logit models in capturing risk perception and safety trust in ride-hailing choices. Extending this to public transit, Lee et al. [16] explored attitudinal behavior changes for crowding impedance, finding that latent fear amplifies disutility differently between natural and human-made disasters. Blandin et al. [17] examined the influence of perceived accessibility on mode choice, showing that low perceived accessibility increases reliance on motorized modes in urban margins. Ingvardson et al. [18] incorporated psychological needs in commute mode choice modeling, demonstrating that latent constructs like relatedness enhance explanations of sustainable mode shifts. Abdulhussein et al. [19] investigated infrastructure as a latent variable in active transportation mode choices, revealing that perceptions of walking and cycling facilities significantly influence ridership among high school students in Baghdad.

Building on these insights, ICLV models have also proven valuable in evaluating vehicle adoption, sustainability initiatives, and policy interventions. They often link sociodemographic variables with latent attitudes to predict broader shifts in transportation patterns. For example, Iogansen et al. [20] examined the adoption of alternative fuel vehicles, linking sociodemographic characteristics, environmental attitudes, and technology acceptance. Gutjar et al. [21] modeled electric vehicle ownership dynamics at the household level, incorporating latent intentions to assess pricing and incentive effects on fleet adaptations. In the realm of incentives and policies, Gong et al. [22] incorporated latent attitudes into mode choice models, showing that carbon credit incentives positively influence green travel. Piras et al. [23] employed experimental methods to evaluate the combined effects of hard and soft transport policies, highlighting how such models can inform effective interventions.

2.3. Significance and Challenges in Applying ICLV to Pedestrian Route Choice

For the study of pedestrian route choice behavior, an ICLV model could also be very fruitful. It overcomes the limitation of traditional route choice models (e.g., DCMs) that only focus on observable pedestrian variables. By incorporating latent pedestrian variables that are difficult to directly measure, it more authentically reconstructs the complex behavioral mechanisms underlying pedestrians’ route decision-making. With the support of the SEM framework, it not only makes it easier to explain certain unobservable pedestrian motivations, but also addresses the “omitted variable bias”, which can improve the accuracy of model predictions and interpretations. In addition, at the level of practical applications, it can also provide more specific directions for the planning of pedestrian-friendly urban walking systems.

Nevertheless, although ICLV models have been used in many transportation studies, their current application for pedestrian route choice behavior is very rare. In recent years, some ICLV studies have explored pedestrians’ discrete choices in urban traffic. For example, Cantillo et al. [24] modeled pedestrian crossing decisions among bridges, signalized crosswalks and direct crossings, incorporating latent perceptions such as safety and convenience. Similarly, Papadimitriou et al. [25] used ICLV models to examine the influence of risk-taking attitudes and walking motivations on midblock versus junction crossings. More recently, Feng et al. [26] applied the ICLV framework to investigate pedestrian decisions on when to cross in autonomous vehicle scenarios. However, these studies focus on specific crossing behaviors, rather than route choice decisions. We think one possible reason for the very limited application of ICLV models to pedestrian route choice is the lack of high-quality pedestrian data, which constrains deeper investigation into the underlying decision-making mechanisms.

3. Methodology

3.1. Conceptual Framework

In this subsection, we briefly introduce the structure of the ICLV model. To capture the complex relationships between latent constructs, observed indicators and explanatory variables, we adopt an SEM approach that integrates both measurement and structural components:

$$\left\{\begin{array}{ll}{y}_{ni}={\Lambda \eta }_{ni}+{\epsilon }_{ni}& (\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l})\\ {\eta }_{ni}=B{\eta }_{ni}+\Gamma x_{ni}+{\zeta }_{ni}& (\mathrm{S}\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{l} \mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l})\end{array}\right.$$

(1)

where

• $y_{ni}\in {\mathbb{R}}^{P\times 1}$: the vector of $P$ observed indicators for individual $i$ and alternative $n$;
• ${\eta }_{ni}\in {\mathbb{R}}^{M\times 1}$: the vector of $M$ latent variables;
• $\mathsf{\Lambda }\in {\mathbb{R}}^{P\times M}$: the factor loading matrix;
• ${\epsilon }_{ni}$: the measurement of error term;
• $B$: the matrix of coefficients representing relationships among latent variables;
• $\mathsf{\Gamma }$: the matrix capturing effects of observed variables $x_{ni}$ on latent variables;
• $x_{ni}$: the vector of observed exogenous variables;
• ${\zeta }_{ni}$: the structural disturbances.

Since our experiment involves two routes, we adopt a Binary Logit (BL) model to analyze participants’ choices. The model estimates the probability that individual $i$ chooses alternative $j$ based on the random utility:

$$U_{ij}={\beta }^{\mathrm{\top }}{X}_{ij}+{\epsilon }_{ij}$$

(2)

where

$U_{ij}$: the total utility of alternative $j$ by individual $i$;

$X_{ij}$: the vector of observed attributes (e.g., travel time, width, density);

${\beta }^T$ the vector of coefficients representing sensitivities to attributes;

${\epsilon }_{ij}$: the random error term, assumed to follow an i.i.d. Gumbel distribution.

The probability of choosing alternative $j$ is given by:

$$P_{ij}={\displaystyle \frac{\exp \left({\beta }^{\mathrm{\top }}{X}_{ij}\right)}{\mathrm{e}\mathrm{x}\mathrm{p}\left({\beta }^{\mathrm{\top }}{X}_{i1}\right)+\mathrm{e}\mathrm{x}\mathrm{p}\left({\beta }^{\mathrm{\top }}{X}_{i2}\right)}}$$

(3)

To incorporate the latent psychological constructs, we extend this model into an ICLV framework. This approach jointly estimates the SEM and the DCM. The utility function is augmented to include the influence of latent variables:

$$U_{ij}={\beta }^{\mathrm{\top }}{X}_{ij}+{\theta }^{\mathrm{\top }}{\eta }_i+{\epsilon }_{ij}$$

(4)

The corresponding choice probability becomes:

$$P_{ij}={\displaystyle \frac{\exp \left({\beta }^{\mathrm{\top }}{X}_{ij}+{\theta }^{\mathrm{\top }}{\eta }_i\right)}{{\sum }_{k\in C_i} \mathrm{e}\mathrm{x}\mathrm{p}\left({\beta }^{\mathrm{\top }}{X}_{ik}+{\theta }^{\mathrm{\top }}{\eta }_i\right)}}$$

(5)

where

${\eta }_i$: the vector of latent variables inferred from observed indicators via the measurement model $Y_i=\mathsf{\Lambda }{\eta }_i+{\epsilon }_i$;

$\theta$: the coefficients capturing the impact of latent variables on utility.

And then, the corresponding flowchart of this study is shown in Figure 1.

3.2. Study Design

In this subsection, we introduce the pedestrian route choice experiments that were carried out in 2020 and 2021. These experiments took place on the Jiulonghu Campus of Southeast University in China, as illustrated in

Table 1. Basic information of the two-route experiments.

Experiment ID	Date	Number of Participants	Run ID
1	23 October 2020	100	1~8 (except 2D)
2	7 November 2020 *	70	9~10
3	27 November 2021	90	11~16 and 2D

* On that day, we also conducted many other experiments, which are out of the scope of this paper.

. All the participants were university students aged 18 to 25. We confirm that this study complies with relevant ethical requirements. All the participants voluntarily joined these experiments. They knew that their route choice behaviors, including some statistical results (e.g., average travel times) will be used for academic research. Their privacy would be protected, and their personal information (e.g., names and student numbers) would not be used.

The routes in the experiments were constructed using plastic stools, as depicted in Figure 2a. These stools were arranged in a rectangular formation. With the origin and destination designated, pedestrians had the option to choose either a shorter route (L = 12 m, refer to the red route) or a longer one (L = 24 m, see the green route). To facilitate recording and tracking, all participants were obliged to wear red caps. An unmanned aerial vehicle (UAV) was employed to record the experiments. The video had a rate of 25 frames per second and a resolution of 2704 × 1520. Additionally, two fixed cameras were set up to track all the participants (Figure 2b). Each participant could be identified by the numbers on their backs.

During each experiment, participants were required to complete multiple runs. In the majority of runs (excluding Run 7 and 8), the pedestrians were instructed to walk at their normal pace for 5 to 6 laps. The initial positions of all participants varied randomly across different runs. At the origin, all pedestrians chose one route and had to proceed all the way to the destination. Once they arrived at the destination, they needed to return to the origin and finish a new lap. The routes from the origin to the destination were restricted by plastic stools, while the return journey was unrestricted, enabling the participants to move freely.

All the variables utilized in this paper are presented in

Table 2. Summary of the designed and observed experimental variables.

Designed Variables	Explanation
L/L1/L2	Lengths of a route/Route 1/Route 2
W/W1/W2	Widths of a route/Route 1/Route 2
BT/BT1/BT2	Pedestrian’s waiting Times at a bottleneck 1/Bottleneck 1/Bottleneck 2
DBT	The Deviation of pedestrian’s waiting Time at the bottleneck
DC	Whether the Distance Control 2 is used for pedestrians (Yes: 1, No: 0)
R	Whether the pedestrians are asked to compete for Reward 3 (Yes: 1, No: 0)
Lap	The order of the Lap in one run
Observed experimental variables	Explanation
N/N1/N2	Pedestrian Numbers on a route/Route 1/Route 2
D/D1/D2	Average pedestrian densities on a route/Route 1/Route 2, $D=N/(L·W)$
T/T1/T2	Travel Times on a route/Route 1/Route 2
V/V1/V2	Average pedestrian speeds on a route/Route 1/Route 2, $V=L/T$
BN/BN1/BN2	Numbers of pedestrians waiting at a bottleneck/Bottleneck 1/Bottleneck 2
RT	The Return Time from the destination to the origin
Cro	Whether the origin is Crowded (Yes: 1, No: 0)
Pair	Whether the pedestrian is moving with others (Yes: 1, No: 0)

. They could be categorized into two types: (1) Some variables are alternative-specific, e.g., the speeds or travel times. The naming convention for these variables is: the first letter of the full variable name plus the route number. (2) Some other variables are non-alternative-specific (Covariates). For relatively short variables, we use their full names, such as Lap. For longer variables, we use their first three letters as abbreviations, such as Cro. Among them, L, W, BT, DBT, DC, R, and Lap are experimental design variables, and the details of each run are presented in the Appendix A. The other variables in Table 2 were extracted and calculated from the video recordings. To minimize errors associated with automated tracking, we manually extracted data using the Tracker software.

For the variables listed above, it should be noted that:

(1)

Bottleneck effect: When a bottleneck exists along a route, all pedestrians must wait. In our experiments, the bottleneck is only set at Route 1 in some runs. Therefore, BN2 and BT2 are always zero.

(2)

Distance control (DC = 1): Participants are required to maintain a 1 m distance from others, simulating the pandemic-related distancing requirements.

(3)

Reward (R = 1): Participants are instructed to complete the route as quickly as possible to earn an extra reward. Pedestrians who complete the experiment faster can receive more rewards.

(4)

Crowding (Cro = 1): The situation of a pedestrian is considered as “crowded” if they experiences body contact with others at the origin.

Table 3. Descriptive statistics of selected experimental outcomes.

Run	T1 (s)	T2 (s)	P1 (%)	Run	T1 (s)	T2 (s)	P1 (%)
1	18.4	17.0	60.3	1x	16.8	21.0	59.6
2	47.3	26.6	15.0	2x	22.6	25.9	21.6
3	68.2	28.1	8.7	2D	54.4	21.9	21.4
4	16.4	13.9	54.8	4x	17.7	14.1	59.3
5	15.2	14.9	56.2	5x	14.5	21.8	50.0
6	11.1	14.2	48.0	6x	10.9	16.6	49.3
7	9.5	11.6	45.5	8	4.9	4.9	47.6
9	16.7	21.6	46.1	10	19.9	22.1	42.6
11	10.9	16.6	54.8	11x	7.8	13.7	52.8
12	49.0	30.1	16.2	12x	23.5	18.5	21.4
13	14.2	12.4	43.4	13x	9.7	9.5	52.9
14	13.7	13.5	50.5	14x	10.7	10.7	63.6
15	11.3	14.4	49.0	15x	10.1	13.0	65.1
16	10.5	14.8	60.1	16x	8.9	13.1	65.8

presents some key statistics from the experimental runs. T₁ and T₂ indicate the average travel times on Routes 1 and 2, respectively, while P₁ represents the proportions choosing Route 1. For further descriptive analysis, please refer to our earlier study about logit models [3].

3.3. Detailed Methodology

In this subsection, we present the results of case study about methodological application of ICLV. To facilitate the comparison between the ICLV models and standard logit models, we analyze four experimental groups based on distinct decision-making mechanisms. As shown in Figure 3, Groups 1, 2, and 3 examine the effects of bottlenecks, distance control, and extra rewards, respectively, while Group 4 focuses on variations in route length and width. Note that in our previous paper about the typical Logit models [3], we had used the same four groups to study the influence of controls. And in this paper, to clarify the advantage of ICLV models, we want to directly compare the results between Logit models and ICLV models. Therefore, we consider the same groups for a better comparison.

3.3.1. SEM Results

Here we present the SEM results prepared for the ICLV model analysis, utilizing AMOS software. The main evaluation metrics for the four structural models are presented in

Table 4. Main metrics of structural models in four groups.

Group	CFI	TLI	RMSEA	SRMR
1	0.986	0.975	0.080	0.0228
2	0.992	0.983	0.075	0.0237
3	0.987	0.989	0.063	0.0078
4	0.991	0.963	0.074	0.0343

. All metrics satisfy the fundamental criteria for SEM, including CFI > 0.9, TLI > 0.9, RMSEA < 0.1, and SRMR < 0.08.

Following adjustments based on Modification Indices, the results for Group 1 (Bottleneck group) are presented in

Table 5. Tests for reliability and validity of Group 1.

Latent Variable	Measured Variable	Factor Loading	AVE	CR	Variance Explained Ratio	Overall Validity and Reliability
L-R1B (Route 1 statistics with Bottleneck)	BT1	0.82	0.67	0.86	11.8%	KMO: 0.821 Sig: 0.000 Cumulative variance explained ratio: 87.4%
	V1	−0.97
	D1	0.63
L-R2 (Route 2 statistics)	T2	0.85	0.71	0.88	9.9%
	D2	0.70
	V2	−0.95
L-O (Occupancy Statistics)	BN1	0.77	0.53	0.70	65.8%
	N2	0.69

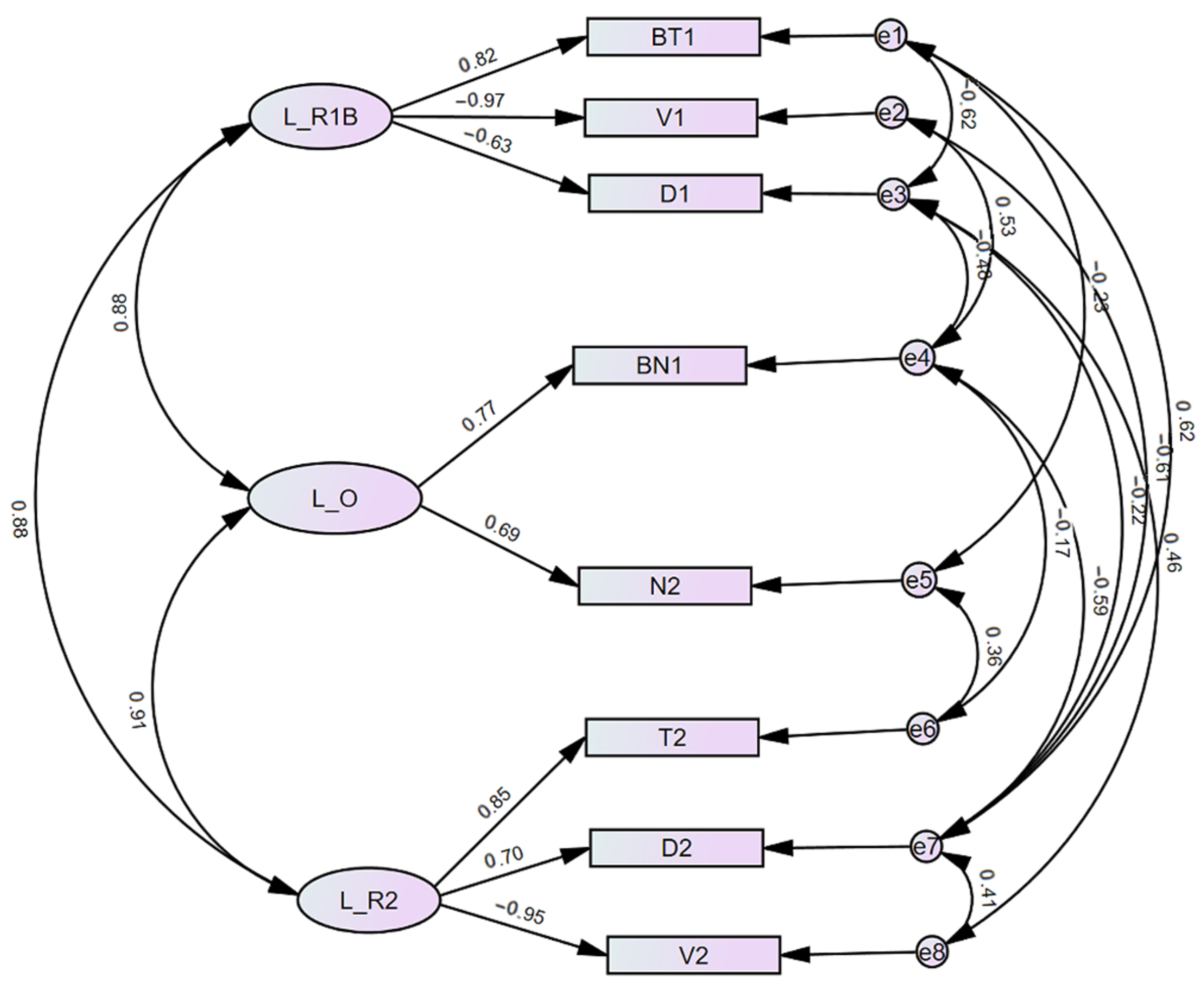
and Figure 4. To clearly differentiate latent variables from observed indicators, we prefix latent variables with “L-”. Specifically, Group 1 includes the latent variables L-R1B (Route 1 with Bottleneck), L-R2 (Route 2), and L-O (Occupancy).

The measurement model demonstrates satisfactory performance. Here all factor loadings exceed 0.5, Composite Reliability (CR) values are above 0.7, Average Variance Extracted (AVE) values surpass 0.5, and the Kaiser-Meyer-Olkin (KMO) measure is greater than 0.7, indicating adequate convergent validity and sampling adequacy. It is important to note that while Cronbach’s Alpha is commonly used as an indicator for measurement models, it is not applicable in this study. This is primarily because many of the independent variables considered, such as route length, width, average speed, and average density, are objective physical quantities rather than items or scales designed to measure latent psychological or abstract constructs. Although some correlation may exist among these variables, this does not align with the concept of internal consistency reliability that Cronbach’s Alpha is intended to assess.

Figure 4 presents the three latent variables and their relationships with the associated coefficients. L-R1B represents the cost of Route 1: an increase in BT₁ and D₁ raises the cost of using Route 1, resulting in positive coefficients. Conversely, a larger V₁ reduces the cost, leading to a negative coefficient. Similarly, L-R2 captures the total cost of Route 2 across various factors. Additionally, L-O represents route occupancy: as the number of pedestrians increases, the cost of using the route also increases.

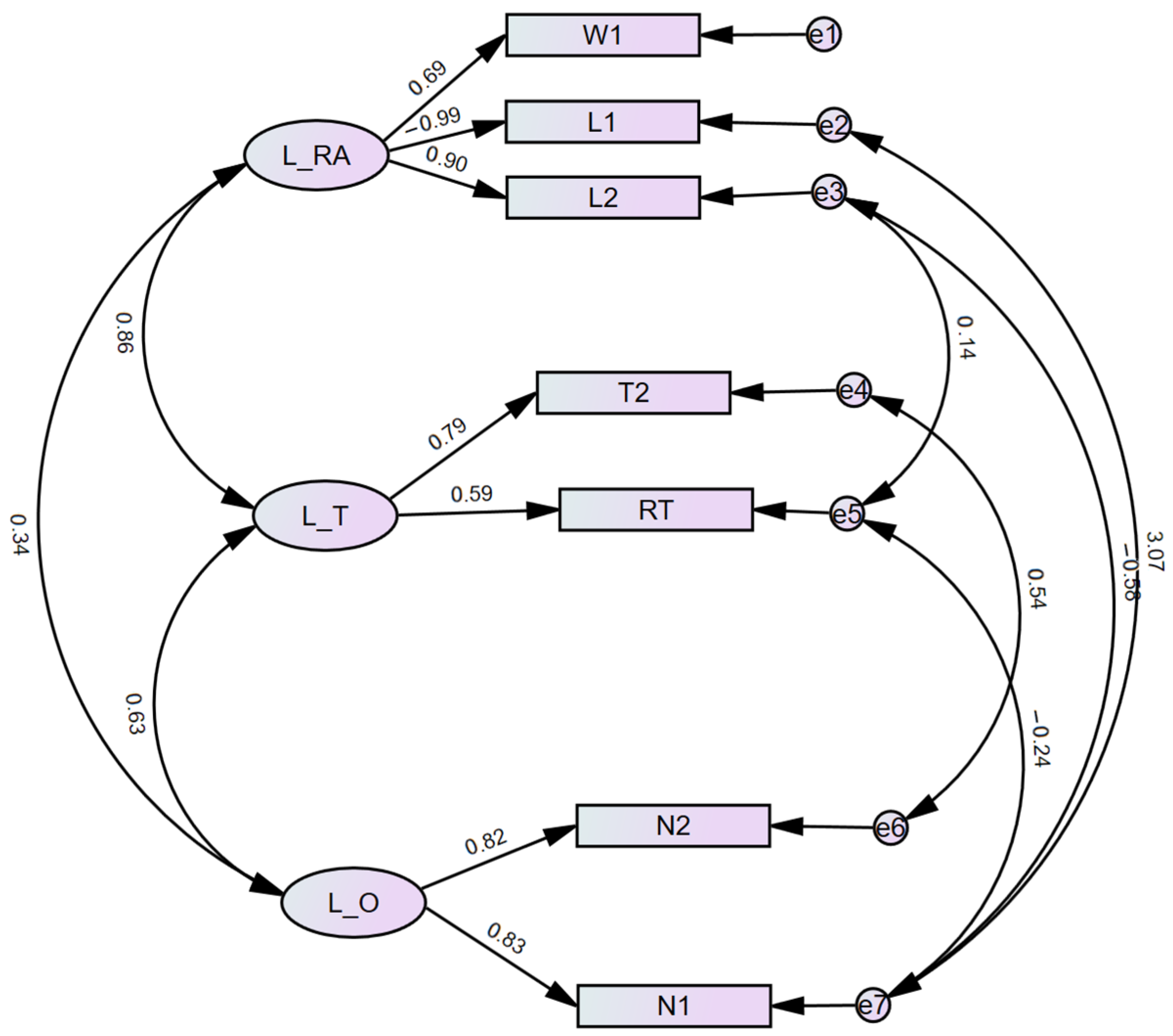
The results for Group 2 (Distance Control group) are presented in

Table 6. Tests for reliability and validity of Group 2.

Latent Variable	Measured Variable	Factor Loading	AVE	CR	Variance Explained Ratio	Overall Validity and Reliability
L-RA (Route Attributes)	W1	0.69	0.76	0.90	53.7%	KMO: 0.756 Sig: 0.000 Cumulative variance explained ratio: 88.8%
	L1	−0.99
	L2	0.90
L-T (Time statistics)	T2	0.79	0.49	0.65	9.0%
	RT	0.59
L-O (Occupancy Statistics)	N1	0.83	0.68	0.81	22.0%
	N2	0.82

and Figure 5. Most of the metrics in Table 4 are satisfactory, except for the AVE of L-T, which is slightly below 0.5. Since there is no bottleneck in this group, the decision-making mechanisms of pedestrians change, and the latent variables used should be different. Here L-RA represents the physical cost of the two routes. In our experimental data, the dependent variable is defined as 0 for Route 1 and 1 for Route 2. Therefore, a positive sign indicates that an increase in the measured variables (W₁ and L₂) raises the cost of choosing Route 2, while a negative sign suggests that L₁ decreases the cost. Additionally, a similar pattern is observed in L-T, and the characteristics of L-O in this group are similar to those shown in Group 1.

Note that the variable about distance control (DC) is not included in the structure model of Group 2. This situation also corresponds to the statistical results in Table 3: when adding distance control in the experiment, the proportions of choosing routes do not significantly change. Nevertheless, the influence of DC could be seen in the column of “variance explained ratios”: since the densities on both routes are low, the ratio for L-O is smaller. But that for L-RA is higher, which means the route lengths and widths are more significant in a distance-controlled environment.

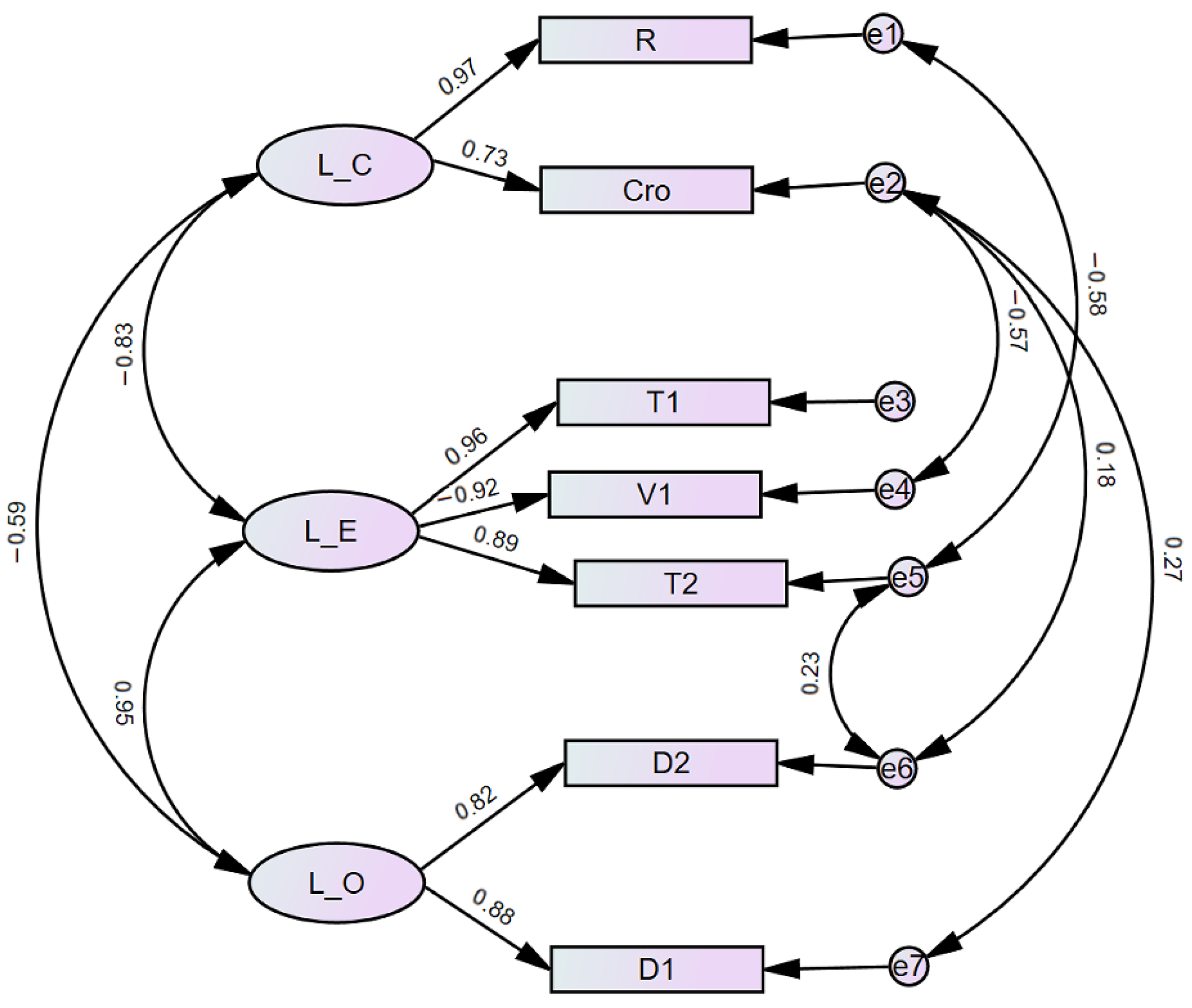
The results of Group 3 (Reward group) are presented in

Table 7. Tests for reliability and validity of Group 3.

Latent Variable	Measured Variable	Factor Loading	AVE	CR	Variance Explained Ratio	Overall Validity and Reliability
L-C (Control Influence)	R	0.97	0.74	0.85	4.9%	KMO:0.846 Sig: 0.000 Cumulative variance explained ratio: 91.0%
	Cro	0.73
L-E (Efficiency statistics)	V1	−0.92	0.88	0.95	72.0%
	T1	0.96
	T2	0.89
L-O (Occupancy statistics)	D1	0.88	0.72	0.84	14.1%
	D2	0.82

and Figure 6. Unlike Group 2, here the influence of control (extra reward) is revealed by L-C. Whether the origin is crowded (Cro) is also useful for the decision-making of pedestrians when racing. At the same time, the other two latent variables are more or less similar to that in Group 2, especially L-O. The signs of the corresponding measured variables are the same as that in the previous models. In addition, the variance explained ratio for L-E is much higher than the others, which corresponds to the special nature of Group 3: many pedestrians pay particular attention to the efficiencies of the two routes during the races.

Finally, the results of Group 4 (Different lengths and widths) are presented in

Table 8. Tests for reliability and validity of Group 4.

Latent Variable	Measured Variable	Factor Loading	AVE	CR	Variance Explained Ratio	Overall Validity and Reliability
L-R1 (Route 1 statistics)	V1	−0.76	0.59	0.74	18.7%	KMO: 0.789 Sig: 0.000 Cumulative variance explained ratio: 80.9%
	W1	0.77
L-T (Time statistics)	T1	0.43	0.58	0.71	9.3%
	RT	0.99
L-R2 (Route 2 statistics)	V2	0.69	0.62	0.83	52.9%
	W2	0.80
	D2	−0.86

and Figure 7. In the absence of control factors, the geometrical characteristics of the routes become the primary determinants of pedestrian route choice. As shown in Figure 7, the three latent variables are L-R1, L-R2, and L-T. Generally speaking, most signs of the measured variables are similar to the previous groups, except V₂. Note that the cumulative variance explained ratio for Group 4 (80.9%) is lower than that of the other groups, suggesting that the model’s performance in this group is less robust. This may be attributed to the complex composition of the experimental runs in this group. Additionally, the highest variance explained ratio in Group 4 is found in L-R2, indicating that the condition of the alternative route (longer Route 2) is the key concern for pedestrians in this no-control environment.

3.3.2. ICLV Results

Next, we present the ICLV models based on the SEM results in Section 3.3.1. Firstly, the results of Group 1 are shown in

Table 9. The effect of bottleneck (Group 1) in ICLV model.

Parameter	MV (BL)	LV	ICLV
BT	−0.176 (−6.50)	/	−0.521 (−10.9)
BN	−0.179 (−7.24)	/	−0.388 (−11.1)
DBT	0.410 (6.03)	/	1.01 (10.6)
RT	−0.033 (−6.09)	/	−0.031 (−5.41)
Pair	0.420 (2.65)	/	0.401 (2.48)
L-R1B	/	0.333 (7.10)	−0.322 (−4.20)
L-O	/	0.396 (10.30)	/
L-R2	/	−0.115 (−5.73)	−0.164 (−7.33)
$\mathrm{LL}(\mathsf{\beta }$)	−1042.0	−1085.7	−975.8
LL(0)	−1466.7	−1466.7	−1466.7
${\rho }^2$	0.290	0.260	0.335
$\mathrm{Adj}. {\rho }^2$	0.286	0.257	0.329

. Here the MV model includes only measured variables, the LV model includes only the latent variables identified in this paper, while the ICLV model integrates both measured and latent variables. Since the discussions of the influential measured variables have been given in the previous paper, in this paper we mainly concentrate on the new findings brought by ICLV model:

(1)

The results of LV model are easy to understand. Since the latent variables are added into the utility function of Route 2 (as covariates), the signs show that an increase in the cost of Route 1 and a decrease in the cost of Route 2 will lead to a higher probability of choosing Route 2. At the same time, higher occupancies of routes, indicating more pedestrians on the road, will have the same influence.

(2)

In the results of LV model, all the latent variables are statistically significant. The large absolute values of t-values further show the validity of the findings from SEM.

(3)

Although the ${\rho }^2$ of LV model is still lower than that of MV model, the effects of these latent variables could be clearly seen in the ICLV model results. The adj ${\rho }^2$ of ICLV model is as high as 0.329, which is impossible for a typical BL model to reach.

(4)

Since some latent variables are also associated with measured ones, the signs and significance of some latent variables could change in ICLV model. To obtain a model result in which all variables are significant, we select some of them for ICLV model, as shown in Table 9. Here L-O is removed: it does not mean the occupancy of routes is not important. On the contrary, this decision is due to the correlation with other measured variables, e.g., BN.

Next, we show the ICLV model results of Group 2, 3, 4 in

Table 10. The effect of distance control (Group 2) in ICLV model.

Parameter	MV (BL)	LV	ICLV
V	0.992 (4.67)	/	1.64 (7.66)
D	−0.719 (−4.98)	/	/
DC	−0.493 (−4.23)	/	/
Cro	1.409 (8.11)	/	1.50 (8.35)
RT	−0.169 (−15.0)	/	−0.311 (−14.8)
Pair	0.492 (3.86)	/	0.381 (2.93)
L-RA	/	0.229 (8.64)	/
L-T	/	0.702 (11.2)	2.09 (9.06)
L-O	/	−1.94 (−11.6)	0.453 (7.31)
$\mathrm{LL}(\mathsf{\beta }$)	−1357.6	−1455.3	−1315.4
LL(0)	−1576.2	−1576.2	−1576.2
${\rho }^2$	0.139	0.077	0.165
$\mathrm{Adj}. {\rho }^2$	0.135	0.074	0.161

,

Table 11. The effect of rewards (Group 3) in ICLV model.

Parameter	MV (BL)	LV	ICLV
D	−1.063 (−10.36)	/	−1.08 (−10.5)
R	−1.094 (−6.14)	/	−0.629 (−5.36)
Cro	1.783 (10.98)	/	1.62 (9.24)
RT	−0.028 (−4.10)	/	−0.038 (−5.20)
Pair	2.051 (8.98)	/	2.05 (8.95)
L-E	/	0.682 (6.01)	−0.33 (−4.06)
L-T	/	0.339 (6.15)	0.265 (3.90)
L-O	/	−10.4 (−11.8)	/
$\mathrm{LL}(\mathsf{\beta }$)	−1722.8	−1822.6	−1715.0
LL(0)	−1937.4	−1937.4	−1937.4
${\rho }^2$	0.111	0.059	0.115
$\mathrm{Adj}. {\rho }^2$	0.108	0.057	0.111

and

Table 12. The situation with different lengths and widths (Group 4) in ICLV model.

Parameter	MV (BL)	LV	ICLV
W	−0.939 (−4.30)	/	−1.56 (−5.58)
L	−0.069 (−6.48)	/	−0.124 (−9.56)
D	−0.311 (−2.70)	/	−0.935 (−6.77)
V	0.971 (4.25)	/	2.98 (8.44)
Cro	1.150 (7.03)	/	0.968 (5.81)
RT	−0.013 (−6.93)	/	−0.379 (−6.72)
Pair	0.503 (4.59)	/	0.584 (5.18)
L-R1	/	−0.211 (−5.10)	6.01 (6.16)
L-T	/	−1.150 (−2.61)	−5.72 (−8.35)
L-R2	/	−0.251 (−2.08)	−1.59 (−5.24)
$\mathrm{LL}(\mathsf{\beta }$)	−1825.9	−1883.2	−1783.9
LL(0)	−1899.2	−1899.2	−1899.2
${\rho }^2$	0.037	0.008	0.061
$\mathrm{Adj}. {\rho }^2$	0.035	0.007	0.056

. Generally speaking, the findings are qualitatively similar to those of Group 1:

(1)

The ${\rho }^2$ of the ICLV model is higher than that of the MV and LV models in all groups, which means the introduction of latent variables is helpful.

(2)

The signs of all the measured variables always remain the same when adding some latent variables.

(3)

The removal of some measured/latent variables is also due to the correlation with other latent/measured variables, e.g., in both Group 2 and 3, D is correlated with L-O. Therefore, only one of them is left.

(4)

The signs of many latent variables in the LV models of different groups are consistent across groups, e.g., the travel times (L-T) and occupancies (L-O) in Group 2 and 3. However, some exceptions exist, such as the travel time in Group 4. As discussed in our previous study on DCMs, the influence of travel times in our experimental data sometimes deviates from typical expectations, partly because the time differences between two routes are usually small.

(5)

The relationship between SEM and ICLV results could be further observed. For example, the explanatory power of Group 4 is not good enough (lower ${\rho }^2$ in Table 12), which corresponds to the lower cumulative variance explained ratio in Table 7. In other words, the model features will not be essentially changed by ICLV model.

After presenting the ICLV results, the significant latent variables in the four ICLV models are further concluded in

Table 13. Significant latent variables in the four ICLV models.

Group	Control	LV1	LV2	LV3
1	Bottleneck	Route 1	Route 2	/
2	Distance control	/	Occupancy	Time
3	Extra reward	Efficiency	/	Time
4	None	Route 1	Route 2	Time

. We can see the differences between the four groups are clear, which corresponds to the different mechanisms of decision-making:

(1)

When a bottleneck exists, or there is no control, the comparison between two routes is important for pedestrians. In other words, the bottleneck on a route actually can be regarded as part of the route features.

(2)

On the contrary, for the other situations, the focus of pedestrians will be shifted to certain characteristics. Under distance control, the occupancies of routes are more important. And when there is extra reward, it is easy to understand that the efficiencies of routes become crucial.

(3)

For most situations, time is usually important for pedestrians, even when the differences between two routes are not large.

4. Discussion

In this section, we will conduct a further discussion on the research findings of this paper, including an assessment of the degree to which the research objectives have been achieved, a comparative analysis with the conclusions in previous studies, and an elaboration on the practical application value of the findings, as well as the existing limitations.

Firstly, the two main research objectives mentioned in the introduction have been met. By using an SEM structure and ICLV models, we successfully build a systematic framework for understanding pedestrian route choice behavior in the experiments. In addition, as shown in Section 5, we have proposed a new ICLV model whose metrics are better. Compared with the results of Logit models without SEM structure, the adjusted R² values of ICLV models in the four groups have been improved. The qualitative results of each group remained unchanged (e.g., the results of Group 1 are the highest, and that of Group 4 are the lowest), while there was a quantitative improvement across all groups. In particular, the differences between various controls could be observed. For most situations, the travel times are always important. The comparisons between two routes are mainly considered when there exists a bottleneck or no control. On the contrary, the main concern of pedestrians during distance control is occupancy, while that with extra reward is efficiency.

Since no prior papers have exactly the same technical approach to this paper (using ICLV models for studying pedestrian route choice behavior in the experiments), the conclusions of this paper cannot be quantitatively compared with that in the previous papers. Nevertheless, we find the results are qualitatively similar to the previous ones [15,17,19]: the ICLV models can help to improve the model performance and its interpretability. They can uncover certain mechanisms that the MNL models fail to demonstrate. The conclusions in various transportation studies are similar, while the topics or backgrounds are different. Therefore, in a word, our findings do not challenge any of the existing literature.

Beyond the academic contributions, the outcomes of this research hold tangible societal benefits that can support evidence-based transportation planning and pedestrian safety management. Firstly, the systematic framework for understanding pedestrian route choice behavior provides urban planners with a data-driven tool to optimize pedestrian infrastructure design. For instance, insights into how bottlenecks, distance controls, and extra rewards influence route preferences can guide the layout of sidewalks, crosswalks, and public space signage, including university campuses, commercial districts, or transit hubs. In addition, the identification of key decision-making mechanisms enables policymakers to implement targeted traffic control strategies. This not only enhances the user experience of pedestrians but also minimizes potential safety risks by aligning infrastructure design with actual pedestrian behavior.

At the end of discussion, the limitations of this study need to be mentioned: Firstly, due to the pandemic of COVID-19 in 2020 and 2021, the university imposed strict restrictions on visitors, which meant that we could only recruit university students to participate in the experiment. Therefore, the experimental results cannot represent the behavior of other people with different ages or backgrounds. Secondly, no subjective variables are considered in the models, which is different from the traditional approach used in some previous papers. Nevertheless, the current model without subjective variables also performs better than the baseline model, which shows the validity and significance of ICLV models. In addition, these experiments are based on some ideal consumptions. For example, the overall pedestrian numbers and densities do not change during the experiments. Thus, whether the experimental results differ from those in real life still needs to be checked in the future.

5. Conclusions

This paper explores the application of an ICLV model in analyzing pedestrian route choice behavior. Four groups of experimental runs were designed, each offering two route options. The first three groups focused on specific control mechanisms, including bottlenecks, distance control, and extra rewards, while the fourth group, without any controls, examined the impact of route geometry (lengths and widths). Firstly, we develop measurement models and structural models for all the groups. The latent variables we considered are different according to the main features of each group. The indicators show that all models perform adequately, providing a solid basis for further analysis.

We then compare three models: a basic binary logit model using only measured variables (MV model), a model using only latent variables (LV model), and the ICLV model incorporating both. The adjusted R² values in the four groups have been improved from 0.286/0.135/0.108/0.035 (MV model) to 0.329/0.161/0.111/0.056 (ICLV model). The qualitative results of each group remained unchanged, while there was a quantitative improvement across all groups. Such a result suggests the integration of SEM-based latent variables enhances our understanding of pedestrian route choice behavior. In addition, the differences of the latent variables explored in various groups further illustrate the distinctions between the mechanisms of pedestrian decision-making under different controls. These results are helpful for the design of pedestrian facilities, and also useful for the control measures when the crowding emerges.

Despite the insights gained, several limitations remain. From a data perspective, the current experiments only involve two-route scenarios with relatively simple route features, and no participant-level questionnaire data were collected, limiting the ability to account for individual heterogeneity. Future research should aim to expand the experimental design to include more complex route configurations and richer individual-level data. From a modeling perspective, a more systematic framework is needed to interpret the ICLV results, especially regarding qualitative shifts in the signs of latent variables when incorporated into the discrete choice model. Furthermore, pedestrian heterogeneity has not yet been incorporated into the analysis, constraining our understanding of diverse decision-making behaviors. In the future, it is necessary to collect more data on pedestrian route choice behavior, and try to consider more variables in the modeling. We believe the potential of the ICLV model in this field remains to be further explored and discussed.