A Spatiotemporal Multi-Model Ensemble Framework for Urban Multimodal Traffic Flow Prediction
Abstract
1. Introduction
- (1)
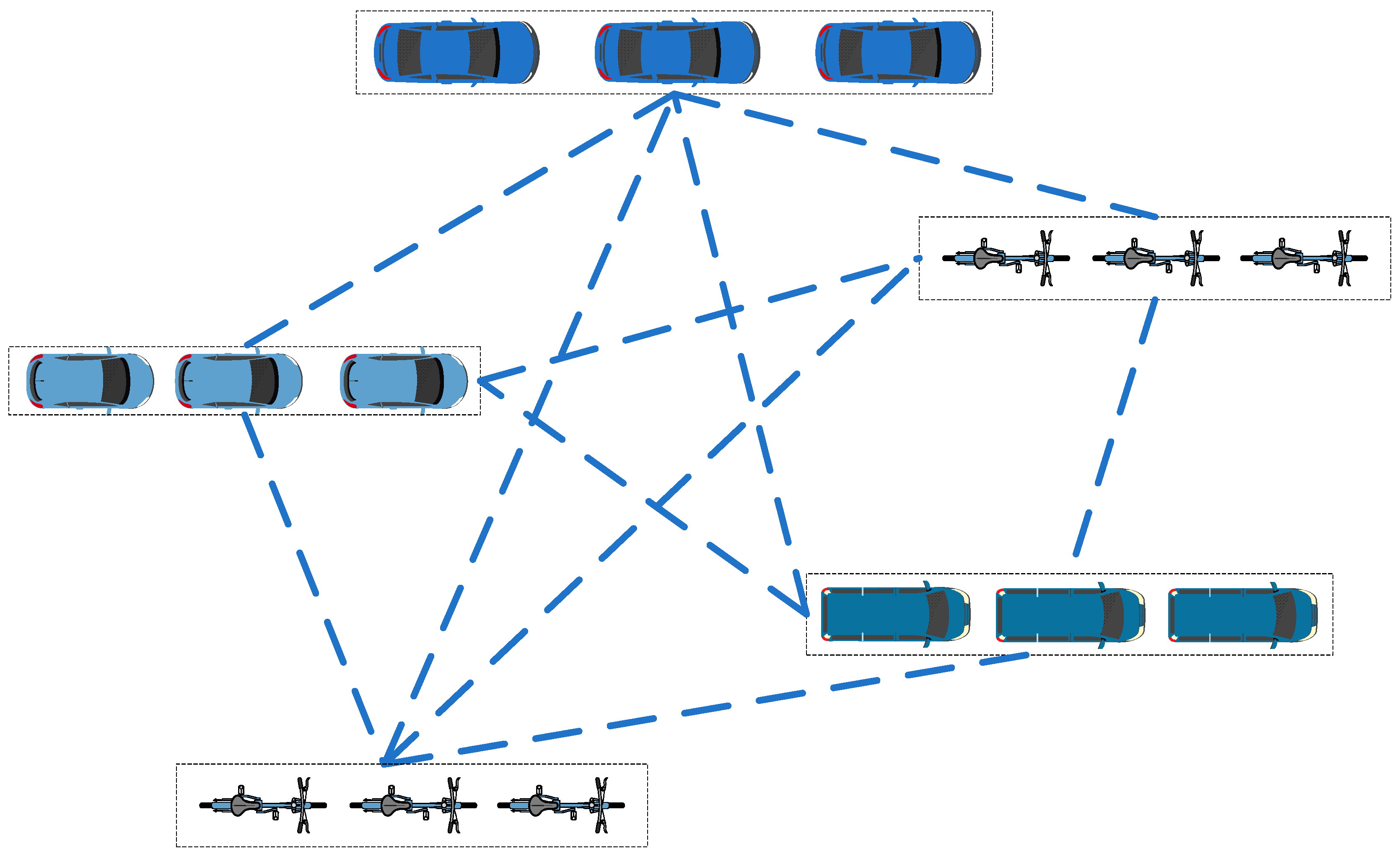
- Dynamic interaction among multimodal travel trajectories. In urban traffic networks, different modes of transportation (such as bike-sharing, taxis, and buses) not only exhibit strong spatiotemporal characteristics, but also generate movement trajectories that demonstrate complex interaction patterns across both spatial and temporal dimensions [6,7].
- (2)
- Multimodal travel trajectory features. The spatiotemporal characteristics of urban multimodal travel trajectories stem from the interaction dependencies and latent correlations among different travel modes across space and time [8]. Based on the different trajectory features, it is necessary to consider the trajectory characteristics of different transportation modes (e.g., bike-sharing, taxis, and buses) for flow prediction.
- (3)
- Multi-model ensemble. Travel trajectories have significant heterogeneity in spatial and temporal dimensions, and different travel characteristics have different requirements for model adaptation [9]. By integrating the features predicted by each model with the multi-model ensemble strategy, the overall traffic flow of multimodal travel in the city can be well reflected.
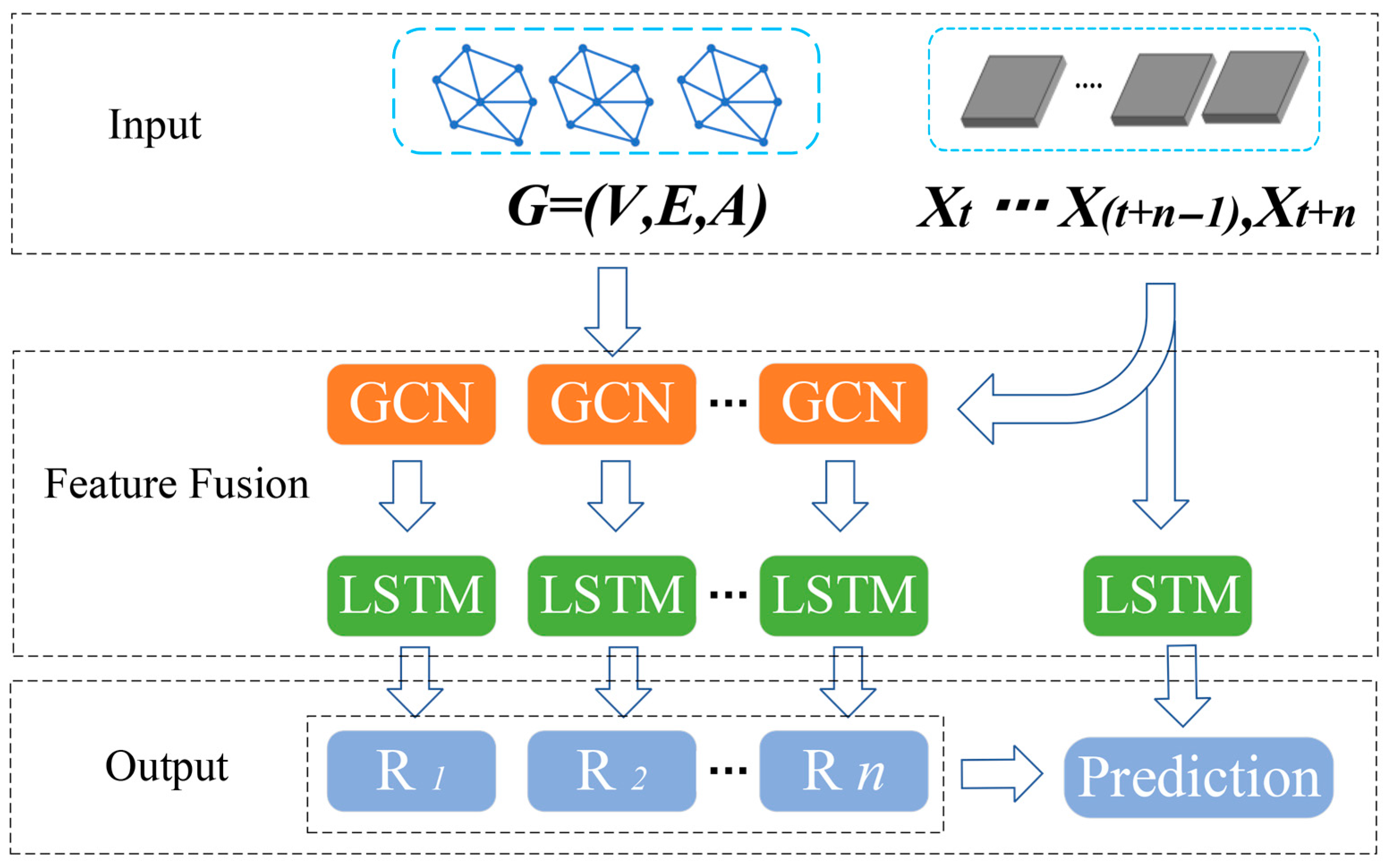
- We propose a feature-adaptive selection mechanism to match travel scenarios with appropriate predictive models (Graph Convolutional Network (GCN) for dynamic and Long Short-Term Memory (LSTM) for fixed-route modes). This approach generates heterogeneous feature representations that serve as inputs for the subsequent multi-model ensemble process.
- We introduce a dynamic weighted integration strategy, and use the traffic fusion calculation method to generate comprehensive traffic flow prediction results through the output of the spatiotemporal grid mapping fusion model.
- Extensive experiments on real datasets demonstrate that the proposed method is significantly superior to existing methods in terms of prediction accuracy.
2. Related Works
3. Basic Definitions
3.1. Trajectory Flow Prediction Problem
3.2. Spatiotemporal Coupling Across Trajectory Modalities
3.3. Multi-Model Ensemble
4. Data and Methods
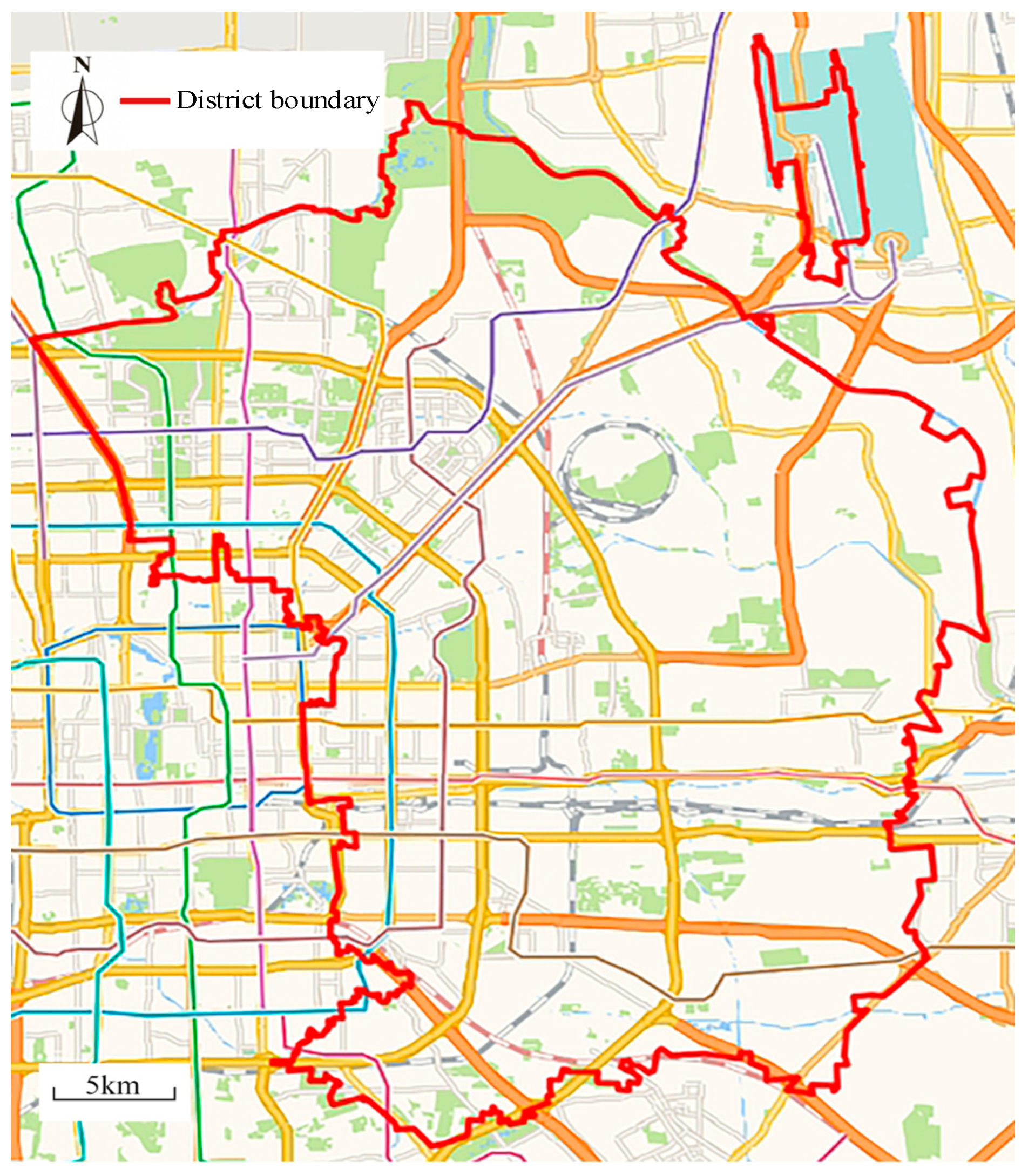
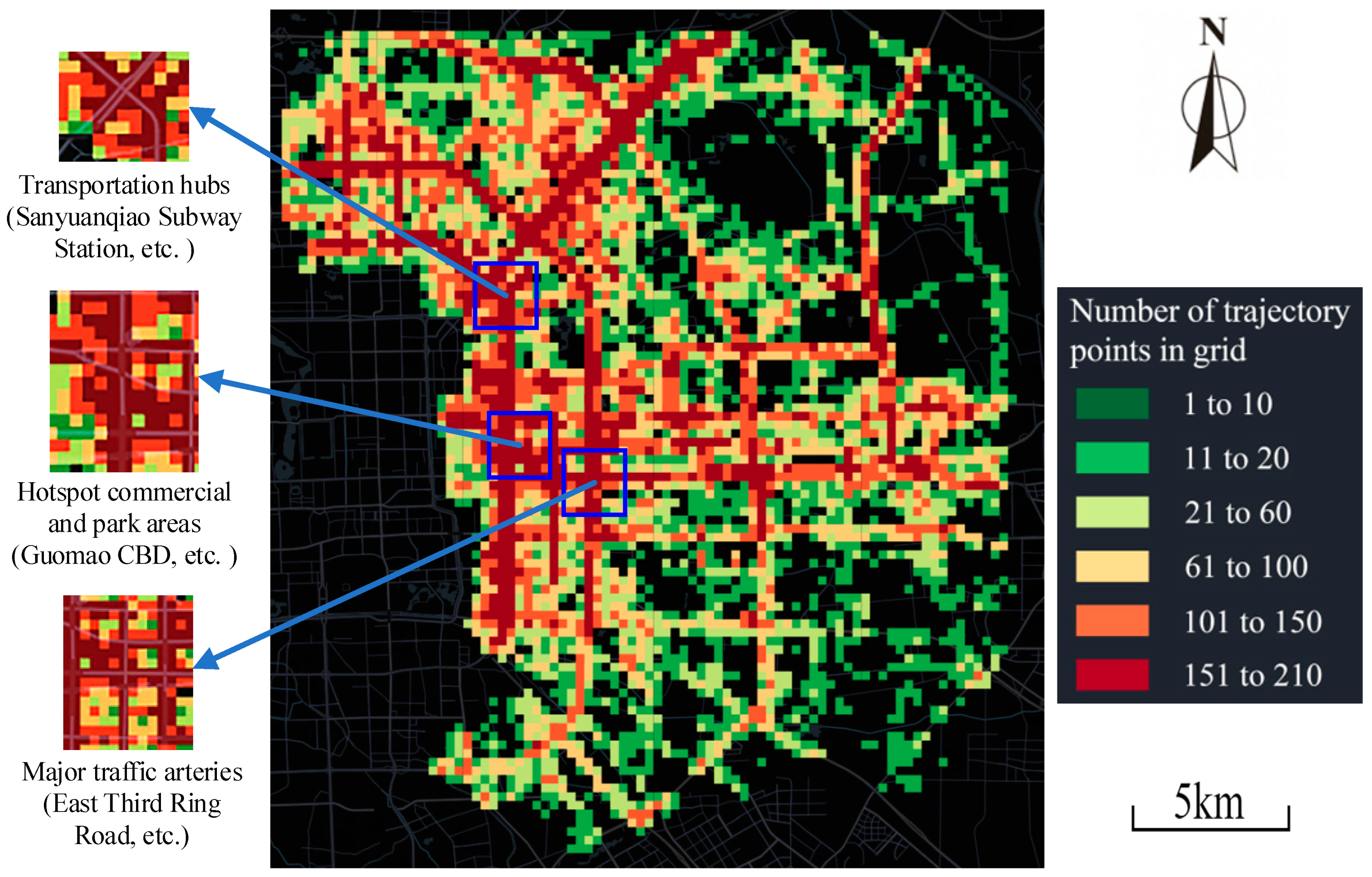
4.1. Studied Area and Dataset
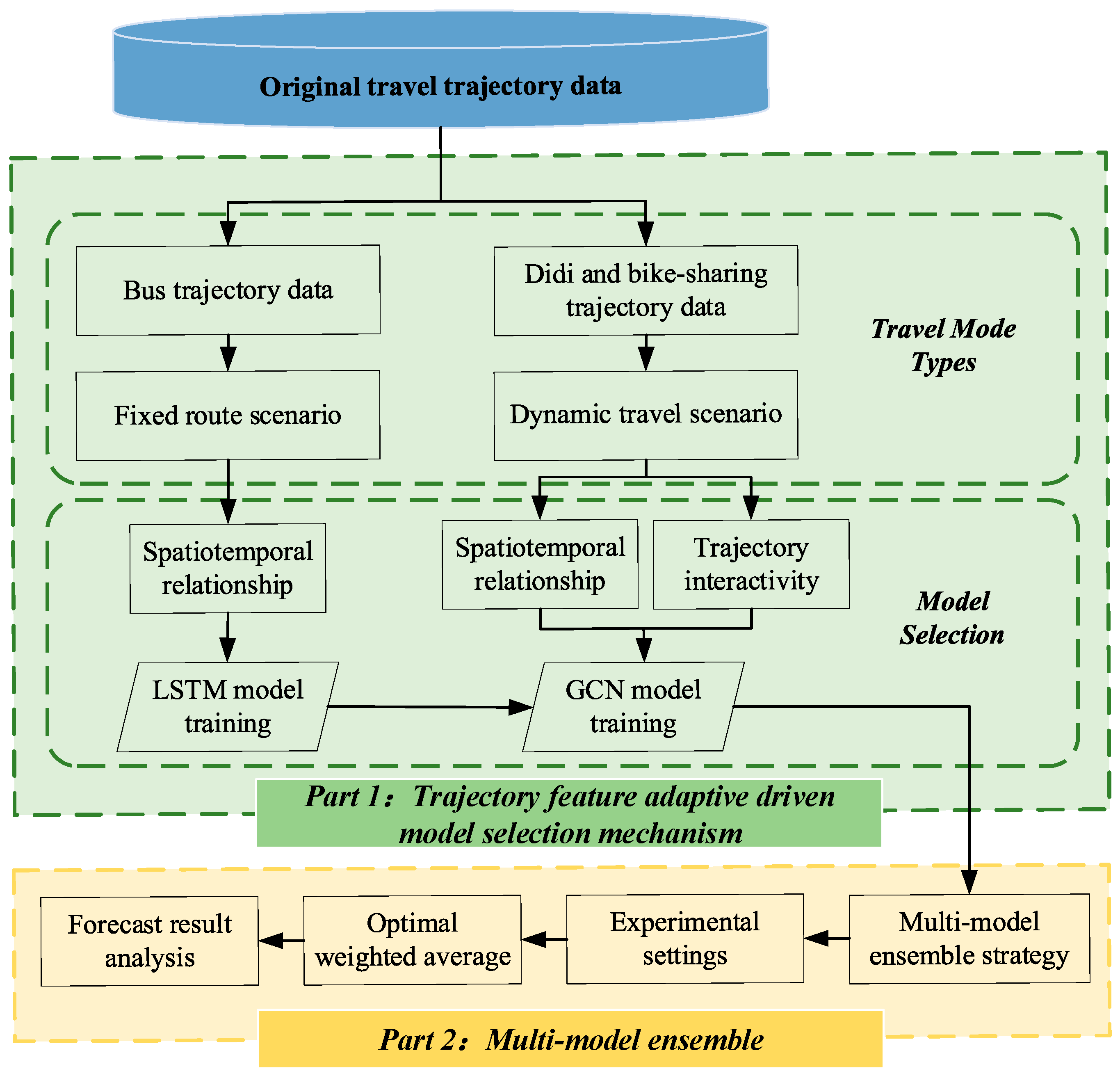
4.2. Overall Spatiotemporal Multi-Model Framework
4.3. Trajectory Feature Adaptive Driven Model Selection Mechanism
4.3.1. Dynamic Trajectory Feature Scenario
4.3.2. Fixed-Route Trajectory Feature Scenario
4.4. Multi-Model Ensemble
4.4.1. Dynamic Weights for the Multi-Model Ensemble Strategy
4.4.2. Flow Fusion Computation
5. Results
5.1. Accuracy Evaluation Metrics of the Model GLEN
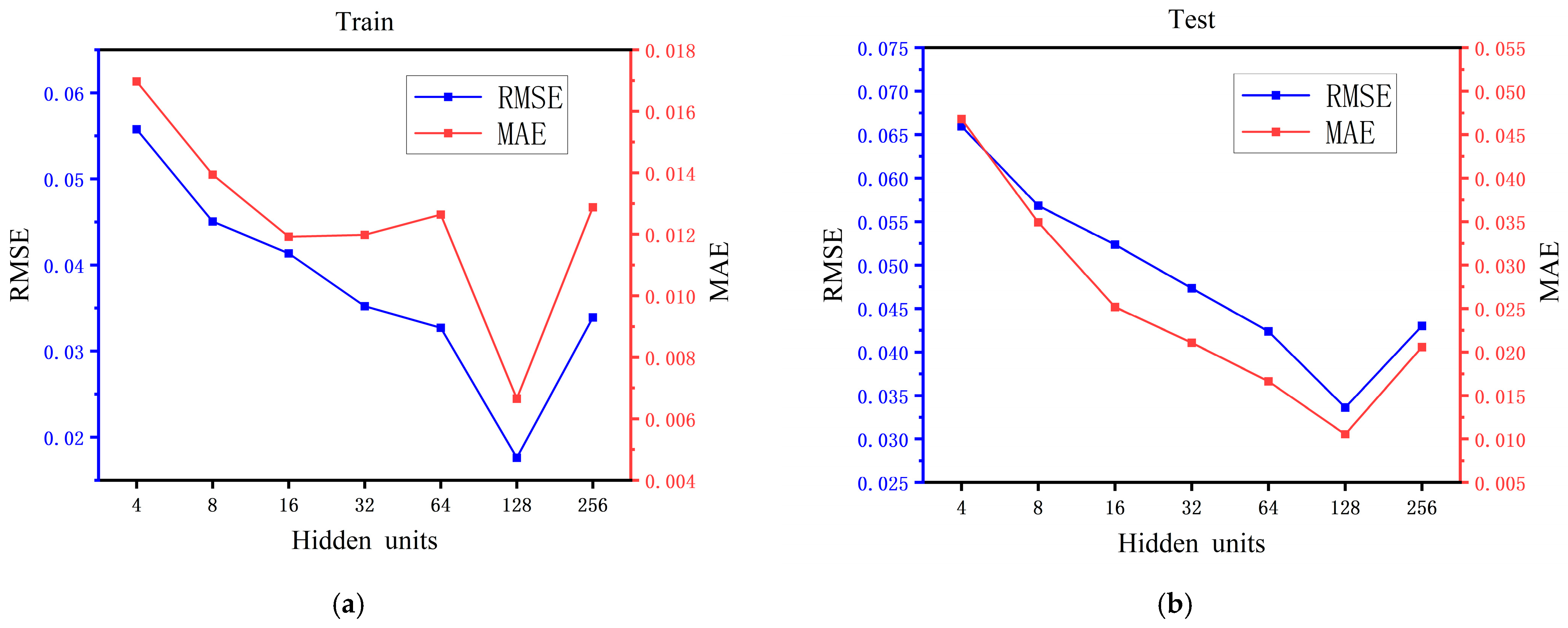
5.2. Parameter Settings of the Prediction Model GLEN
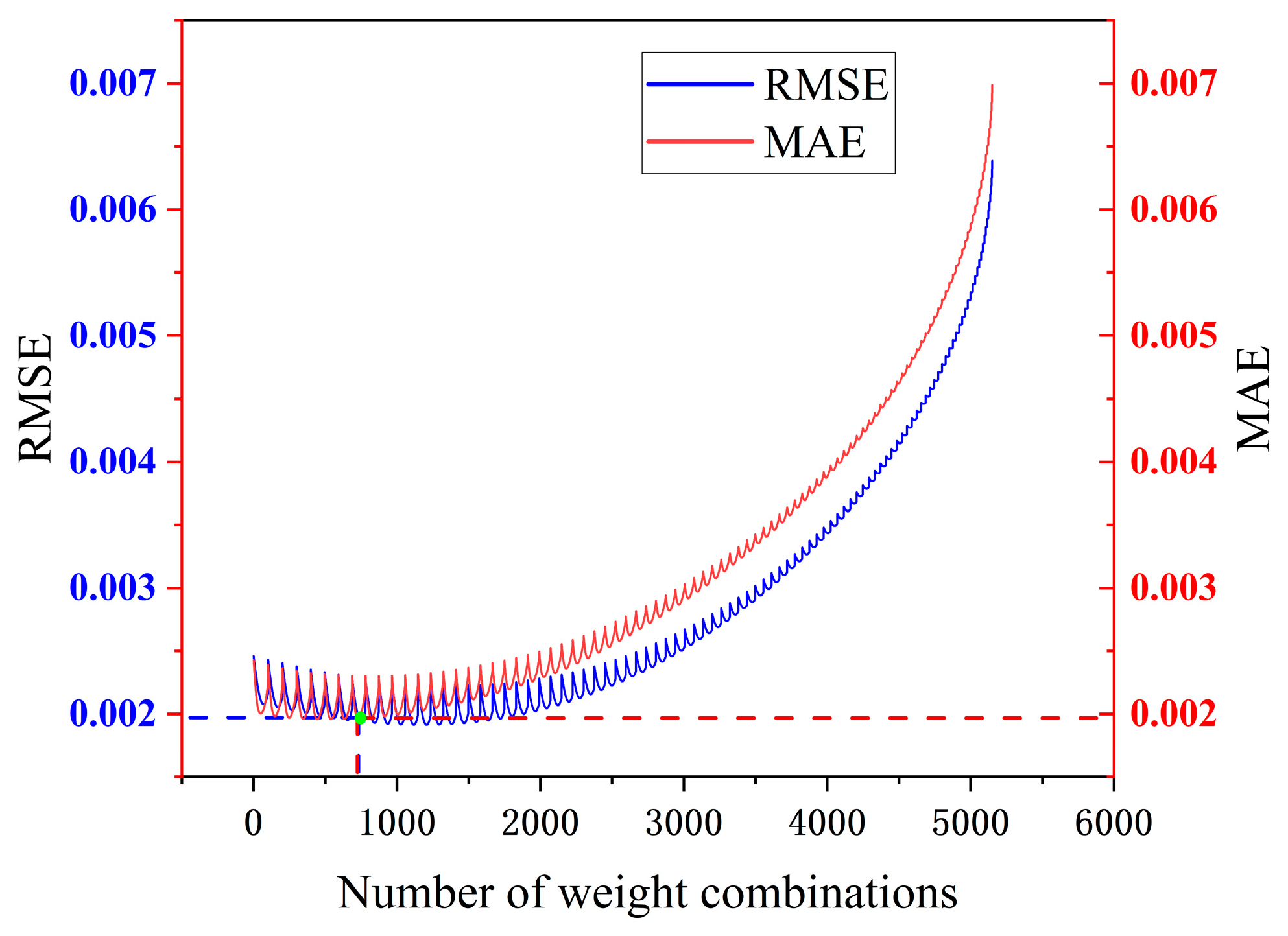
5.3. Dynamic Weights Analysis of Multi-Model Ensemble
5.4. Experimental Results
5.4.1. Comparison with Baselines
5.4.2. Prediction Performance over Different Future Time Horizons
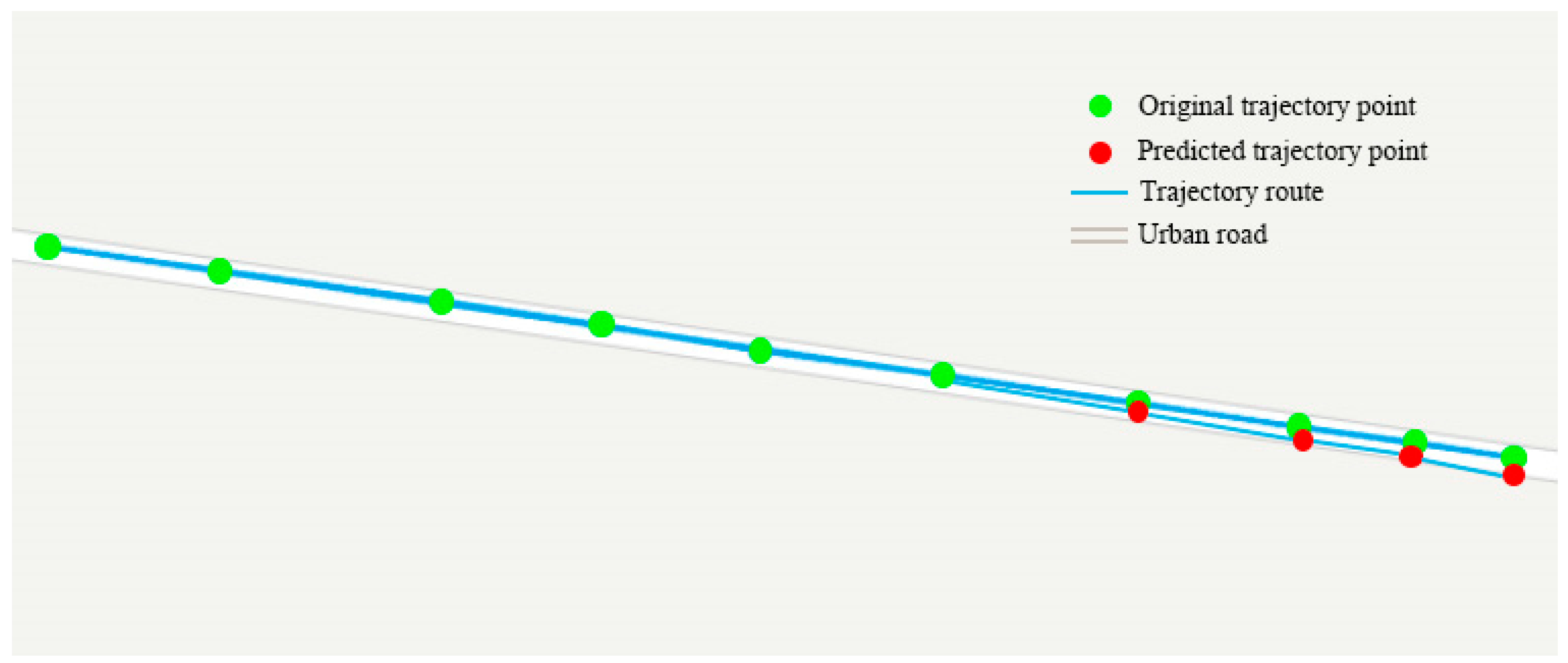
5.4.3. Model Interpretation
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, C.; Dai, G.; Zhou, J. Short-term traffic flow prediction for urban road sections based on time series analysis and LSTM_BILSTM method. IEEE Trans. Intell. Transp. Syst. 2021, 23, 5615–5624. [Google Scholar] [CrossRef]
- Zhou, T.; Huang, B.; Li, R.; Liu, X.; Huang, Z. An attention-based deep learning model for citywide traffic flow forecasting. Int. J. Digit. Earth 2022, 15, 323–344. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, Y.; Wang, S.; Zhao, X.; Hu, Y.; Yin, B. Self-Attention Graph Convolution Imputation Network for Spatio-Temporal Traffic Data. IEEE Trans. Intell. Transp. Syst. 2024, 25, 19549–19562. [Google Scholar] [CrossRef]
- Gao, Y.; Fu, J.; Feng, W.; Xu, T.; Yang, K. Surrounding vehicle trajectory prediction under mixed traffic flow based on graph attention network. Physica A 2024, 639, 129643. [Google Scholar] [CrossRef]
- Cai, S.; Liu, G.; He, J.; Du, Y.; Si, Z.; Jiang, Y. Temporal-Spatial Traffic Flow Prediction Model Based on Prompt Learning. ISPRS Int. J. Geo-Inf. 2025, 14, 11. [Google Scholar] [CrossRef]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion convolutional recurrent neural network: Data-driven traffic forecasting. arXiv 2017, arXiv:1707.01926. [Google Scholar]
- Zhang, J.; Zheng, Y.; Qi, D.; Li, R.; Yi, X.; Li, T. Predicting citywide crowd flows using deep spatio-temporal residual networks. Artif. Intell. 2018, 259, 147–166. [Google Scholar] [CrossRef]
- Dou, Z.; Guo, D. DPSTCN: Dynamic Pattern-Aware Spatio-Temporal Convolutional Networks for Traffic Flow Forecasting. ISPRS Int. J. Geo-Inf. 2025, 14, 10. [Google Scholar] [CrossRef]
- Benterki, A.; Judalet, V.; Maaoui, C.; Boukhnifer, M. Multi-model and learning-based framework for real-time trajectory prediction. In Proceedings of the 28th Mediterranean Conference on Control and Automation (MED), Saint-Raphaël, France, 15–18 September 2020; pp. 776–781. [Google Scholar] [CrossRef]
- Smith, B.L.; Demetsky, M.J. Traffic flow forecasting: Comparison of modeling approaches. J. Transp. Eng. 1997, 123, 261–266. [Google Scholar] [CrossRef]
- Hamed, M.M.; Al-Masaeid, H.R.; Said, Z.M.B. Short-term prediction of traffic volume in urban arterials. J. Transp. Eng. 1995, 121, 249–254. [Google Scholar] [CrossRef]
- Williams, B.M.; Durvasula, P.K.; Brown, D.E. Urban freeway traffic flow prediction: Application of seasonal autoregressive integrated moving average and exponential smoothing models. Transp. Res. Rec. 1998, 1644, 132–141. [Google Scholar] [CrossRef]
- Lee, S.; Fambro, D.B. Application of subset autoregressive integrated moving average model for short-term freeway traffic volume forecasting. Transp. Res. Rec. 1999, 1678, 179–188. [Google Scholar] [CrossRef]
- Davis, G.A.; Nihan, N.L. Nonparametric regression and short-term freeway traffic forecasting. J. Transp. Eng. 1991, 117, 178–188. [Google Scholar] [CrossRef]
- Lefèvre, S.; Laugier, C.; Ibañez-Guzmán, J. Exploiting map information for driver intention estimation at road intersections. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 583–588. [Google Scholar] [CrossRef]
- Hu, W.; Yan, L.; Liu, K.; Wang, H. A short-term traffic flow forecasting method based on the hybrid PSO-SVR. Neural Process. Lett. 2016, 43, 155–172. [Google Scholar] [CrossRef]
- Firl, J.; Stübing, H.; Huss, S.A.; Stiller, C. Predictive maneuver evaluation for enhancement of car-to-x mobility data. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium, Madrid, Spain, 3–7 June 2012; pp. 558–564. [Google Scholar] [CrossRef]
- Hussain, B.; Afzal, M.K.; Ahmad, S.; Mostafa, A.M. Intelligent traffic flow prediction using optimized GRU model. IEEE Access 2021, 9, 100736–100746. [Google Scholar] [CrossRef]
- Jia, Y.; Wu, J.; Du, Y. Traffic speed prediction using deep learning method. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 1217–1222. [Google Scholar] [CrossRef]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.-Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2014, 16, 865–873. [Google Scholar] [CrossRef]
- Sattarzadeh, A.R.; Kutadinata, R.J.; Pathirana, P.N.; Huynh, V.T. A novel hybrid deep learning model with ARIMA Conv-LSTM networks and shuffle attention layer for short-term traffic flow prediction. Transp. A Transp. Sci. 2023, 21, 2236724. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Fang, L.; Jiang, Q.; Zhou, B. Multimodal motion prediction with stacked transformers. arXiv 2021. [Google Scholar] [CrossRef]
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transp. Res. Part C Emerg. Technol. 2015, 54, 187–197. [Google Scholar] [CrossRef]
- Zhang, D.; Kabuka, M.R. Combining weather condition data to predict traffic flow: A GRU-based deep learning approach. IET Intel. Transp. Syst. 2018, 12, 578–585. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, H.; Feng, X.; Chen, Z. Short-term traffic flow prediction with Conv-LSTM. In Proceedings of the 9th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 11–13 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Yu, H.; Wu, Z.; Wang, S.; Wang, Y.; Ma, X. Spatiotemporal recurrent convolutional networks for traffic prediction in transportation networks. Sensors 2017, 17, 1501. [Google Scholar] [CrossRef]
- Wang, J.; Gu, Q.; Wu, J.; Liu, G.; Xiong, Z. Traffic speed prediction and congestion source exploration: A deep learning method. In Proceedings of the IEEE 16th International Conference on Data Mining (ICDM), Barcelona, Spain, 12–15 December 2016; pp. 499–508. [Google Scholar] [CrossRef]
- Gong, S.; Liu, J.; Yang, Y.; Cai, J.; Xu, G.; Cao, R.; Jing, C.; Liu, Y. Self-paced Gaussian-based graph convolutional network: Predicting travel flow and unravelling spatial interactions through GPS trajectory data. Int. J. Digit. Earth 2024, 17, 2353123. [Google Scholar] [CrossRef]
- Qi, T.; Li, G.; Chen, L.; Xue, Y. ADGCN: An asynchronous dilation graph convolutional network for traffic flow prediction. IEEE Internet Things J. 2021, 9, 4001–4014. [Google Scholar] [CrossRef]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H. T-GCN: A temporal graph convolutional network for traffic prediction. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3848–3858. [Google Scholar] [CrossRef]
- Liu, H.; Dong, Z.; Jiang, R.; Deng, J.; Deng, J.; Chen, Q.; Song, X. STAEformer: Spatio-Temporal Adaptive Embedding Makes Vanilla Transformer SOTA for Traffic Forecasting. arXiv 2023. [Google Scholar] [CrossRef]
- Patara, T.; Lee, J.G. DF-TAR: A Deep Fusion Network for Citywide Traffic Accident Risk Prediction with Dangerous Driving Behavior. In Proceedings of the Web Conference 2021 (WWW’21), New York, NY, USA, 19–23 April 2021; pp. 1146–1156. [Google Scholar] [CrossRef]
- Choi, J.; Choi, H.; Hwang, J.; Park, N. Graph neural controlled differential equations for traffic forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Palo Alto, CA, USA, 22 February–1 March 2022; pp. 6367–6374. [Google Scholar] [CrossRef]
- Wang, K.; Ma, C.; Qiao, Y.; Lu, X.; Hao, W.; Dong, S. A hybrid deep learning model with 1DCNN-LSTM-Attention networks for short-term traffic flow prediction. Physica A 2021, 583, 126293. [Google Scholar] [CrossRef]
- Weng, W.; Fan, J.; Wu, H.; Hu, Y.; Tian, H.; Zhu, F.; Wu, J. A Decomposition Dynamic graph convolutional recurrent network for traffic forecasting. Pattern Recognit. 2023, 142, 109670. [Google Scholar] [CrossRef]
- Fernando, T.; Denman, S.; Sridharan, S.; Fookes, C. Soft+ hardwired attention: A lstm framework for human trajectory prediction and abnormal event detection. Neural Netw. 2018, 108, 466–478. [Google Scholar] [CrossRef]
- Li, Y.; Tarlow, D.; Brockschmidt, M.; Zemel, R. Gated graph sequence neural networks. arXiv 2015, arXiv:1511.05493. [Google Scholar]
- Ke, J.; Qin, X.; Yang, H.; Zheng, Z.; Zhu, Z.; Ye, J. Predicting origin-destination ride-sourcing demand with a spatio-temporal encoder-decoder residual multi-graph convolutional network. Transp. Res. Part C Emerg. Technol. 2021, 122, 102858. [Google Scholar] [CrossRef]
- Qin, H.; Yang, X. Iterative Algorithm for Vessel Trajectory Restoration Based on Improved Linear Interpolation. J. Comput.-Aided Des. Comput. Graph. 2019, 31, 1759–1767. [Google Scholar] [CrossRef]
- Wei, X. Analytic Deep Learning: Convolutional Neural Network Principles and Visual Practice, 1st ed.; Publishing House of Electronics Industry: Beijing, China, 2018; pp. 21–109. [Google Scholar]
- Kim, G.; Kim, D.; Ahn, Y.; Huh, K. Hybrid approach for vehicle trajectory prediction using weighted integration of multiple models. IEEE Access 2021, 9, 78715–78723. [Google Scholar] [CrossRef]
- Lv, M.; Hong, Z.; Chen, L.; Chen, T.; Zhu, T.; Ji, S. Temporal multi-graph convolutional network for traffic flow prediction. IEEE Trans. Intell. Transp. Syst. 2020, 22, 3337–3348. [Google Scholar] [CrossRef]


| Date | Order ID | Longitude | Latitude | Passenger Status | Direction Angle |
|---|---|---|---|---|---|
| 2019/5/27 16:00:09 | 861729202470 | 116.4864 | 39.99074 | 0 | 39 |
| 2019/5/27 16:12:32 | 861729202470 | 116.49747 | 40.00511 | 0 | 00 |
| 2019/5/27 16:30:15 | 861729202470 | 116.52434 | 40.01903 | 0 | 63 |
| 2019/5/27 16:46:44 | 861729202470 | 116.43866 | 39.98539 | 0 | 297 |
| 2019/9/27 17:10:15 | 861729202470 | 116.40126 | 39.9896 | 0 | 168 |
| Baseline Methods | Characteristics of Model Methods |
|---|---|
| HMM | The Hidden Markov Model generates unobservable state sequences through a hidden Markov chain and uses these state sequences to generate observed value sequences. |
| LSTM | Traffic trajectory prediction is performed using the LSTM model. In the experiment, two LSTM layers are stacked, with each layer containing 32 units. |
| Transformer | The model uses partial trajectory data. By extracting and analyzing the spatial and temporal characteristics of the trajectory, the future trajectory points of the traveler can be accurately predicted. |
| DCRNN | Traffic trajectories are modeled as diffusion processes on graphs, and a deep learning framework is proposed that combines both spatial and temporal correlations. |
| T-GCN | Combines GCN and GRU for traffic trajectory prediction. It performs graph convolution operations while considering only the topology of the graph. |
| STAEFormer | The autoencoder and Transformer architecture are integrated, and the local and global feature patterns are captured by the self-attention mechanism. The spatiotemporal data is effectively compressed by the autoencoder, and the spatiotemporal relationship is modeled in parallel. |
| 1DCNN-LSTM | Developed an integrated prediction model based on an attentional mechanism and a 1DCNN-LSTM network, which combines the advantages of both models. |
| DDGCRN | This is a dual dynamic graph convolutional recurrent network, which combines RNNs to model complex spatiotemporal dependencies and dynamically adjusts the graph structure. |
| Future Moments | Models | Latitude | Longitude | ||
|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | ||
| HMM | 0.6352 | 0.6785 | 0.6445 | 0.7133 | |
| LSTM | 0.5472 | 0.6173 | 0.5532 | 0.6547 | |
| Transformer | 0.5383 | 0.5962 | 0.5442 | 0.6063 | |
| DCRNN | 0.4981 | 0.5536 | 0.5089 | 0.5434 | |
| 1 | T-GCN | 0.5178 | 0.5632 | 0.4953 | 0.5471 |
| STAEFormer | 0.3857 | 0.4226 | 0.3971 | 0.4158 | |
| 1DCNN-LSTM | 0.3664 | 0.3975 | 0.3321 | 0.3449 | |
| DDGCRN | 0.3289 | 0.3458 | 0.3084 | 0.3244 | |
| GLEN | 0.3227 | 0.3242 | 0.2827 | 0.2962 | |
| Future Moments | Models | Latitude | Longitude | ||
|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | ||
| HMM | 0.6845 | 0.7031 | 0.6768 | 0.7482 | |
| LSTM | 0.6178 | 0.6683 | 0.6228 | 0.6945 | |
| Transformer | 0.5972 | 0.6214 | 0.5863 | 0.6487 | |
| DCRNN | 0.5572 | 0.5843 | 0.5423 | 0.5901 | |
| 2 | T-GCN | 0.5874 | 0.5932 | 0.5674 | 0.5943 |
| STAEFormer | 0.5097 | 0.5376 | 0.5018 | 0.5139 | |
| 1DCNN-LSTM | 0.4534 | 0.4957 | 0.4542 | 0.4587 | |
| DDGCRN | 0.4288 | 0.4413 | 0.4271 | 0.4125 | |
| GLEN | 0.4041 | 0.4458 | 0.4302 | 0.3913 | |
| HMM | 0.7152 | 0.7345 | 0.7162 | 0.7643 | |
| LSTM | 0.6458 | 0.6734 | 0.6254 | 0.6653 | |
| Transformer | 0.5986 | 0.6598 | 0.6052 | 0.6263 | |
| DCRNN | 0.5244 | 0.5437 | 0.5477 | 0.5245 | |
| 3 | T-GCN | 0.5482 | 0.5668 | 0.5535 | 0.5611 |
| STAEFormer | 0.4954 | 0.5212 | 0.5319 | 0.5483 | |
| 1DCNN-LSTM | 0.4757 | 0.4911 | 0.4921 | 0.5171 | |
| DDGCRN | 0.4581 | 0.4312 | 0.4284 | 0.4692 | |
| GLEN | 0.4524 | 0.4332 | 0.4212 | 0.4544 | |
| HMM | 0.8101 | 0.8251 | 0.7740 | 0.7962 | |
| LSTM | 0.7231 | 0.7408 | 0.7006 | 0.7235 | |
| Transformer | 0.6587 | 0.6802 | 0.6577 | 0.6947 | |
| DCRNN | 0.5910 | 0.6128 | 0.6007 | 0.6255 | |
| 4 | T-GCN | 0.6012 | 0.6045 | 0.6301 | 0.6387 |
| STAEFormer | 0.5567 | 0.5736 | 0.5810 | 0.5875 | |
| 1DCNN-LSTM | 0.5381 | 0.5406 | 0.5221 | 0.5351 | |
| DDGCRN | 0.4832 | 0.4896 | 0.4932 | 0.4824 | |
| GLEN | 0.4904 | 0.4868 | 0.4697 | 0.4801 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Hu, L. A Spatiotemporal Multi-Model Ensemble Framework for Urban Multimodal Traffic Flow Prediction. ISPRS Int. J. Geo-Inf. 2025, 14, 308. https://doi.org/10.3390/ijgi14080308
Wang Z, Hu L. A Spatiotemporal Multi-Model Ensemble Framework for Urban Multimodal Traffic Flow Prediction. ISPRS International Journal of Geo-Information. 2025; 14(8):308. https://doi.org/10.3390/ijgi14080308
Chicago/Turabian StyleWang, Zhenkai, and Lujin Hu. 2025. "A Spatiotemporal Multi-Model Ensemble Framework for Urban Multimodal Traffic Flow Prediction" ISPRS International Journal of Geo-Information 14, no. 8: 308. https://doi.org/10.3390/ijgi14080308
APA StyleWang, Z., & Hu, L. (2025). A Spatiotemporal Multi-Model Ensemble Framework for Urban Multimodal Traffic Flow Prediction. ISPRS International Journal of Geo-Information, 14(8), 308. https://doi.org/10.3390/ijgi14080308







