Predicting the Next Location of Urban Individuals via a Representation-Enhanced Multi-View Learning Network
Abstract
1. Introduction
- We propose a novel community-enhanced spatial representation to capture human regional preferences and the relationships between locations. Accurately modeling human mobility patterns at different spatial scales improves the model’s understanding of spatial structure;
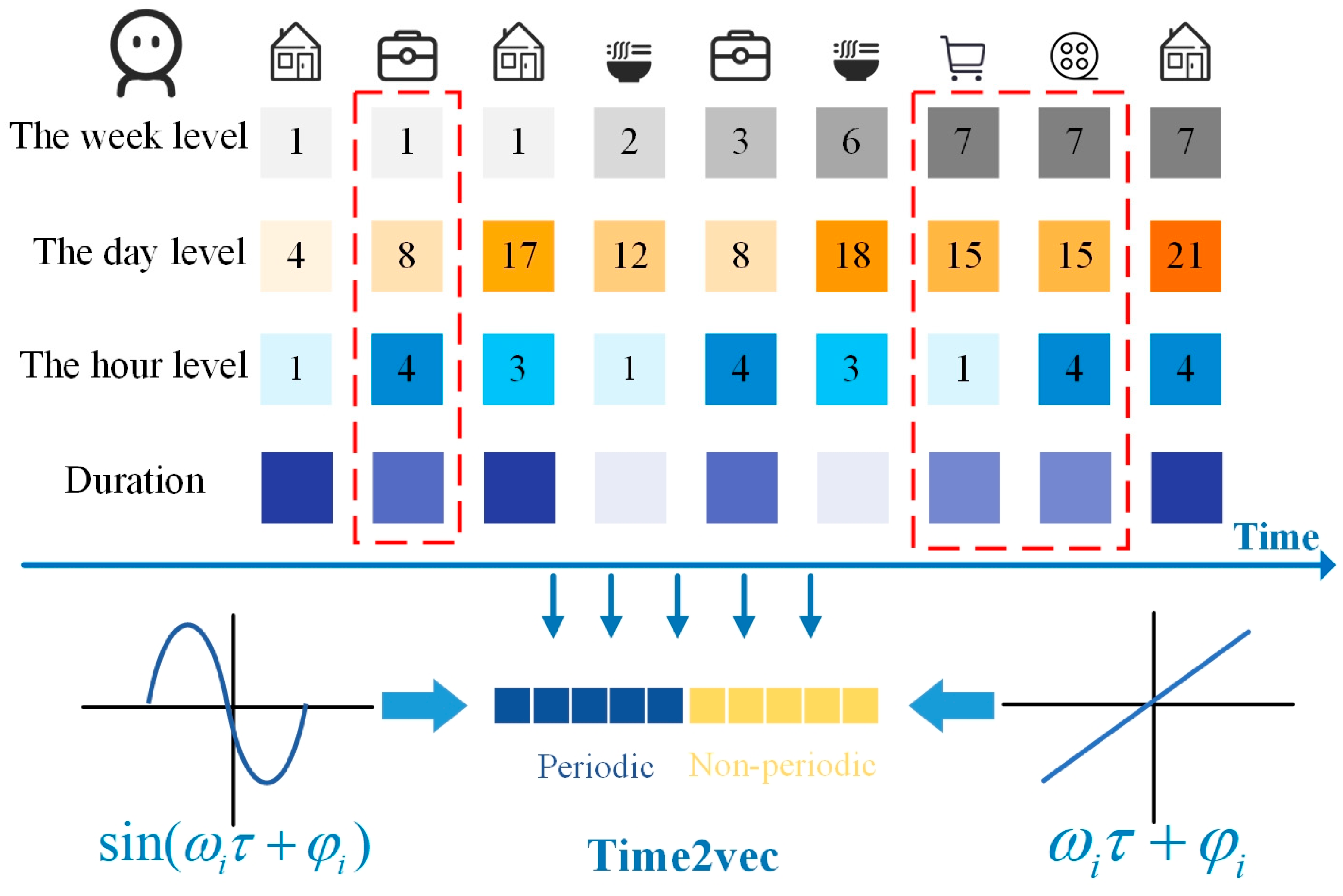
- We introduce a multi-granular enhanced temporal representation to capture complex temporal periodicity. Accurately modeling human mobility at different temporal granularities improves the model’s ability to learn temporal patterns;
- We design a travel semantic recognition mechanism based on rule inference. This mechanism effectively distinguishes the functional meaning of the same location for different individuals, improving the model’s ability to perceive individualized travel intentions;
- We develop a transformer-based framework to capture global context dependencies and design a gated residual network to efficiently integrate spatial–temporal contexts and user features, thereby enhancing the model’s ability to capture the diversity of human mobility patterns.
2. Related Work
2.1. Next Location Prediction Methods
2.2. Multi-View Learning for Next-Location Prediction
2.3. Challenges and Solutions
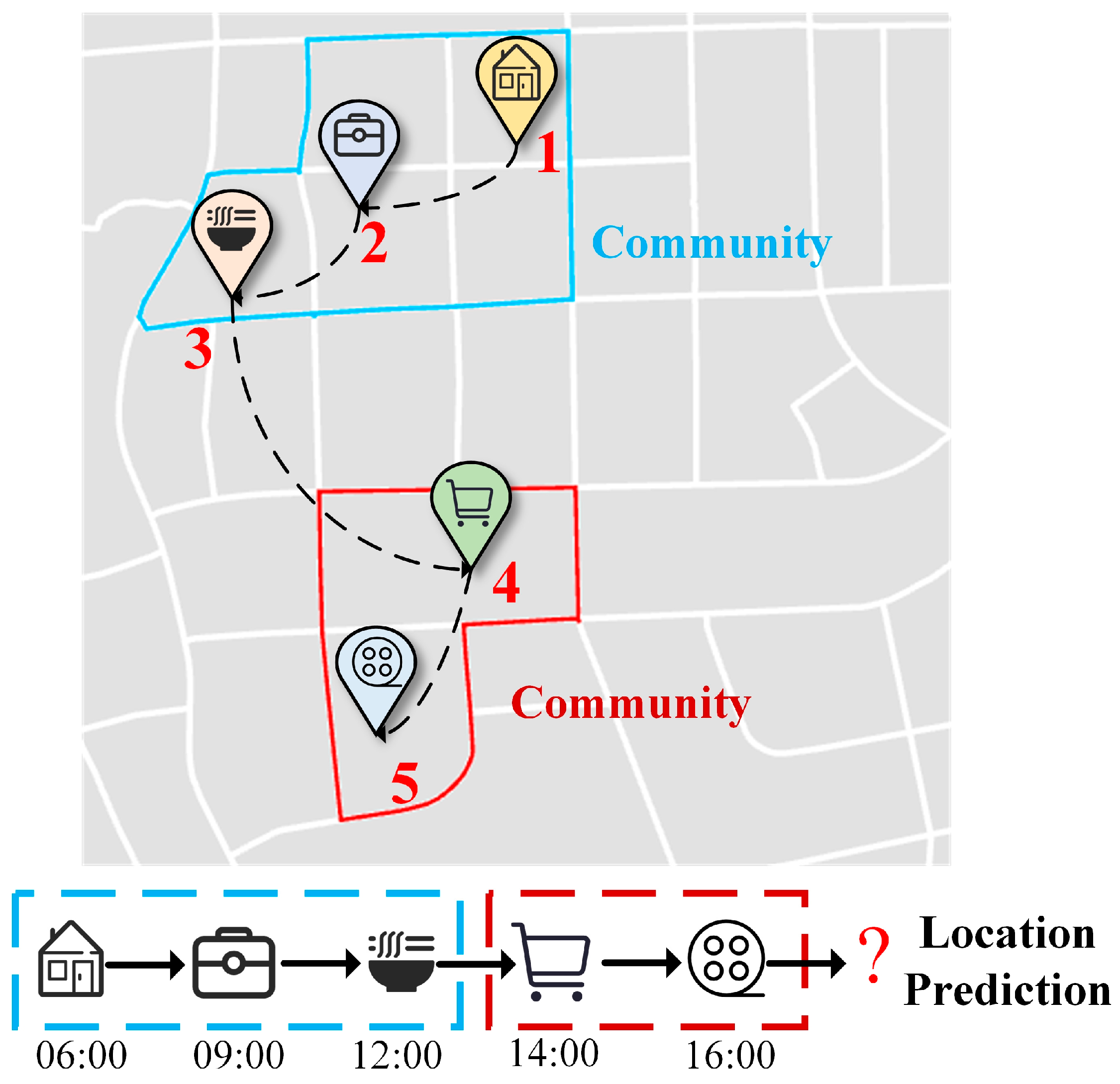
3. Problem Definition
4. Methodology
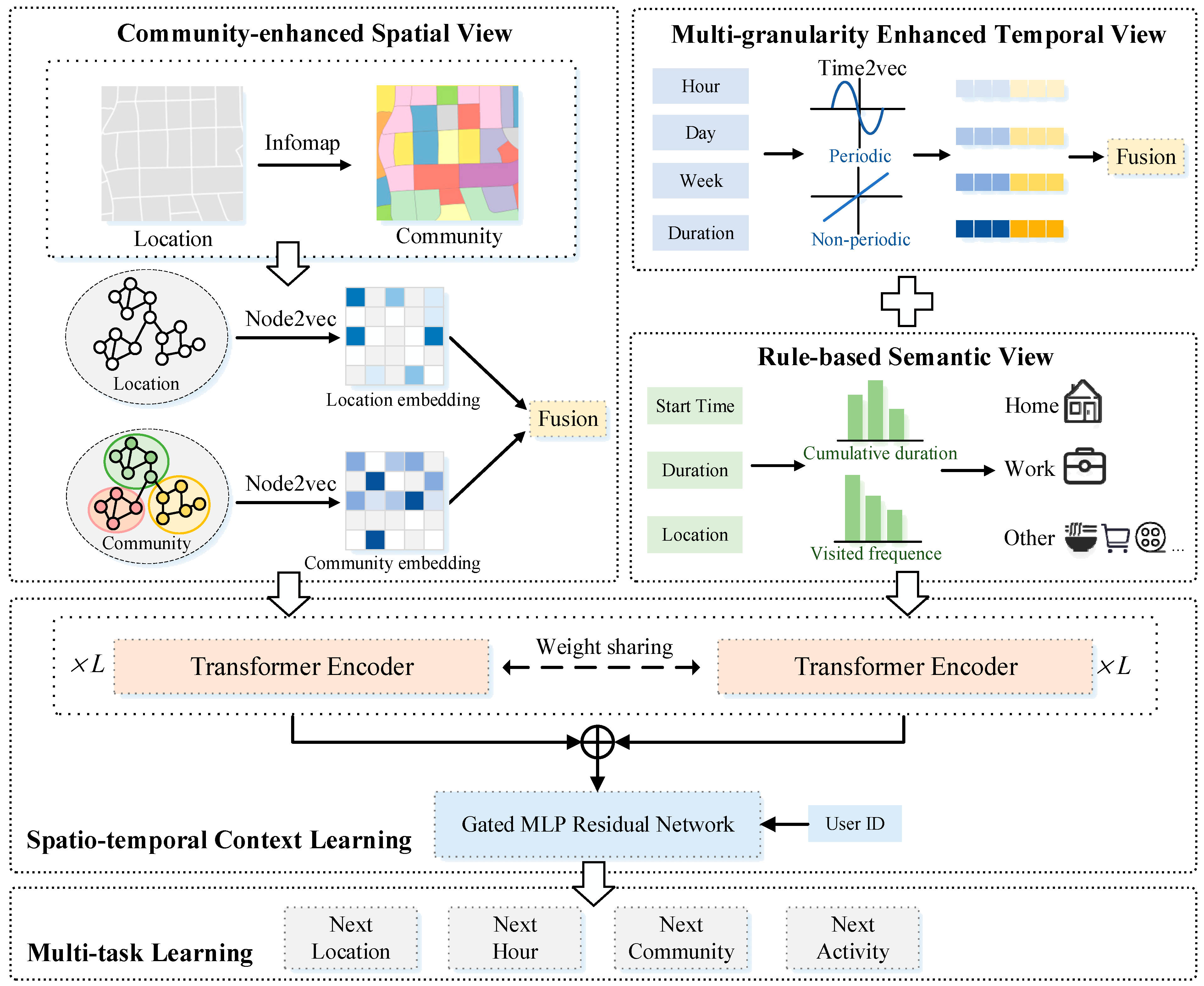
4.1. Overall Framework
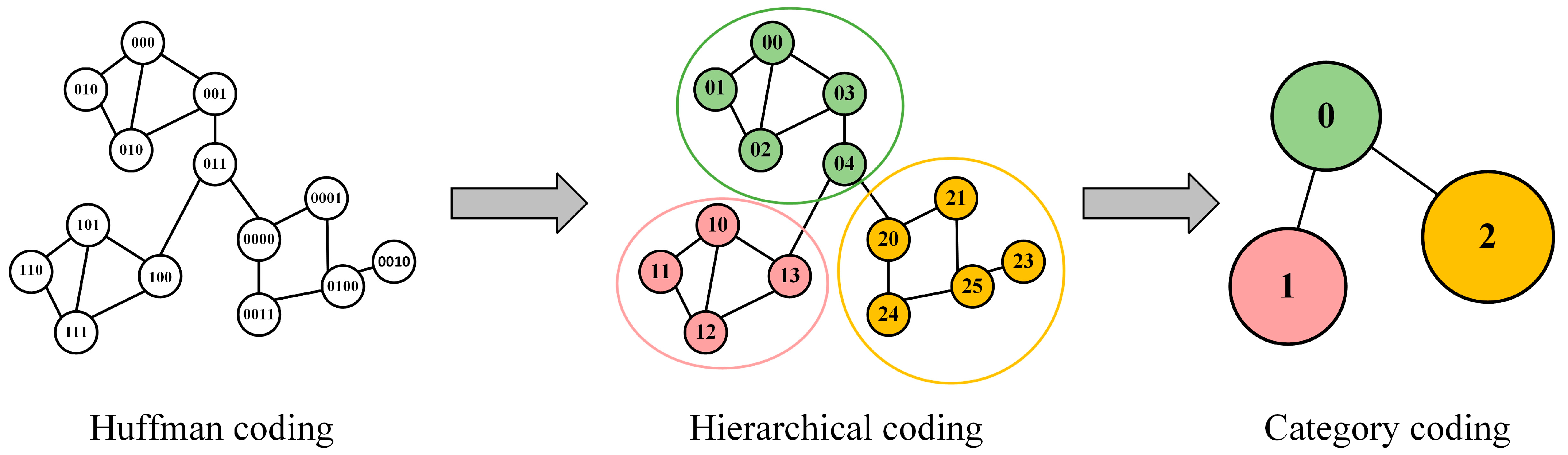
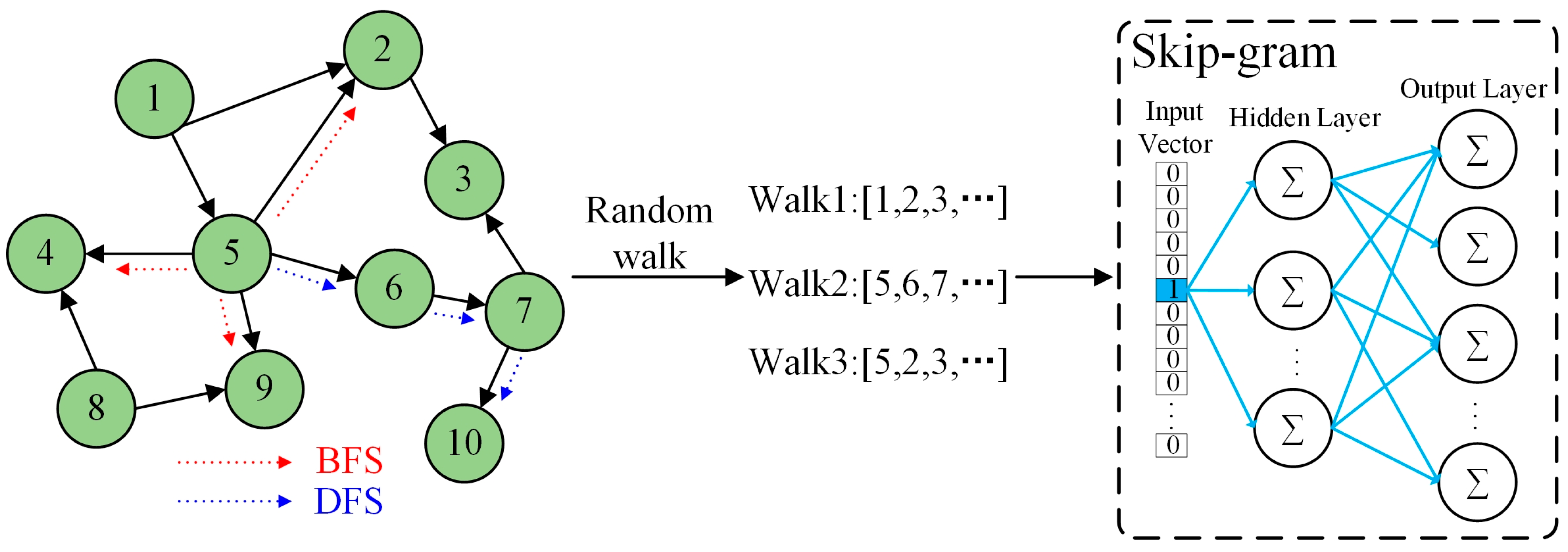
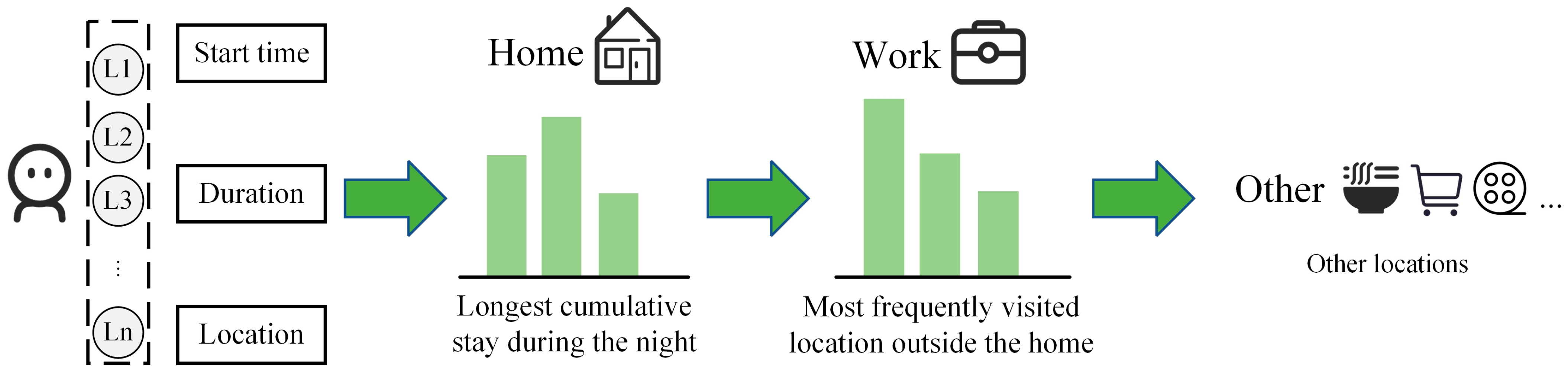
4.2. Community-Enhanced Spatial View
4.3. Multi-Granular Enhanced Temporal View
4.4. Rule-Based Semantic View
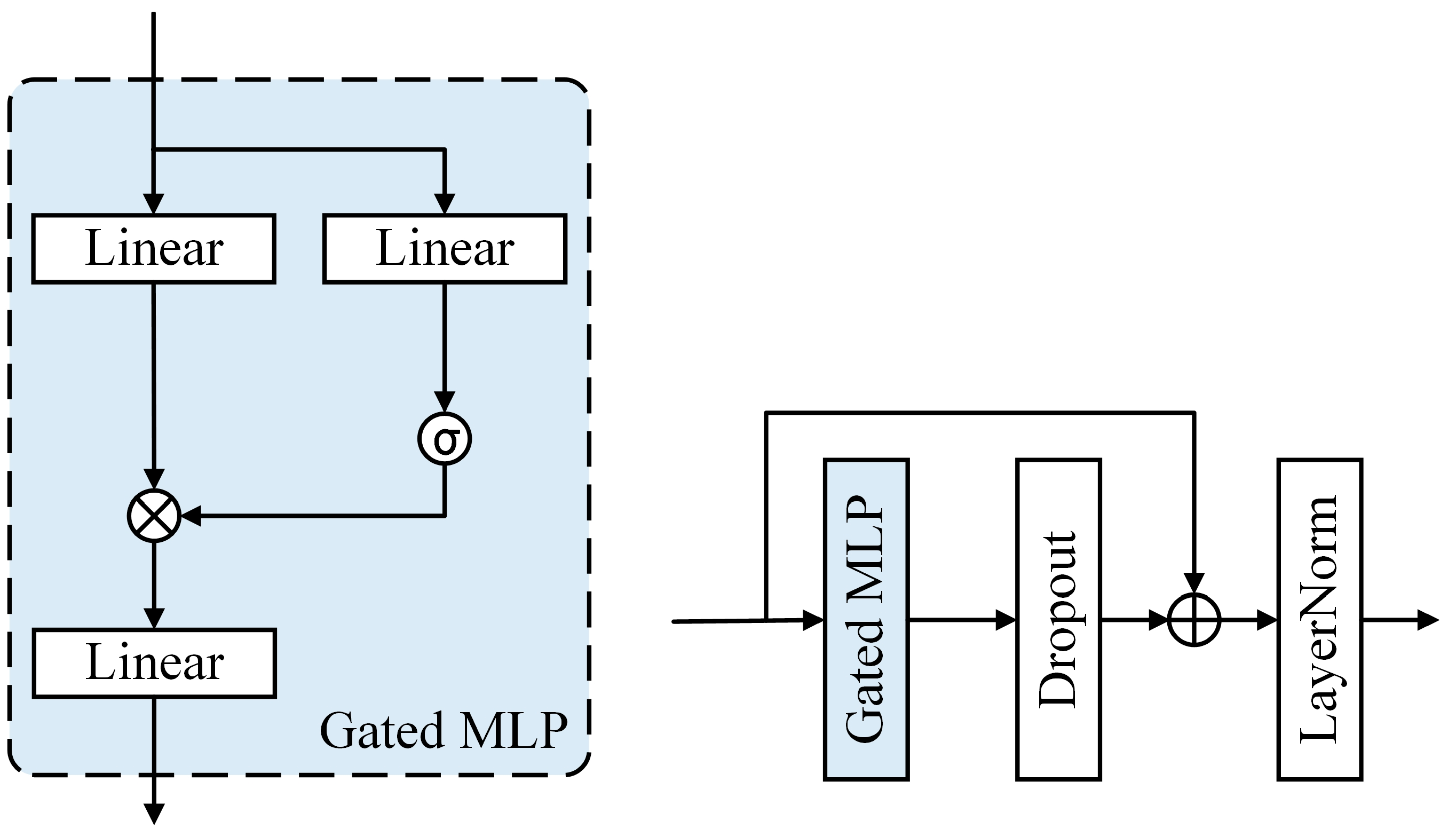
4.5. Spatiotemporal Context Learning
4.6. Multi-Task Learning
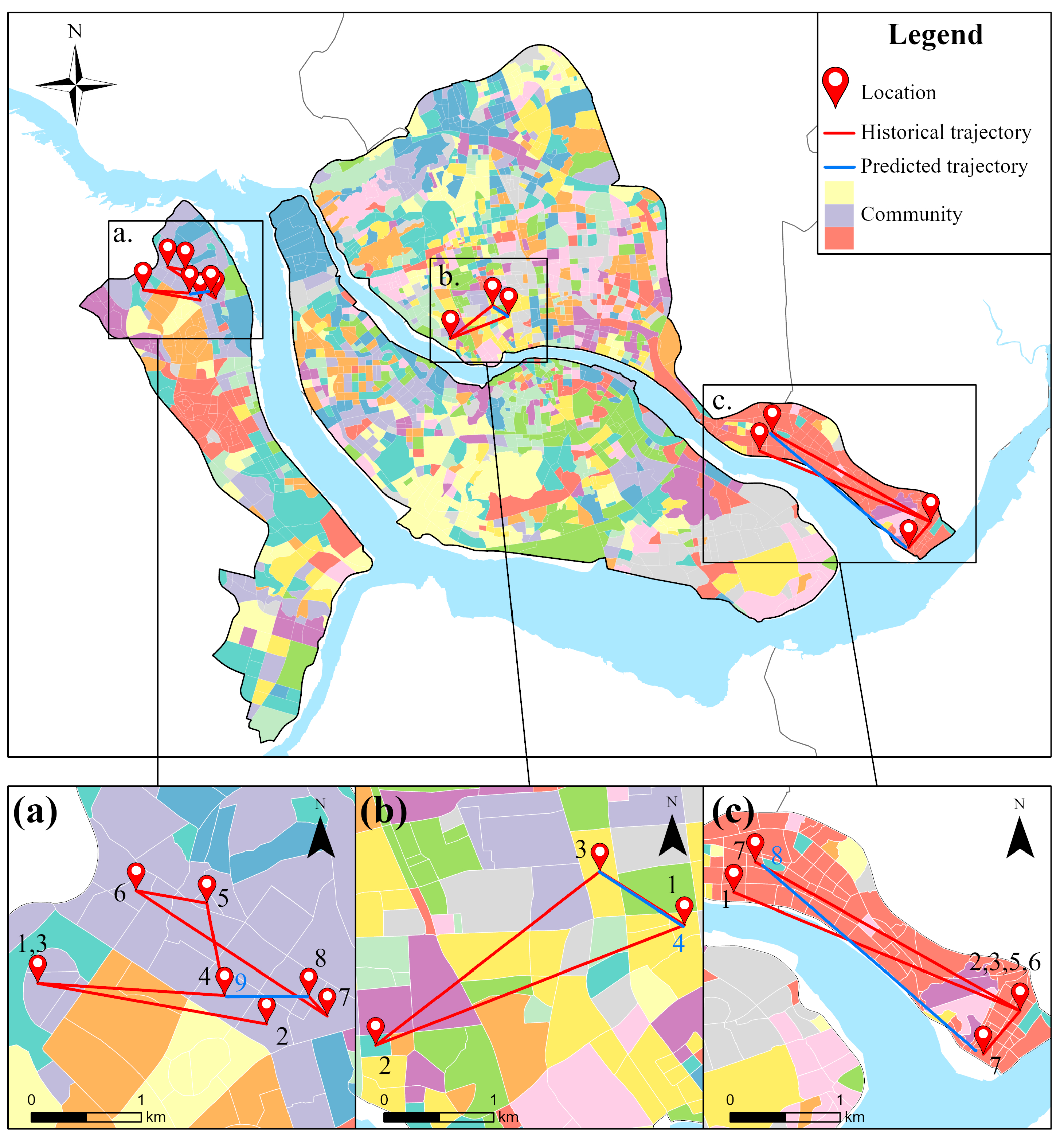
5. Experiment and Analysis
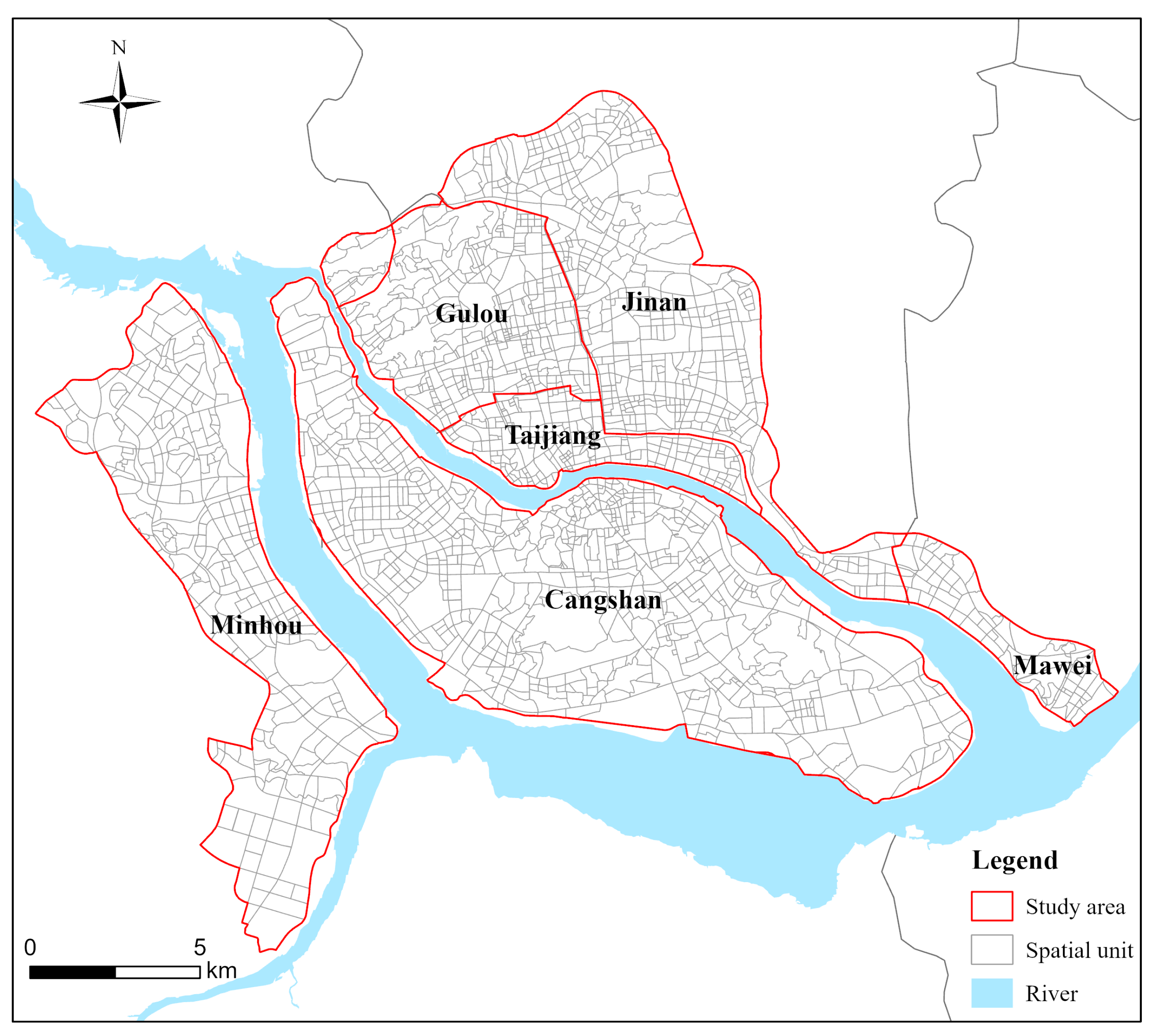
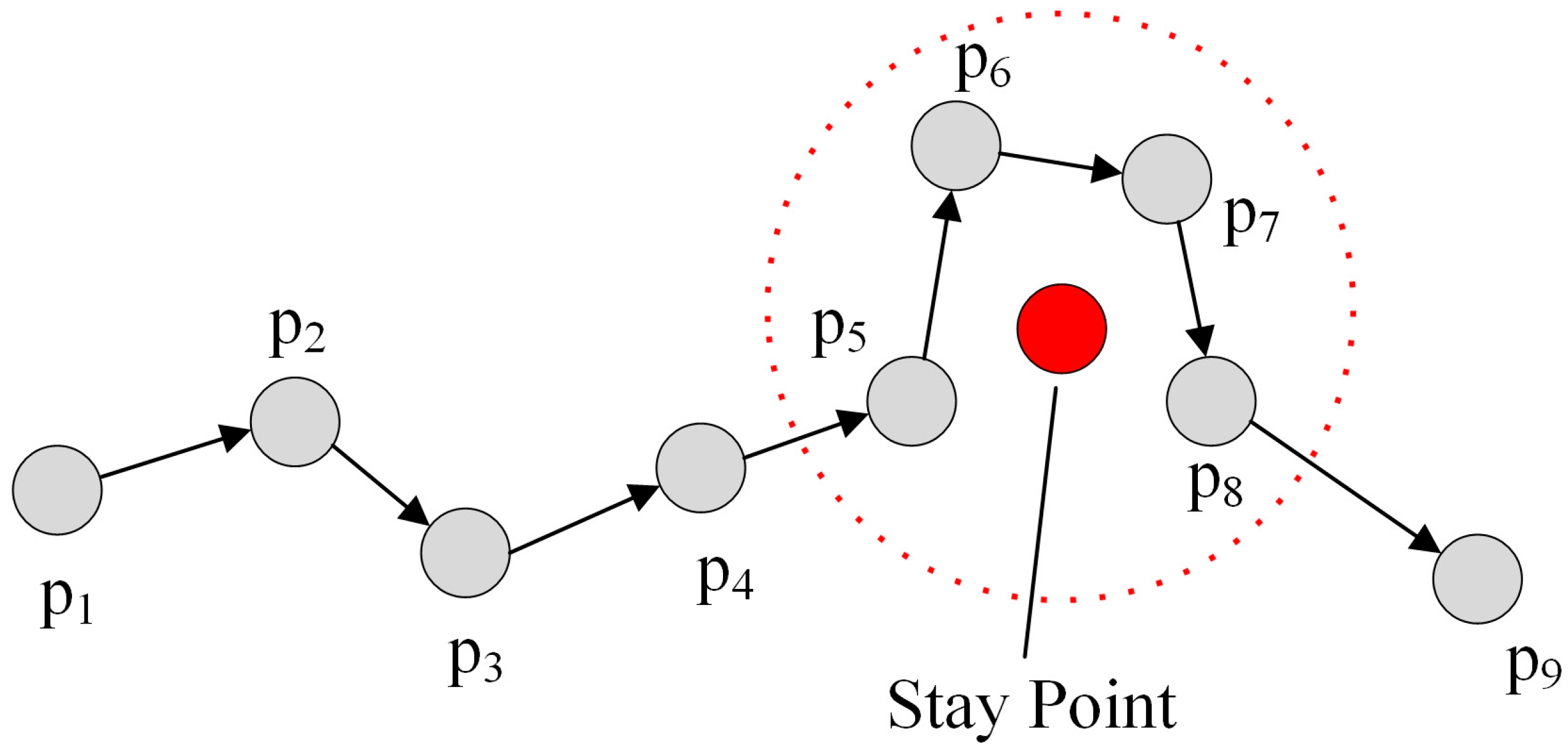
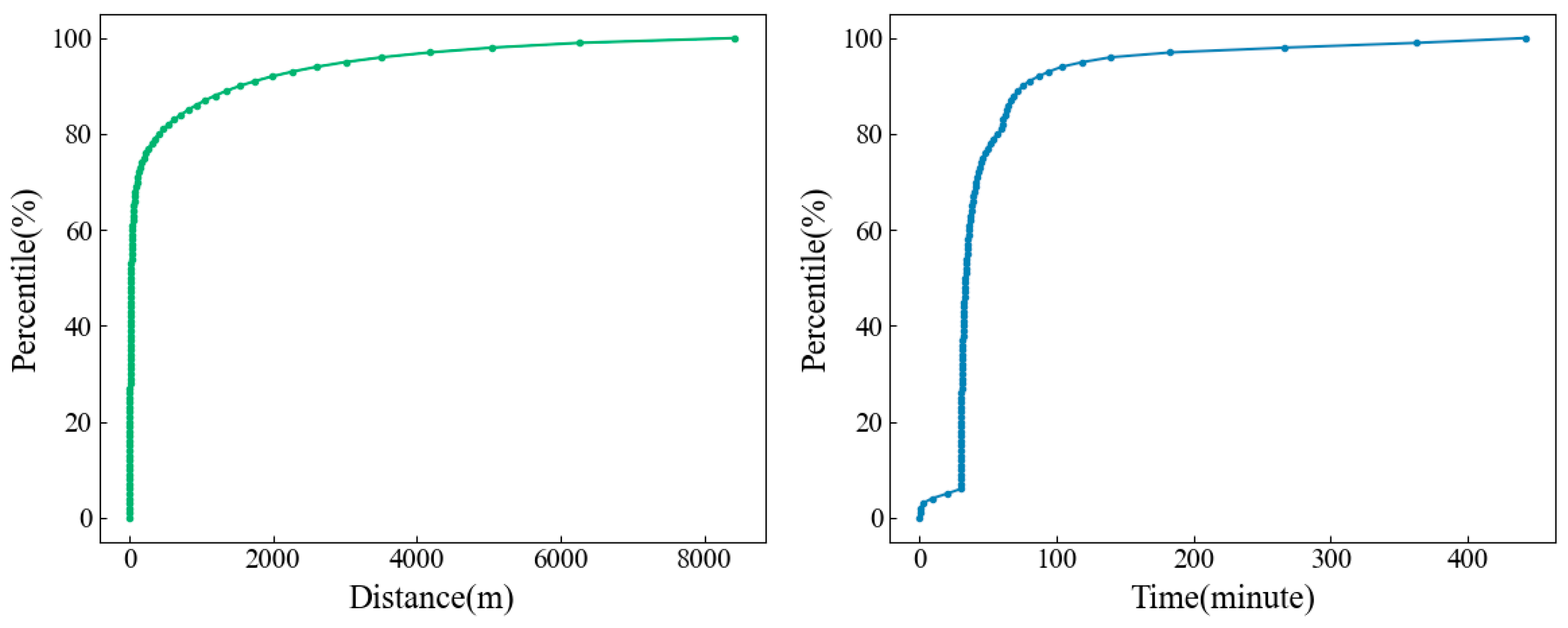
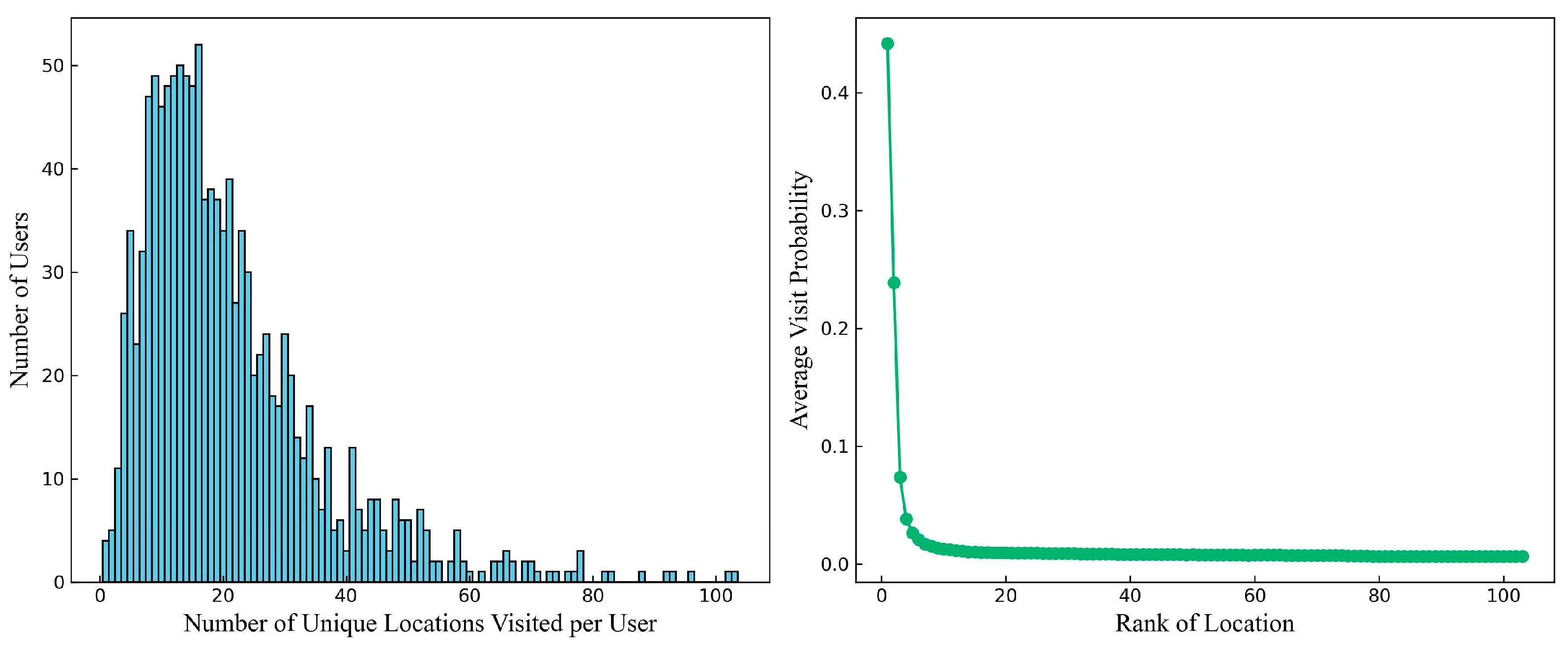
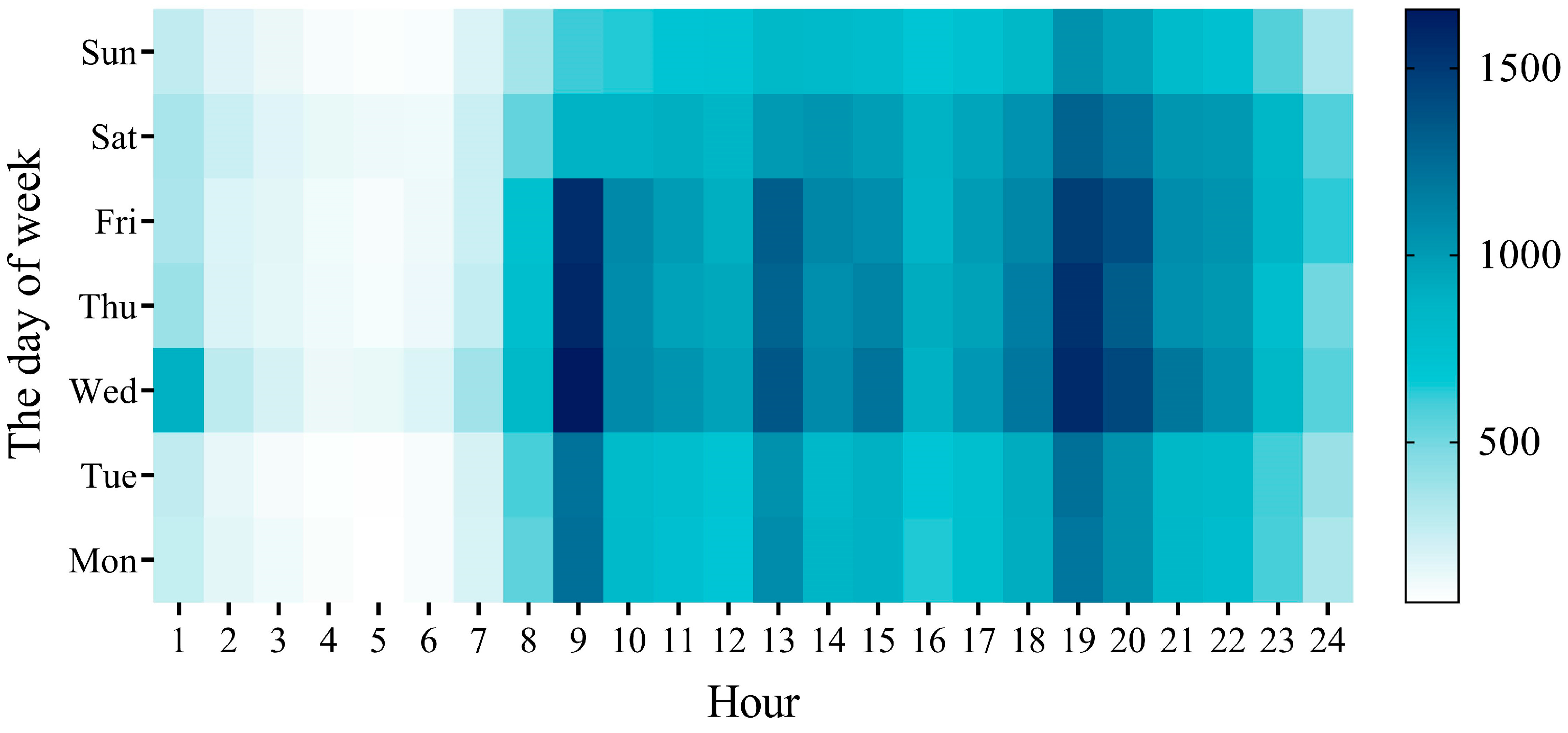
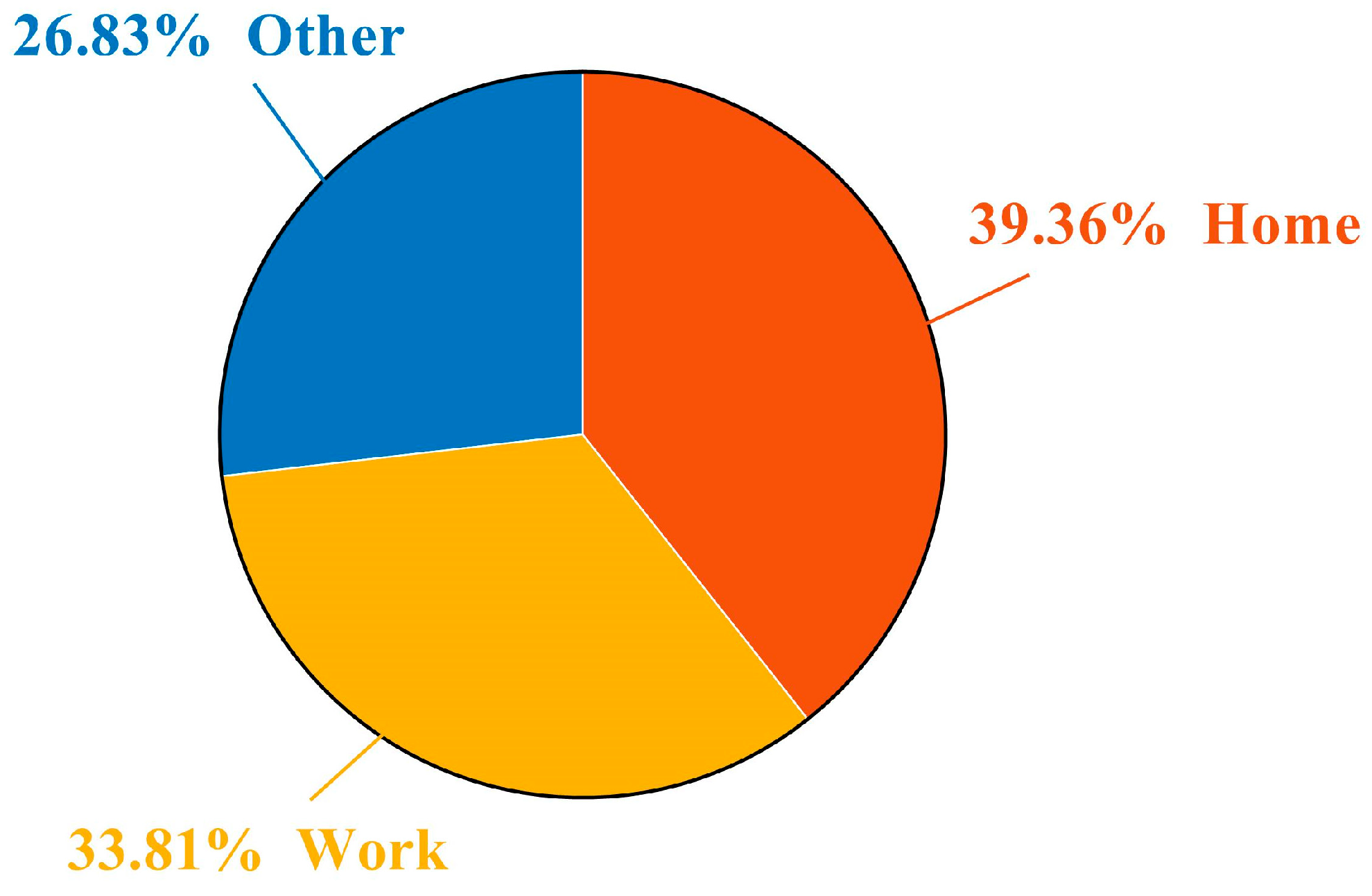
5.1. Study Area and Data
5.2. Comparison of Models
- Markov: This method treats locations as states and constructs a transition probability matrix to describe state transitions. It is a fundamental approach in location prediction;
- RNN: RNN utilizes the output of the previous time step as the input for the current time step, making it well suited for modeling sequential data. It is a widely used deep learning method;
- SERM [32]: Built on the LSTM framework, SERM integrates embeddings of location, temporal, semantics, and user ID to achieve multi-dimensional feature fusion;
- MSSRM [40]: This model enhances location prediction by combining LSTM with self-attention mechanisms. It employs Time2vec and Node2vec to embed temporal and spatial information, improving representation capability;
- MUPT [34]: This model leverages GGNN to learn expressive POI embeddings from a global trajectory graph and uses three dedicated transformer encoders to model temporal, categorical, and sequential user preferences;
- GetNext [33]: This model integrates a graph-enhanced transformer with global trajectory flow modeling. It fuses user preferences, spatiotemporal contexts, and time-aware category embeddings to capture collaborative signals across users;
- MHSA [21]: Based on the multi-head self-attention mechanism, MHSA learns location transition patterns from historical visits, multi-scale temporal features, activity duration, and surrounding land use, facilitating accurate location inference.
5.3. Evaluation Indicators
- Accuracy: Accuracy measures the agreement between the predicted and actual locations. In this study, Acc@K is used to represent the model’s prediction accuracy. Specifically, the model outputs a probability distribution over candidate locations, which is ranked in descending order. Acc@K determines whether the true location appears within the top K predictions. Acc@1 indicates whether the location with the highest probability is correct, while Acc@5 and Acc@10 assess whether the true location is included among the top five and top ten predictions, respectively. The accuracy is computed using the following formula:where represents the total number of test samples, denotes the actual location of the sample, and is the set of the top predicted candidate locations for the sample. The indicator function returns 1 if is included in , and 0 otherwise;
- Mean Reciprocal Rank (MRR): MRR measures the average of the reciprocal ranks of the correct predictions within the candidate outcomes. It evaluates the relative ranking of the actual location among the top K predicted results. A higher MRR value indicates a more accurate prediction. The calculation formula is as follows:where represents the position of the true location for the sample within the predicted candidate list;
- Normalized Discount Cumulative Gain (NDCG): NDCG evaluates both the relevance and ranking of predicted results. It first calculates the discounted cumulative gain (DCG) by applying a discount factor to the relevance score of each predicted outcome, reducing the influence of lower-ranked results. The DCG is then normalized using the ideal discounted cumulative gain (IDCG) to obtain the NDCG value, which ranges from 0 to 1. A value closer to 1 indicates better model performance. NDCG effectively captures the ranking capability of the model and the relevance of its predictions. The calculation formula is as follows:where evaluates the ranking quality of the model based on the top K predicted positions. In this study, NDCG@10 is used as the evaluation metric.
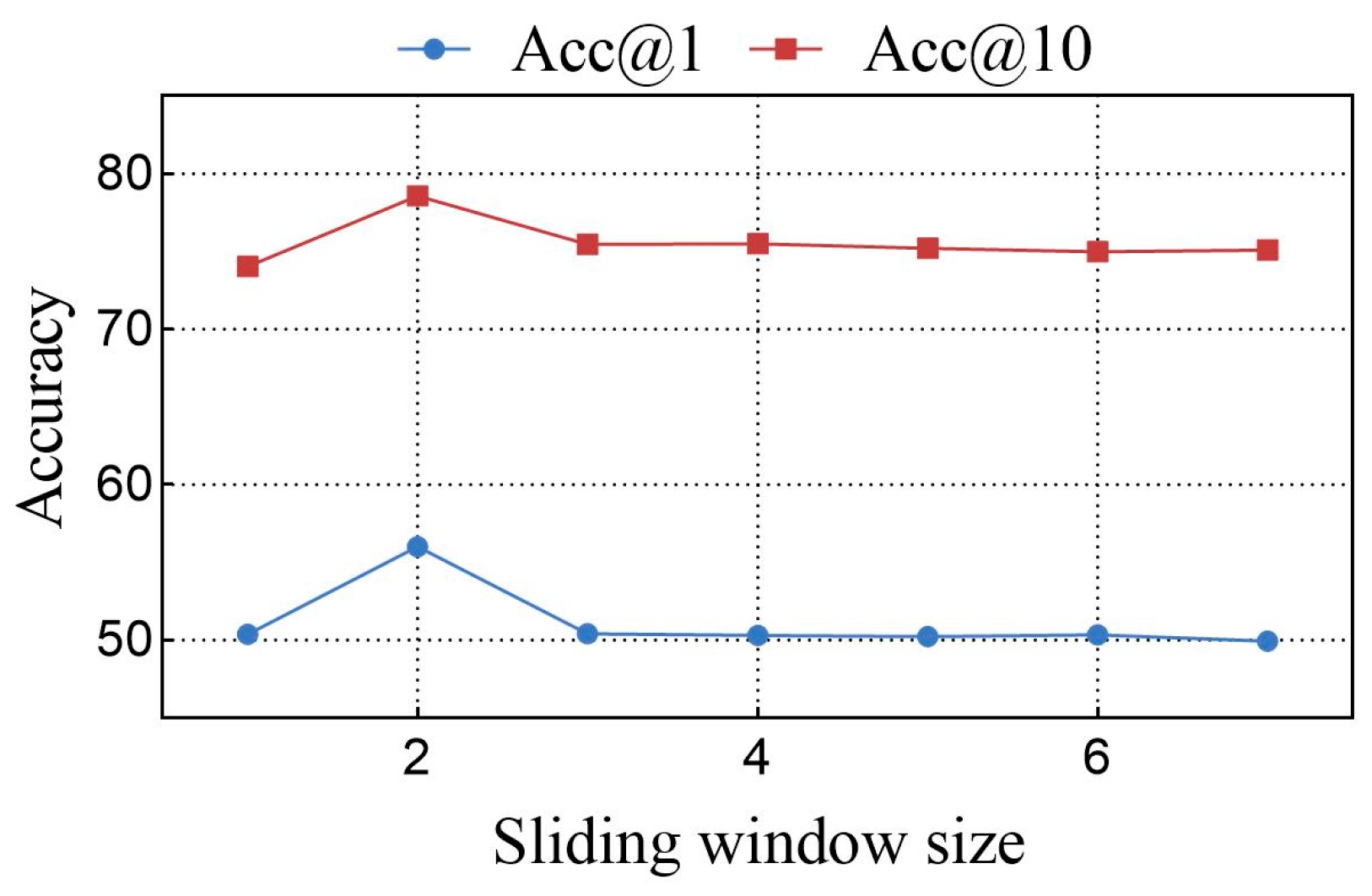
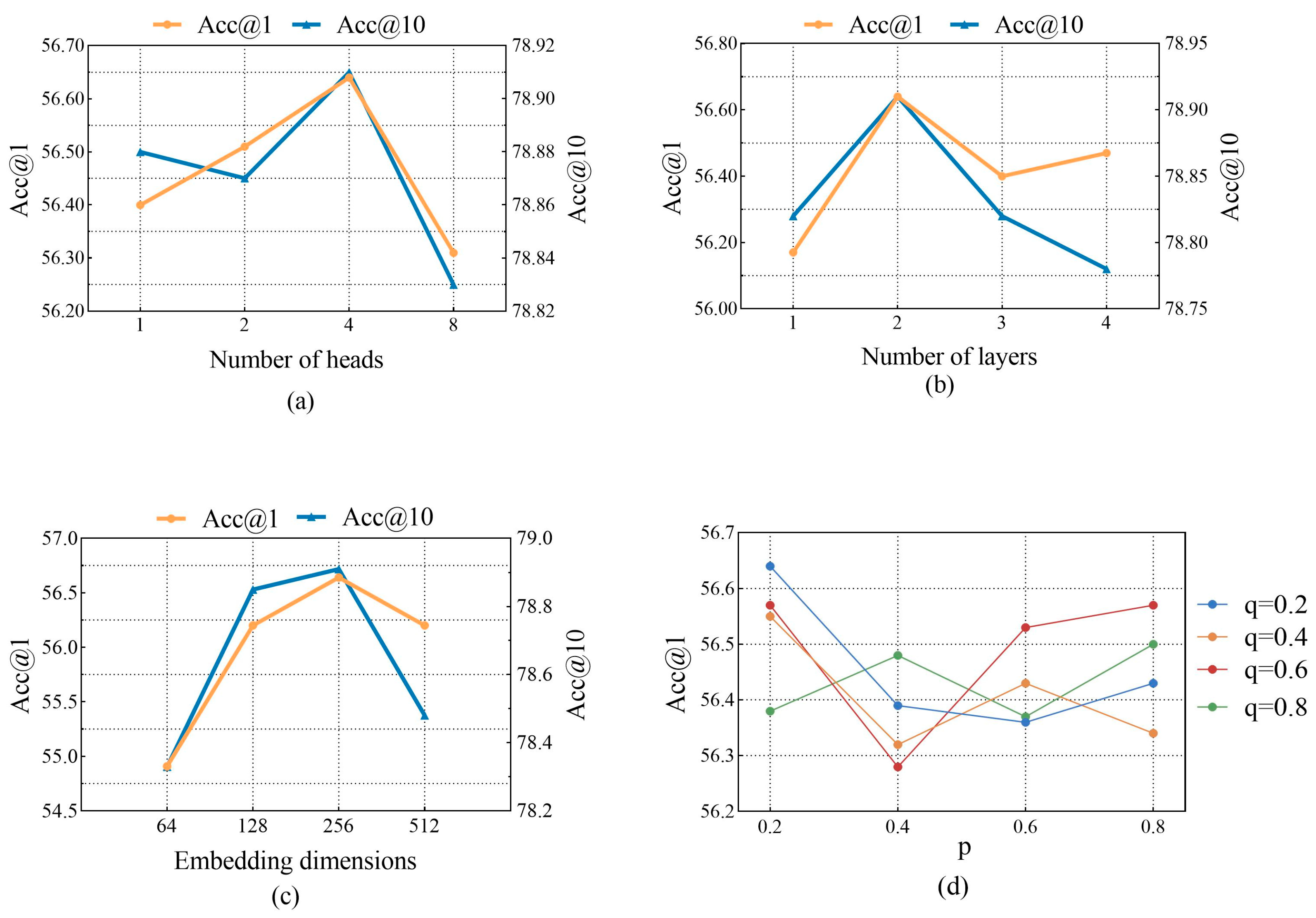
5.4. Hyperparameter Experiment
5.5. Performance Evaluation of Next Location Prediction
5.6. The Influence of Model Components
5.7. The Influence of Multi-Task Learning
5.8. The Influence of Spatiotemporal Context
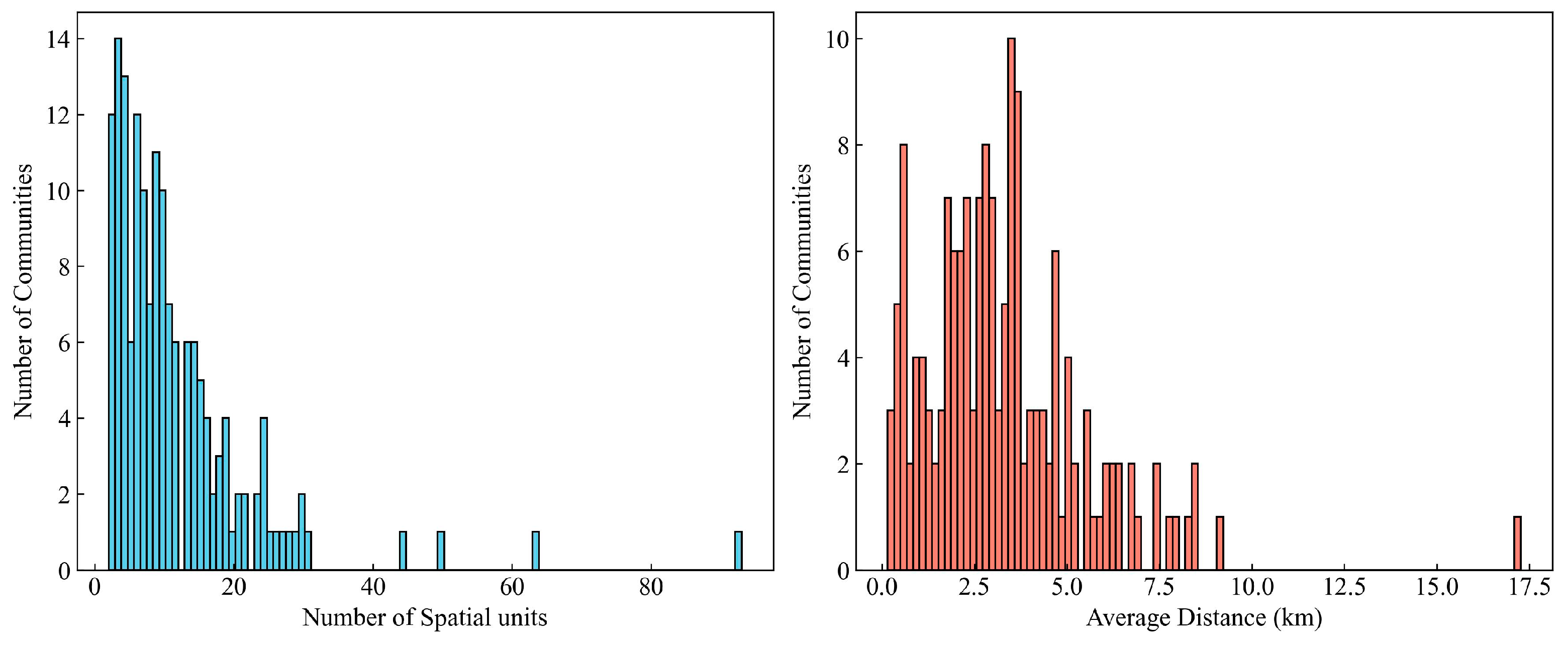
5.8.1. Influence of Community
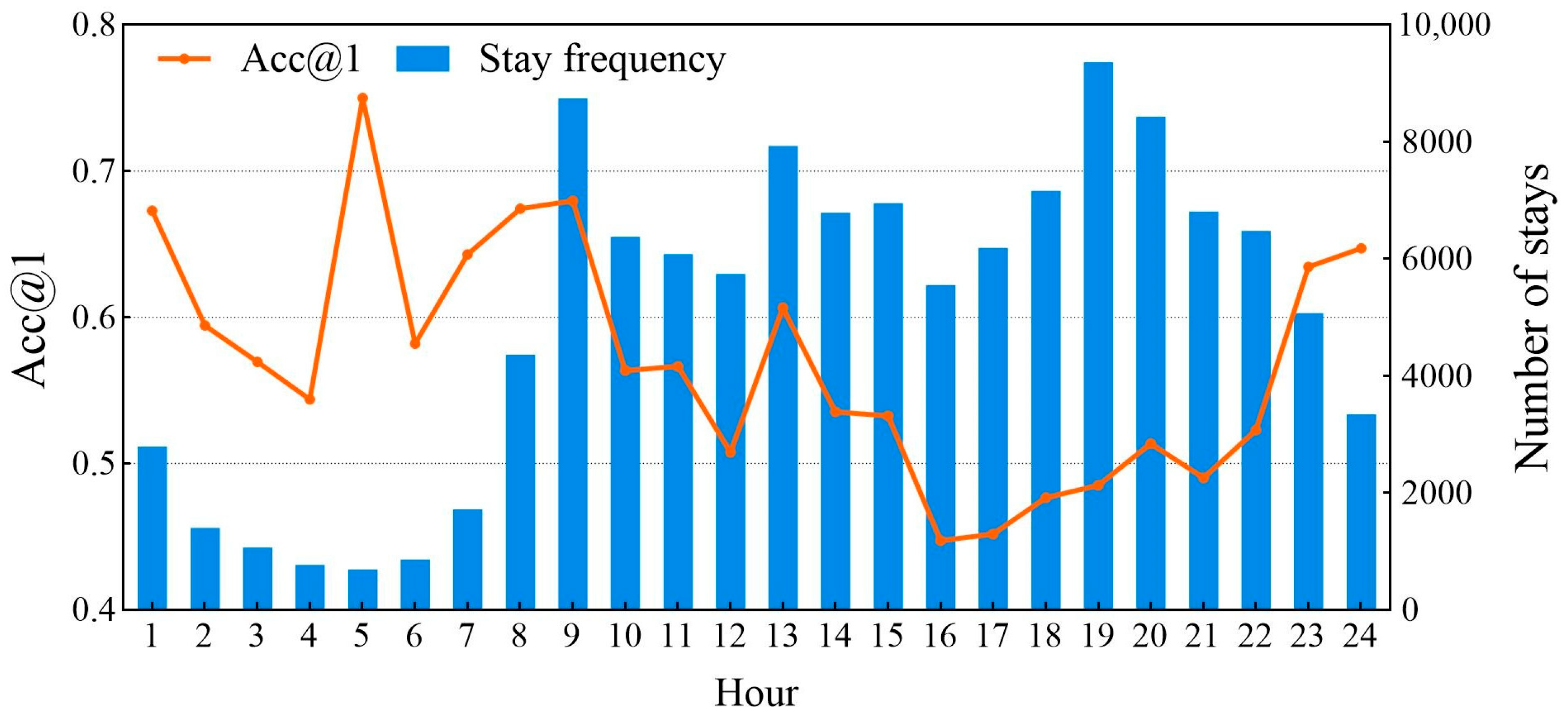
5.8.2. Influence of Temporal Features
5.8.3. Influence of Travel Semantics
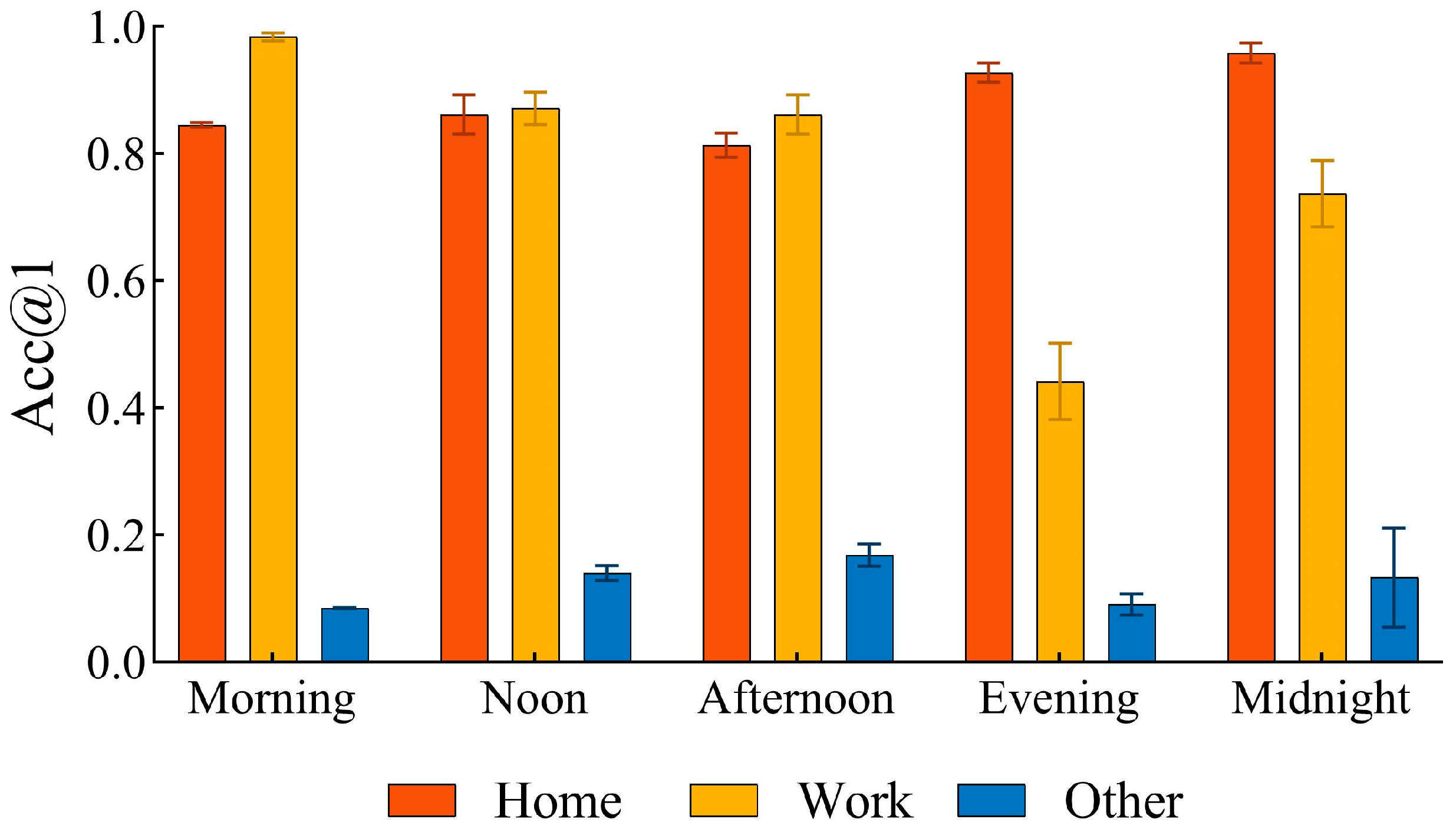
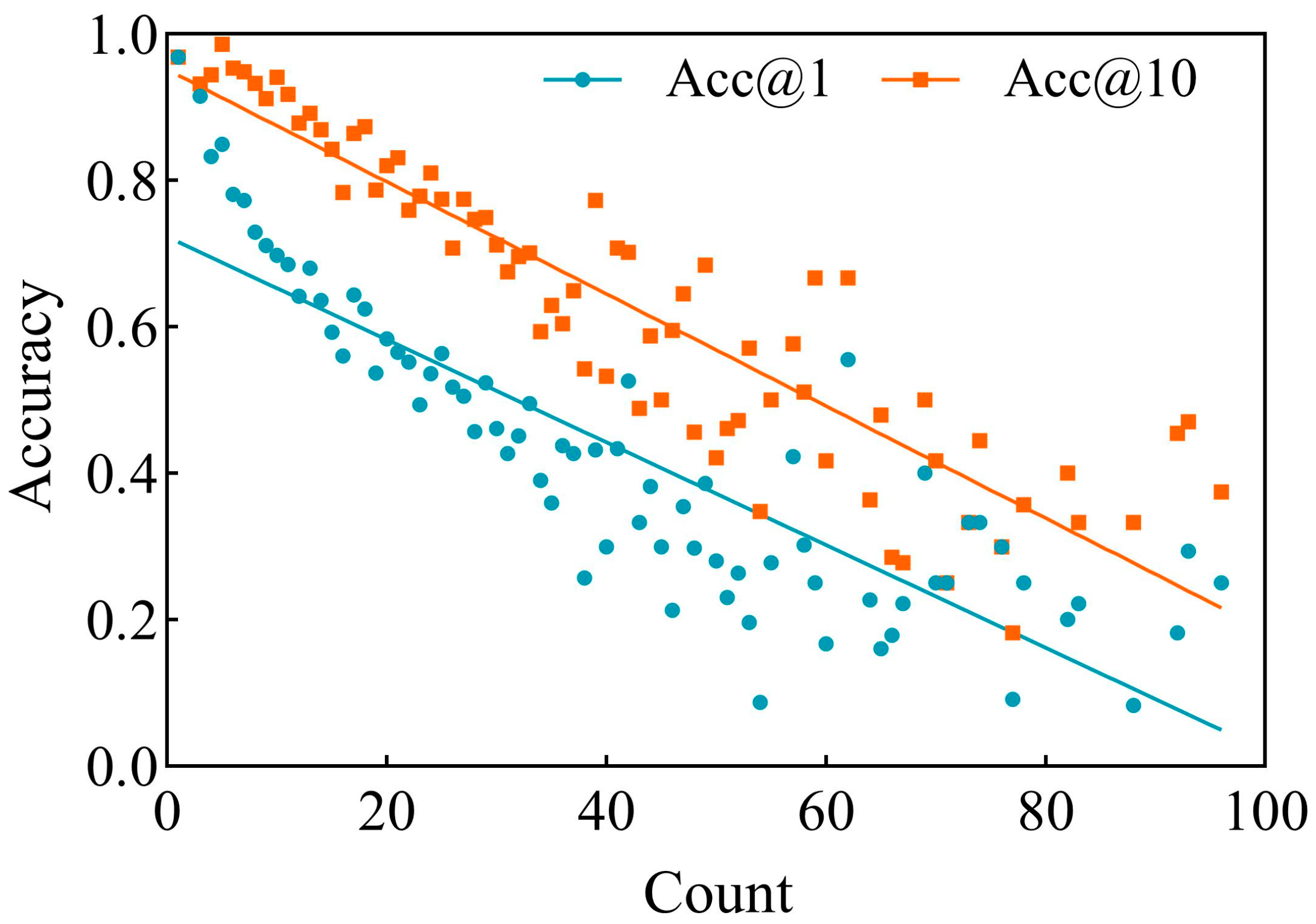
5.8.4. Influence of Individual
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marsico, G.J.C. The borderland. Cult. Psychol. 2016, 22, 206–215. [Google Scholar] [CrossRef]
- Yunshuo, L.; Jiaqi, Y.; Jun, X.; Xuyuan, G.; Jing, Z. High-dimensional urban dynamic patterns perception under the perspective of human activity semantics and spatiotemporal coupling. Sustain. Cities Soc. 2025, 121, 106192. [Google Scholar] [CrossRef]
- Ericsson. Smartphone Users Worldwide 2024 Statista. Available online: https://www.statista.com/statistics/330695/number-of-smartphone-users-worldwide/ (accessed on 6 March 2025).
- Song, C.; Qu, Z.; Blumm, N.; Barabási, A.-L. Limits of Predictability in Human Mobility. Science 2010, 327, 1018–1021. [Google Scholar] [CrossRef] [PubMed]
- González, M.C.; Hidalgo, C.A.; Barabási, A.-L. Understanding individual human mobility patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef]
- Tao, H.; Siqin, W.; Bing, S.; Mengxi, Z.; Xiao, H.; Yunhe, C.; Jacob, K.; Yaxin, H.; Xiaokang, F.; Xiaoyue, W.; et al. Human mobility data in the COVID-19 pandemic: Characteristics, applications, and challenges. Int. J. Digit. Earth 2021, 14, 1126–1147. [Google Scholar] [CrossRef]
- Xia, P.; Yue-yan, N.; Bin, M.; Yingchun, T.; Zhou, H. Big geo-data unveils influencing factors on customer flow dynamics within urban commercial districts. Int. J. Appl. Earth Obs. Geoinf. 2024, 134, 104231. [Google Scholar] [CrossRef]
- Almutairi, A.; Owais, M. Active Traffic Sensor Location Problem for the Uniqueness of Path Flow Identification in Large-Scale Networks. IEEE Access 2024, 12, 180385–180403. [Google Scholar] [CrossRef]
- Owais, M.; Shahin, A.I. Exact and heuristics algorithms for screen line problem in large size networks: Shortest path-based column generation approach. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24829–24840. [Google Scholar] [CrossRef]
- Owais, M. Deep learning for integrated origin–destination estimation and traffic sensor location problems. IEEE Trans. Intell. Transp. Syst. 2024, 25, 6501–6513. [Google Scholar] [CrossRef]
- Owais, M.; Moussa, G.S.; Hussain, K.F. Sensor location model for O/D estimation: Multi-criteria meta-heuristics approach. Oper. Res. Perspect. 2019, 6, 100100. [Google Scholar] [CrossRef]
- Yuhe, Z.; Guangfei, Y.; Bing, Y.; Yuanfeng, C.; Zhiguo, Z. Point-of-interest recommendation model considering strength of user relationship for location-based social networks. Expert Syst. Appl. 2022, 199, 117147. [Google Scholar] [CrossRef]
- Rendle, S.; Freudenthaler, C.; Schmidt-Thieme, L. Factorizing personalized Markov chains for next-basket recommendation. In Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010; pp. 811–820. [Google Scholar]
- Xu, S.; Huang, Q.; Zou, Z. Spatio-Temporal Transformer Recommender: Next Location Recommendation with Attention Mechanism by Mining the Spatio-Temporal Relationship between Visited Locations. ISPRS Int. J. Geo-Inf. 2023, 12, 79. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, L.; Ye, J.; Xu, C. MDLF: A Multi-View-Based Deep Learning Framework for Individual Trip Destination Prediction in Public Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2022, 23, 13316–13329. [Google Scholar] [CrossRef]
- Song, C.; Wen, J.; Li, S. Personalized POI recommendation based on check-in data and geographical-regional influence. In Proceedings of the 3rd International Conference on Machine Learning and Soft Computing, Da Lat, Vietnam, 25–28 January 2019; pp. 128–133. [Google Scholar]
- Sun, Z.; Lei, Y.; Zhang, L.; Li, C.; Ong, Y.-S.; Zhang, J. A Multi-channel Next POI Recommendation Framework with Multi-granularity Check-in Signals. ACM Trans. Inf. Syst. 2023, 42, 15. [Google Scholar] [CrossRef]
- Haifeng, Z.; Yajie, Y.; Ningbo, Z. Human Mobility Prediction Based on DBSCAN and RNN. In Proceedings of the 2021 IEEE 4th International Conference on Computer and Communication Engineering Technology (CCET), Beijing, China, 13–15 August 2021; pp. 146–152. [Google Scholar]
- Shengwen, L.; Renyao, C.; Chenpeng, S.; Hong, Y.; Xuyang, C.; Zhuoru, L.; Tailong, L.; Kang, X. Region-aware neural graph collaborative filtering for personalized recommendation. Int. J. Digit. Earth 2022, 15, 1446–1462. [Google Scholar] [CrossRef]
- Xu, C.; Li, F.; Xia, J. Fusing high-resolution multispectral image with trajectory for user next travel location prediction. Int. J. Appl. Earth Obs. Geoinf. 2023, 116, 103135. [Google Scholar] [CrossRef]
- Hong, Y.; Zhang, Y.; Schindler, K.; Raubal, M. Context-aware multi-head self-attentional neural network model for next location prediction. Transp. Res. Part C Emerg. Technol. 2023, 156, 104315. [Google Scholar] [CrossRef]
- Qiao, Y.; Si, Z.; Zhang, Y.; Abdesslem, F.B.; Zhang, X.; Yang, J. A hybrid Markov-based model for human mobility prediction. Neurocomputing 2018, 278, 99–109. [Google Scholar] [CrossRef]
- Ashbrook, D.; Starner, T. Learning significant locations and predicting user movement with GPS. In Proceedings of the Proceedings. Sixth International Symposium on Wearable Computers, Seattle, WA, USA, 10 October 2002; pp. 101–108. [Google Scholar] [CrossRef]
- Liu, Q.; Wu, S.; Wang, L.; Tan, T. Predicting the Next Location: A Recurrent Model with Spatial and Temporal Contexts. Proc. AAAI Conf. Artif. Intell. 2016, 30, 194–200. [Google Scholar] [CrossRef]
- Choi, S.; Yeo, H.; Kim, J. Network-Wide Vehicle Trajectory Prediction in Urban Traffic Networks using Deep Learning. Transp. Res. Rec. 2018, 2672, 173–184. [Google Scholar] [CrossRef]
- Endo, Y.; Nishida, K.; Toda, H.; Sawada, H. Predicting Destinations from Partial Trajectories Using Recurrent Neural Network. In Proceedings of the Advances in Knowledge Discovery and Data Mining. PAKDD 2017, Jeju, Republic of Korea, 23–26 May 2017; Springer: Cham, Switzerland, 2017; Volume 10234, pp. 160–172. [Google Scholar]
- Feng, J.; Li, Y.; Zhang, C.; Sun, F.; Meng, F.; Guo, A.; Jin, D. DeepMove: Predicting Human Mobility with Attentional Recurrent Networks. In Proceedings of the 2018 World Wide Web Conference, Lyon, France, 23–27 April 2018; pp. 1459–1468. [Google Scholar]
- Kong, X.; Chen, Z.; Li, J.; Bi, J.; Shen, G. Kgnext: Knowledge-graph-enhanced transformer for next poi recommendation with uncertain check-ins. IEEE Trans. Comput. Soc. Syst. 2024, 11, 6637–6648. [Google Scholar] [CrossRef]
- Zhi, L.; Deju, Z.; Chenwei, Z.; Jixin, B.; Junhui, D.; Guojiang, S.; Xiangjie, K. KDRank: Knowledge-driven user-aware POI recommendation. Knowl.-Based Syst. 2023, 278, 110884. [Google Scholar] [CrossRef]
- Seongjin, C.; Jiwon, K.; Hwasoo, Y. Attention-based Recurrent Neural Network for Urban Vehicle Trajectory Prediction. Procedia Comput. Sci. 2019, 151, 327–334. [Google Scholar] [CrossRef]
- Tsiligkaridis, A.; Zhang, J.; Taguchi, H.; Nikovski, D. Personalized Destination Prediction Using Transformers in a Contextless Data Setting. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–7. [Google Scholar]
- Yao, D.; Zhang, C.; Huang, J.; Bi, J. SERM: A Recurrent Model for Next Location Prediction in Semantic Trajectories. In Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, Singapore, 6–10 November 2017; pp. 2411–2414. [Google Scholar]
- Yang, S.; Liu, J.; Zhao, K. GETNext: Trajectory Flow Map Enhanced Transformer for Next POI Recommendation. In Proceedings of the SIGIR’22: Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval, Madrid Spain, 11–15 July 2022; pp. 1144–1153. [Google Scholar]
- Zheng, Y.; Zhou, X. Modeling multi-factor user preferences based on Transformer for next point of interest recommendation. Expert Syst. Appl. 2024, 255, 124894. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, G. Revealing the Spatio-Temporal Heterogeneity of the Association between the Built Environment and Urban Vitality in Shenzhen. ISPRS Int. J. Geo-Inf. 2023, 12, 433. [Google Scholar] [CrossRef]
- Jingwei, S.; Huiming, Z.; Chen, M. Identifying city communities in China by fusing multisource flow data. Int. J. Digit. Earth 2023, 16, 4247–4264. [Google Scholar] [CrossRef]
- Yuan, Q.; Cong, G.; Ma, Z.; Sun, A.; Thalmann, N.M. Time-aware point-of-interest recommendation. In Proceedings of the 36th International ACM SIGIR Conference on Research and Development in Information Retrieval, Dublin, Ireland, 28 July–1 August 2013; pp. 363–372. [Google Scholar]
- Gao, H.; Tang, J.; Hu, X.; Liu, H. Exploring temporal effects for location recommendation on location-based social networks. In Proceedings of the 7th ACM conference on Recommender Systems, Hong Kong, China, 12–16 October 2013; pp. 93–100. [Google Scholar]
- Luo, Y.; Liu, Q.; Liu, Z. STAN: Spatio-Temporal Attention Network for Next Location Recommendation. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 2177–2185. [Google Scholar]
- Wen, S.; Zhang, X.; Cao, R.; Li, B.; Li, Y. MSSRM: A Multi-Embedding Based Self-Attention Spatio-temporal Recurrent Model for Human Mobility Prediction. Hum.-Centric Comput. Inf. Sci. 2021, 11, 37. [Google Scholar] [CrossRef]
- Li, S.; Peter, R.S. A process for trip purpose imputation from Global Positioning System data. Transp. Res. Part C Emerg. Technol. 2013, 36, 261–267. [Google Scholar] [CrossRef]
- Yao, Y.; Guo, Z.; Dou, C.; Jia, M.; Hong, Y.; Guan, Q.; Luo, P. Predicting mobile users’ next location using the semantically enriched geo-embedding model and the multilayer attention mechanism. Comput. Environ. Urban Syst. 2023, 104, 102009. [Google Scholar] [CrossRef]
- Rosvall, M.; Bergstrom, C.T. Maps of random walks on complex networks reveal community structure. Proc. Natl. Acad. Sci. USA 2008, 105, 1118–1123. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.-L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Kazemi, S.M.; Goel, R.; Eghbali, S.; Ramanan, J.; Sahota, J.; Thakur, S.; Wu, S.; Smyth, C.; Poupart, P.; Brubaker, M. Time2Vec: Learning a Vector Representation of Time. arXiv 2019, arXiv:1907.05321. [Google Scholar] [CrossRef]
- Hasan, S.; Schneider, C.M.; Ukkusuri, S.V.; González, M.C. Spatiotemporal Patterns of Urban Human Mobility. J. Stat. Phys. 2013, 151, 304–318. [Google Scholar] [CrossRef]
- Jiang, S.; Ferreira, J.; González, M.C. Clustering daily patterns of human activities in the city. Data Min. Knowl. Discov. 2012, 25, 478–510. [Google Scholar] [CrossRef]
- Liu, K.; Jin, X.; Cheng, S.; Gao, S.; Yin, L.; Lu, F. Act2Loc: A synthetic trajectory generation method by combining machine learning and mechanistic models. Int. J. Geogr. Inf. Sci. 2024, 38, 407–431. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Lu, E.H.-C.; Lin, Y.-R. A Self-Attention Model for Next Location Prediction Based on Semantic Mining. ISPRS Int. J. Geo-Inf. 2023, 12, 420. [Google Scholar] [CrossRef]
- Ye, Y.; Zheng, Y.; Chen, Y.; Feng, J.; Xie, X. Mining Individual Life Pattern Based on Location History. In Proceedings of the 2009 Tenth International Conference on Mobile Data Management: Systems, Services and Middleware, Taipei, China, 18–20 May 2009; pp. 1–10. [Google Scholar]
| User ID | Longitude | Latitude |
|---|---|---|
| 0000269a***292c0c | 119.30889 | 26.112497 |
| 00007ebc***5cdc7c | 119.18924 | 26.068150 |
| … | … | … |
| 00002edc***8ef30a | 119.25607 | 26.109436 |
| Model | Acc@1 | Acc@5 | Acc@10 | MRR | NDCG@10 |
|---|---|---|---|---|---|
| Markov | 42.30 | 59.11 | 61.14 | 49.59 | 52.40 |
| RNN | 46.64 ± 0.23 | 69.32 ± 0.25 | 73.90 ± 0.15 | 56.97 ± 0.18 | 60.75 ± 0.18 |
| SERM | 50.65 ± 0.16 | 73.76 ± 0.21 | 77.50 ± 0.21 | 60.97 ± 0.05 | 64.77 ± 0.06 |
| MSSRM | 53.73 ± 0.12 | 73.51 ± 0.13 | 77.42 ± 0.14 | 62.70 ± 0.10 | 66.00 ± 0.09 |
| MUPT | 53.72 ± 0.25 | 72.34 ± 0.07 | 75.86 ± 0.17 | 62.20 ± 0.16 | 65.26 ± 0.15 |
| MHSA | 53.86 ± 0.10 | 74.16 ± 0.24 | 78.02 ± 0.13 | 62.94 ± 0.08 | 66.36 ± 0.05 |
| GetNext | 55.02 ± 0.18 | 73.41 ± 0.15 | 77.62 ± 0.09 | 63.37 ± 0.08 | 66.53 ± 0.06 |
| ReMVL-Net | 56.64 ± 0.14 | 74.82 ± 0.07 | 78.91 ± 0.18 | 64.90 ± 0.11 | 68.01 ± 0.12 |
| Model | Acc@1 | Acc@5 | Acc@10 | MRR | NDCG@10 |
|---|---|---|---|---|---|
| Full | 56.64 ± 0.14 | 74.82 ± 0.07 | 78.91 ± 0.18 | 64.90 ± 0.11 | 68.01 ± 0.12 |
| w/o Transformer | 56.17 ± 0.08 | 74.62 ± 0.10 | 78.54 ± 0.17 | 64.55 ± 0.08 | 67.67 ± 0.10 |
| w/o Gated MLP | 52.59 ± 0.36 | 71.93 ± 0.26 | 76.18 ± 0.11 | 61.49 ± 0.29 | 64.70 ± 0.24 |
| w/o Node2vec | 56.27 ± 0.08 | 74.75 ± 0.08 | 78.73 ± 0.14 | 64.68 ± 0.07 | 67.81 ± 0.09 |
| w/o Time2vec | 56.31 ± 0.18 | 74.70 ± 0.13 | 78.71 ± 0.16 | 64.68 ± 0.12 | 67.80 ± 0.12 |
| Model | Acc@1 | Acc@5 | Acc@10 | MRR | NDCG@10 |
|---|---|---|---|---|---|
| Full | 56.64 ± 0.14 | 74.82 ± 0.07 | 78.91 ± 0.18 | 64.90 ± 0.11 | 68.01 ± 0.12 |
| w/o Time | 55.05 ± 0.10 | 74.80 ± 0.15 | 78.89 ± 0.07 | 64.01 ± 0.08 | 67.36 ± 0.08 |
| w/o Act | 56.20 ± 0.23 | 74.78 ± 0.16 | 78.85 ± 0.10 | 64.67 ± 0.13 | 67.82 ± 0.10 |
| w/o Com | 56.44 ± 0.14 | 74.61 ± 0.04 | 78.84 ± 0.12 | 64.73 ± 0.11 | 67.87 ± 0.11 |
| Model | Acc@1 | Acc@5 | Acc@10 | MRR | NDCG@10 |
|---|---|---|---|---|---|
| Full | 56.64 ± 0.14 | 74.82 ± 0.07 | 78.91 ± 0.18 | 64.90 ± 0.11 | 68.01 ± 0.12 |
| w/o Week | 56.51 ± 0.18 | 74.65 ± 0.10 | 78.80 ± 0.10 | 64.80 ± 0.12 | 67.91 ± 0.07 |
| w/o Day | 53.53 ± 0.16 | 74.30 ± 0.08 | 78.64 ± 0.14 | 62.92 ± 0.08 | 66.44 ± 0.09 |
| w/o Hour | 56.38 ± 0.12 | 74.79 ± 0.03 | 78.83 ± 0.11 | 64.75 ± 0.06 | 67.88 ± 0.04 |
| w/o Duration | 53.58 ± 0.09 | 74.46 ± 0.19 | 78.67 ± 0.10 | 63.03 ± 0.06 | 66.55 ± 0.07 |
| w/o Act | 55.83 ± 0.08 | 74.71 ± 0.10 | 78.75 ± 0.09 | 64.45 ± 0.06 | 67.63 ± 0.06 |
| w/o Com | 55.68 ± 0.15 | 74.09 ± 0.24 | 78.26 ± 0.24 | 64.06 ± 0.14 | 67.20 ± 0.17 |
| w/o User | 52.79 ± 0.15 | 71.79 ± 0.20 | 76.04 ± 0.21 | 61.47 ± 0.16 | 64.65 ± 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lun, M.; Wang, P.; Wu, S.; Zhang, H.; Cheng, S.; Lu, F. Predicting the Next Location of Urban Individuals via a Representation-Enhanced Multi-View Learning Network. ISPRS Int. J. Geo-Inf. 2025, 14, 302. https://doi.org/10.3390/ijgi14080302
Lun M, Wang P, Wu S, Zhang H, Cheng S, Lu F. Predicting the Next Location of Urban Individuals via a Representation-Enhanced Multi-View Learning Network. ISPRS International Journal of Geo-Information. 2025; 14(8):302. https://doi.org/10.3390/ijgi14080302
Chicago/Turabian StyleLun, Maoqi, Peixiao Wang, Sheng Wu, Hengcai Zhang, Shifen Cheng, and Feng Lu. 2025. "Predicting the Next Location of Urban Individuals via a Representation-Enhanced Multi-View Learning Network" ISPRS International Journal of Geo-Information 14, no. 8: 302. https://doi.org/10.3390/ijgi14080302
APA StyleLun, M., Wang, P., Wu, S., Zhang, H., Cheng, S., & Lu, F. (2025). Predicting the Next Location of Urban Individuals via a Representation-Enhanced Multi-View Learning Network. ISPRS International Journal of Geo-Information, 14(8), 302. https://doi.org/10.3390/ijgi14080302











