Spatiotemporal Patterns of Greening and Their Correlation with Surface Radiative Forcing on the Tibetan Plateau from 1982 to 2021
Abstract
1. Introduction
2. Materials and Methods
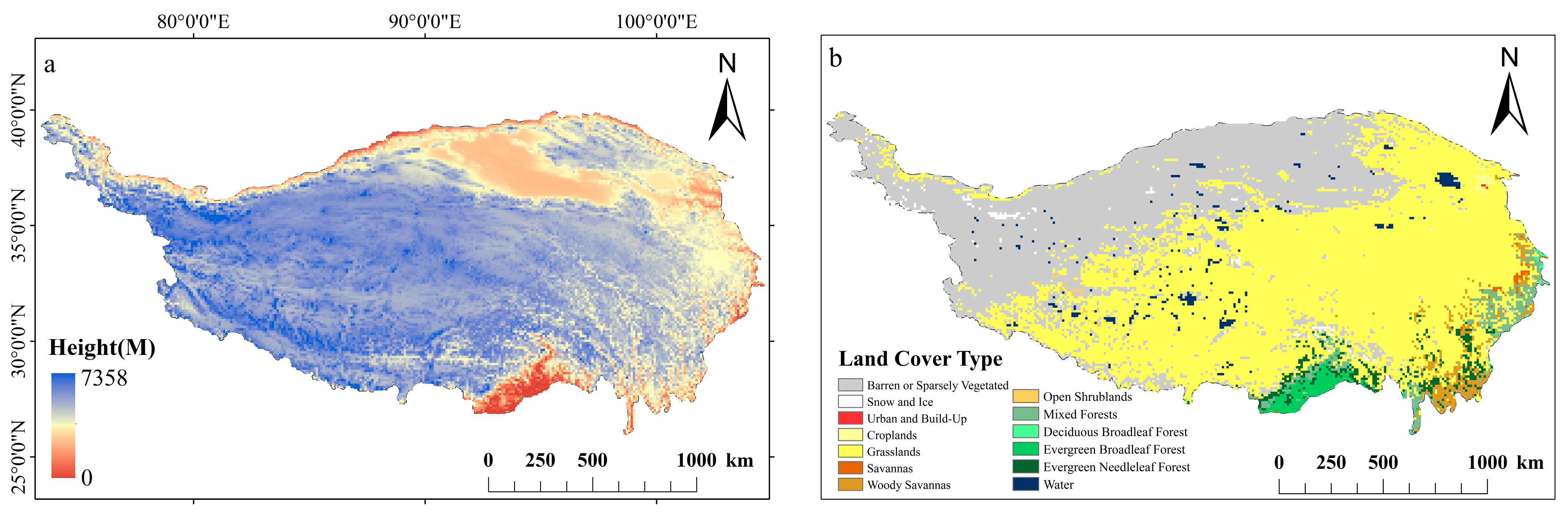
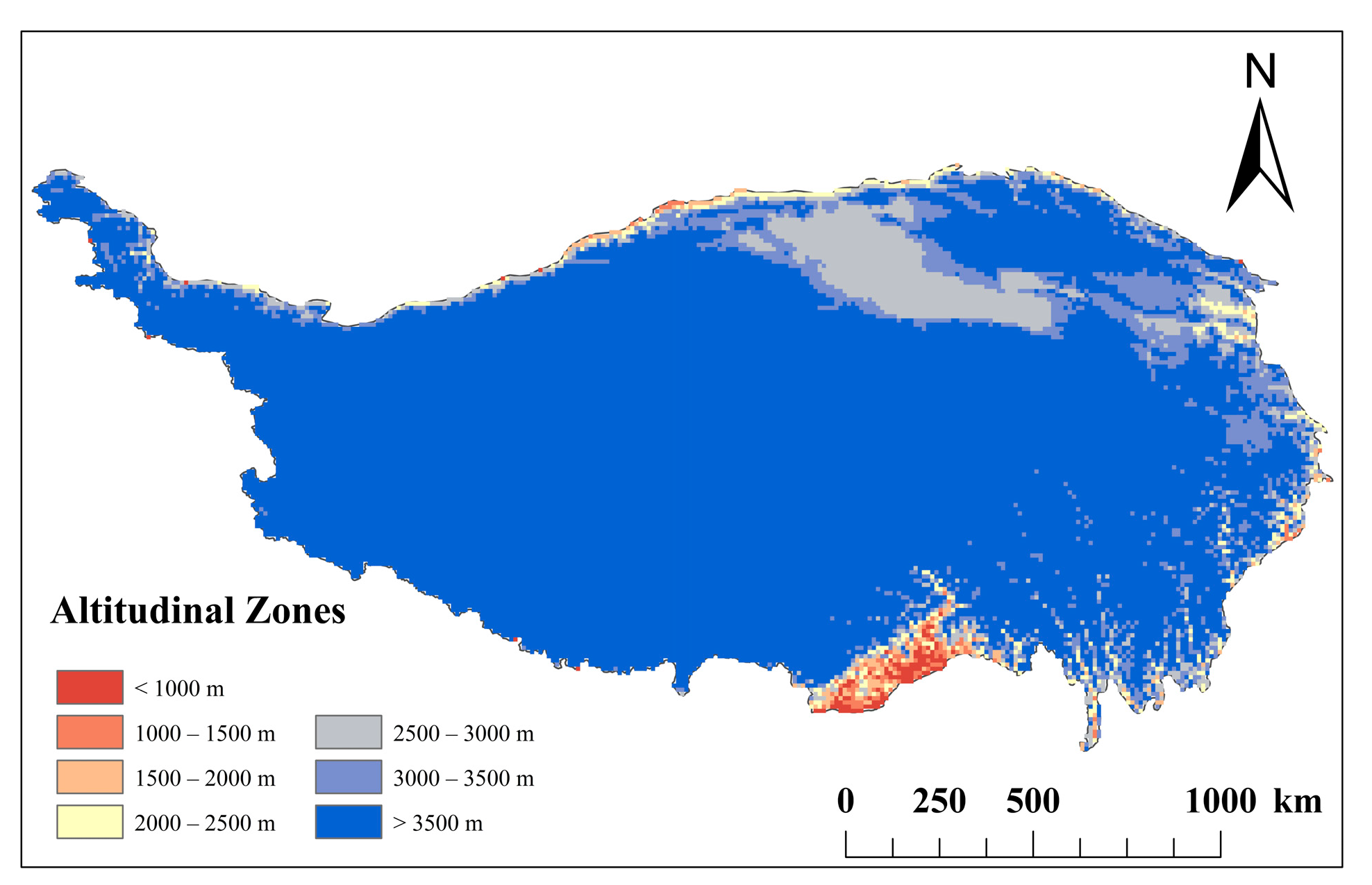
2.1. Study Area
2.2. Datasets
2.3. Analysis
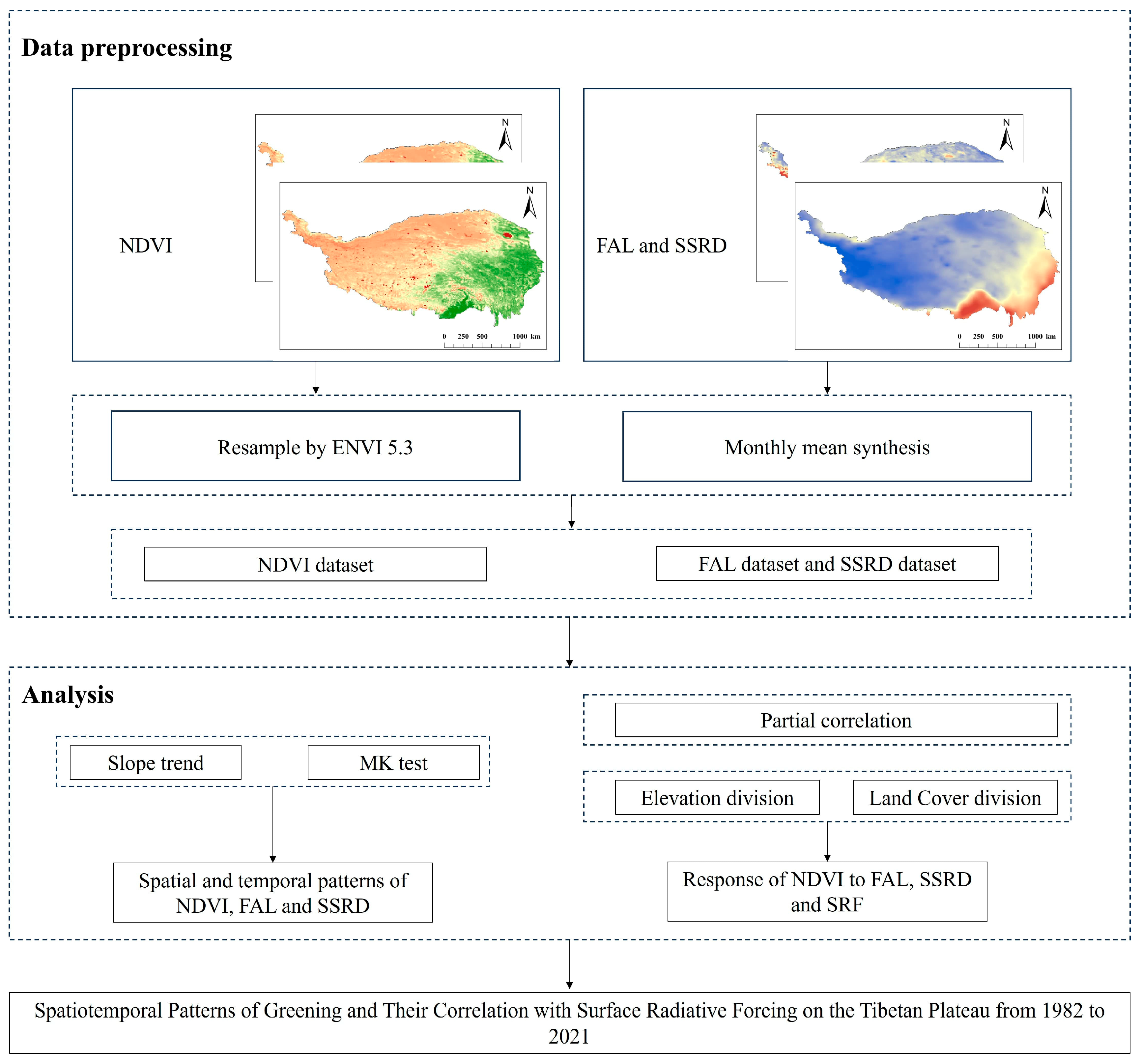
2.3.1. Data Preprocessing
2.3.2. Calculation of Regional Average Surface Radiative Forcing
2.3.3. Slope Trend Analysis
2.3.4. Mann–Kendall Test
2.3.5. Partial Correlation Analysis
2.3.6. Factor Dominance and Contribution
2.3.7. Experimental Procedures
3. Results
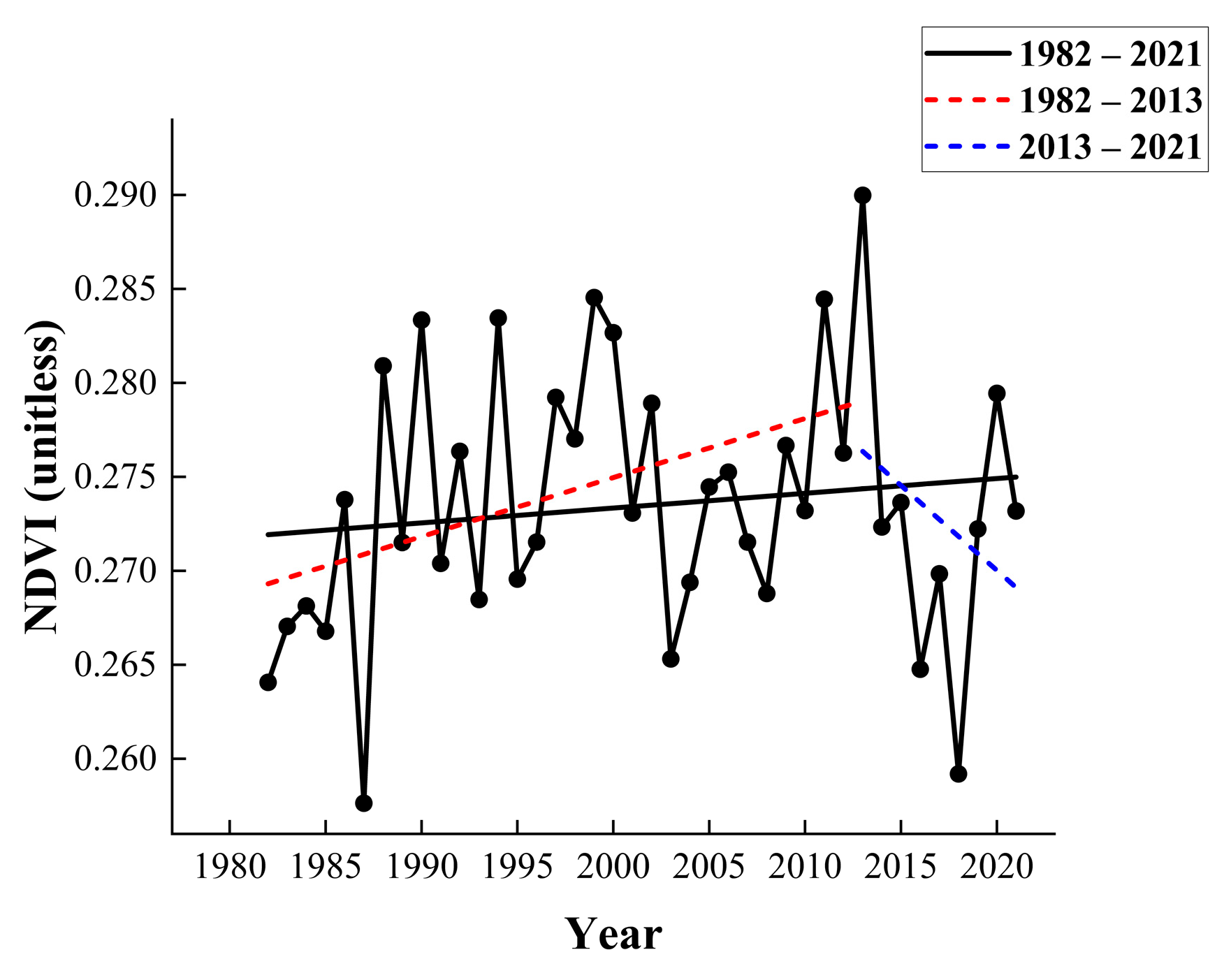
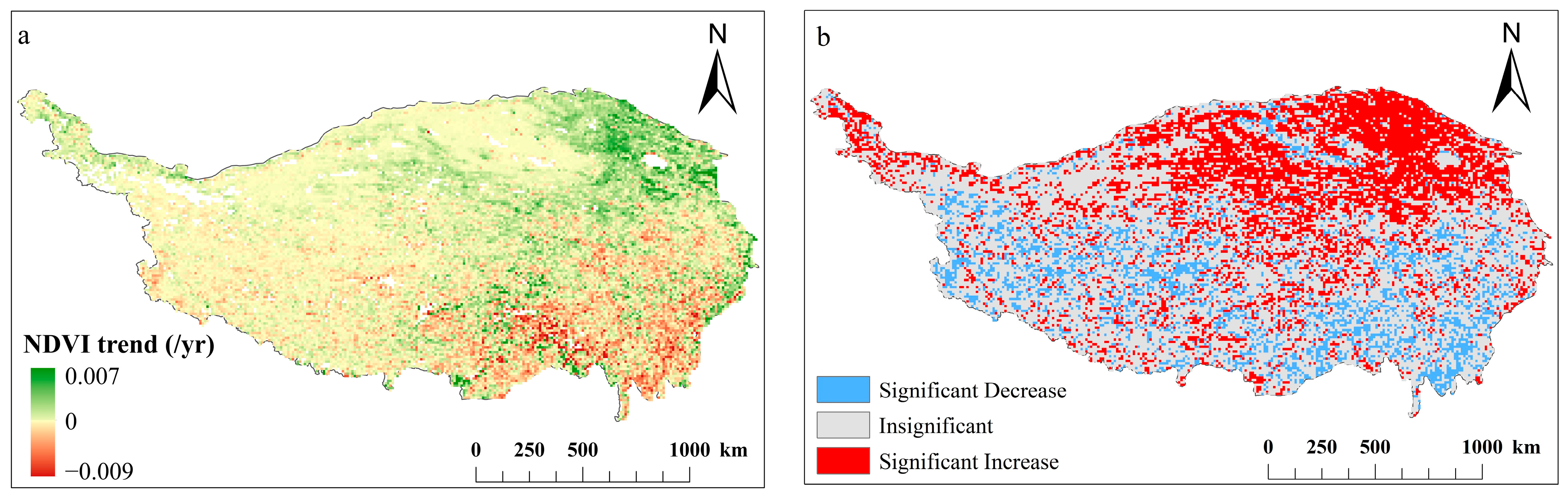
3.1. Spatial and Temporal Variation in NDVI on the Tibetan Plateau
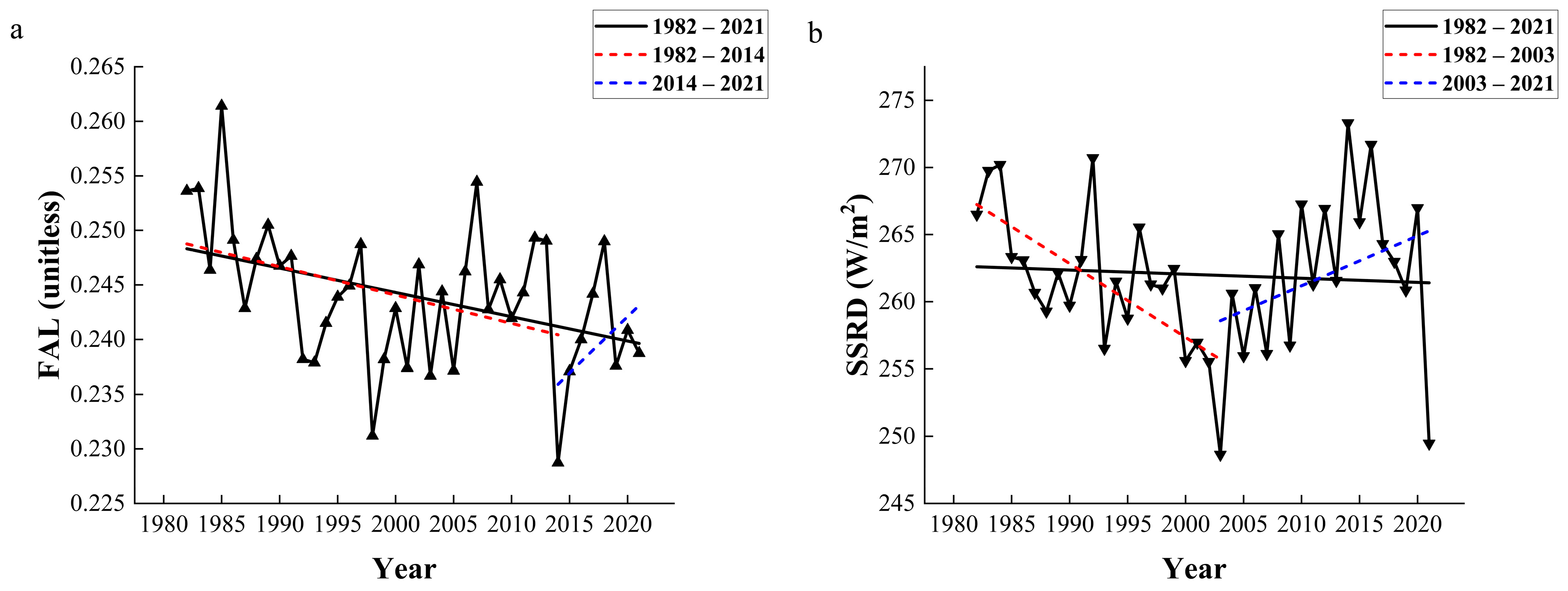
3.2. Temporal Variation in FAL and SSRD on the Tibetan Plateau
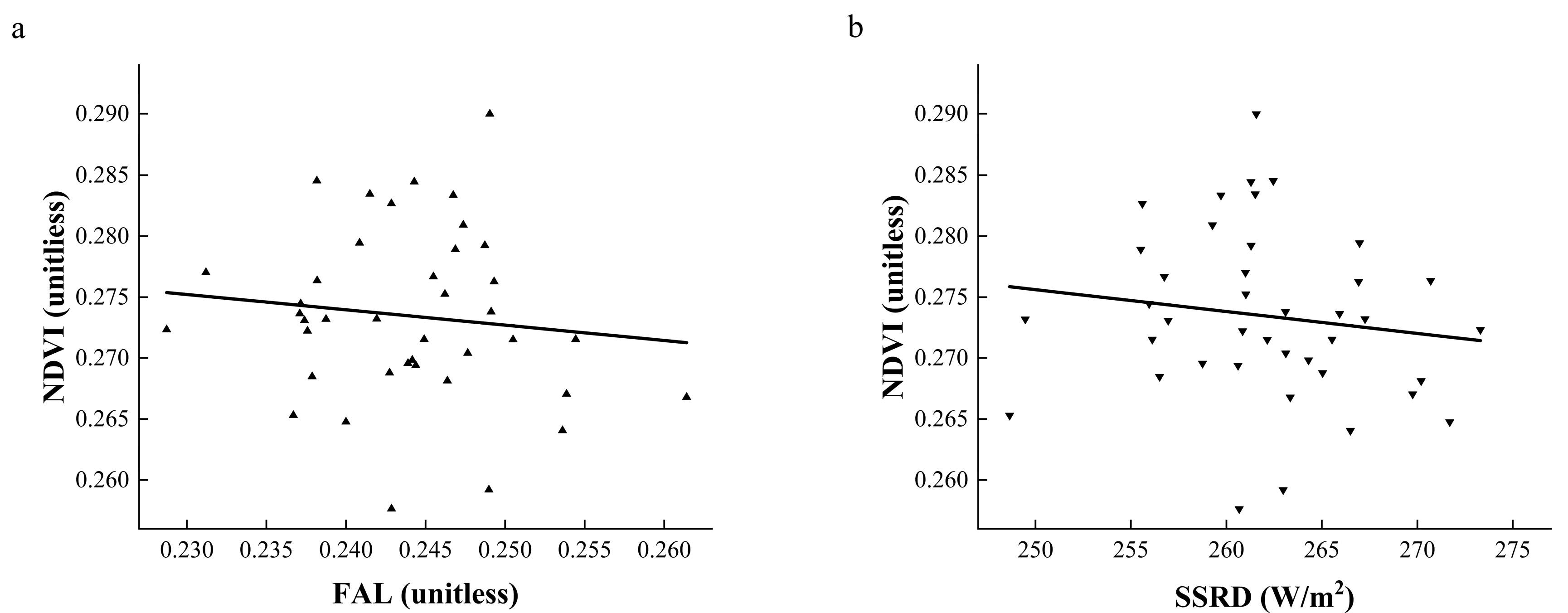
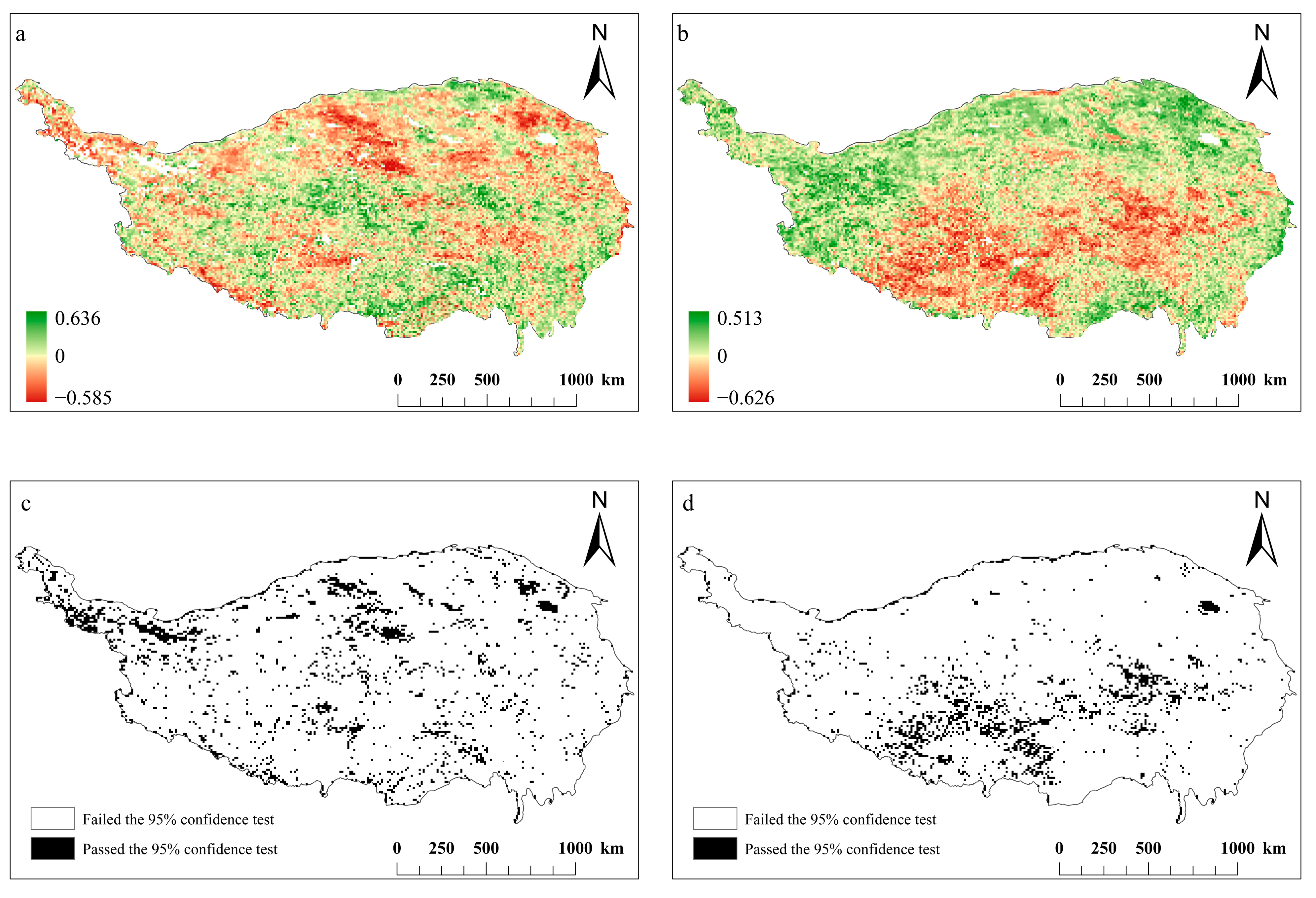
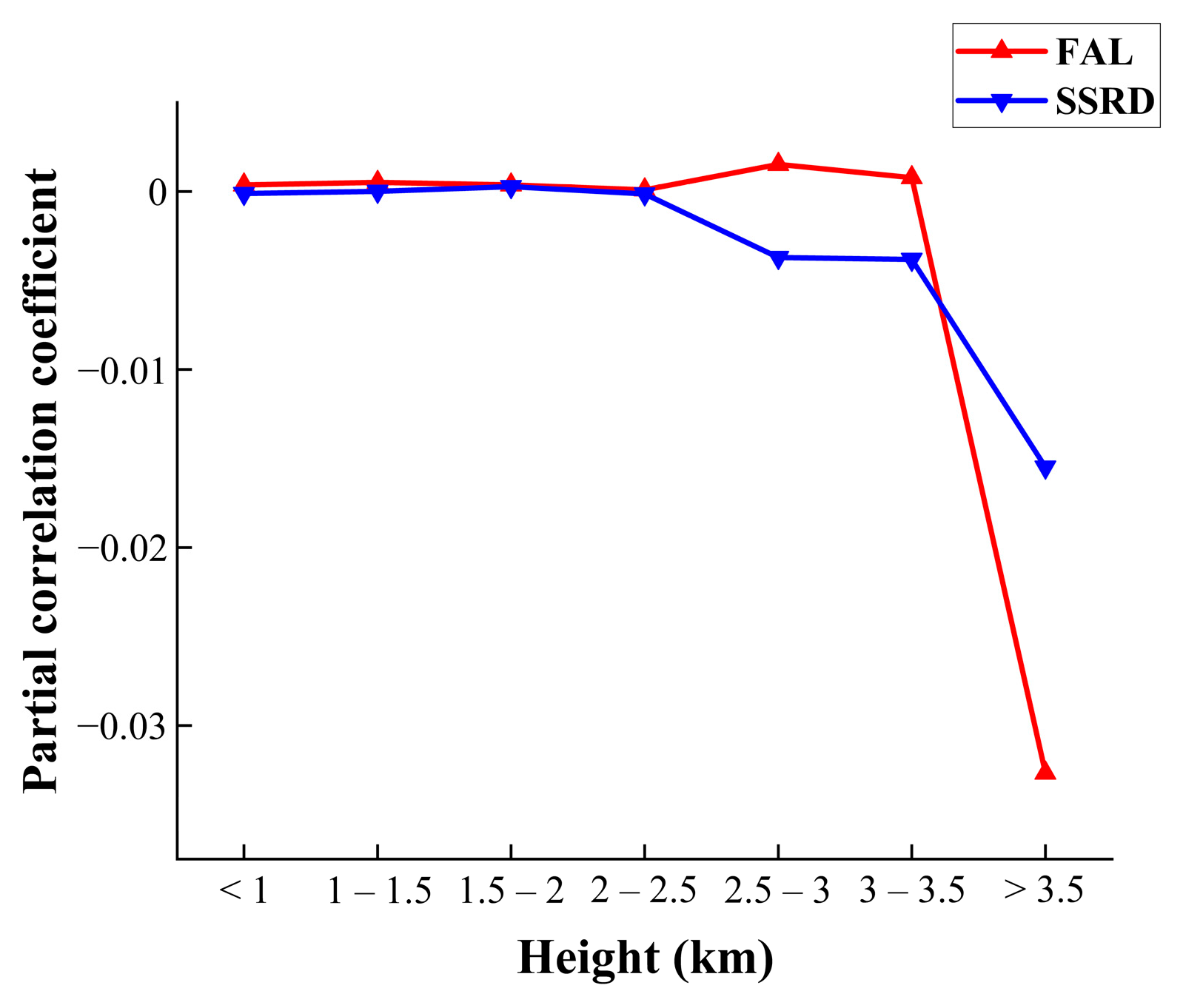
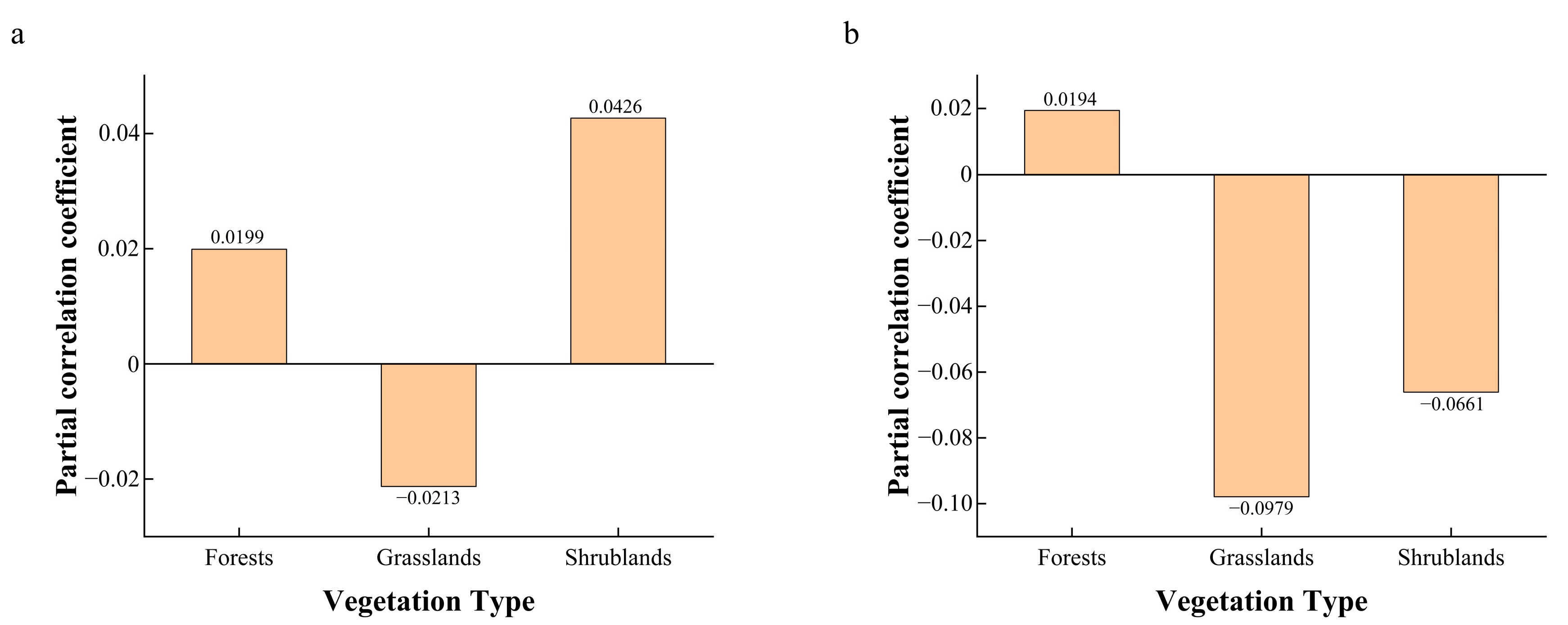
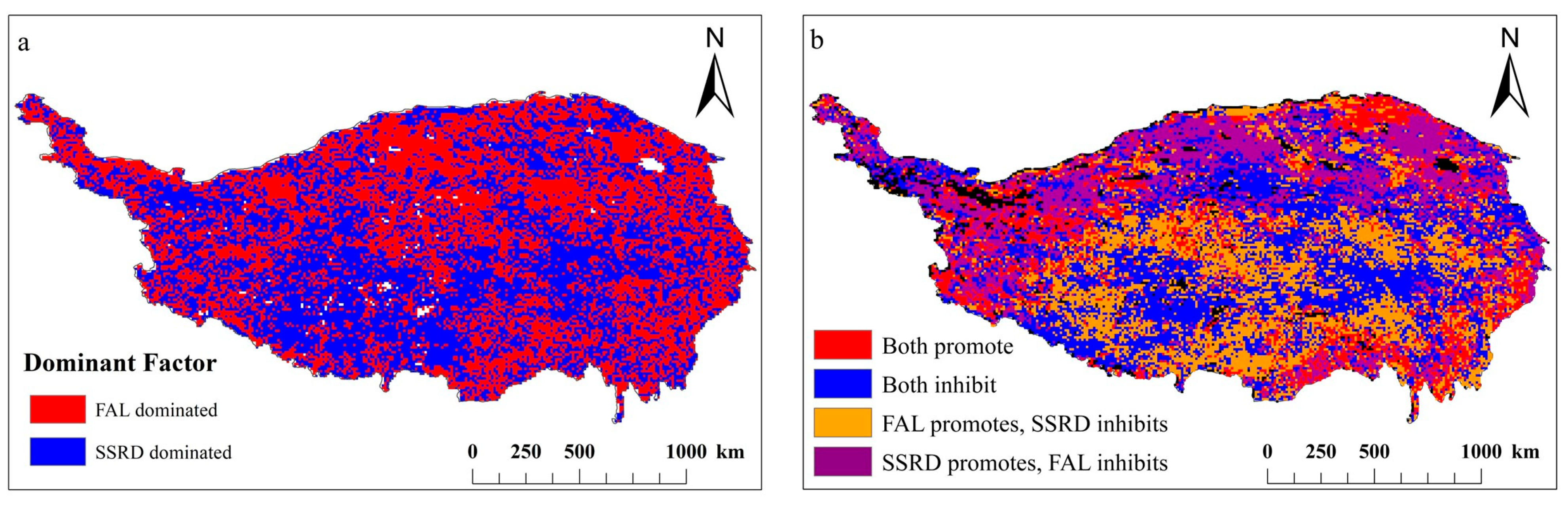
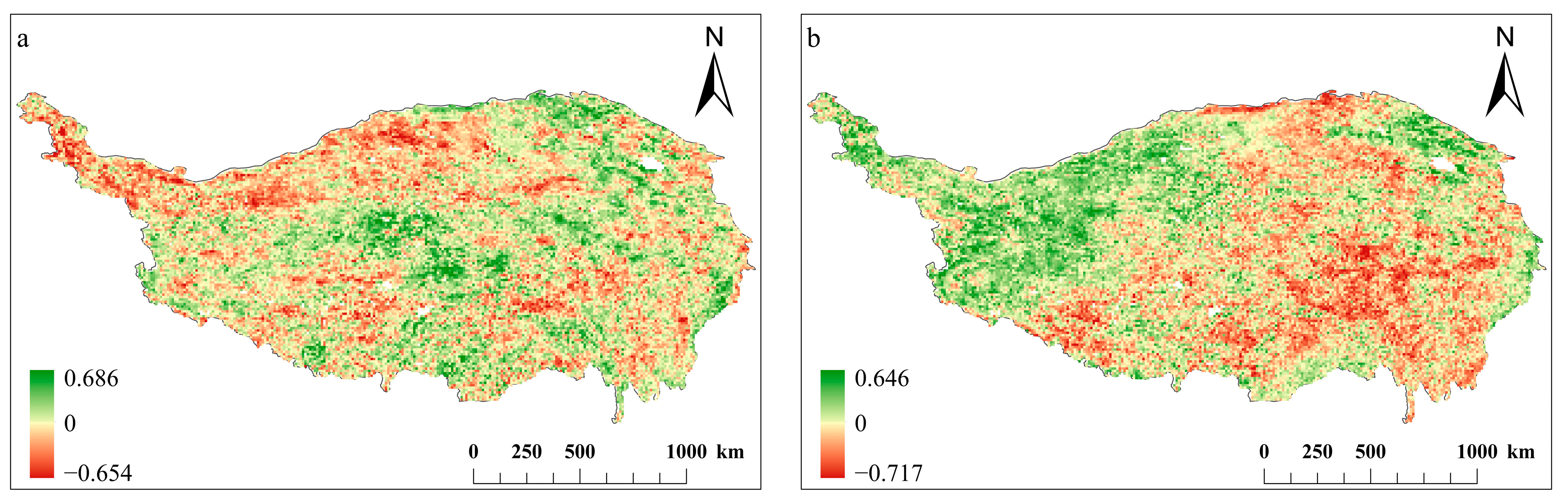
3.3. Change in NDVI and SRF on the Tibetan Plateau
4. Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, J.; Yu, G.; Liu, L.; Hu, S.; Chapin, F.S. Climate Change, Human Impacts, and Carbon Sequestration in China. Proc. Natl. Acad. Sci. USA 2018, 115, 4015–4020. [Google Scholar] [CrossRef] [PubMed]
- Ferrini, F.; Fini, A.; Mori, J.; Gori, A. Role of Vegetation as a Mitigating Factor in the Urban Context. Sustainability 2020, 12, 4247. [Google Scholar] [CrossRef]
- Chaudhry, S.; Sidhu, G.P.S. Climate Change Regulated Abiotic Stress Mechanisms in Plants: A Comprehensive Review. Plant Cell Rep. 2022, 41, 1–31. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Ding, Y.; Shi, H.; Cai, H.; Fu, Q.; Liu, S.; Li, T. Analysis and Prediction of Vegetation Dynamic Changes in China: Past, Present and Future. Ecol. Indic. 2020, 117, 106642. [Google Scholar] [CrossRef]
- Lindén, J.; Gustafsson, M.; Uddling, J.; Watne, Å.; Pleijel, H. Air Pollution Removal through Deposition on Urban Vegetation: The Importance of Vegetation Characteristics. Urban For. Urban Green. 2023, 81, 127843. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Kaskaoutis, D.G.; Kalliampakos, G.K.; Rashki, A.; Wild, M. The Solar Dimming/Brightening Effect over the Mediterranean Basin in the Period 1979–2012. J. Atmos. Sol.-Terr. Phys. 2016, 150–151, 31–46. [Google Scholar] [CrossRef]
- Kang, S.; Xu, Y.; You, Q.; Flügel, W.-A.; Pepin, N.; Yao, T. Review of Climate and Cryospheric Change in the Tibetan Plateau. Environ. Res. Lett. 2010, 5, 015101. [Google Scholar] [CrossRef]
- Yao, T.; Xue, Y.; Chen, D.; Chen, F.; Thompson, L.; Cui, P.; Koike, T.; Lau, W.K.-M.; Lettenmaier, D.; Mosbrugger, V.; et al. Recent Third Pole’s Rapid Warming Accompanies Cryospheric Melt and Water Cycle Intensification and Interactions between Monsoon and Environment: Multidisciplinary Approach with Observations, Modeling, and Analysis. Bull. Am. Meteorol. Soc. 2019, 100, 423–444. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Dong, S.; Fu, M.; Li, Y.; Li, S.; Wu, S.; Ma, C.; Ma, T.; Cao, Y. Evolution of ecological patterns and its driving factors on Qinghai-Tibet Plateau over the past 40 years. Acta Ecol. Sin. 2022, 42, 8941–8952. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Z.; Wu, J.; Niu, B.; He, Y.; Zu, J.; Li, M.; Zhang, X. Vegetation Expansion on the Tibetan Plateau and Its Relationship with Climate Change. Remote Sens. 2020, 12, 4150. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, J.; Chen, L. Effects of vegetation degradation on atmospheric circulation over the Tibetan Plateau and its surrounding areas. Acta Ecol. Sin. 2018, 38, 132–142. (In Chinese) [Google Scholar] [CrossRef]
- Wang, T.; Zhao, Y.; Wang, H. Spatial and temporal changes of vegetation index and their response to temperature and precipitation in the Tibetan Plateau based on GIMMS NDVI. J. Glaciol. Geocryol. 2020, 42, 641–652. (In Chinese) [Google Scholar] [CrossRef]
- Zhong, L.; Ma, Y.; Xue, Y.; Piao, S. Climate Change Trends and Impacts on Vegetation Greening Over the Tibetan Plateau. J. Geophys. Res. Atmos. 2019, 124, 7540–7552. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J.; Cui, X.; Wei, Y.; Sun, J.; Naudiyal, N.; Du, W.; Chen, Q. Spatio-temporal change in vegetation patterns and its climatic drivers in the core region of Three Parallel Rivers in southeast Tibet. Geogr. Res. 2021, 40, 3191–3207. (In Chinese) [Google Scholar] [CrossRef]
- Zhuo, G.; Chen, S.; Zhou, B. Spatio-Temporal Variation of Vegetation Coverage over the Tibetan Plateau and Its Responses to Climatic Factors. Acta Ecol. Sin. 2018, 38, 3208–3218. [Google Scholar] [CrossRef]
- Li, H.; Zhang, C.; Wang, S.; Ma, W.; Liu, F.; Chen, Q.; Zhou, Q.; Xia, X.; Niu, B. Response of vegetation dynamics to hydrothermal conditions on the Qinghai-Tibet Plateau in the last 40 years. Acta Ecol. Sin. 2022, 42, 4770–4783. (In Chinese) [Google Scholar] [CrossRef]
- Yang, D.; Yi, G.; Zhang, Y.; Li, J.; Qin, Y.; Wen, B.; Liu, Z. Spatiotemporal variation and driving factors of growing season NDVI in the Tibetan Plateau, China. Chin. J. Appl. Ecol. 2021, 32, 1361–1372. (In Chinese) [Google Scholar] [CrossRef]
- Yang, L.; Liu, L.; Sun, S. The Dominated Environmental Factors of Vegetation Change on the Qinghai-Tibet Plateau from 1982 to 2015. Acta Ecol. Sin. 2023, 43, 744–755. [Google Scholar] [CrossRef]
- Yao, T.; Wu, G.; Xu, B.; Wang, W.; Gao, J.; An, B. Asian Water Tower Change and Its Impacts. Bull. Chin. Acad. Sci. 2019, 34, 1203–1209. (In Chinese) [Google Scholar] [CrossRef]
- Wang, N.; Yao, T.; Xu, B.; Chen, A.; Wang, W. Spatiotemporal Pattern, Trend, and Influence of Glacier Change in Tibetan Plateau and Surroundings under Global Warming. Bull. Chin. Acad. Sci. 2019, 34, 1220–1232. [Google Scholar] [CrossRef]
- Losapio, G.; Cerabolini, B.E.L.; Maffioletti, C.; Tampucci, D.; Gobbi, M.; Caccianiga, M. The Consequences of Glacier Retreat Are Uneven Between Plant Species. Front. Ecol. Evol. 2021, 8, 616562. [Google Scholar] [CrossRef]
- Charles, C.; Khelidj, N.; Mottet, L.; Tu, B.N.; Adatte, T.; Bomou, B.; Faria, M.; Monbaron, L.; Reubi, O.; de Vere, N.; et al. Plant–Soil Interactions Underline the Development of Novel Ecosystems after Glacier Retreat. EGUsphere 2024, 2024, 1–24. [Google Scholar] [CrossRef]
- Tu, B.N.; Khelidj, N.; Cerretti, P.; De Vere, N.; Ferrari, A.; Paone, F.; Polidori, C.; Schmid, J.; Sommaggio, D.; Losapio, G. Glacier Retreat Triggers Changes in Biodiversity and Plant–Pollinator Interaction Diversity. Alp. Bot. 2024, 134, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.; Gong, W.; Bianchini, S.; Yang, Z. Linking Glacier Retreat with Climate Change on the Tibetan Plateau through Satellite Remote Sensing. EGUsphere 2024, 2024, 1–26. [Google Scholar] [CrossRef]
- Liu, J.; Xu, X.; Shao, Q. Grassland Degradation in the “Three-River Headwaters” Region, Qinghai Province. J. Geogr. Sci. 2008, 18, 259–273. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, L.; Wang, Z.; Bai, W.; Ding, M.; Wang, X.; Yan, J.; Xu, E.; Wu, X.; Zhang, B.; et al. Spatial and Temporal Characteristics of Land Use and Cover Changes in the Tibetan Plateau. Chin. Sci. Bull. 2019, 64, 2865–2875. [Google Scholar] [CrossRef]
- Yang, Z.; Jiang, L.; Xu, Y.; Zhan, W.; Zhu, E.; Chen, H. Responses of vegetation and soil of alpine meadows on the Qinghai-Tibet Plateau to short-term grazing prohibition. Acta Ecol. Sin. 2017, 37, 7903–7911. (In Chinese) [Google Scholar] [CrossRef][Green Version]
- Planque, C.; Carrer, D.; Roujean, J.-L. Analysis of MODIS Albedo Changes over Steady Woody Covers in France during the Period of 2001–2013. Remote Sens. Environ. 2017, 191, 13–29. [Google Scholar] [CrossRef]
- Zheng, L.; Qi, Y.; Qin, Z.; Xu, X.; Dong, J. Assessing Albedo Dynamics and Its Environmental Controls of Grasslands over the Tibetan Plateau. Agric. For. Meteorol. 2021, 307, 108479. [Google Scholar] [CrossRef]
- Hasler, N.; Williams, C.A.; Denney, V.C.; Ellis, P.W.; Shrestha, S.; Terasaki Hart, D.E.; Wolff, N.H.; Yeo, S.; Crowther, T.W.; Werden, L.K.; et al. Accounting for Albedo Change to Identify Climate-Positive Tree Cover Restoration. Nat. Commun. 2024, 15, 2275. [Google Scholar] [CrossRef]
- Zheng, L.; Zhao, G.; Dong, J.; Ge, Q.; Tao, J.; Zhang, X.; Qi, Y.; Doughty, R.B.; Xiao, X. Spatial, Temporal, and Spectral Variations in Albedo Due to Vegetation Changes in China’s Grasslands. ISPRS J. Photogramm. Remote Sens. 2019, 152, 1–12. [Google Scholar] [CrossRef]
- Tu, Y.; Jiang, L.; Liu, R.; Xiao, Z.; Min, J. Spatiotemporal changes of vegetation NDVI and its driving forces in China during 1982-2015. Trans. Chin. Soc. Agric. Eng. 2021, 37, 75–84. (In Chinese) [Google Scholar] [CrossRef]
- Hao, A.; Xue, X.; Duan, H.; Peng, F.; You, Q. Different Spatiotemporal Variations in Seasonal NDVI and Their Climatic Driving Forces of a Typical Grassland on the Qinghai-Tibetan Plateau. Acta Ecol. Sin. 2023, 43, 352–363. [Google Scholar] [CrossRef]
- Zhu, Q.; Chen, J.; Wu, L.; Huang, Y.; Shao, C.; Dong, G.; Xu, Z.; Li, X. Changes in Albedo and Its Radiative Forcing of Grasslands in East Asia Drylands. Ecol. Process. 2024, 13, 17. [Google Scholar] [CrossRef]
- Feng, H.; Ye, S.; Zou, B. Contribution of Vegetation Change to the Surface Radiation Budget: A Satellite Perspective. Glob. Planet. Chang. 2020, 192, 103225. [Google Scholar] [CrossRef]
- Tang, X.; Cui, Y.; Li, N.; Fu, Y.; Liu, X.; Run, Y.; Li, M.; Zhao, G.; Dong, J. Human Activities Enhance Radiation Forcing through Surface Albedo Associated with Vegetation in Beijing. Remote Sens. 2020, 12, 837. [Google Scholar] [CrossRef]
- Yang, K.; Wu, H.; Qin, J.; Lin, C.; Tang, W.; Chen, Y. Recent Climate Changes over the Tibetan Plateau and Their Impacts on Energy and Water Cycle: A Review. Glob. Planet. Chang. 2014, 112, 79–91. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; van Beek, L.P.H.; Bierkens, M.F.P. Climate Change Will Affect the Asian Water Towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef]
- Yao, T.; Wang, W.; Yang, W.; Zhang, G.; Shi, J.; Wu, G.; Gao, J.; Che, T.; Liu, S.; Walter, I.; et al. Imbalance of the Asian Water Tower characterized by glacier and snow melt. Clim. Chang. Res. 2024, 20, 689–698. (In Chinese) [Google Scholar] [CrossRef]
- Duan, H.; Xue, X.; Wang, T.; Kang, W.; Liao, J.; Liu, S. Spatial and Temporal Differences in Alpine Meadow, Alpine Steppe and All Vegetation of the Qinghai-Tibetan Plateau and Their Responses to Climate Change. Remote Sens. 2021, 13, 669. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, W.; Shi, P.; Zhao, C.; Liu, R.; Tang, H.; Wang, J.; He, B. The differences of vegetation characteristics and environmental conditions among main vegetation types on the Qinghai-Tibet Plateau. Acta Ecol. Sin. 2024, 44, 2955–2970. (In Chinese) [Google Scholar] [CrossRef]
- Cheng, W.; Zhou, C.; Chai, H.; Zhao, S.; LI, B. Quantitative Extraction and Analysis of Basic Morphological Types of Land Geomorphology in China: Quantitative Extraction and Analysis of Basic Morphological Types of Land Geomorphology in China. Geo-Inf. Sci. 2010, 11, 725–736. [Google Scholar] [CrossRef]
- Guo, D.; Yu, E.; Wang, H. Will the Tibetan Plateau Warming Depend on Elevation in the Future? J. Geophys. Res. Atmos. 2016, 121, 3969–3978. [Google Scholar] [CrossRef]
- Hu, W.; Yao, J.; He, Q.; Chen, J. Elevation-Dependent Trends in Precipitation Observed over and around the Tibetan Plateau from 1971 to 2017. Water 2021, 13, 2848. [Google Scholar] [CrossRef]
- Tang, R.; Zhao, X.; Tang, B.; Wei, H.; Chen, J.; Peng, Y. Influence of urbanization on radiative forcing in Beijing. J. Beijing Norm. Univ. Sci. 2017, 53, 443–450+376. (In Chinese) [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: Oxford, UK, 1948. [Google Scholar]
- Hamed, K.H.; Ramachandra Rao, A. A Modified Mann-Kendall Trend Test for Autocorrelated Data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Ronald Eastman, J.; Sangermano, F.; Ghimire, B.; Zhu, H.; Chen, H.; Neeti, N.; Cai, Y.; Machado, E.A.; Crema, S.C. Seasonal Trend Analysis of Image Time Series. Int. J. Remote Sens. 2009, 30, 2721–2726. [Google Scholar] [CrossRef]
- Yang, H.; Wu, K.; Chen, J.; Zhong, C.; Hu, Z. Spatiotemporal Variability and Climatic Drivers of Net Primary Productivity on Hainan Island during 2000–2018. Remote Sens. Inf. 2024, 39, 164–172. (In Chinese) [Google Scholar] [CrossRef]
- Li, J.; Sun, Z.; Liu, Y.; You, Q.; Chen, G.; Bao, Q. Top-of-Atmosphere Radiation Budget and Cloud Radiative Effects Over the Tibetan Plateau and Adjacent Monsoon Regions from CMIP6 Simulations. J. Geophys. Res. Atmos. 2021, 126, e2020JD034345. [Google Scholar] [CrossRef]
- Wei, J.; Li, X.; Liu, L.; Christensen, T.R.; Jiang, Z.; Ma, Y.; Wu, X.; Yao, H.; López-Blanco, E. Radiation, Soil Water Content, and Temperature Effects on Carbon Cycling in an Alpine Swamp Meadow of the Northeastern Qinghai–Tibetan Plateau. Biogeosciences 2022, 19, 861–875. [Google Scholar] [CrossRef]
- Shi, S.; Shi, R.; Zhou, D.; Li, T.; De, K.; Gao, X.; Ma, J.; Wang, F. Reduction of PSII Photosynthetic Performance by Low Temperature Is the Reason for the Growing Inhibition of Kobresia Pygmaea Clarke. Braz. J. Bot. 2023, 46, 527–539. [Google Scholar] [CrossRef]
- Gong, J.; Zhang, Z.; Zhang, C.; Zhang, J.; Ran, A. Ecophysiological Responses of Three Tree Species to a High-Altitude Environment in the Southeastern Tibetan Plateau. Forests 2018, 9, 48. (In Chinese) [Google Scholar] [CrossRef]
- Wang, X.; Wang, G.; Song, C.; Sun, J.; Lin, S.; Wang, Y.; Sun, X. Snowmelt Decreases Light Use Efficiency in Qinghai-Tibetan Plateau between 2000 and 2017. J. Environ. Manag. 2025, 373, 123469. [Google Scholar] [CrossRef]
- Chen, S.; Guo, B.; Yang, F.; Han, B.; Fan, Y.; Yang, X.; He, T.; Liu, Y.; Yang, W. Spatial and Temporal Patterns of NPP and Its Response to Climate Change in the Qinghai-Tibet Plateau from 2000 to 2015. J. Nat. Resour. 2020, 35, 2511–2527. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, Y.; Zeng, H.; Tang, Z. Change of NDVI during Growing Season and Its Relationship with Climate in North China and the Adjacent Areas from 1982 to 2014. Acta Sci. Nat. Univ. Pekin. 2021, 57, 153. (In Chinese) [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Gao, Y.; Zou, C.; Yan, S.; Gao, J. Human Impact on Vegetation Dynamics around Lhasa, Southern Tibetan Plateau, China. Sustainability 2016, 8, 1146. [Google Scholar] [CrossRef]




| Name | Data Sources | Web Address | Spatial Resolution | Time Resolution |
|---|---|---|---|---|
| Normalized Difference Vegetation Index (NDVI) | AVHRR GIMMS-3G+ | https://daac.ornl.gov/ (accessed on 12 October 2024) | 0.08° × 0.08° | 15 d |
| Forecast Albedo (FAL) | ERA5-Land | https://cds.climate.copernicus.eu/ (accessed on 12 October 2024) | 0.09° × 0.09° | monthly |
| Surface Solar Radiation Downwards (SSRD) | ERA5-Land | https://cds.climate.copernicus.eu/ (accessed on 12 October 2024) | 0.09° × 0.09° | monthly |
| Elevation (DEM) | GMTED2010 | https://www.usgs.gov/ (accessed on 12 October 2024) | 30 arc-seconds | yearly |
| Land Cover | MODIS | https://svs.gsfc.nasa.gov/ (accessed on 12 October 2024) | 500 m | yearly |
| Time | Linear Regression Equation | R2 | PCC | p-Value |
|---|---|---|---|---|
| 1982–2021 | 0.017 | 0.131 | 0.420 | |
| 1982–2013 | 0.172 | 0.415 | 0.018 | |
| 2013–2021 | 0.081 | −0.286 | 0.455 |
| Time | Linear Regression Equation | R2 | PCC | p-Value |
|---|---|---|---|---|
| 1982–2021 | 0.162 | −0.402 | 0.010 | |
| 1982–2014 | 0.139 | −0.374 | 0.032 | |
| 2014–2021 | 0.185 | −0.431 | 0.287 |
| Time | Linear Regression Equation | R2 | PCC | p-Value |
|---|---|---|---|---|
| 1982–2021 | 0.004 | −0.065 | 0.689 | |
| 1982–2003 | 0.643 | −0.680 | 0.001 | |
| 2003–2021 | 0.102 | 0.320 | 0.182 |
| Linear Regression Equation | R2 | PCC | p-Value | |
|---|---|---|---|---|
| FAL-NDVI | 0.014 | −0.116 | 0.475 | |
| SSRD-NDVI | 0.019 | −0.141 | 0.386 |
| Linear Regression Equation | R2 | PCC | p-Value | |
|---|---|---|---|---|
| SRF-ΔNDVI | 0.037 | −0.194 | 0.238 | |
| ΔSSRD-ΔNDVI | 0.004 | −0.063 | 0.705 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Wu, K.; Yang, H.; Shen, Y. Spatiotemporal Patterns of Greening and Their Correlation with Surface Radiative Forcing on the Tibetan Plateau from 1982 to 2021. ISPRS Int. J. Geo-Inf. 2025, 14, 228. https://doi.org/10.3390/ijgi14060228
Guo J, Wu K, Yang H, Shen Y. Spatiotemporal Patterns of Greening and Their Correlation with Surface Radiative Forcing on the Tibetan Plateau from 1982 to 2021. ISPRS International Journal of Geo-Information. 2025; 14(6):228. https://doi.org/10.3390/ijgi14060228
Chicago/Turabian StyleGuo, Junshan, Kai Wu, Han Yang, and Yao Shen. 2025. "Spatiotemporal Patterns of Greening and Their Correlation with Surface Radiative Forcing on the Tibetan Plateau from 1982 to 2021" ISPRS International Journal of Geo-Information 14, no. 6: 228. https://doi.org/10.3390/ijgi14060228
APA StyleGuo, J., Wu, K., Yang, H., & Shen, Y. (2025). Spatiotemporal Patterns of Greening and Their Correlation with Surface Radiative Forcing on the Tibetan Plateau from 1982 to 2021. ISPRS International Journal of Geo-Information, 14(6), 228. https://doi.org/10.3390/ijgi14060228






