Topology-Aware Multi-View Street Scene Image Matching for Cross-Daylight Conditions Integrating Geometric Constraints and Semantic Consistency

Abstract

While deep learning-based image matching methods excel at extracting high-level semantic features from remote sensing data, their performance degrades significantly under cross-daylight conditions and wide-baseline geometric distortions, particularly in multi-source street-view scenarios. This paper presents a novel illumination-invariant framework that synergistically integrates geometric topology and semantic consistency to achieve robust multi-view matching for cross-daylight urban perception. We first design a self-supervised learning paradigm to extract illumination-agnostic features by jointly optimizing local descriptors and global geometric structures across multi-view images. To address extreme perspective variations, a homography-aware transformation module is introduced to stabilize feature representation under large viewpoint changes. Leveraging a graph neural network with hierarchical attention mechanisms, our method dynamically aggregates contextual information from both local keypoints and semantic topology graphs, enabling precise matching in occluded regions and repetitive-textured urban scenes. A dual-branch learning strategy further refines similarity metrics through supervised patch alignment and unsupervised spatial consistency constraints derived from Delaunay triangulation. Finally, a topology-guided multi-plane expansion mechanism propagates initial matches by exploiting the inherent structural regularity of street scenes, effectively suppressing mismatches while expanding coverage. Extensive experiments demonstrate that our framework outperforms state-of-the-art methods, achieving a 6.4% improvement in matching accuracy and a 30.5% reduction in mismatches under cross-daylight conditions. These advancements establish a new benchmark for reliable multi-source image retrieval and localization in dynamic urban environments, with direct applications in autonomous driving systems and large-scale 3D city reconstruction.

1. Introduction

1.1. Background

Multi-source street-view imagery is acquired through heterogeneous sensors, including smartphone-embedded consumer-grade CMOS devices and unmanned aerial vehicles (UAVs) equipped with oblique photogrammetry modules. These spatiotemporally synchronized multi-view datasets, georeferenced via unified spatiotemporal benchmarks, exhibit sub-meter-level spatiotemporal resolution. The multi-perspective characteristics of such multimodal imagery enable the reconstruction of holographic topological structures for urban scenes [1], providing multi-scale observational foundations for 3D architectural facade analysis and urban spatial digitization [2]. Current research prioritizes multi-view image matching methodologies that integrate geometric priors with semantic–topological relationships, particularly addressing dynamic illumination perturbations under cross-daylight conditions.

The core challenge lies in establishing robust feature correspondences across multi-view images of identical scenes, a prerequisite for image retrieval [3], image registration [4], Structure from Motion (SfM) [5], and Simultaneous Localization and Mapping (SLAM). Cross-daylight multi-view street scene matching confronts three coupled constraints: (1) wide-baseline viewpoint variations induce local appearance distortions, causing a significant performance degradation of traditional feature descriptors under extreme perspective changes; (2) illumination intensity dynamics spanning orders of magnitude lead to contrast inversion and chromatic aberrations; and (3) semantic interference fields arise from repetitive textures and weakly textured regions. Although existing SfM/SLAM frameworks employ RANSAC-based outlier rejection, they fail to ensure topology-consistent feature correspondences, resulting in structural discontinuities and topological distortions in 3D point cloud reconstruction.

To address these challenges, we propose a Topology-Aware Multi-View image Matching (TAMVM) framework that seamlessly integrates geometric constraints and semantic consistency, specifically tailored for cross-daylight conditions. This framework is designed to preserve local geometric consistency while maintaining robust and stable correspondences, even under complex environmental variations such as illumination changes and viewpoint distortions.

1.2. Related Work

Over the past few decades, image matching has been a widely studied topic, encompassing both handcrafted and deep learning-based approaches. Feature matching has been a long-standing challenge in computer vision, especially in multi-source street-view scenarios where images exhibit extreme variations in illumination, viewpoint, and texture patterns. In the field of multi-source imagery, deep learning methods are clearly more advantageous due to their shorter development cycles, lower costs, and ability to efficiently process large-scale data. From the perspective of image matching principles, existing research primarily focuses on three key aspects: feature extraction, feature matching, and the optimization of matches.

1.2.1. Handcrafted Feature-Based Image Matching Methods

Conventional feature detection methods rely heavily on handcrafted criteria and gradient statistics. Representative algorithms such as SIFT and SURF [6] have been refined into improved variants like ASIFT [7] and RIFT [8] to enhance the precision of feature detection and description. Zhang et al. [9] introduced a method based on Gabor filter decomposition and phase consistency to extract feature points within normalized regions, utilizing Gaussian mixture models to establish correspondences and estimate transformation matrices, thereby addressing the low positioning accuracy of affine-invariant feature points. Similarly, Xiao et al. [10] proposed an affine-invariant oblique image matching approach by estimating camera orientation parameters to compute an initial affine matrix, performing inverse affine transformation to rectify the image, and subsequently applying SIFT-based matching [11]. Lee et al. [12] evaluated the performance of different feature descriptors, aggregation strategies, and Nearest Neighbor search algorithms in UAV image retrieval. They proposed an optimal image retrieval method combining SIFT, VLAD, and HNSW, which improves retrieval accuracy and efficiency. Yuan [13] proposed an improved dense matching algorithm based on optical flow fields (OFFDM). While these approaches exhibit robustness in traditional optical image matching tasks, their effectiveness is often hindered in complex scenarios involving diverse geometric deformations, particularly in cross-daylight multi-source street-view imagery. The ambiguity of local descriptors under such conditions leads to challenges such as high computational complexity, reduced robustness, and suboptimal practical performance.

1.2.2. Deep Learning-Based Image Matching Methods

With the advancements in deep learning, image matching has increasingly adopted deep learning-based methods to extract more robust keypoints and descriptors. These approaches learn pixel-wise similarity directly from raw image data, effectively capturing shared features across multi-view imagery. For instance, MatchNet [14] employs a Siamese network to extract feature points and measure descriptor similarity, while KeyNet [15] and R2D2 [16] integrate convolutional networks with multi-scale representations to construct scale- and viewpoint-invariant feature point networks. Peng et al. [17] introduced a method called Radiometric Invariant Phase Correlation (RIPC), designed to simultaneously estimate rotation, scale, and displacement changes in multimodal image pairs. Liao et al. [18] proposed a repetitive feature optimization strategy that dynamically filters and refines matching features in multimodal images (such as optical and SAR), significantly enhancing generalization capability and localization accuracy. Combining parameter-free filtering with enhanced sketch features, Liao et al. [19] proposed an adaptive matching framework to address geometric and radiometric differences in multimodal images under complex scenarios. Methods like ASLFeat [20] and D2Net [21] leverage multi-pyramid architectures to simulate traditional Difference of Gaussian (DoG) principles, generating scale-invariant descriptors.

For feature matching, commonly used strategies include Nearest Neighbor (NN), Fixed Threshold (FT), Mutual Nearest Neighbor (MNN), and Nearest Neighbor Distance Ratio (NNDR). While NNDR improves performance, it remains dependent on stable feature descriptors. SuperGlue [22] addresses this limitation by incorporating an attention mechanism to jointly match sparse keypoints and descriptors within a global context, significantly enhancing matching accuracy. However, its performance remains constrained by the quality of feature point detection. Furthermore, although attention mechanisms demonstrate superior capabilities in image matching, they have been found to lack local consistency in large-scale street-view imagery, exhibiting spatial correlation diffusion effects that degrade performance under substantial scale and viewpoint variations [23].

1.2.3. Geometric Topology-Based Mismatch Removal

To address high-complexity mismatches between affine-transformed image pairs, non-parametric methods enhance matching robustness by relaxing parametric model assumptions under scene deformation smoothness constraints. These approaches primarily include the following categories: graph matching methods, non-parametric interpolation methods, and local geometric constraint methods.

Graph matching methods typically define cost functions using both feature descriptor similarity and spatial geometric consistency of feature distributions. By minimizing structural discrepancies between two graphs through global optimization, these methods effectively eliminate false matches [24], offering substantial flexibility for transformation models.

Non-parametric interpolation methods learn non-parametric functions through prior-conditional interpolation or regression. These approaches map features from one image to another, then verify the consistency of each candidate match within the hypothesized correspondence set against the estimated mapping function, thereby removing inconsistent matches to suppress mismatches [25].

Local geometric constraint methods operate under the assumption that geometric structures among local region features remain preserved in affine-transformed images [26]. Based on this principle, such methods design specialized local geometric structure descriptors to eliminate mismatches.

Inspired by these works, this paper explores a geometric topology-based method for removing mismatches in wide-view-angle street-view image matching. Given the distinct geometric characteristics of building structures in street-view imagery, the proposed method achieves significant reduction in mismatches.

1.2.4. Match Expansion-Based Delaunay Triangle (DT) Constraint

With the widespread adoption of high-resolution imagery, the visual similarity between adjacent ground features has significantly increased, leading to multi-peak response characteristics of target image feature points in reference images (i.e., single points corresponding to multiple candidate matches). This phenomenon substantially elevates the complexity of high-precision image matching [27]. Traditional methods such as brute-force matching and k-Nearest Neighbor (k-NN) matching typically filter matched pairs based on descriptor similarity thresholds [28]. However, due to the lack of geometric structural constraints, these approaches tend to suffer from sparse matching distributions and mismatch propagation.

Studies demonstrate that DT can effectively enhance matching robustness through topological relationship modeling. Due to its strong structural stability, DT constructs topological connections between feature points based on the empty circle criterion, dividing the image plane into triangular meshes. By constraining affine transformation parameters (e.g., homography matrices) between adjacent triangles, DT significantly suppresses mismatches caused by nonlinear deformations [29]. Using initially reliable matches as seeds, DT expands candidate match spaces through hierarchical expansion of triangulation. Zhu et al. [30] proposed a DT-based progressive match expansion strategy, which increases initial match counts via affine consistency verification across triangular meshes. Zhang et al. [31] developed a DT-driven registration framework that improves large-scale image registration efficiency through topology entropy-weighted optimization. Despite extensive research on DT constraints, their adaptability to large viewpoint differences and cross-daylight image matching remains limited. For instance, existing methods predominantly construct fixed DT based on initial matches, which may fail to propagate matches when viewpoint-induced local topological distortions (e.g., building occlusions) occur.

1.3. Research Objectives

Matching multi-source, cross-daylight street-view images presents significant challenges due to extreme variations in illumination, viewpoint, and scale differences. Conventional global attention mechanisms often overlook local consistency, where true matches exhibit spatial proximity, while false matches are randomly distributed. Although attention mechanisms enhance feature aggregation via long-range dependencies, they also introduce irrelevant contextual information, leading to dispersed response distributions. In repetitive textures or abrupt scale variations, misleading information from non-local similar structures (e.g., building facades) may propagate mismatches in a cascading manner. Additionally, under large-scale differences, strict Mutual Nearest Neighbor (MNN) strategies may introduce geometric inconsistencies in block-level matching. While MNN effectively eliminates ambiguous matches via bidirectional constraints, scale variations may cause multiple highly similar regions in a high-resolution image to map onto a single reference block in a lower-resolution image, leading to a “many-to-one” mapping problem. In such cases, simply selecting the highest-confidence match and enforcing mutual testing may result in the unintended rejection of valid correspondences.

To overcome these limitations, we propose a robust TAMVM framework designed to enhance spatial consistency, geometric reliability, and matching robustness in complex urban environments. Our method integrates illumination-invariant feature extraction, multi-scale feature fusion, and geometric topology constraints to establish high-confidence correspondences in challenging urban scenes. A self-supervised learning paradigm is employed to construct robust feature representations that remain stable under extreme viewpoint and lighting variations. A hierarchical feature aggregation mechanism is introduced to refine multi-scale feature correspondence while suppressing ambiguity in repetitive-textured regions. To enforce geometric consistency, we develop a topology-guided refinement strategy based on DT, which stabilizes local feature correspondences and expands the matching set through localized affine transformations. Furthermore, multi-plane homography transformations are utilized to handle perspective distortions in wide-baseline matching scenarios, maintaining structural regularity across viewpoints.

This study makes the following key contributions:

(1)

This study proposes a hierarchical feature fusion framework integrating self-supervised learning with geometric augmentation techniques. By jointly optimizing local descriptors and global geometric structures in multi-view images, it extracts illumination-invariant features to resolve feature degradation under cross-illumination conditions (e.g., varying lighting) and wide-baseline scenarios (e.g., scale variations and perspective distortions).

(2)

A DT-based local homography transformation strategy is designed to stabilize topological structures and expand matches through multi-planar geometric constraints. This method enhances spatial consistency, particularly in complex urban scenes with repetitive textures and multi-scale building facades, thereby significantly improving geometric reliability.

(3)

We present a hierarchical attention model using Graph Neural Networks (GNNs) to dynamically fuse contextual information between local keypoints and semantic–topological graphs. Combined with a dual-branch learning strategy (supervised block alignment + unsupervised spatial consistency constraints) and a topology-guided multi-planar expansion mechanism, it effectively resolves matching ambiguities in occluded regions. Simultaneously, it suppresses mismatch propagation by leveraging inherent structural regularities in street-view imagery, significantly enhancing multi-source image matching performance in complex urban scenes.

The remainder of this paper is organized as follows. Section 2 details the proposed feature matching framework and the multi-plane matching point expansion mechanism. Section 3 and Section 4 present the design of validation experiments and comparative analysis with conventional methods. Finally, Section 5 concludes the paper while discussing the generalizability and limitations of the proposed method.

2. Methods

This study proposes an illumination-robust multi-view matching framework by unifying geometric topology and semantic consistency for cross-daylight urban perception. The main steps include (1) a self-supervised paradigm extracting illumination-agnostic features through the joint optimization of local descriptors and global geometric structures; (2) a homography-aware module stabilizing features under extreme viewpoint variations; (3) a hierarchical-attention graph network aggregating contextual cues from keypoints and semantic topology to address occlusion and texture ambiguity; (4) a dual-branch metric learning strategy combining supervised patch alignment and unsupervised spatial consistency via DT; and (5) a topology-guided multi-plane propagation mechanism leveraging urban structural priors to expand matches while suppressing outliers.

2.1. Overview of the Proposed Method

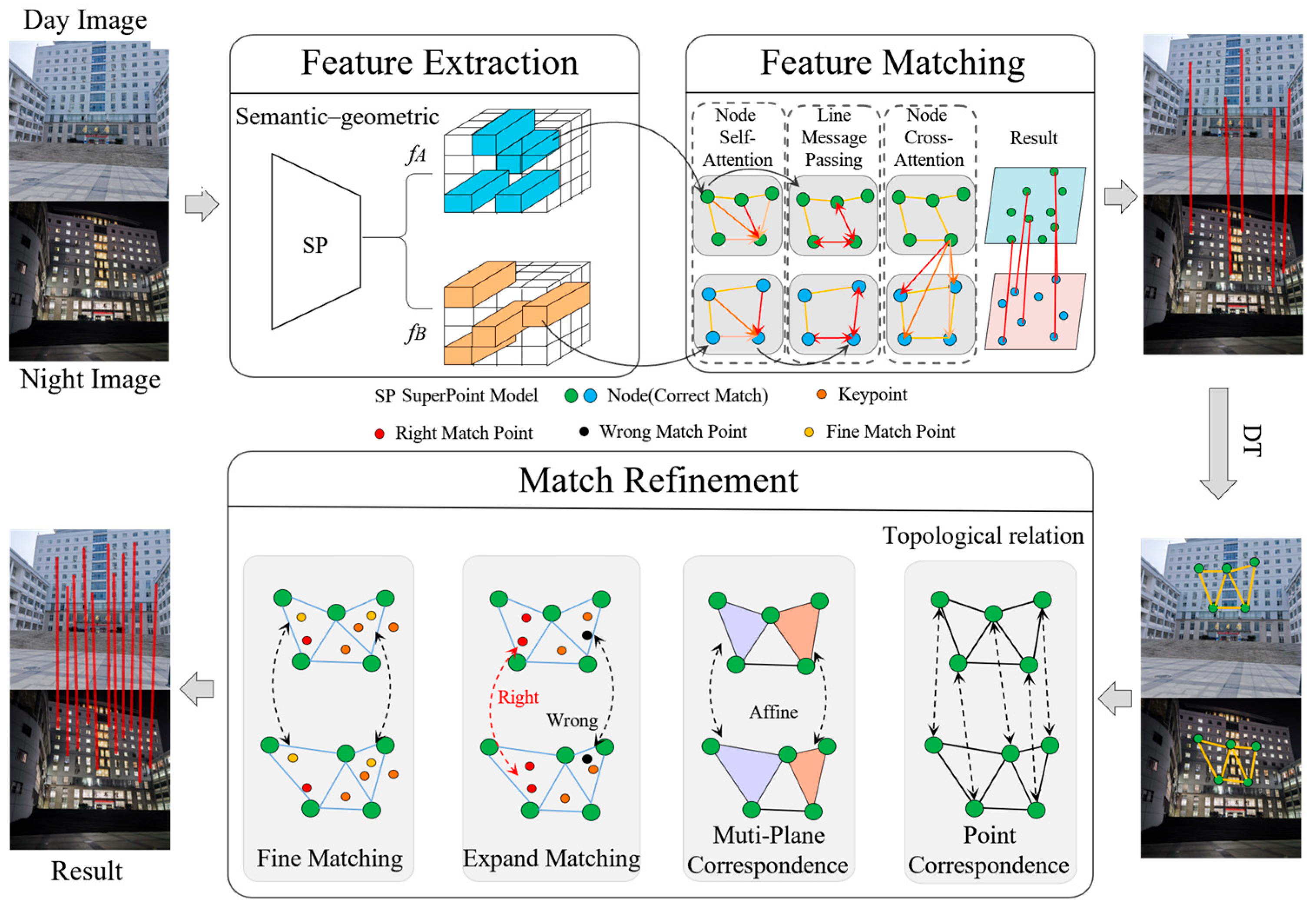
As illustrated in Figure 1, the proposed image matching algorithm, which consists of three key stages: feature extraction, feature matching, and match refinement.

(1)

Feature Extraction: This module extracts local feature maps from the input image pair $I_A$ and $I_B$, leveraging a self-supervised learning paradigm to detect and describe keypoints while incorporating semantic–geometric features. To enhance robustness across varying illumination conditions and acquisition devices, homography transformations are integrated to stabilize feature representations across diverse viewpoints. This ensures that both local descriptors and global geometric structures are preserved, mitigating the impact of extreme perspective variations.

(2)

Feature Matching: To establish high-confidence correspondences, this stage employs a GNN-based method, capturing both local keypoint relationships and high-level semantic topology. Initial correspondences are determined using inner-product similarity between local descriptors and refined via the Sinkhorn algorithm, which enforces optimal matching constraints. Furthermore, self-attention and cross-attention mechanisms dynamically aggregate global contextual information, reducing mismatches in occluded and repetitive-textured regions while improving robustness under large viewpoint variations.

(3)

Match Refinement and Expansion: To increase the spatial consistency and coverage of correspondences, we introduce a DT-based constraint mechanism. A triangulated graph is constructed across the image pair, allowing multi-local homography transformations to extend correspondences into low-confidence regions. By leveraging both geometric regularity and topological constraints, this module refines correspondences and propagates valid matches across structured urban environments, yielding a comprehensive, accurate, and topology-consistent final matching result.

2.2. Robust Learning Feature Extraction

2.2.1. Feature Extraction Network Architecture with Scale and Rotation Invariance

Given an image pair $I_A$ and $I_B$, the SuperPoint [32] feature detector is employed to extract features. The network utilizes a VGG-style backbone to downsample the image dimensions to $H_c=H/8$ and $W_c=W/8$. After the encoder stage, the input image $I\in {\mathcal{R}}^{H\times W}$ is transformed into a tensor $\mathcal{B}\in {\mathbb{R}}^{H_c\times W_c\times F}$. Subsequent bilinear interpolation and descriptor normalization are applied to generate unified-length descriptors, resulting in a feature dimensionality transition from $\mathcal{D}\in {\mathbb{R}}^{H_c\times W_c\times D}$ to ${\mathbb{R}}^{H\times W\times D}$.

2.2.2. Network Training Loss

To comprehensively model the correspondence between positive and negative matches, we adopt the training loss function from SuperPoint, which demonstrates robust performance for both detection and descriptor learning. The loss function is formulated as:

$$\mathcal{L}\left(\mathcal{X},{\mathcal{X}}^{\prime },\mathcal{D},{\mathcal{D}}^{\prime };Y,Y^{\prime },S\right)={\mathcal{L}}_p(\mathcal{X},Y)+{\mathcal{L}}_p\left({\mathcal{X}}^{\prime },Y^{\prime }\right)+\lambda {\mathcal{L}}_d\left(\mathcal{D},{\mathcal{D}}^{\prime },S\right),$$

(1)

where ${\mathcal{L}}_p$ denotes the feature point detection loss and ${\mathcal{L}}_d$ represents the descriptor loss.

2.2.3. Network Training

The network training consists of three stages:

(1)

Synthetic Pretraining: A dataset of virtual 3D objects is used to train the network for corner detection, producing the MagicPoint model.

(2)

Real-World Adaptation: The network is further trained on real-world images, where MagicPoint and homography transformations are applied to extract corner points and geometric–semantic features.

(3)

Keypoint and Descriptor Extraction: From the second stage, additional homography transformations are carried out to generate image pairs with known pose relationships. These pairs are then fed into the SuperPoint network to extract keypoints and descriptors for robust feature representation.

2.3. Feature Matching Under Attention Mechanism

This study introduces an advanced attention-driven feature matching framework that seamlessly integrates feature correspondence estimation with outlier rejection by addressing the differentiable optimal transport problem. The proposed method employs an adaptive feature aggregation mechanism to enhance global contextual understanding, enabling accurate feature matching under significant viewpoint and illumination variations. Unlike conventional methods such as k-Nearest Neighbors (KNNs) and ratio test-based approaches, our framework leverages graph-based message passing to iteratively refine feature assignments. By introducing a learnable matching strategy, it effectively filters unreliable correspondences, achieving highly robust and accurate feature matching in both indoor and outdoor environments.

2.3.1. Feature Matching Framework

Given a pair of images A and B, the initial stages provide detected keypoints and descriptors, represented as $(p,d)$. Each keypoint $p_i:=(x,y,c)$ encodes its spatial position $(x,y)$ and confidence score c, while the descriptor $d_i\in {\mathbb{R}}^D$ encodes the local appearance, where D is the descriptor dimension. The set of keypoints in the two images is denoted as $\mathcal{A}:=\{1,\dots ,M\}$ and $\mathcal{B}:=\{1,\dots ,N\}$.

2.3.2. Assignment Matrix

Feature matching follows a one-to-one constraint, meaning that each keypoint can match at most one keypoint in the other image. This yields a soft assignment matrix $P\in [\mathrm{0,1}{]}^{M\times N}$, constrained as:

$$P{1}_N\le 1_M and P^T{1}_M\le 1_N,$$

(2)

where $1_M$ and $1_N$ are all-one vectors of length $M$ and $N$, respectively.

2.3.3. Attention-Guided Graph Neural Network (GNN)

The attention-based GNN integrates self-attention and cross-attention to iteratively refine feature correspondences. When better candidate matches emerge during feature aggregation, the network re-evaluates and updates the matching relationships, ensuring stability in complex environments. This feature allows the method to significantly reduce mismatches.

For each keypoint $i$ in image $Q$, all corresponding features are retrieved from image $S$, where $(Q,S)\in {\{A,B\}}^2$. Each attention layer follows:

$${\mathit{q}}_i={\mathit{W}}_1^{\left(\mathcal{l}\right)}{\mathit{x}}_i^Q+{\mathit{b}}_1,$$

(3)

$$\left[\begin{array}{c}{\mathit{k}}_j\\ {\mathit{v}}_j\end{array}\right]={\left[\begin{array}{c}{\mathit{W}}_2\\ {\mathit{W}}_3\end{array}\right]}^{\left(\mathcal{l}\right)}{\mathit{x}}_i^S+\left[\begin{array}{c}{\mathit{b}}_2\\ {\mathit{b}}_3\end{array}\right],$$

(4)

where ${\mathit{q}}_i$ represents the query vector, while ${\mathit{k}}_j$ and ${\mathit{v}}_j$ are the key and value vectors for keypoint $j$. The attention mechanism progressively refines feature embeddings by aggregating information across the image pair.

The update function for keypoint $i$ through self-attention and cross-attention is:

$${\mathit{m}}_{\mathcal{E}\to i}={\sum }_{j:(i,j)\in \mathcal{E}}{\alpha }_{ij}{\mathit{v}}_j,$$

(5)

where ${\alpha }_{ij}$ is the attention weight, computed as:

$${\alpha }_{ij}=\mathrm{Softma}{\mathrm{x}}_j\left({\mathit{q}}_i^{\top }{\mathit{k}}_j\right).$$

(6)

The iterative update rule for feature embeddings is:

$${\mathit{x}}_i^{A(\mathcal{l}+1)}={\mathit{x}}_i^{A\left(\mathcal{l}\right)}+\mathrm{MLP}([{\mathit{x}}_i^{A\left(\mathcal{l}\right)}\Vert {\mathit{m}}_{\mathcal{E}\to i}]).$$

(7)

After $L$ layers of refinement, the final attention-enhanced feature descriptors are obtained:

$$f_i^A=W^{\left(L\right)}\cdot x_i^A+b,\forall i\in \mathcal{A},$$

(8)

$$f_j^B=W^{\left(L\right)}\cdot x_j^B+b,\forall j\in \mathcal{B}.$$

(9)

2.3.4. Feature Matching via Optimal Transport

The refined feature descriptors $f_i^A$ and $f_j^B$ are then used to construct a similarity score matrix:

$${\mathit{S}}_{i,j}=<{\mathit{f}}_i^A,{\mathit{f}}_j^B>,\forall (i,j)\in \mathcal{A}\times \mathcal{B}.$$

(10)

To handle unmatched keypoints, an additional dustbin row and column are introduced:

$${\stackrel{-}{\mathit{S}}}_{i,N+1}={\stackrel{-}{\mathit{S}}}_{M+1,j}={\stackrel{-}{\mathit{S}}}_{M+1,N+1}=z,$$

(11)

where $z\in \mathbb{R}$ represents the outlier rejection score. The soft assignment matrix is then constrained by:

$$\overline{\mathit{P}}{1}_{N+1}=\mathit{a},\hspace{1em}{\overline{\mathit{P}}}^{\top }{1}_{M+1}=\mathit{b},$$

(12)

where

$$\mathit{a}={\left[\begin{array}{cc}{1}_M^{\top }& N\end{array}\right]}^{\top },\mathit{b}={\left[\begin{array}{cc}{1}_N^{\top }& M\end{array}\right]}^{\top }.$$

(13)

This ensures that each keypoint in image $A$ is assigned at most one match in image $B$, while allowing for possible unmatched points.

The optimal transport (OT) problem is then formulated as:

$$\mathit{max}{\sum }_{i,j}{\mathit{S}}_{i,j}{\mathit{P}}_{i,j},$$

(14)

which is efficiently solved using the differentiable Sinkhorn algorithm. After removing outliers, the final assignment matrix $P$ is obtained, yielding reliable feature correspondences.

2.3.5. Loss Function

Given known matches $\mathcal{M}=\left\{\right(i,j\left)\right\}\subset \mathcal{A}\times \mathcal{B}$ as positive sample pairs and unmatched points $\mathcal{I}\subseteq \mathcal{A}$ and $\mathcal{J}\subseteq \mathcal{B}$ as negative sample pairs, the loss function aims to jointly maximize matching precision and recall through the following formulation:

$$\begin{array}{ll}\hfill Loss=& -{\displaystyle \sum _{(i,j)\in \mathcal{M}}\log }{\overline{P}}_{i,j}\hfill \\ & -{\displaystyle \sum _{i\in \mathcal{I}}\log }{\overline{P}}_{i,N+1}-{\displaystyle \sum _{j\in \mathcal{J}}\log }{\overline{P}}_{M+1,j}\hfill \end{array}$$

(15)

2.4. Fine Matching Under Multi-Plane Constraints

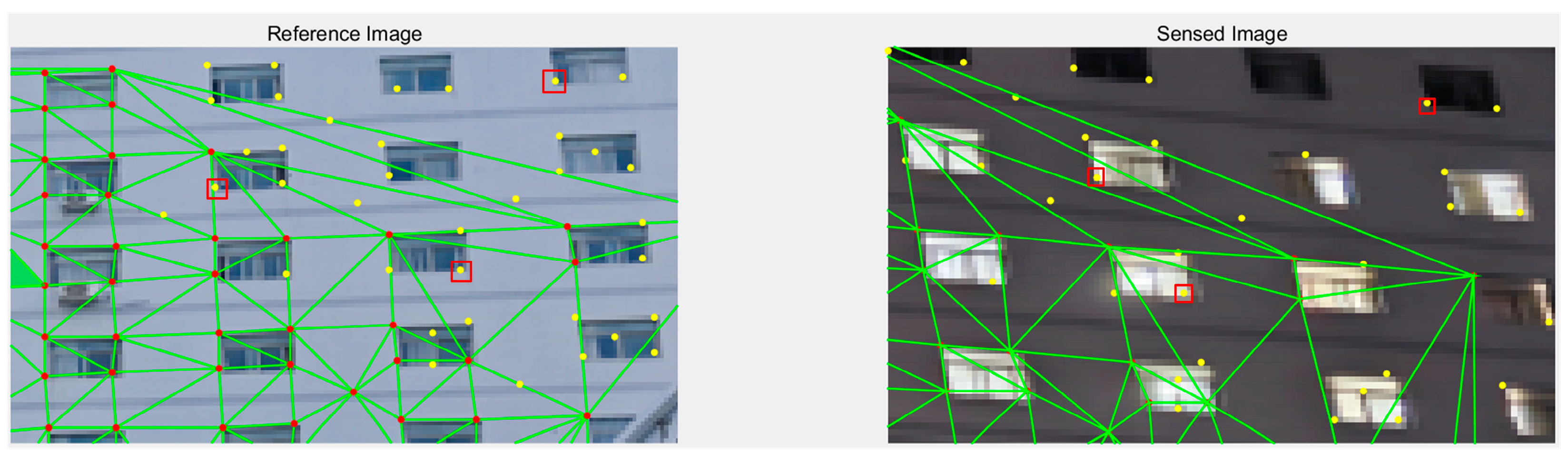
In complex street-view image matching tasks, the initial matches obtained by preceding modules through global feature extraction often fail to comprehensively cover potential matching regions across the entire image. This limitation stems from multi-plane scene structures, viewpoint variations, and heterogeneous imaging conditions. Such deficiencies are particularly pronounced in geometrically distinctive multi-plane objects (e.g., buildings), manifesting as missed and false matches caused by insufficient feature point and descriptor extraction, as shown in Figure 2. The red dots indicate correct matches, and the yellow dots indicate possible missed matches. We mark the correct matches in the yellow dots with red boxes.

To address this, we propose a multi-plane matching point expansion mechanism constrained by DT to enhance geometric consistency and matching stability between images. The proposed method constructs multi-local homography matrices to propagate matches across planar regions under topological constraints, ensuring local consistency between planes and the geometric reliability of correspondences.

2.4.1. DT Construction and Constraints

For an image pair $I_A$ and $I_B$, the initial matching results in a correspondence set $C=\left\{\right(p_i,q_i):i=\mathrm{1,2},\dots ,n\}$, which is used to construct DT networks $G_A$ and their homologous counterparts $G_B$. The DT structures enforce topological constraints among feature points across the image planes, thereby regularizing local feature matching processes. To mitigate triangular deformations, we impose a minimum interior angle threshold (>$\pi /6$ radians) during triangulation, ensuring transformation stability. As analyzed, the core principle of DT-constrained multi-plane matching expansion lies in segmenting images into reliable inter-triangle transformations while constraining the search space for candidate keypoint matches. Through this dual mechanism, the DT cells establish localized consistency frameworks, thereby allowing geometric structures to be extended through affine and perspective transformations.

2.4.2. Local Affine Transformation and Initial Expansion

For each triangle ΔABC in the DT network $G_A$, we utilize three matched vertex pairs from the homologous triangle Δ$A^{\prime }{B}^{\prime }{C}^{\prime }$ in $G_B$ to define the local affine transformation matrix A:

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}{R}_{00}& R_{01}& T_x\\ R_{10}& R_{11}& T_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right],$$

(16)

where $R$ denotes the linear transformation and $T$ represents the translation transformation. With five degrees of freedom in this matrix, three matched point pairs are sufficient to solve the transformation parameters.

As shown in Figure 3, the local affine transformation matrix A, derived from three matched vertex pairs in the corresponding triangles ΔABC and Δ$A^{\prime }{B}^{\prime }{C}^{\prime }$, is applied to propagate candidate matches within the triangular regions. For any unmatched keypoint p (indicated by yellow cross) in ΔABC, its predicted correspondence q (marked with a red cross) is computed as $\mathit{q}=A\mathit{p}$. Candidate matches are then searched within a circular region (dashed red circle in Figure 3) centered at q with radius r. To ensure computational efficiency for subsequent homography estimation, we designate the feature pair $(p_i,q_i)$ with the minimum reprojection error $\left|\right|q_i-A{p}_i|{|}_2$ as propagated matches only if the error is below the predefined radius.

2.4.3. Multi-Local Homography Matrix Construction and Match Expansion

In multi-sourced imagery, most images are captured from varying viewpoints, resulting in significant perspective distortions. Traditional approaches typically employ a global homography matrix to model the transformation between image pairs, which has been widely adopted in photogrammetry and computer vision. Under homogeneous coordinates, the homographic transformation between a point $X\left(x,y,1\right)$ in reference image $A$ and its correspondence $X^{\prime }\left(x^{\prime },y^{\prime },1\right)$ in target image $B$ is expressed as:

$$X^{\prime }=H_{p}X,$$

(17)

where the homography matrix $H_p\in {\mathbb{R}}^{3\times 3}$ possesses eight degrees of freedom (DOFs), requiring at least four matched pairs for estimation—hence the necessity of propagating optimal matches in the preceding step.

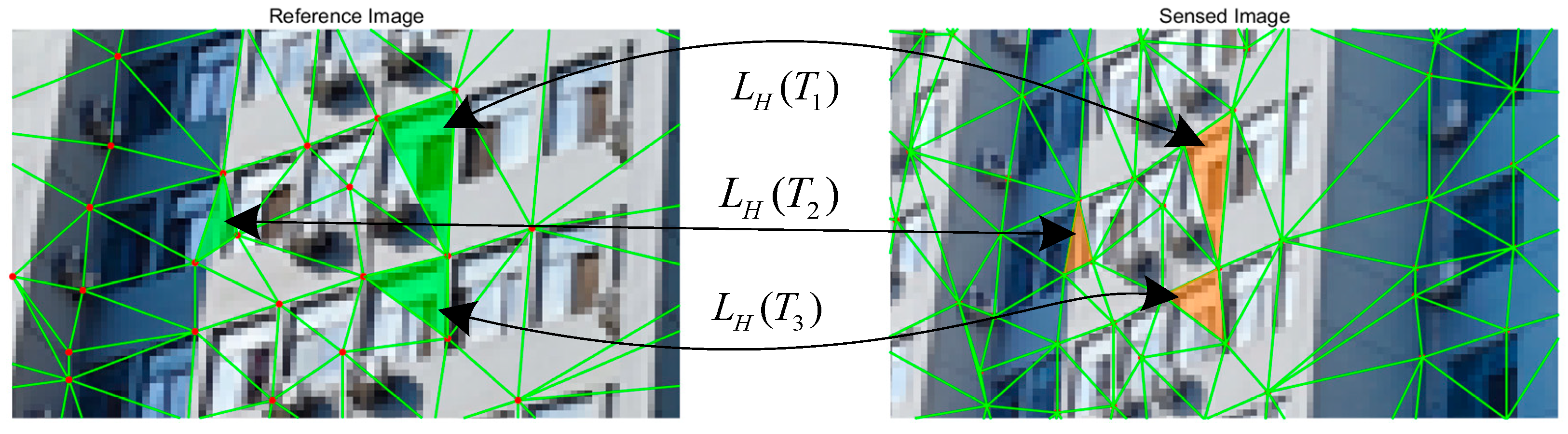
However, building façades often comprise multiple quasi-planar structures, rendering global homography matrices inadequate for capturing localized geometric variations across distinct planes. This limitation introduces reconstruction inaccuracies due to unmodeled perspective distortions. To address this, we propose multi-local homography matrices that independently model transformations for individual planar regions, thereby enhancing structural fidelity and detail preservation. Leveraging the DT framework established earlier, each triangular cell is treated as an independent planar patch, ensuring generalizability across complex urban scenes. The multi-local homography transformation is formulated as:

$$\begin{gathered} L_H(T_1,T_2,\dots ,T_n)=\left\{\right\{H_p|p\in (T_1,T_2,\dots ,T_n\left)\right\}\}, \\ {H}_p=\left[\begin{array}{ccc}{h}_{00}& h_{01}& h_{02}\\ h_{10}& h_{11}& h_{12}\\ h_{20}& h_{21}& 1\end{array}\right], \end{gathered}$$

(18)

where $T_1,T_2,\dots ,T_n$ denote corresponding triangle pairs, and $H_p$ represents the associated homography matrix with entries $h_{00}~h_{21}$. Consequently, the set $L_H$ may encompass multiple homography matrices, as shown in Figure 4.

Subsequently, we employ the multi-local homography matrices to further propagate matches across the image pair. Compared to the previous affine transformation-based expansion approach, this method replaces affine transformations with homography matrices that provide a more stable characterization of inter-triangle geometric relationships. The mathematical formulation is given by:

$$q_i=L_H\left(T_k\right)\times p_i,$$

(19)

where $L_H\left(T_k\right)$ denotes the homography matrix for the triangle $T_k$ planar region.

The homography matrices $L_H$ effectively characterize the perspective transformation relationships between corresponding triangular regions across images. Building upon this, we leverage all initial feature points extracted by SuperPoint and apply the aforementioned methodology to optimize the expansion of matches. Specifically, for both unmatched feature points within each triangular region and low-confidence matches from the initial matching results, we iteratively refine correspondences while eliminating mismatches through geometric verification. This dual process of expansion and pruning ensures the acquisition of optimal matching results, thereby achieving stable and reliable feature match expansion.

The details of the Algorithm 1 for multi-plane match expansion mechanism are shown in the following section.

Algorithm 1: Multi-plane match expansion mechanism

Input: Image pair $(I_A, I_B)$ with feature points $P\in A$ and $Q\in B$; $n$ initial corresponding points $C_{init}$.  Output: Final corresponding points $C_{final}$.  Procedure Delaunay Triangle Construction  1: Extract locations $L$ from feature points P based on initial corresponding points $C_{init}$  2: Construct the DT $G_A$ and homologous counterparts $G_B$ using candidate matches $C_{init}$  3: Corresponding point expansion based on the DT constraint $(C_{opti}\leftarrow C_{init})$  end procedure  Procedure Initial expansion  1: for each $t_A\in triangle\left(G_A\right)$ do  2: Compute affine matrix $A$ using three corresponding points based on two triangles  3: for each $p=\mathrm{inside}\left(t_A\right)$ do  4: Map a location $q_e=p\ast A$ in image $I_B$  5: Search candidate points $q_{list}$ from the circular region around $q_e$ using threshold $t_d$  6: Determine the smallest Euclidean distance d with point $q_e$ of $q$ in $q_{list}$  7: if $d\le t_d$  8:  Append a corresponding point pair $(p, q)$  9:  end if  10: end for  11: end for  end procedure  Procedure Multi-plane match expansion  1: for each $t_A\in triangle\left(G_A\right)$ and $t_B\in triangle\left(G_B\right)$ do  2: Compute local homography matrix $L_H\left(T_k\right)$ using vertex and expansion point coordinates  3: Obtain the extended points $C_{exp}$ by applying the formula $q_e=p\ast L_H\left({\mathrm{T}}_{\mathrm{K}}\right)$ to the initial feature point sets $P_{init}$ and $Q_{init}$  4: Obtain $C_{final}(C_{final}=C_{opti}\cup C_{exp})$  5: end for  end procedure

3. Experiment Results and Analysis

The experimental framework comprises three core modules: feature extraction, initial match, and fine match. To achieve high-precision match expansion under cross-daylight multi-sourced street-view imagery requirements, each component—the feature extraction network, matching network, and optimization module—is rigorously trained and validated using diverse datasets and tailored training strategies.

3.1. Experiment Implementation

Datasets and Evaluation Metrics

In the feature extraction stage, we employ a VGG-based feature extraction network, initially trained on the COCO2014 dataset, to generate generalized initial features and geometrically semantic descriptors. During the feature matching phase, a GNN framework is utilized to model relationships between feature points, also trained on the COCO2014 dataset to improve matching accuracy across image pairs. The feature point optimization method leverages a multi-plane topological structure, expanding and refining initial matches using DT-generated meshes. To ensure the stability of transformation matrices during matching, we enforce a minimum angle constraint (≥π/6) for all triangles in the DT network, thereby enhancing structural consistency and noise robustness.

This study utilizes a dataset of 14 cross-daylight multi-sourced street-view image pairs encompassing diverse device-type combinations, imaging periods, and capture conditions to simulate real-world environmental variations. The dataset configuration is as shown in

Table 1. Detailed description of experimental data.

Category	Pair	Dataset Description		Dataset Presentation
		Reference Image	Sensed Image
Mobile Devices—Daytime	1	Device: Mobile	Device: Mobile
		Size: 1280 × 760	Size: 1280 × 760
		Time: Day (Cloud)	Time: Day (Rain)
	2	Device: Mobile	Device: Mobile
		Size: 1280 × 760	Size: 1280 × 760
		Time: Day (Cloud)	Time: Day (Sun)
	3	Device: Mobile	Device: Mobile
		Size: 1280 × 760	Size: 1280 × 760
		Time: Day (Rain)	Time: Day (Rain)
UAV Devices—Daytime	4	Device: UAV	Device: UAV
		Size: 1280 × 760	Size: 1280 × 760
		Time: Day	Time: Day
Mobile Devices—Night–Daytime	5	Device: Mobile	Device: Mobile
		Size: 1280 × 760	Size: 1280 × 760
		Time: Night	Time: Day
UAV Devices—Night–Daytime	6	Device: UAV	Device: UAV
		Size: 1280 × 760	Size: 1280 × 760
		Time: Night	Time: Day
Mobile–UAV Devices—Daytime	7	Device: Mobile	Device: UAV
		Size: 1280 × 760	Size: 1280 × 760
		Time: Day	Time: Day
Mobile–UAV Devices—Night	8	Device: Mobile	Device: UAV
		Size: 1280 × 760	Size: 1280 × 760
		Time: Night	Time: Night
Mobile–UAV Devices—Night–Daytime	9	Device: Mobile	Device: UAV
		Size: 1280 × 760	Size: 1280 × 760
		Time: Night	Time: Day
	10	Device: Mobile	Device: UAV
		Size: 1280 × 760	Size: 1280 × 760
		Time: Day	Time: Night

. The dataset is sourced from diverse imaging devices, sensors, resolutions, and viewing angles, producing imagery with multi-scale characteristics, heterogeneous textural patterns, and radiometric variations. Such diversity encompasses the complexity encountered in real-world scenarios, ensuring that our experimental findings maintain practical representativeness.

To comprehensively evaluate the method’s performance, we adopt three primary metrics: number of initial matches ($NIM$), number of correct matches ($NCM$), and correct match rate ($NCR$). $NCM$ is calculated as:

$$\mathrm{Cor}(p):‖p_i-{\widehat{p}}_i‖\le \epsilon .$$

(20)

A correspondence is validated as correct if the pixel distance between the matched feature point $p_i$ and its ground-truth projected position ${\widehat{p}}_i$ is below a threshold $\epsilon$.

$NCR$ is calculated as:

$$NCR=NCM/NIM.$$

(21)

During evaluation, correspondences with matching errors below 3 pixels were classified as correct matches $NCM$, based on which the $NCR$ was computed. Experimental results were averaged over three independent trials to mitigate stochastic variability, ensuring statistical significance and maximizing the characterization of the method’s robustness and accuracy in cross-daylight multi-sourced image matching scenarios.

3.2. Methodology Design

Figure 5 delineates the workflow of the proposed method. Figure 5a demonstrates the feature extraction module, which generates densely distributed and geometrically discriminative keypoints to enhance matching robustness. Figure 5b illustrates the initial feature matching results, where high-confidence correspondences are identified to establish precise homologous DT networks. Leveraging these matches, the initial DT structure is constructed under Delaunay criteria (empty circumcircle property; minimum angle ≥ 30°), ensuring geometric stability and point-wise correspondence between triangulated meshes, as shown in Figure 5c. This topology-constrained framework provides foundational support for match propagation. Finally, Figure 5d presents the optimized results after DT-based propagation, where 26 additional geometrically verified correspondences (red lines) are established.

3.3. Experiments and Comparative Analysis

To validate the effectiveness of our algorithm in cross-daylight multi-sourced street-view image matching, qualitative and quantitative comparative experiments were conducted on a custom-built multi-sourced street-view dataset, as detailed in Table 1. Baseline methods include five state-of-the-art approaches: traditional algorithms (ASIFT and WSSF [33]) and deep learning-based methods (SuperPoint, D2-Net, and R2D2 [16]). Matching results are visualized as green lines and matching points are marked in red or green in Figure 6. For fair comparison, all baseline results were generated using the authors’ publicly released code and pretrained models.

3.3.1. Daytime with Different Weather Experimental Results Analysis

As shown in Figure 6, Figure 7, Figure 8 and Figure 9, we conducted experiments on Pairs 1–4 to evaluate the matching performance of mobile and UAV-acquired images under daytime conditions, focusing primarily on scale variations and wide-baseline viewpoint changes. The results demonstrate that traditional methods such as ASIFT and WSSF suffer from low matching accuracy and are susceptible to mismatches under large-scale transformations.

In contrast, deep learning-based approaches like SuperPoint, D2-Net, and R2D2 exhibit stronger robustness in feature extraction and matching quality across challenging perspectives.

Building upon these findings, we further extended the evaluation to consider adverse weather conditions, including rainy, cloudy, sunny, and low-light scenarios. The results indicate that our proposed method—through its integration of geometric topology constraints and semantic consistency—is capable of maintaining high recall rates and substantially reducing false matches even in complex environments affected by illumination shifts and texture degradation. These results underline the framework’s superior adaptability and robustness.

3.3.2. Night Experimental Result Analysis

As shown in Figure 10 and Figure 11, in the Pair5-Pair6 experiments, we evaluated the matching performance of mobile devices and UAV equipment in night–day scenarios. Due to extreme lighting variations, traditional local-feature-based methods (e.g., ASIFT and WSSF) struggled to extract stable features, resulting in sparse matches and numerous mismatches. Deep learning methods (e.g., D2-Net and R2D2) still exhibited matching failures in areas with significant lighting changes, while SuperPoint performed relatively better though some feature points remained unstable. Our method, by integrating geometric topology information with deep feature semantics, more robustly establishes cross-temporal matching relationships and improves match reliability.

3.3.3. Experimental Analysis of Cross-Device Matching Performance

As shown in Figure 12, Figure 13 and Figure 14, which include the results of pairs 7–10, the results show that traditional methods fail to adapt to cross-sensor image matching, while deep learning approaches, despite exhibiting some robustness in feature extraction, inadequately account for global structural relationships, resulting in uneven match distributions.

In contrast, our method achieves more stable matching across different devices by implementing topology constraints based on DT. This method significantly reduces mismatch rates in cross-view and cross-resolution scenarios while enhancing spatial consistency among matched points.

3.4. Quantitative and Qualitative Analysis

3.4.1. Qualitative Matching Result Comparison

We selected representative image pairs (Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14) to perform qualitative analysis. These pairs show large differences in scale, viewpoint, illumination, and imaging devices. For example, Pairs 1 and 3 involve significant scale and viewpoint changes. Pair 4 has both viewpoint and lighting differences. Pairs 1–4 were taken in poor weather. Pairs 6–10 come from different devices. These variations make image matching much harder.

ASIFT shows good affine invariance but performs poorly under strong lighting changes or in scenes with noise, occlusion, or repeated textures. WSSF works well in daylight but fails in night scenes. R2D2 gives reliable results for similar images, but struggles with cross-source matching, especially in textureless areas. D2-Net handles small changes well but breaks down under large scale or lighting differences.

Our method performs best across all pairs. It stays robust under various lighting, viewpoints, weather, and device settings. This shows its strong ability for matching in cross-daylight, multi-source street-view conditions.

3.4.2. Quantitative Matching Result Comparison

Table 2. Result of experiment data.

Category	Metrics	Methods
		ASIFT	WSSF [33]	Super Point [32]	D2Net [21]	R2D2 [16]	Ours
Mobile—Day1 (Cloud–Rain)	NIM	266	2065	474	894	1969	558
	NCM	20	41	276	128	182	360
	NCR	7.52%	1.99%	58.23%	14.32%	9.24%	64.52%
	Time(s)	29.08	13.43	2.46	6.42	7.04	4.5
Mobile—Day2 (Cloud–Sun)	NIM	137	2779	635	844	1775	988
	NCM	44	174	136	225	293	489
	NCR	32.12%	6.26%	21.42%	26.66%	16.51%	49.49%
	Time(s)	17.66	15.62	2.25	6.84	7.18	4.18
Mobile—Day3 (Rain–Rain)	NIM	155	2041	632	1069	2249	888
	NCM	7	17	285	92	29	541
	NCR	4.52%	0.83%	45.09%	8.61%	1.29%	60.92%
	Time(s)	31.51	16.24	2.55	6.75	6.61	4.33
UAV—Day (Cloud–Cloud)	NIM	195	1677	334	1243	2300	416
	NCM	26	94	115	592	595	197
	NCR	13.33%	5.61%	34.43%	47.63%	25.87%	47.36%
	Time(s)	25.96	14.21	2.77	7.15	6.79	3.77
Mobile—Night–Day	NIM	53	1327	523	640	1429	762
	NCM	9	20	203	74	52	442
	NCR	16.98%	1.51%	38.81%	11.56%	3.64%	58.01%
	Time(s)	18.28	16.82	2.81	6.36	6.58	4.47
UAV—Night–Day	NIM	83	1296	721	1070	1921	821
	NCM	13	18	462	184	47	562
	NCR	15.66%	1.39%	64.08%	17.20%	2.45%	68.45%
	Time(s)	23.78	15.31	2.95	7.07	6.52	3.32
Mobile–UAV—Day	NIM	120	1310	540	978	2079	665
	NCM	30	58	300	293	477	425
	NCR	25.00%	4.43%	55.56%	29.96%	22.94%	63.91%
	Time(s)	19.54	18.23	3.03	6.63	6.72	3.43
Mobile–UAV—Night	NIM	115	1727	273	870	2050	320
	NCM	10	301	150	437	537	197
	NCR	8.70%	17.43%	54.95%	50.23%	26.20%	61.56%
	Time(s)	21.53	13.41	2.53	6.6	6.84	1.83
Mobile N–UAV D	NIM	103	2591	227	934	1929	266
	NCM	8	15	114	84	90	153
	NCR	7.77%	0.57%	50.22%	8.99%	4.67%	57.52%
	Time(s)	28.1	15.21	2.75	6.74	7.52	1.33
Mobile D–UAV N	NIM	108	1056	270	691	2040	313
	NCM	18	29	161	129	110	204
	NCR	16.67%	2.75%	59.63%	18.67%	5.39%	65.18%
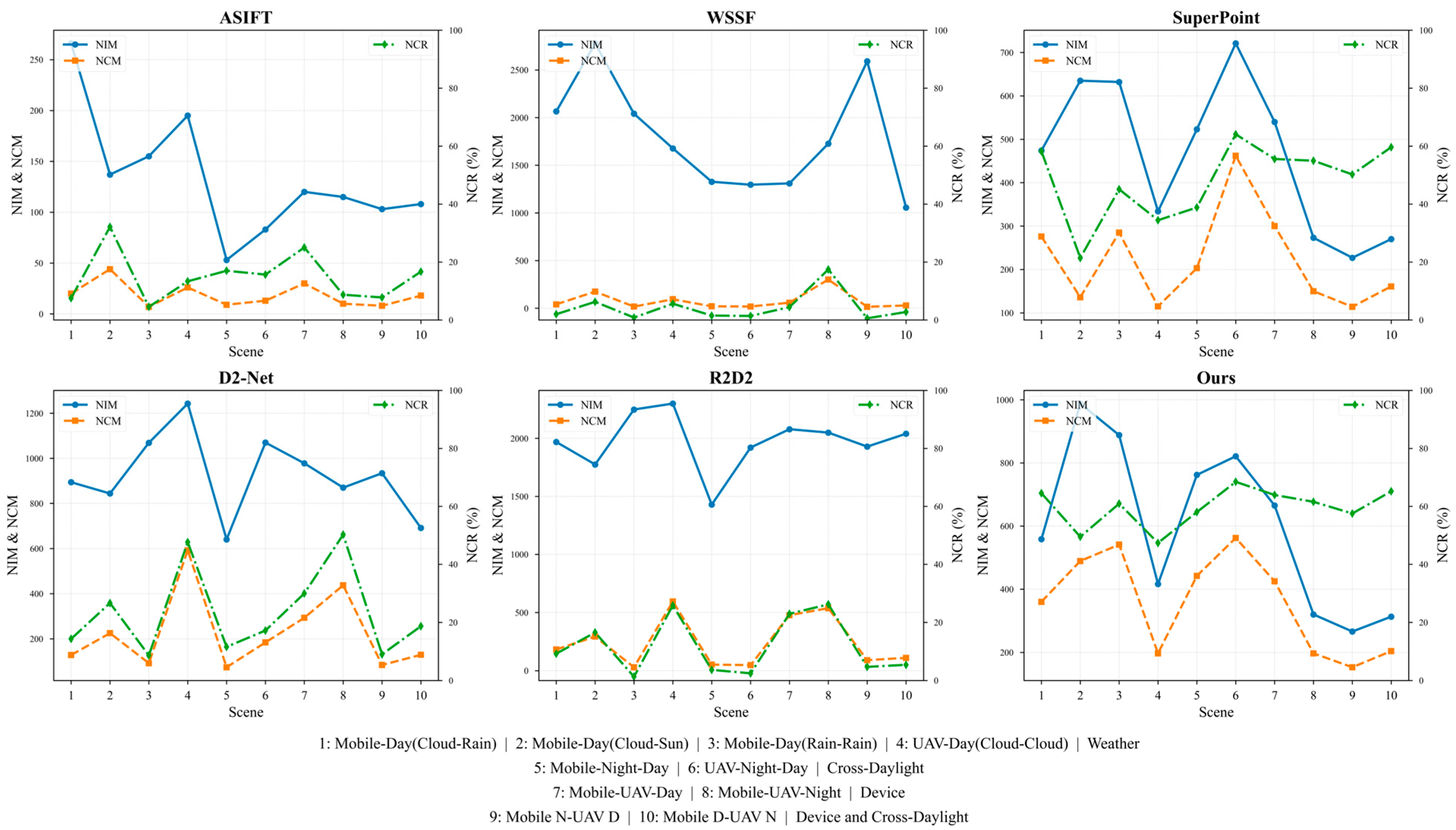
	Time(s)	17.78	13.58	2.60	6.44	6.91	2.47

lists the average quantitative evaluation results across datasets, and Figure 15 shows the results, including the number of initial matches (NIM), number of correct matches (NCM), and correct match rate (NCR). The results indicate that the proposed method achieves significantly higher NCM and NCR values. The traditional ASIFT method performs poorly on cross-device datasets due to its non-robust feature detection. The WSSF method achieves high NIM values but critically low NCR values, primarily limited by low-precision feature matching. The deep learning-based R2D2 and D2-Net methods exhibit instability in both matching quantity and accuracy, particularly under significant illumination and viewpoint variations. In comparison, the proposed method significantly outperforms other approaches in the task of cross-daylight multi-sourced street-view image matching, demonstrating notable improvements in both matching quantity and accuracy, especially under cross-source and cross-scale conditions.

3.5. Ablation Study

To rigorously evaluate the contribution of each module within the TAMVM framework, we conducted an ablation study using cross-daylight datasets collected from street-view imagery across different devices. In this study, we systematically removed or modified individual components—including the feature extractor, the graph-based matcher, and the topology-aware homography module—to observe their individual and combined effects on overall performance. The results are summarized in

Table 3. Ablation studies to test the ability of each module of TAMVM.

Method	Category	NCM	NCR
TAMVM using SIFT	Mobile Night–UAV Day	23	0.70%
	Mobile Day–UAV Night	697	21.44%
TAMVM using BF matcher	Mobile Night–UAV Day	30	4.78%
	Mobile Day–UAV Night	23	5.94%
TAMVM without topology-aware	Mobile Night–UAV Day	114	50.22%
	Mobile Day–UAV Night	161	59.63%
TAMVM full	Mobile Night–UAV Day	153	57.52%
	Mobile Day–UAV Night	204	65.18%

, where the reported metrics represent average values across multiple testing scenarios.

In the feature extraction module, our method demonstrates the ability to produce stable geometric and semantic descriptors even under substantial variations in scale, viewpoint, illumination, and imaging mechanisms. Furthermore, by integrating multi-level local feature representations, the extracted keypoints become more discriminative and robust against geometric distortions and radiometric inconsistencies.

Within the feature matching module, unlike brute-force (BF) matcher approaches that often yield limited correspondences despite high accuracy, our method obtains a richer set of correspondences across diverse street-view scenarios. This improvement stems from the GNN module’s capacity to capture latent 3D structural information, which facilitates more precise and dense matching under geometrically complex scenes—demonstrating the superior geometric perception capability of GNNs.

By jointly applying self-supervised feature extraction, GNN-based matching, and a topology-aware multi-plane homography refinement strategy, our method achieves substantial improvements in the number of correct matches (NCM) and normalized correct ratio (NCR) metrics. Compared with variants that lack topological awareness and semantic constraints, our full model achieves approximately 30.5% improvement in NCM and 6.5% in NCR, affirming the effectiveness of our geometry-aware semantic constraint design.

Interestingly, we observe that the combination of SIFT features, GNN matching, and topology guidance can, in certain favorable conditions, produce even higher NCM values. This is primarily attributed to SIFT’s strong capacity to detect a large number of keypoints in scenes with high image clarity and minimal distortion. However, SIFT suffers from poor robustness under adverse or complex lighting conditions, leading to a dramatic drop in performance in many real-world scenes. In contrast, our proposed framework consistently maintains high accuracy across a wide range of scenarios. Notably, our method achieves the highest matching precision among all evaluated baselines, highlighting its strong robustness and generalization capabilities.

4. Discussion

The superior performance of the proposed method in multi-source street-view image matching can be attributed to three key factors: (1) The deep feature extraction capability of the VGG backbone network enables robust feature representation across diverse imaging conditions. (2) The spatial relationship modeling via GNN further enhances matching precision. (3) The multi-plane topological optimization strategy effectively extends and refines low-confidence matches using DT, thereby increasing both the quantity and accuracy of cross-device and cross-temporal correspondences. Through these technical advancements, the proposed method demonstrates exceptional robustness and adaptability in complex street-view scenarios, fulfilling practical application requirements.

Here follows an analysis of the experimental results as shown in Figure 15: (1) Improved Matching Accuracy: The introduction of geometric topological relationships significantly reduces mismatches and enhances matching precision. (2) Enhanced Robustness: The stability of topological structures across dynamic lighting conditions (e.g., cross-daylight) and complex weather scenarios (e.g., rainy or cloudy scenes) enables the algorithm to maintain high matching fidelity. Unlike traditional feature-based methods that often fail under severe radiometric distortion, our framework effectively preserves structural consistency, ensuring reliable performance in real-world urban settings. (3) Complex Scene Handling: Geometric topological relationships effectively address image matching under large viewpoint differences and wide baselines, broadening applicability to diverse real-world scenarios.

5. Conclusions

This paper proposes a robust cross-daylight, multi-source street-view image matching method by integrating geometric topology and semantic representations. Designed for complex urban environments with drastic viewpoint, illumination, and structural variations, our method refines low-confidence correspondences and expands match coverage via a local homography-based optimization strategy. Furthermore, a Delaunay triangulation (DT)-based topological structure enforces spatial consistency, resulting in stable and uniform matching.

The framework comprises three modules: (1) Feature extraction preserves semantic and geometric cues for robust keypoint detection under challenging conditions. (2) Initial matching utilizes both global and local context for high-quality correspondence generation. (3) Match refinement incorporates geometric constraints and multi-plane homography to improve inlier coverage and matching completeness. The experimental results confirm that our method surpasses ASIFT, WSSF, D2-Net, R2D2, and SuperPoint in both the number of correct matches (NCM) and the matching completeness ratio (NCR), achieving superior precision and spatial consistency across diverse urban scenes.

Despite its advantages, the proposed method still faces challenges under extreme perspective distortions and highly dynamic scenes, where local topological structures may become unstable. Future work will focus on integrating deep learning-based adaptive feature adjustment strategies to enhance generalization and robustness. In addition, we plan to explore high-precision matching techniques suitable for large-angle and multi-view imagery to further refine sub-pixel-level correspondences.

To strengthen the applicability in real-world scenarios, we will expand our experiments towards practical downstream tasks such as autonomous driving and large-scale 3D urban reconstruction. Specifically, future efforts will involve constructing urban-scale benchmarks under varying lighting and traffic conditions, and integrating our method into real-time localization pipelines for autonomous vehicles. Meanwhile, we aim to evaluate the performance of our approach in generating accurate and structurally consistent 3D urban models, with a focus on dense urban areas, occlusion handling, and geometric regularity preservation.