Static–Dynamic Analytical Framework for Urban Health Resilience Evaluation and Influencing Factor Exploration from the Perspective of Public Health Emergencies—Case Study of 61 Cities in Mainland China
Abstract
1. Introduction
2. Materials and Methods
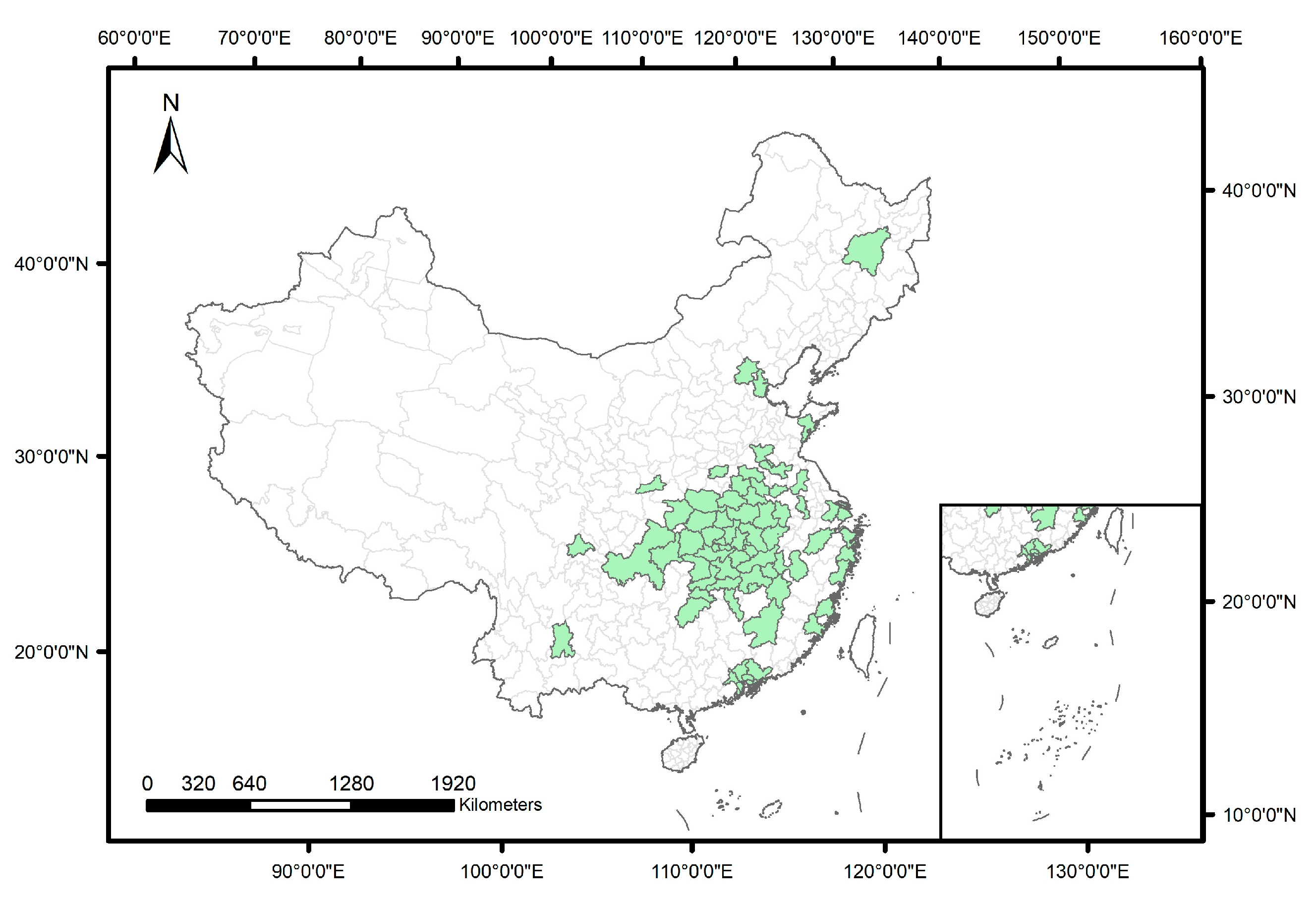
2.1. Study Area
2.2. Methodology
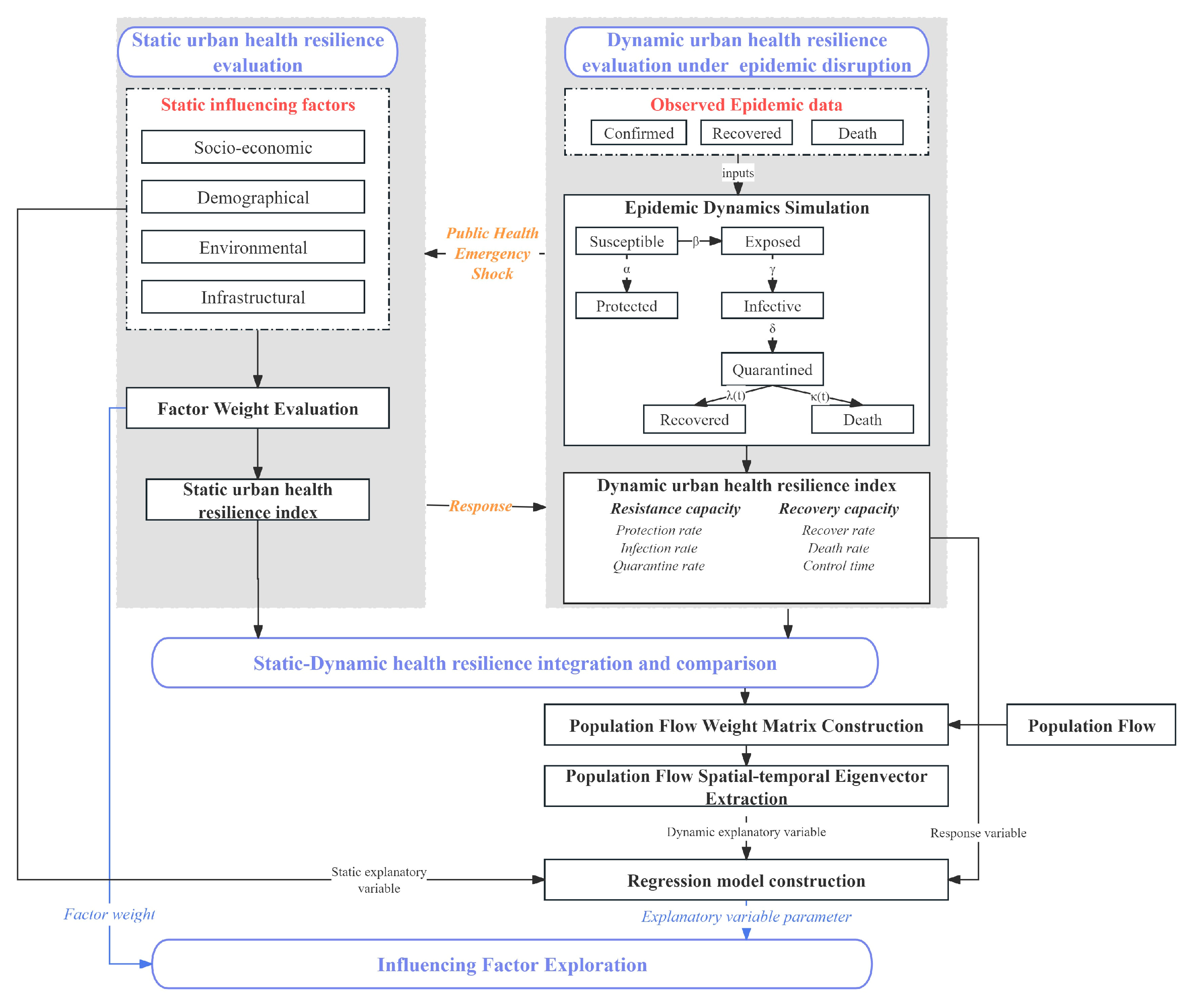
2.2.1. Analytical Framework Construction
2.2.2. Static Urban Health Resilience Index Calculation
2.2.3. Dynamic Urban Health Resilience Index Calculation
2.2.4. Population Flow-Based Spatial–Temporal Eigenvector Filtering Model Construction
2.2.5. Influencing Factor Exploration
3. Results
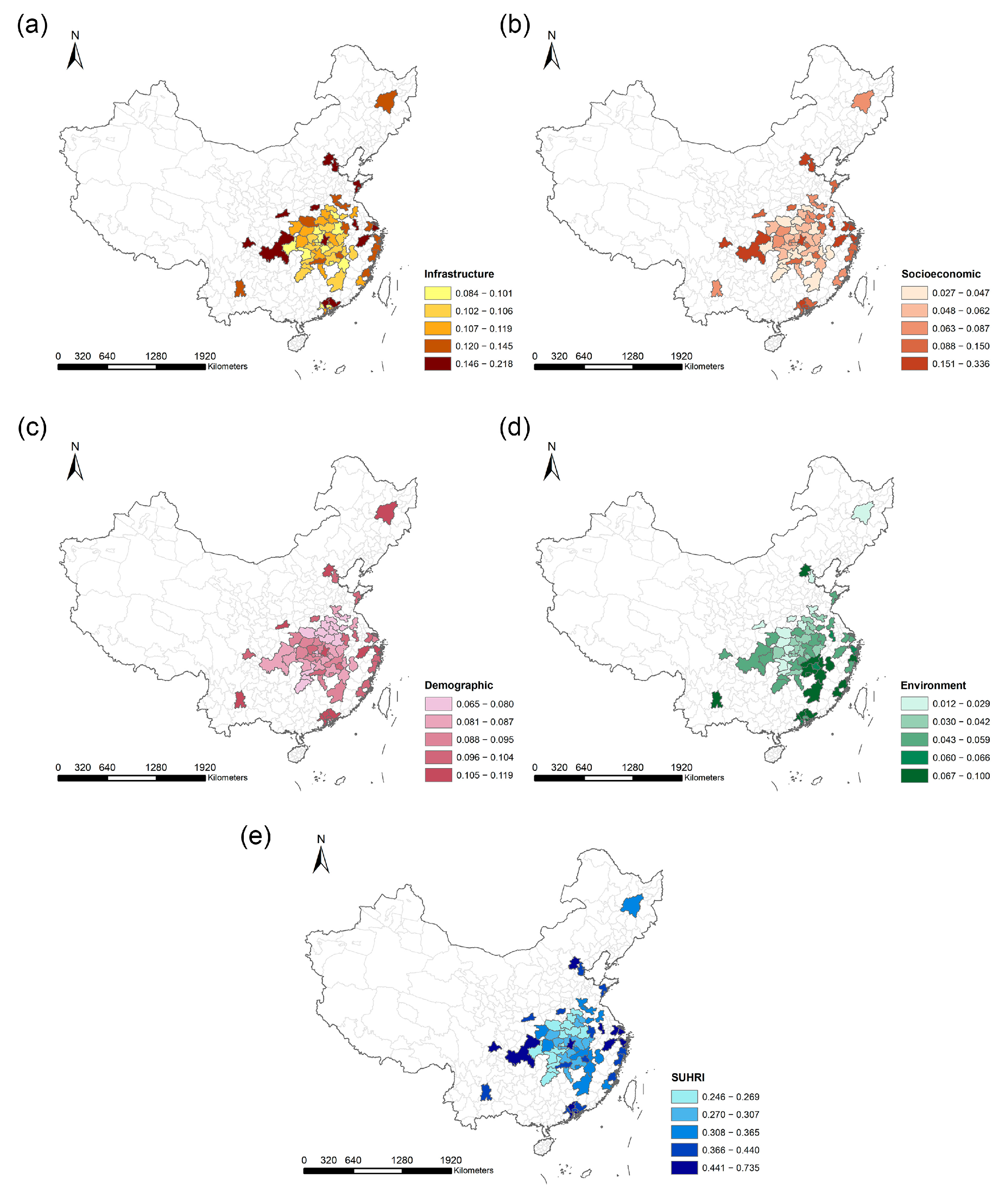
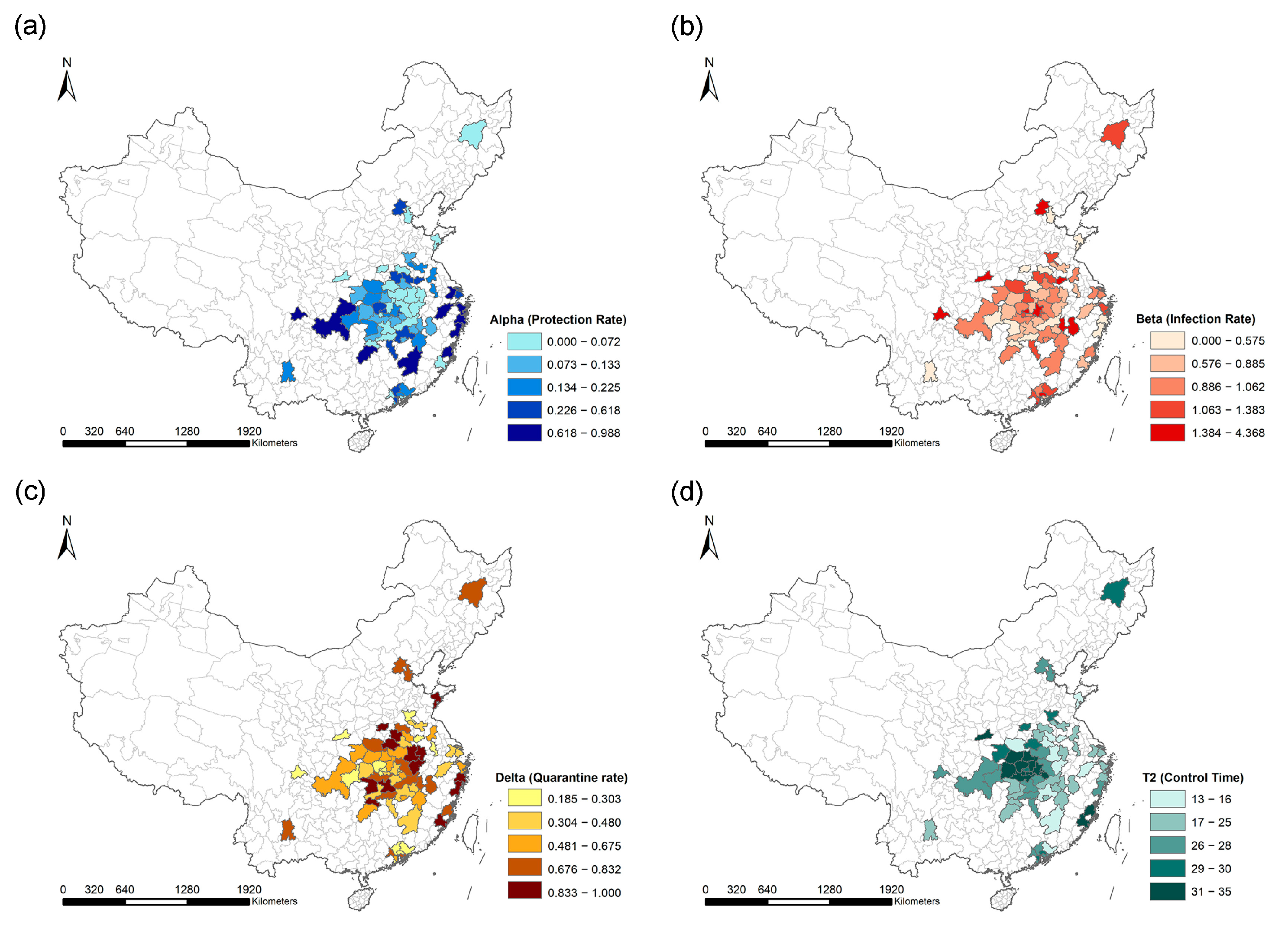
3.1. Static Urban Health Resilience Index Calculation Result
3.2. Dynamic Urban Health Resilience Index Calculation Result
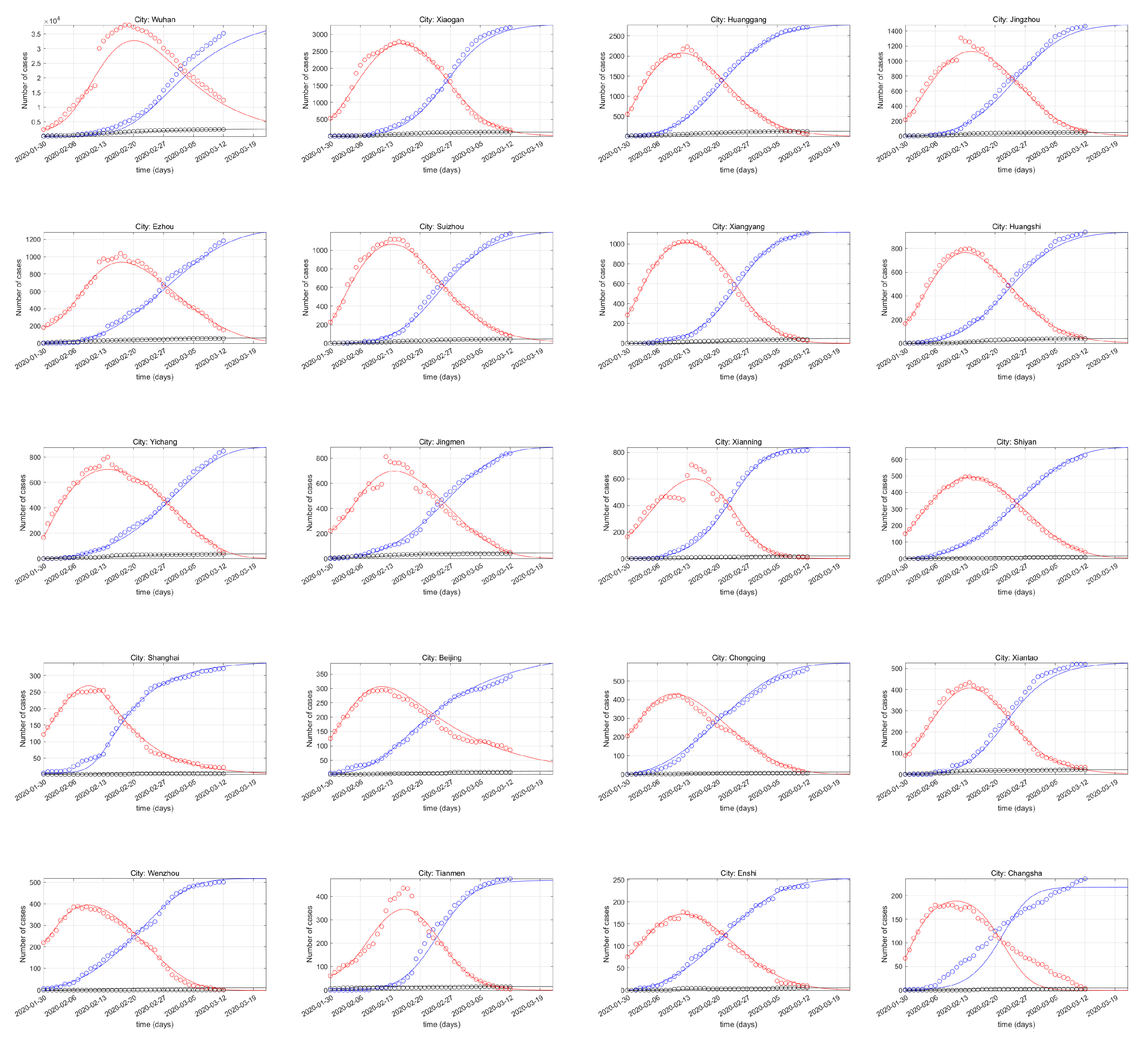
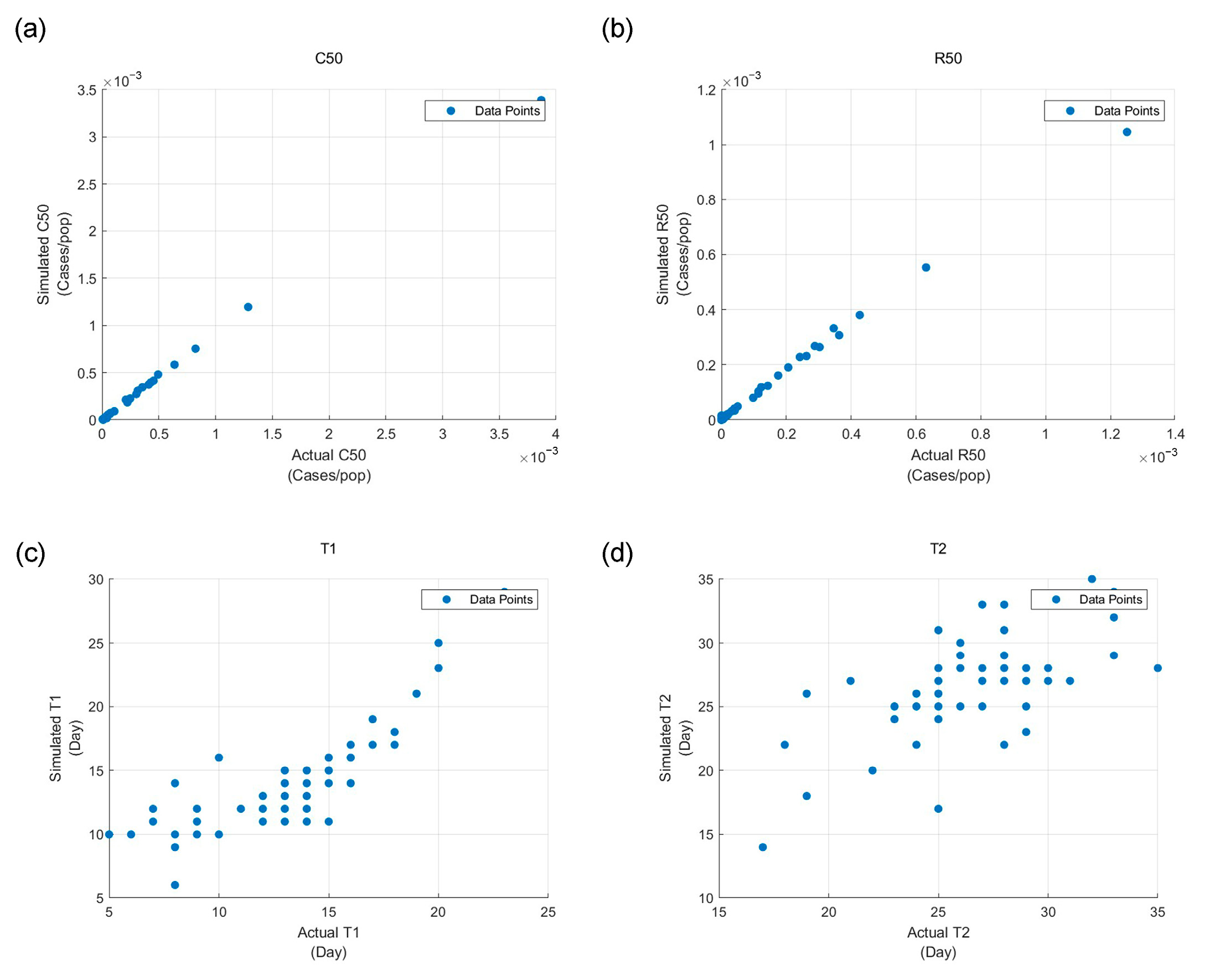
3.2.1. SEIQRDP Model Performance
3.2.2. Public Health Emergency Resistance and Recovery Index Visualization
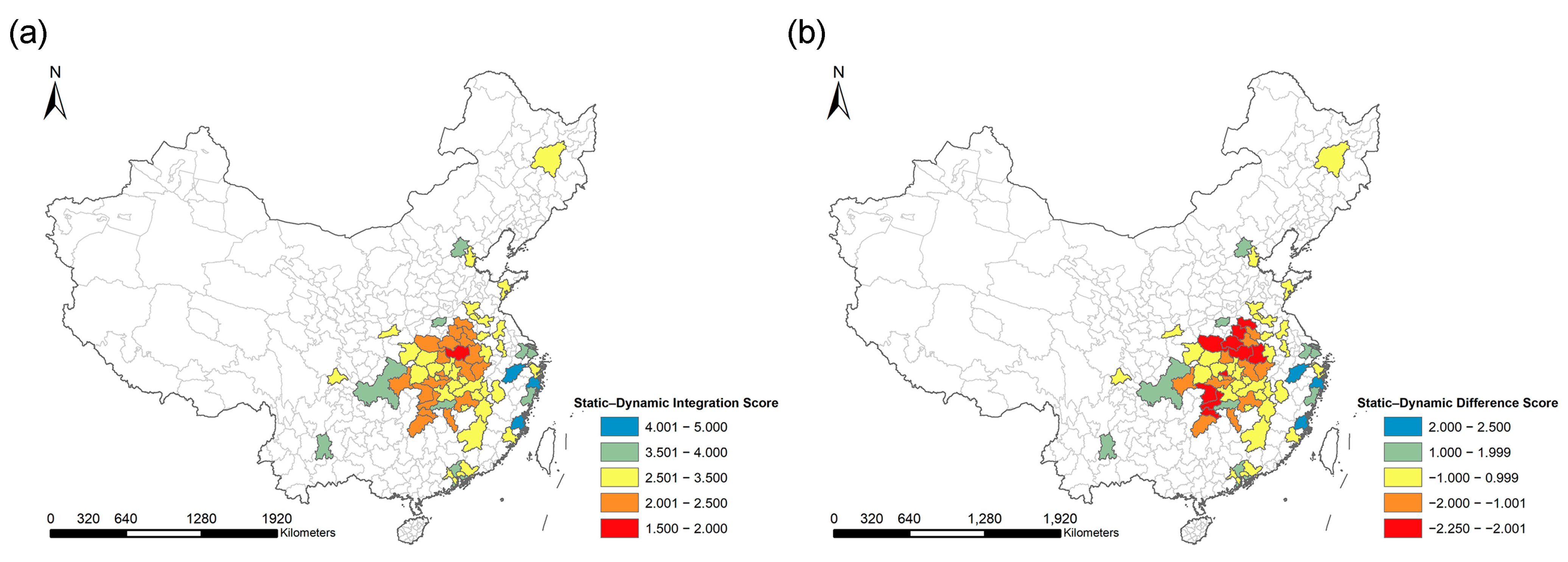
3.3. Static and Dynamic Urban Health Resilience Comparison and Integration
3.4. FLOW-ESTF Regression Model Performance
3.5. Influencing Factor Exploration Result
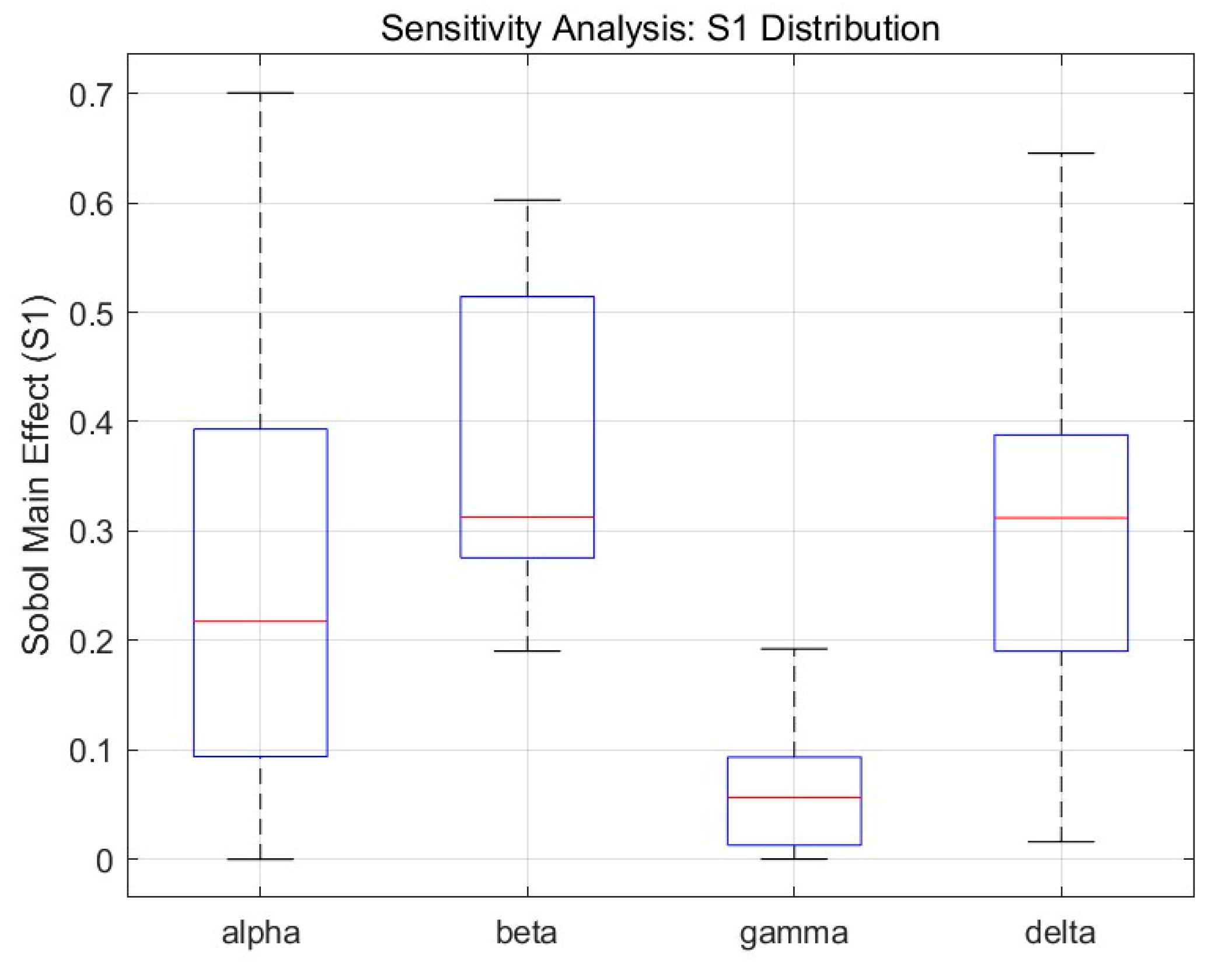
3.5.1. Influencing Factor Contribution for SUHRI
3.5.2. Influencing Factor Contribution for DUHRI
4. Discussion
4.1. Model Performance
4.2. Static and Dynamic Urban Health Resilience Comparison
4.3. Influencing Factor Contribution
4.4. Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, Z.; Qin, Y.; Li, Y.; Shen, W.; Zheng, Z.; Liu, S. Spatial and temporal differentiation of COVID-19 epidemic spread in mainland China and its influencing factors. Sci. Total Environ. 2020, 744, 140929. [Google Scholar] [CrossRef] [PubMed]
- Kostandova, N.; Schluth, C.; Arambepola, R.; Atuhaire, F.; Bérubé, S.; Chin, T.; Cleary, E.; Cortes-Azuero, O.; García-Carreras, B.; Grantz, K.; et al. A systematic review of using population-level human mobility data to understand SARS-CoV-2 transmission. Nat. Commun. 2024, 15, 10504. [Google Scholar] [CrossRef] [PubMed]
- Perofsky, A.C.; Hansen, C.L.; Burstein, R.; Boyle, S.; Prentice, R.; Marshall, C.; Reinhart, D.; Capodanno, B.; Truong, M.; Schwabe-Fry, K.; et al. Impacts of human mobility on the citywide transmission dynamics of 18 respiratory viruses in pre- and post-COVID-19 pandemic years. Nat. Commun. 2024, 15, 4164. [Google Scholar] [CrossRef] [PubMed]
- Benita, F. Human mobility behavior in COVID-19: A systematic literature review and bibliometric analysis. Sustain. Cities Soc. 2021, 70, 102916. [Google Scholar] [CrossRef]
- Guo, C.; Bo, Y.; Lin, C.; Li, H.B.; Zeng, Y.; Zhang, Y.; Hossain, M.S.; Chan, J.W.M.; Yeung, D.W.; Kwok, K.O.; et al. Meteorological factors and COVID-19 incidence in 190 countries: An observational study. Sci. Total Environ. 2021, 757, 143783. [Google Scholar] [CrossRef]
- Mansour, S.; Al Kindi, A.; Al-Said, A.; Al-Said, A.; Atkinson, P. Sociodemographic determinants of COVID-19 incidence rates in Oman: Geospatial modelling using multiscale geographically weighted regression (MGWR). Sustain. Cities Soc. 2021, 65, 102627. [Google Scholar] [CrossRef]
- Holling, C.S. Resilience and Stability of Ecological Systems. Annu. Rev. Ecol. Syst. 1973, 4, 460–482. [Google Scholar] [CrossRef]
- Ahern, J. From fail-safe to safe-to-fail: Sustainability and resilience in the new urban world. Landsc. Urban Plan. 2011, 100, 341–343. [Google Scholar] [CrossRef]
- Meerow, S.; Newell, J.P.; Stults, M. Defining urban resilience: A review. Landsc. Urban Plan. 2016, 147, 38–49. [Google Scholar] [CrossRef]
- Sharifi, A. Resilient urban forms: A macro-scale analysis. Cities 2019, 85, 1–14. [Google Scholar] [CrossRef]
- Adger, W.N. Social and ecological resilience: Are they related? Prog. Hum. Geogr. 2000, 24, 347–364. [Google Scholar] [CrossRef]
- Walker, B.; Holling, C.S.; Carpenter, S.R.; Kinzig, A. Resilience, adaptability and transformability in social–ecological systems. Ecol. Soc. 2004, 9. [Google Scholar] [CrossRef]
- Folke, C. Resilience: The emergence of a perspective for social–ecological systems analyses. Glob. Environ. Change 2006, 16, 253–267. [Google Scholar] [CrossRef]
- Martin, R.; Sunley, P. On the notion of regional economic resilience: Conceptualization and explanation. J. Econ. Geogr. 2015, 15, 1. [Google Scholar] [CrossRef]
- Ardebili pour, M.; Zare, N.; Maknoon, R. Urban flood resilience assessment & stormwater management (case study: District 6 of Tehran). Int. J. Disaster Risk Reduct. 2024, 102, 104280. [Google Scholar] [CrossRef]
- Ignatowicz, A.; Tarrant, C.; Mannion, R.; El-Sawy, D.; Conroy, S.; Lasserson, D. Organizational resilience in healthcare: A review and descriptive narrative synthesis of approaches to resilience measurement and assessment in empirical studies. BMC Health Serv. Res. 2023, 23, 376. [Google Scholar] [CrossRef]
- Zawadzki, M.; Montibeller, G. A framework for supporting health capability-based planning: Identifying and structuring health capabilities. Risk Anal. 2023, 43, 78–96. [Google Scholar] [CrossRef]
- Alizadeh, H.; Sharifi, A. Analysis of the state of social resilience among different socio-demographic groups during the COVID- 19 pandemic. Int. J. Disaster Risk Reduct. IJDRR 2021, 64, 102514. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Q.; Li, X.; Zhang, X.; Qiu, Z. Spatial-temporal evolution characteristics and critical factors identification of urban resilience under public health emergencies. Sustain. Cities Soc. 2024, 102, 105221. [Google Scholar] [CrossRef]
- Galbusera, L.; Cardarilli, M.; Giannopoulos, G. The ERNCIP survey on COVID-19: Emergency & Business Continuity for fostering resilience in critical infrastructures. Saf. Sci. 2021, 139, 105161. [Google Scholar]
- Sun, J.-Y.; Zhou, L.-Y.; Deng, J.-Y.; Zhang, C.-Y.; Xing, H.-G. Spatio-Temporal Analysis of Urban Emergency Response Resilience During Public Health Crises: A Case Study of Wuhan. Sustainability 2024, 16, 9091. [Google Scholar] [CrossRef]
- Díaz-Castro, L.; Díaz de León-Castañeda, C.; Pérez-Hernández, G.; Suárez-Herrera, J.C. COVID-19 policy response: Perspectives of key stakeholders in Mexico’s health system and implications for resilience. Arch. Med. Res. 2025, 56, 103097. [Google Scholar] [CrossRef] [PubMed]
- Santiago-Iglesias, E.; Romanillos, G.; Sun, W.; Schmöcker, J.-D.; Moya-Gómez, B.; García-Palomares, J.C. Light in the darkness: Urban nightlife, analyzing the impact and recovery of COVID-19 using mobile phone data. Cities 2024, 153, 105276. [Google Scholar] [CrossRef]
- Chen, M.; Liu, Y.; Ye, Z.; Wang, S.; Zhang, W. Vivid London: Assessing the resilience of urban vibrancy during the COVID-19 pandemic using social media data. Sustain. Cities Soc. 2024, 115, 105823. [Google Scholar] [CrossRef]
- Liu, R.; Li, X.; Zhang, Z. Urban Resilience of Large Public Health Events Based on NPP-VIIRS Nighttime Light Images: A Case Study of 35 Large Cities in China. Sustainability 2024, 16, 7483. [Google Scholar] [CrossRef]
- Chen, J.; Guo, X.; Pan, H.; Zhong, S. What determines city’s resilience against epidemic outbreak: Evidence from China’s COVID-19 experience. Sustain. Cities Soc. 2021, 70, 102892. [Google Scholar] [CrossRef]
- Shi, C.; Zhu, X.; Wu, H.; Li, Z. Assessment of Urban Ecological Resilience and Its Influencing Factors: A Case Study of the Beijing-Tianjin-Hebei Urban Agglomeration of China. Land 2022, 11, 921. [Google Scholar] [CrossRef]
- Yang, Z.; Cui, X.; Dong, Y.; Guan, J.; Wang, J.; Xi, Z.; Li, C. Spatio-temporal heterogeneity and influencing factors in the synergistic enhancement of urban ecological resilience: Evidence from the Yellow River Basin of China. Appl. Geogr. 2024, 173, 103459. [Google Scholar] [CrossRef]
- Mızrak, S.; Çam, H. Determining the factors affecting the disaster resilience of countries by geographical weighted regression. Int. J. Disaster Risk Reduct. 2022, 81, 103311. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Zhou, Y. Assessing urban resilience in China from the perspective of socioeconomic and ecological sustainability. Environ. Impact Assess. Rev. 2023, 102, 107163. [Google Scholar] [CrossRef]
- Tang, D.; Li, J.; Zhao, Z.; Boamah, V.; Lansana, D.D. The influence of industrial structure transformation on urban resilience based on 110 prefecture-level cities in the Yangtze River. Sustain. Cities Soc. 2023, 96, 104621. [Google Scholar] [CrossRef]
- Fotheringham, S.; Brundson, C.; Charlton, M. Geographically Weighted Regression & Associated Techniques; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Fu, H.; Hong, N.; Liao, C. Spatio-temporal patterns of Chinese urban recovery and system resilience under the pandemic new normal. Cities 2023, 140, 104385. [Google Scholar] [CrossRef]
- Fu, Q.; Zhou, M.; Li, Y.; Ye, X.; Yang, M.; Wang, Y. Flow Spatiotemporal Moran’s I: Measuring the Spatiotemporal Autocorrelation of Flow Data. Geogr. Anal. 2024, 56, 799–824. [Google Scholar] [CrossRef]
- Chen, M.; Chen, Y.; Xu, Y.; An, Q.; Min, W. Population flow based spatial-temporal eigenvector filtering modeling for exploring effects of health risk factors on COVID-19. Sustain. Cities Soc. 2022, 87, 104256. [Google Scholar] [CrossRef]
- Chen, X.; Quan, R. A spatiotemporal analysis of urban resilience to the COVID-19 pandemic in the Yangtze River Delta. Nat. Hazards 2021, 106, 829–854. [Google Scholar] [CrossRef]
- Dong, L.; Longwu, L.; Zhenbo, W.; Liangkan, C.; Faming, Z. Exploration of coupling effects in the Economy–Society–Environment system in urban areas: Case study of the Yangtze River Delta Urban Agglomeration. Ecol. Indic. 2021, 128, 107858. [Google Scholar] [CrossRef]
- World Health Organization; Habitat, U.N. Global Report on Urban Health: Equitable Healthier Cities for Sustainable Development; World Health Organization: Geneva, Switzerland, 2016. [Google Scholar]
- Kruk, M.E.; Gage, A.D.; Arsenault, C.; Jordan, K.; Leslie, H.H.; Roder-DeWan, S.; Adeyi, O.; Barker, P.; Daelmans, B.; Doubova, S.V.; et al. High-quality health systems in the Sustainable Development Goals era: Time for a revolution. Lancet Glob. Health 2018, 6, e1196–e1252. [Google Scholar] [CrossRef]
- Marmot, M. Social determinants of health inequalities. Lancet 2005, 365, 1099–1104. [Google Scholar] [CrossRef]
- Schmiege, D.; Haselhoff, T.; Ahmed, S.; Anastasiou, O.E.; Moebus, S. Associations Between Built Environment Factors and SARS-CoV-2 Infections at the Neighbourhood Level in a Metropolitan Area in Germany. J. Urban. Health Bull. N. Y. Acad. Med. 2023, 100, 40–50. [Google Scholar] [CrossRef]
- Xun, X.; Yuan, Y. Research on the urban resilience evaluation with hybrid multiple attribute TOPSIS method: An example in China. Nat. Hazards 2020, 103, 557–577. [Google Scholar] [CrossRef]
- Zhu, Y.; Xie, J.; Huang, F.; Cao, L. Association between short-term exposure to air pollution and COVID-19 infection: Evidence from China. Sci. Total Environ. 2020, 727, 138704. [Google Scholar] [CrossRef] [PubMed]
- Burgos, D.; Ivanov, D. Food retail supply chain resilience and the COVID-19 pandemic: A digital twin-based impact analysis and improvement directions. Transp. Res. Part E Logist. Transp. Rev. 2021, 152, 102412. [Google Scholar] [CrossRef] [PubMed]
- Oshima, S.M.; Tait, S.D.; Thomas, S.M.; Fayanju, O.M.; Ingraham, K.; Barrett, N.J.; Hwang, E.S. Association of Smartphone Ownership and Internet Use With Markers of Health Literacy and Access: Cross-sectional Survey Study of Perspectives From Project PLACE (Population Level Approaches to Cancer Elimination). J. Med. Int. Res. 2021, 23, e24947. [Google Scholar] [CrossRef] [PubMed]
- Vangeepuram, N.; Mayer, V.; Fei, K.; Hanlen-Rosado, E.; Andrade, C.; Wright, S.; Horowitz, C. Smartphone ownership and perspectives on health apps among a vulnerable population in East Harlem, New York. mHealth 2018, 4, 31. [Google Scholar] [CrossRef]
- Chang, S.; Pierson, E.; Koh, P.W.; Gerardin, J.; Redbird, B.; Grusky, D.; Leskovec, J. Mobility network models of COVID-19 explain inequities and inform reopening. Nature 2021, 589, 82–87. [Google Scholar] [CrossRef]
- Du, F.; Mao, L. Identifying points of interest (POIs) as sentinels for infectious disease surveillance: A COVID-19 study. Spat. Spatio-Temporal Epidemiol. 2024, 51, 100691. [Google Scholar] [CrossRef]
- World Health Organization. Critical Preparedness, Readiness and Response Actions for COVID-19: Interim Guidance, 22 March 2020; World Health Organization: Geneva, Switzerland, 2020. [Google Scholar]
- Hananel, R.; Fishman, R.; Malovicki-Yaffe, N. Urban diversity and epidemic resilience: The case of the COVID-19. Cities 2022, 122, 103526. [Google Scholar] [CrossRef]
- Shankar, M.; Hartner, A.-M.; Arnold, C.R.K.; Gayawan, E.; Kang, H.; Kim, J.-H.; Gilani, G.N.; Cori, A.; Fu, H.; Jit, M.; et al. How mathematical modelling can inform outbreak response vaccination. BMC Infect. Dis. 2024, 24, 1371. [Google Scholar] [CrossRef]
- Dan, Y.Y.; Tambyah, P.A.; Sim, J.; Lim, J.; Hsu, L.Y.; Chow, W.L.; Fisher, D.A.; Wong, Y.S.; Ho, K.Y. Cost-effectiveness analysis of hospital infection control response to an epidemic respiratory virus threat. Emerg. Infect. Dis. 2009, 15, 1909–1916. [Google Scholar] [CrossRef]
- Anderson, R.M.; Heesterbeek, H.; Klinkenberg, D.; Hollingsworth, T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet 2020, 395, 931–934. [Google Scholar] [CrossRef]
- Mosadeghrad, A.M.; Afshari, M.; Isfahani, P.; Ezzati, F.; Abbasi, M.; Farahani, S.A.; Zahmatkesh, M.; Eslambolchi, L. Strategies to strengthen the resilience of primary health care in the COVID-19 pandemic: A scoping review. BMC Health Serv. Res. 2024, 24, 841. [Google Scholar] [CrossRef] [PubMed]
- Hsiang, S.; Allen, D.; Annan-Phan, S.; Bell, K.; Bolliger, I.; Chong, T.; Druckenmiller, H.; Huang, L.Y.; Hultgren, A.; Krasovich, E.; et al. The effect of large-scale anti-contagion policies on the COVID-19 pandemic. Nature 2020, 584, 262–267. [Google Scholar] [CrossRef] [PubMed]
- Verity, R.; Okell, L.C.; Dorigatti, I.; Winskill, P.; Whittaker, C.; Imai, N.; Cuomo-Dannenburg, G.; Thompson, H.; Walker, P.G.T.; Fu, H.; et al. Estimates of the severity of coronavirus disease 2019: A model-based analysis. Lancet Infect. Dis. 2020, 20, 669–677. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Lu, J. Assessment of long and short-term flood risk using the multi-criteria analysis model with the AHP-Entropy method in Poyang Lake basin. Int. J. Disaster Risk Reduct. 2022, 75, 102968. [Google Scholar] [CrossRef]
- Bahloul, M.A.; Chahid, A.; Laleg-Kirati, T.M. Fractional-Order SEIQRDP Model for Simulating the Dynamics of COVID-19 Epidemic. IEEE Open J. Eng. Med. Biol. 2020, 1, 249–256. [Google Scholar] [CrossRef]
- Torky, M.; Torky, M.S.; Ahmed, A.; Hassanein, A.E.; Said, W. Investigating epidemic growth of COVID-19 in saudi arabia based on time series models. Int. J. Adv. Comput. Sci. Appl. 2020, 11. [Google Scholar] [CrossRef]
- Wilta, F.; Chong, A.L.C.; Selvachandran, G.; Kotecha, K.; Ding, W. Generalized Susceptible–Exposed–Infectious–Recovered model and its contributing factors for analysing the death and recovery rates of the COVID-19 pandemic. Appl. Soft Comput. 2022, 123, 108973. [Google Scholar] [CrossRef]
- Fanelli, D.; Piazza, F. Analysis and forecast of COVID-19 spreading in China, Italy and France. Chaos Solitons Fractals 2020, 134, 109761. [Google Scholar] [CrossRef]
- Heuvelink, G.; Griffith, D. Space–Time Geostatistics for Geography: A Case Study of Radiation Monitoring Across Parts of Germany. Geogr. Anal. 2010, 42. [Google Scholar] [CrossRef]
- Hocking, R.R. A Biometrics Invited Paper. The Analysis and Selection of Variables in Linear Regression. Biometrics 1976, 32, 1–49. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically Weighted Regression. J. R. Stat. Soc. Ser. D (Stat.) 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [PubMed]
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.R.; Azman, A.S.; Reich, N.G.; Lessler, J. The Incubation Period of Coronavirus Disease 2019 (COVID-19) From Publicly Reported Confirmed Cases: Estimation and Application. Ann. Intern. Med. 2020, 172, 577–582. [Google Scholar] [CrossRef]
- Quesada, J.A.; López-Pineda, A.; Gil-Guillén, V.F.; Arriero-Marín, J.M.; Gutiérrez, F.; Carratala-Munuera, C. Incubation period of COVID-19: A systematic review and meta-analysis. Rev. Clin. Esp. 2021, 221, 109–117. [Google Scholar] [CrossRef]
- Zaki, N.; Mohamed, E.A. The estimations of the COVID-19 incubation period: A scoping reviews of the literature. J. Infect. Public Health 2021, 14, 638–646. [Google Scholar] [CrossRef]
- Folayan, M.O.; Abeldaño Zuñiga, R.A.; Virtanen, J.I.; Ezechi, O.C.; Yousaf, M.A.; Jafer, M.; Al-Tammemi, A.a.B.; Ellakany, P.; Ara, E.; Ayanore, M.A.; et al. A multi-country survey of the socio-demographic factors associated with adherence to COVID-19 preventive measures during the first wave of the COVID-19 pandemic. BMC Public Health 2023, 23, 1413. [Google Scholar] [CrossRef]
- Jay, J.; Bor, J.; Nsoesie, E.O.; Lipson, S.K.; Jones, D.K.; Galea, S.; Raifman, J. Neighbourhood income and physical distancing during the COVID-19 pandemic in the United States. Nat. Hum. Behav. 2020, 4, 1294–1302. [Google Scholar] [CrossRef]
- Badillo-Goicoechea, E.; Chang, T.-H.; Kim, E.; LaRocca, S.; Morris, K.; Deng, X.; Chiu, S.; Bradford, A.; Garcia, A.; Kern, C.; et al. Global trends and predictors of face mask usage during the COVID-19 pandemic. BMC Public Health 2021, 21, 2099. [Google Scholar] [CrossRef]
- Kale, D.; Herbec, A.; Beard, E.; Gold, N.; Shahab, L. Patterns and predictors of adherence to health-protective measures during COVID-19 pandemic in the UK: Cross-sectional and longitudinal findings from the HEBECO study. BMC Public Health 2022, 22, 2347. [Google Scholar] [CrossRef]
- Zhang, Q.; Phang, C.W.; Zhang, C. Does the internet help governments contain the COVID-19 pandemic? Multi-country evidence from online human behaviour. Gov. Inf. Q. 2022, 39, 101749. [Google Scholar] [CrossRef] [PubMed]
- Urbaczewski, A.; Lee, Y.J. Information Technology and the pandemic: A preliminary multinational analysis of the impact of mobile tracking technology on the COVID-19 contagion control. Eur. J. Inf. Syst. 2020, 29, 405–414. [Google Scholar] [CrossRef]
- Pribadi, D.O.; Saifullah, K.; Putra, A.S.; Nurdin, M.; Iman, L.O.S.; Rustiadi, E. Spatial analysis of COVID-19 outbreak to assess the effectiveness of social restriction policy in dealing with the pandemic in Jakarta. Spat. Spatio-Temporal Epidemiol. 2021, 39, 100454. [Google Scholar] [CrossRef] [PubMed]


| Type | Criterion | Indicator | Abbreviation | Data Sources | |
|---|---|---|---|---|---|
| Influencing factors | Static | Infrastructure | POI density | POI | Baidu map service platform (https://lbsyun.baidu.com/), accessed on 20 June 2023. |
| Hospital capacity (sick bed and doctor number) | HOS | The Statistical year book of 2019 (https://navi.cnki.net/knavi/), accessed on 9 April 2025. | |||
| Mobile phone rate | PHONE | ||||
| Internet Rate | INTER | ||||
| Socioeconomic | Income level | INCOME | |||
| Medical insurance | MISU | ||||
| Elderly care insurance | EISU | ||||
| Education level | ILLE | ||||
| Demographic | Population density | POP | |||
| Aging ratio | A65 | ||||
| Young age ratio | U15 | ||||
| Environmental | Green ratio | GR | |||
| Annual average Air quality | PM25 | ||||
| Dynamic | Human Mobility | Initial inflow from Wuhan before lockdown | Wh_qx | Baidu Qianxi Platform (https://qianxi.baidu.com/), accessed on 27 July 2021. | |
| Population migration flow among cities | / |
| DUHRI | Sub-Index | Description |
|---|---|---|
| Resistance capacity | Population that protected from infected cases, either by vaccination or by strictly quarantined from infected cases. | |
| The possibility of susceptible individuals being infected after being exposed to infected individuals. | ||
| The speed of infected cases entered quarantine. | ||
| Recovery capacity | The ratio of daily recovered cases versus existing active (quarantined) cases. | |
| The ratio of daily death cases versus existing active (quarantined) cases. | ||
| Control time (T2) | The number of day that the existing active cases decline from peak to minimum and kept not rising for more than 7 days at the first wave of pandemic. |
| Type | DURHI Index | Period | MLR | GWR | ESTF | FLOW-ESTF | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | RMSE | RMSE | RMSE | |||||||
| Constant Sub-indices | Total | 0.209 | 0.247 | 0.236 | 0.237 | 0.632 | 0.165 | 0.724 | 0.138 | |
| Total | 0.165 | 0.652 | 0.261 | 0.640 | 0.341 | 0.568 | 0.567 | 0.441 | ||
| Total | 0.158 | 0.235 | 0.240 | 0.219 | 0.288 | 0.212 | 0.446 | 0.181 | ||
| T2 | Total | 0.415 | 8.090 | 0.507 | 7.272 | 0.705 | 5.508 | 0.773 | 4.720 | |
| Time varying sub-indices | Week 1 | 0.075 | 4.642 | 0.091 | 4.663 | 0.367 | 3.767 | 0.536 | 2.535 | |
| Week 2 | 0.084 | 4.367 | 0.098 | 4.398 | 0.326 | 3.728 | 0.750 | 1.633 | ||
| Week 3 | 0.158 | 4.123 | 0.177 | 4.148 | 0.404 | 3.463 | 0.724 | 1.726 | ||
| Week 4 | 0.143 | 4.347 | 0.161 | 4.377 | 0.398 | 3.636 | 0.754 | 1.665 | ||
| Week 5 | 0.150 | 5.097 | 0.165 | 5.131 | 0.305 | 4.339 | 0.730 | 1.925 | ||
| Week 6 | 0.184 | 6.885 | 0.292 | 6.159 | 0.283 | 6.319 | 0.551 | 4.075 | ||
| ) | Week 1 | 0.053 | 0.371 | 0.104 | 0.318 | 0.185 | 0.272 | 0.197 | 0.271 | |
| Week 2 | 0.011 | 0.476 | 0.016 | 0.572 | 0.105 | 0.582 | 0.163 | 0.582 | ||
| Week 3 | 0.022 | 0.410 | 0.095 | 0.609 | 0.103 | 0.552 | 0.104 | 0.459 | ||
| Week 4 | 0.018 | 0.400 | 0.086 | 0.707 | 0.108 | 0.600 | 0.166 | 0.529 | ||
| Week 5 | 0.031 | 0.348 | 0.122 | 0.548 | 0.139 | 0.524 | 0.187 | 0.528 | ||
| Week 6 | 0.005 | 0.377 | 0.027 | 0.335 | 0.066 | 0.283 | 0.107 | 0.272 | ||
| Criterion | Factor Name | Factor Weight | |
|---|---|---|---|
| SUHRI | Infrastructure | POI | 0.067 |
| HOS | 0.160 | ||
| PHONE | 0.057 | ||
| INTER | 0.039 | ||
| Socioeconomic | INCOME | 0.159 | |
| MISU | 0.123 | ||
| EISU | 0.063 | ||
| ILLE | 0.068 | ||
| Demographic | POP | 0.051 | |
| A65 | 0.058 | ||
| U15 | 0.045 | ||
| Environmental | GR | 0.061 | |
| PM25 | 0.050 |
| Coef | Alpha | Beta | Delta | T2 |
|---|---|---|---|---|
| HOS | 0.844 *** | −1.457 *** | / | / |
| POI | −0.865 *** | 1.697 *** | / | / |
| PHONE | 0.606 *** | −0.269 * | 1.088 *** | / |
| INTER | 0.525 *** | −0.213 * | / | / |
| INCOME | 0.103 * | −2.000 *** | / | / |
| MISU | 0.108 * | −0.446 ** | / | / |
| EISU | / | / | / | / |
| POP | −0.513 *** | 0.993 ** | −0.595 ** | 2.632 ** |
| A65 | 0.438 ** | 0.721 ** | / | 7.260 *** |
| U15 | / | / | / | / |
| ILLE | −0.403 ** | 1.129 *** | / | / |
| GR | 1.090 *** | −0.113 * | / | −2.841 ** |
| PM25 | / | / | / | / |
| Wh_qx | −0.033 | / | / | 3.550 ** |
| Flow_ev | −2.436 *** | 5.234 *** | −1.238 *** | 15.489 *** |
| Coef | Week 1 | Week 2 | Week 3 | Week 4 | Week 5 | Week 6 |
|---|---|---|---|---|---|---|
| HOS | 8.798 *** | 3.114 *** | / | / | / | / |
| POI | / | / | / | / | / | / |
| PHONE | 3.545 *** | / | / | / | / | / |
| INTER | / | / | / | / | / | / |
| INCOME | 1.833 ** | / | / | / | / | / |
| MISU | 3.510 *** | 0.820 * | 1.570 *** | 3.305 *** | 2.121 ** | 20.999 *** |
| EISU | / | / | / | / | / | / |
| POP | / | / | / | / | / | / |
| A65 | −2.383 ** | −2.699 *** | −4.100 *** | −3.682 *** | −2.882 ** | −1.769 * |
| U15 | / | / | / | / | / | / |
| ILLE | / | / | / | / | / | / |
| GR | 0.966 * | 1.114 ** | 2.741 *** | 4.482 *** | 4.716 *** | 5.350 *** |
| PM25 | / | / | / | / | / | / |
| Wh_qx | / | / | / | / | / | / |
| Flow_ev | −11.435 *** | −6.280 *** | −7.242 *** | −8.009 *** | −13.034 *** | −12.652 *** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Peng, M.; Li, B.; Cai, Z.; Li, R. Static–Dynamic Analytical Framework for Urban Health Resilience Evaluation and Influencing Factor Exploration from the Perspective of Public Health Emergencies—Case Study of 61 Cities in Mainland China. ISPRS Int. J. Geo-Inf. 2025, 14, 176. https://doi.org/10.3390/ijgi14040176
Chen M, Peng M, Li B, Cai Z, Li R. Static–Dynamic Analytical Framework for Urban Health Resilience Evaluation and Influencing Factor Exploration from the Perspective of Public Health Emergencies—Case Study of 61 Cities in Mainland China. ISPRS International Journal of Geo-Information. 2025; 14(4):176. https://doi.org/10.3390/ijgi14040176
Chicago/Turabian StyleChen, Meijie, Mingjun Peng, Bowen Li, Zhongliang Cai, and Rui Li. 2025. "Static–Dynamic Analytical Framework for Urban Health Resilience Evaluation and Influencing Factor Exploration from the Perspective of Public Health Emergencies—Case Study of 61 Cities in Mainland China" ISPRS International Journal of Geo-Information 14, no. 4: 176. https://doi.org/10.3390/ijgi14040176
APA StyleChen, M., Peng, M., Li, B., Cai, Z., & Li, R. (2025). Static–Dynamic Analytical Framework for Urban Health Resilience Evaluation and Influencing Factor Exploration from the Perspective of Public Health Emergencies—Case Study of 61 Cities in Mainland China. ISPRS International Journal of Geo-Information, 14(4), 176. https://doi.org/10.3390/ijgi14040176






