1. Introduction
Traffic accident prediction studies built based on traditional methods have played a pivotal role in capturing trends and predicting potential accidents based on historical data. Some examples of these methods are statistical models, a rule-based approach, and machine learning. However, the studies that adopt these methods suffer from challenges and limitations, such as data complexity and high dimensionality [
1], handling sparse and imbalanced data [
2], and limited spatiotemporal analysis [
3]. High-dimensional traffic characteristics, such as road geometry, traffic congestion, and weather-related factors, are hardly detected by traditional models [
1]. Traffic accident data is sparse and imbalanced, and traditional models are biased toward the majority classes, resulting in less accurate predictions of rare events [
2]. Traditional models may not effectively capture spatiotemporal dependencies, as they often fail to account for the dynamic nature of traffic patterns and accident occurrences [
3].
Deep learning (DL) overcomes these challenges through its ability to handle complex data and manage non-linear correlation in traffic data [
4,
5]. It even shows greater capabilities in handling a large volume of data by leveraging architectures like dense layers and multi-head attention in transformer models [
6,
7]. Additionally, the adaptability of spatial and temporal dynamics makes it a possible choice for accident prediction, whereas traditional models, such as ARIMA, struggle with the complexity and integration of spatiotemporal data [
8]. Finally, DL models can tackle the missing or noisy data by adapting imputation strategies and latent space, whereas, on the other hand, the traditional model requires a preprocessing step that could skew the results [
5,
9,
10]. However, most existing DL approaches still rely on single-modal inputs, limiting their ability to represent the full complexity of accident-related factors. This gap motivates the exploration of multimodal deep fusion frameworks that integrate spatial, temporal, and environmental data for more comprehensive accident prediction.
Traditional single-modal systems often fail to meet the expectation of capturing the varied and ever-changing factors that play a role in the probability of traffic accident occurrence [
11,
12,
13]. DL, or deep fusion, has the potential to fuse or combine temporal, spatial, and environmental features by leveraging advanced architectures, hierarchical feature learning, and parallel computation [
14,
15,
16,
17,
18]. Multimodal high-dimensional deep fusion refers to integrating diverse types of data (modalities) into high-dimensional spaces to build scalable and efficient DL models for complex tasks [
19,
20,
21]. This approach is especially relevant for problems requiring the combination of multiple data sources, such as text, images, numerical data, or spatial–temporal information [
22]. Building on these insights, this study applies multimodal deep fusion to traffic accident prediction, aiming to enhance accuracy and interpretability through integrated spatial–temporal modeling.
This paper investigates three scenarios of DL models to predict road accidents in Toronto, utilizing a comprehensive dataset consisting of highway accident reports from 2014 to 2015, along with relevant environmental information, road surface conditions, and lighting conditions. The study employs a multi-stage deep fusion methodology, which adapts a Gated Recurrent Unit (GRU) and Convolutional Neural Network (CNN) architecture to effectively analyze the spatiotemporal data associated with highway accidents. The dataset was subjected to preprocessing by removing duplicate and inconsistent entries, validating coordinate integrity, and ensuring consistency across multiple Excel data sheets. Feature engineering was then applied to enhance the dataset’s representation quality. This preprocessing step played a crucial role by enabling the models to learn from refined inputs, resulting in more reliable predictions and a clearer understanding of the factors contributing to highway collisions. The performance of the proposed DL models was compared with that of conventional machine learning approaches, demonstrating the DL models’ superior ability to uncover hidden relationships and patterns that support data-driven decision making in urban planning and roadway safety.
The main contributions of this paper are as follows:
Developing a proactive spatiotemporal prediction model using a high-quality, multimodal dataset that fused multimodal data.
Addressing key limitations in prior work, including the exclusion of demographic and socio-economic diversity that can affect predictive accuracy across different populations and regions.
Exploring multiple deep fusion strategies for scalable, high-dimensional data, including both input- and output-level fusion methodologies.
Comparing the performance of DL models against conventional methods such as AdaBoost, Linear Regression, Random Forest, and Support Vector Regression (SVR), applied to the same dataset.
The paper is structured as follows.
Section 2 reviews related literature on DL adoption in accident prediction.
Section 3 details the methodology, including data acquisition, preprocessing, feature engineering, model architecture, and fusion strategy.
Section 4 discusses the results and the outcomes.
Section 5 concludes the paper and outlines directions for future work.
2. Related Work
In the advancement of smart urban environments, the significance of multimodal data modeling has been emphasized across a diverse range of applications, including traffic management [
13,
23,
24,
25], urban planning and infrastructure development [
26,
27,
28,
29,
30], emergency response optimization [
31,
32], and enhancing autonomous vehicle safety [
33].
In traffic accident prediction, multimodal data often includes geographic coordinates, timestamps, weather conditions, road attributes, and even social media streams. Several key factors, such as availability, usability, scalability, and relevance, determine how effectively these diverse data sources can be integrated. Chen, Tao et al. [
34] adopted six data modalities derived from structured and textual sources to improve predictions of accident durations on expressways in Shaanxi Province, China. Karimi Monsefi, Shiri et al. [
24] used comprehensive datasets that combined accident histories, weather conditions, map imagery, and demographic information to estimate crash risks. Liyong and Vateekul [
35] combined the England Highways and ITIC Traffic datasets to build a more accurate multi-step traffic prediction model. Bao, Liu et al. [
36] utilized a broad set of multimodal datasets for short-term crash risk prediction, incorporating road network attributes (e.g., length, type, intersections, and volume), crash reports from the New York City Police Department, taxi GPS trajectories, land use data, population density, and weather records. These data were spatially and temporally aggregated using PostgreSQL and PostGIS. Collectively, these studies emphasize the importance of integrating heterogeneous data sources for improved accident prediction. However, despite their promise, most approaches remain constrained by fragmented data integration, inconsistent spatiotemporal resolution, and limited cross-modal learning.
Innovations in DL architectures continue to drive progress in traffic and transportation modeling, reinforcing their status as transformative tools within machine learning [
4]. Neural networks, particularly DL models, are widely applied to capture the multi-dimensional and non-linear relationships underlying accident occurrences [
9,
17,
18,
36,
37]. However, due to the complex nature of the road network environment, single-modality data often fails to capture the hidden factors that influence the occurrence of traffic accidents, and to deeply analyze complex patterns. To overcome this, several studies explored deep fusion strategies. For example, Liyong and Vateekul [
35] developed a fusion model that integrates CNN-LSTM, CNN, and attention mechanisms to capture spatial and temporal dependencies for traffic prediction. In their model, a CNN is used for feature extraction, and an LSTM is trained to learn the sequence of time series data. The attention mechanism is used to assess the impact of accidents on traffic and to identify unexpected events that affect traffic conditions. The performance measure of the developed model significantly outperforms baseline models. Likewise, Chen, Tao et al. [
34] investigated different prediction models and evaluated their performance to determine the most effective one for predicting traffic accident duration. The study employed various data types, including structured data, such as accident type, time, weather, and location, unstructured data, such as traffic accident information and treatment measures, multimodal data, such as video and text, and numerical text data. The integration of Bidirectional GRU-CNN outperforms the other tested models. Bao, Liu et al. [
36] introduce a spatiotemporal convolutional long short-term memory network (STCL-Net) model to predict short-term crash risk using multimodal data. The model integrates CNN, LSTM, and ConvLSTM layers. Three temporal categories were investigated: weekly, daily, and hourly. STCL-Net was found to perform better than machine-learning models in terms of positive accuracy rates and lower false positive rates across all three crash risk prediction categories. While these architectures achieved strong predictive accuracy, most still relied on single or simplified data modalities. Few have explored how deep fusion can jointly model spatial, temporal, and contextual factors in a unified framework.
Earlier studies have addressed multiple drawbacks and limitations that negatively impact the effectiveness and accuracy of traffic model predictions. Traditional statistical models, such as logistic regression, decision trees, and random forests, are considered straightforward and interpretable, but they fail to capture the complex, non-linear relationships in dynamic and heterogeneous traffic environments [
38,
39]. Most studies have focused on the time and location of accidents, including factors such as road conditions, weather, and traffic congestion. These studies overlook the roles of spatial heterogeneity and temporal autocorrelation; “Patterns change across different places and over time”. For example, if a model does not consider how crashes in one area can affect nearby places, it might miss important trends in accidents over time, making predictions less accurate [
40,
41].
Another limitation is that many studies handle accident prediction and contributing factors as separate tasks. This limits models’ ability to provide actionable insights for accident prevention [
42,
43]. Similarly, inadequate integration with spatial analysis tools and the absence of advanced optimization techniques weaken the model’s capacity to identify high-risk zones or improve safety planning [
44]. While recent DL models have improved accuracy, their interpretability remains limited, constraining their applicability in real-world decision making [
42,
43]. On top of that, their complexity and computational intensity make them challenging to implement in real-world scenarios, especially in regions with limited computational capacity [
43,
45]. Critical human, vehicle, and environmental elements have often been omitted from the modeling process. This includes limited attention to the quantitative assessment of driver psychology and environmental variables, which affect accident risks, further reducing prediction accuracy [
44,
46].
Finally, several studies continue to face unresolved data challenges. Accident datasets often encounter issues such as imbalanced classes and incomplete or noisy data. Additionally, the heterogeneity of data sources, such as variations in weather patterns, poses challenges for models’ generalization abilities, resulting in models that perform poorly across diverse environments [
40,
41]. Additionally, previous studies overlooked the high number of zero-count “non-accident” points, a challenge called the zero-inflation problem, which reduces the prediction performance in areas with low accident frequencies [
41,
47].
Recent studies have attempted to address these challenges through various strategies, including data resampling, synthetic data generation, and hybrid balancing techniques. However, these methods often struggle to distinguish true non-accident regions from augmented samples, potentially distorting the spatial or temporal structure of the data. Some studies have also applied general oversampling algorithms, such as the Synthetic Minority Oversampling Technique and its regression variant, Synthetic Minority Oversampling Technique for Regression with Gaussian Noise (SMOGN); however, their performance is limited when dealing with sparse spatiotemporal grids and high-dimensional contextual variables [
48,
49,
50,
51,
52,
53,
54].
Despite ongoing research, the existing literature still struggles to integrate multimodal fusion and robust data handling within a single predictive framework. Overall, prior research has laid a solid foundation for traffic accident prediction; however, it remains fragmented across different data types and modeling approaches. This study bridges these gaps by combining multimodal fusion with balanced data augmentation, enabling more robust and generalizable accident prediction in urban contexts. The present study addresses these collective gaps by integrating multimodal fusion with balanced data augmentation, thereby enabling more robust and generalizable accident prediction in urban contexts.
3. Materials and Methods
This section outlines the methodology adopted in this study, which focuses on developing a multimodal, high-dimensional deep fusion framework for predicting highway traffic accidents. The proposed approach integrates diverse accident-related features with external contextual factors using DL-based fusion strategies. The framework is designed to address key challenges in traffic accident prediction, including capturing spatial–temporal dependencies and managing variations introduced by heterogeneous data sources.
As illustrated in
Figure 1, the process consists of five main stages: (1) data collection, which includes traffic accident records and related variables, such as environmental, temporal, and spatial data; (2) data and feature engineering, covering data preparation and attribute generation; (3) data augmentation and feature extraction; (4) model configuration through hyperparameter optimization; and (5) model training, evaluation, and prediction. Each stage contributes to ensuring consistency, generalization, and robustness in the predictive modeling process. The following sections provide a detailed description of the methodological decisions, model configurations, and evaluation procedures.
3.1. Data Engineering
Data engineering is a crucial phase focused on the systematic collection, preprocessing, integration, and storage of data to ensure its accessibility, reliability, and suitability for analysis [
55,
56]. It involves acquiring data from various sources, cleansing and integrating data into large volumes of data, and transforming this data to ensure its consistency and uniformity [
57]. This phase also involves storing and managing data in suitable formats such as databases and data lakes [
55].
3.1.1. Data Collection
For this research purpose, we collected data from two data sources, as follows:
Collision Data: The traffic accident dataset consists of road police reports related to highway collisions in Toronto for the years 2014–2015, obtained from the Ministry of Transportation of Ontario (MTO). The analysis focuses exclusively on highway segments to maintain consistent traffic and reporting conditions. This period was selected for its completeness and reliability, as it represents one of the most consistent reporting intervals in Toronto. The raw data were organized and transformed into a structured Excel database. The comprehensive dataset includes variables such as collision location, time of occurrence, police response time, meteorological conditions, and environmental attributes, shown in
Appendix A,
Table A1.
Population Density by CensusMapper: The CensusMapper population density data provide a visual and quantitative view of how people are distributed across Canadian geographic areas, based on census information from Statistics Canada. The dataset includes population by age group, land area (in square kilometers), and density values. Since Canada conducts full censuses every five years, no official maps exist for the period 2014–2015; therefore, we used the comparable spatial patterns from the 2016 census. The study focuses on the 24–74 age range, as explained in
Section 3.2.3.
3.1.2. Data Visualization and Extraction
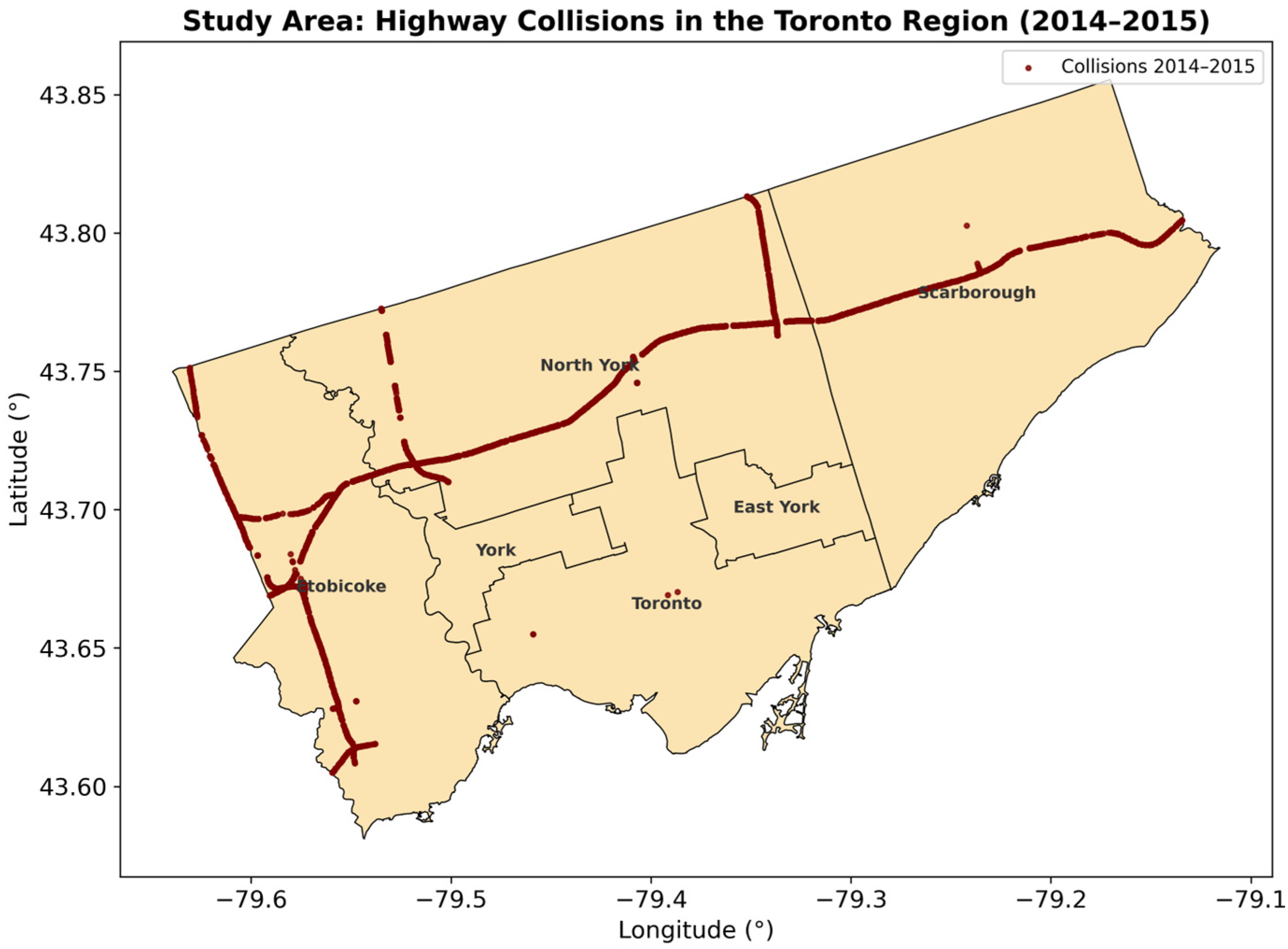
The study focused on Toronto; accordingly, city-specific data were extracted and clipped from the MTO dataset, as shown in
Figure 2. Toronto was selected as the study area because it offers high-quality, publicly available traffic data and exhibits diverse and complex roadway characteristics [
58]. As Canada’s largest metropolitan region, it encompasses a dense mix of expressways, arterials, and local streets, including Highway 401, the busiest and one of the widest highways in North America. The city’s high traffic volumes, urban expansion, and mixed land use create substantial spatial and temporal variation in collision risk, making Toronto a suitable environment for developing and validating multimodal spatiotemporal accident prediction models [
59,
60,
61].
For each year, collision data were organized into four Excel sheets sharing a common MTO collision reference number. Using ArcGIS (Version 3.4) these sheets were integrated into a single table containing all fields for 2014 and 2015.
The collision details sheet, which included longitude and latitude, was projected to map collision locations, with each year visualized separately. The remaining tables were converted to CSV format and joined with the location data using a common reference field, producing a comprehensive feature layer in ArcGIS (Version 3.4). The final attribute table for the study area contained 11,800 recorded highway collisions, including 4100 in 2014 and 7700 in 2015.
3.2. Feature Engineering Process
In DL, feature engineering is a key phase in traffic accident prediction. It converts raw data into a structured and informative format suitable for input into DL and machine learning models [
62]. This process typically involves selecting relevant features, deriving new ones from existing data, and generating attributes based on identified patterns [
63]. In this research, the following feature engineering steps were applied to the MTO dataset.
3.2.1. Temporal Window Selection
The temporal window defines the period over which accident data are analyzed and is fundamental to capturing recurring temporal patterns [
64]. Its selection depends on analytical objectives and the temporal behavior of traffic data. Earlier research has shown that excessively short intervals, such as 15–30 min, may reduce the reliability of accident frequency estimates [
48].
In this study, no temporal binning of time series data in its raw format was applied. Instead, each accident’s timestamp was first parsed as a datetime object and then converted into Portable Operating System Interface (POSIX), or Unix Epoch time, to preserve full temporal granularity. This numeric representation of time allowed the model to learn continuous temporal patterns without compromising minute- or second-level resolution. The resulting timestamp values were included directly as one of the input features in the model’s training sequences.
3.2.2. Definition of Spatial Matrix
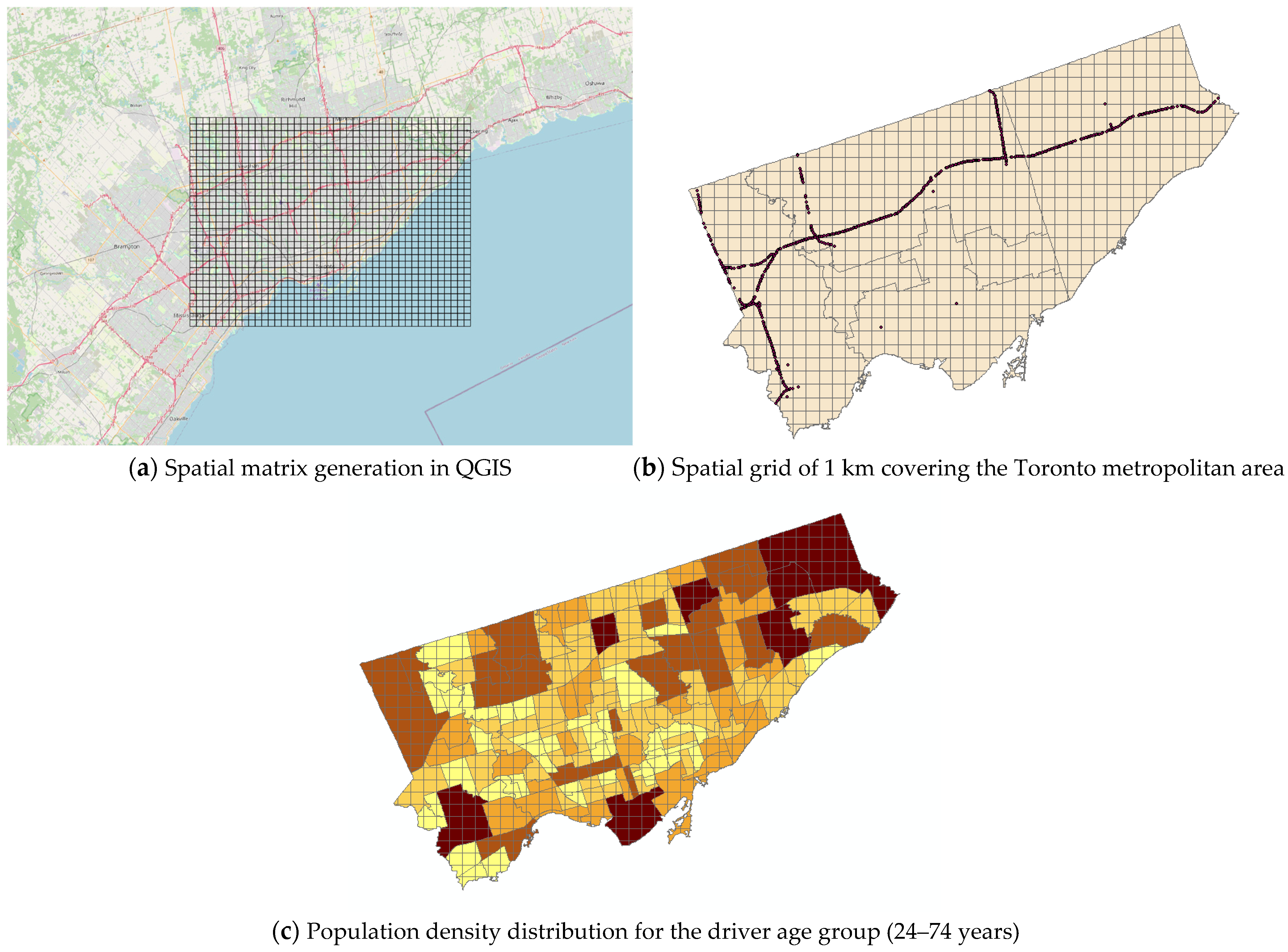
The traffic accident dataset was organized into a two-dimensional spatial matrix. A uniform grid of 1 km × 1 km cells was applied, covering an area of 43 km in the east–west direction and 32 km in the north–south direction, resulting in a 43 × 32 matrix, as shown in
Figure 3a. The grid size decision was made based on previous research conducted by [
36] to ensure the balance between spatial resolution and data sparsity. This guarantees that the occurrence of traffic accidents does not approach zero, preventing sparsity-related degradation in model performance.
The spatial matrix was generated in QGIS using the grid generation tool to define grid corner coordinates. The intersect tool was applied to exclude areas outside the Toronto boundary, as shown in
Figure 3b.
Figure 4 presents the complete grid network for spatial reference. The bottom-left corner was defined as the origin point [0, 0], and the grid extended from Left = 609,553.4701 m, Top = 4,857,446.0757 m, Right = 652,553.4701 m, to Bottom = 4,825,446.0757 m.
Including the full grid network provides spatial clarity and supports the generation of synthetic negative samples by identifying cells without reported accidents. These negative samples help augment the dataset, improving the model’s generalization ability and learning stability.
3.2.3. Density per Spatial Matrix
To calculate the frequency and population for each grid cell, a choropleth map containing population data by age group (2014–2015) was overlaid on the spatial grid. Using the Intersect tool in ArcGIS (Version 3.4), population values were assigned to each grid cell based on spatial overlap, as illustrated in
Figure 3c. The resulting attribute table provided the basis for computing traffic accident probability by relating accident counts to cell coordinates (latitude and longitude).
This study focuses on drivers aged 24 to 74 years, representing the core of the active driving population in Toronto. Individuals younger than 20 are excluded, since most do not possess a Full G license, while those older than 74 are less likely to use highways regularly. National licensing data support this range: in 2009, approximately 75% of Canadians aged 65–74 held valid driver’s licenses, with a substantial decline observed among those aged 75 and older [
65]. A similar pattern is evident in both licensing and driving frequency, which decrease sharply beyond age 74, whereas few individuals under 20 meet the licensing requirements for highway travel [
65,
66,
67].
Accident probability was then derived and normalized using the support metric from association rule mining, as defined in [
68,
69], where
where the fine-grained form of the equation is given in (2)–(7), as follows:
Local Temporal Density of Accidents: This captures short-term local congestion or the clustering of accidents.
Accident Volume per Neighbor: This gives the total number of accidents in each neighborhood.
Combined Risk Factor: This combines the accident intensity in the area and the population density as a demographic risk modifier.
Relative Accident Concentration: This gives the relative weight of local accident clustering compared to the total neighborhood exposure.
PropScore scaled, Clipped Proportion.
Breaking that down, the following is undertaken:
Multiply by 100 to express the ratio as a percentage.
Then caps it at 1, to avoid unrealistic proportions (e.g., if a small denominator makes the ratio huge).
The variable captures the temporal clustering of accidents by indicating the number of collisions that occurred within a 60 min window centered around each incident. This helps identify peak periods of accident occurrence. The reflects spatial clustering, highlighting areas with a high concentration of traffic accidents. Finally, the population density for individuals aged 24 to 74 serves as a proxy for levels of human activity across different areas.
3.3. Data Augmentation Procedure
Data augmentation is crucial for addressing the under-representation of negative traffic accident reports by simulating realistic accident distributions in the real world. It increases the diversity and volume of the training dataset, helping to reduce overfitting and improve the model’s generalization ability, to encompass new, slightly varied data [
48,
49,
50,
51,
52,
53].
3.3.1. Data Augmentation
This study initially explored the Synthetic Minority Oversampling Technique for Regression with Gaussian Noise (SMOGN), as proposed by [
54]. However, SMOGN proved ineffective at distinguishing between accident-related and non-accident-related cases in the Toronto region, particularly in relation to environmental and road surface conditions. This limitation highlighted the need for a more context-specific augmentation method.
To address this, a custom algorithm was developed to generate synthetic samples for areas where no accidents were originally reported, referred to as “negative data.” The algorithm creates tuples with an accident frequency of zero, probability at random times, and coordinates within these regions. An iterative process applies this across the entire spatial matrix, where the number of synthetic samples (N) for each cell matches the number of actual accidents reported in that grid cell. Other attributes, such as date, environmental condition, and road surface type, were duplicated from the original data to maintain consistency [
48,
49,
50,
51,
52,
53].
To prevent spatial bias, synthetic non-accident samples were initially generated across all grid cells to ensure uniform spatial representation. However, since real-world accidents occur only on road networks, grid cells without mapped road segments were subsequently filtered out prior to model training. This step ensured that the final negative dataset accurately represented realistic, road-based non-accident conditions while preserving balanced spatial coverage across the study area.
The final dataset was fused by merging the positive data (actual reported accidents) and the negative data (synthetic non-accident cases). A data cleaning step was applied to remove duplicates and any synthetic tuples that overlapped with real observations. An equal number of positive and negative samples were used to ensure a balanced dataset and prevent model bias; specifically, 11,800 data points from each group were used, thereby supporting effective and unbiased model training. This approach mitigates the zero-inflation problem by ensuring uniform spatial representation and realistic contextual patterns.
3.3.2. Resulting Set of Features
Following data engineering and augmentation, a finalized feature set was generated for training the DL model. These features integrate spatial and temporal dimensions with environmental and contextual attributes relevant to traffic accident prediction. The complete list of variables used as model inputs is presented in
Table 1. This consolidated set captures key patterns required for reliable accident prediction, balancing real and synthetic data sources. Among the included features is the traffic accident probability, computed using the equation derived from the association rule methodology described in
Section 3.2.
3.4. Model Design and Architecture
The DL model developed in this study is designed to capture complex non-linear relationships in large, high-dimensional datasets with minimal manual feature engineering. It integrates multiple neural network architectures, Gated Recurrent Units (GRUs), and Convolutional Neural Networks (CNNs), to extract spatial and temporal dependencies from heterogeneous data.
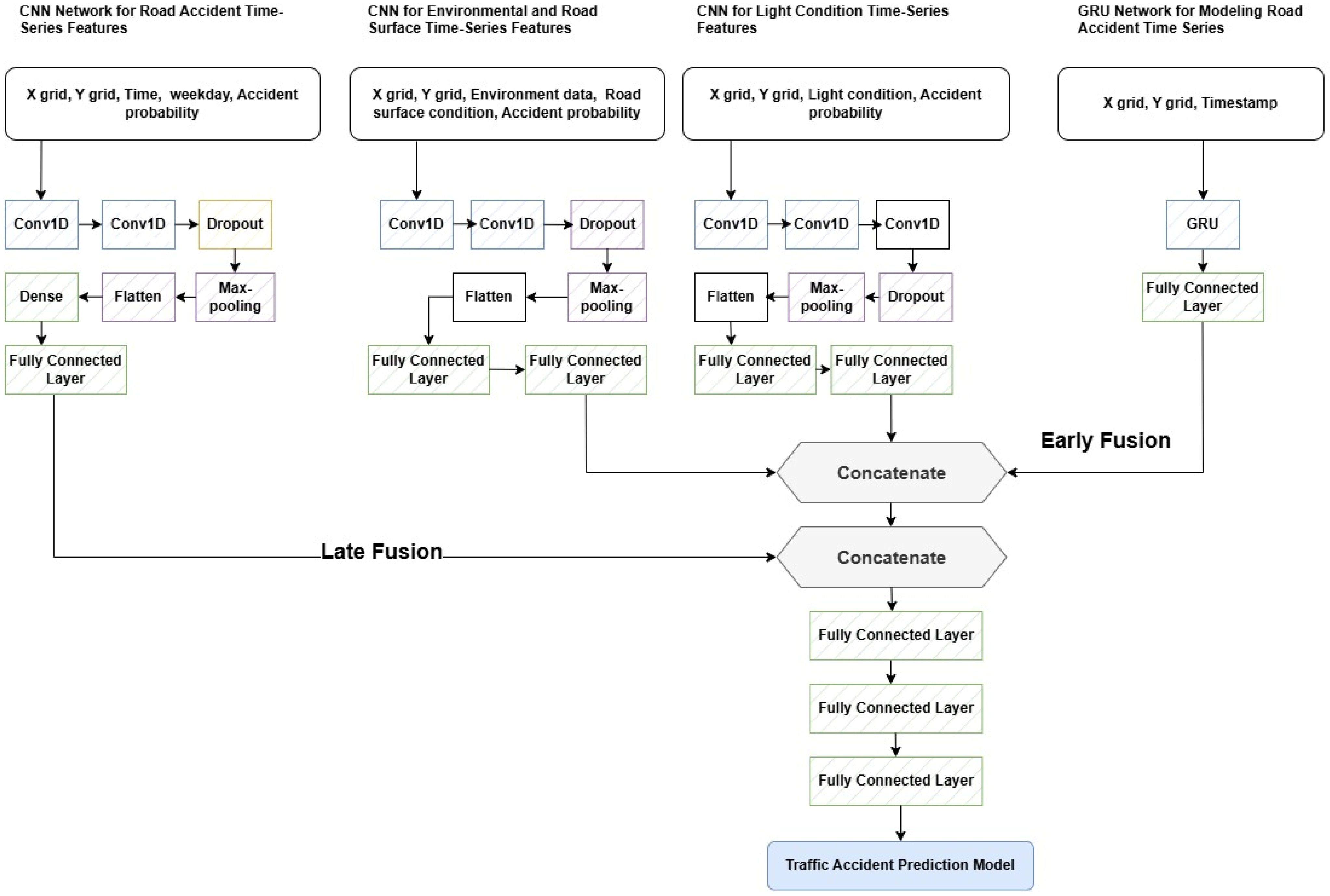
A deep fusion strategy was adopted to integrate multiple data sources and feature types, enhancing the model’s capacity to represent diverse relationships and improving its predictive accuracy by leveraging the complementary strengths of different architectures. Specifically, the GRU and CNN sub-networks were combined to process information related to road accidents, environmental conditions, lighting, and road surface characteristics, thereby enabling accurate estimation of accident probability. The model’s output is a continuous value representing the predicted probability of a traffic accident at a specific location and time, based on the provided spatial and contextual features.
3.4.1. Time Window Granularity Selection
Three temporal windows (6 h, 12 h, and 24 h) were employed to model varying temporal patterns in accident probability. These intervals were chosen for their ability to capture different scales of temporal behavior [
70,
71]. The 6-hour window reflects short-term sequential trends, the 12 h window captures diurnal variations in lighting conditions, and the 24 h window represents the full day of environmental and road surface fluctuations [
72].
These selections were informed by domain knowledge and validated through empirical performance evaluations using the Mean Squared Error (MSE), Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE) metrics. Comparative analysis across these metrics confirmed that each window effectively represented distinct temporal characteristics relevant to accident prediction.
3.4.2. GRU Network for Modeling Road Accident Time Series
This study implemented a GRU network to model temporal patterns in traffic accident data across a spatial grid. GRUs are a variant of recurrent neural networks equipped with two gating mechanisms: the reset gate and the update gate. These control the flow of information within the network, enabling the model to retain relevant historical context and to mitigate the vanishing gradient problem. This makes GRUs well-suited for capturing long-term dependencies in sequential data, such as traffic trends.
The GRU model was trained on structured time series sequences represented as three-dimensional input arrays in the format (samples, time window, and features). Each input sequence consisted of 24 consecutive hourly records, along with three features: standardized X and Y grid coordinates, and a timestamp converted to POSIX format. The target label for each sequence corresponded to the accident probability at the subsequent time step.
To identify the optimal time window for grouping traffic accidents, several durations (1 h, 3 h, 4 h, and 6 h) were tested. The time window has a significant influence on the model’s ability to capture spatiotemporal patterns in traffic data. Based on prior studies and evaluation metrics, including MSE, RMSE, and MAE, a 6 h window was selected as optimal, corresponding to a sequence length of 24 h steps.
This configuration enabled the model to learn the temporal trends in accident probability for each spatial grid cell, allowing it to detect consistent patterns across both time and location. The GRU network’s hyperparameters were tuned using a grid search approach. Several GRUs configurations were trained using different combinations of key hyperparameters, including filter size, kernel size, and dense layer structure. The optimal setup was selected based on MSE, RMSE, AND MAE metrics, as summarized in
Table 2.
3.4.3. CNN for Road Accident Time Series Features
This study employed a one-dimensional convolutional neural network (Conv1D) to model spatial and temporal dependencies in traffic accident data. Conv1D networks are feedforward architectures designed to extract localized feature patterns from structured inputs. By applying convolutional filters to sequential data, they capture interactions among adjacent features, making them suitable for datasets containing embedded spatial and temporal relationships.
The network was trained using three-dimensional tensor input with the shape (samples, features, 1). Each sample included standardized X and Y grid coordinates, a normalized time-of-day value (in seconds), and one-hot-encoded weekday indicators. The target variable represented the computed accident probability.
This configuration enabled the model to capture spatial and contextual dependencies associated with accident probability across varying time intervals and grid cells. Through this process, the Conv1D network learned the localized feature interactions and spatiotemporal relationships important for accurate accident prediction. Several CNN configurations were trained, using different combinations of key hyperparameters, including filter size, kernel size, and dense layer structure. The optimal setup was selected based on MSE, RMSE, and MAE metrics, as summarized in
Table 3.
3.4.4. CNN for Environmental and Road Surface Time Series
In this study, Conv1D was used to estimate traffic accident probability by modeling temporal sequences of environmental and road surface data across spatial grid locations. The Conv1D architecture was selected for its ability to extract sequential patterns from structured time series inputs, enabling the model to learn how traffic-related features evolve over time within each spatial unit.
The input data included standardized X and Y grid coordinates, one-hot-encoded environmental conditions, and road surface types. These features were organized into sequences using a 24 h sliding time window, producing three-dimensional input tensors with the shape (samples, time window, features). The label for each sequence corresponded to the accident probability observed immediately after the 24 h window.
This configuration allowed the network to learn how variations in environmental and road conditions influence accident probability over time at specific spatial locations. Consequently, the Conv1D model captured temporal dependencies and spatial contexts across different road segments. Several CNN configurations were trained using different combinations of key hyperparameters, including filter size, kernel size, and dense layer structure. The optimal setup was selected based on MSE, RMSE, and MAE metrics, as summarized in
Table 4.
3.4.5. CNN for Environmental Conditions Time Series Features
In this study, Conv1D was adapted to estimate accident probability based on environmental conditions at specific spatial grid locations. The model was designed to capture how environmental factors evolve over time and influence accident risks across different grid cells.
The input data consisted of standardized X and Y grid coordinates and one-hot-encoded environmental condition categories. These features were arranged into time series sequences using a fixed window size of 24, corresponding to a 24 h period. Each sequence was represented as a three-dimensional array with the shape (samples, 24, features), and the target variable indicated the accident probability at the subsequent time step.
This configuration enabled the model to learn temporal patterns in environmental conditions and their relationship to accident likelihood. Several CNN configurations were trained, using different combinations of key hyperparameters, including filter size, kernel size, and dense layer structure. The optimal setup was selected based on MSE, RMSE, and MAE metrics, as summarized in
Table 5.
3.4.6. CNN for Light Condition Time Series Features
In this study, Conv1D was developed to evaluate the influence of light conditions on road accident probability. The model analyzed temporal sequences of lighting conditions at specific spatial locations to identify patterns associated with increased accident risk. Light conditions were encoded categorically and modeled over a 12 h window to reflect typical daily variations.
The input features consisted of standardized X and Y grid coordinates, as well as one-hot-encoded light condition categories. These were organized into time series sequences with a fixed window size of 12, producing three-dimensional input arrays with the shape (samples, time window, features). The target variable for each sequence represented the accident probability at the next time step.
This configuration enabled the model to learn temporal dependencies in lighting conditions that contribute to accident risks across the spatial matrix. Several CNN configurations were trained using different combinations of key hyperparameters, including filter size, kernel size, and dense layer structure. The optimal setup was selected based on MSE, RMSE, and MAE metrics, as summarized in
Table 6.
3.5. Deep Fusion Methods Development
In this study, two deep fusion strategies were applied, as described in [
21]: output-based fusion and double-stage-based fusion. These strategies were implemented to integrate specialized neural network models; each trained on different temporal and contextual data sources relevant to traffic accident prediction.
Table 7 summarizes the scenario configuration, time window, deep fusion technique, and input features of each model. The dataset was partitioned into training (60%), validation (20%), and testing (20%) subsets to prevent data leakage and ensure consistent model evaluation.
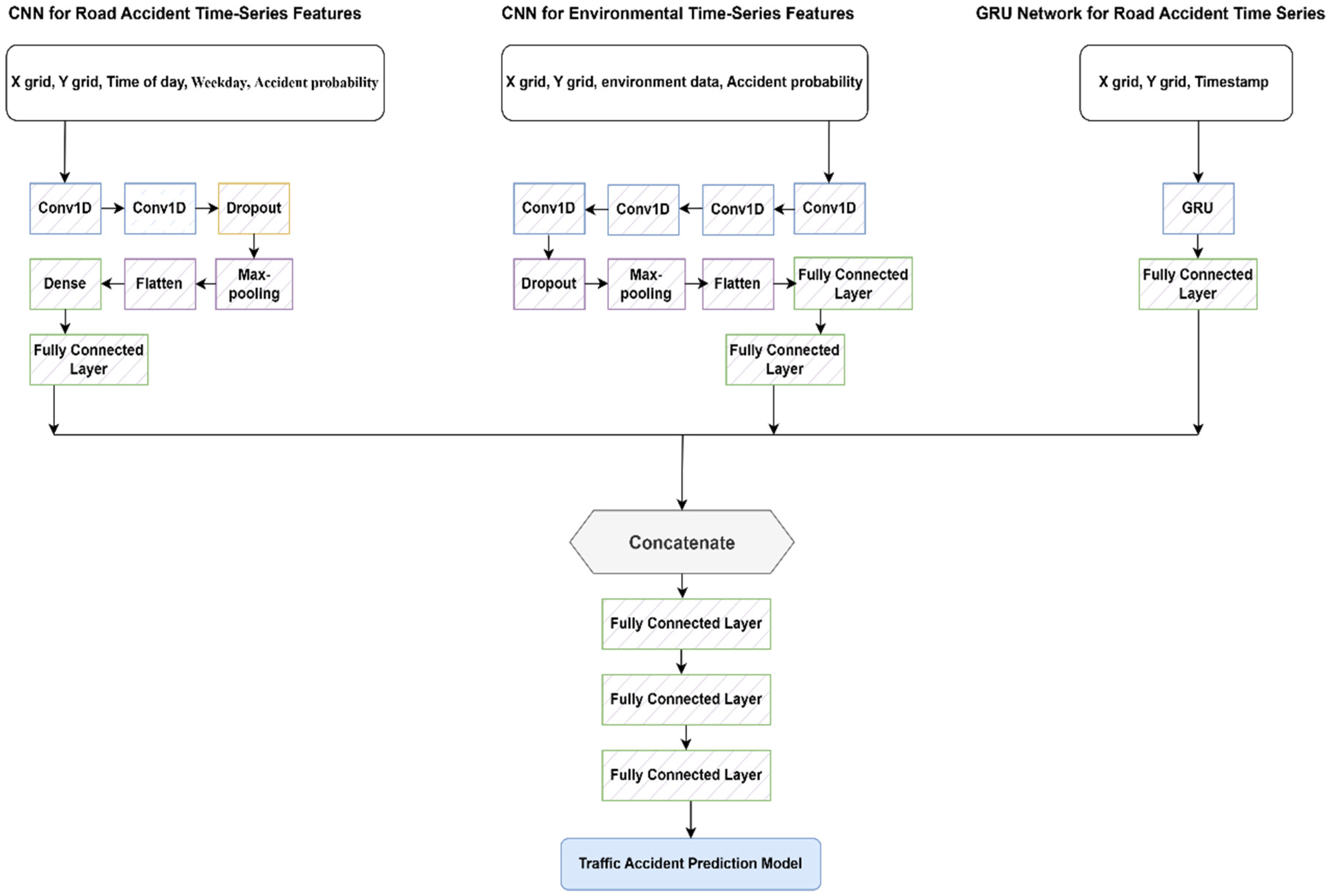
The first scenario (SC1) was implemented with a simplified output-based deep fusion architecture that focused on environmental conditions as a primary contextual factor, as shown in
Figure 5. This configuration fused three distinct models, each trained on different aspects of spatial and temporal data related to environmental inputs. A Conv1D network processed 24 h environmental time series sequences, while another CNN captured spatial–temporal accident trends using X–Y grid coordinates, weekday, time, and accident probability as inputs. In parallel, a GRU sub-network modeled short-term sequential dependencies in spatiotemporal accident data. The outputs from all three sub-networks were concatenated and passed through fully connected layers with ReLU activation, batch normalization, dropout (0.5), and L2 regularization to enhance generalization ability, followed by a final regression layer with linear activation to predict accident probability. This configuration served as a foundation for evaluating the impact of additional contextual features in subsequent scenarios.
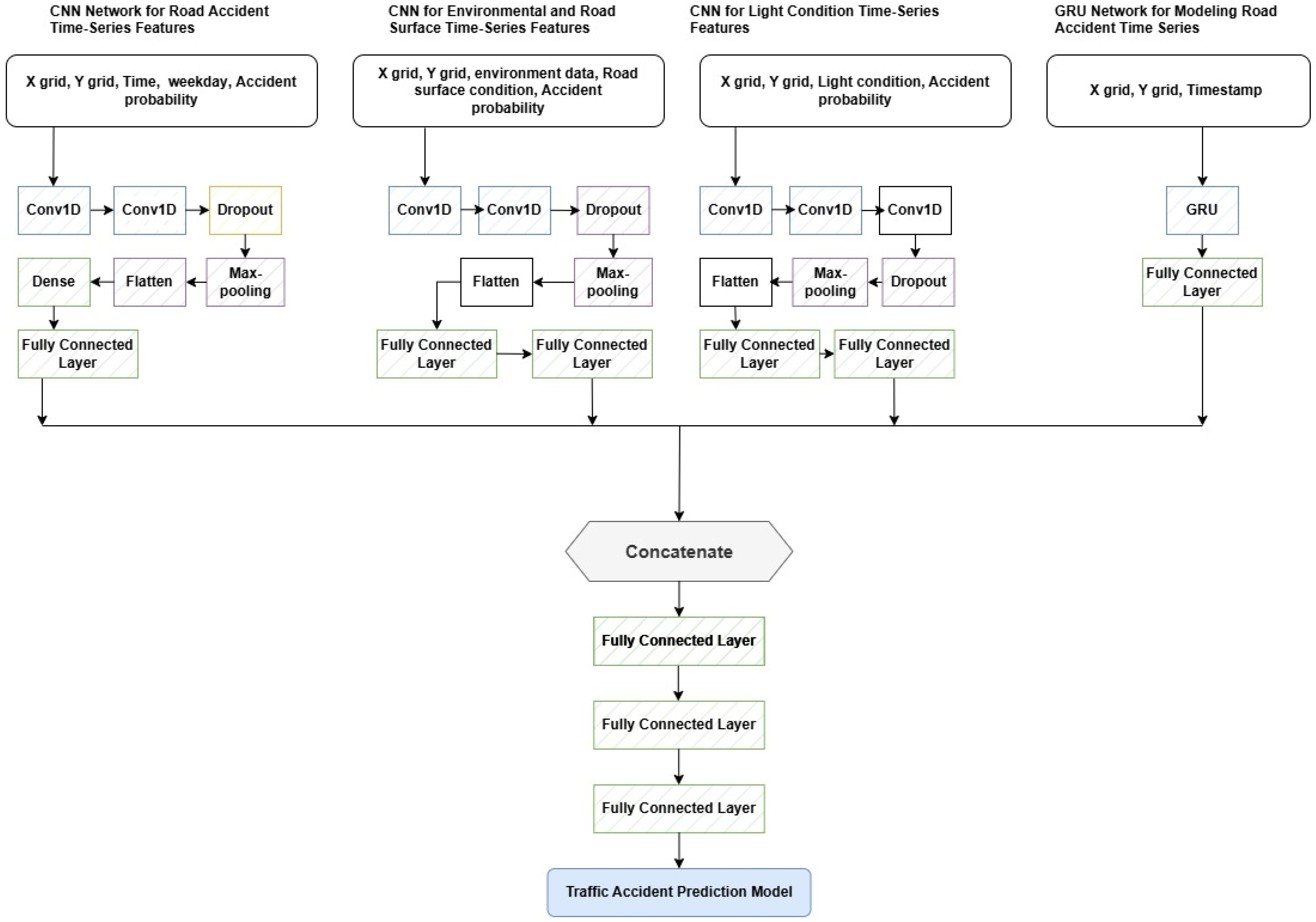
The second scenario (SC2) was developed to enable the model to integrate a broader range of contextual information, supporting a more comprehensive framework for traffic accident prediction, as presented in
Figure 6. SC2 follows an output-level deep fusion strategy that combines the outputs of four neural network sub-models. This configuration includes three CNNs and one GRU. The first CNN models 24 h sequences of accident-related time series inputs, incorporating X and Y grid coordinates, time information, weekday encoding, and accident probability. A second CNN processes 24 h sequences of environmental and road surface conditions, utilizing X and Y grid coordinates, one-hot-encoded environmental and surface categories, and accident probability. A third CNN sub-network captures 12 h lighting condition patterns using spatial grid inputs, one-hot-encoded lighting types, and accident probability. Additionally, a GRU sub-network learns spatiotemporal dependencies from the X- and Y-grid-based accident time series data. Outputs from the four sub-networks are concatenated and passed through fully connected layers with ReLU activation, batch normalization, dropout (0.5), and L2 regularization, followed by a linear regression layer to predict accident probability. This configuration enables SC2 to exploit richer contextual and temporal information than SC1, improving generalization ability across varying traffic and environmental settings.
As shown in
Figure 7, the third SC3 was constructed using a double-stage deep fusion approach, to facilitate a more comprehensive integration of contextual and temporal features. This architecture combines multiple CNN- and GRU-based sub-models to capture diverse patterns of spatial, temporal, lighting, road surface, and environmental conditions. At the early fusion stage, the outputs from the individual time series models, 24 h CNN (environmental and road surface features), 12 h CNN (light condition features), and 6 h GRU (sequential timestamp data), combine their learned representations. At the late fusion stage, the output from the first concatenation layer is combined with the output of the standalone CNN model (for X, Y, hour, day, and accident probability). At the late fusion stage, the output from the first concatenation layer is combined with the output of the standalone CNN model, which is trained on non-sequential spatial–temporal features, including X and Y grid coordinates, hour of day, weekday encoding, and accident probability. The final fused representation is passed through three fully connected layers to generate the accident probability prediction. Both fusion stages use fully connected layers with ReLU activation, batch normalization, dropout (0.5), and L2 regularization to enhance generalization and prevent overfitting. The final output layer employs a linear activation to estimate accident probability.
4. Results and Discussion
This section presents the performance evaluation of each deep fusion scenario, focusing on how different fusion strategies impact the predictive accuracy and the model’s generalization ability. Evaluation metrics are reported across the training, validation, and testing datasets to assess both fitness and generalizability. In addition, training and validation loss curves are analyzed to visualize learning behavior and detect potential issues, such as overfitting. To further contextualize model performance, the three deep fusion scenarios (SC1, SC2, and SC3) are compared against several traditional machine learning models, including regression-based and ensemble techniques. This comparative analysis highlights the advantages of deep fusion methods in modeling complex traffic accident patterns using multimodal data.
4.1. Scenarios Performance Evaluation
The three deep fusion scenarios, SC1, SC2, and SC3, introduced in
Section 3.5, were evaluated using consistent performance metrics: MSE, MAE, and RMSE. These metrics were calculated across the training, validation, and testing datasets to assess the models’ predictive accuracy and generalizability. As shown in
Table 8, SC1 demonstrates acceptable performance during training but shows a noticeable increase in error on the validation and testing sets. This gap between training and validation metrics suggests its limited generalization ability and possible overfitting. SC2 improves upon SC1 by reducing both training and validation errors across all three metrics, indicating better robustness and a more balanced learning process. This improvement can be attributed to the inclusion of additional contextual features, such as light and road surface conditions. SC3 achieves the best overall performance, with the lowest MSE, MAE, and RMSE values across all data splits. These results validate the effectiveness of the double-stage fusion strategy, which integrates both early and late fusion mechanisms, enabling the model to capture complex spatial–temporal and contextual dependencies in traffic accident data more effectively.
4.2. Model Comparison and Validation
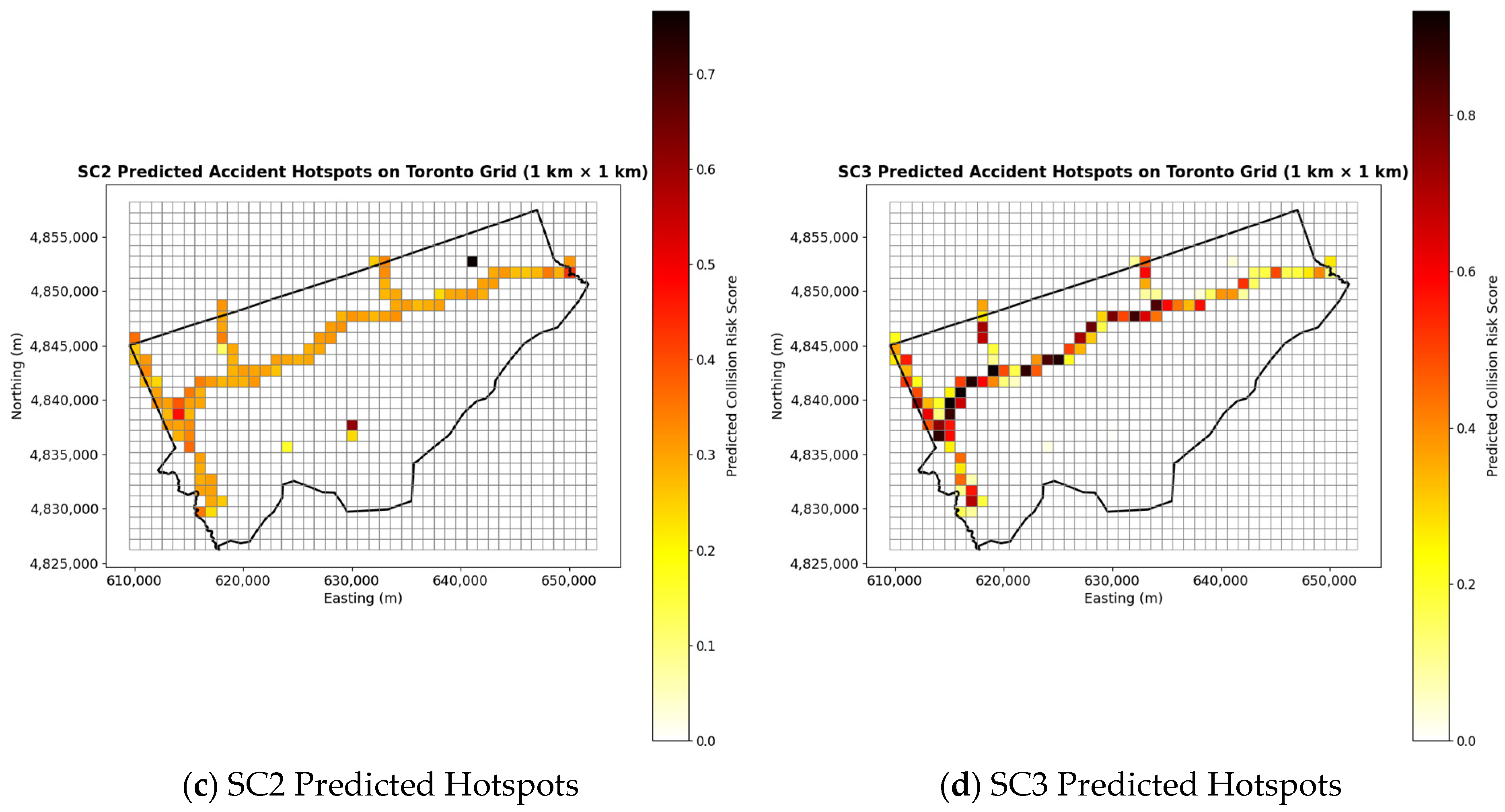
For spatial visualizations of predicted hotspots, we generate figures highlighting high-risk areas and comparative maps across SC1–SC3, along with raw accident counts per grid, as shown in
Figure 8. These hotspot maps provide spatial interpretability of the proposed framework. SC1 produced scattered predictions, consistent with its higher RMSE values. SC2 improved consistency along major road corridors, though gaps remained. SC3 generated the most realistic and corridor-aligned hotspot surfaces, confirming the advantages of the double-stage fusion approach. When compared with observed accident counts from 2014 to 2015, SC3 showed the closest match in both intensity and spatial distribution, while still smoothing local noise to produce more generalizable predictions.
Although DL models are often viewed as “black boxes,” the developed deep fusion framework improves interpretability by structuring feature integration across two levels. The early fusion stage enables the evaluation of how spatial, temporal, and environmental factors jointly influence the predicted risk of accidents, while the late fusion stage isolates the contribution of contextual features, such as lighting and road surface conditions. This flexible design clarifies the relative impact of diverse data sources on model outputs. Furthermore, by converting predictions into spatially interpretable hotspot probability maps, the framework allows transportation authorities to visualize high-risk areas and prioritize safety interventions based on data-driven evidence.
To further validate the effectiveness of the proposed deep fusion models, particularly SC3, we conducted a comparative analysis against several traditional machine learning models using the same dataset and evaluation metrics. This comparison aims to benchmark the performance of DL approaches against established regression and ensemble techniques, providing additional insight into the advantages of multimodal and sequential data integration for traffic accident prediction. The parameters and configurations of each algorithm are detailed in
Table 9. These baseline models were trained using the data from this study. The results of the error metrics are presented in
Table 10.
When comparing deep fusion scenarios to traditional models like AdaBoost and Random Forest, the focus is on testing data metrics, as this reflects how well the model performs on unseen data, which is crucial for real-world applications. As shown in
Table 11, the metric errors for the scenarios were imported from
Table 9, which presents the testing data performance measures for the three scenarios.
Table 10 shows that the developed scenarios outperform traditional machine learning models, especially in capturing complex data relationships and by offering a superior ability to generalize to unseen data. SC3 is the strongest performer across all metrics, and even SC1 and SC2 demonstrate better performance than standard machine learning models, such as Random Forest, AdaBoost, and SVR, particularly in handling real-time traffic prediction scenarios.
To strengthen the claims regarding model superiority and robustness, we conducted a paired
t-test with corresponding
p-values, as shown in
Table 11. The
t-tests were performed on per-sample absolute errors and confirmed that SC3 significantly outperformed SC1 (
p < 0.001), SC2 (
p < 0.05), and all baseline machine learning models (
p < 0.001). These findings validate the robustness and statistical significance of SC3’s improvements.
4.3. Model Optimization and Hyperparameter Tuning
Finally, we developed a training and validation loss curve to assess the performance of deep fusion models during training. This curve helps in diagnosing potential issues such as overfitting, underfitting, and improper learning rates. We encountered an overfitting issue, mitigated it, and enhanced the model’s generalization ability by making adjustments, such as adding dropout layers or applying L1/L2 regularization. This process is called regularization. After adopting regularization, we generated the validation loss curve to evaluate the effect of regularization on the model’s performance and its ability to generalize to unseen data, as shown in
Figure 9.
Figure 9a illustrates the training and validation loss evolution for the SC1 output-based fusion model. The training loss drops quickly at the start and then flattens out, indicating that the model is learning effectively from the training data. The validation loss also decreases but then slightly increases and fluctuates after epoch 15, suggesting potential overfitting or instability in the model’s performance on new, unseen data. The gap between the training and validation loss lines is relatively small, which generally suggests the good generalizability of the model. However, the slight rise in validation loss at later epochs could be a point of concern for the models’ robustness.
Figure 9b represents the Training and validation loss curve of output-based deep fusion for SC2. The training loss decreases sharply from epoch 0 to 2 and then gradually flattens, indicating initial rapid learning, which stabilizes as training progresses. The validation loss decreases in a similar pattern but remains consistently above the training loss, suggesting some overfitting as the model learns to perform better on the training data compared to unseen validation data. The convergence of both lines as epochs increase suggests that the model is becoming stable and learning effectively, though the gap indicates potential for improvement in generalization ability.
Figure 9c shows the training and validation loss trends for double-stage deep fusion for SC3. The training loss decreases sharply initially and then stabilizes, indicating effective learning in the early epochs. The validation loss decreases and closely follows the training loss, suggesting that the model generalizes well without overfitting. The convergence of both lines towards the end implies that further training might not significantly improve the model, indicating an optimal stopping point around epoch 12.
4.4. Use Case and Deployment Potential
The proposed multimodal deep fusion framework shows strong potential for integration into urban intelligent transportation systems (ITS). It can be incorporated into real-time traffic management platforms to assess accident risk levels, provide early warnings, and support proactive safety measures, such as adaptive speed control and dynamic rerouting.
When deployed within geospatial or traffic management systems (e.g., ArcGIS, QGIS, or control centers), the model generates dynamic hotspot maps to assist in resource allocation and road safety planning. Its modular design also supports its integration with additional data sources, including live sensors and vehicular telemetry, to enhance its predictive accuracy.
Experiments were conducted on a Windows 11 Home (version 24H2, build 26100.6584) workstation equipped with an Intel (R) Core (TM) i7-9700 CPU at 3.00 GHz, 128 GB RAM, and a 64-bit operating system. The average training times were 2.5 h (SC1), 3.3 h (SC2), and 4.9 h (SC3), reflecting an increase in computational cost alongside higher model complexity. Inference times remained under 0.3 s per grid cell, demonstrating suitability for near-real-time ITS applications. Deployment challenges primarily involve ensuring real-time data synchronization, managing large model sizes, and maintaining system responsiveness, which can be mitigated through model optimization (e.g., pruning, quantization) and cloud-based distributed deployment.
Overall, the framework offers a scalable, data-driven decision-support tool for smart cities, enabling real-time accident risk monitoring, improved prevention, and more efficient emergency response. Although the present study utilized data from 2014 to 2015, this period provided a comprehensive and well-documented dataset suitable for initial model validation. The framework was intentionally designed to accommodate updated and streaming datasets, allowing retraining with more recent accidents, infrastructure, and mobility information. This adaptability supports the model’s deployment in evolving urban contexts and helps ensure that predictive accuracy remains robust as traffic patterns, technologies, and driver behaviors continue to change over time.
5. Conclusions
This research introduced a comprehensive DL framework for traffic accident probability prediction, leveraging a progressive fusion of temporal, spatial, and contextual data features. By systematically developing and evaluating multiple fusion scenarios, the study demonstrated that integrating diverse information streams, such as environmental factors, lighting conditions, and road surface states, through advanced DL architectures significantly enhances predictive performance.
The double-stage fusion strategy implemented in SC3 represents a novel contribution to the field, as it captures both short-term and long-term dependencies by combining the strengths of multiple CNN and GRU models at different stages of feature integration. The results indicate that models incorporating a broader range of contextual factors, and employing both early and late fusion, can more effectively characterize the complex relationships underlying traffic accidents.
Overall, this approach underscores the value of deep fusion frameworks in transportation safety analytics. The findings suggest that future research and practical implementations should prioritize the integration of rich, multimodal data and adopt flexible DL pipelines capable of modeling the nuanced interactions present in real-world traffic environments. This work lays the groundwork for further exploration of deep ensemble strategies in spatiotemporal risk prediction, offering a scalable path forward for next-generation intelligent transportation systems.
Practical Implications: The framework provides usable guidance for Toronto transportation policymakers. This evidence-based tool enables decision-makers to understand which specific highway segments are at high risk and are vulnerable to safety concerns, thus allowing planners to prioritize proactive measures. These proactive measures may include more efficient resource allocation for routine maintenance and enforcement, targeting the hotspot, and supporting proactive dynamic traffic management during inclement weather conditions.
Limitations: Temporal generalizability may be limited because the analysis is based only on the 2014–2015 Toronto highways dataset. Although this dataset is among the most complete and reliable sources available, changes in population, land use, and infrastructure may influence future model performance. Another limitation involves the model’s inability to distinguish between minor and severe crash risks, due to the absence of real-time traffic flow and severity data.
The study also lacks several key predictors commonly used in traffic safety research, particularly traffic flow variables (e.g., vehicle counts, congestion, and origin–destination demand) and crash severity indicators (e.g., injury counts, fatalities, or property damage). Incorporating these factors into the current framework presented two main challenges. Firstly, traffic flow is a dynamic exposure variable that requires continuous monitoring through sensors or GPS traces, while the accident dataset used here comprises static event reports. Linking continuous flow data to discrete crash events would require additional datasets beyond those analyzed for the 2014–2015 period. Secondly, severity prediction represents a distinct modeling task. While this study focused on estimating the probability of accident occurrence across space and time, severity modeling would involve classifying the crash outcomes conditional to a crash event. Combining both objectives would require a multi-task learning approach and a substantially larger dataset to address the strong class imbalance between minor, injury, and fatal crashes.
Future directions: Future research could incorporate traffic flow and crash severity data to enhance the model’s realism and its predictive capabilities. Extending the framework to urban arterials and cross-regional transportation networks would further test its scalability. Integrating real-time data from IoT-enabled traffic sensors and connected vehicles could enable the dynamic and continuous prediction of accident risks. Additionally, future models could utilize adaptive parameters through online learning and simulation to enhance their responsiveness to changing traffic conditions.