Evaluation of Spatial Variability of Soil Nutrients in Saline–Alkali Farmland Using Automatic Machine Learning Model and Hyperspectral Data
Abstract
1. Introduction
2. Materials and Methods
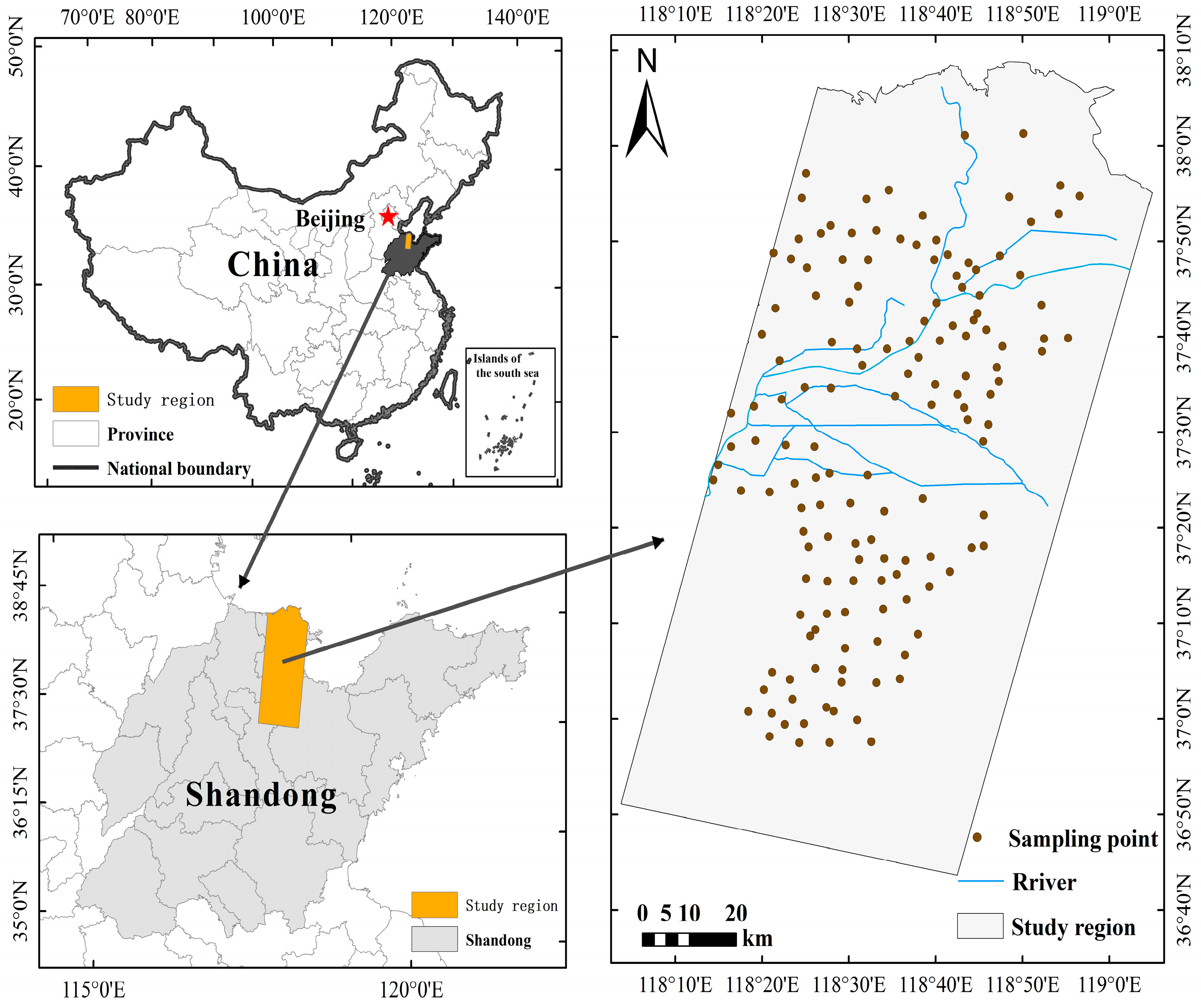
2.1. Study Area
2.2. Data Sources and Preprocessing
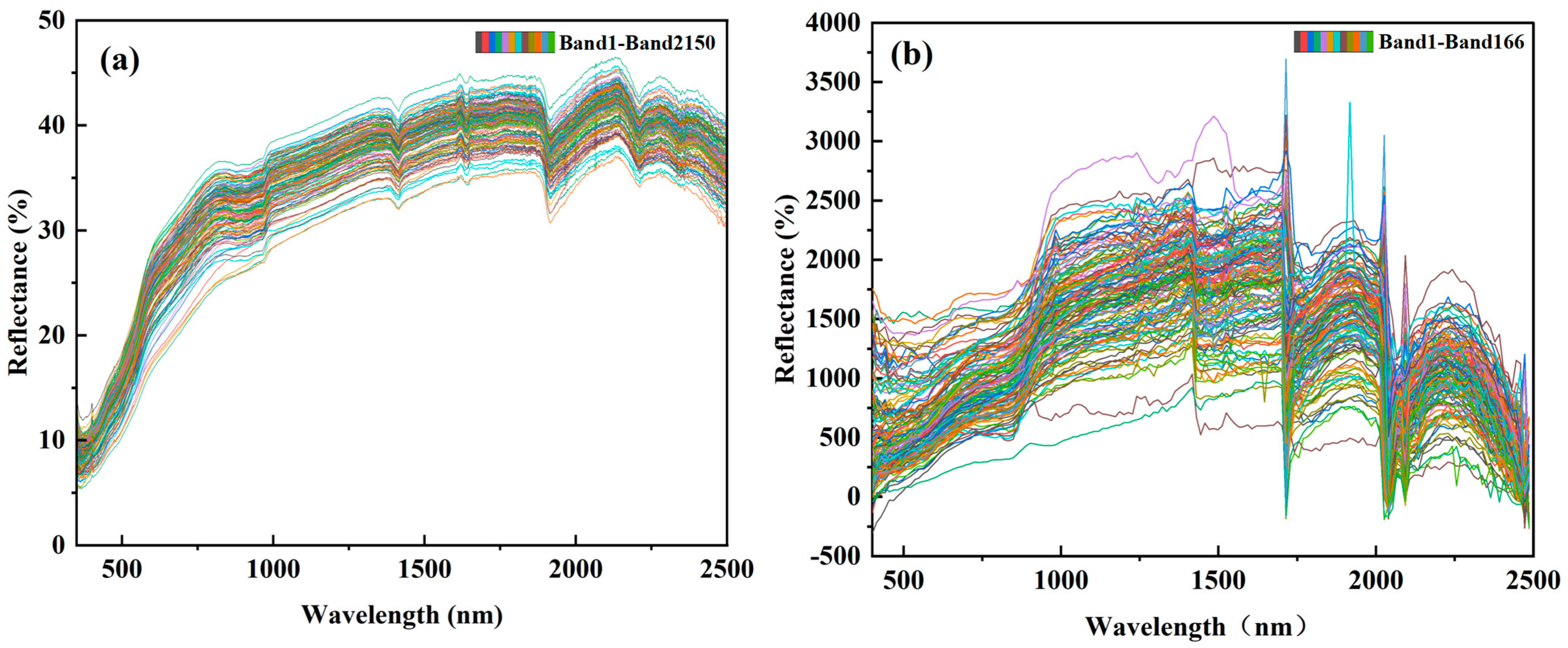
2.2.1. Spectral Data
2.2.2. Soil Nutrient Data
2.2.3. Driving Factor Data
2.3. Band Selection
2.4. TPE Optimization Algorithm
2.5. XGB Model
2.6. Principles of SHAP and Model Interpretation
2.7. Performance Evaluation of TPE-XGB Model
2.8. Hierarchical Partitioning and Variance Decomposition
3. Results and Analysis
3.1. Distribution Characteristics and Variability of Soil Nutrients
3.2. Accuracy Assessment of Soil Nutrient Prediction Models
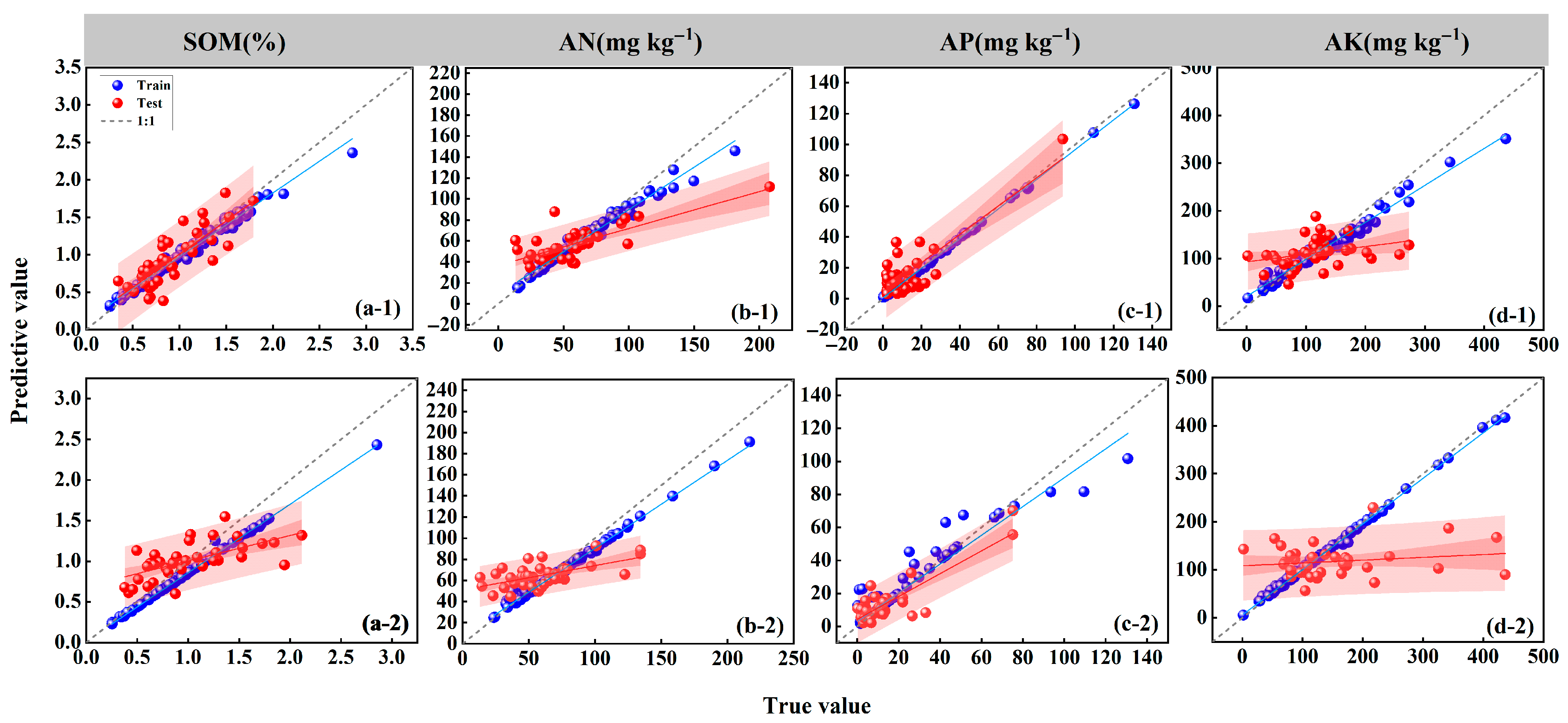
3.3. Evaluation of TPE-XGB Model Fitting Performance Via Scatter Plot Analysis
3.4. Spatial Distribution Mapping of Soil Nutrients Using TPE-XGB Model
3.5. Interpretation of Spectral Contributions Using SHAP Values
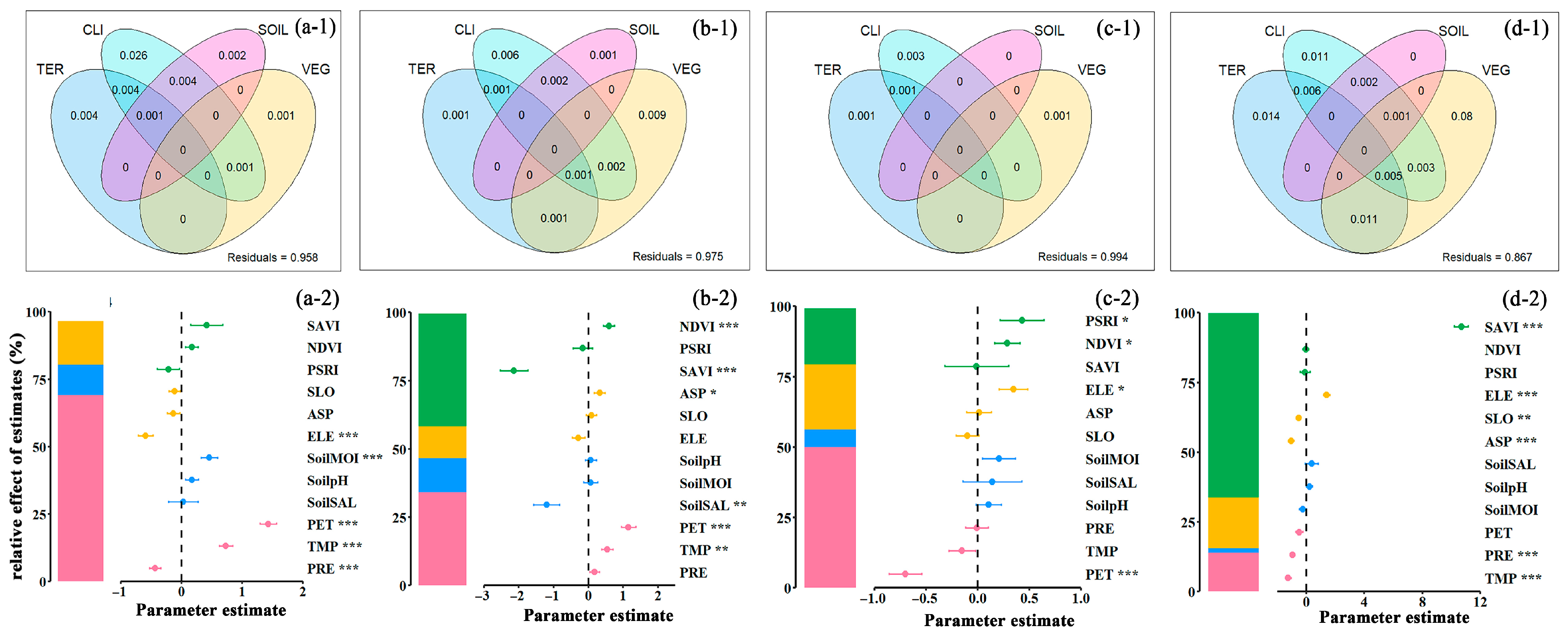
3.6. Analysis of Environmental Drivers of Soil Nutrient Spatial Differences
4. Discussion
4.1. The Driving Mechanism of Factor Synergy on Soil Nutrients
4.2. Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ahmed, U.; Lin, J.C.; Srivastava, G.; Djenouri, Y. A nutrient recommendation system for soil fertilization based on evolutionary computation. Comput. Electron. Agric. 2021, 189, 106407. [Google Scholar] [CrossRef]
- Kim, M.; Gilley, J.E. Artificial neural network estimation of soil erosion and nutrient concentrations in runoff from land application areas. Comput. Electron. Agric. 2008, 64, 268–275. [Google Scholar] [CrossRef]
- Sirsat, M.S.; Cernadas, E.; Fernández-Delgado, M.; Barro, S. Automatic prediction of village-wise soil fertility for several nutrients in india using a wide range of regression methods. Comput. Electron. Agric. 2018, 154, 120–133. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, G.X.; Feng, B.; Wang, C.; Luo, Y.; Li, F.; Shen, C.C.; Ma, D.H.; Zhang, C.Z.; Zhang, J.B. Saline-alkali land reclamation boosts topsoil carbon storage by preferentially accumulating plant-derived carbon. Sci. Bull. 2024, 69, 2948–2958. [Google Scholar] [CrossRef]
- Feng, W.T.; Jiang, J.; Lin, L.T.; Wang, Y.G. Soil calcium prompts organic carbon accumulation after decadal saline-water irrigation in the Taklamakan desert. J. Environ. Manag. 2023, 344, 118421. [Google Scholar] [CrossRef]
- Song, J.S.; Zhang, H.Y.; Chang, F.D.; Yu, R.; Zhang, X.Q.; Wang, X.Q.; Wang, W.N.; Liu, J.M.; Zhou, J.; Li, Y.Y. Humic acid plus manure increases the soil carbon pool by inhibiting salinity and alleviating the microbial resource limitation in saline soils. Catena 2023, 233, 107527. [Google Scholar] [CrossRef]
- Du, X.J.; Hu, H.; Wang, T.H.; Zou, L.; Zhou, W.F.; Gao, H.X.; Ren, X.Q.; Wang, J.; Hu, S.W. Long-term rice cultivation increases contributions of plant and microbial-derived carbon to soil organic carbon in saline-sodic soils. Sci. Total Environ. 2023, 904, 166713. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Yao, X.F.; Li, X.X.; Wang, Q.; Wang, J.H.; Zhu, L.S.; Wang, J. Effects of dibutyl phthalate on microbial community and the carbon cycle in salinized soil. J. Clean. Prod. 2023, 404, 136928. [Google Scholar] [CrossRef]
- Zhang, L.; Su, X.Y.; Meng, H.; Men, Y.Q.; Liu, C.M.; Yan, X.Y.; Song, X.L.; Sun, X.Z.; Mao, L.L. Cotton stubble return and subsoiling alter soil microbial community, carbon and nitrogen in coastal saline cotton fields. Soil Till. Res. 2023, 226, 105585. [Google Scholar] [CrossRef]
- Setia, R.; Gottschalk, P.; Smith, P.; Marschner, P.; Baldock, J.; Setia, D.; Smith, J. Soil salinity decreases global soil organic carbon stocks. Sci. Total Environ. 2012, 465, 267–272. [Google Scholar] [CrossRef] [PubMed]
- Li, S.P.; Zhao, L.; Wang, C.; Huang, H.Y.; Zhuang, M.H. Synergistic improvement of carbon sequestration and crop yield by organic material addition in saline soil: A global meta-analysis. Sci. Total Environ. 2023, 891, 164530. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.X.; Fan, Q.Y.; Ma, J.W.; Cui, L.Q.; Quan, G.X.; Yan, J.L.; Wu, L.M.; Hina, K.; Abdul, B.; Wang, H. Effects of biochar on cadmium (Cd) uptake in vegetables and its natural downward movement in saline-alkali soil. Environ. Pollut. Bioavail. 2020, 32, 36–46. [Google Scholar] [CrossRef]
- Duan, M.L.; Liu, G.H.; Zhou, B.B.; Chen, X.P.; Wang, Q.J.; Zhu, H.Y.; Li, Z.J. Effects of modified biochar on water and salt distribution and water-stable macro-aggregates in saline-alkaline soil. J. Soils Sediments 2021, 21, 2192–2202. [Google Scholar] [CrossRef]
- Liu, K.; Wang, Y.F.; Wang, X.D.; Sun, Z.P.; Song, Y.H.; Di, H.G.; Yan, Q.; Hua, D.X. Characteristic bands extraction method and prediction of soil nutrient contents based on an analytic hierarchy process. Measurement 2023, 220, 111695. [Google Scholar] [CrossRef]
- Qi, H.J.; Paz-Kagan, T.; Karnieli, A.; Jin, X.; Li, S.W. Evaluating calibration methods for predicting soil available nutrients using hyperspectral VNIR data. Soil Tillage Res. 2018, 175, 267–275. [Google Scholar] [CrossRef]
- Lelago, A.; Bibiso, M. Performance of mid infrared spectroscopy to predict nutrients for agricultural soils in selected areas of ethiopia. Heliyon 2022, 8, e11564. [Google Scholar] [CrossRef]
- Shao, W.Y.; Wang, Q.Z.; Guan, Q.Y.; Luo, H.P.; Ma, Y.R.; Zhang, J. Distribution of soil available nutrients and their response to environmental factors based on path analysis model in arid and semi-arid area of northwest china. Sci. Total Environ. 2022, 827, 154346. [Google Scholar] [CrossRef]
- Zuo, W.A.; Xu, L.; Qiu, M.H.; Yi, S.Q.; Wang, Y.M.; Shen, C.; Zhao, Y.L.; Li, Y.L.; Gu, C.H.; Shan, Y.H.; et al. Effects of different exogenous organic materials on improving soil fertility in coastal saline-alkali soil. Agriculture 2023, 13, 61. [Google Scholar] [CrossRef]
- žížala, D.; Minařík, R.; Zádorová, T. Soil organic carbon mapping using multispectral remote sensing data: Prediction ability of data with different spatial and spectral resolutions. Remote Sens. 2019, 11, 2947. [Google Scholar] [CrossRef]
- Li, W.; Liu, Y.; Zheng, H.; Wu, J.; Yuan, H.; Wang, X.; Xie, W.; Qin, Y.; Zhu, H.; Nie, X.; et al. Complex vegetation patterns improve soil nutrients and maintain stoichiometric balance of terrace wall aggregates over long periods of vegetation recovery. Catena 2023, 227, 107141. [Google Scholar] [CrossRef]
- Liu, K.; Liu, Z.C.; Zhou, N.; Shi, X.R.; Lock, T.R.; Kallenbach, R.L.; Yuan, Z.Y. Predicted increased p relative to n growth limitation of dry grasslands under soil acidification and alkalinization is ameliorated by increased precipitation. Soil Biol. Biochem. 2022, 173, 108793. [Google Scholar] [CrossRef]
- Oberholzer, S.; Summerauer, L.; Steffens, M.; Speranza, C.I. Best performances of visible-near-infrared models in soils with little carbonate—A field study in switzerland. Soil 2024, 10, 231–249. [Google Scholar] [CrossRef]
- Pelegrino, M.H.P.; Silva, S.H.G.; de Faria, Á.J.G.; Mancini, M.; Teixeira, A.F.D.S.; Chakraborty, S.; Weindorf, D.C.; Guilherme, L.R.G.; Curi, N. Prediction of soil nutrient content via pxrf spectrometry and its spatial variation in a highly variable tropical area. Precis. Agric. 2022, 23, 18–34. [Google Scholar] [CrossRef]
- Jiao, X.C.; Liu, H.; Wang, W.M.; Zhu, J.J.; Wang, H. Estimation of surface soil nutrient content in mountainous citrus orchards based on hyperspectral data. Agriculture 2024, 14, 873. [Google Scholar] [CrossRef]
- Liu, K.; Wang, Y.F.; Peng, Z.Q.; Xu, X.X.; Liu, J.J.; Song, Y.H.; Di, H.G.; Hua, D.X. Monitoring soil nutrients using machine learning based on uav hyperspectral remote sensing. Int. J. Remote Sens. 2024, 45, 4897–4921. [Google Scholar]
- Ratke, R.F.; Viana, P.R.N.; Teodoro, L.P.R.; Baio, F.H.R.; Teodoro, P.E.; Santana, D.C.; Santos, C.E.D.S.; Zuffo, A.M.; Aguilera, J.G. Multispectral sensors and machine learning as modern tools for nutrient content prediction in soil. AgriEngineering 2024, 6, 4384–4394. [Google Scholar] [CrossRef]
- Li, Y.S.; Chang, C.Y.; Wang, Z.R.; Li, T.; Li, J.W.; Zhao, G.X. Identification of cultivated land quality grade using fused multi-source data and multi-temporal crop remote sensing information. Remote Sens. 2022, 14, 5647. [Google Scholar]
- Vašát, R.; Kodešová, R.; Borůvka, L.; Klement, A.; Jakšík, O.; Gholizadeh, A. Consideration of peak parameters derived from continuum-removed spectra to predict extractable nutrients in soils with visible and near-infrared diffuse reflectance spectroscopy (VNIR-DRS). Geoderma 2014, 232–234, 208–218. [Google Scholar] [CrossRef]
- Ramírez, P.B.; Calderón, F.J.; Jastrow, J.D.; Ping, C.; Matamala, R. Applying nir and mir spectroscopy for c and soil property prediction in northern cold-region ecosystems. Which approach works better? Geoderma Reg. 2023, 32, e00617. [Google Scholar] [CrossRef]
- Yang, J.X.; Yuan, X.Z.; Han, B.; Zhao, L.B.; Sun, J.L.; Shang, M.Y.; Wang, X.C.; Ding, C.B. Phase imbalance analysis of gf-3 along-track insar data and ocean current measurements. Remote Sens. 2021, 13, 269. [Google Scholar] [CrossRef]
- Hu, J.; Peng, J.; Zhou, Y.; Xu, D.; Zhao, R.; Jiang, Q.; Fu, T.; Wang, F.; Shi, Z. Quantitative estimation of soil salinity using UAV-borne hyperspectral and satellite multispectral images. Remote Sens. 2019, 11, 736. [Google Scholar] [CrossRef]
- Metternicht, G.I.; Zinck, J.A. Remote sensing of soil salinity: Potentials and constraints. Remote Sens. Environ. 2003, 85, 1–20. [Google Scholar] [CrossRef]
- Dai, X.; Feng, H.; Xiao, L.; Zhou, J.; Wang, Z.; Zhang, J.; Yao, Y. Ecological vulnerability assessment of a China’s representative mining city based on hyperspectral remote sensing. Ecol. Indic. 2022, 145, 109663. [Google Scholar] [CrossRef]
- Feng, L.; Zhao, Z.; Yang, H.; Chen, Q.; Yang, C.; Zhao, X.; Zhang, G.; Zhang, X.; Dong, X. Clay-Hosted Lithium Exploration in the Wenshan Region of Southeastern Yunnan Province, China, Using Multi-Source Remote Sensing and Structural Interpretation. Minerals 2025, 15, 826. [Google Scholar] [CrossRef]
- Ge, X.Y.; Ding, J.L.; Teng, D.X.; Xie, B.Q.; Zhang, X.L.; Wang, J.J.; Han, L.J.; Bao, Q.L.; Wang, J.Z. Exploring the capability of gaofen-5 hyperspectral data for assessing soil salinity risks. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102928. [Google Scholar] [CrossRef]
- Goetz, A.F.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging spectrometry for earth remote sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef] [PubMed]
- Stuke, A.; Rinke, P.; Todorovic, M. Efficient hyperparameter tuning for kernel ridge regression with bayesian optimization. Mach. Learn. Sci. Technol. 2021, 2, 045024. [Google Scholar] [CrossRef]
- Ghawi, R.; Pfeffer, J. Efficient hyperparameter tuning with grid search for text categorization using kNN approach with BM25 similarity. Int. J. Inf. Retr. Res. 2019, 9, 160–180. [Google Scholar] [CrossRef]
- Scott, M.; Lee, S. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4765–4774. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 2951–2959. [Google Scholar]
- Chen, B.L.; Zheng, H.W.; Luo, G.P.; Chen, C.B.; Bao, A.M.; Liu, T.; Chen, X. Adaptive estimation of multi-regional soil salinization using extreme gradient boosting with bayesian tpe optimization. Int. J. Remote Sens. 2022, 43, 778–811. [Google Scholar] [CrossRef]
- Kim, D.; Kwon, K.; Pham, K.; Oh, J.; Choi, H. Surface settlement prediction for urban tunneling using machine learning algorithms with bayesian optimization. Autom. Constr. 2022, 140, 104331. [Google Scholar] [CrossRef]
- Salamai, A.A. Deep learning framework for predictive modeling of crude oil price for sustainable management in oil markets. Expert Syst. Appl. 2023, 211, 118687. [Google Scholar] [CrossRef]
- Yu, J.; Zheng, W.; Xu, L.; Meng, F.; Li, J.; Zhangzhong, L. Tpe-catboost: An adaptive model for soil moisture spatial estimation in the main maize-producing areas of china with multiple environment covariates. J. Hydrol. 2022, 613, 128465. [Google Scholar] [CrossRef]
- Ozaki, Y.; Tanigaki, Y.; Watanabe, S.; Onishi, M. Multiobjective tree-structured parzen estimator for computationally expensive optimization problems. IEEE Trans. Evol. Comput. 2020, 25, 522–535. [Google Scholar]
- Ha, N.T.; Manley-Harris, M.; Pham, T.D.; Hawes, I. The use of radar and optical satellite imagery combined with advanced machine learning and metaheuristic optimization techniques to detect and quantify above ground biomass of intertidal seagrass in a new zealand estuary. Int. J. Remote Sens. 2021, 42, 4712–4738. [Google Scholar] [CrossRef]
- Liu, X.; Liu, T.; Feng, P. Long-term performance prediction framework based on xgboost decision tree for pultruded frp composites exposed to water, humidity and alkaline solution. Compos. Struct. 2022, 284, 115184. [Google Scholar] [CrossRef]
- Lai, J.; Zou, Y.; Zhang, J.; Peres Neto, P.R. Generalizing hierarchical and variation partitioning in multiple regression and canonical analyses using the rdacca. Hp R package. Methods Ecol. Evol. 2022, 13, 782–788. [Google Scholar] [CrossRef]
- Li, H.; Tian, H.; Wang, Z.; Liu, C.; Nurzhan, A.; Megharaj, M.; He, W. Potential effect of warming on soil microbial nutrient limitations as determined by enzymatic stoichiometry in the farmland from different climate zones. Sci. Total Environ. 2022, 802, 149657. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, P.; Ou, H.; Wei, S.; Wu, L.; Jiang, Y.; Wang, R.; Liu, X.; Wang, Z.; Chen, L. Effects of different vegetation restoration on soil nutrients, enzyme activities, and microbial communities in degraded karst landscapes in southwest china. For. Ecol. Manage. 2022, 508, 120002. [Google Scholar] [CrossRef]
- Yang, X.; Shao, M.; Li, T.; Zhang, Q.; Gan, M.; Chen, M.; Bai, X. Distribution of soil nutrients under typical artificial vegetation in the desert–loess transition zone. Catena 2021, 200, 105165. [Google Scholar] [CrossRef]
- Cui, Y.; Fang, L.; Guo, X.; Han, F.; Ju, W.; Ye, L.; Wang, X.; Tan, W.; Zhang, X. Natural grassland as the optimal pattern of vegetation restoration in arid and semi-arid regions: Evidence from nutrient limitation of soil microbes. Sci. Total Environ. 2019, 648, 388–397. [Google Scholar] [CrossRef]
- Zhang, M.; O’Connor, P.J.; Zhang, J.; Ye, X. Linking soil nutrient cycling and microbial community with vegetation cover in riparian zone. Geoderma 2021, 384, 114801. [Google Scholar] [CrossRef]
- Yuan, C.; Wu, F.; Wu, Q.; Fornara, D.A.; Heděnec, P.; Peng, Y.; Zhu, G.; Zhao, Z.; Yue, K. Vegetation restoration effects on soil carbon and nutrient concentrations and enzymatic activities in post-mining lands are mediated by mine type, climate, and former soil properties. Sci. Total Environ. 2023, 879, 163059. [Google Scholar] [CrossRef]
- Lin, Y.; Deng, H.; Du, K.; Rafay, L.; Zhang, G.; Li, J.; Chen, C.; Wu, C.; Lin, H.; Yu, W. Combined effects of climate, restoration measures and slope position in change in soil chemical properties and nutrient loss across lands affected by the wenchuan earthquake in china. Sci. Total Environ. 2017, 596, 274–283. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Jing, C. Response of the natural grassland vegetation change to meteorological drought in xinjiang from 1982 to 2015. Front. Environ. Sci. 2022, 10, 1047818. [Google Scholar] [CrossRef]
- Qinfei, B.; Yuhai, B.; Yantong, Y.; Jie, Y.; Yanqi, W.; Jie, W. Effects of different vegetation restoration models on soil nutrients in the water level fluctuation zone of a large reservoir. Ecol. Indic. 2024, 169, 112955. [Google Scholar] [CrossRef]
- Ni, Y.; Jian, Z.; Zeng, L.; Liu, J.; Lei, L.; Zhu, J.; Xu, J.; Xiao, W. Climate, soil nutrients, and stand characteristics jointly determine large-scale patterns of biomass growth rates and allocation in pinus massoniana plantations. For. Ecol. Manage. 2022, 504, 119839. [Google Scholar] [CrossRef]
- Dai, L.; Ge, J.; Wang, L.; Zhang, Q.; Liang, T.; Bolan, N.; Lischeid, G.; Rinklebe, J. Influence of soil properties, topography, and land cover on soil organic carbon and total nitrogen concentration: A case study in qinghai-tibet plateau based on random forest regression and structural equation modeling. Sci. Total Environ. 2022, 821, 153440. [Google Scholar] [CrossRef]
- Bi, M.; Zhang, S.; Xu, Q.; Hou, S.; Han, M.; Yu, X. Coupling and synergistic relationships between soil aggregate stability and nutrient stoichiometric characteristics under different microtopographies on karst rocky desertification slopes. Catena 2024, 243, 108142. [Google Scholar] [CrossRef]
- Balasundram, S.K.; Robert, P.C.; Mulla, D.J.; Allan, D.L. Relationship between oil palm yield and soil fertility as affected by topography in an indonesian plantation. Commun. Soil Sci. Plant Anal. 2006, 37, 1321–1337. [Google Scholar] [CrossRef]
- Noorbakhsh, S.; Schoenau, J.; Si, B.; Zeleke, T.; Qian, P. Soil properties, yield, and landscape relationships in south-central saskatchewan canada. J. Plant Nutr. 2008, 31, 539–556. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, M.; Zhao, X.; Li, Y.; Zhao, W.; Li, A.; Chen, S.; Chen, S.; Han, X.; Huang, J. Topography and grazing effects on storage of soil organic carbon and nitrogen in the northern china grasslands. Ecol. Indic. 2018, 93, 45–53. [Google Scholar] [CrossRef]
- Huang, M.; Zhang, L. Hydrological responses to conservation practices in a catchment of the loess plateau, china. Hydrol. Process. 2004, 18, 1885–1898. [Google Scholar] [CrossRef]
- Li, Z.; Liu, C.; Dong, Y.; Chang, X.; Nie, X.; Liu, L.; Xiao, H.; Lu, Y.; Zeng, G. Response of soil organic carbon and nitrogen stocks to soil erosion and land use types in the loess hilly–gully region of china. Soil Till. Res. 2017, 166, 1–9. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, Q.; Wang, H.; Geng, R.; Wang, J.; Yi, Y.; Li, M.; He, D. Optical and molecular techniques are complementary to understand the characteristics of dissolved organic matter in the runoff from sloping croplands with various micro-topographies during rainfall. J. Hydrol. 2025, 648, 132403. [Google Scholar] [CrossRef]
- Fu, B.J.; Meng, Q.H.; Qiu, Y.; Zhao, W.W.; Zhang, Q.J.; Davidson, D.A. Effects of land use on soil erosion and nitrogen loss in the hilly area of the loess plateau, china. Land Degrad. Dev. 2004, 15, 87–96. [Google Scholar] [CrossRef]




| Category | Driving Factor | Acquisition Method |
|---|---|---|
| Soil | SoilMOI, SoilpH, SoilSAL | Drying method, electrode method, mass method |
| Topography | ELE, SLO, ASP | ArcGIS—Surface Analysis |
| Climate | TMP, PRE, PET | ArcGIS—Kriging Interpolation |
| Vegetation | SAVIred, PSRI, NDVI | ENVI—Band Math |
| Hyperparameter | Type | Optimization Range |
|---|---|---|
| min_child_weight | float | [0.1, 5] |
| lambda | float | [1, 100] |
| num_boost_round | int | [10, 200] |
| eta | float | [0.1, 5] |
| subsample | float | [0.1, 5] |
| max_depth | int | [1, 15] |
| colsample_bytree | float | [0.6, 1] |
| colsample_bynode | float | [0.6, 1] |
| Soil Nutrients | Feature | R2 | I(R2) | RMSE | I(RMSE) |
|---|---|---|---|---|---|
| SOM | ISH | 0.65 | 44% | 0.21% | −40% |
| SBH | 0.45 | 0.35% | |||
| AN | ISH | 0.56 | 37% | 23.42 (mg kg−1) | −40% |
| SBH | 0.41 | 39.23 (mg kg−1) | |||
| AP | ISH | 0.70 | 15% | 9.84 (mg kg−1) | −23% |
| SBH | 0.61 | 12.73 (mg kg−1) | |||
| AK | ISH | 0.51 | 21% | 59.82 (mg kg−1) | 17% |
| SBH | 0.42 | 50.94 (mg kg−1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, M.; Rao, Q.; Yang, X.; Wu, X.; Zhan, D.; Zhang, J.; Lu, M.; Song, Y. Evaluation of Spatial Variability of Soil Nutrients in Saline–Alkali Farmland Using Automatic Machine Learning Model and Hyperspectral Data. ISPRS Int. J. Geo-Inf. 2025, 14, 403. https://doi.org/10.3390/ijgi14100403
Xiang M, Rao Q, Yang X, Wu X, Zhan D, Zhang J, Lu M, Song Y. Evaluation of Spatial Variability of Soil Nutrients in Saline–Alkali Farmland Using Automatic Machine Learning Model and Hyperspectral Data. ISPRS International Journal of Geo-Information. 2025; 14(10):403. https://doi.org/10.3390/ijgi14100403
Chicago/Turabian StyleXiang, Meiyan, Qianlong Rao, Xiaohang Yang, Xiaoqian Wu, Dexi Zhan, Jin Zhang, Miao Lu, and Yingqiang Song. 2025. "Evaluation of Spatial Variability of Soil Nutrients in Saline–Alkali Farmland Using Automatic Machine Learning Model and Hyperspectral Data" ISPRS International Journal of Geo-Information 14, no. 10: 403. https://doi.org/10.3390/ijgi14100403
APA StyleXiang, M., Rao, Q., Yang, X., Wu, X., Zhan, D., Zhang, J., Lu, M., & Song, Y. (2025). Evaluation of Spatial Variability of Soil Nutrients in Saline–Alkali Farmland Using Automatic Machine Learning Model and Hyperspectral Data. ISPRS International Journal of Geo-Information, 14(10), 403. https://doi.org/10.3390/ijgi14100403








