Numerical Assessment of a High-Level Rock Failure Potential Based on a Three-Dimensional Discrete Element Model
Abstract
1. Introduction
2. Background
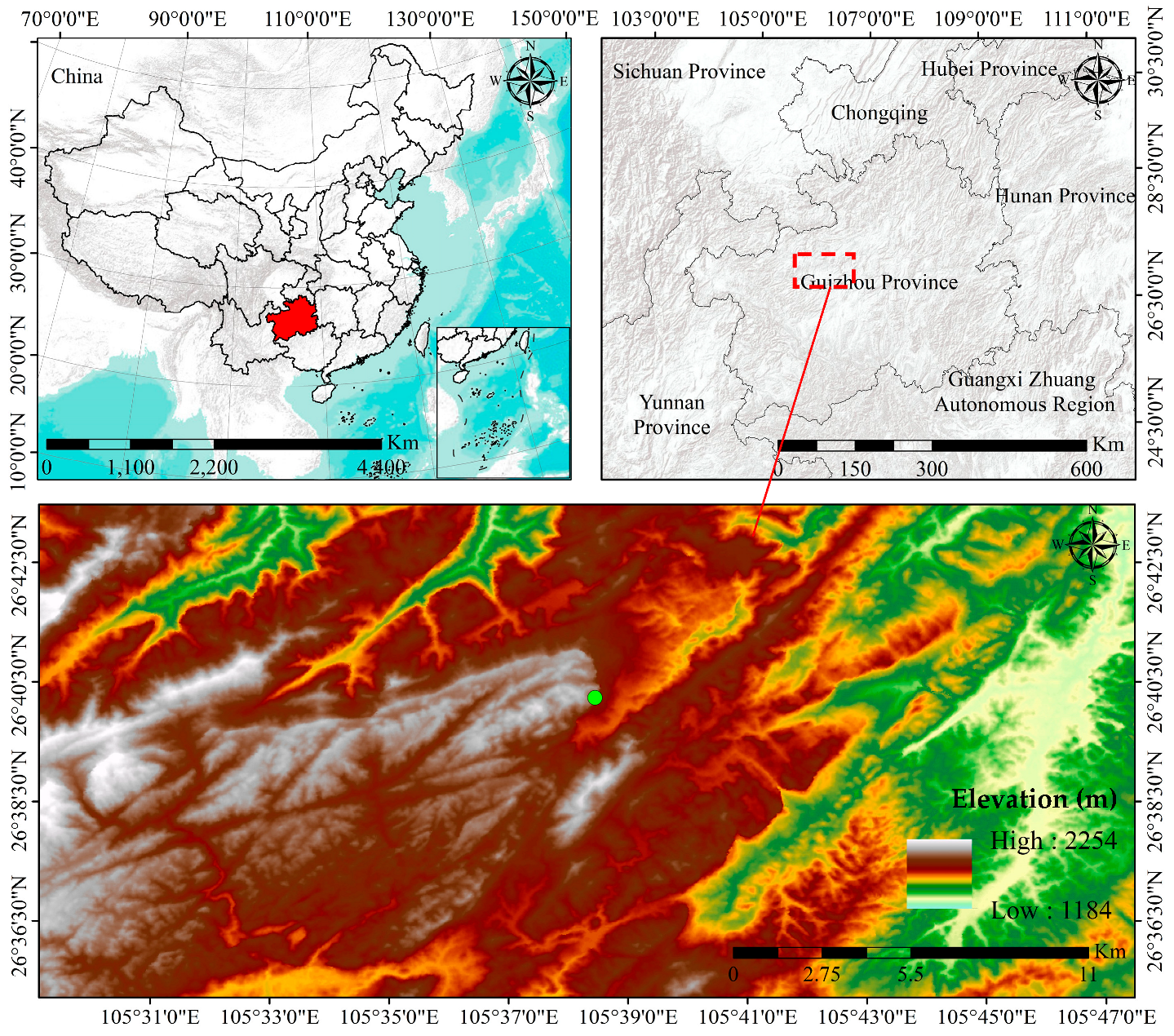
2.1. Study Area
2.2. Geological and Topographical Condition
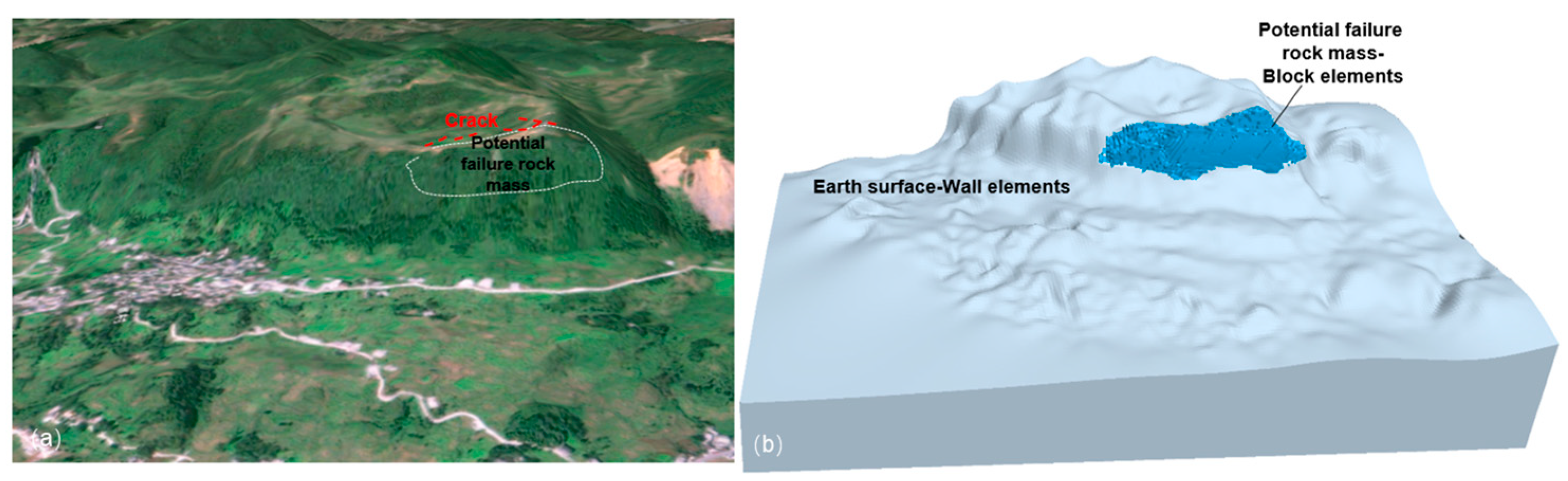
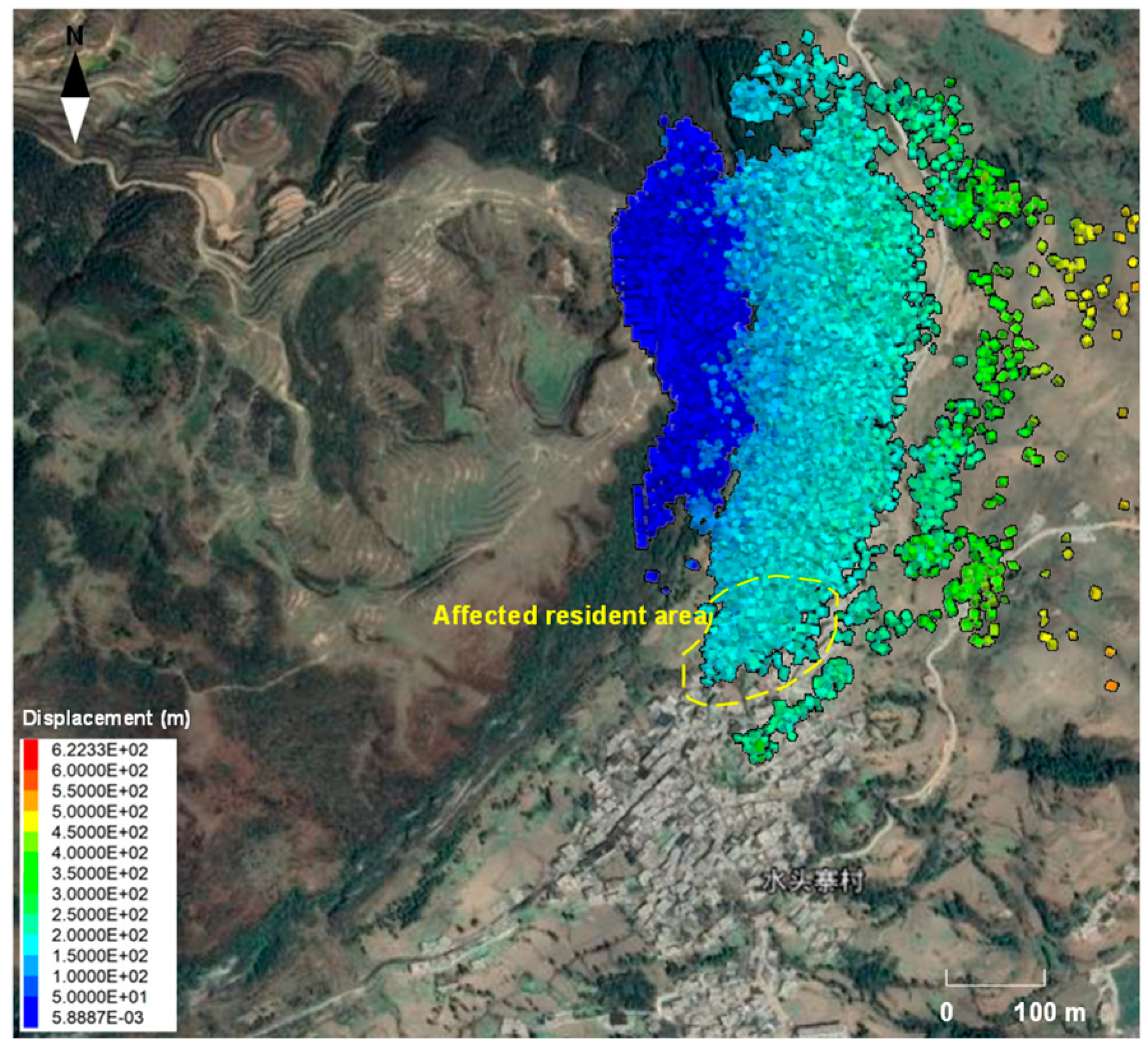
2.3. Deformation Phenomenon
3. Methodology
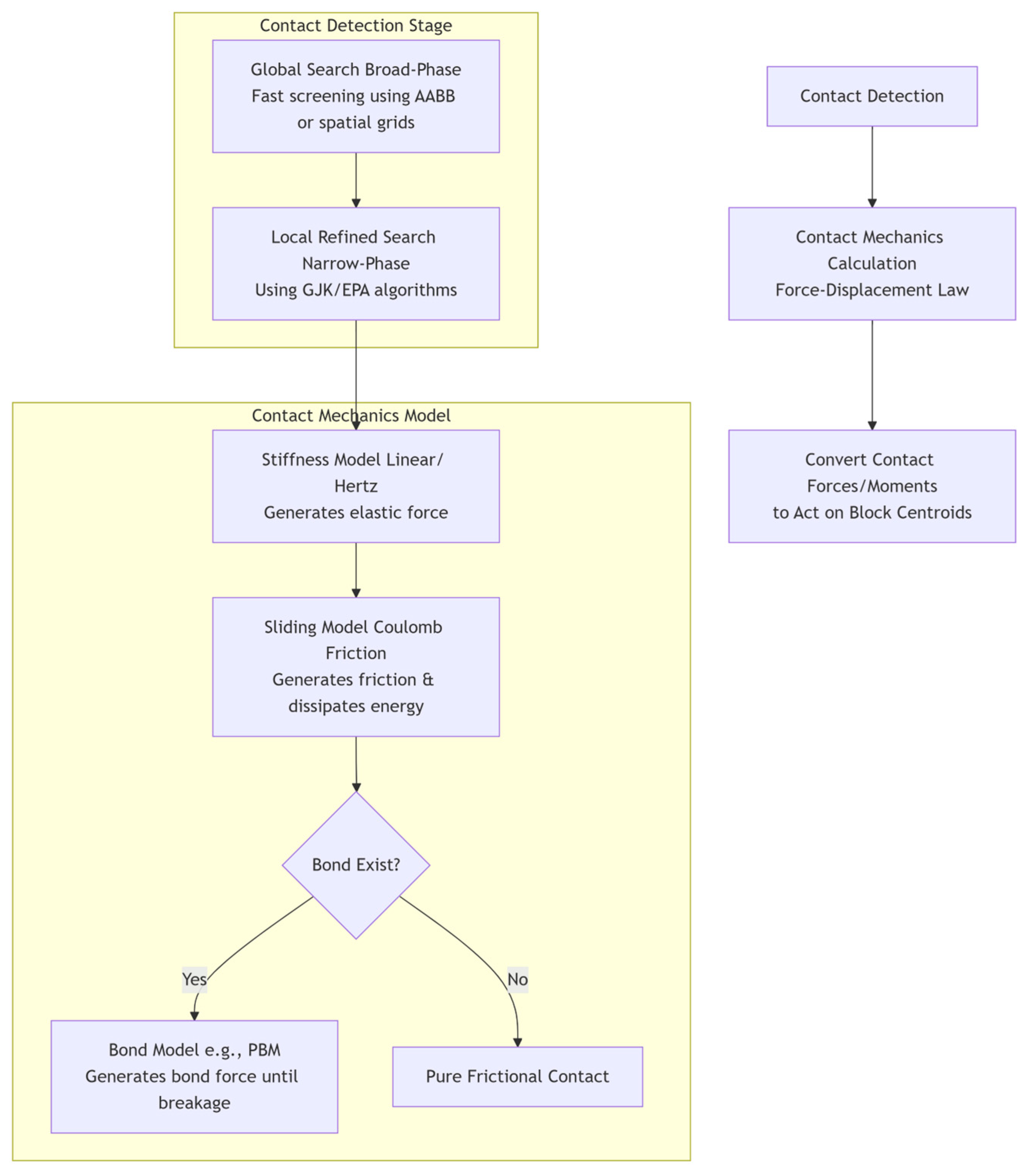
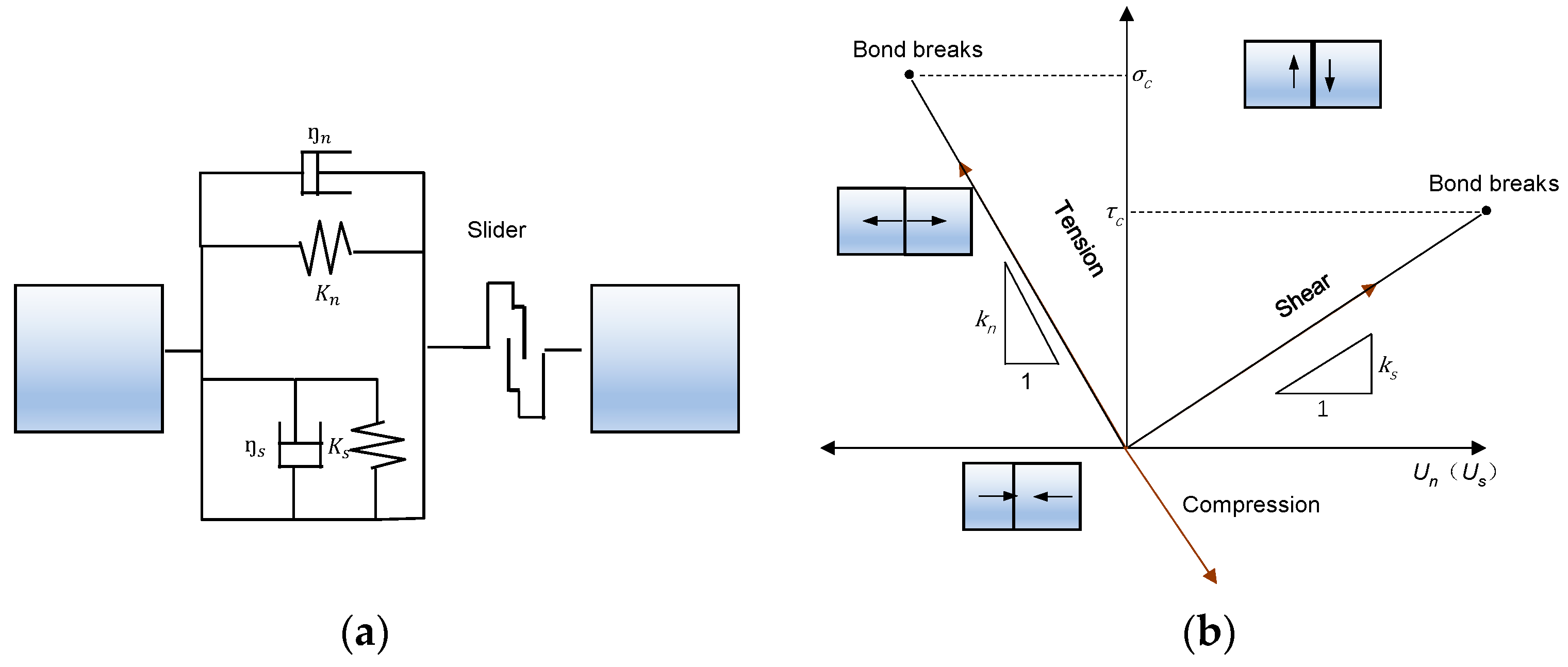
3.1. Discrete Element Method
- Rigid Block Assumption: Each discrete element (block) is treated as an absolutely rigid body, meaning it itself undergoes no elastic or plastic deformation. All system strain energy is stored at the contacts between blocks.
- Finite Displacement and Rotation Assumption: Blocks can undergo arbitrarily large displacements and rotations during loading, making this model particularly suitable for simulating highly nonlinear mechanical processes such as large deformation, disintegration, and collapse.
3.2. Numerical Model Construction and Setting
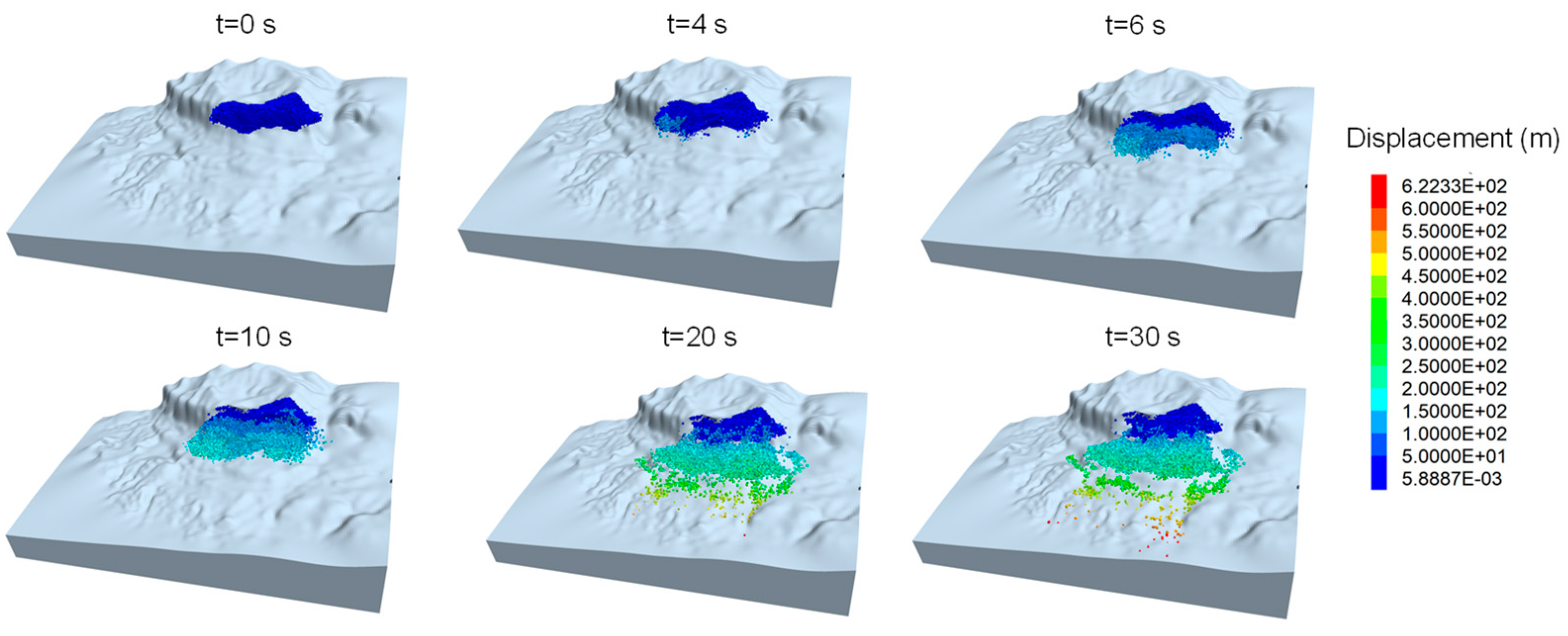
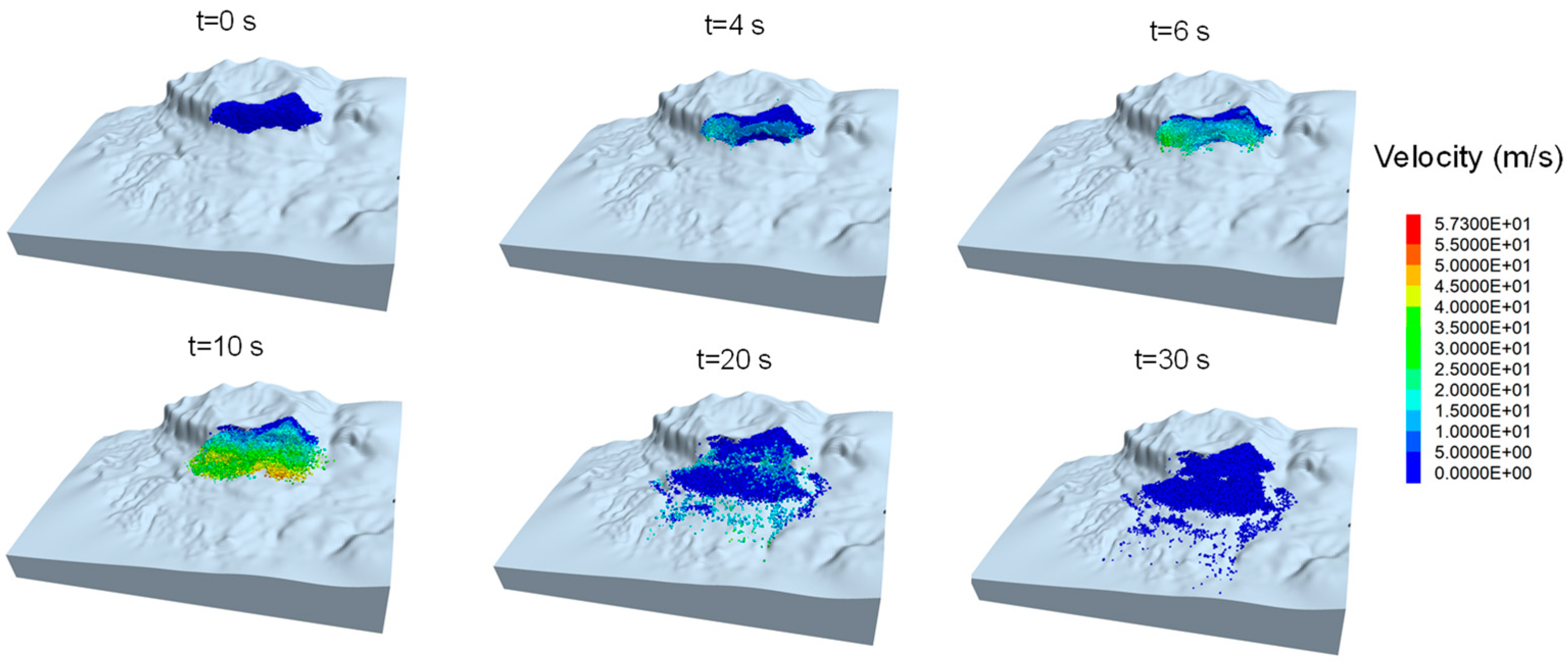
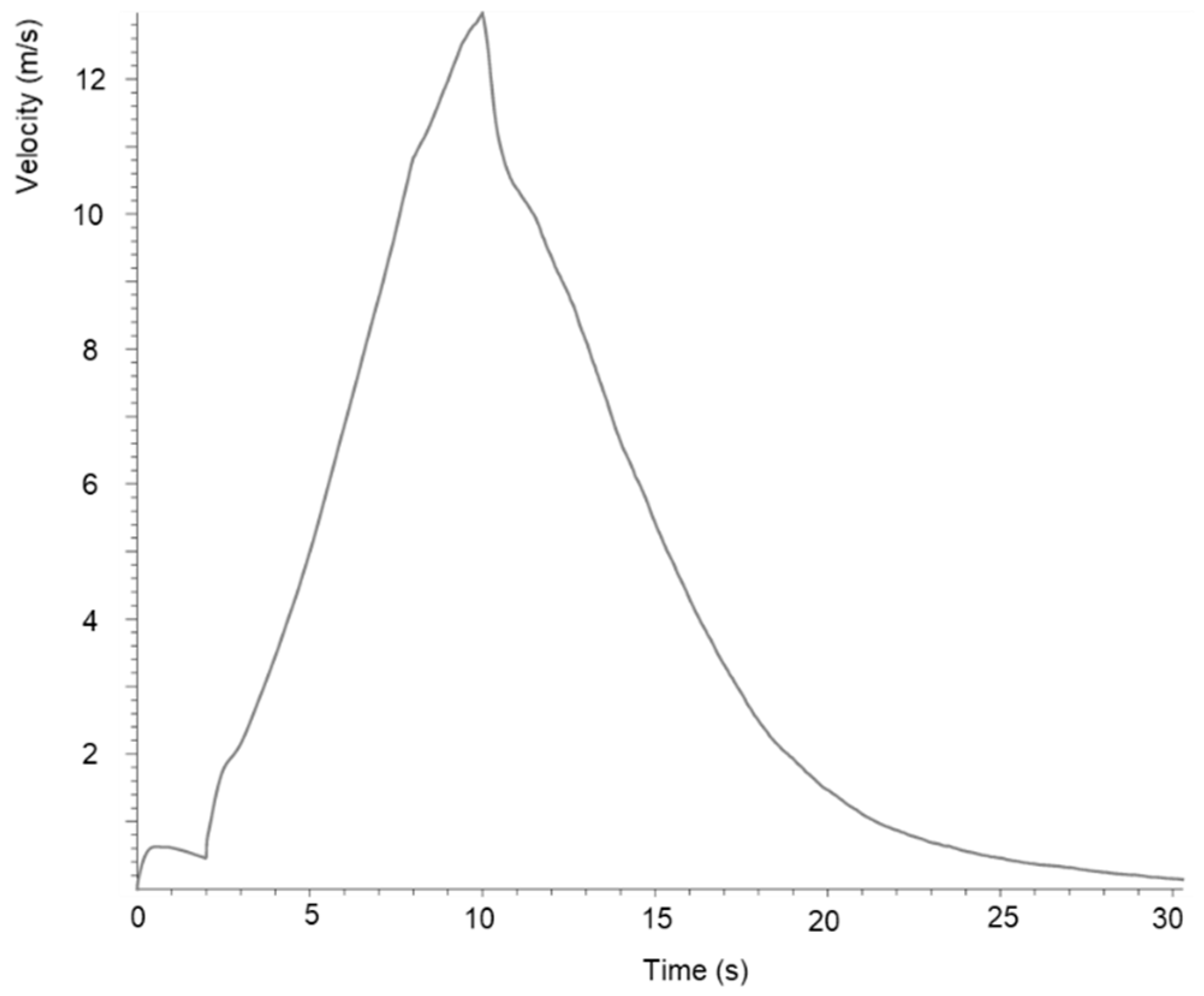
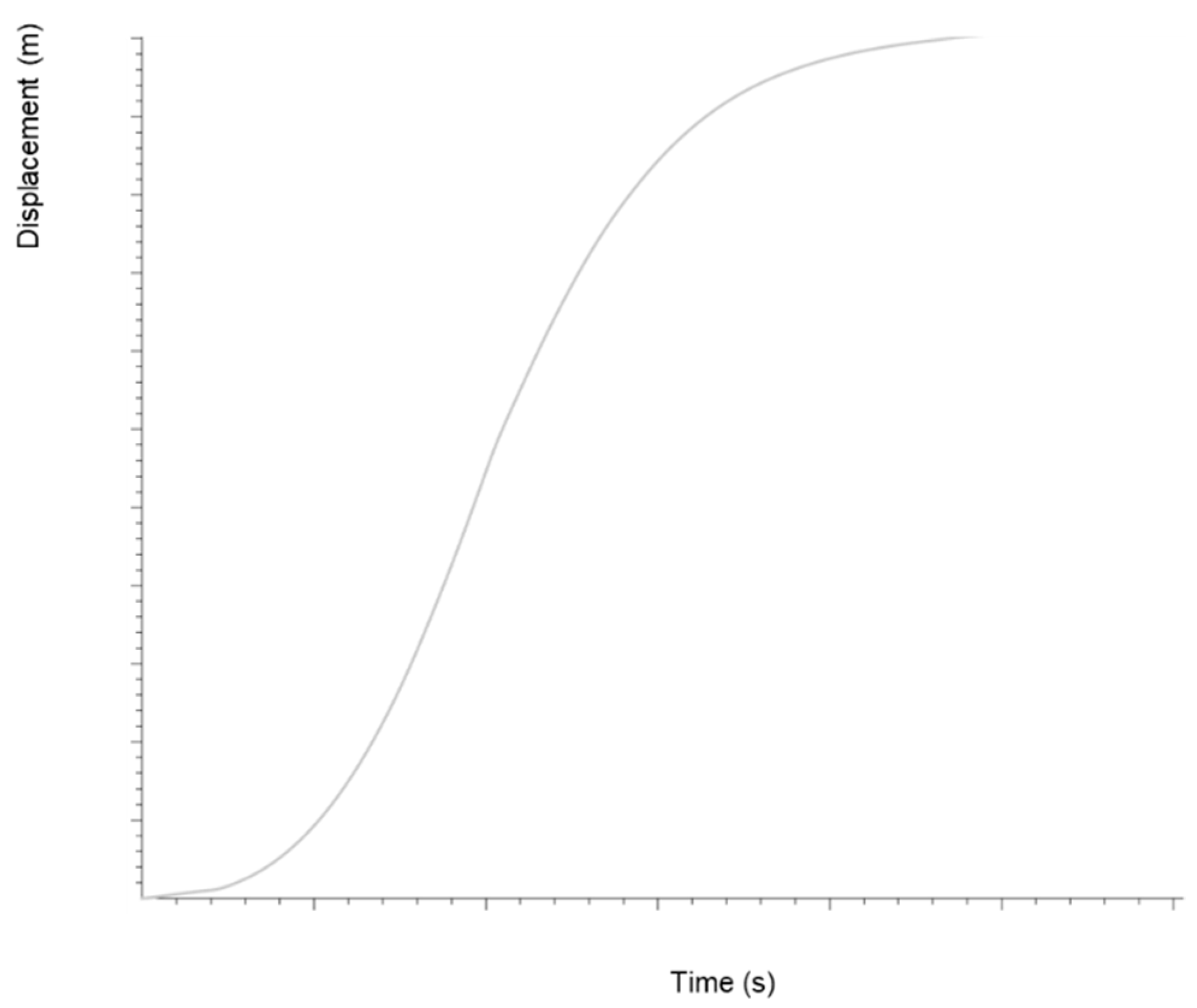
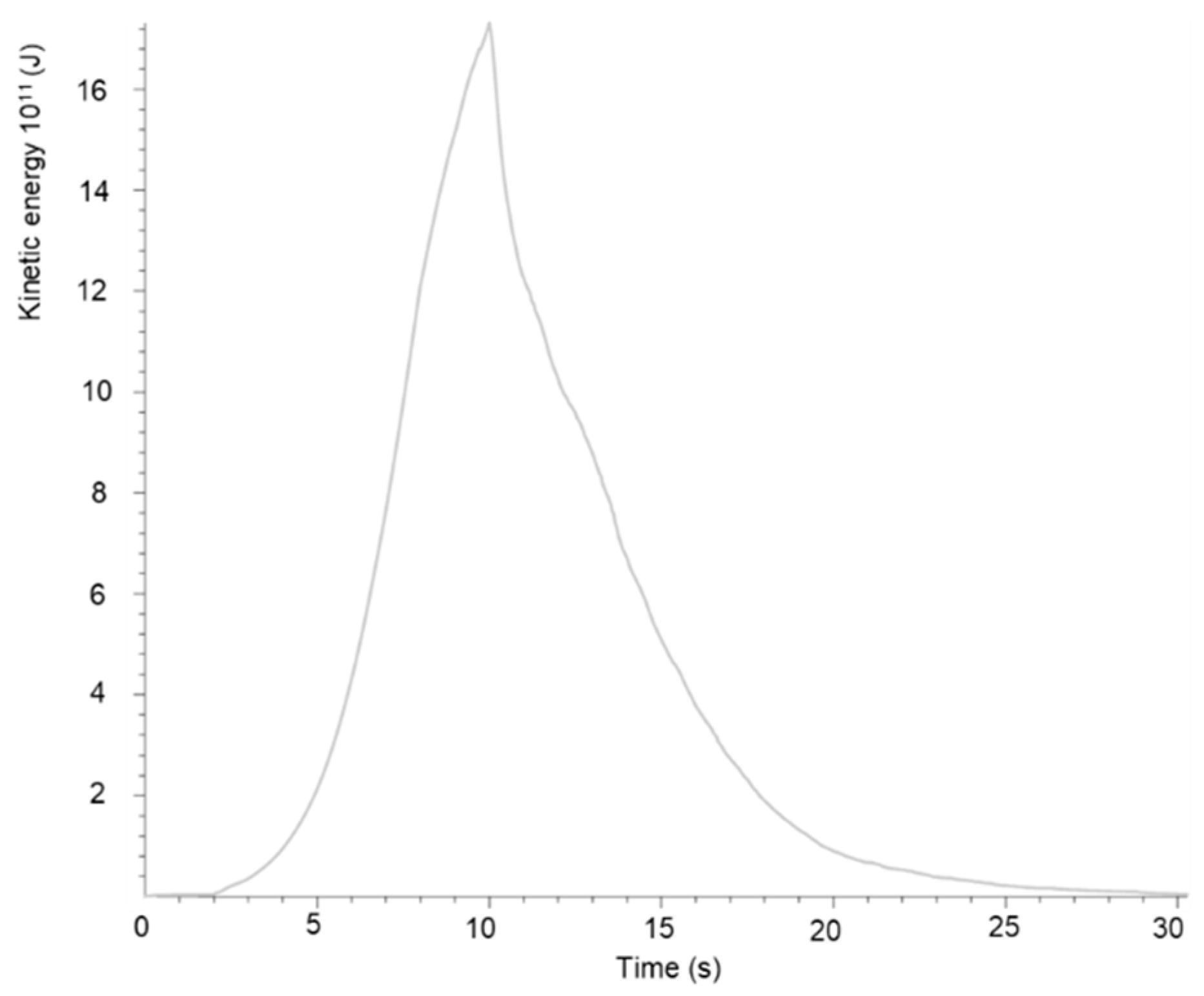
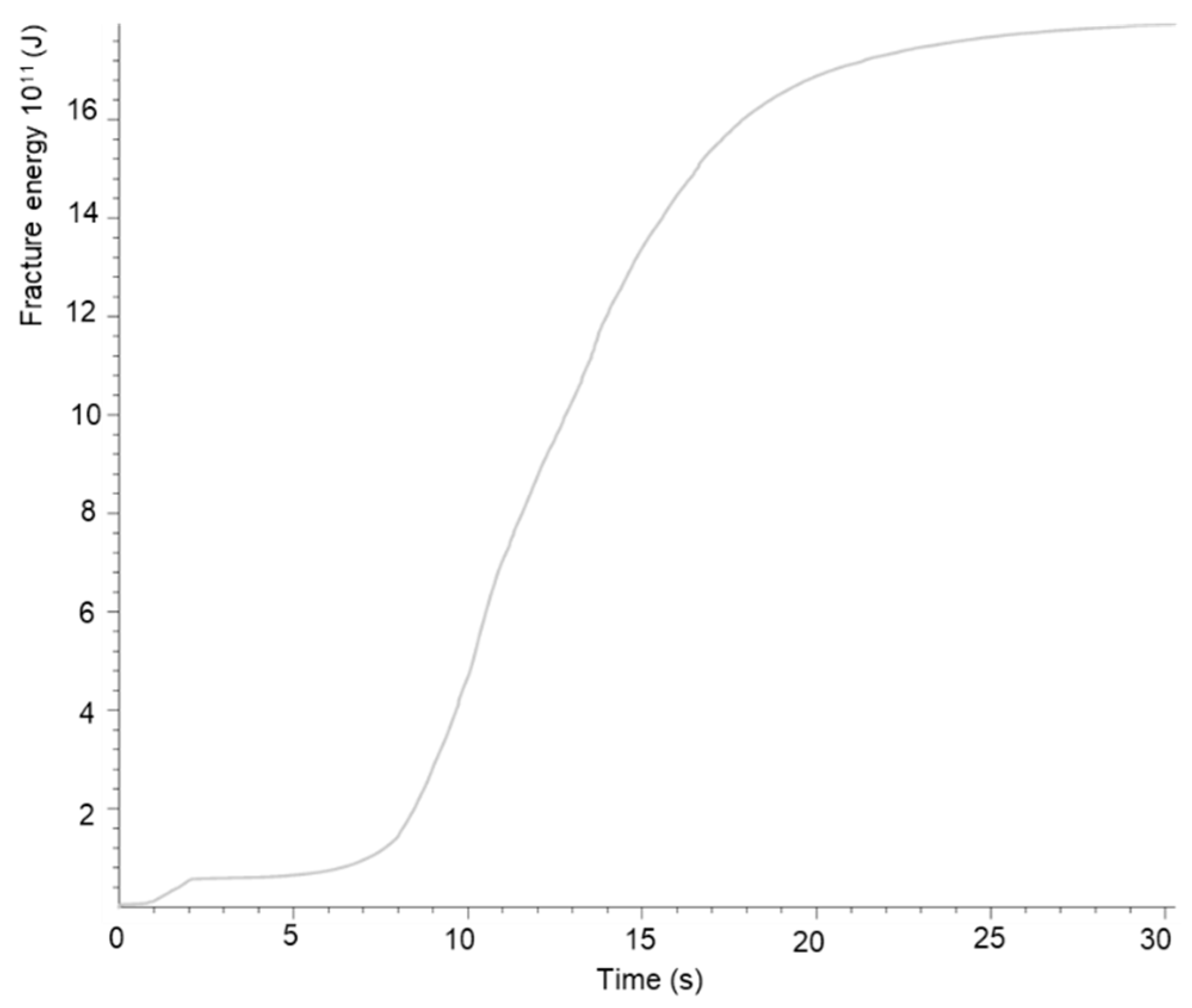
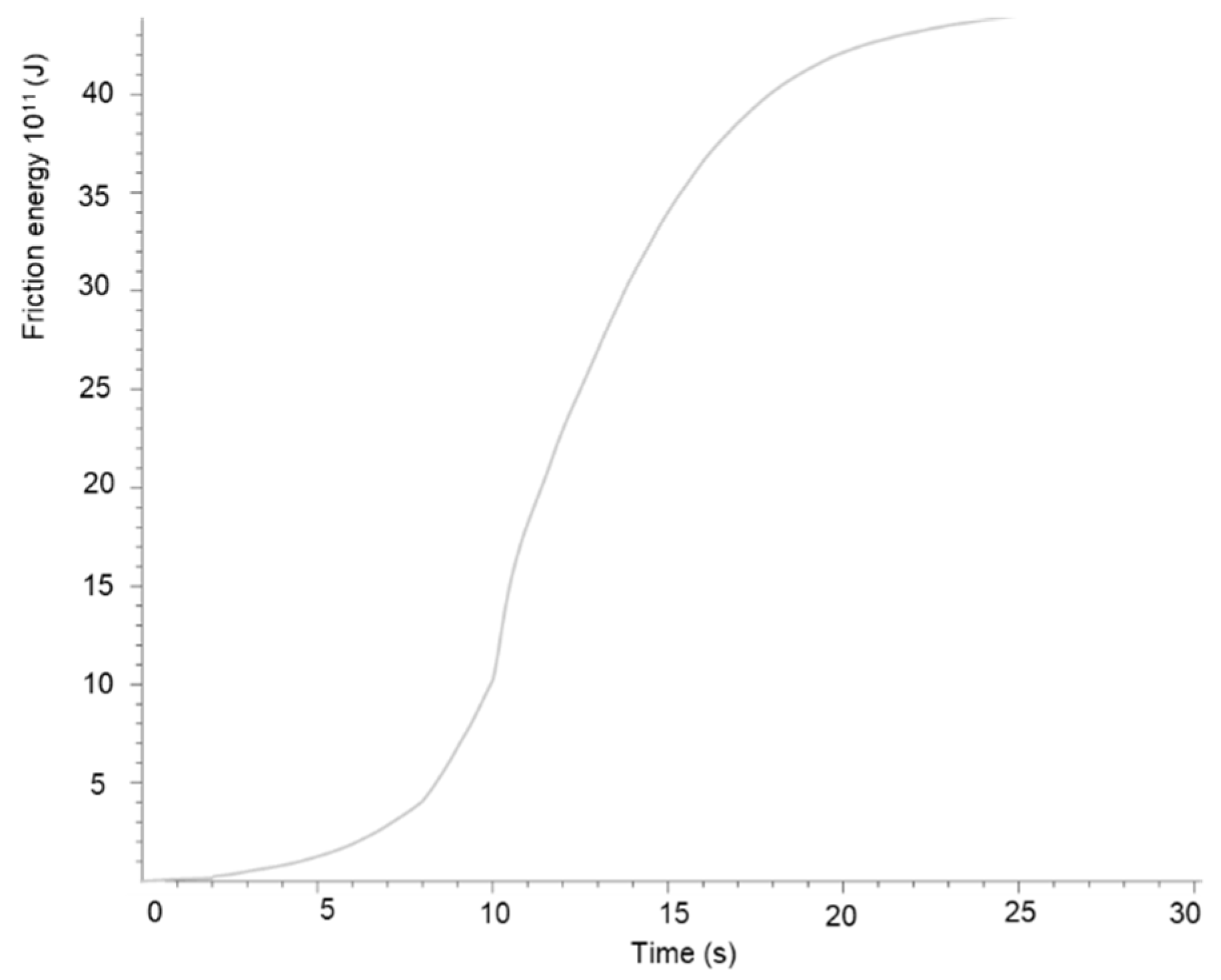
4. Numerical Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Maerz, N.H.; Youssef, A.M.; Pradhan, B.; Bulkhi, A. Remediation and mitigation strategies for rock fall hazards along the highways of Fayfa Mountain, Jazan region, Kingdom of Saudi Arabia. Arab. J. Geosci. 2014, 8, 2633–2651. [Google Scholar] [CrossRef]
- Gerstner, R.; Fey, C.; Kuschel, E.; Valentin, G.; Voit, K.; Zangerl, C. Polyphase rock slope failure controlled by pre-existing geological structures and rock bridges. Bull. Eng. Geol. Environ. 2023, 82, 363. [Google Scholar] [CrossRef]
- Bao, Y.; Han, X.; Chen, J.; Zhang, W.; Zhan, J.; Sun, X.; Chen, M. Numerical assessment of failure potential of a large mine waste dump in Panzhihua City, China. Eng. Geol. 2019, 253, 171–183. [Google Scholar] [CrossRef]
- Peng, W.; Song, S.; Yu, C.; Bao, Y.; Sui, J.; Hu, Y. Forecasting landslides via three-dimensional discrete element modeling: Helong landslide case study. Appl. Sci. 2019, 9, 5242. [Google Scholar] [CrossRef]
- Zito, C.; Mangifesta, M.; Francioni, M.; Guerriero, L.; Di Martire, D.; Calcaterra, D.; Sciarra, N. Cascading landslide: Kinematic and finite element method analysis through remote sensing techniques. Remote. Sens. 2024, 16, 3423. [Google Scholar] [CrossRef]
- Grodecki, M. Landslide triggered by small excavation—Numerical simulations. Arch. Civ. Eng. 2023, 69, 293–301. [Google Scholar] [CrossRef]
- Antoci, C.; Gallati, M.; Sibilla, S. Numerical simulation of fluid–structure interaction by SPH. Comput. Struct. 2007, 85, 879–890. [Google Scholar] [CrossRef]
- Dai, Z.; Huang, Y. A three-dimensional model for flow slides in municipal solid waste landfills using smoothed particle hydrodynamics. Environ. Earth Sci. 2016, 75, 135. [Google Scholar] [CrossRef]
- Li, X.; Yan, Q.; Zhao, S.; Luo, Y.; Wu, Y.; Wang, D. Investigation of influence of baffles on landslide debris mobility by 3D material point method. Landslides 2020, 17, 1129–1143. [Google Scholar] [CrossRef]
- Llano-Serna, M.A.; Farias, M.M.; Pedroso, D.M. An assessment of the material point method for modelling large scale run-out processes in landslides. Landslides 2016, 13, 1057–1066. [Google Scholar] [CrossRef]
- Liu, W.; Wang, D.; Zhou, J.; He, S. Simulating the Xinmo landslide runout considering entrainment effect. Environ. Earth Sci. 2019, 78, 585. [Google Scholar] [CrossRef]
- Bao, Y.; Sun, X.; Zhou, X.; Zhang, Y.; Liu, Y. Some numerical approaches for landslide river blocking: Introduction, simulation, and discussion. Landslides 2021, 18, 3907–3922. [Google Scholar] [CrossRef]
- Troncone, A.; Pugliese, L.; Parise, A.; Mazzuca, P.; Conte, E. Post-failure stage analysis of flow-type landslides using different numerical techniques. Comput. Geotech. 2025, 182, 107152. [Google Scholar] [CrossRef]
- Zhan, L.; Peng, C.; Zhang, B.; Wu, W. A SPH framework for dynamic interaction between soil and rigid body system with hybrid contact method. Int. J. Numer. Anal. Methods Géoméch. 2020, 44, 1446–1471. [Google Scholar] [CrossRef]
- Liang, H.; He, S.; Lei, X.; Bi, Y.; Liu, W.; Ouyang, C. Dynamic process simulation of construction solid waste (CSW) landfill landslide based on SPH considering dilatancy effects. Bull. Eng. Geol. Environ. 2019, 78, 763–777. [Google Scholar] [CrossRef]
- Bhandari, T.; Hamad, F.; Moormann, C.; Sharma, K.; Westrich, B. Numerical modelling of seismic slope failure using MPM. Comput. Geotech. 2016, 75, 126–134. [Google Scholar] [CrossRef]
- Adhav, P.; Feng, Z.; Ni, T.; Peters, B.; Fan, X. Numerical insights into rock–ice avalanche geophysical flow mobility through CFD–DEM simulation. Comput. Part. Mech. 2024, 11, 1403–1419. [Google Scholar] [CrossRef]
- Wu, Z.; Ma, L.; Fan, L. Investigation of the characteristics of rock fracture process zone using coupled FEM/DEM method. Eng. Fract. Mech. 2018, 200, 355–374. [Google Scholar] [CrossRef]
- Lo, C.-M.; Lin, M.-L.; Tang, C.-L.; Hu, J.-C. A kinematic model of the Hsiaolin landslide calibrated to the morphology of the landslide deposit. Eng. Geol. 2011, 123, 22–39. [Google Scholar] [CrossRef]
- Lu, C.-Y.; Tang, C.-L.; Chan, Y.-C.; Hu, J.-C.; Chi, C.-C. Forecasting landslide hazard by the 3D discrete element method: A case study of the unstable slope in the Lushan hot spring district, central Taiwan. Eng. Geol. 2014, 183, 14–30. [Google Scholar] [CrossRef]
- Li, J.; Wang, W.; Chen, G.; Han, Z. Simulating the impact of highway construction to landslides with creep deformation using DDA: A case study of Qinglong landslide in Guizhou Province, China. Arab. J. Geosci. 2022, 15, 140. [Google Scholar] [CrossRef]
- Liu, G.; Kang, J.; Zhong, Z.; Bo, W.; Fan, H.; Yang, C. Laboratory experiments and 3D DDA numerical simulations on rockfall movement characteristics. Rock Mech. Rock Eng. 2025, 58, 9747–9769. [Google Scholar] [CrossRef]
- Liping, L.; Hongyun, F.; Hongliang, L.; Wenfeng, T.; Jingyao, G.; Shangqu, S.; Xinbo, J.; Shen, Z. Analysis of factors influencing tunnel block collapse in blocky rock masses: Insights from large-scale model experiments and DDA simulations. Rock Mech. Rock Eng. 2024, 57, 9847–9864. [Google Scholar] [CrossRef]
- Chen, X.; Wei, J.; Zhao, Z.; Wang, X.; Ren, Z.; Xu, C. Numerical simulation of landslide movement and impact disaster intensity on brick-concrete buildings: A case from Niuti landslide in Shaanxi, China. Landslides 2025, 22, 2363–2377. [Google Scholar] [CrossRef]
- Chang, M.; Dou, X.; Tang, L.; Xu, H. Risk assessment of multi-disaster in Mining Area of Guizhou, China. Int. J. Disaster Risk Reduct. 2022, 78, 103128. [Google Scholar] [CrossRef]
- Wang, Z.F.; Liu, H.; Li, R.; Fang, Y.; Bi, D. Field investigation and dynamic process simulation: A case study of rock avalanche in Pusa Village, Nayong County, Guizhou Province, China. KSCE J. Civ. Eng. 2022, 26, 3764–3775. [Google Scholar] [CrossRef]
- Zhu, Y.; Xu, S.; Zhuang, Y.; Dai, X.; Lv, G.; Xing, A. Characteristics and runout behaviour of the disastrous 28 August 2017 rock avalanche in Nayong, Guizhou, China. Eng. Geol. 2019, 259, 105154. [Google Scholar] [CrossRef]
- Zhang, X.S.; Wang, Z.F.; Wang, L.Q.; Tian, Y.; Shi, F.G.; Xie, S.T. Influence of path materials on rock avalanche dynamics in the Nayong case study. Sci. Rep. 2025, 15, 25093. [Google Scholar] [CrossRef]
- Luo, H.; Xing, A.; Jin, K.; Xu, S.; Zhuang, Y. Discrete element modeling of the Nayong rock avalanche, Guizhou, China constrained by dynamic parameters from seismic signal inversion. Rock Mech. Rock Eng. 2021, 54, 1629–1645. [Google Scholar] [CrossRef]
- Yan, K.; Wang, F.; Liu, W.; Zhang, B.; Gao, J. Two long-runout rock avalanches in 2022 and 2020 in an underground coal mining field in Zhijin, China. Landslides 2023, 20, 1465–1480. [Google Scholar] [CrossRef]
- Tang, L.; Zhao, Z.; Luo, Z.; Sun, Y. What is the role of tensile cracks in cohesive slopes? J. Rock Mech. Geotech. Eng. 2019, 11, 314–324. [Google Scholar] [CrossRef]
- Bao, Y.; Li, Y.; Zhang, Y.; Yan, J.; Zhou, X.; Zhang, X. Investigation of the role of crown crack in cohesive soil slope and its effect on slope stability based on the extended finite element method. Nat. Hazards 2022, 110, 295–314. [Google Scholar] [CrossRef]
- Wang, M.; Shen, W.; Liu, J.; Shao, J. Phase-field modeling of cracking process in partially saturated porous media and application to rainfall-induced landslides. Eng. Geol. 2022, 310, 106884. [Google Scholar] [CrossRef]
- Miao, M.; Tang, H.; Fang, K.; Jiang, Y.; Li, C.; Lv, B. Influence of tensile crack development on the deformation behavior and failure mode of reservoir-induced landslides: Insights from model tests. Landslides 2025, 22, 1989–2004. [Google Scholar] [CrossRef]
- Bao, Y.; Zhai, S.; Chen, J.; Xu, P.; Sun, X.; Zhan, J.; Zhang, W.; Zhou, X. The evolution of the Samaoding paleolandslide river blocking event at the upstream reaches of the Jinsha River, Tibetan Plateau. Geomorphology 2020, 369, 106970. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, K.; Bilal, M.; He, J.; Xing, A. Dynamic characteristics and risk assessment of the Yiziyan rock topples in Jinsha County, Guizhou, China. Rock Mech. Rock Eng. 2024, 57, 7473–7494. [Google Scholar] [CrossRef]
- Lai, Q.; Zhao, J.; Shi, B.; Liu, H.; Ji, L.; Li, Q.; Huang, R. Deformation evolution of landslides induced by coal mining in mountainous areas: Case study of the Madaling landslide, Guizhou, China. Landslides 2023, 20, 2003–2016. [Google Scholar] [CrossRef]
- Fan, X.; Xu, Q.; Scaringi, G.; Zheng, G.; Huang, R.; Dai, L.; Ju, Y. The “long” runout rock avalanche in Pusa, China, on August 28, 2017: A preliminary report. Landslides 2019, 16, 139–154. [Google Scholar] [CrossRef]
- Xu, W.-J.; Xu, Q.; Liu, G.-Y.; Xu, H.-Y. A novel parameter inversion method for an improved DEM simulation of a river damming process by a large-scale landslide. Eng. Geol. 2021, 293, 106282. [Google Scholar] [CrossRef]
- Bao, Y.; Su, L.; Chen, J.; Ouyang, C.; Yang, T.; Lei, Z.; Li, Z. Dynamic process of a high-level landslide blocking river event in a deep valley area based on FDEM-SPH coupling approach. Eng. Geol. 2023, 319, 107108. [Google Scholar] [CrossRef]
- Chen, K.-T.; Wu, J.-H. Simulating the failure process of the Xinmo landslide using discontinuous deformation analysis. Eng. Geol. 2018, 239, 269–281. [Google Scholar] [CrossRef]
- Liu, Z.; Su, L.; Zhang, C.; Iqbal, J.; Hu, B.; Dong, Z. Investigation of the dynamic process of the Xinmo landslide using the discrete element method. Comput. Geotech. 2020, 123, 103561. [Google Scholar] [CrossRef]
- Bao, Y.; Chen, J.; Su, L.; Zhang, W.; Zhan, J. A novel numerical approach for rock slide blocking river based on the CEFDEM model: A case study from the Samaoding paleolandslide blocking river. Eng. Geol. 2023, 312, 106949. [Google Scholar] [CrossRef]
- Zhu, C.; Li, Z.; Bao, Y.; Ning, P.; Zhou, X.; Wang, M.; Wang, H.; Shi, W.; Chen, B. Dynamic analysis of a long run-out rockslide considering dynamic fragmentation behavior in Jichang Town: Insights from the three-dimensional coupled finite-discrete element method. Remote. Sens. 2023, 15, 5708. [Google Scholar] [CrossRef]
- Ye, T.; Jiang, Q.; Zhang, C.; Ma, Z.; Li, C. High-speed long-runout landslide scraping and entrainment effects: A case study on Shuicheng landslide. Eng. Geol. 2024, 341, 107722. [Google Scholar] [CrossRef]


| Effective modulus (Pa) | 1 × 108 |
| Stiffness ratio | 2.5 |
| Friction coefficient | 0.3 |
| Normal bonding strength (Pa) | 3.6 × 107 |
| Tangential bonding strength (Pa) | 2.6 × 107 |
| Damping ratio | 0.5 |
| Block size (m) | 0.5–9 |
| Density (kg/m3) | 2750 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Bao, Y.; Zhang, W.; Zeng, R. Numerical Assessment of a High-Level Rock Failure Potential Based on a Three-Dimensional Discrete Element Model. ISPRS Int. J. Geo-Inf. 2025, 14, 402. https://doi.org/10.3390/ijgi14100402
Zhou X, Bao Y, Zhang W, Zeng R. Numerical Assessment of a High-Level Rock Failure Potential Based on a Three-Dimensional Discrete Element Model. ISPRS International Journal of Geo-Information. 2025; 14(10):402. https://doi.org/10.3390/ijgi14100402
Chicago/Turabian StyleZhou, Xin, Yiding Bao, Weifeng Zhang, and Renzhe Zeng. 2025. "Numerical Assessment of a High-Level Rock Failure Potential Based on a Three-Dimensional Discrete Element Model" ISPRS International Journal of Geo-Information 14, no. 10: 402. https://doi.org/10.3390/ijgi14100402
APA StyleZhou, X., Bao, Y., Zhang, W., & Zeng, R. (2025). Numerical Assessment of a High-Level Rock Failure Potential Based on a Three-Dimensional Discrete Element Model. ISPRS International Journal of Geo-Information, 14(10), 402. https://doi.org/10.3390/ijgi14100402






