Enhancing Land Use Efficiency Assessment Through Built-Up Area–Built-Up Volume Trajectories: Integrating Vertical Urban Growth into SDG 11.3.1 Monitoring
Abstract
1. Introduction
- Does integrating built-up volume with built-up area improve the interpretation of efficiency outcomes under SDG 11.3.1, and if so, how?
- Which global patterns of built form and growth modality emerge when urban centres are analyzed in BUA–BUV trajectory space?
- How do these structural dynamics intersect with efficiency classifications based on LCRPGR?
- To what extent do these dynamics indicate whether observed efficiency outcomes are structurally sustainable in the long term?
2. SDG 11.3.1 Fundamentals and Related Work
2.1. SDG 11.3.1 Formulations
2.2. Applications and Limitations of LCRPGR
2.3. Volumetric Approaches to Measure Urbanization
2.4. Trajectory-Based and 3D Typological Approaches
2.5. Synthesis and Rationale for the BUA–BUV Framework
3. The BUA-BUV Trajectory Framework
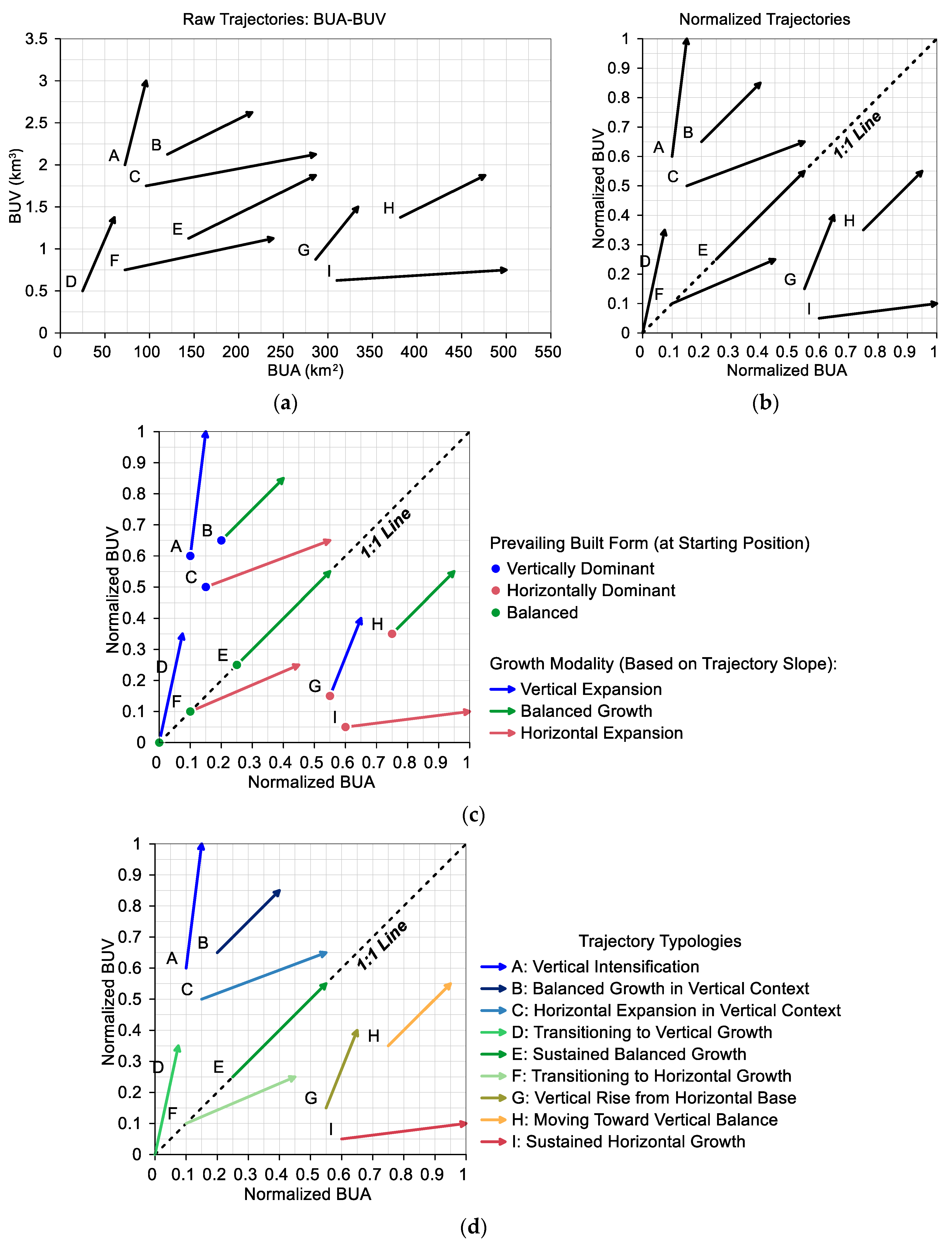
3.1. Conceptual Basis
3.2. Operationalizing the BUA–BUV Framework for Typology Classification
3.3. Comparison with Other Trajectory Typology Classifications
3.4. Interpretation in the Context of SDG Indicator 11.3.1
4. Application of the BUA-BUV Trajectory Framework for Enhanced LUE Assessment of Global Urban Centres
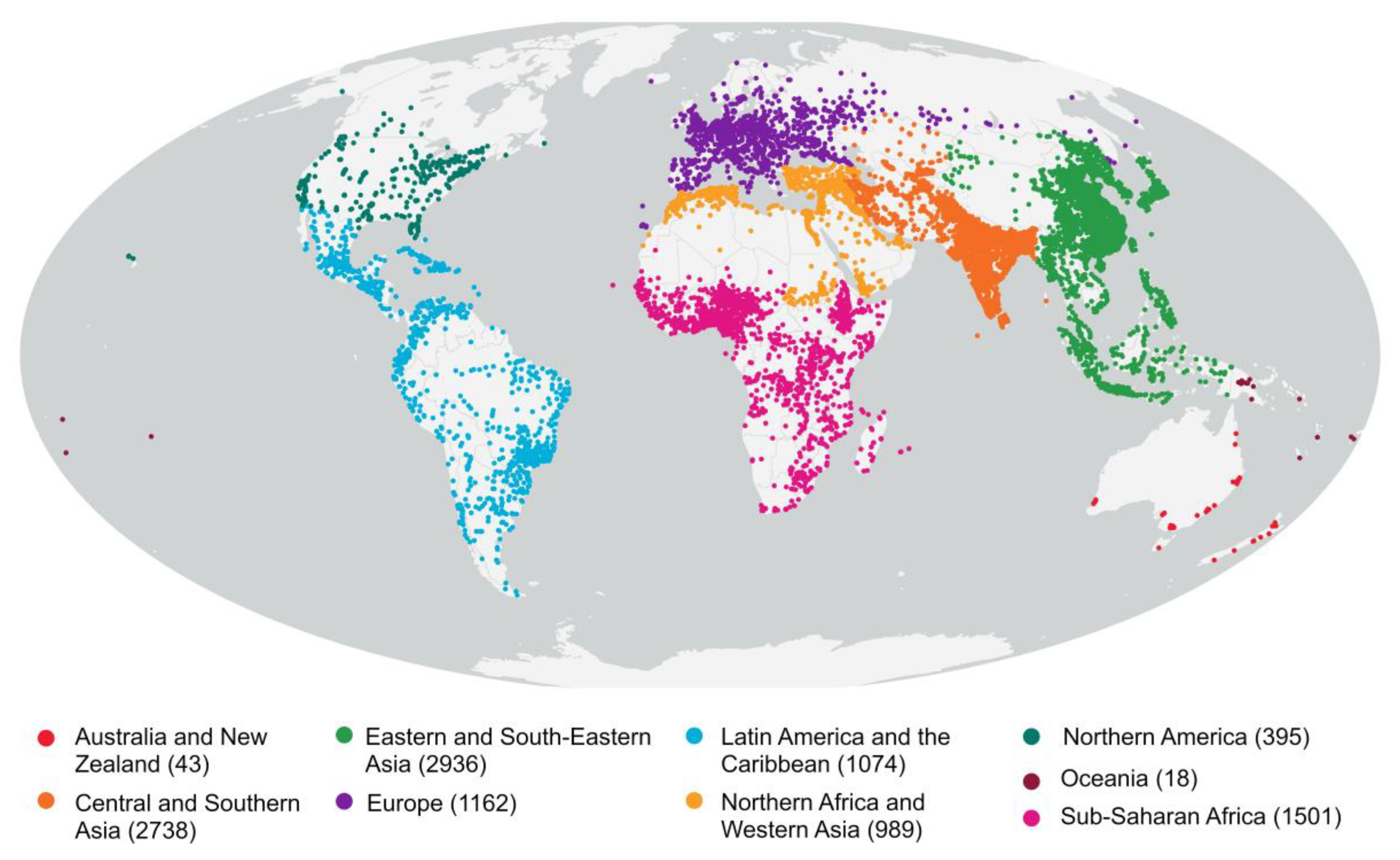
4.1. Data Description and Temporal Scope of Analysis
4.2. Data Preparation
4.3. LUE Assessment
4.4. Trajectory Typology Assignment and Efficiency Evaluation
4.5. Statistical Assessment of Distributional Differences
4.6. Sensitivity Analysis
5. Results
5.1. Temporal Trends in LCR, PGR, and LCRPGR
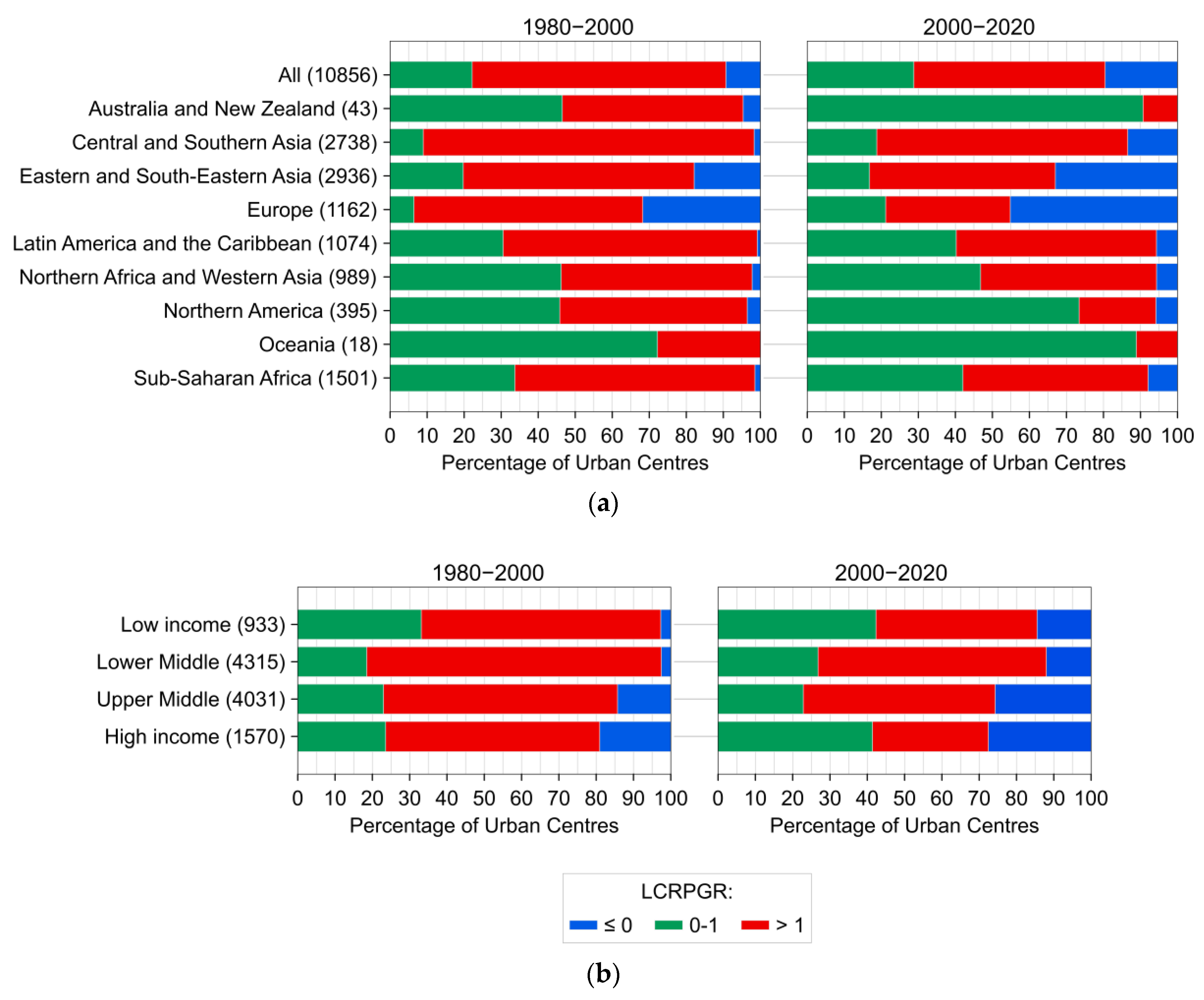
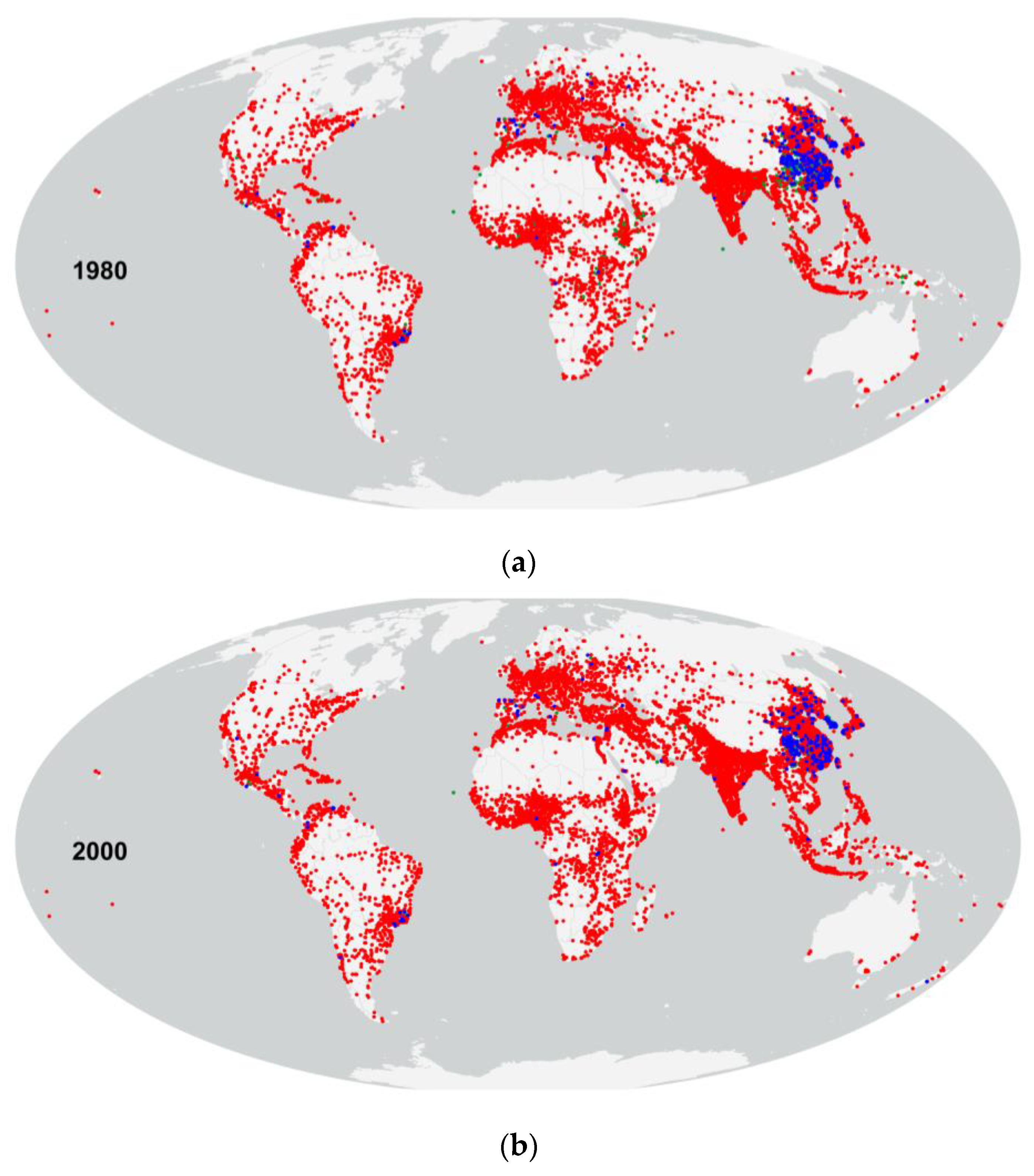
5.2. Spatiotemporal Patterns of Land Use Efficiency (LUE)
5.3. BUA-BUV Trajectories
5.4. Prevailing Built Forms of Urban Centres
5.5. Trajectory Typologies of Urban Centres
5.6. Linking Urban Growth Typologies to Efficiency Outcomes
5.7. Sensitivity of the BUA-BUV Framework
5.7.1. Effect of Thresholds on Prevailing Built Form
5.7.2. Effect of Slope Parameters on Trajectory Typology
6. Discussion
6.1. Enhanced Interpretation of Efficiency Outcomes Through Built-Up Volume Integration
6.2. Global Patterns of Built Form and Growth Modality
6.3. Intersection of Structural Dynamics and Efficiency Metrics
6.4. Structural Sustainability and Policy Implications
- Identify unsustainable pathways early, flagging urban centres where apparent efficiency masks sprawl-driven growth that may lock in high resource use [77].
- Differentiate regional strategies by promoting vertical or balanced growth in land-scarce contexts [81], while focusing on managed expansion in regions with lower demographic pressure.
6.5. Limitations and Future Work
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
Abbreviations
| 3DLUI | 3D Land Use Index |
| B3DI | Building 3D Density Index |
| BUA | Built-up Area |
| BUV | Built-up Volume |
| df | Degrees of Freedom |
| EO | Earth Observation |
| GHS | Global Human Settlement |
| GHSL | Global Human Settlement Layers |
| GHS-UCDB | Global Human Settlement Urban Centre Database |
| κ | Cohen’s kappa index |
| LCR | Land Consumption Rate |
| LCRPGR | Ratio of LCR to PGR |
| LiDAR | Light Detection and Ranging |
| LUE | Land Use Efficiency |
| p | p-value |
| PGR | Population Growth Rate |
| SDG | Sustainable Development Goal |
| UN | United Nations |
| VHG | Vertical-to-Horizontal Growth ratio |
| WB | World Bank |
References
- Stokes, E.C.; Seto, K.C. Characterizing Urban Infrastructural Transitions for the Sustainable Development Goals Using Multi-Temporal Land, Population, and Nighttime Light Data. Remote Sens. Environ. 2019, 234, 111430. [Google Scholar] [CrossRef]
- UN DESA 68% of the World Population Projected to Live in Urban Areas by 2050, Says UN. Available online: https://www.un.org/en/desa/68-world-population-projected-live-urban-areas-2050-says-un (accessed on 31 August 2025).
- Mahendra, A.; Seto, K.C. Upward and Outward Growth: Managing Urban Expansion for More Equitable Cities in the Global South; World Resources Report, Towards a More Equal City; World Resources Institute: Washington, DC, USA, 2019. [Google Scholar]
- UN Department of Economic and Social Affairs. Sustainable Development Goal 11. Available online: https://sdgs.un.org/goals/goal11 (accessed on 7 May 2025).
- UN Statistics Division SDG Indicator Metadata (Harmonized Metadata Template—Format Version 1.0). Last Updated 2021-03-01. Available online: https://unstats.un.org/sdgs/metadata/files/Metadata-11-03-01.pdf (accessed on 27 December 2024).
- Estoque, R.C.; Ooba, M.; Togawa, T.; Hijioka, Y.; Murayama, Y. Monitoring Global Land-Use Efficiency in the Context of the UN 2030 Agenda for Sustainable Development. Habitat Int. 2021, 115, 102403. [Google Scholar] [CrossRef]
- UN-Habitat. Metadata on SDGs Indicator 11.3.1 Indicator Category: Tier II; United Nations Human Settlements Program (UN-Habitat): Nairobi, Kenya, 2018. [Google Scholar]
- Ghazaryan, G.; Rienow, A.; Oldenburg, C.; Thonfeld, F.; Trampnau, B.; Sticksel, S.; Jürgens, C. Monitoring of Urban Sprawl and Densification Processes in Western Germany in the Light of Sdg Indicator 11.3.1 Based on an Automated Retrospective Classification Approach. Remote Sens. 2021, 13, 1694. [Google Scholar] [CrossRef]
- Nicolau, R.; David, J.; Caetano, M.; Pereira, J.M.C. Ratio of Land Consumption Rate to Population Growth Rate-Analysis of Different Formulations Applied to Mainland Portugal. ISPRS Int. J. Geo-Inf. 2019, 8, 10. [Google Scholar] [CrossRef]
- Huang, M.; Liu, F.; Gong, D.; Lin, H.; Chen, Y.; Hu, B.; Ge, Y.; Xiao, C. Spatiotemporal Evolution of Land Use Efficiency in 357 Cities across Mainland China from 2000 to 2020 Based on SDG 11.3.1. Sci. Total Environ. 2024, 954, 176157. [Google Scholar] [CrossRef]
- Zhou, M.; Lu, L.; Guo, H.; Weng, Q.; Cao, S.; Zhang, S.; Li, Q. Urban Sprawl and Changes in Land-Use Efficiency in the Beijing–Tianjin–Hebei Region, China from 2000 to 2020: A Spatiotemporal Analysis Using Earth Observation Data. Remote Sens. 2021, 13, 2850. [Google Scholar] [CrossRef]
- Jaber, S.M. Land Use Efficiency and Governance Disparities: Unveiling the Nexus in the Arab World. Environ. Dev. 2025, 55, 101169. [Google Scholar] [CrossRef]
- Santillan, J.R.; Heipke, C. Assessing Patterns and Trends in Urbanization and Land Use Efficiency Across the Philippines: A Comprehensive Analysis Using Global Earth Observation Data and SDG 11.3.1 Indicators. PFG J. Photogramm. Remote Sens. Geoinf. Sci. 2024, 92, 569–592. [Google Scholar] [CrossRef]
- Li, C.; Cai, G.; Du, M. Big Data Supported the Identification of Urban Land Efficiency in Eurasia by Indicator SDG 11.3.1. ISPRS Int. J. Geo-Inf. 2021, 10, 64. [Google Scholar] [CrossRef]
- Schiavina, M.; Melchiorri, M.; Freire, S.; Florio, P.; Ehrlich, D.; Tommasi, P.; Pesaresi, M.; Kemper, T. Land Use Efficiency of Functional Urban Areas: Global Pattern and Evolution of Development Trajectories. Habitat Int. 2022, 123, 102543. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wu, X.; Li, X.; Xu, X.; Liao, W.; Jiao, L.; Zeng, Z.; Chen, G.; Li, X. Global Mapping of Three-Dimensional Urban Structures Reveals Escalating Utilization in the Vertical Dimension and Pronounced Building Space Inequality. Engineering 2024, 47, 86–99. [Google Scholar] [CrossRef]
- Soltani, A.; Azizi, P.; Rahimioun, A.; Sedaghatfard, M. Volumetric Urban Sprawl: Horizontal and Vertical Growth in Two Metropolitans. J. Urban Manag. 2025. [Google Scholar] [CrossRef]
- Bibri, S.E.; Krogstie, J.; Kärrholm, M. Compact City Planning and Development: Emerging Practices and Strategies for Achieving the Goals of Sustainability. Dev. Built Environ. 2020, 4, 100021. [Google Scholar] [CrossRef]
- Esch, T.; Brzoska, E.; Dech, S.; Leutner, B.; Palacios-Lopez, D.; Metz-Marconcini, A.; Marconcini, M.; Roth, A.; Zeidler, J. World Settlement Footprint 3D—A First Three-Dimensional Survey of the Global Building Stock. Remote Sens. Environ. 2022, 270, 112877. [Google Scholar] [CrossRef]
- Li, M.; Wang, Y.; Rosier, J.F.; Verburg, P.H.; van Vliet, J. Global Maps of 3D Built-up Patterns for Urban Morphological Analysis. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103048. [Google Scholar] [CrossRef]
- Pesaresi, M.; Politis, P. GHS-BUILT-V R2023A—GHS Built-up Volume Grids Derived from Joint Assessment of Sentinel2, Landsat, and Global DEM Data, Multitemporal (1975–2030) 2023. Available online: https://data.jrc.ec.europa.eu/dataset/ab2f107a-03cd-47a3-85e5-139d8ec63283 (accessed on 21 May 2025).
- Pesaresi, M.; Politis, P. GHS-BUILT-H R2023A—GHS Building Height, Derived from AW3D30, SRTM30, and Sentinel2 Composite (2018) 2023. Available online: https://data.jrc.ec.europa.eu/dataset/85005901-3a49-48dd-9d19-6261354f56fe (accessed on 21 May 2025).
- Kamath, H.G.; Singh, M.; Malviya, N.; Martilli, A.; He, L.; Aliaga, D.; He, C.; Chen, F.; Magruder, L.A.; Yang, Z.-L.; et al. GLObal Building Heights for Urban Studies (UT-GLOBUS) for City- and Street- Scale Urban Simulations: Development and First Applications. Sci. Data 2024, 11, 886. [Google Scholar] [CrossRef] [PubMed]
- Che, Y.; Li, X.; Liu, X.; Wang, Y.; Liao, W.; Zheng, X.; Zhang, X.; Xu, X.; Shi, Q.; Zhu, J.; et al. 3D-GloBFP: The First Global Three-Dimensional Building Footprint Dataset. Earth Syst. Sci. Data 2024, 16, 5357–5374. [Google Scholar] [CrossRef]
- Frolking, S.; Mahtta, R.; Milliman, T.; Esch, T.; Seto, K.C. Global Urban Structural Growth Shows a Profound Shift from Spreading out to Building Up. Nat. Cities 2024, 1, 555–566. [Google Scholar] [CrossRef]
- Mahtta, R.; Mahendra, A.; Seto, K.C. Building up or Spreading out? Typologies of Urban Growth across 478 Cities of 1 Million+. Environ. Res. Lett. 2019, 14, 124077. [Google Scholar] [CrossRef]
- Zambon, I.; Colantoni, A.; Salvati, L. Horizontal vs. Vertical Growth: Understanding Latent Patterns of Urban Expansion in Large Metropolitan Regions. Sci. Total Environ. 2019, 654, 778–785. [Google Scholar] [CrossRef]
- Zhao, C.; Weng, Q.; Hersperger, A.M. Characterizing the 3-D Urban Morphology Transformation to Understand Urban-Form Dynamics: A Case Study of Austin, Texas, USA. Landsc. Urban Plan. 2020, 203, 103881. [Google Scholar] [CrossRef]
- Zięba-Kulawik, K.; Skoczylas, K.; Mustafa, A.; Wężyk, P.; Gerber, P.; Teller, J.; Omrani, H. Spatiotemporal Changes in 3D Building Density with LiDAR and GEOBIA: A City-Level Analysis. Remote Sens. 2020, 12, 3668. [Google Scholar] [CrossRef]
- European Commission; Joint Research Centre; Melchiorri, M.; Mari Rivero, I.; Florio, P.; Schiavina, M.; Krasnodebska, K.; Politis, P.; Uhl, J.; Pesaresi, M.; et al. Stats in the City the GHSL Urban Centre Database 2025; Publications Office of the European Union: Luxembourg, 2024. [Google Scholar]
- Faye, B.; Du, G.; Zhang, R. Efficiency Analysis of Land Use and the Degree of Coupling Link between Population Growth and Global Built-Up Area in the Subregion of West Africa. Land 2022, 11, 847. [Google Scholar] [CrossRef]
- Melchiorri, M.; Pesaresi, M.; Florczyk, A.J.; Corbane, C.; Kemper, T. Principles and Applications of the Global Human Settlement Layer as Baseline for the Land Use Efficiency Indicator—SDG 11.3.1. ISPRS Int. J. Geo-Inf. 2019, 8, 96. [Google Scholar] [CrossRef]
- Schiavina, M.; Melchiorri, M.; Corbane, C.; Florczyk, A.J.; Freire, S.; Pesaresi, M.; Kemper, T. Multi-Scale Estimation of Land Use Efficiency (SDG 11.3.1) across 25 Years Using Global Open and Free Data. Sustainability 2019, 11, 5674. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, C.; Feng, Y.; Zhao, M.; Gu, J. Using Earth Observation for Monitoring SDG 11.3.1-Ratio of Land Consumption Rate to Population Growth Rate in Mainland China. Remote Sens. 2020, 12, 357. [Google Scholar] [CrossRef]
- Jiang, H.; Sun, Z.; Guo, H.; Weng, Q.; Du, W.; Xing, Q.; Cai, G. An Assessment of Urbanization Sustainability in China between 1990 and 2015 Using Land Use Efficiency Indicators. npj Urban Sustain. 2021, 1, 34. [Google Scholar] [CrossRef]
- Koroso, N.H.; Lengoiboni, M.; Zevenbergen, J.A. Urbanization and Urban Land Use Efficiency: Evidence from Regional and Addis Ababa Satellite Cities, Ethiopia. Habitat Int. 2021, 117, 102437. [Google Scholar] [CrossRef]
- Li, C.; Cai, G.; Sun, Z. Urban Land-Use Efficiency Analysis by Integrating LCRPGR and Additional Indicators. Sustainability 2021, 13, 13518. [Google Scholar] [CrossRef]
- Calka, B.; Orych, A.; Bielecka, E.; Mozuriunaite, S. The Ratio of the Land Consumption Rate to the Population Growth Rate: A Framework for the Achievement of the Spatiotemporal Pattern in Poland and Lithuania. Remote Sens. 2022, 14, 1074. [Google Scholar] [CrossRef]
- Bhandari, R.; Xue, W.; Virdis, S.G.P.; Winijkul, E.; Nguyen, T.P.L.; Joshi, S. Monitoring and Assessing Urbanization Progress in Thailand between 2000 and 2020 Using SDG Indicator 11.3.1. Sustainability 2023, 15, 9794. [Google Scholar] [CrossRef]
- Wang, Y.; Li, B.; Xu, L. Monitoring Land-Use Efficiency in China’s Yangtze River Economic Belt from 2000 to 2018. Land 2022, 11, 1009. [Google Scholar] [CrossRef]
- Cardenas-Ritzert, O.S.E.; Vogeler, J.C.; Shah Heydari, S.; Fekety, P.A.; Laituri, M.; McHale, M. Automated Geospatial Approach for Assessing SDG Indicator 11.3.1: A Multi-Level Evaluation of Urban Land Use Expansion across Africa. ISPRS Int. J. Geo-Inf. 2024, 13, 226. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Sun, L.; Ning, X.; Li, G. Assessment of Chinese Urban Land-Use Efficiency (SDG11.3.1) Utilizing High-Precision Urban Built-up Area Data. Geogr. Sustain. 2025, 6, 100210. [Google Scholar] [CrossRef]
- Laituri, M.; Davis, D.; Sternlieb, F.; Galvin, K. Sdg Indicator 11.3.1 and Secondary Cities: An Analysis and Assessment. ISPRS Int. J. Geo-Inf. 2021, 10, 713. [Google Scholar] [CrossRef]
- Jiang, H.; Guo, H.; Sun, Z.; Xing, Q.; Zhang, H.; Ma, Y.; Li, S. Projections of Urban Built-up Area Expansion and Urbanization Sustainability in China’s Cities through 2030. J. Clean. Prod. 2022, 367, 133086. [Google Scholar] [CrossRef]
- Angel, S.; Mackres, E.; Guzder-Williams, B. Measuring Change in Urban Land Consumption: A Global Analysis. Land 2024, 13, 1491. [Google Scholar] [CrossRef]
- Santillan, J.R.; Dorozynski, M.; Heipke, C. Uncertainty Quantification and Monte Carlo Simulations to Enhance SDG 11.3.1 Monitoring. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2025, X-G-2025, 753–762. [Google Scholar] [CrossRef]
- Cardenas-Ritzert, O.S.E.; Vogeler, J.C.; Shah Heydari, S.; Fekety, P.A.; Laituri, M.; McHale, M.R. Effects of Land Use Data Spatial Resolution on SDG Indicator 11.3.1 (Urban Expansion) Assessments: A Case Study Across Ethiopia. Sustainability 2024, 16, 9698. [Google Scholar] [CrossRef]
- Aquilino, M.; Adamo, M.; Blonda, P.; Barbanente, A.; Tarantino, C. Improvement of a Dasymetric Method for Implementing Sustainable Development Goal 11 Indicators at an Intra-Urban Scale. Remote Sens. 2021, 13, 2835. [Google Scholar] [CrossRef]
- Wang, H.; Wei, Y.; Liu, Y.; Cao, Y.; Liu, R.; Ning, X. Evaluation of Chinese Urban Land-Use Efficiency (Sdg11.3.1) Based on High-Precision Urban Built-up Area Data. In Proceedings of the IGARSS 2024—2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 858–862. [Google Scholar]
- Koomen, E.; Rietveld, P.; Bacao, F. The Third Dimension in Urban Geography: The Urban-Volume Approach. Environ. Plan. B Plan. Des. 2009, 36, 1008–1025. [Google Scholar] [CrossRef]
- Ruan, L.; He, T.; Xiao, W.; Chen, W.; Lu, D.; Liu, S. Measuring the Coupling of Built-up Land Intensity and Use Efficiency: An Example of the Yangtze River Delta Urban Agglomeration. Sustain. Cities Soc. 2022, 87, 104224. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H. 3-D Land Use Index: Vertical Land Use Analysis Based on Multi-Dimensional Geospatial Data Cube. In Proceedings of the 2024 IEEE International Conference on Big Data (BigData 2024), Washington, DC, USA, 15–18 December 2024; pp. 8719–8721. [Google Scholar]
- Forman, R.T.T. Land Mosaics: The Ecology of Landscapes and Regions; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Camagni, R.; Gibelli, M.C.; Rigamonti, P. Urban Mobility and Urban Form: The Social and Environmental Costs of Different Patterns of Urban Expansion. Ecol. Econ. 2002, 40, 199–216. [Google Scholar] [CrossRef]
- Jabareen, Y.R. Sustainable Urban Forms. J. Plan. Educ. Res. 2006, 26, 38–52. [Google Scholar] [CrossRef]
- Schneider, A.; Woodcock, C.E. Compact, Dispersed, Fragmented, Extensive? A Comparison of Urban Growth in Twenty-Five Global Cities Using Remotely Sensed Data, Pattern Metrics and Census Information. Urban Stud. 2008, 45, 659–692. [Google Scholar] [CrossRef]
- Shi, Y.; Sun, X.; Zhu, X.; Li, Y.; Mei, L. Characterizing Growth Types and Analyzing Growth Density Distribution in Response to Urban Growth Patterns in Peri-Urban Areas of Lianyungang City. Landsc. Urban Plan. 2012, 105, 425–433. [Google Scholar] [CrossRef]
- Sun, Y.; Jiao, L.; Guo, Y.; Xu, Z. Recognizing Urban Shrinkage and Growth Patterns from a Global Perspective. Appl. Geogr. 2024, 166, 103247. [Google Scholar] [CrossRef]
- Santillan, J.R.; Heipke, C. Using GHSL to Analyze Urbanization and Land-Use Efficiency in the Philippines from 1975-2020: Trends and Implications for Sustainable Development. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 10, 413–422. [Google Scholar] [CrossRef]
- European Commission. GHSL Data Package 2023; Publications Office of the European Union: Luxembourg, 2023. [Google Scholar]
- European Commission. Statistical Office of the European Union Applying the Degree of Urbanisation—A Methodological Manual to Define Cities, Towns and Rural Areas for International Comparisons, 2021 ed.; Publications Office of the European Union: Luxembourg, 2021. [Google Scholar]
- Schiavina, M.; Melchiorri, M.; Pesaresi, M. GHS-SMOD R2023A—GHS Settlement Layers, Application of the Degree of Urbanisation Methodology (Stage I) to GHS-POP R2023A and GHS-BUILT-S R2023A, Multitemporal (1975–2030) 2023. Available online: https://data.jrc.ec.europa.eu/dataset/a0df7a6f-49de-46ea-9bde-563437a6e2ba (accessed on 21 May 2025).
- Pesaresi, M.; Politis, P. GHS-BUILT-S R2023A—GHS Built-up Surface Grid, Derived from Sentinel2 Composite and Landsat, Multitemporal (1975–2030) 2023. Available online: https://data.jrc.ec.europa.eu/dataset/9f06f36f-4b11-47ec-abb0-4f8b7b1d72ea (accessed on 21 May 2025).
- Schiavina, M.; Freire, S.; MacManus, K. GHS-POP R2023A—GHS Population Grid Multitemporal (1975–2030) 2023. Available online: https://data.jrc.ec.europa.eu/dataset/2ff68a52-5b5b-4a22-8f40-c41da8332cfe (accessed on 21 May 2025).
- Pesaresi, M.; Schiavina, M.; Politis, P.; Freire, S.; Krasnodębska, K.; Uhl, J.H.; Carioli, A.; Corbane, C.; Dijkstra, L.; Florio, P.; et al. Advances on the Global Human Settlement Layer by Joint Assessment of Earth Observation and Population Survey Data. Int. J. Digit. Earth 2024, 17, 2390454. [Google Scholar] [CrossRef]
- Barbato, G.; Barini, E.M.; Genta, G.; Levi, R. Features and Performance of Some Outlier Detection Methods. J. Appl. Stat. 2011, 38, 2133–2149. [Google Scholar] [CrossRef]
- McHugh, M.L. The Chi-Square Test of Independence. Biochem. Med. 2013, 23, 143–149. [Google Scholar] [CrossRef]
- Congalton, R.G. A Review of Assessing the Accuracy of Classifications of Remotely Sensed Data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The Measurement of Observer Agreement for Categorical Data. Biometrics 1977, 33, 159. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, X.; Chen, W.; Meng, L.; Wu, Q.; Gong, P.; Seto, K.C. Satellite Mapping of Urban Built-up Heights Reveals Extreme Infrastructure Gaps and Inequalities in the Global South. Proc. Natl. Acad. Sci. USA 2022, 119, e2214813119. [Google Scholar] [CrossRef]
- Taubenböck, H.; Mast, J.; Lemoine Rodríguez, R.; Debray, H.; Wurm, M.; Geiß, C. Was Global Urbanization from 1985 to 2015 Efficient in Terms of Land Consumption? Habitat Int. 2025, 160, 103397. [Google Scholar] [CrossRef]
- Lin, Z. Vertical Urbanism: Re-Conceptualizing the Compact City. In Vertical Urbanism; Routledge: London, UK, 2018; ISBN 978-1-351-20682-2. [Google Scholar]
- Pelczynski, J.; Tomkowicz, B. Densification of Cities as a Method of Sustainable Development. IOP Conf. Ser. Earth Environ. Sci. 2019, 362, 012106. [Google Scholar] [CrossRef]
- Munn, K.; Dragićević, S. Spatial Multi-Criteria Evaluation in 3D Context: Suitability Analysis of Urban Vertical Development. Cartogr. Geogr. Inf. Sci. 2021, 48, 105–123. [Google Scholar] [CrossRef]
- OECD. Rethinking Urban Sprawl: Moving Towards Sustainable Cities; OECD: Paris, France, 2018; ISBN 978-92-64-18982-9. [Google Scholar]
- Hasse, J.E.; Lathrop, R.G. Land Resource Impact Indicators of Urban Sprawl. Appl. Geogr. 2003, 23, 159–175. [Google Scholar] [CrossRef]
- Kim, J.H.; Li, X. Building More Housing near Transit: A Spatial Analysis of Residential Densification Dynamics. Transp. Policy 2021, 114, 15–24. [Google Scholar] [CrossRef]
- Yang, W.; Xu, Q.; Yi, S.; Shankar, R.; Chen, T. Enhancing Transit-Oriented Development Sustainability through the Integrated Node-Place-Ecology (NPE) Model. Transp. Res. D Transp. Environ. 2024, 136, 104456. [Google Scholar] [CrossRef]
- Mualam, N.; Salinger, E.; Max, D. Increasing the Urban Mix through Vertical Allocations: Public Floorspace in Mixed Use Development. Cities 2019, 87, 131–141. [Google Scholar] [CrossRef]
- Grace Wong, K.M. Vertical Cities as a Solution for Land Scarcity: The Tallest Public Housing Development in Singapore. Urban. Des. Int. 2004, 9, 17–30. [Google Scholar] [CrossRef]
- Li, Y.; Beeton, R.J.S.; Zhao, X.; Fan, Y.; Yang, Q.; Li, J.; Ding, L. Advancing Urban Sustainability Transitions: A Framework for Understanding Urban Complexity and Enhancing Integrative Transformations. Humanit. Soc. Sci. Commun. 2024, 11, 1064. [Google Scholar] [CrossRef]
- Swilling, M.; Hajer, M. Governance of Urban Transitions: Towards Sustainable Resource Efficient Urban Infrastructures. Environ. Res. Lett. 2017, 12, 125007. [Google Scholar] [CrossRef]
- Giyasov, B.; Giyasova, I. The Impact of High-Rise Buildings on the Living Environment. E3S Web Conf. 2018, 33, 01045. [Google Scholar] [CrossRef]


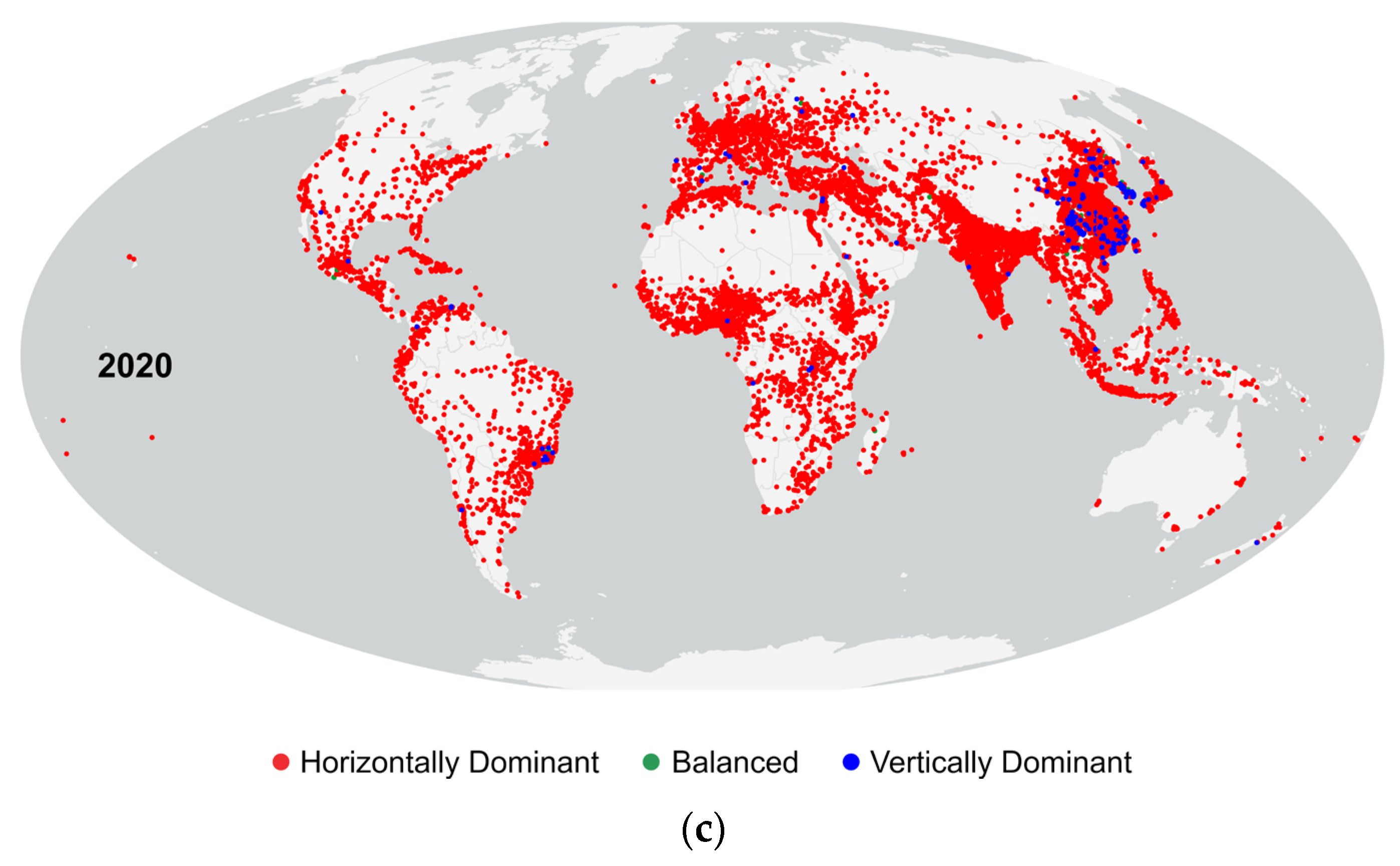
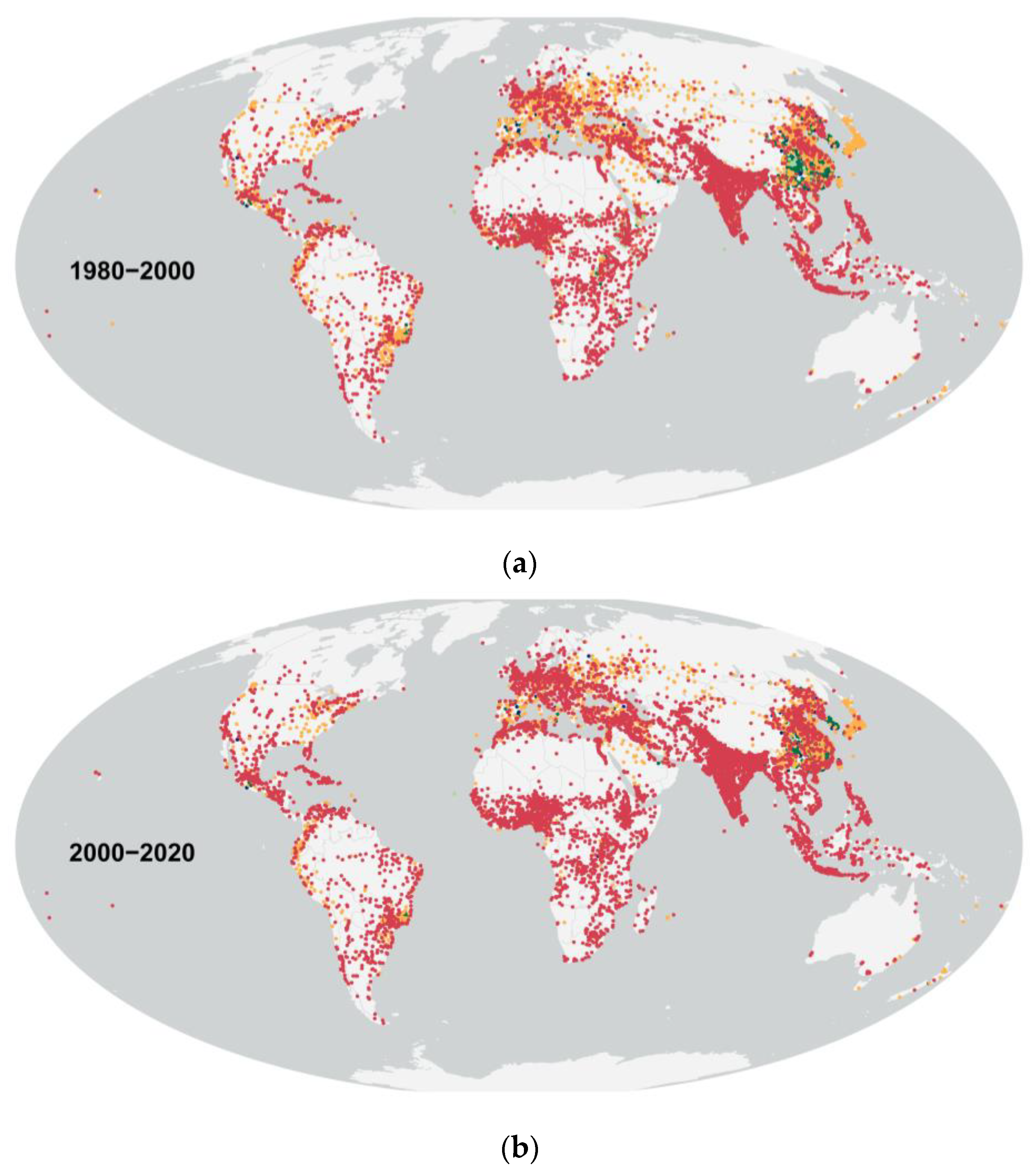



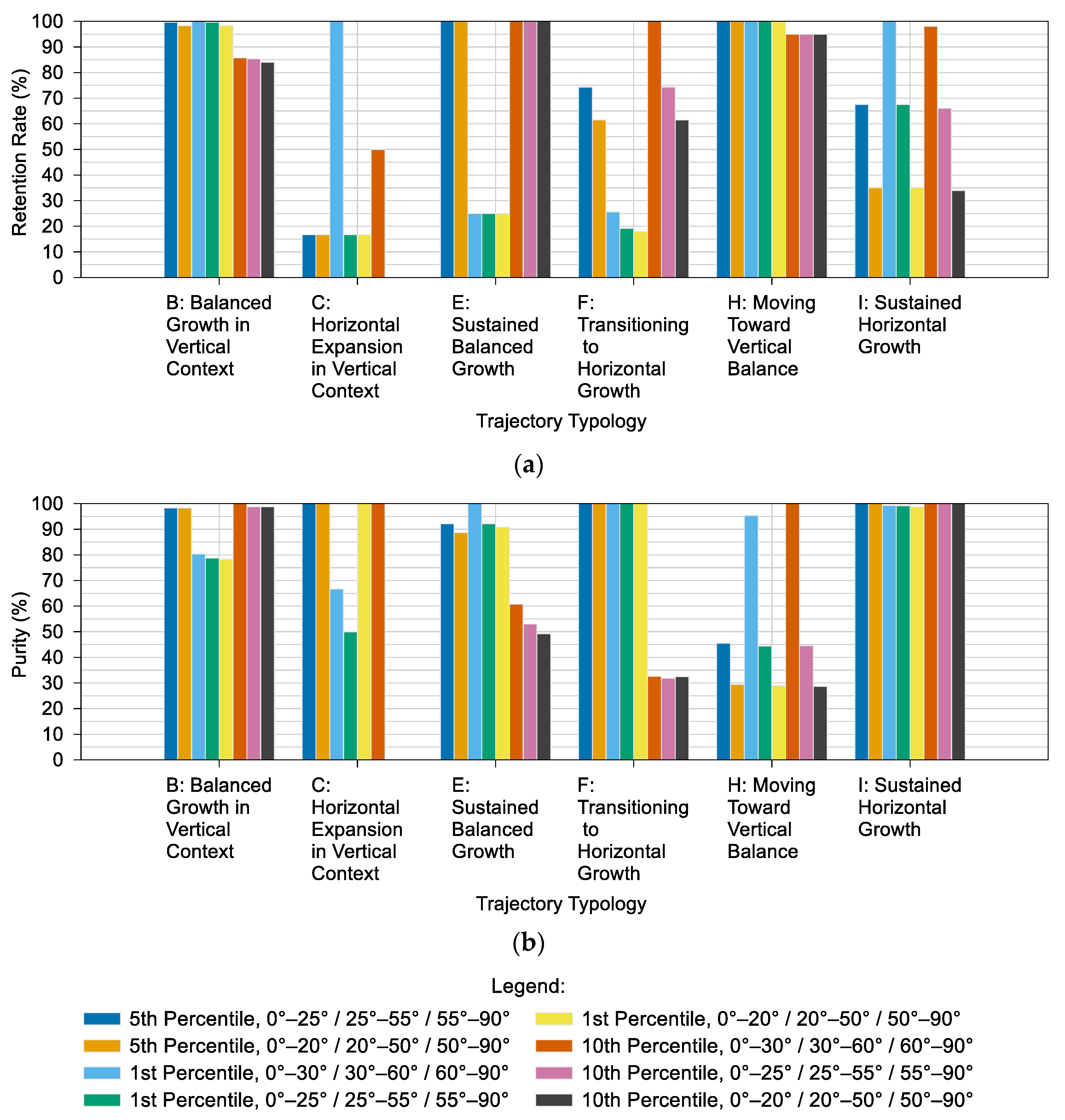
| Case | LCR | PGR | LCRPGR | Interpretation |
|---|---|---|---|---|
| 1A | >0 | >0 | >1 | Land consumption exceeds population growth; indicates inefficient land use (e.g., sprawl, low-density expansion). |
| 1B | >0 | >0 | =1 | Proportional land consumption and population growth; represents the ideal condition for land use efficiency, where the land consumption rate matches the population growth rate, indicating that urban expansion is aligned with demographic demand. |
| 1C | >0 | >0 | <1 | Population grows faster than land expansion; denotes efficient land use, typically via densification or compact growth. |
| 2 | >0 | < 0 | <0 | Urban expansion amid population decline; reflects highly inefficient land use and unsustainable spatial growth. |
| 3 | <0 | >0 | <0 | Built-up area contracts as population increases; may indicate efficient densification, but can also lead to overcrowding if unmanaged. |
| 4A | <0 | <0 | <1 | Both LCR and PGR decline; if LCR declines faster, indicates efficient urban contraction. |
| 4B | <0 | <0 | >1 | Both LCR and PGR decline; if PGR declines faster, it indicates inefficient shrinkage with possible underutilization of urban space. |
| 5 (Special case) | Any | =0 | Undefined | PGR is zero; LCRPGR is undefined. Interpretation depends on LCR: if LCR > 0, it indicates inefficiency; if LCR < 0, it may suggest efficient contraction. |
| 6 (Special case) | =0 | ≠0 | 0 | No change in land consumption. If PGR > 0, it indicates maximum efficiency; if PGR < 0, it reflects ambiguous conditions needing contextual analysis. |
| Vertical Expansion (Steeper, 60–90°) | Balanced Growth (Moderate, 30–60°) | Horizontal Expansion (Shallow, 0–30°) | |
|---|---|---|---|
| Vertically Dominant (Above the 1:1 line) | A: Vertical Intensification (Growth is driven primarily by built-up volume; vertically dominant cities become more compact.) | B: Balanced Growth in Vertical Context (BUA and BUV increase at relatively balanced rates while retaining vertical dominance.) | C: Horizontal Expansion in Vertical Context (BUA increases more rapidly than BUV, but vertical dominance remains.) |
| Balanced (On or near the 1:1 line) | D: Transitioning to Vertical Growth (Urban form shifts from balance toward increasing vertical development.) | E: Sustained Balanced Growth (BUA and BUV grow proportionally; urban structure remains balanced.) | F: Transitioning to Horizontal Growth (Urban form shifts from balance toward increasing horizontal expansion.) |
| Horizontally Dominant (Below the 1:1 line) | G: Vertical Rise from Horizontal Base (Cities previously dominated by BUA show increased BUV; a shift toward vertical development.) | H: Moving Toward Vertical Balance (Both BUA and BUV grow, with vertical development catching up; movement toward balance.) | I: Sustained Horizontal Growth (Horizontal expansion continues to dominate; vertical growth remains limited.) |
| LCR (%) | PGR (%) | LCRPGR | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1980–2000 | 2000–2020 | 1980–2020 | 1980–2000 | 2000–2020 | 1980–2020 | 1980–2000 | 2000–2020 | 1980–2020 | |
| All | 3.47 | 1.72 | 3.44 | 1.97 | 0.95 | 1.52 | 1.67 | 1.05 | 1.94 |
| UN SDG Region | |||||||||
| Australia and New Zealand | 1.19 | 0.63 | 1.06 | 1.64 | 1.48 | 1.60 | 0.96 | 0.54 | 0.77 |
| Central and Southern Asia | 6.02 | 2.15 | 5.55 | 2.21 | 0.96 | 1.60 | 2.75 | 1.63 | 3.45 |
| Eastern and South-Eastern Asia | 4.19 | 2.08 | 4.31 | 1.13 | 0.42 | 0.81 | 1.64 | 1.02 | 2.03 |
| Europe | 1.22 | 0.63 | 1.00 | 0.26 | 0.10 | 0.21 | 1.66 | 0.52 | 1.48 |
| Latin America and the Caribbean | 3.01 | 1.35 | 2.70 | 2.17 | 1.23 | 1.74 | 1.41 | 1.08 | 1.65 |
| Northern Africa and Western Asia | 2.74 | 1.79 | 2.88 | 2.79 | 1.83 | 2.31 | 1.03 | 0.97 | 1.25 |
| Northern America | 1.55 | 0.65 | 1.22 | 1.52 | 1.15 | 1.42 | 1.01 | 0.58 | 0.94 |
| Oceania | 1.89 | 0.60 | 1.29 | 2.64 | 2.16 | 2.51 | 0.66 | 0.45 | 0.61 |
| Sub-Saharan Africa | 3.37 | 2.49 | 3.90 | 2.74 | 2.25 | 2.38 | 1.38 | 1.01 | 1.69 |
| World Bank Income Group | |||||||||
| Low income | 3.52 | 2.25 | 3.84 | 3.01 | 1.87 | 2.38 | 1.43 | 0.82 | 1.74 |
| Lower Middle | 4.67 | 2.09 | 4.54 | 2.37 | 1.28 | 1.87 | 2.12 | 1.32 | 2.48 |
| Upper Middle | 3.50 | 1.77 | 3.43 | 1.48 | 0.69 | 1.18 | 1.44 | 1.06 | 1.73 |
| High income | 1.30 | 0.66 | 1.10 | 0.61 | 0.53 | 0.54 | 1.24 | 0.60 | 1.29 |
| Metric | Year | 1st Percentile | 10th Percentile |
|---|---|---|---|
| Overall Agreement | 2000 | 98% | 97% |
| 2020 | 99% | 99% | |
| Cohen’s kappa (Three-class case: Horizontal, Balanced, Vertical) | 2000 | 0.77 | 0.78 |
| 2020 | 0.81 | 0.85 | |
| Cohen’s kappa (Two-class case: Balanced vs. All Other Built Forms) | 2000 | 0.40 | 0.65 |
| 2020 | 0.40 | 0.72 |
| 5th Percentile | 1st Percentile | 10th Percentile | |
|---|---|---|---|
| 0–30°/30–60°/60–90° | (Baseline) | 98% | 97% |
| 0–25°/25–55°/55–90° | 76% | 74% | 73% |
| 0–20°/20–50°/50–90° | 51% | 50% | 49% |
| 5th Percentile | 1st Percentile | 10th Percentile | |
|---|---|---|---|
| 0–30°/30–60°/60–90° | (Baseline) | 0.94 | 0.93 |
| 0–25°/25–55°/55–90° | 0.55 | 0.51 | 0.51 |
| 0–20°/20–50°/50–90° | 0.27 | 0.24 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santillan, J.; Dorozynski, M.; Heipke, C. Enhancing Land Use Efficiency Assessment Through Built-Up Area–Built-Up Volume Trajectories: Integrating Vertical Urban Growth into SDG 11.3.1 Monitoring. ISPRS Int. J. Geo-Inf. 2025, 14, 404. https://doi.org/10.3390/ijgi14100404
Santillan J, Dorozynski M, Heipke C. Enhancing Land Use Efficiency Assessment Through Built-Up Area–Built-Up Volume Trajectories: Integrating Vertical Urban Growth into SDG 11.3.1 Monitoring. ISPRS International Journal of Geo-Information. 2025; 14(10):404. https://doi.org/10.3390/ijgi14100404
Chicago/Turabian StyleSantillan, Jojene, Mareike Dorozynski, and Christian Heipke. 2025. "Enhancing Land Use Efficiency Assessment Through Built-Up Area–Built-Up Volume Trajectories: Integrating Vertical Urban Growth into SDG 11.3.1 Monitoring" ISPRS International Journal of Geo-Information 14, no. 10: 404. https://doi.org/10.3390/ijgi14100404
APA StyleSantillan, J., Dorozynski, M., & Heipke, C. (2025). Enhancing Land Use Efficiency Assessment Through Built-Up Area–Built-Up Volume Trajectories: Integrating Vertical Urban Growth into SDG 11.3.1 Monitoring. ISPRS International Journal of Geo-Information, 14(10), 404. https://doi.org/10.3390/ijgi14100404







