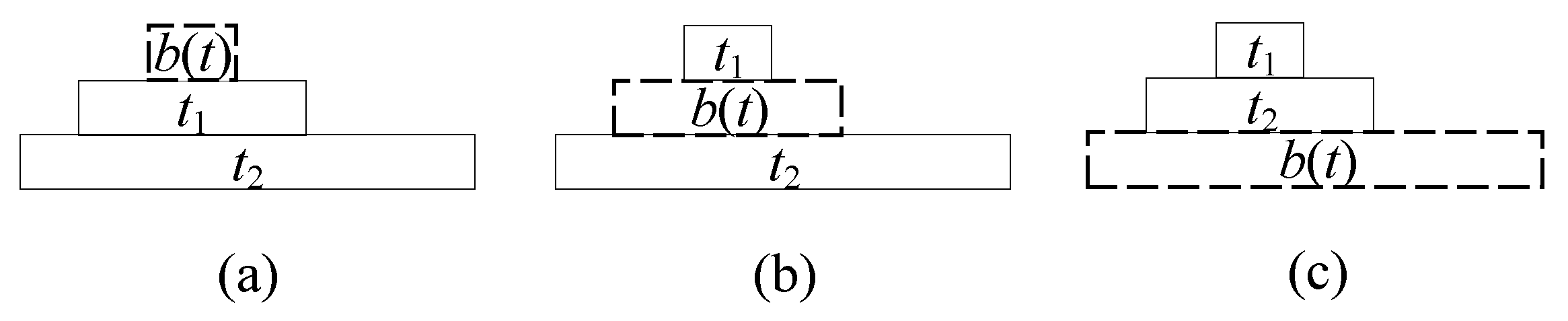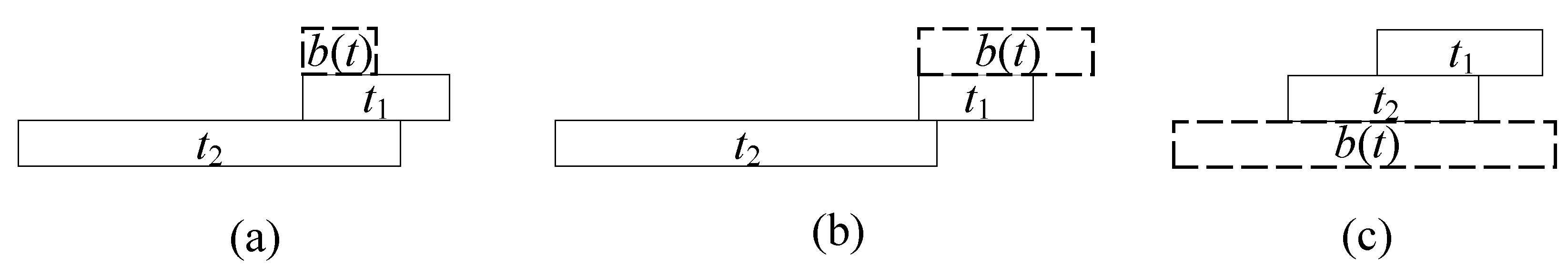A Novel Approach for Mining Spatiotemporal Explicit and Implicit Information in Multiscale Spatiotemporal Data

Abstract

In the era of big data, a significant volume of spatiotemporal data exists in a multiscale format, describing diverse phenomena in the objective world across different spatial and temporal scales. While existing methods focus on analyzing the features and connections of spatiotemporal data at various scales, they often overlook the consideration of uncertainty in spatiotemporal information within the context of multiscale meaning. To effectively harness the potential of spatiotemporal data, it becomes crucial to capture the fuzzy spatiotemporal information inherent in multiscale datasets. This paper proposes a novel multiscale spatiotemporal correlation method that accounts for and quantifies the uncertainty of spatiotemporal information. Spatiotemporal information is categorized into two types, explicit information and implicit information, based on respective levels of uncertainty. The method employs spatiotemporal cubes to interpret the spatiotemporal items within the data, followed by the introduction of a benchmark scale to determine the certainty of each spatiotemporal item based on its range and topological relationships. Subsequently, spatiotemporal confidence and correlation index are proposed to gauge the significance of geographical elements and their interrelationships. To validate the proposed method, a multiscale spatiotemporal transaction dataset is generated and utilized in the experiment. The experimental results demonstrate that the proposed method effectively captures spatiotemporal implicit information and enables better utilization of multiscale spatiotemporal data. Notably, the importance of each object of study varies when analyzed using different benchmark scales, providing valuable insights for professionals to identify novel objects and associations worthy of consideration. The obtained results can be used to construct spatiotemporal knowledge graphs.

1. Introduction

In recent years, human society has entered the era of big data, characterized by the exponential growth in the type and volume of collected data, which has revolutionized the provision of products and services. Big data is widely recognized for its 5 V characteristics, encompassing vast amounts of valuable information crucial for decision-making and management processes. Nevertheless, the inherent nature of big data poses challenges for traditional data mining algorithms [1], including extensive computational requirements, memory limitations, and handling diverse data types. Consequently, mining and analyzing massive datasets have emerged as a central hurdle in the realm of big data. To effectively manage and leverage this wealth of data, a new approach has emerged by incorporating spatiotemporal attributes [2]. These attributes naturally bind data to specific locations and timeframes, enabling filtering and correlation based on a few dimensions. As a result, spatiotemporal big data mining has gained significant traction as a critical aspect of processing and analyzing big data, becoming a prominent and timely topic within the data mining field.

Spatiotemporal data plays a significant role in various fields of study. Its ability to describe both macro and micro activities makes it a natural multiscale feature. In the era of big data, spatiotemporal data sourced from numerous channels inherently exhibits a multiscale character. Current spatiotemporal data mining methods can be classified as single-scale mining or multi-scale mining, depending on the perspective considered. Several data mining algorithms have been proposed to effectively extract relevant information from single-scale spatiotemporal data [3,4]. For instance, Celik et al. [5] introduced the fast mixed-drove co-occurrence pattern (FastMDCOP)-Miner algorithm which prunes temporal infrequent patterns during the mining of spatiotemporal co-occurrence patterns to improve efficiency. Ryu et al. [6] employed a spatiotemporal correlation matrix to express short-term dependencies between adjacent road sections, resulting in improved accuracy for traffic flow prediction. Baer et al. [7] developed a spatiotemporal hybrid Bayesian hierarchical model (STM BHM) that decomposes global random effects in space-time and classifies spatial regions to describe disease risk characteristics. Jin et al. [8] explored the spatiotemporal relationship between regional tourism economies and other variables using a semi-parametric geographically weighted regression (GWR) model capable of capturing both global and local spatiotemporal relationships. Jung et al. [9] utilized generalized linear mixed models (GLMMs) to analyze the association between temperature and aggression in space-time. While these spatiotemporal mining methods effectively consider the dynamic and heterogeneous characteristics of the spatiotemporal dimension by synergizing the temporal and spatial dimensions, a single-scale perspective limits the exploitation of the full information contained in spatiotemporal data, especially when it exists at other scales. Therefore, multiscale spatiotemporal analysis is crucial. Chen et al. [10] proposed a multiscale interactive recurrent network to capture joint multi-scale patterns. Mohamed et al. [11] introduced an algorithm based on a multiscale dynamic time regularization approach using the dynamic time warping (DTW) algorithm within the multiscale iterative framework IMs-DTW for rainfall time series. Deng et al. [12] developed a non-parametric model that considers spatial autocorrelation to construct a zero feature distribution. Wu et al. [13] incorporated scale effects into a geographically and temporally weighted regression model (GTWR) to identify and analyze multi-scale processes, employing flexible bandwidths determined by various covariates. Lawler and Edwards [14] employed an analytical technique based on variance decomposition to quantify cross-scale correlations in multi-scale spatial associations applied in the study of habitat location changes. Zhang et al. [15] utilized a one-sided weighting approach and proposed the MUGTWR method to characterize multi-scale spatiotemporal dynamic regression relationships, improving the efficiency of multi-scale spatiotemporal analysis. These multi-scale spatiotemporal data mining methods offer the flexibility to characterize distribution patterns or correlations of spatiotemporal attributes at each scale effectively.

Whether analyzing spatiotemporal data from a single-scale or multi-scale perspective, it is common for the spatiotemporal attributes of the studied object to be single-scale, known, or precise. However, it is crucial to consider the presence of uncertainty in geographical information, which is inevitable in many cases [16]. The multiscale nature of spatiotemporal data reflects one aspect of this inherent uncertainty. While fine-scale spatiotemporal descriptions often provide accurate information, coarse-scale descriptions tend to introduce information uncertainty. If the range of spatiotemporal attributes describing geographic elements is excessively broad, it can lead to insufficient accuracy that fails to meet actual needs. Therefore, it is essential to flexibly integrate spatiotemporal locations and scales for the analysis of spatiotemporal data [17]. Uncertain spatiotemporal information within the dataset also holds value as it can complement certain spatiotemporal information. In situations where deterministic spatiotemporal information is scarce and inadequate for problem-solving, uncertain spatiotemporal information can provide additional options and enhance the potential for problem resolution.

To mine uncertain spatiotemporal information in multiscale spatiotemporal data, this paper proposes a multiscale spatiotemporal correlation method which attempts to discover and measure uncertain spatiotemporal information from structured spatiotemporal data. Firstly, the ambiguity of spatiotemporal data is considered in terms of its multiscale characteristics and measured by a threshold value related to the spatiotemporal dimension. Secondly, the frequency of geographical elements and the ambiguity of spatiotemporal attributes are combined in assessing their importance. Thirdly, the measure of the strength of the spatiotemporal correlation is achieved by considering the ambiguous correlation of each spatiotemporal piece of data of geographical elements in an integrated manner. Finally, in the experiment, the spatiotemporal information in the spatiotemporal transaction set is displayed with knowledge graphs.

2. Geographic Elements and Their Spatiotemporal Correlation Based on Transaction Data

In the era of big data, spatiotemporal data exhibits the characteristics of multi-source heterogeneity. After processing, it can be transformed into structured data in the form of [“time”, “space”, “attribute1”, “attribute2”,…]. This structured data bears similarities to transactions and can be effectively mined using association rules [18,19]. The spatiotemporal association rule, as a significant algorithm in spatiotemporal data mining, represents an advancement of the association rule algorithm, specifically designed to extract association relationships within spatiotemporal data. This algorithm has been extensively applied in various domains, including traffic congestion research [20], air pollution analysis [21], ecology studies [22], climate investigations [23], marine environment assessments [24], among others. In many studies, spatiotemporal attributes are employed to classify geographic elements within a specific spatiotemporal range, and the correlations between these elements are explored based on classification results. However, the natural ambiguity inherent in spatiotemporal data and its relationships [25] can pose challenges in accurately classifying research objects. Furthermore, the mining of spatiotemporal association rules often relies on known relationships between geographical elements. For example, transaction [t, s, f₁, f₂] not only describes the spatiotemporal attributes of f₁ and f₂ but also implies that they exist within the same spatiotemporal region at a given time. However, in many cases, these correlations are unknown or uncertain. In such scenarios, leveraging the spatiotemporal attributes of elements can reveal correlations that cannot be effectively captured by traditional association rules.

An example of spatiotemporal relevance is the investigation of a suspect. Relevant information about suspects is sometimes scarce or hidden, and their activity trajectory may become the only clue. Bob is a suspect in an accident that occurred in March 2021 in region P. Since Bob’s interpersonal relationships are unknown, the only way to find Bob is to collect information related to “March 2021 in region P” from the available spatiotemporal information. Some of the known information is as follows: (1) Jack and Bob appeared in region A in March 2021. (2) Jack and Alice appeared in region B on 15 March 2021. At the time of the survey, for various reasons (fuzzy memory of the respondents, etc.), some descriptions were vague and could only be described with a wider range of temporal or spatial scope: (3) Donald was active in region W in 2021: (4) Stephen was active in S region in March 2021. Here, S and W are above the administrative level of P. A, B, C and P are at the same administrative level. These data constitute a multi-scale spatiotemporal dataset, and the processed data are shown in

Table 1. Known information from the case.

Time	Space	Objects
2021-03	A	Jack, Bob
2021-03-15	B	Jack, Alice
2021	W	Donald
2021-03	S	Stephen
2021-03	C	Jack, Bob

.

If [2021-03, P] is used as the selection condition, all these transactions cannot be filtered out due to mismatch. However, considering the spatiotemporal implications of their descriptions, these data then have relevance to the search criteria. There is a clear multiscale character to the time items. By further understanding, the range of each location is shown in Figure 1. There are scale differences in the space column in Table 1 space item W contains space item S, while S contains space items A, P, C and B.

Consideration of the topological relationship in the spatiotemporal dimension reveals that all four transactions potentially relate to the search conditions. Stephen and Donald’s activity areas encompass the target area of the search, and the locations described in the first and second transactions are in close proximity to the target area. Consequently, it can be inferred that the objects described in these transactions may also be associated with Bob. By comparing the degree of overlap between each figure and Bob’s action trajectory, along with their respective certainties, it becomes possible to identify the figures that are more closely related to Bob. This example demonstrates that in many situations, direct relationships between objects may not be readily available. In such cases, the spatiotemporal dimension offers a perspective for uncovering correlations that can provide potentially valuable information. To quantify the strength of correlations between pairs of objects, a new metric needs to be introduced. Addressing the aforementioned challenges, this paper proposes an enhanced method for association rules. Differing from previous research approaches, this paper aims to directly correlate geographic elements based on their existing spatiotemporal attributes, without dividing them into spatiotemporal divisions. Before correlating geographic elements or attributes using spatiotemporal attributes, the attributes need to be interpreted and converted into analyzable spatiotemporal data format.

Definition 1. 

Time Item. A time item refers to an item in a transaction that describes a temporal concept, representing either a specific point in time or a time interval. It can be mapped to a one-dimensional timeline, denoted as t.

Definition 2. 

Space Item. A space item represents an item in a transaction that describes a spatial concept, indicating a distinct spatial extent. It can be mapped to a polygon or a three-dimensional region in geospatial space, denoted as s.

Definition 3. 

Attribute Item. Attribute items are items within a transaction that either represent geographical elements or describe various attributes. These items are denoted as a.

Definition 4. 

Space-Time Transaction. A transaction is classified as a spatiotemporal transaction if it includes time, space, and attribute items. A spatiotemporal transaction consists of a time item, a space item, and multiple attribute items. It describes a specific spatiotemporal range, along with the geographic elements and attributes within that range, and is denoted as [t, s, a₁, a₂,...]. Here, t represents the time item, s represents the space item, and a₁, a₂, and other items represent the attribute items.

The time and space items include the spatiotemporal information associated with the attribute items. By mapping the time items to realistic time ranges and the space items to realistic spatial ranges, the spatiotemporal transactions satisfy the essential conditions for conducting spatiotemporal analysis. As shown in Figure 2, it can be observed that [t₁, s₁] is disjointed from [t₂, s₂], and the length of t₁, t₂ and the area of s₁, s₂ can be calculated. Therefore, objects or events located in [t₁, s₁] and [t₂, s₂] can be considered unrelated.

In massive spatiotemporal data, the precise spatiotemporal locations of many geographic elements may be uncertain due to various factors. Consequently, the ranges described in the data may be broader than the actual locations. However, the time and space items still enable further analysis, even if they describe fuzzy spatiotemporal location information of geographic elements.

3. Methods for Measuring Spatiotemporal Information Uncertainty

Nowadays, a considerable number of spatiotemporal datasets contain uncertainties or ambiguities in their spatiotemporal information. Unfortunately, these uncertainties are frequently overlooked or disregarded, leading to a loss of valuable information. Nevertheless, the disregarded fuzzy information can provide additional options and opportunities when other information is insufficient to address a problem. Therefore, to fully leverage spatiotemporal data, it is crucial to explore and utilize fuzzy spatiotemporal information. The key step in mining fuzzy spatiotemporal information is to identify uncertain spatiotemporal information and quantify its level of uncertainty, as shown in Figure 3.

Definition 5. 

Spatiotemporal explicit information. Subset E in spatiotemporal dataset D means a spatiotemporal range that satisfies a specific and required precision. There are explicit correlations (co-occurrence, causality, etc.) when it comes to the spatiotemporal properties of each data. This kind of spatiotemporal information obtained directly or indirectly from E is defined as spatiotemporal explicit information, which can be described by certain indicators. In other words, spatiotemporal explicit information is a collection consisting of various indicators that express certain spatiotemporal information. The spatiotemporal explicit information obtained from E is denoted as ε_E.

Definition 6. 

Spatiotemporal Implicit Information. A spatiotemporal range expressed by subset I in spatiotemporal dataset D does not meet the accuracy requirements of a specific need, and the information obtained from it has uncertainty. This kind of spatiotemporal information with uncertainty is called spatiotemporal implicit information. Specifically, spatiotemporal implicit information is a collection of various indicators that means fuzzy spatiotemporal information. Spatiotemporal implicit information obtained from I is denoted as φ_I.

Spatiotemporal datasets consist of both spatiotemporal explicit information, which represents certain spatiotemporal details, and spatiotemporal implicit information, which represents uncertain aspects. These two types of information play distinct roles in addressing practical problems. Spatiotemporal explicit information, being deterministic in nature, is typically prioritized and proves effective in problem solving. On the other hand, spatiotemporal implicit information is characterized by uncertainty and cannot be directly relied upon for decision-making. However, in scenarios where spatiotemporal explicit information is limited and insufficient, spatiotemporal implicit information offers additional options and opportunities to tackle complex problems.

To effectively mine and differentiate spatiotemporal implicit information from spatiotemporal explicit information in datasets, it is necessary to measure the uncertainty of spatiotemporal data. Moreover, comparisons can be made regarding the extent of spatiotemporal information across different datasets. We posit that the uncertainty of spatiotemporal information in datasets manifests in two aspects: the uncertainty of spatiotemporal information pertaining to individual geographic elements and the uncertainty of spatiotemporal associations among geographic elements. In this paper, we propose a method to quantify the uncertainty of spatiotemporal information, providing a benchmark for identifying these two types of spatiotemporal information.

The spatial relationships between geographic elements are categorized into four cases: separation, adjacency, intersection, and containment. In this study, we specifically discuss the intersection and inclusion of spatial relationships in the temporal dimension. We contend that geographic elements within the same spatiotemporal range exhibit spatiotemporal correlations. When mining spatiotemporal information, we first examine the relationships among spatiotemporal transactions. Subsequently, we synthesize the spatiotemporal correlations from multiple spatiotemporal data to derive the spatiotemporal correlations between geographic elements.

3.1. Uncertainty Measures for Spatiotemporal Correlation between Spatiotemporal Data

Different geographic elements or phenomena could cover different spatiotemporal scales, so it is necessary to choose a suitable scale according to the spatiotemporal data to measure its uncertainty. In general, it could be considered that the smaller the spatiotemporal range covered by a spatiotemporal attribute, the higher the certainty of its spatiotemporal information. When the spatiotemporal range is small enough, we consider that the spatiotemporal data contains spatiotemporal explicit information. Based on this premise, we adopt a quantifiable benchmark for measuring the uncertainty of spatiotemporal information.

Definition 7. 

Benchmark Scale. A benchmark scale is a spatiotemporal scale that distinguishes spatiotemporal information as explicit or implicit. The benchmark scale is used to measure the certainty of the spatiotemporal range. The uncertainty of each spatiotemporal attribute is determined by the range on the benchmark scale it occupies. In the spatiotemporal dimension, it consists of two parts, time benchmark and space benchmark, denoted as b(t, s).

If the spatiotemporal range represented by the time and space items falls within the designated benchmark scale, the spatiotemporal data is categorized as containing spatiotemporal explicit information. Conversely, if it exceeds the benchmark scale, it is considered as spatiotemporal implicit information. For instance, if “2022-04-01” is chosen as the time benchmark, the temporal information encompassed by “2022-04” is implicit, whereas the temporal information included in “2022-04-01” is explicit. However, if “2022-04” is used as the benchmark, both “2022-04” and “2022-04-01” are deemed to have explicit temporal information. The determination of the benchmark scale is influenced by a combination of objective and subjective factors, including the requirements of real-world applications, the level of geographic information technology, and the individuals’ subjective judgment.

Definition 8. 

Spatiotemporal Correlation Degree. Many spatiotemporal transactions are considered to have the possibility of spatiotemporal correlation if they intersect in both time and space. The strength of the spatiotemporal correlation between transactions at the benchmark scale is called the spatiotemporal correlation degree. The spatiotemporal correlation degree is jointly determined by the time and space items of spatiotemporal transactions and the benchmark scale, reflecting the uncertainty of spatiotemporal correlation between spatiotemporal data.

When calculating the spatiotemporal correlation between two elements, we first determine whether there is an intersection of the ranges covered by their spatiotemporal data. After that, we use the probability that the geographic elements are within the spatiotemporal range of the same benchmark scale as the strength of the correlation between the geographic elements. We use R() to denote the range (time or space) and P() to denote the probability of the existence of correlation. We suppose the spatiotemporal transactions T₁ = {t₁,s₁,f₁} and T₂ = {t₂,s₂,f₂}. The temporal extent is measured by the length of the time slice, and the spatial extent is measured by the area. t₁, t₂, s₁, s₂ express a specific spatial or temporal extent, implying location, scale, and range information, and are represented by solid lines. b(t, s) is represented by dashed lines. We discuss the spatiotemporal relationship between f₁ and f₂ in each case in terms of the correlations in the temporal and spatial dimensions, respectively.

3.1.1. Measuring Correlation in Time Dimension

When there is an intersection or containment relationship in time dimension of two spatiotemporal elements, it is considered that there is a possibility of temporal correlation between them. Factors that affect the correlation between time periods include the scale of temporal attributes, the range of temporal attributes, and the benchmark scale. The correlation of two temporal attributes t₁ and t₂ is

$$P(t_1,t_2)=\frac{R{(b(t))}^2}{R(t_1)R(t_2)}$$

(1)

R(b(t)) denotes the size of the benchmark time range, R(t₁), R(t₂) denote the sizes of the range of t₁ and t₂, respectively.

Next, we discuss the more special cases that exist between two spatiotemporal transactions from the perspective of scales, considering the containment and intersection cases, respectively. The spatiotemporal correlation degree can be used more efficiently to obtain the corresponding results by understanding these cases.

• Containment

The containment relation is the main topological relation that exists in multi-scale spatiotemporal data, and is also a special intersection case. We discuss the temporal correlations according to three special examples separately, as shown in Figure 4.

(1)

R(b(t)) ≤ R(t₁) ≤ R(t₂)

In this example, multiple benchmark scales are covered by both t₁ and t₂. t₂ has the probability of being within the time range of one of the benchmark scales of t₁. The probability of the existence of correlation between t₁ and t₂ is the product of the probability that t₁ lies in b(t) and the probability that t₂ lies in b(t).

$$P(t_1,t_2)=\frac{R{(b(t))}^2}{R(t_1)R(t_2)}$$

(2)

(2)

R(t₁) ≤ R(b(t)) ≤ R(t₂)

In this example, t₁ involves only one time slice on the benchmark scale. At this point, the possibility that t₂ is in the range of the benchmark scale where t₁ is located is considered, so

$$P(t_1,t_2)=\frac{R(b(t_1))}{R(t_2)}$$

(3)

(3)

R(t₁) ≤ R(t₂) ≤ R(b(t))

When t₁ and t₂ are in the same time slice in the benchmark time, then t₁ and t₂ are considered to have a time correlation. Therefore, P(t₁,t₂) = 1.

• Intersection

When considering the intersection relationship, the connection between t₁ and t₂ in the benchmark scale is discussed. Three special cases are included equally. We discuss the probability of t₁ and t₂ being in the same benchmark time for each case separately, as shown in Figure 5.

(1)

R(b(t) ≤ R(t₁) ≤ R(t₂)

When t₁ and t₂ cover multiple time slices under the benchmark scale, t₁ and t₂ are correlated when they are simultaneously in the time slice at the b(t) scale of the intersection of t₁ and t₂. In this condition,

$$P(t_1,t_2)=\frac{R{(b(t))}^2}{R(t_1)R(t_2)}$$

(4)

(2)

R(t₁) ≤ R(b(t) ≤ R(t₂)

When t₁ is sufficiently precise and covers only one benchmark scale, t₁ and t₂ co-exist in the range of one cell under the benchmark scale. t₁ and t₂ are correlated when t₂ is in the time slice of the benchmark scale where that t₁ exists, so

$$P(t_1,t_2)=\frac{R(t_2)\cap R(b(t))}{R(t_2)}$$

(5)

(3)

R(t₁) ≤ R(t₂) ≤ R(b(t))

In the last example, the ranges represented by both t₁ and t₂ are sufficiently fine and the total time range of t₁ and t₂ is in a time period on a benchmark scale, which means that T₁ and T₂ are sufficiently precise and closely linked in time and therefore temporally correlated, i.e., P(t₁,t₂) = 1.

• Adjacent and disjoint

The topological relations of time slices are adjacent and disjoint in addition to intersection and containment, and the general situation is shown in Figure 6. There is no intersection between t₁ and t₂ in the two cases of (a,d) in Figure 6, and the length of b(t) is short, thus there is no correlation, i.e., P(t₁,t₂) = 0. There is an intersection between t₂ and t₁ in the benchmark time slice in (b,e), which can be calculated by using Equation (6). The case of (c,f) t₁ and t₂ exists in the same benchmark time, and it can be considered that P(t₁,t₂) = 1 at this time.

Using the data in Table 1 as an example, assuming a temporal benchmark scale of March 2021, the correlation between Donald and Stephen in the time dimension is the probability that their time items are in March 2021, i.e., P(t₁, t₂) = 31/365.

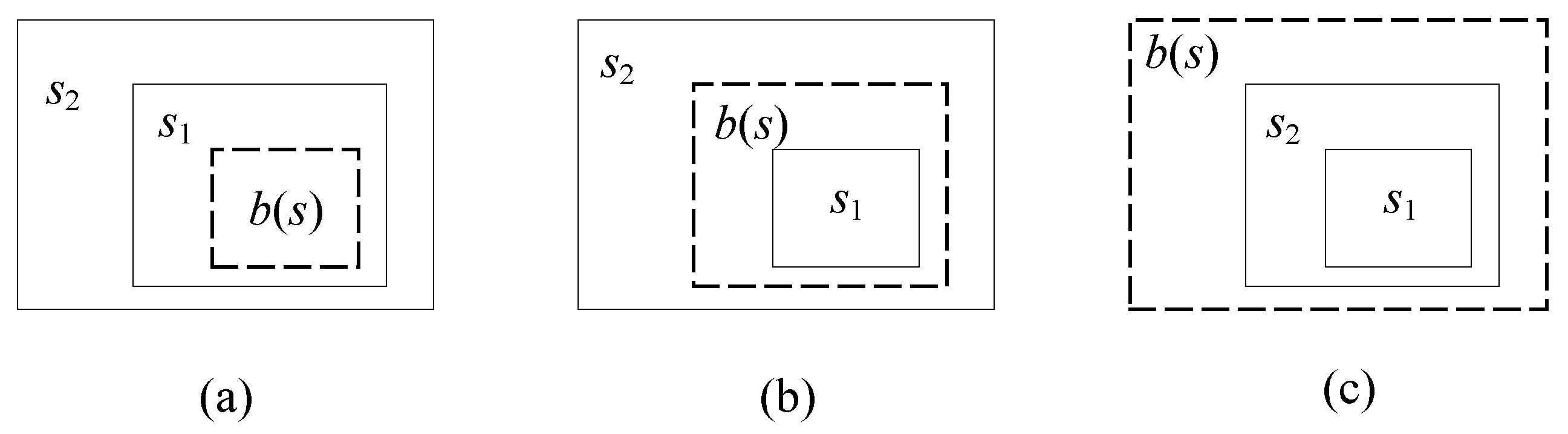
3.1.2. Measuring Correlation in Spatial Dimension

Similar to the temporal dimension, in the spatial dimension, we consider two cases of containment and intersection and analyze the uncertainty of their correlation separately. When the geographic elements are contained, R(s₁), R(s₂) denote the range of s₁, s₂, respectively, including three cases in Figure 7.

According to these three examples, the spatial correlations of T₁ and T₂ are calculated as follows:

$$P(s_1,s_2)=\left\{\begin{array}{cc}\frac{R{(b(s))}^2}{R(s_1)R(s_2)}& R(b(s))\le R\left(s_1\right)\le R\left(s_2\right)\\ \frac{R(b(s))}{R(s_2)}& R\left(s_1\right)\le R(b(s))\le R\left(s_2\right)\\ 1& R\left(s_1\right)\le R\left(s_2\right)\le R(b(s))\end{array}\right.$$

(6)

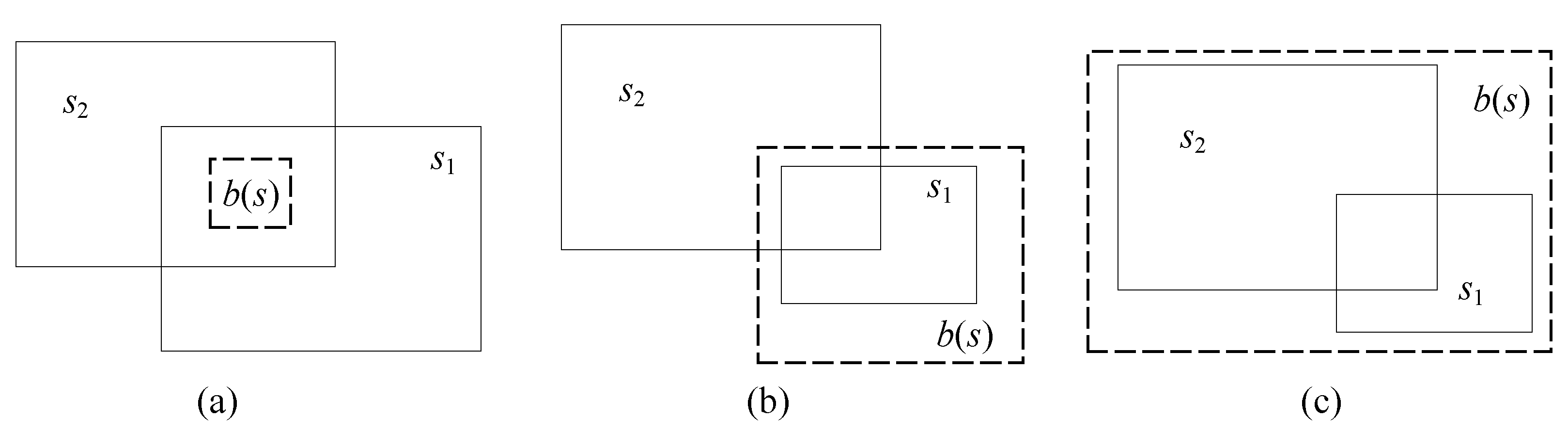
The examples of geographical elements spatially intersecting with each other are shown in Figure 8.

Referring to the analysis of temporal correlation, we can obtain the spatial correlation for these three cases:

$$P(s_1,s_2)=\left\{\begin{array}{cc}\frac{R{(b(s))}^2}{R(s_1)R(s_2)}& R(b(s))\le R\left(s_1\right)\le R\left(s_2\right)\\ \frac{R(s_2)\cap R(b(s))}{R(s_2)}& R\left(s_1\right)\le R(b(s))\le R\left(s_2\right)\\ 1& R\left(s_1\right)\le R\left(s_2\right)\le R(b(s))\end{array}\right.$$

(7)

Similar to the temporal dimension, the same adjacency or disjoint relationship exists in the spatial dimension, as shown in Figure 9. P(s₁,s₂) = 0 in the case (a,d), and (b,e) whose spatiotemporal correlation is as the second equation in Equation (9). P(s₁,s₂) = 1 in the case of (c,f).

In the temporal dimension, the benchmark scale provides known temporal units, enabling straightforward comparisons. However, in the spatial dimension, the situation is different, particularly when dealing with vector data. The range of spatial units at each benchmark scale can be complex or unknown. Consequently, comparing the correlation between two spatial attributes of larger scales becomes challenging, as it cannot be easily calculated based on the size of a specific spatial region’s range.

Using the data in Table 1 as an example again, assuming a temporal benchmark scale of S, the areas of W and S are 200 and 100, respectively. The correlation between Donald and Stephen in the space dimension is the probability that their space items are in S, i.e., P(s₁, s₂) = 1/2.

Considering time and space together, the spatiotemporal correlation of transactions T₁ and T₂ is

$$P(T_1,T_2)=P(t_1,t_2)P(s_1,s_2)$$

(8)

When the temporal correlation degree and spatial correlation degree of T₁ and T₂ are both 1, the spatiotemporal correlation degree between them is 1, i.e., P(T₁, T₂) = 1. At this time, we consider that there is an obvious spatiotemporal correlation between T₁ and T₂. This correlation is considered into spatiotemporal explicit information.

In calculating the spatiotemporal correlation, the length of the time period is used to quantify the temporal attributes and the area of the planar region is utilized to quantify the spatial attributes. Then, the uncertainty or credibility of the spatiotemporal information contained by the spatiotemporal attributes is measured according to the benchmark scale. In many cases, the spatiotemporal data that can be obtained are ambiguous because their spatiotemporal range is much larger than the range of the benchmark scale. Therefore, mining spatiotemporal implicit information is usually the main task of massive spatiotemporal data mining. After understanding the meaning and calculation method of spatiotemporal correlation degree, the uncertainty of spatiotemporal information can be measured.

Definition 9 

. Spatiotemporal Support. Given condition d_c, which could be a spatiotemporal range or geographical element, there are m records in the spatiotemporal transaction set OD = [d₁,d₂,...,d_n] that have a correlation with d_c which can form the candidate dataset CD = [r₁,r₂,...,r_m]. The spatiotemporal correlations with the benchmark scale b(t,s) are calculated for each record in CD and summed to obtain the spatiotemporal support of CD, denoted as δ_CD. The spatiotemporal support is affected by the amount and accuracy of the candidate dataset as well as the benchmark scale.

$${\delta }_{CD}={\displaystyle \sum _{i=1}^{m}P(r_i,b(t,s))}$$

(9)

Definition 10. 

Spatiotemporal Confidence. In a candidate spatiotemporal transaction set CD, there exists a geographical element o. The weight of the spatiotemporal support of the spatiotemporal transaction set T = [u₁,u₂,...,u_m] of o to the spatiotemporal support of CD is called the spatiotemporal confidence of o in CD, denoted as η(o,CD).

$$\eta (o,CD)=\frac{{\delta }_o}{{\delta }_{CD}}=\frac{{\displaystyle \sum _{j=1}^{n}P(u_j,b(t,s))}}{{\displaystyle \sum _{i=1}^{m}P(r_i,b(t,s))}}$$

(10)

Spatiotemporal confidence describes the strength of the correlation between the candidate transaction set and the geographic element. The higher the spatiotemporal confidence of a geographic element, the higher the correlation between the geographic element and the candidate transaction set, and the stronger the correlation with the selection conditions for generating the candidate transaction set.

3.2. Uncertainty Measures of Spatiotemporal Correlation between Geographical Elements

The spatiotemporal correlation degree can easily be calculated and can measure the spatiotemporal correlation between spatiotemporal transactions. Geographic elements often exist in multiple spatiotemporal transactions, so all their transactions with spatiotemporal correlation should be considered when analyzing the correlation between different geographic elements.

Definition 11. 

Element Fuzzy Correlation Degree. Given the condition d_c and the benchmark scale b(t,s), the candidate dataset CD = [r₁,r₂,...,r_m] is filtered from OD, and r_m describes a specific geographic element. We let the set composed of these objects be O = [o₁,o₂,...,o_i], and in order to describe the strength of spatiotemporal correlation among geographic elements, the concept of element fuzzy correlation degree is introduced, which is denoted as κ. The element fuzzy correlation degree of m objects is calculated as follows:

$$\begin{array}{cc}\kappa (o_1,o_2,\dots ,o_m)={\omega }_i{\displaystyle \sum P(T_1^{k_1},T_2^{k_2},\dots ,T_m^{k_m})}& k_m=1,2,\dots ,n\end{array}$$

(11)

where m denotes the serial number of the target, k_m denotes the marker in the set of spatiotemporal transactions of the mth element, and n is the number of spatiotemporal transactions of the mth target. ω_i is the weight value of the spatiotemporal correlation between the elements involved in the association, which is used to measure the influence brought by other factors affecting the spatiotemporal association between elements, such as the trustworthiness of data sources, the accuracy of spatiotemporal transaction extraction, etc. Its value ranges from 0 to 1. The spatiotemporal correlation of these spatiotemporal transactions is calculated by selecting one transaction from the set of transactions of each target to form a combination. The spatiotemporal correlations of all the combinations are summed to obtain the elemental fuzzy correlations of these targets κ. The size of κ is related to the amount of data and the accuracy of the data for each target. Precise spatiotemporal data contain reliable information, on the other hand, more correlated data indicate a stronger connection between geographic elements. They both reflect the possibility of the existence of connections between geographic elements and the strength of the connections.

The element fuzzy correlation degree of two geographic elements is convenient to calculate and can be used as the basis for more complex correlation judgment. It could be the most commonly used element fuzzy correlation degree. Its calculation method is presented in Equation (12).

$$\kappa (o_a,o_b)={\omega }_{ab}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m}P(T_a^i,T_b^j)}}$$

(12)

where n and m denote the number of spatiotemporal transactions of geographic elements O_a and O_b, respectively, T_a and T_b denote the spatiotemporal transactions existing in a and b, respectively, and ω_ab is the weight value of the spatiotemporal correlation between o_a and o_b. Since both spatiotemporal explicit information and spatiotemporal implicit information may exist between each geographical element, to distinguish them, we measure them by element explicit correlation degree and element implicit correlation degree, which are denoted as κ_e and κ_i, respectively. Their formulas are as follows:

$$\kappa (o_a,o_b)\left\{\begin{array}{cc}{\kappa }_e(o_a,o_b)={\omega }_{ab}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m}P(T_a^i,T_b^j)}}& P(T_a^i,T_b^j)=1\\ {\kappa }_i(o_a,o_b)={\omega }_{ab}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m}P(T_a^i,T_b^j)}}& 0<P(T_a^i,T_b^j)<1\end{array}\right.$$

(13)

Spatiotemporal correlation obtained by taking one transaction from the spatiotemporal transaction set of each of the two elements is obtained as a value equal to 1 or less than 1. The value of 1 expresses spatiotemporal explicit information, and summing all the values of less than 1 produces the κ_e value between these two elements. Summing all the values of less than 1, the value of κ_i between the elements can be obtained. κ_e reflects the obvious spatiotemporal correlation between the elements and can be considered as spatiotemporal explicit information. κ_i reflects the ambiguous spatiotemporal correlation between two elements and is considered as spatiotemporal implicit information between the geographical elements.

Using the data in Table 1 as an example again, we suppose the baseline scale is (2021-03-15, S), and the areas of A, B, S, and C are, respectively, 8, 7, 100, and 6. Then, the elemental fuzzy correlation degree between Stephen and Jack includes two parts, i.e., Κ_e = 0, Κ_i = 1/31 × 1/31 × 1 + 1/31 × 1 × 1 + 1/31 × 1/31 × 1 = 33/961.

Definition 12. 

Correlation Index. Given a set C of element fuzzy correlations, it contains all the associated elements in C and their corresponding element fuzzy correlations, including explicit correlations and implicit correlations. The proportion of the element fuzzy correlation degree of an association (o_a,o_b) to the sum of the element fuzzy correlations of all the associations is called the correlation index of the association, which is denoted as ζ(o_a,o_b). Similarly, when calculating the correlation index of each relation, the uncertainty is taken into account and divided into explicit and implicit relatedness indexes, denoted as ζ_e and ζ_i. We let sum(κ_e) be the sum of explicit relatedness of all elements and sum(κ_i) be the sum of implicit relatedness of all elements. The correlation index of any two elements is calculated as in Equation (14).

$$\xi (o_a,o_b)=\left\{\begin{array}{c}{\xi }_e(o_a,o_b)=\frac{{\kappa }_e(o_a,o_b)}{sum({\kappa }_e)}\\ {\xi }_i(o_a,o_b)=\frac{{\kappa }_i(o_a,o_b)}{sum({\kappa }_i)}\end{array}\right.$$

(14)

Correlation index can reflect the reliability of a specific association relationship under specified conditions. When the selection conditions change, the set of spatial and temporal affairs of each geographic element also changes, and the magnitude of the change may vary. When the range of filtering conditions or the benchmark scale is expanded, the element fuzzy correlation degree between individual elements increases, but it does not mean that each association relationship is stronger. The correlation index can be used to eliminate the effect of data volume on the strength of correlation between geographic elements.

3.3. Flow of Multiscale Spatiotemporal Correlation Algorithm

Based on the relevant concepts introduced above, the correlation analysis algorithm of multiscale spatiotemporal data is designed to mine the spatiotemporal explicit implicit information of multiscale spatiotemporal data. The process of multiscale spatiotemporal correlation algorithm is introduced with the example of mining the element fuzzy correlation degree between every two geographical elements under a certain spatiotemporal condition. The exact process is shown in Figure 10.

In the first step, relevant transactions are selected using topological relationships. The topological relationships between spatiotemporal data and spatiotemporal conditions are analyzed according to the temporal and spatial extent of the spatiotemporal data. In this paper, two topological relationships, intersection and containment, are considered. Multiscale spatiotemporal data with these two topological relationships with spatiotemporal conditions are filtered out for the next step of processing. According to a certain spatiotemporal condition d_c = {t_c, s_c}, data d_i(i = 1,2,...,n) in the original multiscale spatiotemporal data set OD = [d₁,d₂,...,d_n] are sequentially compared to that spatiotemporal condition. If d_i is associated with d in both time and space, the data are selected and their spatiotemporal correlation with d_c is calculated to form the candidate data set CD = [r₁,r₂,...,r_m], where r_i = {t_i, s_i,...,p_i}, i ≤ m ≤ n. p_i denotes the spatiotemporal correlation degree of r_i with d_c.

The second step is to iterate through CD, filter out all the elements in it and generate the element dataset FD. Each element is classified according to the elements in FD to generate a spatiotemporal transaction set ST(f), which constitutes a spatiotemporal list FL = [[f₁, ST(f₁)],[f₂, ST(f₂)],…,[f_n, ST(f_n)]].

In the third step, the benchmark scale b(t,s) is determined and the spatiotemporal confidence of each element in FL to d_c is calculated, which can find the correlation between geographic elements and d_c and serve as a basis for evaluating the importance of each geographic element.

In the fourth step, element correlation degree is analyzed. The topological relationship between each spatiotemporal transaction in the spatiotemporal transaction set of one and another element in TL is judged. If there is an association, the corresponding spatiotemporal correlation degree is calculated. The explicit correlation degree κ_e of two elements and the implicit correlation degree κ_i of two elements are calculated. Finally, all the explicit correlation degrees are divided by the sum of explicit correlation degrees, and all the implicit correlation degrees are divided by the sum of explicit implicit correlation degrees to obtain correlation index ζ_e and ζ_i for each correlation.

4. Simulation Experiment

4.1. Basic Hypotheses and Experimental Targets

The algorithm proposed in this paper can be used to handle spatiotemporal transactions after the extraction of spatiotemporal data by semantic analysis. However, obtaining spatiotemporal transaction datasets that adhere to multiscale characteristics is challenging. The primary reason is that the majority of current spatiotemporal datasets concentrate on a specific domain, resulting in usually uniform spatiotemporal scales. Constructing multiscale spatiotemporal data necessitates a vast amount of spatiotemporal data as raw materials, sourced from a wide range of domains. The extraction process of multisource heterogeneous spatiotemporal data is complicated and out of the scope of this study. Therefore, to implement the ideas proposed in this paper, experiments are conducted using artificially generated data. Before conducting the experiments, some assumptions are made to simplify the complex real-life situation: (1) All transactions record different events. (2) Each transaction contains only one geographic element, which is an object. The goal of the experiment is to analyze the importance of each object in the multiscale spatiotemporal transaction set and to mine the explicit and implicit information between the two objects. The results of mining are used to judge the importance of geographic elements and to discover important correlations.

4.2. Generating Multiscale Spatiotemporal Data

Firstly, an accurate spatiotemporal dataset was generated by following a series of preparation steps. Preparation involved gathering time items, space items, and attribute items. Subsequently, space-time transactions were generated through random combinations. To create these transactions, specific dates were randomly selected with a “day” level of accuracy. Similarly, place names were randomly chosen, and the coordinates of the boundary points corresponding to these places were collected. The selected places covered three administrative levels, namely “point of interest (POI)”, “district”, and “city”, thus encompassing different spatial scales. The polygons formed by connecting the boundary points served as the spatiotemporal representation of the space items. They were employed to determine the topological relationships and calculate the area. Next, a random number of objects were generated, each associated with a set of attributes. For each spatiotemporal transaction, one time item, one space item, and one attribute item were randomly selected. This experiment yielded 10,000 spatiotemporal transactions, forming the set of spatiotemporal transactions.

Then, spatiotemporal transaction sets were processed into the multiscale. The locations we chose were inherently multiscale, so only the time attributes needed to be multiscale to generate spatiotemporal transaction sets that are temporally ambiguous. All time items were randomly kept at one of the scales “year”, “year–month” and “year–month–day”. For example, “2021-01-01” can be randomly converted to “2021”, “2021-01”, or itself. The generated multi-scale spatiotemporal transaction set was used as the original data set OD = [d₁,d₂,…, d_n].

4.3. Mining Spatiotemporal Explicit and Implicit Information and Building Knowledge Graphs

In this section, we mine the spatiotemporal information of each object in a certain spatiotemporal range. The result of mining can reflect the importance of each object in that spatiotemporal and the strength of elemental correlations between them and is presented in the form of a knowledge graph. The knowledge graph can represent knowledge and information figuratively, and can also be used for mining and representation of geographic knowledge, such as natural language quizzing in virtual geographic environments [26], geographic entity and relationship prediction [27], etc. To reflect the influence of benchmark scales on mining results, the experiments took d_c = [2022-05, Erqi District] as the spatiotemporal condition and used three spatiotemporal regions Ω₁ = (2022-05-23, Zhengzhou University South Campus), Ω₂ = (2022-05, Erqi District), and Ω₃ = (2022-05, Zhengzhou City) as the benchmark scales to analyze the importance of each object and the spatiotemporal correlation between objects. The spatiotemporal correlations between these spatiotemporal regions are scaled differently. In the following experiments, transactions with explicit spatiotemporal information are referred to as explicit transactions and those with implicit spatiotemporal information are referred to as implicit transactions.

4.3.1. Object Importance Analysis

In the previous section, we used the spatiotemporal confidence to measure the importance of each geographical element. In order to calculate the spatiotemporal confidence of each object, we needed to select the data related to d_c from the data and classify the selected results according to the elements to obtain the spatiotemporal transaction set of each element. In this experiment, a total of 366 relevant transactions were selected as the candidate transaction set CD, and the number of spatiotemporal transactions for each object is shown in

Table 2. The number of related objects and their transactions.

Objects	o1	o2	o3	o4	o5	o6	o7	o8	o9	o10	Total
Transactions	32	42	40	29	29	40	45	46	30	33	366

. Filtering the transactions in which each object is located by each object constituted the spatiotemporal transaction set ST(f).

Table 3. The number of related transactions and support of each object obtained using association rule.

Objects	Ω1		Ω2		Ω3
	N	sup	N	sup	N	sup
o1	0	0	1	0.142857	0	0
o2	0	0	1	0.142857	1	0.25
o3	0	0	0	0	0	0
o4	2	1	0	0	0	0
o5	0	0	1	0.142857	0	0
o6	0	0	2	0.285714	0	0
o7	0	0	1	0.142857	1	0.25
o8	0	0	0	0	1	0.25
o9	0	0	1	0.142857	1	0.25
o10	0	0	0	0	0	0

shows the number of transactions N and the corresponding support sup for each object at different benchmark scales mined using association rules.

Table 4. The number of related transactions and spatiotemporal support obtained by considering the spatiotemporal properties.

Objects	Ω1			Ω2			Ω3
	Ne	Ni	δ	Ne	Ni	δ	Ne	Ni	δ
o1	0	9	0.011068	15	17	16.277517	15	17	16.443836
o2	0	17	0.022045	10	32	12.340201	12	30	14.547945
o3	0	11	0.075491	15	25	16.745681	17	23	18.953425
o4	2	5	2.013699	12	17	13.315707	14	15	15.273973
o5	0	10	0.040594	12	17	13.149388	14	15	15.273973
o6	0	11	0.040695	21	19	22.466475	22	18	23.528767
o7	0	12	0.037849	19	26	20.664294	21	24	23.038356
o8	0	13	0.013709	14	32	15.962595	14	32	20.378082
o9	0	9	0.000127	11	19	12.172027	11	19	15.358904
o10	0	10	0.013715	7	26	8.766548	10	23	11.953425

shows the number of transactions and the corresponding spatiotemporal support for each object at the benchmark scale. Ne is the number of explicit transactions, Ni is the number of implicit transactions, and δ denotes spatiotemporal support.

The calculation of the support of each object in Table 3 is performed on a specific benchmark scale, and thus the sup obtained can be considered as the confidence of the set of items in that benchmark space-time for that object, e.g., the confidence of Ω₂ for o₆ is conf(Ω₂ → o₆) = 0.285714. Since the association rules cannot consider the spatiotemporal properties of items, and thus the explicit and implicit characteristics of transactions cannot be found, many transactions with correlation were ignored, resulting in partial loss of information. Table 4 shows the explicit and implicit spatiotemporal information by considering the spatiotemporal attributes. It can be seen that when the spatiotemporal range was Ω₁, the overall number of explicit transactions was the least; only o₄ had two explicit transactions, and the other objects contained only implicit transactions. Accordingly, the spatiotemporal support of o₄ was much higher than that of other objects. When the spatiotemporal range was Ω₂, the explicit and implicit transactions of each object increased significantly, and the spatiotemporal support of each object increased substantially. When the spatiotemporal range was further expanded to Ω₃, the explicit transactions of each object were increasing, the implicit transactions were decreasing, and the spatiotemporal support increased slightly. Combined with Table 2, it can be found that when the spatiotemporal range was Ω₂, all relevant transactions of each object were considered, and thus only the transformation of implicit transactions into explicit transactions occurred when the spatiotemporal range was expanded from Ω₂ to Ω₃.

From Table 3 and Table 4, it can be clearly found that the association rules are not flexible enough when dealing with spatiotemporal transaction data. The spatiotemporal explicit and implicit information and spatiotemporal support can well describe the importance of each object in a specific spatiotemporal condition and the strength of the correlation between the object and the spatiotemporal condition.

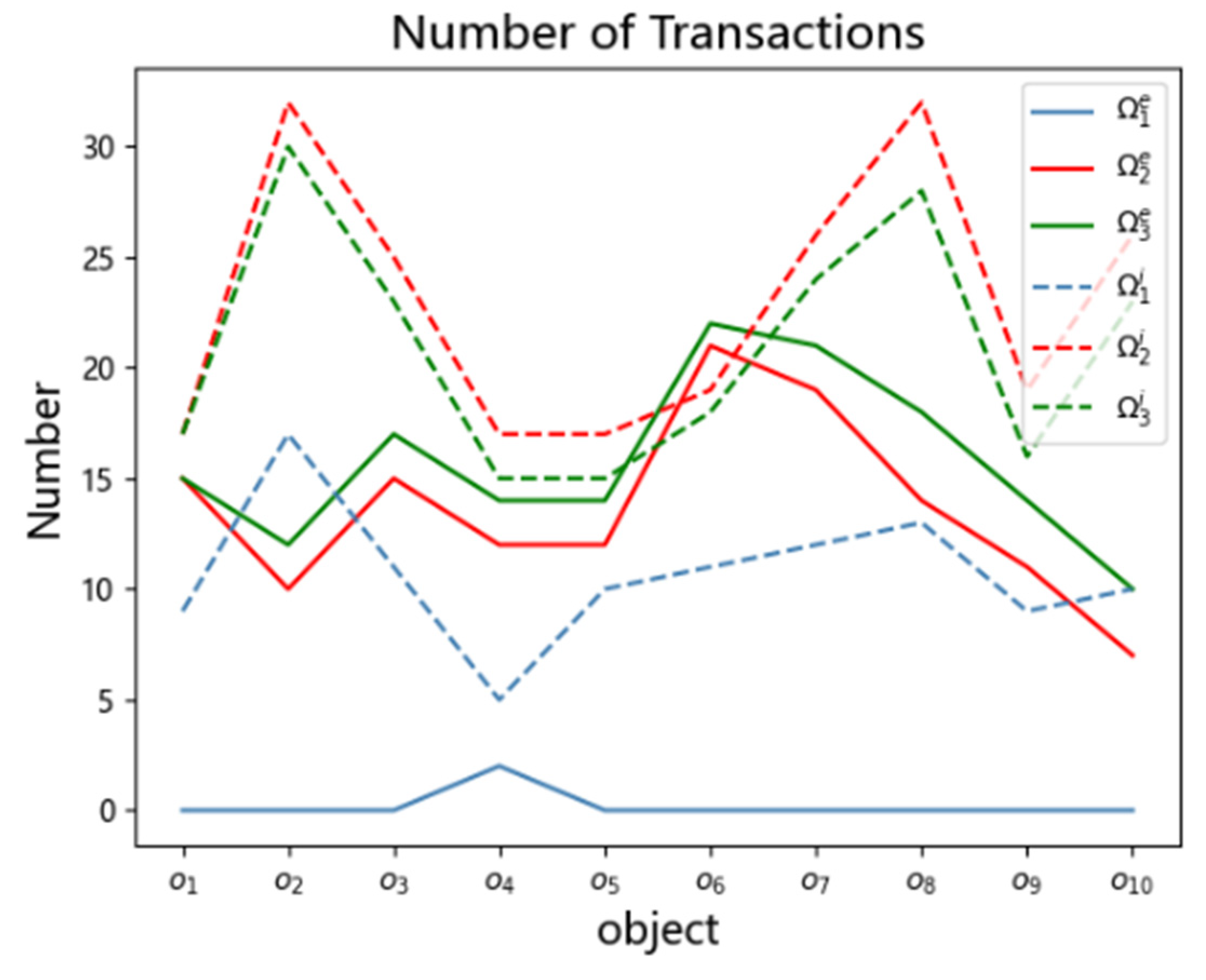
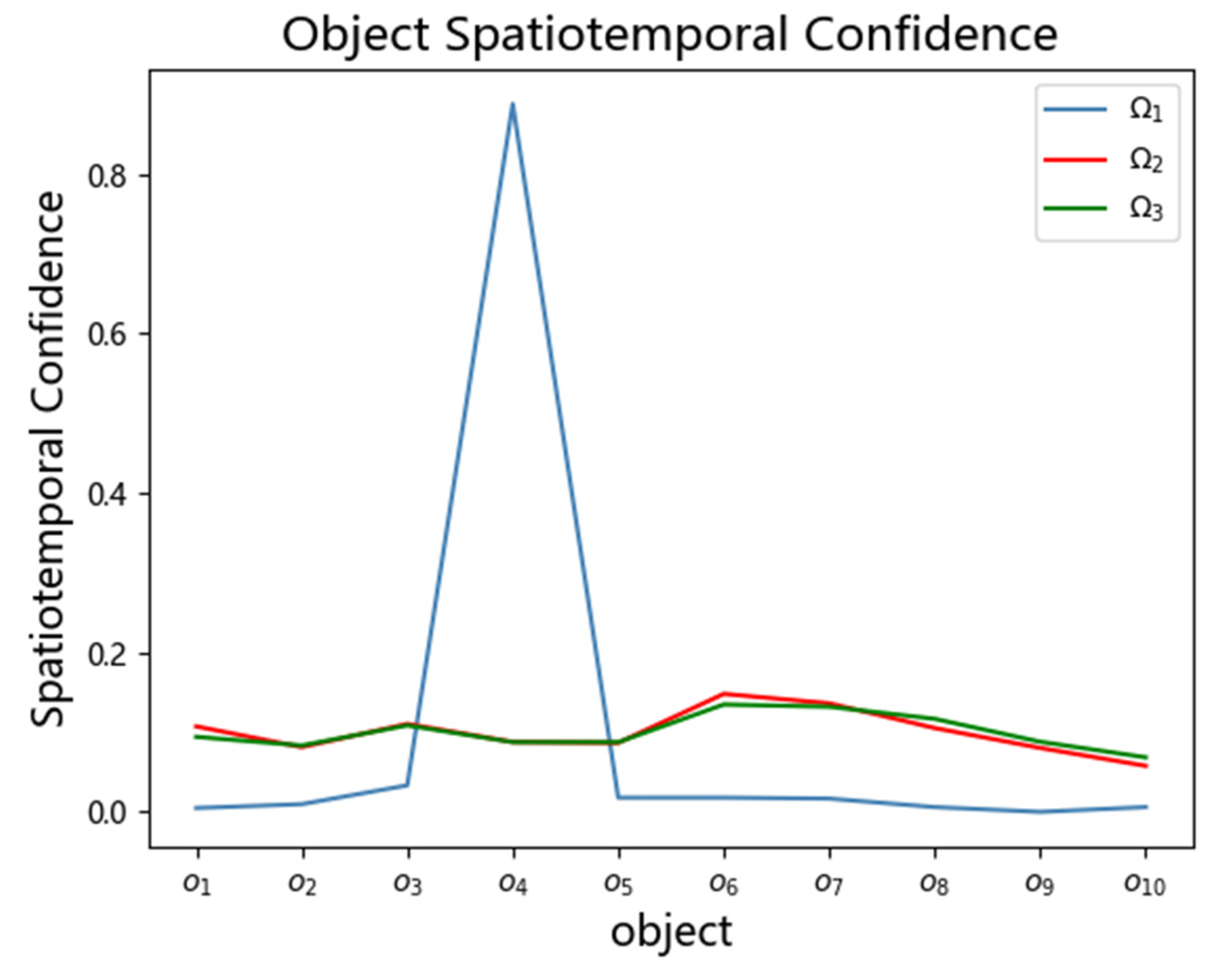
Figure 11 shows the spatiotemporal transactions of each object when the spatiotemporal range was changed, where Ω^e and Ωⁱ indicate the number of explicit and implicit transactions at the spatiotemporal range, respectively. Figure 12 shows the spatiotemporal confidence of each object at different benchmark space-time. It is obvious that the spatiotemporal confidence of o₄ was much higher than that of other objects when the spatiotemporal range was Ω₁. The spatiotemporal confidence of each object was approximately the same after the spatiotemporal range was expanded to Ω₂.

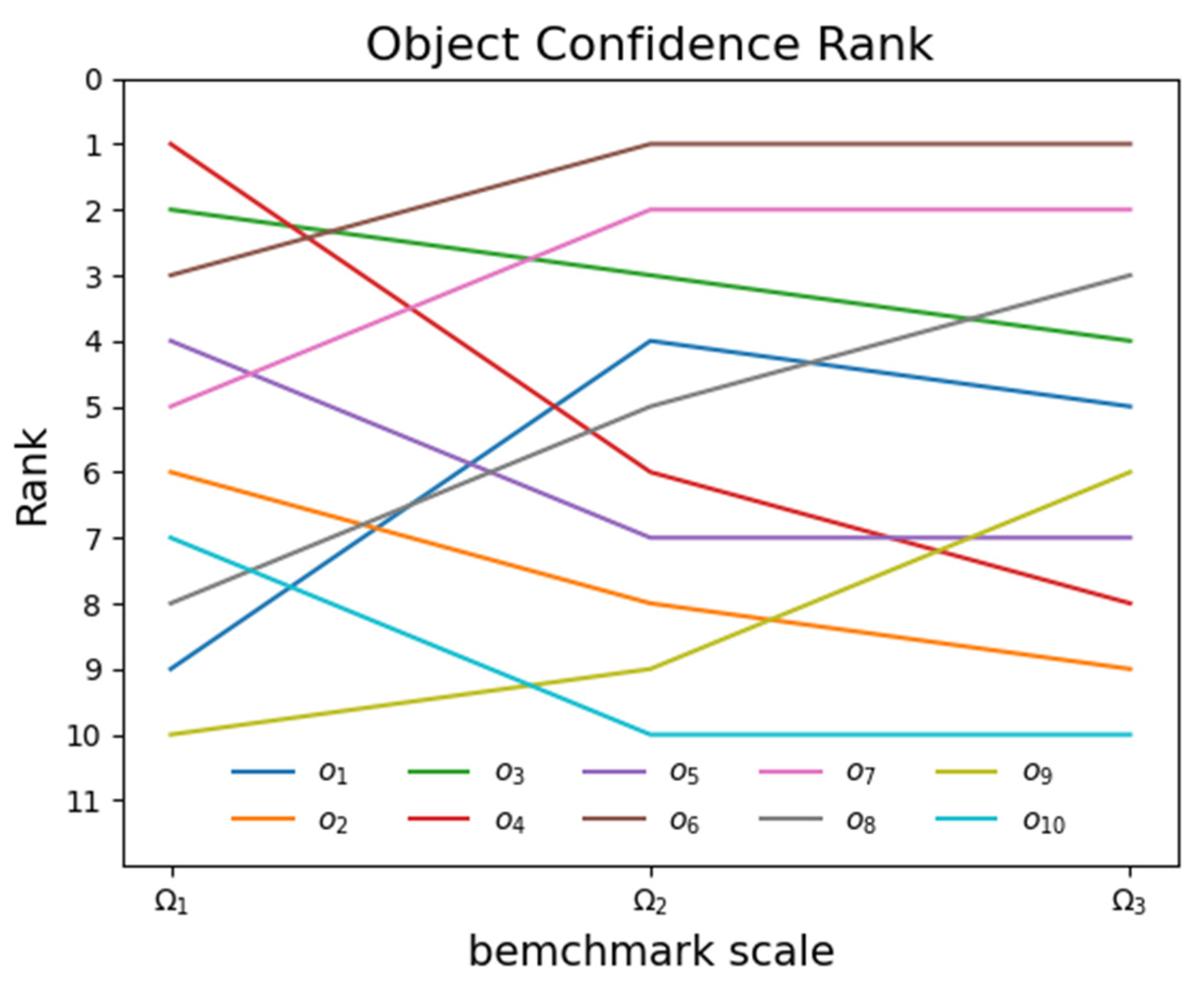
Figure 13 illustrates the impact of the benchmark scale on the ranking of each object. It is evident that the ranking of objects is influenced not only by the spatiotemporal confidence level but also by the chosen benchmark scale. Modifying the benchmark scale allows the alteration of the spatiotemporal confidence ranking of objects, thereby presenting new potential options that could prove valuable for specific problems.

Based on the aforementioned experimental results, it is apparent that smaller benchmark scales tend to concentrate explicit spatiotemporal transactions in a limited number of objects. The number of transactions with explicit information significantly influences the importance of objects. As the benchmark scale expands to a certain extent, the number of spatiotemporal transactions, both explicit and implicit, increases for individual objects, leading to a decrease in the spatiotemporal confidence of individual objects that were previously prominent. However, when the benchmark scale is expanded to a certain extent, most of the potentially relevant transactions are considered, resulting in a lesser change in the total number of spatiotemporal transactions. The transformation of implicit information into explicit information plays a crucial role in determining the degree of object importance. Consequently, the ranking of objects may change as their importance is affected by the chosen benchmark scale. This underscores the significance of carefully selecting the benchmark scale when examining the objects relevant to a specific problem.

4.3.2. Object Correlation Analysis

The spatiotemporal transaction lists of any two objects were selected, and all transactions of these two spatiotemporal transaction lists were compared to calculate the correlation index between the two objects. In calculating the element fuzzy correlation degree between objects, it was assumed to be the ideal case where all the correlations are given a weight ω of 1. The results are shown in

Table 5. Element fuzzy relevance between objects.

Related Objects	Ω1		Ω2		Ω3
	κe	κi	κe	κi	κe	κi
(“o1”, “o2”)	0	0.000244	150	50.867840	180	59.224020
(“o1”, “o3”)	0	0.000836	225	47.578107	255	56.666999
(“o1”, “o4”)	0	0.022288	180	36.746641	210	41.162695
…	…	…	…	…	…	…
(“o8”, “o9”)	0	1.743080	154	40.297137	252	60.985010
(“o8”, “o10”)	0	0.000188	98	41.936849	180	63.587870
(“o9”, “o10”)	0	1.743775	77	29.706660	140	43.591503

.

Some of the results of the element fuzzy correlation degree calculation are shown in Table 5. When the benchmark scale was Ω₁, it can be obtained from Figure 11 that only o₄ transactions with explicit information existed; thus, there was no explicit correlation between the objects. All correlations between objects were implicit. When the benchmark scale was expanded from Ω₁ to Ω₂, some of the implicit and irrelevant transactions had explicit correlation, and the explicit and implicit correlation index changed at the same time. When it was increased to Ω₃, more implicit correlations were transformed into explicit ones. Each object was affected by a different proportion of data, and thus its explicit and implicit fuzzy correlations changed.

Based on the above experimental results, it is clear that the range of the benchmark scale may affect the results of the analysis. The reason is that the benchmark scale reflects the requirement for data accuracy and is used to judge the ambiguity of spatiotemporal information, and as its range expands, some information previously considered implicit or irrelevant is converted into explicit information. In addition, the importance of the object changes somewhat because the data volume and scale distribution of each spatiotemporal data is different and is influenced differently. This means that the appropriate benchmark scale is important when analyzing specific problems.

Each relation contains two objects and their correlation index, and this structure is similar to the triad structure of “entity–relationship–entity” in the knowledge graph, so the results of this experiment can be used to construct the spatiotemporal knowledge graph related to spatiotemporal scope d_c. The spatiotemporal knowledge graph of objects is shown in Figure 14 with the help of Echarts, using Ω₂ as the benchmark scale and measuring the strength of the previous correlation of each object with the correlation index. Object nodes are represented by blue circles, and there are explicit and implicit correlations between objects, which are connected by solid and dashed lines, respectively. The spatiotemporal confidence of each object was used as an attribute of the object node. According to the graph, it can be quickly determined that the spatiotemporal correlation between two objects exists, while the strength of the spatiotemporal association can be determined roughly.

After obtaining the correlation index between objects, the objects related to the object of interest were ranked according to the correlation index. Implicit correlation index as a kind of implicit information is used as a supplement to explicit information, so the explicit correlation index was compared first, and the implicit correlation index was second. Taking the object relationship of o₇ under Ω₂ as the benchmark scale as an example, the ranking of other objects with their relatedness is shown in Table 5, and it can be found that the spatiotemporal correlation between o₆ and o₇ was the strongest, and the association between o₁₀ and o₇ was the weakest.

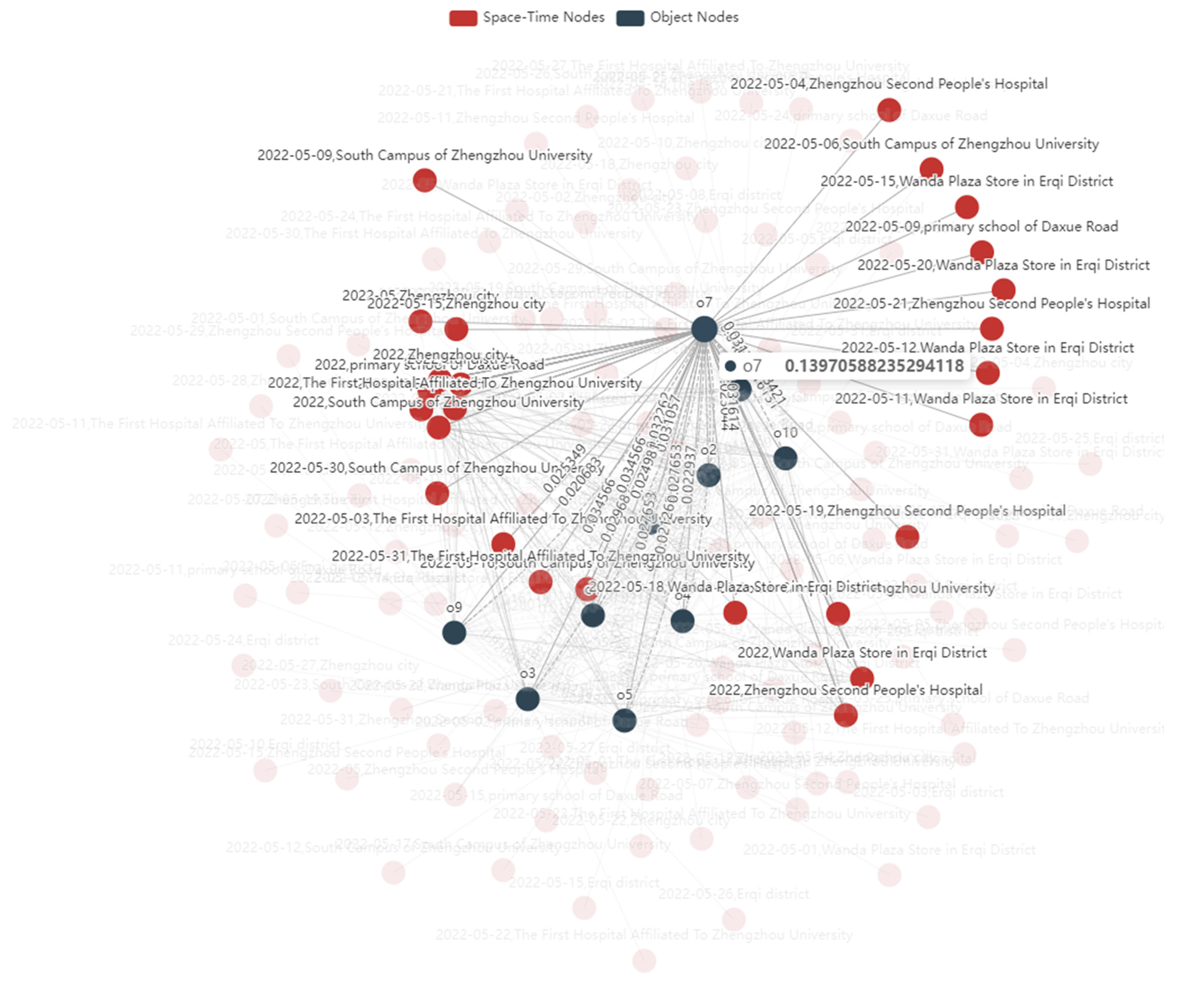
The Echarts tool utilized in generating the relationship graph offers a node-focusing feature, enabling users to concentrate on specific elements and comprehend related information without the need for an additional knowledge graph. By focusing on an element, the prompt box displays its corresponding spatiotemporal confidence, reflecting its level of importance. Figure 14 serves as the basis for such focus.

In Figure 15, the information from

Table 6. Ranking of correlations related to o₇ when the benchmark scale is Ω₂.

Related Objects	ζe	ζi
o6	0.048393	0.031737
o3	0.034566	0.029687
o1	0.034566	0.024981
o8	0.032262	0.031057
o4	0.027653	0.022937
o5	0.027653	0.021265
o9	0.025349	0.020683
o2	0.023044	0.031614
o10	0.016131	0.023421

is presented within the knowledge graph. It exhibits the explicit and implicit correlations of each object with o₇, allowing clear visualization. However, directly determining the order of association strength from the knowledge graph can be challenging.

The spatiotemporal attributes encompass the spatiotemporal information of each object, serving as the foundation for establishing correlations between objects. For a more comprehensive understanding of object-specific spatiotemporal information, additional spatiotemporal data selected based on spatiotemporal conditions can be incorporated into the knowledge graph. The results obtained are depicted in Figure 15, where the red circles represent spatiotemporal attributes. The connections between objects and spatiotemporal attributes derived from the data are depicted as solid lines, forming the basis of spatiotemporal information. Moreover, by focusing on individual objects, as demonstrated in Figure 16, users can gain detailed insights into the object’s spatiotemporal characteristics. The spatiotemporal knowledge graph effectively facilitates rapid comprehension of other objects related to the object of interest and their co-existing spatiotemporal attributes, ensuring readability and visualization.

4.4. Discussion

Based on the aforementioned experimental results, it is evident that the proposed method effectively mines both explicit and implicit information from multi-scale spatiotemporal data. The process involves several key steps. Firstly, the data relevant to the specified spatiotemporal conditions are filtered, enabling the calculation of spatiotemporal confidence for the involved objects based on data volume and accuracy. This step ensures the selection of reliable and informative data. Secondly, the spatiotemporal datasets of two objects are utilized to analyze their spatiotemporal correlations, which are expressed as element fuzzy correlation degrees. Additionally, comparisons are made between the spatiotemporal information extracted from different benchmark scales. It is observed that as the benchmark scale covers a wider range, the spatiotemporal correlation between objects becomes stronger. The presence of varying data amounts and proportions at each spatiotemporal scale for different objects leads to changes in the order of object importance to varying degrees. Furthermore, with the expansion of the benchmark scale, some implicit associations are transformed into explicit associations, enriching the understanding of the relationships between objects. Finally, the results obtained from the experiments can be employed to construct a spatiotemporal knowledge graph, effectively visualizing the information derived from the spatiotemporal mining process. The knowledge graph serves as a valuable tool for comprehending the interrelationships and characteristics of objects in the spatiotemporal domain.

5. Conclusions

In this paper, a novel method is proposed to effectively mine both certain and uncertain spatiotemporal information from spatiotemporal data. The specific steps of the method are described in detail. Initially, topological relations are utilized to determine the potential associations between spatiotemporal data, and indicators reflecting the uncertainty of spatiotemporal information are calculated based on the benchmark scale. The spatiotemporal information is then divided into two categories: spatiotemporal explicit information and spatiotemporal implicit information, depending on their respective levels of uncertainty. The results are quantitatively expressed. Subsequently, several concepts are introduced to measure the strength of correlations among objects.

The experimental results demonstrate that this method enables the discovery of significant geographical elements and facilitates the identification and quantification of both certain and uncertain correlations between these elements in the spatiotemporal domain. These results can be used to construct spatiotemporal knowledge graphs, offering valuable insights into the relationships and characteristics of the studied phenomena. However, it is worth noting that the method still has several areas that can be further improved. Firstly, spatiotemporal correlations between geographic elements may exist even in separated spatiotemporal regions, which requires further exploration. Secondly, the analysis of fuzzy spatiotemporal data relies on considering data within the same spatiotemporal region, emphasizing the need for further investigation in this aspect. Lastly, the probability distribution of geographic elements should be considered based on the actual situation. Therefore, mining uncertain spatiotemporal information represents a comprehensive and essential approach to gain a more thorough understanding of the data.