A Multi-Objective Roadside Unit Deployment Model for an Urban Vehicular Ad Hoc Network

Abstract

Vehicular ad hoc networks (VANETs) are a type of mobile ad hoc network that forms a unified wireless communication network between vehicles and roadside nodes. Roadside units (RSUs), as the infrastructure and key component of VANETs, play a critical role in improving the performance of VANETs. Their deployment can effectively improve the communication performance of the network. The goal of the RSU deployment (RSUD) problem is to install as few RSUs as possible on both sides of roads or intersections so that they can cover most areas and achieve better communication performance. This paper proposes a multi-objective optimization model to solve the RSUD problem using the characteristics of RSUDs on urban roads. Our optimized target includes three performance indicators, which are the deployment cost of RSUs, their coverage area, and communications. Since these three indicators cannot achieve consensus, this paper proposes a multi-objective evolutionary algorithm, the NSGA-II Pareto optimal solution, to solve the RSUD problem. The simulation results show the effectiveness of the multi-objective model and method. Finally, we present an experiment featuring RSU deployment that is based on a real traffic environment and uses OpenStreetMap; this experiment proves that our proposed method is practical.

1. Introduction

Vehicle ad hoc networks (VANETs) are self-organizing and open communication networks between vehicles. They are an application of mobile ad hoc networks (MANETs) in the traffic field and have become an important part of intelligent transportation systems (ITSs). VANETs merge wireless networking technology, sensor technology, and transmission technology and realize the interaction of information between pedestrians, vehicles, and roadside facilities through direct communications or multi-hop communications [1]. The widespread deployment of VANETs will ensure that they play a vital role in improving traffic efficiency, warnings about accidents, traffic safety, and driving experiences. Therefore, VANETs have attracted the attention of an increasing number of researchers.

VANETs are mainly composed of on-board units (OBUs) and roadside units (RSUs). Generally, OBUs are installed on vehicles and RSUs are usually installed on both sides of roads or intersections. VANETs provide two communication modes, namely vehicle-to-vehicle (V2V) communications and vehicle-to-RSU (V2R) communications [2]. In V2V communications, vehicles communicate directly with each other through their own OBUs; this method of communication can therefore be categorized as a distributed communication mode. In V2R communications, vehicles with priority coverage of RSU signals communicate with RSUs through their OBU, and then the RSUs communicate with other vehicles. This method of communication can be categorized as a centralized communication mode. However, it is easy to cause network delays and data packet loss in V2V communications because high-speed vehicles change their network topology frequently. Moreover, the roadside environment will also affect the wireless channel quality of V2V communications in urban environments [3]. This issue can be overcome by adopting a single-hop communication mode in V2R communications, which can effectively improve the success rate of data transmission and network throughput. It is necessary to deploy a large number of RSU devices to increase the coverage of vehicular ad hoc networks, although this will also bring great facility costs and maintenance costs. However, if the RSUs are too densely located, there will be a large number of overlapping areas, which will interfere with the communication between RSUs and reduce the performance of VANETs [4].

Due to budget and other factors, the number of RSUs deployed in a certain area is usually limited; therefore, the number of vehicle nodes in urban areas far exceeds the number of RSUs. The demand for information from vehicle nodes is growing rapidly, which makes RSUs the bottleneck on the capacity to transmit information between vehicle networks and external networks. Therefore, the deployment location of RSUs should be optimized to meet the communication needs of urban vehicle nodes as much as possible [5]. Since the location of deployment and quantity of RSUs have a significant effect on the communication performance and quality of VANETs in urban environments, it is very important to study the RSUD problem for the application and development of VANETs based on an analysis of vehicle traffic conditions and urban road structures.

The main goal of the RSUD problem is to choose an optimized location to deploy a limited number of RSUs that are best able to cover and improve the communication performance of the network. Moreover, the objectives of the RSUD problem affect and conflict with each other. For instance, when the number of RSUs is small, the coverage area of V2X communication is reduced. In this case, V2V communications are used to replace the faster V2I communications, which may cause communication delays. Financial costs are greatly increased when the number of RSU devices increases, and their resources will be wasted when there are fewer vehicles. Therefore, the RSUD problem is an NP-hard problem and a multi-objective optimization problem that has computational complexity and engineering complexity.

In this paper, we study the RSUD problem in an urban VANET. Through a comprehensive consideration of urban traffic conditions, a multi-objective optimization model is built with consideration of deployment costs (number of RSUs), coverage area, and data transmission delay in an urban area with fewer vehicles accessing the VANET. In order to solve the problem of the difficult selection of weight factors, the NSGA-II algorithm is used to obtain Pareto optimal solutions. Finally, the proposed method is verified and analyzed through simulation experiments and actual traffic maps. The rest of this paper is organized as follows. Section 2 summarizes the research status of the RSUD problem, which is followed by an introduction of our multi-objective optimization model and the NSGA-II algorithm in Section 3. In Section 4, the method of this paper is verified using an RSU deployment problem in a simulated urban environment with 8*8 intersections, and it is then applied in a real traffic environment based on OpenStreetMap (OSM). Finally, Section 5 concludes with the current work and prospects.

2. Related Work

Many researchers have recently dedicated themselves to solving the RSUD problem. Some research on RSUD is aimed at the fixed-location RSU deployment method, while other research considers the unfixed-location RSU deployment problem. Kim et al. proposed deploying RSUs on a customized vehicle that can drive on a fixed route while covering many areas at the same time [6]. This study focus on fixed-location RSU deployment because this is more widely used in urban areas. The optimization objectives of the RSU deployment in urban areas mainly include deployment cost, coverage range, and communication performance. Therefore, researchers studied a number of methods to solve the RSUD problem for different optimization objectives.

The common optimization objective is to minimize the number of RSU deployments, i.e., reduce the cost of deployment. Barrachina et al. proposed a density-based roadside unit (D-RSU) deployment strategy for remote areas. Under high vehicle density, good results are obtained at the lowest possible cost. The altered message can inform the emergency service department when accidents happen [7]. Nikookaran et al. used the sum of capital expenditure (CAPEX) and operating expenditure (OPEX) as optimization objectives of RSU deployment, and calculated the minimum cost allocation according to the historical traffic trajectory and candidate positions of vehicles. The RSU deployment scheme is obtained by solving the integer linear programming (ILP) problem with the minimum cost [8]. Lin and Deng minimized costs and covered as much areas as possible by deploying RSUs along both sides of a two-lane road and the middle island, and proposed a central particle swarm optimization method to obtain the lowest-cost RSU deployment scheme [9]. Shi et al. proposed an RSUD message propagation model based on the V2X network in an urban area, and used a control node selection algorithm (CNSA) based on central rules to obtain the optimal candidate installation location of RSUs within a given budget [10].

Another important optimization objective is to reduce the overlap of RSU signals coverage areas, which will help to reduce the search space of the RSU deployment scheme. Cheng et al. proposed the sparse coverage protocol “GeoCover” based on geometry to maximize the coverage area of RSU deployment and improve the performance of information transmission [11]. Zhu et al. proposed the complex city environment model (CCEM) to transform the area coverage problem into the street coverage problem and proposed a greedy polynomial (GBP) time approximation algorithm to obtain the optimal deployment scheme to minimize the number of RSUs in a specific area [12]. Rizk et al. proposed a greedy method for RSU deployment that mainly takes the coverage radius and overlap rate and prioritizes the more important candidate sites.The simulation results show that this method can be effectively applied to urban and rural roads [13]. Taoufik and Sabri proposed a minimum mobility patterns coverage (MPC) strategy to achieve high coverage and low deployment cost of RSUs, where MPC can extract the model of the moving vehicles with as few RSUs as possible through the tracking file [14].

The communication performance of an RSU deployment is also a very important optimization objective. This mainly refers to the data transmission performance of vehicles on the road, which is generally expressed by the expected packet-forwarding delay at both ends of the road [15]. Researchers nowadays use delay bounds as the constraint condition of the RSUD problem, that is, the communication delay on each road cannot exceed the given delay bound for data transmission. Mehar et al. treated the RSU deployment as a layout optimization problem and established a two-step solution model to solve it. First, the candidate location of the RSU was found according to the road connection information, then the deployment cost and communication delay were taken as the optimization objectives. The optimal deployment scheme of the RSU was obtained by using the genetic algorithm and Dijkstra algorithm [16]. Li et al. proposed a greedy algorithm and a two-stage algorithm to obtain the optimal deployment location of two kinds of RSUs with different costs and communication ranges. The simulation results show that this method can effectively reduce the total cost and meets the communication delay boundary in a given area [17]. Manuel et al. designed a genetic algorithm based on an RSU deployment system with the delay of traffic warning notification time in an urban area. The simulation results show that the algorithm can provide an RSU deployment scheme with a given road map and improve the vehicle communication ability in different density scenes [18]. Jalooli et al. aimed to minimize the communication delay using a security-based disconnected RSU placement algorithm. The experimental results show that this method can reduce the message propagation delay to a certain extent [19]. Yang et al. treated the RSUD problem as an NP-hard problem whose optimization objectives include bounded communication delay and RSU deployment cost, and proposed an improved binary differential evolution algorithm to solve this problem with the largest number of roads covered under the constraint of communication laying boundary and cost budget [5].

At present, the optimization objectives of the RSUD problem mainly include deployment cost, coverage area, and data transmission performance, etc. The selection of optimization objectives has a great impact on the RSU deployment scheme, and different scenarios require different optimization objectives. Therefore, researchers choose one or two optimization targets to solve the RSUD problem according to different needs. A few researchers consider RSUD as the Pareto optimal solution set of the multi-objective optimization problem to solve the problem directly [20], but most of them still use the weight method to transform it into a single-objective problem for optimization. Hence, there is still a lack of a comprehensive optimization method to solve the problem of RSU deployment.

3. Model and Algorithm

This paper proposes a new multi-objective optimization model for RSUD with the evolutionary algorithm NSGA-II in the urban road environment, with the deployment cost, coverage areas of RSUs, and total expected delay of data transmission as the optimization objectives.

3.1. Multi-Objective Model of RSUD

Firstly, the RSUD problem is defined in a simulation environment. Assume $G=(V,E)$, where $V=\{v_1,v_2,\dots ,v_N\}$ represents the set of all vertices (i.e., road intersections) in the road graph. N is the number of intersections. $E=\{e_1,e_2,\dots ,e_M\}$ represents the collection of all road segments and M is the number of edges between two adjacent vertices. If the two vertices of an edge are $v_i$ and $v_j$, the edge $e_k$ can also be expressed as $e_{ij}=\{l_{ij},{\rho }_{ij},v_{ij}\}$, where $l_{ij}$, ${\rho }_{ij}$, $v_{ij}$ are the European distance, vehicle density, and average speed of the segment, respectively. R is the communication radius between the vehicle and RSU. Figure 1 shows the description of the RSU deployment.

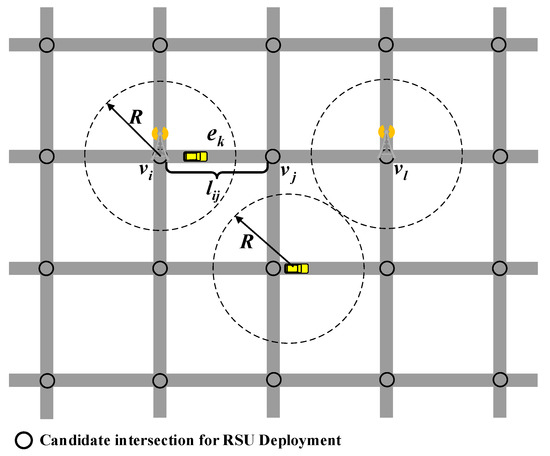
Figure 1. The simulated RSU deployment diagram.

Considering the impact of urban road environment on RSU deployment and VANET networking, this paper selected the number of RSUs, the coverage area of RSUs, and the expected data transmission delay as the optimization objectives. The multi-objective optimization model of RSUD in urban environment is as follows.

$$\begin{gathered} F\left(x\right)=\left\{f_1\right(x),f_2(x),f_3(x\left)\right\} \\ \mathrm{s}.\mathrm{t}.x_i=\left\{\begin{array}{c}1,\mathrm{R}\mathrm{S}\mathrm{U}\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{l}\mathrm{o}\mathrm{y}\mathrm{e}\mathrm{d}\\ 0,No\mathrm{R}\mathrm{S}\mathrm{U}\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{l}\mathrm{o}\mathrm{y}\mathrm{e}\mathrm{d}\end{array}\right. \end{gathered}$$

(1)

In Equation (1), $f_1\left(x\right)$ is the deployment cost of RSUs. As there is only one type of RSU deployed in this paper, we used the sum of RSUs to express the deployment cost. $f_2\left(x\right)$ is the coverage area, that is, the sum of the coverage areas of all RSUs. $f_3\left(x\right)$ is the sum of expected data transmission delays of all roads in the area where the RSU is to be deployed, where $x=\{x_1,x_2,\dots ,x_N\}$. N is the number of intersections. When the RSU is deployed at intersection $i$, the value of $x_i$ is 1. Otherwise, it is 0.

3.1.1. RSU Deployment Cost

In general, the deployment cost depends on the price of RSUs and the number of RSUs, which can be represented with $c\cdot f_1$, where c is the price of RSU. To simplify the calculation, the $c$ is neglected in this paper. We could only consider the sum of the number of RSUs as the deployment cost. Moreover, assuming the deployment cost as the optimization goal, the number of RSUs in the deployment scheme is a variable. Therefore, this paper aims to achieve the largest VANET communication coverage by deploying the fewest RSUs while minimizing the expected delay of roads. Equation (2) for the optimization objective of RSU quantity is shown below.

$$f_1=\mathit{min}{\sum }_{i=1}^N{x}_i$$

(2)

3.1.2. Coverage Area

Due to the dense urban roads, this paper aims to improve the utilization rate of RSUs. Assuming RSUs are all deployed at intersections so that each RSU can cover multiple streets, the coverage area of RSUs is considered as the optimization objective, that is, the total coverage area of all RSUs minus the overlapping area with other RSUs. According to this assumption, the larger the coverage area of the RSUs, the better the performance will be. To simplify the calculation, we assumed the coverage area is a negative value. Equation (3) for the coverage optimization objective is as follows.

$$f_2=\mathit{min}{\sum }_{i=1}^N-(\pi R^2-{\sum }_{j=i+1}^N\mathsf{\Delta }{A}_{ij})\cdot x_i$$

(3)

where $\mathsf{\Delta }{A}_{ij}$ is the overlapping area of any two RSU coverage areas, also known as interference area.

3.1.3. Expected Data Transmission Delay

In the previous research, the bounded delay for data transmission was generally used as a constraint condition to evaluate whether the RSU deployment scheme was feasible [5]. The expected data transmission delay is closely related to the vehicle density and average speed on the road, so it is difficult to obtain accurate data. Therefore, this paper directly used the total expected data transmission delay as the optimization objective to measure the VANET communication performance of the entire area. Equations (4)–(6) are the communication delay optimization objectives.

$$f_3=\mathit{min}{\sum }_{k=1}^M{T}_k$$

(4)

$$T_k=\left\{\begin{array}{c}{t}_{hop}=\frac{p_{size}}{s},0\le d_{ij}\le R\\ t(i,j),d_{ij}>R\end{array}\right.$$

(5)

$$t(i,j)=(1-e^{-R\cdot {\rho }_{ij}})\cdot \frac{l_{ij}\cdot t_{hop}}{R}+e^{-R\cdot {\rho }_{ij}}\cdot \frac{l_{ij}}{v_{ij}}$$

(6)

where $T_k$ is the expected delay of road section $e_k$ and $d_{ij}$ is the distance from the two endpoints $v_i$ and $v_j$ of road section $e_k$ to the nearest RSU device.

Significantly, when the road is covered within the range of the RSU, the vehicle single-hop communication delay can be calculated directly. When the road is beyond the coverage of the RSU, the multi-hop communication delay needs to be calculated based on the vehicle density. Multi-hop communication means that the vehicle cannot communicate directly with the RSU and needs to jump through other vehicles.

3.2. NSGA-II Algorithm

In order to verify the effectiveness of the proposed model, a multi-objective evolutionary algorithm is required to find the Pareto optimal front face and obtain the non-dominant solution set. At present, the most representative multi-objective algorithms are NSGA-II [21] and MOEA/D [22]. Since this study focused on the improvement of the problem model rather than the algorithm, we chose the multi-objective evolutionary algorithm NSGA-II to solve it. The NSGA-II algorithm has the advantages of simple structure and fast computation speed, and obtains the optimal solution set based on Pareto non-dominant relation. The flow chart of the NSGA-II algorithm is shown in Figure 2. It is notable that the single-point crossover and Gaussian variation are used to avoid local optimality in the algorithm.

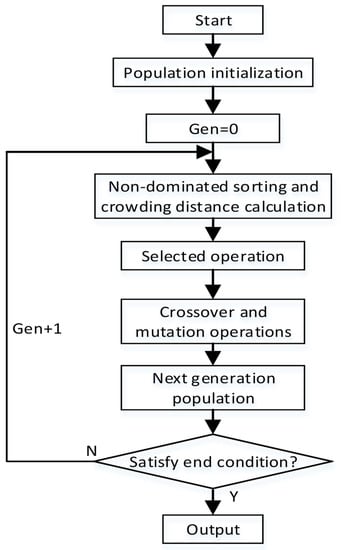
Figure 2. Flow chart of NSGA-II algorithm.

According to the demand of the multi-objective optimization model of RSUD, the NSGA-II algorithm in this paper adopted a 0–1 integer coding mode. and it determines The number of genes of each algorithm individual is determined by the candidate position of RSUs. In this paper, we consider each road intersection to be a candidate position of RSUs, and assume that this deployment has the highest utilization. Therefore, the NSGA-II algorithm adopted a 0–1 integer coding, and each solution represents all candidate intersections. In each gene of solution, 1 indicates that the RSU is deployed at this intersection, and 0 indicates that the RSU is not deployed.

An example is shown below. There are 64 road intersections in an area where RSUs can be deployed. Each solution in the algorithm population contains 64 genes, and each gene represents whether there is an RSU deployment at an intersection. It is necessary to decode the algorithm individuals when calculating the objective function. When the value is equal to 1, the corresponding RSU candidate position coordinates according to the gene sequence will be obtained. The coverage area and expected data delay of the deployment scheme are then calculated. As shown in Figure 2, after algorithm population initialization, it is necessary to perform a non-dominated ranking calculation according to the objective function value to rank all the individuals in the population, and to rank the non-dominated solutions of the same level by calculating the crowding distance between two individuals. Furthermore, the selection operation is performed according to the non-dominant grades of the two individuals, and then the preferences of the high grades are compared. If the grades are the same, the crowding distance is compared. The individual with the larger crowding distance will be preferred.

After the selection operation, a new offspring population is generated by crossing and mutating the selected parent population. The $(\mu +\lambda )$ strategy is adopted as the elite retention mechanism to retain the excellent individuals in the parent and offspring populations. The principle of strategy $(\mu +\lambda )$ is as follows. When $\mu$ parents in the population generate $\lambda$ offspring through cross and mutation operations, the number of better $\mu$ are selected from the set consisting of $\mu$ parents and $\lambda$ offspring through non-dominant sorting to enter the next generation. In each generation of the NSGA-II algorithm, the parent population and the newly born offspring population are combined to generate the next generation of the population using non-dominated sorting and the crowding distance. Finally, the mixed population is clipped to obtain the next generation population, and the fixed population size is maintained. This process can be repeated until the end condition is reached. It is worth noting that the elite retention mechanism of NSGA-II does not necessarily retain all non-dominant individuals, and if the number of non-dominant individuals is insufficient, excellent dominant individuals will also be retained.

4. Simulation and Analysis

To verify the effectiveness of the proposed multi-objective model of RSUD, the algorithm is calculated in a simulated traffic environment and a real traffic environment based on OpenStreetMap (OSM). The experimental results are then discussed and analyzed.

4.1. Preliminary Simulation Environment

In the simulation environment, we apply the model to the urban road environment with an 8 by 8 intersection matrix. As is shown in in Figure 3, the length and width of the entire area are 3600 m in the simulation. The map only includes vertical and horizontal roads, and the length of each road section is 400 m. It has been proven that it is easier for RSU devices to cover more roads at intersections [23]. Hence, the deployment locations of RSUs in this paper are only selected from 64 intersections. The communication range between RSU and vehicle is 250 m, packet size $p_{size}$ is 1 KB, and data rate is 3 Mb/s.

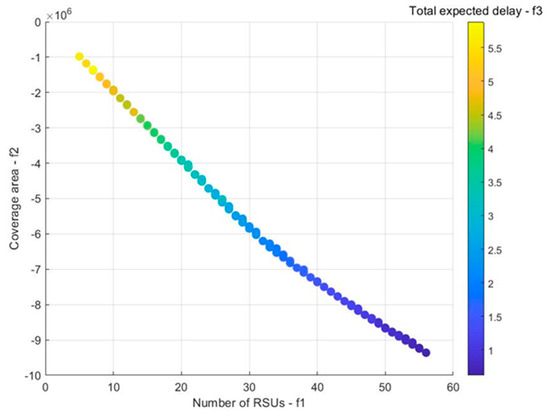
Figure 3. Simulation environment case: Pareto-optimal solution.

The vehicle density ${\rho }_{ij}$ on each road section is randomly generated according to the uniform distribution of 10–120 vehicles/km, and the average vehicle speed is generated according to the vehicle density. When the density of vehicles on the road is low, the speed will be high. In contrast, when the density of vehicles is high, the speed of traffic will be reduced. According to different traffic congestion levels, the relationship between vehicle density and average speed can be estimated through linear, logarithmic, and exponential relationships [24]. In this paper, the traffic density on the road is assumed to be moderate, so the linear relationship between the vehicle density and the average speed is used for estimation, as shown in Equation (7).

$$v=A-B\rho$$

(7)

where A and B are undetermined constants. The relationship between average vehicle speed and the density of each road section is as follows.

$$v_{ij}=64-0.4\ast {\rho }_{ij}$$

(8)

Moreover, the NSGA-II algorithm in this paper uses 0–1 integer coding. Each in the algorithm population contains 64 genes, and each gene represents whether there is an RSU deployment at an intersection. After conducting many experiments, we set the crossover rate as 0.7, the mutation rate as 0.3, the population size as 100, and the generation as 500. The maximum number of generations is obtained after many experiments.

4.2. Simulation Results and Discussion

In this paper, the NSGA-II algorithm was used to solve the multi-objective optimization model and obtain the optimal Pareto solution. It can be seen in Figure 3 that the x-axis indicates the number of RSUs deployed on the map, while the y-axis shows the total coverage area of all RSUs. The bar chart on the right shows the total expected delay for all roads. The color of the bar graph gradually darkens toward the bottom, which is suitable for values with a small total expected delay. It can be seen from Figure 3 that the Pareto optimal front face obtained through this method is evenly distributed. The optimal solution of coverage area and expected delay in the optimization target is at the right end of the Pareto front face, and the optimal solution of RSU number is at the left end of the Pareto front face. When one of the RSUD objectives achieves the optimal value, one of the other objectives may obtain a poor value. It is impossible to obtain the unique solution when all three objectives are optimal. Therefore, we can only choose a compromise solution from its Pareto optimal solution for this kind of multi-objective optimization problem.

Based on the analysis of the representative scheme in the Pareto optimal solution, we explore the characteristics of RSUD and the targeted scheme selection method. Four deployment schemes with 20, 30, 40, and 50 RSUs were selected from the Pareto optimal solution, and the mean value and mean square error of the whole solution are given, as shown in Table 1. When the number of RSUs is increased from 20 to 30, the average coverage area is increased by 48.96% and the average total expected delay is shortened by 33.13%. When the number of RSUs is from 30 to 40, the average coverage area is increased by 25.88% and the average total expected delay is shortened by 37.96%. When the number of RSUs is from 40 to 50, the average coverage area is increased by 17.78% and the average total expected delay is shortened by 30.57%.

Table 1. Objective function values in the Pareto front.

Objective Function	Number of RSUs f1	Coverage Area f2	Total Expected Delay f3	Number of Solutions
20 RSUs	20	3,926,990.817	479.401	3
30 RSUs	30	5,849,610.948	320.582	5
40 RSUs	40	7,363,478.308	198.905	3
50 RSUs	50	8,672,969.281	138.093	4
Overall Mean	31.275	5,736,473.210	355.206	--
Overall Std	14.808	2,458,829.988	203.059	--

This clearly shows that the average coverage area gradually decreases as the number of RSUs increases. The average total expected delay is the largest when there are 40 RSUs. The different numbers of RSU deployments are shown in Figure 4. When 20 RSUs are deployed, it can be seen there are fewer RSU deployments in the upper left corner and the upper right corner, which results in a low coverage level. When the number of RSUs increases to 30, the coverage area in the bottom area is not improved. However, there are fewer RSUs overlapping and the utilization rate of each RSU is higher. In the deployment of 40 and 50 RSUs, the RSUs can almost cover all roads, but the overlapping areas increase significantly. Therefore, it is better to deploy more than 40 RSUs to achieve better coverage and expected delay in the simulated traffic environment. Also, researchers can determine and select the Pareto optimal solution to maximize its coverage area according to specific RSUs’ cost budget and expected delay requirements.

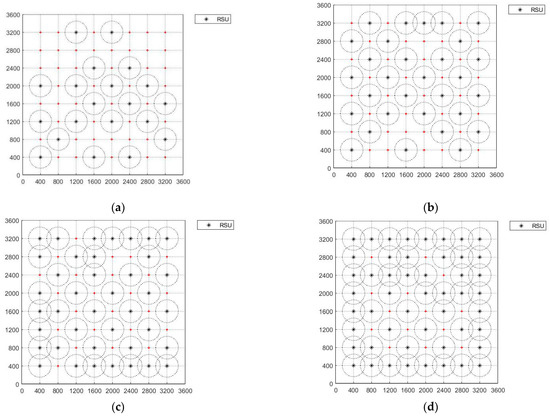
Figure 4. Representative deployment based on different quantities of RSUs. (a) Deployment of 20 RSUs; (b) deployment of 30 RSUs; (c) deployment of 40 RSUs; (d) deployment of 50 RSUs.

After conducting a numerical simulation, the effectiveness of this model and algorithm are preliminarily verified. However, there are several limitations compared to actual traffic. In the simulation environment, all intersections evenly distributed, and the distances between intersections are equal. We assumed the number of intersections is small, which means it is hard to apply the model to complicated scenarios. Overlap between RSUs rarely occurs, which reduces the requirement for RSU coverage. In response to these problems, the multi-objective model is applied to the actual traffic environment to verify the algorithm proposed in the next section.

4.3. Real Traffic Environment Test

In this section, we use OSM to verify the effectiveness of the multi-objective model and algorithm for the real traffic environment. OSM [25] is an open-source map that can be exported from its official website. It mainly includes spatial data and attribute data. OSM maps can be easily imported into simulation software such as SUMO and Veins, which is widely used in VANET. Combining OSM maps with onboard sensors can generate more accurate digital maps, such as for relating vehicle positions and identifying different road features, which are often used in the deployment of traffic assistance facilities and test case planning in automatic driving [26].

4.3.1. Test Environment Description and Configuration

The range of 36.6598–36.6470 N and 117.0204–117.0407 E was selected as the RSU deployment experiment in Jinan, Shandong Province, China, as shown in Figure 5a. Firstly, the downloaded OSM map is analyzed. According to the data of nodes and ways, the intersections are identified as candidate location points for RSU deployment, and the latitude and longitude coordinates in the waypoint data are converted into WGS 84 coordinates. To make the display more intuitive, the waypoint map is rotated by the Web Mercator projection, as shown in Figure 5b. According to map data preprocessing, this area includes 178 candidate sites of RSUs and 173 roads with different lengths. The setting of RSUs is the same as that of the last case. The communication range between RSU and vehicle is 250 m, and packet size and data rate are 1 KB and 3 MB/s, respectively. Each one in the NSGA-II algorithm population contains 178 genes, and each gene represents whether there is RSU deployment at an intersection. After running many experiments on the algorithm parameters, the crossover rate is set as 0.7, the mutation rate is set as 0.3, the population size is 200, and the generation is 1000.

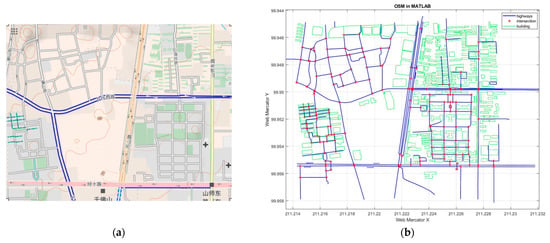
Figure 5. Real traffic environment schematic. (a) The original map; (b) RSU candidate points.

4.3.2. Real Traffic Test Results and Discussion

The NSGA-II algorithm is applied to the multi-objective optimization model, and the Pareto optimal solution set of RSUD problems in a real traffic environment is obtained, as shown in Figure 6. The x-axis in the figure shows the number of RSUs deployed on the map, the y-axis shows the total coverage area of all RSUs, and the bar chart on the right shows the total expected delay of all roads. It can be seen from Figure 6 that the expected delay increases with the increase in the coverage area. The bar chart also becomes darker with the expected delay reducing. Similarly to the simulated environment case, the Pareto optimal front-end distribution of the real traffic environmental case is relatively uniform, and the three optimization objectives conflict with each other. This is in agreement with the characteristics of multi-objective optimization problems.

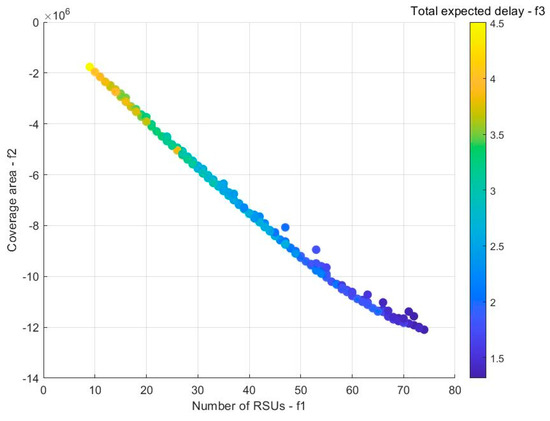
Figure 6. Real environment case: Pareto optimal solution.

Although the problem contains 178 RSU candidate points, it is only possible to have 74 solutions in Pareto’s optimal front face. This implies that continuing to increase the RSU has no effect on improving the coverage area and reducing the communication delay in the real traffic environment. However, when the number of RSUs is too small, the coverage area and communication performance will significantly decrease. Therefore, how to choose the number of RSUs according to the specific traffic environment is one of the challenging issues to be solved. The Pareto optimal solution set gives the optimal deployment schemes of different numbers of RSUs for designers to choose.

To further explore the characteristics of deployment schemes with different numbers of RSUs, the deployment schemes with 20, 30, 40, 50, 60, and 70 RSUs as representatives from the Pareto optimal solution set were selected, and then the objective function values were analyzed. Table 2 provides the average objective function values of the six representative RSU quantitative schemes, and also gives the average value and mean square deviation of the whole Pareto solution set.

Table 2. Objective function values in the Pareto front.

Objective Function	Number of RSUs f1	Coverage Area f2	Total Expected Delay f3	Number of Solutions
20 RSUs	20	3,914,775.836	483.365	4
30 RSUs	30	5,727,824.148	380.909	4
40 RSUs	40	7,513,408.303	324.868	2
50 RSUs	50	9,200,991.955	279.866	2
60 RSUs	60	10,611,066.285	233.905	3
70 RSUs	70	11,752,034.586	208.232	4
Overall Mean	39.580	7,203,486.487	371.505	--
Overall Std	18.142	3,010,101.743	112.509	--

As shown in Table 2, when the number of RSUs is increased from 20 to 30, the average coverage area is increased by 46.31% and the average total expected delay is shortened by 21.20%. When the number of RSUs is increased from 30 to 40, the average coverage area is increased by 31.17% and the average total expected delay is shortened by 14.71%. Similarly, when the number of RSUs is increased from 40 to 50, the average coverage area is increased by 22.46% and the average total expected delay is shortened by 13.85%. When the number of RSUs is increased from 50 to 60, the average coverage area is increased by 15.33% and the average total expected delay is shortened by 16.42%. When the number of RSUs is increased from 60 to 70, the average coverage area is increased by 10.75% and the average total expected delay is shortened by 10.98%.

Representative schemes of different quantities of RSU deployment are shown in Figure 7, in which it is obvious that the 20, 30, and 40 RSUs deployment schemes are not able to cover the whole area of the map but only cover the communication performance of the main roads of the environmental map. Starting from the scheme of 50 RSUs, they can cover most areas of the environmental map and achieve better communication performance. In the 60 RSUs deployment scheme, the overlapping area of RSU coverage begins to increase, while in the 70 RSUs deployment scheme, the overlapping area of RSU coverage is serious and there is a great redundancy. Therefore, in this real traffic environment, the better solution is to deploy more than 50 RSUs, which achieves better coverage and expected delay. If there is a higher requirement for communication delay, it is necessary to choose a scheme with more RSUs.

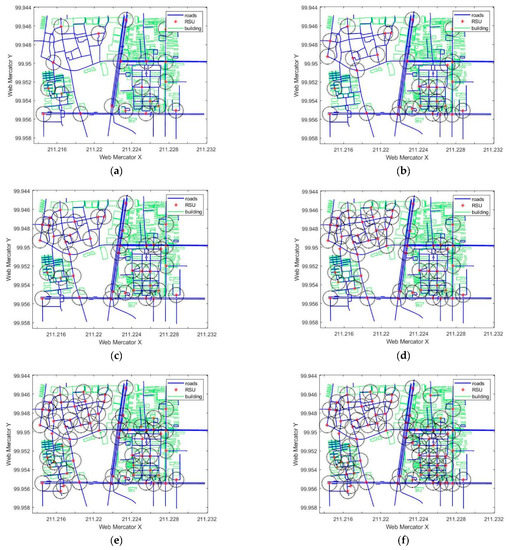
Figure 7. Different quantity of RSUs representative deployment plan. (a) Represents 20 RSUs; (b) represents 30 RSUs; (c) represents 40 RSUs; (d) represents 50 RSUs; (e) represents 60 RSUs; (f) represents 70 RSUs.

To conclude, through the simulation and real environment case verification, we have shown that the multi-objective model in this paper can effectively reflect the characteristics of the RSUD problem, and the Pareto optimal solution set obtained covers a variety of representativeness for designers to choose.

5. Conclusions and Future Work

In this paper, a multi-objective optimization model is proposed for the RSU deployment problem, which includes the optimization objectives deployment cost (number of RSUs), coverage area, and data transmission delay in the urban area with lower VANET. It aims to solve the difficulties of determining the weight coefficient, and only the unique preferred solution can be obtained in the RSUD optimization problem. The multi-objective evolutionary algorithm NSGA-II is used to solve the problem, and it obtains the Pareto optimal solution set. The method is verified using a simulated and a real environment case with urban traffic, respectively. According to the characteristics of the Pareto optimal front surface obtained, the model in this paper can effectively reflect the characteristics of the RSUD problem. Finally, the experimental results are analyzed, and some suggestions are provided for the selection of the deployment scheme.

Although the verification of a real traffic case shows that this method can provide an effective solution to the RSUD problem in an urban area, there is still a certain gap with the actual application. Due to the irregularity of real roads, RSU deployment at intersections alone cannot achieve full coverage of the entire area of communication. Especially for long lengths of roads, it is necessary to deploy RSUs on both sides of the road, which will increase the difficulty of selecting the deployment location. For the road area without RSU communication coverage, this study estimates the communication delay by calculating the expected data transmission time between vehicles, which is influenced by road vehicle density and average vehicle speed. Moreover, the road vehicle density is randomly generated by a linear relationship; it is difficult to truly reflect the data of actual road vehicle density and average vehicle speed. After obtaining the Pareto optimal solution set of the RSUD problems, engineers can also choose a deployment scheme by themselves despite the three optimization objectives. The multi-objective optimization model in this paper only considers three optimization objectives, and there are still other important optimization objectives. For example, it does not consider the signal attenuation of the RSU data transmission. Therefore, the multi-objective optimization model still has much room for improvement.

To address the multi-objective RSUD problems, the researchers plan to investigate the following aspects. First, it is necessary to find more candidate locations and deployment methods of RSUs by combining various elements such as nodes, ways, and relations in the real road OSM. This will eliminate blind spots of signal coverage when RSUs are deployed on roads in the whole region. Next, the data transmission attenuation and other optimization objectives will potentially be increased to expand the evaluation index in the future. Finally, the configuration and modeling of the vehicle–road cloud-networked system can be studied based on the deployment of RSUs, which can provide support for the research of vehicle–road coordinated control.