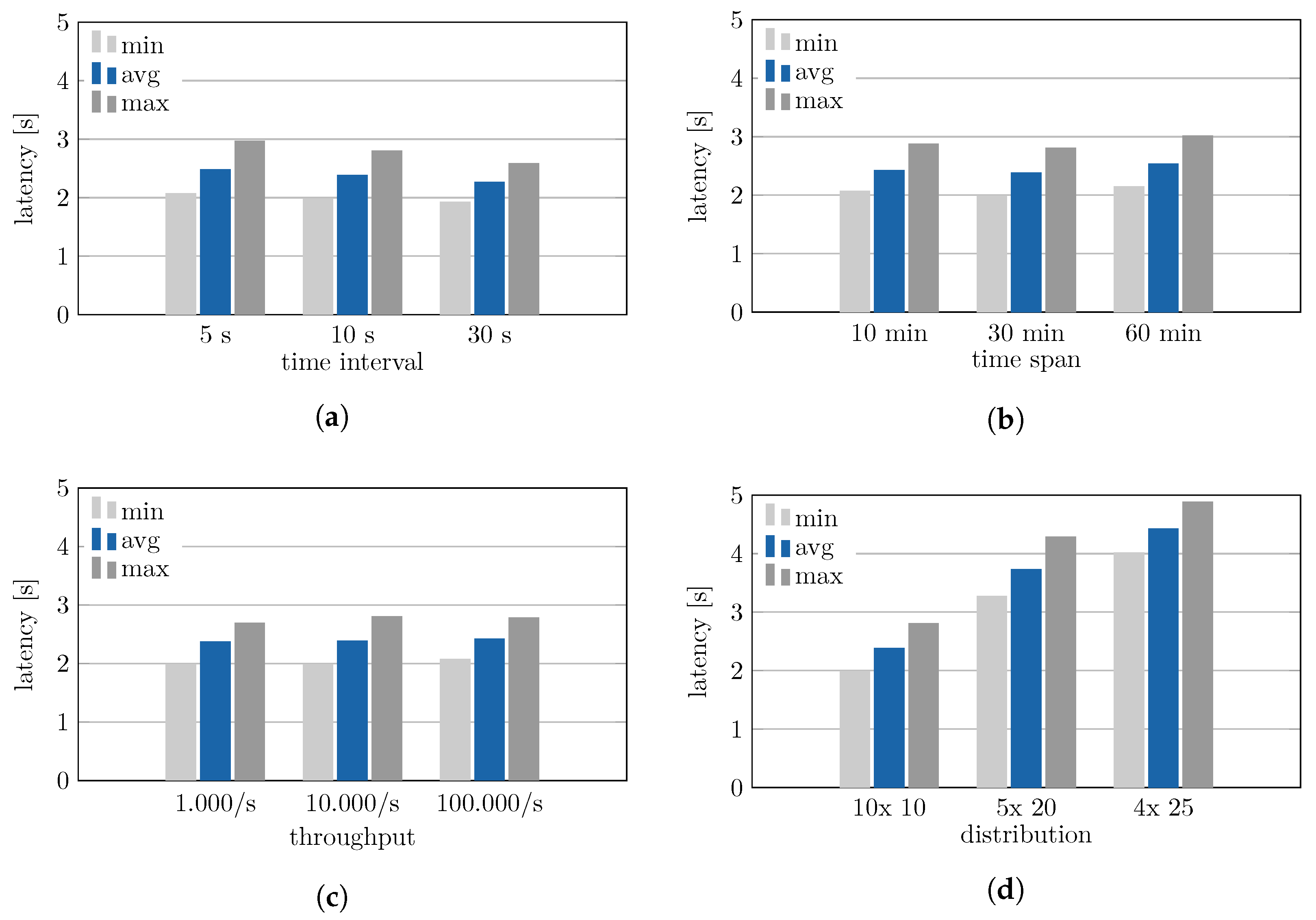Geostatistics on Real-Time Geodata Streams—An Extended Spatiotemporal Moran’s I Index with Distributed Stream Processing Technologies

Abstract

The availability of geodata with high spatial and temporal resolution is increasing steadily. Often, these data are continuously generated by distributed sensor networks and provided as geodata streams. Geostatistical analysis methods, such as spatiotemporal autocorrelation, have thus far been applied primarily to historized data. As such, the advantages of continuous and up-to-date acquisition of geodata have not yet been transferred to the analysis phase. At the same time, open-source frameworks for distributed stream processing have been developed into powerful real-time data processing tools. In this paper a methodology is developed to apply analyses of spatiotemporal autocorrelation directly to geodata streams through a distributed streaming process using open-source software frameworks. For this purpose, we adapt the extended Moran’s I index for continuous and up-to-date computation, then apply it to simulated geospatial data streams of recorded taxi trip data. Various application scenarios for the developed methodology are tested and compared on a distributed computing cluster. The results show that the developed methodology can provide geostatistical analysis results in real time. This research demonstrates how modern datastream processing technologies have the potential to significantly advance the way geostatistical analysis can be performed and used in the future.

1. Introduction

The increasing use of sensor networks for the collection of various traffic and environmental parameters offers tremendous potential for the analysis of current processes in urban areas. Due to these possibilities of distributed data collection in the context of the Internet of Things (IoT), the availability of geodata for such processes in mobility events and in the environment is skyrocketing. Many of these sensor networks provide collected data continuously and instantaneously. Accordingly, the resulting geospatial data streams lend themselves to equally continuous and immediate processing and analysis. Some of these sensor networks also provide data with high spatial and temporal resolution. Due to these continuously available high-resolution geodata streams, the temporal reference of the geodata tuples is of particular importance. This timeliness of available data is often not reflected in retrospective analyses based on historicized data. An analysis procedure based on equally continuous processing would be able to do justice to the timeliness and immediacy of the data collection. Such an application has the potential to bridge the gap between continuous data collection and traditional data analysis. Thus, the potential of additional knowledge gained from continuous data acquisition can be transferred to the analysis phase of the data, allowing for detection of patterns and dependencies within the data in real time. This opens up various possibilities for gaining insights into current real-world processes. In this way, continuous analyses of geodata streams may become a supplement to traditional geospatial analysis methods that use historicized data.

As the amount of high-resolution spatiotemporal data grows, the need for new geostatistical analysis methods is increasing as well. One of the most common geostatistical analysis methods when using spatial data sets is spatial autocorrelation. The availability of both, a spatial and a temporal component in contemporary geodata streams opens up the possibility of conducting investigations regarding spatiotemporal autocorrelation. Spatiotemporal autocorrelation analyzes geospatial data for relationships regarding their relative spatial position with respect to their time of occurrence, allowing for statistical assessment of found patterns. This raises the question of the extent to which these extensive geodata streams can be processed in real time for geostatistical analysis. In particular, the computation of test statistics, which allow the significance of observations to be assessed, conflicts with continuous analysis. Often, the computation of such test statistics requires a large number of repetitions before becoming meaningful. In combination with the large amounts of data in these calculations, a large number of repetitions requires processing resources, which in turn relies on powerful computers. Thus, traditional geostatistical methods are not yet compatible with real-time analysis.

This challenge may be tackled using stream processing. Stream processing is a methodology from computer-aided data processing that is designed to process large amounts of streaming data continuously and efficiently. Modern systems of this type are not limited to trivial computing operations; they are able to perform complex computational processes on data streams as well. For processing large data streams in real time, distributed stream processing (DSP) is a particularly suitable approach. With DSP, the processing of tuples in the data stream is distributed among several computing nodes in a network to facilitate processing in parallel. This concept makes it possible to bundle large resources for a common processing purpose. Ongoing advances in DSP provide the technical prerequisites for elaborate geostatistical analyses with high-resolution geodata streams in real time. In recent years, a variety of open-source frameworks for distributed stream processing have been developed. In this paper, three of these open-source frameworks (Apache Flink, Apache Storm, and Apache Spark Streaming) are compared in order to assess their suitability for implementing real-time spatiotemporal autocorrelation analysis. Subsequently, the most suitable solution (Apache Flink) is used to implement and evaluate such a real-time analysis methodology on a set of New York taxi trip data.

The innovation of this approach is its adaption of an extended spatiotemporal Moran’s I index as a distributed streaming process. This brings with it with multiple novelties in the geostatistical analysis of geodata streams:

• Continuously updated geostatistical analysis as a result of the stream processing pipeline;
• Continuously created test statistics through parallel computation during permutation tests;
• A processing delay on the scale of seconds while processing hundreds of thousands of geospatial events;
• Real-time exploration of spatiotemporal autocorrelation in spatial big data.

In this work, we have developed a methodology for analyzing spatiotemporal autocorrelation in geodata streams using the mechanisms of distributed stream processing. The background and related works regarding the concepts used in this paper are described in Section 2. The essential steps of the presented development are illustrated in Section 3. These include the adaption of the spatiotemporal autocorrelation approach by Gao et al. (2019) as a streaming process, its implementation with open-source frameworks, and the procedure used to evaluate the methodology [1]. The results of this evaluation are covered in Section 4, with our conclusions provided at the end of the paper.

2. Background and Related Work

The application of real-time geostatistics to sensor data streams has been proposed in the literature several times. The study of spatiotemporal autocorrelation in road traffic networks by Cheng et al. (2012) and the study of inner-city air quality using spatiotemporal regression by van Zoest et al. (2020) both suggested that implementation of their geostatistical analysis methods in real-time applications could represent a promising future development [2,3]. A summary of the challenges arising from large real-time sensor data streams and their management along with a discussion of suitable data management technologies was provided by Nittel (2015) [4]; who highlighted the relevance of real-time data analysis technologies such as stream processing in geospatial sensor data handling.

2.1. Spatiotemporal Autocorrelation

In geostatistics, autocorrelation is a proven method for discovering and evaluating dependencies within large datasets, and has been continuously developed over a long period of time. Spatial autocorrelation is used to detect dependencies between events based on their spatial proximity. The most commonly used measure of spatial autocorrelation is Moran’s I, first introduced by Moran (1950) and further developed by Cliff and Ord (1973) [5,6]. In addition to this, Anselin (1995) added local indicators to Moran’s I, which had previously been exclusively global [7]. This development has enabled the use of Moran’s I in the investigation of local influencing factors. Over the course of the last several years, a number of approaches to the investigation of spatiotemporal autocorrelation have been developed. In particular, an extended Moran’s I index was presented by Gao et al. to analyze collective human mobility data [1]. This extended Moran’s I index is designed to handle time series data; it measures the deviation of two time series based on the difference in their accumulative magnitude, then adjusts it using their temporal dissimilarity. This feature is advantageous for use with data streams. A data stream can be considered as a time series that is continuously updated. Thus, extensive modification of the method originally presented by Gao et al. can be avoided [1]. As such, this extended spatiotemporal Moran’s I index is well suited for the adaption as a streaming process, and is the approach used in our work.

$$I^T=\frac{N}{{\sum }_i^N{\sum }_j^N{W}_{ij}}\frac{{\sum }_i^N{\sum }_j^N{W}_{ij}{Z}_i^T{Z}_j^T}{{\sum }_i^N{Z}_i^{T^2}}\mathrm{and}{I}_i^T=\frac{N{Z}_i^T{\sum }_j^N{W}_{ij}{Z}_j^T}{{\sum }_i^N{Z}_i^{T^2}}$$

(1)

Equation (1) shows the global ($I^T$) and local ($I_i^T$) extended Moran’s I indices, where W is the spatial weight matrix, N the number of localities, and $Z_i^T$ and $Z_j^T$ are the deviations from the series of mean values between the time series at locations i and j, respectively. The global extended Moran’s I index indicates the presence of spatiotemporal autocorrelation within the whole dataset. The local indicators estimate the associated impact of individual local values. Depending on the standardization of the weights matrix, the sum of all local indicators $I_i^T$ divided by N is equal to the value of the global indicator $I^T$.

2.2. Stream Processing in the Geospatial IoT

The Internet of Things (IoT) refers to a variety of information-gathering devices that connect to the internet in order to form a larger network. The main characteristics of this concept were summarized by Tao Liu and Dongxin Lu (2012) [8] as follows:

• By using sensors and similar technologies, the relevant operating information of devices can be obtained any time and anywhere;
• Through reliable transmission over a variety of telecommunication networks and internet convergence, it is possible to pass on this information accurately and in real time.
• Through intelligent computing technologies, it is possible to process and analyze the vast amounts of resulting data and information, allowing for intelligent control of the devices of interest.

Sensor networks for recording environmental and mobility data in urban areas should be seen in this context. These sensor networks collect corresponding data in a spatially distributed manner and make it available as geodata streams. Such an exchange of geospatial information in the IoT leads to the concept of a Geospatial IoT. A Geospatial IoT architecture was designed by Herlé (2019) [9]. This work covers principles regarding an infrastructure for the Geospatial IoT and its integration into established geoinformation technologies.

Processing systems based on direct processing of data streams, so-called stream processing, are characterized by the fact that there is no time at which all data are available. Instead, the incoming data in the form of events in the data stream is constantly in motion through the system. In other words, the data are processed continuously, not in individual batches. Stream processing can be seen as a kind of data pipeline in which there is only one possible direction of movement as the data pass through the system, allowing for low processing delays. The basic challenges involved in stream processing of data sourced from IoT contexts have been summarized by Liu et al. (2016) [10]. There have been many studies concerning the streaming of geodata, which is known as geo-streaming. Most of these approaches have focused on the aggregation, filtering, and management of geodata acquired from streaming data sources. Lorkowski and Brinkhoff (2015) presented a system to filter, process, interpolate, monitor, and archive sensor data streams based on kriging [11]. Their developed methodology allowed for timely updating of kriging calculations by recalculation of data from a data grid in only those regions where the variance of the new grid was significantly lower. Hwang et al. (2013) presented a methodology for near real-time aggregation of geo-referenced social media data [12]. The goal of this approach is to provide a pipeline to serve as a data source for spatiotemporal analytical methods. Furthermore, Lee et al. (2011) provided a toolkit for streaming geodata management based on the Open Geospatial Consortium (OGC) GeoSPARQL recommendations and a time-annotated RDF streaming data management service [13]. A study of spatiotemporal data streams in stream processing was presented by Laska et al. (2018) [14]. In this case study, IoT data streams were integrated into open source stream processing tools to implement a state-of-the-art map matching algorithm in a distributed manner. Zhong et al. (2016) developed two strategies for improving the performance of an ordinary kriging interpolator adapted to a stream processing environment [15]. They were able to significantly reduce calculation times when performing interpolation, and suggested real-time spatial interpolation with large streaming datasets as an aim for further investigations.

These developments provide methods to manage and process geodata streams. Support for direct geostatistical analysis of such data as a distributed streaming process in real-time, however, remains absent from the field of geodata stream analysis. Due to the ongoing growth of the geospatial IoT, billions of geo-referenced devices and other sensors and actuators are expected to become connected to the internet, resulting in the creation of spatial big data in the near future [16].

The work presented in the present paper bridges the gap between the availability of real-time spatial big data and its spatiotemporal analysis in a distributed real-time stream processing environment. For this purpose, a scalable, distributed, and high performance analytical method is developed, delivering results with only seconds of latency while including hundreds of thousands of sensor measurements per second. The geostatistical approach in the developed process is represented by an explorative analysis of spatiotemporal autocorrelation based on the extended Moran’s I index introduced above in Section 2.1.

3. Spatiotemporal Autocorrelation in Data Streams

In this section, major challenges concerning the development of a distributed stream processing approach for spatiotemporal autocorrelation are described. These include the adaption of the extended Moran’s I index to the mechanisms of stream processing as well as the selection of values that provide meaningful and comprehensible results with high update frequencies. A comparison of adequate open-source frameworks for the implementation of such an approach is provided as well. Lastly, we present the settings of the conducted evaluation and the computing cluster used for the same.

3.1. Adaption of Extended Moran’s I for Stream Processing

Applying geostatistics on geodata streams in real-time comes with a specific set of challenges.

The first challenge concerns the lack of a beginning or end of the data in a data stream. New data arrive in the processing system constantly. Therefore, these data need to be processed by a temporal system that produces reliable analysis results while allowing for fast calculation in real-time.

The second challenge derives from the way calculations are performed in streaming environments. In stream processing, data tuples are passed from one transformation to the other inside of a data pipeline. It is necessary to derive multiple streaming-ready transformations from the analytical mathematical procedure. These transformations, when chained together, combine to allow for complex calculation of the global and local extended Moran’s I indices and build the desired processing pipeline. The processing of geodata, in particular in geostatistical analysis, demands further consideration of the spatial relations between the data. Certain transformations can be performed for different localities separately, while others need to comprise data from all localities in order to be meaningful.

This leads to the third challenge. Conducting parallel calculations to achieve real-time analysis with respect to the correct inclusion of spatial relations in the data is critical for the geostatistical analysis in real time. To solve this challenge, a definition of tasks that can be performed as parallel processing pipelines is needed. Furthermore, it is necessary to partition the processed data into virtual datastreams within the tasks to allow for parallel calculation of transformations inside the pipelines.

The last major challenge is the effective provision of the results of the geostatistical analysis. For the presented approach using an extended Moran’s I index, a test statistic needs to be produced in order to compare the calculated indices to it. For this test statistic, results from multiple processing pipelines need to be merged. Furthermore, the presentation of spatiotemporal analysis results demands the sophisticated selection and design of the resulting values. Quickly produced and updated results need to be interpretable and comprehensible for humans in order to be valuable. Therefore, it is necessary to present the resulting values in a way that combines the statistical result values with their spatial relations and meaning.

The following subsections address the challenges described above and present the methodology used to solve them.

3.1.1. Limiting Endless Data Streams with Windowing Operations

Data streams generated by sensor networks have neither a beginning nor an end. New and current measured values are constantly generated. However, if there is no defined beginning and end within the scope of a calculation, it is hardly possible to perform complex evaluations. The calculation of geostatistical analyses, on the other hand, requires that multiple non-trivial transformations be performed.

This problem can be addressed by a temporal processing system applied to the data stream. This temporal processing system allows for proper computation of the required data transformations while permitting powerful real-time processing. For this purpose, the data stream is subdivided continuously and broken down into finite sequences of tuples. This subdivision must be small-stepped enough to allow computation to be as continuous as possible while reliably including all the data required for meaningful analysis. In the DSP, limitations of the data stream are applied using windowing operations. In the presented approach, two different kinds of windows are used, namely, tumbling windows and sliding windows. In order to create tumbling windows, elements are placed into non-overlapping windows with a fixed size. In case of sliding windows, the data stream elements are assigned to fixed-size windows that are shifted by a specific slide interval [17].

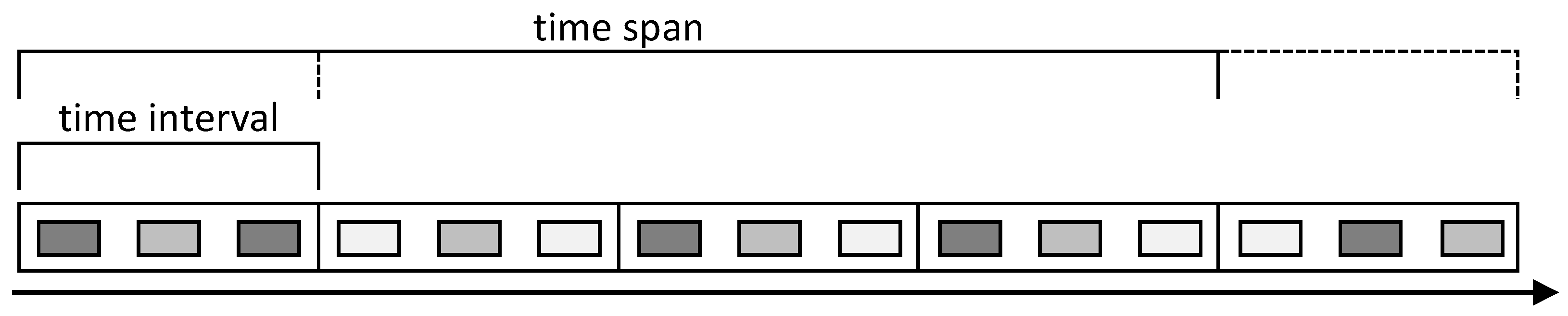
In the context of this work, the subdivision of the data stream to limit the considered data corresponds to the length of the time series considered within the calculation of the extended Moran’s I index. In the following, this length of the time series is referred to as the time span, and is schematically shown in Figure 1. Accordingly, the subdivision of the data stream can be implemented directly in the geostatistical method. As this time period has to be chosen for the analysis anyway, the validity of the geostatistical procedure is not changed at this point by implementation in the DSP.

In addition to the time span, a time interval must be defined. This time interval determines the period of time over which incoming data are summarized. In the context of the extended Moran’s I index, occurring events are accumulated within this time interval. Thus, individual events sum up to frequencies resolved over time. Accordingly, the time interval defines the maximum limit within which the results can be updated in the DSP. The choice of such a time interval has the effect of discretizing the continuously occurring events. Similar to the time interval, this containment is already provided in the geostatistical method, and can be implemented directly in the DSP.

This temporal system is implemented using a combination of tumbling and sliding windows. The summary of the incoming events is performed using tumbling windows with sizes that correspond to the time interval. In turn, these tumbling windows are then combined into a larger sliding window with a length provided by the time span. By using tumbling windows to accumulate and discretize the data, it is ensured that each event is uniquely assigned to a time window. Sliding windows represent the time series formed from the event frequencies. This makes it possible to update the analysis of these time series step by step. Consequently, an analysis result can be produced for each time interval based on the data of a time span. In this way, the analysis can continuously produce temporal highly resolved results by taking into account data from a much longer period of time.

3.1.2. Mathematical Preparation

Complex calculations such as those required for the extended Moran’s I index cannot be readily implemented in DSP. The necessary transformations must be derived from the calculation rules of the global and local extended Moran’s I indices. These calculation rules are decomposed into individual self-contained terms. They are chosen in such a manner that they can be performed as transformations, then the partial results can be passed on to the next operation. During this process, it is determined whether there are any recurring terms and partial results. These can be used several times during processing to reduce the computational effort.

When comparing the calculation estimates for the global and the local extended Moran’s I indices in Equation (1), it is noticeable that they are composed of the same partial results. These are the deviations $Z_i^T$ and $Z_j^T$ of the time series at the localities i and j from the time series of the mean values, the number of localities N, and the weighting factors in the matrix $W_{ij}$. 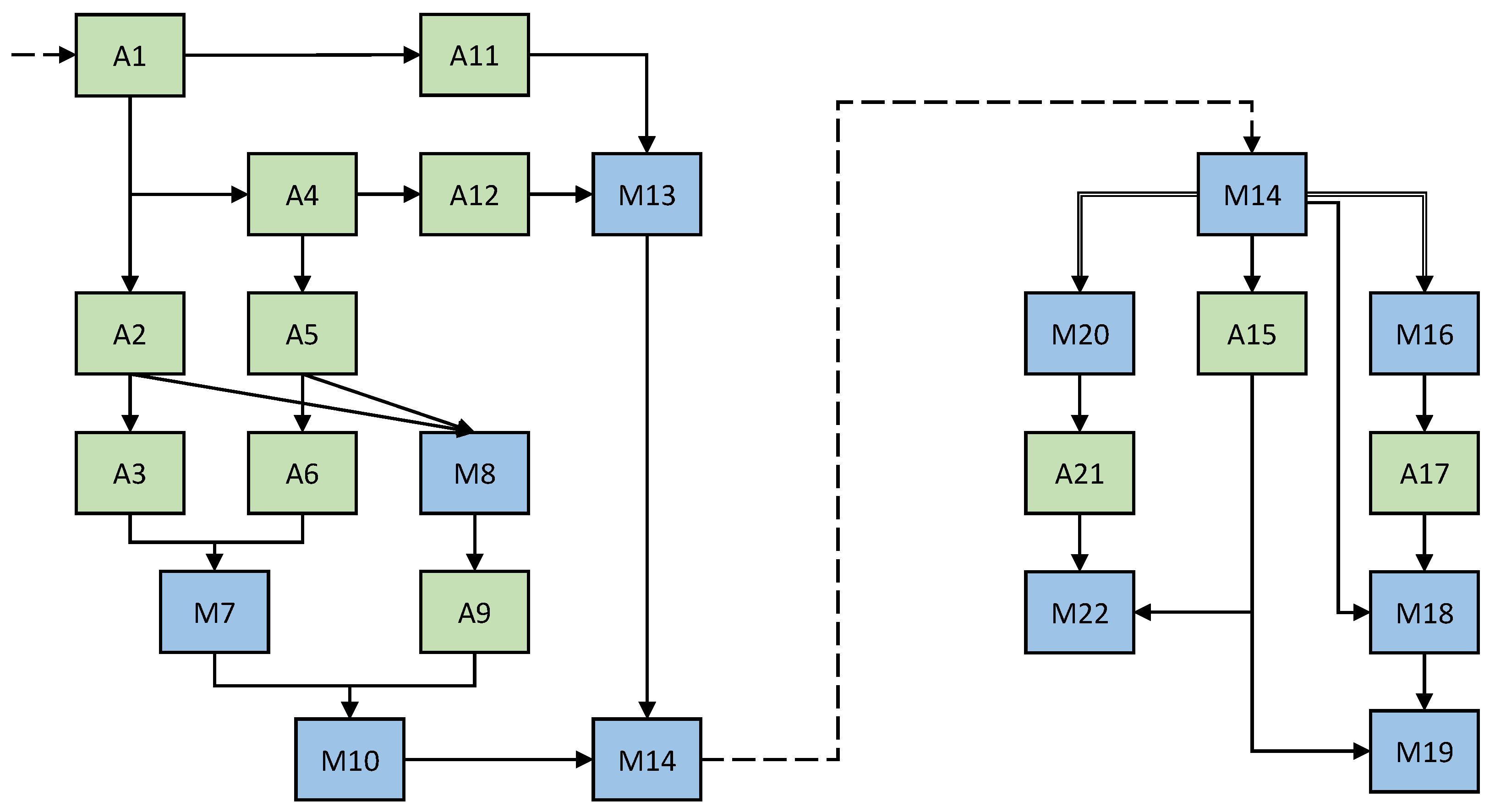The factors N and $W_{ij}$ are constant, and only the deviations $Z_i^T$ and $Z_j^T$ have to be determined. Consequently, it is advisable to calculate these partial results and afterwards perform further transformations separately for the local and global Moran’s I indices. In the context of the DSP, the data streams with time series deviations are duplicated, and continue henceforth in two detached processing pipelines. This principle is illustrated in Figure 2. It can be seen that the M14 transformation is duplicated downstream in order to compute two different results.

According to the principles explained above, the entire calculation rule can be broken down into a total of 22 individual transformations. These can be found in

Table 1. Detailed description of transformations.

Name	Input	Operation	Output
A1		Aggregation of events per locality and time interval	R1
A2	R1	Difference of two consecutive values per locality and time interval	R2
A3	R2	Sum of squared values over the time span per locality and time interval	R3
A4	R1	Mean value from values of all localities per time interval	R4
A5	R4	Difference of two consecutive values of all localities per time interval	R5
A6	R5	Sum of squared values of all localities over the time span per time interval	R6
M7	R3, R6	Product of the square roots of the values per locality and time interval	R7
M8	R2, R5	Product of the values per locality and time interval	R8
A9	R8	Sum over the time span per locality and time interval	R9
M10	R7, R9	Quotient of the values per locality and time interval	R10
A11	R1	Sum over the time span per locality and time interval	R11
A12	R4	Sum of the values of all localities over the time span per time interval	R12
M13	R11, R12	Product of values per locality and time interval	R13
M14	R10, R13	Application of the tuning function and product of the values per locality and time interval	R14
A15	R14	Sum of squared values of all localities over the time span per time interval	R15
M16	R14, R14	Product of value and weighting factor per locality and time interval	R16
A17	R16	Product of values per locality and time interval	R17
M18	R14, R17	Product of values and factor per locality and time interval	R18
M19	R15, R18	Quotient of values per locality and time interval	R19
M20	R14, R14	Product of values for all combinations and weighting factor per locality and time interval	R20
A21	R20	Sum of values of all localities per time interval	R21
M22	R15, R21	Quotient of the values of all localities per time interval	R22

. The corresponding partial results, which are passed on between the transformations, are denoted with R*. Transformations that process only one input from their upstream transformation are named A* and illustrated in green, while transformations that rely on multiple partial results are named M* and illustrated in blue. In the descriptions of the transformations in Table 1, the addition per locality indicates that a separate partial result is produced for each locality i. The addition per time interval indicates that a current partial result is produced for each time interval.

3.1.3. Parallel Computing and Data Partitioning

In modern stream processing systems, multiple logical data streams are processed in parallel. The individual logical data streams are distributed among several computing units. This type of parallel processing is called data parallelism. The processed data are partitioned and the partitions are each processed individually. The use of data parallelism is particularly useful when processing large amounts of data [17]. This differs from so-called task parallelism, in which multiple tasks are executed in parallel. These tasks can be performed on the same or different data. With the help of task parallelism, computing resources can be used more efficiently [17]. For real-time analysis, these principles of parallelism must be incorporated into the computation of the extended Moran’s I index.

For this purpose, we consider which tasks can be differentiated in the analysis procedure. The achievable task parallelism is derived from these tasks. The tasks are chosen in such a way that they can be performed in a self-contained manner and do not depend on the exchange of data with other tasks during processing. This does not include the transfer of results to subsequent tasks. Individual tasks that process results of preceding tasks can be performed in parallel. This is possible because continuous data streams are being processed, meaning that there are always new results to be processed on an ongoing basis. The tasks into which the analysis procedure can be divided are listed in

Table 2. Chosen tasks for task parallelism.

Task	Quantity
Calculation of the global and local extended Moran’s I indices for the observed data set	1
Calculation of the global and local extended Moran’s I indices for a permuted data set	n
Preparation of the data for the Moran scatterplot and the calculation of the linear regression	1
Preparation of the data from the permutation tests for the histogram and calculation of the pseudo-p-value	1
Comparison of the check values	1

. These five tasks can be performed in parallel. It should be noted that computation of the extended Moran’s I indices of a permuted dataset occurs multiple times. Thus, this task exists for as many times as there are permutations of the dataset. Consequently, with a number of permutations n there are $n+4$ tasks that can be performed in parallel.

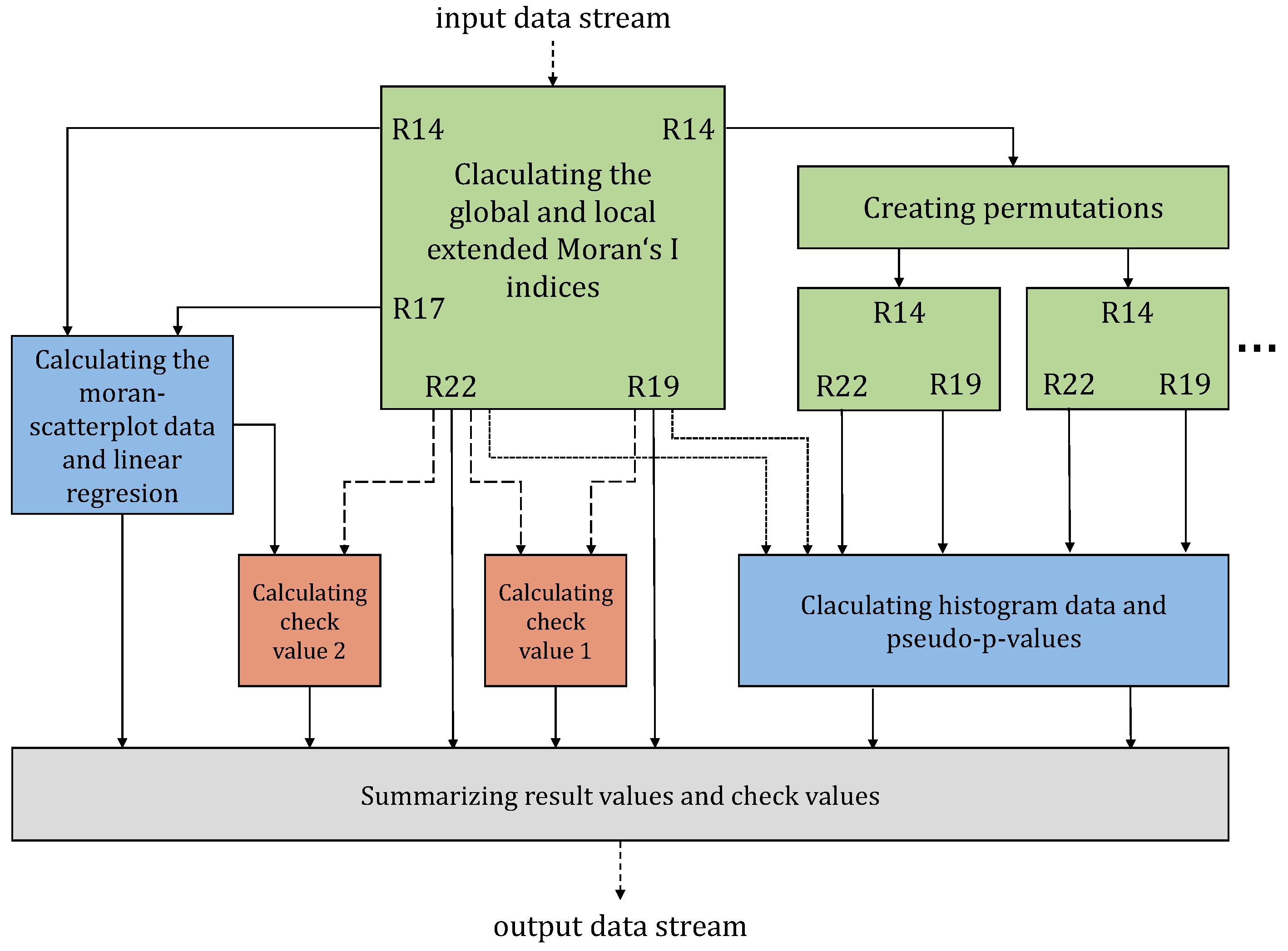
The arrangement of tasks within the overall process is illustrated in Figure 3. The calculation of the extended Moran’s I indices for the analysis of spatiotemporal autocorrelation is performed according to the methodology in Section 3.1.2. The calculated coefficients are output as result values and passed on as intermediate results for calculation of the check values (see Section 3.1.4). In parallel with computation of the coefficients from the incoming data stream, permutation tests are performed for the global and local extended Moran’s I indices. For this purpose, the deviations of the time series from the time series of means $Z_i^T$ are spatially permuted and the extended Moran’s I indices are calculated for each permutation. These deviations correspond to the intermediate results R14 from the single operation M14 (see Table 1). Complete recalculation of the time series data is not necessary, as an exclusively spatial rearrangement takes place. The temporal trend of the observed events is not changed. Recalculating the variances using the spatially permuted data would result in the same results, with only the assigned localities being different.

Consequently, the single operations A1 to M14 can be omitted. It is sufficient to spatially rearrange the intermediate results R14, then perform the individual operations A15 to M22 for each permutation. Subsequently, the calculated global indices can summarized and a histogram generated from them (see Section 3.1.4). In addition, pseudo-p values (see Section 3.1.4) can be calculated for all local and global indices from the permutations.

In addition to the described task parallelism, data parallelism within the individual tasks is examined as well. The achievable parallelism results from the intended transformations within each task. Unless all incoming data are considered in their entirety, it is not possible to prepare the data for generation of the Moran scatterplot or calculation of the linear regression, perform permutation tests for the histogram, calculate of the pseudo-p-values, or compare the check values. For this reason, data parallelism is not applicable for these tasks. When calculating the global and local extended Moran’s I indices for the observed dataset, however, such data parallelism is indeed applicable. For this purpose, the data are partitioned within the data stream. When a data stream is partitioned, it is divided into several logical data streams which can then be processed in parallel. In the case of the time series data used here, every tuple is assigned to a locality. The locality is represented as the ID of the district the tuple was produced in, and data partitioning is performed based on that locality. Consequently, the data are partitioned according to their locality, and the corresponding transformation is performed separately and in parallel for each locality. However, such partitioning is not possible for all transformations. Certain transformations produce partial results considering the entire set of localities. For these transformations, the partitioned data are merged again and processed in their entirety. Thus, these transformations cannot be performed in parallel in the form of multiple logical data streams. Accordingly, data parallelism is not an option for transformations A4, A5, A6, A12, A15, A21, or A22. For the transformations A1, A2, A3, M7, M8, A9, M10, A11, M13, M14, M16, A17, M18, M19, and M20, however, partitioning can be provided according to the respective localities. This applies in the same way to calculation of the global and the local extended Moran coefficients of a permuted dataset, which follows the same calculation procedure without performing the single operations A1 to M14. Transformations M16 and M20 introduce the spatial relations into the calculation process, and connect data from neighboring localities for further processing by accessing a spatial weights matrix.

3.1.4. Effective Provision of Results

The results of the analysis should be summarized in the form of meaningful values. Two categories of values can be distinguished: result values, which represent the geostatistical statements, and check values, which allow for assessing the reliability with which the processing is progressing. The result values for the geostatistical analysis include the global and local extended Moran’s I indices, a summary of the permutation tests, and a Moran scatterplot. In parallel with the calculation of the extended Moran’s I indices, permutation tests are performed to assess their statistical significance. Subsequently, the results of the permutation tests are summarized in a histogram. In addition, a pseudo-p value is calculated for the global and each local index based on these results. Such a pseudo-p-value indicates how often an equal or more extreme value for the corresponding coefficient occurred in the permutation tests. In the permutation tests, the observed events are permuted in spatial terms. Thus, while the existing time series data are spatially redistributed, the time series themselves are not changed. For this purpose, each time series is randomly assigned one of the existing localities. This results in a dataset that is identical to the original dataset in terms of temporal behavior and event occurrence, and where only the spatial relationships have been permuted. In this way, it is possible to examine the temporal course of the occurring events for the presence of spatial correlations. In addition to the extended Moran’s I index and the histogram, a Moran scatterplot is created. The Moran scatterplot is a tool for visualizing and identifying the degree of spatial instability in a spatial association by means of Moran’s I [18]. It provides a graphical and quickly comprehensible way to display the manner of the present autocorrelation.

Furthermore, we define two check values ${\mathsf{\Psi }}_1$ and ${\mathsf{\Psi }}_2$ to assess the reliability of the continuous calculation processes. These check values verify whether the different result values are mathematically plausible among each other. For this purpose, mathematical dependencies between the result values are utilized. The first of these check values (${\mathsf{\Psi }}_1$) results from the relationship between the global and the local Moran’s I indices. Bearing in mind the chosen spatial weights, the values of the global Moran’s I index equals the sum of the local indices divided by the number of localities. The second check value (${\mathsf{\Psi }}_2$) is derived from the regression line of the Moran scatterplot. The slope in this regression provides a legitimate estimate of the Moran’s I [18]. Consequently, this second check value observes the difference between the slope of the regression line and the global extended Moran’s I index.

3.2. Implementation with Open-Source Frameworks

The number of complex and powerful software solutions available as open-source software is constantly increasing. In particular, a variety of promising open-source software applications are available in the area of distributed data processing and distributed stream processing. Several of these have been developed with a range of high-performance functions, meaning that implementation of geostatistical analyses in real time can be carried out directly within geodata streams.

The presented methodology requires two types of software solutions for its application. First, a so-called distributed stream processing framework (DSPF) is required to implement the simultaneously continuous and distributed computation of the geodata streams. A DSPF is a software solution that provides the necessary functions for transforming and partitioning data streams. A distributed messaging system (DMS) is required to implement the data transfer between distributed computations. Such a DMS provides functions that ensure successful communication between the individual components of the analysis procedure.

Several requirements must be met, both for the implementation of the analysis procedure itself and for data transfer between the individual subtasks. To implement the presented methodology, the DSPF needs to provide the ability to define tumbling and sliding time windows and to execute nontrivial transformations while ensuring low latency and high data throughput. Furthermore, the realization of a meaningful and reliable analysis requires the ability to process incoming data based on their event time while handling late data in a reasonable fashion, to guarantee data safety on a high level, to build up backpressure in order to prevent data loss in case of load peaks, and to scale out the analysis process horizontally. The DMS should implement an architecture based on the publish–subscribe model to allow for flexible integration of the various analysis tasks, the ability to keep the incoming data (messages) in order, and to guarantee a high level data safety. Low latency and high data throughput are crucial aspects for both this software element and for the DSPF.

In order to select the most suitable DSPF with respect to our requirements, we compared the open source frameworks Apache Flink (available online: https://flink.apache.org, accessed on 14 September 2022), Apache Storm (available online: https://storm.apache.org, accessed on 14 September 2022), and Apache Spark Streaming (available online: https://spark.apache.org/streaming, accessed on 14 September 2022). These are currently the most popular DSPFs, which is due in part to their fault-tolerant architecture and support for scalability in stream processing [19]. All three software solutions are based on the so-called manager–worker architecture, and allow horizontal process scaling. A comparison of the respective features and capabilities of these frameworks can be found in

Table 3. Comparison of the considered open-source DSPFs.

		Apache Flink	Apache Storm	Apache Spark Streaming
	Organization 4	manager-worker	manager-worker	manager-worker
	Parallelism 4	yes	yes	yes
	Scalability	horizontal	horizontal	horizontal
Processing		+	+	−
	Processing model 1	tuple-at-a-time	tuple-at-a-time	micro-batching
Window operations		+	−	+
	Window types	tumbling, sliding	tumbling, sliding	tumbling, sliding
	Event time	yes	no	yes
Complex transformations		+	−	+
	Statefulness 3	yes	no	yes
	Non-trivial	yes	yes	yes
Reliability		+	−	+
	Guarantee 2	exactly-once	at-least-once	exactly-once
	Failure mechanism 2	check-pointing	upstream backup *	parallel recovery **
Dynamic data streams		+	−	−
	Backpressure	yes	yes	yes
	Late data handling	yes	no	no
Performance		+	−	−
	Latency 1	very low	very low	high
	Throughput 1	high	low	high

¹ [20]. ² [21]. ³ [19]. ⁴ [10]. * by using Trident. ** by using DStreams. Rating of the suitability for this application: suitable (+)/unsuitable (−).

.

While Apache Storm and Apache Spark Streaming lack required data handling features and performance, Apache Flink fulfills all requirements. Therefore, it is the most suitable for implementing the analysis procedure.

For use as a DMS, the open source software solutions Apache Kafka (available online: https://kafka.apache.org, accessed on 14 September 2022), RabbitMQ (available online: https://www.rabbitmq.com, accessed on 14 September 2022), and NATS Streaming (available online: https://nats.io, accessed on 14 September 2022) were considered. These systems correspond to a distributed architecture and support the publish–subscribe model.

Table 4. Comparison of the considered open-source DMS options.

		Apache Kafka	RabbitMQ	NATS Streaming
Data transfer model		+	+	+
	Publish/subscribe 1	yes	yes	yes
Reliability		+	−	−
	Guarantee 1	exactly-once	at-least-once	at-least-once
	Message ordering 1	yes	yes	yes
Performance		+	−	−
	Latency 1	low	low/medium	high
	Throughput 1	high	medium/high	high

¹ [22]. Rating of the suitability for this application: suitable (+)/unsuitable (−).

shows the capabilities of these three systems. Based on this comparison, the software solution Apache Kafka was selected for the implementation.

For implementation of the procedure for processing the extended Moran’s I index into the DSPF, the Apache Flink DataStream API was used. This DataStream API provides several interfaces which can be used to implement transformations. Afterwards, these transformations can be chained together into processing pipelines. To pass the data through this pipeline and the included transformations, special data tuples were defined and implemented as data classes. The UML class diagram shown in Figure 4 describes the four defined tuples.

The event tuple is used to carry the original data streaming into the processing procedure. It holds the event time of a beginning or ending taxi trip and the location ID of the corresponding district. A detailed description of the taxi trip data we used is provided in Section 3.3. The tuples LocalValue, GlobalValue, and CrossValue contain intermediate results from the transformations. For this purpose, they store a value and the start and end of the corresponding time window. GlobalValues are output by transformations that process data from all localities, while LocalValues instead store additionally a locality and are used in transformations that produce results for different localities separately. The CrossValue tuple is needed for intermediate results derived from data from two neighboring localities.

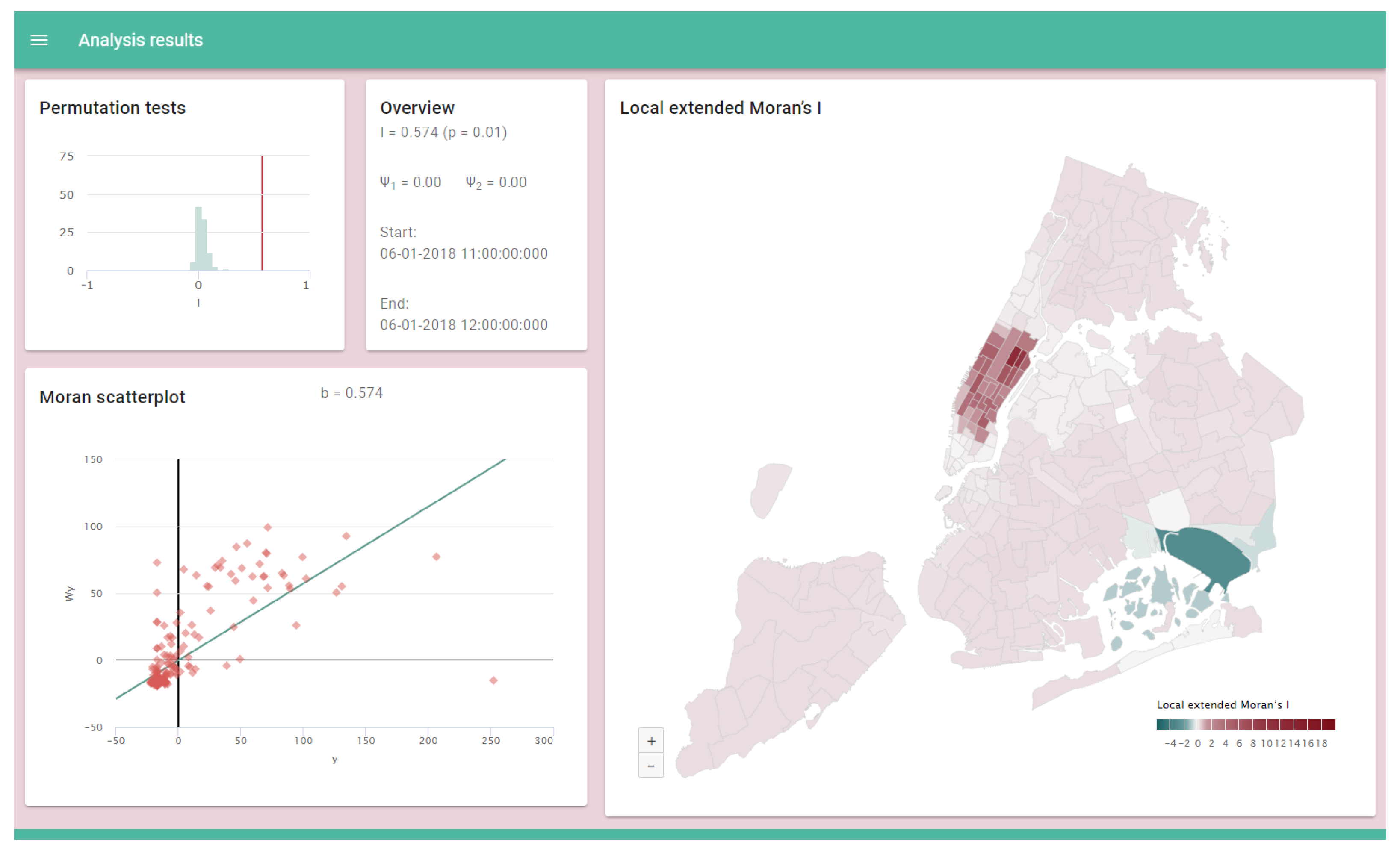
Furthermore, we implemented a dashboard for dynamic display of the analysis results in real time. The dashboard displays and continuously updates the results and check values of the spatiotemporal autocorrelation analysis. It is designed as a web application using the open source javascript framework Nuxt.js (available online: https://nuxtjs.org, accessed on 14 September 2022). The produced analysis results are pushed to the web application via web sockets. Thus, the dashboard can provide results with wide coverage and low delay over computer networks such as the internet. As envisioned, the Moran scatterplot along with the distribution of permutation tests and local extended Moran’s I indices are presented in the form of dynamic and interactive diagrams and maps. These graphics were implemented using the Highcharts software library (available online: https://www.highcharts.com, accessed on 14 September 2022). The structure of the dashboard is shown in Figure 5.

Such an up-to-date visual representation by dynamic diagrams and maps allows for fast and comprehensive understanding of the analysis results. This is particularly advantageous for the presentation of results that change rapidly over time. Figure 6 highlights the importance of such dynamic visualization by comparing four result sets with a time distance of 15 min. Even though the dashboard is capable of an update rate in the range of seconds, the time distance of 15 min was chosen to illustrate the changing display in an easily comprehensible manner.

3.3. Evaluation and Test Data Simulation

Our evaluation of data processing examined the technical influencing factors and limitations of the process, with the processing latency being of particular interest. A series of test runs with different configurations were conducted while varying both methodological and technical aspects of the configuration. In this way, influences from the configuration of the method and from technical boundary conditions were compared with each other. Based on the results, it is possible to assess the effects of the different configurations on the processing latency.

The TLC Trip Record Data [23] dataset was used for evaluation. This dataset contains data tuples on taxi trips recorded in New York City. Each tuple covers origin and destination locations as well as trip start and end times for each taxi trip. In addition, distance traveled, billing data, and number of passengers are available. However, only the origin and destination locations and the start and end times of the trips are of interest in this paper.

In methodological terms, the parameters of the temporal configuration (the time interval and the time span) are varied. The extent to which the processing latency is affected by different time intervals (the step size at which the results are updated) is of substantial interest as well. Another point of interest is whether the time interval may be too small to be executed reliably. Different time spans deliver insights into the way processing latency is affected by the consideration of large amounts of data from long time periods. In technical terms, the number of computing nodes used, available RAM of the corresponding computing nodes, and data throughput were all investigated. The number of computing nodes limits the possible parallelism, and it is of interest to see how distributing the tasks to a larger or smaller number of computing nodes affects the processing latency. Likewise, different amounts of available working memory were tested and the data throughput was varied. For this purpose, data streams containing different numbers of events per second were simulated and streamed into the calculation procedure. Within the scope of this simulation, the recorded events were replayed in their original order with increased speed and constant spacing. The time of occurrence of the original events was replaced with the current time of their replay. In this way, constant data streams could be simulated, which is suitable for processing based on event time.

In order to determine the processing latency as well as the data throughput, the definitions from Karimov et al. (2018) were used to define corresponding metrics for these parameters [24]. Within the conducted test runs, the event time delay could be determined because simulated data streams were used for the performance tests. Thus, the interval between the actual occurrence of an event and the output from the processing system could be determined either. For this reason, only the processing time delay occurring during processing was considered. In addition, we defined how the processing time latency was determined when windowing operations were used in the following manner:

• Processing Time of Window Operations: the processing time of events that have been combined into a time window is the maximum processing time of all events that have contributed to that time window.

This definition was applied accordingly when determining the processing time latency. Data throughput was defined as the number of events processed by the processing system within a given time period.

The performance tests were conducted on a distributed computing cluster. The cluster comprised a total of twelve computing nodes in two different configurations. One of these nodes was particularly powerful, and is referred to as the manager in the following. The other eleven nodes are referred to as workers. The configurations of the computing nodes are provided in

Table 5. Configuration of the computing nodes.

	Manager	Worker
CPU	1× Intel Xeon 4215 (2.5 GHz)	1× Intel Xeon 4215 (2.5 GHz)
RAM	8 GB	2 GB (4 GB)
Network	1000 MBit/s	1000 MBit/s

.

4. Results and Discussion

In the evaluation, fourteen performance tests were conducted. The performance tests ran for a duration of one hour each plus the duration of the time span. In this way, the ramp-up time required to accumulate the data in the system for the first computational step over a complete time series was taken into account. In each performance test, 100 permutation tests were run in parallel and the processing latencies were measured for each. Instead of 99 tests, as typically expected, 100 tests were run, as this number could be evenly distributed among the available computational nodes. In this way, the same workload was ensured on all computational nodes, ensuring comparable results for all of the permutation tests. While varying specific parameters, all other parameters were fixed to default values. These fixed values were defined as ten seconds for the time interval, 30 min for the time span, 10,000 events per second for the throughput, and a distribution of ten permutations per worker node. In the results presented below, the latencies of all time steps over the runtime of one hour of all parallel permutation tests are taken into account. According to the definition of processing latency in the context of windowing operations, the highest value is determined for each time step. These maximum values are subsequently used for further evaluation. The results are shown in Figure 7. Each performance test contains the arithmetic mean along with the minimum and maximum of the measured latencies.

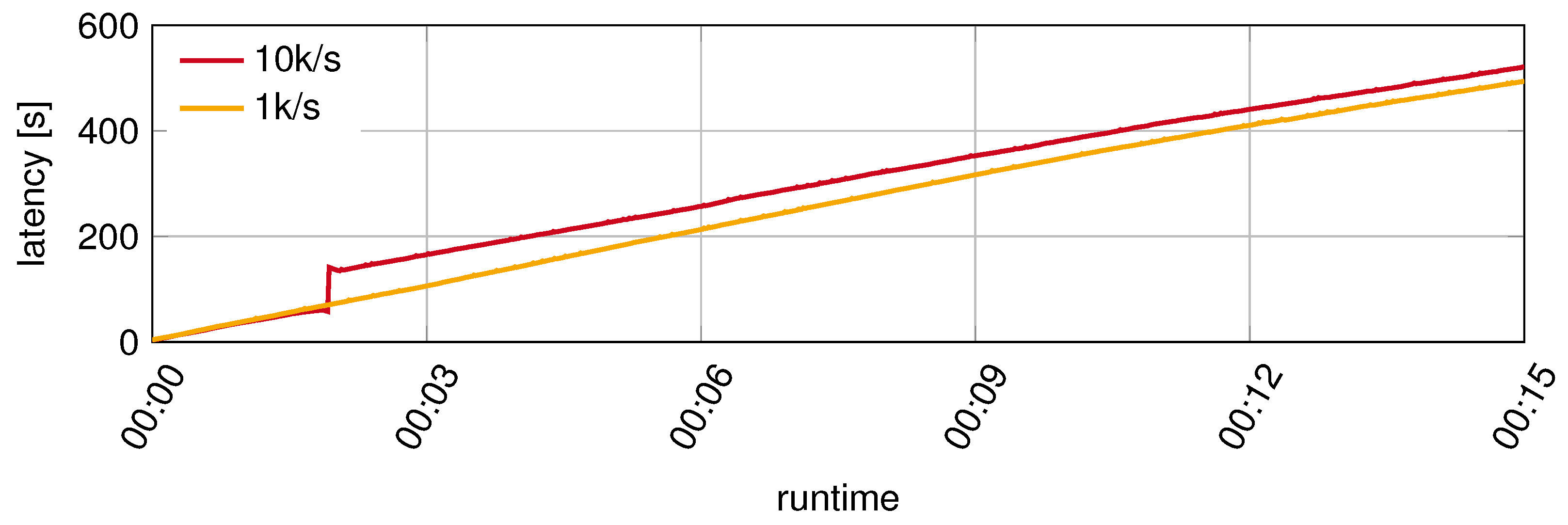
The results show an increase in latency for decreasing time intervals. However, the average latency remains between two and three seconds in all three test runs. The minimum and maximum values lie within a narrow range around the mean value. Consequently, a latency between two and three seconds was measured for the entire runtime. Based on this, two further tests were conducted with a time interval of one second and a data throughput of 1000 and 10,000 events per second. In both cases, stable processing latencies could not be achieved. The results in Figure 8 show the progression of latency over a runtime of 15 min. In both tests, the processing latency increased steadily. This means that the system cannot cope with the input frequency, leading to failure after a certain amount of time.

The results for the different time spans show little difference in processing latency (see Figure 7, diagram b); no significant influence of the time span can be detected. Moreover, no significant difference can be seen in the results for the varied throughput. This can be explained by the fact that in the first single operation the incoming data stream is aggregated into time windows, which are then subjected to further processing. Consequently, a very large amount of incoming data can be processed with little latency. The maximum amount of incoming data that can be processed at this point could not be determined during the performance tests. It was found that the technical performance of the manager node limited the distributed messaging system to a maximum data throughput of 240,000 events per second in the incoming data stream. Again, no increase in processing latency was observed for this data throughput.

The influence of task distribution was investigated by distributing the one hundred permutation tests among the computing nodes in three different configurations. The results in Figure 7 (diagram d) show a significant increase in processing latency when a higher number of permutation tests are run on one node. Clearly, the distribution of the computational tasks has a significant impact on data processing performance.

In addition to these investigations, the influence of the available working memory of the computing nodes was measured. For this purpose, the three setups of the permutation tests from the previous evaluation were repeated on computing nodes with 4 GB of RAM instead of 2 GB. The results are shown in Figure 9. In order to obtain another comparative value, a setup with ten computing nodes and five permutation tests each was tested as well. However, in this configuration only 50 tests could be run in parallel. The latencies from all of the separate calculation are shown using the original data. It can be seen that a larger amount of available memory can reduce the processing latency, and that this effect is stronger as the workload of each computing node increases.

The results of the performance tests show that processing latencies of a few seconds can be achieved. Thus in principle, applying the method for analyses of geodata streams in real-time is possible. It is crucial that adequately short time intervals can be used. Nevertheless, the performance tests carried out with a time interval of one second revealed a limit on the possible update rate of the results. This behavior is expected, as the time interval is shorter than the processing latency itself. Especially important for practical applications is the stability of the achieved delays. The minimum and especially the maximum processing latencies are within a time range of less than one second from the mean. Consequently, no significant fluctuations in data processing occurred over the runtime of the performance tests, meaning that an application of the method with a very short time interval for updating the analysis results can be realized reliably. When using these very short time intervals, much larger time spans can be selected at the same time. Increasing the time spans has little effect on the latencies measured in the performance tests. Therefore, it is possible to consider long time series in the calculation of the spatiotemporal autocorrelation and to update the analysis results regularly within a few seconds. Moreover, the amount of incoming data in the analysis procedure has little effect on the processing latency. As a result, significant amounts of data can be processed reliably and in real time. Even in the event of large fluctuations in the data streams, increased latency or disruption of the calculation process is not expected.

The most significant impact on processing latency is found in the distribution of permutation tests among the available computing nodes. This strong influence on performance clearly shows the suitability of the DSP for such an analysis in real-time. The required permutation tests can be arbitrarily distributed to additional computing nodes. Accordingly, the processing latency can be reduced. Likewise, it is possible to increase the number of permutation tests without negatively affecting the processing latency. Thus, the developed method can be scaled for different applications in a flexible way.

Repeating the performance tests with twice the amount of available memory shows that processing latency can be reduced in this way as well. The reduction achieved is more pronounced with lower task parallelism. Thus, adjusting the amount of available memory can be a remedy for excessive processing latency when low parallelism is used. However, the influence due to a larger number of computing nodes is much stronger. Computer nodes with one processor core each were used to perform the performance tests. Thus, the number of computer nodes used corresponds to the number of processor cores used. It is noticeable that doubling the processor cores resulted in a significantly greater reduction in processing latency than doubling the main memory. This implies that the achieved performance is primarily limited by the available processor cores. This observation is important for scaling the analysis procedure in the context of practical applications. As such, the increase in parallelism should be considered preferentially with the planning of the computer capacities. However, it should be noted that our investigation of the results of changing the number of processor cores only examined horizontal scaling, as vertical scaling with an increase in the computing power of the respective processor cores could not be performed.

Overall, our evaluation of the data processing performance shows that the developed methodology is feasible for continuous analysis of geospatial data streams for spatiotemporal autocorrelation using DSP. Both the distributed computation and the continuous processing of the data enabled by the DSP are appropriate concepts for implementing this analysis procedure. The chosen temporal configuration of the method influences the technical performance only to a very small extent. For this reason, it is not necessary to counterbalance aspects such as the amount and timeliness of the data or the desired processing latency. Thus, the temporal configuration of the analysis mostly does not have to take into account the technical conditions, and can be determined specifically for the methodological requirements. If a sufficiently powerful computing cluster is available, very low processing latencies can be reliably achieved.

In addition to the capabilities and added value, the limitations of the implemented methodology can be identified. The application of geostatistical analysis techniques such as spatiotemporal autocorrelation requires a sufficiently large amount of data to provide robust results. This type of analysis requires a critical mass of data tuples. This is needed to ensure the statistical effects on which the analyses are based. For this reason, our methodology is bound by these limitations. An application is only possible for data streams that provide a sufficiently large amount of measured values. In particular, the dynamic consideration of current processes limits the amount of data that can be included in the analysis. Preprocessing methods such as aggregation of the measured data over long periods of time, as in batch analysis of historized data, cannot be performed on data streams. Thus, a data source that collects and provides measured values with high spatial and temporal resolution is necessary to meet these requirements. For this reason, an application of the developed methodology is particularly reasonable in the context of extensive distributed sensor networks. Continuous collection of mobility and environmental data in urban areas can meet these requirements. This problem was identified during the evaluation. The dataset we used, consisting of data on started and ended taxi trips, could only be used in a limited form for evaluation of the achievable performance. Accordingly, and as stated earlier, the evaluation was performed with simulated data streams. This allowed for a sufficient amount of events to be introduced into the processing pipelines, making it possible to investigate the limitations of the system.

Another limitation of the developed methodology arises from the required performance of the computing cluster. Complex calculations, such as those performed to determine the extended Moran’s I index, require several costly transformations to be implemented in the DSP. In addition to this, a large number of these calculations are required as part of the permutation tests, which need to be calculated simultaneously. In the evaluation of the developed methodology, 100 of these permutations were calculated, respectively. However, larger numbers in the range of 1000 or 10,000 of these permutation tests are often used to provide an even more reliable statistical estimate. For simultaneously fast application of this methodology with a larger number of parallel permutation tests, an equally larger computing cluster is required.

Beyond these limiting factors, possible sources of error with respect to the analysis results of the developed methodology are considered as well. As described, dynamic data streams may contain late data. These late data can be taken into account in the calculations if an appropriate waiting time is specified. However, while such delayed data are often present in the incoming data stream, they can arise within the processing pipeline as well. Following the parallel execution of the permutation tests, their results are merged and pseudo-p values are calculated from them. This merging of results is implemented by forming time windows. If the results of individual permutation tests arrive late, not all tests are included in this calculation of the pseudo-p values. This problem must be met by selecting an appropriate waiting time. In doing so, a trade-off must be done between a high waiting time, which entails either a high degree of certainty that all data will be acquired, or a low waiting time, which allows a lower processing latency. Thus, speeding up processing in this case may result in a decrease in the reliability of the analysis results. A delay of individual intermediate results within the overall process is expected, especially in case of a low task parallelism. The more permutation tests are executed on one computing node, the larger the processing latency. Consequently, the time interval between the output of the results of the individual permutation tests increases, as the corresponding computation tasks within a computer node cannot take place in parallel. This increases the probability of individual results arriving late for merging. This problem can only be addressed by a longer waiting time or greater parallelism, meaning a larger computing cluster.

5. Conclusions

In this work, a method for the analysis of spatiotemporal autocorrelation in geodata streams using open source distributed stream processing technology was successfully developed and applied. It was found that modern data processing technologies such as the DSP represent a significant advance in the way geostatistical analyses can be performed and used in the future.

The ability to perform geostatistical analysis in real time is associated with the existing approach to collecting mobility and environmental data through powerful sensor networks in urban areas. Thus, indicators for spatiotemporal autocorrelation as well as associated test statistics are available within only a few seconds. This opens up new applications for geostatistical analysis methods. The extended Moran’s I index by Gao et al. (2019) used here is not the only method in this area [1]; a variety of other methods for spatiotemporal autocorrelation exist as wwll. In addition, there are many other geostatistical analysis methods. For a number of of these procedures, adaptation for data streams using DSP may be an option. The proposals in the literature for performing geostatistical methods in real time and the associated application possibilities can find confirmation in the results of this work.

Beyond this, it can be noted that the temporal configuration of the analysis procedure used in this work, that is, with a time interval and a time span, has a notable characteristic. The time interval is a parameter which defines two different aspects of the analysis procedure. On the one hand, it defines the interval over which the incoming data are aggregated and further processed. Thus, the time interval defines a methodological aspect which directly affects the analysis results. On the other hand, the use of windowing operations to calculate the analysis results over the time interval defines the interval for updating the results. Accordingly, a technical aspect of the analysis is influenced by this. An advanced development of the presented methodology in which these two parameters are decoupled can further improve applicability.

By providing analysis results in real time, they can be used in real-time decision-making processes for the initiation of managing measures. By developing this, the application of geostatistical methods can evolve from passive data analysis to active management of events. In particular, local observations of what is happening, such as local extended Moran’s I indices, can play a crucial role in such applications.

In addition to the data on started and ended taxi trips used in this work, many other application areas for geostatistical analysis with geodata streams exist. Spatially and temporally resolved data on overall traffic volumes, rental vehicles, e-bikes, and e-scooters are available in many urban areas. Mobility data in particular offers the necessary temporal resolution for continuous processing in real time. Continuously recorded environmental data, such as air quality or weather events, can be analyzed in this way as well. With the progressive development of powerful sensor networks in the context of the IoT, even more fields of application can be expected in the future.

Further developments can be made with regard to the provisioning of analysis results. The implemented dashboard already provides possibilities for displaying dynamic and interactive graphics. Such a presentation method in combination with web-based provisioning can serve as a basis for making results and findings from the analysis available to a broad public in a processed and comprehensible form. Thus, it would be conceivable to develop information portals about current events in urban areas based on geostatistical analysis.

An in-depth analysis of the geostatistical interpretation of the real-time analysis results from the presented methodology is part of our future work.