Towards a Sensitivity Analysis in Seismic Risk with Probabilistic Building Exposure Models: An Application in Valparaíso, Chile Using Ancillary Open-Source Data and Parametric Ground Motions
Abstract
:1. Introduction
- Presenting the capabilities of integrating a freely available dataset gathered from VGI (without having to inspect individual buildings) to derive a probabilistic exposure model for residential buildings in Valparaíso and Viña del Mar (Chile), based on the inferred building footprint area for certain typologies.
- In addition to better characterising the building composition, this approach has improved its spatial representation by downscaling a coarser existing exposure model onto higher-resolution regular grids. Then, a large magnitude earthquake scenario can be defined, and a related set of exhaustive seismic ground motion fields through the variation of some of its driving parameters can be constructed.
- Use the former set of groung motions along with the three exposure models as inputs to independently calculate the direct economic losses that are expected from the building portfolio subjected to such a worst-case earthquake scenario. This vulnerability assessment allows us to propagate and compare the uncertainties embedded in the exposure models with respect to the parameters used to constrain the seismic ground motions.
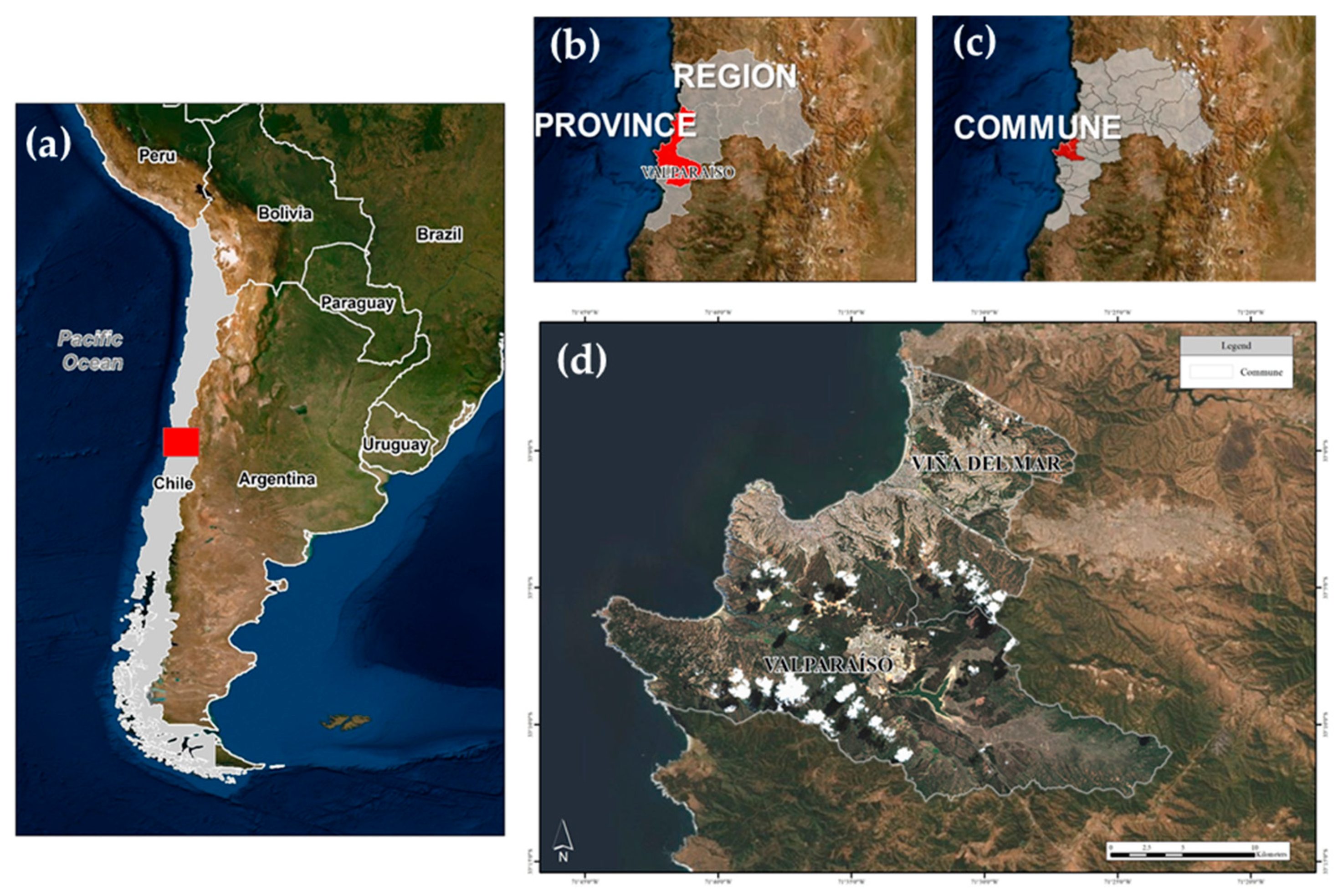
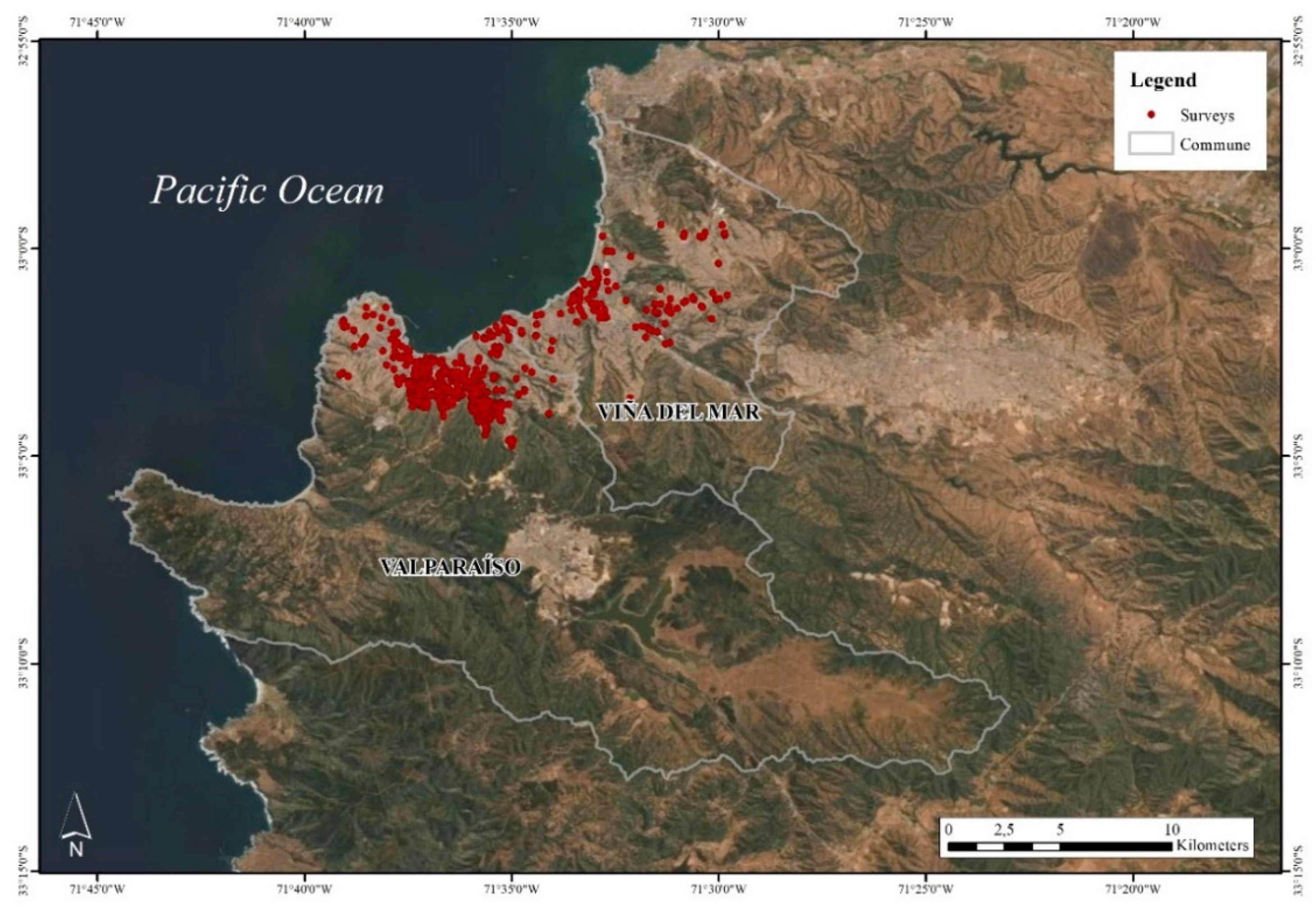
2. Context of the Study Area
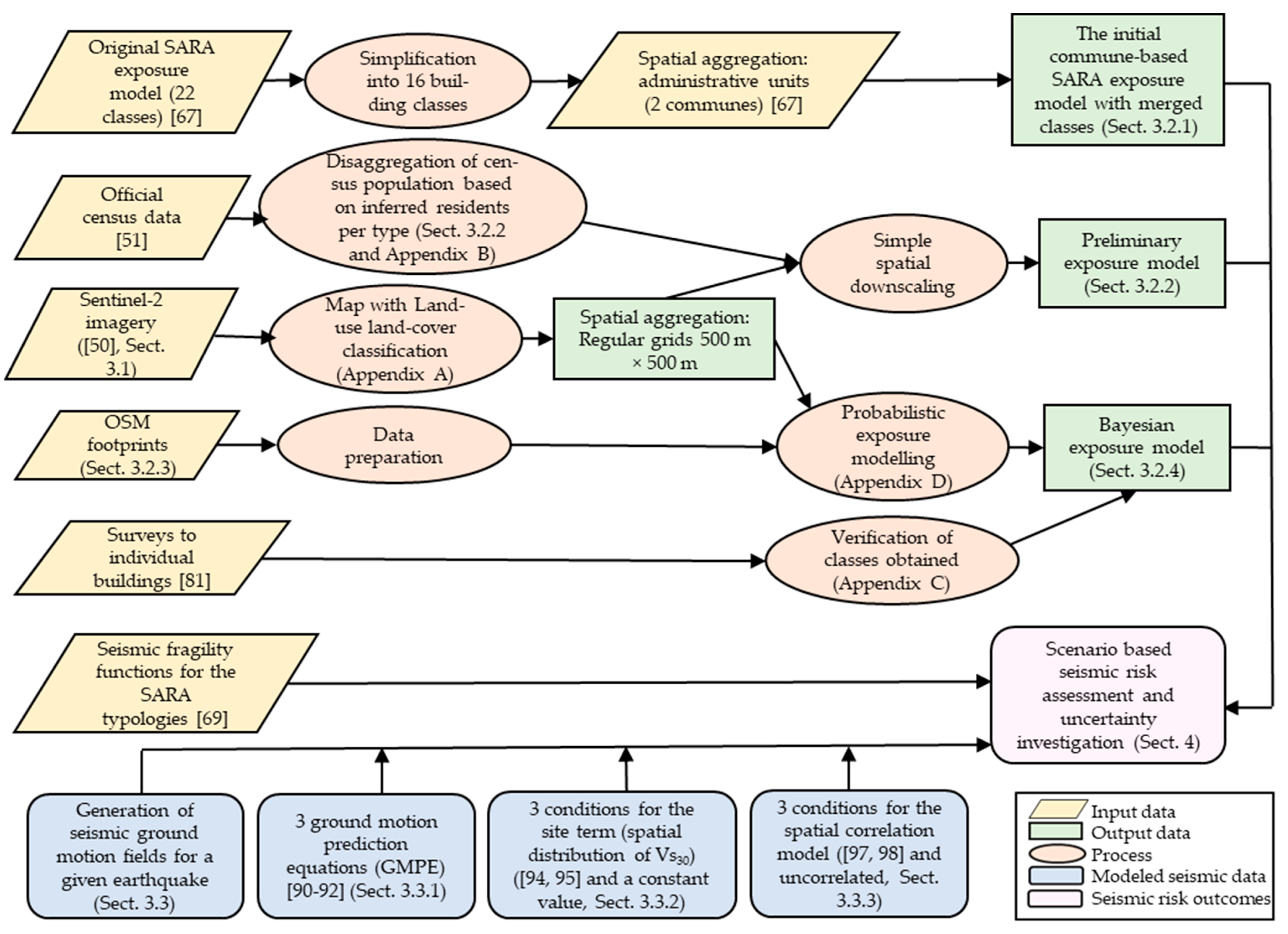
3. Materials and Methods
3.1. Delimitation of the Urban Area and Some Initial Features
3.2. Building Exposure and Vulnerability Models for Valparaíso
3.2.1. The Initial Commune-Based SARA Exposure Model with Merged Classes
- We did not consider the class “UNK” (unknown) because it lacked observable attributes. Its proportion (~10%) was redistributed to the other classes.
- We combined five pairs of classes into a more generic enclosing typology that had a similar taxonomic description and only differed in their storey ranges. These were ER-ETR-H1 within ER-ETR-H1-2, MCF-DNO-H1 within MCF-DNO-H1-3, MUR-ADO-H1 within MUR-ADO-H1-2, W-WLI-H1 within W-WLI-H1-3, and W-WS-H1 within W-WS-H1-2.
3.2.2. Preliminary Model: A Simple Downscaling Using Spatial Disaggregation of Population
3.2.3. Ancillary Data Available for Valparaíso
OpenStreetMap (OSM)
Data Collection of Taxonomic Attributes in Valparaíso and Building Classification
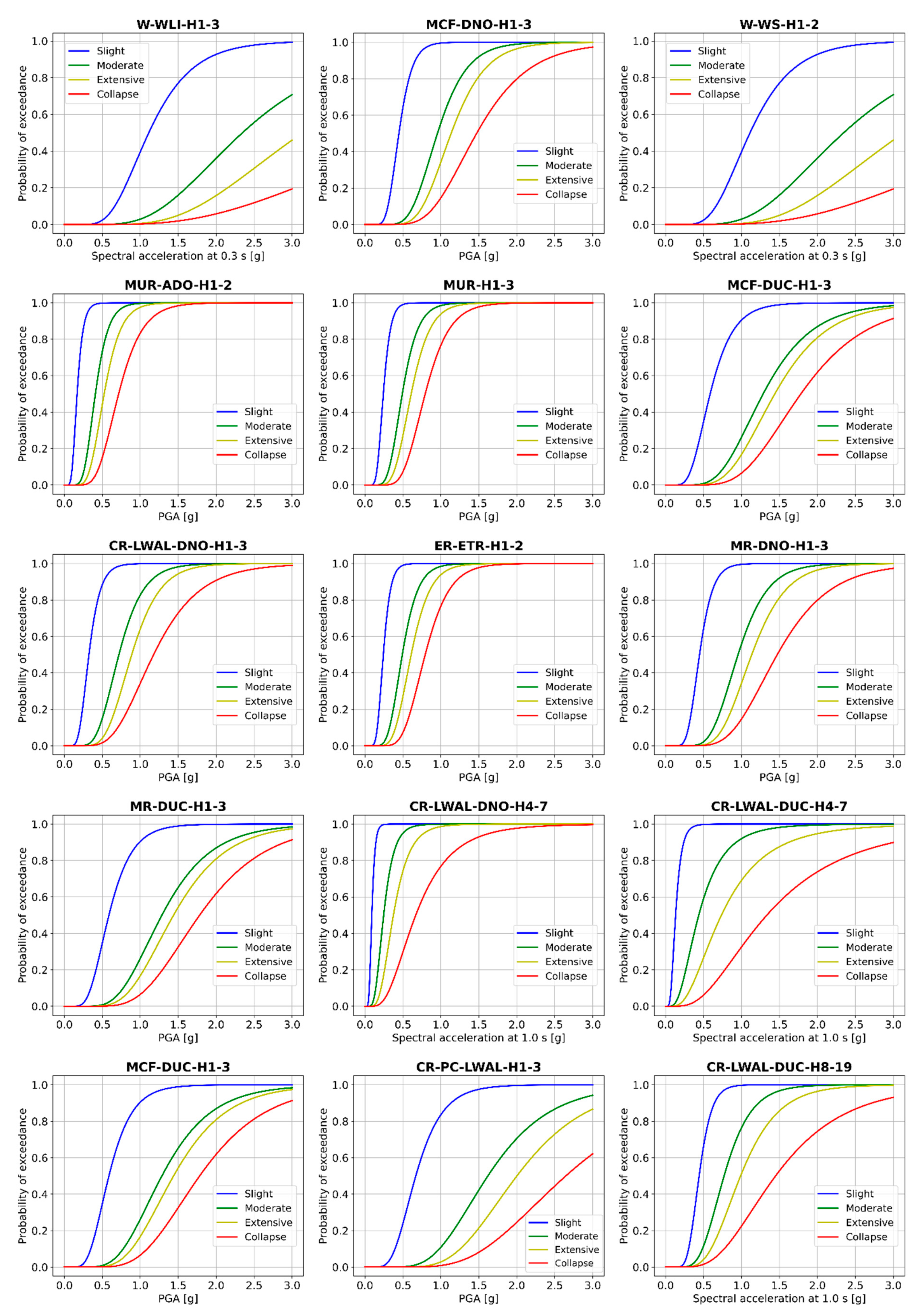
3.2.4. Bayesian Exposure Model for Valparaíso
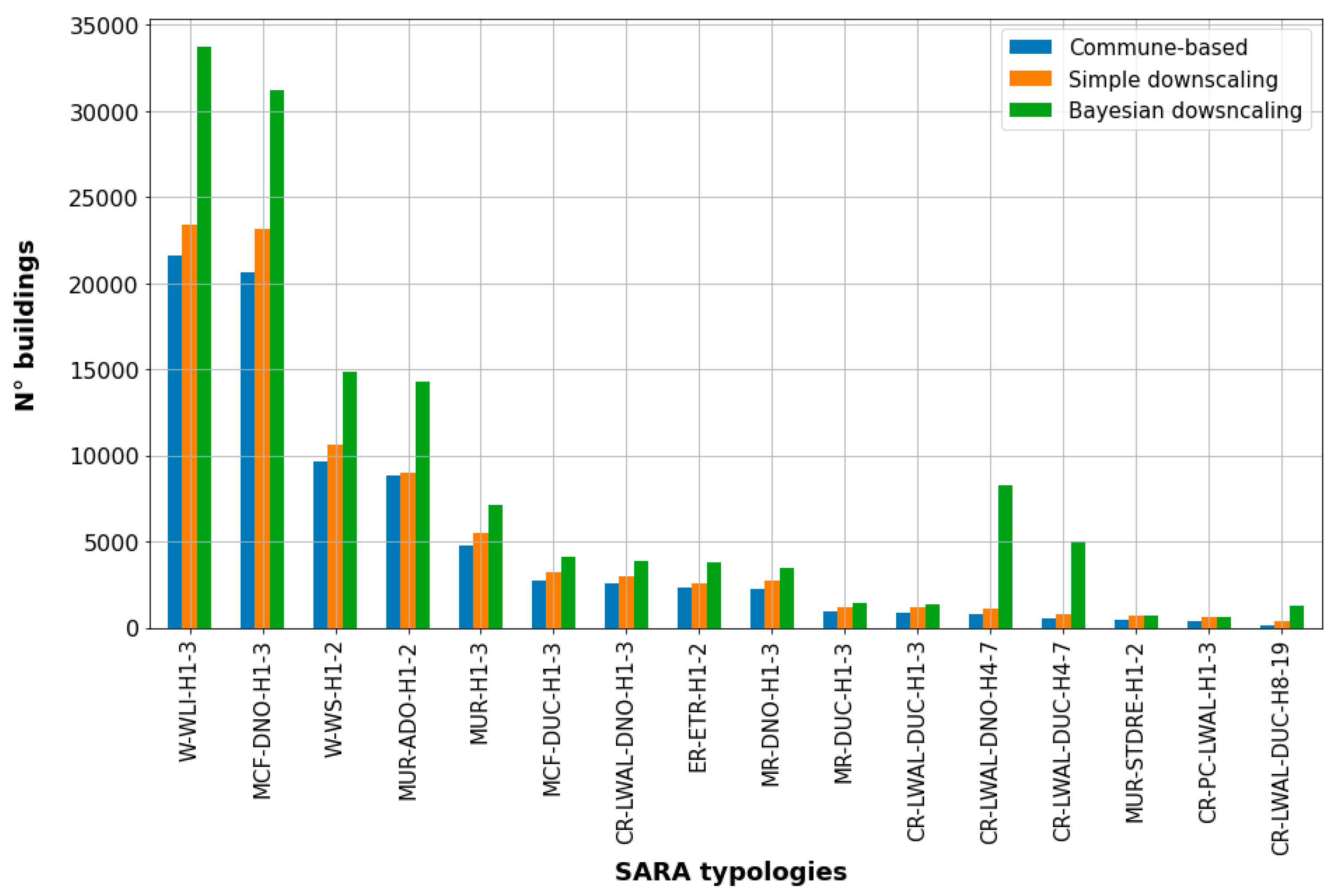
3.2.5. Comparison of Exposure Models Available for Valparaíso
- The first model (Section 3.2.1) is quite similar to the original SARA model, since it maintains its spatial representation over the administrative units. Its composition consists of the combination of similar classes in terms of their height.
- The second model (preliminary downscaled model, Section 3.2.2) constitutes the spatial disaggregation of the former onto higher resolutions of regular grid cells (500 m × 500 m). The total number of buildings was estimated by disaggregating the population at the block level from the 2017 official Chilean census.
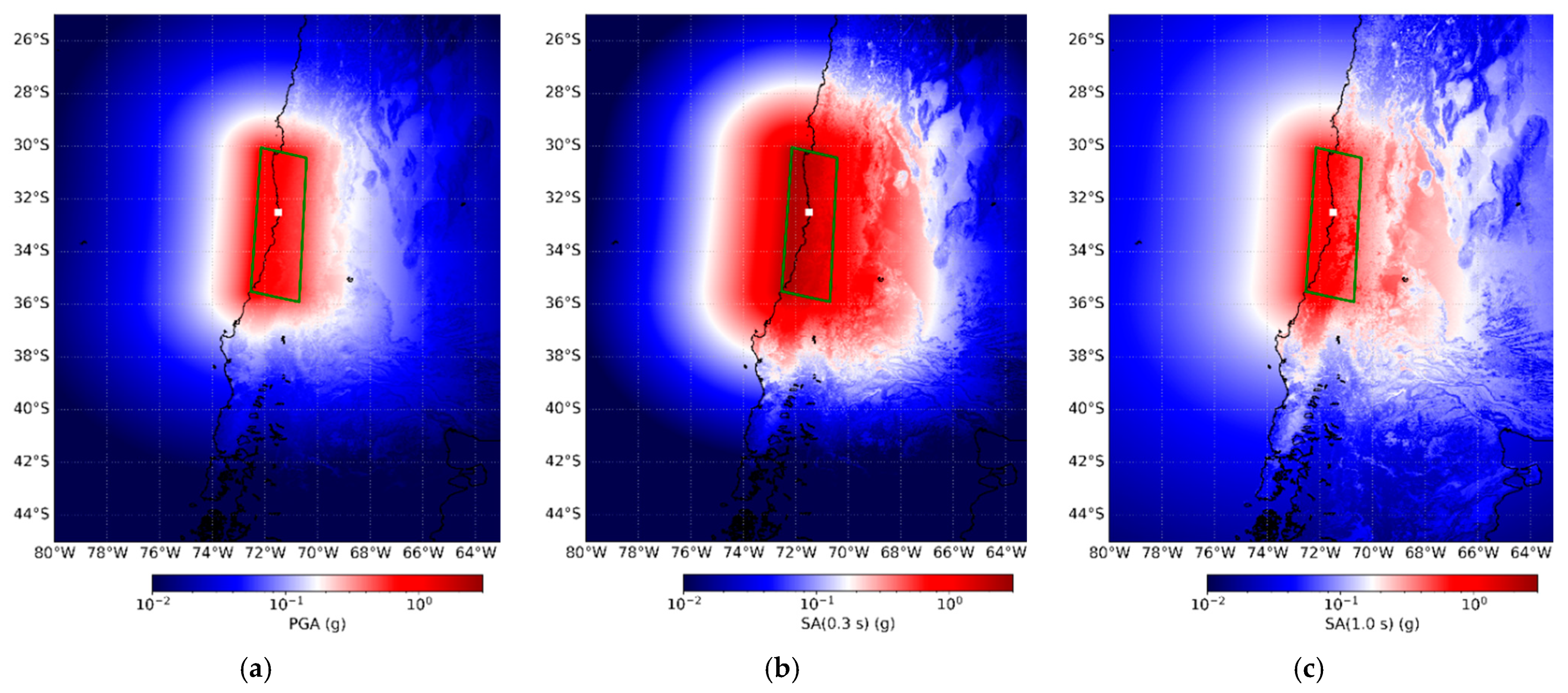
3.3. Generation of Seismic Ground Motion Fields for an Earthquake Scenario
3.3.1. Ground Motion Prediction Equation (GMPE)
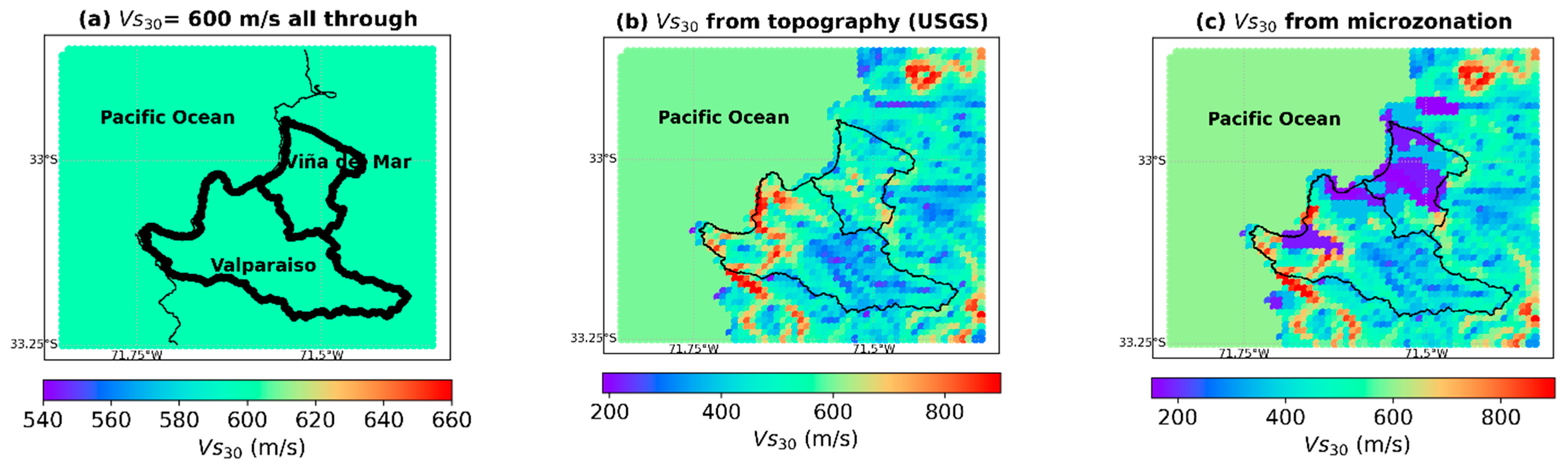
3.3.2. Site Term (Spatial Distribution of Vs30)
- Assuming Vs30 values of 600 m/s uniformly distributed throughout the study area. This emulated the presence of a moderately homogenous weathered rock with similar values assumed for the seabed rocks (Figure 13a).
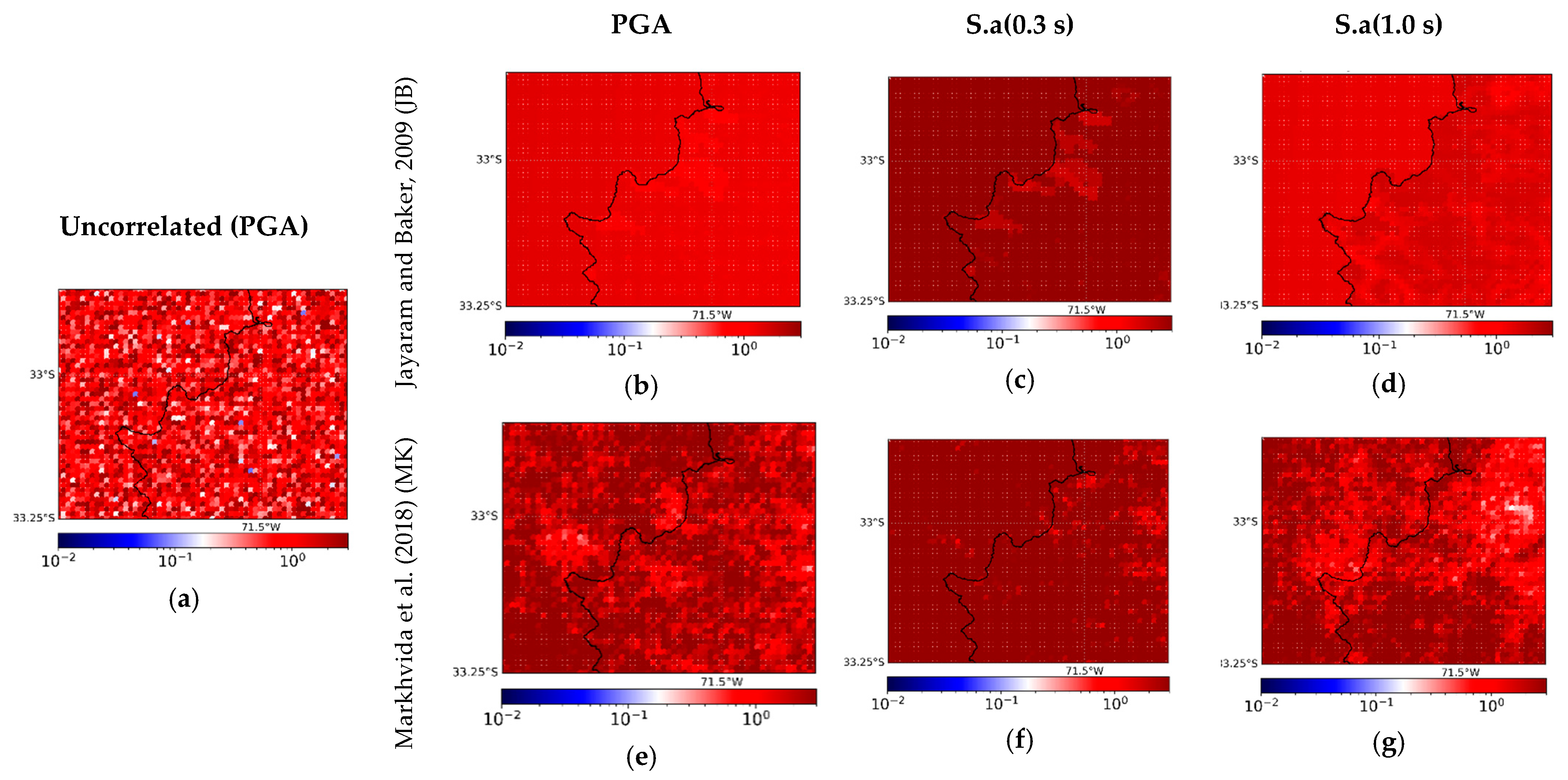
3.3.3. Spatial Correlation Model
- Uncorrelated ground motion fields (Figure 14a);
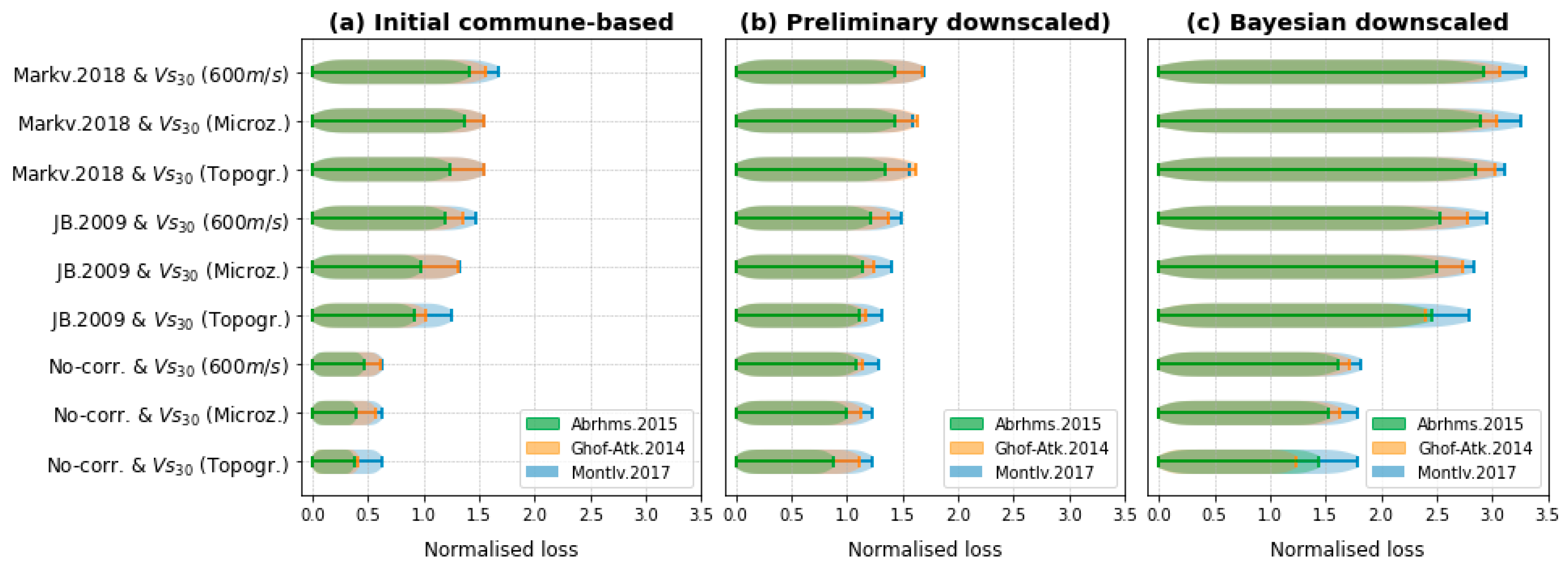
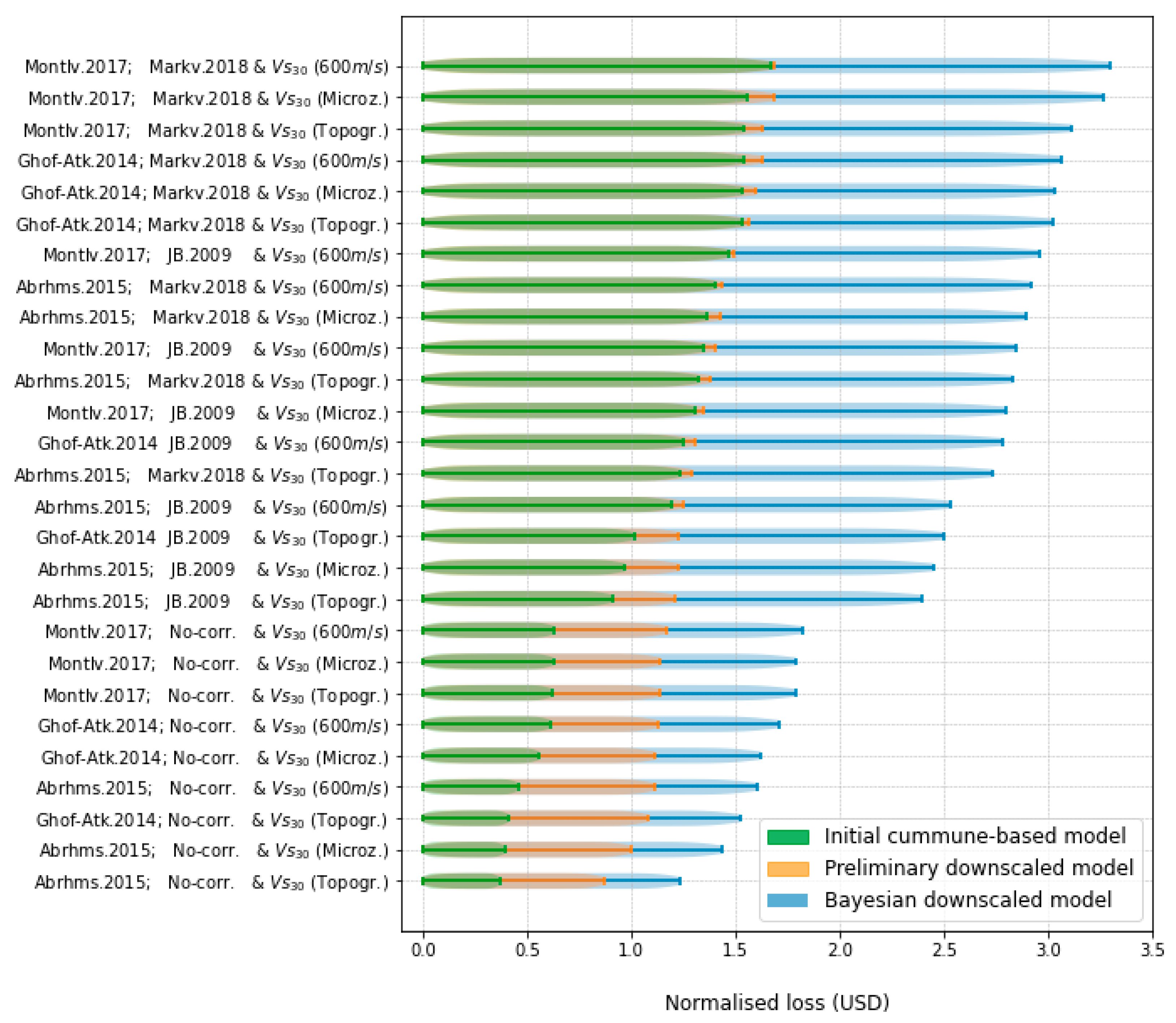
4. Sensitivity Analyses of Scenario-Based Seismic Risk Assessment
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Spatial Delimitation of the Urban Area and Available Data Sources for Building Exposure Modelling


Appendix B. Assumptions Followed in the Prelimary Model to Obtain Building Counts from Population and Footprint Areas per Typology
| Taxonomy | Dwellings | Buildings | Mean Number of Storeys | Reference Average Area per Dwelling (m2) | Population | Construction Quality | Area m2 Dwellings | Floor Area (m) | Floor Area (m2) per Building | Average Floor Area per Building | Sub-Categories |
|---|---|---|---|---|---|---|---|---|---|---|---|
| W + WS/H:1,2 | 1464.4 | 1464.4 | 1 | 80 | 5420 | Low | 117,152 | 117,152.1 | 80.00 | 73.24 | A |
| ER + ETR/H:1,2 | 2348.8 | 5909.5 | 1.25 | 70 | 30,771 | Low | 582,001 | 465,600.8 | 78.79 | ||
| MUR + ADO/H:1,2 | 9185.9 | 7472.5 | 1.25 | 70 | 33,997 | Low | 643,013 | 514,410.4 | 68.84 | ||
| MUR + STDRE/H:1,2 | 5747.8 | 4928 | 1.25 | 70 | 21,273 | Low | 402,346 | 321,876.8 | 65.32 | ||
| MCF/DNO/H:1,3 | 6841.9 | 876.4 | 1.5 | 70 | 3244 | Low | 61,348 | 40,898.7 | 46.67 | 65.56 | B |
| MUR/H:1,3 | 2732.5 | 1821.7 | 1.5 | 70 | 10,113 | Low | 191,275 | 127,516.7 | 70.00 | ||
| W + WLI/H:1,3 | 16,254.2 | 10,836.1 | 1.5 | 80 | 60,157 | Low | 1,300,336 | 866,890.7 | 80.00 | ||
| CR/LWAL/DNO/H:1,3 | 4384.3 | 1096.1 | 2 | 80 | 16,226 | Low | 350,744 | 175,372 | 160.00 | 153.33 | C |
| CR/LWAL/DUC/H:1,3 | 1461.1 | 365.3 | 2 | 70 | 5408 | Low | 102,277 | 51,138.5 | 140.00 | ||
| MCF/DUC/H:1,3 | 4501.3 | 1125.3 | 2 | 80 | 16,659 | Low | 360,104 | 180,052 | 160.00 | ||
| CR + PC/LWAL/H:1,3 | 1016.9 | 203.4 | 2.5 | 80 | 3764 | Low | 81,352 | 32,540.8 | 160.00 | 153.33 | D |
| MR/DNO/H:1,3 | 4652.5 | 930.5 | 2.5 | 80 | 17,219 | Low | 372,200 | 148,880 | 160.00 | ||
| MR/DUC/H:1,3 | 2077.7 | 415.5 | 2.5 | 70 | 7690 | Low | 145,439 | 58,175.6 | 140.00 | ||
| CR/LWAL/DNO/H:4,7 | 4316 | 287.7 | 5 | 80 | 15,974 | Medium | 345,280 | 69,056 | 240.03 | 225.04 | E |
| CR/LWAL/DUC/H:4,7 | 2076.6 | 138.4 | 5 | 70 | 76,856 | Medium | 145,362 | 29,072.4 | 210.00 | ||
| CR/LWAL/DUC/H:8,19 | 1656.9 | 34.5 | 12 | 70 | 6132 | High | 115,983 | 9665.3 | 280.15 | 280.15 | F |
Appendix C. Data Collection of Building Attributes in Valparaíso and Their Classification

| Attribute Type | Attribute Value |
|---|---|
| Material type | MCF |
| Material technology | CL99 |
| Material property | MO99 |
| Lateral load-resisting system (LLRS) | LWAL |
| Non-structural exterior walls | EWMA |
| Roof shape | RSH2 |
| Roof coverage material | RMT6 |
| Roof system material | RWO |
| Roof system type | RWO1 |
| Floor material | FC |
| Floor type | FC99 |
| Floor connections | FWCP |
| Number of storeys | 2 |
| Ductility of the LRRS | DU99 |
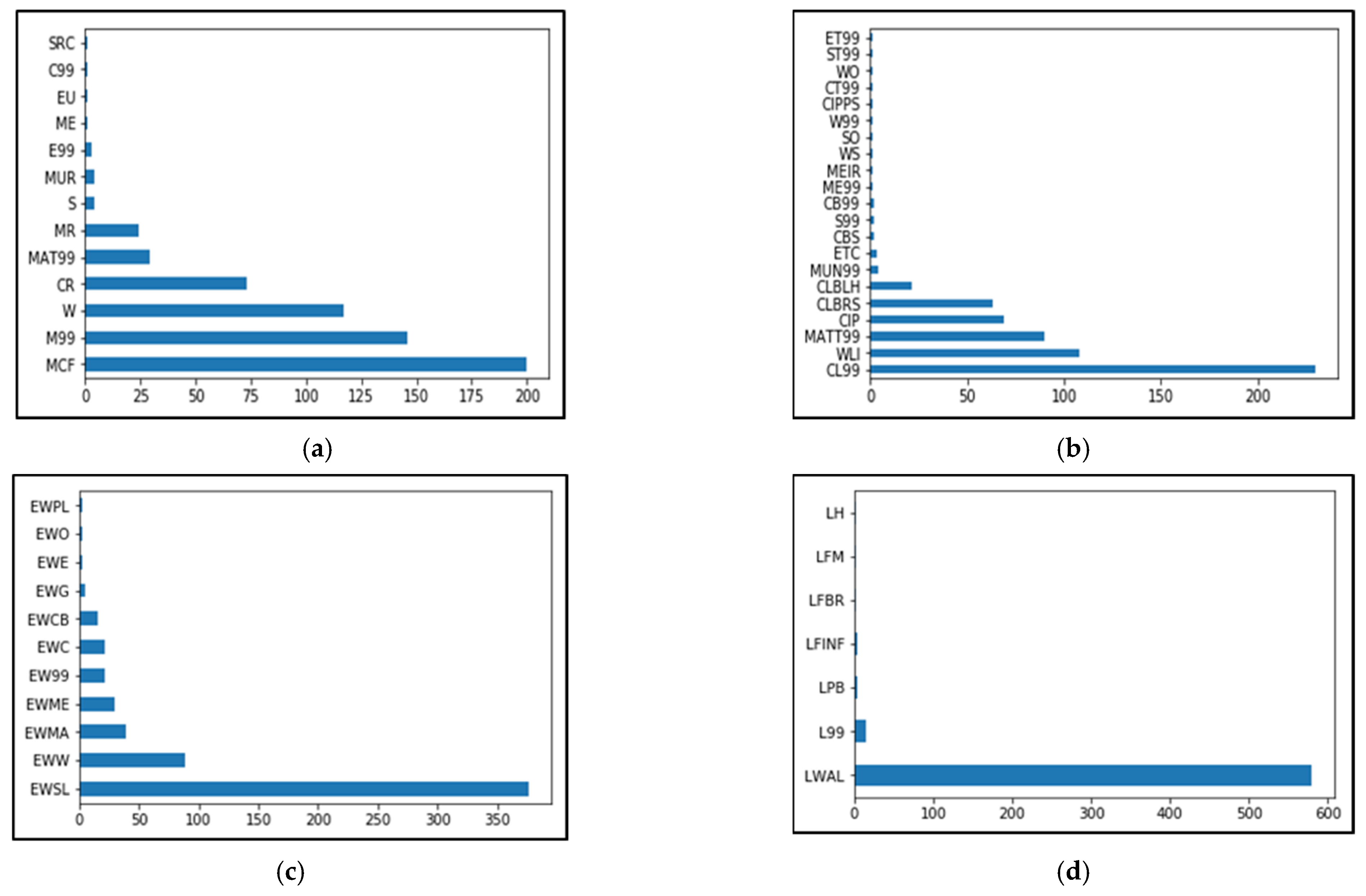
| (a) Material Type SRC: Concrete, composite with steel section C99: Concrete, unknown reinforcement EU: Earth, unreinforced ME: Metal (except steel) E99: Earth, unknown reinforcement MUR: Masonry, unreinforced [MUR] S: Steel MR: Masonry, reinforced MAT99: Unknown material CR: Concrete, reinforced W: Wood M99: Masonry, unknown reinforcement MCF: Masonry, confined (MCF) | (b) Material Technology ET99: Unknown earth technology ST99: Stone, unknown technology WO: Wood, other WS: Solid wood MEIR: Iron ME99: Metal, unknown CB99: Concrete blocks, unknown type S99: Steel, unknown CBS: Concrete blocks, solid ETC: Cob or wet construction MUN99: Masonry unit, unknown CLBLH: Fired clay hollow blocks or tiles CLBRS: Fired clay solid bricks CIP: Cast-in-place concrete MATT99: Unknown material WLI: Light wood members CL99: Fired clay unit, unknown type |
| (c) Non- Structural Exterior Walls EWPL: Plastic or vinyl exterior walls, various EWO: Material of exterior walls, other EWE: Earthen exterior walls EWG: Glass exterior walls EWCB: Cement-based boards for exterior walls EWC: Concrete exterior walls EW99: Unknown material of exterior walls EWME: Metal exterior walls EWMA: Masonry exterior walls EWW: Wooden exterior walls EWSL: Stucco finish on light framing for exterior walls | (d) Lateral Load Resisting System LH: Hybrid lateral load-resisting system LFM: Moment frame LFBR: Braced frame LFINF: Infilled frame LPB: Post and beam L99: Unknown lateral load-resisting system LWAL: Wall |
Appendix D. Basic Overview of the Probabilistic Exposure Modelling Approach

References
- UNISDR. UNISDR Terminology on Disaster Risk Reduction, United Nations International Strategy for Disaster Reduction; UNISDR-20-2009: Geneva, Switzerland, 2009. [Google Scholar]
- Calvi, G.M.; Pinho, R.; Magenes, G.; Crowley, H.; Bommer, J.J.; Restrepo-Velez, L.F. Development of seismic vulnerability assessment methodologies over the past 30 years. ISET J. Earthq. Technol. 2006, 43, 75–104. [Google Scholar]
- Crowley, H.; Bommer, J.J. Modelling seismic hazard in earthquake loss models with spatially distributed exposure. Bull. Earthq. Eng. 2006, 4, 275. [Google Scholar] [CrossRef]
- Crowley, H. Earthquake risk assessment: Present shortcomings and future directions. In Perspectives on European Earthquake Engineering and Seismology: Volume 1; Ansal, A., Ed.; Springer International Publishing: Cham, Switzerland, 2014; pp. 515–532. ISBN 978-3-319-07118-3. [Google Scholar]
- Corbane, C.; Hancilar, U.; Ehrlich, D.; De Groeve, T. Pan-European seismic risk assessment: A proof of concept using the earthquake loss estimation routine (ELER). Bull. Earthq. Eng. 2017, 15, 1057–1083. [Google Scholar] [CrossRef]
- Silva, V.; Akkar, S.; Baker, J.; Bazzurro, P.; Castro, J.M.; Crowley, H.; Dolsek, M.; Galasso, C.; Lagomarsino, S.; Monteiro, R.; et al. Current challenges and future trends in analytical fragility and vulnerability modeling. Earthq. Spectra 2019, 35, 1927–1952. [Google Scholar] [CrossRef]
- Haas, M. Towards Time- and State-Dependent Seismic Risk over Urban Scales. Ph.D. Thesis, der Technischen Universität Berlin, Berlin, Germany, 2018. [Google Scholar]
- Martins, L.; Silva, V. Development of a fragility and vulnerability model for global seismic risk analyses. Bull. Earthq. Eng. 2020. [Google Scholar] [CrossRef]
- Jaiswal, K.; Wald, D.; Porter, K. A global building inventory for earthquake loss estimation and risk management. Earthq. Spectra 2010, 26, 731–748. [Google Scholar] [CrossRef]
- Gunasekera, R.; Ishizawa, O.; Aubrecht, C.; Blankespoor, B.; Murray, S.; Pomonis, A.; Daniell, J. Developing an adaptive global exposure model to support the generation of country disaster risk profiles. Earth-Sci. Rev. 2015, 150, 594–608. [Google Scholar] [CrossRef] [Green Version]
- Silva, V.; Amo-Oduro, D.; Calderon, A.; Costa, C.; Dabbeek, J.; Despotaki, V.; Martins, L.; Pagani, M.; Rao, A.; Simionato, M.; et al. Development of a global seismic risk model. Earthq. Spectra 2020, 36, 372–394. [Google Scholar] [CrossRef]
- Rao, A.; Dutta, D.; Kalita, P.; Ackerley, N.; Silva, V.; Raghunandan, M.; Ghosh, J.; Ghosh, S.; Brzev, S.; Dasgupta, K. Probabilistic seismic risk assessment of India. Earthq. Spectra 2020, 36, 345–371. [Google Scholar] [CrossRef]
- Crowley, H.; Despotaki, V.; Rodrigues, D.; Silva, V.; Toma-Danila, D.; Riga, E.; Karatzetzou, A.; Fotopoulou, S.; Zugic, Z.; Sousa, L.; et al. Exposure model for European seismic risk assessment. Earthq. Spectra 2020, 36, 252–273. [Google Scholar] [CrossRef]
- Ma, J.; Rao, A.; Silva, V.; Liu, K.; Wang, M. A township-level exposure model of residential buildings for mainland China. Nat. Hazards 2021, 108, 389–423. [Google Scholar] [CrossRef]
- Xin, D.; Daniell, J.E.; Tsang, H.-H.; Wenzel, F. Residential building stock modelling for mainland China targeted for seismic risk assessment. Nat. Hazards Earth Syst. Sci. 2021, 21, 3031–3056. [Google Scholar] [CrossRef]
- Rivera, F.; Rossetto, T.; Twigg, J. An interdisciplinary study of the seismic exposure dynamics of santiago de chile. Int. J. Disaster Risk Reduct. 2020, 48, 101581. [Google Scholar] [CrossRef]
- Calderón, A.; Silva, V. Exposure forecasting for seismic risk estimation: Application to Costa Rica. Earthq. Spectra 2021, 37, 1806–1826. [Google Scholar] [CrossRef]
- Yepes-Estrada, C.; Silva, V.; Valcárcel, J.; Acevedo, A.B.; Tarque, N.; Hube, M.A.; Coronel, G.; María, H.S. Modeling the residential building inventory in South America for seismic risk assessment. Earthq. Spectra 2017, 33, 299–322. [Google Scholar] [CrossRef]
- Dabbeek, J.; Crowley, H.; Silva, V.; Weatherill, G.; Paul, N.; Nievas, C.I. Impact of exposure spatial resolution on seismic loss estimates in regional portfolios. Bull. Earthq. Eng. 2021, 19, 5819–5841. [Google Scholar] [CrossRef]
- Wieland, M.; Pittore, M. A spatio-temporal building exposure database and information life-cycle management solution. ISPRS Int. J. Geo-Inf. 2017, 6, 114. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Giovinazzi, S. Macroseismic and mechanical models for the vulnerability and damage assessment of current buildings. Bull. Earthq. Eng. 2006, 4, 415–443. [Google Scholar] [CrossRef]
- Wieland, M.; Pittore, M.; Parolai, S.; Zschau, J.; Moldobekov, B.; Begaliev, U. Estimating building inventory for rapid seismic vulnerability assessment: Towards an integrated approach based on multi-source imaging. Soil Dyn. Earthq. Eng. 2012, 36, 70–83. [Google Scholar] [CrossRef]
- Riedel, I.; Guéguen, P.; Dalla Mura, M.; Pathier, E.; Leduc, T.; Chanussot, J. Seismic vulnerability assessment of urban environments in moderate-to-low seismic hazard regions using association rule learning and support vector machine methods. Nat. Hazards 2015, 76, 1111–1141. [Google Scholar] [CrossRef]
- Liuzzi, M.; Aravena Pelizari, P.; Geiß, C.; Masi, A.; Tramutoli, V.; Taubenböck, H. A Transferable remote sensing approach to classify building structural types for seismic risk analyses: The case of val d’agri area (Italy). Bull. Earthq. Eng. 2019, 17, 4825–4853. [Google Scholar] [CrossRef]
- Torres, Y.; Arranz, J.J.; Gaspar-Escribano, J.M.; Haghi, A.; Martínez-Cuevas, S.; Benito, B.; Ojeda, J.C. Integration of LiDAR and multispectral images for rapid exposure and earthquake vulnerability estimation. Application in Lorca, Spain. Int. J. Appl. Earth Obs. Geoinf. 2019, 81, 161–175. [Google Scholar] [CrossRef] [Green Version]
- Aravena Pelizari, P.; Geiß, C.; Aguirre, P.; María, H.S.; Peña, Y.M.; Taubenböck, H. Automated building characterization for seismic risk assessment using street-level imagery and deep learning. ISPRS J. Photogramm. Remote Sens. 2021, 180, 370–386. [Google Scholar] [CrossRef]
- Rueda-Plata, D.; González, D.; Acevedo, A.B.; Duque, J.C.; Ramos-Pollán, R. Use of deep learning models in street-level images to classify one-story unreinforced masonry buildings based on roof diaphragms. Build. Environ. 2021, 189, 107517. [Google Scholar] [CrossRef]
- Geiß, C.; Thoma, M.; Pittore, M.; Wieland, M.; Dech, S.W.; Taubenbock, H. Multitask active learning for characterization of built environments with multisensor earth observation data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5583–5597. [Google Scholar] [CrossRef]
- Zafrir, R.; Pittore, M.; Gomez-Zapata, J.C.; Aravena, P.; Geiß, C. Bayesian downscaling of building exposure models with remote sensing and ancillary information. In Proceedings of the EGU General Assembly Conference Abstracts, Online. 4–8 May 2020; p. 18240. [Google Scholar]
- Geiß, C.; Aravena Pelizari, P.; Priesmeier, P.; Calderon, A.R.S.; Schoepfer, E.; Langbein, M.; Riedlinger, T.; Santa María, H.; Gómez Zapata, J.C.; Pittore, M.; et al. Earth observation techniques for spatial disaggregation of exposure data. In Proceedings of the EGU General Assembly Conference Abstracts, Online. 19–30 April 2021; p. EGU21-8574. [Google Scholar]
- Pittore, M.; Wieland, M.; Errize, M.; Kariptas, C.; Güngör, I. Improving post-earthquake insurance claim management: A novel approach to prioritize geospatial data collection. ISPRS Int. J. Geo-Inf. 2015, 4, 2401–2427. [Google Scholar] [CrossRef] [Green Version]
- Pittore, M.; Wieland, M.; Fleming, K. Perspectives on global dynamic exposure modelling for geo-risk assessment. Nat. Hazards 2017, 86, 7–30. [Google Scholar] [CrossRef]
- Brzev, S.; Scawthor, C.; Charleson, A.W.; Allen, L.; Greene, M.; Jaiswal, K.; Silva, V. GEM Building Taxonomy Version 2.0; GEM Foundation: Pavia, Italy, 2013. [Google Scholar]
- Pittore, M.; Haas, M.; Megalooikonomou, K.G. Risk-oriented, bottom-up modeling of building portfolios with faceted taxonomies. Front. Built Environ. 2018, 4, 41. [Google Scholar] [CrossRef]
- Nicodemo, G.; Pittore, M.; Masi, A.; Manfredi, V. Modelling exposure and vulnerability from post-earthquake survey data with risk-oriented taxonomies: AeDES form, GEM taxonomy and EMS-98 typologies. Int. J. Disaster Risk Reduct. 2020, 50, 101894. [Google Scholar] [CrossRef]
- Shinde, S.; Gomez-Zapata, J.C.; Pittore, M.; Arroyo, O.; Merino-Peña, Y.; Aguirre, P.; Santa María, H. Development of multi-hazard exposure models from individual building observations for multi-risk assessment purposes. In Proceedings of the EGU General Assembly Conference Abstracts, Online. 4–8 May 2020; p. 11719. [Google Scholar]
- Polese, M.; d’Aragona, M.G.; Prota, A. Simplified approach for building inventory and seismic damage assessment at the territorial scale: An application for a town in Southern Italy. Soil Dyn. Earthq. Eng. 2019, 121, 405–420. [Google Scholar] [CrossRef]
- Kechidi, S.; Castro, J.M.; Monteiro, R.; Marques, M.; Yelles, K.; Bourahla, N.; Hamdache, M. Development of exposure datasets for earthquake damage and risk modelling: The case study of Northern Algeria. Bull. Earthq. Eng. 2021, 19, 5253–5283. [Google Scholar] [CrossRef]
- Tocchi, G.; Polese, M.; Di Ludovico, M.; Prota, A. Regional based exposure models to account for local building typologies. Bull. Earthq. Eng. 2021, 20, 193–228. [Google Scholar] [CrossRef]
- Pittore, M.; Haas, M.; Silva, V. Variable resolution probabilistic modeling of residential exposure and vulnerability for risk applications. Earthq. Spectra 2020, 36, 321–344. [Google Scholar] [CrossRef]
- Hecht, R.; Kunze, C.; Hahmann, S. Measuring completeness of building footprints in openstreetmap over space and time. ISPRS Int. J. Geo-Inf. 2013, 2, 1066–1091. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, Q.; Tian, Y. Understanding completeness and diversity patterns of OSM-based land-use and land-cover dataset in China. ISPRS Int. J. Geo-Inf. 2020, 9, 531. [Google Scholar] [CrossRef]
- Feldmeyer, D.; Meisch, C.; Sauter, H.; Birkmann, J. Using OpenStreetMap data and machine learning to generate socio-economic indicators. ISPRS Int. J. Geo-Inf. 2020, 9, 498. [Google Scholar] [CrossRef]
- Sousa, L.; Silva, V.; Bazzurro, P. Using open-access data in the development of exposure data sets of industrial buildings for earthquake risk modeling. Earthq. Spectra 2017, 33, 63–84. [Google Scholar] [CrossRef]
- Tumurbaatar, Z.; Miura, H.; Tsamba, T. Development of building inventory data in ulaanbaatar, mongolia for seismic loss estimation. ISPRS Int. J. Geo-Inf. 2022, 11, 26. [Google Scholar] [CrossRef]
- Nievas, C.I.; Pilz, M.; Prehn, K.; Schorlemmer, D.; Weatherill, G.; Cotton, F. Calculating earthquake damage building by building: The case of the city of Cologne, Germany. Bull. Earthq. Eng. 2022. [Google Scholar] [CrossRef]
- Figueiredo, R.; Martina, M. Using open building data in the development of exposure data sets for catastrophe risk modelling. Nat. Hazards Earth Syst. Sci. 2016, 16, 417–429. [Google Scholar] [CrossRef] [Green Version]
- Cerri, M.; Steinhausen, M.; Kreibich, H.; Schröter, K. Are OpenStreetMap building data useful for flood vulnerability modelling? Nat. Hazards Earth Syst. Sci. 2021, 21, 643–662. [Google Scholar] [CrossRef]
- Soman, S.; Beukes, A.; Nederhood, C.; Marchio, N.; Bettencourt, L.M.A. Worldwide detection of informal settlements via topological analysis of crowdsourced digital maps. ISPRS Int. J. Geo-Inf. 2020, 9, 685. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Beutin, T.; Cotton, F.; Garcia Ospina, N.; Hirata, N.; Ma, K.-F.; Nievas, C.; Prehn, K.; Wyss, M. Global dynamic exposure and the OpenBuildingMap—A big-data and crowd-sourcing approach to exposure modeling. In Proceedings of the EGU General Assembly Conference Abstracts, Online. 4–8 May 2020; p. 18920. [Google Scholar]
- Zafrir, R. Downscaling Building Exposure Models: A Probabilistic Approach Using Remote Sensing Products and Open Source Auxiliary Information; Stuttgart Technology University of Applied Sciences (Hochschule für Technik Stuttgart—HFT Stuttgart): Stuttgart, Germany, 2020. [Google Scholar]
- INE. Base Cartográfica Censal. Alcances y Consideraciones Para el Usuario; Departamento de Demografía y Censos, Instituto Nacional de Estadísticas: Santiago, Chile, 2018. [Google Scholar]
- Gomez-Zapata, J.C.; Pittore, M.; Cotton, F.; Lilienkamp, H.; Simantini, S.; Aguirre, P.; Hernan, S.M. Epistemic uncertainty of probabilistic building exposure compositions in scenario-based earthquake loss models. Bull. Earthq. Eng. 2022. [Google Scholar] [CrossRef]
- Carvajal, M.; Cisternas, M.; Catalán, P.A. Source of the 1730 Chilean earthquake from historical records: Implications for the future tsunami hazard on the coast of metropolitan Chile. J. Geophys. Res. Solid Earth 2017, 122, 3648–3660. [Google Scholar] [CrossRef]
- Montessus de Ballore, F. Historia sísmica de los Andes Meridionales al sur del paralelo XVI, Cuarta Parte; Imprenta Cervantes: Santiago, Chile, 1914. [Google Scholar]
- Indirli, M.; Razafindrakoto, H.; Romanelli, F.; Puglisi, C.; Lanzoni, L.; Milani, E.; Munari, M.; Apablaza, S. Hazard evaluation in Valparaíso: The MAR VASTO project. Pure Appl. Geophys. 2011, 168, 543–582. [Google Scholar] [CrossRef]
- Comte, D.; Eisenberg, A.; Lorca, E.; Pardo, M.; Ponce, L.; Saragoni, R.; Singh, S.K.; Suarez, G. The 1985 central Chile earthquake: A repeat of previous great earthquakes in the region? Science 1986, 233, 449. [Google Scholar] [CrossRef]
- de la Llera, J.C.; Rivera, F.; Mitrani-Reiser, J.; Jünemann, R.; Fortuño, C.; Ríos, M.; Hube, M.; Santa María, H.; Cienfuegos, R. Data collection after the 2010 Maule earthquake in Chile. Bull. Earthq. Eng. 2017, 15, 555–588. [Google Scholar] [CrossRef]
- Gómez Zapata, M.; Jiménez Martínez, M.; Romero-Jarén, R. How resilient is the labour market against natural disaster? Evaluating the effects from the 2010 earthquake in Chile. Nat. Hazards 2020, 104, 1481–1533. [Google Scholar] [CrossRef]
- Nealy, J.L.; Herman, M.W.; Moore, G.L.; Hayes, G.P.; Benz, H.M.; Bergman, E.A.; Barrientos, S.E. 2017 Valparaíso earthquake sequence and the megathrust patchwork of central Chile. Geophys. Res. Lett. 2017, 44, 8865–8872. [Google Scholar] [CrossRef] [Green Version]
- Jiménez, B.; Pelà, L.; Hurtado, M. Building survey forms for heterogeneous urban areas in seismically hazardous zones. Application to the historical center of Valparaíso, Chile. Int. J. Arch. Herit. 2018, 12, 1076–1111. [Google Scholar] [CrossRef]
- GEM. Report on the SARA Exposure and Vulnerability Workshop in Medellin, Colombia. 2014. Available online: https://sara.openquake.org/_media/risk:03_2014_-_workshop_medellin_-_exposure.pdf (accessed on 21 December 2021).
- Geiß, C.; Schauß, A.; Riedlinger, T.; Dech, S.; Zelaya, C.; Guzmán, N.; Hube, M.A.; Arsanjani, J.J.; Taubenböck, H. Joint use of remote sensing data and volunteered geographic information for exposure estimation: Evidence from Valparaíso, Chile. Nat. Hazards 2017, 86, 81–105. [Google Scholar] [CrossRef] [Green Version]
- CIESIN. Documentation for the Gridded Population of TheWorld, Version 4 (GPWv4), Revision 11 Data Sets. Available online: https://doi.org/10.7927/H45Q4T5F (accessed on 21 December 2021).
- ESA European Space Agency. Sentinel-2 MSI; European Space Agency: Paris, France, 2018. [Google Scholar]
- ERDAS. ERDAS Imagine 2014; Hexagon Geospatial, Peachtree Corners Circle Norcross: Norcross, GA, USA, 2014. [Google Scholar]
- Mohammadi, A.; Karimzadeh, S.; Valizadeh Kamran, K.; Matsuoka, M. Extraction of land information, future landscape changes and seismic hazard assessment: A case study of Tabriz, Iran. Sensors 2020, 20, 7010. [Google Scholar] [CrossRef]
- INE. Censo de Población y Vivienda 2002; Instituto Nacional de Estadística de Chile: Santiago, Chile, 2002. [Google Scholar]
- Villar-Vega, M.; Silva, V.; Crowley, H.; Yepes, C.; Tarque, N.; Acevedo, A.B.; Hube, M.A.; Gustavo, C.D.; María, H.S. Development of a fragility model for the residential building stock in South America. Earthq. Spectra 2017, 33, 581–604. [Google Scholar] [CrossRef]
- INITN. Instituto Nacional de Investigaciones Tecnológica y Normalizaciones, Cálculo Antisísmico de Edificios, NCh.433 of 72; Technical Report; INITN: Santiago de Chile, Chile, 1972. [Google Scholar]
- INN. Instituto Nacional de Normalización Diseño Sísmico de Edificios, NCh.433 of 96; Technical Report; INN: Santiago de Chile, Chile, 1996. [Google Scholar]
- Dell’Acqua, F.; Gamba, P.; Jaiswal, K. Spatial aspects of building and population exposure data and their implications for global earthquake exposure modeling. Nat. Hazards 2013, 68, 1291–1309. [Google Scholar] [CrossRef]
- Bal, I.E.; Bommer, J.J.; Stafford, P.J.; Crowley, H.; Pinho, R. The influence of geographical resolution of urban exposure data in an earthquake loss model for Istanbul. Earthq. Spectra 2010, 26, 619–634. [Google Scholar] [CrossRef]
- Senouci, A.; Bard, P.-Y.; Beck, E.; Farsi, M.N.; Cartier, S. Mapping seismic vulnerability at urban scale: Discussion on relevant cartography representations and smoothing for urban planning purposes on the oran case study. Soil Dyn. Earthq. Eng. 2018, 115, 545–563. [Google Scholar] [CrossRef]
- Scheingraber, C.; Käser, M. Spatial seismic hazard variation and adaptive sampling of portfolio location uncertainty in probabilistic seismic risk analysis. Nat. Hazards Earth Syst. Sci. 2020, 20, 1903–1918. [Google Scholar] [CrossRef]
- Gomez-Zapata, J.C.; Brinckmann, N.; Harig, S.; Zafrir, R.; Pittore, M.; Cotton, F.; Babeyko, A. Variable-resolution building exposure modelling for earthquake and tsunami scenario-based risk assessment. An application case in Lima, Peru. Nat. Hazards Earth Syst. Sci. 2021, 21, 3599–3628. [Google Scholar] [CrossRef]
- OSM Task Manager. #502—Valparaíso, Chile Fires/Fuegos En Valparaíso, Chile. 2014. Available online: https://tasks.hotosm.org/projects/502 (accessed on 21 December 2021).
- OSM Task Manager. #508—Valparaíso, Chile Fires 2/Fuegos En Valparaíso, Chile. 2014. Available online: https://tasks.hotosm.org/projects/508 (accessed on 21 December 2021).
- Reszka, P.; Fuentes, A. The great valparaiso fire and fire safety management in Chile. Fire Technol. 2015, 51, 753–758. [Google Scholar] [CrossRef] [Green Version]
- Haas, M.; Wieland, M.; Pittore, M. DEMO: Remote Rapid Visual Screening (RRVS). Available online: https://vimeo.com/158600573 (accessed on 21 December 2021).
- Merino-Peña, Y.; Pittore, M.; Gomez-Zapata, J.C. RRVS building survey for building exposure modelling in valparaiso and viña del mar (Chile). V. 1.0. GFZ Data Serv. 2021. [Google Scholar] [CrossRef]
- Acevedo, A.B.; Jaramillo, J.D.; Yepes, C.; Silva, V.; Osorio, F.A.; Villar, M. Evaluation of the seismic risk of the unreinforced masonry building stock in Antioquia, Colombia. Nat. Hazards 2017, 86, 31–54. [Google Scholar] [CrossRef]
- Arroyo, O.; Feliciano, D.; Carrillo, J.; Hube, M.A. Seismic performance of mid-rise thin concrete wall buildings lightly reinforced with deformed bars or welded wire mesh. Eng. Struct. 2021, 241, 112455. [Google Scholar] [CrossRef]
- Vásquez, J.A.; Jünemann, R.; de la Llera, J.C.; Hube, M.A.; Chacón, M.F. Three-dimensional nonlinear response history analyses for earthquake damage assessment: A reinforced concrete wall building case study. Earthq. Spectra 2021, 37, 235–261. [Google Scholar] [CrossRef]
- Weatherill, G.; Pittore, M.; Haas, M.; Brinckmann, N.; Rüster, M.; Gomez-Zapata, J.C. Shakyground: A web service to serve GMPE-based ground motion fields. V. 1.0. GFZ Data Serv. 2021. [Google Scholar] [CrossRef]
- Pagani, M.; Monelli, D.; Weatherill, G.; Danciu, L.; Crowley, H.; Silva, V.; Henshaw, P.; Butler, L.; Nastasi, M.; Panzeri, L.; et al. OpenQuake engine: An open hazard (and risk) software for the global earthquake model. Seism. Res. Lett. 2014, 85, 692–702. [Google Scholar] [CrossRef] [Green Version]
- Kalakonas, P.; Silva, V.; Mouyiannou, A.; Rao, A. Exploring the impact of epistemic uncertainty on a regional probabilistic seismic risk assessment model. Nat. Hazards 2020, 104, 997–1020. [Google Scholar] [CrossRef]
- Kotha, S.R.; Bazzurro, P.; Pagani, M. Effects of epistemic uncertainty in seismic hazard estimates on building portfolio losses. Earthq. Spectra 2018, 34, 217–236. [Google Scholar] [CrossRef] [Green Version]
- Hussain, E.; Elliott, J.R.; Silva, V.; Vilar-Vega, M.; Kane, D. Contrasting seismic risk for Santiago, Chile, from near-field and distant earthquake sources. Nat. Hazards Earth Syst. Sci. 2020, 20, 1533–1555. [Google Scholar] [CrossRef]
- Ghofrani, H.; Atkinson, G.M. Ground-motion prediction equations for interface earthquakes of M7 to M9 based on empirical data from Japan. Bull. Earthq. Eng. 2014, 12, 549–571. [Google Scholar] [CrossRef]
- Abrahamson, N.; Gregor, N.; Addo, K. BC hydro ground motion prediction equations for subduction earthquakes. Earthq. Spectra 2016, 32, 23–44. [Google Scholar] [CrossRef]
- Montalva, G.A.; Bastías, N.; Rodriguez-Marek, A. Ground-motion prediction equation for the chilean subduction zone. Bull. Seism. Soc. Am. 2017, 107, 901–911. [Google Scholar] [CrossRef]
- Peyghaleh, E.; Mahmoudabadi, V.; Martin, J.R.; Shahjouei, A.; Chen, Q.; Javanbarg, M.; Khoshnevisan, S. Impact of local site conditions on portfolio earthquake loss estimation for different building types. Nat. Hazards 2018, 94, 121–150. [Google Scholar] [CrossRef]
- Heath, D.C.; Wald, D.J.; Worden, C.B.; Thompson, E.M.; Smoczyk, G.M. A global hybrid VS30 map with a topographic slope–Based default and regional map insets. Earthq. Spectra 2020, 36, 1570–1584. [Google Scholar] [CrossRef]
- Mendoza, L.; Ayala, F.; Fuentes, B.; Soto, V.; Sáez, E.; Yañez, G.; Montalva, G.; Gález, C.; Sepúlveda, N.; Lazo, I.; et al. Estimación Cuantitativa de la Amenaza Sísmica en Base a Métodos Geofísicos: Aplicación a las Localidades Costeras del Segmento los Vilos—San Antonio; Congreso SOCHIGE: Valparaiso, Chile, 2018. [Google Scholar]
- Weatherill, G.A.; Silva, V.; Crowley, H.; Bazzurro, P. Exploring the impact of spatial correlations and uncertainties for portfolio analysis in probabilistic seismic loss estimation. Bull. Earthq. Eng. 2015, 13, 957–981. [Google Scholar] [CrossRef]
- Jayaram, N.; Baker, J.W. Correlation model for spatially distributed ground-motion intensities. Earthq. Eng. Struct. Dyn. 2009, 38, 1687–1708. [Google Scholar] [CrossRef]
- Markhvida, M.; Ceferino, L.; Baker, J.W. Modeling spatially correlated spectral accelerations at multiple periods using principal component analysis and geostatistics. Earthq. Eng. Struct. Dyn. 2018, 47, 1107–1123. [Google Scholar] [CrossRef]
- Silva, V. Critical issues in earthquake scenario loss modeling. J. Earthq. Eng. 2016, 20, 1322–1341. [Google Scholar] [CrossRef]
- Pittore, M.; Gomez-Zapata, J.C.; Brinckmann, N.; Rüster, M. Assetmaster and modelprop: Web services to serve building exposure models and fragility functions for physical vulnerability to natural-hazards. V. 1.0. GFZ Data Serv. 2021. [Google Scholar] [CrossRef]
- Brinckmann, N.; Gomez-Zapata, J.C.; Pittore, M.; Rüster, M. DEUS: Damage-exposure-update-service. V. 1.0. GFZ Data Serv. 2021. [Google Scholar] [CrossRef]
- Beven, K.J.; Aspinall, W.P.; Bates, P.D.; Borgomeo, E.; Goda, K.; Hall, J.W.; Page, T.; Phillips, J.C.; Simpson, M.; Smith, P.J.; et al. Epistemic uncertainties and natural hazard risk assessment—Part 2: What should constitute good practice? Nat. Hazards Earth Syst. Sci. 2018, 18, 2769–2783. [Google Scholar] [CrossRef] [Green Version]
- Vamvatsikos, D.; Panagopoulos, G.; Kappos, A.J.; Nigro, E.; Rossetto, T.; Lloyd, T.O.; Stathopoulos, T. Structural vulnerability assessment under natural hazards: A review. In Urban Habitat Constructions under Catastrophic Events; Chapter 3–4; Mazzolani, F.M., Ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Stafford, P.J. Evaluation of structural performance in the immediate aftermath of an earthquake: A case study of the 2011 christchurch earthquake. Int. J. Forensic Eng. 2012, 1, 58–77. [Google Scholar] [CrossRef]
- Aguirre, P.; Vásquez, J.; de la Llera, J.C.; González, J.; González, G. Earthquake damage assessment for deterministic scenarios in Iquique, Chile. Nat. Hazards 2018, 92, 1433–1461. [Google Scholar] [CrossRef]
- Zuccaro, G.; De Gregorio, D.; Leone, M.F. Theoretical model for cascading effects analyses. Int. J. Disaster Risk Reduct. 2018, 30, 199–215. [Google Scholar] [CrossRef]
- Pilz, M.; Cotton, F. Does the one-dimensional assumption hold for site response analysis? A study of seismic site responses and implication for ground motion assessment using KiK-Net strong-motion data. Earthq. Spectra 2019, 35, 883–905. [Google Scholar] [CrossRef]
- Candia, G.; Poulos, A.; de la Llera, J.C.; Crempien, J.G.F.; Macedo, J. Correlations of spectral accelerations in the Chilean subduction zone. Earthq. Spectra 2020, 36, 788–805. [Google Scholar] [CrossRef]
- Abbasnejadfard, M.; Bastami, M.; Fallah, A.; Garakaninezhad, A. Analyzing the effect of anisotropic spatial correlations of earthquake intensity measures on the result of seismic risk and resilience assessment of the portfolio of buildings and infrastructure systems. Bull. Earthq. Eng. 2021, 19, 5791–5817. [Google Scholar] [CrossRef]
- Cabrera, T.; Hube, M.; Santa María, H. Empirical fragility curves for reinforced concrete and timber houses, using different intensity measures. In Proceedings of the 17th World Conference on Earthquake Engineering, Sendai, Japan, 13–18 September 2020. [Google Scholar]
- Sousa, L.; Silva, V.; Marques, M.; Crowley, H. On the treatment of uncertainty in seismic vulnerability and portfolio risk assessment. Earthq. Eng. Struct. Dyn. 2018, 47, 87–104. [Google Scholar] [CrossRef]
- Pittore, M.; Graziani, L.; Maramai, A.; Haas, M.; Parolai, S.; Tertulliani, A. Bayesian estimation of macroseismic intensity from post-earthquake rapid damage mapping. Earthq. Spectra 2018, 34, 1809–1828. [Google Scholar] [CrossRef]
- Contreras, D.; Wilkinson, S.; James, P. Earthquake reconnaissance data sources, a literature review. Earth 2021, 2, 1006–1037. [Google Scholar] [CrossRef]
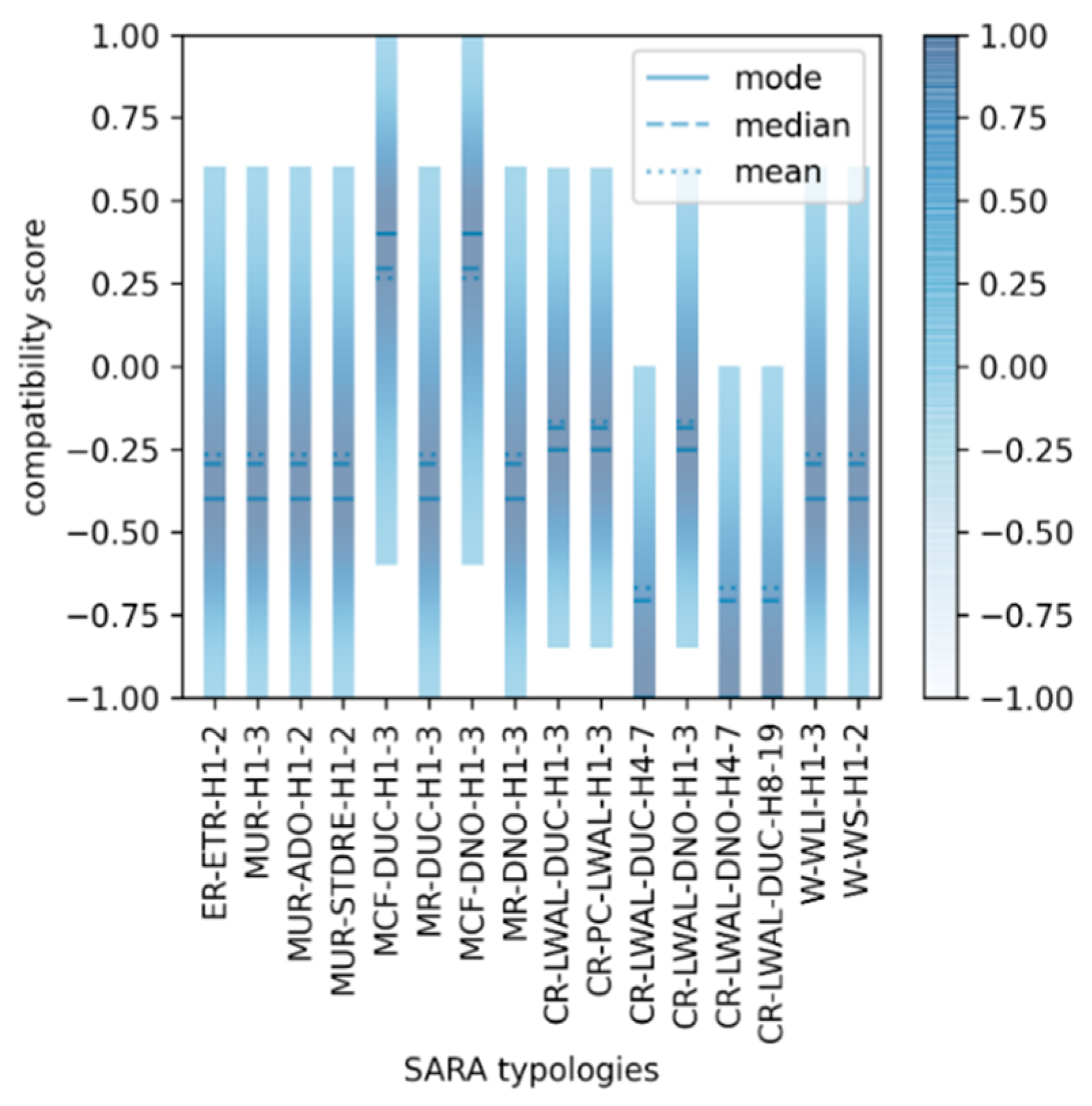
- Gomez-Zapata, J.C.; Shinde, S.; Pittore, M.; Merino-Peña, Y. Scripts to generate (1) Attribute-based fuzzy scores for SARA and HAZUS building classes, and (2) Probabilistic inter-scheme compatibility matrices. An application on the residential building stock of Valparaiso (Chile) for seismic risk applications. GFZ Data Serv. 2021. [Google Scholar] [CrossRef]
- Xing, E.P. 19: Bayesian Nonparametrics: Dirichlet Processes. Probabilistic Graphical Models 10-708. 2014. Available online: https://www.cs.cmu.edu/~epxing/Class/10708-14/scribe_notes/scribe_note_lecture19.pdf (accessed on 21 December 2021).
- Pittore, M.; Wieland, M. Toward a rapid probabilistic seismic vulnerability assessment using satellite and ground-based remote sensing. Nat. Hazards 2013, 68, 115–145. [Google Scholar] [CrossRef]
- Lynch, S.M. Introduction to Applied Bayesian Statistics and Estimation for Social Scientists; Springer: New York, NY, USA, 2007; ISBN 978-0-387-71264-2. [Google Scholar]
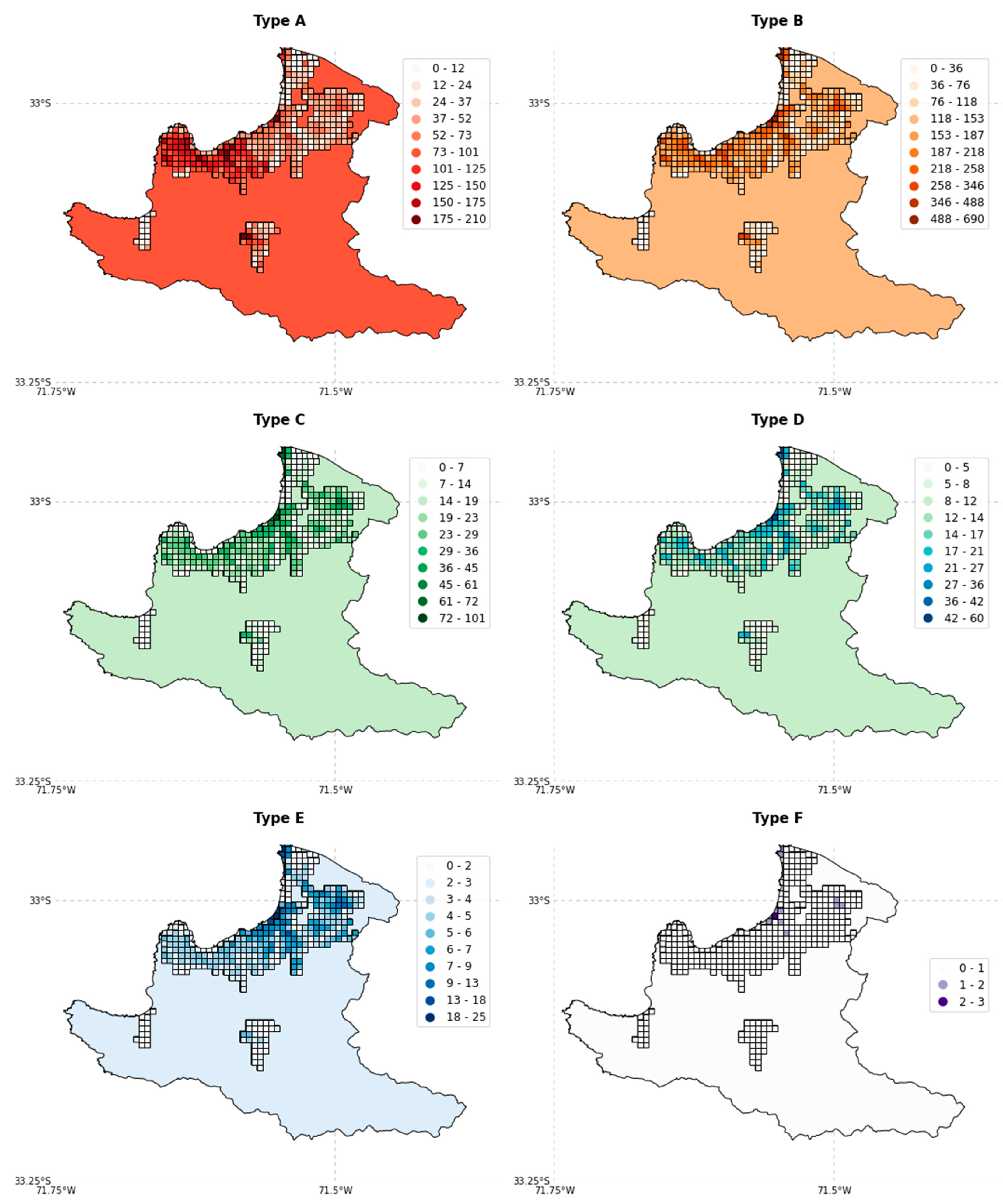
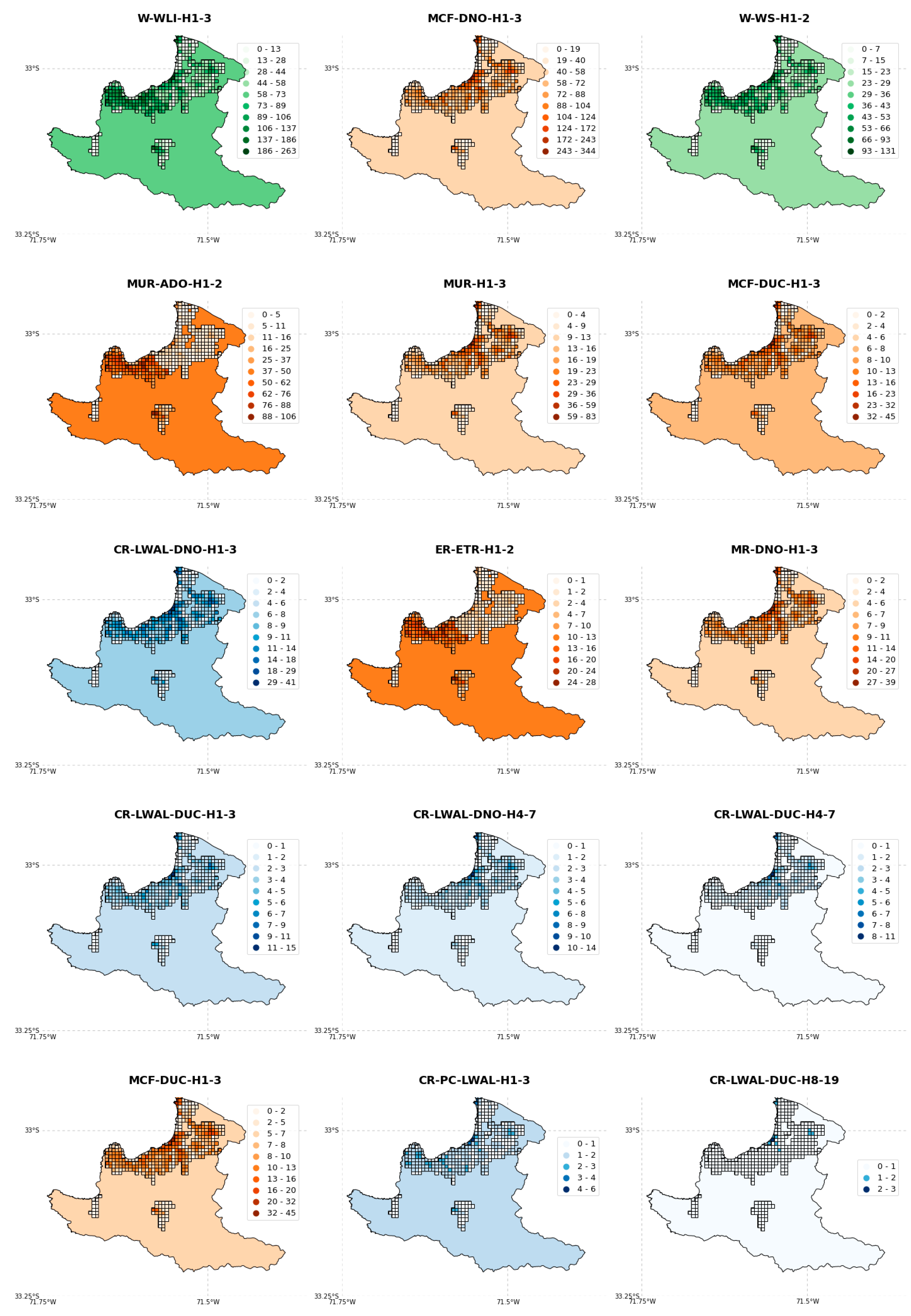

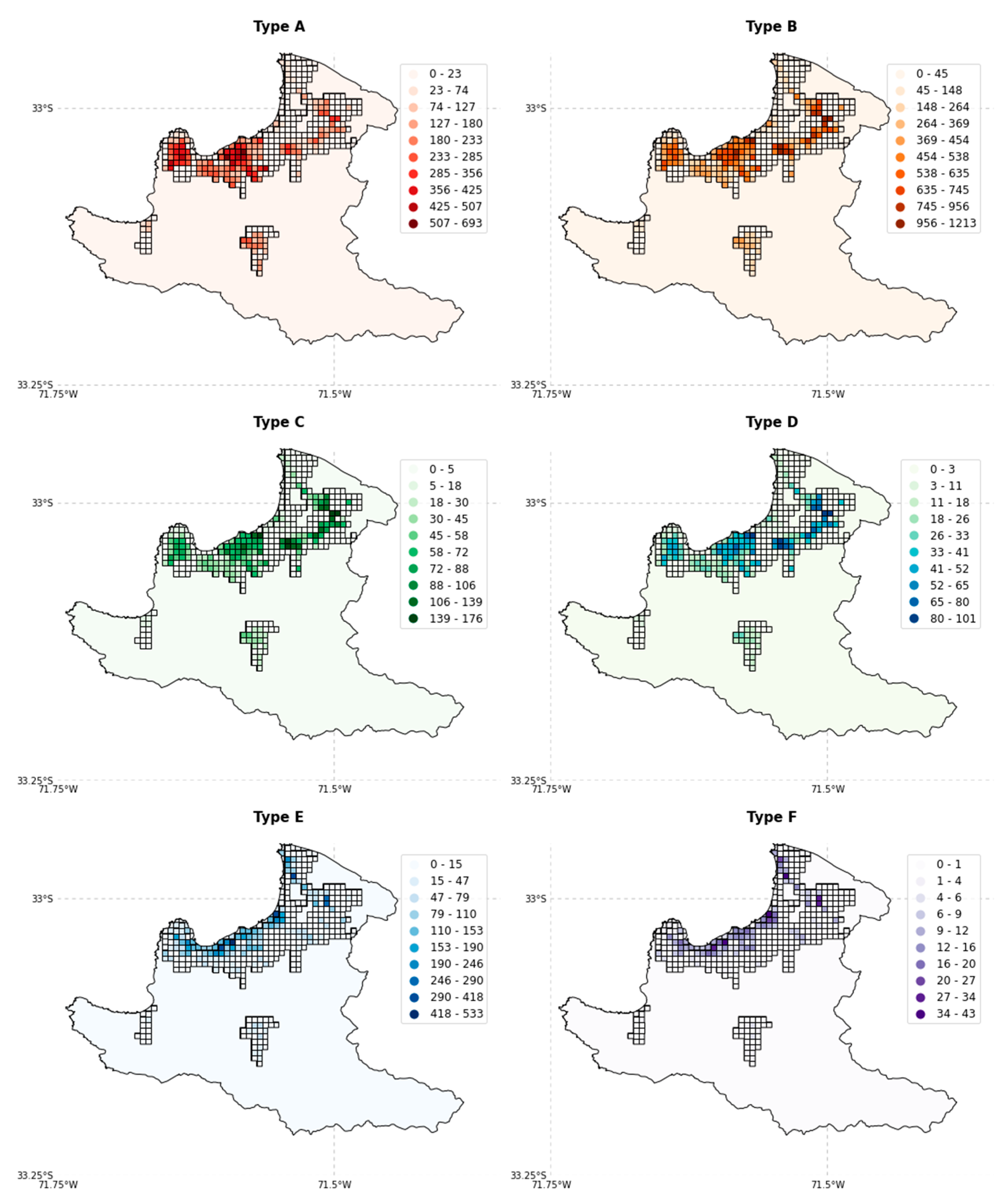
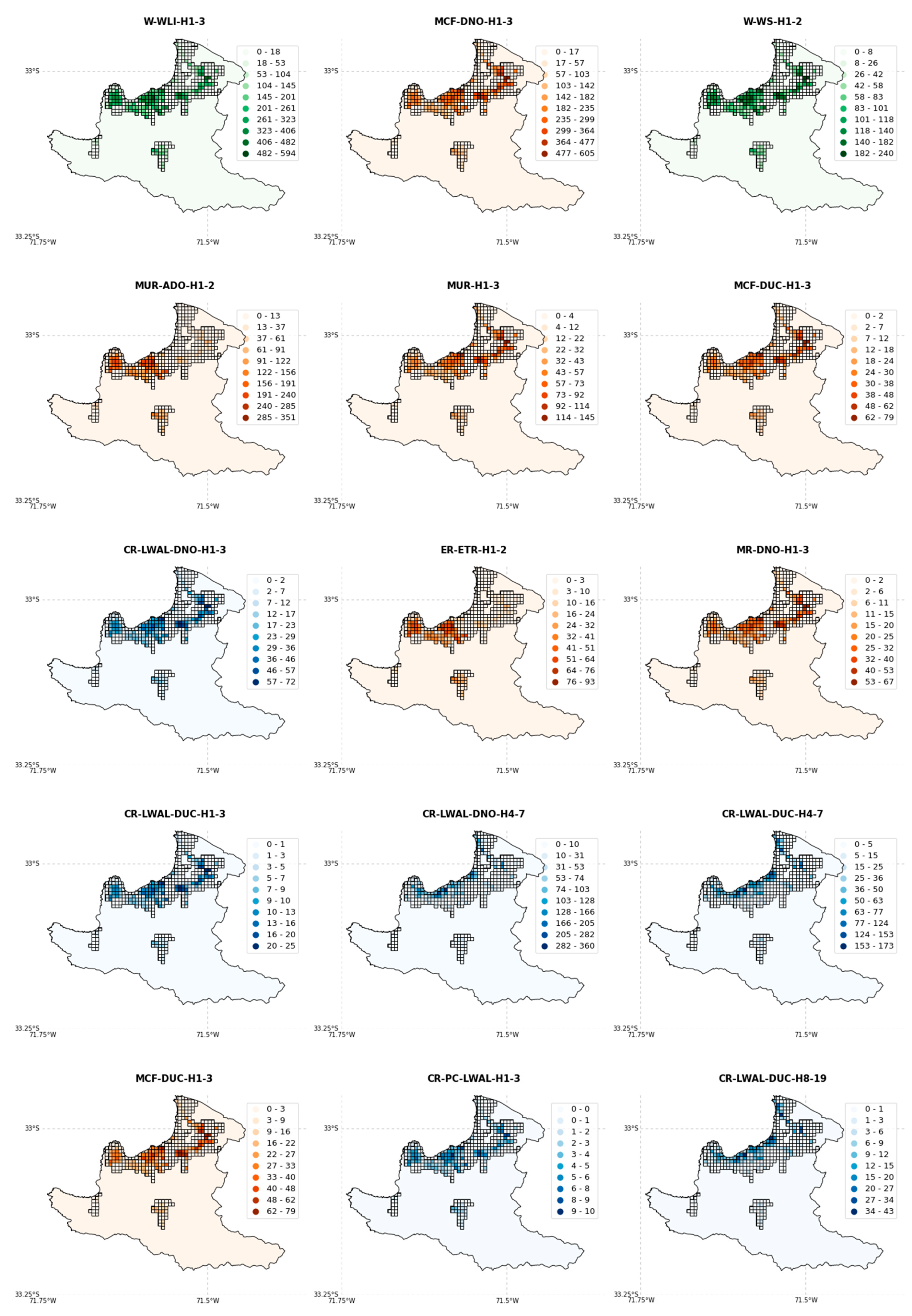
| Typologies | Description | Dwel/bdg. | Ft/bdg. (m2) | Res./ bdg. | Repl. Cost (USD) | New Type |
|---|---|---|---|---|---|---|
| ER + ETR/H:1,2 | Rammed earth, 1–2 stories | 1.25 | 78.79 | 4 | 43,750 | A |
| MUR + ADO/H:1,2 | Unreinforced masonry with adobe blocks, 1–2 stories | 1.25 | 66.84 | 4 | 43,750 | |
| MUR + STDRE/H:1,2 | Unreinforced masonry, dressed stone, 1–3 stories | 1.25 | 65.32 | 5 | 43,750 | |
| W + WS/H:1,2 | Solid wood, between 1–2 stories | 1.25 | 80.00 | 4 | 108,000 | |
| MCF/DNO/H:1,3 | Confined masonry (non-ductile), 1–3 stories | 4 | 46.67 | 5 | 94,500 | B |
| MUR/H:1,3 | Unreinforced masonry, 1–3 stories | 1.5 | 70.00 | 6 | 52,500 | |
| W + WLI/H:1,3 | Light wood members, 1–3 stories | 1.5 | 80.00 | 5 | 108,000 | |
| CR/LWAL/DNO/H:1,3 | Reinforced concrete wall system (non-ductile), 1–3 stories | 4 | 160.00 | 14 | 288,000 | C |
| CR/LWAL/DUC/H:1,3 | Reinforced concrete wall system (ductile), 1–3 stories | 4 | 140.00 | 15 | 336,000 | |
| MCF/DUC/H:1,3 | Confined masonry (ductile), 1–3 stories | 4 | 160.00 | 5 | 288,000 | |
| CR + PC/LWAL/H:1,3 | Precast reinforced concrete wall system, 1–3 stories | 5 | 160.00 | 18 | 360,000 | D |
| MR/DNO/H:1,3 | Reinforced masonry (non-ductile), 1–3 stories | 5 | 160.00 | 18 | 360,000 | |
| MR/DUC/H:1,3 | Reinforced masonry (ductile), 1–3 stories | 5 | 140.00 | 18 | 360,000 | |
| CR/LWAL/DNO/H:4,7 | Reinforced concrete wall system (non-ductile), 4–7 stories | 15 | 240.00 | 54 | 1,080,000 | E |
| CR/LWAL/DUC/H:4,7 | Reinforced concrete wall system (ductile), 4–7 stories | 15 | 210.00 | 54 | 1,260,000 | |
| CR/LWAL/DUC/H:8,19 | Reinforced concrete wall system (ductile), 8–19 stories | 48 | 218.15 | 173 | 4,032,000 | F |
| Typology | Average Height (m) | In Viña del Mar | In Valparaíso | ||
|---|---|---|---|---|---|
| Average Footprint Area (m2) | Proportion | Average Footprint Area (m2) | Proportion | ||
| A | 3.75 | 67.5 | 21% | 73 | 38% |
| B | 4.5 | 71 | 59% | 66 | 50% |
| C | 6 | 153 | 11% | 153 | 7% |
| D | 7.5 | 115 | 5% | 153 | 3% |
| E | 15 | 225 | 3% | 225 | 1% |
| F | 36 | 280 | 1% | 280 | 1% |
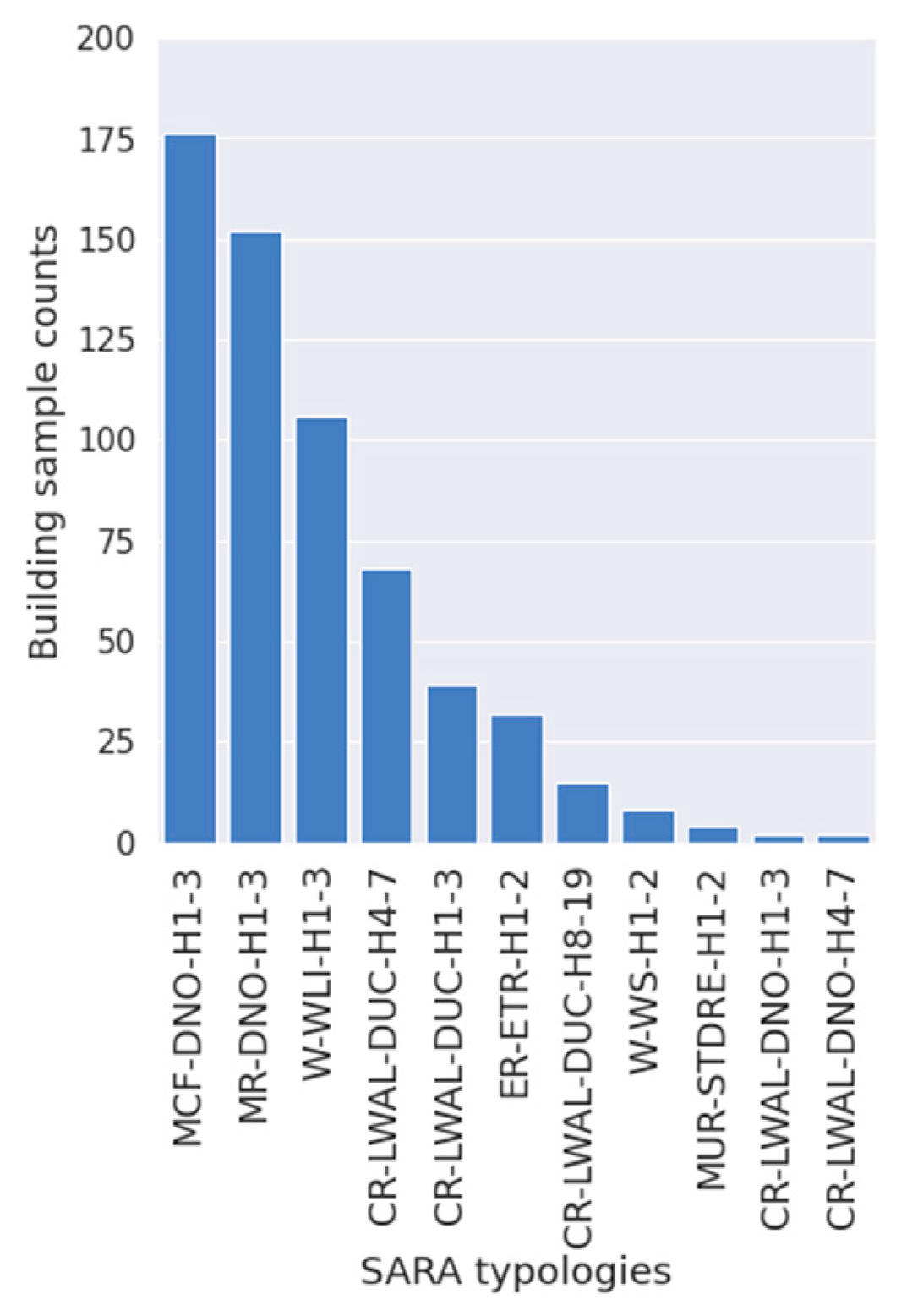
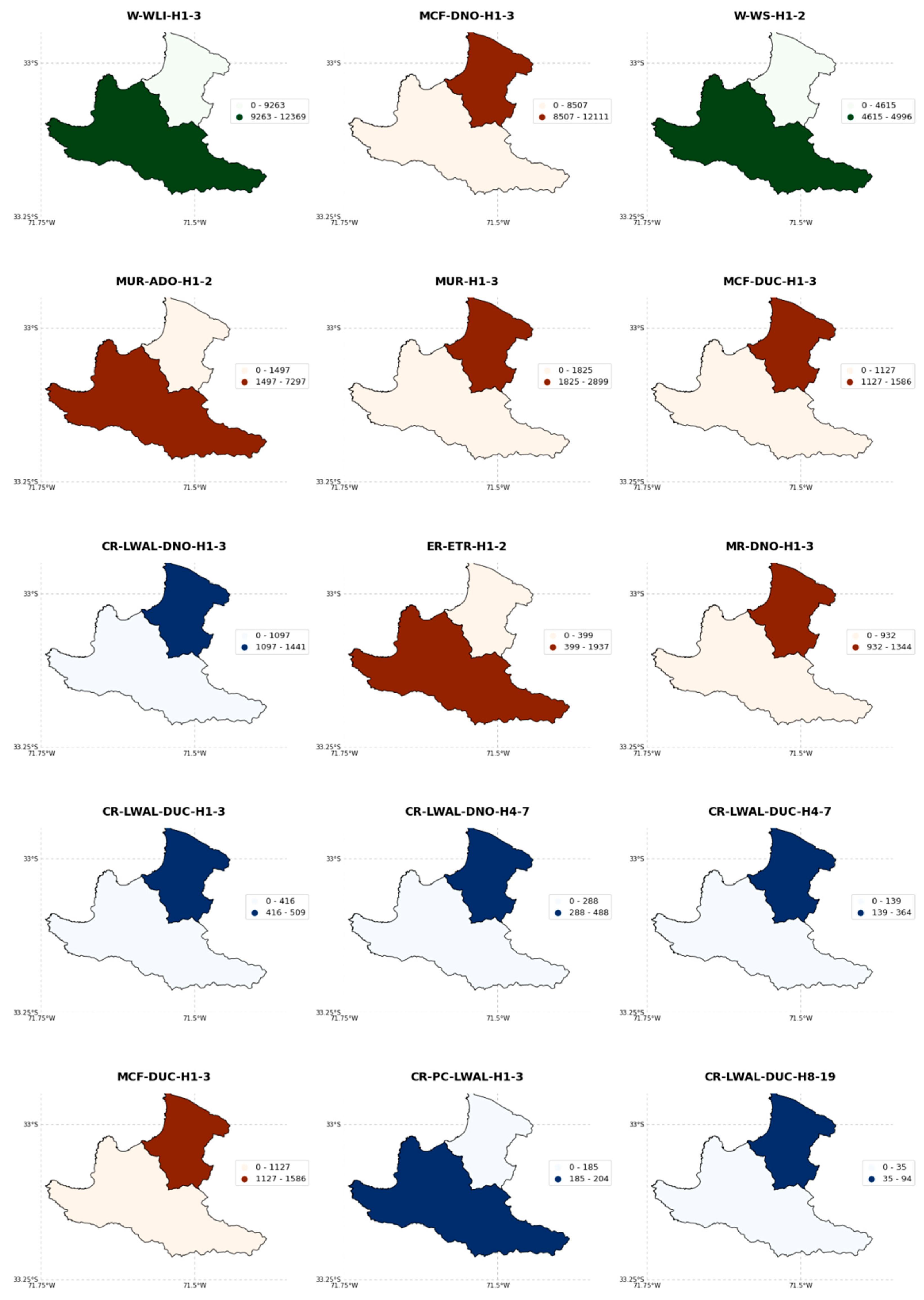
| Initial Model (Commune-Based with Merged Classes, Section 3.2.1) | Freq. (%) | Preliminary Model (Simple Downscaling, Section 3.2.2) | Freq. (%) | Probabilistic Model (Bayesian Dowsncaling, Section 3.2.4) | Freq. (%) | |
|---|---|---|---|---|---|---|
| W-WLI-H1-3 | 21,631 | 27.29 | 23,374 | 26.22 | 33,695 | 24.97 |
| MCF-DNO-H1-3 | 20,617 | 26.01 | 23,146 | 25.97 | 31,244 | 23.15 |
| W-WS-H1-2 | 9610 | 12.12 | 10,619 | 11.91 | 14,835 | 10.99 |
| MUR-ADO-H1-2 | 8793 | 11.09 | 9013 | 10.11 | 14,298 | 10.59 |
| MUR-H1-3 | 4723 | 5.96 | 5494 | 6.16 | 7128 | 5.28 |
| MCF-DUC-H1-3 | 2712 | 3.42 | 3216 | 3.61 | 4111 | 3.05 |
| CR-LWAL-DNO-H1-3 | 2537 | 3.2 | 3006 | 3.37 | 3854 | 2.86 |
| ER-ETR-H1-2 | 2335 | 2.95 | 2542 | 2.85 | 3801 | 2.82 |
| MR-DNO-H1-3 | 2274 | 2.87 | 2728 | 3.06 | 3449 | 2.56 |
| MR-DUC-H1-3 | 924 | 1.17 | 1222 | 1.37 | 1407 | 1.04 |
| CR-LWAL-DUC-H1-3 | 865 | 1.09 | 1166 | 1.31 | 1311 | 0.97 |
| CR-LWAL-DNO-H4-7 | 775 | 0.98 | 1065 | 1.19 | 8293 | 6.14 |
| CR-LWAL-DUC-H4-7 | 502 | 0.63 | 792 | 0.89 | 4980 | 3.69 |
| MUR-STDRE-H1-2 | 452 | 0.57 | 723 | 0.81 | 689 | 0.51 |
| CR-PC-LWAL-H1-3 | 388 | 0.49 | 633 | 0.71 | 603 | 0.45 |
| CR-LWAL-DUC-H8-19 | 129 | 0.16 | 398 | 0.45 | 1265 | 0.94 |
| ∑ total | 79,267 | 100 | 89,137 | 100 | 134,963 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez Zapata, J.C.; Zafrir, R.; Pittore, M.; Merino, Y. Towards a Sensitivity Analysis in Seismic Risk with Probabilistic Building Exposure Models: An Application in Valparaíso, Chile Using Ancillary Open-Source Data and Parametric Ground Motions. ISPRS Int. J. Geo-Inf. 2022, 11, 113. https://doi.org/10.3390/ijgi11020113
Gómez Zapata JC, Zafrir R, Pittore M, Merino Y. Towards a Sensitivity Analysis in Seismic Risk with Probabilistic Building Exposure Models: An Application in Valparaíso, Chile Using Ancillary Open-Source Data and Parametric Ground Motions. ISPRS International Journal of Geo-Information. 2022; 11(2):113. https://doi.org/10.3390/ijgi11020113
Chicago/Turabian StyleGómez Zapata, Juan Camilo, Raquel Zafrir, Massimiliano Pittore, and Yvonne Merino. 2022. "Towards a Sensitivity Analysis in Seismic Risk with Probabilistic Building Exposure Models: An Application in Valparaíso, Chile Using Ancillary Open-Source Data and Parametric Ground Motions" ISPRS International Journal of Geo-Information 11, no. 2: 113. https://doi.org/10.3390/ijgi11020113
APA StyleGómez Zapata, J. C., Zafrir, R., Pittore, M., & Merino, Y. (2022). Towards a Sensitivity Analysis in Seismic Risk with Probabilistic Building Exposure Models: An Application in Valparaíso, Chile Using Ancillary Open-Source Data and Parametric Ground Motions. ISPRS International Journal of Geo-Information, 11(2), 113. https://doi.org/10.3390/ijgi11020113