Ambulances Deployment Problems: Categorization, Evolution and Dynamic Problems Review

Abstract

In this paper, an analytic review of the recent methodologies tackling the problem of dynamic allocation of ambulances was carried out. Considering that state-of-the-art is moving to deal with more extensive and dynamic problems to address in a better way real-life instances, this research looks to identify the evolution and recent applications of this kind of problem once the basic models are explored. This extensive review allowed us to identify the most recent developments in this problem and the most critical gaps to be addressed. In this sense, it is essential to point out that the dynamic location of emergency medical services (EMS) is nowadays a relevant topic considering its impact on the healthcare system outcomes. Issues related to forecasting, simulation, heterogeneous fleets, robustness, and solution speed for real-life problems, stand out in the identified gaps. Applications of machine learning the deployment challenges during epidemic outbreaks such as SARS and COVID-19 were also explored. At the same time, a proposed notation tries to tackle the fact that the word problem in this kind of work refers to a model on many occasions. The proposed notation eases the comparison between the different model proposals found in the literature.

1. Introduction

Diseases such as stroke and heart arrest result in high costs to the economy alongside prolonged periods of stay in clinics, hospitals, and care homes. This situation has turned the global attention to healthcare systems, considering that its outcome has a significant impact on the quality of life of people, a nation’s productivity, and a nation’s finances [1]. Additionally, due to the inversion in the population pyramid worldwide, it has become more important that people live longer, having a good quality of life. These unbalanced proportions affect the retirement-income (pension) system, forcing the elderly to work to more advanced ages, making it necessary that the elderly have good health [2]. Healthcare systems are a critical element for this purpose. Therefore, investments to improve different aspects of the healthcare system are crucial [3].

On the other hand, the outcome of daily activities taking place in an Emergency Room (ER) requires not only innovation in medical research but also speed in procedures and promptness in taking the patients to ER to increase their chances to recover well [4,5]. For example, in the case of acute stroke, the benefits of using the rtPa treatment are evident if given in less than 4.5 h after the stroke event [1]. In the case of a heart attack, each minute of delay in the patient receiving treatment decreases the probability of survival by 10%. Additionally, the likelihood that the patient remains with some disabilities increases with time [5,6,7]. These disabilities may cause other conditions such as dementia, causing the person to reenter the system to receive additional treatment, increasing system costs and affecting the patient’s quality of life [1,8].

In many cases, continuing life depends on a career to carry out the activities of daily life [1,8,9]. This impact is evident in cardiovascular diseases (CVD) such as stroke. According to WHO (World Health Organization), CVD caused the death of 17.9 million people in 2016, representing a total cost of around EUR 900 billion [10], of which 50% is described by direct costs of care, including hospitalization, external consultation, medication costs, and home care [11]. Likewise, 27% of the total charges are given by indirect expenses and the rest by indirect costs to the economy due to premature death and disability [12].

Therefore, ambulances’ fast response is a crucial factor in the good outcomes in ER, impacting both the probability of survival and having disabilities [13], making it essential for all countries [14,15,16,17]. In this sense, different reviews have been undertaken previously. Still, none of them tried to cover both the ambulance routing problem and the ambulance deployment problem at the same time despite these problems being closely interrelated. Additionally, this survey attempts to combine the most recent research related to dynamic redeployment and Artificial Intelligence (AI) to tackle different aspects of the problem, such as demand forecasting and redeployment.

The paper is organized as follows: Section 2 describes the methodology used in the review process. Section 3 contains a characterization of the ambulance service process from the moment the emergency call enters to the moment the patient is received at the hospital. The now free ambulance needs to head to a defined location to wait for the next call. Section 4 presents a classification of the ambulance location and routing problems. Section 5 describes the ambulance location problem by analyzing main objectives, constraints, heuristics, and other aspects considered for this problem by different researchers and analyzes the literature review results regarding dynamic approaches. Finally, in Section 6, some conclusions with the research gaps identified in the process are described.

2. Review Methodology

This work, conducted as a systematic literature review of dynamic ambulance location problems, was led in four stages, following PRISMA guidelines and the methodology described by Sanchez et al. [18]. In the first stage, we constructed the query strings; the second stage focused on gathering potential results in the Web of Science (WoS) database; the third focused on excluding and including results based on criteria. Finally, the fourth stage consisted of characterizing and analyzing the selected literature.

The search was carried out using the following keywords: Ambulances, EMS, Dynamic deployment, Dynamic location, relocation, and redeployment. The review did not consider gray literature. Although WoS and Scopus share many quality journal characteristics, they also differ in coverage and accuracy, according to [19]. According to Sanchez et al. [18], even though Scopus covers more journals than WoS, it tends to neglect indexing more papers, causing the loss of possibly relevant information. Additionally, WoS has a strong reputation indexing journals in the science and technology field and better accuracy in journal classification [18,19], allowing us to access more updated and better-classified information. The relevance of the accessed journals allows us to be confident that the information used in the review is pertinent.

The above, in conjunction with the review method and the inclusion and exclusion criteria, helped to reduce the efforts of exploring quality scientific information, as the review seeks to determine the most recent and relevant developments and applications in the dynamic ambulance location problems. A complete view of the whole review process is shown in Figure 1 The initial query string (QS) was:

EMS relocation* OR EMS redeployment* OR EMS dynamic location* OR EMS dynamic deployment* OR ambulance*

The filtering process depicted in Figure 1 allowed us to review 49 documents. The trends in the selected papers’ publications can be observed in Figure 2. From this figure, it can be concluded that the number of publications related to this topic is increasing, showing that this is a relevant research topic in the scientific community. This topic is critical, considering its impact, as described in the introduction.

The search process followed the steps described by Sanchez et al. [18]. The keywords used in the process are location, relocation, ambulances, deployment, machine learning, forecasting, and redeployment. According to Figure 3, simulation and EMS are the most relevant topics within the ambulance location/relocation problems. This fact indicates that simulation is a frequent solution approach for this type of problem. From the diagram, it can also be concluded that there is considerable concern regarding the inclusion of equity issues.

Nevertheless, the classical covering concept is still relevant within the filtered papers. This figure also shows the need for standardization within this kind of problem. For example, the words, deployment, and location are used to deal with the same situation. A similar situation happens with the words redeployment and relocation.

In addition, it is not clear when this relocation is considered static or dynamic. It is also important to point out the static relevance redeployment has, considering the number of papers that use this approach. This kind of approach is usually implemented with compliance tables. Likewise, the concept of coverage is often related to response time. Nevertheless, the quest for lower mean response times does not imply obtaining a better survival rate [7] in many cases. Therefore, an integrated deployment/dispatching decision approach is vital for the outcomes of the system. As mentioned before, equity measures, whether in the objective function or the decision process, are gaining prominence. It is also important to point out that equity measures are not single-dimensional. Still, different facets force a multi-objective optimization in the objective function and heuristics in the decision process. The use of heuristics also tries to deal with the need to obtain fast results in dynamic redeployment.

From each paper, the critical information is related to:

• Tackled problem;
• Model used;
• Optimization objective;
• Optimization tools;
• Results.

This information was processed and organized to analyze the recent developments regarding dynamic ambulance location problems.

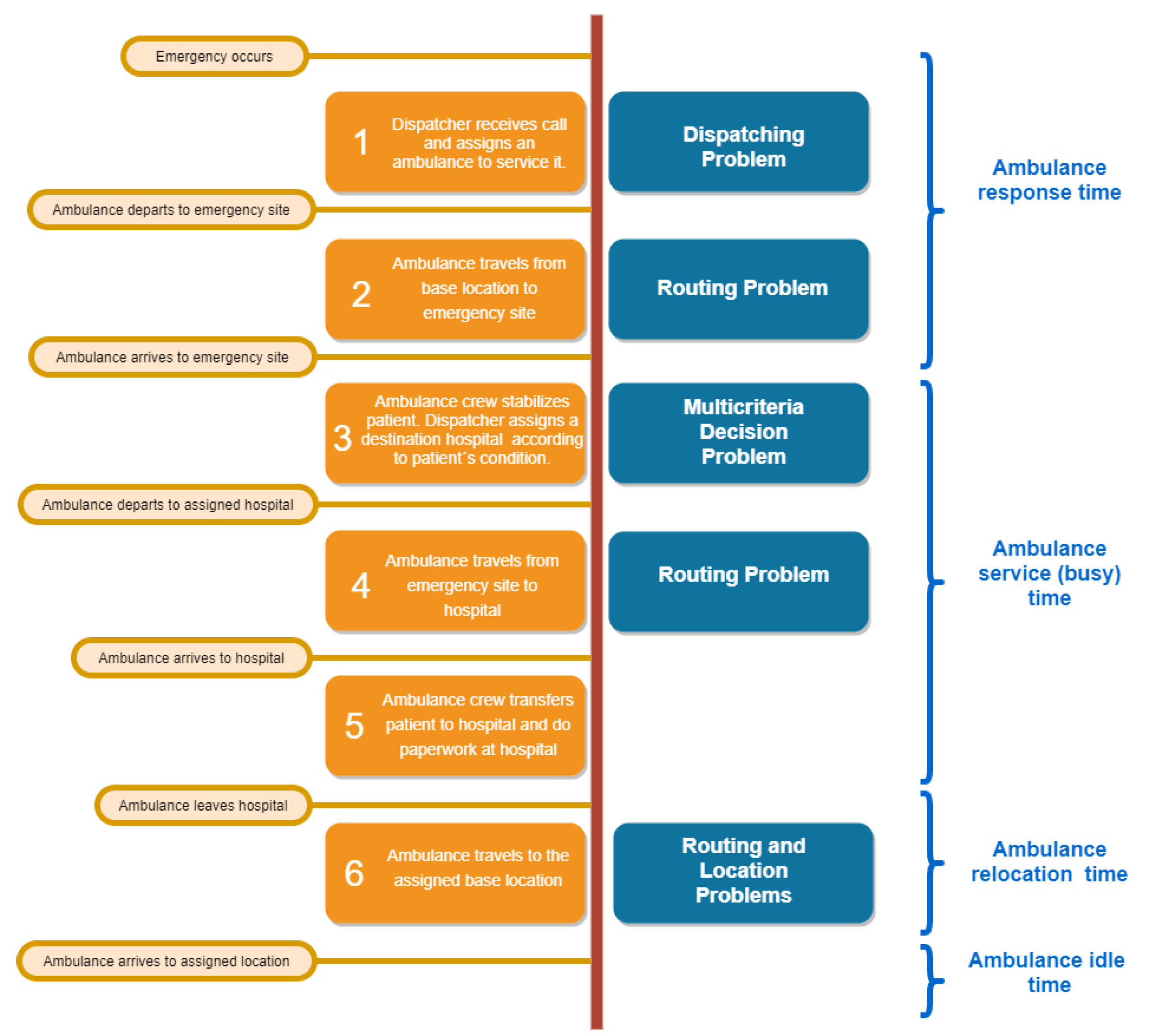
3. The Ambulance Service Process

Emergency medical services (EMS) essentially refers to the provision of out-of-hospital acute medical care and the transport of patients to hospitals for definitive care [20]. Nevertheless, to better understand the process, its improvement opportunities, and the different agents involved in it and affect its performance, it is necessary to describe the process.

In the ambulance service process, a group of activities is carried out that usually begins with the reception of a call and a request for the information necessary to identify the severity of the patient to make decisions to determine which vehicle is the best alternative to send to the emergency site. The distance from idle vehicles influences this decision-making process to the emergency site, the type of ambulance required due to the severity of the emergency, and the availability of idle ambulances. There are different procedures to decide which ambulance could service a particular emergency, differing between each order in the factors considered in the process and the tools used to make the decision [5].

Once the vehicle arrives at the event site, the crew performs pre-hospital care; then, if necessary, the patient is assigned and moved to a hospital, considering the hospital-enabled services and its closeness to the emergency site. Then, after delivering the patient to the hospital, the ambulance should position itself at a particular point and wait for the next service assignment [5,7,20]. The positioning activity can be executed considering a fixed position or a dynamic positioning depending on emergency occurrence forecasts.

Figure 4 shows that some operations in the process, such as stabilizing the patient at the emergency site, are within the medical field. Other procedures are in the administrative area, as the hospital time, in which the crew may perform some auxiliary medical operations. Still, the main objective is to transfer information regarding the patient, vital signs, applied medical procedures, among others. The dispatcher performs administrative functions with the assistance of an information system. This information system should allow the dispatcher to determine the position of the different idle ambulances and the distance from the emergency site to the destination hospital. The dispatcher, in this step, evaluates the emergency report and determines the degree of severity of the incident to proceed with the dispatching decision. This decision involves determining the type and quantity of vehicles needed to service the emergency call, which is available at the time of the emergency. Once the dispatcher assigns an ambulance(s) to an emergency or determines a destination hospital, the ambulance(s) should reach their destination as soon as possible; in these cases, a routing problem emerges.

Nevertheless, it is essential to point out that the dispatching policy is relevant in the decision and may affect the outcome of the system in terms of survival rate. Therefore, this administrative decision, which the dispatcher often makes, has recently become more integrated with the location/relocation decision. Finally, the idle ambulance needs to reach its location point, dealing again with a routing problem. The decision of the ambulance location/relocation can be dynamic or static. When dynamic, this position may change in time depending on received calls, i.e., the system adapts itself to the evolution of the traffic requirements in time. When static, the ambulance always returns to the same location point once it becomes idle or relocates with a fixed schedule or condition. It is essential to point out that routing and location problems are significant for ambulance service performance. The fact that routing problems appear more times in the scheme does not mean routing problems are more important than location problems. A good location can reduce ambulance travel times. In this sense, both routing and location problems can be considered operational decisions. Nevertheless, these operational decisions follow specific policies defined at a strategic level.

In the process represented in Figure 4, two conditions that affect the ambulance service’s performance must be addressed. These conditions occur when the dispatcher sends an ambulance to an emergency and when the vehicle becomes available again to service a new event. In the first case, one or several ambulances are no longer available because they are serving other emergencies. In this case, the available ambulances cannot locate close to where the next emergency occurs. In the second case, one or more unavailable vehicles change their status to available. The dispatcher must decide which location to send each ambulance to wait for the next emergency.

When addressing the location decision as a dynamic one, and the operation of the medical system is centralized, the supervisors of the medical system must, over time, determine the location of the fleet of medical care vehicles within the geographical space where the service is required. The location must consider that in future emergencies, the response times be adequate. Depending on each particular case, the location decision may include the following issues: types of vehicle to locate (heterogeneous fleet); authorized locations for these ambulances; the number of ambulances that can be allocated in each particular place at the same time (location capacity); the different types of emergencies; and the constraints due to the different kinds of vehicles available to respond to specific types of emergencies.

4. Ambulance Location and Routing Problems Classification

Looking at the EMS planning process helps to understand the ambulance routing and location problems. According to Reuter-Oppermann et al. [21], EMS planning divides into the following parts: the general design of the services, the logistics to fulfill the benefits, and the services’ analytics.

Existing laws and regulations mainly determine the design of the services. Moreover, general decisions must be made. For example, is it always the best decision to assign the closest ambulance to the emergency. On the other hand, two additional critical factors for the proper system performance must be considered. These two factors are logistics and analytics. The primary purpose of logistics is to guarantee that the system fulfills all the country’s regulation, standards, and laws and simultaneously deliver an appropriate service.

On the other hand, the system’s analytics relates to processing all the information related to the system, such as travel times, duration of paramedical care on-site, time from the emergency site to hospital, and others. These data can be used to forecast future demand and assist in defining the number of ambulances required and their location. Finally, this data can also be used to monitor the system’s performance and check if standards, laws, and regulations are being fulfilled. Both logistics and analytics are in the field of operations research regarding the EMS planning process. This planning process covers strategic (determination of the size of the system), tactical (when determining location based on upcoming expected demand), and operational levels (when working on real-time data and deciding on relocation).

These three planning horizons interact and affect many other decisions in the system. For example, relocation policy, the number of ambulances, and the type of ambulances affect workload decisions. These situations also require a decision process to find the best way to assign the shifts, guaranteeing that all the locations and relocation can be accomplished and the crew does not get exhausted, considering that this will affect the quality of the service. Regarding the type of ambulance, the most common type of ambulance is Advanced Life Support (ALS) and Basic Life Support Advanced Life (BLS). Required crews are different for each class. Figure 5 portrays the relations between the various disciplines and problems involved in EMS planning.

According to Reuter-Oppermann et al. [21], EMS planning involves different disciplines such as Logistics, Service Design, and Analytics. The three domains themselves contain various problems. In Figure 5, the dotted line shows the disciplinary area to which ambulance routing and location problems belong. Many researchers try to address this problem using different tools, considering other constraints or assumptions. In most cases, it is necessary to read the paper to determine the scope of the researcher’s approach. Even so, in some cases, some aspects of the problem do not become apparent.

Additionally, in some cases, the proposed models are called problems, creating confusion. Therefore, the comparison between the different problems found in literature becomes difficult. It is necessary to have a notation that eases the comparison of the different approaches by clarifying the assumptions considered in the problem, among other aspects. A triplet notation is proposed to tackle this situation. The following fields form the triplet:

$\alpha$: The letter alpha represents the first field. This field represents the scope of the problem. This fact means if the problem tries to tackle a routing or a location problem or both. The letters used are:

• SL—for static location or deployment problems. This fact means that ambulances have a fixed location or base point through time.
• DL—for dynamic location problems. This fact refers to situations in which the ambulances change their position over time.
• BER—for routing problems considering base to emergency site routing.
• EHR—for routing problems considering an emergency site to hospital routing.
• HLR—for routing problems considering hospital to location routing.
• FR—for complete routing problems, i.e., includes the three routing problems.

When this field is empty it means that a particular aspect is not included in the scope of the problem; for example, the combination (DL-FR) refers to a dynamic location and a complete routing problem. On the other hand, the notation (DL) refers only to a dynamic location problem.

$\beta$: The letter beta represents the second field of the triplet. This field represents the constraints considered in the problem. These constraints refer to some problem characteristics affecting the solution depending on whether they are included or not. In this field, the following letters are used:

• VF—for problems considering vehicle failures.
• MP—for multiperiod problems.
• Po—for problems considering relocation as a consequence of emergency events.
• DPl—for problems involving issues related to the dispatching policy.
• WF—for problems considering workforce shifts and workdays.
• SF—for problems addressing scenarios with stochastic demand.
• DF—for problems considering the demand forecast.
• ST—for problems considering stochastic routing times.
• RS—for problems considering the resilience of the system.
• At—for problems considering the ambulance type. For example, if the problem is A1—all the ambulances considered in the model are equal, i.e., there is one type of ambulance in the model. If the model is A2, there are two types of ambulances (ALS and BLS).
• BU—for problems considering Back-Up ambulances, such as double standard problems.
• FI—for problems considering financial issues.

In this case, if a letter code is not included in the triplet field, it is assumed that the problems do not consider this constraint. For example, suppose the declared letters are (SF-BU). In that case, the problem considers stochasticity in forecasts and backup ambulances to have at least two ambulances covering a region. The other fields mean that ambulances do not have mechanical failures, the workforce is always available, the travel times are deterministic, the problem considers a single period, the dispatching policy is the closest available idle server, the localization policy is a priority (a planned relocation in case a particular ambulance becomes busy). There is only one type of ambulance in the problem.

$\gamma$: the third field is represented by the letter gamma. This field represents the optimization objective(s) considered in the model. In this field, the following letters will be used:

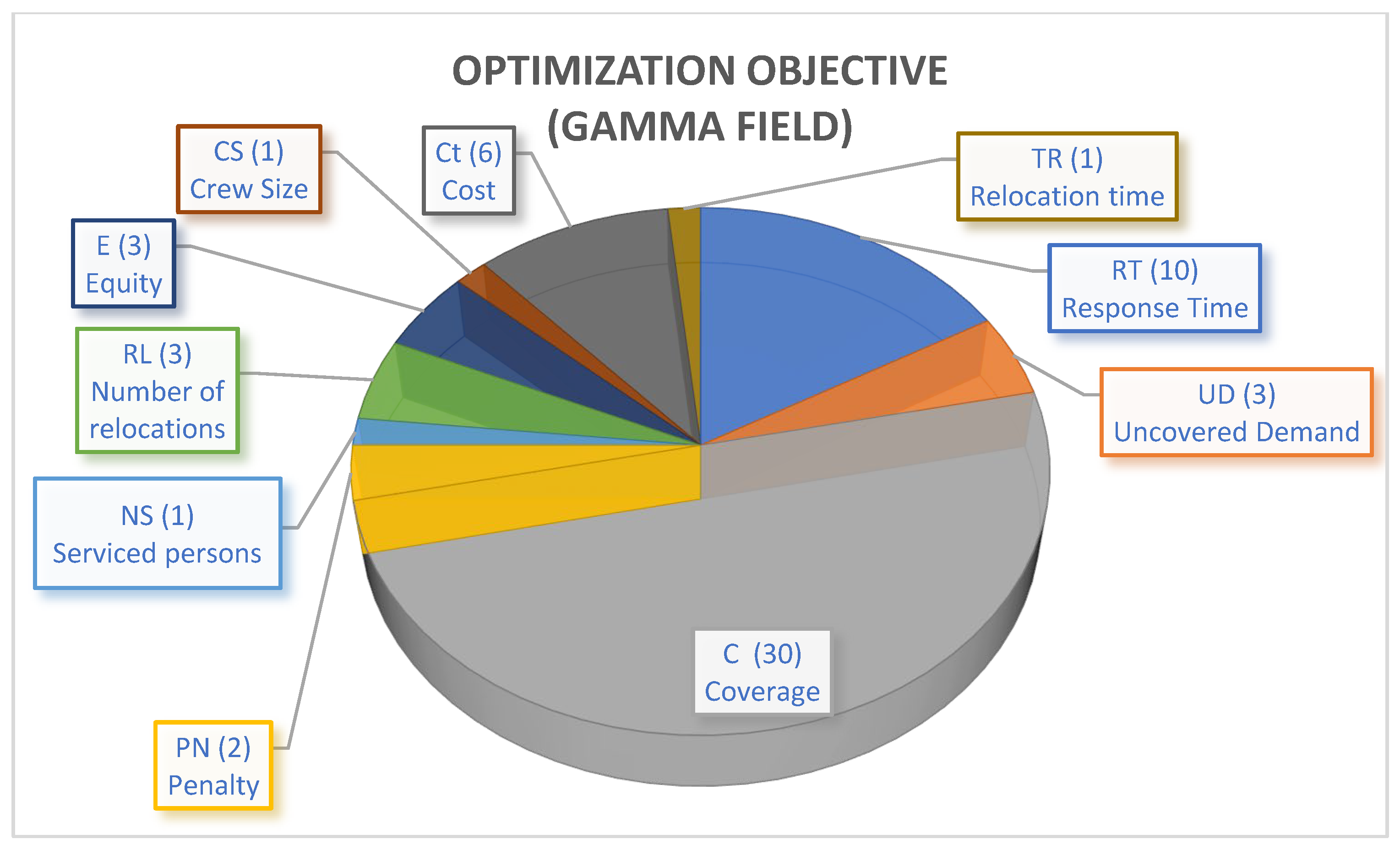
• PS—probability of survival (maximization).
• E—equity (maximization).
• NS—number of serviced persons (maximization).
• RT—response time (minimization).
• D—distance (minimization).
• C—coverage (maximization).
• PN—penalty (minimization).
• UD—uncovered demand (minimization).
• S—survivors (maximization).
• RL—number of relocations (minimization).
• CS—crew size (minimization).
• Ct—cost (minimization).
• TR—relocation time (minimization).

5. Ambulance Location Problems

5.1. Basic Static Problems

To locate ambulances accurately, Hakimi [22] proposed the p-media model. The p-media model’s objective is to minimize the average distance envisaged given a finite number of installations (p) and cover all the demand. Hakimi [22] also proposed a p-center model, looking to minimize the maximal distance for all demand points to the installation to which they are assigned.

Toregas [23] proposed an integer linear formulation for EMS location based on the principle that EMS should meet a response time threshold value to maximize the survival probability of injured people. The objective of this formulation was to minimize the number of facilities required to meet the demand within the response time threshold value. This model is known as the Location Set Covering Problem (LSCP). This first approach lets them identify that reducing this threshold value may exponentially increase the number of facilities required (Figure 6).

Meeting the same service standard for rural and urban situations was not economically viable, considering that too many ambulances would be required in rural areas. Therefore, Toregas [24] suggested setting different service standards for urban and rural areas to obtain the most viable solutions.

On the other hand, healthcare systems usually have a maximum amount of money to spend, i.e., a fixed number of ambulances to deploy or locate. Therefore, it is reasonable to state the problem as maximizing the covered demand within the service standard(s). This model is known as the Maximal Covering Location Problem (MCLP) and was proposed by Church and Revelle [25]. The solution of this approach shows that the marginal coverage gain reduces as the number of ambulances increases, obtaining a similar plot, as shown in Figure 7. Altogether, these four approaches (P-central, P-media, LSCM, and MCLP) form the basis on which most ambulance location models have been developed. All of them are well suited for the EMS facility (i.e., ambulance) allocation, depending on the objective and particular conditions of the problem.

Torregas [23] introduced extensions of these basic models. The extensions of the basic models consider that the number of ambulances required to service a particular region should be greater than 1. These Multi-Service extensions are the MS-LSCP and the MS-MCLP. In these problems, the objective is to give α service coverage. Suppose an ambulance is busy and cannot service a new emergency call in its area. In that case, only another facility located within the response standard can serve this new emergency.

The consideration of different types of ambulances is a topic gaining relevance throughout the globe, considering that the presence of the two types of ambulances in the fleet (ALS and BLS) may help to improve the outcome of the system [16,25,26]. When this is the case, it is necessary to prioritize calls, considering the severity of the patient’s condition requiring the ambulance service. For priority 1, for example, ALS could be mandatory and an alternative for priority two calls. On the other hand, BLS could be mandatory for priority two calls and an option for priority one calls [25,26]. This problem type, in which the demand can be segmented, and there are different ambulances to service the different priority types, is known as the MCLP-FT [16]. The problem is also known as the TEAM (Tandem Equipment Allocation Model) [27,28].

This model is a direct extension of MCLP but imposes a hierarchy between the two vehicle types. This constraint can be removed depending on the circumstances. On the other hand, in the facility-location, equipment-emplacement technique (FLEET) model [27,29], the imposition of a hierarchy between different ambulance types is relaxed. Still, only p location sites may be used.

A common challenge for all the above models is to deal with coverage when ambulances get busy. To face this situation, Daskin and Stern [26] and Hogan and Revelle [27] proposed a second objective within MCLP and a hierarchical approach to tackle the problem. The first objective aims to maximize the number of points covered by more than one ambulance—the second objective aims to maximize the twice-covered total demand.

Another LSCP extension aims to cover each demand point while maximizing the number of backup coverage instances among demand areas [16]. This problem is known as LSCP with Backup or LSCP-B. This problem is addressed with a two-objective optimization approach. The first objective is the minimization of the total number of facilities. The second objective involves maximizing the number of times that demand is covered beyond a single facility. These models are similar to the BACOP1 (Backup Coverage Problem 1) proposed in [27], aiming to cover twice at least a fraction of the demand. A slightly different model (BACOP2) is also presented in [27]. This model’s objective function aims to maximize a combination, using parameter θ, of the demands covered once and twice. The coverage of all urban areas is not required in this case. It is impossible to guarantee full coverage in many real-life systems while meeting the service standard.

Another proposal to address coverage in-between ambulances came from Moon and Chaudhry [28]. Their model stated that facilities were required to cover demand points and other ambulances. This model is known as the double set covering. Their model aims to minimize the number of servers to cover all demand points considering primary and secondary coverage. Revelle et al. [29] also used this approach for ambulance location. This model is known as the location set covering problems with conditional coverage (LSCP-CC).

On the other hand, Gendreau et al. [30] proposed the so-called Double Standard Model (DSM). This model works with two coverage standards. Their model aimed for the complete coverage of demand considering coverage from each facility to a distance r2 from the location. Additionally, at least a proportion of demand, denoted by α, should be covered within a distance of r1 from the location. They also set the condition that r1 < r2, as specified by the United States Emergency Medical Services Act of 1973 [31]. DSM looks for maximizing the twice covered need within r1 using p ambulances [32].

Another significant extension of classic MCLP, LSCP models is the inclusion of multiple objectives. The purposes may vary and include distance, cost, numbers of locations, among others. Considering that ambulance location is a complex problem, with social, health, and economic implications (among others), it is necessary to tackle the problem considering more than a single objective to capture in a better way its complexity, and in doing so, to obtain more valid and integral solutions.

5.2. Probabilistic Static Approaches

The models described up to this point assume for sure the fact that an ambulance is available when an emergency call is received. Models such as BACOP1, BACOP2, DSM, and LSCP-CC partially deal with the fact that an ambulance may be busy, and therefore additional coverage is required. Nevertheless, in some cases, ambulance unavailability could be caused for different situations, such as mechanical failures or accidents [16].

Researchers have proposed different models to deal with facilities’ unavailability. These models include the Maximal Expected Coverage Location Problem (MEXCLP), the Probabilistic Location Set Covering Problem (PLSCP), the Maximum Availability Location Problem (MALP), among others [16]. Facility unavailability will affect, without any doubt, the outcome of the process. Therefore, in this new problem, the aim is that the ambulance fulfills the service at least a threshold value of times of the demand points in its range. These goals are set considering the regulation of each city or country and become an operational parameter. The literature often refers to this using the symbol α [16].

Chapman and White [33] were the first to deal with availability in the problem formulation. Their model, named the Probabilistic Location Set Covering Problem (PLSCP), essentially extends the LSCP by defining suitable temporal availability and geographical proximity coverage. In their model, the expected probability of the ambulance being unavailable can be extracted from historical data and equipment user manuals. In order to guarantee that at least another ambulance is available to service a given need with at least a certain probability (a minimum value of availability), it requires that multiple ambulances adequately cover that demand point. This value is commonly represented as α and known as the α-reliable coverage level. In this sense, the goal of PLSCP is to minimize the number and locations but to ensure that every demand point receives at least α-reliable coverage. This principle must be accomplished for all demand points.

On the other hand, Daskin [34] proposed a stochastic version of the MCLP, calling it the Maximal Expected Covering Problem (MEXCLP). MEXCLP differs from PLCSP in that MEXCLP considers availability as a binomial probability function. In doing so, any level of coverage provides some benefit rather than requiring a minimum coverage reliability threshold. MEXCLP seeks to maximize expected coverage by considering the probability that each facility may be unavailable to serve a specific portion of the time. In this formulation, it is essential to consider the limitations of the number of facilities to exactly p facilities, which is a specific form of a budget constraint. When considering a hypercube correction factor suggested by Larson [35], this model is known as the Adjusted Maximum Expected Location Model (AMEXCLP) in the literature. Along this same line of thinking, Mandell [36] proposed the “two-tiered system model” (TTM). This model of expected demand maximization considers a mixed fleet and a waiting queue model to determine the probabilities used by the model, in this way integrating stochastic optimization, queue theory, and heterogeneous fleet modeling. Likewise, Batta et al. [37] also tackled the problem dealing with service as a queuing system. They intended to address facility independence, different busyness probabilities, and location influence on busyness probabilities. On the other hand, Goldberg et al. [38] relied on queuing and simulation to derive and update facility response and service probabilities.

In the formulation of MEXCLP, it is necessary to check two availability perspectives. In the first place, a facility’s unavailability or busyness may be considered from a system-wide perspective, i.e., the probability of a facility being busy and unavailable for service is the same across a region. On the other hand, the model may consider heterogeneous loads due to variations in demand across a region. Accordingly, MEXCLP’s objective function must be modified to fit this situation. Second, facility siting may permit only one service entity at a location or allow the co-location of facilities [16].

Marianov and Revelle [39] used a queuing model to estimate within each demand region how many servers would be necessary to satisfy the reliability constraint for that neighborhood. In their model, they assumed that the queue of one district is independent of the servers of other areas or vice versa. Nevertheless, this assumption has not been thoroughly tested, and there remain doubts regarding the validity of this assumption [40]. In another study, Marianov and Serra [41] suggested a queuing based form of the maximal covering problem, which explicitly addressed the capacity of individual servers. While queuing is an improvement in some ways, especially when considering the servers’ ability, as in MCLP-Q, many developed models rely on system-wide or local busyness measures. Murray and Church [16] pointed out that this kind of approach can overestimate service potential in a given demand area, considering that not all of the sited facilities are available to service every time.

On the other hand, Revelle and Hogan [42] introduced a formulation that seeks to maximize the covered demand provided for an α-reliable value. This model is known as the Maximal Availability Location Problem (MALP) and aims to maximize the demand that has α-reliable coverage. The model ignores the condition of covering all demand points with the α-level of reliability included in the PLSCP.

Probabilistic models support many applications because they represent real-life conditions better. For example, Aytug et al. [43] addressed solving the MEXCLP for large-scale problems. They solved several instances based on heuristic approaches in their research, specifically, the work developed by Daskin et al. [44] and two methods using genetic algorithms. They found that the genetic algorithm can comply with acceptable computational times of solution for large-scale problems, yielding close to the optimum results. Saydam [45] proposed another study validating the use of genetic algorithms. Sorensen and Church [46] suggested a further extension to MEXCLP. They tackled the problem with a combination of the objective function of the MEXCLP together with the MALP approach to calculate the minimum number of ambulances that should provide coverage to each zone in advance of the mathematical modeling. They did this to obtain the confidence level of the response time to an emergency call. The results showed a moderate improvement in the performance of the system when compared with the solution given by the basic deterministic models.

On the other hand, Erkut et al. [47] validated five optimization models for ambulance location while using actual case data. An approximate hypercube model of queues measured the performance of the models, finding that the models that incorporate uncertainty into their components present better solution performance.

Likewise, Ingolfsson et al. [14] proposed a model that explicitly models the variation in pre-dispatch time and the variation in the response time and the availability of ambulances. Other researchers that tackled the issue of the stochastic location were Lightner [48] and Erkut et al. [49]. Lightner [48] proposed a model that minimizes the fraction of unanswered calls; its main contribution lies in a genetic algorithm adjusted using discrete simulation tools. Likewise, Erkut et al. [49] proposed the Maximal Survival Location Problem (MSLP). Their research addresses the insufficiency of considering service times and coverage as indicators for the correct location of emergency vehicles; instead, they postulate a location model that considers patients’ survival rates. They achieve this by incorporating a survival function based on a log-logistic distribution that considers the type of emergency and the time requirements necessary to respond to it. The approach was developed for both deterministic and stochastic problems.

5.3. Gradual Coverage in Static Approaches

Up to this point, the concept of coverage has been considered only in a crisp way. This fact means that all the described models have a maximum allowed response time (service standard). Crisply meeting this service standard means that the quality of service is the same for all the demands within the standard service radius. For example, suppose the service standard is 9 min. In that case, the quality of service is the same for demand one minute away from the ambulance location or 9 min away from the ambulance location. The quality of service is rated as zero for demand sites 10 min away from the ambulance location. This fact is considered to be a radical criterion. In the case of a stroke emergency, maybe this additional minute is crucial for the person’s survival, but in the majority of the cases is not that way, for example, a broken arm or leg. When EMS location models do not consider the coverage a crisp rule, the models are considered as continuous coverage. EMS location models in which the quality of service is not the same when moving away from the ambulance site are known as gradual coverage. Researchers can address this condition in two ways. The quality of service is considered the same within the service standard radius. Once the service standard radius boundary is surpassed, the service quality is assumed to decrease gradually. Furthermore, in a second approach, the quality of service is considered different even within the standard service radius. The way this quality of service decreases can be modeled with a linear, polynomial, or logistic curve, depending on how the drop in the quality of service will be penalized. This concern was evident since the early EMS location works [50,51]. Different strategies for the gradual covering can be found in Murray [52], Drezner et al. [53], Berman et al. [54,55], and Peker and Kara [56].

Restrepo et al. [57], Davari et al. [58], and Zarandi et al. [32] developed other approaches to these static models. For example, Restrepo et al. [57] incorporated a model to minimize the number of calls not addressed in time through a loss function modeled with an Erlang distribution. This model captures the dependence among ambulances located in the same station. Additionally, variations such as the fuzzy logic considerations of the MCLP model, as proposed by Davari [58], have been incorporated into these models. This author used fuzzy logic to estimate the travel times of the ambulances. This proposal also includes the development of a simulated annealing algorithm for the solution of the problem. Additionally, Zarandi et al. [32] developed a genetic algorithm for MCLP instances of up to 2500 nodes. The results recorded less than 2% gaps and computational times less than four minutes.

Yin and Mu [59] proposed two extensions of the MCLP, which consider the location stations and the number of ambulances to be located there. The proposed models consider the facilities’ capacity and aim to maximize the number of demand points covered while minimizing the average distance from facilities to the demand points not covered.

5.4. Dynamic Approaches

The first and basic ambulance location models looked for the best location of ambulances, trying to minimize penalty functions, or maximize coverage, among other objectives. At the same time, more realistic conditions were progressively included in the models. Among these conditions, one can consider gradual coverage, the probability of ambulance failure, or the ambulance being busy. Nevertheless, all the cases described address the problem of ambulances’ location as a static one. Static models imply that ambulances have fixed location sites, which remain fixed in number and position across the timeline. This fact could cause a drop in the perceived quality of service if, for example, two contiguous ambulances are busy, and either of these two ambulances should service the incoming call.

Given that the rest of the fleet remains at their assigned location, it is very probable that the service given to that call exceeds the service standard. In such a situation, it would have been preferable that the rest of the fleet had redeployed to a new location to increase the chance of giving service meeting the service standard. To tackle this drawback of the static models, researchers started to tackle the EMS location problem dynamically, adjusting the fleet’s location, if necessary, if some ambulances become busy. This fact encouraged the development of a new family of problems known as dynamic location problems. This family of problems is often referred to as the DPLMEV (Dynamic Problem of Locating Medical Emergency Vehicles), redeployment or relocation problems. In this paper, we use these three names interchangeably to refer to the situation previously described. Relocation is beneficial for maximizing coverage and reducing response times [60,61].

Additionally, relocation improves flexibility to respond to fluctuating patient demand [62] and dynamic traffic conditions [7]. Although in the process of dynamically locating the ambulances, decision-makers try to reduce the movements of the ambulances by setting some constraints on the problem, the rise of ambulances movements as a consequence of dynamic relocation may also bring some advantages. For example, it is more likely to receive a call while on the road, causing a drop in response times, considering that the crew is ready and already on the road. If the staff were at the ambulance base, they might require some time to prepare, increasing the system’s response time [63].

Relocation problems are challenging since they have to be solved more frequently and considerably faster. Therefore, using more powerful solution approaches in these cases is necessary. The availability of faster heuristics and advanced computer technologies makes it possible to solve ambulance location problems in real-time, making it possible to compute a new ambulance deployment strategy at any time t, using real-time data. In this sense, Gendreau et al. [64] used the DSM to generate the first dynamic problem modeling. In their model, Gendreau et al. [64] consider several practical considerations inherent to the dynamic nature of the problem. For example, they stated that the ambulances moved in successive redeployments cannot always be the same. They avoided the repeated round trips between the same two location sites and the long trips between the initial and final location sites. The objective function considers these conditions with the inclusion of a parameter M. This parameter represents the cost of redeploying a particular ambulance to a specific site at instant t. They solved the problem at each instant at which a call is registered. They named the problem as Maximum Expected Covering Relocation Problem (MECRP), taking into account that each time they solved a MEXCLP.

However, despite the mighty computation power available nowadays, on some occasions, the number of calls and the size of the problem make it difficult to solve the problem for each call [65]. Gendreau et al. [60] tackled the (MECRP) with compliance tables to handle this situation. Each row indicates the desired waiting sites for the available ambulances. If these ambulances are at their selected location sites, the system complies. The number of available ambulances changes when a request arrives or when an ambulance becomes available again. Then, each idle ambulance may be assigned to a different waiting site. A strength of the compliance table policy is that it is simple to explain to and to be used by dispatchers: the number of available ambulances only describes the state of the Emergency Medical Services (EMS) system. Another strength is calculating compliance tables offline instead of real-time methods that compute new relocation decisions whenever an event occurs. These advantages have led to compliance tables, a commonly used policy structure for the ambulance relocation problem [66,67]. Van Barneveld [68] addressed this problem but assumed penalty functions, incorporating the gradual covering of the problem. It is also important to point out that Lim et al. [69] and Sudtachat et al. [70] had recognized and evaluated by simulation that a static configuration of the ambulance fleet generates underutilization. This fact, in turn, caused a lower performance of the proposed optimization objectives. However, Nair and Miller-Hooks [71] suggested that a too flexible policy is not realistic because of the burden it represents for fleet personnel. To respond to this problem, the authors compared the two types of policies through an analytical model, finding that when the fleet of vehicles is large enough, there are no significant differences in the response times between policies. On the other hand, when there are few vehicles, the strategy of the relocation of ambulances shows a better performance in the response time. This fact is explained because, under these circumstances, when dispatching an ambulance, it leaves a vast area without coverage compared to a system with a more significant number of ambulances, so relocating ambulances has better results when the objective is to decrease the future response times.

Bélanger et al. [72] conducted a robust study assessing different location policies (static and flexible policy) using simulation for this purpose. The authors found that the flexible strategy (called “dynamic strategies”) presented better results in the response times to emergencies than the static approach. Still, they show that these results are obtained with high relocation costs. On the other hand, Van Barneveld et al. [73] found that the better results of the relocation policies in rural areas are obtained by increasing the crew’s workload. Maxwell et al. [74] proposed a method to calculate a lower bound on the fraction of calls serviced in a response time higher than the service standard. This lower bound is computed by modeling the ambulance system as a multiserver queuing model and can be used to determine effective redeployment policies.

Gendreau et al. [60] stated two solution approaches for the ambulance dynamic location problem. In their work, they stated that there is an a priori approach and a posteriori approach. The tools designed with the first approach (a priori) seek to find a solution for specific system conditions (even if they involve long computational times of solution), to consolidate, in advance, how the vehicles should be located and operated in that specific situation. Once the system has these conditions in actual operation, operators need only look for the previously found solution and use it to support decision-making. This problem may also be considered a static multiperiod type and the basis for relocation strategies such as the compliance tables.

On the other hand, the a posteriori approach tools are designed to give an immediate response to the operator when a relevant change in the system takes place; usually, these changes are called events, among which one can find the arrival of a request for dispatch or the entry of a vehicle into operation. In general, tools with this approach seek to work in real-time. Therefore, there must be a substantial computational capacity to get fast solutions.

The table in Appendix A summarizes the relevant contributions of the studies found in this review. This table organizes the studies considering the optimization objective, constraints considered in the model, solution approach, and the proposed triplet notation. Additionally, the proposed triplet notation is given for each study. The MEXCLP is the basis for several of these proposals regarding the basic model. The contributions are analyzed regarding the optimization objective, constraints considered in the model, location capacity, fleet type, and dispatching policy.

5.4.1. Dispatching Policies

Roa et al. [75], Carvalho et al. [76], and Lee [77] based their dispatching policy on the calculation of the system’s preparedness. Their studies are based on the dispatching algorithm proposed by Andersson et al. [78]. They concluded that dispatching based on this criterion could contribute significantly to the response time of the EMS as long as it is applied appropriately; that is, taking into consideration current and future calls. Another study aiming to validate dispatch policies is that of Lim et al. [69]. The authors validated various dispatch policies through applied simulation and five published location models. In this study, the authors concluded that no dispatch policy exceeds the others; all have their advantages and disadvantages; therefore, the best approach should be chosen according to the objectives of the EMS and the context of the application. Nevertheless, the authors show that emergency response times can be improved through different dispatch policies. Moreover, they emphasize that by giving the system the possibility of changing the assignment of a given ambulance, despite having already been dispatched, for one of higher priority, it can improve the response time in critical emergencies.

Mayorga et al. [79] proposed a methodology to establish a districting/dispatching strategy. Unlike schemes based on response times, the authors determined the districts based on a survival function. This fact is a feature that can better balance the system’s workload. This priority can be assigned, considering the TRIAGE evaluation. Sudtachat et al. [70] applied an ordered preference list heuristic algorithm based on this approach. The results obtained from evaluating policies using a discrete event simulation model built on an actual database suggest that the priority-based policy generates better results than the closest server dispatch criterion.

Jagtenberg et al. [65] obtained similar results in their study. The authors presented alternative dispatch policies based on Markov chains and on a heuristic algorithm that can handle regions with large numbers of ambulances. The authors found that with this heuristic algorithm, it is possible that the number of calls attended within a threshold time can be improved. The study suggests that the dispatching criteria of the closest server are not necessarily the best to attend emergencies.

Previous studies like Zhen et al. [80] showed that dispatching decisions cannot be as simple as assigning the closest available server. In their study, Zhen et al. [80] proposed a decision algorithm for dispatching ambulances designed to operate with a real-time deployment system. The algorithm considers the priority of the call, how fast an ambulance can return to its base, the number of available ambulances in a given location, and the number of requests which may emerge in the neighborhood of the ambulance locations. Once the indicator is computed for each possible dispatching decision, the ambulance with a less negative impact on the system performance is dispatched. The structure of this algorithm, created for the real-time application, has become for recent studies that also consider location and relocation.

Similarly, Van Barneveld et al. [68] considered two types of vehicles in their approach. One of them is Rapid Responder Ambulances (RRAs) and the other is Regular Transport Ambulances (RTAs). The critical difference between them is that RRAs are faster, but they cannot transport patients to the hospital. In their proposal, Van Barneveld et al. [68] assumed the dispatch policy is as follows: if the patient is reachable by at least one RRA within the service standard, then the closest RRA is assigned to that emergency. If not, and an available RTA can reach the patient meeting the service standard, this available RTA will be dispatched. If neither an RRA nor an RTA can get to the patient timely, the nearest vehicle is assigned, regardless of its type. Such a response counts as a late arrival. If no unit at all is available, the call enters a first-come-first-served queue: the first unit that becomes available is dispatched.

Van Barneveld et al. [68] considered that it is typically difficult to determine the severity of the incident based on the caller’s descriptions, considering that the caller is usually upset and may give an inadequate description of the patient’s status. Therefore, they stated that it is impossible to know beforehand if the patient needs transportation to a hospital. Once the ambulance crew report to the dispatch center that the patient needs transportation, the following scenarios are possible. If the patient requires transportation to the hospital and an RRA is on the emergency site, the closest available RTA is sent to the emergency site. If there is no available RTA, the call enters the first-come-first-served queue. The RRA stays on-site and gives care to the patient until RTA arrives. The RTA can arrive at the site before or after on-scene care finishes. If on-scene care finishes before RTA arrival, RRA must wait for RTA arrival at the emergency site. Once RTA departs with the patient, RRA will become available for the system. Janosikova et al. [81] described a similar procedure.

The dispatching policy is not explicitly mentioned in many studies. On the other hand, the closest available server policy is prevalent. Different studies tackling the dispatching decision of the location problem can be found in Appendix A. For example, the studies undertaken by Van Barneveld et al. [73,82] addressed the dispatching decision using a heuristic approach that considers the severity of the call and the status of the ambulance. The status deals with the activity the ambulance is performing at the moment of the incoming call. They stated that the ambulance could idle at its location in any of the following phases, giving treatment at the emergency site, driving to the hospital, or giving treatment at the hospital. From these four phases, only phase 3 (going to hospital) makes an ambulance not eligible for the assignation process. Priority rules that can include a preparedness measure of the system and the type of emergency associated with the incoming call can be found in [83,84]. Likewise, Jagtenberg et al. [85] and Park and Lee [86] use dispatching rules based on a Markov decision process, in which at each states, an action from the set of allowed actions must be followed. The process evolves in time according to transition probabilities that depend on the selected activities. They dealt with an infinite planning horizon. Finally, Van Barneveld et al. [68] address the dispatching problem with two types of servers in the following way. They split the dispatching process into two moments. The first one refers to the decision of sending an emergency vehicle at the moment the call is received. The second is when the crew arrives at the emergency site, and it becomes clear that the patient must be taken to a hospital.

5.4.2. Modeling Issues

Regarding the features included in the model, Chanta et al. [87] proposed incorporating equity criteria in the management of EMS. This fact is essential for these systems since they are expected to serve with equity. To achieve this, the authors use an envy minimization approach, a measure that considers the differences in service quality between all possible customers. To build the envy function, they used the survival function; thus, envy is defined regarding survival probabilities, such that higher survival probabilities are associated with satisfaction. The concept of equity has also been considered with the Gini coefficient. This metric has been used by Lee [77] and Enayati et al. [88]. Equity was also addressed by Tsai et al. [89]. In this case, one of the objectives in the multi-objective optimization aims to balance the services between the different areas.

On the other hand, Van den Berg et al. [90] dealt with the location problem, proposing a linearization of the MEXCLP with fractional coverage to reduce the computational time necessary to solve the problem.

Janosikova et al. [81] based on the work of Jánošíková et al. [91] and Ball and Lin [92] to develop a stochastic model based on the concept of failure probability. Jánošíková et al. [91] introduced the probability of failure in the objective function to be maximized. The model was validated through agent-based simulation. OpenStreetMap (OSM) information was used to model the road network. The travel times between nodes are calculated according to the distance to travel and the maximum speed per section, considering the six types of sections of the OSM. Variations of Dijkstra’s algorithm are used to determine the travel time. The simulation results suggest that the configuration of the ambulances proposed by the developed model does not improve the behavior of the average response time; however, it does enhance the fairness of the service.

Maxwell et al. [63,93] aimed to improve the system’s coverage with an approximate dynamic programming scheme. The results showed that the approach could be applied to real problems to determine relocation policies. It was one of the first studies designed for a possible application in real-time; however, relocation decisions are only considered when an ambulance completes a service. This constraint ignores the possibility of improvements obtained from the fleet’s partial or total relocation. The authors evaluated solutions employing a static and flexible policy framework, finding that the flexible policy outperforms the static approach.

McCormack and Coates [94], Park and Lee [86], Abensur et al. [95], worked in the same line of Knight et al. [96], including survival functions to capture the problem of addressing heterogeneous patient types.

Shariat-Mohaymany et al. [97] considered stochasticity in the problem as an extension of the MEXCLP in which the probability of usage of the ambulances is not modeled explicitly; however, it is established based on a level of confidence and the total time of attention required (for a given period) at each point of demand. Likewise, Maleki et al. [98] proposed an extension of the MEXCRP model, as proposed by Gendreau et al. [60]. Another related study was carried out by Van den Berg and Aardal [90]; in this study, the authors addressed the problem employing a multiperiod model based on the MEXCLP. The authors proposed an extension of the model considering time-dependent parameters. Subsequently, Jagtenberg et al. [65] suggested a heuristic algorithm that obtains the marginal contribution to the expected coverage by locating the ambulance in each station to send the location orders. They calculated this contribution using the MEXCLP objective function obtained by locating the ambulance in each station.

Liu et al. [84] presented another contribution in the modeling schemes; thus, extending the DYNAROC model proposed by Andersson and Värbrand [78] with a “chance-constrained programming” modeling approach for the optimal relocation of ambulances. The model integrates other interesting modeling features, such as the approximate hypercube model used to compute the availability of ambulances. Furthermore, travel times and demand are taken into account as arbitrary elements.

In addition, Naoum-Sawaya and Elhedhli [99] proposed a stochastic two-stage model. This model minimizes the number of relocations for a planning horizon while maintaining an acceptable level of service. Another relevant stochastic approach was proposed by Toro-Díaz et al. [100]. This approach defines a queuing model within the internal structure of a mathematical model corresponding to a Markov process of continuous-time and finite states. Consequently, a hypercube model of queues is used to represent the requirements on hold and the dispatch decisions.

On the other hand, Saydam et al. [45] extended the dynamic available coverage location model to a multiperiod model that uses Jarvis hypercube approximation to calculate vehicle-specific busy probabilities. The authors’ main contribution is a new approach that minimizes the number of servers and redeployments.

Billhardt et al. [101] developed a tool that addresses the problem in real-time, generating solutions as events occur. The tool has two modules that work together. One of the modules solves the dispatch problem using an allocation heuristic, known as the auction algorithm of Bertsekas [102]. The location module proposes modeling based on a Voronoi graph approach. When considering the ambulances, this is equivalent to minimizing EMS response time.

Degel et al. [103] developed a multi-period model of location and relocation. Its main contribution is the introduction of the concept of “flexible coverage” in its modeling scheme. Unlike the models that work with a single or double coverage, the authors propose a new approach to determine the number k of vehicles needed to cover each requested zone. This number is calculated based on the definition of a confidence level and the simultaneous demand empirical probability distribution at each area. After analytically defining this level of coverage, the value calculated in the model is used in describing the decision variable involved in the objective function, not as the classic binary variable of single or double coverage, but as a binary variable of the coverage level k (different for each zone). This approach is an improvement over previous works because it considers the different time-based needs of each area. Moreover, the model considers time dependence in all the parameters that the authors deemed relevant.

Andrade and Cunha [104] propose a multi-period linear optimization model based on coverage. The model seeks to maximize double coverage minus the cost of ambulance relocation. The model considers two types of vehicles and decisions to locate ambulance stations, the location of ambulances and the re-location of ambulances. It also incorporates the stochastic component. An analytical queuing theory model helped determine the minimum number of ambulances required for each demand point. The authors defined a confidence level for the probability of the ambulance being available within a designated service standard. The model was used to support the design of the emergency care system in Sao Paulo, Brazil.

Another tool is the so-called “Compliance Table Policies,” commonly used for dynamic ambulance management. As mentioned before, these tables indicate where the ambulances should locate when there is an available number of ambulances. If all the ambulances are in the assigned areas, it is considered that the system is in “compliance.” As ambulances are dispatched or enter into operation in the system, operators use these pre-calculated tables to make relocation decisions. Likewise, Lam et al. [105] modeled the dynamic location of ambulances based on compliance tables (called by the authors “System Status Plan,” SSP). Similar models were developed by Van Barneveld [106], Van Barneveld et al. [68], and Van Barneveld et al. [73].

Sudtachat et al. [67] also proposed a nested-compliance table model for the dynamic management of ambulances. Unlike other approaches, the compliance table constructed by the authors retains the assigned locations even as the number of ambulances increases. This aspect poses an advantage from the perspective of the number of relocations, causing that when there is a change in the system’s state, at most, only one relocation movement is generated. Due to the last characteristic, the authors called their approach the “nested-compliance table.” The table is constructed based on a linear programming model, oriented towards maximizing the expected coverage using steady-state probabilities of a Markov chain model with relocation as input parameters.

Nickel et al. [107] proposed a stochastic model in which the ambulance stations to be enabled are simultaneously decided upon and the number of ambulances that need to be assigned to these stations, using a two-stage decision scheme. Unlike the classic two-stage stochastic models that work with the expected value in the target function, the authors used a coverage restriction that ensures that the expected number of ambulances assigned to the region is greater than or equal to a predefined coverage level.

Van Barneveld et al. [73] developed the Dynamic Ambulance Management model for rural regions with limited ambulances and modeled it as a discrete-time Markov decision process. The computational times of an optimal relocation policy are not efficient; thus, they developed a one-step look-ahead heuristic so that, at each step, ambulances are relocated to minimize the expected response time. Van Barneveld et al. [73] also computed compliance tables, considering two different ambulances: higher speed and better patient attention capacity. The authors restricted the number of relocations by ambulance type and relocation time to construct these tables. The resulting compliance table guarantees that long trips are not considered. The model uses the modification of the Jarvis Hypercube model [108] to estimate busy fractions. The model applicability was validated through discrete event simulation.

On the other hand, Van Barneveld [109] considered the same problem, but from the construction of compliance tables. To achieve this, the author used a mathematical programming model called the minimum expected penalty relocation problem (MEXPREP). Computational results suggest that the compliance table constructed based on the MEXPREP (minimum expected penalty relocation problem) outperforms both the MECRP compliance table and the static policy.

In addition, Van Barneveld et al. [68] proposed a heuristic for ambulance relocation based on an indicator called “unpreparedness.” If relocation avoids an increase in this indicator, then the relocation is performed. A particular proposal’s feature is that although relocation identifies an origin and a destination, an ambulance does not need to move from the point of origin to the destination. Instead, the authors allow for several movements; for example, the ambulance that is at the node of origin can be moved to a central location while, at the same time, the ambulance at the intermediate location moves to the destination. This type of movement allows for bringing the system to the desired state more quickly; however, due to the increased number of moving ambulances, the authors restricted the number of these intermediate movements. Another innovative feature of the tool is that these intermediate movements are determined through mathematical programming. This hybrid heuristic configuration with optimization is of recent application, known as Matheuristic. Actual data was used to simulate the system’s behavior using the tool. The results show that the system’s performance improves with the relocation strategy; however, there is a point where the increased number of relocations no longer enhances the system’s behavior, leading, in fact, to a worsening of it.

Enayati et al. [110] proposed a real-time optimization to tackle managerial decisions related to ambulance fleets. In their model, the authors implement two linear programming models in series. The first model maximizes coverage (Maximum Covering Location Problem with Workload restriction). The second is to minimize relocation time (Minimum total Travel Time Location Problem with Workload restriction). Computational tests show the practicality and applicability of the model. Likewise, the relocation scheme improves the coverage against the static policy scheme while respecting the operators’ workload.

Vile et al. [111] tackled the Welsh Ambulance Service Trust (WAST) operations. In this case, they aimed to minimize the crew workforce by improving the forecast for each time of the day. In their study, they used singular spectrum analysis (SSA) to improve the demand estimates. Then they used this forecast to optimize the number of crews in each shift keeping a high quality of service. The developed techniques were integrated into a workforce capacity planning tool that WAST planners might independently operate.

The types of location policies were discussed and evaluated in the study carried out by Lam et al. [105]. In their study, the authors examined different location models oriented towards static policies and dynamic models, which integrate all aspects of the problem and operational approach. The authors evaluated both methods using simulation, and they concluded that dealing with the problem operationally improves EMS response times. This finding is also suggested in the study by Peyravi et al. [112]. However, Lam et al. [105] highlight that these types of solutions need the support of both georeferencing [113] and information exchange systems in real-time. Including these two factors increases complexity, partially explaining why most research focuses on static policies.

Considering better computing capabilities available nowadays, many researchers include more features in the modeling process to obtain more realistic models. In this sense, it is important to highlight the inclusion of stochasticity in demand in [67,81,86,88,89,95,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128]. There are different ways to address stochasticity, but one of the prominent research areas is machine learning. The most recent studies try to forecast demand using different machine learning approaches, such as random forest [119], convolutional neural networks [127], clustering combined with Gaussian mixture models [129]. Other approaches found in these studies also try to make spatiotemporal emergency forecasts to allocate or relocate ambulances in a better way. For example, Tsai et al. [89] use time series smoothing to tackle stochasticity to make better relocation decisions. Other researchers deal with demand stochasticity with hypercube models like in [100,110,114,115,126,128]. Other studies deal with stochasticity in travel times using machine learning [130], as Olave-Rojas and Nickel [131] have previously done.

On the other hand, an essential application of machine learning in the ambulance service is the ability of this kind of technology to give healthcare systems to detect or monitor the progress of potential epidemic outbreaks or bioterrorist attacks. In this sense, it is vital to consider ambulances as one of the critical elements of the first line of defense in this kind of scenario. Therefore, many countries have created Real-Time Syndromic Surveillance (ReSS), of which ambulances are one of the critical elements. The purpose of ReSS to monitor disease indicators in real-time or near real-time to detect epidemic outbreaks of disease earlier than would otherwise be possible and monitor disease trends in the community and ensure that a large-scale outbreak is not occurring in the community. According to Sugishita [132] and Todkill [133], a system based on ambulance data provides an additional measure of the severity of the clinical disease spectrum. These ambulance-supported syndromic surveillance systems (ADSSSS) allow the healthcare authorities to determine trends and key epidemiological characteristics of patients, and automated statistical algorithms and machine learning techniques can be employed to detect the daily increase in the expected number of calls [132,133]. ADSSS is timely in detecting seasonal changes in patterns of respiratory infections and growths in case numbers during seasonal events [133]. Machine learning techniques allow authorities to detect outliers or abnormal conditions of patients serviced with ambulances that can be considered early alerts of a new epidemic outbreak or just that a seasonal disease (flu) is starting its seasonal cycle [132]. If the ambulances are dynamically located, it is necessary to have an efficient data acquisition system to adequately summarize the data, considering that each ambulance will be servicing different districts due to the dynamic location policy. Data management is a little easier in a static policy, considering that each ambulance will serve only a particular community.

Older studies focused on a priori type solutions due to computation limitations. However, current computational technology, information technology, and geographic information systems motivate a posteriori type tools development. Several authors (Yue et al. [134], Majzoubi et al. [135], Mason [83], Billhardt et al. [101], Jagtenberg et al. [65], Lam et al. [105], Van Barneveld, [106,109]; Enayati et al. [110], Sudtachat et al. [67], Yoon and Albert [136], Roa et al. [75], Sun et al. [137], Yuangyai et al. [138], Nilsang et al. [139], van Buuren et al. [140], Tsai et al. [89]) worked on real-time response tools, which, in the current context, are self-evident as a promising research development line in the future of these tools.

The use of social networks to detect special events is a new prominent field in ambulance dynamic relocation. Nilsang et al. [139] and Yuangyai et al. [138] monitor social networks to assist relocation decision processes.

5.4.3. Optimization Objectives

Regarding the optimization objectives used within the different approaches, the most frequent goal is coverage and derivative goals such as survival, the fraction of late arrival, number of survivors, and fuzzy coverage. Davari et al. [58] addressed the problem considering fuzzy travel times leading to a fuzzy coverage objective. The service measure depends entirely on the value of service standard. If managers choose a large time limit (service standard), the coverage indicator shows excellent system performance. However, this does not necessarily mean operation with the best response times. Erkut et al. [49] analyzed this situation and consequently proposed the survival function as a better criterion for ambulance location decisions. This objective was also used in [86,94,141].

In summary, the majority of objective functions aim for the wellness of patients. Additionally, in recent developments, other objectives have been proposed, such as the survival functions (Erkut et al. [49]) or the concept of envy (Chanta et al. [87]). Another common objective used in these kinds of problems is response time, which considers the time elapsed since the call is received until the arrival of the ambulance to the emergency site [82,91,117,142].

On the other hand, some authors considered that excessive relocations could negatively impact the system’s performance. Excessive relocations may cause excessive round trips between locations and the excessive number of long trips [99,106,143], and these may produce crew fatigue [45]. The excessive number of relocations will also impact the operational costs of the system [74,93,135]. On the other hand, Nickel et al. [107] address the problem looking for the minimization of the expected cost but considering mainly the fixed cost associated with ambulance bases, guaranteeing a service level. Liu et al. [84] proposed the maximization of an objective based on a preparedness measure of the system.

Some authors have considered objectives integration to address the problem as a multiobjective one. Among these studies are [76,82,88,95,110,136,141,144,145]. All of them used different ways to weigh the objective functions. Some objectives included in these studies are Gini coefficient, survival, uncovered demand, penalization, relocation costs, and preparedness.

5.4.4. Fleet Type

Another relevant issue is that most studies consider only one type of vehicle; this means a fleet with similar vehicles. This issue is crucial because it can structurally change any proposed tool. It is vital to point out that researchers globally are trying to include the concept of a heterogeneous fleet more frequently in their models. The relevance of a heterogeneous fleet lies in the fact that a heterogeneous fleet can save money, considering that BLS ambulances have less equipment than the others. This fact is significant because, with the same amount of money, it is possible to have more ambulances, and the more ambulances available, the lesser response time of the system. This fact helps increase service quality and could impact equity indicators [73]. Although ALS and BLS are the most common classification of ambulances type, it is essential to point out that in some cases, this classification can vary, depending on the conditions or regulation of the country or region under study. In this sense, van Barneveld et al. [68] use two different ambulance types in their model, and they called them Rapid Responder Ambulances (RRAs) and Regular Transport Ambulances (RTAs), highlighting that the main difference is that RRAs are faster. Still, they cannot transport a patient to the hospital.

Some problems do not specify the fleet type, making it evident again the need to introduce the proposed triplet notation to have a clear view of the scope of the problem tackled in each case.

5.4.5. Location Capacity

Another aspect that needs to be considered is whether the solution method allows several vehicles at the same geographic point. Zarandi et al. [32], Toro-Díaz et al. [100], Chanta et al. [87], Billhardt et al. [101], Maleki et al. [98], Van Barneveld et al. [73], among others, do not include this option in their models.

5.4.6. Solution Approaches

The following solution techniques were used in the studied papers: (i) the exact solution technique, which includes all the techniques (linear programming, stochastic programming, among others) that use exact algorithms that are mainly applied through commercial software such as CPLEX, (ii) heuristic algorithms, (iii) metaheuristic algorithms, (iv) machine learning, and (v) simulation. The specific solution procedures found in the studies are mainly non-linear programming, linear programming, simulation-optimization, stochastic programming, integrated simulation with metaheuristics and linear programming, geometric optimization, geographical analysis, heuristic, sampling approach, matheuristic, and compliance tables.

The studies proposed by Firooze and Rafiee et al. [146], Van Barneveld [106], Degel et al. [103], Andersson et al. [141], Moeini et al. [125], Shariat-Mohayma et al. [97], Maleki et al. [98], and Van den Berg et al. [90] are based on linear programming and are solved accurately using general-purpose solvers. Nevertheless, one disadvantage of using mixed-integer linear programming and exact algorithms is that such sophisticated models with large-scale applications cannot be solved in a short computational time. Another disadvantage is the complexity of explicitly modeling the stochastic behavior of the problem. This fact partially explains the fact that many of the tools that use this approach tend to be geared towards the generation of solutions of a strategic nature and a priori application, restricted to small-scale cases or, at most, medium-scale cases.

Naoum-Sawaya and Elhedhli [99] used a two-step stochastic programming to tackle the problem. The model presents an innovative way of explicitly modeling stochastic behaviors. However, the stochastic model is solved only once, and no suggested techniques are used to obtain a more robust solution. Boujemaa et al. [126] used Sample Average Approximation (SAA) to find the approximated optimal solution via sampling.

On the other hand, some tools seek to include stochastic behavior based on non-linear approaches [81,138].

In the study carried out by Zarandi et al. [32], a dynamic extension of the MCLP for treating large-scale problems was proposed. The authors developed a simulated annealing algorithm to solve the problem considering ambulance occupancy probabilities. The algorithm was able to solve instances with 2500 nodes.

Schmid and Doerner [4] used the variable neighborhood search algorithm to solve the problem regarding approaches. Knight et al. [96] and Tozan and Donmez [147] used genetic algorithms. Specifically, Tozan and Donmez [147] developed a genetic algorithm for the capacitated versions of the already known MCLP and the LSCM.

Another metaheuristic approach is the artificial bee colony algorithm proposed by Andrade and Cunha [104]. This latest algorithm shows that the approach produces reasonable solutions with an optimality gap, generally below 5%, with a maximum gap of 8.24%. The application of this type of technique substantially improves the computational times of the solution, thus making it possible to approach the problems of significant scale; however, an optimal solution is not guaranteed. Other metaheuristics approaches can be found in [32,88,89,110,111,115,148], where the use of tabu search and simulated annealing is described. On the other hand, Roa et al. [75] used a matheuristic approach to deal with the challenge of obtaining fast solutions.

On the other hand, Jagtenberg et al. [65] proposed a heuristic algorithm based on dispatching and relocation policies given the system’s state in real-time. The algorithm aims at minimizing the expected fraction of accidents that occur outside the given standard of time for coverage. The design of the algorithm guarantees that it can deal with large-scale problems.

On the other hand, Lam et al. [105] used geographic analysis techniques. They performed a hot spots analysis in the first place. Secondly, the analysis of displacement polygons was used. Displacement polygon is a technique that allows for the delineation of zones around a geographical point for a predetermined travel time. This zone indicates that if one moves from the geographical point, one can reach the maximum boundaries of the area delineated within the stipulated travel time. These techniques allowed locating ambulances in such a way to guarantee that any point of the space could be reached below the threshold time. These results were compared, and it was determined through simulation that the mathematical approach allows for the best results. However, they do not differ significantly from those derived from the geographical analysis. GIS techniques are also integrated in [113].

Zhen et al. [80] developed a tool that combines optimization and simulation methods. The authors first solve the location problem. They fragmented several time windows and generated random solutions to each period’s location problem to achieve this. Next, each of these solutions is evaluated through simulation, assessing its behavior with 400 emergency scenarios that were randomly generated. These simulations allowed calculating the expected ambulance response time. This criterion is used as an optimization objective by a genetic algorithm responsible for improving the solutions obtained. The process was performed repeatedly using the simulation module to calculate the expected average response time.

McCormack and Coates [94] developed a tool that integrates discrete event simulation with a genetic algorithm. Their simulation model uses a list of historical data with the type and the time of events (emergencies). Each solution generated by the algorithm is evaluated using the simulation model and repeatedly searching for a better solution. McCormack and Coates [94] considered the survival probability in their integrated optimization-simulation scheme as a performance indicator.

Yue et al. [134] integrated discrete event simulation with a greedy algorithm to efficiently consolidate a viable tool for real-time applications. The authors integrated the application of the SAA into the tool. The last hybrid simulation–modeling scheme analyzed is proposed by Liu et al. [84]. The method integrates Monte Carlo simulation as an integral part of the tool. The base optimization scheme is a genetic algorithm that uses simulation to evaluate the solutions generated during its execution.

Nickel et al. [107] used a sampling approach to solve the stochastic linear programming model. The authors assumed that the probability distribution of the demand of each zone is known. They solved the model by employing a general-purpose solver for N demand scenarios; then, they solved the best model M times. Next, the optimal values of the objective function and the decision variables are estimated, and the average of the M values of the objective function is calculated.

Regarding uncertainty topics, but not only related to demand but also with ambulance failure, crew absenteeism, among others, it is vital to include resilience in the analysis to improve the system’s performance across time. To achieve this, robust optimization to enhance system performance was used in [117,118]. In the case of Bertsimas et al. [118], row and column generation approaches were used to obtain fast solutions.

The need for a more capable posteriori approaches (ambulance repositioning depending on real-time emergency calls evolution) has been posed as a relevant issue considering the impact of these approaches on the quality of service [69].

In many studies, problems are tackled with heuristic approaches. These heuristic approaches can support other techniques such as Markov decision processes [85,86], approximate dynamic programming [122], and hypercube models [123].

Simulation is one of the most relevant solution approaches in the studies. It can be found in [68,72,82,94,126] and is commonly used to address the stochasticity of demand and travel times.

In a novel application, game theory was used by Abensur et al. [95] to select the best location for one emergency service provider in order to obtain better results in a competitive environment.

6. Concluding Remarks and Future Directions

The purpose of this paper was to present a general description of the EMS location problem, both static and dynamic, its applications, and recent developments to detect the gaps in the subject and to establish possible lines of research. Closing these gaps will help in obtaining better outcomes in healthcare systems worldwide. The impact of EMS in healthcare systems is very relevant due to the correlation it has with the survival rate and sequels in emergencies related to conditions such as stroke and heart attacks. This fact also has a significant economic and social impact on any nation.

This paper provides a detailed review of EMS location problems’ evolution and dynamic problems’ recent developments. Papers published in 2015 or more recently on the WoS database were included in the review. The reviewed papers showed that many proposals are under development to better assist decision-makers in ambulance allocation and dispatching. Nevertheless, as shown in Figure 8, the most common approach to address the problem is mixed-integer linear programming (MILP) models (26 papers). MILP is the preferred approach due to getting an exact solution.

Nevertheless, addressing the problem with linear programming may affect the model’s ability to represent real-life situations or include some optimization objectives in the model. In some cases, constraints are the model’s elements that could be better expressed nonlinearly. In the cases where the MILP model is implemented, the most common solver is CPLEX (14 papers), Xpress, and Gurobi (three papers each). Metaheuristics approach amount with six papers and matheuristic with one. This is very important because due to the size of the problem, it was expected that the proportion of metaheuristic approaches would be higher. The high proportion of exact approaches, evidence of two things, the power of solvers has increased, and the available computation power has also increased, making it possible to tackle bigger problems.

On the other hand, nonlinear optimization is used in four papers and solved through metaheuristics and general-purpose solvers. It is essential to point out how robust optimization is only used in two papers, even though the system must be resilient considering that people’s lives may be affected. Figure 8 also shows the relevance of heuristic approaches in this type of problem. Finally, only one paper bases on game theory to address the problem.

In some cases, the problem is tackled recursively, optimizing and simulating iteratively. This kind of approach seems to make the problem more adaptative. Finally, it is essential to point out that though many problems use geographical information to estimate travel time or distances, there are only two papers where GIS is incorporated in the modeling.

Regarding the features considered in the problem, as shown in Figure 9, the majority of the papers consider stochastic demand. Some of them also consider stochastic travel times. In seven papers, the demand stochasticity drove into a posteriori relocation approach. Some other researchers (six papers) addressed this situation as a multiperiod problem through compliance tables. Only three papers incorporated demand forecast into the model. This is relevant considering that relocation policy should consider the past and the present of the system and the possible upcoming events to make a relocation decision or even a dispatching decision.

In Figure 10 that coverage is the predominant objective pursued in most of the research. Other objectives, such as penalty and equity, try to include fairness in the service. Coverage has the drawback of tending to locate ambulances in highly populated areas.

It is essential to point out that most EMS covering problems can be classified into two types: (1) cover every demand using the smallest number of facilities. This is the main objective of the models based on the Location Set Covering Problem (LSCP), or (2) maximize the demand that is covered while locating a fixed number of facilities. The main objective of problems based on the Maximal Covering Location Problem (MCLP) is maximizing covered demand. These two problems form the basis of most models developed after that. Many detailed models represent sophisticated extensions of the LSCP and the MCLP, addressing expected, multiple level, probabilistic, and capacity-constrained coverage.

It is also evident that these problems have been broadly studied, but significant challenges still must be addressed. Taking into account the analysis of the previous sections and the above conclusions, we consider that the most critical challenges and lines of research regarding EMS location and deployment are the following:

6.1. Holistic Models

Many optimization objectives are used in the literature; nevertheless, there is no consensus about prioritizing them or at least some basic measures that should be included in multiobjective EMS problems. In this sense, the selection of criteria seems arbitrary by authors and does not reflect a holistic approach in many cases. Therefore, it is necessary to explore the possibility of including multi-criteria decision-making in ambulances’ dynamic relocation. The use of TOPSIS, PROMETHEE, and other multicriteria decision rank tools could be integrated with optimization or heuristics approaches to get deployments schemes that comply better with the need and thinking of the citizens.

6.2. Algorithms for More Extensive and Realistic Models

Currently, cities are becoming huge metropolises not only in developed countries but also in developing countries. Cities have become extensive, and at the same time, they have become highly densely inhabited, increasing the possible demand and potential location points. The increase in demand and potential location sites makes solving ambulance deployment a challenging task. The size of the problem is critical when trying to address EMS dynamic redeployment or considering multi-objective problems, in which the problem must be solved within seconds. Therefore, it is necessary to develop new and more capable solution strategies. These strategies can include optimal, heuristic, metaheuristic (hyperheuristics and matheuristics) for current and future problems. It is essential to point out that the relevance of dynamic relocation relies on the fact that it improves the outcome of the system. Another critical topic is the system’s resilience, in an ambulance accident or only due to traffic jams or mechanical failure. In this sense, solution approaches based on cooperative game theory could be helpful.

Another important topic in EMS relocation is minimizing the distance to reach the demand point. Still, it could also be essential to build a more holistic model in which not the base to emergency site journey is minimized, but the global travel (EMS base–emergency site–hospital). It is also essential to include more applications related to continuous coverage, multiple type ambulance fleet use, and workforce exhaustion.

Regarding constructing more realistic models, Aringhieri et al. [149] identified that it is necessary to develop models that simultaneously incorporate actual information and several uncertainty sources. Most existing studies in the literature focus on only one or two stochastic aspects, and there is a lack of location models handling all sources of uncertainty simultaneously. It is also essential to study the robustness of EMS systems. Additionally, some tools, such as stochastic programming, are susceptible to improvement [99]. An aspect that has been highlighted by Li et al. [150] is the lack of goal programming and non-linear models. Aringhieri et al. [149] suggested combining optimization techniques with (generalized) stochastic Petri nets.

6.3. Absence of Open Datasets

Many studies show the benefits of addressing the problems somehow, and these benefits are supported by the improvements of some indicators in simulated scenarios. Nevertheless, in many cases, the results obtained by simulation in the studies are not easily reproducible. In some cases, the input data of the simulation model is not described nor published. Other significant problems with these studies are details that are not clearly defined, such as the parameters and policies used for road infrastructure and traffic behavior and the transportation times used in those simulations.

Open datasets could compare all approaches in terms of their performance regarding quality and timeliness. This fact could help set a standard for solving EMS location problems.

6.4. Artificial Intelligence and Machine Learning

Artificial intelligence and machine learning models are significant improvement opportunities in these problems. Machine learning can be used both as a solution approach and to improve some problem inputs. Forecasting when, where, and the severity of the following emergency call could enhance the performance of the systems. The gap between optimum and MEXCLP (with dynamic relocation) is currently 90% approximately [151]. This means that the percentage of location-to-emergency-site trips meeting the service standard is almost doubled when working with online data. These results were obtained with a simulation model. In the first place, the simulation was run with the locations obtained with the MEXCLP. The simulation was run again but supplying where the next emergency will occur, allowing the model to make better decisions [151]. Therefore, it is necessary to explore the use of machine learning to forecast the EMS demand dynamically and predict future demand considering the system’s current status. There is also a lack of integration of spatiotemporal demand forecasting with optimization processes. For example, it is necessary to include in the regressor time-series information, weather features, socioeconomic features, and cooccurrence of demand to improve the prediction. Good predictions will help make better decisions regarding relocation or at least compliance time if the problem is addressed as a multiperiod one. Another prominent area of research related to machine learning is its use to assist dispatchers in assigning ambulances once they have delivered the patient to the hospital. Although there are some applications of these tools, further applications must be implemented, including different metrics such as envy, number of relocations costs, survival functions, among others.

It is relevant to continue research on machine learning techniques to the data acquired during ambulance services to better predict the possible start of epidemic outbreaks. Early detection of epidemic outbreaks will help authorities establish containment actions for the outbreak and a better chance to detect patient zero. These situations may also affect location decisions due to the concentration of outbreak cases in some city districts and could have been very useful in the containment of the COVID-19 outbreak.

6.5. Resilience

The inclusion of resilience in the design of location policies of EMS is critical to face special events such as the current COVID-19 pandemic. It is necessary to consider the different scenarios that have faced EMS systems worldwide when special events such as H1N1, SARS, and EVD occur. The system must be aware of the changes in protocols related to the sanitization of ambulances and crew members, which will affect the system’s availability and preparedness. Consequently, the system-covered demand will be reduced. Another issue that will affect the system’s robustness and must be considered is that ambulances may assist the system with common emergencies at home to avoid ED in the cases of highly infectious outbreaks. This situation should be considered in robust models considering that demand distribution and quantity will affect the whole EMS system.

Serving patients with highly contagious diseases such as SARS or Ebola Virus Disease (EVD) requires specific policies to be implemented rapidly by emergency ambulance services to adequately support and protect all personnel [152]. There must be changes in policies, personnel behavior, training, and education of ambulance crew members in this sense. This situation substantially impacts ambulance services’ costs and the system’s performance, considering that the new policies may include the complete disinfection of ambulance and crew. This situation affects ambulances’ preparedness and consequently the capacity and costs of the system [152]. Therefore, the location policy may be affected.

6.6. Models for Rural Areas

The studies found in this review focus mainly on ambulances’ locations in highly populated areas. These areas can be big cities or small cities, but there are many people concentrated in one area in either of the cases. When addressing rural areas with city areas, it is necessary to include constraints that guarantee that the people from rural areas will be served. The problem lies in maximizing the covered demand; the model will always to try to locate ambulances in highly populated areas, leaving low-density areas without coverage. Therefore, it is necessary to continue developing models that can be successfully implemented in rural areas. It is required to look for other performance measures in these kinds of problems for the relocation actions for idle ambulances. In this sense, Van Barneveld et al. [73] considered that ambulances do not need to return to a base station. This means that ambulances are allowed to idle at any node. This brings forth a high degree of complexity of the state space. Therefore, they presented a heuristic approach to compute redeployment actions. These strategies combined with machine learning and multidimensional objectives encouraging the system’s equity are vital for rural areas, especially in nations like Colombia, where rural regions are perceived as being abandoned by the government.

Finally, it is essential to point out that ambulances are getting more involved in executing more preventive tasks to avoid hospitalization of patients and patients reentering hospitals. This can be achieved by making joint visits with nurses to monitor discharged patients’ recovery or the evolution of patients under different treatments. In this sense, the ambulance will also become an essential actor for data gathering for the whole system, performing preventing tasks, and triggering alerts of unusual conditions of a particular patient or a group of patients, representing an early alert for epidemics.