Mitigating Imbalance of Land Cover Change Data for Deep Learning Models with Temporal and Spatiotemporal Sample Weighting Schemes
Abstract
1. Introduction
2. Methodology
2.1. Study Area and Datasets
2.2. Capturing Neighborhood Effects in Land Cover Data Samples
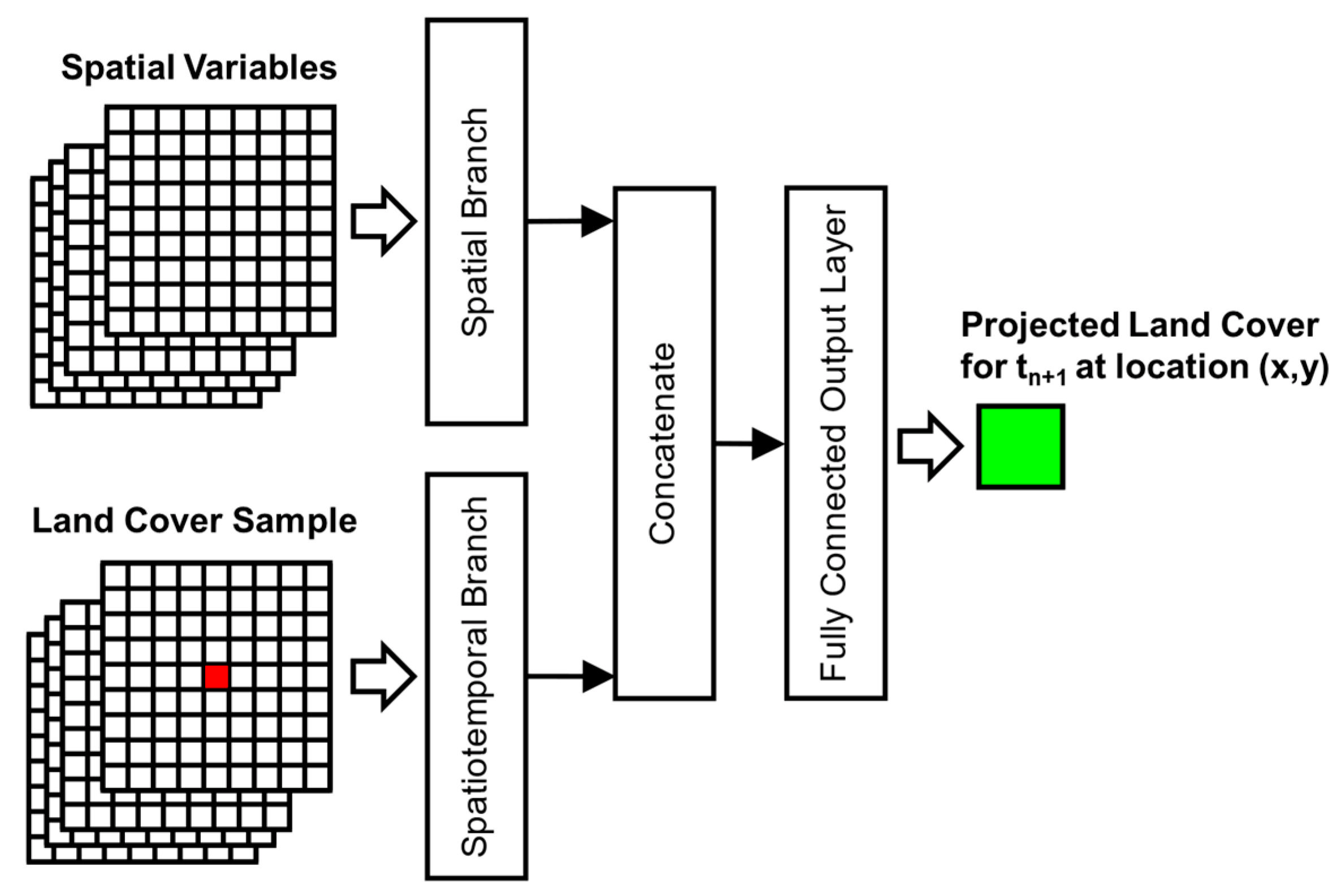
2.3. Model Specifications
2.4. Categorical Cross-Entropy Loss
2.5. Calculating Temporal and Spatiotemporal Sample Weights
- Unweighted (base case or “none”), where no sample weights were used;
- Binary weights (BW), where a traditional inverse frequency weighting scheme used the inverse frequency of changed versus persistent sample counts to assign sample weights;
- Temporal weighting scheme 1 (TW1), where the inverse temporal distance weight was computed with respect to the most recent change of the central cell;
- Temporal weighting scheme 2 (TW2), where the inverse temporal distance weight was computed with respect to the most recent change of the cell’s neighborhood;
- Spatiotemporal weighting scheme (STW), where the inverse spatiotemporal distance weight was calculated with respect to the most recent change that occurred within the neighborhood of the central cell.
2.6. Model Assessment
2.7. Experiment Settings
3. Results
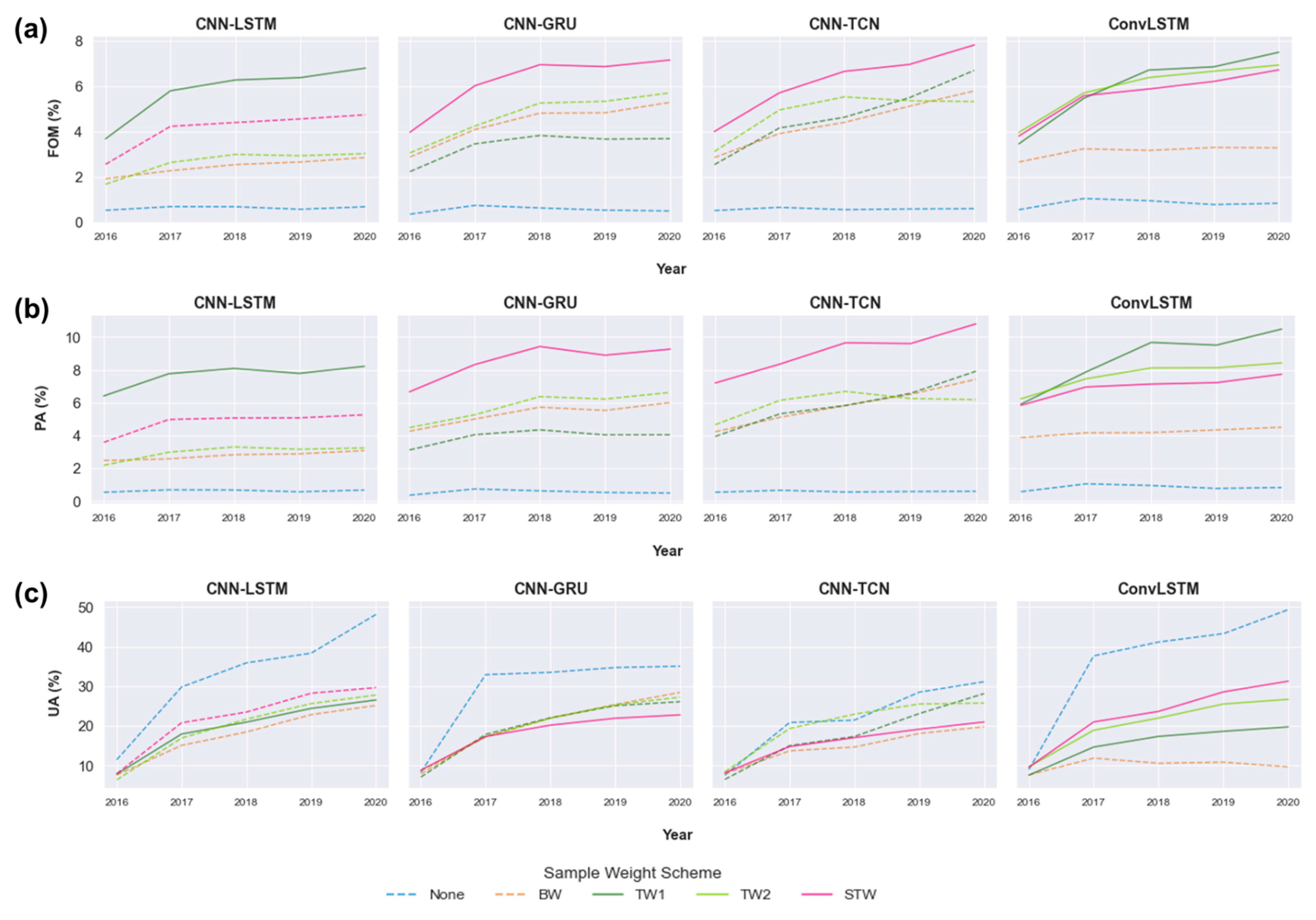
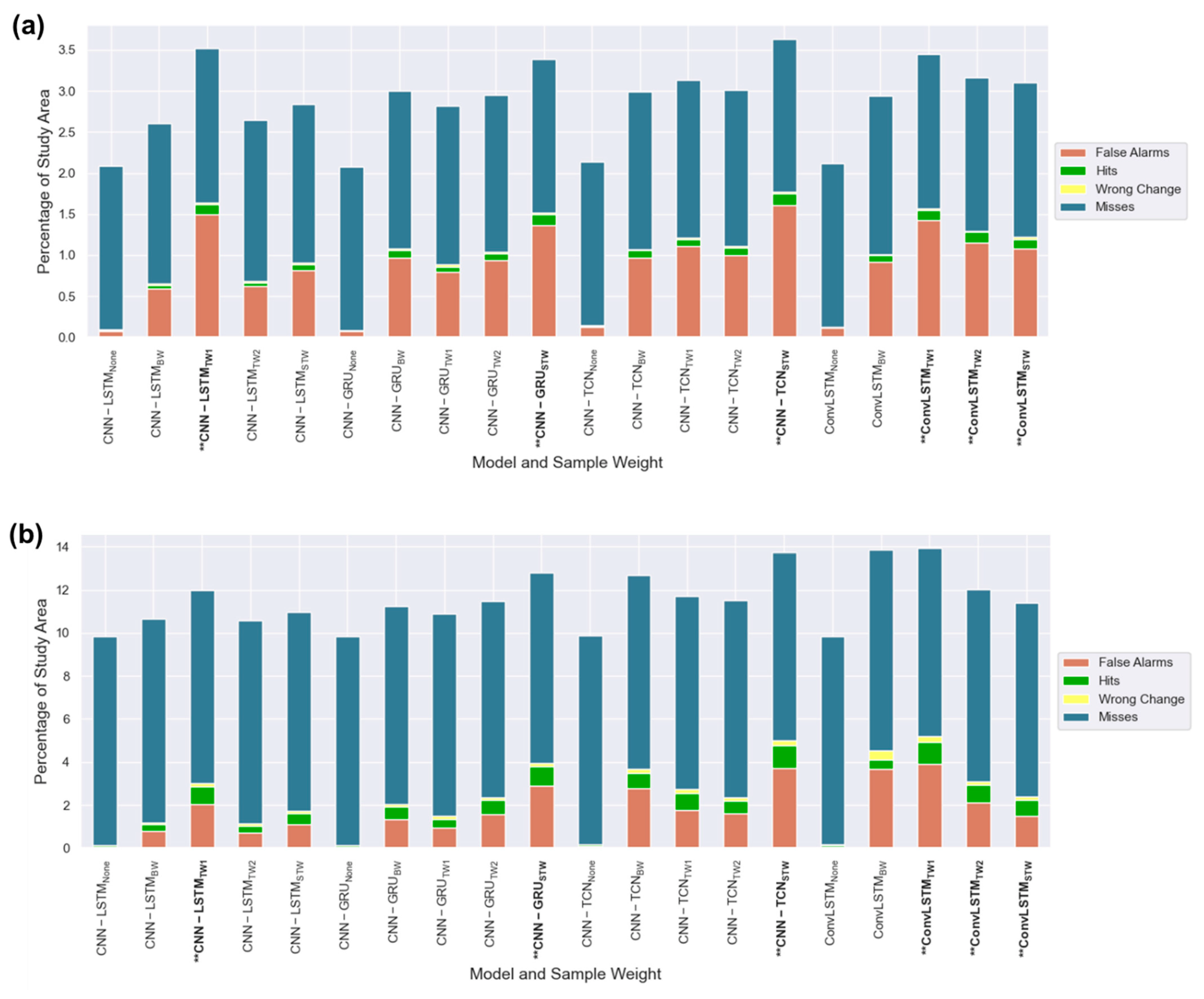
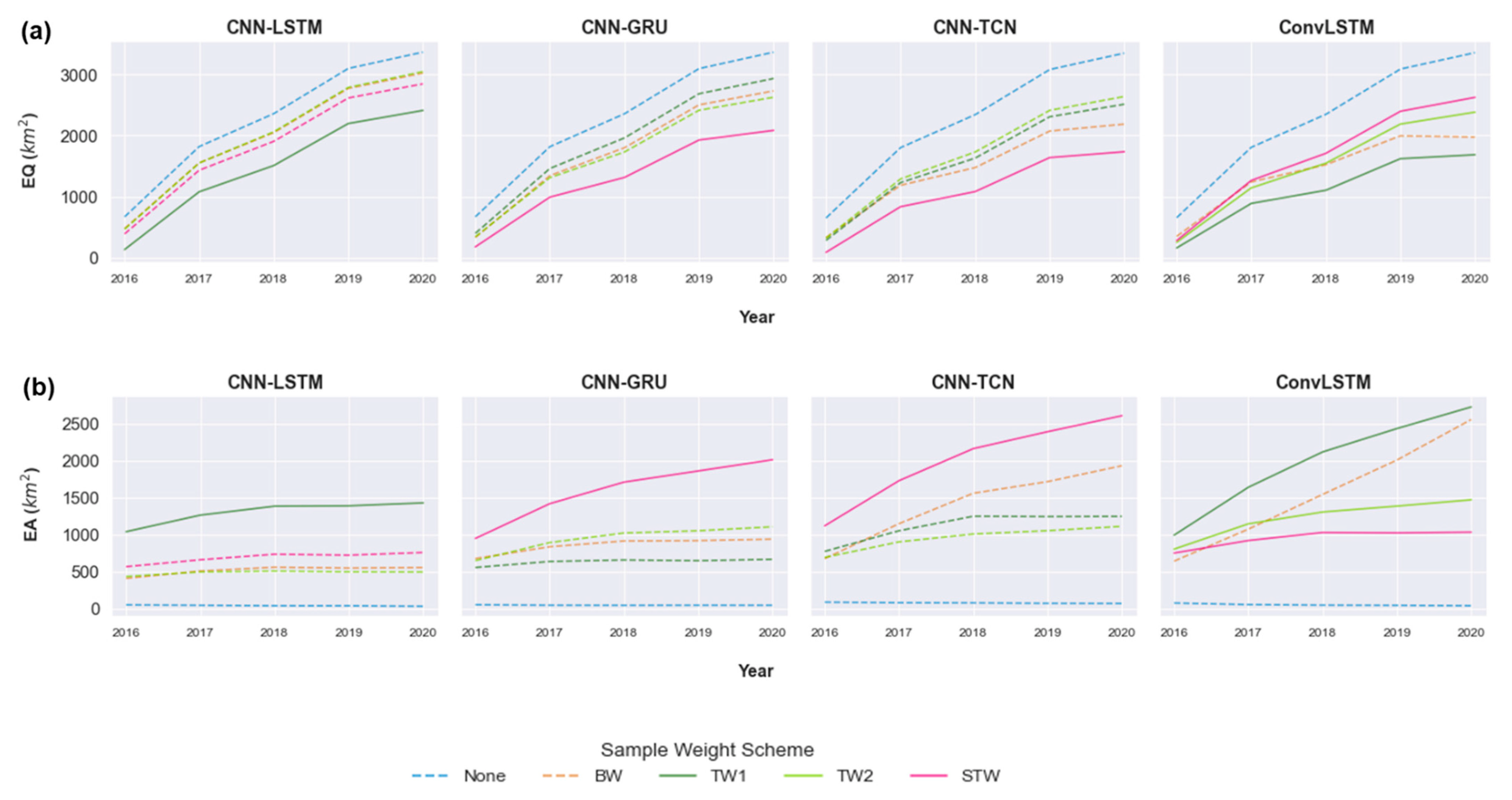
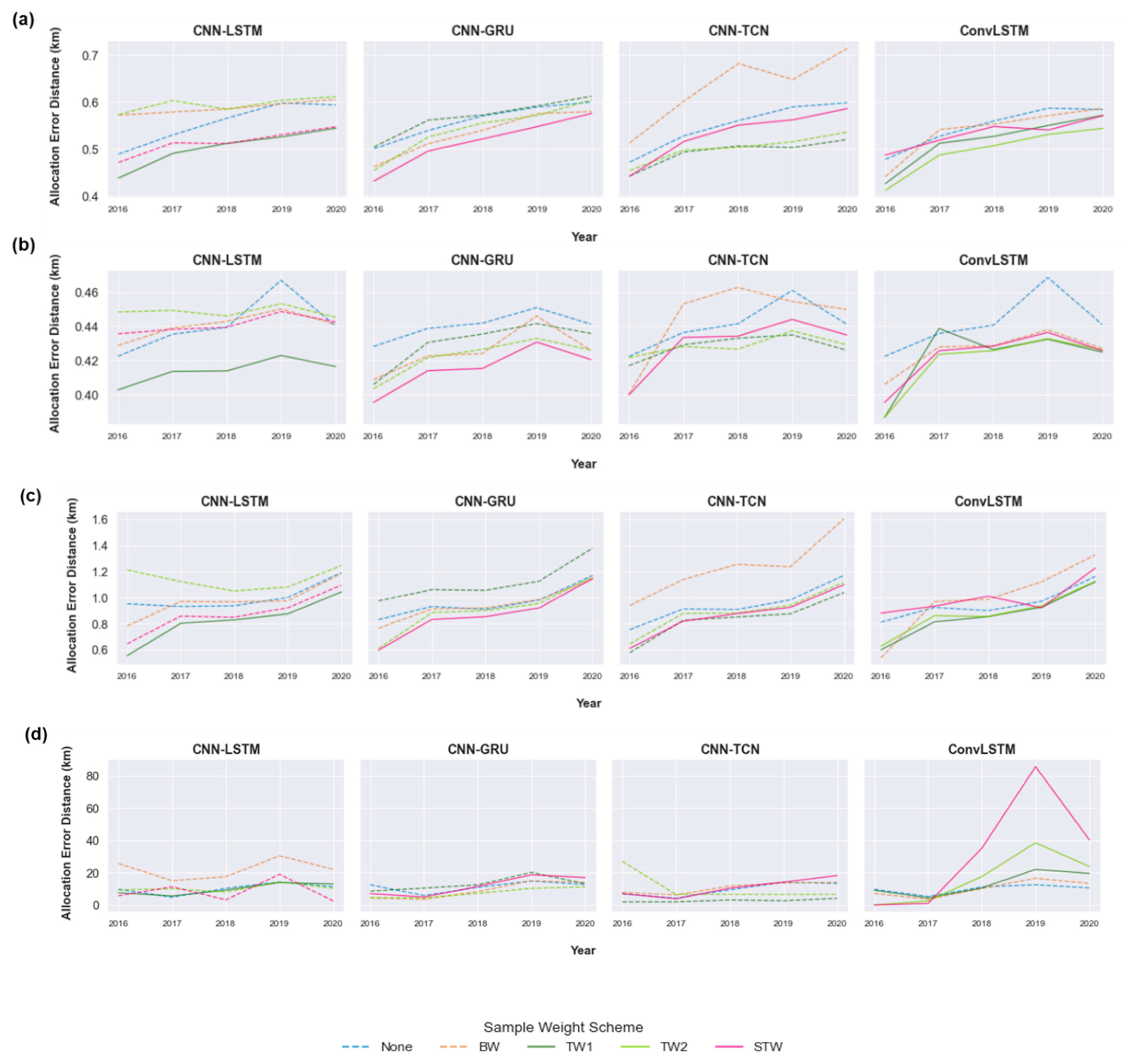
3.1. Multi-Year Change Assessment
3.2. Multi-Year Error Analysis
3.3. Visual Assessment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, W.; Zhang, M.; Zhang, R.; Chen, S.; Zhan, Z. Change detection based on artificial intelligence: State-of-the-art and challenges. Remote Sens. 2020, 12, 1688. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Prabhat Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Aburas, M.M.; Ahamad, M.S.S.; Omar, N.Q. Spatio-temporal simulation and prediction of land-use change using conventional and machine learning models: A review. Environ. Monit. Assess. 2019, 191, 205. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Bretz, M.; Dewan, M.A.A.; Delavar, M.A. Machine learning in modelling land-use and land cover-change (LULCC): Current status, challenges and prospects. Sci. Total Environ. 2022, 822, 153559. [Google Scholar] [CrossRef] [PubMed]
- Rußwurm, M.; Körner, M. Multi-Temporal Land Cover Classification with Sequential Recurrent Encoders. ISPRS Int. J. Geo-Inf. 2018, 7, 129. [Google Scholar] [CrossRef]
- Lee, C.; Lee, J.; Park, S. Forecasting the urbanization dynamics in the Seoul metropolitan area using a long short-term memory–based model. Environ. Plan. B Urban Anal. City Sci. 2022, 59. in press. [Google Scholar] [CrossRef]
- Xiao, B.; Liu, J.; Jiao, J.; Li, Y.; Liu, X.; Zhu, W. Modeling dynamic land use changes in the eastern portion of the hexi corridor, China by cnn-gru hybrid model. GIScience Remote Sens. 2022, 59, 501–519. [Google Scholar] [CrossRef]
- Kubat, M.; Matwin, S. Addressing the curse of imbalanced data sets: One-sided sampling. In Proceedings of the Fourteenth International Conference on Machine Learning, Nashville, TN, USA, 8–12 July 1997; pp. 179–186. [Google Scholar]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef]
- Buda, M.; Maki, A.; Mazurowski, M.A. A systematic study of the class imbalance problem in convolutional neural networks. Neural Netw. 2018, 106, 249–259. [Google Scholar] [CrossRef] [PubMed]
- Pontius, R.G.; Shusas, E.; McEachern, M. Detecting important categorical land changes while accounting for persistence. Agric. Ecosyst. Environ. 2004, 101, 251–268. [Google Scholar] [CrossRef]
- Karpatne, A.; Jiang, Z.; Vatsavai, R.R.; Shekhar, S.; Kumar, V. Monitoring land-cover changes: A machine-learning perspective. IEEE Geosci. Remote Sens. Mag. 2016, 4, 8–21. [Google Scholar] [CrossRef]
- Samardžić-Petrović, M.; Kovačević, M.; Bajat, B.; Dragićević, S. Machine Learning Techniques for Modelling Short Term Land-Use Change. ISPRS Int. J. Geo-Inf. 2017, 6, 387. [Google Scholar] [CrossRef]
- Karimi, F.; Sultana, S.; Babakan, A.S.; Suthaharan, S. Urban expansion modeling using an enhanced decision tree algorithm. Geoinformatica 2021, 25, 715–731. [Google Scholar] [CrossRef]
- Ahmadlou, M.; Karimi, M.; Pontius, R.G. A new framework to deal with the class imbalance problem in urban gain modeling based on clustering and ensemble models. Geocarto Int. 2022, 37, 5669–5692. [Google Scholar] [CrossRef]
- Douzas, G.; Bacao, F.; Fonseca, J.; Khudinyan, M. Imbalanced learning in land cover classification: Improving minority classes’ prediction accuracy using the geometric SMOTE algorithm. Remote Sens. 2019, 11, 3040. [Google Scholar] [CrossRef]
- Yu, X.; Wu, X.; Luo, C.; Ren, P. Deep learning in remote sensing scene classification: A data augmentation enhanced convolutional neural network framework. GIScience Remote Sens. 2017, 54, 741–758. [Google Scholar] [CrossRef]
- Kamel, A.; Issam, B. Data Augmentation for Land Cover Classification Using Generative Adversarial Networks. Int. Geosci. Remote Sens. Symp. 2021, 2021, 2309–2312. [Google Scholar] [CrossRef]
- Lu, J.; Ren, K.; Li, X.; Zhao, Y.; Xu, Z.; Ren, X. From reanalysis to satellite observations: Gap-filling with imbalanced learning. Geoinformatica 2022, 26, 397–428. [Google Scholar] [CrossRef]
- Ren, X.; Mi, Z.; Georgopoulos, P.G. Comparison of Machine Learning and Land Use Regression for fine scale spatiotemporal estimation of ambient air pollution: Modeling ozone concentrations across the contiguous United States. Environ. Int. 2020, 142, 105827. [Google Scholar] [CrossRef] [PubMed]
- Lian, D.; Wu, Y.; Ge, Y.; Xie, X.; Chen, E. Geography-Aware Sequential Location Recommendation. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery, San Diego, CA, USA, 23–27 August 2020; pp. 2009–2019. [Google Scholar]
- Sun, P.; Lu, Y.; Zhai, J. Mapping land cover using a developed U-Net model with weighted cross entropy. Geocarto Int. 2021, in press. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Crespo, R.; Yao, J. Geographical and Temporal Weighted Regression (GTWR). Geogr. Anal. 2015, 47, 431–452. [Google Scholar] [CrossRef]
- Li, D.; Wen, G.; Kuai, Y.; Wang, L. Spatio-temporally weighted multiple instance learning for visual tracking. Optik 2018, 171, 904–917. [Google Scholar] [CrossRef]
- Statistics Canada “Population and Dwelling Counts: Canada and Census Subdivisions”. Available online: https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=9810000201 (accessed on 1 June 2022).
- Sulla-Menashe, D.; Friedl, M. The Terra and Aqua Combined Moderate Resolution Imaging Spectroradiometer (MODIS) Land Cover Type (MCD12Q1) Version 6 Data Product. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mcd12q1_v006 (accessed on 30 January 2022).
- Wang, M.; Sun, X.; Fan, Z.; Yue, T. Investigation of Future Land Use Change and Implications for Cropland Quality: The Case of China. Sustainability 2019, 11, 3327. [Google Scholar] [CrossRef]
- Singh, V.G.; Singh, S.K.; Kumar, N.; Singh, R.P. Simulation of land use/land cover change at a basin scale using satellite data and markov chain model. Geocarto Int. 2022, in press. [Google Scholar] [CrossRef]
- Van Berkel, D.; Shashidharan, A.; Mordecai, R.S.; Vatsavai, R.; Petrasova, A.; Petras, V.; Mitasova, H.; Vogler, J.B.; Meentemeyer, R.K. Projecting urbanization and landscape change at large scale using the FUTURES model. Land 2019, 8, 144. [Google Scholar] [CrossRef]
- Stobbe, T.E.; Eagle, A.J.; Cotteleer, G.; van Kooten, G.C. Farmland Preservation Verdicts-Rezoning Agricultural Land in British Columbia. Can. J. Agric. Econ. 2011, 59, 555–572. [Google Scholar] [CrossRef]
- NASA/METI/AIST/Japan Spacesystems and U.S./Japan ASTER Science Team. “ASTER Global Digital Elevation Model V003”. Available online: https://lpdaac.usgs.gov/products/astgtmv003/ (accessed on 10 June 2022).
- Statistics Canada. “2016 Census-Boundary Files”. Available online: https://www12.statcan.gc.ca/census-recensement/2011/geo/bound-limit/bound-limit-2016-eng.cfm (accessed on 10 May 2022).
- Statistics Canada. “2016 Census Road Network File”. Available online: https://open.canada.ca/data/en/dataset/57d5ffae-3048-4a19-9b4c-eab12f6322c5 (accessed on 29 July 2022).
- van Vliet, J.; Naus, N.; van Lammeren, R.J.A.; Bregt, A.K.; Hurkens, J.; van Delden, H. Measuring the neighbourhood effect to calibrate land use models. Comput. Environ. Urban Syst. 2013, 41, 55–64. [Google Scholar] [CrossRef]
- Roodposhti, M.S.; Hewitt, R.J.; Bryan, B.A. Towards automatic calibration of neighbourhood influence in cellular automata land-use models. Comput. Environ. Urban Syst. 2020, 79, 101416. [Google Scholar] [CrossRef]
- Masolele, R.N.; De Sy, V.; Herold, M.; Marcos Gonzalez, D.; Verbesselt, J.; Gieseke, F.; Mullissa, A.G.; Martius, C. Spatial and temporal deep learning methods for deriving land-use following deforestation: A pan-tropical case study using Landsat time series. Remote Sens. Environ. 2021, 264, 112600. [Google Scholar] [CrossRef]
- Gray, P.C.; Chamorro, D.F.; Ridge, J.T.; Kerner, H.R.; Ury, E.A.; Johnston, D.W. Temporally Generalizable Land Cover Classification: A Recurrent Convolutional Neural Network Unveils Major Coastal Change through Time. Remote Sens. 2021, 13, 3953. [Google Scholar] [CrossRef]
- van Duynhoven, A.; Dragićević, S. Assessing the Impact of Neighborhood Size on Temporal Convolutional Networks for Modeling Land Cover Change. Remote Sens. 2022, 14, 4957. [Google Scholar] [CrossRef]
- Verburg, P.H.; de Nijs, T.C.M.; van Eck, J.R.; Visser, H.; de Jong, K. A method to analyse neighbourhood characteristics of land use patterns. Comput. Environ. Urban Syst. 2004, 28, 667–690. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 26–28 October 2014; Association for Computational Linguistics: Stroudsburg, PA, USA, 2014; pp. 1724–1734. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Yin, G.; Huang, Z.; Bao, Y.; Wang, H.; Li, L.; Ma, X.; Zhang, Y. ConvGCN-RF: A hybrid learning model for commuting flow prediction considering geographical semantics and neighborhood effects. Geoinformatica 2022, in press. [Google Scholar] [CrossRef]
- Yan, J.; Chen, X.; Chen, Y.; Liang, D. Multistep Prediction of Land Cover from Dense Time Series Remote Sensing Images with Temporal Convolutional Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5149–5161. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 2015, 802–810. [Google Scholar]
- Chen, R.; Wang, X.; Zhang, W.; Zhu, X.; Li, A.; Yang, C. A hybrid CNN-LSTM model for typhoon formation forecasting. Geoinformatica 2019, 23, 375–396. [Google Scholar] [CrossRef]
- Huang, C.-J.; Kuo, P.-H. A Deep CNN-LSTM Model for Particulate Matter (PM2.5) Forecasting in Smart Cities. Sensors 2018, 18, 2220. [Google Scholar] [CrossRef]
- Sefrin, O.; Riese, F.M.; Keller, S. Deep learning for land cover change detection. Remote Sens. 2021, 13, 78. [Google Scholar] [CrossRef]
- Pham, V.; Bluche, T.; Kermorvant, C.; Louradour, J. Dropout Improves Recurrent Neural Networks for Handwriting Recognition. In Proceedings of the 2014 14th International Conference on Frontiers in Handwriting Recognition, Crete, Greece, 1–4 September 2014; pp. 285–290. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Gordon-Rodriguez, E.; Loaiza-Ganem, G.; Pleiss, G.; Cunningham, J.P. Uses and Abuses of the Cross-Entropy Loss: Case Studies in Modern Deep Learning. In Proceedings of the Proceedings on “I Can’t Believe It’s Not Better!” at NeurIPS Workshops, online, 12 December 2020; Volume 137, pp. 1–10. [Google Scholar]
- Maretto, R.V.; Fonseca, L.M.G.; Jacobs, N.; Körting, T.S.; Bendini, H.N.; Parente, L.L. Spatio-Temporal Deep Learning Approach to Map Deforestation in Amazon Rainforest. IEEE Geosci. Remote Sens. Lett. 2021, 18, 771–775. [Google Scholar] [CrossRef]
- Zimmerman, D.; Pavlik, C.; Ruggles, A.; Armstrong, M.P. An experimental comparison of ordinary and universal kriging and inverse distance weighting. Math. Geol. 1999, 31, 375–390. [Google Scholar] [CrossRef]
- Kang, M.; Liu, Y.; Wang, M.; Li, L.; Weng, M. A random forest classifier with cost-sensitive learning to extract urban landmarks from an imbalanced dataset. Int. J. Geogr. Inf. Sci. 2022, 36, 496–513. [Google Scholar] [CrossRef]
- Tong, X.; Feng, Y. A review of assessment methods for cellular automata models of land-use change and urban growth. Int. J. Geogr. Inf. Sci. 2020, 34, 866–898. [Google Scholar] [CrossRef]
- Pontius, R.G.; Boersma, W.; Castella, J.-C.C.; Clarke, K.; de Nijs, T.; Dietzel, C.; Duan, Z.; Fotsing, E.; Goldstein, N.; Kok, K.; et al. Comparing the input, output, and validation maps for several models of land change. Ann. Reg. Sci. 2008, 42, 11–37. [Google Scholar] [CrossRef]
- Camacho Olmedo, M.T.; Pontius, R.G.; Paegelow, M.; Mas, J.F. Comparison of simulation models in terms of quantity and allocation of land change. Environ. Model. Softw. 2015, 69, 214–221. [Google Scholar] [CrossRef]
- Paegelow, M.; Camacho Olmedo, M.T.; Mas, J.; Houet, T. Benchmarking of LUCC modelling tools by various validation techniques and error analysis. Cybergeo Eur. J. Geogr. 2014, 701. [Google Scholar] [CrossRef]
- van Rossum, G. Python Language Reference; Python Software Foundation: Amsterdam, The Netherlands, 2009; ISBN 9780954161781. [Google Scholar]
- Chollet, F. Keras: The Python Deep Learning Library. Available online: https://keras.io/ (accessed on 26 May 2022).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar] [CrossRef]
- Remy, P. Temporal Convolutional Networks for Keras. Available online: https://github.com/philipperemy/keras-tcn (accessed on 1 May 2022).
- Naushad, R.; Kaur, T.; Ghaderpour, E. Deep transfer learning for land use and land cover classification: A comparative study. Sensors 2021, 21, 8083. [Google Scholar] [CrossRef]
- Xiao, C.; Chen, N.; Hu, C.; Wang, K.; Xu, Z.; Cai, Y.; Xu, L.; Chen, Z.; Gong, J. A spatiotemporal deep learning model for sea surface temperature field prediction using time-series satellite data. Environ. Model. Softw. 2019, 120, 104502. [Google Scholar] [CrossRef]
- van Duynhoven, A.; Dragićević, S. Exploring the sensitivity of recurrent neural network models for forecasting land cover change. Land 2021, 10, 282. [Google Scholar] [CrossRef]
- Ma, J.; Ding, Y.; Gan, V.J.L.; Lin, C.; Wan, Z. Spatiotemporal Prediction of PM2.5 Concentrations at Different Time Granularities Using IDW-BLSTM. IEEE Access 2019, 7, 107897–107907. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal Loss for Dense Object Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 318–327. [Google Scholar] [CrossRef] [PubMed]
- Gupta, J.; Molnar, C.; Xie, Y.; Knight, J.; Shekhar, S. Spatial Variability Aware Deep Neural Networks (SVANN): A General Approach. ACM Trans. Intell. Syst. Technol. 2021, 12, 1–21. [Google Scholar] [CrossRef]
- Costa, H.; Almeida, D.; Vala, F.; Marcelino, F.; Caetano, M. Land cover mapping from remotely sensed and auxiliary data for harmonized official statistics. ISPRS Int. J. Geo-Inf. 2018, 7, 157. [Google Scholar] [CrossRef]
- da Silva, M.V.; Pandorfi, H.; de Oliveira-Júnior, J.F.; da Silva, J.L.B.; de Almeida, G.L.P.; de Assunção Montenegro, A.A.; Mesquita, M.; Ferreira, M.B.; Santana, T.C.; Marinho, G.T.B.; et al. Remote sensing techniques via Google Earth Engine for land degradation assessment in the Brazilian semiarid region, Brazil. J. South Am. Earth Sci. 2022, 120, 104061. [Google Scholar] [CrossRef]


| Sample Weight Scheme for Changed Locations | Formula | Description |
|---|---|---|
| Binary weight (BW) | The inverse proportion of changed versus persistent samples | |
| Cell-change temporal weight (TW1) | Temporal distance () between most recent year () and the year of the most recent change event of the central cell () | |
| Neighborhood-change temporal weight (TW2) | Temporal distance () from the most recent year () and the year of change event occurring in the neighborhood of the central cell () | |
| Spatiotemporal weight (STW) | Spatiotemporal distance () from the central cell () to the nearest changed cell in its neighborhood () |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
van Duynhoven, A.; Dragićević, S. Mitigating Imbalance of Land Cover Change Data for Deep Learning Models with Temporal and Spatiotemporal Sample Weighting Schemes. ISPRS Int. J. Geo-Inf. 2022, 11, 587. https://doi.org/10.3390/ijgi11120587
van Duynhoven A, Dragićević S. Mitigating Imbalance of Land Cover Change Data for Deep Learning Models with Temporal and Spatiotemporal Sample Weighting Schemes. ISPRS International Journal of Geo-Information. 2022; 11(12):587. https://doi.org/10.3390/ijgi11120587
Chicago/Turabian Stylevan Duynhoven, Alysha, and Suzana Dragićević. 2022. "Mitigating Imbalance of Land Cover Change Data for Deep Learning Models with Temporal and Spatiotemporal Sample Weighting Schemes" ISPRS International Journal of Geo-Information 11, no. 12: 587. https://doi.org/10.3390/ijgi11120587
APA Stylevan Duynhoven, A., & Dragićević, S. (2022). Mitigating Imbalance of Land Cover Change Data for Deep Learning Models with Temporal and Spatiotemporal Sample Weighting Schemes. ISPRS International Journal of Geo-Information, 11(12), 587. https://doi.org/10.3390/ijgi11120587






