1. Introduction
Emergency evacuation is a process in which people in dangerous areas have to be guided or transported to safe places. It plays an essential part in crisis management, saving people’s lives and property. Since the occurrences of some notable emergency events, such as terrorist attacks on 11 September 2001 and the 2005 London bombing (which occurred in indoor environments), increased attention has been paid to indoor emergency evacuation [
1,
2,
3,
4]. We could classify the practical usages of this type of research into three categories: (1) to optimize the spatial designs of indoor environments; (2) to improve the configurations of the emergency response facilitates (exit lights, fire hose) for firefighting; (3) to assist with generating evaluation plans.
Indoor emergency evacuation is a complex phenomenon influenced by many factors, such as human awareness and interactions, hazard spread, and indoor environments. With the increased interest in indoor emergencies in recent years, many researchers have conducted studies to study the influences of these factors on evacuation efficiency in indoor environments during emergencies. The authors of [
2] proposed an agent simulation model that combines human behaviors to predict the spatial accessibility of a specific building under fire disaster situations. The authors of [
1] combined 3D spatial neighboring with topological relationships to implement a CA-based building evacuation simulation system. In [
3], the authors applied a multigrid model to study the pedestrian evacuation process under blind conditions and discovered several critical characteristics of the evacuees. The study in [
5] checked potential bioterrorism attacks on subway stations and inspected the influences of hazardous materials on the evacuees. However, the studies mentioned above mainly focused on human behaviors and interactions during evacuations. To the best of our knowledge, few works have evaluated spatial units’ connectivity in 3D environments for indoor emergency evacuation.
2. Related Works
An important aspect related to indoor emergency evacuation is navigation. During emergencies, various obstacles (e.g., fires, floods, and plumes) can affect road networks, and people in dangerous places need guidance to reach safe areas [
6]. Unlike outdoor navigation, indoor navigation occurs in 3D spaces and requires both the topological and geometric 3D information of route planning environments. Many efforts have shed light on developing models and methods for the efficient representation of 3D data for indoor navigation purposes [
7,
8,
9,
10,
11]. In recent decades, with the increased attention paid to indoor emergencies, many researchers have directed their interests to indoor navigation in disastrous situations and have developed new models and methods to support routing in indoor environments. The studies in [
12,
13,
14,
15] systematically exploited a 3D graph network model integrated with the metric distance measure to help emergency responders and evacuees determine the safest egress paths quickly. The authors of [
16] fully applied a three-dimensional geometric network to compute evacuation routes for evacuees and generated two types of “almost-optimal” and “almost feasible” solutions considering time constraints. However, these above works only addressed route generation in different disaster situations, and few researchers have paid attention to analyzing the robustness of networks affected by hazards. Because 3D networks play a major role in the generation of indoor routes, there is also a need to analyze the indoor routing network understudy’s status to facilitate route calculations during emergencies.
Network representations have been used in various fields to model real-world problems, such as social networks, traffic networks, and power networks. Researchers have developed a rich set of methods to address these problems and analyze networks for various purposes [
17,
18]. The authors of [
19] proposed multiple centrality assessment systems to evaluate the nature of a network from a primal perspective. This system can show the metric distances and other indices of the centrality features of the studied graphs. For general cases regarding network connectivity statuses, References [
20,
21] explored some essential characteristics and dynamics for urban street network gridlocks and developed a model to reproduce hysteresis and network gridlocks. They applied the developed model to significant city networks and discovered some phenomena from the whole network’s perspective. In [
22], the authors proposed a robustness analysis model based on short-term variations in supplies. This model is efficient for demonstrating the vulnerabilities of specific networks. In [
23], the authors conducted a systematic structural vulnerability analysis for a large-scale power grid structure according to complex network principles. This model can identify the vulnerable spots in a network. The authors of [
24,
25,
26] studied the community structures existing in several large networks and the influences of their effects during random and infectious attacks. In [
27,
28], the authors investigated the impacts of illness carriers among a complex network and found that the most influential spreaders are the nodes that have the highest k-decomposition values instead of the considerable connectivity values suggested by the classical evaluation methods. Although these existing network studies have provided insights into navigation networks’ evaluation from a topological aspect, they lack consideration for 3D geometric information, limiting their applicability concerning the analysis of indoor navigation networks.
In this study, we investigate the evaluation of networks for indoor emergencies and propose a method to analyze networks’ robustness under emergencies. In this method, we use the 3D spatial distance as the edge weight for the generation of navigation paths and consider both the network topology and 3D spatial distance in the network analysis. The 3D spatial distance usage allows us to evaluate the given 3D network more realistically and holistically. Furthermore, we introduce hazard models to evaluate the connectivity status of the indoor network. Thus, by integrating hazard models, we can estimate the influence of hazards on the network structure over time (i.e., by dynamically dividing the main network into isolated subnetworks) and update the weights of edges in the indoor navigation network. We propose a set of indices for the evaluation of nodes and the whole network. These indices can help us examine the network’s status in a 3D environment affected by hazards and identify vulnerable nodes and edges, facilitating the generation of evacuation plans for indoor emergencies. We organize the rest of this paper as follows: in
Section 3.1, we present the indices proposed for the connectivity analysis of 3D indoor navigation networks. In
Section 3.2–
Section 3.4, we take a fire event as an example and present our method to study the isolation phenomena of an indoor network affected by fires. In these sections, we carry out experiments and test our method with two buildings’ datasets.
Section 3.5 describes our experiments and
Section 4 presents the experiments results. Finally, in
Section 5, we provide our conclusions and suggest future research directions.
In the next part, we present a set of indices that define network connectivity at the global and local levels. At the global level, we use selected indices to examine the connection efficiency of the entire network. We evaluate the connection effectiveness for the neighborhood of specifically studied graphs and estimate the local influences of the considered neighboring nodes or edges at the local level. The developed indices use nodes as fundamental elements for examining purposes and integrating spatial correlations with nearby objects to describe the same spatial characteristics in the indoor navigation network. We generally elaborate on the classical indices that play the function of measuring the graph statuses below:
The gamma index is a measure of connectivity that considers the relationship between the number of observed links and possible links. The value of gamma is between 0 and 1, where a value of 1 indicates a completely connected network, which would be extremely unlikely in reality. We use this index to measure the progression of a network over time.
- B.
General transitivity
Transitivity is the overall probability of having its adjacent nodes be interconnected, thus revealing tightly connected communities. We use the measure of general transitivity that is calculated by the average clustering coefficient for all nodes.
- C.
Average node path length
The average shortest path length is a measure of efficiency representing the average number of steps needed to reach two distant nodes in the graph. The lower the result is, the more efficient the network in providing ease of circulation. In this paper, we use a node as the unit of measuring the average path length.
- D.
Graph diameter
The graph diameter is the length of the shortest path between the most distanced nodes of a graph. It measures the extent of a graph and the topological length between two nodes.
- E.
Local connectivity
Connectivity is the minimum number of deletion elements to separate the remaining nodes into isolated sub-graphs. We introduce the concept of local connectivity generated by the arithmetic mean of all nodes’ connectivity values.
3. Research Methodology
3.1. The Proposed Method
In the following part, we show the six indices definitions of the proposed method for network evaluation. The first index is the clustering coefficient and an indicator for describing the spatial influence of removing a specific node in the network. The second index is the average cost of local neighbor node counts and depicts the number of neighboring nodes of a specific node covered by the ordinary node distance scope. The third index is the 3D spatial distance, which describes a neighboring node’s spatial closeness from a specific node, and so it is a spatial influence indicator for this source node. The fourth index is the meaningful result count used to depict the mean count for the generated path result. The path results mentioned in this paper are all generated by the Dijkstra algorithm. The fifth index is the average time cost of pathfinding and describes the general case of the time cost spent on the pathfinding process. The last index is the average length of the path used to demonstrate the general distances of output paths; two sub-indices implement it: the average path lengths measured by the node distance and spatial distance. Moreover, in Equations (
1)–(
9), we use the symbol
v to represent a specific node; the symbol
e to represent an edge; the symbol
V to represent the complete node set; and the symbols
p and
P to represent the generated path and complete path set in the corresponding graph, respectively.
Table 1 summarizes the index symbols used in this paper.
- A.
Node clustering coefficient
Equation (
1) produces the clustering coefficient for a specific node
v. To compute this index, we first calculate the number of edges in node
v’s neighboring node-set
after the deletion of node
v from the navigation network.
represents the edge collection formed by nodes
u and
w in the set
.
is the size of set
, which equals the number of nodes in this set. This index illustrates the influence of a selected node on the entire navigation network. Since this index’s value represents the importance of the considered node in the system, a larger value means that this node’s deletion would have a lesser impact on the system’s passing efficiency.
- B.
The average cost of the local connectivity index
When calculating the average cost of the regional connectivity index for all nodes in the network, we aim to measure the node deletion process’s average influence level in the system. This value indicates a general perspective of the neighborhood clustering status in Equation (
2).
- C.
3D spatial distance and spatial closeness of a neighboring node
Aiming to demonstrate the considered navigation network’s 3D spatial distribution, we introduce two coefficients generated by Equations (
3) and (
4). In Equation (
3),
represents the 3D distance between any two connected nodes
v and
w in the navigation network, and
represents the number of edges in the same system. The average spatial distance cost of edge
shows the mean travel distance for existing edges. Currently, these edges are undirected; we will consider directed edges in future work.
Equation (
4) generates a quantitative index
Q for illustrating the spatial closeness of neighboring nodes in the navigation network, and two steps accomplish the computation of this index computation. The first step computes the number of nodes spread in the spatial scope around the considered node
v. In detail, this scope is a 3D ball formed by using the 3D coordinates of
v as the center and the value generated by Equation (
3) as the radius
. In other words, there are the nodes with spatial distances
smaller than
, where
w represents any neighboring node of the current considered node
v. After setting up covering balls, we generate an adjacent set of
that contains every ball’s covering nodes. Then, in the second step, we calculate the arithmetic mean
Q for the entire navigation network with the previously defined
values for all nodes by dividing this sum by the total node number
n.
- D.
Meaningful result count
Let us first define a result count
that originates from calculating the meaningful evacuation paths passing a specific node marked with the label
t. Therefore, the meaningful result counts,
, equals the sum of elements
neither in the zero nor null set (
) that either cover the case of the considered node as the evacuation target or the case in which there is no accessible, safe evacuation path to the target node. Moreover, these values mostly come from a test that cannot generate any meaningful evacuation path or exceeds each path generation process’s time threshold.
- E.
The average time cost of path finding
The average time cost
of pathfinding is the mean value among every specific type of path generating principle for the compared methods. Moreover, it is the average sum (generated by subdividing the path node number
) of the time cost
for each path
p in the complete evacuation path set
P.
- F.
Average length of generated paths
The average length of path finding
is the average value (generated by subdividing the path node number
) of the generated path distance
for each successfully generated path
p in the complete path search set
P. This value is introduced to reflect the effect of applying different optimization principles for our solution. For each path
,
,
I is the number of nodes along path
p, and we use two distance types: the node distance and spatial distance; thus, the following two subsections describe these two distances for the average length of a path in detail.
The node distance
is the count
of every successive node pair along a path and is measured in counts (Equation (
8)). Moreover, it reflects how the generated evacuation path traverses many critical nodes. Here,
denotes a node in the complete node set
I for the generated path
p.
The spatial distance
is the sum of the spatial distances
of every two successive nodes along a path measured in meters (Equation (
9)). It shows the geometric space that is covered by the generated evacuation path. Here,
denotes a node of the complete node set
I for the generated path
p.
3.2. Isolation Study and Recovery of the Spatial Navigation Network for a Spreading Fire
Unlike the static environments of typical navigation situations, evacuation navigation must take the dynamics of the spreading hazards into account. As a threat develops, many edges and nodes in the navigation network become affected and unavailable. This situation can deteriorate when the threats block all main egresses. Under this circumstance, many isolated subnetworks can emerge due to their egress routes becoming blocked, and we call this situation the isolation of the navigation network.
The isolation phenomenon can significantly hinder evacuation efficiency, and under extreme situations, it can even paralyze the entire evacuation network due to the unavailability of all safe egress routes. Nevertheless, emergency responders can apply ladders or personnel lowering devices to construct new egress paths. Therefore, the resilience of the navigation network for evacuation purposes is also crucial. From our perspective, we can split fire disasters’ primary development process into three phases: the ignition phase, the entire development phase, and the egress closure phase. These phases have different spatial influences on the navigation network. In the first phase, only the fire source and its nearby surrounding region are inaccessible. In the second phase, fire development is severe, and it paralyzes a large part of the navigation network. In the final stage, hazards block most critical nodes in the navigation network, and no safe egress paths are available. We are currently only considering a particular ignition position and carefully studying the multiple ignition positions in future work. Furthermore, we would also conclude the difference of the fire resistance features of various building and furniture materials, for example, plastic, wood, and paint, in future research on the fire spreading models.
3.3. Estimation of the Spread of Fire in a 3D Navigation Network
As previously mentioned, the spread of a fire has a spatial influence on the navigation network. We can describe this process by marking the passage statuses of nodes covered by the hazard, such as transit areas filled with fire plumes and flames, as blocked. Therefore, a fire model must estimate fires’ spatial influence on the navigation network and obtain information about the building’s navigation conditions during disasters.
In this study, we use a fire model (Equation (
10)) to estimate the fire’s spatial influence during the full development phase. In this equation,
,
, and
represent the fire source’s initial coordinates;
,
, and
represent the speed of the spread of the developing fire across three axes.
represents the starting time of the current phase, and
t represents the present time.
and
represent the current minimum and maximum coverage of the fire along the
X-axis. The same explanation also applies to
and
for the
Y-axis and
and
for the
Z-axis. Here,
t represents the development time for the fire event.
3.4. Pre-Measures for the Recovery Analysis of an Indoor Navigation Network
As discussed at the beginning of
Section 3, the spread of a disaster can reorganize the original navigation network. This phenomenon can demonstrate the isolation between several nodes and their neighbors due to the blockage of their connecting edges by hazards. This situation can result in two critical issues affecting navigation operations. The first issue is to find the minimum influence paths between these nodes, which are generated by checking the
values from
Section 2 and are named as
isolated subnetworks. The second issue is to use the smallest number of nodes possible to address the dynamically deteriorating navigation network. To address these two issues, we rely on the spatial sorting of nodes across both the primary and isolated subnetworks, and these nodes are the same as the nodes in the building structure’s skeletal framework. We have not discussed furniture, fixtures, and equipment (FF&E) in the current research stage due to the lack of reliable data for these objects. Moreover, according to the sorting results, only some sorted nodes are introduced to generate minimum influence paths across the navigation network.
3.4.1. Spatial Sorting of Nodes
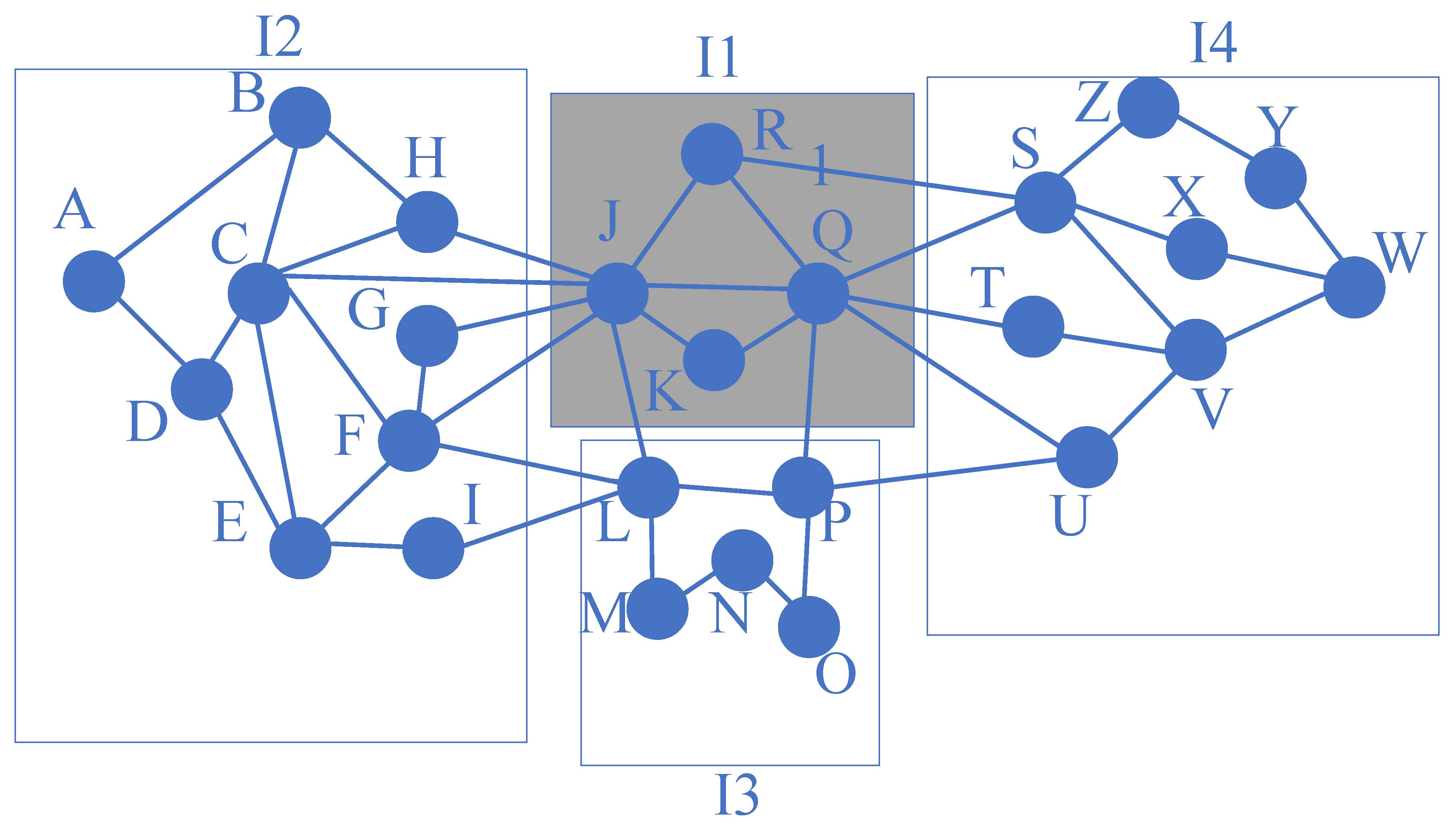
We can choose different principles for sorting nodes, such as sorting them by their node distances to the fire region or their spatial distances to the fire region and applying them in this study. In our opinion, the most critical issue for evacuation navigation is to determine the effect of the 3D spatial distance weights on the network. Therefore, we set different groups of nodes by evaluating the node distances to the fire region and the fire region’s spatial distances. We demonstrate this concept in
Figure 1. There are 26 nodes to search for the emergency evacuation solutions in this figure. We optimize the evacuation searching process by assigning different priorities to the 22 nodes (the 4 nodes in isolated-region 1 are filtered out due to disaster coverage), as shown in
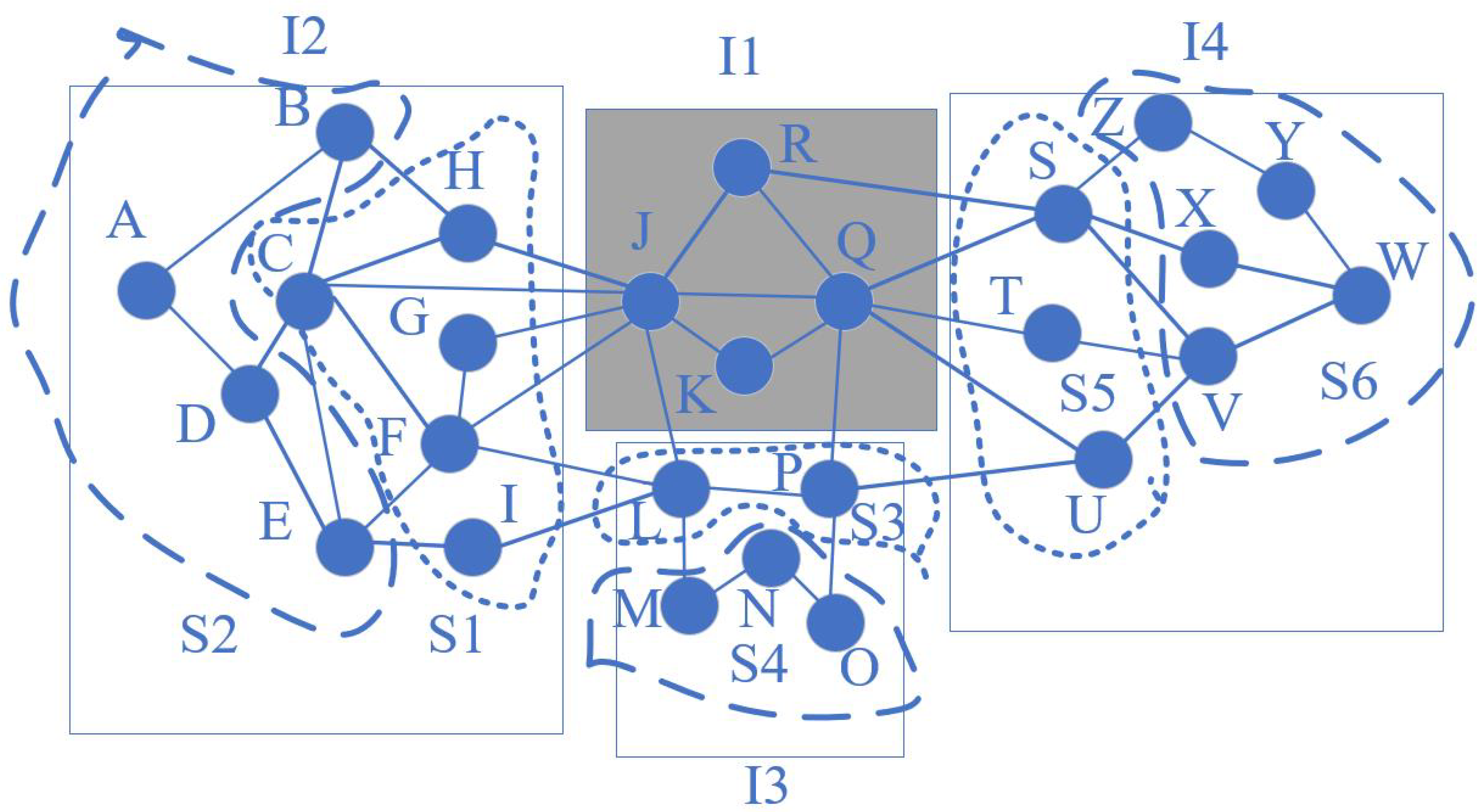
Table 2. Next, we take nodes C and F as examples to explain the sorting principle. Because node C connects isolated region 1 with the minimum depth 1 to node J, the ’node distance’ for node C from isolated region 1 is 1. Following this principle, node F’s ’node distance’ is also 1 for isolated regions 1 and 3. Therefore, we can receive the sorted region S1’ composed of nodes C, F, G, H, and I. We can finally generate three sorted regions: S1, S3, and S5, with node distances of 1 to the isolated-region 1. Thus, we select these regions with higher priorities than those of other sorted regions with node distances larger than 1 to isolated-region 1 in
Figure 2.
3.4.2. Partial Selection of Nodes for Path Finding
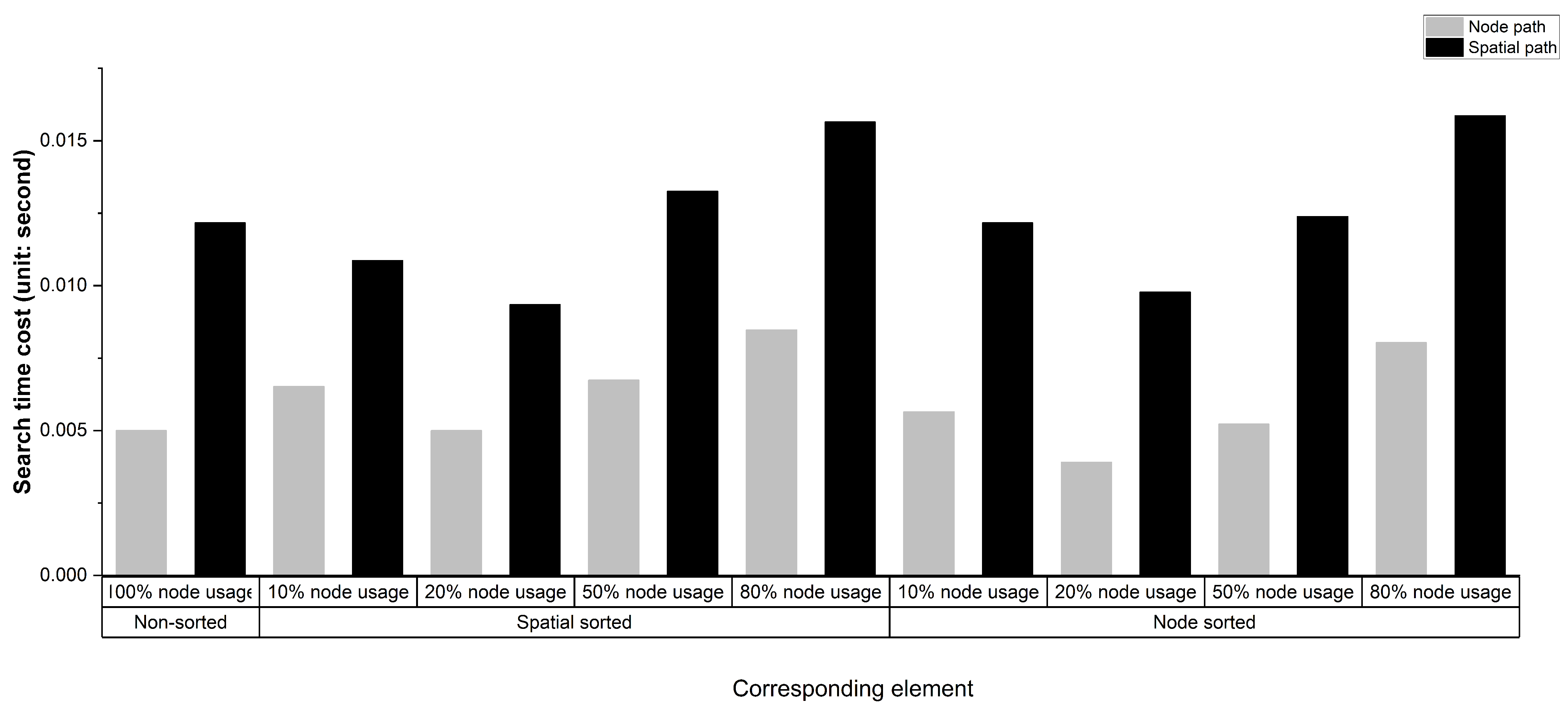
For the spatial sorting of nodes, we arrange the sequence of nodes by a specific standard, such as the node distance to the fire region, and we fetch only the nodes relevant to the pathfinding process. For this purpose, we utilize the first 20% of the sorted nodes for evacuation path generation according to the Pareto principle [
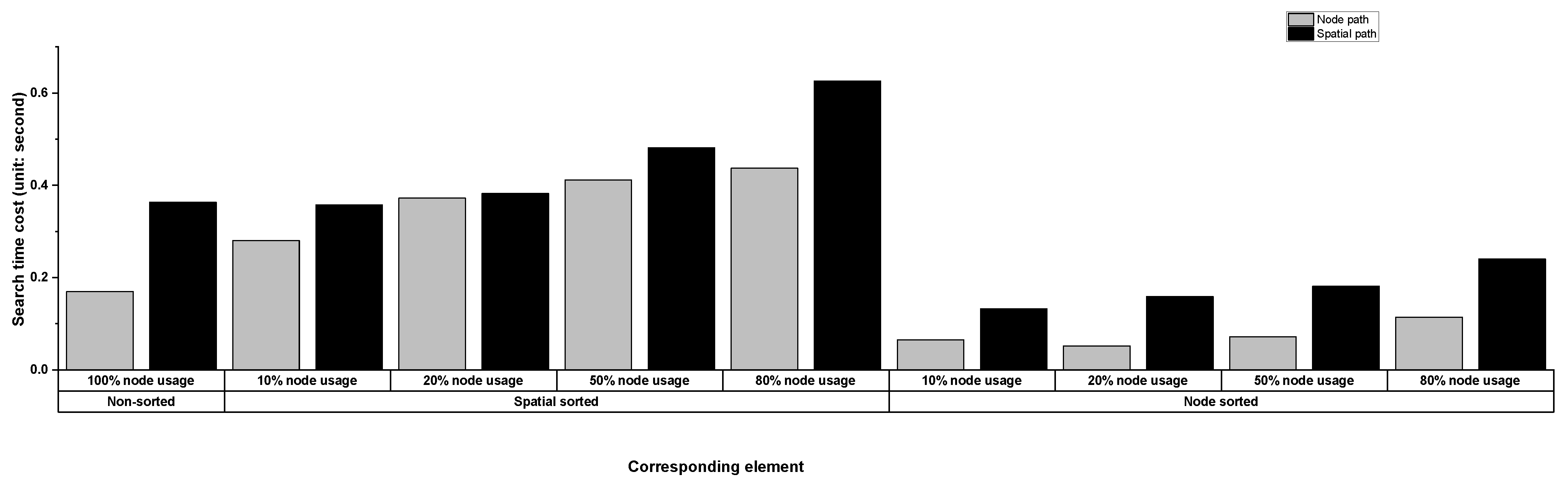
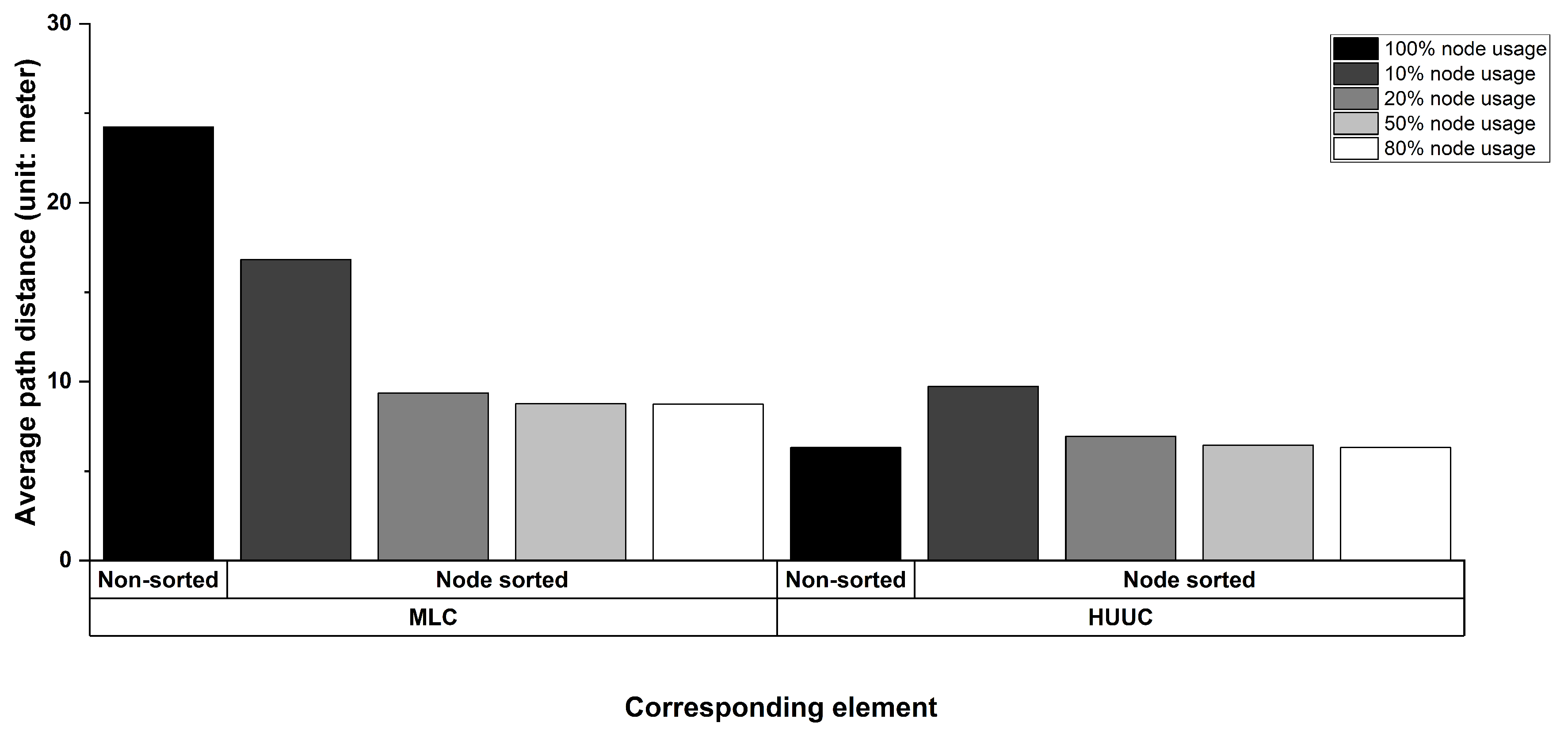
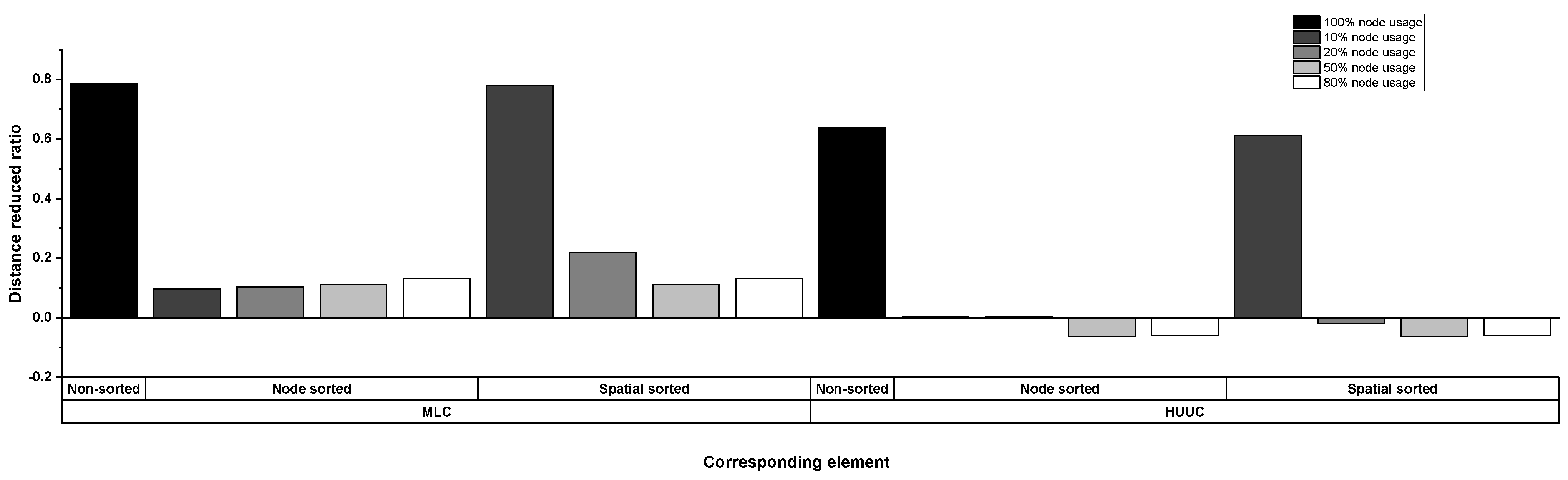
29]. Additionally, we introduce the 10%, 50%, and 80% cases of all nodes as the comparison group. The purpose of using a different number of nodes during navigation is to balance the volume of node data and the accuracy of the generated evacuation paths. When the number of nodes is extensive, using all nodes in the evacuation path generation is not optimal for saving time. Using the necessary number of nodes for the required computation is a wiser option. To this end, we can only select the exact number of nodes by fully understanding which of the nodes are crucial during evacuation path generation operations.
3.5. Introduction of the Studied Buildings
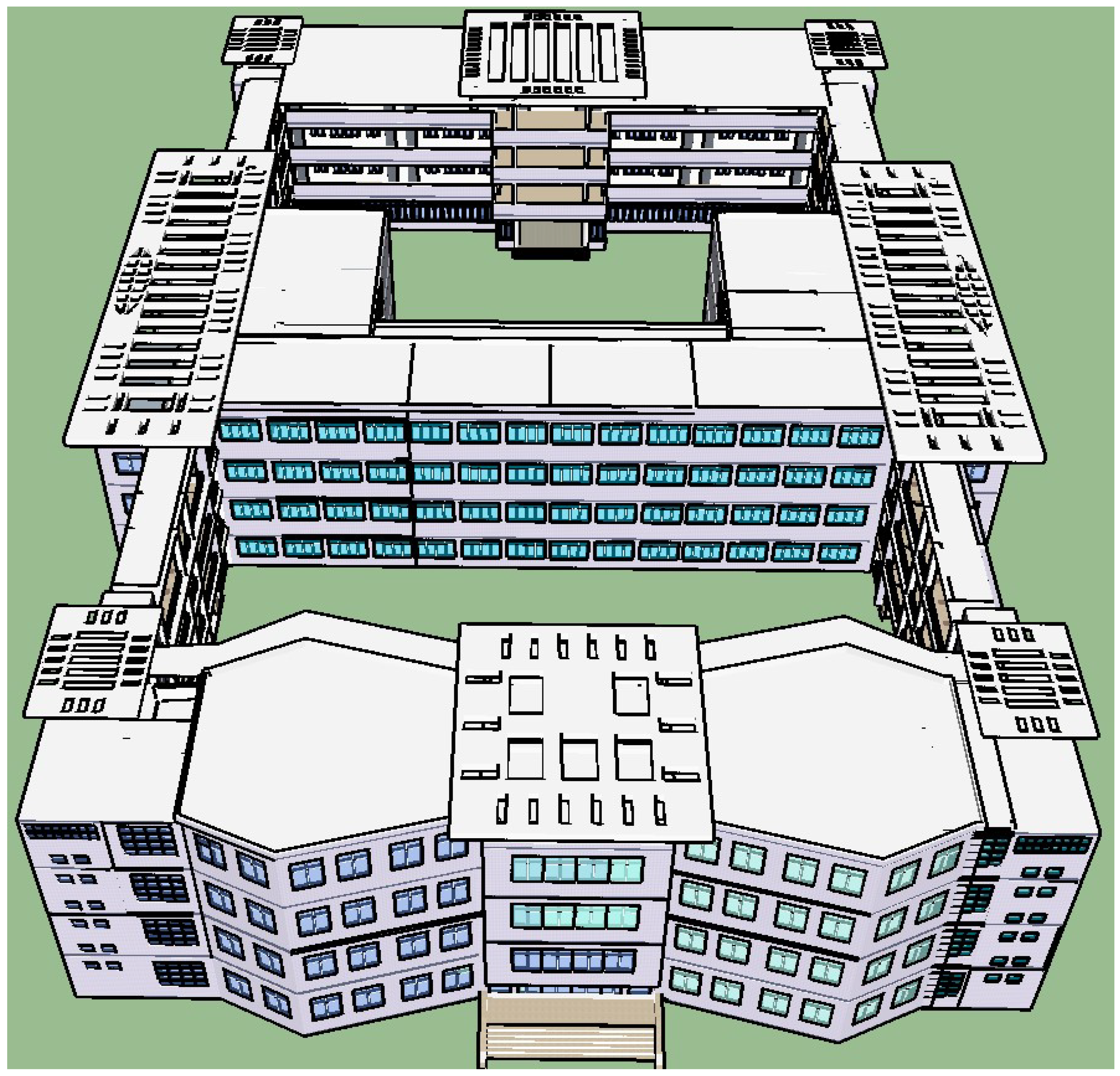
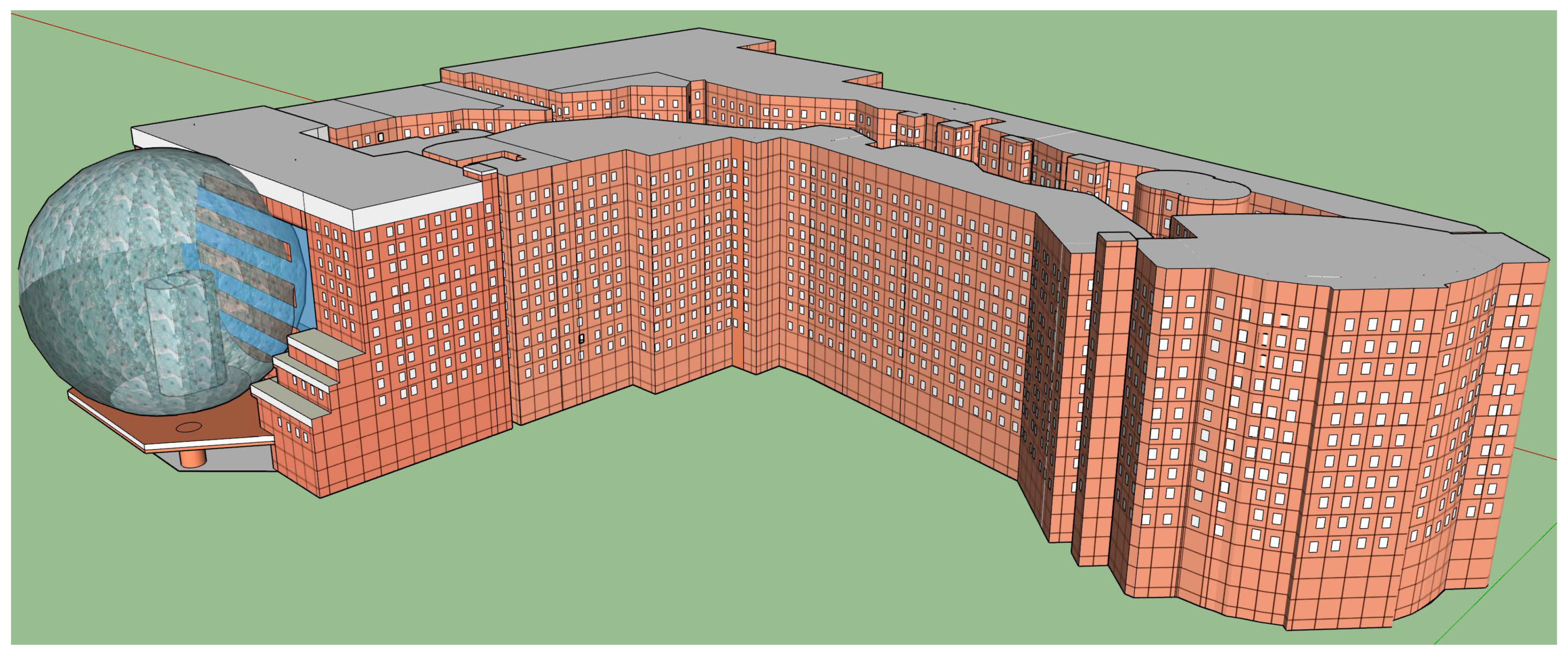
We evaluate our method with the datasets of two buildings. The first is a building at the Henan University of Urban Construction (HUUC) (
Figure 3). The other one is the Meiluocheng (MLC) building (
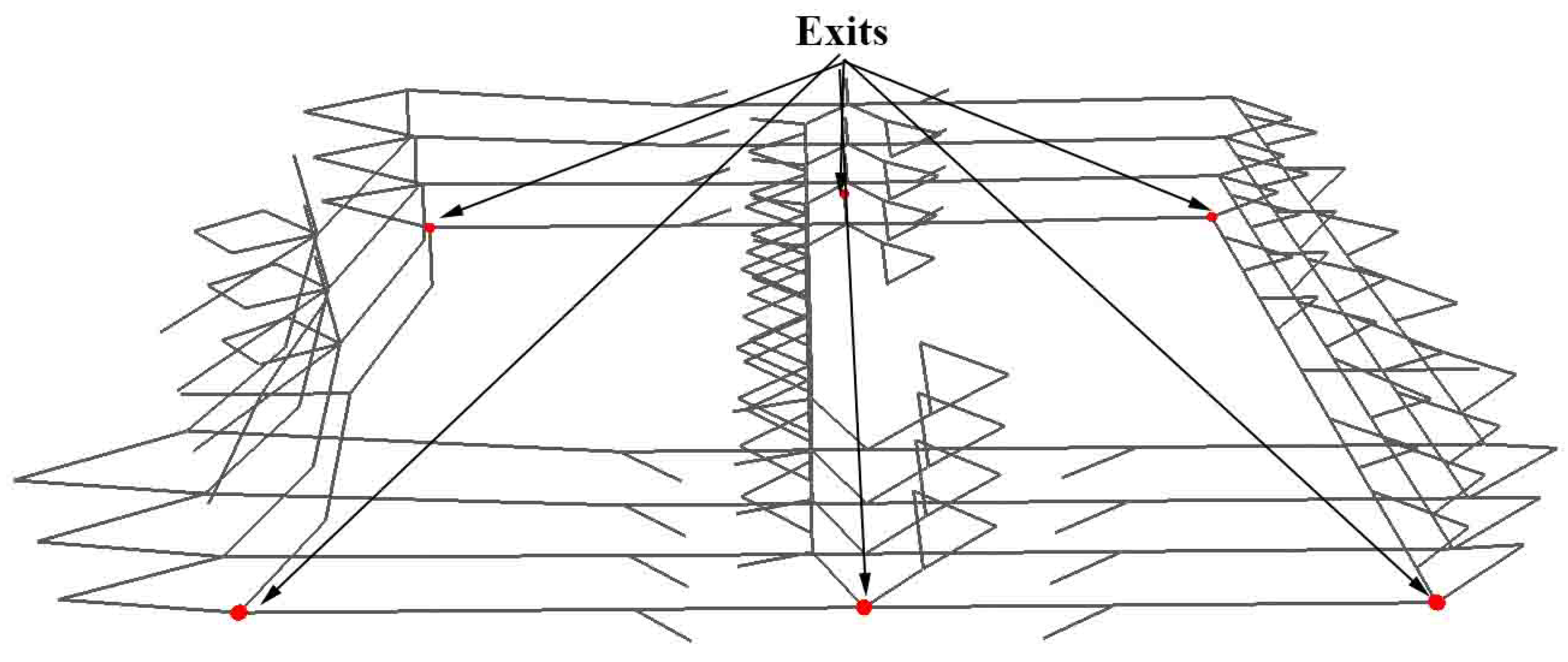
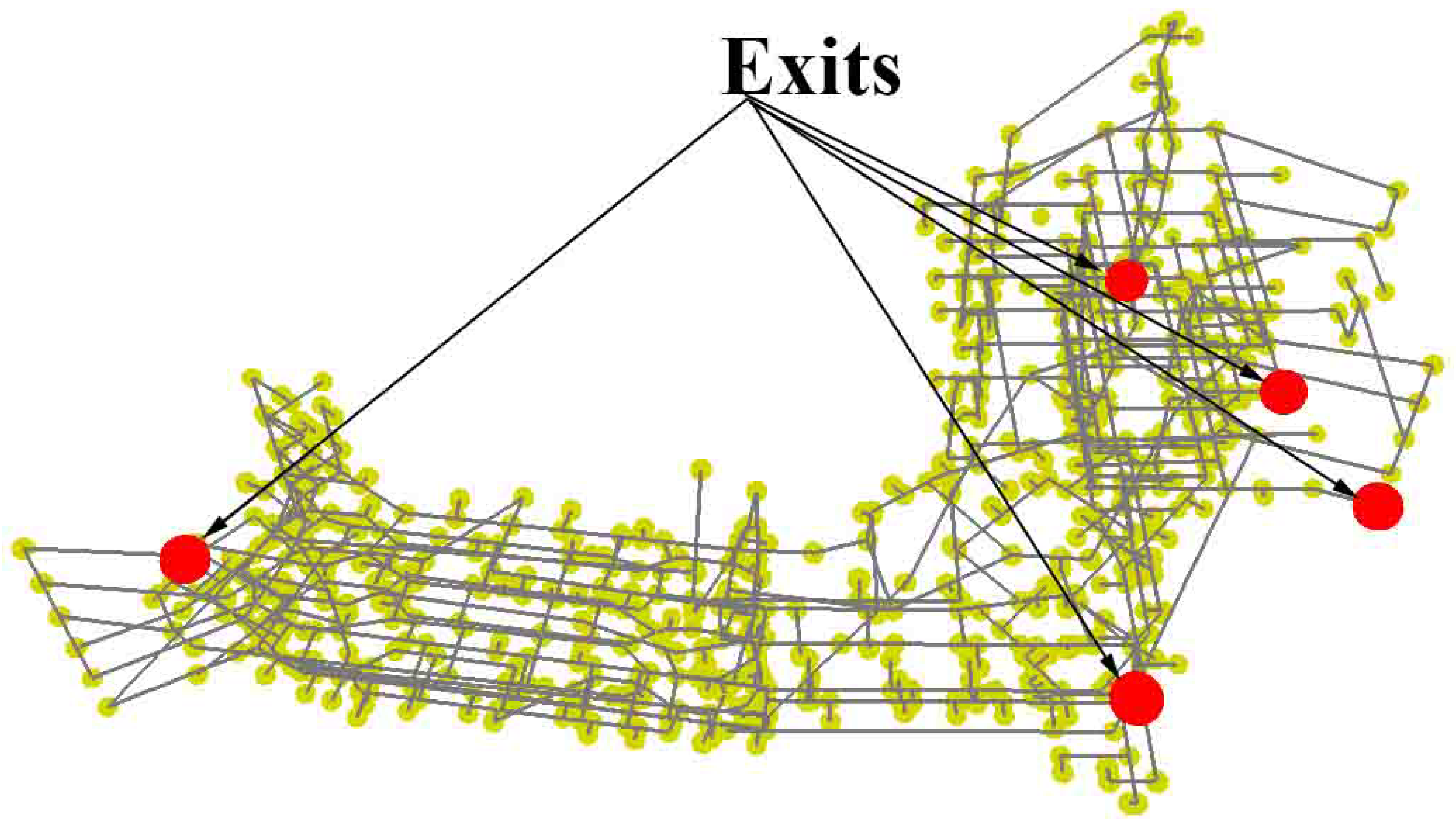
Figure 4). The first building is located on Longxiang Road, Xincheng District, Pingdingshan, China, and comprises three sub-buildings, named parts A, B, and C (part A in the north, part B in the middle, and part C in the south). All three parts are connected by corridors distributed along the west and east wings. The HUUC building has four floors and is currently the primary teaching and research facility occupied by the school of surveying and urban spatial information. Therefore, evaluating this building’s navigation network connectivity can reduce the risk of losing a life when facing fire events. The MLC building is on Zhaojiabang Road in Xuhui District, Shanghai, China; it has eight floors in the main structure and is famous for its giant glass ball, a landmark of Shanghai City.
First, we establish the two test buildings’ graphs by applying middle axis extraction and key node extraction to the doors, corners, and stairs. Next, we set the fire sources with the following settings: we place the fire source at one node at a time and traverse the entire navigation network after all simulations, and the initial phase for the fire emergency is phase 2. In this phase, the accessibility of the neighbor nodes within a specific range of the fire source is disabled. We set this scope with parameters defined in the SFPE handbook [
30] under normal fire spreading conditions: the fire-affected areas increase with a speed of 0.0015 m/s for 280 s and with a developing rate of 0.30 m/s for 140 s. The exit nodes for the MLC building are nodes 1111, 111,122, 111,164, 111,155, and 111,158. The exit nodes for the HUUC building are nodes 15, 16, 22, 25, 26, and 37.
As demonstrated in
Figure 5, the navigation graph of the HUUC building clearly shows its four-layer distribution and three-part spatial division. Additionally, we can observe that part A contains many small spatial subdivisions, part B has the most intensive spatial connections among the three parts, and part C has the largest span of distributed objects. We can explain this spatial phenomenon as follows: part A contains many midsized classrooms for fewer than 50 students to use. Part B has many school offices, staff conference rooms, bathrooms, and two lecture halls. From
Figure 6, we can see that the MLC building has two main groups of navigation nodes and another group to connect them. Additionally, due to the fire safety code, many egress routes lie around these groups of nodes to quickly evacuate customers and employees during emergencies.
3.6. Experimental Configuration
We aim to introduce four new characteristic indices for the studied navigation graph: the number of edges outside the 3D covering ball formed by using as the radius and the current node as the center, the number of edges inside this ball, the sum of the nodes outside this ball, and the sum of the nodes inside this ball. These four indices illustrate the edge weights compared with and the node quantity relative to the average length, and they show the experimental navigation graph’s spatial distribution features. In addition to the above indices, we provide additional IDs to identify multiple pathfinding results for the two experimental buildings. We use these IDs with the four levels of nodes searching percentage to design the main practical scheme, which we use to demonstrate the search time efficiency and egress path quality achieved by considering the 3D evacuation network’s spatial weights.
5. Conclusions and Future Works
In this paper, we have proposed a method to evaluate indoor navigation networks’ connectivity for emergency evacuations. We have defined a set of indices to describe navigation networks’ statuses during disasters from the graph view and the spatial metric perspective. In this method, we use both the 3D geometric distance measure and the fire spread model, and this allows us to estimate the fires’ influences on the neighboring clusters of accessible nodes in the 3D network. We can link the isolated groups of accessible nodes through the spatial sorting of nodes, facilitating the process of generating and selecting the minimum-risk evacuation paths and reducing the search time cost.
We suggest several directions for future research: First, currently, a simple fire model is used in this paper to estimate the influence of fires on indoor networks. The model breaks down the continuous fire spreading process into discrete steps and assumes that the fire spreads with a static speed in all directions. In the next step, we can drive a more complex fire simulation model (e.g., [
31]) by real-time data and better predict how fires spread to estimate the influence of fires on indoor environments. Second, heuristic routing methods such as A*, which can consider the proposed indices, will also be developed to generate feasible and safe routes in disastrous situations. Third, we will improve the definitions of the index by considering human behaviors. During emergencies, the network’s connectivity status is affected by hazards and influenced by evacuees’ movements, which could result in congestion at specific nodes and edges. Therefore, there is also a need to integrate the human factor in the network robustness analysis. Finally, we may apply our network robustness evaluation method to flooding and other emergency evacuation networks after a thorough investigation of the considered network features.