Upside-Down Robots: Modeling and Experimental Validation of Magnetic-Adhesion Mobile Systems
Abstract
:1. Introduction
- mathematical modeling of a class of magnetic-adhesion mobile robots that are capable of climbing walls thanks to a sandwich configuration. Furthermore, this design allows the master robot to autonomously detach itself from the follower, which is a novel contribution to the state of the art;
- numerical analysis through simulations, taking into account the interaction between the two carts, and between the robot and the support sheet (planar driving, behavior during detachment, and driving on a curved sheet);
- experimental validation of the prototype of an upside-down robot, both in the detachment phase as well as on the curved surface.
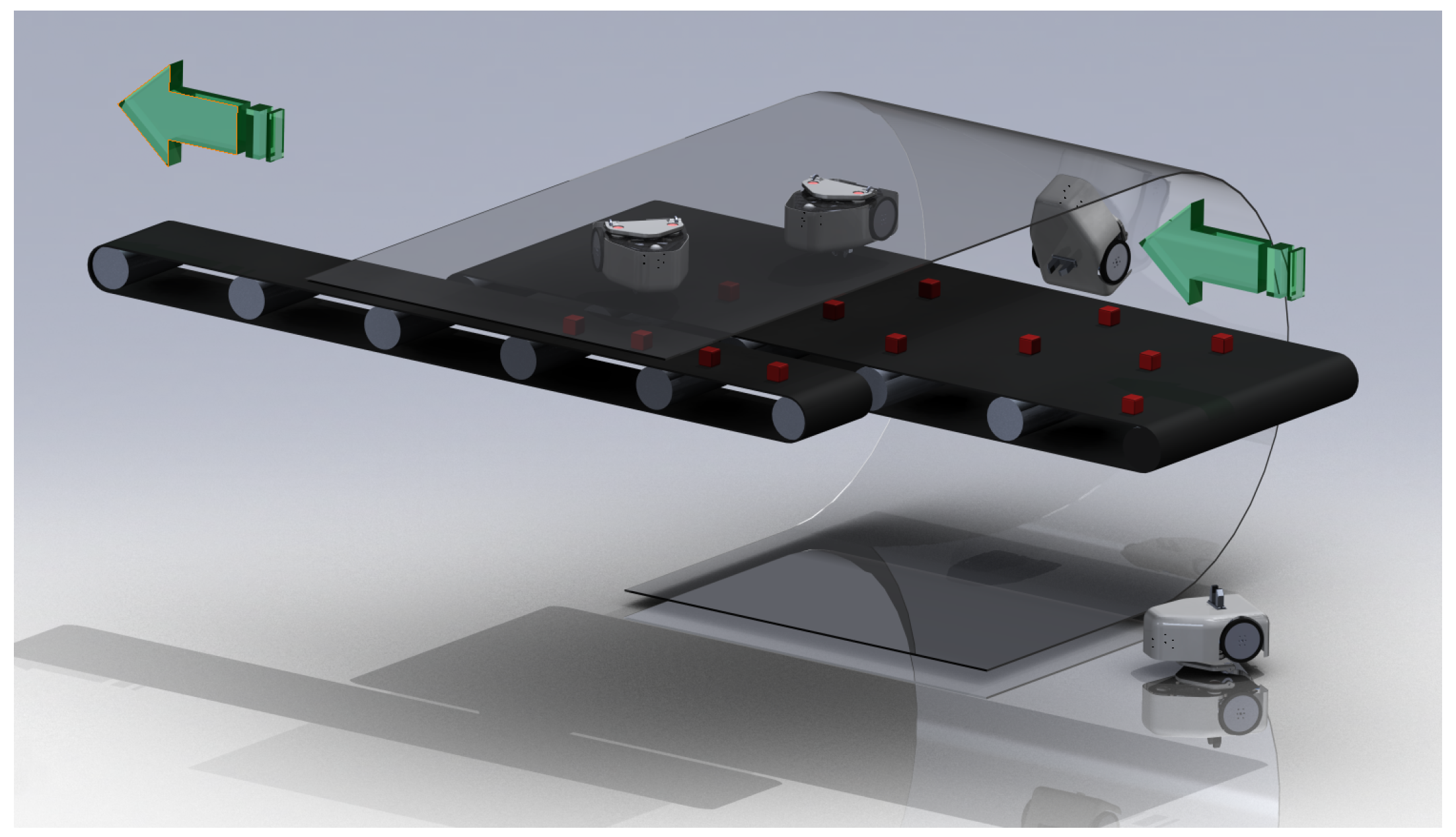
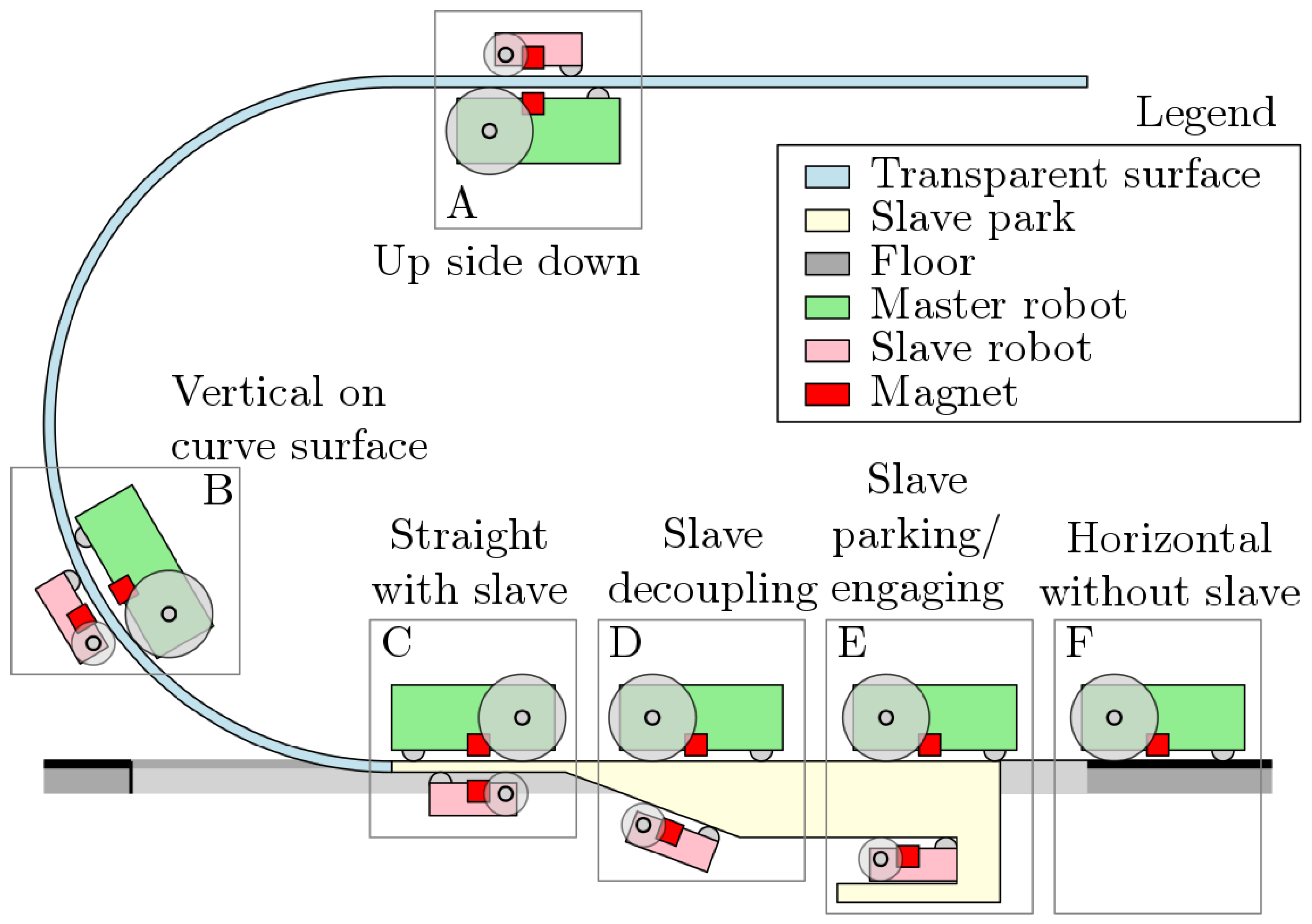
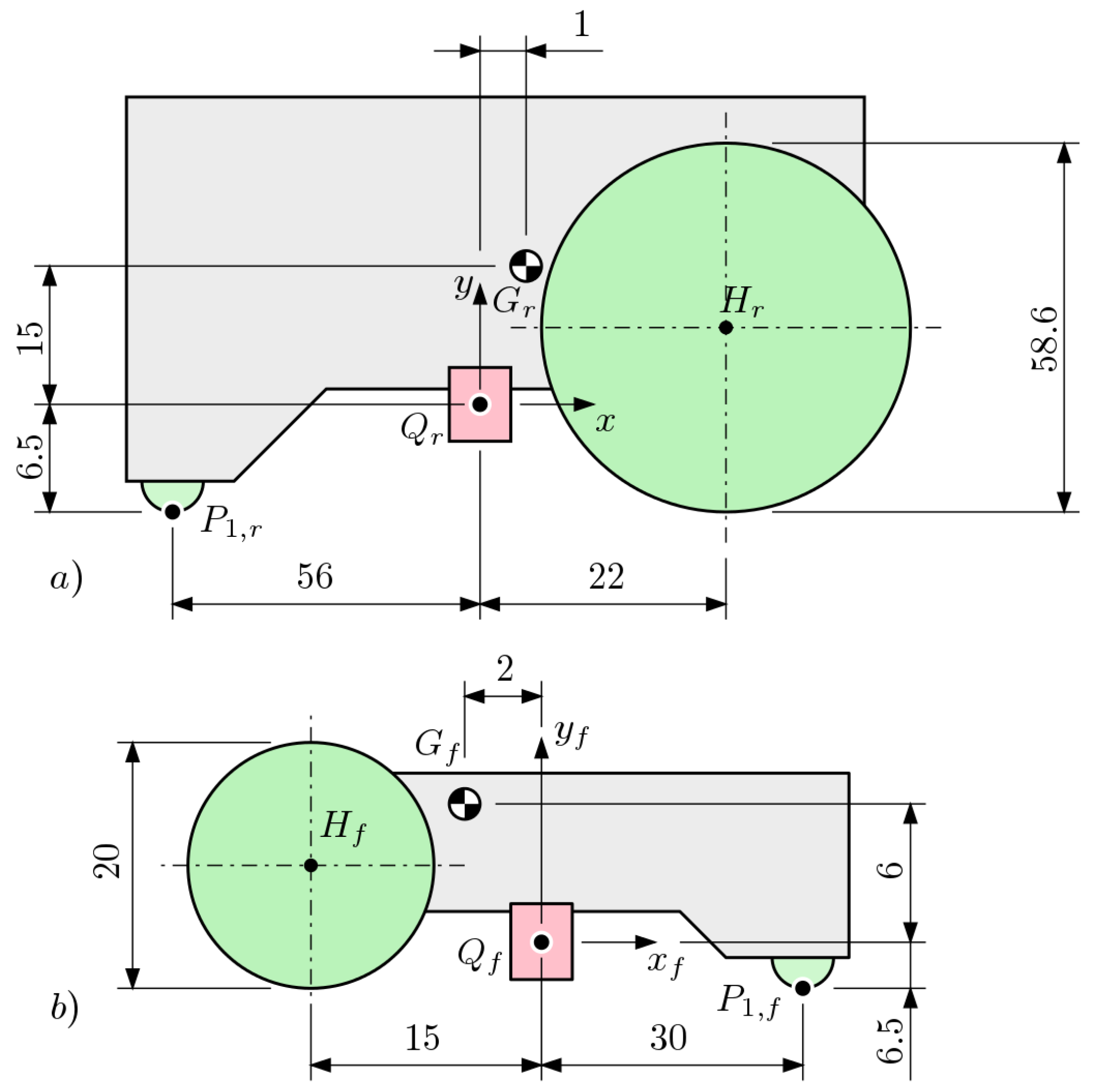
2. Robot Architecture
- upside-down driving phase (A);
- curved-surface driving phase (B);
- slave-decoupling phase (D); and
- slave parking/engaging (E).
- the master robot always has to be pressed against the master surface;
- the master robot has to be able to drive away from the influence of the magnetic field of the slave during parking; and
- the slave robot has to always be pressed against the slave surface except when parked.
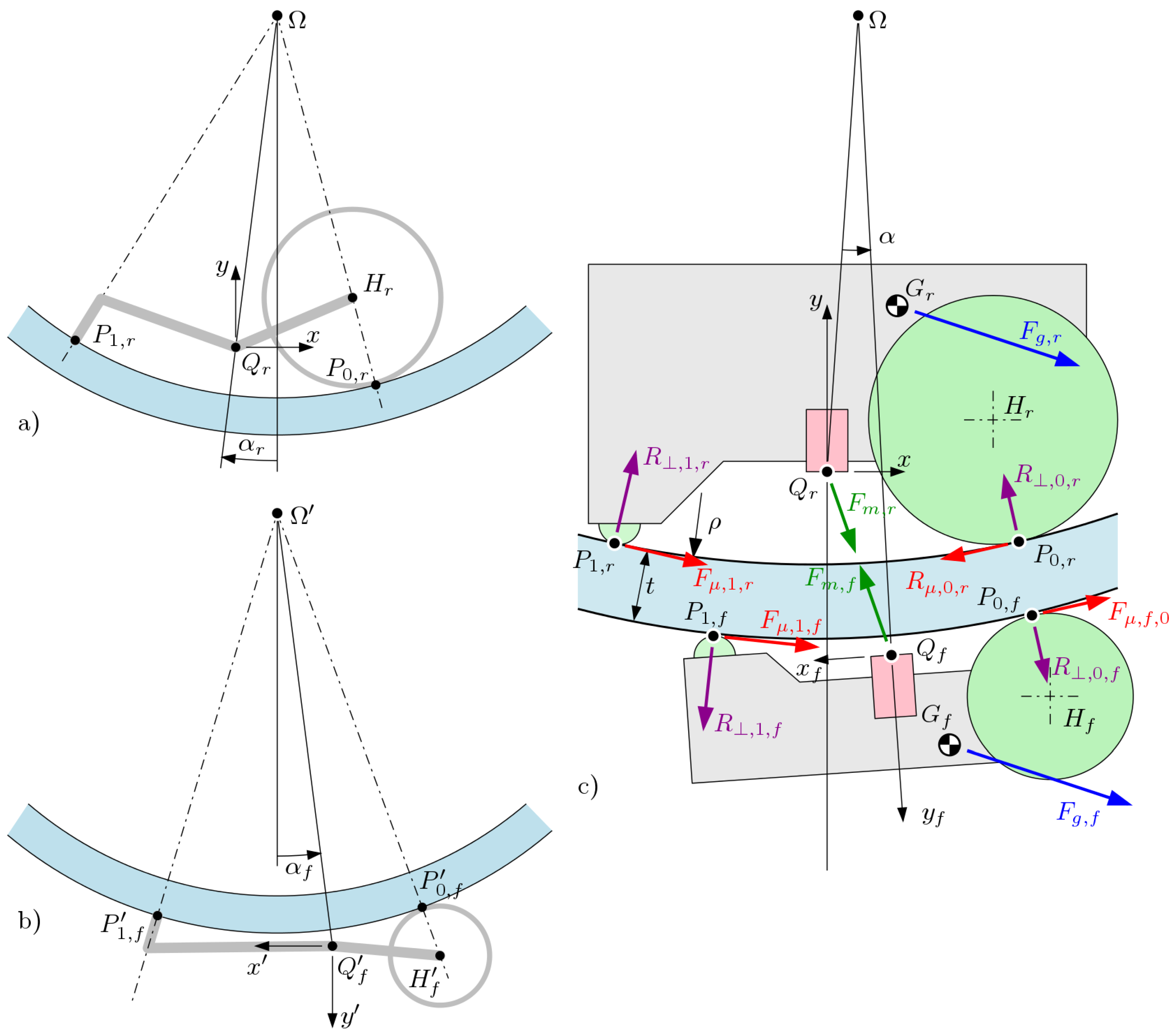
3. Mathematical Model
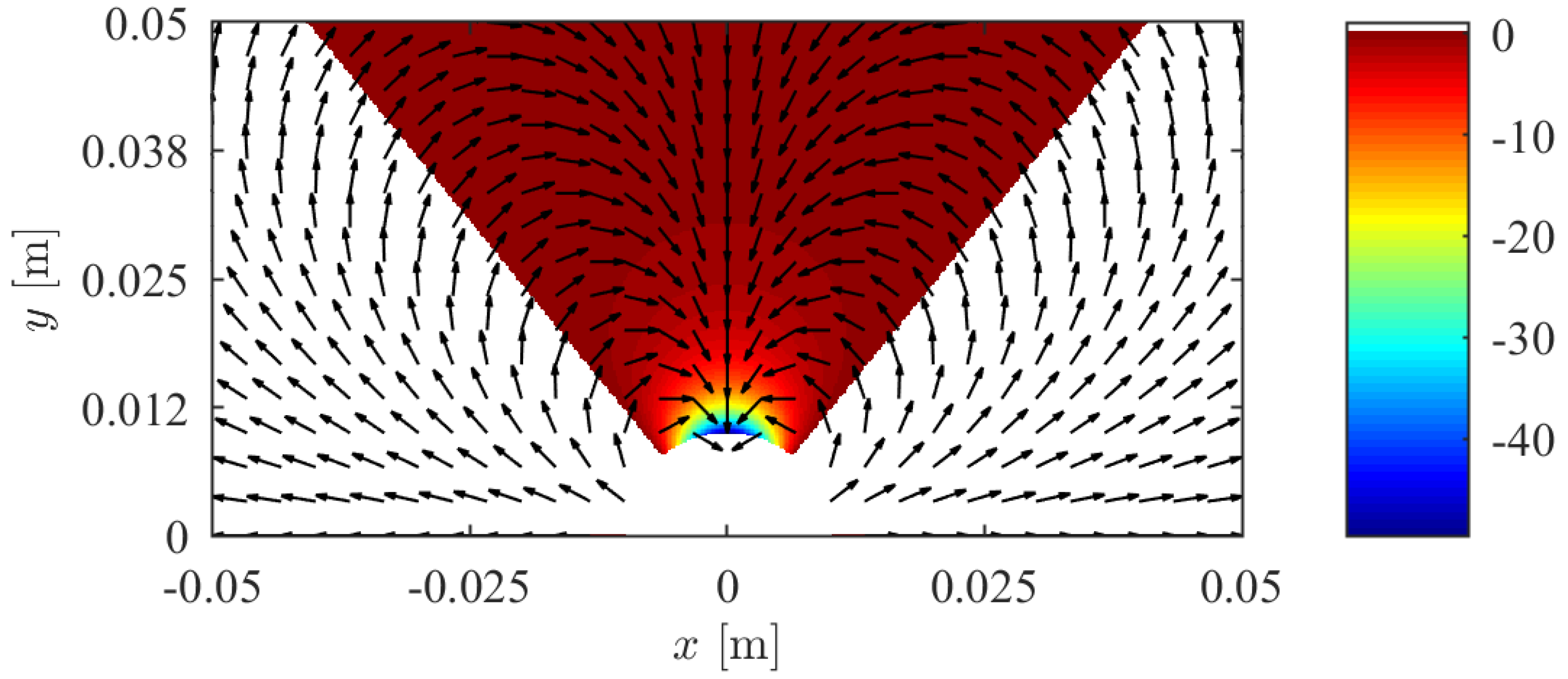
3.1. Magnetic Model
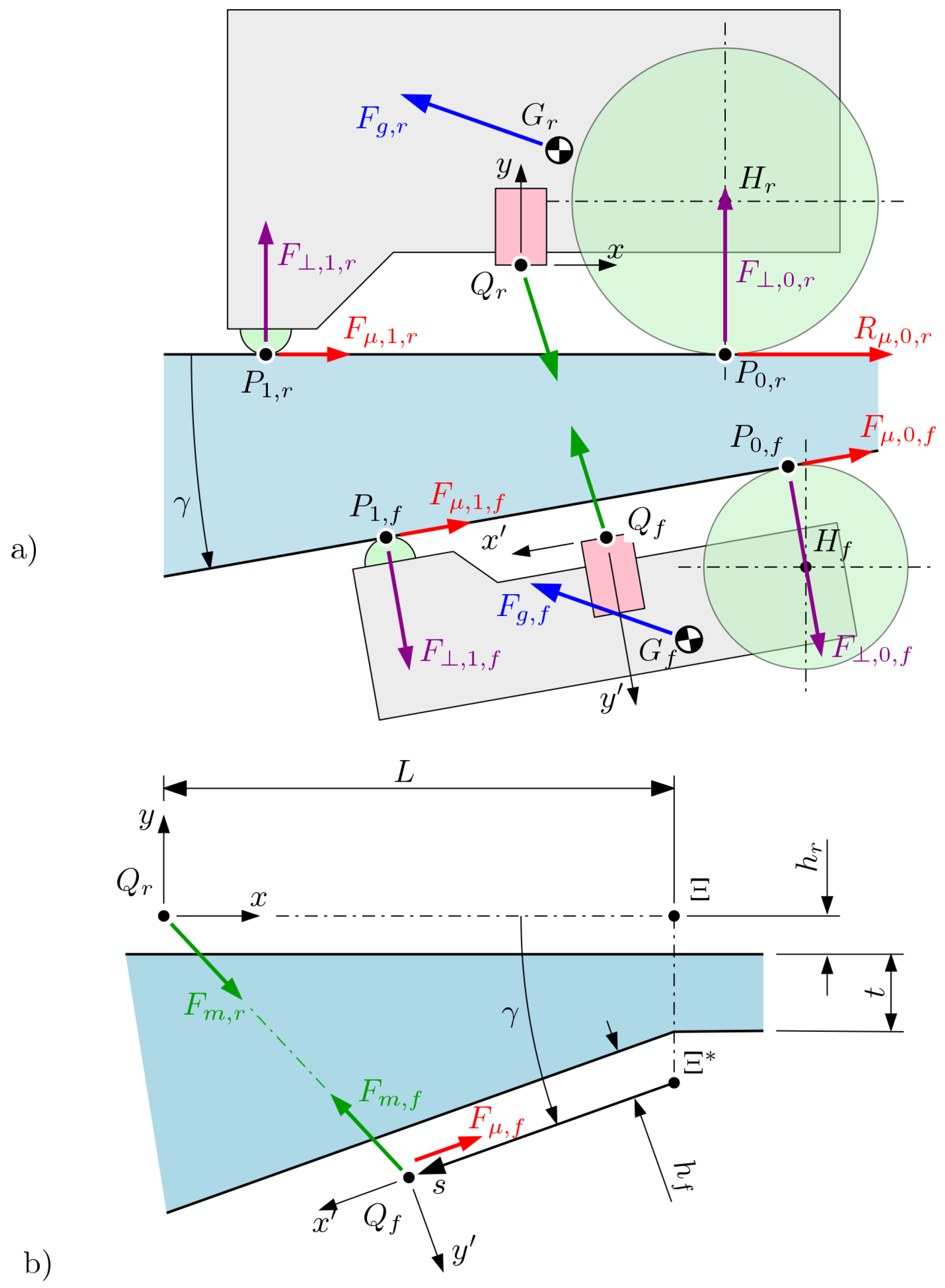
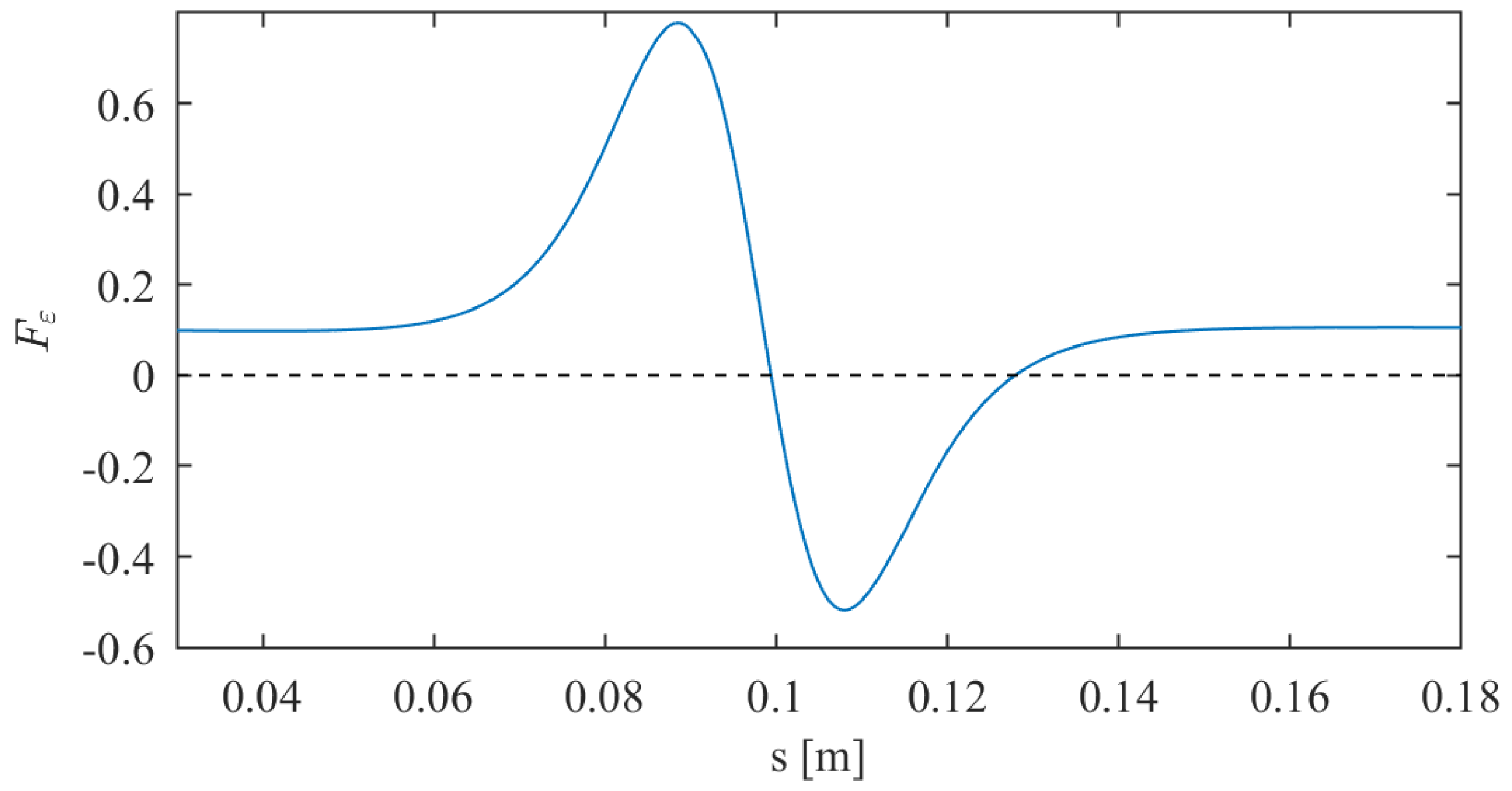
3.2. Planar-Surface Model
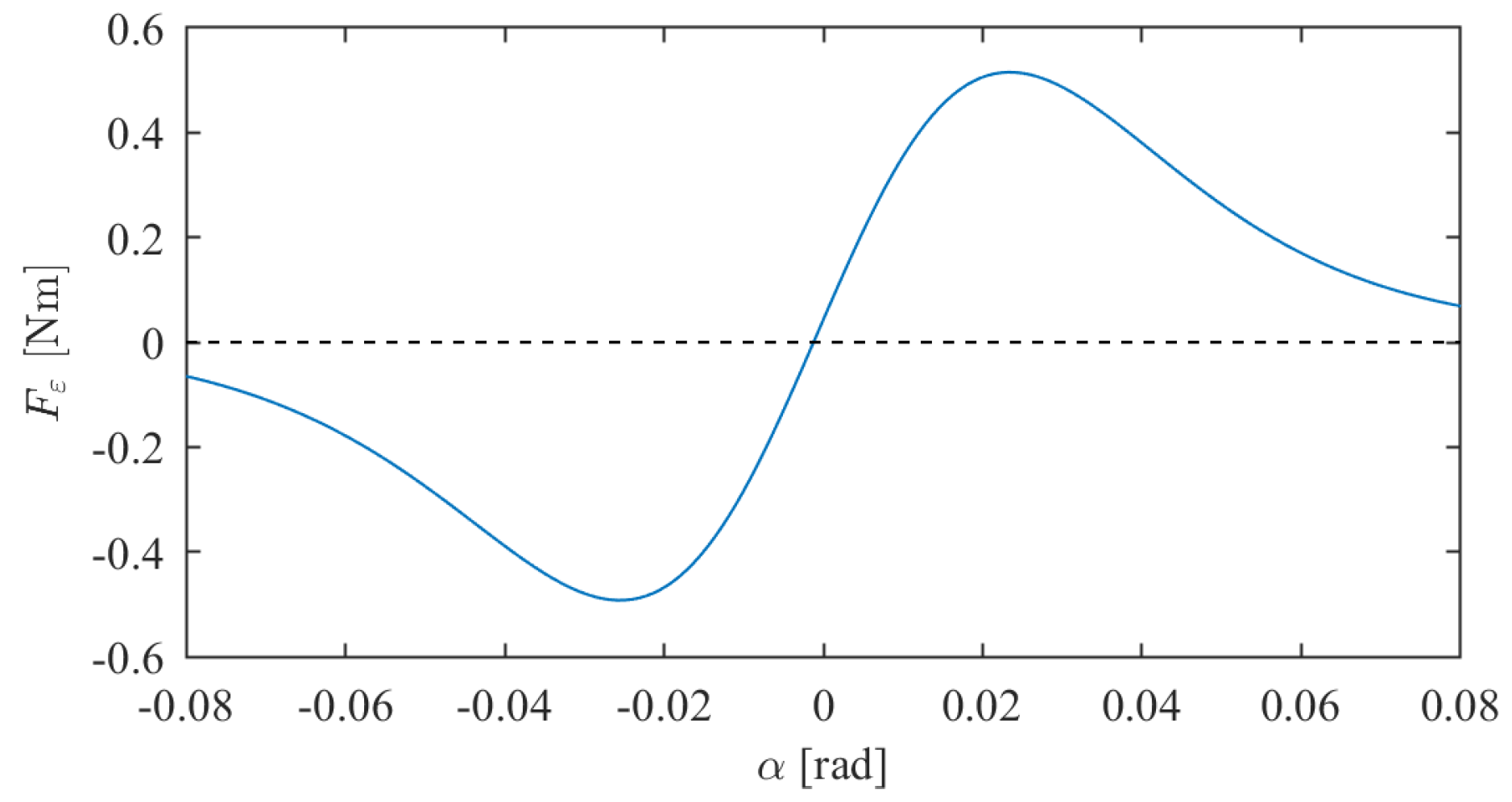
3.3. Cylindrical Surfaces
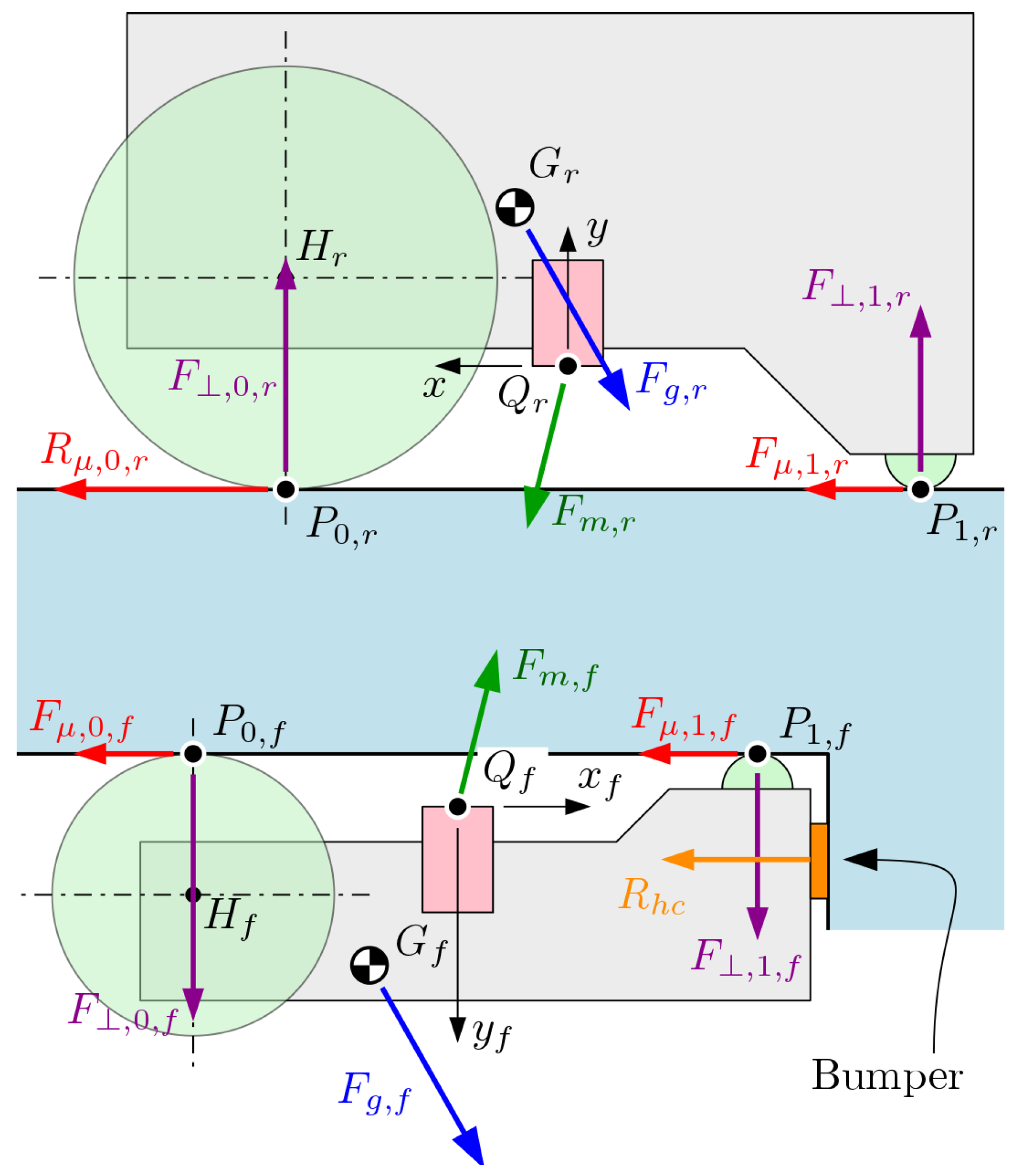
3.4. Slave Parking/Engaging
- Magnetic force acting on the master robot should be sufficiently small to allow it to drive away; indeed, maximum traction force of the master robot should be larger than , i.e., the reaction force produced by the external forces on the wheel contact point;
- magnetic force acting on the slave robot should be sufficiently high (before contact with the bumper) to allow it to both be pulled along by the master robot and remain attached to the ceiling of the support surface; this is to say, and .
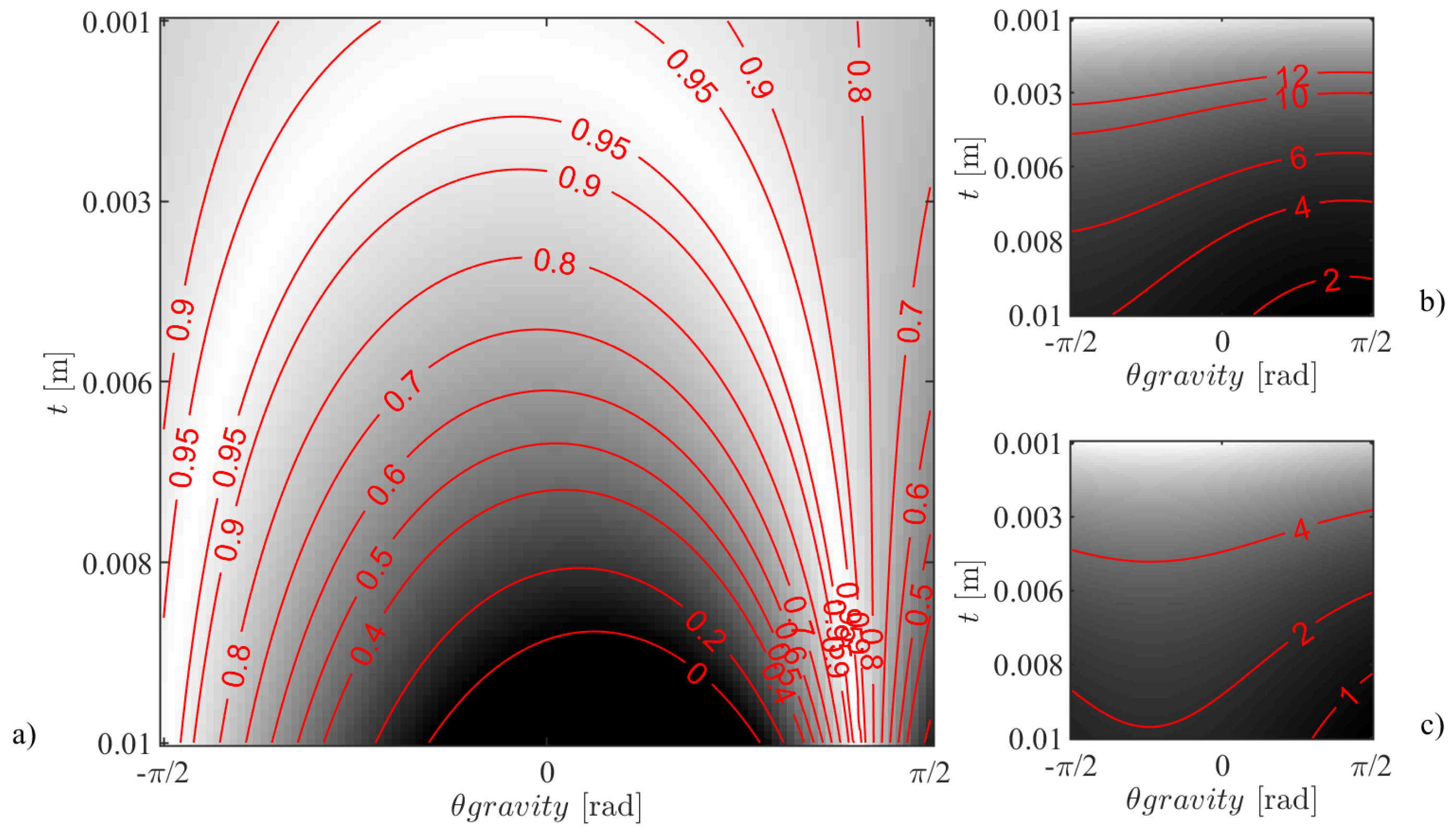
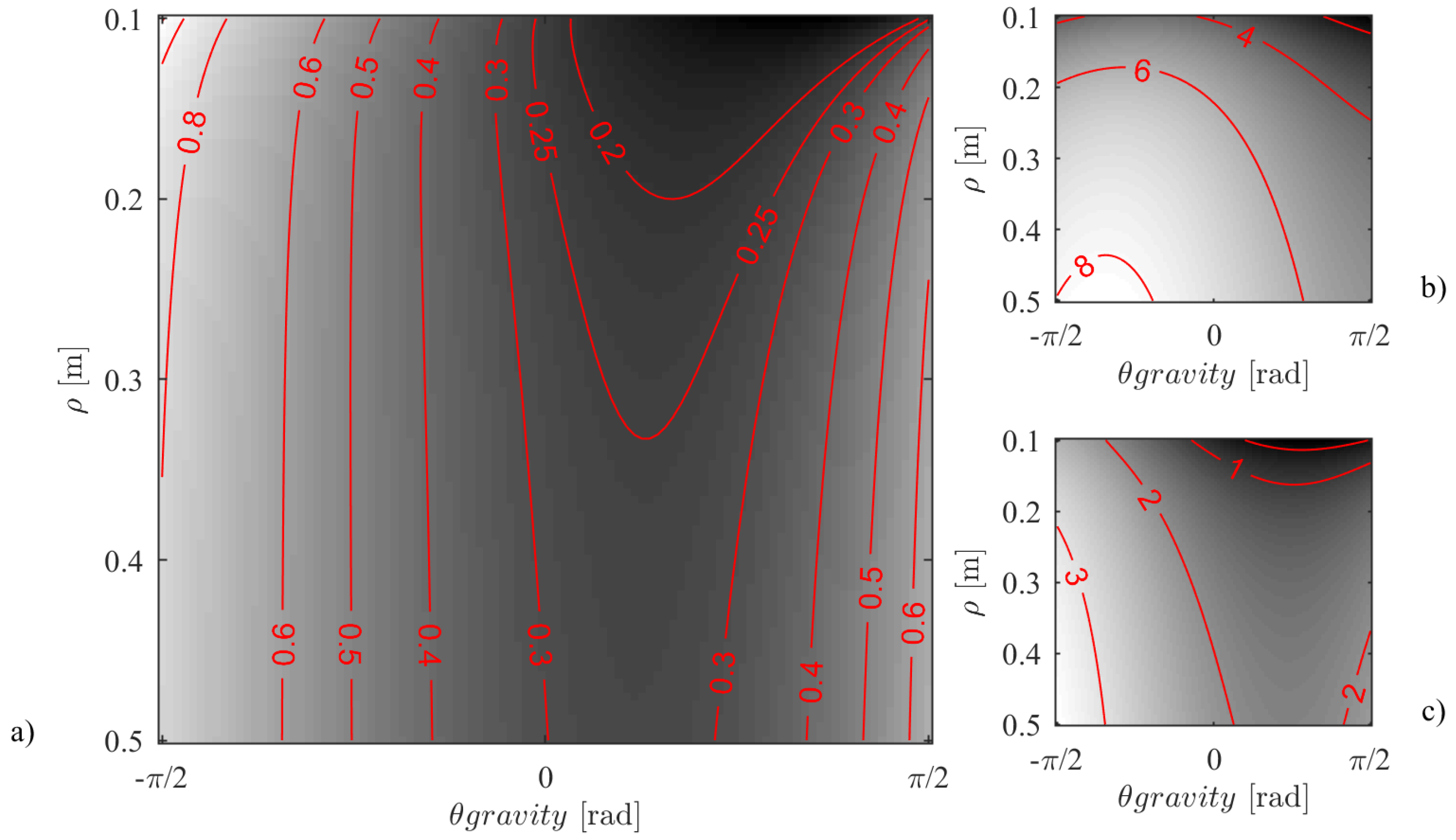
3.5. Traction Margin and Contact Forces
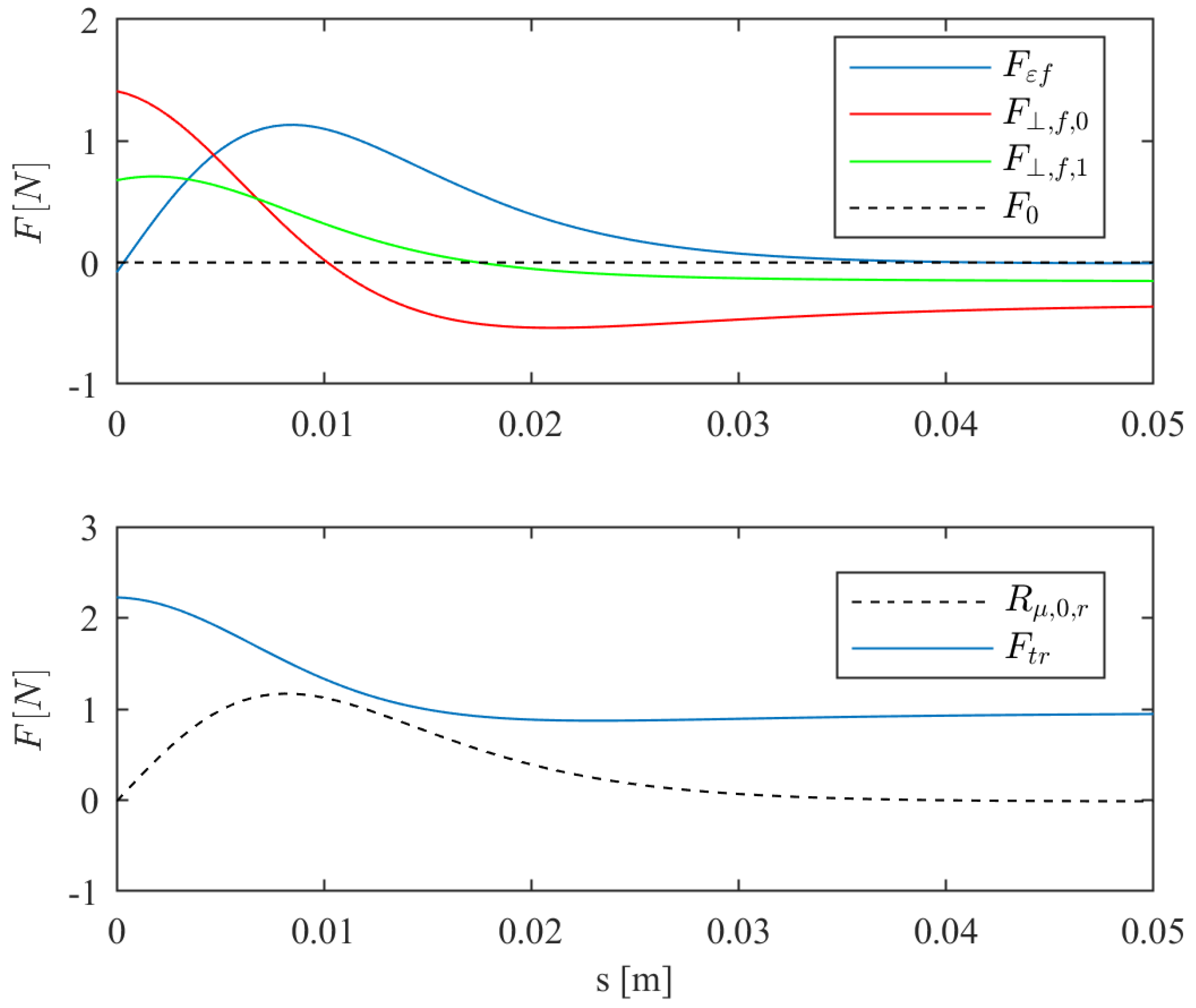
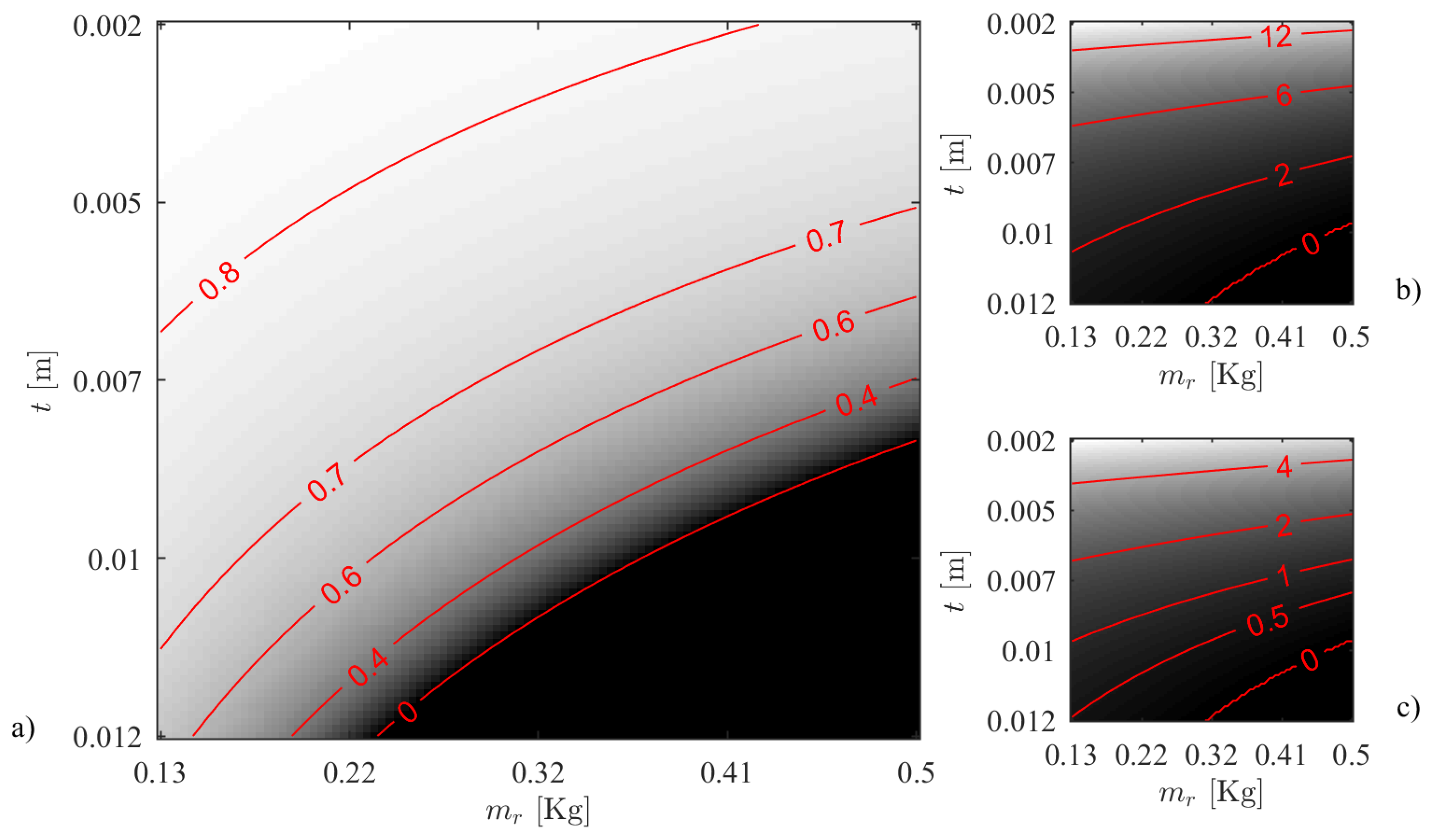
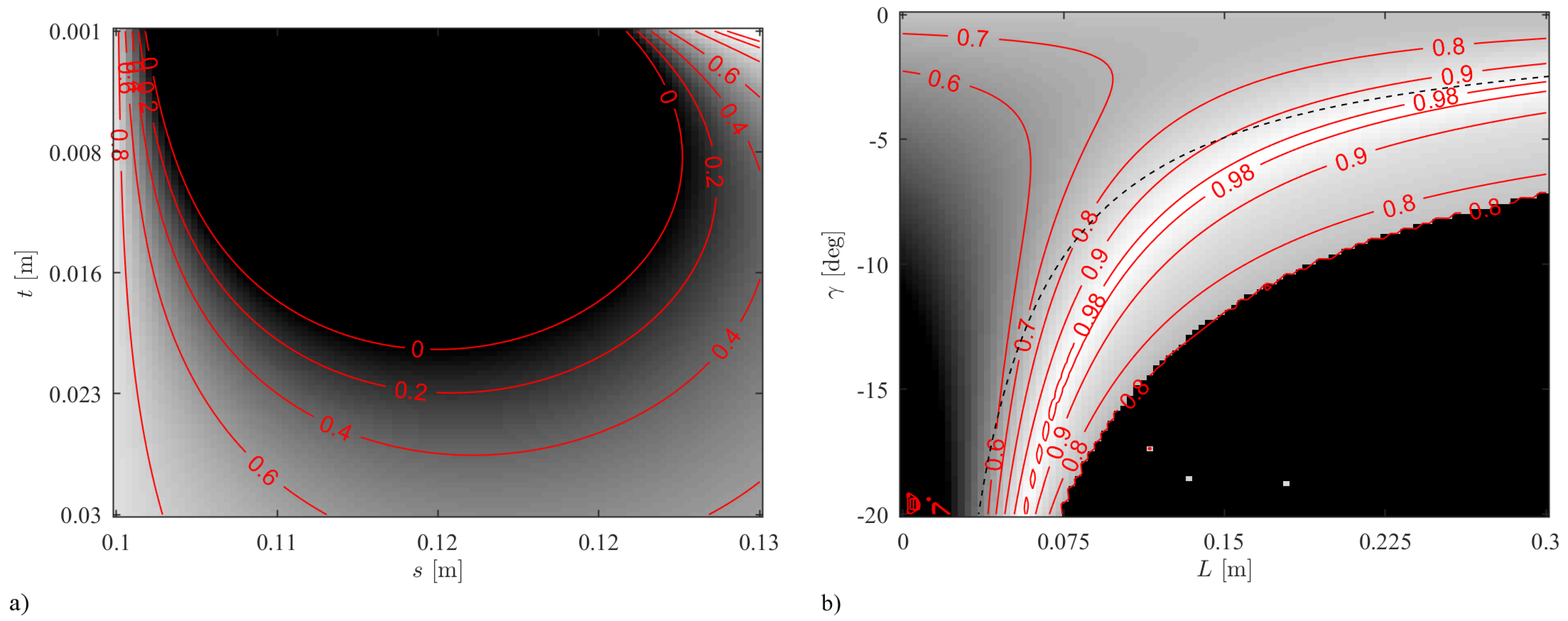
4. Numerical Implementation and Discussion
5. Prototype and Experiment Validation
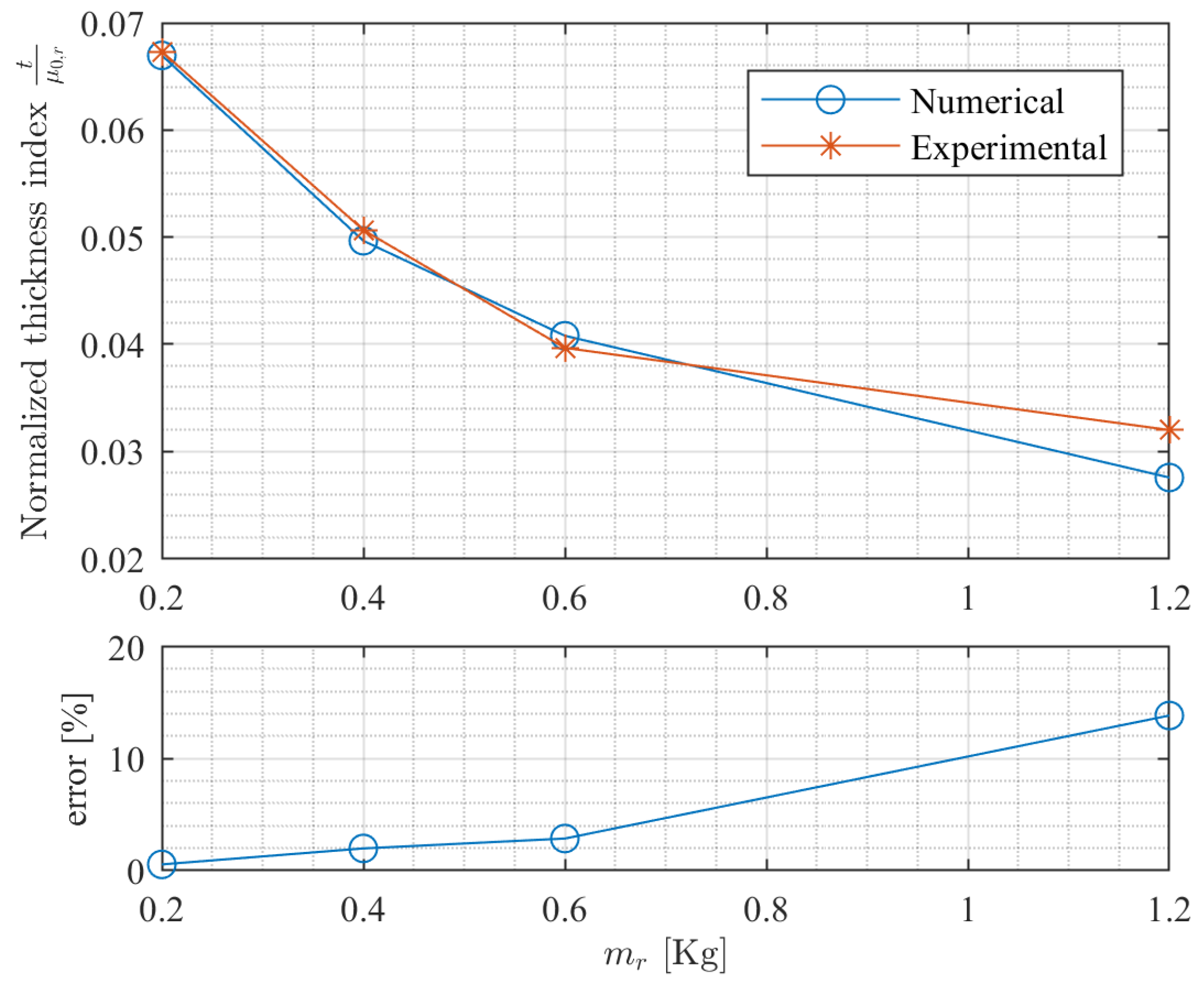
5.1. Experiment 1
- friction of the master with respect to the support sheet and
- magnetic interaction between master and slave.
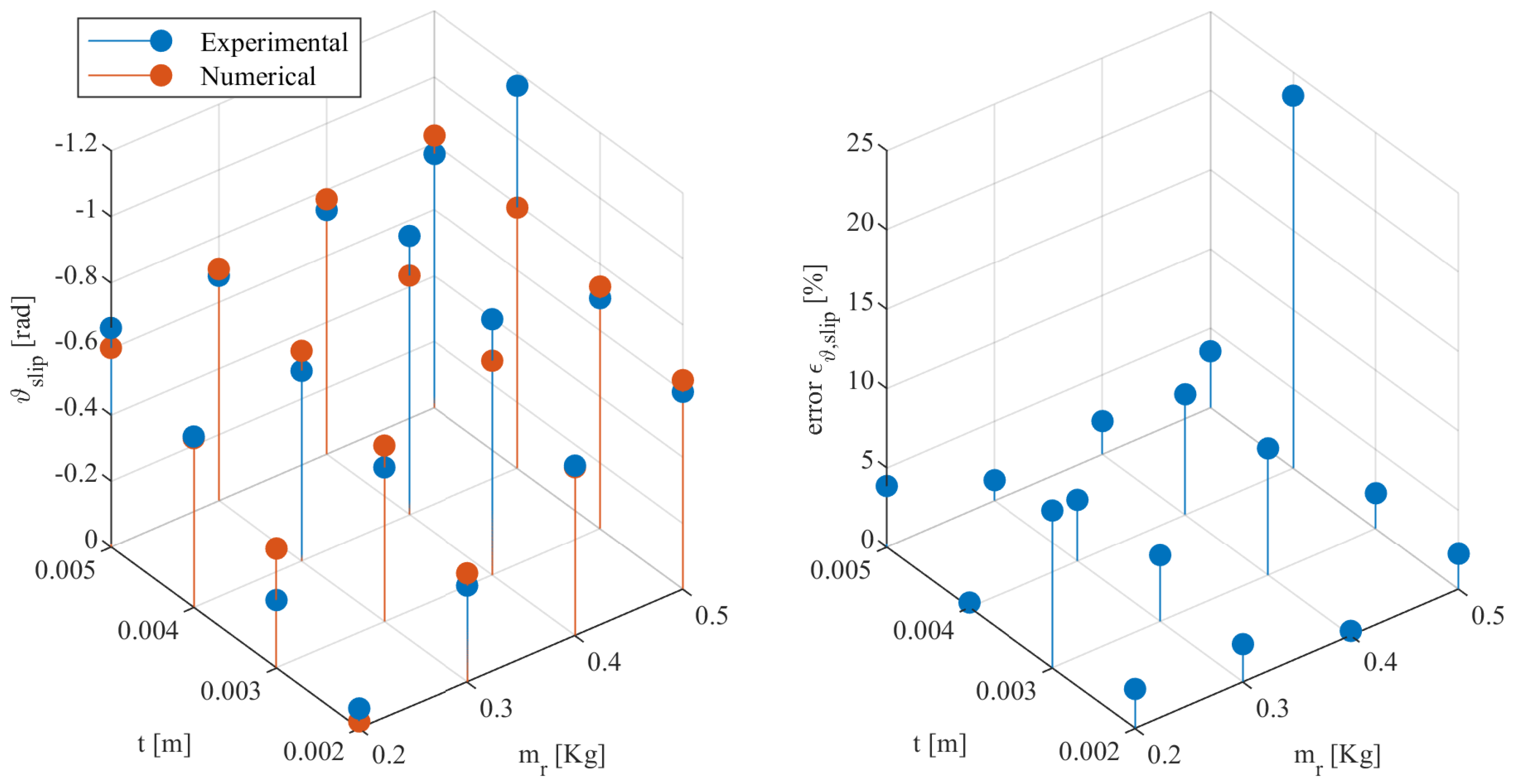
5.2. Experiment 2
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cesetti, A.; Scotti, C.; Di Buo, G.; Longhi, S. A service oriented architecture supporting an autonomous mobile robot for industrial applications. In Proceedings of the 18th IEEE Mediterranean Conference on Control and Automation (MED’10), Marrakech, Morocco, 23–25 June 2010; pp. 604–609. [Google Scholar]
- Bietresato, M.; Carabin, G.; D’Auria, D.; Gallo, R.; Ristorto, G.; Mazzetto, F.; Vidoni, R.; Gasparetto, A.; Scalera, L. A tracked mobile robotic lab for monitoring the plants volume and health. In Proceedings of the 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Auckland, New Zealand, 29–31 August 2016. [Google Scholar]
- Vidoni, R.; Gallo, R.; Ristorto, G.; Carabin, G.; Mazzetto, F.; Scalera, L.; Gasparetto, A. ByeLab: An agricultural mobile robot prototype for proximal sensing and precision farming. In Proceedings of the ASME 2017 International Mechanical Engineering Congress and Exposition. American Society of Mechanical Engineers, Tampa, FL, USA, 3–9 November 2017. [Google Scholar]
- Palacín, J.; Palleja, T.; Valgañón, I.; Pernia, R.; Roca, J. Measuring coverage performances of a floor cleaning mobile robot using a vision system. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 4236–4241. [Google Scholar]
- Quaglia, G.; Bruzzone, L.; Bozzini, G.; Oderio, R.; Razzoli, R.P. Epi. q-TG: Mobile robot for surveillance. Ind. Robot Int. J. 2011, 38, 282–291. [Google Scholar] [CrossRef]
- Ristorto, G.; Gallo, R.; Gasparetto, A.; Scalera, L.; Vidoni, R.; Mazzetto, F. A Mobile Laboratory for Orchard Health Status Monitoring in Precision Farming. Chem. Eng. Trans. 2019, 58, 661–666. [Google Scholar]
- Carbone, G.; Tedeschi, F.; Gallozzi, A.; Cigola, M. A robotic mobile platform for service tasks in cultural heritage. Int. J. Adv. Robot. Syst. 2015, 12, 88. [Google Scholar] [CrossRef]
- Seriani, S.; Gallina, P.; Wedler, A. A modular cable robot for inspection and light manipulation on celestial bodies. Acta Astronaut. 2016, 123, 145–153. [Google Scholar] [CrossRef]
- Seriani, S.; Gallina, P.; Wedler, A. Dynamics of a tethered rover on rough terrain. In Advances in Italian Mechanism Science; Springer: New York, NY, USA, 2017; pp. 355–361. [Google Scholar]
- Seriani, S.; Scalera, L.; Gasparetto, A.; Gallina, P. Preloaded structures for space exploration vehicles. In Mechanisms and Machine Science; Springer: New York, NY, USA, 2018; pp. 129–137. [Google Scholar]
- Silva, M.F.; Machado, J.T.; Tar, J.K. A survey of technologies for climbing robots adhesion to surfaces. In Proceedings of the 2008 IEEE International Conference on Computational Cybernetics, Stara Lesna, Slovakia, 27–29 November 2008; pp. 127–132. [Google Scholar]
- Longo, D.; Muscato, G. Design of a single sliding suction cup robot for inspection of non porous vertical wall. In Proceedings of the (ISR 2004) 35th International Symposium on Robotics, Paris-Nord Villepinte, France, 23–26 March 2004. [Google Scholar]
- Gao, X.; Kikuchi, K. Study on a kind of wall cleaning robot. In Proceedings of the 2004 IEEE International Conference on Robotics and Biomimetics, Shenyang, China, 22–26 August 2004; pp. 391–394. [Google Scholar]
- Yoshida, Y.; Ma, S. Design of a wall-climbing robot with passive suction cups. In Proceedings of the 2010 IEEE International Conference on Robotics and Biomimetics, Tianjin, China, 14–18 December 2010; pp. 1513–1518. [Google Scholar]
- Sintov, A.; Avramovich, T.; Shapiro, A. Design and motion planning of an autonomous climbing robot with claws. Robot. Autom. Syst. 2011, 59, 1008–1019. [Google Scholar] [CrossRef]
- Balaguer, C.; Gimenez, A.; Jardón, A. Climbing robots’ mobility for inspection and maintenance of 3D complex environments. Autonom. Robot. 2005, 18, 157–169. [Google Scholar] [CrossRef]
- Seidl, T.; Vidoni, R. Adhesion to flat surfaces: From spiders to stickers. In Spider Ecophysiology; Springer: New York, NY, USA, 2013; pp. 463–473. [Google Scholar]
- Gasparetto, A.; Seidl, T.; Vidoni, R. A mechanical model for the adhesion of spiders to nominally flat surfaces. J. Bionic Eng. 2009, 6, 135–142. [Google Scholar] [CrossRef]
- Boscariol, P.; Henrey, M.A.; Li, Y.; Menon, C. Optimal gait for bioinspired climbing robots using dry adhesion: A quasi-static investigation. J. Bionic Eng. 2013, 10, 1–11. [Google Scholar] [CrossRef]
- Henrey, M.; Ahmed, A.; Boscariol, P.; Shannon, L.; Menon, C. Abigaille-III: A versatile, bioinspired hexapod for scaling smooth vertical surfaces. J. Bionic Eng. 2014, 11, 1–17. [Google Scholar] [CrossRef]
- Cai, J.; He, K.; Fang, H.; Chen, H.; Hu, S.; Zhou, W. The design of permanent-magnetic wheeled wall-climbing robot. In Proceedings of the 2017 IEEE International Conference on Information and Automation (ICIA), Macau, China, 18–20 July 2017; pp. 604–608. [Google Scholar]
- Howlader, M.O.F.; Sattar, T.P. Development of magnetic adhesion based climbing robot for non-destructive testing. In Proceedings of the 2015 7th Computer Science and Electronic Engineering Conference (CEEC), Colchester, UK, 24–25 September 2015; pp. 105–110. [Google Scholar]
- Howlader, M.O.F.; Sattar, T.P. Design and Optimization of Permanent Magnet Based Adhesion Module for Robots Climbing on Reinforced Concrete Surfaces. In Intelligent Systems and Applications; Springer: New York, NY, USA, 2016; pp. 153–171. [Google Scholar]
- Zhang, Y.; Dodd, T.; Atallah, K.; Lyne, I. Design and optimization of magnetic wheel for wall and ceiling climbing robot. In Proceedings of the IEEE International Conference on Mechatronics and Automation, Xi’an, China, 4–7 August 2010; pp. 1393–1398. [Google Scholar]
- Ishihara, H. Basic study on wall climbing root with magnetic passive wheels. In Proceedings of the IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 6–9 August 2017; pp. 1964–1969. [Google Scholar]
- Hu, S.; Peng, R.; He, K.; Li, J.; Cai, J.; Zhou, W. Structural design and magnetic force analysis of a new crawler-type permanent magnetic adsorption wall—Climbing. In Proceedings of the 2017 IEEE International Conference on Information and Automation (ICIA), Macau, China, 18–20 July 2017; pp. 598–603. [Google Scholar]
- Huang, H.; Li, D.; Xue, Z.; Chen, X.; Liu, S.; Leng, J.; Wei, Y. Design and performance analysis of a tracked wall-climbing robot for ship inspection in shipbuilding. Ocean Eng. 2017, 131, 224–230. [Google Scholar] [CrossRef]
- Milella, A.; Maglietta, R.; Caccia, M.; Bruzzone, G. Robotic inspection of ship hull surfaces using a magnetic crawler and a monocular camera. Sens. Rev. 2017, 37, 425–435. [Google Scholar] [CrossRef]
- Mao, J.; He, K.; Li, J.; Sun, X. Simulation and experimental verification of permanent magnet adsorption unit for wall-climbing robot. In Proceedings of the 2016 IEEE International Conference on Information and Automation (ICIA), Ningbo, China, 1–3 August 2016; pp. 1189–1194. [Google Scholar]
- Tummala, R.L.; Mukherjee, R.; Xi, N.; Aslam, D.; Dulimarta, H.; Xiao, J.; Minor, M.; Dangi, G. Climbing the walls. IEEE Robot. Autom Mag. 2002, 9, 10–19. [Google Scholar] [CrossRef]
- Seriani, S.; Scalera, L.; Gasparetto, A.; Gallina, P. A new family of magnetic adhesion based wall-climbing robots. In Proceedings of the 2nd International Conference of IFToMM ITALY, Cassino, Italy, 29–30 November 2018; pp. 223–230. [Google Scholar]
- Belforte, G.; Gay, P.; Aimonino, D.R. Robotics for improving quality, safety and productivity in intensive agriculture: Challenges and opportunities. In Industrial Robotics: Programming, Simulation and Applications; IntechOpen: London, UK, 2006. [Google Scholar]
- Fiorini, P.; Botturi, D. Introducing service robotics to the pharmaceutical industry. Intell. Serv. Robot. 2008, 1, 267–280. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics, 3rd ed.; Benjamin Cummings: San Francisco, CA, USA, 1998. [Google Scholar]
- Landecker, P.B.; Villani, D.D.; Yung, K.W. Analytic solution for the torque between two magnetic dipoles. Magn. Electr. Sep. 1999, 10, 29–33. [Google Scholar] [CrossRef]

| Quantity | Symbol | Value | Unit |
|---|---|---|---|
| Magnetic permeability | 1.257 × 10 | N/A | |
| Magnetic moment (master) | Am | ||
| Magnetic moment (slave) | Am | ||
| Mass (master) | kg | ||
| Mass (slave) | kg | ||
| Frict. coeff. of wheel (master) | – | ||
| Frict. coeff. of skid (master) | – | ||
| Rolling resistance coeff. (slave) | – | ||
| Skid coefficient of friction (slave) | – |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seriani, S.; Scalera, L.; Caruso, M.; Gasparetto, A.; Gallina, P. Upside-Down Robots: Modeling and Experimental Validation of Magnetic-Adhesion Mobile Systems. Robotics 2019, 8, 41. https://doi.org/10.3390/robotics8020041
Seriani S, Scalera L, Caruso M, Gasparetto A, Gallina P. Upside-Down Robots: Modeling and Experimental Validation of Magnetic-Adhesion Mobile Systems. Robotics. 2019; 8(2):41. https://doi.org/10.3390/robotics8020041
Chicago/Turabian StyleSeriani, Stefano, Lorenzo Scalera, Matteo Caruso, Alessandro Gasparetto, and Paolo Gallina. 2019. "Upside-Down Robots: Modeling and Experimental Validation of Magnetic-Adhesion Mobile Systems" Robotics 8, no. 2: 41. https://doi.org/10.3390/robotics8020041
APA StyleSeriani, S., Scalera, L., Caruso, M., Gasparetto, A., & Gallina, P. (2019). Upside-Down Robots: Modeling and Experimental Validation of Magnetic-Adhesion Mobile Systems. Robotics, 8(2), 41. https://doi.org/10.3390/robotics8020041








