Kinematics of the 3(RPSP)-S Fully Spherical Parallel Manipulator by Means of Screw Theory
Abstract
1. Introduction
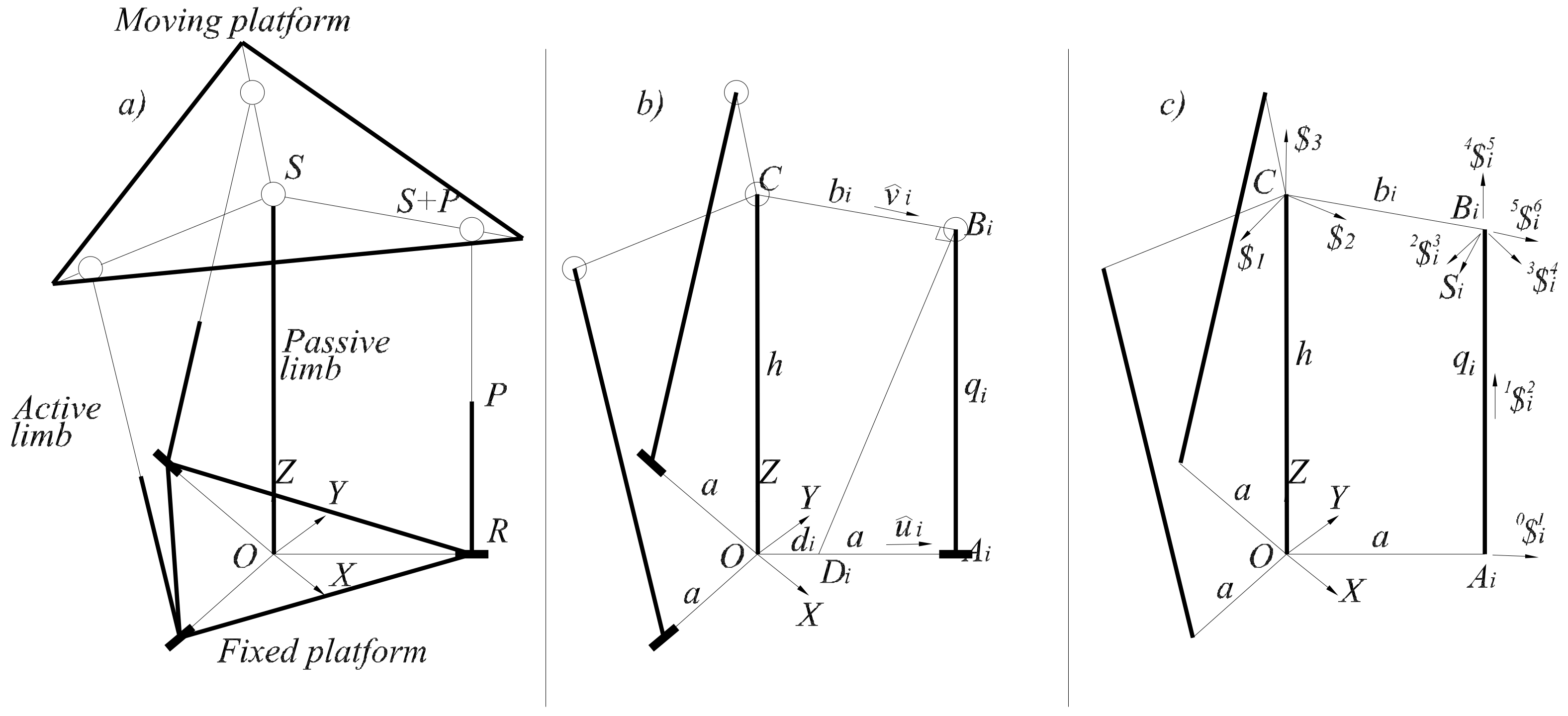
2. Architecture of the Spherical Parallel Manipulator
3. Displacement Analysis
4. Input-Output Equation of Velocity
- is the forward Jacobian matrix,
- is the inverse Jacobian matrix,
- where is the first order driver matrix and
- is an operator of polarity generated with the zero matrix 0 and the identity matrix .
5. Input-Output Equation of Acceleration
- where is the second-order driver matrix and
- is the complementary matrix of acceleration.
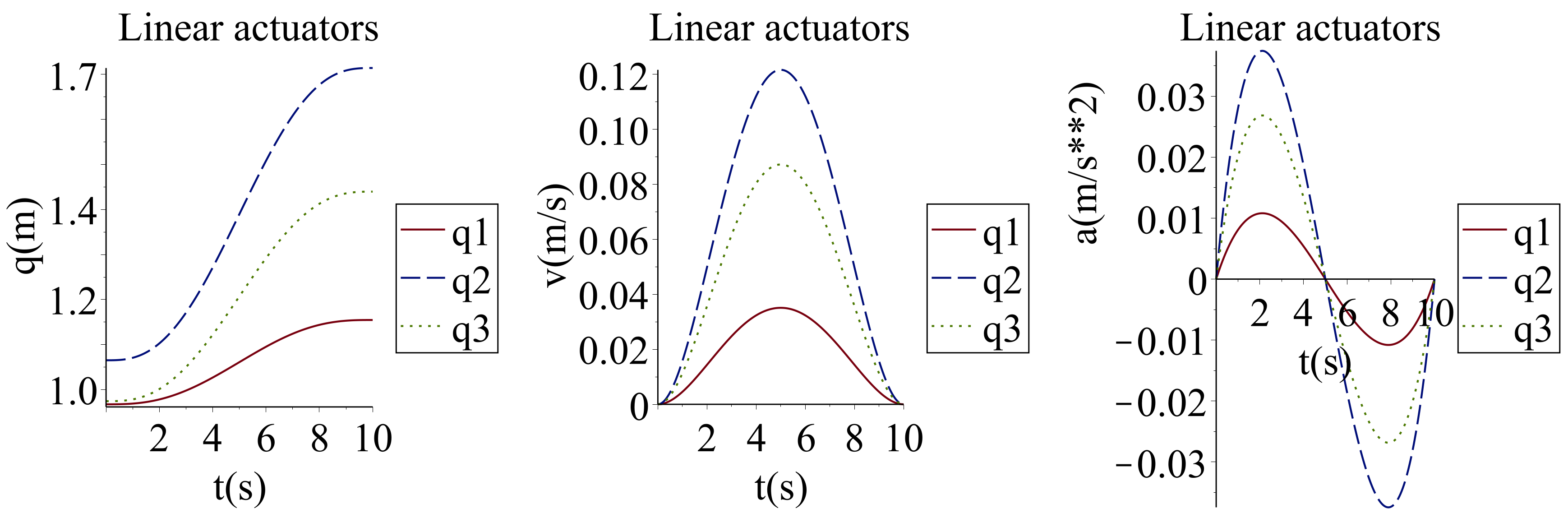
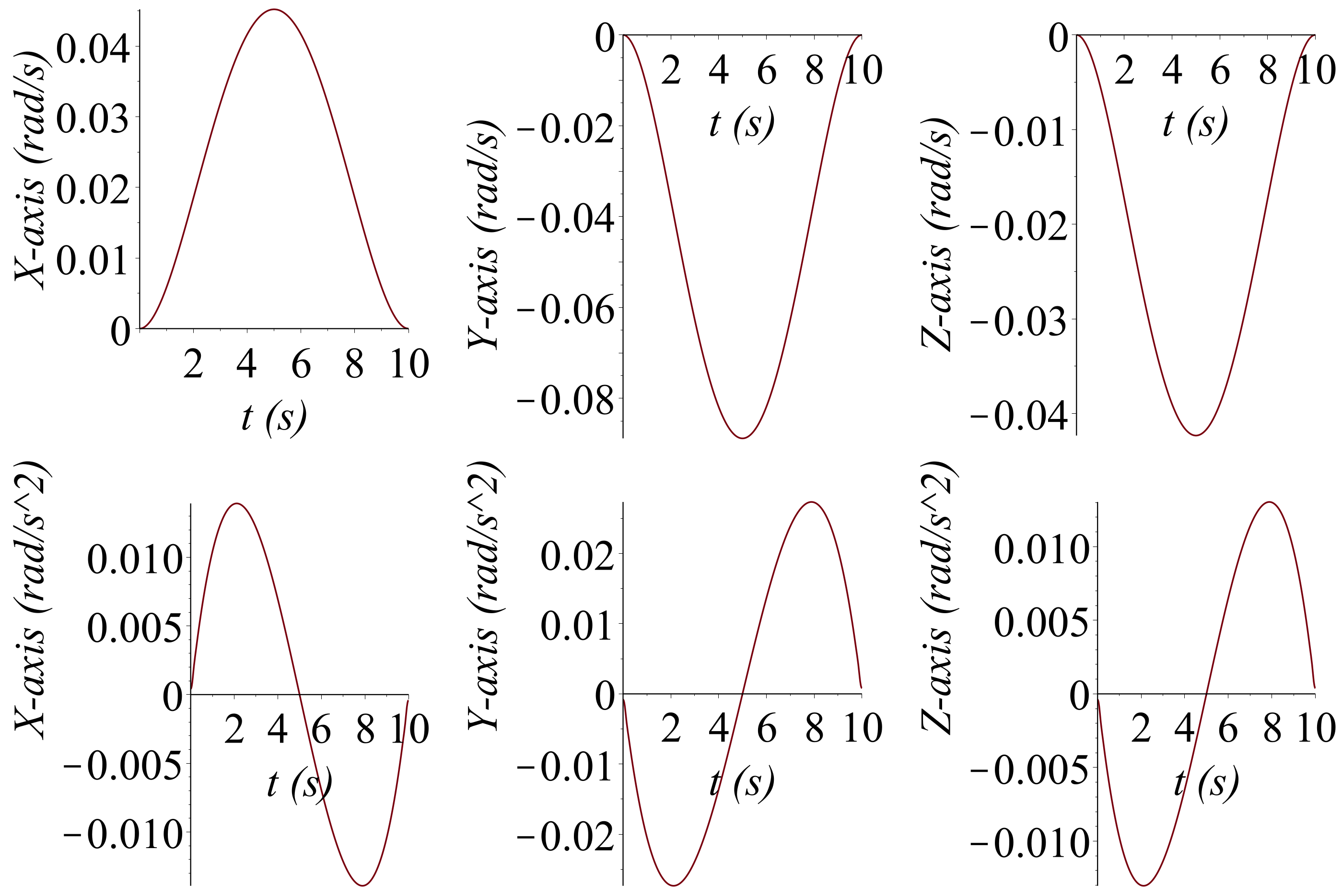
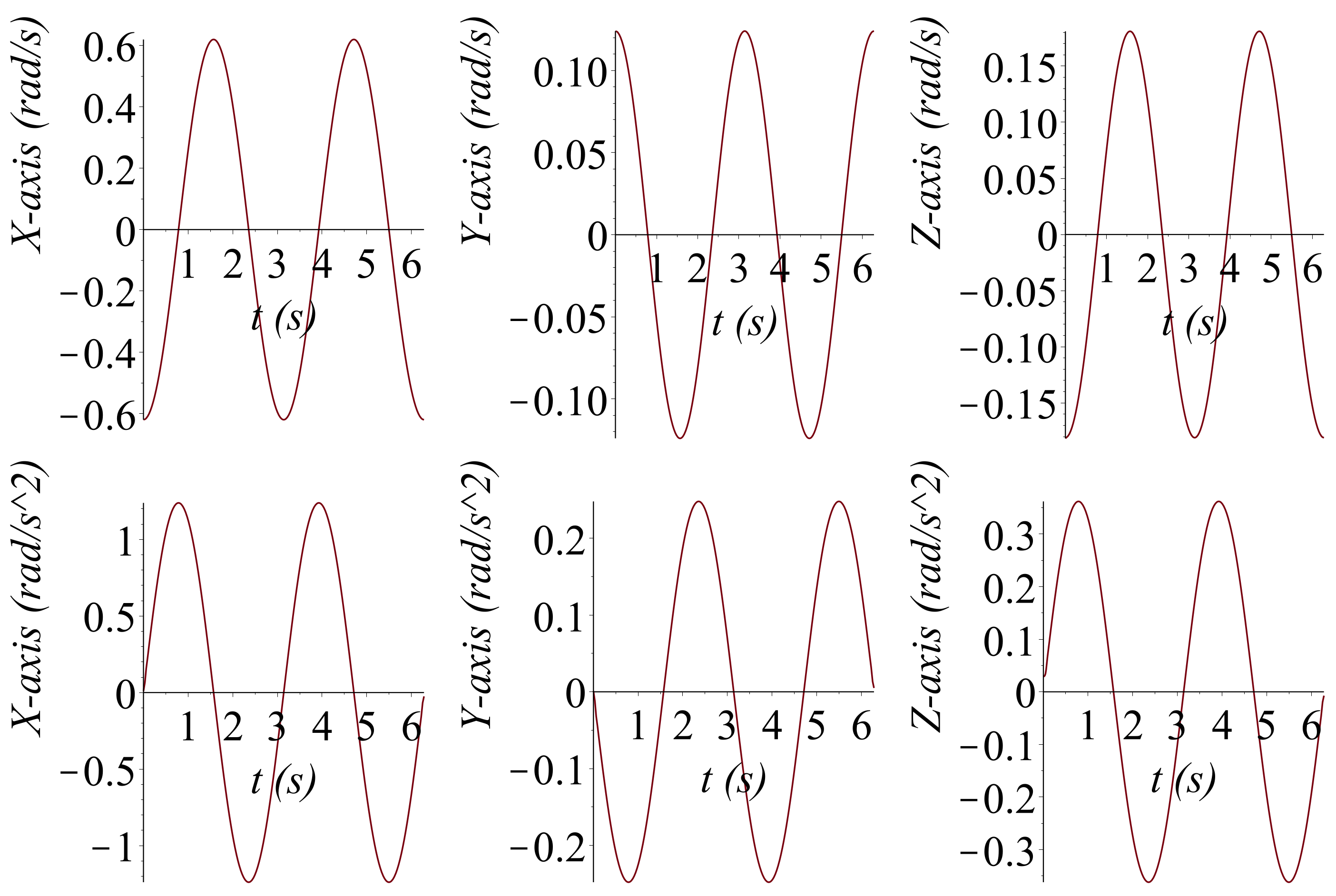
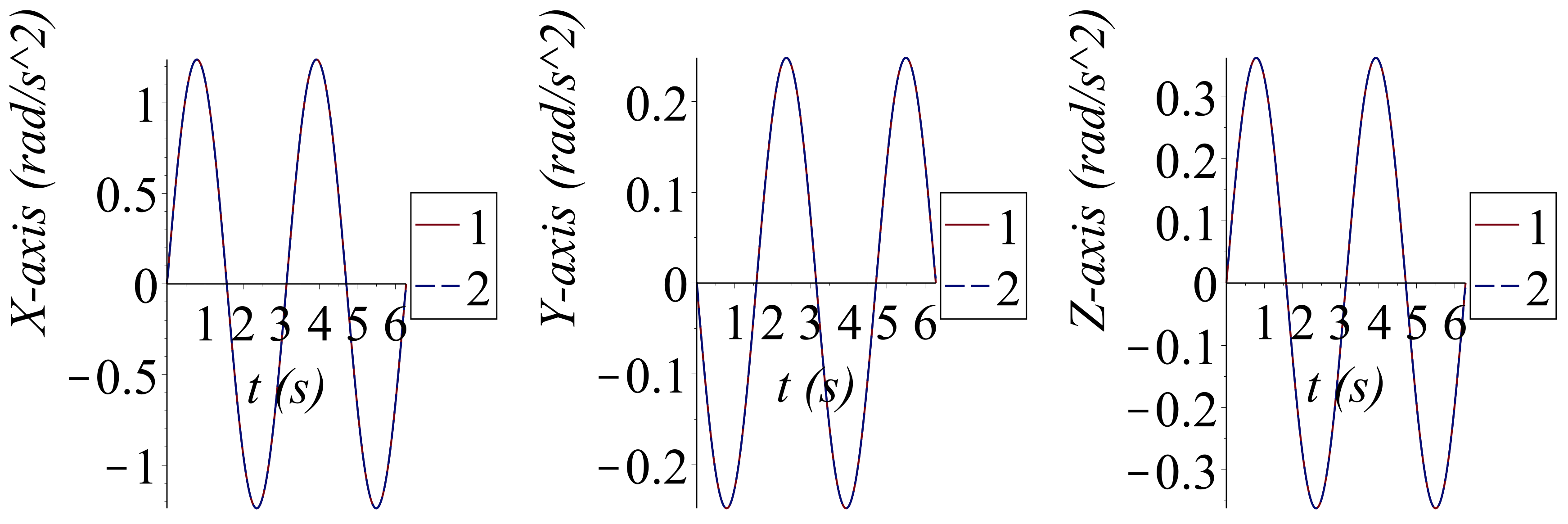
6. Numerical Applications
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Peres, A. Finite rotations and angular velocity. Am. J. Phys. 1980, 48, 70–71. [Google Scholar] [CrossRef]
- Ting, K.-L.; Soni, A.H. Instantaneous kinematics of a plane in spherical motion. ASME J. Mech. Trans. Autom. Des. 1983, 105, 560–567. [Google Scholar] [CrossRef]
- Nikravesh, P.E.; Wehage, R.A.; Kwon, O.K. Euler parameters in computational kinematics and dynamics. Part 1. ASME J. Mech. Trans. Autom. Des. 1985, 107, 358–365. [Google Scholar] [CrossRef]
- Angeles, J. Rational Kinematics; Springer: New York, NY, USA, 1988. [Google Scholar]
- Chiang, C.H. Kinematics of Spherical Mechanisms; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Rico-Martinez, J.M.; Gallardo-Alvarado, J. A simple method for the determination of angular velocity and acceleration of a spherical motion through quaternions. Meccanica 2000, 35, 111–118. [Google Scholar] [CrossRef]
- Chase, R.; Pandya, A. A Review of active mechanical driving principles of spherical robots. Robotics 2012, 1, 3–23. [Google Scholar] [CrossRef]
- McCarthy, J.M.; Bodduluri, R.M. Avoiding singular configurations in finite position synthesis of spherical 4R linkages. Mech. Mach. Theory 2000, 35, 451–462. [Google Scholar] [CrossRef]
- McCarthy, J.M.; Soh, G.S. Geometric Design of Linkages, 2nd ed.; Springer: Berlin, Germany, 2011. [Google Scholar]
- Cervantes-Sánchez, J.J.; Medellín-Castillo, H.I.; Rico-Martínez, J.M.; González-Galván, E.J. Some improvements on the exact kinematic synthesis of spherical 4R function generators. Mech. Mach. Theory 2009, 44, 103–121. [Google Scholar] [CrossRef]
- Yang, T.; Jian, Y.H.; Lai, R.Y. A Simple Synthesis Method of Spherical 4R Linkages Reaching Four Positions. Adv. Mater. Res. 2011, 199–200, 1236–1239. [Google Scholar] [CrossRef]
- Mendoza-Trejo, O.; Cruz-Villara, C.A.; Peón-Escalante, R.; Zambrano-Arjona, M.A.; Peñuñuri, F. Synthesis method for the spherical 4R mechanism with minimum center of mass acceleration. Mech. Mach. Theory 2015, 93, 53–64. [Google Scholar] [CrossRef]
- Asada, H.; Granito, J. Kinematic and static characterization of wrist joints and their optimal design. In Proceedings of the IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; pp. 244–250. [Google Scholar]
- Lo, H.S.; Xie, S. Optimization and analysis of a redundant 4R spherical wrist mechanism for a shoulder exoskeleton. Robotica 2014, 32, 1191–1211. [Google Scholar] [CrossRef]
- Gosselin, C.M.; Hamel, J.F. The Agile Eye: A high-performance three-degree-of-freedom camera-orienting device. In Proceedings of the IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 781–786. [Google Scholar]
- Gosselin, C.M.; St-Pierre, É. Development and experimentation of a fast 3-DOF camera-orienting device. Int. J. Robot. Res. 1997, 16, 619–630. [Google Scholar] [CrossRef]
- Li, T.; Payandeh, S. Design of spherical parallel mechanisms for application to laparoscopic surgery. Robotica 2002, 20, 133–138. [Google Scholar] [CrossRef]
- Hong, M.B.; Jo, Y.-H. Design of a novel 4-DOF wrist-type surgical instrument with enhanced rigidity and dexterity. IEEE ASME Trans. Mechatron. 2014, 19, 500–511. [Google Scholar] [CrossRef]
- Erdman, A.G. Lessons learned from kinematics research applied to medical device design. ASME J. Biomech. Eng. 2018, 140, 021006-1-15. [Google Scholar] [CrossRef] [PubMed]
- Gosselin, C.M.; Angeles, J. The optimum kinematic design of a spherical three-degree-of-freedom parallel manipulator. ASME J. Mech. Transm. Autom. Des. 1989, 111, 202–207. [Google Scholar] [CrossRef]
- Gosselin, C.M.; Angeles, J. A global performance index for the kinematic optimization of robotic manipulators. ASME J. Mech. Des. 1991, 113, 220–226. [Google Scholar] [CrossRef]
- Alici, G.; Shirinzadeh, B. Topology optimisation and singularity analysis of a 3-SPS parallel manipulator with a passive constraining spherical joint. Mech. Mach. Theory 2004, 39, 215–235. [Google Scholar] [CrossRef]
- Bonev, I.A.; Gosselin, C.M. Singularity loci of spherical parallel mechanisms. In Proceedings of the IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 2957–2962. [Google Scholar]
- Bai, S.; Hansen, M.R.; Andersen, T.O. Modelling of a special class of spherical parallel manipulators with Euler parameters. Robotica 2009, 27, 161–170. [Google Scholar] [CrossRef]
- Bai, S. Optimum design of spherical parallel manipulator for a prescribed workspace. Mech. Mach. Theory 2010, 45, 200–211. [Google Scholar] [CrossRef]
- Kong, X.; Gosselin, C. A formula that produces a unique solution to the forward displacement analysis of a quadratic spherical parallel manipulator: The agile eye. ASME J. Mech. Robot. 2010, 2, 044501. [Google Scholar] [CrossRef]
- Wu, G. Multiobjective optimum design of a 3-RRR spherical parallel manipulator with kinematic and dynamic dexterities. Model. Identif. Control 2012, 33, 111–121. [Google Scholar] [CrossRef]
- Saafi, H.; Laribi, M.; Zeghloul, S. Redundantly actuated 3-RRR spherical parallel manipulator used as a haptic device: Improving dexterity and eliminating singularity. Robotica 2015, 33, 1113–1130. [Google Scholar] [CrossRef]
- Shintemirov, A.; Niyetkaliyev, A.; Rubagotti, M. Numerical optimal control of a spherical parallel manipulator based on unique kinematic solutions. IEEE ASME Trans. Mechatron. 2016, 21, 98–109. [Google Scholar] [CrossRef]
- Wu, G.; Caro, S.; Wang, J. Design and transmission analysis of an asymmetrical spherical parallel manipulator. Mech. Mach. Theory 2015, 94, 119–131. [Google Scholar] [CrossRef]
- Saafi, H.; Laribi, M.A.; Zeghloul, S. Optimal torque distribution for a redundant 3-RRR spherical parallel manipulator used as a haptic medical device. Robot. Auton. Syst. 2017, 89, 40–50. [Google Scholar] [CrossRef]
- Arrouk, K.A.; Bouzgarrou, B.C.; Gogu, G. Workspace characterization and kinematic analysis of general spherical parallel manipulators revisited via graphical based approaches. Mech. Mach. Theory 2018, 122, 404–431. [Google Scholar] [CrossRef]
- Landuré, J.; Gosselin, C. Kinematic analysis of a novel kinematically redundant spherical parallel manipulator. ASME J. Mech. Robot. 2018, 10, 021007. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.; Chen, W.; Bai, S. Integrated design, modeling and analysis of a novel spherical motion generator driven by electromagnetic principle. Robot. Auton. Syst. 2018, in press. [Google Scholar] [CrossRef]
- Enferadi, J.; Shahi, A. A closed-form solution for the position analysis of a novel fully spherical parallel manipulator. Robotica 2015, 33, 2114–2136. [Google Scholar] [CrossRef]
- Gallardo-Alvarado, J.; Abedinnasab, M.H.; Lichtblau, D. Simplified kinematics for a parallel manipulator generator of the Schönflies motion. ASME J. Mech. Robot. 2016, 8, 061020. [Google Scholar] [CrossRef]
- Craig, J.J. Introduction to Robotics: Mechanics & Control; Addison-Wesley Publishing Company: Boston, MA, USA, 1986. [Google Scholar]
- Joshi, S.A.; Tsai, L.W. Jacobian analysis of limited-DOF parallel manipulators. ASME J. Mech. Des. 2002, 124, 254–258. [Google Scholar] [CrossRef]
- Gallardo-Alvarado, J. Kinematic Analysis of Parallel Manipulators by Algebraic Screw Theory; Springer International Publishing: Berlin, Germany, 2016. [Google Scholar]
- Choi, H.-B.; Ryu, J. Singularity analysis of a four degree-of-freedom parallel manipulator based on an expanded 6×6 Jacobian matrix. Mech. Mach. Theory 2012, 57, 51–61. [Google Scholar] [CrossRef]

| Sol. | ||
|---|---|---|
| 13 | ( −0.9969563613,0.0348994966,0.0697139786) | ( 0.5572283259,−0.0627464056,0.8279851940) |
| 16 | (−0.9970863751,0.0347732475,−0.0678939009) | ( 0.4382165437,−0.0627290151,0.8966779419) |
| 45 | ( 0.9970863751,−0.0347732475,0.0678939009 | ( −0.4382165437,0.0627290151,−0.8966779419) |
| 48 | ( 0.9969563613,−0.0348994966,−0.0697139786) | (−0.5572283259,0.0627464056,−0.8279851940) |
| m, m, , , |
|---|
| m, m, m |
| , , |
| m, m, m |
| m, m, m |
| - |
| - |
| m |
| m |
| m |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallardo-Alvarado, J.; Rodriguez-Castro, R.; Perez-Gonzalez, L.; Aguilar-Najera, C.R. Kinematics of the 3(RPSP)-S Fully Spherical Parallel Manipulator by Means of Screw Theory. Robotics 2018, 7, 29. https://doi.org/10.3390/robotics7020029
Gallardo-Alvarado J, Rodriguez-Castro R, Perez-Gonzalez L, Aguilar-Najera CR. Kinematics of the 3(RPSP)-S Fully Spherical Parallel Manipulator by Means of Screw Theory. Robotics. 2018; 7(2):29. https://doi.org/10.3390/robotics7020029
Chicago/Turabian StyleGallardo-Alvarado, Jaime, Ramon Rodriguez-Castro, Luciano Perez-Gonzalez, and Carlos R. Aguilar-Najera. 2018. "Kinematics of the 3(RPSP)-S Fully Spherical Parallel Manipulator by Means of Screw Theory" Robotics 7, no. 2: 29. https://doi.org/10.3390/robotics7020029
APA StyleGallardo-Alvarado, J., Rodriguez-Castro, R., Perez-Gonzalez, L., & Aguilar-Najera, C. R. (2018). Kinematics of the 3(RPSP)-S Fully Spherical Parallel Manipulator by Means of Screw Theory. Robotics, 7(2), 29. https://doi.org/10.3390/robotics7020029







