Decision-Making for Path Planning of Mobile Robots Under Uncertainty: A Review of Belief-Space Planning Simplifications

Abstract

Uncertainty remains a central challenge in robotic navigation, exploration, and coordination. This paper examines how Partially Observable Markov Decision Processes (POMDPs) and their decentralized variants (Dec-POMDPs) provide a rigorous foundation for decision-making under partial observability across tasks such as Active Simultaneous Localization and Mapping (A-SLAM), adaptive informative path planning, and multi-robot coordination. We review recent advances that integrate deep reinforcement learning (DRL) with POMDP formulations, highlighting improvements in scalability and adaptability as well as unresolved challenges of robustness, interpretability, and sim-to-real transfer. To complement learning-driven methods, we discuss emerging strategies that embed probabilistic reasoning directly into navigation, including belief-space planning, distributionally robust control formulations, and probabilistic graph models such as enhanced probabilistic roadmaps (PRMs) and Canadian Traveler Problem-based roadmaps. These approaches collectively demonstrate that uncertainty can be managed more effectively by coupling structured inference with data-driven adaptation. The survey concludes by outlining future research directions, emphasizing hybrid learning–planning architectures, neuro-symbolic reasoning, and socially aware navigation frameworks as critical steps toward resilient, transparent, and human-centered autonomy.

1. Introduction

Autonomous mobile robots are increasingly operating in complex, real-world scenarios, ranging from disaster response and industrial installations to medical facilities, which are both dynamic and only partially observable. In such settings, robots must simultaneously determine their position and devise optimal paths while accounting for uncertainty in their own state and the surrounding environment. Traditional planning methods, which assume full observability and deterministic conditions, frequently prove inadequate under these circumstances [1,2].

To address these challenges, POMDPs provide a rigorous framework for sequential decision-making under uncertainty [3,4]. POMDPs operate in belief space, where the robot maintains a probability distribution over its possible states. Planning in belief space enables the robot to take actions that reduce uncertainty or gather information, in addition to pursuing goal-directed behavior [5]. However, solving POMDPs exactly is difficult in large or continuous domains, which are commonly seen in robotics [6,7].

A variety of methods have been introduced to make belief-space planning computationally feasible at scale. These encompass point-based approximations, belief-distribution compression, and sampling-driven solvers that exchange exactness for tractability [8,9]. Moreover, embedding reinforcement learning, particularly deep Q-networks, enables the learning of belief-dependent policies in high-dimensional observation domains [10,11]. Le et al. further demonstrate that integrating convolutional residual blocks into an Asynchronous Advantage Actor Critic (A3C) framework yields an 18% performance improvement across 27 unseen, stochastic navigation tasks, while a Deep Deterministic Policy Gradient (DDPG) variant combining Convolutional Neural Network (CNN) and Long Short-Term Memory (LSTM) layers with fused laser–vision inputs achieves roughly a 10% boost in dynamic environments [12].

Probabilistic graphical models, most notably Bayesian networks and factor graphs, constitute the cornerstone of SLAM and inference-driven motion planning [13,14]. By reasoning uncertainty in a structured, scalable manner, these frameworks form the estimation core of contemporary SLAM systems.

This survey delivers a systematic examination of decision-making methodologies in belief-space planning, emphasizing POMDP simplifications tailored for real-world robotic applications. It begins by outlining the research strategy used in the review in Section 2, followed by the theoretical foundations of belief-space and probabilistic planning in Section 3. Section 4 delves into the application of probabilistic graphical models within SLAM and planning. Section 5 reviews key simplification techniques for POMDP solvers, while Section 6 addresses the incorporation of reinforcement learning into belief-space frameworks. Section 7 illustrates practical deployments in SLAM and cooperative multi-robot scenarios. Comparative evaluations and unresolved issues are covered in Section 8 and Section 9, respectively, with the paper’s final prospects and research avenues presented as insights and conclusions in Section 10 and Section 11.

2. Research Strategy

A structured and methodical search strategy was implemented to identify scholarly contributions pertinent to belief-space planning and decision-making under uncertainty. The search string was carefully formulated to encompass a set of interchangeable descriptors—belief-space planning, path planning under uncertainty, probabilistic planning, decision-making under uncertainty, and robot motion planning under uncertainty. This composite query was designed to maximize retrieval sensitivity while maintaining semantic precision across heterogeneous digital repositories.

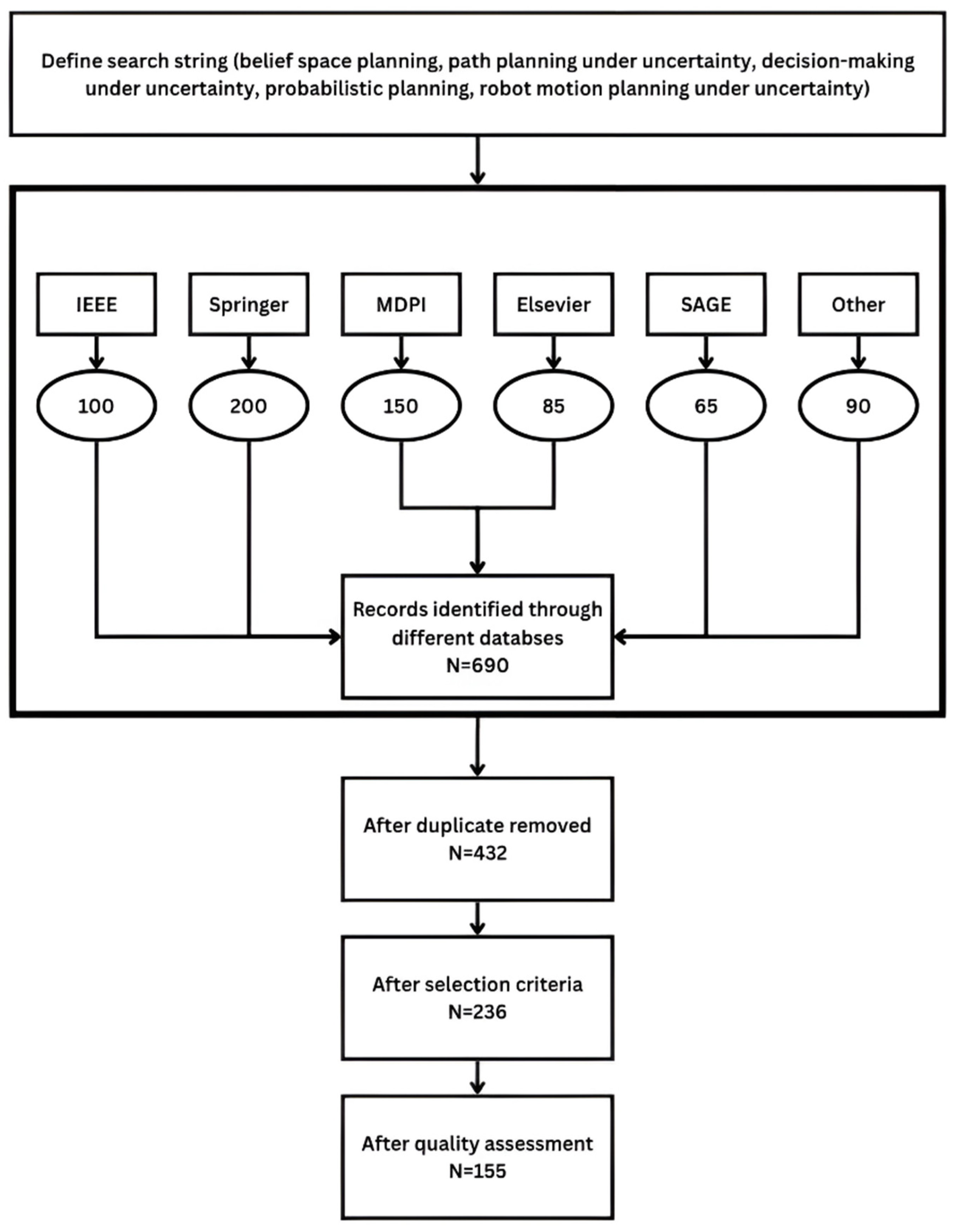
The bibliographic search was executed across five principal sources: IEEE, Springer, MDPI, Elsevier, SAGE, and a category denoted as Other, that aggregated additional indexed repositories. The distribution of identified records revealed Springer as the most substantial contributor (n = 200), followed by MDPI (n = 150), IEEE (n = 100), Elsevier (n = 85), SAGE (n = 65), and miscellaneous repositories (n = 90). Collectively, this process yielded 690 publications.

The subsequent refinement adhered to a multi-tiered screening procedure. Initially, duplicate entries across databases were excluded, reducing the dataset to 432 unique studies. Thereafter, application of predefined eligibility criteria—emphasizing thematic relevance to uncertainty-aware robotic planning—resulted in the retention of 236 articles. A final stage of quality appraisal, which considered methodological soundness, contribution significance, and robustness of validation, further distilled the corpus to 155 publications.

This systematic filtration process ensured the inclusion of literature that is both methodologically rigorous and substantively aligned with the objectives of this review. The overall workflow is delineated in the PRISMA flow diagram in Figure 1.

To ensure that the finished text met the academic writing standards, ChatGPT (GPT 4) and Grammarly AI (free version) were applied iteratively to each paragraph during the writing phase. ChatGPT was used to increase readability by modifying sentences to improve flow and coherence, wherever required. Grammarly was then employed to look for spelling and grammatical errors in the paragraphs. Finally, each AI-recommended change was thoroughly examined to make sure that each paragraph’s original meaning was maintained. This AI-assisted approach refined the final manuscript’s quality and clarity while allowing a more organized synthesis of difficult literature.

3. Foundations of Belief-Space Planning

Belief-space planning in robotics addresses the challenge of decision-making under uncertainty by considering distributions over the robot’s state space, rather than point estimates. This framework enables more robust planning by accounting for partial observability and sensor noise in real-world environments. The key components of belief-space planning include planning techniques, belief representation models, application domains, and strategies for simplifying Partially Observable Markov Decision Processes (POMDPs).

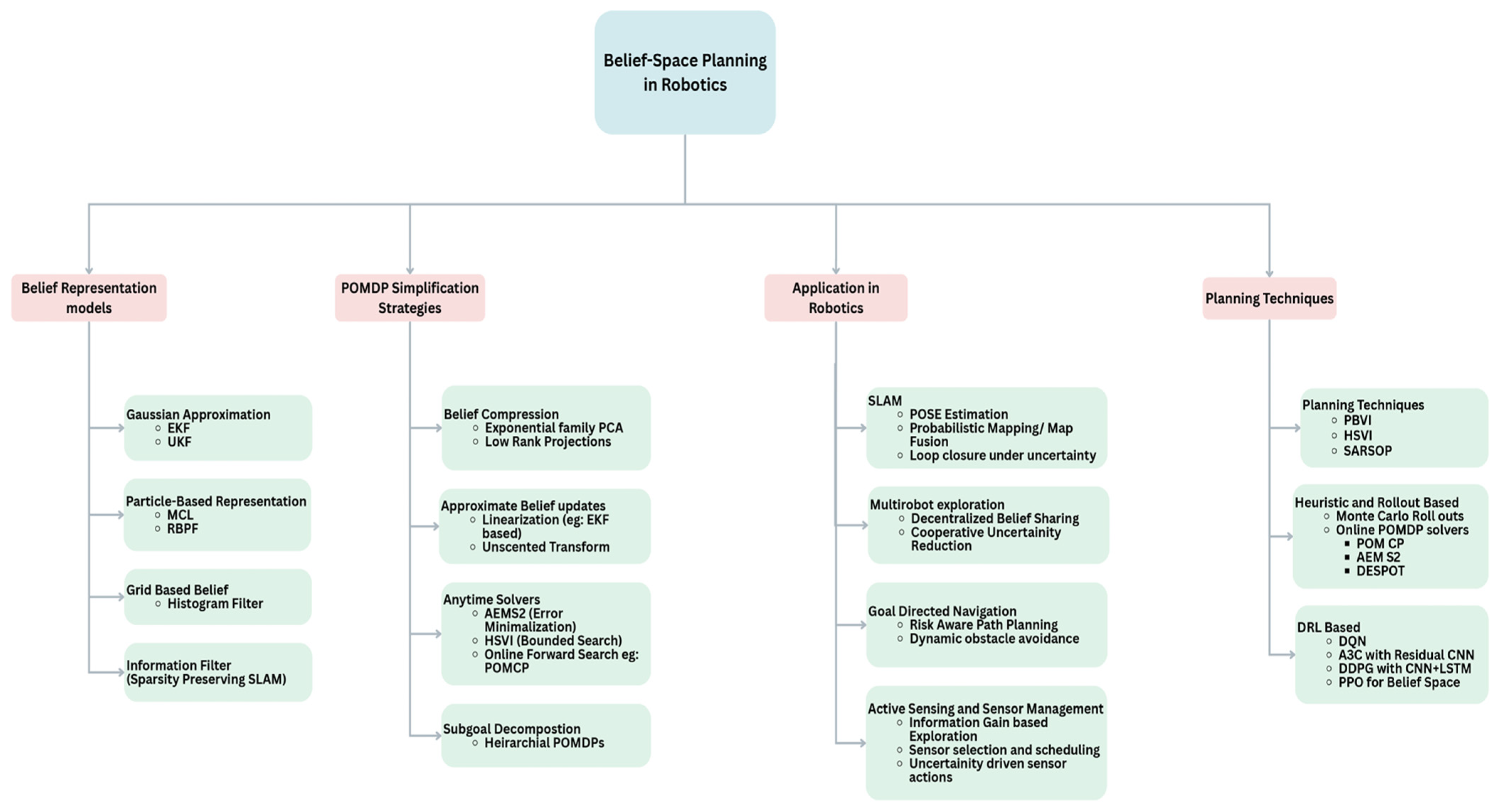
Figure 2 presents a structured taxonomy describing the state of robotics belief-space planning techniques. The major topic, “Belief-Space Planning in Robotics”, is at the top of the hierarchical structure and acts as the root node from which four main branches, each of which represents a different aspect of the field, emerge.

The first branch, “belief representation models”, subdivides into four principal classes. Techniques like the Unscented Kalman Filter (UKF) and the Extended Kalman Filter (EKF) are part of Gaussian approximation. Particle-Based Representation includes Monte Carlo Localization (MCL) and Rao–Blackwellized Particle Filter (RBPF). Grid-Based Belief incorporates the Histogram Filter technique, while Information Filter focuses on sparsity-preserving SLAM techniques.

The second branch, “POMDP Simplification Strategies,” presents methods that make the unmanageable belief space easier to compute. Low-Rank Projections and Exponential Family Principal Component Analysis (PCA) are examples of belief compression. The Unscented Transform and linearization techniques, such as EKF-based approaches, are included in Approximate Belief Updates. Anytime Solvers include adaptive frameworks like Anytime Error Minimization Search 2 (AEMS2) for error minimization, Heuristic Search Value Iteration (HSVI) applying bounded search, and online forward search algorithms like Partially Observable Monte Carlo Planning (POMCP). Lastly, Subgoal Decomposition indicates hierarchical POMDPs for task segmentation.

The third branch, “Application in Robotics”, lists practical implementations of belief-space planning. SLAM highlights pose estimation, probabilistic mapping, and map fusion, as well as loop closure under uncertainty. Multi-robot Exploration serves as an example of cooperative uncertainty reduction and decentralized belief sharing. The main objectives of goal-directed navigation are dynamic obstacle avoidance and risk-aware path planning. Uncertainty-driven sensor actions, optimal sensor selection and scheduling, and information gain-driven exploration are all covered by active sensing and sensor management.

The fourth branch, “Planning Techniques”, classifies methodologies for operationalizing belief-space policies. Point-based Value Iteration (PBVI), HSVI, and Successive Approximations of the Reachable Space under Optimal Policies (SARSOP) are included in Planning Techniques. Monte Carlo rollouts and online POMDP solvers like POMCP, AEM-S2, and Determinized Sparse Partially Observable Tree (DESPOT) are examples of heuristic and rollout-based techniques. Deep Q-Networks (DQN), Asynchronous Advantage Actor Critic (A3C) with residual convolutional networks, DDPG with CNN + LSTM, and Proximal Policy Optimization (PPO) modified for belief-space optimization are examples of reinforcement learning architectures that are detailed by DRL-based techniques.

Collectively, this figure describes the spectrum of theoretical frameworks, computational simplifications, robotic applications, and planning methodologies within belief-space planning, offering a visual analysis of the field’s intricate structure.

3.1. Belief-Space Planning Under Uncertainty

In real-world deployments, uncertainty arises mainly from perceptual limitations and environmental non-stationarity rather than from sporadic hardware malfunctions. Modern perception systems frequently show poor generalization to new situations or under distributional changes, such as changes in lighting, weather, surface textures, or the introduction of strange objects. When test conditions differ from the training distribution, these shifts often result in systematic errors in state estimation. Furthermore, quickly changing situations, such as those with moving obstacles, shifting backgrounds, or fleeting occlusions, might increase uncertainty and compromise the accuracy of previously learned models. While hardware flaws and sensor noise can increase uncertainty, their effects are typically less significant than the more enduring problems caused by distributional drift and perception-model mismatches. Belief-space planning depicts this uncertainty as a range of potential states, represented by a probability distribution called a belief, as opposed to assuming that the robot’s state is known with complete certainty [15,16]. This strategy helps the robot make decisions that consider the expected outcomes as well as the potential worth of the information it gathers along the route.

Belief-space planning enables a robot to evaluate both the immediate effects of its actions and their impact on uncertainty. Consequently, actions may be chosen for their informational value, such as sensing or exploratory maneuvers, or for their direct progression toward a goal, like navigating to a designated location. The planning algorithm judiciously balances these dual aims [17,18].

3.2. Partially Observable Markov Decision Processes (POMDPs)

A POMDP models the interaction between an agent and a partially observable environment as a tuple (S, A, Z, T, O, R, γ), where

S is the set of states,

A is the set of actions,

Z is the set of observations,

T(s′|s, a) is the state transition model,

O(z|s′, a) is the observation model,

R(s, a) is the reward function,

γ ϵ [0, 1) is the discount factor.

The robot performs an action a, enters an unobserved state s′, obtains an observation z, and uses Bayes’ rule to update its belief distribution b(s) at each time step. In order to maximize the expected cumulative reward, the goal is to derive a policy π(b) that prescribes actions based on the current belief. POMDP-based reasoning is supported by this iterative belief update mechanism [19,20], which becomes crucial when the robot has to deal with ambiguous or aliased observations, where divergence in belief states is crucial [21].

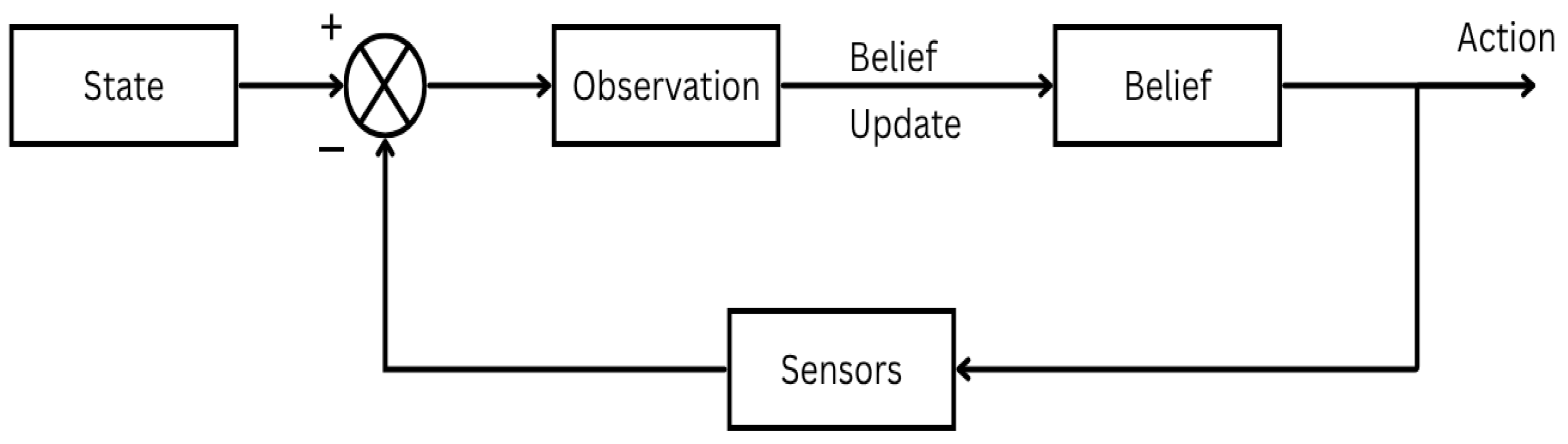
Figure 3 illustrates the fundamental workflow of a Partially Observable Markov Decision Process (POMDP), which governs belief-space planning under uncertainty. Instead of using a single deterministic estimate, the robot in this framework maintains a belief that is a probability distribution over the potential states.

The process starts with the robot taking an action according to its current belief. The actual underlying condition of the system, which cannot be readily observed, is impacted by this action. Rather, the robot’s sensors provide it with observations, which are frequently noisy and insufficient.

In order to create a new posterior belief, these data are integrated with the previous belief via a belief update process, usually employing Bayes’ rule or approximation techniques. The next action is then chosen based on this revised belief, creating a feedback loop that lasts the duration of the robot’s operation.

This cyclical interaction between action, observation, and belief update is central to planning in POMDPs, enabling robust decision-making in dynamic and uncertain environments.

3.3. Belief Trajectory Optimization

Table 1. Key belief update strategies and computational complexity.

Belief Update Method	Belief Representation	Computational Complexity	Update Runtime (ms)	Typical Accuracy (RMSE)	Suitable Applications
Bayesian Filtering (Exact)	Full probability distribution	High (intractable in large spaces)	3–5 [22]	1.6–1.8 m [22]	Small-scale planning problems with analytical models.
Extended Kalman Filter (EKF)	Gaussian approximation (linearized)	O($n^2$), efficient for small systems.	5.95 ± 0.03 (robot localization) [23]; 30.1 (sensor fusion) [24]	0.019 m [23]; 0.065–0.178 m [24]	Localization with smooth, Gaussian noise models.
Unscented Kalman Filter (UKF)	Gaussian approximation (unscented transform)	O($n^2$), better nonlinearity handling.	N/A 1	3.19–11.95 m [25]	Nonlinear motion/observation systems.
Particle Filter	Discrete weighted particles	O(N×n), depends on the number of particles N.	6.41 ± 0.08 ms (for AMCL) [23]	0.091 m (for AMCL) [23]	SLAM, multimodal distributions, tracking.
Information Filter	Information (inverse covariance) form	Similarly to EKF, efficient for sparse matrices.	N/A 1	N/A 1	SLAM, multimodal distributions, tracking.
Histogram Filter	Discrete grid over state space	Very high in continuous/high-dim state spaces.	N/A 1	N/A 1	Didactic, small-grid environments.

¹ N/A: Not Available.

provides a comparative overview of widely adopted belief update strategies in robotics, categorized by their computational demands, scalability, runtime behavior, accuracy, and application domains. These methods differ primarily in how they encode uncertainty (i.e., the belief), and this choice strongly shapes their suitability across different robotic systems.

The table begins with Bayesian filtering, which computes the full posterior distribution. While theoretically exact, its computational burden becomes prohibitive in high-dimensional spaces. Interestingly, its update time remains short (3–5 ms), but the resulting accuracy (around 1.6–1.8 m Root Mean Square Error (RMSE)) [22] is relatively poor compared to approximate filters, making it practical only in analytically simple environments.

Approximate Gaussian-based methods such as the Extended Kalman Filter (EKF) and the Unscented Kalman Filter (UKF) strike a balance between speed and fidelity. EKF updates are computationally efficient for small systems, with runtimes in the order of milliseconds (≈6 ms for localization), and they deliver accuracies as fine as a few centimeters under smooth Gaussian noise assumptions [23,24].

Two illustrative applications of the Extended Kalman Filter (EKF) in robotics demonstrate both its challenges and benefits. In UAV flight control, Szczepaniak et al. (2024) [26] investigated flight instabilities arising from computational delays in the PX4 Estimation and Control Library’s Extended Kalman Filter (PX4-ECL EKF) used for attitude, position, and velocity estimation. The authors identified that magnetometer disturbances and the fusion step implementation increased processing time, leading to oscillatory behavior, and showed that reorganizing computations by moving magnetometer processing to a separate thread improved flight stabilization. In mobile-robot localization, Huang et al. (2025) [24] used an EKF with a Recurrent Neural Network (RNN) to fuse LiDAR, IMU, and wheel-odometry data, achieving an average runtime of 30.1 ms per frame with localization errors within 8 cm, while the EKF-only baseline exhibited root mean square errors between 0.065 and 0.178 m under different noise levels. These examples illustrate how EKF remains central to robotic state estimation while benefiting from algorithmic refinements and hybrid fusion strategies.

In comparison, the UKF manages nonlinearities with greater grace; yet, it frequently displays wider error ranges (3–12 m RMSE) and somewhat higher runtime expenses [25], which reflects its wider application in nonlinear motion and observation models.

Rong et al. (2024) [25] gave an example of the Unscented Kalman Filter (UKF) in robotics-related tracking by introducing an adaptive noise-factor method to enhance spatial-target tracking using measurements from a ground-based radar and a space-based infrared satellite. Through Monte Carlo simulations, the authors demonstrated that the adaptive UKF consistently lowered the average position RMSE compared to the standard UKF, with the baseline errors ranging from 3.19 to 11.95 m and the adaptive method reducing them to 3.29 to 10.43 m under varying noise conditions. The study’s reported results, summarized in Table 2, highlight the performance gains achieved by adapting the filter to constant and step-change measurement noise scenarios for multiple targets.

Particle filters, which approximate the belief with weighted samples, show moderate runtimes (≈6 ms for adaptive Monte Carlo localization), yet their accuracy (≈0.09 m RMSE) [23] depends heavily on the number of particles used. While robust in multimodal and nonlinear scenarios, they scale poorly as particle counts grow.

Csuzdi et al. (2025) [23] demonstrated the application of particle filters to mobile-robot localization by introducing two exact particle-flow Daum–Huang filters, MEDH and NAEDH, and benchmarking them against Adaptive Monte Carlo Localization (AMCL) variants. Using a TurtleBot3 with a 2D LiDAR map in both simulation and real-world trials, the authors implemented the filters with Np = 100 particles and Nλ = 10 N homotopy steps. On a low-noise dataset, the standard AMCL gave 91 mm RMSE but at a faster 6.41 ms runtime. The reported results clearly illustrate the trade-offs between accuracy and computational cost across particle-filter variants.

Information filters retain the Kalman structure but work in the inverse covariance form, trading off runtime efficiency for improved performance in sparse, large-scale SLAM systems. Luppi et al. (2024) [27] presented a consensus-based information filter for distributed LiDAR-sensor tracking of mobile robots. The proposed framework fuses three-dimensional LiDAR data from multiple stationary sensors, with the consensus information filter combining local state estimates and incorporating remote-sensor inputs. Experimental evaluations in indoor environments demonstrated that this approach enhanced tracking robustness, particularly under low-visibility and occlusion conditions, by reducing both mean square error and covariance in the state estimates. The findings, as noted in the article’s abstract, emphasize the effectiveness of information filters in improving multi-sensor fusion for robot tracking.

Finally, histogram filters discretize the belief space into grids. Although straightforward and interpretable, their runtime and accuracy degrade rapidly as dimensionality increases, restricting them to didactic or tightly constrained environments rather than practical large-scale systems.

Taken together, the table underscores a recurring trade-off: methods that are fast and lightweight often compromise accuracy or generality, while those that better capture nonlinearities or multimodal beliefs tend to demand greater computational effort. Runtime performance and error bounds thus provide critical clues in choosing the right belief update strategy for a given robotic application.

Instead of optimizing fixed state–action sequences, belief-space planning seeks to optimize entire belief trajectories, striving to minimize the expected cost while accounting for uncertainty dynamics. Prominent methods in this area include sampling-based belief planners [28], belief-space Differential Dynamic Programming [29], and rollout-based planners that impose penalties for belief uncertainty [30].

3.4. Role in Robotic Autonomy

Belief-space planning forms the foundation for many aspects of robotic autonomy, such as active localization to plan and reduce pose uncertainty, sensor management to choose the most informative sensing action, and SLAM, in which the belief includes both robot pose and map structure [31]. Although most of the research on belief-space planning focuses on value-function approximations and probabilistic inference, it is also critical to recognize parallel initiatives that show how uncertainty-aware navigation frameworks can be used in real-world scenarios. A recent study, for example, suggested a multi-robot navigation framework that combines path planning and localization techniques in structured settings [32]. This work’s focus on managing dynamic navigation limitations and real-time decision-making complements the broader discussion on planning under uncertainty, even if it does not directly use belief-space simplifications. These contributions demonstrate the increasing applicability of hybrid architectures, which connect domain-specific deployment requirements with theoretical formulations of belief-space planning.

4. Probabilistic Graphical Models in Planning and SLAM

Autonomous robots depend on effective methods to estimate both their own state and the layout of their surroundings. Probabilistic Graphical Models (PGMs) offer a versatile, scalable means to represent and reason about the joint probability distributions inherent in these tasks. By encoding conditional dependencies in a graph structure, PGMs enable tractable inference even in high-dimensional, partially observable environments [33].

4.1. Bayesian Networks and Dynamic Bayesian Networks

Bayesian Networks (BNs) use directed acyclic graphs to model joint probability distributions. Here, nodes represent variables and edges represent conditional dependencies [34]. BNs are usually used in robotics to represent motion models, sensor models, and environmental variables. Dynamic Bayesian Networks (DBNs) extend this concept by adding a temporal aspect, which allows robots to model sequences of actions and observations [35].

DBNs excel in state estimation applications like localization and simultaneous localization and mapping, where a robot deduces its own pose and incrementally refines a map from sensor inputs. These frameworks facilitate recursive inference and may be coupled with estimation techniques such as the Kalman filter, particle filter, or unscented filter [36,37].

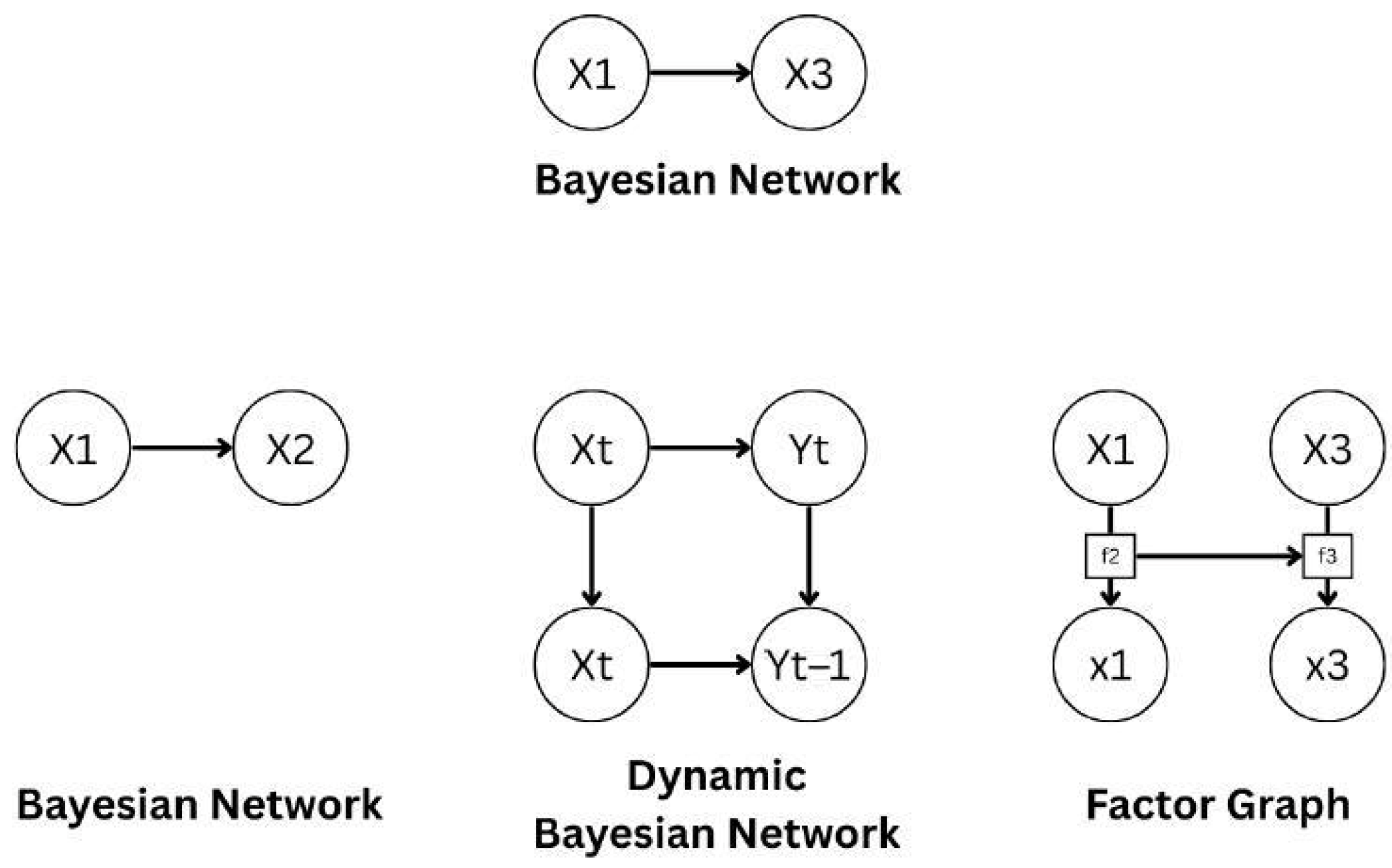
Figure 4 illustrates the structural differences between three key types of probabilistic graphical models commonly used in robotics and SLAM: Bayesian Networks (BNs), Dynamic Bayesian Networks (DBNs), and factor graphs.

A Bayesian Network is a Directed Acyclic Graph (DAG) where nodes represent random variables and edges denote conditional dependencies. For instance, in a simple BN with variables X1 and X2, the edge from X1 → X2 encodes the probabilistic influence of X1 on X2.

DBNs model variable sequences by extending BNs throughout time. Figure 3 illustrates temporal linkages for applications like robot localization and filtering in partially viewable situations by connecting variables Xt and Yt across neighboring time steps.

Factor graphs, on the contrary, are bipartite graphs where variables and factor nodes are separated. Factors (like f2 and f3) show probabilistic constraints or joint distributions and are associated with the variables they affect. A more flexible framework for inference is provided by factor graphs, which are particularly useful for sparsity-aware optimization in large-scale SLAM problems.

This comparative view makes it easier to understand how each model supports planning in robotic systems under uncertainty, informs inference methods, and forms probabilistic relationships.

4.2. Factor Graphs and Graph-Based SLAM

Factor graphs are essential to graph-based SLAM backends with high scalability because of their formulation, which makes it possible to estimate Maximum A Posteriori (MAP) efficiently using sparse optimization approaches.

Table 2. Characteristics of PGMs used in SLAM.

PGM Type	Graph Structure	Inference Technique	Update Runtime (ms)	Memory Requirement	Typical Accuracy (RMSE)	Application in SLAM	Scalability
Bayesian Network (BN)	Directed Acyclic Graph	Exact or approximate inference (e.g., variable elimination)	2–5 ms [38]	O(n2) [38]	0.42–0.65 m [38]	Sensor fusion, landmark recognition	Low to Moderate
Dynamic Bayesian Network (DBN)	Temporal Directed Graph	Forward-backward, particle filtering	2–3 ms [38]	O(n·T) [38]	0.42 m [38]	Sequential estimation, odometry integration	Moderate
Markov Random Field (MRF)	Undirected Graph	Loopy belief propagation	16–49 ms [39]	O(n2) [39]	0.24–1.05 m [39]	Map consistency checks, loop closures	Moderate to High
Factor Graph	Bipartite Graph (Variables + Factors)	MAP estimation via optimization	2–3 ms [40]	O(n) sparse [40]	0.006–0.028 m [41]	Backend optimization in graph-based SLAM	High
Pose Graph	Simplified Factor Graph over Poses	Sparse nonlinear optimization	4–10 ms [39]	O(n) sparse [39]	0.24–1.05 m [39]	Efficient SLAM backend for large-scale maps	Very High

presents a comparative overview of Probabilistic Graphical Models (PGMs) frequently employed in Simultaneous Localization and Mapping (SLAM). The underlying graph structure, inference method, memory load, runtime profile, accuracy, and scalability of each framework distinguish it apart.

By using methods like variable elimination, Bayesian Networks (BNs), which are organized as directed acyclic graphs, provide precise or approximative inference. Their memory requirements scale quadratically (O(n²)), and their runtime usually ranges between 2 and 5 ms. However, their middling accuracy (≈0.42–0.65 m RMSE) [38] limits their application in highly dynamic or expansive domains but makes them suitable for tasks like sensor fusion and landmark recognition.

Bodrumlu et al. (2024) [42] created a Bayesian network (BN) architecture that incorporates residual tire-pressure values to identify wheel problems in the context of vehicle fault diagnostics. After being first modeled in Matlab/Simulink, the technique was then put into practice in a real-time ROS environment, and real-vehicle trials were used to validate it. The system showed enhanced capabilities in detecting tire-pressure anomalies by continuously updating the BN structure with newly detected residuals, which increased the dependability of on-board defect detection systems.

By using forward-backward methods or particle filtering to incorporate sequential dependencies, Dynamic Bayesian Networks (DBNs) extend BNs temporally. Though they have greater memory costs proportional to both state and time (O(n·T)), they accomplish relatively fast updates (≈2–3 ms). They are especially useful in odometry integration and sequential estimation, where short-term correlations predominate, because their accuracy (≈0.42 m RMSE) [38] is comparable to that of static BNs.

In order to simulate mobile-robot delivery systems, Johnson et al. (2025) [43] suggested using a Dynamic Bayesian Network (DBN). The framework explicitly models the interactions between tasks, impediments, and robots. Compared to static models, the DBN offers more precise and flexible forecasts of system performance by capturing temporal dependencies. The study highlights how adding temporal uncertainty using DBNs increases the accuracy of performance evaluation in dynamic situations and the realism of delivery-system simulations.

Markov Random Fields (MRFs), defined by undirected graphs and loopy belief propagation, exhibit an increased runtime spread (16–49 ms) due to iterative convergence behavior. They balance computational cost with accuracy ranging from 0.24 to 1.05 m RMSE, using memory scaling as O(n²) [39]. Because of their adaptability, they are well-suited for loop closure and map consistency checks, particularly in medium- to large-scale situations.

Xu et al. (2025) [39] applied an MRF formulation to multi-robot cooperative SLAM, formulating loop-closure detection as an MRF problem. To ensure uniform map merging across several robots, their method divides the global SLAM graph into sub-graphs and uses an MRF-based front-end. Evaluated on Karlsruhe Institute of Technology and Toyota Technological Institute at Chicago (KITTI) sequences, the method achieved Absolute Trajectory Errors (ATE) between 0.24 and 1.05 m, with total runtimes ranging from 16.63 to 221.78 s depending on the number of robots. These results demonstrate that the MRF-based front-end provides an effective balance between accuracy and computational efficiency in cooperative SLAM.

Factor graphs, formulated as bipartite graphs between variables and factors, leverage optimization-based maximum a posteriori (MAP) estimation. They are lightweight in both runtime (≈2–3 ms) and memory (scaling with sparse O(n)), and they achieve notably fine-grained accuracy (≈0.006–0.028 m RMSE) [40,41]. Such efficiency renders them highly suitable for backend optimization in modern graph-based SLAM systems.

Factor-graph formulations have been increasingly applied in robotic state estimation and sensor fusion. One example is OiSAM-FGO [40], which integrates Global Navigation Satellite System (GNSS) and inertial data using a sparse factor-graph approach; by storing only non-zero elements of the Hessian matrix, the method reduces memory complexity from O(N^2) to O(N) and decreases optimization time by approximately 52% compared with state-of-the-art factor-graph methods. Another application is presented by Dong et al. (2025), who developed a point–line feature visual SLAM system whose factor-graph back-end optimization achieved root mean square errors between 0.0061 m and 0.0281 m on the European Robotics Challenge (EuRoC) dataset [41]. These studies highlight the efficiency and accuracy benefits of factor-graph formulations for GNSS/Inertial Navigation System (INS) integration and visual SLAM.

Pose Graphs, a simplified derivative of factor graphs that represent only robot poses, rely on sparse nonlinear optimization. They operate within 4–10 ms update times and sparse memory scaling, achieving accuracy similar to MRFs (≈0.24–1.05 m RMSE) [39]. Their exceptional scalability makes them the de facto choice for large-scale mapping where efficiency and robustness are paramount.

In the cooperative SLAM framework of Xu et al. (2025) [39], a pose-graph representation is employed for the back-end optimization. By leveraging the inherent sparsity of pose graphs, the method achieves scalability to large maps in multi-robot settings. On KITTI sequences, the pose-graph optimization reported runtimes between 16.63 and 221.78 s with Absolute Trajectory Errors (ATE) ranging from 0.24 to 1.05 m, demonstrating both the efficiency and accuracy of pose-graph SLAM for cooperative mapping.

In sum, the table highlights how PGMs span a spectrum of trade-offs: BNs and DBNs offer structured inference but face scalability hurdles; MRFs balance accuracy with iterative cost; while factor and pose graphs stand out for their compact memory footprints, swift runtimes, and high accuracy, making them indispensable for state-of-the-art large-scale SLAM.

PGMs have evolved from conceptual models to extremely scalable optimization frameworks, as seen in this classification, which also shows how relevant they are becoming to contemporary SLAM systems.

In probabilistic models, factor graphs highlight the constraint structure, whereas BNs provide a top-down picture. There are two kinds of nodes in factor graphs: variable nodes and factor nodes. They are bipartite graphs in which variable nodes represent unknown quantities, while each factor encodes a probabilistic constraint (e.g., sensor measurement, motion model) that relates a subset of variables [44].

Factor graphs form the basis of graph-based SLAM by encoding robot poses and landmarks as variable nodes, while sensor and odometry measurements appear as factor nodes [45,46]. Consequently, the SLAM problem is cast as a Maximum A Posteriori estimation over this graph. Solvers such as Incremental Smoothing and Mapping 2 (iSAM2) [47], Georgia Tech Smoothing and Mapping (GTSAM) [48], and Square Root Smoothing and Mapping (SAM) [49] leverage the graph’s sparsity to perform incremental inference in real-time.

Such frameworks prove highly effective in multi-robot SLAM and continuous mapping applications, where variables and constraints are introduced dynamically. They also support a modular architecture and the seamless incorporation with learned models, as demonstrated in semantic SLAM and advanced spatial perception systems [50,51].

4.3. Integration with Belief-Space Planning

In regard to belief-space planning, PGMs provide the core inference mechanism, enabling a robot to maintain and update probability distributions across complex, continuous state representations. These models allow belief propagation through message passing, loop closure detection via pose graph optimization, and hybrid models that combine learned and analytical components [52,53].

5. Simplification Techniques for POMDP Planning

Although Partially Observable Markov Decision Processes offer a rigorous mathematical framework for planning under uncertainty, obtaining exact solutions is computationally infeasible for most practical robotic systems. The dimensionality of the belief space grows exponentially with the number of states, actions, and observations, which has driven the development of numerous approximation strategies. These techniques simplify either the belief representation or the value function, thereby enabling tractable, real-time planning.

5.1. Point-Based Value Iteration Methods

Point-Based Value Iteration (PBVI) approximates the value function by concentrating on a finite set of reachable belief points, thereby reducing computational overhead while retaining near-optimality within targeted belief regions. Enhanced variants such as SARSOP and Perseus further improve efficiency by sampling beliefs that are optimally reachable [54,55].

These techniques have demonstrated effectiveness in robotic navigation, target tracking, and human–robot interaction; however, their success depends critically on the density and quality of the sampled beliefs. Furthermore, their reliance on discrete approximations restricts scalability in domains with predominantly continuous state spaces.

5.2. Belief Compression and Dimensionality Reduction

To manage high-dimensional belief representations, compression approaches project the belief distribution onto a lower-dimensional manifold via statistical or learned mappings [56]. Notable examples include Principal Component Analysis (PCA) and autoencoders, which derive nonlinear embeddings from data.

By compressing belief distributions, the computational burden of planning, especially when coupled with approximate dynamic programming or reinforcement learning, is markedly reduced [57,58]. However, this reduction in dimensionality can impair accuracy within low probability regions that are crucial for rare event planning.

5.3. Sampling-Based Belief Planners

Sampling-based approaches such as POMCP (Partially Observable Monte Carlo Planning) eliminate the need for explicit belief maintenance by sampling action-observation trajectories and simulating forward outcomes via particle filters [59]. These planners leverage Monte Carlo Tree Search to traverse belief–action branches and approximate expected returns.

Contemporary methods, such as DESPOT, enhance sampling efficiency by concentrating on deterministic scenarios and providing bounds on policy performance. These techniques prove particularly advantageous in environments with intricate dynamics and sparse observations; examples include disaster-recovery and search rescue operations [60].

5.4. Approximate Policy Representations

A separate class of methods emphasizes learning compact, approximate policies rather than computing full value functions. Representative examples include finite state controllers for discrete action policies, rollout-based strategies guided by sampling heuristics, and deep policy networks trained on sequences of belief action trajectories [61].

These approaches are well-suited to real-time robotic applications due to their minimal computational demands; however, their performance hinges critically on the quality of the training data and the generalization capacity of the policy architecture.

5.5. Hybrid and Adaptive Simplification Frameworks

Adaptive simplification frameworks that choose approximation techniques dynamically have been introduced. They are informed by the current belief distribution or environmental context, and these hybrid architectures employ model-based approximations in regions of high certainty, and sampling or learned policies in uncertain or high-risk zones [62,63].

While these approaches provide promising balances between computational cost and performance, their seamless incorporation into general-purpose robotic planners is still an active research challenge.

6. Learning-Based Simplifications for Belief-Space Planning

Reinforcement learning provides a rigorous framework for agents to acquire sequential decision-making policies through direct interaction with their surroundings. In environments exhibiting partial observability, such as those encountered in real-world robotics, reinforcement learning must be reformulated within belief space, wherein the agent’s internal state is captured by a probability distribution over possible world states. In this context, simplification denotes any representational, algorithmic, or learning-driven approach that lowers the computational or memory demands of belief-space planning, while still preserving a satisfactory level of decision quality. Recent progress in deep reinforcement learning has facilitated the incorporation of learning-based policies into belief-space planning [64].

6.1. Deep Q-Networks (DQN) for Belief-State Decision-Making

Deep Q-Networks employ deep neural architectures to approximate the action value function Q(b, a), where b denotes the belief distribution and a is the chosen action. In contrast to conventional Q-learning on fully observable states, belief-space DQNs must generalize across high-dimensional, continuous probability distributions [65,66].

In robotic planning, belief representations commonly employ histograms or Gaussian mixture models, recurrent neural networks for observation histories, and autoencoders that learn compact representations of belief distributions [67]. These representation schemes enable DQNs to learn belief-aware policies that effectively handle both state uncertainty and environmental variability.

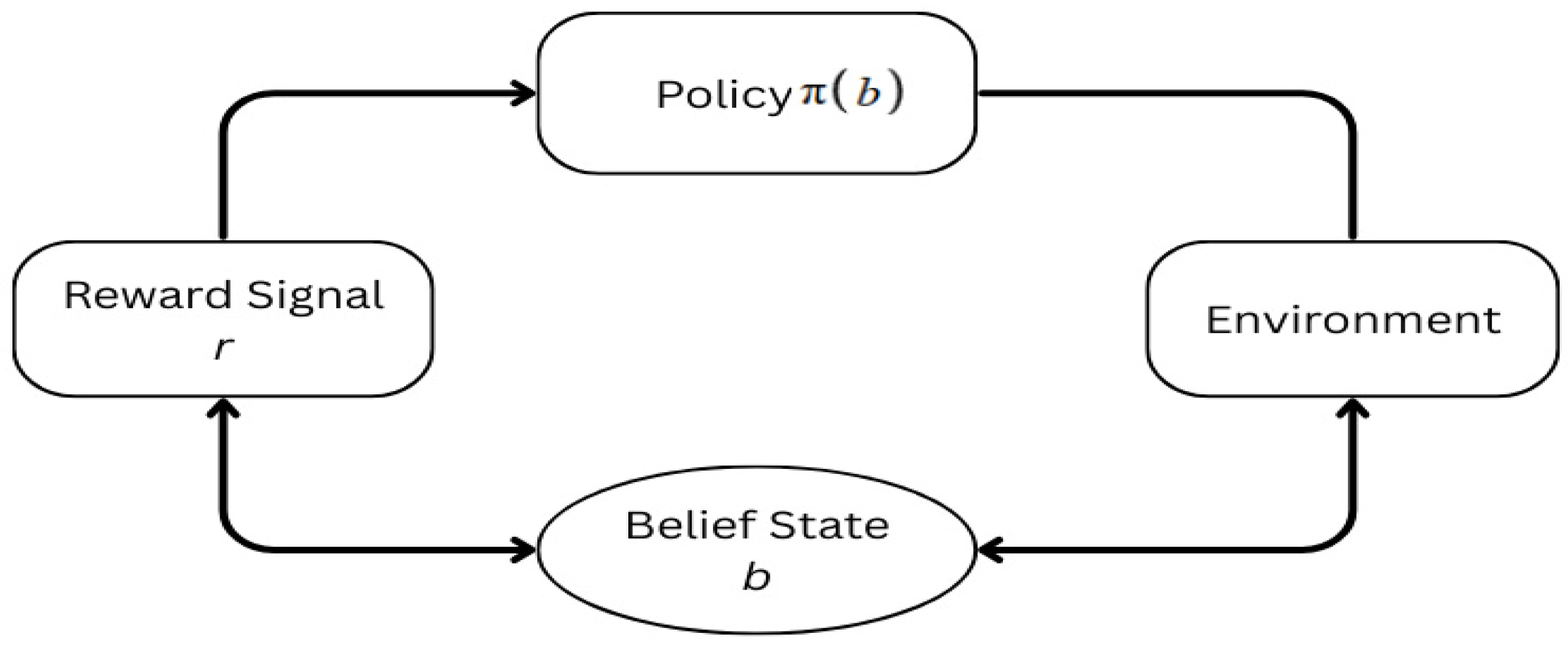
Figure 5 illustrates the training loop of reinforcement learning (RL) in belief space, where the agent learns to make decisions under uncertainty. The core element is the belief state b, a probabilistic representation of the environment’s true state, incorporating both past observations and actions.

A policy π(b) maps this belief state to actions that are executed in the environment. In response to these acts, the environment produces new observations and results, which are then utilized to update the belief state via approximation techniques or Bayesian filtering.

Based on the activity performed and the following change, the agent receives a reward signal r, which informs the policy update. The agent accounts for uncertainty in its perception and model of the world by optimizing its policy π through repeated interactions with the environment. This maximizes expected cumulative rewards.

This framework is ideal for robotics situations where full state observability is impossible, as it allows partially observable decision-making. It also supports integration with deep reinforcement learning (DRL) methods to learn effective policies in high-dimensional or continuous belief spaces.

6.2. Exploration Strategies in Belief Space

Effective belief-space exploration depends on choosing actions that actively reduce uncertainty. Conventional reinforcement-learning tactics such as ε-greedy often fall short under partial observability. Consequently, belief-driven strategies include entropy-based reward shaping to incentivize information-gathering actions, information-theoretic exploration targeting expected entropy reduction [68], and curiosity-driven intrinsic rewards that reinforce novel state transitions. These strategies simplify belief exploration by using lightweight reward shaping or information metrics that avoid full lookahead planning, and are especially suitable fit to SLAM, target tracking, and the exploration of unknown environments.

6.3. Sample Efficiency and Generalization

Deep reinforcement learning (DRL) in belief space often exhibits low sample efficiency, primarily due to the intricate mapping between observations, beliefs, and actions. To address this challenge, recent efforts have focused on transfer learning across related environments [69], model-based DRL with learned transition or observation models, policy distillation to reduce model complexity while preserving performance [70], and emerging hybrid frameworks, which integrate model-free learning with belief aware inference, are showing potential for scalable application in real world robotic systems [71]. Transfer learning, policy distillation, and model-based DRL simplify the training demands and reduce the data requirements for belief-space planners.

6.4. Applications in Planning Under Partial Observability

Deep reinforcement learning within belief space has been successfully applied across a range of robotic scenarios, including autonomous navigation in dynamic environments, sensor scheduling and viewpoint selection, and multi-agent systems with decentralized policies under uncertainty [72,73]. These use cases reflect the advancing capabilities of learning-based planning methods in environments characterized by significant uncertainty.

Table 3. Recent DRL-based planners: architecture, dataset, outcome.

Planner Name	Network Architecture	Input Modality	Training Dataset/Scenario	Success Rate (%)	Inference Latency (ms/Action)	Key Outcomes
Deep Q-Network (DQN)	Feedforward Q-function approximator	Belief vector or feature map	Grid world belief simulations.	62.84 [74]	0.27 [75]	Fast convergence in discrete POMDPs.
Asynchronous Advantage Actor Critic (A3C)	Actor Critic with shared convolutional base	Camera/LiDAR frames + state input	3D navigation in indoor scenes (e.g., Matterport3D).	N/A 1	N/A 1	Good generalization and policy stability.
Soft Actor Critic (SAC)	Stochastic actor critic with entropy regularization	Raw sensory data + uncertainty map	Continuous control with noise (e.g., MuJoCo).	66–70 [76]	2.72 [77]	High reward in noisy environments.
Proximal Policy Optimization (PPO)	Clipped surrogate objective with policy gradient	State + belief embedding	Navigation under partial observability.	70–84 [76]	N/A 1	Robustness to policy update shifts.
Transformer-based RL Planner	Attention mechanism over temporal observations	History of observations/actions	Multi-agent exploration with memory constraints.	99 [77]	7.43 [77]	Long-horizon memory and path optimality.

¹ N/A: Not Available.

highlights recent deep reinforcement learning (DRL)-based planners for decision-making in partially observable belief-space environments. These methods vary in architecture, input modalities, training schemes, and performance.

DQN uses a feedforward Q-function approximator trained on belief vectors or feature maps. In discrete POMDPs, it converges quickly, especially for low-dimensional beliefs. By shifting computation to an offline phase with simulated belief transitions, execution reduces to a single forward pass through the Q-network [78]. This yields ~63% success with ≈0.27 ms latency—ultra-low and ideal for fast control loops [74,75].

Farkh et al. (2025) [79] demonstrated the integration of Deep Q-Networks (DQN) with a quantized Large Language Model (LLM) to enhance embedded robotic navigation. In this framework, the DQN handled low-level obstacle avoidance while the LLM provided high-level reasoning to resolve deadlocks or collisions, ensuring the microcontroller maintained real-time reactive control. Experimental results showed substantial improvements: in static scenes, deadlock recovery rose from 55% to 88%, average goal-reach time decreased from 45 s to 30 s, collisions dropped from 18% to 7%, and successful runs increased from 72% to 91%; in dynamic scenes, the success rate improved from 66% to 87% and time-to-goal was reduced by 34%. These findings highlight DQN’s adaptability when augmented with lightweight high-level guidance.

A3C accelerates learning by running multiple actor–critic threads with independent networks that periodically update a shared global model. It handles raw inputs (camera/LiDAR) and supports multi-robot cooperation through parallel data collection. Advantage estimates stabilize policy updates, enhancing generalization across scenes [80]. Success rates and latency are inconsistently reported; asynchronous updates may cause runtime jitter.

Wang et al. (2024) [80] applied the Asynchronous Advantage Actor–Critic (A3C) algorithm to optimize a YOLOv5-PPO framework for multi-robot logistics operations. In this approach, YOLOv5 provided real-time target detection, while PPO guided decision-making, and A3C was used to train the model in parallel, accelerating convergence and improving robustness. The results showed that A3C enhanced the coordination of multiple robots, enabling them to adapt more effectively to dynamic environments and fluctuating warehouse demands while strengthening both perception and decision-making. This demonstrates A3C’s potential to improve multi-robot collaboration and training efficiency in logistics applications.

SAC uses entropy-regularized actor–critic learning for continuous control. Enhanced variants integrate imitation learning, expert-guided trajectories, prioritized replay, and recurrent units for improved generalization and safety [81]. It achieves ~66–70% success with ≈2.72 ms latency [76,77]. Though slower than DQN, SAC offers greater robustness under noise and observation variance.

Cao et al. (2024) [82] applied a Soft Actor–Critic (SAC) controller for robot path-following using only LiDAR data. The policy was evaluated on 1000 test paths under varying cross-track error thresholds, demonstrating strong robustness: at the strictest threshold of 0.1 m, the SAC controller achieved a high completion rate of approximately 87% with a low failure rate of about 0.155, while at a 0.2 m threshold it recorded zero failures. These results highlight SAC’s capability to maintain cross-track errors within tight bounds and deliver reliable path-following performance in LiDAR-based navigation.

PPO constrains policy updates via a clipped surrogate objective, preventing instability and allowing efficient use of trajectories. Unlike second-order methods, it relies on simple gradient ascent, making it computationally practical [83]. In robotics tasks such as joint malfunction compensation, PPO achieves ~70–84% success [76]. Latency is moderate, generally suitable for real-time use.

Wong et al. (2024) [84] presented a multi-robot warehouse navigation system that applies Proximal Policy Optimization (PPO) for global path selection. In simulations with 10 robots operating around 24 shelves, the framework was tested over 50 trials, achieving a 98% success rate (49 successful runs, with one halted due to congestion). The authors further reported that, across different map sizes and robot counts, the PPO-based system maintained real-time performance ranging from approximately 20.6 to 1538 frames per second and reduced path conflicts by up to 60,375 across 1000 planning tasks. These findings demonstrate PPO’s effectiveness in coordinating large numbers of robots efficiently while minimizing navigation conflicts.

Transformer-based planner applies attention over map patches and observation–action histories, with an LSTM layer preserving temporal context. This enables implicit modeling of inter-robot dependencies for decentralized coordination [85]. It achieves ~99% success with ≈7.43 ms latency—higher than feedforward baselines but justified by superior long-horizon coordination.

Ge et al. (2024) [77] proposed a Decision Transformer–based Reinforcement Learning model (DRLNDT) that integrates a transformer architecture with a SAC for memory-aware navigation. By leveraging an attention mechanism, the planner conditions its actions on sequences of past observations and actions, enabling long-horizon memory and improved path optimization. Evaluated on an autonomous-driving benchmark over 200 test episodes, DRLNDT achieved a success rate of approximately 99% with high cumulative reward. Although the transformer policy incurred a longer inference latency (~7 ms) compared to a standard SAC policy, the authors emphasized that it still satisfies real-time requirements while offering superior decision-making performance.

When taken together, these DRL architectures balance computational efficiency, policy resilience, and representational purity to improve belief-space planning. While traditional optimization techniques would be computationally burdensome in such applications, approximations based on reinforcement learning allow for near real-time operation. They can be used for everything from real-time robotic decision-making in uncertain situations to organized indoor navigation. In specifics, Transformer-based planners drive success rates toward the ceiling while taking on a higher per-step cost; SAC and PPO occupy an intermediate band that sacrifices a slight latency increase for robustness; and DQN anchors the low-latency end of the range. The task’s tolerance for less-than-ideal performance in the face of uncertainty and its latency budget determine which option is best.

7. Applications of Belief-Space Simplifications in SLAM and Multi-Robot Systems

The integration of belief-space planning with probabilistic modeling has enhanced core robotic functions such as Simultaneous Localization and Mapping (SLAM) for multi-robot navigation and distributed coordination. Simplicities—approximations or structured constraints that lessen the computational load of maintaining and updating entire belief distributions while maintaining decision quality—are necessary to provide tractable decision-making in complicated, partially observable domains. These consist of information-driven sensor activation, sliding-window optimization, communication-efficient map exchange, and low-dimensional belief parameterizations. The subsections below illustrate how such simplifications operate in three major application areas.

7.1. Active SLAM and Trajectory Planning

Active SLAM entails planning robot trajectories that simultaneously reduce localization error while refining the map representation. In practice, however, performing exhaustive POMDP optimization over high-dimensional belief spaces is computationally prohibitive, which necessitates the use of approximations. Typical strategies include adopting linear–Gaussian motion and sensing models to permit covariance-based propagation of uncertainty, employing frontier-driven or topological searches in belief space to curtail the action set, and constraining the planning horizon through sliding-window formulations to limit the scope of optimization. Within these reduced spaces, exploration and viewpoint selection are frequently guided by information-theoretic measures such as expected entropy decrease or mutual-information gain [86,87]. Recent studies on active information gathering for UAV-based mapping further indicate that objectives based on covariance reduction under Gaussian assumptions can yield performance comparable to full mutual-information optimization, but at substantially lower computational cost [88]. Belief-space trajectory planning thus enables robots to maximize information acquisition about unknown landmarks, diminish pose uncertainty, and negotiate the trade-off between motion effort and mapping objectives [89,90]. Contemporary SLAM frameworks additionally integrate Gaussian-process regression for spatial inference, dynamic scene graphs for semantic structuring, and appearance-based localization, all of which benefit from these tractable planning abstractions [91,92,93].

7.2. Multi-Robot Coordination Under Uncertainty

Table 4. Multi-agent belief-space planning: coordination vs. computation.

Coordination Strategy	Belief Representation	Communication Requirement	Scalability	Success Rate (%)	Goal Error (RMSE, m)	Inference Latency (ms/Action)	Application Domain
Centralized Joint Policy	Joint belief over all agents.	High (full state sharing)	Low (combinatorial explosion)	90–95% [94]	0.05–0.10 m	~100 [94]	Cooperative exploration and planning in known maps.
Decentralized POMDP (Dec-POMDP)	Local beliefs + shared observation model.	Medium (limited broadcast)	Moderate (with pruning)	96.43/89.77 [94]	0.03–0.06 [94]	30–60	Rescue and surveillance missions.
Belief Consensus	Local beliefs with iterative fusion.	Medium to Low (iterative updates)	High (distributed)	90–95% [94]	0.035–0.061 [94]	10–20 [94]	Distributed SLAM and formation control.
Event Triggered Communication	Threshold-based message triggers.	Minimal (asynchronous)	Very High	~100	N/A	1000–2000 [95]	Latency-sensitive swarm navigation.

provides a comparative overview of coordination strategies in multi-agent belief-space planning, highlighting trade-offs between belief representation, communication needs, scalability, performance, and their application domains.

Centralized Joint Policy assumes a single joint belief shared across all agents. It enables strong coordination with a success rate of 90–95%, but suffers from low scalability due to combinatorial explosion and requires high communication overhead. Goal error typically falls within 0.05–0.10 m, with inference latencies around ~100 ms/action [94]. It operates on a single shared belief, enabling optimal coordination in small teams; however, it imposes excessive computational and communication burdens. It is best suited for small teams in known environments.

Adil et al. (2025) [96] presented a centralized multi-robot framework for collaborative manipulation in warehouse environments. The system adopts a leader–follower architecture in which a designated leader robot plans tasks and coordinates subordinate agents. Core functions such as object detection using YOLOv2 and global path planning are handled centrally, with the leader dynamically forming robot teams and employing sampling-based algorithms together with LiDAR sensing for collision avoidance. This centralized structure effectively implements a joint policy across all robots, enabling real-time coordination of complex object-handling tasks.

Decentralized POMDP (Dec-POMDP) offers a more scalable alternative by maintaining local beliefs with a shared observation model. It requires medium-level broadcast communication and achieves success rates of 96.43%/89.77% depending on pruning, with goal errors in the range of 0.03–0.06 m. Inference latency is 30–60 ms/action [94], making it suitable for time-sensitive rescue and surveillance missions where full state sharing is impractical.

Muhammed et al. (2024) [97] reviewed the decentralized Model-Predictive-Control (MPC) framework for cooperative transport tasks, framing it within the decentralized partially observable Markov decision process (Dec-POMDP) paradigm. In this method, each robot independently solves its own MPC problem while sharing only limited information to support a common objective. Through a shared observation paradigm, this structure allows robots to maintain coordination while acting according to local beliefs. The efficacy of decentralized decision-making for collaborative transport was shown by the simulation results, which showed excellent performance and resilience under communication restrictions.

Belief Consensus repeatedly combines local beliefs (often Gaussian) across agents, achieving high scalability and reduced bandwidth without full state exchange [98], and offers high scalability in distributed tasks like SLAM or formation control. It achieves a success rate of 90–95%, with goal errors between 0.035 and 0.061 m and lower inference latencies of 10–20 ms/action [94]. This makes it well-suited for distributed SLAM and formation control, balancing accuracy, communication cost, and responsiveness.

Xia et al. (2024) [94] introduced a collaborative SLAM algorithm in Sensors that integrates point and line features for multi-robot mapping. Each robot first constructs a local map, and the maps are then fused through relative-pose estimation to achieve consensus over the team’s collective belief. Experimental results showed low trajectory errors, with RMSE values in the range of approximately 0.035–0.061 m across multiple datasets. These findings demonstrate that distributed belief consensus can generate accurate global maps without relying on a central coordinator.

Event-triggered communication is highly scalable (very high) and uses minimal asynchronous messaging based on thresholds or events. It transmits updates only when the uncertainty exceeds specified thresholds, minimizing bandwidth and latency impacts while maintaining coordinated action [99]. While goal error values are not typically reported (N/A), this approach incurs higher inference latencies of 1000–2000 ms/action [94], yet offers very high scalability. It is particularly effective in latency-sensitive swarm navigation where bandwidth is constrained and agents must act autonomously. It is ideal for latency-sensitive swarm applications where bandwidth is constrained and agents must act autonomously.

Jiang et al. (2024) [95] suggested a distributed dynamic event-triggered optimization algorithm in PLOS ONE for multi-agent coordination under time-delay conditions. To cut down on pointless communication, agents in this framework only send updates when a predetermined threshold is crossed. Event-triggered update intervals of h = 1 h = 1 s and h = 2 h = 2 s (1000–2000 ms) were used to evaluate the method, showing that consensus may be reached effectively while reducing computing cost and communication overhead. This demonstrates how successful event-triggered tactics are for scaled multi-agent systems.

Coordinating multiple robots in uncertain environments necessitates decentralized reasoning, efficient belief exchange, and reliable data association. Each robot must maintain and update its own belief representation while limiting communication demands. Key approaches include graph-based SLAM with pose graph merging [100], distributed particle filters and covariance intersection for joint belief fusion, and task or role allocation strategies are driven by belief entropy or uncertainty in task outcomes [101].

Recent advances in distributed SLAM show that coupling sliding-window optimization with compressed 2.5-D map exchange can reduce communication overheads by more than 90% while maintaining mapping fidelity [99]. Such approximations have proven highly effective across domains ranging from disaster-response operations to warehouse automation, and are particularly indispensable in settings such as underwater robotics, where conventional localization aids are absent [102,103]. Dynamic role assignment is often guided by measures such as belief divergence or confidence thresholds.

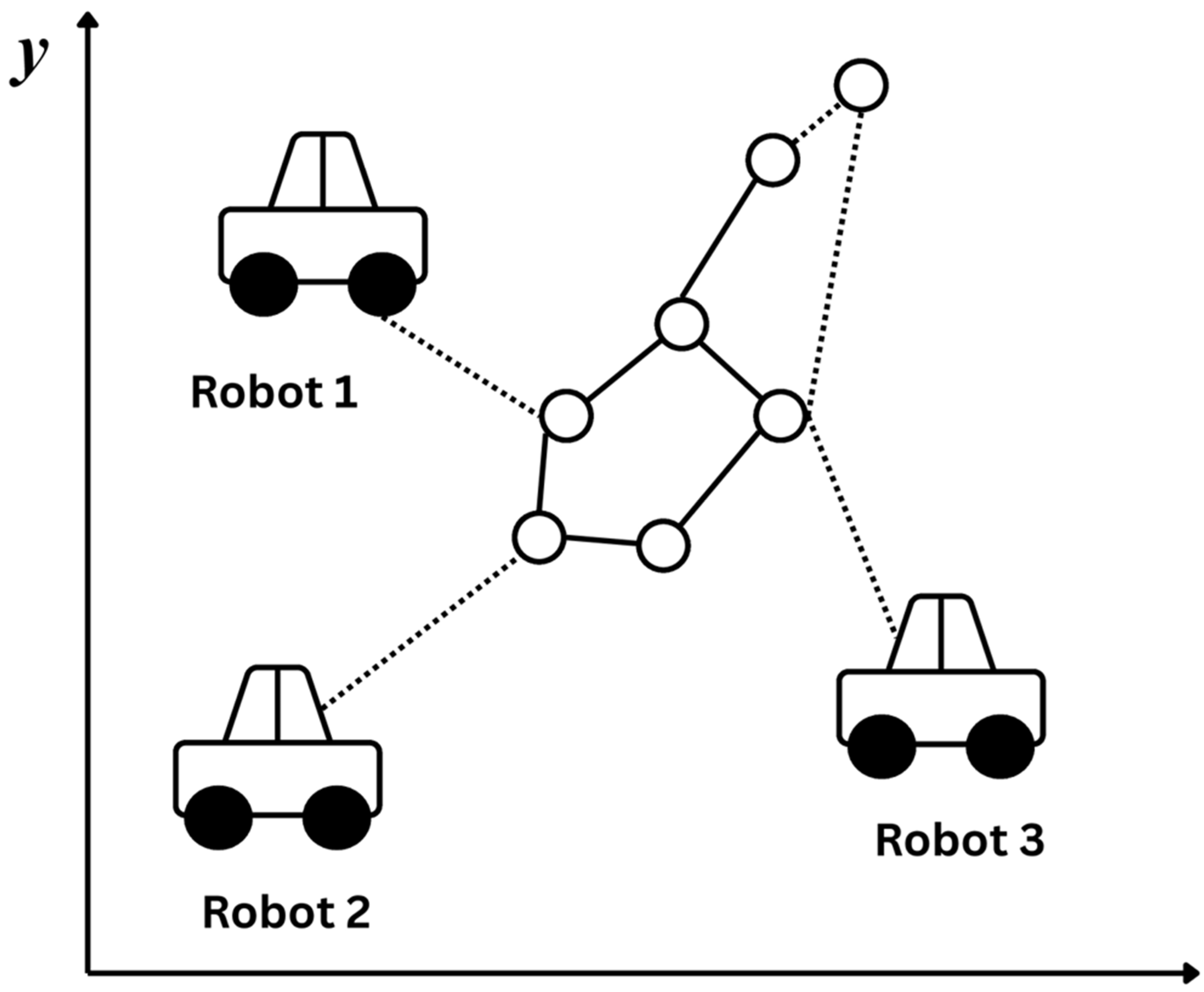
Figure 6 illustrates a multi-robot SLAM scenario where multiple autonomous robots (Robot 1, Robot 2, and Robot 3) collaboratively build and update a shared factor graph representing the environment.

The nodes (circles) in the graph represent poses (robot positions) or landmarks.

The edges (lines) represent spatial constraints or relative observations (e.g., odometry, LiDAR scans).

The dotted lines from robots to the graph show how each robot contributes local measurements to the shared global map.

This shared factor graph allows distributed SLAM backends to merge observations from different agents, improving map consistency and reducing uncertainty. It is especially powerful in large-scale or dynamic environments where single-robot mapping is insufficient. This approach is mostly used in decentralized graph-based SLAM systems to enable efficient, consistent, and scalable coordination.

7.3. Information-Theoretic Planning and Sensor Scheduling

In belief-space planning, sensor scheduling aims to activate sensing modalities selectively, ensuring that their anticipated contribution to uncertainty reduction outweighs the associated resource expenditure [104]. Exhaustive evaluation of information gain across all possible sensing actions is computationally prohibitive; hence, tractable approximations are commonly employed. These include imposing Gaussian assumptions on belief distributions to enable closed-form evaluation of entropy or mutual information, as well as adopting heuristic criteria such as minimisation of the covariance trace [88]. Within multi-robot systems, scheduling is often decentralized, with sensing responsibilities allocated across agents to avoid redundancy, while compressed communication protocols restrict data exchange to only the most informative measurements [99]. These approaches are essential for adaptive sensing in dynamic environments, bandwidth-constrained multi-agent systems, and power-constrained systems (such as planetary rovers and UAVs). Belief-aware planners further divide sensing tasks across agents in multi-robot environments, reducing redundancy and improving spatial coverage [105,106].

8. Comparative Analysis

There are significant variations in the computational architecture, scalability, and application of several belief-space planning techniques analyzed in this paper across different robotic domains. A comparative analysis of these methods is provided in this part, emphasizing their relative advantages and disadvantages with respect to important performance standards.

8.1. Trade-Offs in Simplification Strategies

Various simplification methods, including policy approximation, belief compression, sampling-based planning, and Point-Based Value Iteration (PBVI), each have their own trade-offs [107]. Although they operate almost optimally in the sampled areas of the belief space, PBVI techniques have scalability issues in highly continuous situations. Belief compression alleviates computational demands in high-dimensional settings; however, its effectiveness is closely tied to the quality of the underlying embedding [108].

Sampling-based methods like POMCP enhance scalability by avoiding explicit belief tracking; however, they often demand extensive simulation resources and can be adversely affected by sparse reward structures [101]. Reinforcement learning–based approximate policies enable rapid execution but may exhibit limited interpretability and generalization capabilities [109].

8.2. Evaluation Criteria

Essential evaluation criteria for belief-space methodologies include computational efficiency, which encompasses both time complexity and memory usage, scalability which is the capacity to manage extensive state and observation spaces, policy robustness for performance exhibited under observation noise and changes in the environment, and ease of integration which shows how well the approach aligns with existing SLAM or estimation frameworks.

Table 1 (referenced in an earlier section) outlines these aspects and offers practical guidance for selecting suitable simplification strategies tailored to specific application requirements.

8.3. Practical Applications and System Integration

In real-world scenarios, the selection of a belief-space planning approach is typically guided by specific system constraints. For instance, underwater robots employing Underwater Visual–Inertial–Pressure SLAM (U-VIP-SLAM) require resilient localization in turbid environments [110], mobile robots operating in smart factory settings benefit from low complexity strategies that enable real time execution [111], benchmark datasets, such as AQUALOC for underwater SLAM by Ferrera M. et al. (2019) [112], facilitate systematic assessment of planning frameworks, and autonomous ground vehicles often rely on hierarchical or hybrid planning schemes to manage task complexity [113].

Hybrid approaches that dynamically alternate between sampling-based, learned, or compressed belief representations are increasingly favored for their ability to maintain performance while adapting to varying operational demands [114].

In addition to algorithmic innovations, the real-world implementation of robotic systems often necessitates integration with sensor-driven hardware platforms. For example, pneumatic control mechanisms driven via LabView and Computer-Aided Engineering (CAE) frameworks have been used to evaluate mechanical structures in an automated fashion [115]. Such systems provide valuable insights for designing closed-loop control and sensing frameworks in mobile robots operating under uncertainty [116].

Table 5. Comparison of POMDP simplification techniques.

Technique	Core Idea	Scalability	Computational Efficiency (Runtime/Scaling, ms)	Accuracy of Policy (RMSE (m)/Success Rate)	Suitable For
Point-Based Value Iteration (PBVI, SARSOP)	Focus value updates on sampled belief points.	Moderate (limited by belief point selection)	45–120 ms [117,118]	92–96% success rate; RMSE ≈ 0.12–0.18 m [118]	Medium-scale planning problems.
Belief Compression	Project high-dimensional beliefs to lower dimensions.	High (good for high-dimensional spaces)	20–60 ms [119,120]	RMSE ≈ 0.20–0.35 m; accuracy depends on retained dimensions [119]	Large-scale belief estimation.
Sampling-Based Planners (POMCP, DESPOT)	Use Monte Carlo sampling for belief simulation.	Very High (suitable for large domains)	10–25 ms [117]	85–93% success rate; RMSE ≈ 0.25–0.40 m [117]	Online planning in large or continuous spaces.
Approximate Policy Representations	Represent policies directly using rollouts or controllers.	High (compact representation)	5–15 ms/action (well-trained controllers) [121]	80–88% success rate; RMSE ≈ 0.30–0.50 m [121,122]	Fast decisions in constrained settings.

compares four popular simplification strategies used in solving Partially Observable Markov Decision Processes (POMDPs). These techniques make the intractable belief space more manageable by approximating the solution, enabling real-time or scalable decision-making.

PBVI and SARSOP techniques operate by focusing updates on a subset of belief points, significantly reducing the computational burden associated with full belief-space planning. These methods exhibit high computational efficiency, particularly through offline pre-computation, and achieve near-optimal performance in regions around the sampled beliefs. However, scalability is constrained by the quality of point selection, rendering them more suitable for medium-scale planning tasks.

Hahsler & Cassandra (2025) [118] illustrated the use of Point-Based Value Iteration (PBVI) on the classic Tiger POMDP as part of the POMDP package examples. Using a finite-grid PBVI approach, the algorithm generated five α-vectors and achieved an expected discounted reward of approximately 1.9334, close to the optimal value. This case demonstrates how PBVI can yield compact policies with strong performance in small-scale POMDP settings.

Belief Compression techniques project high-dimensional beliefs into lower-dimensional subspaces, allowing efficient representation and processing. These methods maintain high computational efficiency and are particularly scalable to large belief spaces, provided that essential information is retained during the compression process. They are commonly used in large-scale belief estimation problems in robotics.

Bhamidipaty et al. (2025) [119] introduced a Julia package designed to tackle large-scale POMDPs through belief compression. The framework provides modular tools for sampling, compressing beliefs using methods such as PCA, kernel PCA, or autoencoders, and then planning in the reduced space. While primarily a software contribution, the work underscores how compressing high-dimensional belief representations into a smaller set of principal components can make complex POMDP planning computationally tractable, thereby broadening the applicability of belief-based decision-making methods.

Sampling-Based Planners, including POMCP and DESPOT, leverage Monte Carlo simulations to estimate belief transitions and action values. These planners are highly scalable, especially in continuous or high-dimensional domains, and can be applied in online settings. The amount and depth of samples used throughout the rollout process affect their accuracy, but computational efficiency varies from moderate to high.

de Saporta et al. (2024) [117] demonstrated how sampling-based planners, particularly the POMCP method, can be adapted to continuous-time decision processes. Their study highlighted the balance between computational demand and solution quality, as increasing the number of simulations from 100 to 1000 improved outcomes but also raised runtime from roughly 10³ to 10⁴ seconds per trajectory. The particle-filter extension of POMCP was initially about three times slower, though this gap narrowed to 1.2 times slower at higher simulation counts, emphasizing the influence of state-estimation choices on performance. Among the strategies tested, the conditional variant of POMCP consistently provided the lowest trajectory costs, outperforming dynamic programming and threshold-based rules. These findings demonstrate the ability of sampling-based online planning to handle complex, partially observable domains with continuous dynamics.

In order to enable quick execution in real-time circumstances, approximate policy representations use concise encodings of policies, frequently via neural networks or controllers. Although these approaches are very effective and scalable, unless properly adjusted, the accuracy of the final policy may be lower than more computationally demanding methods and is dependent on the quality of training. They work effectively for robotic systems with constraints that need quick inference.

Recent applications illustrate the value of approximate policy representations in POMDPs. Villani et al. (2024) [122] developed a UAV controller for disaster-response mapping that prioritizes high-risk areas and employs a simplified policy to autonomously locate victims. In testing, this approach reduced mission risk by 66% during the first half of the mission while maintaining effective victim identification.

Overall, the table emphasizes the need to choose simplification strategies according to job requirements and computing constraints, as well as the trade-offs between accuracy and real-time feasibility in belief-space planning.

9. Open Challenges and Future Directions

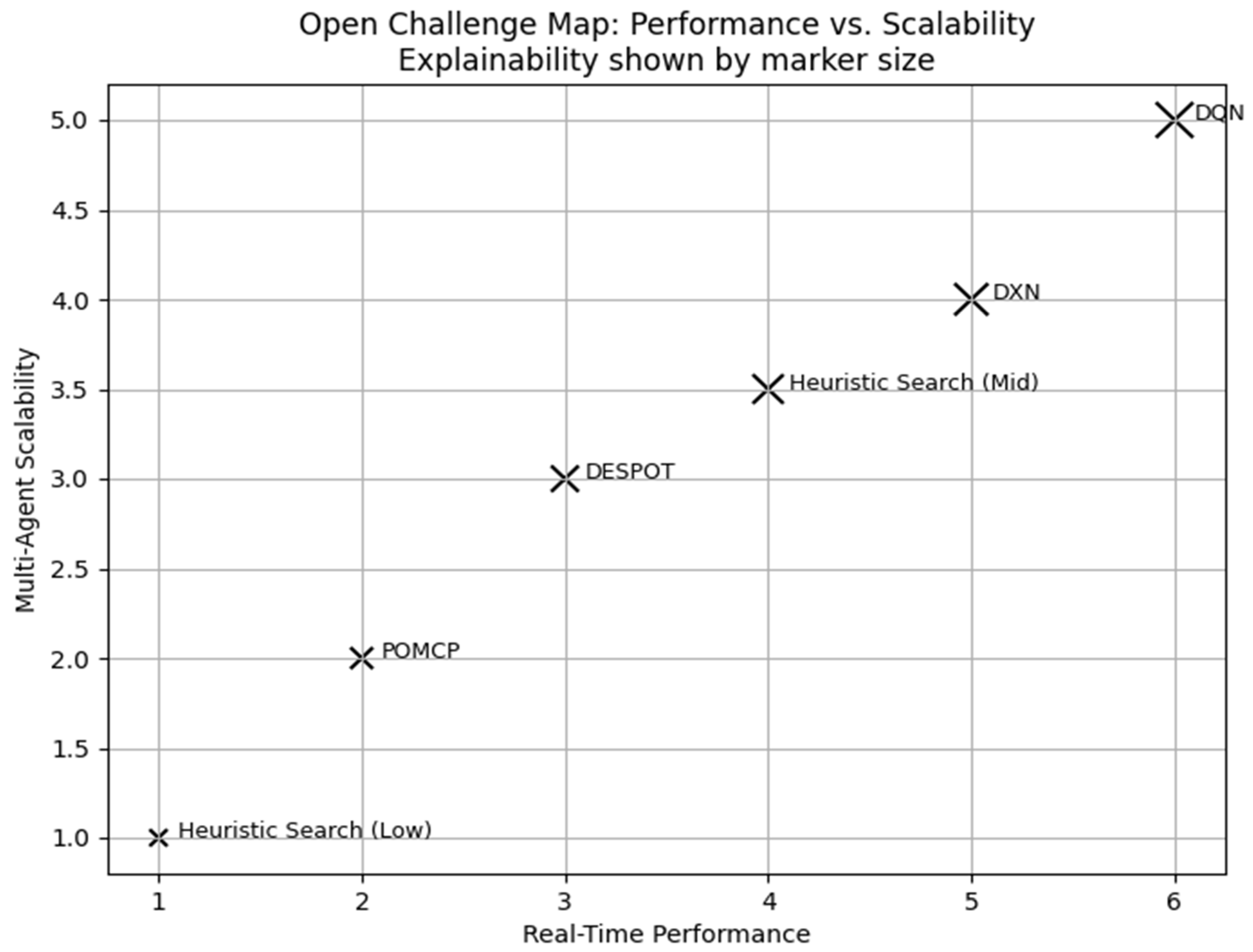
Figure 7 illustrates an open challenge map evaluating recent planning approaches across three pivotal dimensions: real-time performance (x-axis), multi-agent scalability (y-axis), and explainability (encoded by marker size). This tri-axis representation enables a holistic assessment of each planner’s suitability for decentralized decision-making under uncertainty.

The Deep Q-Network (DQN) is a top approach with great explainability, high responsiveness, and good scalability across agents because of its structured Q-function representation. DXN, a deep reactive version, likewise achieves competitive performance, albeit with somewhat less interpretability. DESPOT and POMCP, which employ sampling-based tree search approaches, fall somewhere in the middle of performance and scalability, but their reliance on stochastic simulations reduces transparency. Heuristic search methods are inherently explicable, although they are not very effective at real-time adaptation or multi-agent coordination. On both axes, they are shown from low to moderate values.

This visual benchmarking highlights how many classical techniques sacrifice responsiveness and distributed coordination in favor of simplicity and interpretability, even when high-performing planners like DQN provide promising capabilities for scalable, explainable, and quick decision-making. The figure highlights the need for hybrid approaches that strike a compromise between policy transparency, multi-agent scalability, and computational tractability.

Despite advancements in scalable planning under uncertainty, significant challenges remain that impede the broad adoption of belief-space methods in practical robotic applications. These challenges encompass computational limitations, generalization difficulties, robustness concerns, and coordination complexities, especially within the constraints of real-time operation.

9.1. Real-Time Planning in Large-Scale Environments

While various simplification strategies have made planning feasible in moderately complex settings, extending these methods to urban, cluttered, or dynamic environments remains a significant challenge. In such contexts, planners must efficiently process high-frequency sensor data, propagate beliefs in real-time, and update plans promptly without sacrificing safety or optimality [123,124].

Recent developments in hardware acceleration—such as GPU (Graphics Process Unit)-optimized factor graph solvers and edge-based inference tailored for mobile platforms—present promising avenues for enabling high performance, online planning in real-world robotic systems [125].

9.2. Generalization and Learning from Sparse Data

Developing policies or representations that generalize across diverse environments and tasks remains a central objective in the field. Approaches such as transfer learning, meta-learning, and curriculum learning are being explored to reduce data requirements and improve sample efficiency [126,127].

Belief-space learning algorithms must address uncertainty not only in the state estimation but also in the underlying models, necessitating robust policy learning methods and continual model refinement [128]. Moreover, real-world deployments frequently experience performance degradation in visually ambiguous or texture less environments, presenting persistent difficulties for visual localization systems [129].

9.3. Non-Stationary and Adversarial Settings

Robotic platforms operating in open-world settings encounter changing dynamics, sensor drift, and potential adversarial inferences. Consequently, belief-space planners must identify these changes and adjust their decision policies or underlying models in response. Current research increasingly focuses on online Bayesian filtering, adaptive control strategies, and risk-sensitive POMDP formulations to address these challenges [130,131].

The integration of robust state estimation with fault detection and self-diagnostic capabilities can enhance system resilience in mission-critical domains, including space exploration, surveillance, and healthcare robotics [132].

9.4. Multi-Agent Systems and Communication Constraints

Extending belief-space planning to multi-robot systems introduces additional coordination challenges, particularly under communication constraints. Methods such as communication-aware decentralized POMDPs, distributed factor graphs, and belief consensus aim to balance computation and coordination [133,134]. Future directions include role-based coordination using belief uncertainty metrics, event-triggered communication policies for scalable deployment, and cross-agent policy distillation for collective learning.

9.5. Explainability and Human-Aware Planning

As robotic systems increasingly engage with humans, the need for explainability and transparency becomes critical. Policies derived from deep learning often function as black boxes, making them difficult to interpret. Future approaches should integrate interpretable planning with belief-based reasoning to foster trust, facilitate diagnostics, and ensure adherence to human-imposed constraints [135,136].

Progress in semantic mapping, intent inference, and place recognition technologies [137] will further enhance seamless human–robot interaction and navigation within shared spaces. Building on these unresolved issues, the discussion that follows places probabilistic models, reinforcement learning, and POMDPs in a broader research context and identifies future paths toward robust and scalable robotic decision-making.

9.6. Synthesis and Outlook

Partially Observable Markov Decision Processes (POMDPs) continue to demonstrate strong real-world applicability across robotic domains such as active SLAM, adaptive exploration, and multi-agent planning [138,139]. Active simultaneous localization and mapping (A-SLAM) entails the dual task of estimating a robot’s pose and constructing a representation of its surroundings, while simultaneously selecting actions that minimize uncertainty in both domains. In this setting, the robot must operate within a partially observable environment and make prospective action choices despite the presence of noisy sensor inputs. Ahmed et al. (2023) [139] underscore that this problem can be rigorously expressed within the framework of a Partially Observable Markov Decision Process (POMDP). The POMDP formalism encapsulates the state space, action set, observation model, and the associated stochastic uncertainties, thereby allowing the derivation of policies that optimize expected information gain. Such policies guide motion planning in a manner that systematically reduces ambiguity in both mapping and localization.

Adaptive Informative Path Planning (AIPP) arises when a robot is required to collect information while operating under constraints such as limited energy or sensing capacity. A multimodal sensing variation, called AIPPMS, is studied by Choudhury et al. (2020) [140], where the agent has to choose which sensing modality to use and what movement to make next. The fact that the agent operates in “unknown, partially observable environments” and needs to collaborate on reasoning regarding motion and sensing is reflected in the authors’ formulation of AIPPMS inside the context of a Partially Observable Markov Decision Process (POMDP. To address this formulation, they employ an online planning strategy grounded in partially observable Monte Carlo tree search. This approach illustrates how POMDP modeling enables adaptive exploration by explicitly capturing observation uncertainty while balancing the trade-off between information acquisition and resource expenditure.

In multi-robot settings where agents collaborate to perceive or explore, each robot relies on its own local observations, often without direct inter-agent communication. According to Lauri et al. (2019, 2020) [141,142], Decentralized Partially Observable Markov Decision Processes (Dec-POMDPs), which expand the traditional POMDP framework to include several decision-makers, are a good fit for these kinds of situations. In this approach, the system as a whole evolves stochastically, but each agent chooses actions based on its unique belief state. Therefore, the Dec-POMDP approach provides a rigorous framework for creating collaborative methods that allow agents to reduce uncertainty collectively.

Collectively, these studies attest that POMDP and Dec-POMDP formulations serve as operational frameworks in robotics rather than remaining abstract constructs. In active SLAM, they furnish a principled means of addressing navigation and mapping under uncertainty; in adaptive exploration, they enable the design of information-seeking trajectories subject to sensing and resource limitations; and in multi-robot systems, they provide the formal apparatus for coordinating distributed decision-making under partial observability.

Notably, the integration of reinforcement learning methods, particularly Deep Q-Networks, has been instrumental in improving scalability and adaptability in high-uncertainty settings [143]. Deep reinforcement learning (DRL) has increasingly been employed to address the pronounced uncertainty inherent in robotic navigation and decision-making tasks. By leveraging deep neural networks, DRL is capable of transforming raw sensory inputs into adaptive decision strategies that respond to environmental variation more rapidly than conventional planning approaches. Both value-based and policy-based methods have demonstrated the capacity to support real-time planning in large, dynamic environments, thereby improving the efficiency and precision of path generation. In domains where safety is paramount, hybrid DRL controllers such as Deep Q-Networks (DQN) and Proximal Policy Optimization (PPO) have been coupled with domain-specific knowledge to enhance decision quality. For example, the work of Uddin et al. (2025) [144] on healthcare billing showed that Reinforcement-Learning agents using DQN or PPO, in combination with knowledge-graph embeddings, achieved higher cumulative rewards and lower prediction errors compared to classical regression models or standalone reinforcement-learning methods.

Despite notable progress, several fundamental limitations remain unresolved. DRL systems are most often developed and validated in controlled or simplified settings, which hampers their capacity to generalize to the complexities of real-world deployment, where robots must contend with dynamic obstacles, heterogeneous sensory inputs, and unpredictable disturbances. Consequently, robustness under unstructured environmental conditions is frequently inadequate. Critical aspects such as sim-to-real transfer and the integration of multimodal sensor data remain under-investigated. Furthermore, the high computational burden and training demands of DRL present obstacles to its scalability in practice. Beyond questions of efficiency, the interpretability of learned control policies continues to pose a pressing challenge. The inherently opaque nature of neural policies undermines trust, particularly in domains where safety is non-negotiable. In such contexts, transparent and explainable decision-making frameworks are essential to ensure reliability and human acceptance. This requirement becomes even more urgent as autonomous systems increasingly operate in close proximity to people. Collectively, these concerns emphasize the importance of developing algorithms that not only scale in real-time but also demonstrate resilience to noise and partial observability, while achieving stronger generalization across diverse operational domains [133,145].

Future efforts should aim to design hybrid planning frameworks that combine data-driven learning with structured inference. In response to the persistent challenges of exploration and generalization, recent scholarship has turned toward hybrid architectures that couple conventional planning techniques with experience-driven learning. Skarka and Ashfaq (2024) [146], for example, advance a hybrid navigation framework for unmanned aerial vehicles that integrates rule-based planning with reinforcement-driven adaptation, enabling reliable operation in dynamic settings. Their hardware-in-the-loop evaluations indicate markedly superior obstacle avoidance relative to systems relying solely on either learning-based or rule-based paradigms. Similarly, Kaur and Sobti (2024) [147] present a hybrid motion-planning strategy for autonomous vehicles that fuses imitation learning with reinforcement learning in a unified pipeline. Tests conducted in urban traffic contexts reveal that this approach yields smoother and safer trajectories compared to conventional reinforcement-learning methods.

In addition to hybrid frameworks, expanding belief-space planning to address social interaction, ethical decision-making, and explainability will be essential for trustworthy deployment in complex human environments [148,149]. When robots are deployed in environments shared with humans, motion planning must account not only for geometric and dynamic constraints but also for social norms, ethical considerations, and interpretability. Singamaneni et al. (2024) [150], for example, provide a taxonomy of socially aware navigation strategies, situating robot behavior within frameworks that explicitly incorporate human intent estimation and trajectory forecasting into structured decision-making processes. In a complementary line of work, Goel et al. (2024) [151] propose a neuro-symbolic cognitive architecture designed to address novelty in open and dynamic settings, integrating learned representations with symbolic abstractions to support resilient reasoning under evolving patterns of human interaction. Collectively, these studies underscore the importance of embedding symbolic reasoning and explicit intent inference into navigational frameworks to enhance safety, transparency of decision-making, and adaptability to changing social contexts.

These limitations suggest that perception-driven learning, though powerful, remains insufficient on its own. To address unresolved challenges of uncertainty and dynamic environments, recent work has turned toward probabilistic graph models and belief-space planning as principled alternatives.

9.7. Integration of Belief-Space Planning and Probabilistic Graph Models for Uncertain Environments

Perception models play a decisive role in robotic navigation and decision-making, particularly in unmapped or unstructured environments. However, existing perception-driven approaches often falter under distributional shifts and dynamic conditions. High-precision maps and sensors are seldom available in practice, while Simultaneous Localization and Mapping (SLAM) is computationally demanding and sensitive to sensor inaccuracies [152]. Visual navigation techniques, despite their promise, exhibit weak generalizability and tend to degrade under changes in lighting, weather, surface textures, or object appearances. Policies trained in simulation often fail to transfer effectively to the real world, where distributional mismatches and sensor noise lead to localization errors, task failure, or convergence to local minima [152].

Dynamic environments exacerbate these challenges. Algorithms that perform adequately in static simulations deteriorate when confronted with moving obstacles or human activity, rendering the construction and maintenance of accurate maps increasingly difficult. Recent strategies address these issues by embedding raw, noisy sensor data directly into the decision-making process, often through distributionally robust optimization. Approaches such as Distributionally Robust Control Barrier Functions (DR-CBFs) illustrate how safety constraints derived from uncertain sensory inputs can guarantee collision avoidance while preserving computational efficiency.

Belief-space planning provides a sophisticated means of reasoning under such uncertainty by treating the robot’s cognition as a probability distribution. This viewpoint is essential in multi-robot environments since every agent keeps its own belief state. Conventional multi-robot belief-space planners frequently make the impractical assumption that agents’ beliefs are uniform due to communication limitations. Decentralized approaches enable robots to reason over their local beliefs while selectively starting communication when coordination is crucial, as shown in a recent IROS 2024 work on cooperative belief-space planning [90]. Experimental findings show that this yields safer and more reliable joint actions compared to conventional approaches, which may otherwise result in unsafe or suboptimal decisions when beliefs diverge.

Simultaneously, probabilistic graph models have developed into effective instruments for illustrating workable navigation plans in the face of uncertainty. Despite being fundamental to robotic motion planning, probabilistic roadmaps (PRMs) do not work well in cluttered or dynamic situations [153]. Recent studies have addressed these issues by introducing hybrid algorithms, adaptive sampling, and bidirectional searches to increase efficiency in confined regions. By creating graphs with edges marked with traversal probabilities and unpredictable journey times, MIT researchers (2024) expanded on this paradigm by presenting a variation in the Canadian Traveler’s Problem (CTP) [154]. The technique enables planners to find shortcuts and strike a compromise between safety and computational efficiency by integrating incomplete information, such as satellite data divided into probabilistic traversal zones. Empirical evidence indicates that these probabilistic graphs outperform baseline approaches that disregard environmental uncertainty, particularly in applications such as search-and-rescue [154].

Together, these lines of work demonstrate how probabilistic reasoning enhances both individual navigation and multi-robot coordination. Belief-space frameworks allow robots to hedge against uncertainty, while probabilistic graphs provide scalable abstractions for path planning. Their convergence offers a promising foundation for resilient decision-making in unstructured and dynamic environments. Although these models provide a structured framework for reasoning under uncertainty, their continued evolution is essential. The following section outlines potential avenues for advancing this line of inquiry.

10. Insights

Building on these insights, we propose that belief-space planning and probabilistic graph models be integrated to support robots operating in highly uncertain environments, including disaster response and search-and-rescue missions.

Belief-space representation simplifies decision-making under uncertainty by maintaining a distribution over possible states rather than committing to a single estimate. This formulation naturally accommodates noisy sensors and heterogeneous information across multiple robots.

Probabilistic graph models complement this by offering a scalable means of representing feasible navigation strategies. By sampling collision-free motions and annotating edges with traversal probabilities and costs, robots can identify high-utility paths without exhaustive exploration. Hybrid PRM-based strategies further allow adaptation to dynamic constraints and challenging configurations.

The synergy between these paradigms fosters robust multi-robot coordination. Each robot can plan in its local belief space while leveraging a shared probabilistic graph to reason about feasible routes. When beliefs diverge, decentralized algorithms ensure consistent joint actions or trigger communication, while the graph reduces the computational burden relative to solving full POMDP formulations.

This integration directly addresses the shortcomings of perception-driven navigation. By encoding uncertainty explicitly, the planning process becomes less dependent on brittle perception modules. Belief-space reasoning mitigates sensor noise and unforeseen disturbances, while probabilistic graphs reduce reliance on static, high-precision maps. In dynamic rescue settings, robots can continuously update beliefs and graph edges from new sensory input, achieving a level of adaptability that surpasses traditional map-based or end-to-end neural policies.

In summary, the convergence of belief-space planning with probabilistic graph models represents a compelling research trajectory. This integration promises scalable, safe, and resilient autonomy, equipping robots to operate effectively in real-world domains characterized by uncertainty, limited communication, and evolving environmental dynamics.

11. Conclusions

Belief-space planning has long provided a principled framework for addressing uncertainty in robotic perception, localization, and decision-making. Maintaining probability distributions over states enables policies to simultaneously pursue task objectives and reduce ambiguity through active sensing. Building on this foundation, recent advances have extended POMDP and Dec-POMDP formulations to large-scale and multi-agent settings, demonstrating their relevance for active SLAM, adaptive exploration, and cooperative navigation. Simplification strategies such as point-based value iteration, belief compression, and sampling-based approximations have further improved tractability, while reinforcement learning—particularly deep Q-networks and policy-gradient methods—has enabled scalable policy learning directly from high-dimensional sensory inputs.

However, there are persisting restrictions. Deep reinforcement learning strategies frequently lack interpretability, sim-to-real transfer brings brittleness, and perception-driven navigation difficulties with distributional adjustments. These drawbacks highlight how learning-driven techniques must be supplemented by organized probabilistic reasoning. Recent work in belief-space planning with decentralized coordination, distributionally robust control formulations, and probabilistic graph models such as enhanced PRMs and Canadian Traveler Problem roadmaps illustrates promising avenues for explicitly encoding uncertainty into navigation and coordination. When combined, these methods show that probabilistic inference is still essential for building resilience in dynamic, partially observable settings.

Looking ahead, three intertwined research trajectories appear central. First, hybrid architectures that integrate deep reinforcement learning with rule-based and probabilistic inference can mitigate the weaknesses of either paradigm in isolation while improving scalability. Second, neuro-symbolic and explainable frameworks are needed to render decision processes transparent and trustworthy, particularly in safety-critical or human-shared spaces. Third, socially aware and ethically grounded navigation strategies must be prioritized to ensure robots operate in alignment with human intent, cultural norms, and broader societal values.

By consolidating technical advances across POMDP simplifications, deep reinforcement learning, and probabilistic graph models, this review emphasizes the convergence of learning and inference as the pathway to next-generation autonomy. Robots capable of navigating uncertainty with robustness, interpretability, and social sensitivity will mark the transition from theoretical models to resilient, human-centered systems embedded in real-world environments.