Non-Orthogonal Serret–Frenet Parametrization Applied to Path Following of B-Spline Curves by a Mobile Manipulator

Abstract

A tool for path following for a mobile manipulator is herein presented. The control algorithm is obtained by projecting a local frame associated with the robot onto the desired path, thus obtaining a non-orthogonal moving frame. The Serret–Frenet frame moving along the curve is considered as a reference. A curve resulting from the control points of a B-spline in 2D or 3D is investigated as the desired path. It is used to show how the geometric continuity of the path has an impact on the performance of the robot in terms of undesired force spikes. This can be understood by looking at the curvature and, in 3D, at the torsion of the path. These unwanted effects vanish and better performance is achieved thanks to the change of the B-spline order. The theoretical results are confirmed by the simulation study for a mobile manipulator consisting of a non-holonomic wheeled base coupled with a holonomic robotic arm with three degrees of freedom (rotational and prismatic).

1. Introduction

Collaborative robots (cobots) are a recent and important field of study in robotics and in human–robot interaction (HRI). Manipulators and robotic arms are adopted in many industrial and productive contexts for different tasks and purposes [1]. They are typically attached to a fixed base, like a working table or another type of support, to perform their activities. This can be a limit of the their operational space for certain applications, for instance, picking objects from a place, even in the proximity of the working space, that are out of their grasping reach. An example is a robot that needs to refill the container of components used to assemble a product, which are stored in a drawer or in a warehouse outside the robot’s immediate proximity. Typical cases are given by robots in automated warehouses [2,3,4].

In this field of research, robotic arms mounted over a mobile platform are becoming popular. The scientific challenge of controlling them is that they combine holonomic with non-holonomic constraints. Indeed, typically, the mobile base is a wheeled robot, e.g., unicycle or car-like, whereas the arm is a combination of rotational and prismatic joints. Such a robot is named a mobile manipulator. In the literature, four types of mobile manipulators are distinguished [5]:

• type (h,h): holonomic mobile platform with a holonomic on-board manipulator;
• type (nh,h): non-holonomic mobile platform with a holonomic on-board manipulator;
• type (h,nh): holonomic mobile platform with a non-holonomic on-board manipulator;
• type (nh,nh): non-holonomic mobile platform with a non-holonomic on-board manipulator. Such a combination is also noted as a doubly non-holonomic mobile manipulator.

In this work, we propose a tool to perform the path-following task of a mobile manipulator [6] constituted by a non-holonomic wheeled base and a holonomic robotic arm; overall, this is a robot of type (nh,h). Such a construction is frequently used in many applications [7,8,9].

The presented control algorithm is suitable for any mobile manipulator of type $(nh,h)$. In our research, we consider an example model consisting of a unicycle base and a manipulator with three degrees of freedom (rotational, prismatic, rotational—a RPR robot); see the scheme of Figure 1. The robotic arm is mounted at distance l from the origin of the mobile platform local frame $X_p{Y}_p{Z}_p$. The manipulator local frame $X_m{Y}_m{Z}_m$ is located at that point.

Following the classic paradigm, we split the problem of the trajectory design into geometric path and speed profile, the latter being generated by the proposed control algorithm. We briefly introduce our contribution, which will then be detailed in the following sections.

We model the geometric path with B-splines [10], which are an established way of designing paths starting from a conveniently shaped control polygon. There are several advantages in using B-splines:

• They are defined over a polynomial basis with only local support, that is, changing a piece of the curve does not require a change in the whole spline;
• They extend the concept of the Bézier curve and inherit their good properties, like positivity, partition of unity of the basis, etc;
• They can be used in ${\mathbb{R}}^2$ or in ${\mathbb{R}}^3$ (or in ${\mathbb{R}}^n$) without any particular changes in the code;
• Their definition, as well as their derivatives, are recursive and, therefore, numerically, they are very stable.

The main disadvantage of B-splines (depending on the application) is that they cannot represent certain curve primitives [10] like ellipses, hyperbolas, parabolas, and more notably, circles, thus, biarcs [11,12] are also excluded. These curves appear typically in milling and machining processes resulting in G-code. However, for a robot moving in space this is not a problem. Moreover, we want to stress that our approach is not dependent on B-splines, which we selected just as an example, but other classes of curves will be possible without changing the essence of our method. Possible alternatives could be other polynomial splines like $\eta 3D$ splines, Tychonov-regularised splines, and Pythagorean Hodographs; non-polynomial solution can be biarcs, clothoids, Dubins and Reeds–Shepp curves, Fermat spirals, or more general log-aesthetic curves.

The design of the control law follows two steps, as depicted in a diagram in Section 6. The controller consists of two control laws working in parallel. Firstly, kinematic constraints have to be taken into account. They result from the robot description with respect to the path and are similar to non-integrable constraints of the first order, and other constraints, which usually result from the robot non-holonomy. In particular, the non-holonomic constraints may be introduced to the system by a certain class of the mobile platform. In the case considered in this paper, it is caused by the mobile robot of class $(2,0)$, namely a unicycle [13]. Based on the kinematic model, a kinematic controller is designed. This gives a formula for the robot velocities to satisfy the kinematic constraints. As the robot velocities cannot be commanded directly, the kinematic controller can be treated as a motion planner, and a layer to perform the reference velocities is required. Therefore, the second layer of the controller, the dynamic controller, is designed based on the robot dynamics model. It plays the role of an execution system. Although some solutions to the path-following problem are limited only to the investigation of a kinematic layer [14,15], in the presented paper the robot dynamics are taken into account as an important aspect for the control law design. The overall process builds a cascaded system following the backstepping integrator philosophy [16]. Such an approach has been eagerly used in many robotic applications considering non-holonomic constraints, e.g., [17,18,19]. The backstepping method was also used for the path-following task in the previous research. For instance, in papers [20,21], control laws for fixed-base manipulators were provided. It shows that this methodology allows us to obtain an effective path-following controller.

Paper Contribution and Structure

We present a tool to perform the path-following task based on the desired control points resulting from a simple motion planner. Background material for the Serret–Frenet frame is introduced in Section 2. In this paper, we consider a non-holonomic mobile manipulator, as it is a complex system of increasing importance in industrial solutions. We provide the robot description in Section 3. In order to obtain the robot description with respect to the path, we use equations introduced in Section 2 and Section 3. We project the robot guidance point onto the orthonormal frame located on the path. In Section 4, the details of the non-orthogonal projection are provided and robot equations with respect to the path are derived. The projection method does not introduce any additional constraints to the robot description, so it is an effective global approach. Combined with the Serret–Frenet frame, it results in the non-orthogonal projection onto the desired path. These results are then applied to a path made of a specific family of curves, the B-splines, which are detailed and analysed in Section 5. In particular, we discuss how the continuity of the path impacts the robot performance in terms of undesired force spikes and how this can be avoided using a proper spline order. Furthermore, we show how to tailor the algorithm based on the non-orthogonal Serret–Frenet parametrization to control a mobile manipulator performing the path-following task. The control law to generate and perform reference velocities that allow the robot to track the path is discussed in Section 6. The overall system is simulated and validated in Section 7. Finally, in Section 8 we draw the conclusions.

2. Serret–Frenet Parametrization

Curvilinear parametrization methods allow defining a local frame associated with a geometrical curve. The frame evolution along the curve is strictly defined by its geometry. One can distinguish different types of the parametrization, namely the normalized description and the general one [22].

In the normalized parametrization, a curve is described with respect to the so-called curvilinear distance, s. It can be interpreted as the length of a string mounted at the point of the motion beginning and laid precisely on the path [23,24]. However, for many curves it is difficult to obtain the explicit normalized equation. It results from the non-linear dependency on the general parameter u.

$$s\left(u\right)=\underset{0}{\overset{u}{\int }}∥{\displaystyle \frac{\mathrm{d}\mathit{r}\left(x\right)}{\mathrm{d}x}}∥\mathrm{d}x,$$

(1)

where $\mathit{r}$ is the analytical equation of a curve. Therefore, curves are frequently described in terms of general parametrization.

The most popular parametrization method was proposed by Serret [25] and Frenet [26]. This mathematical heritage of the previous century is commonly used in many contemporary problems in robotics, mathematics, or graphics [21,24,27,28]. The Serret–Frenet frame consists of three vectors spanning an orthonormal basis in ${\mathbb{R}}^3$ space:

• tangent to a curve, $\mathit{T}$;
• normal to a curve, $\mathit{N}$;
• binormal to a curve, $\mathit{B}$.

They can be derived with the following equations [29]:

$$\begin{array}{cc}\hfill \mathit{T}\left(u\right)& ={\displaystyle \frac{\frac{\mathrm{d}\mathit{r}\left(u\right)}{\mathrm{d}u}}{∥\frac{\mathrm{d}\mathit{r}\left(u\right)}{\mathrm{d}u}∥}},\hfill \end{array}$$

(2a)

$$\begin{array}{cc}\hfill \mathit{B}\left(u\right)& ={\displaystyle \frac{\frac{\mathrm{d}\mathit{r}\left(u\right)}{\mathrm{d}u}\times \frac{{\mathrm{d}}^2\mathit{r}\left(u\right)}{\mathrm{d}{u}^2}}{∥\frac{\mathrm{d}\mathit{r}\left(u\right)}{\mathrm{d}u}\times \frac{{\mathrm{d}}^2\mathit{r}\left(u\right)}{\mathrm{d}{u}^2}∥}},\hfill \end{array}$$

(2b)

$$\begin{array}{cc}\hfill \mathit{N}\left(u\right)& =\mathit{B}\left(u\right)\times \mathit{T}\left(u\right).\hfill \end{array}$$

(2c)

The geometrical parameters describing a curve are curvature and torsion. They define a curve swerve from a straight line and a plane, respectively. They are defined with the following equations [22,24]:

$$\begin{array}{cc}\hfill \kappa \left(u\right)& ={\displaystyle \frac{∥\frac{\mathrm{d}\mathit{r}\left(u\right)}{\mathrm{d}u}\times \frac{{\mathrm{d}}^2\mathit{r}\left(u\right)}{\mathrm{d}{u}^2}∥}{{∥\frac{\mathrm{d}\mathit{r}\left(u\right)}{\mathrm{d}u}∥}^3}},\hfill \end{array}$$

(3a)

$$\begin{array}{cc}\hfill \tau \left(u\right)& ={\displaystyle \frac{〈\frac{\mathrm{d}\mathit{r}\left(u\right)}{\mathrm{d}u}\times \frac{{\mathrm{d}}^2\mathit{r}\left(u\right)}{\mathrm{d}{u}^2},\frac{{\mathrm{d}}^3\mathit{r}\left(u\right)}{\mathrm{d}{u}^3}〉}{{∥\frac{\mathrm{d}\mathit{r}\left(u\right)}{\mathrm{d}u}\times \frac{{\mathrm{d}}^2\mathit{r}\left(u\right)}{\mathrm{d}{u}^2}∥}^2}},\hfill \end{array}$$

(3b)

where $\langle ·,·\rangle$ denotes the scalar product of vectors. The definition of torsion, given by Equation (3b), indicates that the parametrized curve should be of at least class ${\mathcal{C}}^3$.

The evolution of the Serret–Frenet frame is given with the following relation [22,24]:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}\mathit{T}\left(u\right)}{\mathrm{d}u}}& =\upsilon \kappa \left(u\right)\mathit{N}\left(u\right),\hfill \end{array}$$

(4a)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}\mathit{N}\left(u\right)}{\mathrm{d}u}}& =-\upsilon \left(\kappa \left(u\right)\mathit{T}\left(u\right)-\tau \left(u\right)\mathit{B}\left(u\right)\right),\hfill \end{array}$$

(4b)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}\mathit{B}\left(u\right)}{\mathrm{d}u}}& =-\upsilon \tau \left(u\right)\mathit{N}\left(u\right).\hfill \end{array}$$

(4c)

where $\upsilon ={\displaystyle \frac{\mathrm{d}s}{\mathrm{d}u}}=∥{\displaystyle \frac{\mathrm{d}\mathit{r}\left(u\right)}{\mathrm{d}u}}∥$, which results from Equation (1). Let us denote matrix $\mathit{S}\left(u\right)\in \mathbb{SO}\left(3\right)$, comprising the base vectors of the Serret–Frenet frame, i.e., $\mathit{S}\left(u\right)=\left[\begin{array}{ccc}\mathit{T}\left(u\right)& \mathit{N}\left(u\right)& \mathit{B}\left(u\right)\end{array}\right]$. Then, Equation (4) can be rewritten in the concise matrix form

$${\displaystyle \frac{\mathrm{d}\mathit{S}\left(u\right)}{\mathrm{d}u}}=\left[\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}\mathit{T}\left(u\right)}{\mathrm{d}u}}& {\displaystyle \frac{\mathrm{d}\mathit{N}\left(u\right)}{\mathrm{d}u}}& {\displaystyle \frac{\mathrm{d}\mathit{B}\left(u\right)}{\mathrm{d}u}}\end{array}\right]=\upsilon \mathit{S}\left(u\right)\mathit{W}\left(u\right),$$

(5)

where $\mathit{W}\left(u\right)$ is the skew-symmetric matrix comprising the geometric parameters of a curve:

$$\mathit{W}\left(u\right)=\left[\begin{array}{ccc}0& -\kappa \left(u\right)& 0\\ \kappa \left(u\right)& 0& -\tau \left(u\right)\\ 0& \tau \left(u\right)& 0\end{array}\right].$$

(6)

Hence, the frame evolution in time is expressed with the equation

$$\dot{\mathit{S}}\left(u\right)={\displaystyle \frac{\mathrm{d}\mathit{S}\left(u\right)}{\mathrm{d}t}}={\displaystyle \frac{\mathrm{d}\mathit{S}\left(u\right)}{\mathrm{d}u}}\dot{u}=\dot{u}\upsilon \mathit{S}\left(u\right)\mathit{W}\left(u\right)=\dot{s}\mathit{S}\left(u\right)\mathit{W}\left(u\right).$$

(7)

3. Non-Holonomic Mobile Manipulator

A mobile manipulator is a robotic system consisting of a mobile platform and an on-board robotic arm [30]. In the paper, we consider a mobile manipulator of type (nh,h), i.e., with a non-holonomic platform and a holonomic manipulator. Hence, the robot state can be denoted as

$$\mathit{q}=\left(\begin{array}{c}{\mathit{q}}_p\\ {\mathit{q}}_m\end{array}\right),$$

(8)

where ${\mathit{q}}_p\in {\mathbb{R}}^p$ is the mobile platform state, while ${\mathit{q}}_m\in {\mathbb{R}}^m$ is the vector of manipulator configuration.

Non-holonomic constraints of the mobile platform can be expressed in the Pfaffian form [13]

$$\mathit{A}\left({\mathit{q}}_p\right){\dot{\mathit{q}}}_p=\mathbf{0},$$

(9)

where $\mathit{A}\in {\mathbb{R}}^{l\times p}$ and l is the number of independent non-holonomic constraints. The system (9) can be equivalently transformed to the driftless system [23]

$${\dot{\mathit{q}}}_p=\mathit{G}\left({\mathit{q}}_p\right)\eta ,$$

(10)

where $\eta \in {\mathbb{R}}^n$ is the vector of auxiliary velocities and $\mathit{G}\left({\mathit{q}}_p\right)\in {\mathbb{R}}^{p\times n}$, $n=p-l$, is the control matrix spanning the kernel of the Pfaff matrix $\mathit{A}\left({\mathit{q}}_p\right)$, i.e., $\mathit{A}·\mathit{G}\equiv \mathbf{0}$.

Let us denote $\mathit{p}\left(\mathit{q}\right)$ as the position of the manipulator end-effector with respect to the inertial frame. Thus, the end-effector velocities are expressed as

$$\dot{\mathit{p}}={\displaystyle \frac{\partial \mathit{p}}{\partial \mathit{q}}}\dot{\mathit{q}}=\left[\begin{array}{cc}{\displaystyle \frac{\partial \mathit{p}}{\partial {\mathit{q}}_p}}& {\displaystyle \frac{\partial \mathit{p}}{\partial {\mathit{q}}_m}}\end{array}\right]\dot{\mathit{q}}=\left[\begin{array}{ccc}{\mathit{J}}_1& \mid & {\mathit{J}}_2\end{array}\right]\dot{\mathit{q}}=\mathit{J}({\mathit{q}}_p,{\mathit{q}}_m)\dot{\mathit{q}}=\mathit{J}\left(\mathit{q}\right)\dot{\mathit{q}},$$

(11)

where $\mathit{J}\left(\mathit{q}\right)$ is the Jacobian. Considering the non-holonomic constraints of the mobile platform, Equation (11) can be rewritten as

$$\dot{\mathit{p}}=\left[\begin{array}{cc}{\mathit{J}}_1& {\mathit{J}}_2\end{array}\right]\left(\begin{array}{c}{\dot{\mathit{q}}}_p\\ {\dot{\mathit{q}}}_m\end{array}\right)=\left[\begin{array}{cc}{\mathit{J}}_1& {\mathit{J}}_2\end{array}\right]\left(\begin{array}{c}\mathit{G}\eta \\ {\dot{\mathit{q}}}_m\end{array}\right)=\left[\begin{array}{cc}{\mathit{J}}_1\mathit{G}& {\mathit{J}}_2\end{array}\right]\left(\begin{array}{c}\eta \\ {\dot{\mathit{q}}}_m\end{array}\right)=\left[\begin{array}{cc}{\mathit{J}}_1^{*}& {\mathit{J}}_2\end{array}\right]\mathit{z}={\mathit{J}}^{*}\left(\mathit{q}\right)\mathit{z},$$

(12)

where $\mathit{z}={\left(\begin{array}{cc}\mathit{\eta }& {\dot{\mathit{q}}}_m\end{array}\right)}^T$ is the velocity vector comprising the auxiliary velocities of the mobile platform and general velocities of the on-board manipulator.

Due to the non-holonomy of the mobile platform, the dynamics of the mobile manipulator is derived using the d’Alembert principle [30]. In the general coordinates, it takes the form

$$\left[\begin{array}{cc}{\mathit{Q}}_{11}& {\mathit{Q}}_{12}\\ {\mathit{Q}}_{21}& {\mathit{Q}}_{22}\end{array}\right]\left(\begin{array}{c}{\ddot{\mathit{q}}}_p\\ {\ddot{\mathit{q}}}_m\end{array}\right)+\left[\begin{array}{cc}{\mathit{C}}_{11}& {\mathit{C}}_{12}\\ {\mathit{C}}_{21}& {\mathit{C}}_{22}\end{array}\right]\left(\begin{array}{c}{\dot{\mathit{q}}}_p\\ {\dot{\mathit{q}}}_m\end{array}\right)+\left(\begin{array}{c}\mathbf{0}\\ {\mathit{D}}_2\end{array}\right)=\left[\begin{array}{c}{\mathit{A}}^T\lambda \\ \mathbf{0}\end{array}\right]+\left[\begin{array}{cc}{\mathit{B}}_p& \mathbf{0}\\ \mathbf{0}& {\mathit{I}}_m\end{array}\right]\left(\begin{array}{c}{\mathit{u}}_p\\ {\mathit{u}}_m\end{array}\right),$$

(13)

where the different elements have the following meanings:

• $\mathit{Q}\left(\mathit{q}\right)=\left[\begin{array}{cc}{\mathit{Q}}_{11}& {\mathit{Q}}_{12}\\ {\mathit{Q}}_{21}& {\mathit{Q}}_{22}\end{array}\right]\in {\mathbb{R}}^{(p+m)\times (p+m)}$ is the inertia matrix;
• $\mathit{C}(\mathit{q},\dot{\mathit{q}})=\left[\begin{array}{cc}{\mathit{C}}_{11}& {\mathit{C}}_{12}\\ {\mathit{C}}_{21}& {\mathit{C}}_{22}\end{array}\right]\in {\mathbb{R}}^{(p+m)\times (p+m)}$ is the matrix of Coriolis and centrifugal forces;
• $\mathit{D}\left(\mathit{q}\right)=\left(\begin{array}{c}\mathbf{0}\\ {\mathit{D}}_2\end{array}\right)\in {\mathbb{R}}^{p+m}$ is the vector of gravity terms. It is assumed that the mobile platform moves on a plane;
• $\lambda \in {\mathbb{R}}^l$ is the vector of Lagrange multipliers. The non-holonomic constraints are defined only for the mobile platform;
• $\mathit{u}=\left(\begin{array}{c}{\mathit{u}}_p\\ {\mathit{u}}_m\end{array}\right)\in {\mathbb{R}}^{n+m}$ is the control vector. The vector ${\mathit{u}}_p\in {\mathbb{R}}^n$ represents the control torques applied to the platform wheels. It is noteworthy that there are less controls ${\mathit{u}}_p$ than the platform state variables ${\mathit{q}}_p$, that is, $n<p$. This results from the platform non-holonomy. Moreover, ${\mathit{u}}_m\in {\mathbb{R}}^m$ denotes generalized forces to control the manipulator joints;
• $\mathit{B}=\left[\begin{array}{cc}{\mathit{B}}_p& \mathbf{0}\\ \mathbf{0}& {\mathit{I}}_m\end{array}\right]\in {\mathbb{R}}^{(p+m)\times (n+m)}$ is the input matrix, where the matrix ${\mathit{B}}_p\in {\mathbb{R}}^{p\times n}$ indicates how controls applied to the mobile platform, ${\mathit{u}}_p$, influence the platform state, ${\mathit{q}}_p$, and ${\mathit{I}}_m\in {\mathbb{R}}^{m\times m}$ is the identity matrix as torques and forces generated by actuators of the holonomic robotic arm, ${\mathit{u}}_m$, impact directly every respective state variable, ${\mathit{q}}_m$.

The elements ${\mathit{Q}}_{12}$, ${\mathit{Q}}_{21}$, ${\mathit{C}}_{12}$, and ${\mathit{C}}_{21}$ in the dynamic model (13) result from the dynamic coupling between the mobile platform and the manipulator. Model (13) can be expressed with respect to the auxiliary velocities vector, $\mathit{z}$. Considering Equation (10) and its derivative, the following relation is obtained:

$${\mathit{Q}}^{*}\left(\mathit{q}\right)\dot{\mathit{z}}+{\mathit{C}}^{*}(\mathit{q},\dot{\mathit{q}})\mathit{z}+{\mathit{D}}^{*}\left(\mathit{q}\right)={\mathit{B}}^{*}\mathit{u},$$

(14)

where ${\mathit{Q}}^{*}\in {\mathbb{R}}^{(n+m)\times (n+m)}$, ${\mathit{C}}^{*}\in {\mathbb{R}}^{(n+m)\times (n+m)}$, ${\mathit{D}}^{*}\in {\mathbb{R}}^{n+m}$, and ${\mathit{B}}^{*}\in {\mathbb{R}}^{(n+m)\times (n+m)}$.

It is noteworthy that, for mobile manipulators, the skew-symmetry between the inertia matrix, ${\mathit{Q}}^{*}$, and the Coriolis matrix, ${\mathit{C}}^{*}$, does not hold [30]. Therefore, a correction matrix, ${\mathit{C}}_{\mathit{K}}^{*}$, is defined, so that

$${\dot{\mathit{Q}}}^{*}=({\mathit{C}}^{*}+{\mathit{C}}_K^{*})+{({\mathit{C}}^{*}+{\mathit{C}}_K^{*})}^T.$$

(15)

4. Robot Description with Respect to a Path

In order to describe a robot with respect to the desired path, the robot guidance point has to be projected onto the considered curve. Let us associate the robot guidance point E with the manipulator end-effector. Then, its location in the inertial frame is equal to $\mathit{p}$. Next, let the projection of point E onto the path be denoted as $E^{\prime }$. Without loss of the generality, we can associate point $E^{\prime }$ with the origin of the Serret–Frenet frame, which is defined with the vectors $\{\mathit{T},\mathit{N},\mathit{B}\}$ and evolves along the path. The origin of the Serret–Frenet frame in the inertial frame is equal to $\mathit{r}$. Subsequently, the projection onto the path is performed so that no constraints, e.g., regarding the distance between point E and the frame origin, are introduced. Hence, it is the non-orthogonal projection, which is free of singularities and is global and valid in every point of the space. As the Serret–Frenet frame and the particular projection method are considered, we denote this approach to the description of a robot with respect to the path as non-orthogonal Serret–Frenet parametrization. The essence of the method is to define a vector with three coordinates, $\mathit{d}={\left(\begin{array}{ccc}{d}_1& d_2& d_3\end{array}\right)}^T$, which denotes the position of the robot guidance point E in the local frame on the path. The schematic presentation of the projection procedure is presented in Figure 2.

In fact, the position of the robot guidance point with respect to the Serret–Frenet frame can be computed using the following equation:

$$\mathit{d}={\mathit{S}}^T(\mathit{p}-\mathit{r})=\left(\begin{array}{c}\langle \mathit{T},\mathit{p}-\mathit{r}\rangle \\ \langle \mathit{N},\mathit{p}-\mathit{r}\rangle \\ \langle \mathit{B},\mathit{p}-\mathit{r}\rangle \end{array}\right)=\left(\begin{array}{c}{d}_1\\ d_2\\ d_3\end{array}\right).$$

(16)

The position $\mathit{d}$ changes in time according to the relation obtained by differentiating Equation (16):

$$\dot{\mathit{d}}={\mathit{S}}^T(\dot{\mathit{p}}-\dot{\mathit{r}})+{\dot{\mathit{S}}}^T(\mathit{p}-\mathit{r}).$$

(17)

Let us notice that the element ${\mathit{S}}^T\dot{\mathit{r}}$ defines the linear velocity of the frame associated with the path expressed in that frame. It corresponds to the velocity in the body frame. Therefore, this element is equal to

$${\mathit{S}}^T\left(u\right)\dot{\mathit{r}}\left(u\right)=\left(\begin{array}{c}〈\mathit{T},{\displaystyle \frac{\mathrm{d}\mathit{r}}{\mathrm{d}u}}〉\\ \\ 〈\mathit{N},{\displaystyle \frac{\mathrm{d}\mathit{r}}{\mathrm{d}u}}〉\\ \\ 〈\mathit{B},{\displaystyle \frac{\mathrm{d}\mathit{r}}{\mathrm{d}u}}〉\end{array}\right)\dot{u}=\left(\begin{array}{c}〈\mathit{T},\mathit{T}〉\\ 〈\mathit{N},\mathit{T}〉\\ 〈\mathit{B},\mathit{T}〉\end{array}\right)\dot{u}∥{\displaystyle \frac{\mathrm{d}\mathit{r}}{\mathrm{d}u}}∥=\left(\begin{array}{c}\dot{u}\upsilon \\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}\dot{s}\\ 0\\ 0\end{array}\right).$$

(18)

Moreover, based on Equations (7) and (16), it is observed that

$${\dot{\mathit{S}}}^T(\mathit{p}-\mathit{r})=\dot{s}{\mathit{W}}^T{\mathit{S}}^T(\mathit{p}-\mathit{r})=-\dot{s}\mathit{W}\mathit{d},$$

(19)

where ${\mathit{W}}^T=-\mathit{W}$ according to Equation (6). Hence, considering (12), (18), and (19), the final form of Equation (17) is derived as

$$\dot{\mathit{d}}={\mathit{S}}^T\dot{\mathit{p}}-\left(\begin{array}{c}\dot{s}\\ 0\\ 0\end{array}\right)-\dot{s}\mathit{W}\mathit{d}=\underset{\mathit{L}}{\underbrace{{\mathit{S}}^T{\mathit{J}}^{*}}}\mathit{z}\underset{\mathit{F}}{\underbrace{-\dot{s}\left(\begin{array}{c}1-\kappa d_2\\ \kappa d_1-\tau d_3\\ \tau d_2\end{array}\right)}}=\mathit{L}\mathit{z}+\mathit{F}.$$

(20)

The relation (20) has the form of a non-integrable constraint of the first order. It can be treated as a constraint introduced to the robotic system. If the constraint is satisfied, the robot follows the desired path correctly.

5. B-Spline Curve

According to [10], a B-spline curve of order k is the polynomial given by the equation

$$\mathit{r}\left(u\right)=\sum _{i=0}^r{N}_{i,k}\left(u\right)P_i,$$

(21)

where $P_i$, for $i\in \{0,\dots ,r\}$, are the control points defining the convex surrounding of the curve, and $N_{i,k}$ are base functions of order k, defined on the set of knots

$$U=\{\underset{k+1}{\underbrace{a,\dots ,a}},u_{k+1},\dots ,u_r,\underset{k+1}{\underbrace{b,\dots ,b}}\},$$

(22)

while the domain of the curve is given by $u\in [a,b]$.

The $N_{i,k}$ functions are piecewise polynomial functions. They create a base for the vector space of all piecewise polynomial functions of given order and continuity for the set of knots U. Moreover, the base functions have properties similar to Bézier curves [10], e.g., invariance of the transformation or locality. The i-th function is non-zero only on a certain interval of the domain. As a result, the control point $P_i$ shapes a curve only if the corresponding base function is non-zero. The base functions of order k are defined as [10]

$$\begin{array}{cc}\hfill N_{i,0}\left(u\right)& =\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{u}_i\le u<u_{i+1}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.,\hfill \end{array}$$

(23a)

$$\begin{array}{cc}\hfill N_{i,k}\left(u\right)& ={\displaystyle \frac{u-u_i}{u_{i+k}-u_i}}{N}_{i,k-1}\left(u\right)+{\displaystyle \frac{u_{i+k+1}-u}{u_{i+k+1}-u_{i+1}}}{N}_{i+1,k-1}\left(u\right),\hfill \end{array}$$

(23b)

but in the case of a vanishing denominator in Equation (23b), the whole element is assumed to be equal to zero.

The definition of B-spline curves proposed in [10] guarantees certain properties, including the following:

• If $r=k$ and $U=\{0,\dots ,0,1,\dots ,1\}$, the B-spline curve is equal to the Bézier curve. The base functions have the form of Bernstein polynomials;
• The base polynomial functions, creating a B-spline curve, are defined on intervals of the domain. The curve is of order k and defined for $r+1$ control points. The number of knots is equal to $r+k+2$;
• The boundary conditions $\mathit{r}\left(a\right)=P_0$ and $\mathit{r}\left(b\right)=P_k$ are satisfied;
• The polygon defined by the control points is equal to the linear approximation of the B-spline curve. The lower the order of base polynomials, the more precise is the polygon mapped by the B-spline curve. The comparison of B-spline curves built on the same set of control points on a plane is presented in Figure 3. Also, the curvature of the B-spline curves is plotted. It is noteworthy that, in this example, the splines have curvatures equal to zero at certain point. Moreover, for $k=2$ the curvature is discontinuous.
• Continuity and differentiability of B-spline curves result directly from the properties of the base functions. Hence, the curve of order k is smooth inside the intervals defined by knots and at least $k-d$ times differentiable in the knot point with multiplicity d.

The derivative of order p of a B-spline curve (21) is given by

$${\displaystyle \frac{{\mathrm{d}}^p\mathit{r}\left(u\right)}{\mathrm{d}{u}^p}}={\mathit{r}}^{\left(p\right)}\left(u\right)=\sum _{i=0}^n{N}_{i,k}^{\left(p\right)}\left(u\right)P_i.$$

(24)

Therefore, the derivatives of the base functions along the curve have to be calculated. One of the methods proposed in [10] is defined with the following relation:

$$N_{i,k}^{\left(p\right)}={\displaystyle \frac{k!}{(k-p)!}}\sum _{j=0}^p{a}_{p,j}{N}_{i+j,k-p},$$

(25)

where the coefficients $a_{p,j}$ are given according to the formulas

$$\begin{array}{cc}\hfill a_{0,0}& =1,\hfill \\ \hfill a_{p,0}& ={\displaystyle \frac{a_{p-1,0}}{u_{i+k-p+1}-u_i}},\hfill \\ \hfill a_{p,j}& ={\displaystyle \frac{a_{p-1,j}-a_{p-1,j-1}}{u_{i+k+j-p+1}-u_{i+j}}},j=1,\dots ,k-1,\hfill \\ \hfill a_{p,p}& ={\displaystyle \frac{-a_{p-1,p-1}}{u_{i+k+1}-u_{i+p}}},\hfill \end{array}$$

where $p\le k$. Again, it is assumed that in the case of a vanishing denominator, the whole coefficient $a_{p,j}$ is equal to 0.

6. Control Law Formulation

The considered control problem is the path-following task performed by a non-holonomic mobile manipulator.

The path-following task is to force a robot to approach the desired path, defined as a purely geometrical curve, and move along it [31]. Moreover, the velocity profile along the path has to be asymptotically tracked. However, it does not influence the geometrical description of the path, which can be defined independently.

The desired path is defined as a B-spline curve. It is assumed that the input data is a set of control points, which can be obtained with the usage of motion planning algorithms. The control points are located in the robot workspace. A collision-free environment is considered.

The control law is formulated for a mobile manipulator of type (nh,h). Therefore, in the robotic system exist kinematic constraints resulting from the platform non-holonomy, Equations (9) and (10), and from the robot description with respect to the path, Equation (20). In order to satisfy the constraints, proper velocities, $\mathit{z}$, have to be performed. However, the auxiliary velocities, $\mathit{z}$, belong to the state trajectories and cannot be commanded directly. Hence, the robot dynamics, Equation (13), must be considered. As a result, the system has a cascaded structure in which kinematic and dynamic layers can be distinguished.

In order to design a control law for a cascaded system, the backstepping integrator algorithm [16] can be used. Firstly, a kinematic control law needs to be designed to satisfy the kinematic constraints. Secondly, a dynamic controller is proposed to execute the reference velocity profiles generated on the previous level. The resulting structure of the control system is presented in Figure 4.

Based on the backstepping integrator method, the following control law is proposed to guarantee asymptotic convergence of path-following errors to zero. The kinematic controller takes the form

$${\mathit{z}}_{\mathit{ref}}={\mathit{L}}^{\#}({\dot{\mathit{d}}}_d-{\mathit{K}}_k{\mathit{e}}_{\mathit{d}}-\mathit{F}),$$

(26)

where ${\mathit{z}}_{\mathit{ref}}$ are the reference velocity profiles to satisfy the robot kinematic constraints, ${\mathit{d}}_d$ is the desired state with respect to the path, ${\mathit{e}}_{\mathit{d}}=\mathit{d}-{\mathit{d}}_d$ is the vector of path-following errors, ${\mathit{K}}_k=\mathrm{diag}\left\{k_k\right\}$ is the positive-definite matrix of kinematic controller coefficients, and # denotes the Moore–Penrose pseudo-inverse of matrix $\mathit{L}$, i.e., ${\mathit{L}}^{\#}={\mathit{L}}^T{\left(\mathit{L}{\mathit{L}}^T\right)}^{-1}$. The reference velocity profiles are performed via the dynamic layer for which the model-based control law is proposed,

$$\mathit{u}={\left({\mathit{B}}^{*}\right)}^{-1}\left({\mathit{Q}}^{*}{\dot{\mathit{z}}}_{\mathit{ref}}+{\mathit{C}}^{*}{\mathit{z}}_{\mathit{ref}}+{\mathit{D}}^{*}-{\mathit{K}}_d{\mathit{e}}_{\mathit{z}}-{\mathit{C}}_K^{*}{\mathit{e}}_{\mathit{z}}\right),$$

(27)

where ${\mathit{e}}_{\mathit{z}}=\mathit{z}-{\mathit{z}}_{\mathit{ref}}$ is the vector of velocity profile following errors, and ${\mathit{K}}_d=\mathrm{diag}\left\{k_d\right\}$ is the positive-definite matrix of control gains. For the proposed controllers, the following theorem is stated.

Theorem 1.

The kinematic controller, Equation (26), and the dynamic controller, Equation (27), working in parallel as a cascaded controller guarantee asymptotic convergence of path-following errors, ${\mathit{e}}_{\mathit{d}}$, and velocity profile following errors, ${\mathit{e}}_{\mathit{z}}$, to zero.

Proof. 

To begin with, the kinematic controller is considered. According to the backstepping methodology, it is treated as though there were no higher layers of the control cascade. Hence, the kinematic constraints are satisfied if the system trajectories tend to the reference velocity profiles, ${\mathit{z}}_{\mathit{ref}}$. Therefore, system (20) in the closed control loop with the virtual control defined by (26) is described with the equation

$${\dot{\mathit{e}}}_{\mathit{d}}+{\mathit{K}}_k{\mathit{e}}_{\mathit{d}}=0.$$

(28)

It is easily observed that system (28) is the Hurwitz system for a positive-definite matrix ${\mathit{K}}_k$. It corresponds to the assumed properties of the gain matrix. Hence, the kinematic layer is asymptotically stable.

The reference velocity profiles, ${\mathit{z}}_{\mathit{ref}}$, generated on the kinematic level, are asymptotically tracked by the proposed dynamic controller. The trajectories planned by the kinematic controller are strictly performed on the dynamic level. The control loop at the second stage of the control cascade is closed by putting control law (27) to the robot dynamics model (14). As a result, the following equation is obtained:

$${\mathit{Q}}^{*}{\dot{\mathit{e}}}_{\mathit{z}}+{\mathit{C}}^{*}{\mathit{e}}_{\mathit{z}}+{\mathit{K}}_d{\mathit{e}}_{\mathit{z}}+{\mathit{C}}_K^{*}{\mathit{e}}_{\mathit{z}}=0.$$

(29)

Let us propose a candidate Lyapunov-like function for the system (29):

$$V\left({\mathit{e}}_{\mathit{z}}\right)={\displaystyle \frac{1}{2}}{\mathit{e}}_{\mathit{z}}^T{\mathit{Q}}^{*}\left(\mathit{q}\right){\mathit{e}}_{\mathit{z}}.$$

(30)

The derivative of function (30) along the system trajectories is equal to

$$\begin{array}{cc}\hfill \dot{V}\left({\mathit{e}}_{\mathit{z}}\right)& ={\mathit{e}}_{\mathit{z}}^T{\mathit{Q}}^{*}{\dot{\mathit{e}}}_{\mathit{z}}+{\displaystyle \frac{1}{2}}{\mathit{e}}_{\mathit{z}}^T{\dot{\mathit{Q}}}^{*}{\mathit{e}}_{\mathit{z}}=\hfill \\ \hfill & ={\mathit{e}}_{\mathit{z}}^T\underset{\left(29\right)}{\underbrace{\left(-{\mathit{C}}^{*}{\mathit{e}}_{\mathit{z}}-{\mathit{C}}_K^{*}{\mathit{e}}_{\mathit{z}}-{\mathit{K}}_d{\mathit{e}}_{\mathit{z}}\right)}}+{\mathit{e}}_{\mathit{z}}^T\underset{\left(15\right)}{\underbrace{\left({\mathit{C}}^{*}+{\mathit{C}}_K^{*}\right)}}{\mathit{e}}_{\mathit{z}}=\hfill \\ \hfill & =-{\mathit{e}}_{\mathit{z}}^T{\mathit{K}}_d{\mathit{e}}_{\mathit{z}}=-W\left({\mathit{e}}_{\mathit{z}}\right).\hfill \end{array}$$

(31)

As $W\left({\mathit{e}}_{\mathit{z}}\right)$ is a quadratic form of the positive-definite matrix, ${\mathit{K}}_d$, it is always non-negative. Thus, the following relation holds

$$\dot{V}\left({\mathit{e}}_{\mathit{z}}\right)=-W\left({\mathit{e}}_{\mathit{z}}\right)\le 0.$$

(32)

By virtue of the LaSalle invariance principle [13], it is concluded that velocity profiles following errors converge to zero asymptotically. As a result, system trajectories tend to the reference velocity profiles, $\mathit{z}\to {\mathit{z}}_{\mathit{ref}}$. Hence, the kinematic constraints are satisfied and it is proven that the robot controlled by the designed cascade controller follows the desired path correctly. □

7. Simulation Results and Discussion

The presented theoretical results were validated in a simulation study. A mobile manipulator of type (nh,h) was considered. It consisted of a mobile platform of class $(2,0)$ [13] and a robotic arm of three degrees of freedom (rotational, prismatic, rotational). A schematic view of the mobile manipulator is presented in Figure 1.

A B-spline curve was commanded as the desired path. The curve was defined by the arbitrarily chosen set of control points

$$\begin{array}{c}{P}_i\in \left\{{\left(\begin{array}{ccc}1& 0& 1\end{array}\right)}^T,{\left(\begin{array}{ccc}2& 0& 0\end{array}\right)}^T,{\left(\begin{array}{ccc}2& 2& 0\end{array}\right)}^T,{\left(\begin{array}{ccc}3& 3& 1\end{array}\right)}^T,{\left(\begin{array}{ccc}4& 2& 0\end{array}\right)}^T,\right.\hfill \\ \hfill \left.{\left(\begin{array}{ccc}6& 0& 0\end{array}\right)}^T,{\left(\begin{array}{ccc}5& -1& 1\end{array}\right)}^T,{\left(\begin{array}{ccc}2& -1/2& 1/2\end{array}\right)}^T\right\},\end{array}$$

(33)

whereas the domain was selected as $u\in [0,20]$ and the single knot points were uniformly distributed. In the simulation study, spline curves of various order k, namely $k\in \{3,4\}$, were taken into account. As a result, curves of classes ${\mathcal{C}}^2$ and ${\mathcal{C}}^3$ were obtained, respectively. Such a choice is purposeful. As indicated in Section 5, the lower the order k, the better the control points are mapped by a B-spline curve. On the other hand, the Serret–Frenet parametrization requires at least class ${\mathcal{C}}^3$. Therefore, it will be verified within the study what happens in the critical step of the requirement violation.

In order to validate the proposed control law, the parameters of the example were selected arbitrarily:

• control gains: $k_k=50$, $k_d=500$;
• robot initial state: ${\mathit{q}}_0={\left(\begin{array}{cccccc}0& 0& \pi /2& \pi /4& 1& -\pi /2\end{array}\right)}^T$, ${\mathit{z}}_0=\mathbf{0}$;
• velocity profile along the path: $\dot{u}\left(t\right)={\displaystyle \frac{1}{2}}{\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}$, $u\left(0\right)=0$.

Furthermore, the desired position with respect to the path, ${\mathit{d}}_d$, was defined so that the mobile manipulator approached the desired path smoothly from the initial state.

In the following subsections, simulation results obtained for different desired paths are presented and discussed.

7.1. The Desired Path of Class ${\mathcal{C}}^2$

Firstly, the performance of the robot was investigated, when the commanded B-spline curve was of order $k=3$, which resulted in the class of continuity ${\mathcal{C}}^2$ in the knot points. It is the violation of the requirement necessary for the Serret–Frenet frame definition.

Nevertheless, the path performed by the robot is consistent with the desired path, which is presented in Figure 5. Moreover, no discontinuity can be observed in the local frame evolution along the path. Also, the reference signals, shown in Figure 6, seem to be preserved at a feasible level. The control errors, presented in Figure 7, are also maintained at a satisfactorily low level. Despite the fact that the mobile manipulator is outside the path in the initial state, the path-following errors, shown in Figure 7a, are maintained at low level during the whole manoeuvre. The smooth approach to the desired path results from the value of the desired position with respect to the path, ${\mathit{d}}_d$, which is presented in Figure 6a. During the first few seconds, the manipulator is smoothly brought to the origin of the Serret–Frenet frame, i.e., zero position with respect to the path. All in all, it can be concluded that, in this case, the path is followed correctly.

However, in the trajectory of torsion, discontinuities are revealed, as presented in Figure 8. In the knot points, the path class is ${\mathcal{C}}^2$, which is too low and results in step changes of the torsion value. This causes unachievable values of control commands; see Figure 9. The desired path is performed correctly in the simulation as the requirements are violated only in the knot points. However, this might not be applicable to the physical robot. The controls would have to be saturated and the robot behaviour in the knot points should be better operated. This case highlights the necessity of the precise modeling of B-spline curves, which are a convenient tool to derive an equation of the desired path, based on the set of control points.

7.2. The Desired Path of Class ${\mathcal{C}}^3$

In contrast to the case described in the previous section, here the desired path created with base functions of order $k=4$ is analysed. The curve is modelled appropriately and, as a result, it has the continuity class ${\mathcal{C}}^3$ in the knot points. This guarantees the continuity of the Serret–Frenet frame evolution.

In Figure 10, the desired path and the Serret–Frenet frame evolution along the curve are presented. In addition, in Figure 11, the geometric parameters of the desired curve are shown. It should be noticed that both curvature and torsion values are variable in time. However, they are continuous due to the chosen order of the base functions, i.e., $k=4$.

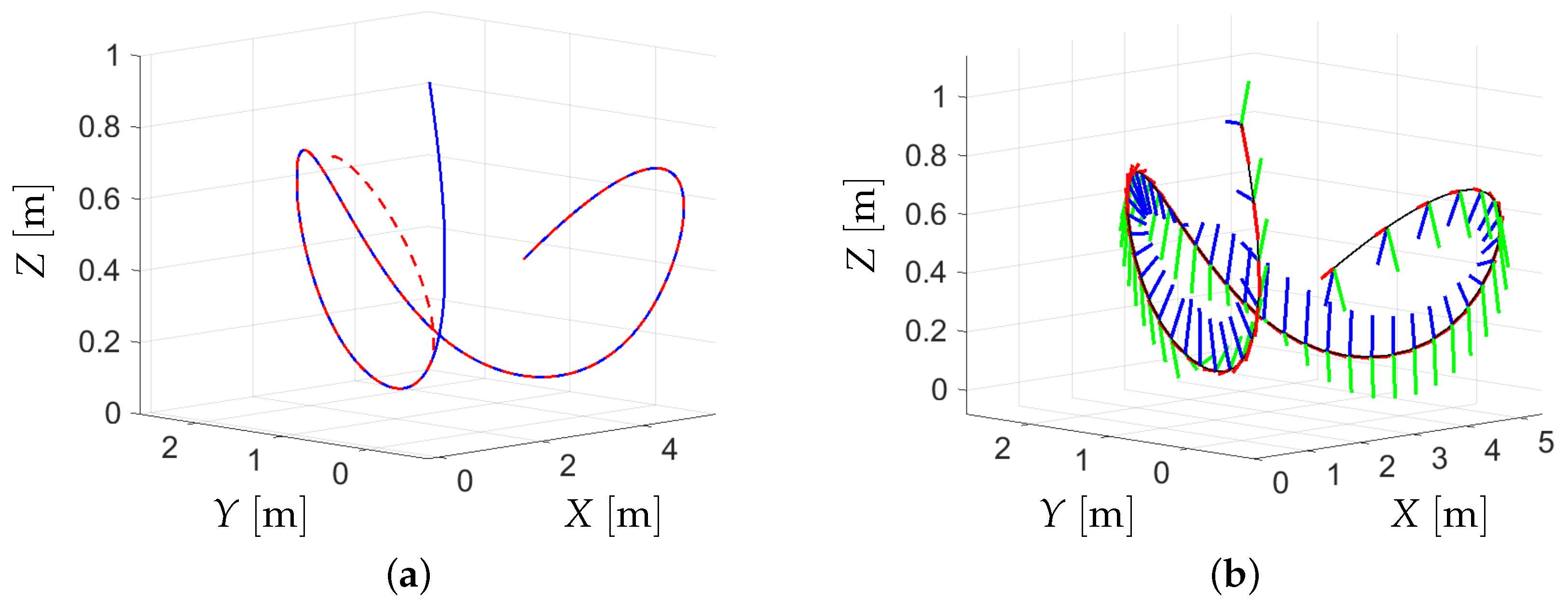
Moreover, in Figure 12, the performance of the considered mobile manipulator is visualized. The robot smoothly approaches the given path, and its end-effector, which is associated with the robot guidance point, moves precisely along the curve determined by the control points, Equation (33).

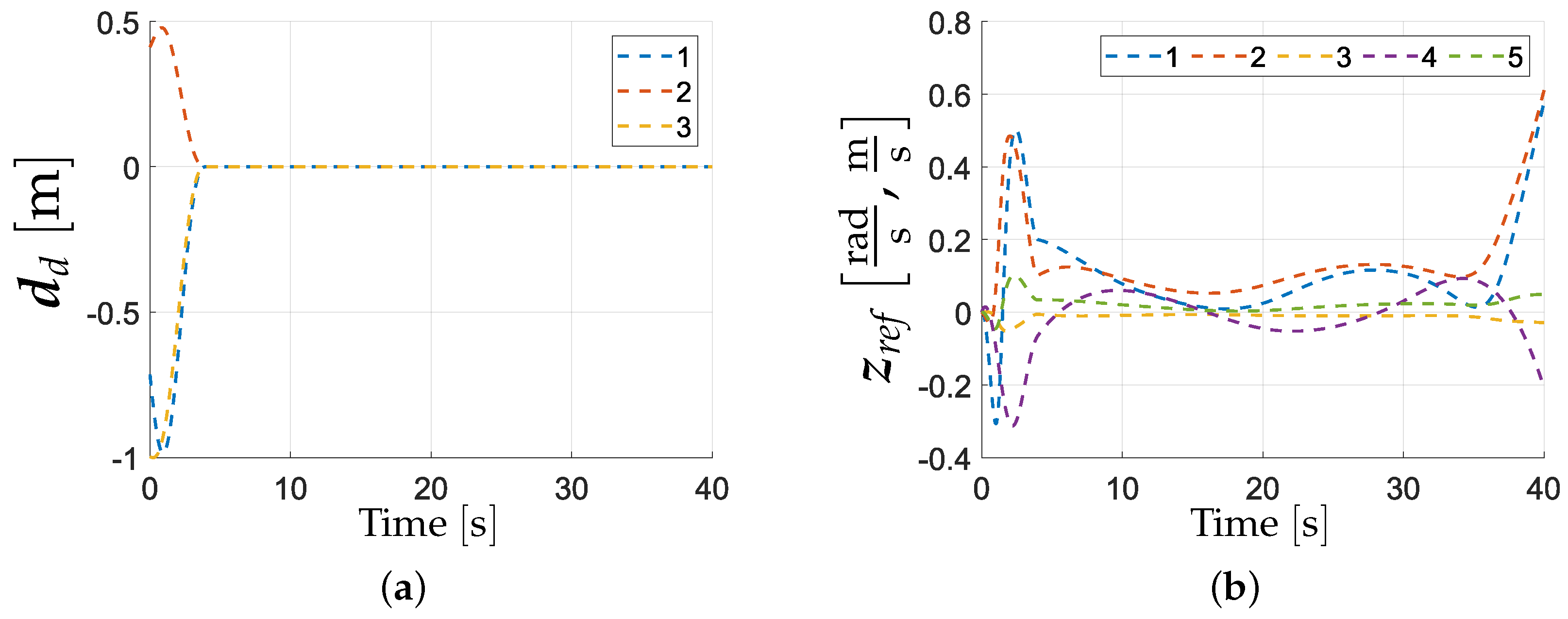
Subsequently, in Figure 13, the reference values for the controllers on both layers of the cascade are presented. The desired position with respect to the path smoothly converges from the initial value to the origin, to follow the desired path correctly; see Figure 13a. Simultaneously, the reference velocity profiles commanded by the kinematic controller can be observed. In the same graph, reference velocities for the platform wheels (indexes 1 and 2), rotational joints (3 and 5), and prismatic joint (4) are plotted. It is noteworthy that the values are rapidly increasing in the sense of absolute value in the last stage of motion. This might result from the fact that the constant velocity profile along the curve, ${\dot{u}}_d$, is considered.

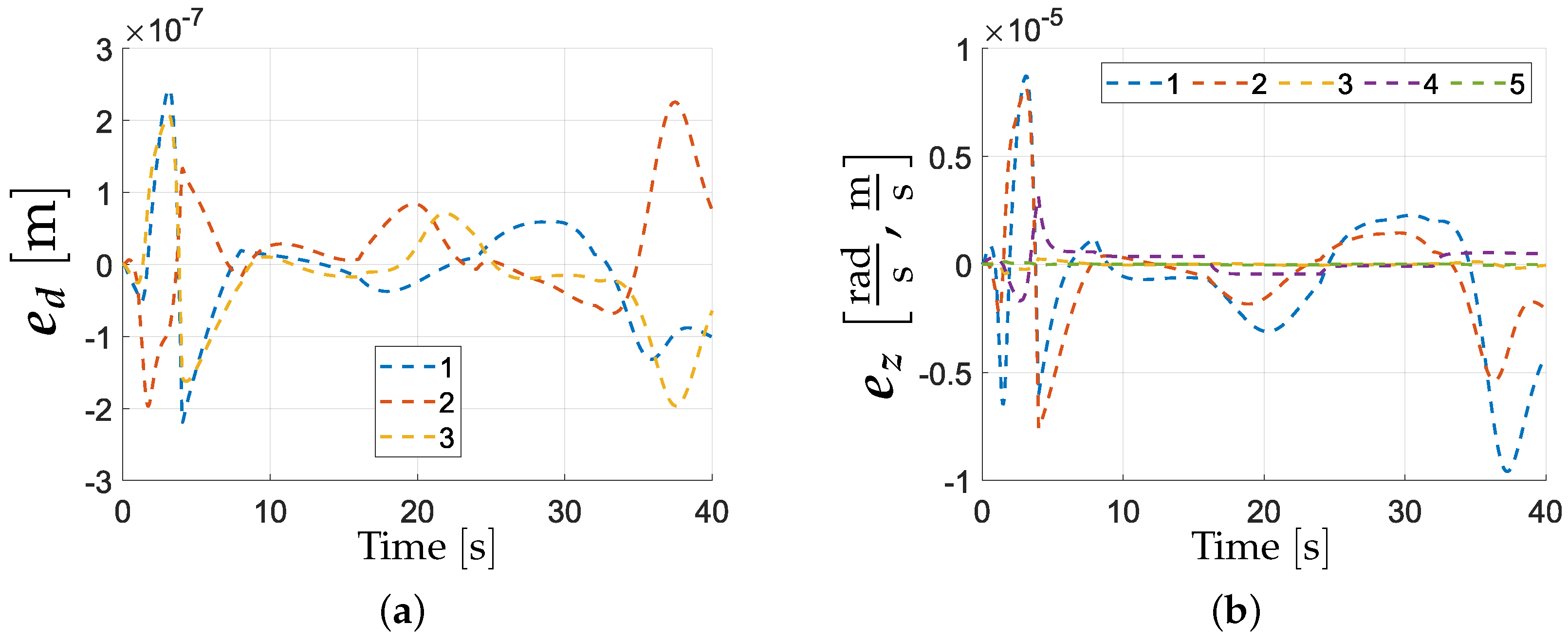
The reference signals can be compared with the errors, which are shown in Figure 14. For both kinematic and dynamic layers, the errors are maintained at a low level. In particular, the path-following errors, Figure 14a, are low during the whole manoeuvre due to the design of the reference value; see Figure 13a. The graphs prove the successful performance of the controller. In fact, the errors are below the precision of the sensors, which indicates that the controller performance is satisfactory. The proposed control law guarantees the successful following of the desired path. At the end of the motion, a negligible excitation can be noticed. This results from the mentioned changes of the reference value. Nonetheless, the excitation is well compensated by the controller. As a result, the errors demonstrate the expected behaviour at satisfactory precision.

Finally, in Figure 15 the generated control commands are presented. The control torques for the platform wheels and rotational joints are shown separately from the control force for the prismatic joint. For a properly modelled path, the obtained control values are acceptable and achievable by real actuators. Therefore, it is indicated that the control law can be successfully applied to practical problems.

8. Conclusions

In the paper, a path-following algorithm based on the Serret–Frenet parametrization and non-orthogonal projection is presented. Its applicability was verified in a simulation study for a non-holonomic mobile manipulator following a B-spline curve.

The considered class of B-spline curves is particularly interesting. It can be easily defined based on the given set of control points. A considerable advantage of B-spline curves is the fact that the desired properties can be simply obtained by tuning the curve parameters. For instance, in Section 5 it was shown how the order of base polynomials impacts the curvature of a spline and the class of continuity in the knot points. The second aspect is particularly important in terms of satisfying the minimal requirements of the selected path parametrization method. In the example simulation study, presented in Section 7, we showed how to model the desired path in order to achieve a continuous performance of the controller. Although the followed curve is complex, as its curvature and torsion are variable along the curve, the proposed controller allows following the path successfully.

Moreover, it is noteworthy that the lower the order of the B-spline curve, the better the control points are mapped. Therefore, the requirement of the Serret–Frenet parametrization for the a class of at least ${\mathcal{C}}^3$ may sometimes be too strict, and other methods, e.g., the Bishop method, should be considered to describe the path. As a result, a more precise performance in the path-following task may be achieved.

The presented study highlights the usability of the algorithm to control mobile manipulators, since their importance in robotic solutions is constantly increasing. Indeed, in future research, an experimental validation should be additionally performed. The validation methodology may be inspired by the one proposed for a fixed-base manipulator in [32]. Such a process will be important in order to confirm the practical suitability of the control law presented in this paper. It would also be essential to verify the control system behaviour in the knot points of the reduced continuity class.