Robust Adaptive-Sliding-Mode Control for Teleoperation Systems with Time-Varying Delays and Uncertainties ^†

Abstract

Master–slave teleoperation systems with haptic feedback enable human operators to interact with objects or perform tasks in remote environments. This paper presents a sliding-mode control scheme tailored for bilateral teleoperation systems operating in the presence of unknown uncertainties and time-varying delays. To address unknown but bounded uncertainties, adaptive laws are derived alongside controller design. Additionally, a linear matrix inequality is solved to determine the allowable bound of delays. Stability of the closed-loop system is ensured through Lyapunov–Krasovskii functional analysis. Two-degree-of-freedom mechanisms are self-built as haptic devices. Free-motion and force-perception scenarios are examined, with experimental results validating and comparing performances. The proposed adaptive-sliding-control method increases the position performance from 58.48% to 82.55% and the force performance from 83.48% to 99.77%. The proposed control scheme demonstrates enhanced position tracking and force perception in bilateral teleoperation systems.

1. Introduction

The structure of teleoperation systems typically consists of several key components: human operator, master manipulator, slave manipulator, and communication channel. The interactions between these components form the basis of teleoperation systems, enabling human operators to control systems and interact with remote environments effectively [1,2]. In a teleoperation system, the human operator controls the master manipulator, usually through prescribed trajectories or specific tasks. The slave robot then follows the movements of the master manipulator in a free space, replicating the actions performed by the operator in the remote environment. Integrating haptic feedback into teleoperation systems enhances the operator’s situational awareness and dexterity, enabling more intuitive and precise control of the master manipulator while interacting with the remote environment. This contributes to improved task performance and overall efficiency in various teleoperation applications. The applications of teleoperation systems are versatile, such as in unmanned aerial vehicles [3,4,5], virtual reality [6,7], medical training [8,9,10], and telesurgery [11,12,13,14,15,16].

In recent years, significant advancements have been made in the development of teleoperation systems, with several methods and techniques being addressed to improve their performance, robustness, and versatility. In [17], an event-triggered mechanism combined with a PD-like controller was presented for bilateral teleoperation systems to address communication channel congestion. In [18], an adaptive proportional damping controller utilizing an RBF neural network and adaptive control strategy was proposed to enhance stability and performance in a telerobotic system. On the other hand, time-domain-passivity control is a widely used approach to preserve the stability of teleoperation systems. In general, it is expected to maintain the passivity of the system to ensure a safe and stable operation [19,20]. Bavili et al. [21] investigated the problem of asymptotic stability and position tracking in nonlinear teleoperation systems when interacting with non-passive operators and environments. In [22], a passivity controller was presented to compensate for the non-passivity induced by longitudinal slipping and lateral sliding of wheeled robots. In [23], a passivity-based delay predictor was proposed to improve the transparency of a four-channel bilateral teleoperation system. Passivity-based control was utilized to ensure energy stability, and shared variable impedance control can facilitate smooth collaboration in teleoperation [24]. Additionally, a passivity-based nonlinear controller was introduced for bilateral teleoperation system under variable time delay and load disturbance [25]. In [26], a neural network-based four-channel-time-domain-passivity approach was proposed for a teleoperation system with time-varying delays.

Obtaining precise dynamic models for both master and slave manipulators in a teleoperation system can be challenging due to various factors such as nonlinearities, uncertainties, and complex mechanical structures. Adaptive tuning methods have been proposed to overcome this problem. Yang et al. [27] addressed the problem of adaptive tracking control for a teleoperation system with uncertainties in both kinematics and dynamics. In [28], an adaptive fuzzy neural network-backstepping-control scheme was developed for bilateral teleoperation systems to handle time delays and uncertainties. In [29], a fixed-time adaptive neural network-synchronization control was presented for teleoperation systems, handling position-error constraints and time-varying delays. In [30], a type-2 fuzzy neural network was proposed to deal with time-varying delays and uncertainties. In [31], a type-2 fuzzy-based observer was introduced to estimate external force/torque information and simultaneously filter out system disturbances. In [32], an adaptive bilateral control strategy was introduced for underwater manipulator teleoperation, with adaptive RBF network compensation for slave-manipulator uncertainties. In [33], a radial basis function-neural network-based-sliding-mode-control design was developed for nonlinear bilateral teleoperation system with transmission delays and uncertainties. In addition, a sliding-mode controller combined with a nonlinear-disturbance observer was proposed, such that the asymptotical stability can be preserved [34]. Due to the superiority of its robustness, the sliding-mode control has become an effective scheme for network control systems that are subject to time delays, packet losses, uncertainties, disturbances, and/or faults [35].

The presence of communication time delays and model uncertainties can significantly impact the transparency and stability of teleoperation systems [36,37]. For constant delays, a terminal sliding-mode controller was discussed for time-delayed nonlinear teleoperation systems [38]. In [39], an observer-based force control scheme was proposed to guarantee the position and force tracking in nonlinear teleoperation systems, subject to a constant communication time delay. Moreover, a bilateral neural network adaptive controller was designed for a class of teleoperation systems with constant time delays, external disturbances, and internal friction [40]. In practice, it is more attractive to investigate the tracking stability of teleoperation systems subject to time-varying delays. In [41], a general framework was presented to analyze and optimize the transparency of multilateral systems under time-varying delays. In [42], an adaptive control framework was developed to simultaneously handle both unknown kinematics/dynamics and time-varying delays. In [43], a finite-time control method was presented for bilateral teleoperators to ensure the coordination of master and slave manipulators in the presence of time-varying delays, external disturbances, and dynamic uncertainties. Zakerimanesh et al. [44] presented a control framework for bilateral teleoperation systems experiencing bounded time-varying delays in their communication channels.

When analyzing time-delay issues, delay-dependent approaches are generally less conservative than delay-independent approaches. However, the derivation of delay-dependent stability conditions can be more complex than that for delay-independent approaches, particularly because delays are explicitly considered in the design of stabilizing controllers. In general, when dealing with time-delay systems, ensuring closed-loop stability is crucial for the overall performance and reliability of the system. To achieve this, various conditions related to controller parameters are often desired, especially those that explicitly consider the time delays. Lyapunov–Krasovskii functions and linear matrix inequalities (LMIs) are commonly employed tools for investigating the stability of time-delay systems [45,46,47,48,49,50,51].

The synthesis problem in time-delayed teleoperation systems involves designing stabilizing controllers to ensure closed-loop stability while minimizing conservatism and preserving transparency in teleoperation. This entails finding less conservative stabilizing controllers that can effectively handle time delays, especially those that vary over time. Delay-dependent approaches are preferred due to their ability to explicitly consider time delays, which leads to more accurate estimation of stability conditions and efficient controller designs. By addressing practical considerations such as time-varying delays, teleoperation systems can achieve robust performance and seamless interaction between the operator and the remote environment. In the works of [52], both symmetric and asymmetric time-varying delays in communication were addressed. Symmetry of the communication delays means that the delays of the forward and backward channels are equal. Symmetric delays could exist in a constrained environment such as a local wire-connected network with a strictly defined protocol. On the other hand, asymmetric communication delays would be more practical in internet or wireless networks. In existing works of asymmetric time-varying delays, the bounds of time-varying delays are usually given in advance, then a delay-dependent controller can be obtained to ensure closed-loop stability. In this paper, it is desired to find the allowable boundary of time-varying communication delays. For the purpose of concise computations, a symmetric teleoperation system is addressed. How to relax this assumption of symmetry would be another interesting topic.

Transparency is a critical issue in teleoperations. Ensuring precise force feedback across versatile environments is a primary task. Our proposed control strategies are designed to maintain high transparency by accurately replicating forces encountered in the remote environment, thus enhancing the user’s sense of presence and control. In this work, a novel adaptive-sliding-mode control scheme is proposed for bilateral teleoperation systems encountering model uncertainties and time-varying delays. The main contributions are as follows:

• The proposed method allows for the determination of admissible bounds of time-varying delays by solving linear matrix inequalities (LMIs), thus providing valuable insights into temporal constraints.
• The derived adaptive laws enable the estimation of bounds for unknown uncertainties, thereby enhancing the robustness of the controller against model uncertainties.
• Utilizing delay-dependent Lyapunov–Krasovskii functional analysis ensures the closed-loop stability of the teleoperation system, offering theoretical assurances even in the presence of delays and uncertainties.
• The control scheme addresses both free-motion and force-perception aspects of a general non-passive teleoperation system, thereby expanding its applicability across various scenarios.
• Conducting master–slave experiments validates the feasibility and effectiveness of the proposed control scheme in real-world settings, demonstrating its practical applicability and performance.

2. Materials and Methods

2.1. Preliminaries

The dynamic model for an nth degree master–slave robotic system can be described using the following equations:

$${\mathit{M}}_m\left({\mathit{q}}_m\right){\ddot{\mathit{q}}}_m+{\mathit{C}}_m\left({\mathit{q}}_m,{\dot{\mathit{q}}}_m\right){\dot{\mathit{q}}}_m+{\mathit{g}}_m\left({\mathit{q}}_m\right)+{\mathit{\delta }}_m={\mathit{\tau }}_m+{\mathit{f}}_h$$

(1)

$${\mathit{M}}_s\left({\mathit{q}}_s\right){\ddot{\mathit{q}}}_s+{\mathit{C}}_s\left({\mathit{q}}_s,{\dot{\mathit{q}}}_s\right){\dot{\mathit{q}}}_s+{\mathit{g}}_s\left({\mathit{q}}_s\right)+{\mathit{\delta }}_s={\mathit{\tau }}_s-{\mathit{f}}_e$$

(2)

where the subscripts m and s represent the master and slave, respectively, ${\mathit{q}}_m$ and ${\mathit{q}}_s\in {\mathcal{R}}^n$ are the vectors joint positions, ${\mathit{M}}_m\left({\mathit{q}}_m\right)$ and ${\mathit{M}}_s\left(q_s\right)\in {\mathcal{R}}^{n\times n}$ are the inertia matrices, ${\mathit{C}}_m\left({\mathit{q}}_m,{\dot{\mathit{q}}}_m\right)$ and ${\mathit{C}}_s\left({\mathit{q}}_s,{\dot{\mathit{q}}}_s\right)\in {\mathcal{R}}^{n\times n}$ are the Coriolis matrices, ${\mathit{g}}_m\left({\mathit{q}}_m\right)$ and ${\mathit{g}}_s\left({\mathit{q}}_s\right)\in {\mathcal{R}}^n$ are the gravitational vectors, ${\mathit{\tau }}_m$ and ${\mathit{\tau }}_s\in {\mathcal{R}}^n$ are vectors of input torques, ${\mathit{f}}_h$ and ${\mathit{f}}_e\in {\mathcal{R}}^n$ are the human operation force and the environmental force, and ${\mathit{\delta }}_m$ and ${\mathit{\delta }}_s$ are the unknown uncertainties of the master and slave robots, respectively. In this paper, the human operator’s force ${\mathit{f}}_h$ and the environmental force ${\mathit{f}}_e$ are non-passive [53,54]:

$${\mathit{f}}_h={\mathit{k}}_h-{\mathit{D}}_h{\dot{\mathit{q}}}_m-{\mathit{K}}_h{\mathit{q}}_m$$

(3)

$${\mathit{f}}_e={\mathit{k}}_e-{\mathit{D}}_e{\dot{\mathit{q}}}_s-{\mathit{K}}_e{\mathit{q}}_s$$

(4)

where ${\mathit{k}}_h$ and ${\mathit{k}}_e$ are constant vectors of ${\mathcal{R}}^n$, and ${\mathit{D}}_h$ and ${\mathit{K}}_h\in {\mathcal{R}}^{n\times n}$ are the damping and spring-constant matrices for human force, respectively. In addition, ${\mathit{D}}_e$ and ${\mathit{K}}_e\in {\mathcal{R}}^{n\times n}$ represent the damping and spring-constant matrices for the environmental force, respectively.

Property 1.

The inertia matrix ${\mathit{M}}_i\left({\mathit{q}}_i\right)$ is symmetric and positive definite. Let ${\overline{\lambda }}_i$ be the maximum eigenvalue of ${\mathit{M}}_i\left({\mathit{q}}_i\right)$. Then, ${\mathit{M}}_i\left({\mathit{q}}_i\right)\le {\overline{\lambda }}_i{\mathit{I}}_n$ where ${\mathit{I}}_n\in {\mathcal{R}}^{n\times n}$ is the identity matrix, $i\in \{m,s\}$.

Property 2.

The matrix ${\dot{\mathit{M}}}_i\left({\mathit{q}}_i\right)-2{\mathit{C}}_i({\mathit{q}}_i,{\dot{\mathit{q}}}_i)$ is skewed symmetric, $i\in \{m,s\}$.

Property 3.

There exists a positive constant $c_i$ such that ${‖{\mathit{C}}_i({\mathit{q}}_i,{\dot{\mathit{q}}}_i)‖}_2\le c_i$, where ${‖·‖}_2$ represents the ${\mathcal{L}}_2$ norm, $i\in \{m,s\}$.

Assumption 1.

Let ${\mathit{\delta }}_i={[{\delta }_{i1}\hspace{1em}{\delta }_{i2}\hspace{1em}\dots \hspace{1em}{\delta }_{in}]}^T$ be bounded by ${\overline{\mathit{\delta }}}_i={\left[\begin{array}{cc}\begin{array}{cc}{\overline{\delta }}_{i1}& {\overline{\delta }}_{i2}\end{array}& \begin{array}{cc}\dots & {\overline{\delta }}_{in}\end{array}\end{array}\right]}^T,$ $\left|{\delta }_{ij}\right|<{\overline{\delta }}_{ij}$, where ${\overline{\delta }}_{ij}$ is an unknown constant, $i\in \{m,s\}$, $j=1, 2,\dots n$.

Lemma 1.

[55] Given a positive-definite matrix R, the following inequality holds

$$2{\mathit{X}}^T\mathit{Y}\le {\mathit{X}}^T\mathit{R}\mathit{X}+{\mathit{Y}}^T{\mathit{R}}^{-1}\mathit{Y},$$

(5)

where $X$ and $Y$ are two matrices with proper dimensions.

Lemma 2.

[56] Let $\mathit{O}=\left[\begin{array}{cc}{\mathit{O}}_{11}& {\mathit{O}}_{12}\\ {\mathit{O}}_{12}^T& {-\mathit{O}}_{22}\end{array}\right]$ be a matrix with proper dimensions, ${\mathit{O}}_{22}>0$. Then the following equation holds:

$$\mathit{O}<0⟺{\mathit{O}}_{11}+{\mathit{O}}_{12}{\mathit{O}}_{22}^{-1}{\mathit{O}}_{12}^T<0.$$

(6)

2.2. Adaptive-Sliding-Mode-Controller Design

In the context of the time-delayed teleoperation system described by Equations (1) and (2), a sliding-mode controller will be designed to achieve asymptotically stable sliding motion.

Assumption 2.

The forward and backward communication delays are symmetric, and the time-varying delay $d\left(t\right)$ satisfies the conditions that

$$0<\mathit{d}\left(\mathit{t}\right)\le \overline{\mathit{d}}<\mathit{\infty }, \dot{\mathit{d}}\left(\mathit{t}\right)\le \mathit{\mu }<1,$$

(7)

where $\overline{d}$ and $\mu$ are positive constants.

Remark 1.

If $\dot{d}\left(t\right)\ge 1$, then the delay will grow faster than the increase in time. As the manipulator devices are required to track some delayed trajectories, the control loop becomes open. Under this circumstance, the controller design and related stability analysis opens a new theoretical problem, which cannot be solved at current stage and needs to be investigated separately [42].

In the following equations, the notations ${\mathit{q}}_{\mathit{m},\mathit{d}}$ and ${\mathit{q}}_{\mathit{s},\mathit{d}}$ are used to stand for ${\mathit{q}}_{\mathit{m}}\left(t-d\left(t\right)\right)$ and ${\mathit{q}}_{\mathit{s}}\left(t-d\left(t\right)\right)$, respectively, for simplicity. The sliding surfaces for the master and slave robots are defined, respectively, as

$${\mathit{s}}_{\mathit{m}}={\dot{\mathit{q}}}_{\mathit{m}}+{\mathit{K}}_{\mathit{m}}({\mathit{q}}_{\mathit{m}}-{\mathit{q}}_{\mathit{s},\mathit{d}})$$

$${\mathit{s}}_{\mathit{s}}={\dot{\mathit{q}}}_{\mathit{s}}+{\mathit{K}}_{\mathit{s}}({\mathit{q}}_{\mathit{s}}-{\mathit{q}}_{\mathit{m},\mathit{d}})$$

(8)

where ${\mathit{K}}_{\mathit{m}}=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\left\{k_{m1},k_{m2},\dots ,k_{mn}\right\}\in {\mathcal{R}}^{n\times n}$ and ${\mathit{K}}_{\mathit{s}}=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\left\{k_{s1},k_{s2},\dots ,k_{sn}\right\}\in {\mathcal{R}}^{n\times n},$ $k_{mj}>0$, and $k_{sj}>0$, $j=\mathrm{1,2},\dots ,n$. Then, the sliding mode of (8), ${\mathit{s}}_{\mathit{m}}={\mathit{s}}_{\mathit{s}}=\mathbf{0}$, can be equivalently described as

$${\dot{\mathit{q}}}_{\mathit{m}}=-{\mathit{K}}_{\mathit{m}}({\mathit{q}}_{\mathit{m}}-{\mathit{q}}_{\mathit{s},\mathit{d}})$$

$${\dot{\mathit{q}}}_{\mathit{s}}=-{\mathit{K}}_{\mathit{s}}({\mathit{q}}_{\mathit{s}}-{\mathit{q}}_{\mathit{m},\mathit{d}})$$

(9)

Let the error functions of the master and slave sides, respectively, be defined as

$${\mathit{e}}_{\mathit{m}}={\mathit{q}}_{\mathit{m}}-{\mathit{q}}_{\mathit{s}}, {\mathit{e}}_{\mathit{s}}={\mathit{q}}_{\mathit{s}}-{\mathit{q}}_{\mathit{m}}$$

(10)

From (9) and (10), it can be determined that

$$\dot{\mathit{e}}=-{\mathit{A}}_{\mathbf{1}}\mathit{e}-{\mathit{A}}_{\mathbf{1}}{\mathit{e}}_{\mathit{d}}$$

(11)

where $\mathit{e}={\left[\begin{array}{cc}{\mathit{e}}_{\mathit{m}}^{\mathit{T}}& {\mathit{e}}_{\mathit{s}}^{\mathit{T}}\end{array}\right]}^{\mathit{T}}$, ${\mathit{e}}_{\mathit{d}}=\mathit{e}(\mathit{t}-\mathit{d}\left(\mathit{t}\right))$, and ${\mathit{A}}_{\mathbf{1}}=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\left\{{\mathit{K}}_{\mathit{m}},{\mathit{K}}_{\mathit{s}}\right\}$.

Theorem 1.

The error functions of (10) are asymptotically convergent if the following inequality holds:

$$\left[\begin{array}{cccc}{\mathit{\Theta }}_{\mathbf{11}}& {\mathit{A}}_{\mathbf{1}}{\mathit{P}}_{\mathit{s}}& {\mathbf{0}}_{\mathbf{2}\mathit{n}}& {\mathit{A}}_{\mathbf{1}}\\ {\mathit{P}}_{\mathit{s}}{\mathit{A}}_{\mathbf{1}}& -{\overline{\mathit{d}}}^{-\mathbf{1}}{\mathit{R}}_{\mathit{s}}& {\mathbf{0}}_{\mathbf{2}\mathit{n}}& {\mathbf{0}}_{\mathbf{2}\mathit{n}}\\ {\mathbf{0}}_{\mathbf{2}\mathit{n}}& {\mathbf{0}}_{\mathbf{2}\mathit{n}}& -\tilde{\mathit{\mu }}{\mathit{Q}}_{\mathit{s}}& {\mathit{A}}_{\mathbf{1}}\\ {\mathit{A}}_{\mathbf{1}}& {\mathbf{0}}_{\mathbf{2}\mathit{n}}& {\mathit{A}}_{\mathbf{1}}& {-\left(\overline{\mathit{d}}{\mathit{R}}_{\mathit{s}}\right)}^{-\mathbf{1}}\end{array}\right]<\mathbf{0}$$

(12)

where ${\mathit{P}}_{\mathit{s}}$, ${\mathit{Q}}_{\mathit{s}}$, and ${\mathit{R}}_{\mathit{s}}$ are symmetric positive-definite matrices of ${\mathcal{R}}^{2n\times 2n}$, ${\mathit{\Theta }}_{\mathbf{11}}=-\mathbf{4}{\mathit{P}}_{\mathit{s}}{\mathit{A}}_{\mathbf{1}}+{\mathit{Q}}_{\mathit{s}}$, $\tilde{\mu }=1-\mu$, and ${\mathbf{0}}_{\mathbf{2}\mathit{n}}$ is a zero matrix of dimension $2n\times 2n$.

Proof. 

A Lyapunov–Krasovskii function is chosen as

$${\mathit{V}}_{\mathit{s}}={\mathit{e}}^{\mathit{T}}{\mathit{P}}_{\mathit{s}}\mathit{e}+{\int }_{\mathit{t}-\mathit{d}\left(\mathit{t}\right)}^{\mathit{t}}{\mathit{e}}^{\mathit{T}}(\mathit{s}){\mathit{Q}}_{\mathit{s}}\mathit{e}(\mathit{s})\mathit{d}\mathit{s}+{\int }_{-\overline{\mathit{d}}}^{\mathbf{0}}{\int }_{\mathit{t}+\mathit{\theta }}^{\mathit{t}}{\dot{\mathit{e}}}^{\mathit{T}}(\mathit{s}){\mathit{R}}_{\mathit{s}}\dot{\mathit{e}}(\mathit{s})\mathit{d}\mathit{s}\mathit{d}\mathit{\theta }.$$

(13)

The time derivative of ${\mathit{V}}_{\mathit{s}}$ from (11) is derived as

$$\begin{gathered} {\dot{\mathit{V}}}_{\mathit{s}}\le \mathbf{2}{\mathit{e}}^{\mathit{T}}{\mathit{P}}_{\mathit{s}}\left(-{\mathit{A}}_{\mathbf{1}}\mathit{e}-{\mathit{A}}_{\mathbf{1}}{\mathit{e}}_{\mathit{d}}\right)+{\mathit{e}}^{\mathit{T}}{\mathit{Q}}_{\mathit{s}}\mathit{e}-\tilde{\mu }{\mathit{e}}_{\mathit{d}}^{\mathit{T}}{\mathit{Q}}_{\mathit{s}}{\mathit{e}}_{\mathit{d}} \\ +\overline{d}{(-{\mathit{A}}_{\mathbf{1}}\mathit{e}-{\mathit{A}}_{\mathbf{1}}{\mathit{e}}_{\mathit{d}})}^{\mathit{T}}{\mathit{R}}_{\mathit{s}}\left(-{\mathit{A}}_{\mathbf{1}}\mathit{e}-{\mathit{A}}_{\mathbf{1}}{\mathit{e}}_{\mathit{d}}\right)-{\int }_{\mathit{t}-\overline{\mathit{d}}}^{\mathit{t}}{\dot{\mathit{e}}}^{\mathit{T}}\left(\mathit{s}\right){\mathit{R}}_{\mathit{s}}\dot{\mathit{e}}(\mathit{s})\mathit{d}\mathit{s} \end{gathered}$$

(14)

It is noted that ${\mathit{e}}_{\mathit{d}}=\mathit{e}-{\int }_{\mathit{t}-\mathit{d}\left(\mathit{t}\right)}^{\mathit{t}}\dot{\mathit{e}}\left(\mathit{s}\right)\mathit{d}\mathit{s}$. Then, from Lemma 1 and Assumption 2, it leads to the following inequality

$$\begin{gathered} {\dot{\mathit{V}}}_{\mathit{s}}\le -\mathbf{4}{\mathit{e}}^{\mathit{T}}{\mathit{P}}_{\mathit{s}}{\mathit{A}}_{\mathbf{1}}\mathit{e}+\overline{\mathit{d}}{\mathit{e}}^{\mathit{T}}{\mathit{P}}_{\mathit{s}}{\mathit{A}}_{\mathbf{1}}{\mathit{R}}_{\mathit{s}}^{-\mathbf{1}}{\mathit{A}}_{\mathbf{1}}{\mathit{P}}_{\mathit{s}}\mathit{e}+{\mathit{e}}^{\mathit{T}}{\mathit{Q}}_{\mathit{s}}\mathit{e}{-\tilde{\mathit{\mu }}\mathit{e}}_{\mathit{d}}^{\mathit{T}}{\mathit{Q}}_{\mathit{s}}{\mathit{e}}_{\mathit{d}}+\overline{\mathit{d}}{\mathit{e}}^{\mathit{T}}{\mathit{A}}_{\mathbf{1}}{\mathit{R}}_{\mathit{s}}{\mathit{A}}_{\mathbf{1}}\mathit{e} \\ +\mathbf{2}\overline{\mathit{d}}{\mathit{e}}^{\mathit{T}}{\mathit{A}}_{\mathbf{1}}{\mathit{R}}_{\mathit{s}}{\mathit{A}}_{\mathbf{1}}{\mathit{e}}_{\mathit{d}}+\overline{\mathit{d}}{\mathit{e}}_{\mathit{d}}^{\mathit{T}}{\mathit{A}}_{\mathbf{1}}{\mathit{R}}_{\mathit{s}}{\mathit{A}}_{\mathbf{1}}{\mathit{e}}_{\mathit{d}}={\left[\begin{array}{c}\mathit{e}\\ {\mathit{e}}_{\mathit{d}}\end{array}\right]}^{\mathit{T}}\mathit{\Theta }\left[\begin{array}{c}\mathit{e}\\ {\mathit{e}}_{\mathit{d}}\end{array}\right] \end{gathered}$$

(15)

where

$$\mathit{\Theta }=\left[\begin{array}{cc}{\mathit{\Theta }}_{\mathbf{1}}& \overline{d}{\mathit{A}}_{\mathbf{1}}{\mathit{R}}_{\mathit{s}}{\mathit{A}}_{\mathbf{1}}\\ \overline{d}{\mathit{A}}_{\mathbf{1}}{\mathit{R}}_{\mathit{s}}{\mathit{A}}_{\mathbf{1}}& \overline{d}{\mathit{A}}_{\mathbf{1}}{\mathit{R}}_{\mathit{s}}{\mathit{A}}_{\mathbf{1}}-\tilde{\mu }{\mathit{Q}}_{\mathit{s}}\end{array}\right],{ \mathit{\Theta }}_{\mathbf{1}}=-\mathbf{4}{\mathit{P}}_{\mathit{s}}{\mathit{A}}_{\mathbf{1}}+{\mathit{Q}}_{\mathit{s}}+\overline{d}{\mathit{P}}_{\mathit{s}}{\mathit{A}}_{\mathbf{1}}{\mathit{R}}_{\mathit{s}}^{-\mathbf{1}}{\mathit{A}}_{\mathbf{1}}{\mathit{P}}_{\mathit{s}}+\overline{d}{\mathit{A}}_{\mathbf{1}}{\mathit{R}}_{\mathit{s}}{\mathit{A}}_{\mathbf{1}}$$

(16)

From Lemma 2, ${\dot{\mathit{V}}}_{\mathit{s}}$ is negative if (12) holds. This implies that the error dynamics of (11) is asymptotically stable. This completes the proof. □

The sliding-mode-based controllers for the torques acting on the delayed teleoperation system are designed as

$${\mathsf{\tau }}_{\mathit{m}}={\mathit{\tau }}_{\mathit{e}\mathit{q},\mathit{m}}+{\mathit{\tau }}_{\mathit{s}\mathit{w},\mathit{m}}$$

(17)

$${\mathit{\tau }}_{\mathit{s}}={\mathit{\tau }}_{\mathit{e}\mathit{q},\mathit{s}}+{\mathit{\tau }}_{\mathit{s}\mathit{w},\mathit{s}}$$

(18)

where ${\mathit{\tau }}_{\mathit{e}\mathit{q},\mathit{m}}$ and ${\mathit{\tau }}_{\mathit{e}\mathit{q},\mathit{s}}$ are the equivalent control actions and ${\mathit{\tau }}_{\mathit{s}\mathit{w},\mathit{m}}$ and ${\mathit{\tau }}_{\mathit{s}\mathit{w},\mathit{s}}$ are the switching controllers. From (1) and (2), considering the uncertainty-free case, the equivalent controllers ${\mathit{\tau }}_{\mathit{e}\mathit{q},\mathit{m}}$ and ${\mathit{\tau }}_{\mathit{e}\mathit{q},\mathit{s}}$ can be determined as

$${\mathit{\tau }}_{\mathit{e}\mathit{q},\mathit{m}}=-{\mathit{M}}_{\mathit{m}}{\mathit{K}}_{\mathit{m}}\left({\dot{\mathit{q}}}_{\mathit{m}}-{\dot{\mathit{q}}}_{\mathit{s},\mathit{d}}\right)+{\mathit{C}}_{\mathit{m}}{\dot{\mathit{q}}}_{\mathit{m}}+{\mathit{g}}_{\mathit{m}}$$

(19)

$${\mathit{\tau }}_{\mathit{e}\mathit{q},\mathit{s}}=-{\mathit{M}}_{\mathit{s}}{\mathit{K}}_{\mathit{s}}\left({\dot{\mathit{q}}}_{\mathit{s}}-{\dot{\mathit{q}}}_{\mathit{m},\mathit{d}}\right)+{\mathit{C}}_{\mathit{s}}{\dot{\mathit{q}}}_{\mathit{s}}+{\mathit{g}}_{\mathit{s}}$$

(20)

It is noted that the uncertain terms ${\mathit{\delta }}_{\mathit{m}}$ and ${\mathit{\delta }}_{\mathit{s}}$ of (1) and (2) are unknown but bounded. To estimate ${\overline{\mathit{\delta }}}_{\mathit{m}}={\left[\begin{array}{cc}\begin{array}{cc}{\overline{\delta }}_{m1}& {\overline{\delta }}_{m2}\end{array}& \begin{array}{cc}\dots & {\overline{\delta }}_{mn}\end{array}\end{array}\right]}^{\mathit{T}}$ and ${\overline{\mathit{\delta }}}_{\mathit{s}}={\left[\begin{array}{cc}\begin{array}{cc}{\overline{\delta }}_{s1}& {\overline{\delta }}_{s2}\end{array}& \begin{array}{cc}\dots & {\overline{\delta }}_{sn}\end{array}\end{array}\right]}^{\mathit{T}}$, the adaptive laws are designated as follows:

$${\dot{\widehat{\overline{\mathit{\delta }}}}}_{\mathit{m}}=\left\{\begin{array}{cc}\mathit{\Gamma }{\mathit{M}}_{\mathit{m}}^{-\mathbf{1}}\left|{\mathit{s}}_{\mathit{m}}\right|,& if {\mathit{f}}_{\mathit{h}}=\mathbf{0},\\ \mathbf{0},& if {\mathit{f}}_{\mathit{h}}\ne \mathbf{0}.\end{array}\right.$$

(21)

$${\dot{\widehat{\overline{\mathit{\delta }}}}}_{\mathit{s}}=\left\{\begin{array}{cc}\mathit{\Gamma }{\mathit{M}}_{\mathit{s}}^{-\mathbf{1}}\left|{\mathit{s}}_{\mathit{s}}\right|,& if {\mathit{f}}_{\mathit{e}}=\mathbf{0},\\ \mathbf{0},& if {\mathit{f}}_{\mathit{e}}\ne \mathbf{0}.\end{array}\right.$$

(22)

where ${\widehat{\overline{\mathit{\delta }}}}_{\mathit{m}}$ and ${\widehat{\overline{\mathit{\delta }}}}_{\mathit{s}}\in {\mathcal{R}}^n$, $\mathit{\Gamma }=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\{{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\}\in {\mathcal{R}}^{n\times n}$, ${\gamma }_j>0,j=1,2,\dots ,n,$ $\left|{\mathit{s}}_{\mathit{m}}\right|={\left[\begin{array}{cc}\begin{array}{cc}\left|{\mathit{s}}_{\mathit{m}\mathbf{1}}\right|& \left|{\mathit{s}}_{\mathit{m}\mathbf{2}}\right|\end{array}& \begin{array}{cc}\dots & \left|{\mathit{s}}_{\mathit{m}\mathit{n}}\right|\end{array}\end{array}\right]}^{\mathit{T}}$, and $\left|{\mathit{s}}_{\mathit{s}}\right|={\left[\begin{array}{cc}\begin{array}{cc}\left|{\mathit{s}}_{\mathit{s}\mathbf{1}}\right|& \left|{\mathit{s}}_{\mathit{s}\mathbf{2}}\right|\end{array}& \begin{array}{cc}\dots & \left|{\mathit{s}}_{\mathit{s}\mathit{n}}\right|\end{array}\end{array}\right]}^{\mathit{T}}$.

In this paper, the switching controllers are formulated as

$${\mathit{\tau }}_{\mathit{s}\mathit{w},\mathit{m}}=-({\mathit{\Phi }}_{\mathit{m}}+{\widehat{\mathsf{\Delta }}}_{\mathit{m}})\mathit{s}\mathit{g}\mathit{n}\left({\mathit{s}}_{\mathit{m}}\right),$$

(23)

$${\mathit{\tau }}_{\mathit{s}\mathit{w},\mathit{s}}=-({\mathit{\Phi }}_{\mathit{s}}+{\widehat{\mathsf{\Delta }}}_{\mathit{s}})\mathit{s}\mathit{g}\mathit{n}\left({\mathit{s}}_{\mathit{s}}\right),$$

(24)

in which ${\mathit{\Phi }}_{\mathit{m}}=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\left\{{\varphi }_{m1},{\varphi }_{m2},\dots ,{\varphi }_{mn}\right\}\in {\mathcal{R}}^{n\times n},{\mathit{\Phi }}_{\mathit{s}}=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\left\{{\varphi }_{s1},{\varphi }_{s2},\dots ,{\varphi }_{sn}\right\}\in {\mathcal{R}}^{n\times n},$ ${\varphi }_{mj}>0$, ${\varphi }_{sj}>0$, $j=1,2,\dots ,n$, and $\mathit{s}\mathit{g}\mathit{n}(·)$ is a standard sign function. In addition, ${\widehat{\mathsf{\Delta }}}_{\mathit{m}}=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\{{\widehat{\overline{\delta }}}_{m1},{\widehat{\overline{\delta }}}_{m2},\dots ,{\widehat{\overline{\delta }}}_{mn}\}$ and ${\widehat{\mathsf{\Delta }}}_{\mathit{s}}=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\{{\widehat{\overline{\delta }}}_{s1},{\widehat{\overline{\delta }}}_{s2},\dots ,{\widehat{\overline{\delta }}}_{sn}\}$.

Remark 2.

The required input torques on the master and slave sides are shown in (17) and (18). The input torques include both equivalent and switching control actions. For example, the input torque ${\mathit{\tau }}_{\mathit{m}}$ can be obtained from ${\mathit{\tau }}_{\mathit{e}\mathit{q},\mathit{m}}$ and ${\mathit{\tau }}_{\mathit{s}\mathit{w},\mathit{m}}$ in Equations (17), (19) and (23). In (23), an adaptive law for the unknown bounded uncertainties is designed as (21). Similarly, the input torque ${\mathit{\tau }}_{\mathit{s}}$ can be implemented with Equations (18), (20), (22), and (24). The scheme diagram of the proposed teleoperation system is shown in Figure 1.

Remark 3.

There could be a potential issue of chattering associated with the use of the sign function in the controller (23) and (24). To address this common chattering problem, a smoothing technique can be employed by replacing the sign function with a continuous approximation, such as a saturation function or a boundary-layer approach.

Theorem 2.

Consider the bilateral teleoperation systems (1) and (2). In free motion, ${\mathit{f}}_{\mathit{h}}={\mathit{f}}_{\mathit{e}}=\mathbf{0}$, and the state trajectories of teleoperation systems (1) and (2) will be driven onto the sliding surfaces (8) with the controllers (17) and (18) and the adaptive laws (21), (22).

Proof. 

Let a Lyapunov function be chosen as

$${\mathit{V}}_{\mathit{c}}=\frac{\mathbf{1}}{\mathbf{2}}\left({\mathit{s}}_{\mathit{m}}^{\mathit{T}}{\mathit{s}}_{\mathit{m}}+{\tilde{\mathit{\delta }}}_{\mathit{m}}^{\mathit{T}}{\mathit{\Gamma }}^{-\mathbf{1}}{\tilde{\mathit{\delta }}}_{\mathit{m}}+{\mathit{s}}_{\mathit{s}}^{\mathit{T}}{\mathit{s}}_{\mathit{s}}+{\tilde{\mathit{\delta }}}_{\mathit{s}}^{\mathit{T}}{\mathit{\Gamma }}^{-\mathbf{1}}{\tilde{\mathit{\delta }}}_{\mathit{s}}\right)$$

(25)

where ${\tilde{\mathit{\delta }}}_{\mathit{m}}={\overline{\mathit{\delta }}}_{\mathit{m}}-{\widehat{\overline{\mathit{\delta }}}}_{\mathit{m}}$, and ${\tilde{\mathit{\delta }}}_{\mathit{s}}={\overline{\mathit{\delta }}}_{\mathit{s}}-{\widehat{\overline{\mathit{\delta }}}}_{\mathit{s}}$ are the estimation errors. The derivative of (8) is obtained as

$${\dot{\mathit{s}}}_{\mathit{m}}={\ddot{\mathit{q}}}_{\mathit{m}}+{\mathit{K}}_{\mathit{m}}({\dot{\mathit{q}}}_{\mathit{m}}-{\dot{\mathit{q}}}_{\mathit{s},\mathit{d}}),$$

$${\dot{\mathit{s}}}_{\mathit{s}}={\ddot{\mathit{q}}}_{\mathit{s}}+{\mathit{K}}_{\mathit{s}}({\dot{\mathit{q}}}_{\mathit{s}}-{\dot{\mathit{q}}}_{\mathit{m},\mathit{d}}).$$

(26)

The derivative of ${\mathit{V}}_{\mathit{c}}$ along (26) is

$$\begin{gathered} {\dot{\mathit{V}}}_{\mathit{c}}={\mathit{s}}_{\mathit{m}}^{\mathit{T}}\left({\mathit{M}}_{\mathit{m}}^{-\mathbf{1}}\left({\mathit{\tau }}_{\mathit{m}}-{\mathit{C}}_{\mathit{m}}{\dot{\mathit{q}}}_{\mathit{m}}-{\mathit{g}}_{\mathit{m}}-{\mathit{\delta }}_{\mathit{m}}\right)+{\mathit{K}}_{\mathit{m}}\left({\dot{\mathit{q}}}_{\mathit{m}}-{\dot{\mathit{q}}}_{\mathit{s},\mathit{d}}\right)\right) \\ {+\mathit{s}}_{\mathit{s}}^{\mathit{T}}\left({\mathit{M}}_{\mathit{s}}^{-\mathbf{1}}\left({\mathit{\tau }}_{\mathit{s}}-{\mathit{C}}_{\mathit{s}}{\dot{\mathit{q}}}_{\mathit{s}}-{\mathit{g}}_{\mathit{s}}-{\mathit{\delta }}_{\mathit{s}}\right)+{\mathit{K}}_{\mathit{s}}\left({\dot{\mathit{q}}}_{\mathit{s}}-{\dot{\mathit{q}}}_{\mathit{m},\mathit{d}}\right)\right)-{\tilde{\mathit{\delta }}}_{\mathit{m}}^{\mathit{T}}{\mathit{\Gamma }}^{-\mathbf{1}}{\dot{\widehat{\overline{\mathit{\delta }}}}}_{\mathit{m}}-{\tilde{\mathit{\delta }}}_{\mathit{s}}^{\mathit{T}}{\mathit{\Gamma }}^{-\mathbf{1}}{\dot{\widehat{\overline{\mathit{\delta }}}}}_{\mathit{s}}. \end{gathered}$$

(27)

From Assumption 1, this gives the following:

$$\begin{gathered} {\dot{\mathit{V}}}_{\mathit{c}}<{\mathit{s}}_{\mathit{m}}^{\mathit{T}}\left({\mathit{M}}_{\mathit{m}}^{-\mathbf{1}}\left({\mathit{\tau }}_{\mathit{m}}-{\mathit{C}}_{\mathit{m}}{\dot{\mathit{q}}}_{\mathit{m}}-{\mathit{g}}_{\mathit{m}}\right)+{\mathit{K}}_{\mathit{m}}\left({\dot{\mathit{q}}}_{\mathit{m}}-{\dot{\mathit{q}}}_{\mathit{s},\mathit{d}}\right)\right) \\ {+\mathit{s}}_{\mathit{s}}^{\mathit{T}}\left({\mathit{M}}_{\mathit{s}}^{-\mathbf{1}}\left({\mathit{\tau }}_{\mathit{s}}-{\mathit{C}}_{\mathit{s}}{\dot{\mathit{q}}}_{\mathit{s}}-{\mathit{g}}_{\mathit{s}}\right)+{\mathit{K}}_{\mathit{s}}\left({\dot{\mathit{q}}}_{\mathit{s}}-{\dot{\mathit{q}}}_{\mathit{m},\mathit{d}}\right)\right) \\ +{\left|{\mathit{s}}_{\mathit{m}}\right|}^{\mathit{T}}{\mathit{M}}_{\mathit{m}}^{-\mathbf{1}}{\overline{\mathit{\delta }}}_{\mathit{m}}+{\left|{\mathit{s}}_{\mathit{s}}\right|}^{\mathit{T}}{\mathit{M}}_{\mathit{s}}^{-\mathbf{1}}{\overline{\mathit{\delta }}}_{\mathit{s}}-{\tilde{\mathit{\delta }}}_{\mathit{m}}^{\mathit{T}}{\mathit{\Gamma }}^{-\mathbf{1}}{\dot{\widehat{\overline{\mathit{\delta }}}}}_{\mathit{m}}-{\tilde{\mathit{\delta }}}_{\mathit{s}}^{\mathit{T}}{\mathit{\Gamma }}^{-\mathbf{1}}{\dot{\widehat{\overline{\mathit{\delta }}}}}_{\mathit{s}}. \end{gathered}$$

(28)

Substituting (17), (18), and (21) into (28), it yields

$${\dot{\mathit{V}}}_{\mathit{c}}<-{\mathit{s}}_{\mathit{m}}^{\mathit{T}}{\mathit{\Phi }}_{\mathit{m}}{\mathit{M}}_{\mathit{m}}^{-\mathbf{1}}\mathit{s}\mathit{g}\mathit{n}\left({\mathit{s}}_{\mathit{m}}\right)-{\mathit{s}}_{\mathit{s}}^{\mathit{T}}{\mathit{\Phi }}_{\mathit{s}}{\mathit{M}}_{\mathit{s}}^{-\mathbf{1}}\mathit{s}\mathit{g}\mathit{n}\left({\mathit{s}}_{\mathit{s}}\right)$$

(29)

From (25) to (29), it is evident that the negative definiteness of ${\mathit{V}}_{\mathit{c}}$ can be preserved, which means that ${\mathit{s}}_{\mathit{m}}$, ${\mathit{s}}_{\mathit{s}}$, ${\tilde{\mathit{\delta }}}_{\mathit{m}}$, and ${\tilde{\mathit{\delta }}}_{\mathit{m}}$ are bounded. Therefore, the systems (1) and (2) are stable. Hence, the states of the teleoperation system (1) and (2) will reach the sliding surface (8). The proof is completed. □

2.3. Stability Analysis

Substituting (3), (4), (17), and (18) into (1) and (2), the closed-loop teleoperation systems can be represented as

$${\mathit{M}}_{\mathit{m}}{\ddot{\mathit{q}}}_{\mathit{m}}=-{\mathit{M}}_{\mathit{m}}{\mathit{K}}_{\mathit{m}}\left({\dot{\mathit{q}}}_{\mathit{m}}-{\dot{\mathit{q}}}_{\mathit{s},\mathit{d}}\right)+{\mathit{ϵ}}_{\mathit{m}}+{\mathit{k}}_{\mathit{h}}-{\mathit{D}}_{\mathit{h}}{\dot{\mathit{q}}}_{\mathit{m}}-{\mathit{K}}_{\mathit{h}}{\mathit{q}}_{\mathit{m}}$$

$${\mathit{M}}_{\mathit{s}}{\ddot{\mathit{q}}}_{\mathit{s}}=-{\mathit{M}}_{\mathit{s}}{\mathit{K}}_{\mathit{s}}\left({\dot{\mathit{q}}}_{\mathit{s}}-{\dot{\mathit{q}}}_{\mathit{m},\mathit{d}}\right)+{\mathit{ϵ}}_{\mathit{s}}+{\mathit{k}}_{\mathit{e}}-{\mathit{D}}_{\mathit{e}}{\dot{\mathit{q}}}_{\mathit{s}}-{\mathit{K}}_{\mathit{e}}{\mathit{q}}_{\mathit{s}}.$$

(30)

where ${\mathit{ϵ}}_{\mathit{m}}=-{\mathit{\delta }}_{\mathit{m}}-{\widehat{\mathsf{\Delta }}}_{\mathit{m}}\mathit{s}\mathit{g}\mathit{n}\left({\mathit{s}}_{\mathit{m}}\right)-{\mathit{\Phi }}_{\mathit{m}}\mathit{s}\mathit{g}\mathit{n}({\mathit{s}}_{\mathit{m}})$ and ${\mathit{ϵ}}_{\mathit{s}}=-{\mathit{\delta }}_{\mathit{s}}-{\widehat{\mathsf{\Delta }}}_{\mathit{s}}\mathit{s}\mathit{g}\mathit{n}\left({\mathit{s}}_{\mathit{s}}\right)-{\mathit{\Phi }}_{\mathit{s}}\mathit{s}\mathit{g}\mathit{n}({\mathit{s}}_{\mathit{s}})$.

Remark 4.

According to Assumption 1 and Theorem 2, the uncertainty terms ${\mathit{\delta }}_{\mathit{m}}$ and ${\mathit{\delta }}_{\mathit{s}}$ are bounded and the estimated terms ${\widehat{\mathsf{\Delta }}}_{\mathit{m}}$ and ${\widehat{\mathsf{\Delta }}}_{\mathit{s}}$ are bounded. Thus, both the ${\mathit{ϵ}}_{\mathit{m}}$ and ${\mathit{ϵ}}_{\mathit{s}}$ are bounded.

Theorem 3.

With non-passive human and environment forces (3) and (4), the closed-loop teleoperation system (30) is asymptotic stable if the following LMI holds:

$$\mathit{\Omega }=\left[\begin{array}{cccc}{\mathit{\Omega }}_{\mathbf{11}}& {\mathbf{0}}_{\mathit{n}}& {\mathbf{0}}_{\mathit{n}}& {\mathbf{0}}_{\mathit{n}}\\ {\mathbf{0}}_{\mathit{n}}& {\overline{\mathit{\lambda }}}_{\mathit{s}}{\mathit{K}}_{\mathit{s}}-\tilde{\mathit{\mu }}\mathit{Q}& {\mathbf{0}}_{\mathit{n}}& {\mathbf{0}}_{\mathit{n}}\\ {\mathbf{0}}_{\mathit{n}}& {\mathbf{0}}_{\mathit{n}}& {\mathit{\Omega }}_{\mathbf{33}}& {\mathbf{0}}_{\mathit{n}}\\ {\mathbf{0}}_{\mathit{n}}& {\mathbf{0}}_{\mathit{n}}& {\mathbf{0}}_{\mathit{n}}& {\overline{\mathit{\lambda }}}_{\mathit{m}}{\mathit{K}}_{\mathit{m}}-\tilde{\mathit{\mu }}\mathit{Q}\end{array}\right]<\mathbf{0}$$

(31)

where $\mathit{Q}\in {\mathcal{R}}^{n\times n}$ is a symmetric positive-definite matrix, and

$${\mathit{\Omega }}_{\mathbf{11}}=-{\overline{\mathit{\lambda }}}_{\mathit{m}}{\mathit{K}}_{\mathit{m}}+\left(\mathbf{2}{\mathit{c}}_{\mathit{m}}+{\mathit{\alpha }}_{\mathit{m}}\right){\mathit{I}}_{\mathit{n}}+\mathit{Q}-\mathbf{2}{\mathit{D}}_{\mathit{h}}$$

$${\mathit{\Omega }}_{\mathbf{33}}=-{\overline{\mathit{\lambda }}}_{\mathit{s}}{\mathit{K}}_{\mathit{s}}+\left(\mathbf{2}{\mathit{c}}_{\mathit{s}}+{\mathit{\alpha }}_{\mathit{s}}\right){\mathit{I}}_{\mathit{n}}+\mathit{Q}-\mathbf{2}{\mathit{D}}_{\mathit{e}}$$

(32)

in which αm and αs are positive constants and 0n is a zero matrix of ${\mathcal{R}}^{n\times n}$.

Proof. 

Consider a Lyapunov–Krasovskii function candidate as follows:

$$\begin{gathered} \mathit{V}={\dot{\mathit{q}}}_{\mathit{m}}^{\mathit{T}}{\mathit{M}}_{\mathit{m}}{\dot{\mathit{q}}}_{\mathit{m}}+{\mathit{q}}_{\mathit{m}}^{\mathit{T}}{\mathit{K}}_{\mathit{h}}{\mathit{q}}_{\mathit{m}}+{\int }_{\mathit{t}-\mathit{d}\left(\mathit{t}\right)}^{\mathit{t}}{\dot{\mathit{q}}}_{\mathit{m}}^{\mathit{T}}(\mathit{s})\mathit{Q}{\dot{\mathit{q}}}_{\mathit{m}}(\mathit{s})\mathit{d}\mathit{s}+{\dot{\mathit{q}}}_{\mathit{s}}^{\mathit{T}}{\mathit{M}}_{\mathit{s}}{\dot{\mathit{q}}}_{\mathit{s}} \\ +{\mathit{q}}_{\mathit{s}}^{\mathit{T}}{\mathit{M}}_{\mathit{s}}{\mathit{q}}_{\mathit{s}}+{\int }_{\mathit{t}-\mathit{d}\left(\mathit{t}\right)}^{\mathit{t}}{\dot{\mathit{q}}}_{\mathit{s}}^{\mathit{T}}(\mathit{s})\mathit{Q}{\dot{\mathit{q}}}_{\mathit{s}}(\mathit{s})\mathit{d}\mathit{s} \end{gathered}$$

(33)

From Property 2, the time derivative of $\mathit{V}$ along (30) can be reformulated as

$$\begin{gathered} \mathit{V}\le 2{\dot{\mathit{q}}}_{\mathit{m}}^{\mathit{T}}\left(-{\mathit{M}}_{\mathit{m}}{\mathit{K}}_{\mathit{m}}\left({\dot{\mathit{q}}}_{\mathit{m}}-{\dot{\mathit{q}}}_{\mathit{s},\mathit{d}}\right)+{\mathit{C}}_{\mathit{m}}{\dot{\mathit{q}}}_{\mathit{m}}+{\mathit{ϵ}}_{\mathit{m}}+{\mathit{k}}_{\mathit{h}}-{\mathit{D}}_{\mathit{h}}{\dot{\mathit{q}}}_{\mathit{m}}\right) \\ +2{\dot{\mathit{q}}}_{\mathit{s}}^{\mathit{T}}\left(-{\mathit{M}}_{\mathit{s}}{\mathit{K}}_{\mathit{s}}\left({\dot{\mathit{q}}}_{\mathit{s}}-{\dot{\mathit{q}}}_{\mathit{m},\mathit{d}}\right)+{\mathit{C}}_{\mathit{s}}{\dot{\mathit{q}}}_{\mathit{s}}+{\mathit{ϵ}}_{\mathit{s}}+{\mathit{k}}_{\mathit{e}}-{\mathit{D}}_{\mathit{e}}{\dot{\mathit{q}}}_{\mathit{s}}\right) \\ +{\dot{\mathit{q}}}_{\mathit{m}}^{\mathit{T}}\mathit{Q}{\dot{\mathit{q}}}_{\mathit{m}}-\tilde{\mathit{\mu }}{\dot{\mathit{q}}}_{\mathit{m},\mathit{d}}^{\mathit{T}}\mathit{Q}{\dot{\mathit{q}}}_{\mathit{m},\mathit{d}}+{\dot{\mathit{q}}}_{\mathit{s}}^{\mathit{T}}\mathit{Q}{\dot{\mathit{q}}}_{\mathit{s}}-\tilde{\mathit{\mu }}{\dot{\mathit{q}}}_{\mathit{s}}^{\mathit{T}}\mathit{Q}{\dot{\mathit{q}}}_{\mathit{s},\mathit{d}}. \end{gathered}$$

(34)

From Lemma 1, the following inequalities can be obtained:

$$2{\dot{\mathit{q}}}_{\mathit{m}}^{\mathit{T}}\left({\mathit{ϵ}}_{\mathit{m}}+{\mathit{k}}_{\mathit{h}}\right)\le {\alpha }_m{\dot{\mathit{q}}}_{\mathit{m}}^{\mathit{T}}{\dot{\mathit{q}}}_{\mathit{m}}+\frac{1}{{\alpha }_m}{‖{\mathit{ϵ}}_{\mathit{m}}+{\mathit{k}}_{\mathit{h}}‖}_{\mathbf{2}}^{\mathbf{2}}$$

$$2{\dot{\mathit{q}}}_{\mathit{s}}^{\mathit{T}}\left({\mathit{ϵ}}_{\mathit{s}}+{\mathit{k}}_{\mathit{e}}\right)\le {\alpha }_s{\dot{\mathit{q}}}_{\mathit{s}}^{\mathit{T}}{\dot{\mathit{q}}}_{\mathit{s}}+\frac{1}{{\alpha }_s}{‖{\mathit{ϵ}}_{\mathit{s}}-{\mathit{k}}_{\mathit{e}}‖}_{\mathbf{2}}^{\mathbf{2}}$$

(35)

and

$$2{\dot{\mathit{q}}}_{\mathit{m}}^{\mathit{T}}{\mathit{K}}_{\mathit{m}}{\mathit{M}}_{\mathit{m}}{\dot{\mathit{q}}}_{\mathit{s},\mathit{d}}\le {\dot{\mathit{q}}}_{\mathit{m}}^{\mathit{T}}{\mathit{K}}_{\mathit{m}}{\mathit{M}}_{\mathit{m}}{\dot{\mathit{q}}}_{\mathit{m}}+{\dot{\mathit{q}}}_{\mathit{s},\mathit{d}}^{\mathit{T}}{\mathit{K}}_{\mathit{m}}{\mathit{M}}_{\mathit{m}}{\dot{\mathit{q}}}_{\mathit{s},\mathit{d}}$$

$$2{\dot{\mathit{q}}}_{\mathit{s}}^{\mathit{T}}{\mathit{K}}_{\mathit{s}}{\mathit{M}}_{\mathit{s}}{\dot{\mathit{q}}}_{\mathit{m},\mathit{d}}\le {\dot{\mathit{q}}}_{\mathit{s}}^{\mathit{T}}{\mathit{K}}_{\mathit{s}}{\mathit{M}}_{\mathit{s}}{\dot{\mathit{q}}}_{\mathit{s}}+{\dot{\mathit{q}}}_{\mathit{m},\mathit{d}}^{\mathit{T}}{\mathit{K}}_{\mathit{s}}{\mathit{M}}_{\mathit{s}}{\dot{\mathit{q}}}_{\mathit{m},\mathit{d}}$$

(36)

where ${‖·‖}_2$ represents the L2 norm of the signals.

From Properties 1 and 3, substituting (35) and (36) into (34) yields

$$\dot{\mathit{V}}\le {\dot{\mathit{q}}}^{\mathit{T}}\mathit{\Omega }\dot{\mathit{q}}+\frac{1}{{\alpha }_m}{‖{\mathit{ϵ}}_{\mathit{m}}+{\mathit{k}}_{\mathit{h}}‖}_{\mathbf{2}}^{\mathbf{2}}+\frac{1}{{\alpha }_s}{‖{\mathit{ϵ}}_{\mathit{s}}-{\mathit{k}}_{\mathit{e}}‖}_{\mathbf{2}}^{\mathbf{2}}$$

(37)

where $\dot{\mathit{q}}={\left[\begin{array}{cc}\begin{array}{cc}{\dot{\mathit{q}}}_{\mathit{m}}^{\mathit{T}}& {\dot{\mathit{q}}}_{\mathit{m},\mathit{d}}^{\mathit{T}}\end{array}& \begin{array}{cc}{\dot{\mathit{q}}}_{\mathit{s}}^{\mathit{T}}& {\dot{\mathit{q}}}_{\mathit{s},\mathit{d}}^{\mathit{T}}\end{array}\end{array}\right]}^{\mathit{T}}$. Furthermore, it leads to the following condition,

$$\mathit{V}\le {\overline{\lambda }}_{\Omega }{‖\dot{\mathit{q}}‖}_{\mathbf{2}}^{\mathbf{2}}+\rho$$

(38)

where ${\overline{\lambda }}_{\Omega }<0$ is the maximum eigenvalue of the matrix $\mathit{\Omega }$, $\rho =\frac{1}{{\alpha }_m}{‖{\mathit{ϵ}}_{\mathit{m}}+{\mathit{k}}_{\mathit{h}}‖}_{\mathbf{2}}^{\mathbf{2}}+\frac{1}{{\alpha }_s}{‖{\mathit{ϵ}}_{\mathit{s}}-{\mathit{k}}_{\mathit{e}}‖}_{\mathbf{2}}^{\mathbf{2}}$. Noting that $\rho$ is bounded, $\rho \le \overline{\rho }$, $\overline{\rho }$ is a constant. Hence, $\dot{\mathit{V}}$ is negative, if ${‖\dot{\mathit{q}}‖}_{\mathbf{2}}>\sqrt{\frac{\overline{\mathit{\rho }}}{-{\overline{\mathit{\lambda }}}_{\mathit{\Omega }}}}$. The controller parameters ${\mathit{K}}_{\mathit{m}}$ and ${\mathit{K}}_{\mathit{s}}$ can be chosen such that $\dot{\mathit{q}}$ will be arbitrarily small. Therefore, the closed-loop system (30) is asymptotically stable. □

3. Experimental Results

In this paper, the master and slave devices are a pair of two-degrees-of-freedom-revolute-prismatic robots. The configuration illustration and 3D framework of the teleoperation devices are shown in Figure 2.

The system parameters of the master and slave robots are listed in

Table 1. System parameters of teleoperation systems.

$m_1$	Mass of link 1	0.36 kg
$m_2$	Mass of link 2	0.027 kg
$l$	Distance between joint o and center of link 1	0.02 m
$g$	Gravitational constant	9.8 m/${\mathrm{s}}^2$

.

The dynamic models of (1) and (2) are obtained as

$${\mathit{M}}_{\mathit{i}}\left({\mathit{q}}_{\mathit{i}}\right)=\left[\begin{array}{cc}{m}_1{l}^2+m_2{h}_i^2& 0\\ 0& m_2\end{array}\right], {\mathit{C}}_{\mathit{i}}\left({\mathit{q}}_{\mathit{i}},{\mathit{q}}_{\mathit{i}}\right)=\left[\begin{array}{cc}0& 2m_2{h}_i{\dot{\theta }}_i\\ -m_2{h}_i{\dot{\theta }}_i& 0\end{array}\right],$$

$${\mathit{G}}_{\mathit{i}}\left({\mathit{q}}_{\mathit{i}}\right)=\left[\begin{array}{c}\left(m_{1}l+m_2{h}_i\right)gcos\left({\theta }_i\right)\\ m_{2}gsin\left({\theta }_i\right)\end{array}\right]$$

(39)

${\mathit{q}}_{\mathit{i}}={\left[\begin{array}{cc}{\theta }_i& h_i\end{array}\right]}^{\mathit{T}}$, ${\ddot{\mathit{q}}}_{\mathit{i}}={\left[\begin{array}{cc}{\ddot{\theta }}_i& {\ddot{h}}_i\end{array}\right]}^{\mathit{T}}$, ${\mathit{\tau }}_{\mathit{i}}={\left[\begin{array}{cc}{\tau }_{1i}& {\tau }_{2i}\end{array}\right]}^{\mathit{T}}$, ${\mathit{f}}_{\mathit{h}}={\left[\begin{array}{cc}{f}_{h1}& f_{h2}\end{array}\right]}^{\mathit{T}},{\mathit{f}}_{\mathit{e}}={\left[\begin{array}{cc}{f}_{e1}& f_{e2}\end{array}\right]}^{\mathit{T}},i\in \{m,s\}$. In addition, $h_i$ is the length of the joint 2 between the point o and the center of mass of the second link, and ${\theta }_i$ is the angle of the joint 1.

The parameters of the adaptive-sliding-mode controller are set as ${\mathit{K}}_{\mathit{i}}=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\left\{\mathrm{2,2}\right\}$, ${\mathit{\Phi }}_{\mathit{i}}=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\left\{\mathrm{2.5,2.5}\right\}$, and $\mathit{\Gamma }=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\{0.5,0.1\}\times {10}^{-3}$, $i\in \{m,s\}$. The disturbance parts are assumed as ${\mathit{\delta }}_{\mathit{i}}=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\{0.5,0.1\}\times \mathit{r}\mathit{a}\mathit{n}\mathit{d}(·)\times {10}^{-3}$ and $\mathit{r}\mathit{a}\mathit{n}\mathit{d}(·)$ is a uniformly distributed random number. From Theorem 1, the allowable delay bound can be obtained as $\overline{d}=0.5$ s by solving LMI (12). In experiments, the time delay is chosen as $d\left(t\right)=0.25+0.2\sin \left(t\right)$ s. The initial states of the master and slave robots are set as ${\mathit{q}}_{\mathit{m}}={\mathit{q}}_{\mathit{s}}={\left[\begin{array}{cc}0& 0.145\end{array}\right]}^{\mathit{T}}$, and the initial velocities and acceleration are zero. Three types of controllers are adopted for comparison, including the proportional plus damping controller (P + dC) [17,18,45], sliding-mode controller (SC), and the proposed adaptive-sliding-mode controller (ASC). The following indices are considered for performance comparisons: the integral absolute error (IAE), the integral time absolute error (ITAE), the integral square error (ISE), and the integral time square error (ITSE) [57].

In the following, the cases of both free motion and force perception are performed. The experimental setup of a bilateral teleoperation system is shown in Figure 3. The position responses of the master and slave robots are measured by encoders. The control algorithms and signal interfacing are implemented by Raspberry Pi and a PIC18F4331 microprocessor. The sampling time is selected as 20 ms. In these experiments, the time delay is realized by software programming. Furthermore, all of the controller parameters of the teleoperation system are the same as the settings in simulations. The allowable delay bound is determined to be 0.5 s. The behavior of a delay can be accurately captured if the delay is multiple times the length of the sampling time.

3.1. Case 1: Free Motion (Experiment)

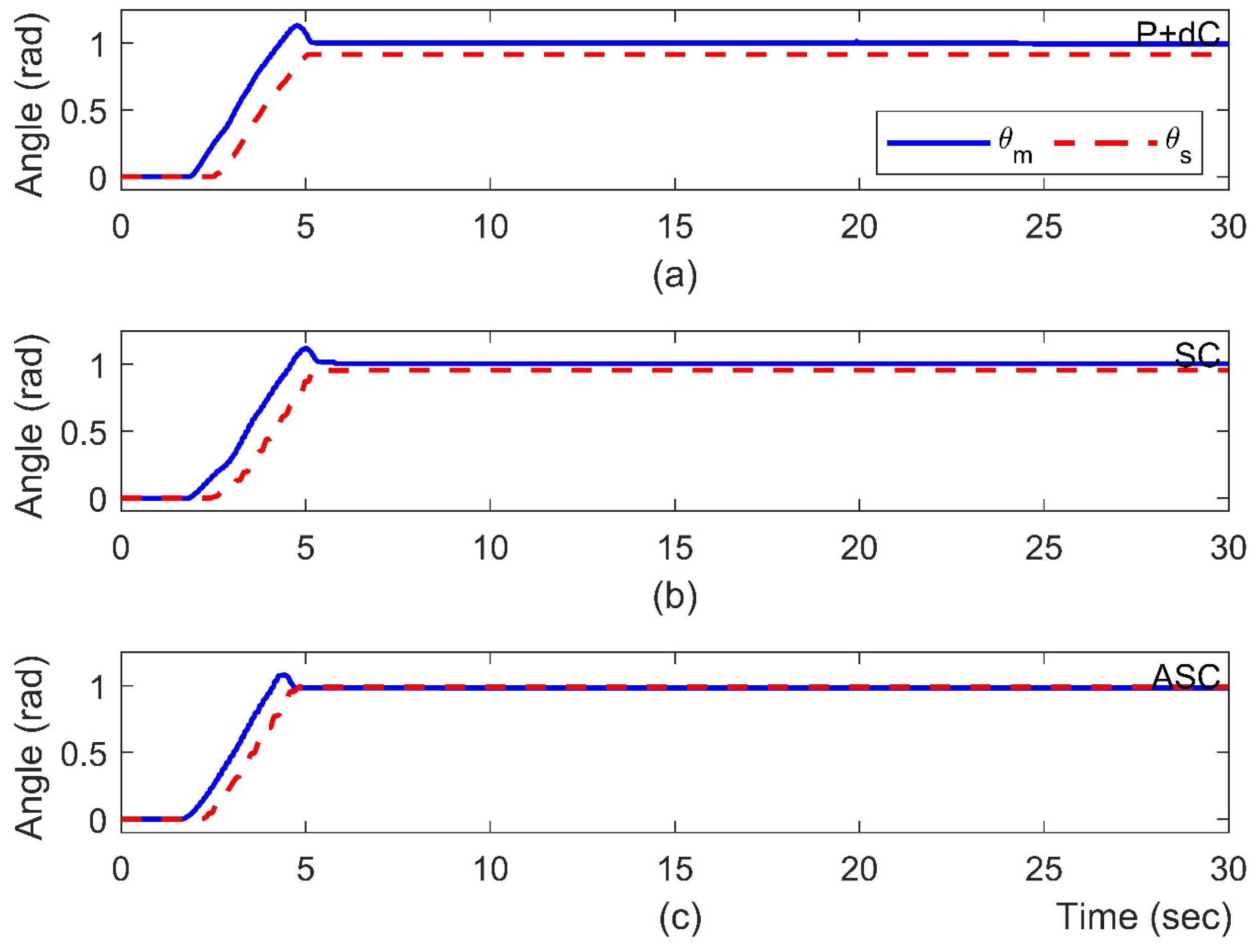
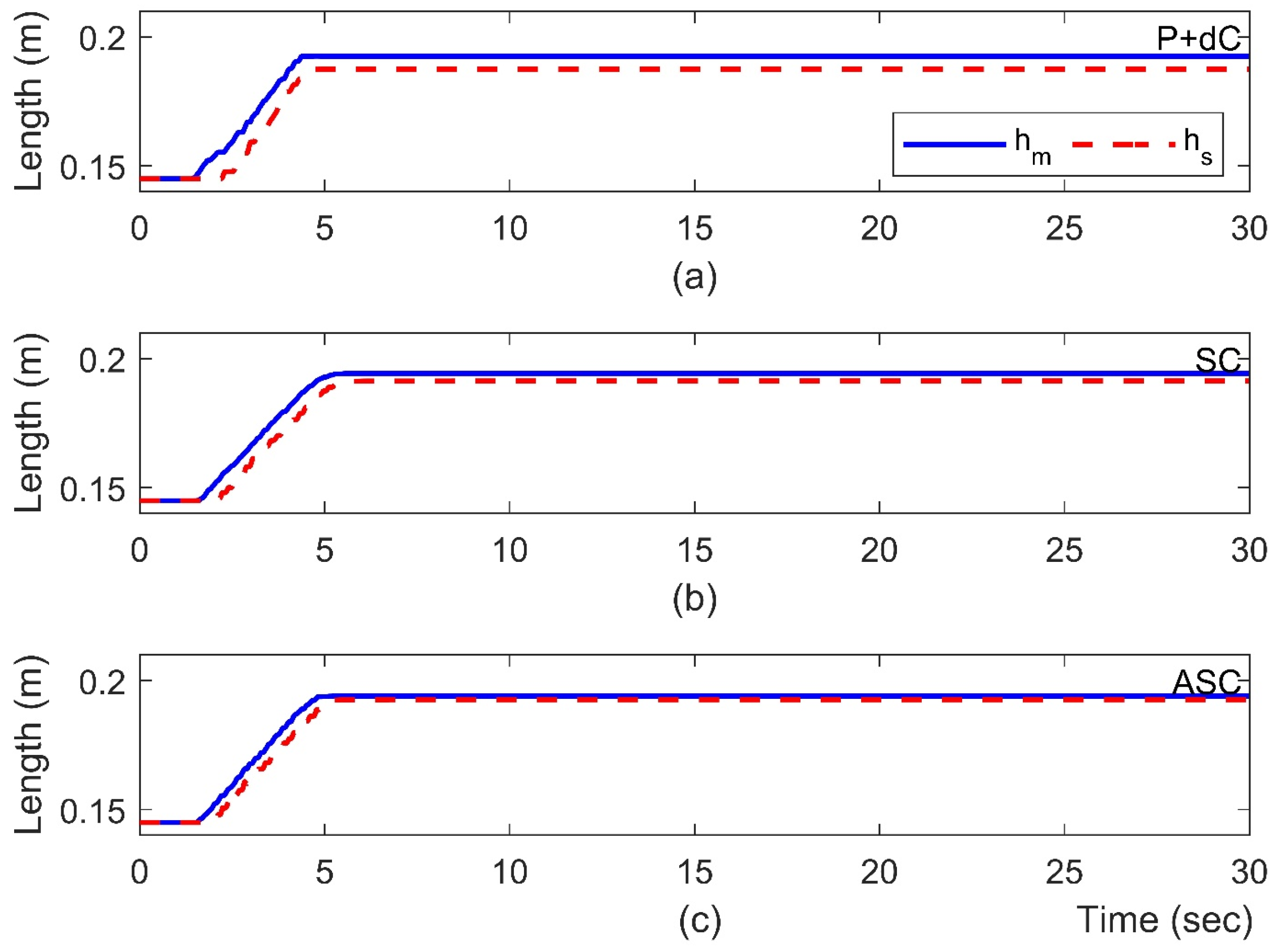
During the free-motion operation, the human operator moves the master robot towards ${\theta }_m=1$ rad and $h_m=0.195$ m, and the operator leaves the device standing still alone for $t>5$ s. It is desired to see whether the slave robot can track the motion trajectory of the master device stably. As shown in Figure 4 and Figure 5, the steady-state position errors are significantly reduced using the ASC method. Quantitative analyses of different methods are shown in

Table 2. Experimental comparisons of position errors in Case 1.

		IAE	ITAE	ISE	ITSE
P + dC	Joint 1	21.38	147.72	1983.70	199.68
	Joint 2	0.045	7.79	115.41	0.60
SC	Joint 1	13.38	99.21	1199.80	92.06
	Joint 2	0.019	4.81	68.24	0.21
ASC	Joint 1	6.26	36.91	248.95	22.71
	Joint 2	0.008	2.70	33.85	0.06

unit: joint 1 (rad), joint 2 (m).

. The proposed ASC method increases the performance improvement from 70.70% to 90.00%. The video snapshots captured from the ASC are depicted in Figure 6, where the recording time of each snapshot is indicated on the bottom right.

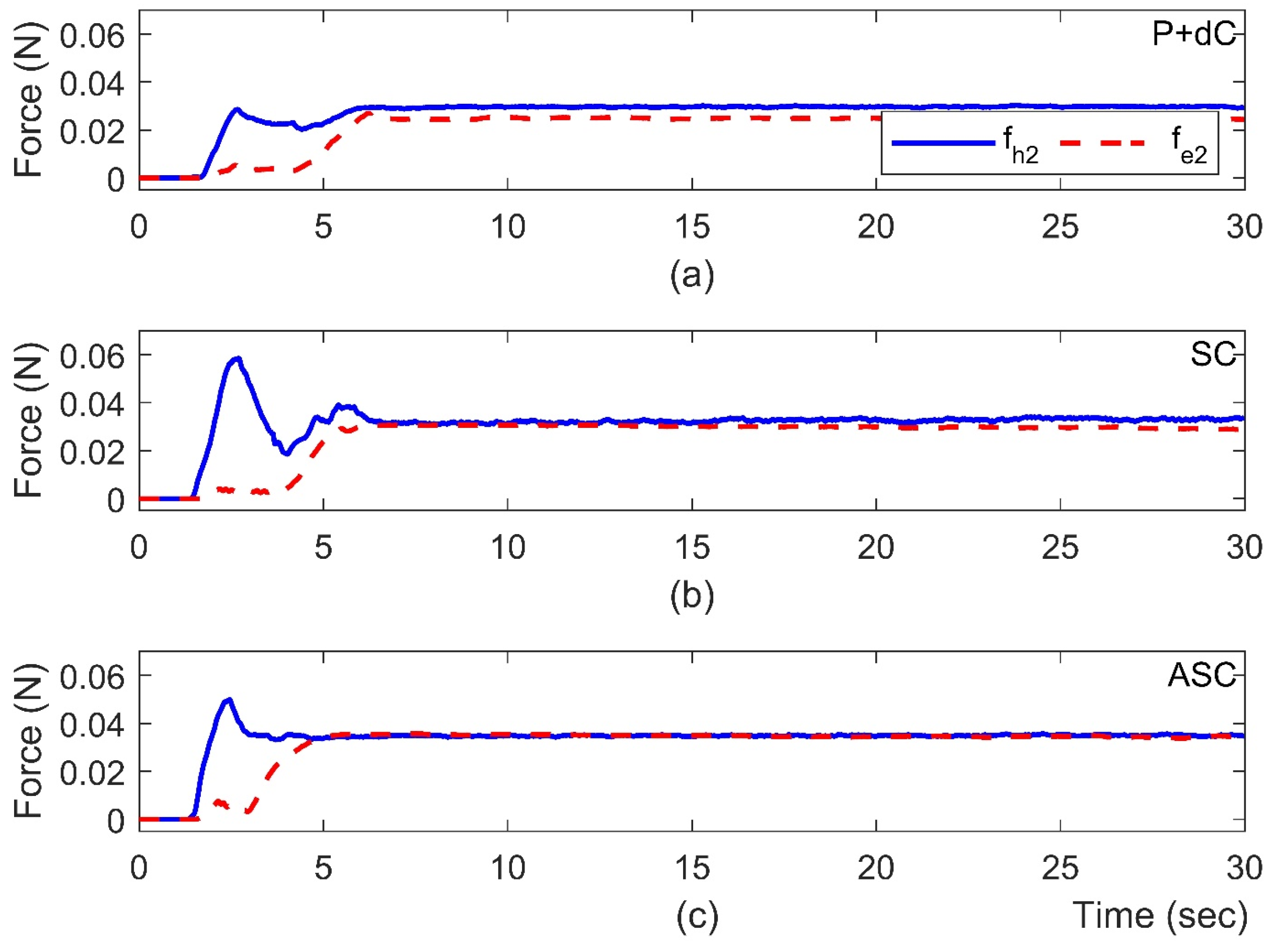
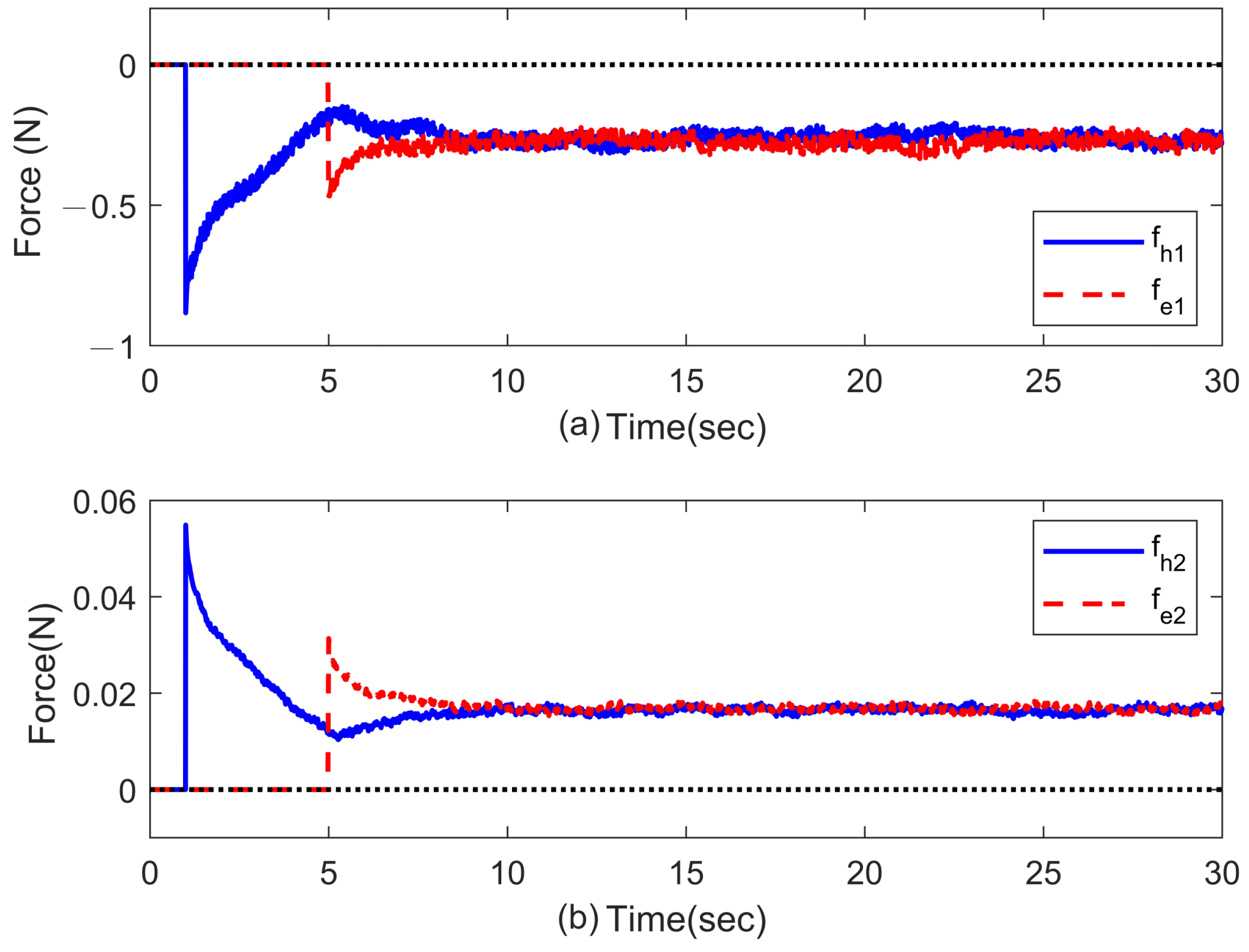
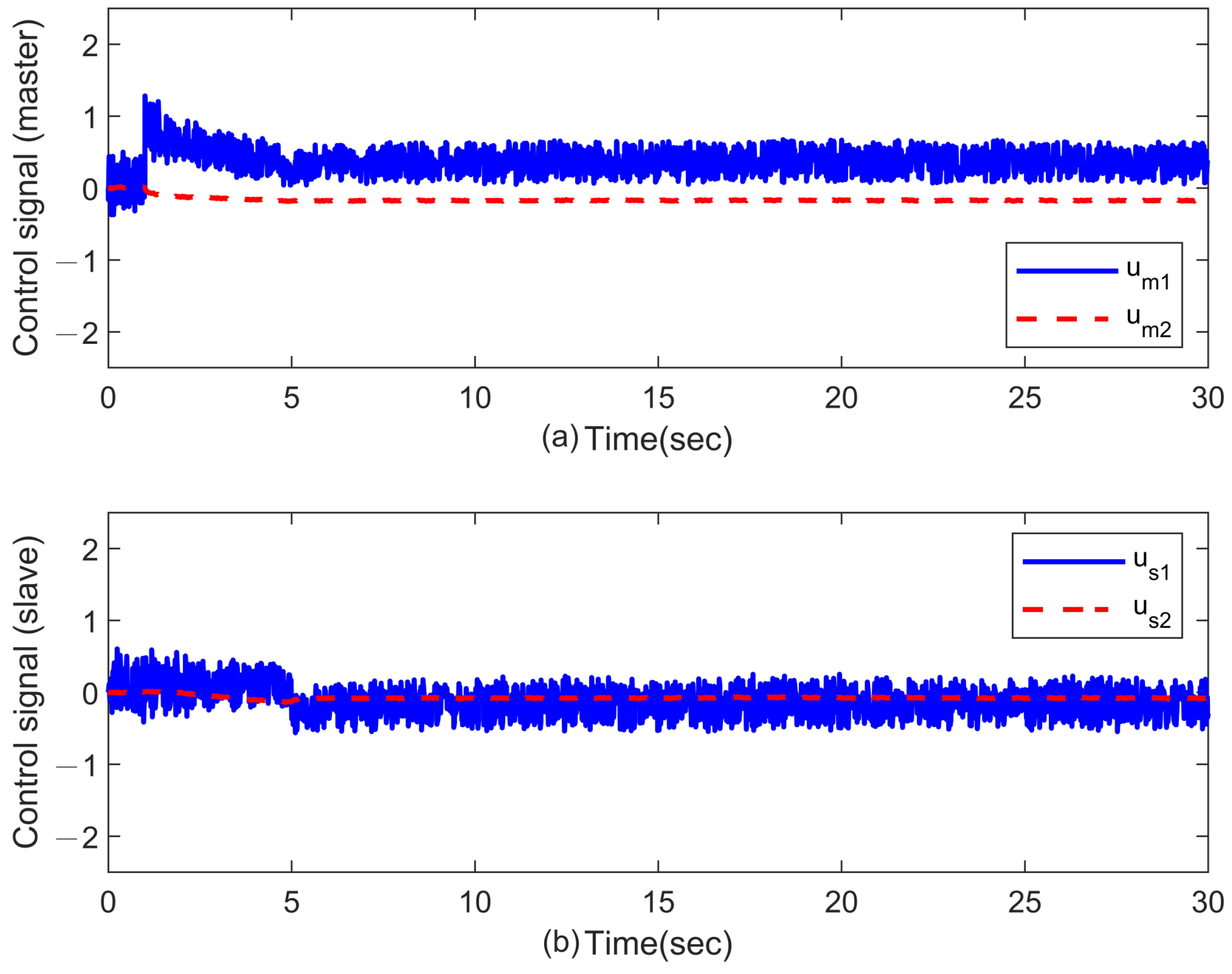
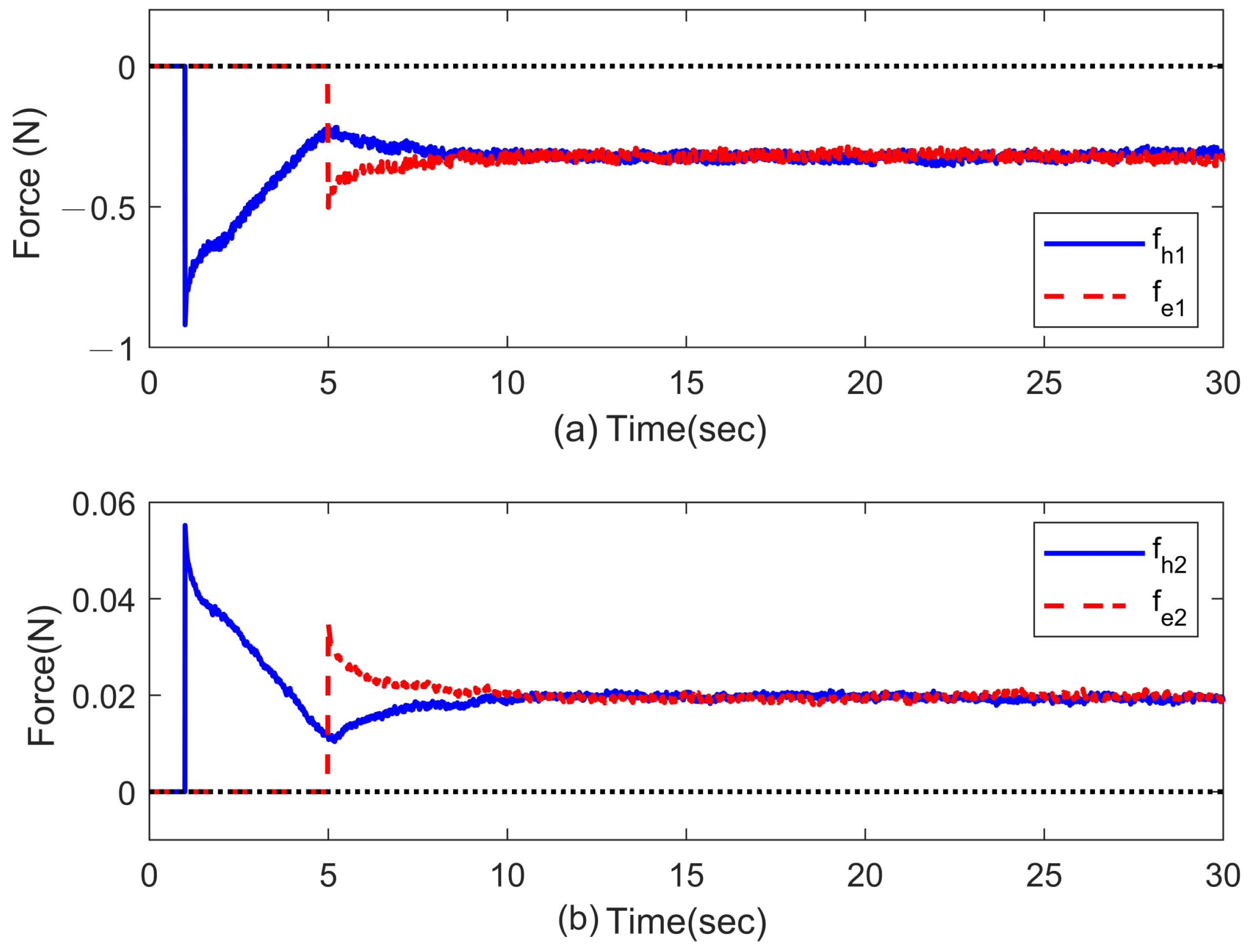
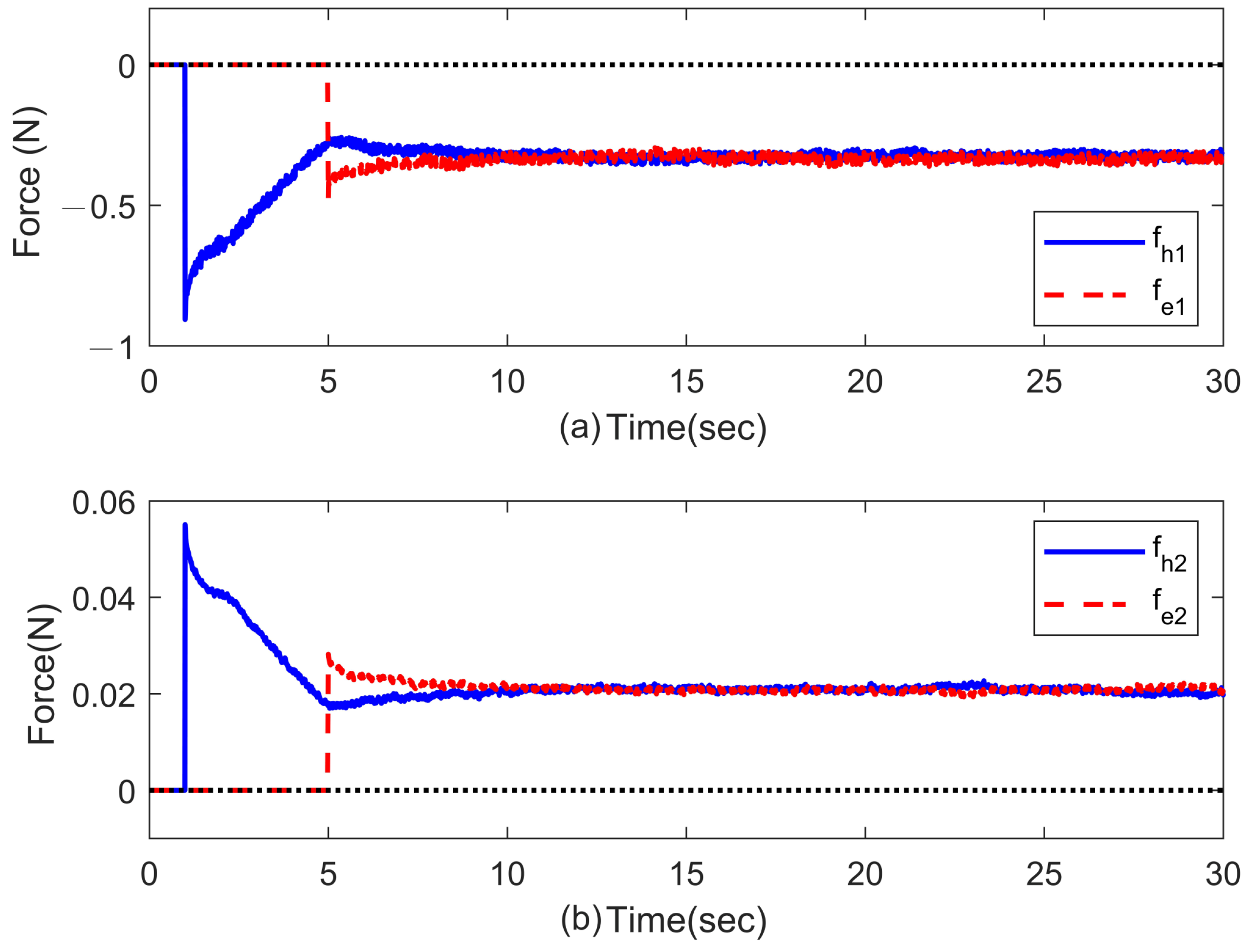
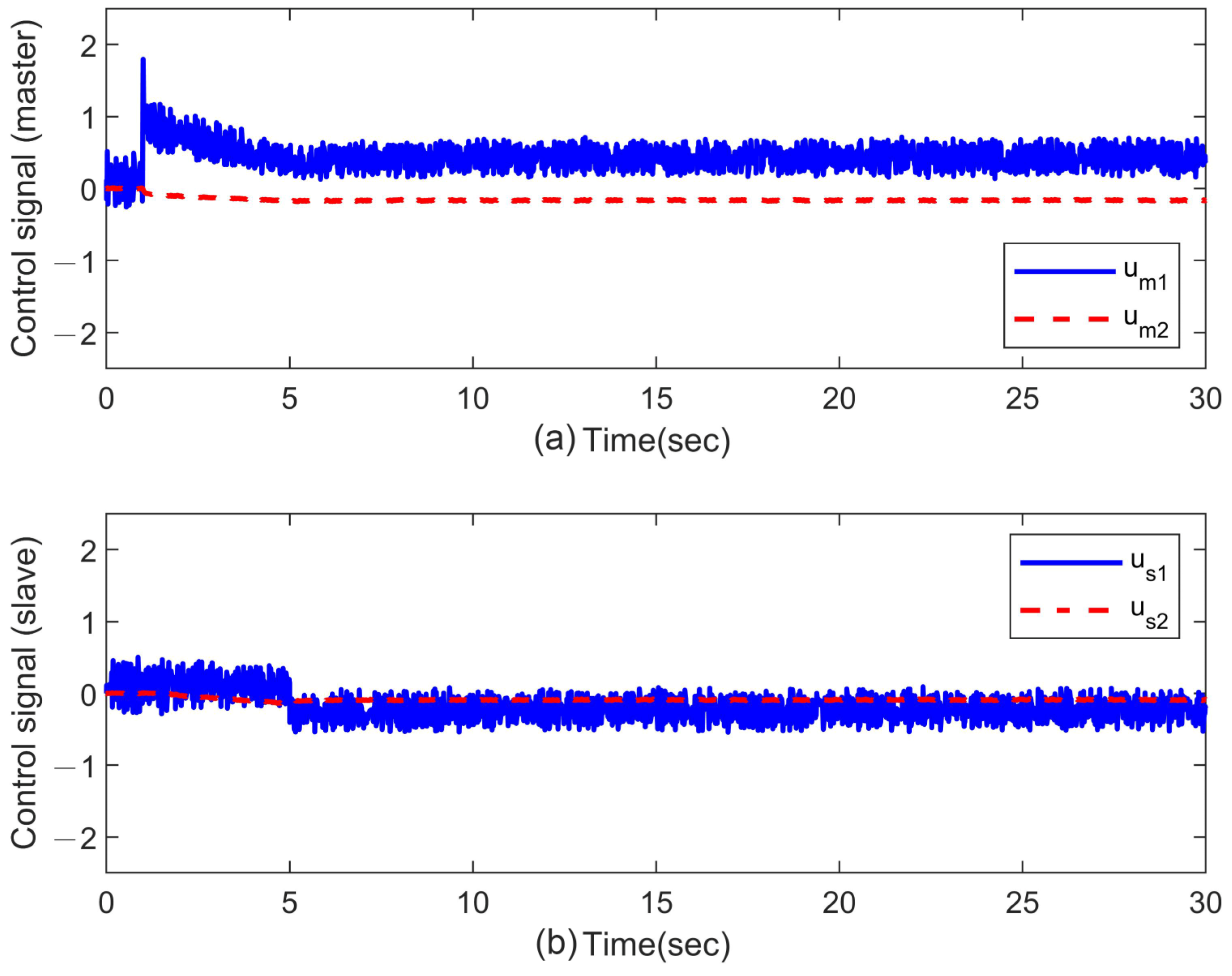
3.2. Case 2: Force Perception (Experiment)

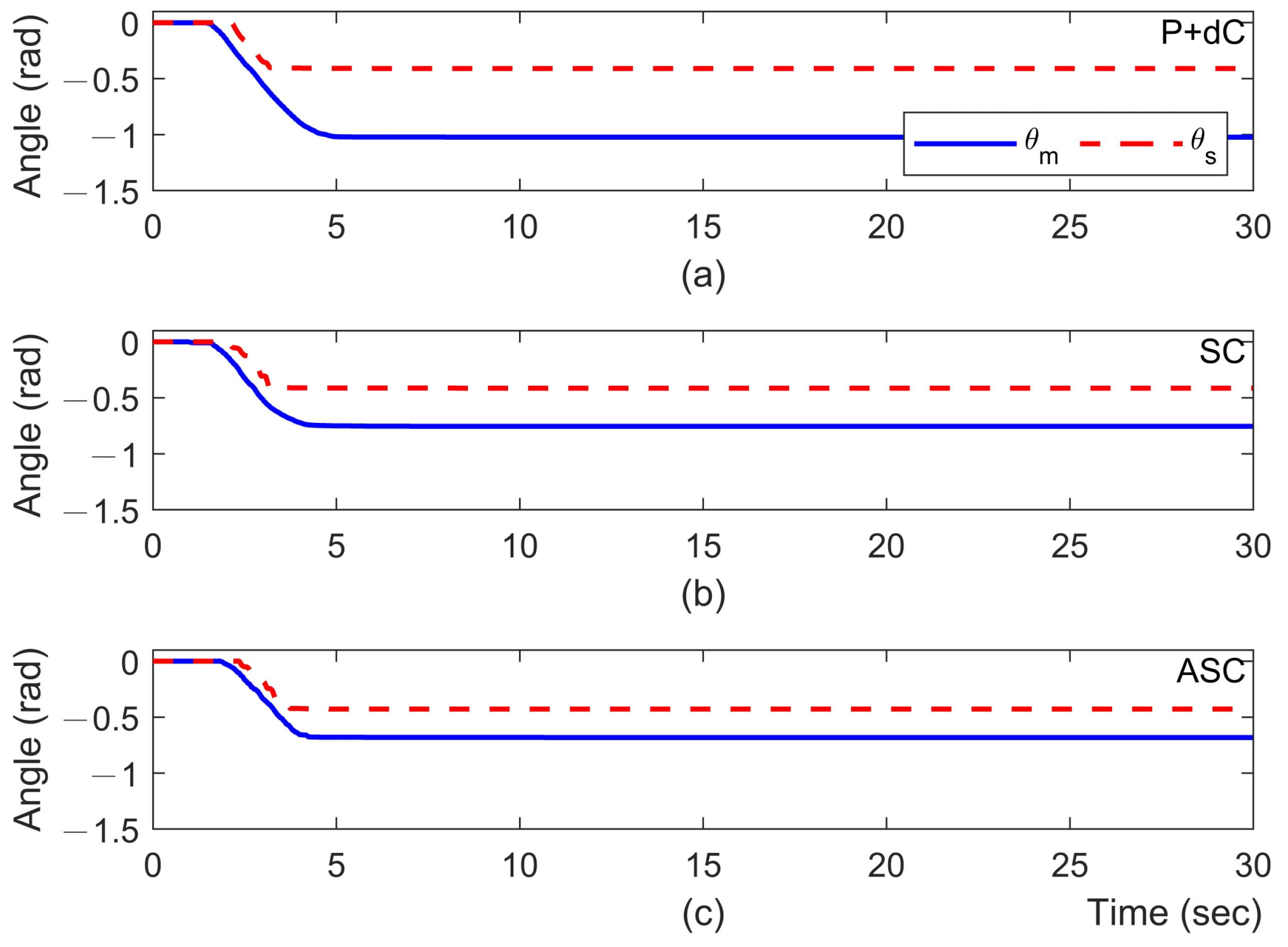
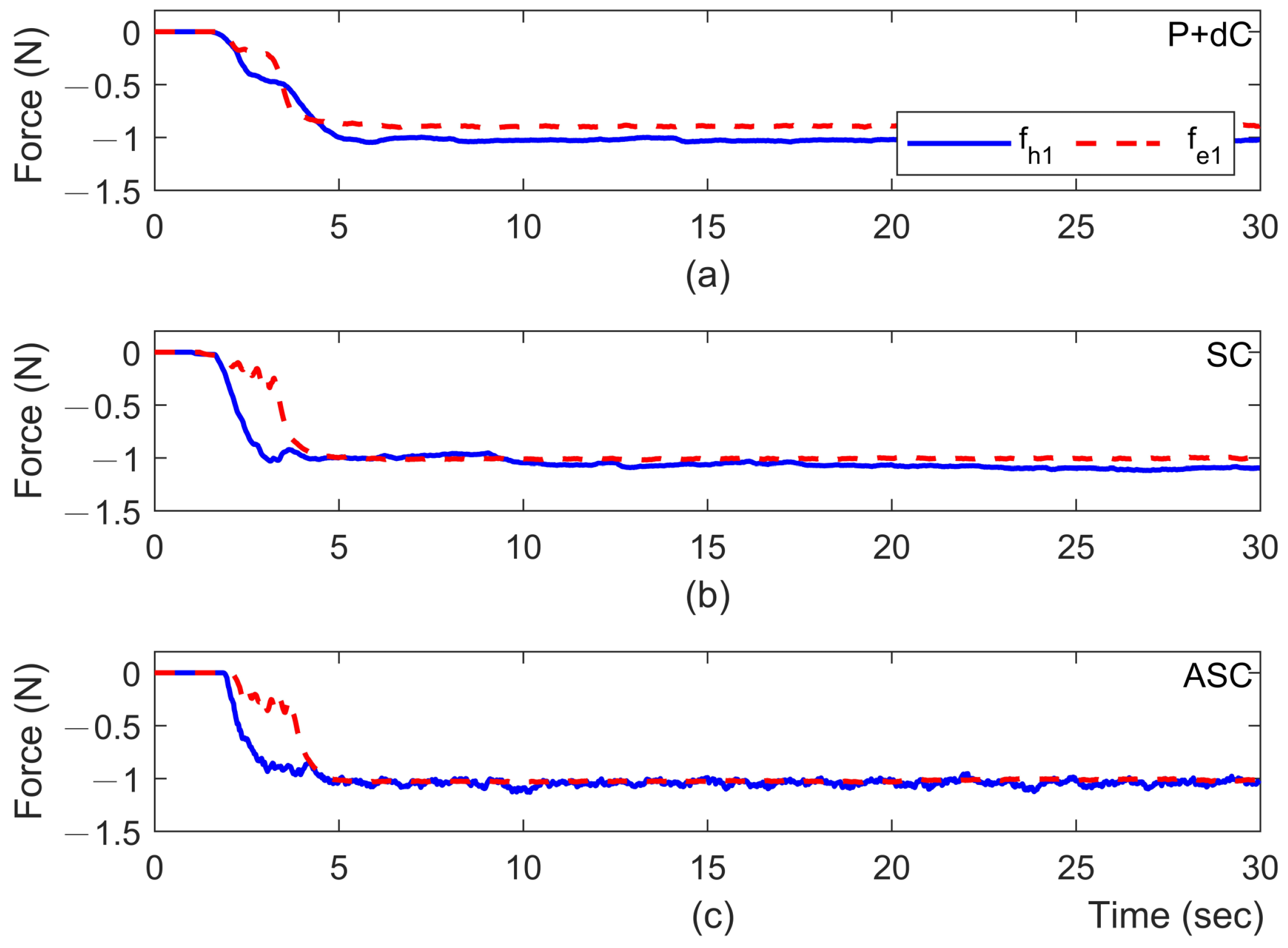
In this case, an obstacle is placed on the slave side of the system at a position of roughly $h_s=0.175$ m and ${\theta }_s=-0.5$ rad, respectively. As it is following the scheduled movement of the master, the slave robot will contact the pre-placed obstacle. Like in the in the simulation discussions, the force feedback will be conducted in turn for each joint. The experimental results corresponding to different methods are presented in Figure 7, Figure 8, Figure 9 and Figure 10, where the slave robot contacts the obstacle around $t=4$ s. From Figure 7 and Figure 8, it can be observed that there exist quite clear biases between the joint positions of master and slave robots with the P + dC method. On the other hand, the proposed ASC controller can provide significant improvements in position tracking and force perception. As the force perception in Figure 9 and Figure 10, the proposed ASC control method has superiority in stably and accurately tracking for $t>4$ s. Quantitative analyses of the experimental results are summarized in

Table 3. Experimental comparisons of position responses in Case 2.

		IAE	ITAE	ISE	ITSE
P + dC	Joint 1	493.82	822.78	13,620.00	8319.10
	Joint 2	0.53	27.06	453.25	9.23
SC	Joint 1	155.35	465.18	7588.70	2575.70
	Joint 2	0.18	15.84	262.65	3.09
ASC	Joint 1	85.66	343.22	5655.00	1432.80
	Joint 2	0.17	15.69	241.20	2.60

unit: joint 1 (rad), joint 2 (m).

and

Table 4. Experimental comparisons of force errors in Case 2.

		IAE	ITAE	ISE	ITSE
P + dC	Joint 1	24.45	178.45	2497.80	351.22
	Joint 2	0.048	7.23	85.57	0.435
SC	Joint 1	13.28	93.91	1348.60	112.79
	Joint 2	0.036	4.77	54.07	0.195
ASC	Joint 1	2.87	34.35	412.59	15.84
	Joint 2	0.001	0.93	10.41	0.001

unit: joint 1 (N), joint 2 (N).

. They indicate that the proposed ASC method increases position performance from 58.48% to 82.55% and improves force performance from 83.48% to 99.77%. The video snapshots of ASC are depicted in Figure 11, where the recording time of each snapshot is indicated on the bottom right.

Remark 5.

To enhance the reader’s understanding of the experimental process and results, experimental videos have been uploaded to YouTube (accessed on 11 June 2024).

• https://www.youtube.com/watch?v=M0uSr1mg5YU
• https://www.youtube.com/watch?v=buR8rsf2_ls
• https://www.youtube.com/watch?v=0H8ogvjg2TU
• https://www.youtube.com/watch?v=jYd8kWvERj0

4. Discussion

A non-passive environment in the context of teleoperation systems refers to an environment where the forces exerted on the slave’s side are not purely passive. This means that the slave’s side does not simply follow the master’s movements passively but may exert forces or exhibit behaviors that are independent or reactive to the master’s commands. Building an experimental setup to replicate a non-passive environment presents several challenges due to its inherent complexity and unpredictability. To address these challenges, we conduct a simulation scenario in this study. Key performance indicators in a non-passive teleoperation environment include the closeness of position responses between the master and slave sides and the consistency of force tracking. Smaller errors in position and force tracking generally indicate better system performance.

4.1. Case 3: Free Motion (Simulation)

Additionally, a more general free-motion case is considered, where the joint 1 of the master moves approximately up to 1 rad and then gradually returns to its original position. During the same period, joint 2 smoothly pulls out. The simulation responses are shown in Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17, and the comparisons of position errors with different control methods are summarized in

Table 5. Simulation comparisons of position errors in Case 3.

		IAE	ITAE	ISE	ITSE
P + dC	Joint 1	1366.5	15,168.1	179.2	1456.9
	Joint 2	26.8	296.3	0.09	0.61
SC	Joint 1	710.1	7420.9	54.4	410.4
	Joint 2	20.5	249.7	0.04	0.32
ASC	Joint 1	643.1	7295.7	44.5	369.0
	Joint 2	18.7	209.6	0.03	0.29

unit: joint 1 (rad), joint 2 (m).

. Furthermore, the related control signals regarding to P + dC, SC, and ASC are shown in Figure 13, Figure 15 and Figure 17, respectively. It can be observed that the proposed ASC method can provide better trajectory-tracking capability.

4.2. Case 4: Non-Passive Human and Environment (Simulation)

Consider the case that the human operator and environment forces are all non-passive, such as

$${\mathit{f}}_{\mathit{h}}=\left\{\begin{array}{cc}{\mathit{k}}_{\mathit{h}}-{\mathit{D}}_{\mathit{h}}{\dot{\mathit{q}}}_{\mathit{m}}-{\mathit{K}}_{\mathit{h}}{\mathit{q}}_{\mathit{m}},& 1\le t\le 30 \mathrm{s}\\ \mathbf{0}& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right.$$

(40)

$${\mathit{f}}_{\mathit{e}}=\left\{\begin{array}{cc}{\mathit{k}}_{\mathit{e}}-{\mathit{D}}_{\mathit{e}}{\dot{\mathit{q}}}_{\mathit{s}}-{\mathit{K}}_{\mathit{e}}{\mathit{q}}_{\mathit{s}},& 5\le t\le 30 \mathrm{s}\\ \mathbf{0}& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right.$$

(41)

where ${\mathit{k}}_{\mathit{h}}={\left[\begin{array}{cc}-0.9& 0.2\end{array}\right]}^{\mathit{T}}$, ${\mathit{k}}_{\mathit{e}}={\left[\begin{array}{cc}0.1& -0.15\end{array}\right]}^{\mathit{T}}$, ${\mathit{D}}_{\mathit{h}}={\mathit{D}}_{\mathit{e}}=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\left\{\mathrm{1,1}\right\}$, and ${\mathit{K}}_{\mathit{h}}={\mathit{K}}_{\mathit{e}}=\mathit{d}\mathit{i}\mathit{a}\mathit{g}\left\{\mathrm{1,1}\right\}$.

The simulation results of this case are depicted in Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25 and Figure 26, including the position responses, force responses, and control signals of the master and slave robots. The observation revolves around the responses after the addition of the environment force, i.e., from 5 to 30 s. From Figure 24, compared to Figure 18 and Figure 21, the position errors of the master and slave robots are significantly improved using the proposed ASC method. As regards the force responses shown in Figure 19, Figure 22 and Figure 25, all three methods can support a certain degree of inconsistency in the human and environment forces. Similarly, the average position and force errors of 20 repetitions are summarized, from 5 to 30 s, in

Table 6. Simulation comparisons of position errors in Case 4.

		IAE	ITAE	ISE	ITSE
P + dC	Joint 1	66,092.74	116,329.60	1753.97	30,999.84
	Joint 2	413.14	7264.24	6.85	120.94
SC	Joint 1	4312.21	75,538.54	747.91	13,093.91
	Joint 2	271.31	4772.02	2.95	52.16
ASC	Joint 1	3328.01	58,510.62	444.31	7840.92
	Joint 2	207.80	3637.15	1.73	30.30

unit: joint 1 (rad), joint 2 (m).

and

Table 7. Simulation comparisons of force errors in Case 4.

		IAE	ITAE	ISE	ITSE
P + dC	Joint 1	655.09	8101.66	49.21	355.33
	Joint 2	44.38	508.72	0.24	1.61
SC	Joint 1	643.66	7720.72	44.83	322.15
	Joint 2	35.56	353.51	0.19	1.08
ASC	Joint 1	572.32	5399.46	23.56	153.96
	Joint 2	26.39	168.89	0.08	0.19

unit: joint 1 (N), joint 2 (N).

. It can be observed that the proposed ASC scheme has better performance in both position following and force perception.

5. Conclusions

This paper introduces an adaptive-sliding-mode controller that has been designed for a bilateral teleoperation system that is characterized by time-varying communication delays and unknown but bounded uncertainties. The master and slave devices utilized in the system are self-made by the authors, with certain components manufactured using CNC milling and lathe machines. The controller design involves deriving a delay-dependent condition for stability and determining the admissible bound of time delays through linear matrix inequalities. The closed-loop stability of the teleoperation system is ensured via Lyapunov–Krasovskii stability analysis, aligning the stability analysis with the designed controllers and adaptive laws. Both passive and non-passive scenarios involving the human operator and the environment are considered in the design process. A real experimental setup is employed to validate the proposed control scheme, covering free-motion and force-perception tasks. Results indicate that the proposed adaptive-sliding-control method increases position performance from 58.48% to 82.55% and force performance from 83.48% to 99.77%. In conclusion, the proposed control algorithm shows promising potential for application in generalized haptic devices with expanded degrees of freedom. Additionally, our control strategies have successfully addressed a wide range of scenarios and environments, including free motion, force perception, and also both passive and non-passive situations. Furthermore, our experimental results underscore its viability for real-world applications.