DDPG-Based Adaptive Sliding Mode Control with Extended State Observer for Multibody Robot Systems
Abstract
:1. Introduction
2. Preliminaries
2.1. Multibody Dynamics Description
2.2. Sliding Mode Control
2.3. Problem Forumlation
3. Proposed Algorithm
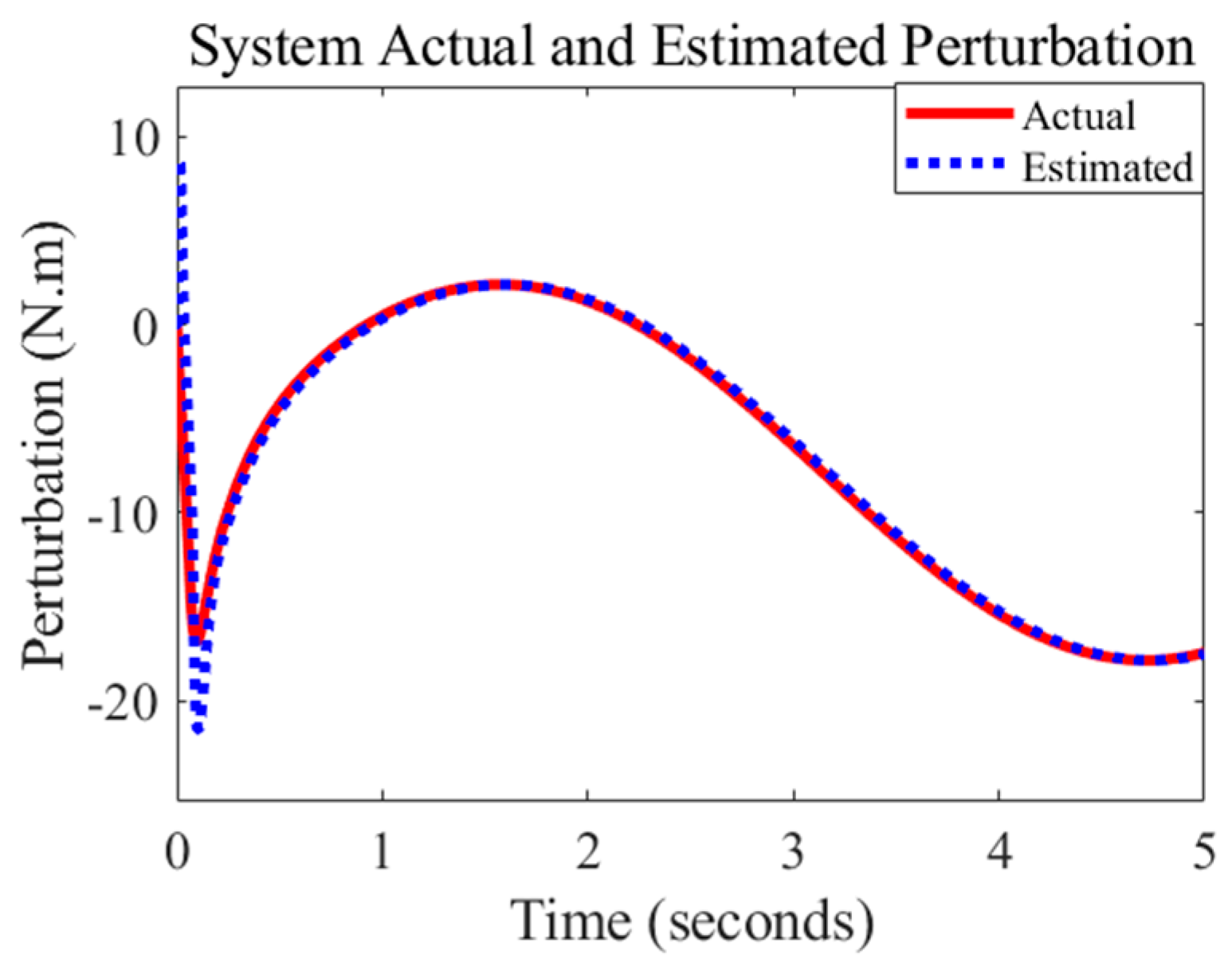
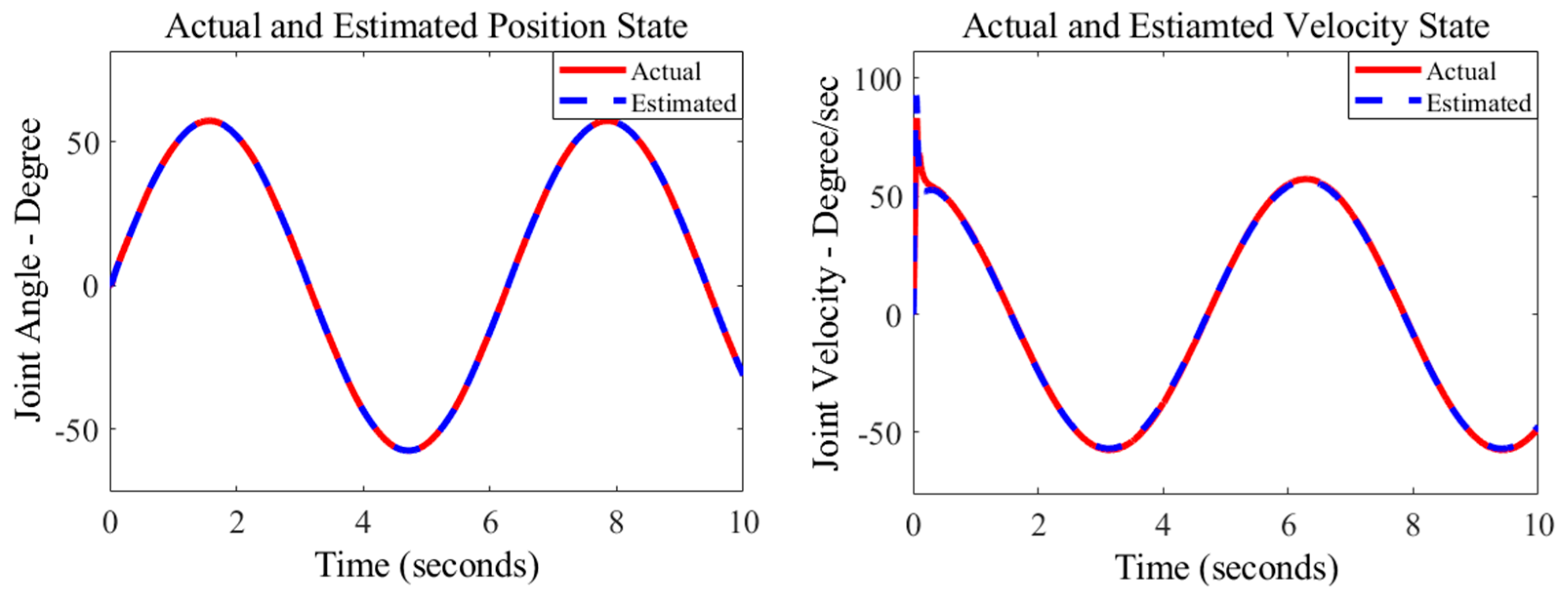
3.1. Extended State Observer
3.2. Extended State Observer-Based Sliding Mode Control (SMCESO)
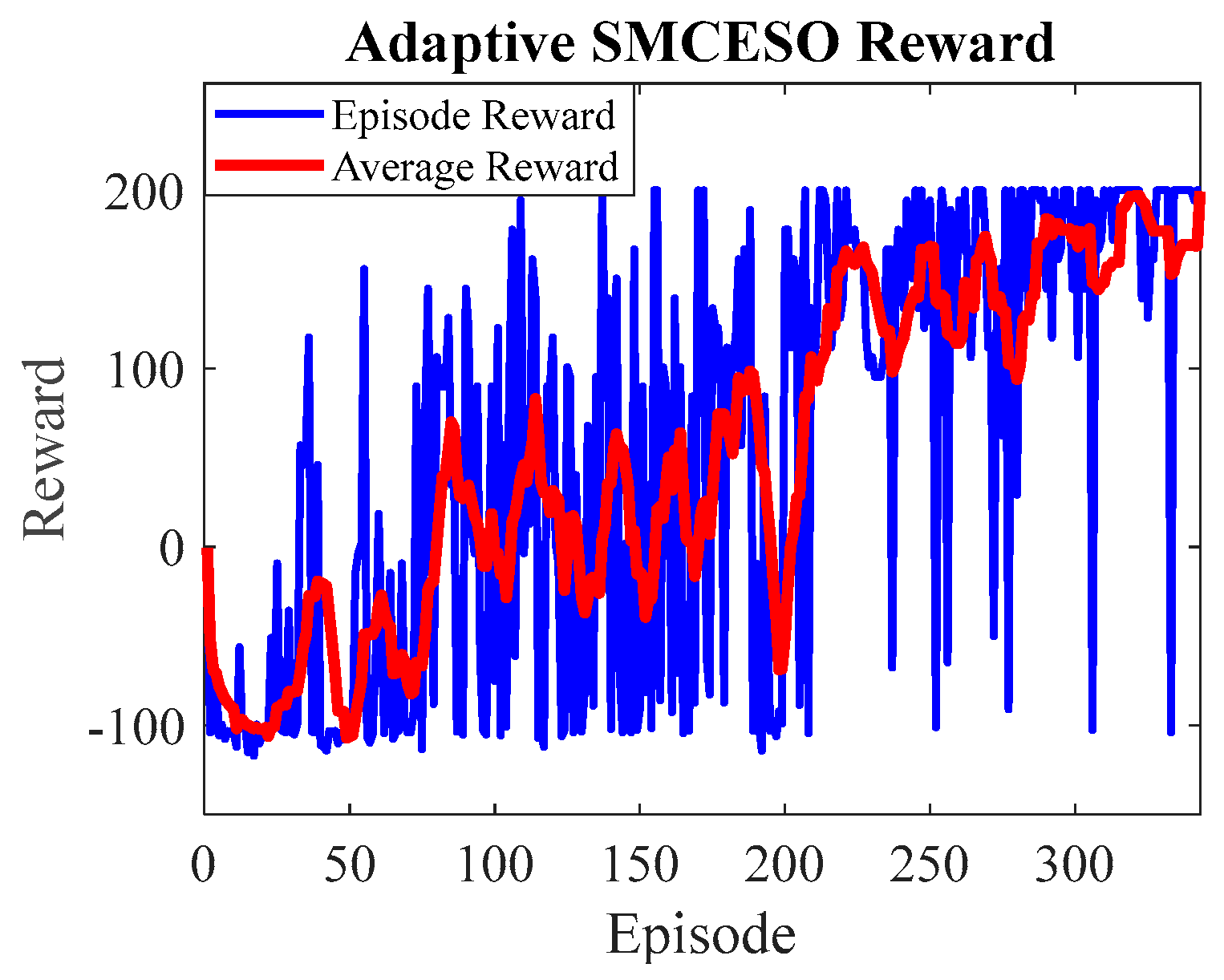
3.3. DDPG-Based SMCESO
| Algorithm 1: Training DDPG Agent |
| Initialize the networks and randomly. Initialize the target network , and with weights. Initialize the replay buffer. While Randomly initialize the process for action exploration. Receive the states while . Execute the environment to update the reward . Store in replay buffer R. Sample a random minibatch of transitions from R. Set target Update the critic by minimizing the loss function Update the actor using the sampled policy gradient . Update the target network with soft update . If Reset. End if end while k if Stop training. End end |
4. Simulations and Discussion
4.1. System and Environment Descrption
4.2. Simulations
4.2.1. Simple System Implementation
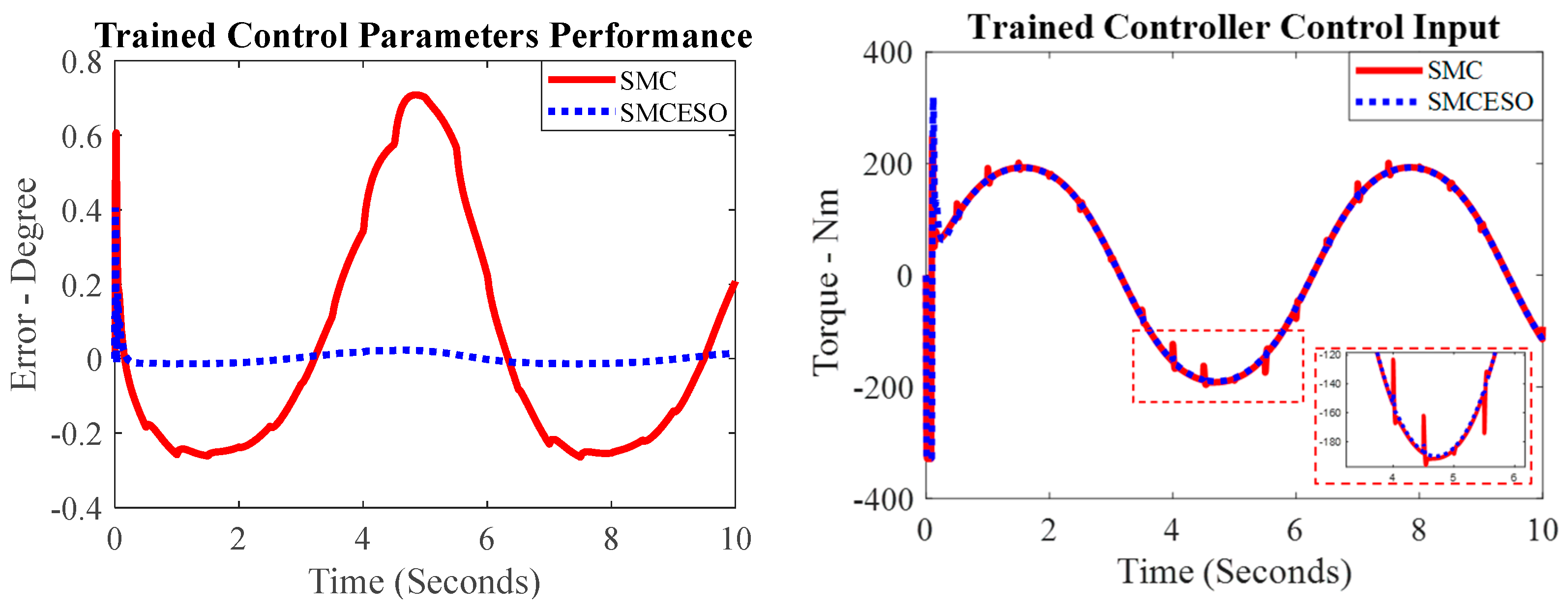
4.2.2. Adaptive SMCESO with Multibody Robot
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Introduction: Intuitive Theory of Sliding Mode Control. In Sliding Mode Control and Observation; Control Engineering; Birkhäuser: New York, NY, USA, 2014; pp. 1–42. [Google Scholar]
- Afifa, R.; Ali, S.; Pervaiz, M.; Iqbal, J. Adaptive Backstepping Integral Sliding Mode Control of a MIMO Separately Excited Dc Motor. Robotics 2023, 12, 105. [Google Scholar] [CrossRef]
- Khan, H.; Abbasi, S.J.; Lee, M.C. DPSO and Inverse Jacobian-based Real-time Inverse Kinematics with Trajectory Tracking using Integral SMC for Teleoperation. IEEE Access 2020, 8, 159622–159638. [Google Scholar] [CrossRef]
- Hollweg, G.V.; de Oliveira Evald, P.J.; Milbradt, D.M.; Tambara, R.V.; Gründling, H.A. Design of continuous-time model reference adaptive and super-twisting sliding mode controller. Math. Comput. Simul. 2022, 201, 215–238. [Google Scholar] [CrossRef]
- Mobayen, S.; Bayat, F.; ud Din, S.; Vu, M.T. Barrier function-based adaptive nonsingular terminal sliding mode control technique for a class of disturbed nonlinear systems. ISA Trans. 2023, 134, 481–496. [Google Scholar] [CrossRef] [PubMed]
- Khan, H.; Abbasi, S.J.; Lee, M.C. Robust Position Control of Assistive Robot for Paraplegics. Int. J. Control Autom. Syst. 2021, 19, 3741–3752. [Google Scholar] [CrossRef]
- Abbasi, S.J.; Khan, H.; Lee, J.W.; Salman, M.; Lee, M.C. Robust Control Design for Accurate Trajectory Tracking of Multi-Degree-of-Freedom Robot Manipulator in Virtual Simulator. IEEE Access 2022, 10, 17155–17168. [Google Scholar] [CrossRef]
- Humaidi, A.J.; Hasan, A.F. Particle Swarm Optimization-Based Adaptive Super-Twisting Sliding Mode Control Design for 2-Degree-of-Freedom Helicopter. Meas. Control 2019, 52, 1403–1419. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, K.; Yan, F.; Chen, B. Adaptive Super-Twisting Nonsingular Fast Terminal Sliding Mode Control for Cable-Driven Manipulators using Time-Delay Estimation. Adv. Eng. Softw. 2019, 128, 113–124. [Google Scholar] [CrossRef]
- Wang, H.; Fang, L.; Song, T.; Xu, J.; Shen, H. Model-free Adaptive Sliding Mode Control with Adjustable Funnel Boundary for Robot Manipulators with Uncertainties. Rev. Sci. Instrum. 2021, 92, 065101. [Google Scholar] [CrossRef]
- Xi, R.-D.; Xiao, X.; Ma, T.-N.; Yang, Z.-X. Adaptive Sliding Mode Disturbance Observer-Based Robust Control for Robot Manipulators Towards Assembly Assistance. IEEE Robot. Autom. Lett. 2022, 7, 6139–6146. [Google Scholar] [CrossRef]
- Jing, C.; Xu, H.; Niu, X. Adaptive Sliding Mode Disturbance Rejection Control with Prescribed Performance for Robotic Manipulators. ISA Trans. 2019, 91, 41–51. [Google Scholar] [CrossRef]
- Zhao, H.; Tao, B.; Ma, R.; Chen, B. Manipulator trajectory tracking based on adaptive fuzzy sliding mode control. Concurr. Comput. Pract. Exp. 2023, 35, e7620. [Google Scholar] [CrossRef]
- Khan, H.; Lee, M.C. Extremum Seeking-Based Adaptive Sliding Mode Control with Sliding Perturbation Observer for Robot Manipulators. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 5284–5290. [Google Scholar]
- Razmi, H.; Afshinfar, S. Neural Network-Based Adaptive Sliding Mode Control Design for Position and Attitude Control of a Quadrotor UAV. Aerosp. Sci. Technol. 2019, 91, 12–27. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, F.; Chen, W.; Zhang, W.; Sun, W.; Chen, J.; Zhu, S.; Gu, J. RBFNN-Based Adaptive Sliding Mode Control Design for Delayed Nonlinear Multilateral Telerobotic System with Cooperative Manipulation. IEEE Trans. Ind. Inform. 2020, 16, 1236–1247. [Google Scholar] [CrossRef]
- Wang, D.; Shen, Y.; Sha, Q.; Li, G.; Kong, X.; Chen, G.; He, B. Adaptive DDPG Design-Based Sliding-Mode Control for Autonomous Underwater Vehicles at Different Speeds. In Proceedings of the IEEE Underwater Technology (UT), Kaohsiung, Taiwan, 16–19 April 2019; pp. 1–5. [Google Scholar]
- Mosharafian, S.; Afzali, S.; Bao, Y.; Velni, J.M. A Deep Reinforcement Learning-Based Sliding Mode Control Design for Partially Known Nonlinear Systems. In Proceedings of the European Control Conference (ECC), London, UK, 12–15 July 2022; pp. 2241–2246. [Google Scholar]
- Lei, C.; Zhu, Q. U-Model-Based Adaptive Sliding Mode Control using a Deep Deterministic Policy Gradient. Math. Probl. Eng. 2022, 2022, 8980664. [Google Scholar] [CrossRef]
- Pantoja-Garcia, L.; Parra-Vega, V.; Garcia-Rodriguez, R.; Vázquez-García, C.E. A Novel Actor—Critic Motor Reinforcement Learning for Continuum Soft Robots. Robotics 2023, 12, 141. [Google Scholar] [CrossRef]
- Abbasi, S.J.; Lee, S. Enhanced Trajectory Tracking via Disturbance-Observer-Based Modified Sliding Mode Control. Appl. Sci. 2023, 13, 8027. [Google Scholar] [CrossRef]
- Raoufi, M.; Habibi, H.; Yazdani, A.; Wang, H. Robust Prescribed Trajectory Tracking Control of a Robot Manipulator Using Adaptive Finite-Time Sliding Mode and Extreme Learning Machine Method. Robotics 2022, 11, 111. [Google Scholar] [CrossRef]
- Saleki, A.; Fateh, M.M. Model-free control of electrically driven robot manipulators using an extended state observer. Comput. Electr. Eng. 2020, 87, 106768. [Google Scholar] [CrossRef]
- Zheng, Y.; Tao, J.; Sun, Q.; Zeng, X.; Sun, H.; Sun, M.; Chen, Z. DDPG-Based Active Disturbance Rejection 3D Path-Following Control for Powered Parafoil Under Wind Disturbances. Nonlinear Dyn. 2023, 111, 1–17. [Google Scholar] [CrossRef]
- Sun, M.; Zhang, W.; Zhang, Y.; Luan, T.; Yuan, X.; Li, X. An Anti-Rolling Control Method of Rudder Fin System Based on ADRC Decoupling and DDPG Parameter Adjustment. Ocean. Eng. 2023, 278, 114306. [Google Scholar] [CrossRef]
- Yang, J.; Peng, W.; Sun, C. A Learning Control Method of Automated Vehicle Platoon at Straight Path with DDPG-Based PID. Electronics 2021, 10, 2580. [Google Scholar] [CrossRef]
- Dey, N.; Mondal, U.; Mondal, D. Design of a H-Infinity Robust Controller for a DC Servo Motor System. In Proceedings of the 2016 International Conference on Intelligent Control Power and Instrumentation (ICICPI), Kolkata, India, 21–23 October 2016; pp. 27–31. [Google Scholar]




| Reinforcement | Parameters | |
|---|---|---|
| Parameter | Value | |
| Critic | Learn rate | |
| Gradient Threshold | ||
| Actor | Learn rate | |
| Gradient threshold | ||
| Agent | Sample time | |
| Target smooth factor | ||
| Discount factor | ||
| Minibatch size | ||
| Experience buffer length | ||
| Noise variance | ||
| Noise variance decay rate | ||
| Training | Maximum episode | 2000 |
| Maximum steps | 20 | |
| Average reward window length | 10 | |
| Control Algorithm | Gains |
|---|---|
| PID | . |
| SMC | . |
| SMCESO | . |
| Parameter | Value |
|---|---|
| Gear Ratio | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, H.; Khan, S.A.; Lee, M.C.; Ghafoor, U.; Gillani, F.; Shah, U.H. DDPG-Based Adaptive Sliding Mode Control with Extended State Observer for Multibody Robot Systems. Robotics 2023, 12, 161. https://doi.org/10.3390/robotics12060161
Khan H, Khan SA, Lee MC, Ghafoor U, Gillani F, Shah UH. DDPG-Based Adaptive Sliding Mode Control with Extended State Observer for Multibody Robot Systems. Robotics. 2023; 12(6):161. https://doi.org/10.3390/robotics12060161
Chicago/Turabian StyleKhan, Hamza, Sheraz Ali Khan, Min Cheol Lee, Usman Ghafoor, Fouzia Gillani, and Umer Hameed Shah. 2023. "DDPG-Based Adaptive Sliding Mode Control with Extended State Observer for Multibody Robot Systems" Robotics 12, no. 6: 161. https://doi.org/10.3390/robotics12060161
APA StyleKhan, H., Khan, S. A., Lee, M. C., Ghafoor, U., Gillani, F., & Shah, U. H. (2023). DDPG-Based Adaptive Sliding Mode Control with Extended State Observer for Multibody Robot Systems. Robotics, 12(6), 161. https://doi.org/10.3390/robotics12060161







