PInteract: Detecting Aromatic-Involving Motifs in Proteins and Protein-Nucleic Acid Complexes
Abstract
1. Introduction
2. Materials and Methods
2.1. Types of Interactions
2.2. Design Principles
- The distance between the two interacting partners. Sometimes, this distance is defined as the distance between the centroids of the two interacting functional groups. In other studies, like here, it is defined as the closest distance between any two atoms of the two functional groups. We chose this distance definition because the considered aromatic moieties carry various substituents which influence how the ring interacts with other partners and breaks the symmetry around the ring’s center. Similarly, the electron delocalization in other functional groups is better captured by selecting the closest atom rather than the functional group’s centroid.
- The angle; it is typically defined as the angle between the vector linking the centroids of both partners and the vector normal to the aromatic ring of the aromatic partner or of one of the aromatic partners in the case of - interactions. The complement of , i.e., , is called elevation angle and is sometimes also used.
- The angle; it only applies to interactions in which the two functional groups are planar, i.e., contain an aromatic moiety (Phe, Tyr, Trp, His), a guanidinium group (Arg) or an formamide group (Asn, Gln). It is defined as the angle between the vectors normal to the planes of the two interacting functional groups and measures the degree of parallellism between the planes.
2.3. Technical Implementation
2.3.1. Functional Groups
- Aromatic moiety: all atoms that make up the aromatic ring or rings, as well as their centers referred to as mC5 or mC6 depending on whether the ring is 5- or 6-membered;
- Positive charge: NH1, NH2, CZ and NE for Arg; and NZ, CE, H1 for Lys; ND1, CE1, NE2 for His if its caonsidered as a cation;
- Partial positive charge: NE2, CD and OE1 for Gln; ND2, CG and OD1 for Asn;
- Sulfur: SG for Cys; SD for Met.
2.3.2. Distance Criterion
- Å for - interactions;
- Å for sulfur- interactions;
- Å for cation-, amino-, and His- interactions.
2.3.3. Angle Criterion
- for cation-, His-, amino- and sulfur- interactions;
- for - interactions.
2.3.4. Plane Parallelism Angle
2.4. Structure Datasets’ Construction
- : 5590 protein monomers;
- : 3940 protein homodimers;
- : 1037 protein heterodimers;
- : 51 complexes between a T-cell receptor (TCR) and a peptide-bound major histocompatibility complex (pMHC);
- : 495 antibody-antigen complexes;
- : 573 protein-DNA or protein-RNA complexes.
3. Results
3.1. The PInteract Algorithm
3.2. Examples of -Involving Interactions
3.3. Large-Scale Analysis of -Involving Interactions
3.4. Relationship Between Interactions and Protein Solubility and Aggregation
3.5. PInteract: Fast, Scalable, and User-Friendly
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Salonen, L.M.; Ellermann, M.; Diederich, F. Aromatic rings in chemical and biological recognition: Energetics and structures. Angew. Chem. Int. Ed. 2011, 50, 4808–4842. [Google Scholar] [CrossRef]
- Calinsky, R.; Levy, Y. Aromatic Residues in Proteins: Re-Evaluating the Geometry and Energetics of π–π, Cation-π, and CH-π Interactions. J. Phys. Chem. B 2024, 128, 8687–8700. [Google Scholar] [CrossRef] [PubMed]
- Burley, S.; Petsko, G.A. Aromatic-aromatic interaction: A mechanism of protein structure stabilization. Science 1985, 229, 23–28. [Google Scholar] [CrossRef] [PubMed]
- Dougherty, D.A. Cation-π interactions in chemistry and biology: A new view of benzene, Phe, Tyr, and Trp. Science 1996, 271, 163–168. [Google Scholar] [CrossRef] [PubMed]
- Wintjens, R.; Liévin, J.; Rooman, M.; Buisine, E. Contribution of cation-π interactions to the stability of protein-DNA complexes. J. Mol. Biol. 2000, 302, 393–408. [Google Scholar] [CrossRef]
- Dougherty, D.A. The Cation-π Interaction in Chemistry and Biology. Chem. Rev. 2025, 125, 2793–2808. [Google Scholar] [CrossRef]
- Imai, Y.N.; Inoue, Y.; Nakanishi, I.; Kitaura, K. Amide–π interactions between formamide and benzene. J. Comput. Chem. 2009, 30, 2267–2276. [Google Scholar] [CrossRef]
- Cauët, E.; Rooman, M.; Wintjens, R.; Liévin, J.; Biot, C. Histidine-aromatic interactions in proteins and protein- ligand complexes: Quantum chemical study of X-ray and model structures. J. Chem. Theory Comput. 2005, 1, 472–483. [Google Scholar] [CrossRef]
- Shimba, N.; Serber, Z.; Ledwidge, R.; Miller, S.M.; Craik, C.S.; Dötsch, V. Quantitative identification of the protonation state of histidines in vitro and in vivo. Biochemistry 2003, 42, 9227–9234. [Google Scholar] [CrossRef]
- Calinsky, R.; Levy, Y. Histidine in Proteins: PH-Dependent Interplay between π–π, Cation–π, and CH–π Interactions. J. Chem. Theory Comput. 2024, 20, 6930–6945. [Google Scholar] [CrossRef]
- Reid, K.; Lindley, P.; Thornton, J. Sulphur-aromatic interactions in proteins. FEBS Lett. 1985, 190, 209–213. [Google Scholar] [CrossRef]
- Motherwell, W.B.; Moreno, R.B.; Pavlakos, I.; Arendorf, J.R.; Arif, T.; Tizzard, G.J.; Coles, S.J.; Aliev, A.E. Noncovalent interactions of π systems with sulfur: The atomic chameleon of molecular recognition. Angew. Chem. 2018, 130, 1207–1212. [Google Scholar] [CrossRef]
- Nunar, L.; Aliev, A.E. Quantification of the Strength of π-Noncovalent Interactions in Molecular Balances using Density Functional Methods. Chemistry-Methods 2023, 3, e202200044. [Google Scholar] [CrossRef]
- Daeffler, K.N.M.; Lester, H.A.; Dougherty, D.A. Functionally important aromatic–aromatic and sulfur-π interactions in the D2 dopamine receptor. J. Am. Chem. Soc. 2012, 134, 14890–14896. [Google Scholar] [CrossRef] [PubMed]
- Lanzarotti, E.; Biekofsky, R.R.; Estrin, D.A.; Marti, M.A.; Turjanski, A.G. Aromatic–aromatic interactions in proteins: Beyond the dimer. J. Chem. Inf. Model. 2011, 51, 1623–1633. [Google Scholar] [CrossRef] [PubMed]
- Rooman, M.; Liévin, J.; Buisine, E.; Wintjens, R. Cation–π/H-bond stair motifs at protein–DNA interfaces. J. Mol. Biol. 2002, 319, 67–76. [Google Scholar] [CrossRef]
- Biot, C.; Wintjens, R.; Rooman, M. Stair motifs at protein- DNA interfaces: Nonadditivity of H-bond, stacking, and cation-π interactions. J. Am. Chem. Soc. 2004, 126, 6220–6221. [Google Scholar] [CrossRef]
- Kumar, K.; Woo, S.M.; Siu, T.; Cortopassi, W.A.; Duarte, F.; Paton, R.S. Cation–π interactions in protein–ligand binding: Theory and data-mining reveal different roles for lysine and arginine. Chem. Sci. 2018, 9, 2655–2665. [Google Scholar] [CrossRef]
- Kumar, N.; Gaur, A.S.; Sastry, G.N. A perspective on the nature of cation-π interactions. J. Chem. Sci. 2021, 133, 97. [Google Scholar] [CrossRef]
- Shah, D.; Li, J.; Shaikh, A.R.; Rajagopalan, R. Arginine–aromatic interactions and their effects on arginine-induced solubilization of aromatic solutes and suppression of protein aggregation. Biotechnol. Prog. 2012, 28, 223–231. [Google Scholar] [CrossRef]
- Zauhar, R.J.; Colbert, C.L.; Morgan, R.S.; Welsh, W.J. Evidence for a strong sulfur-aromatic interaction derived from crystallographic data. Biopolymers 2000, 53, 233–248. [Google Scholar] [CrossRef]
- Krainer, G.; Welsh, T.J.; Joseph, J.A.; Espinosa, J.R.; Wittmann, S.; De Csilléry, E.; Sridhar, A.; Toprakcioglu, Z.; Gudiškytė, G.; Czekalska, M.A.; et al. Reentrant liquid condensate phase of proteins is stabilized by hydrophobic and non-ionic interactions. Nat. Commun. 2021, 12, 1085. [Google Scholar] [CrossRef]
- Zhao, H.; Tang, L.; Fang, Y.; Liu, C.; Ding, W.; Zang, S.; Chen, Y.; Xu, W.; Yuan, Y.; Fang, D.; et al. Manipulating Cation–π Interactions of Reader Proteins in Living Cells with Genetic Code Expansion. J. Am. Chem. Soc. 2023, 145, 16406–16416. [Google Scholar] [CrossRef]
- Valley, C.C.; Cembran, A.; Perlmutter, J.D.; Lewis, A.K.; Labello, N.P.; Gao, J.; Sachs, J.N. The Methionine-aromatic Motif Plays a Unique Role in Stabilizing Protein Structure. J. Biol. Chem. 2012, 287, 34979–34991. [Google Scholar] [CrossRef]
- Kumar, Y.B.; Kumar, N.; John, L.; Mahanta, H.J.; Vaikundamani, S.; Nagamani, S.; Sastry, G.M.; Sastry, G.N. Analyzing the cation-aromatic interactions in proteins: Cation-aromatic database V2.0. Proteins Struct. Funct. Bioinform. 2024, 92, 179–191. [Google Scholar] [CrossRef]
- Chourasia, M.; Sastry, G.M.; Sastry, G.N. Aromatic–Aromatic Interactions Database, A2ID: An analysis of aromatic π-networks in proteins. Int. J. Biol. Macromol. 2011, 48, 540–552. [Google Scholar] [CrossRef] [PubMed]
- Tina, K.G.; Bhadra, R.; Srinivasan, N. PIC: Protein Interactions Calculator. Nucleic Acids Res. 2007, 35, W473–W476. [Google Scholar] [CrossRef] [PubMed]
- Biot, C.; Buisine, E.; Kwasigroch, J.M.; Wintjens, R.; Rooman, M. Probing the energetic and structural role of amino acid/nucleobase cation-π interactions in protein-ligand complexes. J. Biol. Chem. 2002, 277, 40816–40822. [Google Scholar] [CrossRef] [PubMed]
- Biot, C.; Buisine, E.; Rooman, M. Free-energy calculations of protein- ligand cation-π and amino- π interactions: From vacuum to proteinlike environments. J. Am. Chem. Soc. 2003, 125, 13988–13994. [Google Scholar] [CrossRef] [PubMed]
- Minoux, H.; Chipot, C. Cation-π Interactions in Proteins: Can Simple Models Provide an Accurate Description? J. Am. Chem. Soc. 1999, 121, 10366–10372. [Google Scholar] [CrossRef]
- Gallivan, J.P.; Dougherty, D.A. A Computational Study of Cation-π Interactions vs Salt Bridges in Aqueous Media: Implications for Protein Engineering. J. Am. Chem. Soc. 2000, 122, 870–874. [Google Scholar] [CrossRef]
- McDonald, I.K.; Thornton, J.M. Satisfying hydrogen bonding potential in proteins. J. Mol. Biol. 1994, 238, 777–793. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The protein data bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef]
- Wang, G.; Dunbrack, R.L., Jr. PISCES: A protein sequence culling server. Bioinformatics 2003, 19, 1589–1591. [Google Scholar] [CrossRef]
- HomodimerDB. Available online: https://seq2fun.dcmb.med.umich.edu/HomodimerDB (accessed on 9 August 2025).
- Gowthaman, R.; Pierce, B.G. TCR3d: The T cell receptor structural repertoire database. Bioinformatics 2019, 35, 5323–5325. [Google Scholar] [CrossRef] [PubMed]
- Pierce, B.G.; Weng, Z. A flexible docking approach for prediction of T cell receptor–peptide–MHC complexes. Protein Sci. 2013, 22, 35–46. [Google Scholar] [CrossRef]
- Dunbar, J.; Krawczyk, K.; Leem, J.; Baker, T.; Fuchs, A.; Georges, G.; Shi, J.; Deane, C.M. SAbDab: The structural antibody database. Nucleic Acids Res. 2014, 42, D1140–D1146. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.; Raybould, M.I.; Deane, C.M. SAbDab in the age of biotherapeutics: Updates including SAbDab-nano, the nanobody structure tracker. Nucleic Acids Res. 2022, 50, D1368–D1372. [Google Scholar] [CrossRef]
- Raybould, M.I.; Marks, C.; Lewis, A.P.; Shi, J.; Bujotzek, A.; Taddese, B.; Deane, C.M. Thera-SAbDab: The therapeutic structural antibody database. Nucleic Acids Res. 2020, 48, D383–D388. [Google Scholar] [CrossRef] [PubMed]
- Mitra, R.; Cohen, A.S.; Sagendorf, J.M.; Berman, H.M.; Rohs, R. DNAproDB: An updated database for the automated and interactive analysis of protein–DNA complexes. Nucleic Acids Res. 2025, 53, D396–D402. [Google Scholar] [CrossRef]
- Mitra, R.; Cohen, A.S.; Tang, W.Y.; Hosseini, H.; Hong, Y.; Berman, H.M.; Rohs, R. RNAproDB: A Webserver and Interactive Database for Analyzing Protein–RNA Interactions. J. Mol. Biol. 2025, 437, 169012. [Google Scholar] [CrossRef]
- Dalkas, G.A.; Teheux, F.; Kwasigroch, J.M.; Rooman, M. Cation–π, amino–π, π–π, and H-bond interactions stabilize antigen–antibody interfaces. Proteins Struct. Funct. Bioinform. 2014, 82, 1734–1746. [Google Scholar] [CrossRef]
- Akiba, H.; Tsumoto, K. Thermodynamics of antibody–antigen interaction revealed by mutation analysis of antibody variable regions. J. Biochem. 2015, 158, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Wilson, K.A.; Kellie, J.L.; Wetmore, S.D. DNA–protein π-interactions in nature: Abundance, structure, composition and strength of contacts between aromatic amino acids and DNA nucleobases or deoxyribose sugar. Nucleic Acids Res. 2014, 42, 6726–6741. [Google Scholar] [CrossRef]
- Wu, D.; Sun, J.; Xu, T.; Wang, S.; Li, G.; Li, Y.; Cao, Z. Stacking and energetic contribution of aromatic islands at the binding interface of antibody proteins. Immunome Res. 2010, 6, S1. [Google Scholar] [CrossRef]
- Varadi, M.; Bertoni, D.; Magana, P.; Paramval, U.; Pidruchna, I.; Radhakrishnan, M.; Tsenkov, M.; Nair, S.; Mirdita, M.; Yeo, J.; et al. AlphaFold Protein Structure Database in 2024: Providing structure coverage for over 214 million protein sequences. Nucleic Acids Res. 2024, 52, D368–D375. [Google Scholar] [CrossRef] [PubMed]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Hou, Q.; Bourgeas, R.; Pucci, F.; Rooman, M. Computational analysis of the amino acid interactions that promote or decrease protein solubility. Sci. Rep. 2018, 8, 14661. [Google Scholar] [CrossRef]
- Vernon, R.M.; Chong, P.A.; Tsang, B.; Kim, T.H.; Bah, A.; Farber, P.; Lin, H.; Forman-Kay, J.D. Pi-Pi contacts are an overlooked protein feature relevant to phase separation. eLife 2018, 7, e31486. [Google Scholar] [CrossRef]
- Gazit, E. A possible role for π-stacking in the self-assembly of amyloid fibrils. FASEB J. 2002, 16, 77–83. [Google Scholar] [CrossRef]
- Warwicker, J.; Charonis, S.; Curtis, R.A. Lysine and arginine content of proteins: Computational analysis suggests a new tool for solubility design. Mol. Pharm. 2014, 11, 294–303. [Google Scholar] [CrossRef]
- Hou, Q.; Kwasigroch, J.M.; Rooman, M.; Pucci, F. SOLart: A structure-based method to predict protein solubility and aggregation. Bioinformatics 2020, 36, 1445–1452. [Google Scholar] [CrossRef] [PubMed]
- Niwa, T.; Ying, B.W.; Saito, K.; Jin, W.; Takada, S.; Ueda, T.; Taguchi, H. Bimodal protein solubility distribution revealed by an aggregation analysis of the entire ensemble of Escherichia coli proteins. Proc. Natl. Acad. Sci. USA 2009, 106, 4201–4206. [Google Scholar] [CrossRef] [PubMed]
- Uemura, E.; Niwa, T.; Minami, S.; Takemoto, K.; Fukuchi, S.; Machida, K.; Imataka, H.; Ueda, T.; Ota, M.; Taguchi, H. Large-scale aggregation analysis of eukaryotic proteins reveals an involvement of intrinsically disordered regions in protein folding. Sci. Rep. 2018, 8, 678. [Google Scholar] [CrossRef] [PubMed]
- Stanković, I.M.; Niu, S.; Hall, M.B.; Zarić, S.D. Role of aromatic amino acids in amyloid self-assembly. Int. J. Biol. Macromol. 2020, 156, 949–959. [Google Scholar] [CrossRef]
- van der Kant, R.; Louros, N.; Schymkowitz, J.; Rousseau, F. Thermodynamic analysis of amyloid fibril structures reveals a common framework for stability in amyloid polymorphs. Structure 2022, 30, 1178–1189. [Google Scholar] [CrossRef]
- Kollmer, M.; Close, W.; Funk, L.; Rasmussen, J.; Bsoul, A.; Schierhorn, A.; Schmidt, M.; Sigurdson, C.J.; Jucker, M.; Fändrich, M. Cryo-EM structure and polymorphism of Aβ amyloid fibrils purified from Alzheimer’s brain tissue. Nature Comm. 2019, 10, 4760. [Google Scholar] [CrossRef]


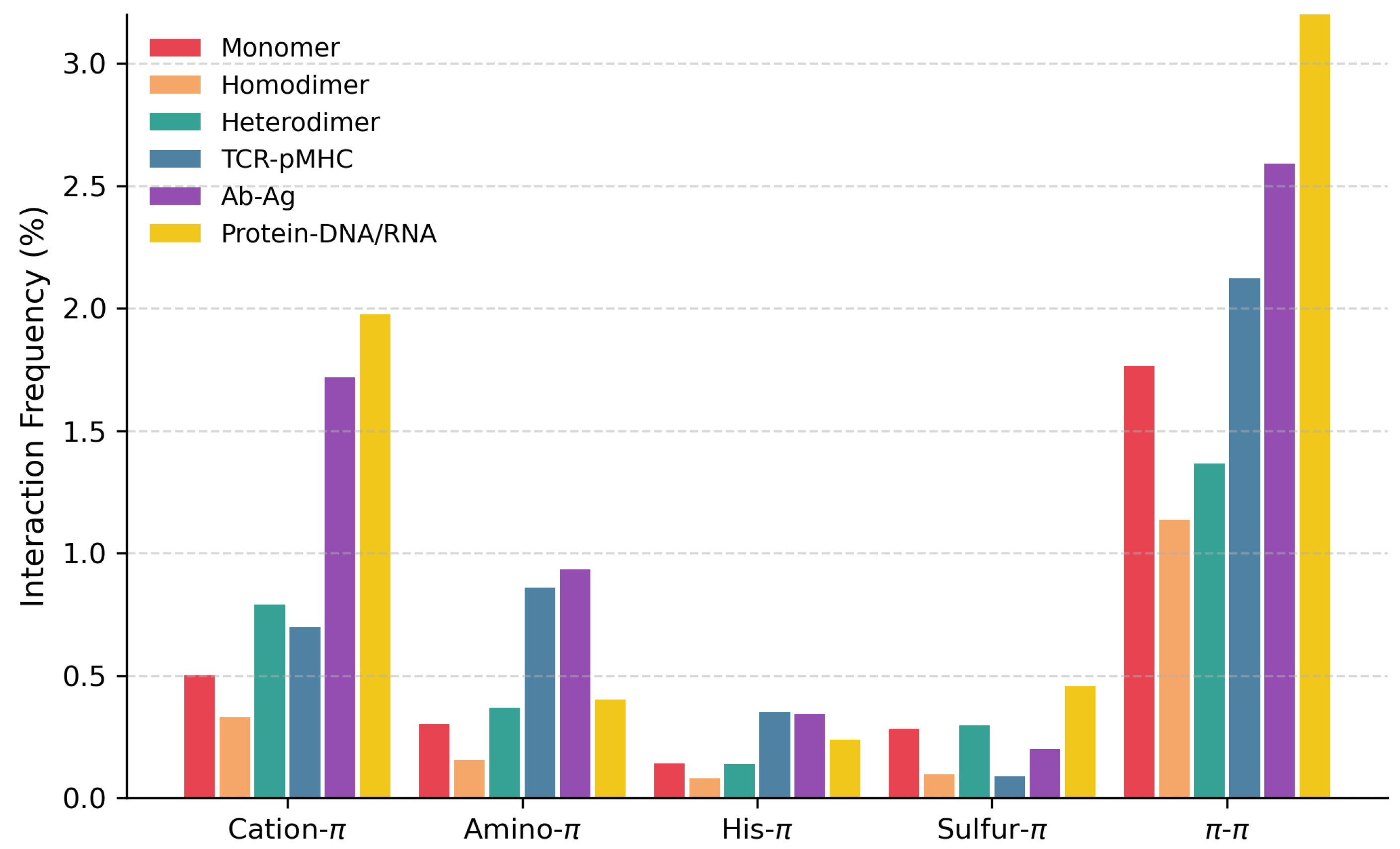
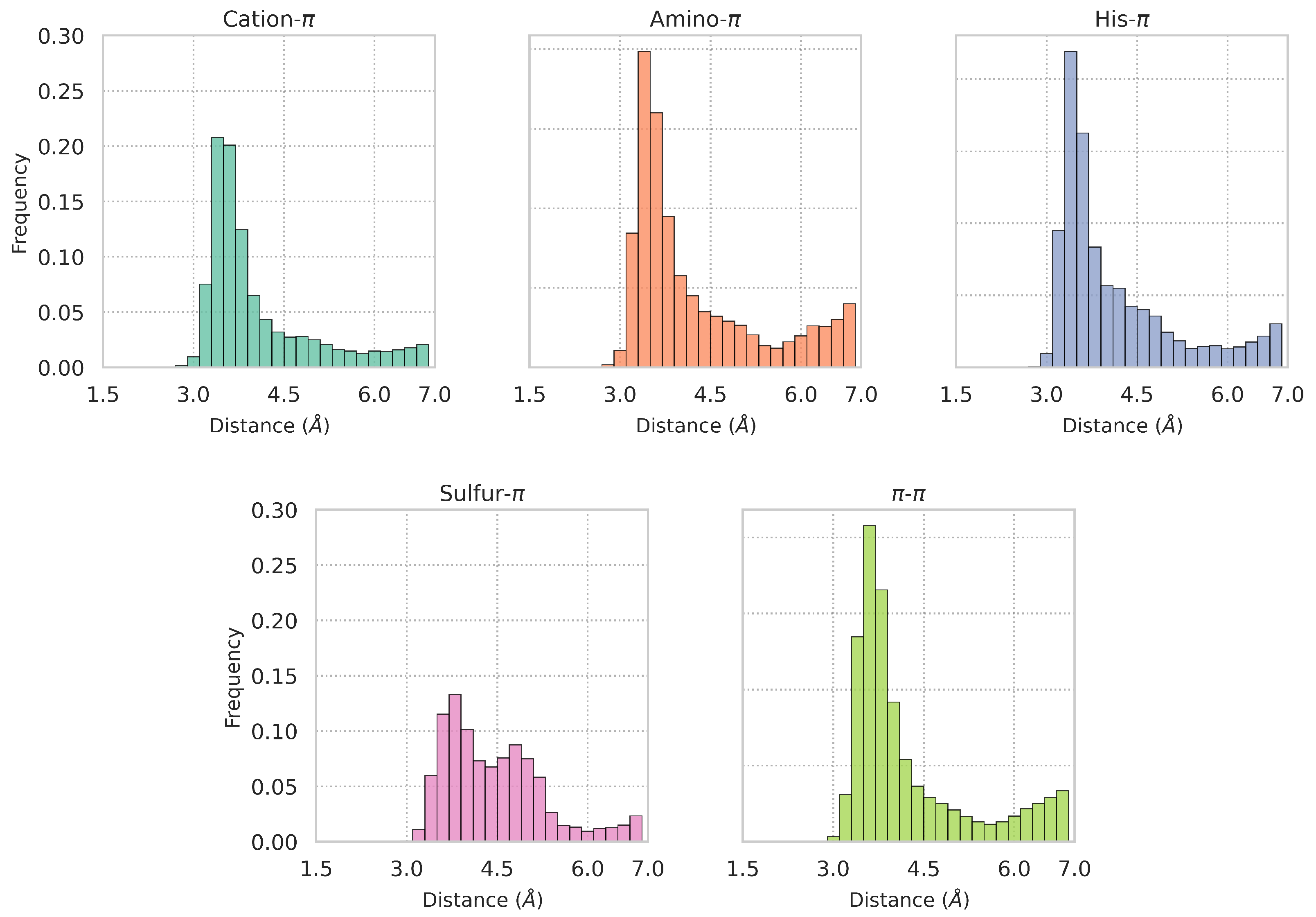


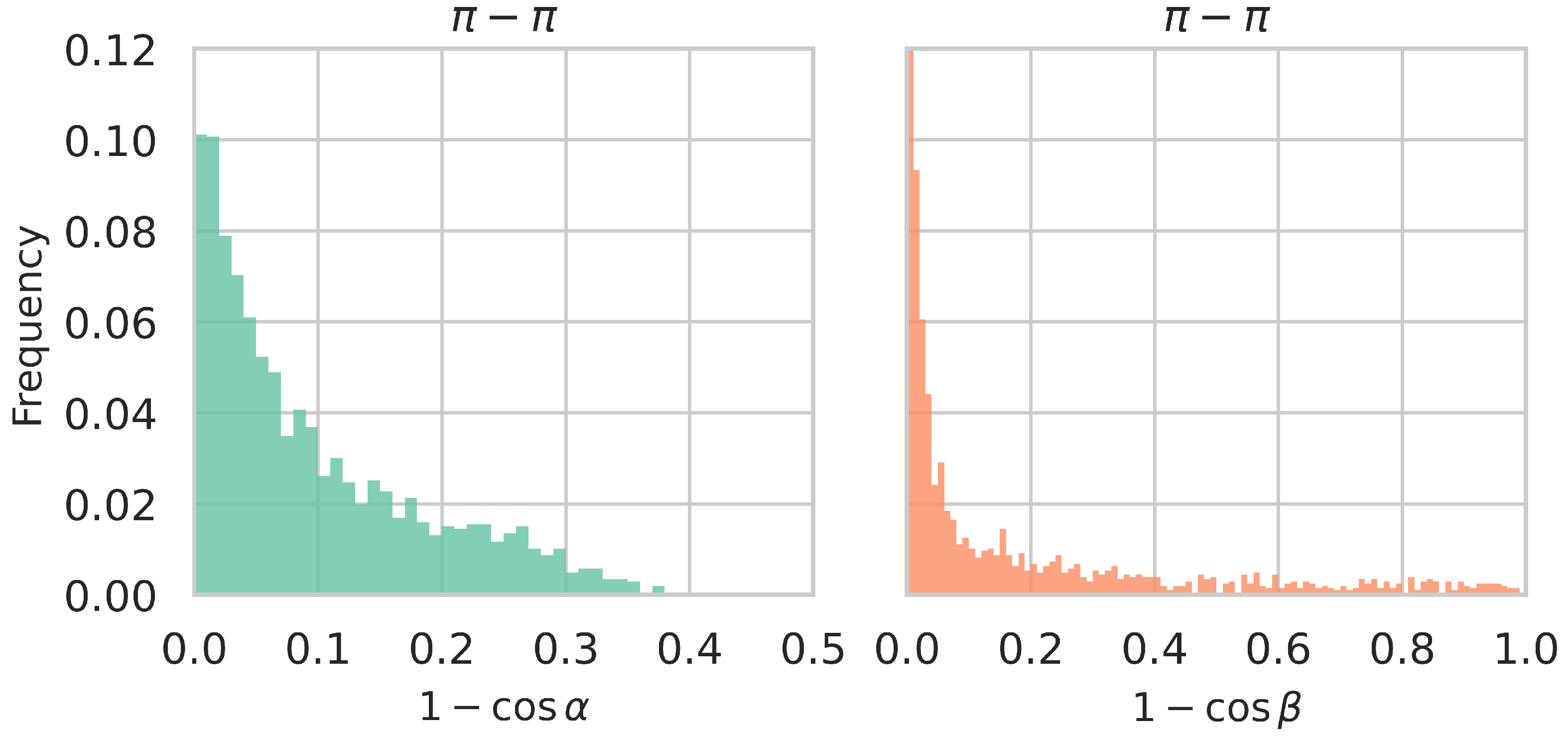
| Dataset | Cation- | Amino- | His- | Sulfur- | - |
|---|---|---|---|---|---|
| 0.50 (0.46) | 0.30 (0.33) | 0.14 (0.22) | 0.28 (0.37) | 1.77 (1.13) | |
| 0.33 (1.14) | 0.17 (0.81) | 0.09 (0.51) | 0.10 (0.56) | 1.13 (2.00) | |
| 0.79 (1.80) | 0.37 (1.36) | 0.14 (0.73) | 0.30 (0.89) | 1.37 (2.38) | |
| 0.70 (1.22) | 0.86 (1.73) | 0.35 (0.84) | 0.09 (0.44) | 2.12 (2.97) | |
| 1.72 (3.21) | 0.93 (1.93) | 0.34 (1.15) | 0.20 (0.78) | 2.59 (3.89) | |
| 2.02 (12.67) | 0.41 (1.08) | 0.23 (0.89) | 0.47 (4.29) | 3.73 (10.41) |
| Arg | Lys | Phe/Tyr/Trp | Asn/Gln | His | Met/Cys | |
|---|---|---|---|---|---|---|
| F | −0.09 | 0.14 | −0.17 | − | − | |
| −0.14 | − | −0.23 | − | − | −0.15 | |
| − | 0.15 | − | − |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Pucci, F.; Rooman, M. PInteract: Detecting Aromatic-Involving Motifs in Proteins and Protein-Nucleic Acid Complexes. Biomolecules 2025, 15, 1204. https://doi.org/10.3390/biom15081204
Li D, Pucci F, Rooman M. PInteract: Detecting Aromatic-Involving Motifs in Proteins and Protein-Nucleic Acid Complexes. Biomolecules. 2025; 15(8):1204. https://doi.org/10.3390/biom15081204
Chicago/Turabian StyleLi, Dong, Fabrizio Pucci, and Marianne Rooman. 2025. "PInteract: Detecting Aromatic-Involving Motifs in Proteins and Protein-Nucleic Acid Complexes" Biomolecules 15, no. 8: 1204. https://doi.org/10.3390/biom15081204
APA StyleLi, D., Pucci, F., & Rooman, M. (2025). PInteract: Detecting Aromatic-Involving Motifs in Proteins and Protein-Nucleic Acid Complexes. Biomolecules, 15(8), 1204. https://doi.org/10.3390/biom15081204







