An Efficient Bayesian Method for Estimating the Degree of the Skewness of X Chromosome Inactivation Based on the Mixture of General Pedigrees and Unrelated Females
Abstract
1. Introduction
2. Materials and Methods
2.1. Notations
2.2. Building Bayesian Models
2.3. Eigenvalue Decomposition and Cholesky Decomposition for Accelerating Computation Speed
2.4. HMC Algorithm and Priors
2.5. Situations When Considering General Pedigrees and Unrelated Females, Respectively
2.6. Situation When There Are Missing Genotypes for Some Individuals from General Pedigrees
2.7. Simulation Settings
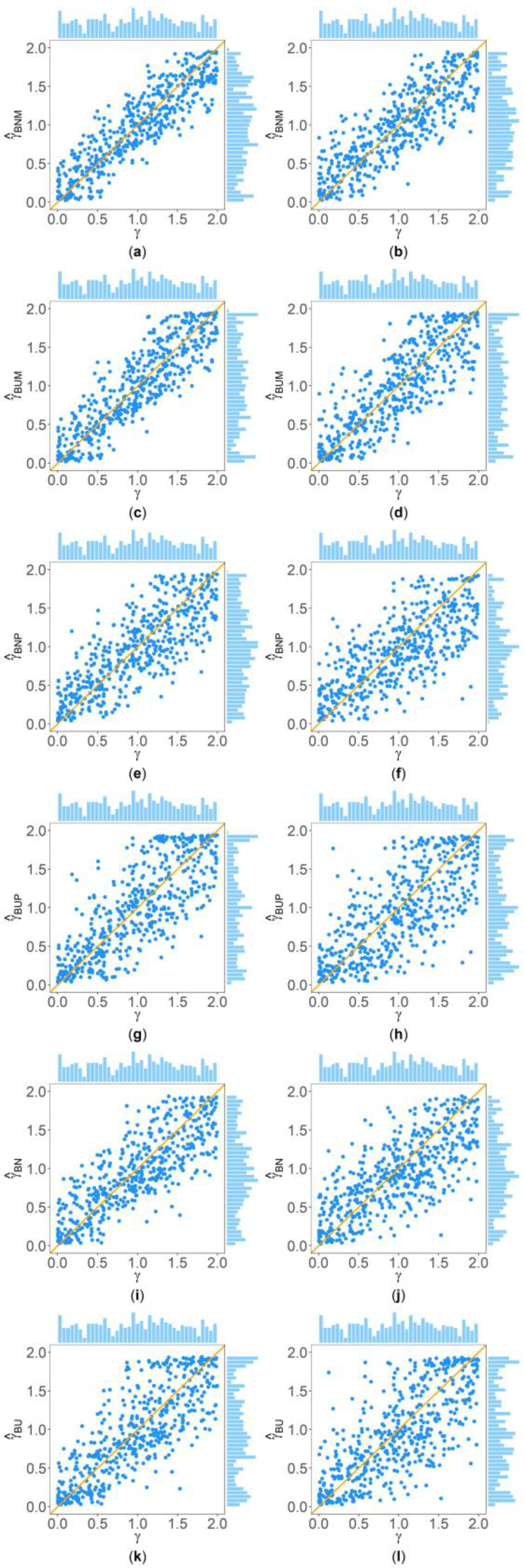
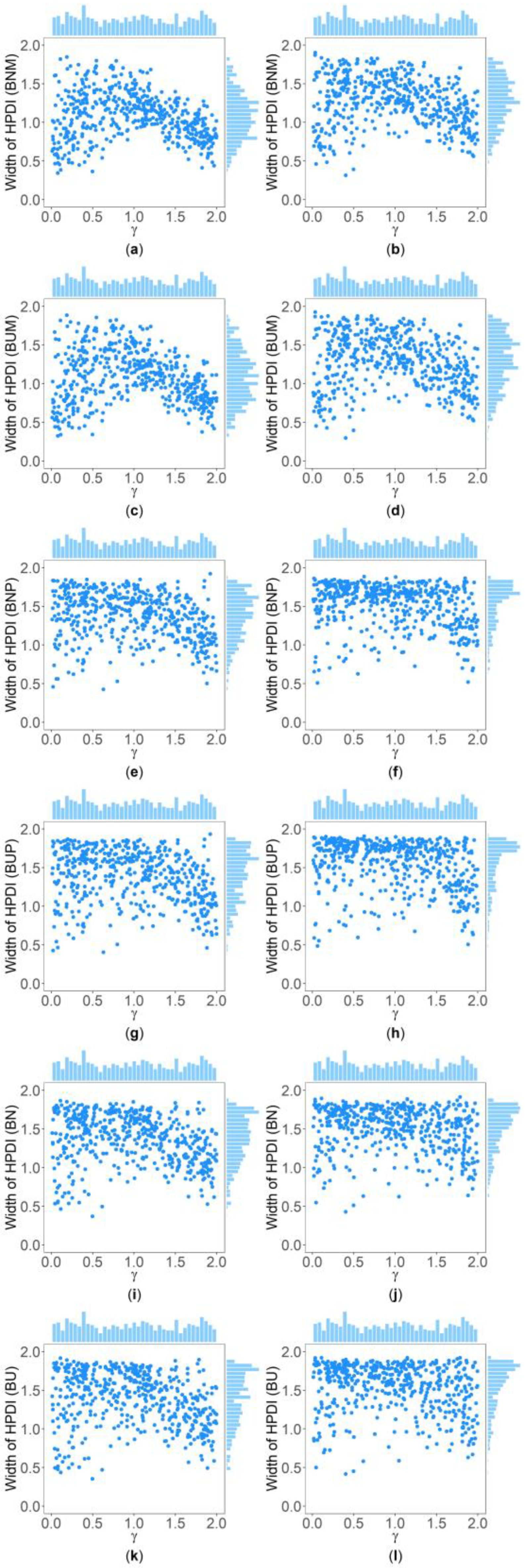
3. Results
3.1. Simulation Results under the Situations of Homoscedasticity and Allele Frequencies in Females and Males Being the Same
3.2. Simulation Results When Allele Frequencies in Females and Males Being Different
3.3. Simulation Results under Heteroscedasticity
3.4. Application to MCTFR Data
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lyon, M.F. Gene action in the X-chromosome of the mouse (Mus musculus L.). Nature 1961, 190, 372–373. [Google Scholar] [CrossRef]
- Zito, A.; Davies, M.N.; Tsai, P.C.; Roberts, S.; Andres-Ejarque, R.; Nardone, S.; Bell, J.T.; Wong, C.; Small, K.S. Heritability of skewed X-inactivation in female twins is tissue-specific and associated with age. Nat. Commun. 2019, 10, 5339. [Google Scholar] [CrossRef]
- Amos-Landgraf, J.M.; Cottle, A.; Plenge, R.M.; Friez, M.; Schwartz, C.E.; Longshore, J.; Willard, H.F. X chromosome-inactivation patterns of 1,005 phenotypically unaffected females. Am. J. Hum. Genet. 2006, 79, 493–499. [Google Scholar] [CrossRef]
- Peeters, S.B.; Cotton, A.M.; Brown, C.J. Variable escape from X-chromosome inactivation: Identifying factors that tip the scales towards expression. Bioessays 2014, 36, 746–756. [Google Scholar] [CrossRef]
- Posynick, B.J.; Brown, C.J. Escape from X-chromosome inactivation: An evolutionary perspective. Front. Cell Dev. Biol. 2019, 7, 241. [Google Scholar] [CrossRef]
- Deng, X.; Berletch, J.B.; Nguyen, D.K.; Disteche, C.M. X chromosome regulation: Diverse patterns in development, tissues and disease. Nat. Rev. Genet. 2014, 15, 367–378. [Google Scholar] [CrossRef] [PubMed]
- Medema, R.H.; Burgering, B.M. The X factor: Skewing X inactivation towards cancer. Cell 2007, 129, 1253–1254. [Google Scholar] [CrossRef] [PubMed]
- Shvetsova, E.; Sofronova, A.; Monajemi, R.; Gagalova, K.; Draisma, H.; White, S.J.; Santen, G.; Chuva, D.S.L.S.; Heijmans, B.T.; van Meurs, J.; et al. Skewed X-inactivation is common in the general female population. Eur. J. Hum. Genet. 2019, 27, 455–465. [Google Scholar]
- Bajic, V.; Mandusic, V.; Stefanova, E.; Bozovic, A.; Davidovic, R.; Zivkovic, L.; Cabarkapa, A.; Spremo-Potparevic, B. Skewed X-chromosome inactivation in women affected by Alzheimer’s disease. J. Alzheimers Dis. 2015, 43, 1251–1259. [Google Scholar] [CrossRef]
- Giliberto, F.; Radic, C.P.; Luce, L.; Ferreiro, V.; de Brasi, C.; Szijan, I. Symptomatic female carriers of duchenne muscular dystrophy (DMD): Genetic and clinical characterization. J. Neurol. Sci. 2014, 336, 36–41. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Jin, T.; Liang, H.; Tu, Y.; Zhang, W.; Gong, L.; Su, Q.; Gao, G. Skewed X-chromosome inactivation in patients with esophageal carcinoma. Diagn. Pathol. 2013, 8, 55. [Google Scholar] [CrossRef] [PubMed]
- Sangha, K.K.; Stephenson, M.D.; Brown, C.J.; Robinson, W.P. Extremely skewed X-chromosome inactivation is increased in women with recurrent spontaneous abortion. Am. J. Hum. Genet. 1999, 65, 913–917. [Google Scholar] [CrossRef] [PubMed]
- Simmonds, M.J.; Kavvoura, F.K.; Brand, O.J.; Newby, P.R.; Jackson, L.E.; Hargreaves, C.E.; Franklyn, J.A.; Gough, S.C. Skewed X chromosome inactivation and female preponderance in autoimmune thyroid disease: An association study and meta-analysis. J. Clin. Endocrinol. Metab. 2014, 99, E127–E131. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Fan, J.; Wang, Y. X-chromosome inactivation and related diseases. Genet. Res. 2022, 2022, 1391807. [Google Scholar] [CrossRef]
- Okumura, K.; Fujimori, Y.; Takagi, A.; Murate, T.; Ozeki, M.; Yamamoto, K.; Katsumi, A.; Matsushita, T.; Naoe, T.; Kojima, T. Skewed X chromosome inactivation in fraternal female twins results in moderately severe and mild haemophilia B. Haemophilia 2008, 14, 1088–1093. [Google Scholar] [CrossRef]
- Ozbalkan, Z.; Bagislar, S.; Kiraz, S.; Akyerli, C.B.; Ozer, H.T.; Yavuz, S.; Birlik, A.M.; Calguneri, M.; Ozcelik, T. Skewed X chromosome inactivation in blood cells of women with scleroderma. Arthritis Rheum. 2005, 52, 1564–1570. [Google Scholar] [CrossRef]
- Chen, Z.; Ng, H.K.; Li, J.; Liu, Q.; Huang, H. Detecting associated single-nucleotide polymorphisms on the X chromosome in case control genome-wide association studies. Stat. Methods Med. Res. 2017, 26, 567–582. [Google Scholar] [CrossRef]
- Chen, B.; Craiu, R.V.; Strug, L.J.; Sun, L. The X factor: A robust and powerful approach to X-chromosome-inclusive whole-genome association studies. Genet. Epidemiol. 2021, 45, 694–709. [Google Scholar] [CrossRef]
- Clayton, D. Testing for association on the X chromosome. Biostatistics 2008, 9, 593–600. [Google Scholar] [CrossRef]
- Deng, W.Q.; Mao, S.; Kalnapenkis, A.; Esko, T.; Sun, L. Analytical strategies to include the X-chromosome in variance heterogeneity analyses: Evidence for trait-specific polygenic variance structure. Genet. Epidemiol. 2019, 43, 815–830. [Google Scholar] [CrossRef]
- Ding, J.; Lin, S.; Liu, Y. Monte carlo pedigree disequilibrium test for markers on the X chromosome. Am. J. Hum. Genet. 2006, 79, 567–573. [Google Scholar] [CrossRef]
- Gao, F.; Chang, D.; Biddanda, A.; Ma, L.; Guo, Y.; Zhou, Z.; Keinan, A. XWAS: A software toolset for genetic data analysis and association studies of the X chromosome. J. Hered. 2015, 106, 666–671. [Google Scholar] [CrossRef]
- Ma, L.; Hoffman, G.; Keinan, A. X-inactivation informs variance-based testing for X-linked association of a quantitative trait. BMC Genom. 2015, 16, 241. [Google Scholar] [CrossRef]
- Wang, J.; Yu, R.; Shete, S. X-chromosome genetic association test accounting for X-inactivation, skewed X-inactivation, and escape from X-inactivation. Genet. Epidemiol. 2014, 38, 483–493. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Martin, E.R.; Morris, R.W.; Li, Y.J. Association test for x-linked QTL in family-based designs. Am. J. Hum. Genet. 2009, 84, 431–444. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; Joo, J.; Zhang, C.; Geller, N.L. Testing association for markers on the X chromosome. Genet. Epidemiol. 2007, 31, 834–843. [Google Scholar] [CrossRef]
- Zhou, X.; Stephens, M. Genome-wide efficient mixed-model analysis for association studies. Nat. Genet. 2012, 44, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.Q.; Zhang, Y.; Wang, P.; Liu, W.; Wu, X.B.; Zhou, J.Y. A statistical measure for the skewness of X chromosome inactivation based on family trios. BMC Genet. 2018, 19, 109. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Zhang, Y.; Wang, B.Q.; Li, J.L.; Wang, Y.X.; Pan, D.; Wu, X.B.; Fung, W.K.; Zhou, J.Y. A statistical measure for the skewness of X chromosome inactivation based on case-control design. BMC Bioinform. 2019, 20, 11. [Google Scholar] [CrossRef]
- Li, B.H.; Yu, W.Y.; Zhou, J.Y. A statistical measure for the skewness of X chromosome inactivation for quantitative traits and its application to the MCTFR data. BMC Genom. Data 2021, 22, 24. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Xu, S.; Wang, Y.X.; Wu, B.; Fung, W.K.; Gao, G.; Liang, Z.; Liu, N. Penalized fieller’s confidence interval for the ratio of bivariate normal means. Biometrics 2021, 77, 1355–1368. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.Y.; Zhang, Y.; Li, M.K.; Yang, Z.Y.; Fung, W.K.; Zhao, P.Z.; Zhou, J.Y. BEXCIS: Bayesian methods for estimating the degree of the skewness of X chromosome inactivation. BMC Bioinform. 2022, 23, 193. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Zhou, J.; Sobel, E.M.; Lange, K. Fast genome-wide pedigree quantitative trait loci analysis using mendel. BMC Proc. 2014, 8, S93. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Blangero, J.; Dyer, T.D.; Chan, K.K.; Lange, K.; Sobel, E.M. Fast genome-wide QTL association mapping on pedigree and population data. Genet. Epidemiol. 2017, 41, 174–186. [Google Scholar] [CrossRef]
- Annis, J.; Miller, B.J.; Palmeri, T.J. Bayesian inference with stan: A tutorial on adding custom distributions. Behav. Res. Methods 2017, 49, 863–886. [Google Scholar] [CrossRef]
- Zhao, J.H.; Luan, J.A.; Congdon, P. Bayesian linear mixed models with polygenic effects. J. Stat. Softw. 2018, 85, 1–27. [Google Scholar] [CrossRef]
- Lange, K. Mathematical and Statistical Methods for Genetic Analysis, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2002; p. 384. [Google Scholar]
- Sinnwell, J.P.; Therneau, T.M.; Schaid, D.J. The kinship2 R package for pedigree data. Hum. Hered. 2014, 78, 91–93. [Google Scholar] [CrossRef]
- Bae, H.T.; Perls, T.T.; Sebastiani, P. An efficient technique for Bayesian modeling of family data using the bugs software. Front. Genet. 2014, 5, 390. [Google Scholar] [CrossRef] [PubMed]
- Runcie, D.E.; Crawford, L. Fast and flexible linear mixed models for genome-wide genetics. PLoS Genet. 2019, 15, e1007978. [Google Scholar] [CrossRef]
- Kruschke, J.K. Bayesian data analysis. Wiley Interdiscip. Rev.-Cogn. Sci. 2010, 1, 658–676. [Google Scholar] [CrossRef]
- Ma, C.; Boehnke, M.; Lee, S. Evaluating the calibration and power of three gene-based association tests of rare variants for the X chromosome. Genet. Epidemiol. 2015, 39, 499–508. [Google Scholar] [CrossRef] [PubMed]
- Schifano, E.D.; Epstein, M.P.; Bielak, L.F.; Jhun, M.A.; Kardia, S.L.; Peyser, P.A.; Lin, X. SNP set association analysis for familial data. Genet. Epidemiol. 2012, 36, 797–810. [Google Scholar] [CrossRef]
- Won, S.; Lange, C. A general framework for robust and efficient association analysis in family-based designs: Quantitative and dichotomous phenotypes. Stat. Med. 2013, 32, 4482–4498. [Google Scholar] [CrossRef] [PubMed]
- Saad, M.; Wijsman, E.M. Association score testing for rare variants and binary traits in family data with shared controls. Brief. Bioinform. 2019, 20, 245–253. [Google Scholar] [CrossRef] [PubMed]
- Vehtari, A.; Gelman, A.; Simpson, D.; Carpenter, B.; Bürkner, P. Rank-normalization, folding, and localization: An improved R for assessing convergence of MCMC. Bayesian Anal. 2020, 16, 667–718. [Google Scholar] [CrossRef]
- Miller, M.B.; Basu, S.; Cunningham, J.; Eskin, E.; Malone, S.M.; Oetting, W.S.; Schork, N.; Sul, J.H.; Iacono, W.G.; Mcgue, M. The Minnesota Center for Twin and Family Research genome-wide association study. Twin Res. Hum. Genet. 2012, 15, 767–774. [Google Scholar] [CrossRef]
- Mcgue, M.; Zhang, Y.; Miller, M.B.; Basu, S.; Vrieze, S.; Hicks, B.; Malone, S.; Oetting, W.S.; Iacono, W.G. A genome-wide association study of behavioral disinhibition. Behav. Genet. 2013, 43, 363–373. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, S.; Li, Z.; Morrison, A.C.; Boerwinkle, E.; Lin, X. ACAT: A fast and powerful p value combination method for rare-variant analysis in sequencing studies. Am. J. Hum. Genet. 2019, 104, 410–421. [Google Scholar] [CrossRef]
- Mccaw, Z.R.; Lane, J.M.; Saxena, R.; Redline, S.; Lin, X. Operating characteristics of the rank-based inverse normal transformation for quantitative trait analysis in genome-wide association studies. Biometrics 2020, 76, 1262–1272. [Google Scholar] [CrossRef]
- Ng, K.T.; Yeung, O.W.; Liu, J.; Li, C.X.; Liu, H.; Liu, X.B.; Qi, X.; Ma, Y.Y.; Lam, Y.F.; Lau, M.Y.; et al. Clinical significance and functional role of transmembrane protein 47 (TMEM47) in chemoresistance of hepatocellular carcinoma. Int. J. Oncol. 2020, 57, 956–966. [Google Scholar] [CrossRef]
- Li, R.; Guo, M.; Song, L. PAS domain containing repressor 1 (PASD1) promotes glioma cell proliferation through inhibiting apoptosis in vitro. Med. Sci. Monitor 2019, 25, 6955–6964. [Google Scholar] [CrossRef] [PubMed]
- Weeks, D.E.; Ott, J.; Lathrop, G.M. SLINK: A general simulation program for linkage analysis. Am. J. Hum. Genet. 1990, 47, A204. [Google Scholar]
- Cheng, H.; Qu, L.; Garrick, D.J.; Fernando, R.L. A fast and efficient Gibbs sampler for Bayes in whole-genome analyses. Genet. Sel. Evol. 2015, 47, 80. [Google Scholar] [CrossRef] [PubMed]
- Mbatchou, J.; Barnard, L.; Backman, J.; Marcketta, A.; Kosmicki, J.A.; Ziyatdinov, A.; Benner, C.; O’Dushlaine, C.; Barber, M.; Boutkov, B.; et al. Computationally efficient whole-genome regression for quantitative and binary traits. Nat. Genet. 2021, 53, 1097–1103. [Google Scholar] [CrossRef]



| Quantitative Trait | Qualitative Trait | |||
|---|---|---|---|---|
| EVD a | Original b | Cholesky a | Original b | |
| 150 | 10 s | 1.8 h | 1.3 min | 7.2 h |
| 600 | 40 s | 7 days | 47 min | 30 days |
| Trait | Mixed Data | Pedigrees | Unrelated Females | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Quantitative | (150, 650) | 0.3 | 1/3 | 0 | 0.0643 | 0.0707 | 0.1167 | 0.1342 | 0.1123 | 0.1258 |
| 0.3 | 1/3 | 0.4 | 0.0943 | 0.1032 | 0.1564 | 0.1757 | 0.1532 | 0.1704 | ||
| 0.3 | 1 | 0 | 0.0889 | 0.0966 | 0.1528 | 0.1646 | 0.1391 | 0.1556 | ||
| 0.3 | 1 | 0.4 | 0.1323 | 0.1473 | 0.2086 | 0.2409 | 0.2017 | 0.2354 | ||
| 0.1 | 1/3 | 0 | 0.1850 | 0.1968 | 0.2959 | 0.3247 | 0.2284 | 0.2499 | ||
| 0.1 | 1/3 | 0.4 | 0.2455 | 0.2670 | 0.3781 | 0.4325 | 0.3304 | 0.3706 | ||
| 0.1 | 1 | 0 | 0.2010 | 0.2192 | 0.3399 | 0.3792 | 0.3260 | 0.3595 | ||
| 0.1 | 1 | 0.4 | 0.2754 | 0.3064 | 0.4224 | 0.4900 | 0.4046 | 0.4709 | ||
| (600, 2600) | 0.3 | 1/3 | 0 | 0.0229 | 0.0236 | 0.0407 | 0.0421 | 0.0377 | 0.0383 | |
| 0.3 | 1/3 | 0.4 | 0.0359 | 0.0377 | 0.0570 | 0.0606 | 0.0558 | 0.0596 | ||
| 0.3 | 1 | 0 | 0.0256 | 0.0260 | 0.0543 | 0.0576 | 0.0540 | 0.0571 | ||
| 0.3 | 1 | 0.4 | 0.0416 | 0.0445 | 0.0805 | 0.0879 | 0.0764 | 0.0813 | ||
| 0.1 | 1/3 | 0 | 0.0786 | 0.0846 | 0.1210 | 0.1300 | 0.1169 | 0.1209 | ||
| 0.1 | 1/3 | 0.4 | 0.1147 | 0.1205 | 0.1689 | 0.1750 | 0.1593 | 0.1684 | ||
| 0.1 | 1 | 0 | 0.0962 | 0.1039 | 0.1650 | 0.1773 | 0.1512 | 0.1660 | ||
| 0.1 | 1 | 0.4 | 0.1353 | 0.1415 | 0.2080 | 0.2252 | 0.1910 | 0.2056 | ||
| Qualitative | (150, 650) | 0.3 | 1/3 | 0 | 0.0862 | 0.0926 | 0.1551 | 0.1774 | 0.1499 | 0.1621 |
| 0.3 | 1/3 | 0.4 | 0.1243 | 0.1298 | 0.2181 | 0.2593 | 0.1922 | 0.2197 | ||
| 0.3 | 1 | 0 | 0.1175 | 0.1249 | 0.2112 | 0.2381 | 0.1923 | 0.2138 | ||
| 0.3 | 1 | 0.4 | 0.1588 | 0.1863 | 0.2768 | 0.3405 | 0.2459 | 0.2793 | ||
| 0.1 | 1/3 | 0 | 0.2654 | 0.2815 | 0.3911 | 0.4343 | 0.3822 | 0.4107 | ||
| 0.1 | 1/3 | 0.4 | 0.4051 | 0.4250 | 0.5403 | 0.6122 | 0.5383 | 0.6103 | ||
| 0.1 | 1 | 0 | 0.2910 | 0.3316 | 0.4342 | 0.5159 | 0.4322 | 0.4921 | ||
| 0.1 | 1 | 0.4 | 0.4430 | 0.5020 | 0.6024 | 0.6967 | 0.5978 | 0.6838 | ||
| (600, 2600) | 0.3 | 1/3 | 0 | 0.0344 | 0.0347 | 0.0551 | 0.0599 | 0.0540 | 0.0562 | |
| 0.3 | 1/3 | 0.4 | 0.0564 | 0.0581 | 0.0847 | 0.0921 | 0.0811 | 0.0885 | ||
| 0.3 | 1 | 0 | 0.0441 | 0.0459 | 0.0816 | 0.0872 | 0.0667 | 0.0700 | ||
| 0.3 | 1 | 0.4 | 0.0727 | 0.0743 | 0.1154 | 0.1261 | 0.1045 | 0.1091 | ||
| 0.1 | 1/3 | 0 | 0.1092 | 0.1214 | 0.2405 | 0.2546 | 0.1549 | 0.1615 | ||
| 0.1 | 1/3 | 0.4 | 0.1577 | 0.1665 | 0.3585 | 0.3722 | 0.2225 | 0.2273 | ||
| 0.1 | 1 | 0 | 0.1429 | 0.1496 | 0.2427 | 0.2570 | 0.1718 | 0.1832 | ||
| 0.1 | 1 | 0.4 | 0.1783 | 0.2017 | 0.3614 | 0.3857 | 0.2472 | 0.2614 | ||
| Trait | Mixed Data | Pedigrees | Unrelated Females | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BNM | BUM | BNP | BUP | BN | BU | |||||
| Quantitative | (150, 650) | 0.3 | 1/3 | 0 | 94.6 | 96.2 | 95.4 | 96.2 | 95.2 | 94.8 |
| 0.3 | 1/3 | 0.4 | 95.0 | 95.6 | 95.2 | 95.6 | 95.4 | 96.0 | ||
| 0.3 | 1 | 0 | 95.0 | 95.0 | 93.8 | 94.6 | 95.2 | 95.2 | ||
| 0.3 | 1 | 0.4 | 94.4 | 95.2 | 94.2 | 95.0 | 94.0 | 94.4 | ||
| 0.1 | 1/3 | 0 | 93.8 | 93.6 | 95.8 | 94.4 | 95.0 | 95.2 | ||
| 0.1 | 1/3 | 0.4 | 93.4 | 95.4 | 95.0 | 94.2 | 94.4 | 95.4 | ||
| 0.1 | 1 | 0 | 96.2 | 94.6 | 94.0 | 95.0 | 94.2 | 94.8 | ||
| 0.1 | 1 | 0.4 | 94.4 | 95.8 | 94.2 | 95.4 | 93.8 | 94.2 | ||
| (600, 2600) | 0.3 | 1/3 | 0 | 94.2 | 94.2 | 94.0 | 94.4 | 94.8 | 95.0 | |
| 0.3 | 1/3 | 0.4 | 94.2 | 94.4 | 95.6 | 95.4 | 95.6 | 95.4 | ||
| 0.3 | 1 | 0 | 95.0 | 96.4 | 95.6 | 95.8 | 95.2 | 95.2 | ||
| 0.3 | 1 | 0.4 | 95.8 | 95.8 | 94.6 | 94.6 | 95.4 | 94.8 | ||
| 0.1 | 1/3 | 0 | 94.2 | 94.2 | 95.0 | 94.6 | 94.4 | 95.4 | ||
| 0.1 | 1/3 | 0.4 | 94.0 | 95.0 | 94.6 | 95.2 | 95.2 | 96.2 | ||
| 0.1 | 1 | 0 | 95.6 | 95.6 | 95.6 | 96.0 | 93.6 | 95.2 | ||
| 0.1 | 1 | 0.4 | 95.0 | 95.4 | 94.8 | 95.6 | 95.6 | 94.6 | ||
| Qualitative | (150, 650) | 0.3 | 1/3 | 0 | 95.8 | 94.8 | 95.0 | 94.8 | 94.2 | 95.2 |
| 0.3 | 1/3 | 0.4 | 94.8 | 95.0 | 94.2 | 95.0 | 94.6 | 95.2 | ||
| 0.3 | 1 | 0 | 95.2 | 95.6 | 95.4 | 94.8 | 95.0 | 95.6 | ||
| 0.3 | 1 | 0.4 | 94.8 | 96.4 | 94.2 | 95.4 | 94.8 | 93.8 | ||
| 0.1 | 1/3 | 0 | 95.4 | 94.8 | 95.2 | 94.8 | 95.4 | 94.6 | ||
| 0.1 | 1/3 | 0.4 | 95.2 | 95.0 | 94.8 | 95.2 | 94.8 | 95.6 | ||
| 0.1 | 1 | 0 | 93.6 | 94.6 | 95.0 | 95.8 | 95.4 | 94.8 | ||
| 0.1 | 1 | 0.4 | 94.8 | 95.2 | 94.6 | 94.8 | 95.0 | 95.4 | ||
| (600, 2600) | 0.3 | 1/3 | 0 | 95.4 | 94.8 | 95.0 | 94.8 | 96.2 | 95.6 | |
| 0.3 | 1/3 | 0.4 | 93.8 | 95.2 | 94.2 | 95.4 | 95.0 | 94.2 | ||
| 0.3 | 1 | 0 | 94.2 | 94.2 | 95.0 | 94.8 | 94.2 | 95.4 | ||
| 0.3 | 1 | 0.4 | 95.6 | 95.2 | 95.0 | 95.6 | 95.8 | 94.4 | ||
| 0.1 | 1/3 | 0 | 93.6 | 94.6 | 96.0 | 94.4 | 94.6 | 95.8 | ||
| 0.1 | 1/3 | 0.4 | 95.0 | 95.0 | 94.4 | 95.6 | 94.0 | 95.0 | ||
| 0.1 | 1 | 0 | 94.2 | 93.8 | 95.2 | 93.4 | 95.2 | 95.0 | ||
| 0.1 | 1 | 0.4 | 95.6 | 95.2 | 94.4 | 95.4 | 95.0 | 95.8 | ||
| Trait | Mixed Data | Pedigrees | Unrelated Females | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BNM | BUM | BNP | BUP | BN | BU | |||||
| Quantitative | (150, 650) | 0.3 | 1/3 | 0 | 0.9770 | 0.9815 | 1.2152 | 1.2336 | 1.2103 | 1.2249 |
| 0.3 | 1/3 | 0.4 | 1.1601 | 1.1801 | 1.4467 | 1.4781 | 1.3937 | 1.4373 | ||
| 0.3 | 1 | 0 | 1.0627 | 1.0636 | 1.3667 | 1.3966 | 1.3405 | 1.3653 | ||
| 0.3 | 1 | 0.4 | 1.2572 | 1.2627 | 1.5525 | 1.6017 | 1.5260 | 1.5821 | ||
| 0.1 | 1/3 | 0 | 1.4258 | 1.4452 | 1.5863 | 1.6305 | 1.5729 | 1.6297 | ||
| 0.1 | 1/3 | 0.4 | 1.5502 | 1.5935 | 1.6720 | 1.7201 | 1.6584 | 1.7103 | ||
| 0.1 | 1 | 0 | 1.5453 | 1.5940 | 1.6713 | 1.7166 | 1.6637 | 1.7112 | ||
| 0.1 | 1 | 0.4 | 1.6493 | 1.6999 | 1.7109 | 1.7633 | 1.7106 | 1.7629 | ||
| (600, 2600) | 0.3 | 1/3 | 0 | 0.5350 | 0.5378 | 0.7332 | 0.7324 | 0.7292 | 0.7278 | |
| 0.3 | 1/3 | 0.4 | 0.6658 | 0.6642 | 0.8894 | 0.8840 | 0.8639 | 0.8650 | ||
| 0.3 | 1 | 0 | 0.6216 | 0.6272 | 0.8754 | 0.8861 | 0.8388 | 0.8433 | ||
| 0.3 | 1 | 0.4 | 0.7755 | 0.7868 | 1.0389 | 1.0515 | 1.0265 | 1.0282 | ||
| 0.1 | 1/3 | 0 | 1.0073 | 1.0217 | 1.2340 | 1.2505 | 1.2201 | 1.2450 | ||
| 0.1 | 1/3 | 0.4 | 1.1494 | 1.1790 | 1.3633 | 1.3885 | 1.3538 | 1.3814 | ||
| 0.1 | 1 | 0 | 1.1208 | 1.1298 | 1.3468 | 1.3654 | 1.3392 | 1.3562 | ||
| 0.1 | 1 | 0.4 | 1.3067 | 1.3313 | 1.4664 | 1.5054 | 1.4634 | 1.5038 | ||
| Qualitative | (150, 650) | 0.3 | 1/3 | 0 | 1.0719 | 1.0821 | 1.4111 | 1.4353 | 1.3991 | 1.4332 |
| 0.3 | 1/3 | 0.4 | 1.2857 | 1.3103 | 1.6186 | 1.6573 | 1.5767 | 1.6258 | ||
| 0.3 | 1 | 0 | 1.2224 | 1.2394 | 1.5703 | 1.6178 | 1.5559 | 1.6176 | ||
| 0.3 | 1 | 0.4 | 1.4206 | 1.4531 | 1.6704 | 1.7288 | 1.6644 | 1.7193 | ||
| 0.1 | 1/3 | 0 | 1.5167 | 1.5485 | 1.6562 | 1.7093 | 1.6551 | 1.6972 | ||
| 0.1 | 1/3 | 0.4 | 1.5914 | 1.6449 | 1.7038 | 1.7543 | 1.6725 | 1.7236 | ||
| 0.1 | 1 | 0 | 1.6121 | 1.6757 | 1.7135 | 1.7649 | 1.6907 | 1.7450 | ||
| 0.1 | 1 | 0.4 | 1.6751 | 1.7284 | 1.7203 | 1.7690 | 1.7160 | 1.7642 | ||
| (600, 2600) | 0.3 | 1/3 | 0 | 0.6888 | 0.6920 | 0.8648 | 0.8684 | 0.8369 | 0.8448 | |
| 0.3 | 1/3 | 0.4 | 0.8207 | 0.8274 | 1.0530 | 1.0555 | 1.0117 | 1.0057 | ||
| 0.3 | 1 | 0 | 0.7781 | 0.7777 | 1.0235 | 1.0199 | 0.9527 | 0.9559 | ||
| 0.3 | 1 | 0.4 | 0.9714 | 0.9739 | 1.1988 | 1.2089 | 1.1522 | 1.1660 | ||
| 0.1 | 1/3 | 0 | 1.1414 | 1.1550 | 1.3164 | 1.3447 | 1.3027 | 1.3380 | ||
| 0.1 | 1/3 | 0.4 | 1.3028 | 1.3184 | 1.4463 | 1.4831 | 1.4182 | 1.4421 | ||
| 0.1 | 1 | 0 | 1.2614 | 1.2848 | 1.4063 | 1.4336 | 1.4022 | 1.4294 | ||
| 0.1 | 1 | 0.4 | 1.4044 | 1.4328 | 1.5227 | 1.5681 | 1.5185 | 1.5555 | ||
| Trait | Mixed Data | Pedigrees | Unrelated Females | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BNM | BUM | BNP | BUP | BN | BU | |||||
| Quantitative | (150, 650) | 0.3 | 1/3 | 0 | 0.3333 | 0.3700 | 0.4620 | 0.5268 | 0.4530 | 0.5122 |
| 0.3 | 1/3 | 0.4 | 0.4106 | 0.4680 | 0.4760 | 0.5466 | 0.4435 | 0.4987 | ||
| 0.3 | 1 | 0 | 0.4218 | 0.4755 | 0.4739 | 0.5418 | 0.4291 | 0.5261 | ||
| 0.3 | 1 | 0.4 | 0.4351 | 0.5176 | 0.4162 | 0.4673 | 0.4069 | 0.4314 | ||
| 0.1 | 1/3 | 0 | 0.4058 | 0.4620 | 0.3309 | 0.3603 | 0.3193 | 0.3392 | ||
| 0.1 | 1/3 | 0.4 | 0.3389 | 0.3812 | 0.2603 | 0.2690 | 0.2267 | 0.2243 | ||
| 0.1 | 1 | 0 | 0.3345 | 0.3817 | 0.2612 | 0.2806 | 0.2586 | 0.2585 | ||
| 0.1 | 1 | 0.4 | 0.2467 | 0.2585 | 0.1618 | 0.1658 | 0.1590 | 0.1488 | ||
| (600, 2600) | 0.3 | 1/3 | 0 | 0.1590 | 0.1629 | 0.2391 | 0.2655 | 0.2272 | 0.2582 | |
| 0.3 | 1/3 | 0.4 | 0.2184 | 0.2344 | 0.3295 | 0.3803 | 0.2823 | 0.3190 | ||
| 0.3 | 1 | 0 | 0.1946 | 0.2087 | 0.3241 | 0.3795 | 0.2968 | 0.3297 | ||
| 0.3 | 1 | 0.4 | 0.2733 | 0.3080 | 0.3892 | 0.4434 | 0.3643 | 0.4125 | ||
| 0.1 | 1/3 | 0 | 0.3785 | 0.4380 | 0.3878 | 0.4345 | 0.3790 | 0.4319 | ||
| 0.1 | 1/3 | 0.4 | 0.4386 | 0.4744 | 0.3998 | 0.4649 | 0.3880 | 0.4338 | ||
| 0.1 | 1 | 0 | 0.3744 | 0.4297 | 0.4101 | 0.4489 | 0.3670 | 0.4449 | ||
| 0.1 | 1 | 0.4 | 0.3653 | 0.3961 | 0.3640 | 0.4160 | 0.3524 | 0.4152 | ||
| Qualitative | (150, 650) | 0.3 | 1/3 | 0 | 0.4290 | 0.4922 | 0.4841 | 0.5399 | 0.4561 | 0.5148 |
| 0.3 | 1/3 | 0.4 | 0.4542 | 0.5314 | 0.3988 | 0.4512 | 0.3902 | 0.4319 | ||
| 0.3 | 1 | 0 | 0.4539 | 0.5204 | 0.4009 | 0.4466 | 0.3970 | 0.4309 | ||
| 0.3 | 1 | 0.4 | 0.4424 | 0.5062 | 0.2980 | 0.3132 | 0.2893 | 0.3005 | ||
| 0.1 | 1/3 | 0 | 0.3811 | 0.4325 | 0.2866 | 0.3086 | 0.2694 | 0.2752 | ||
| 0.1 | 1/3 | 0.4 | 0.3118 | 0.3636 | 0.2822 | 0.3342 | 0.2245 | 0.2540 | ||
| 0.1 | 1 | 0 | 0.3195 | 0.3387 | 0.2239 | 0.2082 | 0.1856 | 0.1867 | ||
| 0.1 | 1 | 0.4 | 0.2468 | 0.2913 | 0.1973 | 0.2209 | 0.1932 | 0.2027 | ||
| (600, 2600) | 0.3 | 1/3 | 0 | 0.1886 | 0.2109 | 0.2929 | 0.3232 | 0.2715 | 0.3036 | |
| 0.3 | 1/3 | 0.4 | 0.2580 | 0.2884 | 0.3947 | 0.4478 | 0.3536 | 0.4152 | ||
| 0.3 | 1 | 0 | 0.2680 | 0.2937 | 0.3801 | 0.4009 | 0.3617 | 0.3981 | ||
| 0.3 | 1 | 0.4 | 0.3576 | 0.4061 | 0.4404 | 0.5107 | 0.4060 | 0.4630 | ||
| 0.1 | 1/3 | 0 | 0.3826 | 0.4368 | 0.3421 | 0.4035 | 0.3350 | 0.3903 | ||
| 0.1 | 1/3 | 0.4 | 0.3333 | 0.3700 | 0.4620 | 0.5268 | 0.4530 | 0.5122 | ||
| 0.1 | 1 | 0 | 0.4106 | 0.4680 | 0.4760 | 0.5466 | 0.4435 | 0.4987 | ||
| 0.1 | 1 | 0.4 | 0.4218 | 0.4755 | 0.4739 | 0.5418 | 0.4291 | 0.5261 | ||
| SNP | Position | Alleles | MAF a | Trait | p-Value | Gene |
|---|---|---|---|---|---|---|
| rs10522027 | 34630163 | G > A | 0.141 | DEP | TMEM47 | |
| rs12860832 | 151643064 | G > A | 0.263 | DEP | PASD1 | |
| rs12849233 | 151645704 | C > A | 0.329 | DEP | PASD1 |
| SNP | Point Estimate | 95% HPDI | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BNM | BUM | BNP | BUP | BN | BU | |||||||
| rs10522027 | 0.6922 | 0.6895 | 0.6394 | 0.6494 | 0.7238 | 0.7429 | (0.2451, 1.3518) | (0.2316, 1.4420) | (0.0156, 1.5816) | (0.0063, 1.5567) | (0.1791, 1.6615) | (0.1870, 1.6384) |
| rs12860832 | 0.8371 | 0.8288 | 0.9422 | 0.9448 | 0.7281 | 0.7200 | (0.3266, 1.4935) | (0.3942, 1.5788) | (0.1878, 1.6258) | (0.2077, 1.6698) | (0.0945, 1.6294) | (0.1214, 1.6503) |
| rs12849233 | 0.7633 | 0.7426 | 0.8843 | 0.8736 | 0.6906 | 0.6968 | (0.2236, 1.2934) | (0.2133, 1.3054) | (0.1054, 1.5392) | (0.1361, 1.5964) | (0.0211, 1.5229) | (0.0764, 1.5490) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, Y.-F.; Li, S.-Z.; Wang, K.-W.; Zhu, B.; Yuan, Y.-X.; Li, M.-K.; Zhou, J.-Y. An Efficient Bayesian Method for Estimating the Degree of the Skewness of X Chromosome Inactivation Based on the Mixture of General Pedigrees and Unrelated Females. Biomolecules 2023, 13, 543. https://doi.org/10.3390/biom13030543
Kong Y-F, Li S-Z, Wang K-W, Zhu B, Yuan Y-X, Li M-K, Zhou J-Y. An Efficient Bayesian Method for Estimating the Degree of the Skewness of X Chromosome Inactivation Based on the Mixture of General Pedigrees and Unrelated Females. Biomolecules. 2023; 13(3):543. https://doi.org/10.3390/biom13030543
Chicago/Turabian StyleKong, Yi-Fan, Shi-Zhu Li, Kai-Wen Wang, Bin Zhu, Yu-Xin Yuan, Meng-Kai Li, and Ji-Yuan Zhou. 2023. "An Efficient Bayesian Method for Estimating the Degree of the Skewness of X Chromosome Inactivation Based on the Mixture of General Pedigrees and Unrelated Females" Biomolecules 13, no. 3: 543. https://doi.org/10.3390/biom13030543
APA StyleKong, Y.-F., Li, S.-Z., Wang, K.-W., Zhu, B., Yuan, Y.-X., Li, M.-K., & Zhou, J.-Y. (2023). An Efficient Bayesian Method for Estimating the Degree of the Skewness of X Chromosome Inactivation Based on the Mixture of General Pedigrees and Unrelated Females. Biomolecules, 13(3), 543. https://doi.org/10.3390/biom13030543













