Advanced Sampling Methods for Multiscale Simulation of Disordered Proteins and Dynamic Interactions
Abstract
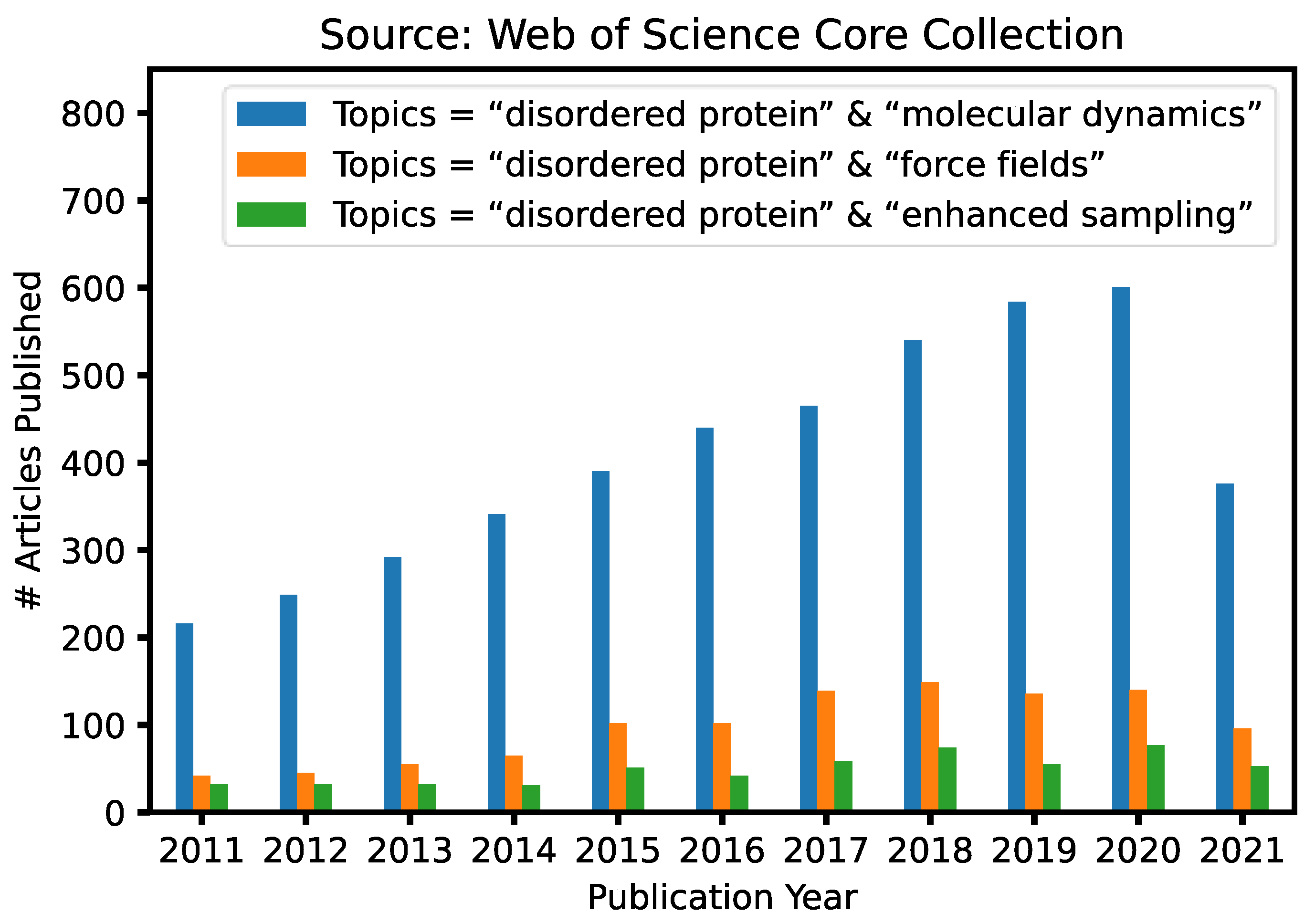
1. Introduction
2. Challenges of Simulating IDP Conformational Equilibria
3. The State-of-the-Art Protein Force Fields for Describing IDP Conformations
3.1. Nonpolarizable Protein Force Fields
3.2. Polarizable Protein Force Fields
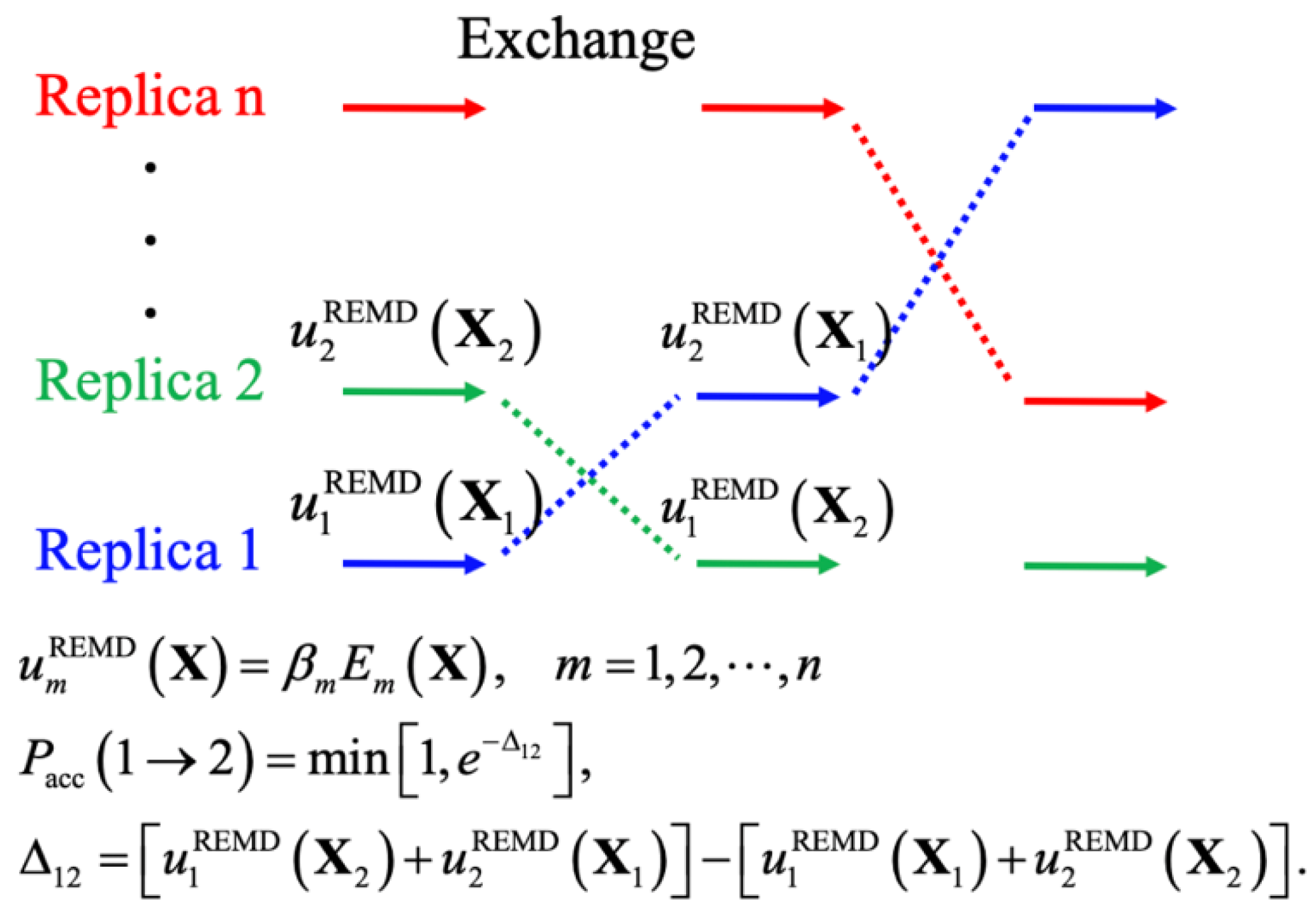
4. Enhanced Sampling Methods for Sampling IDP Conformational Ensembles
4.1. Collective Variables-Based Sampling Methods and Optimization
4.2. Collective Variables-Free Sampling Methods and Optimization
4.3. Reweighting Techniques for Generating Unbiased Ensembles
5. Multi-Scale Approaches for Overcoming Sampling Problems of Large Systems
5.1. Implicit Solvent Models for Removing Solvent DOFs
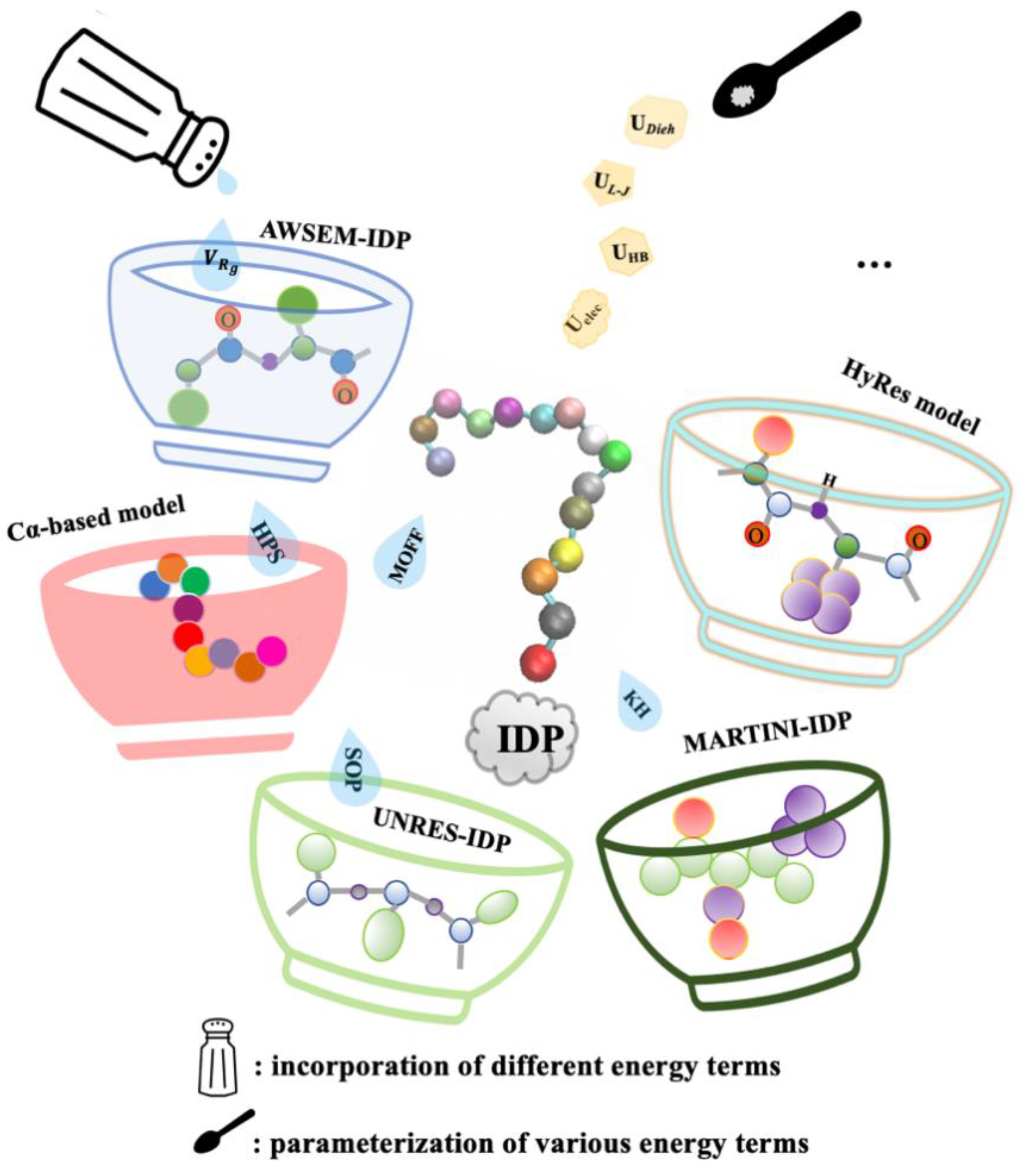
5.2. Coarse-Grain Models for Reducing the DOFs of Proteins
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Csizmok, V.; Follis, A.V.; Kriwacki, R.W.; Forman-Kay, J.D. Dynamic Protein Interaction Networks and New Structural Paradigms in Signaling. Chem. Rev. 2016, 116, 6424–6462. [Google Scholar] [CrossRef]
- Oldfield, C.J.; Dunker, A.K. Intrinsically Disordered Proteins and Intrinsically Disordered Protein Regions. Annu. Rev. Biochem. 2014, 83, 553–584. [Google Scholar] [CrossRef]
- Wright, P.E.; Dyson, H.J. Intrinsically disordered proteins in cellular signalling and regulation. Nat. Rev. Mol. Cell Biol. 2015, 16, 18–29. [Google Scholar] [CrossRef]
- Uversky, V.N. Intrinsically disordered proteins and their (disordered) proteomes in neurodegenerative disorders. Front. Aging Neurosci. 2015, 7, 18. [Google Scholar] [CrossRef]
- Dyson, H.J.; Wright, P.E. Intrinsically unstructured proteins and their functions. Nat. Rev. Mol. Cell Biol. 2005, 6, 197–208. [Google Scholar] [CrossRef] [PubMed]
- Owen, I.; Shewmaker, F. The Role of Post-Translational Modifications in the Phase Transitions of Intrinsically Disordered Proteins. Int. J. Mol. Sci. 2019, 20, 5501. [Google Scholar] [CrossRef] [PubMed]
- Chen, J. Towards the physical basis of how intrinsic disorder mediates protein function. Arch. Biochem. Biophys. 2012, 524, 123–131. [Google Scholar] [CrossRef] [PubMed]
- Das, R.K.; Ruff, K.M.; Pappu, R.V. Relating sequence encoded information to form and function of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2015, 32, 102–112. [Google Scholar] [CrossRef]
- Hatos, A.; Hajdu-Soltesz, B.; Monzon, A.M.; Palopoli, N.; Alvarez, L.; Aykac-Fas, B.; Bassot, C.; Benitez, G.I.; Bevilacqua, M.; Chasapi, A.; et al. DisProt: Intrinsic protein disorder annotation in 2020. Nucleic Acids Res. 2020, 48, D269–D276. [Google Scholar] [CrossRef]
- Vacic, V.; Iakoucheva, L.M. Disease mutations in disordered regions—Exception to the rule? Mol. Biosyst. 2012, 8, 27–32. [Google Scholar] [CrossRef]
- Kulkarni, P.; Uversky, V.N. Intrinsically Disordered Proteins in Chronic Diseases. Biomolecules 2019, 9, 147. [Google Scholar] [CrossRef]
- Oldfield, C.J.; Cheng, Y.; Cortese, M.S.; Brown, C.J.; Uversky, V.N.; Dunker, A.K. Comparing and Combining Predictors of Mostly Disordered Proteins. Biochemistry 2005, 44, 1989–2000. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Liu, X.; Chen, J. Targeting Intrinsically Disordered Proteins through Dynamic Interactions. Biomolecules 2020, 10, 743. [Google Scholar] [CrossRef] [PubMed]
- Mittag, T.; Marsh, J.; Grishaev, A.; Orlicky, S.; Lin, H.; Sicheri, F.; Tyers, M.; Forman-Kay, J.D. Structure/Function Implications in a Dynamic Complex of the Intrinsically Disordered Sic1 with the Cdc4 Subunit of an SCF Ubiquitin Ligase. Structure 2010, 18, 494–506. [Google Scholar] [CrossRef] [PubMed]
- McDowell, C.; Chen, J.; Chen, J. Potential Conformational Heterogeneity of p53 Bound to S100B(betabeta). J. Mol. Biol. 2013, 425, 999–1010. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wu, H.; Fuxreiter, M. The Structure and Dynamics of Higher-Order Assemblies: Amyloids, Signalosomes, and Granules. Cell 2016, 165, 1055–1066. [Google Scholar] [CrossRef]
- Krois, A.S.; Ferreon, J.C.; Martinez-Yamout, M.A.; Dyson, H.J.; Wright, P.E. Recognition of the disordered p53 transactivation domain by the transcriptional adapter zinc finger domains of CREB-binding protein. Proc. Natl. Acad. Sci. USA 2016, 113, E1853–E1862. [Google Scholar] [CrossRef]
- Csizmok, V.; Orlicky, S.; Cheng, J.; Song, J.; Bah, A.; Delgoshaie, N.; Lin, H.; Mittag, T.; Sicheri, F.; Chan, H.S.; et al. An allosteric conduit facilitates dynamic multisite substrate recognition by the SCFCdc4 ubiquitin ligase. Nat. Commun. 2017, 8, 13943. [Google Scholar] [CrossRef]
- Borgia, A.; Borgia, M.B.; Bugge, K.; Kissling, V.M.; Heidarsson, P.O.; Fernandes, C.B.; Sottini, A.; Soranno, A.; Buholzer, K.J.; Nettels, D.; et al. Extreme disorder in an ultrahigh-affinity protein complex. Nature 2018, 555, 61–66. [Google Scholar] [CrossRef]
- Clark, S.; Myers, J.B.; King, A.; Fiala, R.; Novacek, J.; Pearce, G.; Heierhorst, J.; Reichow, S.L.; Barbar, E.J. Multivalency regulates activity in an intrinsically disordered transcription factor. Elife 2018, 7, e36258. [Google Scholar] [CrossRef]
- Fuxreiter, M. Fuzziness in Protein Interactions-A Historical Perspective. J. Mol. Biol. 2018, 430, 2278–2287. [Google Scholar] [CrossRef] [PubMed]
- Weng, J.; Wang, W. Dynamic multivalent interactions of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2019, 62, 9–13. [Google Scholar] [CrossRef]
- Miskei, M.; Antal, C.; Fuxreiter, M. FuzDB: Database of fuzzy complexes, a tool to develop stochastic structure-function relationships for protein complexes and higher-order assemblies. Nucleic Acids Res. 2017, 45, D228–D235. [Google Scholar] [CrossRef] [PubMed]
- Ganguly, D.; Chen, J. Structural interpretation of paramagnetic relaxation enhancement-derived distances for disordered protein states. J. Mol. Biol. 2009, 390, 467–477. [Google Scholar] [CrossRef] [PubMed]
- Fisher, C.K.; Stultz, C.M. Constructing ensembles for intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2011, 21, 426–431. [Google Scholar] [CrossRef]
- Ferreon, A.C.; Ferreon, J.C.; Wright, P.E.; Deniz, A.A. Modulation of allostery by protein intrinsic disorder. Nature 2013, 498, 390–394. [Google Scholar] [CrossRef]
- Garcia-Pino, A.; Balasubramanian, S.; Wyns, L.; Gazit, E.; De Greve, H.; Magnuson, R.D.; Charlier, D.; van Nuland, N.A.; Loris, R. Allostery and intrinsic disorder mediate transcription regulation by conditional cooperativity. Cell 2010, 142, 101–111. [Google Scholar] [CrossRef]
- Berlow, R.B.; Dyson, H.J.; Wright, P.E. Expanding the Paradigm: Intrinsically Disordered Proteins and Allosteric Regulation. J. Mol. Biol. 2018, 430, 2309–2320. [Google Scholar] [CrossRef] [PubMed]
- Levine, Z.A.; Shea, J.-E. Simulations of disordered proteins and systems with conformational heterogeneity. Curr. Opin. Struct. Biol. 2017, 43, 95–103. [Google Scholar] [CrossRef]
- Knott, M.; Best, R.B. A preformed binding interface in the unbound ensemble of an intrinsically disordered protein: Evidence from molecular simulations. PLoS Comput. Biol. 2012, 8, e1002605. [Google Scholar] [CrossRef]
- Mao, A.H.; Crick, S.L.; Vitalis, A.; Chicoine, C.L.; Pappu, R.V. Net charge per residue modulates conformational ensembles of intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA 2010, 107, 8183–8188. [Google Scholar] [CrossRef]
- Ganguly, D.; Chen, J. Atomistic details of the disordered states of KID and pKID. implications in coupled binding and folding. J. Am. Chem. Soc. 2009, 131, 5214–5223. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Ganguly, D.; Chen, J. Residual structures, conformational fluctuations, and electrostatic interactions in the synergistic folding of two intrinsically disordered proteins. PLoS Comput. Biol. 2012, 8, e1002353. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, J. Accelerate Sampling in Atomistic Energy Landscapes Using Topology-Based Coarse-Grained Models. J. Chem. Theory Comput. 2014, 10, 918–923. [Google Scholar] [CrossRef] [PubMed]
- Moritsugu, K.; Terada, T.; Kidera, A. Scalable free energy calculation of proteins via multiscale essential sampling. J. Chem. Phys. 2010, 133, 224105. [Google Scholar] [CrossRef] [PubMed]
- Sugita, Y.; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar] [CrossRef]
- Liu, P.; Kim, B.; Friesner, R.A.; Berne, B.J. Replica exchange with solute tempering: A method for sampling biological systems in explicit water. Proc. Natl. Acad. Sci. USA 2005, 102, 13749–13754. [Google Scholar] [CrossRef]
- Mittal, A.; Lyle, N.; Harmon, T.S.; Pappu, R.V. Hamiltonian Switch Metropolis Monte Carlo Simulations for Improved Conformational Sampling of Intrinsically Disordered Regions Tethered to Ordered Domains of Proteins. J. Chem. Theory Comput. 2014, 10, 3550–3562. [Google Scholar] [CrossRef] [PubMed]
- Peter, E.K.; Shea, J.E. A hybrid MD-kMC algorithm for folding proteins in explicit solvent. Phys. Chem. Chem. Phys. 2014, 16, 6430–6440. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Ma, J. Enhanced sampling and applications in protein folding in explicit solvent. J. Chem. Phys. 2010, 132, 244101. [Google Scholar] [CrossRef]
- Zheng, L.Q.; Yang, W. Practically Efficient and Robust Free Energy Calculations: Double-Integration Orthogonal Space Tempering. J. Chem. Theory Comput. 2012, 8, 810–823. [Google Scholar] [CrossRef]
- Best, R.B. Computational and theoretical advances in studies of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2017, 42, 147–154. [Google Scholar] [CrossRef]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Lin, X. Recent Advances in Computational Protocols Addressing Intrinsically Disordered Proteins. Biomolecules 2019, 9, 146. [Google Scholar] [CrossRef]
- Wang, W. Recent advances in atomic molecular dynamics simulation of intrinsically disordered proteins. Phys. Chem. Chem. Phys. 2021, 23, 777–784. [Google Scholar] [CrossRef] [PubMed]
- Shea, J.-E.; Best, R.B.; Mittal, J. Physics-based computational and theoretical approaches to intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2021, 67, 219–225. [Google Scholar] [CrossRef]
- Arai, M. Unified understanding of folding and binding mechanisms of globular and intrinsically disordered proteins. Biophys. Rev. 2018, 10, 163–181. [Google Scholar] [CrossRef] [PubMed]
- Rauscher, S.; Gapsys, V.; Gajda, M.J.; Zweckstetter, M.; de Groot, B.L.; Grubmüller, H. Structural Ensembles of Intrinsically Disordered Proteins Depend Strongly on Force Field: A Comparison to Experiment. J. Chem. Theory Comput. 2015, 11, 5513–5524. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.; Mittal, J.; Feig, M.; Mackerell, A.D., Jr. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone phi, psi and side-chain chi(1) and chi(2) dihedral angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef]
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; MacKerell, A.D. Force field development and simulations of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2018, 48, 40–48. [Google Scholar] [CrossRef] [PubMed]
- Piana, S.; Donchev, A.G.; Robustelli, P.; Shaw, D.E. Water Dispersion Interactions Strongly Influence Simulated Structural Properties of Disordered Protein States. J. Phys. Chem. B 2015, 119, 5113–5123. [Google Scholar] [CrossRef]
- Wu, H.-N.; Jiang, F.; Wu, Y.-D. Significantly Improved Protein Folding Thermodynamics Using a Dispersion-Corrected Water Model and a New Residue-Specific Force Field. J. Phys. Chem. Lett. 2017, 8, 3199–3205. [Google Scholar] [CrossRef] [PubMed]
- Mu, J.; Liu, H.; Zhang, J.; Luo, R.; Chen, H.-F. Recent Force Field Strategies for Intrinsically Disordered Proteins. J. Chem. Inf. Modeling 2021, 61, 1037–1047. [Google Scholar] [CrossRef] [PubMed]
- Song, D.; Liu, H.; Luo, R.; Chen, H.-F. Environment-Specific Force Field for Intrinsically Disordered and Ordered Proteins. J. Chem. Inf. Modeling 2020, 60, 2257–2267. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Liu, H.; Zhang, Y.; Lu, H.; Chen, H. Residue-Specific Force Field Improving the Sample of Intrinsically Disordered Proteins and Folded Proteins. J. Chem. Inf. Modeling 2019, 59, 4793–4805. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grubmüller, H.; MacKerell, A.D. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef] [PubMed]
- Tian, C.; Kasavajhala, K.; Belfon, K.A.A.; Raguette, L.; Huang, H.; Migues, A.N.; Bickel, J.; Wang, Y.; Pincay, J.; Wu, Q.; et al. ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2020, 16, 528–552. [Google Scholar] [CrossRef]
- Rahman, M.U.; Rehman, A.U.; Liu, H.; Chen, H.-F. Comparison and Evaluation of Force Fields for Intrinsically Disordered Proteins. J. Chem. Inf. Modeling 2020, 60, 4912–4923. [Google Scholar] [CrossRef]
- Abriata, L.A.; Dal Peraro, M. Assessment of transferable forcefields for protein simulations attests improved description of disordered states and secondary structure propensities, and hints at multi-protein systems as the next challenge for optimization. Comput. Struct. Biotechnol. J. 2021, 19, 2626–2636. [Google Scholar] [CrossRef]
- Piana, S.; Robustelli, P.; Tan, D.; Chen, S.; Shaw, D.E. Development of a Force Field for the Simulation of Single-Chain Proteins and Protein–Protein Complexes. J. Chem. Theory Comput. 2020, 16, 2494–2507. [Google Scholar] [CrossRef]
- Song, D.; Luo, R.; Chen, H.-F. The IDP-Specific Force Field ff14IDPSFF Improves the Conformer Sampling of Intrinsically Disordered Proteins. J. Chem. Inf. Modeling 2017, 57, 1166–1178. [Google Scholar] [CrossRef] [PubMed]
- Jing, Z.; Liu, C.; Cheng, S.Y.; Qi, R.; Walker, B.D.; Piquemal, J.-P.; Ren, P. Polarizable Force Fields for Biomolecular Simulations: Recent Advances and Applications. Annu. Rev. Biophys. 2019, 48, 371–394. [Google Scholar] [CrossRef]
- Bedrov, D.; Piquemal, J.-P.; Borodin, O.; MacKerell, A.D.; Roux, B.; Schröder, C. Molecular Dynamics Simulations of Ionic Liquids and Electrolytes Using Polarizable Force Fields. Chem. Rev. 2019, 119, 7940–7995. [Google Scholar] [CrossRef] [PubMed]
- Inakollu, V.S.S.; Geerke, D.P.; Rowley, C.N.; Yu, H. Polarisable force fields: What do they add in biomolecular simulations? Curr. Opin. Struct. Biol. 2020, 61, 182–190. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; MacKerell, A.D., Jr. Induction of Peptide Bond Dipoles Drives Cooperative Helix Formation in the (AAQAA)3 Peptide. Biophys. J. 2014, 107, 991–997. [Google Scholar] [CrossRef] [PubMed]
- Kamenik, A.S.; Handle, P.H.; Hofer, F.; Kahler, U.; Kraml, J.; Liedl, K.R. Polarizable and non-polarizable force fields: Protein folding, unfolding, and misfolding. J. Chem. Phys. 2020, 153, 185102. [Google Scholar] [CrossRef]
- Wang, A.; Zhang, Z.; Li, G. Higher Accuracy Achieved in the Simulations of Protein Structure Refinement, Protein Folding, and Intrinsically Disordered Proteins Using Polarizable Force Fields. J. Phys. Chem. Lett. 2018, 9, 7110–7116. [Google Scholar] [CrossRef]
- Wang, A.; Peng, X.; Li, Y.; Zhang, D.; Zhang, Z.; Li, G. Quality of force fields and sampling methods in simulating pepX peptides: A case study for intrinsically disordered proteins. Phys. Chem. Chem. Phys. 2021, 23, 2430–2437. [Google Scholar] [CrossRef]
- Yang, Y.I.; Shao, Q.; Zhang, J.; Yang, L.; Gao, Y.Q. Enhanced sampling in molecular dynamics. J. Chem. Phys. 2019, 151, 070902. [Google Scholar] [CrossRef]
- Wang, A.H.; Zhang, Z.C.; Li, G.H. Advances in Enhanced Sampling Molecular Dynamics Simulations for Biomolecules. Chin. J. Chem. Phys. 2019, 32, 277–286. [Google Scholar] [CrossRef]
- Barducci, A.; Bonomi, M.; Parrinello, M. Metadynamics. WIREs Comput. Mol. Sci. 2011, 1, 826–843. [Google Scholar] [CrossRef]
- Barducci, A.; Bussi, G.; Parrinello, M. Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method. Phys. Rev. Lett. 2008, 100, 020603. [Google Scholar] [CrossRef]
- Hamelberg, D.; Mongan, J.; McCammon, J.A. Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J. Chem. Phys. 2004, 120, 11919–11929. [Google Scholar] [CrossRef] [PubMed]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Kästner, J. Umbrella sampling. WIREs Comput. Mol. Sci. 2011, 1, 932–942. [Google Scholar] [CrossRef]
- Gao, Y.Q. An integrate-over-temperature approach for enhanced sampling. J. Chem. Phys. 2008, 128, 064105. [Google Scholar] [CrossRef]
- MacCallum, J.L.; Muniyat, M.I.; Gaalswyk, K. Online Optimization of Total Acceptance in Hamiltonian Replica Exchange Simulations. J. Phys. Chem. B 2018, 122, 5448–5457. [Google Scholar] [CrossRef]
- Liu, N.; Guo, Y.; Ning, S.; Duan, M. Phosphorylation regulates the binding of intrinsically disordered proteins via a flexible conformation selection mechanism. Commun. Chem. 2020, 3, 123. [Google Scholar] [CrossRef]
- Dickson, A.; Ahlstrom, L.S.; Brooks III, C.L. Coupled folding and binding with 2D Window-Exchange Umbrella Sampling. J. Comput. Chem. 2016, 37, 587–594. [Google Scholar] [CrossRef]
- Sidky, H.; Chen, W.; Ferguson, A.L. Machine learning for collective variable discovery and enhanced sampling in biomolecular simulation. Mol. Phys. 2020, 118, e1737742. [Google Scholar] [CrossRef]
- Chen, W.; Tan, A.R.; Ferguson, A.L. Collective variable discovery and enhanced sampling using autoencoders: Innovations in network architecture and error function design. J. Chem. Phys. 2018, 149, 072312. [Google Scholar] [CrossRef] [PubMed]
- Marinari, E.; Parisi, G. Simulated Tempering: A New Monte Carlo Scheme. EPL (Europhys. Lett.) 1992, 19, 451–458. [Google Scholar] [CrossRef]
- Kamiya, M.; Sugita, Y. Flexible selection of the solute region in replica exchange with solute tempering: Application to protein-folding simulations. J. Chem. Phys. 2018, 149, 072304. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Friesner, R.A.; Berne, B.J. Replica Exchange with Solute Scaling: A More Efficient Version of Replica Exchange with Solute Tempering (REST2). J. Phys. Chem. B 2011, 115, 9431–9438. [Google Scholar] [CrossRef]
- Miao, Y.; Sinko, W.; Pierce, L.; Bucher, D.; Walker, R.C.; McCammon, J.A. Improved Reweighting of Accelerated Molecular Dynamics Simulations for Free Energy Calculation. J. Chem. Theory Comput. 2014, 10, 2677–2689. [Google Scholar] [CrossRef]
- Kokubo, H.; Tanaka, T.; Okamoto, Y. Two-dimensional replica-exchange method for predicting protein–ligand binding structures. J. Comput. Chem. 2013, 34, 2601–2614. [Google Scholar] [CrossRef]
- Oshima, H.; Re, S.; Sugita, Y. Replica-Exchange Umbrella Sampling Combined with Gaussian Accelerated Molecular Dynamics for Free-Energy Calculation of Biomolecules. J. Chem. Theory Comput. 2019, 15, 5199–5208. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, Y.; Li, Y.; Liu, Q.; Chu, H.; Zhang, D.; Li, G. Integrating Multiple Accelerated Molecular Dynamics to Improve Accuracy of Free Energy Calculations. J. Chem. Theory Comput. 2018, 14, 1216–1227. [Google Scholar] [CrossRef]
- Bussi, G.; Laio, A. Using metadynamics to explore complex free-energy landscapes. Nat. Rev. Phys. 2020, 2, 200–212. [Google Scholar] [CrossRef]
- Galvelis, R.; Sugita, Y. Replica state exchange metadynamics for improving the convergence of free energy estimates. J. Comput. Chem. 2015, 36, 1446–1455. [Google Scholar] [CrossRef] [PubMed]
- Piana, S.; Laio, A. A Bias-Exchange Approach to Protein Folding. J. Phys. Chem. B 2007, 111, 4553–4559. [Google Scholar] [CrossRef]
- Galvelis, R.; Re, S.; Sugita, Y. Enhanced Conformational Sampling of N-Glycans in Solution with Replica State Exchange Metadynamics. J. Chem. Theory Comput. 2017, 13, 1934–1942. [Google Scholar] [CrossRef]
- Do, T.N.; Choy, W.-Y.; Karttunen, M. Binding of Disordered Peptides to Kelch: Insights from Enhanced Sampling Simulations. J. Chem. Theory Comput. 2016, 12, 395–404. [Google Scholar] [CrossRef]
- Guo, J.; Zhou, H.X. Protein Allostery and Conformational Dynamics. Chem. Rev. 2016, 116, 6503–6515. [Google Scholar] [CrossRef]
- Gianni, S.; Freiberger, M.I.; Jemth, P.; Ferreiro, D.U.; Wolynes, P.G.; Fuxreiter, M. Fuzziness and Frustration in the Energy Landscape of Protein Folding, Function, and Assembly. Acc. Chem. Res. 2021, 54, 1251–1259. [Google Scholar] [CrossRef]
- Neupane, K.; Manuel, A.P.; Woodside, M.T. Protein folding trajectories can be described quantitatively by one-dimensional diffusion over measured energy landscapes. Nat. Phys. 2016, 12, 700–703. [Google Scholar] [CrossRef]
- Pfaendtner, J.; Bonomi, M. Efficient Sampling of High-Dimensional Free-Energy Landscapes with Parallel Bias Metadynamics. J. Chem. Theory Comput. 2015, 11, 5062–5067. [Google Scholar] [CrossRef] [PubMed]
- Prakash, A.; Fu, C.D.; Bonomi, M.; Pfaendtner, J. Biasing Smarter, Not Harder, by Partitioning Collective Variables into Families in Parallel Bias Metadynamics. J. Chem. Theory Comput. 2018, 14, 4985–4990. [Google Scholar] [CrossRef] [PubMed]
- Awasthi, S.; Nair, N.N. Exploring high dimensional free energy landscapes: Temperature accelerated sliced sampling. J. Chem. Phys. 2017, 146, 094108. [Google Scholar] [CrossRef]
- Chen, W.; Ferguson, A.L. Molecular enhanced sampling with autoencoders: On-the-fly collective variable discovery and accelerated free energy landscape exploration. J. Comput. Chem. 2018, 39, 2079–2102. [Google Scholar] [CrossRef]
- Galvelis, R.; Sugita, Y. Neural Network and Nearest Neighbor Algorithms for Enhancing Sampling of Molecular Dynamics. J. Chem. Theory Comput. 2017, 13, 2489–2500. [Google Scholar] [CrossRef]
- Salawu, E.O. DESP: Deep Enhanced Sampling of Proteins’ Conformation Spaces Using AI-Inspired Biasing Forces. Front. in Mol. Biosci. 2021, 8, 121. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Chen, M. Unfolding Hidden Barriers by Active Enhanced Sampling. Phys. Rev. Lett. 2018, 121, 010601. [Google Scholar] [CrossRef] [PubMed]
- Brown, S.; Head-Gordon, T. Cool walking: A new Markov chain Monte Carlo sampling method. J. Comput. Chem. 2003, 24, 68–76. [Google Scholar] [CrossRef] [PubMed]
- Neal, R.M. Annealed importance sampling. Stat. Comput. 2001, 11, 125–139. [Google Scholar] [CrossRef]
- Fukunishi, H.; Watanabe, O.; Takada, S. On the Hamiltonian replica exchange method for efficient sampling of biomolecular systems: Application to protein structure prediction. J. Chem. Phys. 2002, 116, 9058–9067. [Google Scholar] [CrossRef]
- Huang, Y.-m.M.; McCammon, J.A.; Miao, Y. Replica Exchange Gaussian Accelerated Molecular Dynamics: Improved Enhanced Sampling and Free Energy Calculation. J. Chem. Theory Comput. 2018, 14, 1853–1864. [Google Scholar] [CrossRef]
- Wang, J.; Arantes, P.R.; Bhattarai, A.; Hsu, R.V.; Pawnikar, S.; Huang, Y.-m.M.; Palermo, G.; Miao, Y. Gaussian accelerated molecular dynamics: Principles and applications. WIREs Comput. Mol. Sci. 2021, 11, e1521. [Google Scholar] [CrossRef]
- Miao, Y.; Bhattarai, A.; Wang, J. Ligand Gaussian Accelerated Molecular Dynamics (LiGaMD): Characterization of Ligand Binding Thermodynamics and Kinetics. J. Chem. Theory Comput. 2020, 16, 5526–5547. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Miao, Y. Peptide Gaussian accelerated molecular dynamics (Pep-GaMD): Enhanced sampling and free energy and kinetics calculations of peptide binding. J. Chem. Phys. 2020, 153, 154109. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Chen, J. Residual Structures and Transient Long-Range Interactions of p53 Transactivation Domain: Assessment of Explicit Solvent Protein Force Fields. J. Chem. Theory Comput. 2019, 15, 4708–4720. [Google Scholar] [CrossRef]
- Shrestha, U.R.; Smith, J.C.; Petridis, L. Full structural ensembles of intrinsically disordered proteins from unbiased molecular dynamics simulations. Commun. Biol. 2021, 4, 243. [Google Scholar] [CrossRef] [PubMed]
- Hicks, A.; Zhou, H.-X. Temperature-induced collapse of a disordered peptide observed by three sampling methods in molecular dynamics simulations. J. Chem. Phys. 2018, 149, 072313. [Google Scholar] [CrossRef] [PubMed]
- Brown, A.H.; Rodger, P.M.; Evans, J.S.; Walsh, T.R. Equilibrium Conformational Ensemble of the Intrinsically Disordered Peptide n16N: Linking Subdomain Structures and Function in Nacre. Biomacromolecules 2014, 15, 4467–4479. [Google Scholar] [CrossRef]
- Pang, X.; Zhou, H.-X. Disorder-to-Order Transition of an Active-Site Loop Mediates the Allosteric Activation of Sortase A. Biophys. J. 2015, 109, 1706–1715. [Google Scholar] [CrossRef]
- Liu, X.; Jia, Z.; Chen, J. Enhanced Sampling of Intrinsic Structural Heterogeneity of the BH3-Only Protein Binding Interface of Bcl-xL. J. Phys. Chem. B 2017, 121, 9160–9168. [Google Scholar] [CrossRef]
- Liang, C.; Savinov, S.N.; Fejzo, J.; Eyles, S.J.; Chen, J. Modulation of Amyloid-beta42 Conformation by Small Molecules Through Nonspecific Binding. J. Chem. Theory Comput. 2019, 15, 5169–5174. [Google Scholar] [CrossRef]
- Liu, X.; Chen, J. Modulation of p53 Transactivation Domain Conformations by Ligand Binding and Cancer-Associated Mutations. Pac. Symp. Biocomput. 2020, 25, 195–206. [Google Scholar]
- Schrag, L.G.; Liu, X.; Thevarajan, I.; Prakash, O.; Zolkiewski, M.; Chen, J. Cancer-Associated Mutations Perturb the Disordered Ensemble and Interactions of the Intrinsically Disordered p53 Transactivation Domain. J. Mol. Biol. 2021, 433, 167048. [Google Scholar] [CrossRef]
- Zhao, J.; Blayney, A.; Liu, X.; Gandy, L.; Jin, W.; Yan, L.; Ha, J.H.; Canning, A.J.; Connelly, M.; Yang, C.; et al. EGCG binds intrinsically disordered N-terminal domain of p53 and disrupts p53-MDM2 interaction. Nat. Commun. 2021, 12, 986. [Google Scholar] [CrossRef]
- Wang, L.; Wu, Y.; Deng, Y.; Kim, B.; Pierce, L.; Krilov, G.; Lupyan, D.; Robinson, S.; Dahlgren, M.K.; Greenwood, J.; et al. Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field. J. Am. Chem. Soc. 2015, 137, 2695–2703. [Google Scholar] [CrossRef]
- Zhou, H.X. Theoretical frameworks for multiscale modeling and simulation. Curr. Opin. Struct. Biol. 2014, 25C, 67–76. [Google Scholar] [CrossRef][Green Version]
- Lee, K.H.; Chen, J.H. Multiscale Enhanced Sampling of Intrinsically Disordered Protein Conformations. J. Comput. Chem. 2016, 37, 550–557. [Google Scholar] [CrossRef]
- Liu, X.R.; Gong, X.P.; Chen, J.H. Accelerating atomistic simulations of proteins using multiscale enhanced sampling with independent tempering. J. Comput. Chem. 2021, 42, 358–364. [Google Scholar] [CrossRef]
- Lee, K.H.; Chen, J.H. Optimization of the GBMV2 implicit solvent force field for accurate simulation of protein conformational equilibria. J. Comput. Chem. 2017, 38, 1332–1341. [Google Scholar] [CrossRef]
- Liu, Y.; Pezeshkian, W.; Barnoud, J.; de Vries, A.H.; Marrink, S.J. Coupling Coarse-Grained to Fine-Grained Models via Hamiltonian Replica Exchange. J. Chem. Theory Comput. 2020, 16, 5313–5322. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.I.; Niu, H.; Parrinello, M. Combining Metadynamics and Integrated Tempering Sampling. J. Phys. Chem. Lett. 2018, 9, 6426–6430. [Google Scholar] [CrossRef] [PubMed]
- Shirts, M.R.; Chodera, J.D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008, 129, 124105. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Sinko, W.; Miao, Y.; de Oliveira, C.A.F.; McCammon, J.A. Population Based Reweighting of Scaled Molecular Dynamics. J. Phys. Chem. B 2013, 117, 12759–12768. [Google Scholar] [CrossRef]
- Ilie, I.M.; Caflisch, A. Simulation Studies of Amyloidogenic Polypeptides and Their Aggregates. Chem. Rev. 2019, 119, 6956–6993. [Google Scholar] [CrossRef]
- Zhou, H.X.; Pang, X. Electrostatic Interactions in Protein Structure, Folding, Binding, and Condensation. Chem. Rev. 2018, 118, 1691–1741. [Google Scholar] [CrossRef]
- Fassler, J.S.; Skuodas, S.; Weeks, D.L.; Phillips, B.T. Protein Aggregation and Disaggregation in Cells and Development. J. Mol. Biol. 2021, 433, 167215. [Google Scholar] [CrossRef] [PubMed]
- Alberti, S.; Gladfelter, A.; Mittag, T. Considerations and Challenges in Studying Liquid-Liquid Phase Separation and Biomolecular Condensates. Cell 2019, 176, 419–434. [Google Scholar] [CrossRef]
- Holehouse, A.S.; Pappu, R.V. Functional Implications of Intracellular Phase Transitions. Biochemistry 2018, 57, 2415–2423. [Google Scholar] [CrossRef] [PubMed]
- Brangwynne, C.P.; Tompa, P.; Pappu, R.V. Polymer physics of intracellular phase transitions. Nat. Phys. 2015, 11, 899–904. [Google Scholar] [CrossRef]
- Mathieu, C.; Pappu, R.V.; Taylor, J.P. Beyond aggregation: Pathological phase transitions in neurodegenerative disease. Science 2020, 370, 56–60. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Brooks, C.L.; Khandogin, J. Recent advances in implicit solvent based methods for biomolecular simulations. Curr. Opin. Struct. Biol. 2008, 18, 140–148. [Google Scholar] [CrossRef] [PubMed]
- Haberthür, U.; Caflisch, A. FACTS: Fast analytical continuum treatment of solvation. J. Comput. Chem. 2008, 29, 701–715. [Google Scholar] [CrossRef] [PubMed]
- Hawkins, G.D.; Cramer, C.J.; Truhlar, D.G. Parametrized Models of Aqueous Free Energies of Solvation Based on Pairwise Descreening of Solute Atomic Charges from a Dielectric Medium. J. Phys. Chem. 1996, 100, 19824–19839. [Google Scholar] [CrossRef]
- Onufriev, A.; Bashford, D.; Case, D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins Struct. Funct. Bioinform. 2004, 55, 383–394. [Google Scholar] [CrossRef]
- Mongan, J.; Simmerling, C.; McCammon, J.A.; Case, D.A.; Onufriev, A. Generalized Born Model with a Simple, Robust Molecular Volume Correction. J. Chem. Theory Comput. 2007, 3, 156–169. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.; Roe, D.R.; Simmerling, C. Improved Generalized Born Solvent Model Parameters for Protein Simulations. J. Chem. Theory Comput. 2013, 9, 2020–2034. [Google Scholar] [CrossRef]
- Gallicchio, E.; Levy, R.M. AGBNP: An analytic implicit solvent model suitable for molecular dynamics simulations and high-resolution modeling. J. Comput. Chem. 2004, 25, 479–499. [Google Scholar] [CrossRef] [PubMed]
- Gallicchio, E.; Paris, K.; Levy, R.M. The AGBNP2 Implicit Solvation Model. J. Chem. Theory Comput. 2009, 5, 2544–2564. [Google Scholar] [CrossRef]
- Im, W.; Lee, M.S.; Brooks Iii, C.L. Generalized born model with a simple smoothing function. J. Comput. Chem. 2003, 24, 1691–1702. [Google Scholar] [CrossRef]
- Lee, M.S.; Salsbury, F.R.; Brooks, C.L. Novel generalized Born methods. J. Chem. Phys. 2002, 116, 10606–10614. [Google Scholar] [CrossRef]
- Lee, M.S.; Feig, M.; Salsbury, F.R., Jr.; Brooks, C.L., III. New analytic approximation to the standard molecular volume definition and its application to generalized Born calculations. J. Comput. Chem. 2003, 24, 1348–1356. [Google Scholar] [CrossRef]
- Chen, J.; Im, W.; Brooks, C.L. Balancing solvation and intramolecular interactions: Toward a consistent generalized born force field. J. Am. Chem. Soc. 2006, 128, 3728–3736. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Brooks, C.L. Implicit modeling of nonpolar solvation for simulating protein folding and conformational transitions. Phys. Chem. Chem. Phys. 2008, 10, 471–481. [Google Scholar] [CrossRef]
- Chen, J. Intrinsically disordered p53 extreme C-terminus binds to S100B(betabeta) through “fly-casting”. J. Am. Chem. Soc. 2009, 131, 2088–2089. [Google Scholar] [CrossRef]
- Wang, Y.; Fisher, J.C.; Mathew, R.; Ou, L.; Otieno, S.; Sublet, J.; Xiao, L.; Chen, J.; Roussel, M.F.; Kriwacki, R.W. Intrinsic disorder mediates the diverse regulatory functions of the Cdk inhibitor p21. Nat. Chem. Biol. 2011, 7, 214–221. [Google Scholar] [CrossRef]
- Ganguly, D.; Chen, J. Modulation of the disordered conformational ensembles of the p53 transactivation domain by cancer-associated mutations. PLoS Comput. Biol. 2015, 11, e1004247. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.; Maier, J.; Huang, H.; Perrone, V.; Simmerling, C. Folding Simulations for Proteins with Diverse Topologies Are Accessible in Days with a Physics-Based Force Field and Implicit Solvent. J. Am. Chem. Soc. 2014, 136, 13959–13962. [Google Scholar] [CrossRef]
- Maffucci, I.; Contini, A. An Updated Test of AMBER Force Fields and Implicit Solvent Models in Predicting the Secondary Structure of Helical, β-Hairpin, and Intrinsically Disordered Peptides. J. Chem. Theory Comput. 2016, 12, 714–727. [Google Scholar] [CrossRef] [PubMed]
- Tao, P.; Xiao, Y. Using the generalized Born surface area model to fold proteins yields more effective sampling while qualitatively preserving the folding landscape. Phys. Rev. E 2020, 101, 062417. [Google Scholar] [CrossRef]
- Gong, X.; Chiricotto, M.; Liu, X.; Nordquist, E.; Feig, M.; Brooks Iii, C.L.; Chen, J. Accelerating the Generalized Born with Molecular Volume and Solvent Accessible Surface Area Implicit Solvent Model Using Graphics Processing Units. J. Comput. Chem. 2020, 41, 830–838. [Google Scholar] [CrossRef] [PubMed]
- Vitalis, A.; Pappu, R.V. ABSINTH: A new continuum solvation model for simulations of polypeptides in aqueous solutions. J. Comput. Chem. 2009, 30, 673–699. [Google Scholar] [CrossRef]
- Vitalis, A.; Caflisch, A. Micelle-Like Architecture of the Monomer Ensemble of Alzheimer’s Amyloid-β Peptide in Aqueous Solution and Its Implications for Aβ Aggregation. J. Mol. Biol. 2010, 403, 148–165. [Google Scholar] [CrossRef]
- Mittal, A.; Holehouse, A.S.; Cohan, M.C.; Pappu, R.V. Sequence-to-Conformation Relationships of Disordered Regions Tethered to Folded Domains of Proteins. J. Mol. Biol 2018, 430, 2403–2421. [Google Scholar] [CrossRef]
- Choi, J.-M.; Pappu, R.V. Improvements to the ABSINTH Force Field for Proteins Based on Experimentally Derived Amino Acid Specific Backbone Conformational Statistics. J. Chem. Theory Comput. 2019, 15, 1367–1382. [Google Scholar] [CrossRef] [PubMed]
- Pak, A.J.; Voth, G.A. Advances in coarse-grained modeling of macromolecular complexes. Curr. Opin. Struct. Biol. 2018, 52, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Wolynes, P.G. Recent successes of the energy landscape theory of protein folding and function. Q. Rev. Biophys. 2005, 38, 405–410. [Google Scholar] [CrossRef]
- Hills, R.D.; Brooks, C.L. Insights from Coarse-Grained Gō Models for Protein Folding and Dynamics. Int. J. Mol. Sci. 2009, 10, 889. [Google Scholar] [CrossRef]
- Law, S.M.; Gagnon, J.K.; Mapp, A.K.; Brooks, C.L., 3rd. Prepaying the entropic cost for allosteric regulation in KIX. Proc. Natl. Acad. Sci. USA 2014, 111, 12067–12072. [Google Scholar] [CrossRef] [PubMed]
- Chu, X.; Wang, J. Position-, disorder-, and salt-dependent diffusion in binding-coupled-folding of intrinsically disordered proteins. Phys. Chem. Chem. Phys. 2019, 21, 5634–5645. [Google Scholar] [CrossRef] [PubMed]
- Ganguly, D.; Otieno, S.; Waddell, B.; Iconaru, L.; Kriwacki, R.W.; Chen, J. Electrostatically Accelerated Coupled Binding and Folding of Intrinsically Disordered Proteins. J. Mol. Biol. 2012, 422, 674–684. [Google Scholar] [CrossRef]
- Ganguly, D.; Zhang, W.; Chen, J. Electrostatically Accelerated Encounter and Folding for Facile Recognition of Intrinsically Disordered Proteins. PLoS Comput. Biol. 2013, 9, e1003363. [Google Scholar] [CrossRef]
- Liu, X.; Chen, J.; Chen, J. Residual Structure Accelerates Binding of Intrinsically Disordered ACTR by Promoting Efficient Folding upon Encounter. J. Mol. Biol. 2019, 431, 422–432. [Google Scholar] [CrossRef]
- Liu, Z.R.; Huang, Y.Q. Advantages of proteins being disordered. Protein Sci. 2014, 23, 539–550. [Google Scholar] [CrossRef]
- Ganguly, D.; Chen, J. Topology-based modeling of intrinsically disordered proteins: Balancing intrinsic folding and intermolecular interactions. Proteins: Struct. Funct. Bioinform. 2011, 79, 1251–1266. [Google Scholar] [CrossRef] [PubMed]
- Ganguly, D.; Zhang, W.; Chen, J. Synergistic folding of two intrinsically disordered proteins: Searching for conformational selection. Mol. Biosyst. 2012, 8, 198–209. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Baul, U.; Chakraborty, D.; Mugnai, M.L.; Straub, J.E.; Thirumalai, D. Sequence Effects on Size, Shape, and Structural Heterogeneity in Intrinsically Disordered Proteins. J. Phys. Chem. B 2019, 123, 3462–3474. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Chen, J. HyRes: A coarse-grained model for multi-scale enhanced sampling of disordered protein conformations. Phys. Chem. Chem. Phys. 2017, 19, 32421–32432. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Wolynes, P.G.; Papoian, G.A. AWSEM-IDP: A Coarse-Grained Force Field for Intrinsically Disordered Proteins. J. Phys. Chem. B 2018, 122, 11115–11125. [Google Scholar] [CrossRef]
- Ashbaugh, H.S.; Hatch, H.W. Natively Unfolded Protein Stability as a Coil-to-Globule Transition in Charge/Hydropathy Space. J. Am. Chem. Soc. 2008, 130, 9536–9542. [Google Scholar] [CrossRef]
- Kim, Y.C.; Hummer, G. Coarse-grained Models for Simulations of Multiprotein Complexes: Application to Ubiquitin Binding. J. Mol. Biol. 2008, 375, 1416–1433. [Google Scholar] [CrossRef]
- Dignon, G.L.; Zheng, W.; Best, R.B.; Kim, Y.C.; Mittal, J. Relation between single-molecule properties and phase behavior of intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA 2018, 115, 9929. [Google Scholar] [CrossRef]
- Latham, A.P.; Zhang, B. Maximum Entropy Optimized Force Field for Intrinsically Disordered Proteins. J. Chem. Theory Comput. 2020, 16, 773–781. [Google Scholar] [CrossRef]
| Types | Sampling Methods | Key Features | References |
|---|---|---|---|
| CV-based | WT-MTD | History-based adaptive bias potentials | [72,73] |
| Bias-exchange MTD | Multiple replicas with bias on different CVs | [79] | |
| Umbrella sampling | Pre-determined bias potentials | [80] | |
| Machine learning | On-the-fly discover optimal CVs | [81,82] | |
| Tempering-based | Simulated tempering | Random walk in the temperature space | [83] |
| Parallel tempering | Multiple replicas to avoid the need for estimating the density of states | [36] | |
| Integrated tempering | Integral of Boltzmann distributions over a range of temperatures as the bias | [77] | |
| Solute tempering | Scaling the energies of only selected atoms or terms to achieve effective tempering | [37,84,85] | |
| Accelerated MD | GaMD | Boost potentials to accelerate barrier crossing | [86] |
| Combinations | MSES | Temperature/Hamiltonian replica exchange simulation by coupling CG and atomistic models | [34] |
| REUS/REST | Combined REUS and REST | [87] | |
| REUS/GaMD | Combined REUS and GaMD | [88] | |
| Integrated aMD | Integrated aMD and integrated tempering | [69,89] | |
| PT-MTD | Combined the WT-MTD with PT | [79] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, X.; Zhang, Y.; Chen, J. Advanced Sampling Methods for Multiscale Simulation of Disordered Proteins and Dynamic Interactions. Biomolecules 2021, 11, 1416. https://doi.org/10.3390/biom11101416
Gong X, Zhang Y, Chen J. Advanced Sampling Methods for Multiscale Simulation of Disordered Proteins and Dynamic Interactions. Biomolecules. 2021; 11(10):1416. https://doi.org/10.3390/biom11101416
Chicago/Turabian StyleGong, Xiping, Yumeng Zhang, and Jianhan Chen. 2021. "Advanced Sampling Methods for Multiscale Simulation of Disordered Proteins and Dynamic Interactions" Biomolecules 11, no. 10: 1416. https://doi.org/10.3390/biom11101416
APA StyleGong, X., Zhang, Y., & Chen, J. (2021). Advanced Sampling Methods for Multiscale Simulation of Disordered Proteins and Dynamic Interactions. Biomolecules, 11(10), 1416. https://doi.org/10.3390/biom11101416






